Go through the Math in Focus Grade 8 Workbook Answer Key Cumulative Review Chapters 3-4 to finish your assignments.
Math in Focus Grade 8 Course 3 A Cumulative Review Chapters 3-4 Answer Key
Concepts and Skills
Solve each equation. Show your work. (Lesson 3.1)
Question 1.
0.2(x + 2) – 2 = 0.4
Answer:
0.2x + 0.4 – 2 = 0.4
0.2x = 2
x = 2/0.2
x = 10
Question 2.
2(x – 5) – 3(3 – x) = \(\frac{1}{2}\) (x – 2)
Answer:
2x – 10 – 9 + 3x = \(\frac{1}{2}\)x – 1
5x – 18 = \(\frac{1}{2}\)x
4 \(\frac{1}{2}\)x = 18
4x = 36
x = 36/4 = 9
Question 3.
\(\frac{x}{3}\) + \(\frac{3+x}{6}\) = 3
Answer:
\(\frac{x}{3}\) + \(\frac{3+x}{6}\) = 3
2x + 3 + x = 18
3x = 18 – 3
3x = 15
x = 15/3
x = 5
Question 4.
\(\frac{2(x+3)}{5}\) – \(\frac{x-1}{2}\) = 2
Answer:
\(\frac{2(x+3)}{5}\) – \(\frac{x-1}{2}\) = 2
\(\frac{2x+6}{5}\) – \(\frac{x-1}{2}\) = 2
4x + 12 – 5x + 5 = 10
-x + 17 = 10
-x = 10 – 17
-x = -7
x = 7
Express each decimal as a fraction, without the use of calculator. (Lesson 3.1)
Question 5.
\(0 . \overline{5}\)
Answer:
\(\frac{5}{9}\)
Question 6.
\(0 . \overline{8}\)
Answer: \(\frac{8}{9}\)
Question 7.
\(0.2 \overline{7}\)
Answer: \(\frac{5}{18}\)
Question 8.
\(0 . \overline{09}\)
Answer: \(\frac{90}{999}\)
Tell whether each equation has one solution, no solution, or an infinite number of solutions. Show your work. (Lesson 3.2)
Question 9.
3x – 2 = -3(\(\frac{2}{3}\) – x)
Answer:
3x – 2 = -3(\(\frac{2}{3}\) – x)
3x – = -2 + 3x
3x – 3x + 2 = 0
2
Infinite solutions
Question 10.
3x + 6 = -2(\(\frac{3}{2}\) – x)
Answer:
3x + 6 = -2(\(\frac{3}{2}\) – x)
3x + 6 = -3 + 2x
3x – 2x = -3 – 6
x = -9
One solution
Question 11.
5(6a – 6) + 40 = 3(10a – 7) + 31
Answer:
5(6a – 6) + 40 = 3(10a – 7) + 31
30a – 30 + 40 = 30a – 21 + 31
Infinte solution
Question 12.
3x + 7 = -8(\(\frac{3}{4}\) – x)
Answer:
3x + 7 = -8(\(\frac{3}{4}\) – x)
3x + 7 = -6 + 8x
3x – 8x = -6 – 7
-5x = -13
x = 13/5
One solution
Question 13.
\(\frac{1}{4}\)(2x – 1) = \(\frac{1}{2}\)x + \(\frac{3}{8}\)
Answer:
Given,
\(\frac{1}{4}\)(2x – 1) = \(\frac{1}{2}\)x + \(\frac{3}{8}\)
\(\frac{1}{4}\)x – \(\frac{1}{4}\) = \(\frac{1}{2}\)x + \(\frac{3}{8}\)
\(\frac{1}{4}\)x – \(\frac{1}{2}\)x = \(\frac{1}{4}\) + \(\frac{3}{8}\)
–\(\frac{1}{4}\)x = \(\frac{5}{8}\)
x = –\(\frac{5}{2}\)
No solution
Question 14.
\(\frac{1}{8}\)x + 6 = \(\frac{1}{16}\)(2x – 96)
Answer:
Given,
\(\frac{1}{8}\)x + 6 = \(\frac{1}{16}\)(2x – 96)
\(\frac{1}{8}\)x + 6 = \(\frac{1}{8}\)x – 6
No solution
Find the value of y when x = 4. (Lesson 3.3)
Question 15.
2x – 1 = \(\frac{1}{2}\) + y
Answer:
2x – 1 = \(\frac{1}{2}\) + y
x = 4
2(4) – 1 = \(\frac{1}{2}\) + y
7 = \(\frac{1}{2}\) + y
y = 7 – \(\frac{1}{2}\)
y = 6 \(\frac{1}{2}\) or 6.5
Question 16.
\(\frac{1}{4}\)(2y – 1) = 0.6 + \(\frac{5x}{8}\)
Answer:
Given,
\(\frac{1}{4}\)(2y – 1) = 0.6 + \(\frac{5x}{8}\)
X = 4
\(\frac{1}{4}\)(2y – 1) = 0.6 + \(\frac{5(4)}{8}\)
\(\frac{1}{4}\)(2y – 1) = 0.6 + \(\frac{20}{8}\)
0.25 (2y – 1) = 0.6 + 2.5
0.5y – 0.25 = 3.1
0.5y = 3.1 + 0.25
0.5y = 3.35
y = 6.7
Express y in terms of x. Find the value of y when x = 4. (Lesson 3.4)
Question 17.
6(3x + y) = 3
Answer:
Given equation
6(3x + y) = 3
18x + 6y = 3
Substitute the value of x in the given equation
x = 4
18(4) + 6y = 3
72 + 6y = 3
24 + 2y = 1
2y = -23
y = -23/2
y = -11 1/2
Question 18.
\(\frac{2 x-1}{4}\) = 3y
Answer:
Given,
\(\frac{2 x-1}{4}\) = 3y
Substitute the value of x in the given equation
3y = \(\frac{2 x-1}{4}\)
3y = (2(4) – 1)4
3y = 7/4
y = 7/12
Express x in terms of y. Find the value of x when y = -2. (Lesson 3.4)
Question 19.
(\(\frac{2x-y}{5}\)) = 9
Answer:
Given,
(\(\frac{2x-y}{5}\)) = 9
2x – y = 9 × 5
2x – y = 45
Substitute the value of y in the given equation
y = -2
2x – (-2) = 45
2x + 2 = 45
2x = 45 – 2
2x = 43
x = 43/2
x = 21.5
Question 20.
0.75(x + y) = 12
Answer:
Given,
0.75(x + y) = 12
0.75x + 0.75y = 12
Substitute the value of y in the given equation
y = -2
0.75x + 0.75 (-2) = 12
0.75x – 1.5 = 12
0.75x = 12 – 1.5
0.75x = 10.5
x = 14
Find the slope of the line passing through each pair of points. (Lesson 4.1)
Question 21.
A (1, 2), B (4, 8)
Answer:
The line passes through the points (1, 2) and (4, 8).
Slope m = \(\frac{8-2}{4-1}\)
= \(\frac{6}{3}\)
= 2
Thus the slope, m = 2
Question 22.
C(1, 4), D(2, 7)
Answer:
The line passes through the points (1, 4) and (2, 7).
Slope m = \(\frac{7-4}{2-1}\)
= \(\frac{3}{1}\)
= 3
Thus the slope, m = 3
Question 23.
E (0, 0), F (-7, 7)
Answer:
The line passes through the points (0, 0) and (-7, 7).
Slope m = \(\frac{7-0}{-7-0}\)
= \(\frac{7}{-7}\)
= -1
Thus the slope, m =-1
Question 24.
G (-3, 0), F (0, -6)
Answer:
The line passes through the points (-3, 0) and (0, -6).
Slope m = \(\frac{-6-0}{0+3}\)
= \(\frac{-6}{3}\)
= -2
Thus the slope, m = -2
Identify the y-intercept. Then calculate the slope using the points indicated. (Lessons 4.1, 4.2)
Question 25.
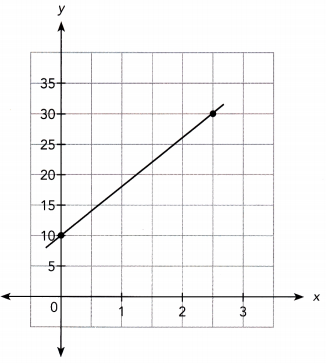
Answer:
The line passes through the points (0, 10) and (2.5, 30).
Slope m = \(\frac{30-10}{2.5-0}\)
= \(\frac{20}{2.5}\)
= 8
Thus the slope, m = 8
y-intercept = 10
Question 26.
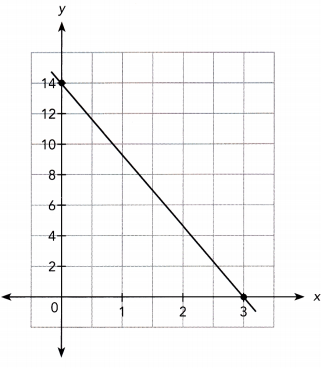
Answer:
The line passes through the points (0, 3) and (0, 14).
m = 14/3
y-intercept = 14
For each equation, find the slope and the y-intercept of the graph of the equation. (Lesson 4.3)
Question 27.
y = 7x + 1
Answer:
Given,
y = 7x + 1
slope, m = 7
y-intercept, b = 1
Question 28.
y = -2x – 5
Answer:
Given,
y = -2x – 5
slope, m = -2
y-intercept, b = -5
Question 29.
2y = 4x + 6
Answer:
Given,
2y = 4x + 6
y = 2x + 3
slope, m = 2
y-intercept, b = 3
Question 30.
4y + 3x = 8
Answer:
Given,
4y + 3x = 8
4y = -3x + 8
y = 3/4 x + 2
slope, m = 3/4
y-intercept, b = 2
Use the given slope and y-intercept of a line to write an equation in slope-intercept form. (Lesson 4.3)
Question 31.
Slope, m = 3
y-intercept, b = 2
Answer:
Slope, m = 3
y-intercept, b = 2
The equation in slope-intercept is y = mx + b
y = 3x + 2
Question 32.
Slope, m = -1
y-intercept, b = 4
Answer:
Slope, m = -1
y-intercept, b = 4
The equation in slope-intercept is y = mx + b
y = -1x + 4
Question 33.
Slope, m = 5
y-intercept, b = -2
Answer:
Slope, m = 5
y-intercept, b = -2
The equation in slope-intercept is y = mx + b
y = 5x – 2
Question 34.
Slope, m = –\(\frac{3}{2}\)
y-intercept, b = -5
Answer:
Slope, m = –\(\frac{3}{2}\)
y-intercept, b = -5
The equation in slope-intercept is y = mx + b
y = –\(\frac{3}{2}\)x – 5
Solve. Show your work. (Lesson 4.3)
Question 35.
Write an equation of the line parallel to 2y = 4x + 3 that has a y-intercept of 4.
Answer: y = 2x + 4
Question 36.
A line has slope -4 and passes through the point (\(\frac{3}{4}\), 3). Write an equation of the line.
Answer:
y = -4x + 6
Question 37.
Write an equation of the line that passes through the point (2, 3) and is parallel to 3y + 2x = 7.
Answer:
y = –\(\frac{2}{3}\)x + \(\frac{13}{3}\)
Use graph paper. Graph each linear equation. Use 1 grid scale to represent 1 unit on both axes for the interval -5 to 5. (Lesson 4.4)
Question 38.
y = -2x + 8
Answer:
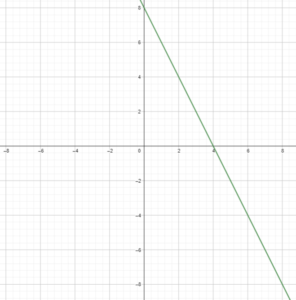
Question 39.
y = -2 – 3x
Answer:
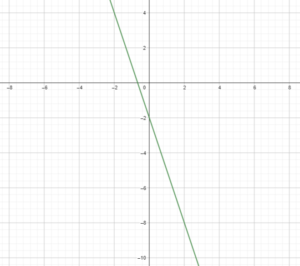
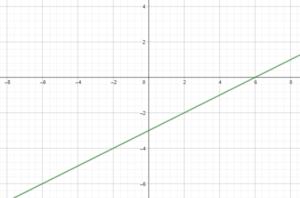
Question 40.
y = \(\frac{1}{2}\)x – 3
Answer:
Solve. Show your work. (Lesson 4.5)
Question 41.
Bobby and Chloe each have a bank account. The balance, y dollars, in each account for x weeks, is shown in the graph.
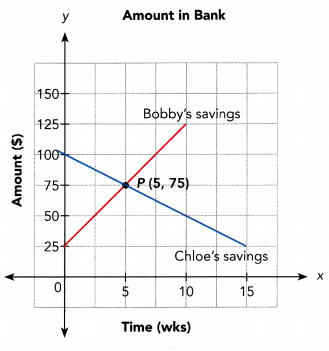
a) Who saved money and who withdrew money during the 10 weeks?
Answer: Bobby’s savings increased, so he saved money. Chloe’s savings decreased, so she withdrew money.
b) Whose balance changed more over 10 weeks?
Answer:
Bobby changed by $100, Chloe’s changed by -$50; Bobby’s changed more.
c) Explain what information the coordinates of P give about the situation.
Answer:
After 5 weeks, Bobby and Chloe have the same amount of money, which is $75.
Problem Solving
Solve. Show your work.
Question 42.
The diagram shows a sheet of metal of width y inches. It is bent into a U-shaped gutter that is used to channel rain from a roof. The horizontal section of the gutter shown on the right is 10 inches wide and the heights are in the ratio of 2 : 3. (Chapter 3).
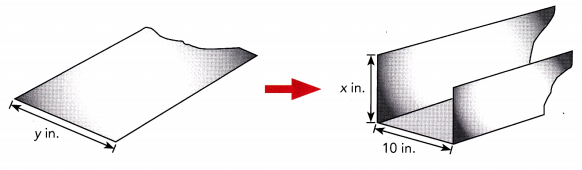
a) Let x represents the longer height of the gutter, in inches. Write a linear equation for the width of the sheet of metal, y inches-, in terms of the longer height of the gutter, x inches.
Answer: y = 5/3 x + 10
b) The width of the sheet of metal is 30 inches. Calculate the longer height of the gutter.
Answer: 12 in
Question 43.
In a grocery store, each apple costs $0.50, each orange costs $0.40, and each pear costs $0.30. Mrs. Fortney bought y apples, three times as many oranges as apples, and 7 fewer pears than apples. $he spent a total of $19.90 on the fruits. (Chapter 3)
a) Write a linear equation to find the amount spent on each fruit.
Answer: 50y + 120y + 30y – 210 = 1990
200y = 2200
b) Find the total cost spent on apples and pears.
Answer: $6.70
Question 44.
Jack traveled from his home to Denver at an average speed of x miles per hour. He arrived in \(\frac{3}{4}\) hour and took a 15-minute break. From Denver, he traveled at an average speed of (x + 2) miles per hour and reached his grandmother’s place in 1.5 hours. (Chapter 3)
a) Write a linear equation for the total distance traveled, D miles, in terms of average speed, x miles per hour.
Answer:
D = \(\frac{3}{4}\)x + \(\frac{3}{2}\)
D = \(\frac{3}{4}\)x + 1.5
D = \(\frac{9}{4}\)x + 3
b) The total distance traveled for the whole journey was 120 miles. Find the average speed for both parts of the journey.
Answer:
First part: 52 mi/h
Second part: 54 mi/h
Use graph paper. Solve.
Question 45.
Xavier walks into an elevator in the basement of a building. Its control panel displays “0” for the floor number. As Xavier goes up, the numbers increase one by one on the display. The table shows the floor numbers and the distance from ground level. (Chapter 4)

a) Graph the relationship between the distance of the elevator from ground level at different floor numbers. Use 1 grid square to represent 1 unit on the horizontal axis for the x interval 0 to 4, and 1 grid square for 10 units on the vertical axis for the y interval -10 to 30.
Answer:
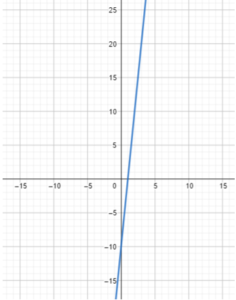
b) Find the vertical intercept of the graph and explain what information it gives about the situation.
Answer: -10
It is the distance of the elevator from ground level, 10 ft below ground level when it is at the basement level.
c) Find the slope of the graph and explain what information it gives about the situation.
Answer: 10
The slope represents the increase in distance, in ft, of the elevator from ground level for every increase of the 1-floor number
d) Write an equation relating the distance of the elevator from ground level and the floor number on the display.
Answer: y = 10x – 10
e) What is the distance of the elevator from the ground level of the highest floor that is less than 165 feet? Is there a floor number with a distance from the ground level of exactly 165 feet?
Answer: 160 ft
There is no floor number with distance from ground level for exactly 165 ft.