Go through the Math in Focus Grade 6 Workbook Answer Key Cumulative Review Chapters 1-3 to finish your assignments.
Math in Focus Grade 6 Course 1 A Cumulative Review Chapters 1-3 Answer Key
Concepts and Skills
Draw a horizontal number line to represent each set of numbers. (Lesson 1.1)
Question 1.
Mixed numbers from 3 to 7, with an interval of \(\frac{1}{3}\) between each pair of mixed numbers
Answer:
![]()
Explanation:
Mixed Fractions on Number Line Mixed fractions have two parts,
one whole number and one proper fraction.
To represent mixed fractions on a number line,
first, mark two points: the whole number part on the left and its successor on the right.
Question 2.
Decimals between 4.2 and 5.4, with an interval of 0.3 between each pair of decimals
Answer:
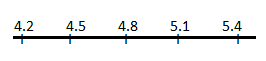
Explanation:
To represent a decimal on a number line,
divide each segment of the number line into ten equal parts.
Then mark the numbers with given intervals.
Express each number as a product of its prime factors. (Lesson 1.2)
Question 3.
84
Answer:
Factors of 84 are 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 and 84.
The prime factorization of 84 is 2 × 2 × 3 × 7 or 22 × 3 × 7.
Explanation:
Factors of 84 are the numbers that divide the original number evenly,
since 84 divided by 2 is equal to 42,
42 divided by 2 is equal to 21,
21 divided by 3 is equal to 7.
So, The prime factorization of 84 is 2 × 2 × 3 × 7 or 22 × 3 × 7.
where 2, 3 and 7 are the prime numbers.
240
Answer:
Factors of 240 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120 and 240.
Prime Factorization of 240 is 2 × 2 × 2 × 2 × 3 × 5 or 24 × 3 × 5.
Explanation:
Factors of 240 are the numbers that divide the original number evenly,
since 240 divided by 2 is equal to 120,
120 divided by 2 is equal to 60,
60 divided by 2 is 30,
30 divided by 2 is 15,
15 divided by 3 is 5.
So, Prime Factorization of 240 is 2 × 2 × 2 × 2 × 3 × 5 or 24 × 3 × 5.
Find the greatest common factor of each pair of numbers. (Lesson 1.3)
Question 5.
16 and 60
Answer:
GCF = 4
Explanation:
Find the prime factorization of 16
16 = 2 × 2 × 2 × 2
Find the prime factorization of 60
60 = 2 × 2 × 3 × 5
To find the GCF, multiply all the prime factors common to both numbers.
Therefore, GCF = 2 × 2
GCF = 4
Question 6.
63 and 96
Answer:
GCF = 3
Explanation:
The factors of 63 are 1,3,7,9,21,63;
The factors of 96 are 1,2,3,4,6,8,12,16,24,32,48,96.
To find the GCF, take the common factor to both numbers.
3 is the greatest number that 63 and 96 divides into.
Therefore, GCF = 3
Find the least common multiple of each pair of numbers. (Lesson 1.3)
Question 7.
9 and 12
Answer:
LCM = 36
Explanation:
To find the least common multiple of 9 and 12,
we need to find the multiples of 9 and 12
multiples of 9 = 9, 18, 27, 36;
multiples of 12 = 12, 24, 36, 48
choose the smallest multiple that is exactly divisible by 9 and 12, i.e., 36.
So, the LCM of 9 and 12 is 36.
Question 8.
15 and 18
Answer:
LCM = 90
Explanation:
To find the least common multiple of 15 and 18,
we need to find the multiples of 15 and 18.
multiples of 15 = 15, 30, 45, 60, 75, 90;
multiples of 18 = 18, 36, 54, 72, 90.
choose the smallest multiple that is exactly divisible by 15 and 18, i.e., 90.
So, the LCM of 15 and 18 is 90.
Find the square root of each number. (Lesson 1.4)
Question 9.
256
Answer:
The square root of 256 is 16.
Explanation:
Determine the prime factors using prime factorization.
Prime factorization of 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
Group the prime factors obtained for 256 in pairs.
Pick one factor from each pair and they can be written in the form:
256 = (2 × 2 × 2 × 2)2
we get, √256 = √(162)
The square root of 256 is 16.
Question 10.
676
Answer:
The square root of 676 is 26.
Explanation:
676 is a perfect square hence,
we can express it as (2 × 2 × 13 × 13).
The numbers within square root which get repeated are 2 and 13.
Hence, the square root of 676 is 2 × 13 = 26 .
Find the cube root of each number. (Lesson 1.5)
Question 11.
1,728
Answer:
The cube root of 1,728 is 12
Explanation:
To find the cube root of 1728 through the prime factorization method,
1728 = 2 × 2 ×2 × 2 × 2 × 2 ×3 × 3 × 3
Pair the similar factors in a group of them and represent them as cubes.
1728 = (2 × 2 × 2) × (2 × 2 × 2 ) × (3 × 3 ×3)
1728 = 23 × 23 × 33
1728 = 2 x 2 x 3 = 12
Hence, the cube root of 1,728 is 12.
Question 12.
5,832
Answer:
The cube root of 5,832 is 18.
Explanation:
To find the cube root of 1728 through the prime factorization method,
1728 = 2 × 2 × 2 × 3 × 3 × 3 ×3 × 3 × 3
Pair the similar factors in a group of them and represent them as cubes.
1728 = (2 × 2 × 2) × (3 × 3 × 3 ) × (3 × 3 ×3)
1728 = 23 × 33 × 33
1728 = 2 x 3 x 3 = 18
Hence, the cube root of 5,832 is 18.
Find the value of each of the following. (Lesson 1.5)
Question 13.
53 – 112 + 73
Answer: 347
Explanation:
Write the cubes and square roots of given numbers.
53 = 5 x 5 x 5 = 125
73 = 7 x 7 x 7 = 343
112 = 11 x 11 = 121
According to BOADMAS first add the numbers of positive integers and then subtract the negative integers.
53 + 73 = 468
53 – 112 + 73 = 468 – 121 = 347
Question 14.
43 ÷ 82 × 123
Answer: 1,728
Explanation:
Apply the order of mathematical operations,
BODMAS stands for B-Brackets, O-Orders, D-Division, M-Multiplication, A-Addition, S-Subtraction.
43 ÷ 82
4x4x4 = 64
8×8 = 64
So, 64 ÷ 64 = 1
123 = 12 x 12 12 = 1,728
43 ÷ 82 × 123 = 1,728
Solve. (Lesson 1.5).
Question 15.
Given that 562 = 3,136, find the square of 112.
Answer:
112 x 112 = 12,544
Explanation:
Square root is the number that we multiply by itself to get the original number.
56 x 56 = 3,136
112 x 112 = 12,544
Question 16.
Given that 133 = 2,197, find the cube root of 17,576.
Answer:
The cube root of 17,576 is 26.
Explanation:
To find the cube root of 17,576 through the prime factorization method,
17,576 = 2 × 2 × 2 × 13 x 13 x 13
Pair the similar factors in a group of them and represent them as cubes.
17,576 = (2 × 2 × 2) × (13 × 13 × 13 )
17,576 = 23 × 133
17,576 = 2 x 13 = 26
Hence, the cube root of 17,576 is 26.
Draw a vertical number line to represent each set of numbers. (Lessons 1.3, 2.1)
Question 17.
Multiples of 3 between 81 and 110
Answer:
84, 87, 90, 93, 96, 99, 102, 105, 108.
Explanation:
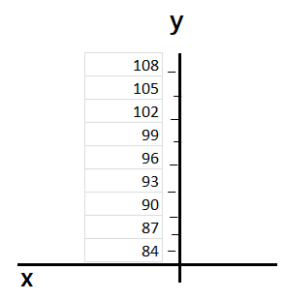
3 x 28 = 84
3 x 29 = 87
3 x 30 = 90
3 x 31 = 93
3 x 32 = 96
3 x 33 = 99
3 x 34 = 102
3 x 35 = 105
3 x 36 = 108
Question 18.
Even numbers greater than -37 but less than -25
Answer:
-36, -34, -32. -30, -28, -26
Explanation:
Even numbers after -37 and -25 given number are
-36
-36+2 = -34
-34 + 2 = -32
-32 + 2 = 30
-30 + 2 = 28
-28 + 2 = -26
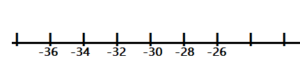
Write a positive or negative number to represent each situation. (Lesson 2.1)
Question 19.
Getting a pay raise of $320 per year
Answer:
Getting a pay raise of $320 per year, means increase to the previous pay.
Explanation:
positive number
Pay raise of $320 per year
it means adding to the previous number
Question 20.
214°F below zero
Answer:
-214°F
Explanation:
Measurement of temperature
0 degrees Fahrenheit is equal to -17.77778 degrees Celsius:
0°F = -17.77778 °C
The temperature T in degrees Celsius (°C) is equal to 214 degrees Fahrenheit (°F) minus 32, times 5/9. To convert 214 Fahrenheit to Celsius we can use the formula below:
Question 21.
Riding an elevator down 15 floors
Answer:
negative number
Explanation:
It means Elevator is moving down.
Elevator down from 15, to 14 , 13 …….. to zero (it means ground floor)
Copy and complete each inequality using > or <. (Lesson 2.1)
Question 22.
121 ![]() -388
-388
Answer:
121 > -388
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number,
smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.
Question 23.
-795 ![]() 347
347
Answer:
-795 < 347
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number,
smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.
Question 24.
-78 ![]() -132
-132
Answer:
-78 > -132
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number, smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.
Question 25.
-234 ![]() -243
-243
Answer:
-234 > -243
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number, smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.
Write an inequality for each of the following statements using > or <. (Lesson 2.1)
Question 26.
185°F is colder than 209°F.
Answer:
Yes,
Explanation:
According to the Fahrenheit scale 185°F is less then 209°F, according to the number system 185 is less then the 209, hence the 185°F is colder then 209°F

Question 27.
Town A, which is 84 kilometers from Town B, is farther from Town B than Town C, which is 76 kilometers from Town B.
Answer:
Copy and complete each inequality using > or <. (Lesson 2.2)
Question 28.
|-356| ![]() |368|
|368|
Answer:
356 < 368
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number, smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.
Question 29.
|232| ![]() |-324|
|-324|
Answer:
232 < 324
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number, smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.
Question 30.
|264| ![]() |246|
|246|
Answer:
264 > 246
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number, smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.
Question 31.
|-311| ![]() |-389|
|-389|
Answer:
311 < 389
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number, smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.
Divide. (Lesson 3.1)
Question 32.
28 ÷ \(\frac{1}{5}\)
Answer: 140
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
28 ÷ \(\frac{1}{5}\)
\(\frac{28}{1}\) x \(\frac{5}{1}\)
28 x 5 = 140
Question 33.
42 ÷ \(\frac{2}{3}\)
Answer: 63
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
42 ÷ \(\frac{2}{3}\)
\(\frac{42}{2}\) x \(\frac{3}{1}\)
\(\frac{126}{2}\) = 63
Question 34.
\(\frac{3}{8}\) ÷ 12
Answer: 32
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
\(\frac{3}{8}\) ÷ 12
\(\frac{8×12}{3}\)\(\frac{96}{3}\) = 32
Question 35.
\(\frac{5}{14}\) ÷ \(\frac{10}{21}\)
Answer: 0.75
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
\(\frac{5}{14}\) ÷ \(\frac{10}{21}\)
\(\frac{5×21}{10×14}\)\(\frac{105}{140}\) = 0.75
Multiply. (Lesson 3.2)
Question 36.
0.3 × 3.8
Answer: 1.14
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
and then the number of decimal places in the product is equal to the total number of decimal places in the given numbers.
Question 37.
6.3 × 4.7
Answer: 29.61
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
and then the number of decimal places in the product is equal to the total number of decimal places in the given numbers.
Question 38.
0.28 × 474
Answer: 132.72
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
and then the number of decimal places in the product is equal to the total number of decimal places in the given numbers.
Question 39.
8.23 × 9.107
Answer: 74.95061
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
and then the number of decimal places in the product is equal to the total number of decimal places in the given numbers.
Divide. (Lesson 3.3)
Question 40.
72 ÷ 0.3
Answer: 240
Explanation:
When we divide decimals,
we change the divisor to a whole number by moving the decimal point all the way to the right.
Then, we move the decimal point of the dividend up to the same number of places to the right,
and divide the resultant numbers in the normal way as we do regular division.
Question 41.
8.1 ÷ 0.3
Answer: 27
Explanation:
When we divide decimals,
we change the divisor to a whole number by moving the decimal point all the way to the right.
Then, we move the decimal point of the dividend up to the same number of places to the right,
and divide the resultant numbers in the normal way as we do regular division.
Question 42.
2.88 ÷ 1.2
Answer: 240
Explanation:
When we divide decimals,
we change the divisor to a whole number by moving the decimal point all the way to the right.
Then, we move the decimal point of the dividend up to the same number of places to the right,
and divide the resultant numbers in the normal way as we do regular division.
Question 43.
128 ÷ 0.02
Answer: 6,400
Explanation:
When we divide decimals,
we change the divisor to a whole number by moving the decimal point all the way to the right.
Then, we move the decimal point of the dividend up to the same number of places to the right,
and divide the resultant numbers in the normal way as we do regular division.
Problem Solving
Solve. Show your work.
Question 44.
Alison paid $21.75 for a number of packs of rice crackers. Three packs of rice crackers cost $1.45. How many packs of rice crackers did Alison buy? If she were to buy 60 packs of the same rice crackers, would $30 be enough to pay for them? (Chapter 3)
Answer:
60 packs
Explanation:
Find the x, the unit price 3x = 1.45
\(\frac{3x}{3}\)
= \(\frac{1.45}{3x}\)
x = 0.483 cost per pack.
the number of packs bought 21.75 = 0.483 x 0.483x = 21.75
0.483x / 0.483 = 21.75 / 0.483 x = 45 packs bought
total cost of 60 packs x = 0.483(60) x = 28.98 is the total cost.
$30 is more than enough to pay for 60 packs.
Question 45.
Find two consecutive numbers whose cubes differ by 169. (Chapter 1)
Answer:
8 and 7 are 2 consecutive numbers.
Explanation:
cube of 8 = 8 x 8 x 8 = 512
cube of 7 = 7 x 7 x 7 = 343
Difference of 8 cube and 7 cube
512 – 343 = 169
Question 46.
Two light houses flash their lights every 30 seconds and 40 seconds respectively. Given that they last flashed together at 10:40 A.M., when will they next flash together? (Chapter 1)
Answer:
10:42 AM
Explanation:
for every 120 seconds the lights will flash together
30 x 4 = 120 sec
40 x 3 = 120 sec
10:40 AM flash
10:42 AM
Question 47.
\(\frac{7}{8}\) of a rectangle is colored red. Damien cuts this red part into a number of pieces so that each piece is \(\frac{1}{24}\) of the whole rectangle. Find the number of red pieces Damien has. (Chapter 3)
Answer:
21 red pieces
Explanation:
\(\frac{7}{8}\) of a rectangle is colored red.
Damien cuts this red part into a number of pieces so that each piece is \(\frac{1}{24}\) The number of red pieces Damien has
\(\frac{7}{8}\) ÷ \(\frac{1}{24}\)
\(\frac{7×24}{8}\) = \(\frac{168}{8}\) = 21
Question 48.
Jon spent \(\frac{1}{3}\) of his allowance on baseball cards, \(\frac{1}{4}\) on baseball souvenirs, and \(\frac{3}{8}\) on a baseball ticket. If he had $5 left, how much allowance did he have to start with? (Chapter 3)
Answer:
$120
Explanation:
Let x is total allowance Jan started
Allowance spent on baseball = \(\frac{1}{3}\)
Allowance spent on baseball souvenirs = \(\frac{3}{4}\)
Allowance spent on baseball ticket = \(\frac{3}{8}\)
Remaining allowances = Total allowance – baseball – souvenirs – ticket
= x -(\(\frac{1}{3}\)) x – (\(\frac{3}{4}\))x – (\(\frac{3}{8}\)) x
= x – \(\frac{x}{3}\) – \(\frac{x}{4}\) – \(\frac{3x}{8}\)
L.C.M of the denominators = 24
Multiply each term with 24
24x – 8x – 6x – 9x ÷ 24
Jane left with $5
\(\frac{x}{24}\) = 5
Multiply 24 on both sides
\(\frac{x}{24}\) x 24 = 5 x 24
= 120
Question 49.
A baker baked some loaves of bread. 240 loaves were sold by the end of the day. The baker was then left with \(\frac{9}{25}\) of the number of loaves that were baked. How many loaves of bread did the baker bake on that day? (Chapter 3)
Answer:
375 loaves
Explanation:
x- 240 = \(\frac{x9}{25}\)
x – \(\frac{x9}{25}\) = 240
25 x -9x = 240 x 25
16x = 6000
x = 6000/25
x = 375
Question 50.
Front and back row tickets to a performance are available. There are 18 front rows with 39 seats in each row, and 27 back rows with 4 seats in each row. If \(\frac{5}{6}\) of all the front row seats and \(\frac{7}{9}\) of the back row seats are sold, how much is the total ticket sales? (Chapter 3)
Answer:
669 seats
Explanation:
18 front rows with 39 seats in each row =
=18 x 39 = 702
702 x \(\frac{5}{6}\) = 585 seats
27 back rows with 4 seats in each row
27 x 4 = 108
108x\(\frac{7}{9}\)
=84
the total ticket sales
= 585 + 84
= 669 seats
Question 51.
A charitable organization packed 195 bags of rice, 325 blankets, and 455 bottles of water equally into boxes. (Chapter 1)
a) Find the greatest possible number of boxes that the items can be packed into.
Answer:
5 boxes
Explanation:
195/5 = 35
325/5 =65
445/5= 91
packed 195 bags of rice, 325 blankets, and 455 bottles of water equally into 5 boxes.
b) Find the number of bags of rice, blankets, and bottles of water in each box.
Answer:
35 rice bags, 65 blankets and 91 water bottles.
Explanation:
195/5 = 35 rice
325/5 =65 blankets
445/5= 91 water bottles