Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 5 Lesson 5.3 Solving Direct Proportion Problems to score better marks in the exam.
Math in Focus Grade 7 Course 2 A Chapter 5 Lesson 5.3 Answer Key Solving Direct Proportion Problems
Math in Focus Grade 7 Chapter 5 Lesson 5.3 Guided Practice Answer Key
Solve.
Question 1.
At a factory, the number of cars produced is directly proportional to the number of hours factory workers are making the cars. It takes 45 hours to make 60 cars. Use a proportion to find how long it will take to make 250 cars.
Method 1
Use a proportion.

Method 2
Use a direct proportion equation.
Let x be the number of hours.
Let y be the number of cars. Define the variables.
Constant of proportionality:
\(\frac{y}{x}=\frac{?}{?}\)
Substitute y = ![]() and x =
and x = ![]()
Simplify.
Direct proportion equation:
y = ![]() x Write an equation.
x Write an equation.
When y = 250 and y = ![]() x, 250 =
x, 250 = ![]() • x Evaluate y =
• x Evaluate y = ![]() x when y = 250.
x when y = 250.
![]() • x = 250 Write an equivalent equation.
• x = 250 Write an equivalent equation.
\(\frac{? \cdot x}{?}=\frac{250}{?}\) Divide both sides by ![]() .
.
x = ![]() Simplify.
Simplify.
It takes ![]() hours to produce 250 cars.
hours to produce 250 cars.
Answer:
It takes 187.5 hours to produce 250 cars.
Explanation:
Method 1:
Use a proportion.
Let number of hours for making 250 cars be x.
60 cars ÷ 45 hours = 250 cars ÷ x hours
=>60:45 = 250:x
=> 60 × x = 250 × 45
=> x = 11250 ÷ 60
=> x = 187.5 hours.
Method 2:
Use a direct proportion equation.
Let x be the number of hours.
Let y be the number of cars. Define the variables.
Constant of proportionality:
\(\frac{y}{x}=\frac{?}{?}\)
Substitute y = 60 and x = 45
\(\frac{y}{x}=\frac{60}{45}\)
y = 1.33 × x
=> y = 1.33x.
Direct proportion equation:
y = kx.
When y = 250
y = 1.33 x
=> 250 = 1.33 • x
=> 250 ÷ 1.33 = x
=> 187.5 hours.
It takes 187.5 hours to produce 250 cars.
Solve.
Question 2.
The number of pears for sale at an orchard, P, is directly proportional to the number of crates used to pack the pears, C. The table shows the relationship between the total number of pears for sale and the number of crates.
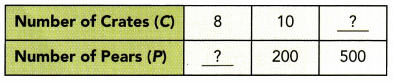
a) Write a direct proportion equation that relates P and C.
Answer:
Direct proportion equation:
P = kC
Explanation:
direct proportion equation:
P = 200.
C = 10.
P = kC
200 = k × 10
200 ÷ 10 = k
20 = k.
b) Find the missing values in the table.
Answer:
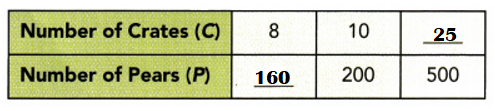
Explanation:
P = ?? C = 8.
P = kC
=> P = 20 ×8
=> P = 160.
P = 500 C = ??.
P = kC
=> 500 = 20 × C
=> 500 ÷ 20 = C
=> 25 = C.
Question 3.
A store owner bought some handbags for $32 each from the manufacturer. Later, the store owner marked up the price of each handbag by $8. Use a proportion to find the percent increase in the price of the handbags.
Answer:
Percent increase in the price of the handbags = 20%.
Explanation:
Cost of the handbags a store owner bought from the manufacturer = $32 each.
Marked up price of the handbags a store owner bought later = $8 each.
Total price of the each handbag = Cost of the handbags a store owner bought from the manufacturer + Marked up price of the handbags a store owner bought later
= $32 + $8
= $40.
Percent increase in the price of the handbags = Marked up price of the handbags a store owner bought later ÷ Total price of the each handbag × 100
= 8 ÷ 40 × 100
= 0.2 × 100
= 20%.
Math in Focus Course 2A Practice 5.3 Answer Key
Write a direct variation equation and find the indicated value.
Question 1.
m varies directly as n, and m = 14 when n = 7.
a) Write an equation that relates m and n.
Answer:
Direct variation equation:
m = kn.
Explanation:
m = 14 when n = 7
m = kn
=> 14 = k × 7
=> 14 ÷ 7 = k
=> 2 = k.
b) Find m when n = 16.
Answer:
m = 32.
Explanation:
Direct variation equation:
m = kn.
=> m = 2 × 16
=> m = 32.
c) Find n when m = 30.
Answer:
n = 15.
Explanation:
m = 30.
Direct variation equation:
m = kn.
=> 30 = 2 × n
=> 30 ÷ 2 = n.
=> 15 = n.
Question 2.
p varies directly as q, and p = 6 when q = 30.
a) Write an equation that relates p and q.
Answer:
Direct variation equation:
q = kp.
Explanation:
p = 6 when q = 30.
Direct variation equation:
q = kp.
=> 30 = k × 6
=> 30 ÷ 6 = k
=> 5 = k.
b) Find q when p = 10.
Answer:
q = 50.
Explanation:
p = 10.
Direct variation equation:
q = kp.
=> q = 5 × 10
=> q = 50.
c) Find p when q = 7.
Answer:
p = 1.4.
Explanation:
q = 7.
Direct variation equation:
q = kp.
=> 7 = 5 × p
=> 7 ÷ 5 = p
=> 1.4 = p.
In each table, b is directly proportional to a. Copy and complete the table.
Question 3.

Answer:
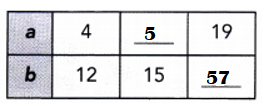
Explanation:
b = 12. a = 4.
Direct variation equation:
b = ka
=> 12 = k × 4
=> 12 ÷ 4 = k
=> 3 = k.
b = 15 a = ??
b = ka
=> 15 = 3 × a
=> 15 ÷ 3 = a
=> 5 = a.
a = 19 b = ??
b = ka
=> b = 3 × 19
=> b = 57.
Question 4.
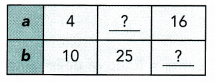
Answer:
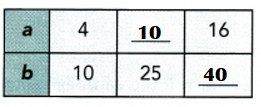
Explanation:
b = 10. a = 4.
Direct variation equation:
b = ka
=> 10 = k × 4
=> 10 ÷ 4 = k
=> 2.5 = k.
b = 25 a = ??
b = ka
=> 25 = 2.5 × a
=> 25 ÷ 2.5 = a
=> 10 = a.
a = 16 b = ??
b = ka
=> b = 2.5 × 16
=> b = 40.
Solve. Show your work.
Question 5.
The amount of blood in a person’s body, a quarts, is directly proportional to his or her body weight, w pounds. A person who weighs 128 pounds has about 4 quarts of blood.
a) Find the constant of proportionality.
Answer:
Constant of proportionality: 32.
Explanation:
The amount of blood in a person’s body, a quarts, is directly proportional to his or her body weight, w pounds.
Direct variation equation:
w = k a.
=> 128 = k × 4
=> 128 ÷ 4 = k
=> 32 = k.
b) Write an equation that relates the amount of blood in a person’s body to his or her body weight.
Answer:
Equation: w = ka.
Explanation:
Direct variation equation:
w = k a.
=> 128 = k × 4
=> 128 ÷ 4 = k
=> 32 = k.
c) Find the weight of a person whose body has about 5 quarts of blood.
Answer:
160 is the weight of a person whose body has about 5 quarts of blood.
Explanation:
a = 5 quarts.
Direct variation equation:
w = k a.
=> w = 32 × 5
=> w = 160.
Question 6.
The height of a stack of books, H inches, is directly proportional to the number of books, n. The height of a stack of 10 books is 12 inches.
a) Find the constant of proportionality.
Answer:
Constant of proportionality:1.2
Explanation:
The height of a stack of books = H inches.
The number of books = n.
Direct variation equation:
H = kn
=> 12 = k × 10
=> 12 ÷ 10 = k.
=> 1.2 = k.
b) Write an equation that relates H and n.
Answer:
Direct variation equation:
H = kn
Explanation:
The height of a stack of books = H inches.
The number of books = n.
Direct variation equation:
H = kn.
c) Find the height of a stack of 24 books.
Answer:
28.8 inches is the height of a stack of 24 books.
Explanation:
The height of a stack of books = 24 inches.
The number of books = 24.
Direct variation equation:
H = kn
=> H = 1.2 × 24
=> H = 28.8 inches.
Question 7.
The total weight of n soccer balls is m ounces, m is directly proportional to n, and n = 12 when m = 54.
a) Find the weight per soccer ball.
Answer:
4.5 ounces is the weight per soccer ball.
Explanation:
The total weight of n soccer balls is m ounces.
Direct variation equation:
m = kn
=> 54 = k × 12
=> 54 ÷ 12 = k
=> 4.5 ounces.
b) Write an equation that relates n and m.
Answer:
m = kn is an equation that relates n and m.
Explanation:
The total weight of n soccer balls is m ounces.
Direct variation equation:
m = kn.
c) Find the value of m when n = 30.
Answer:
m = 135 ounces when n = 30.
Explanation:
n = 30.
Direct variation equation:
m = kn.
=> m = 4.5 × 30
=> m = 135 oounces.
Question 8.
The cost of CD cases, C, is directly proportional to the number of CD cases, n. The cost of 6 CD cases is $2.34.
a) Find the cost per CD case.
Answer:
Cost per CD case = $0.39.
Explanation:
The cost of CD cases = C.
Number of CD cases = n.
Total Cost of 6 CD cases = $2.34.
Cost per CD case = Total Cost of 6 CD cases ÷ Number of CD cases
= $2.34 ÷ 6
= $0.39
b) Write an equation that relates C and n.
Answer:
C = kn is an equation that relates C and n.
Explanation:
Direct variation equation:
C = kn.
c) Find the value of C when n is 7.
Answer:
C = $2.73 ; n = 7.
Explanation:
n = 7.
Direct variation equation:
C = kn.
=> C = $0.39 × 7
=> C = $2.73.
Use a proportion to solve each question. Show your work.
Question 9.
Five oranges cost $2. Find the cost of two dozen oranges.
Answer:
Cost of two dozen oranges = $0.96.
Explanation:
Number of oranges = 5.
Cost of 5 oranges = $0.2.
Cost of each orange = Cost of 5 oranges ÷ Number of oranges
= $0.2 ÷ 5
= $0.04.
dozen oranges = 12.
2 dozen oranges = 2 × 12 = 24.
Cost of two dozen oranges = Cost of each orange × 24
= $0.04 × 24
= $0.96.
Question 10.
It costs $180 to rent a car for 3 days. Find the cost of renting a car for 1 week.
Answer:
Cost of renting a car for 1 week = $420.
Explanation:
Cost of car for 3 days = $180.
Number of days = 3.
Cost of renting a car for a day = Cost of car for 3 days ÷ Number of days
=> $180 ÷ 3
=> $60.
Number of days in a week = 7.
Cost of renting a car for 1 week = Cost of renting a car for a day × Number of days in a week
= $60 × 7
= $420.
Question 11.
John drove 48 miles and used 2 gallons of gasoline. How many gallons of gasoline will he use if he drives 78 miles?
Answer:
Number of gallons of gasoline will he use if he drives 78 miles = 3.25.
Explanation:
Number of miles John drove = 48.
Number of gallons of gasoline = 2.
Number of gallons of gasoline used per mile = Number of miles John drove ÷ Number of gallons of gasoline
= 48 ÷ 2
= 24 miles per gasoline.
Number of miles if John drives = 78.
Number of gallons of gasoline will he use if he drives 78 miles = Number of miles if John drives ÷ Number of gallons of gasoline used per mile
= 78 ÷ 24
= 3.25.
Question 12.
Based on past experience, a caterer knows that the ratio of the number of glasses of juice to the number of people at a party should be 3 : 1. If 15 people are coming to a party, how many glasses of juice should the caterer have ready?
Answer:
Number of people are coming to a party = 45.
Explanation:
A caterer knows that the ratio of the number of glasses of juice to the number of people at a party should be 3 : 1.
=> Ratio of Number of glasses of juice to the number of people at a party = 3:1.
Number of people are coming to a party = 15.
Number of glasses of juices = ??
=> 3 ÷ 1 = ?? ÷ 15
=> 3 × 15 = ?? × 1
=> 45 = ??.
Question 13.
A recipe for meatloaf requires 10 ounces of ground beef. The recipe serves five people, and you would like to make enough for 8. How much ground beef should you use?
Answer:
Quantity of ground beef should be used = 16 ounces.
Explanation:
Quantity of ground beef a recipe for meatloaf requires = 10 ounces.
Number of people the recipe serves = 5.
Quantity of ground beef for one person = Quantity of ground beef a recipe for meatloaf requires ÷ Number of people the recipe serves
= 10 ÷ 5
= 2 ounces.
Number of people the recipe serves would to make enough = 8.
Quantity of ground beef should be used = Number of people the recipe serves would to make enough × Quantity of ground beef for one person
= 8 × 2 ounces
= 16 ounces.
Question 14.
George has to pay $30 in taxes for every $100 that he earns. Last summer he earned $3,680. How much did he pay in taxes?
Answer:
Amount of money he pays for tax = $1,104.
Explanation:
Amount of money George has to pay in taxes = $30.
Amount of money he earns = $100.
Amount of money he earns last summer = $3680.
Ratio:
Amount of money he earns ÷ Amount of money George has to pay in taxes
= $30 ÷ $100 = 30%
Amount of money he pays for tax = Amount of money he earns last summer × 30%
= $3680 × 30 ÷ 100
= $110400 ÷ 100
= $1,104.
Question 15.
Ti Marina wants to buy a sound system that costs $540. The sales tax rate in ‘ her state is 8.25%. How much sales tax must she pay?
Answer:
Amount of sales tax she must pay = $44.55.
Explanation:
Cost of sound system Ti Marina wants to buy = $540.
Sales percentage = 8.25%
Amount of sales tax she must pay = Cost of sound system Ti Marina wants to buy × Sales percentage
= $540 × 8.25%
= $4455 ÷ 100
= $44.55.
Question 16.
Jason mixes cans of yellow and blue paint to make green paint. The ratio of the number of cans of yellow paint to the number of cans of blue paint is 4 : 3. Jason needs to make more paint. He has 2 cans of yellow paint. How many cans of blue paint does he need to make the same shade of green?
Answer:
Number of blue paint cans he needs = 1.5.
Explanation:
The ratio of the number of cans of yellow paint to the number of cans of blue paint is 4 : 3.
Number of yellow cans he has = 2.
Number of blue paint cans he needs = ??
=> 4 ÷ 3 = 2 ÷ ??
=> 4 × ?? = 2 × 3
=> ?? = 6 ÷ 4
=> ?? = 1.5.
Question 17.
The area, A square feet, of the wall Ivan is painting is directly proportional to the time he spends painting the wall, T hours. It takes Ivan 4 hours to paint 113.6 square feet of the wall. How long will he take to paint 227.2 square feet of the wall?
Answer:
Time taken to paint 227.2 square feet = 8 hours.
Explanation:
Length of the wall Ivan is painting = A square feet.
Time he spends to paint the wall = T hours.
It takes Ivan 4 hours to paint 113.6 square feet of the wall.
Time taken to paint 227.2 square feet = ??
=> Ratio: 113.6 ÷ 4 = 227.2 ÷ ??
=> 113.6 × ?? = 227.2 × 4
=> ?? = 908.8 ÷ 113.6
=> ?? = 8 hours.
Question 18.
It takes Christy 2 hours to paint 5 model boats.
a) How long will it take her to paint 10 model boats?
Answer:
Number of hours she paints 10 model boats = 4.
Explanation:
Number of model boats Christy paints = 5.
Number of hours she paints = 2.
Number of hours she paints one model boats = Number of model boats Christy paints ÷ Number of hours she paints
= 5 ÷ 2
= 2.5.
Number of hours she paints 10 model boats = 10 ÷ Number of hours she paints one model boats
= 10 ÷ 2.5
= 4.
b) How many model boats can she paint in 10 hours?
Answer:
Number of model boats Christy paints in 10 hours = 25.
Explanation:
Number of hours she paints one model boats = Number of model boats Christy paints ÷ Number of hours she paints
= 5 ÷ 2
= 2.5.
Number of model boats Christy paints in 10 hours = Number of hours she paints one model boats × 10hours
= 2.5 × 10
= 25.
Question 19.
A commission is an amount of money earned by a sales person, based on the amount of sales the person makes. James works at a shop and earns 5.5% commission on his sales. Last month, he earned $265.32 in commission. Calculate his sales for that month.
Answer:
Sales he made that month = $4,824.
Explanation:
Commission James works at a shop and earns on his sales= 5.5%
Amount of money he earned last month = $265.32.
Let the sales be X.
Sales he made that month × 5.5% = Amount of money he earned last month
=> x × 5.5% = $265.32
=> x = $265.32 ÷ 5.5%
=> x = $26532 ÷ 5.5
=> x = $4,824.
Question 20.
An initial amount of money deposited in a bank account that earns interest is called the principal. In the table below, P stands for principal, and P stands for the interest earned by that principal for a period of one year at a particular bank. At this bank, the interest earned for a period of one year is directly proportional to the principal amount deposited.

a) Write a direct proportion equation that relates l and P.
Answer:
Direct proportion equation: P = kI
Explanation:
Principal = $600.
Interest earned = $15
Direct proportion equation: P = kI
=> $600 = k × $15
=> $600 ÷ $15 = k
=> $40 = k.
b) Copy and complete the table.
Answer:

Explanation:
Principal = $600.
Interest earned = $15
Direct proportion equation: P = kI
=> $600 = k × $15
=> $600 ÷ $15 = k
=> $40 = k.
Principal = $1000.
Interest earned = $??
Direct proportion equation: P = kI
=> $1000 = $40 × I
=> $1000 ÷ $40 = I
=> $25 = I.
Principal = $??
Interest earned = $56.
Direct proportion equation: P = kI
=> P = $40 × $56
=> P = $2,240.
Question 21.
Math journal y varies directly as x. Describe how the value of y changes when the value of x is tripled.
Answer:
The value of y changes when the value of x is tripled because y is directly proportional to x.
Explanation:
Direct variation describes a simple relationship between two variables.
y = kx.
Question 22.
Math Journal Jenny wants to buy some blackberries. Three stores sell blackberries at different prices:

Which store has the best deal? Give your reasons.
Answer:
Store A sells the best deal because cost of 16 strawberries is $0.15 ounces less than other two stores.
Explanation:
1 pound(lb) is equal to 16 ounces(oz).
Cost of blackberries Store A sells = $2.40 per lb.
=> $2.40 ÷ 16 = $0.15 per ounces.
Cost of blackberries Store B sells = $1.28 per 8 ounces.
=> $1.28 ÷ 8 = $0.16 per ounces.
Cost of blackberries Store C sells = $1.08 per 6 ounces.
=> $1.08 ÷ 6 = $0.18 per ounces.