Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 2 Lesson 2.5 Operations with Rational Numbers to finish your assignments.
Math in Focus Grade 7 Course 2 A Chapter 2 Lesson 2.5 Answer Key Operations with Rational Numbers
Math in Focus Grade 7 Chapter 2 Lesson 2.5 Guided Practice Answer Key
Copy and Complete
Question 1.

Answer:
–\(\frac{1}{9}\) + \(\frac{2}{-5}\)
Write equivalent fractions using the LCD
\(\frac{(-1)(-5)}{(9)(-5)}\) + \(\frac{2(9)}{(-5)(9)}\)
= \(\frac{5}{-45}\) + \(\frac{18}{-45}\)
= \(\frac{5+18}{-45}\)
= \(\frac{23}{-45}\)
Question 2.

Answer:
-1 \(\frac{1}{6}\) + 3\(\frac{4}{9}\)
= -1 – \(\frac{1}{6}\) + 3 + \(\frac{4}{9}\)
= -1 + 3 = 2
= –\(\frac{1}{6}\) + \(\frac{4}{9}\)
LCD of \(\frac{1}{6}\) and \(\frac{4}{9}\) is 18
= –\(\frac{3}{18}\) + \(\frac{8}{18}\) = \(\frac{5}{18}\)
2 + \(\frac{5}{18}\) = 2\(\frac{5}{18}\)
Question 3.
\(\frac{1}{6}\) + \(\left(\frac{-5}{9}\right)\) + \(\left(\frac{-1}{3}\right)\)
Add two rational numbers at a time, working from left to right.

Answer:

Method 2
Use a common denominator for all three fractions.

Answer:
\(\frac{1}{6}\) + \(\left(\frac{-5}{9}\right)\) + \(\left(\frac{-1}{3}\right)\)
= \(\frac{3}{18}\) + \(\left(\frac{-10}{18}\right)\) + \(\left(\frac{-6}{18}\right)\)
= (3 -10 – 6)/18
= -13/18
Evaluate each expression.
Question 4.
\(\frac{1}{4}\) – \(\frac{3}{10}\)
Answer:
The fractions have unlike denominators.
So, find the LCD for 1/4 and 3/10 that is 20.
\(\frac{1}{4}\) × \(\frac{5}{5}\) – \(\frac{3}{10}\) × \(\frac{2}{2}\)
\(\frac{5}{20}\) – \(\frac{6}{20}\) = – \(\frac{1}{20}\)
Question 5.
\(\frac{7}{8}\) – \(\frac{9}{10}\)
Answer:
Given,
\(\frac{7}{8}\) – \(\frac{9}{10}\)
The fractions have unlike denominators.
LCD of 8 and 10 is 40
\(\frac{7}{8}\) × \(\frac{5}{5}\) – \(\frac{9}{10}\) × \(\frac{4}{4}\)
\(\frac{35}{40}\) – \(\frac{36}{40}\) = – \(\frac{1}{40}\)
Question 6.
3\(\frac{1}{4}\) – 7\(\frac{5}{6}\)
Answer:
Given
3\(\frac{1}{4}\) – 7\(\frac{5}{6}\)
Rewriting the equation
3 + \(\frac{1}{4}\) – 7 – \(\frac{5}{6}\)
3 – 7 = -4
Now subtract the fractions
\(\frac{1}{4}\) – \(\frac{5}{6}\)
LCM of 4 and 6 is 12
\(\frac{1}{4}\) × \(\frac{3}{3}\) – \(\frac{5}{6}\) × \(\frac{2}{2}\)
\(\frac{3}{12}\) – \(\frac{10}{12}\) = – \(\frac{7}{12}\)
-4 – \(\frac{7}{12}\) = -4\(\frac{7}{12}\)
Question 7.
\(\frac{3}{7}\) – \(\frac{27}{28}\) – \(\frac{3}{14}\)
Answer:
Given
\(\frac{3}{7}\) – \(\frac{27}{28}\) – \(\frac{3}{14}\)
LCM of 7, 14, 28 is 28.
\(\frac{3}{7}\) × \(\frac{4}{4}\) – \(\frac{27}{28}\) × \(\frac{1}{1}\) – \(\frac{3}{14}\) × \(\frac{2}{2}\)
\(\frac{12}{28}\) – \(\frac{27}{28}\) – \(\frac{6}{28}\)
= (12 – 27 – 6)/28
= -21/28
= -3/4
Solve.
Question 8.
Philadelphia suffered a severe snowstorm in 1996 that left 30\(\frac{7}{10}\) inches of snow on the ground. Another severe snowstorm occured in 2010, when 28\(\frac{1}{2}\) inches of snow fell.
a) Write a subtraction expression for the difference in depth of these two record snowfalls.
Answer:
30\(\frac{7}{10}\) – 28\(\frac{1}{2}\)
b) Rewrite the expression as an addition expression.
Answer: – 28\(\frac{1}{2}\) + 30\(\frac{7}{10}\)
c) Find the difference in these two record snowfalls.
Answer:
30\(\frac{7}{10}\) – 28\(\frac{1}{2}\)
Rewriting the equation
30 + \(\frac{7}{10}\) – 28 – \(\frac{1}{2}\)
30 – 28 = 2
\(\frac{7}{10}\) – \(\frac{1}{2}\)
LCD = 10
\(\frac{7}{10}\) – \(\frac{5}{10}\) = \(\frac{2}{10}\) = \(\frac{1}{5}\)
2 + \(\frac{1}{5}\) = 2 \(\frac{1}{5}\)
Copy and Complete.
Question 9.

Answer:
–\(\frac{4}{5}\) × \(\frac{20}{21}\)
Multiply the numerators and multiply the denominators
= (-4 × 20)/(5 × 21)
= –\(\frac{80}{105}\)
Question 10.

Answer:
-3\(\frac{1}{4}\) × -2\(\frac{2}{3}\)
Write as improper fractions
–\(\frac{13}{4}\) × –\(\frac{8}{3}\)
= \(\frac{104}{12}\)
= \(\frac{52}{6}\)
= \(\frac{26}{3}\)
= 8\(\frac{2}{3}\)
Evaluate each quotient.
Question 11.
\(\frac{3}{20}\) ÷ \(\left(-\frac{6}{35}\right)\)
Answer:
Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.
\(\frac{3}{20}\) × –\(\frac{35}{6}\)
= (3 × -35)/(20 × 6)
= -105/120
= -7/8
Question 12.
-3\(\frac{1}{3}\) ÷ \(\left(-1 \frac{1}{4}\right)\)
Answer:
Given,
-3\(\frac{1}{3}\) ÷ \(\left(-1 \frac{1}{4}\right)\)
\(\frac{10}{3}\) ÷ \(\frac{5}{4}\)
LCD of 3 and 4 is 12.
\(\frac{10}{3}\) × \(\frac{4}{4}\) ÷ \(\frac{5}{4}\) × \(\frac{3}{3}\)
\(\frac{40}{12}\) ÷ \(\frac{15}{12}\)
\(\frac{40}{12}\) = 2 \(\frac{2}{3}\)
Question 13.
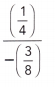
Answer:
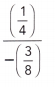
Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.
\(\frac{1}{4}\) ÷ \(\frac{-3}{8}\) = \(\frac{-2}{3}\)
Solve. Show your work.
Question 14.
A pancake recipe requires 1\(\frac{2}{3}\) cups of flour to make 20 pancakes and you have 9 cups of flour.
a) How many pancakes can you make with 1 cup of flour?
Answer:
Given,
A pancake recipe requires 1\(\frac{2}{3}\) cups of flour to make 20 pancakes
Let 1 cup of flour is x
1 \(\frac{2}{3}\) x = 20
x = 12
b) How many pancakes can you make with 9 cups of flour?
Answer:
1 cup = 12 pancakes
9 cups = 9 × 12 = 108
Thus you can make 81 pancakes with 9 cups of flour.
c) Do you have enough to make 100 pancakes? Explain your reasoning.
Answer:
1 cup of flour = 12 pancakes
9 cups = 9 × 12 = 108
Thus you can make 81 pancakes with 9 cups of flour.
As I can make 108 pancakes with 9 cups of flour, I can conclude that I have enough flour to make 100 pancakes
Math in Focus Course 2A Practice 2.5 Answer Key
Evaluate each expression. Give your answer in simplest form.
Question 1.
\(\frac{1}{2}\) + \(\left(-\frac{5}{6}\right)\)
Answer:
Given,
\(\frac{1}{2}\) + \(\left(-\frac{5}{6}\right)\)
The fractions of the denominators are not the same. So, we have to find the LCD of the denominators and rewrite the fractions.
\(\frac{1}{2}\) – \(\frac{5}{6}\)
LCD of 2 and 6 is 6.
\(\frac{1}{2}\) × \(\frac{3}{3}\) – \(\frac{5}{6}\) × \(\frac{1}{1}\)
\(\frac{3}{6}\) – \(\frac{5}{6}\) = – \(\frac{2}{6}\) or – \(\frac{1}{3}\)
Question 2.
–\(\frac{6}{7}\) + \(\frac{3}{14}\)
Answer:
Given,
–\(\frac{6}{7}\) + \(\frac{3}{14}\)
The fractions of the denominators are not the same. So, we have to find the LCD of the denominators and rewrite the fractions.
LCD of 7 and 14 is 14.
–\(\frac{12}{14}\) + \(\frac{3}{14}\) = –\(\frac{9}{14}\)
Question 3.
–\(\frac{1}{7}\) + \(\left(\frac{-3}{5}\right)\)
Answer:
Given,
–\(\frac{1}{7}\) + \(\left(\frac{-3}{5}\right)\)
The fractions of the denominators are not the same. So, we have to find the LCD of the denominators and rewrite the fractions.
-(\(\frac{1}{7}\) + \(\frac{3}{5}\))
LCD of 7 and 5 is 35
-(\(\frac{5}{35}\) + \(\frac{21}{35}\))
–\(\frac{26}{35}\)
Question 4.
\(\frac{1}{2}\) + \(\left(-\frac{2}{5}\right)\) + \(\frac{1}{4}\)
Answer:
Given,
\(\frac{1}{2}\) + \(\left(-\frac{2}{5}\right)\) + \(\frac{1}{4}\)
The fractions of the denominators are not the same. So, we have to find the LCD of the denominators and rewrite the fractions.
\(\frac{1}{2}\) + \(\frac{1}{4}\) – \(\frac{2}{5}\)
\(\frac{3}{4}\) – \(\frac{2}{5}\)
LCD of 4 and 5 is 20.
\(\frac{15}{20}\) – \(\frac{8}{20}\) = \(\frac{7}{20}\)
Question 5.
–\(\frac{1}{7}\) + \(\left(\frac{-5}{6}\right)\) + \(\left(\frac{-1}{3}\right)\)
Answer:
Given,
–\(\frac{1}{7}\) + \(\left(\frac{-5}{6}\right)\) + \(\left(\frac{-1}{3}\right)\)
The fractions of the denominators are not the same. So, we have to find the LCD of the denominators and rewrite the fractions.
–\(\frac{1}{7}\) – \(\frac{5}{6}\) – \(\frac{1}{3}\)
– (\(\frac{1}{7}\) + \(\frac{5}{6}\) + \(\frac{1}{3}\) )
LCD of 7, 6 and 3 is 42.
– (\(\frac{6}{42}\) + \(\frac{35}{42}\) + \(\frac{14}{42}\))
– (6 + 35 + 14)/42
– \(\frac{55}{42}\)
Question 6.
\(\frac{3}{5}\) – \(\frac{2}{3}\)
Answer:
Given,
\(\frac{3}{5}\) – \(\frac{2}{3}\)
The fractions of the denominators are not the same. So, we have to find the LCD of the denominators and rewrite the fractions.
LCD of 5 and 3 is 15.
\(\frac{9}{15}\) – \(\frac{10}{15}\) = – \(\frac{1}{15}\)
Question 7.
–\(\frac{1}{7}\) – \(\frac{3}{14}\)
Answer:
Given,
–\(\frac{1}{7}\) – \(\frac{3}{14}\)
The fractions of the denominators are not the same. So, we have to find the LCD of the denominators and rewrite the fractions.
LCD of 7 and 14 is 14.
-(\(\frac{1}{7}\) + \(\frac{3}{14}\))
-(\(\frac{2}{14}\) + \(\frac{3}{14}\))
– \(\frac{5}{14}\)
Question 8.
–\(\frac{1}{5}\) – \(\left(\frac{-2}{7}\right)\)
Answer:
Given,
–\(\frac{1}{5}\) – \(\left(\frac{-2}{7}\right)\)
The fractions of the denominators are not the same. So, we have to find the LCD of the denominators and rewrite the fractions.
– \(\frac{1}{5}\) + \(\frac{2}{7}\)
LCD of 7 and 5 is 35
-(\(\frac{7}{35}\) + \(\frac{10}{35}\))
–\(\frac{17}{35}\)
Question 9.
\(\frac{1}{3}\) – \(\left(-\frac{2}{5}\right)\) – \(\frac{3}{4}\)
Answer:
Given,
\(\frac{1}{3}\) – \(\left(-\frac{2}{5}\right)\) – \(\frac{3}{4}\)
The fractions of the denominators are not the same. So, we have to find the LCD of the denominators and rewrite the fractions.
\(\frac{1}{3}\) + \(\frac{2}{5}\) – \(\frac{3}{4}\)
LCD of 3, 5, and 7 is 60.
\(\frac{20}{60}\) + \(\frac{24}{60}\) – \(\frac{45}{60}\)
\(\frac{44}{60}\) – \(\frac{45}{60}\) = – \(\frac{1}{60}\)
Evaluate each product. Give your answer in simplest form.
Question 10.
–\(\frac{7}{25}\) • \(\frac{5}{14}\)
Answer:
Given,
–\(\frac{7}{25}\) • \(\frac{5}{14}\)
-(7 × 5)/(25 × 14)
= -1/10
Question 11.
\(\frac{5}{8}\) • \(\left(-\frac{4}{15}\right)\)
Answer:
Given,
\(\frac{5}{8}\) • \(\left(-\frac{4}{15}\right)\)
(5 × -4)/(8 × 15)
= -20/120
= -1/6
Question 12.
\(\frac{7}{30}\) • \(\left(-\frac{6}{7}\right)\)
Answer:
Given,
\(\frac{7}{30}\) • \(\left(-\frac{6}{7}\right)\)
(7 × -6)/(30 × 7)
= -1/5
Question 13.
–\(\frac{8}{27}\) • \(\left(-\frac{9}{40}\right)\)
Answer:
Given,
–\(\frac{8}{27}\) • \(\left(-\frac{9}{40}\right)\)
= (-8 × -9)/(27 × 40)
= 1/15
Question 14.
–\(\frac{11}{16}\) • \(\left(-\frac{4}{33}\right)\)
Answer:
Given,
–\(\frac{11}{16}\) • \(\left(-\frac{4}{33}\right)\)
(-11 × -4)/(16 × 33)
1/12
Question 15.
\(\frac{5}{8}\) • \(\left(-2 \frac{4}{5}\right)\)
Answer:
Given,
\(\frac{5}{8}\) • \(\left(-2 \frac{4}{5}\right)\)
\(\frac{5}{8}\) • \(\left(\frac{-6}{5}\right)\)
(5 × -6)/(8 × 5)
-3/4
Question 16.
–\(\frac{3}{22}\) • 1\(\frac{5}{6}\)
Answer:
Given,
–\(\frac{3}{22}\) • 1\(\frac{5}{6}\)
Convert from mixed fraction to the improper fraction to find the product of two fractions.
–\(\frac{3}{22}\) • \(\frac{11}{6}\)
= –\(\frac{3×11}{22×6}\)
= –\(\frac{33}{132}\)
= –\(\frac{1}{4}\)
Question 17.
3\(\frac{1}{8}\) • \(\left(-\frac{3}{10}\right)\)
Answer:
Given,
3\(\frac{1}{8}\) • \(\left(-\frac{3}{10}\right)\)
Convert from mixed fraction to the improper fraction to find the product of two fractions.
\(\frac{25}{8}\) • –\(\frac{3}{10}\)
= –\(\frac{75}{80}\)
= –\(\frac{15}{16}\)
Question 18.
-4\(\frac{1}{2}\) • \(\left(-1 \frac{8}{9}\right)\)
Answer:
Given,
-4\(\frac{1}{2}\) • \(\left(-1 \frac{8}{9}\right)\)
Convert from mixed fraction to the improper fraction to find the product of two fractions.
–\(\frac{9}{2}\) • –\(\frac{17}{9}\)
minus × minus = plus
We get
\(\frac{9}{2}\) • \(\frac{17}{9}\)
= \(\frac{51}{6}\)
= \(\frac{17}{2}\)
Evaluate each quotient. Give your answer in simplest form.
Question 19.
-10 ÷ \(\left(-\frac{5}{6}\right)\)
Answer:
Given,
-10 ÷ \(\left(-\frac{5}{6}\right)\)
First cancel the negative signs
We get
10 ÷ \(\frac{5}{6}\)
(10 × 6)/(1 × 5)
= 60/5
= 12
Question 20.
\(\frac{9}{25}\) ÷ (-18)
Answer:
Given,
\(\frac{9}{25}\) ÷ (-18)
(9 × 1)/25 × -28
=\(\frac{9}{-450}\)
= –\(\frac{1}{50}\)
Question 21.
–\(\frac{3}{8}\) ÷ \(\left(-\frac{1}{8}\right)\)
Answer:
Given,
–\(\frac{3}{8}\) ÷ \(\left(-\frac{1}{8}\right)\)
First cancel the negative signs
We get
\(\frac{3}{8}\) ÷ \(\frac{1}{8}\) = 3
Question 22.
–\(\frac{1}{4}\) ÷ \(\frac{3}{8}\)
Answer:
Given,
–\(\frac{1}{4}\) ÷ \(\frac{3}{8}\)
= -(1 × 8)/(4 × 3) = -8/12
= -2/3
Question 23.
\(\frac{5}{12}\) ÷ \(\left(-\frac{1}{6}\right)\)
Answer:
Given,
\(\frac{5}{12}\) ÷ \(\left(-\frac{1}{6}\right)\)
(5 × 6)/(-12 × 1)
= -30/12
= -5/2
= \(\left(-2 \frac{1}{2}\right)\)
Question 24.
-1\(\frac{1}{4}\) ÷ \(\frac{3}{4}\)
Answer:
Given,
-1\(\frac{1}{4}\) ÷ \(\frac{3}{4}\)
Convert from mixed fraction to the improper fraction
–\(\frac{5}{4}\) ÷ \(\frac{3}{4}\)
= -(5 × 4)/(4 × 3)
= –\(\frac{20}{12}\)
= -1\(\frac{2}{3}\)
Question 25.
\(\frac{8}{15}\) ÷ \(\left(-2 \frac{2}{3}\right)\)
Answer:
Given,
\(\frac{8}{15}\) ÷ \(\left(-2 \frac{2}{3}\right)\)
Convert from mixed fraction to the improper fraction
\(\frac{8}{15}\) ÷ –\(\frac{8}{3}\)
= (8 × 3)/(15 × -8)
= –\(\frac{1}{5}\)
Question 26.
3\(\frac{3}{4}\) ÷ \(\left(-\frac{1}{4}\right)\)
Answer:
Given,
3\(\frac{3}{4}\) ÷ \(\left(-\frac{1}{4}\right)\)
Convert from mixed fraction to the improper fraction
\(\frac{15}{4}\) ÷ –\(\frac{1}{4}\)
= (15 × 4)/(4 × -1)
= –\(\frac{60}{4}\)
= -15
Question 27.
2\(\frac{1}{2}\) ÷ \(\left(-1 \frac{2}{3}\right)\)
Answer:
Given,
2\(\frac{1}{2}\) ÷ \(\left(-1 \frac{2}{3}\right)\)
Convert from mixed fraction to the improper fraction
\(\frac{5}{2}\) ÷ –\(\frac{5}{3}\)
= -(5 × 3)/(2 × 5)
= –\(\frac{3}{2}\) or -1\(\frac{1}{2}\)
Question 28.
-2\(\frac{2}{7}\) ÷ \(\left(-1 \frac{3}{7}\right)\)
Answer:
Given,
-2\(\frac{2}{7}\) ÷ \(\left(-1 \frac{3}{7}\right)\)
Convert from mixed fraction to the improper fraction
–\(\frac{16}{7}\) ÷ –\(\frac{10}{7}\)
Cancel the negative signs and then perform division operation
\(\frac{16}{7}\) ÷ \(\frac{10}{7}\)
= (16 × 7)/(7 × 10)
= \(\frac{8}{5}\)
= 1 \(\frac{3}{5}\)
Question 29.
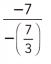
Answer:
Given,
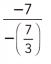
-7 ÷ –\(\frac{7}{3}\)
Cancel the negative signs and then perform division operation
(7 × 3)/(7)
= 21/7
= 3
Question 30.
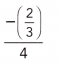
Answer:
Given,
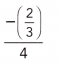
–\(\frac{2}{3}\) ÷ 4
= -(2 × 1)/(3 × 4)
= -2/12
= –\(\frac{1}{6}\)
Question 31.
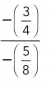
Answer:
Given,
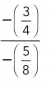
Cancel the negative signs and then perform division operation
\(\frac{3}{4}\) ÷ \(\frac{5}{8}\)
= (3 × 8)/(4 × 5)
= 24/20
= 1\(\frac{1}{5}\)
Question 32.
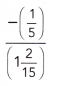
Answer:
Given,
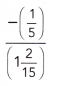
–\(\frac{1}{5}\) ÷ 1\(\frac{2}{15}\)
–\(\frac{1}{5}\) ÷ \(\frac{17}{15}\)
= -(1 × 15)/(5 × 17)
= –\(\frac{3}{17}\)
Solve. Show your work.
Question 33.
David hiked 15\(\frac{9}{10}\) miles on Saturday and 6\(\frac{7}{10}\) miles on Sunday. How much farther did David bike on Saturday than on Sunday?
Answer:
David hiked 15\(\frac{9}{10}\) miles on Saturday and 6\(\frac{7}{10}\) miles on Sunday.
15\(\frac{9}{10}\) – 6\(\frac{7}{10}\) = 9 \(\frac{1}{5}\)
Question 34.
A recipe calls for \(\frac{3}{4}\) cup of flour, but Kelli has only \(\frac{1}{4}\) cup of flour. How much more flour does she need?

Answer:
Given,
A recipe calls for \(\frac{3}{4}\) cup of flour, but Kelli has only \(\frac{1}{4}\) cup of flour.
\(\frac{3}{4}\) – \(\frac{1}{4}\) = \(\frac{1}{2}\)
Thus Kelli needs \(\frac{1}{2}\) cup of flour.
Question 35.
A weather report showed that the rainfall in Janesville was 2\(\frac{2}{3}\) inches during the first half of January. At the end of January, the total rainfall was 3\(\frac{1}{4}\) inches. How much did it rain in the second half of January?
Answer:
Given,
A weather report showed that the rainfall in Janesville was 2\(\frac{2}{3}\) inches during the first half of January.
At the end of January, the total rainfall was 3\(\frac{1}{4}\) inches.
3\(\frac{1}{4}\) – 2\(\frac{2}{3}\)
Convert from mixed fraction to the improper fraction
\(\frac{13}{4}\) – \(\frac{8}{3}\)
LCD of 4 and 3 is 12
\(\frac{39}{12}\) – \(\frac{32}{12}\) = \(\frac{7}{12}\)
Question 36.
The sum of two rational numbers is 5\(\frac{1}{2}\). If one of the numbers is 6\(\frac{3}{14}\), find the other number.
Answer:
The sum of two rational numbers is 5\(\frac{1}{2}\). If one of the numbers is 6\(\frac{3}{14}\)
x + 6\(\frac{3}{14}\) = 5\(\frac{1}{2}\)
x = 5\(\frac{1}{2}\) – 6\(\frac{3}{14}\)
x = 5 + \(\frac{1}{2}\) – 6 – \(\frac{3}{14}\)
x = -1 + \(\frac{2}{7}\) = –\(\frac{5}{7}\)
Question 37.
MathJournal Peter adds \(\frac{1}{a}\) + \(\left(-\frac{1}{b}\right)\) and says the answer is \(\frac{1}{a-b}\). Give an example to show that Peter is wrong.
Answer:
\(\frac{1}{a}\) + \(\left(-\frac{1}{b}\right)\)
\(\frac{1}{a}\) – \(\frac{1}{b}\)
LCD of a and b is ab
\(\frac{b}{ab}\) – \(\frac{a}{ab}\)
\(\frac{b-a}{ab}\)
By this we can say that Peter is wrong.
Question 38.
MathJournal Jo multiplies two mixed numbers, -4\(\frac{3}{5}\) and 1\(\frac{2}{7}\) as follows:
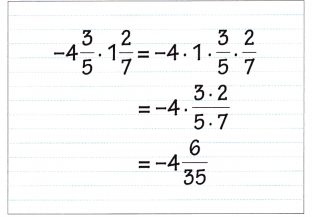
Describe Jo’s mistakes. What is the correct answer?
Answer:
-4\(\frac{3}{5}\) × 1\(\frac{2}{7}\)
Convert from mixed fraction to the improper fraction
–\(\frac{23}{5}\) × \(\frac{9}{7}\)
–\(\frac{207}{35}\)
-5\(\frac{32}{35}\)
Question 39.
A clock’s battery is running low. Every 6 hours, it slows down by \(\frac{1}{2}\) hour. By how much does it slow down in 1 hour?
Answer:
If its running low and every six hours it slows down half an hour, we need to divide 6 from 1/2.
6 divided by 1/2 is 12
It will slow down 12 minutes every hour.
Question 40.
A weighs 5\(\frac{1}{2}\) pounds and package B weighs 1\(\frac{1}{4}\) pounds. Find the average weight of the two packages.
Answer:
Given,
A weighs 5\(\frac{1}{2}\) pounds and package B weighs 1\(\frac{1}{4}\) pounds.
5\(\frac{1}{2}\) + 1\(\frac{1}{4}\) = 6 \(\frac{3}{4}\)
Convert from mixed fraction to the improper fraction
6 \(\frac{3}{4}\) = \(\frac{27}{4}\)
Average of two packets
\(\frac{27}{4}\) ÷ 2 = \(\frac{27}{8}\) = 3 \(\frac{3}{8}\)
Question 41.
A scientist measured the weight of some damp soil. After exposing the soil to the air for 4\(\frac{1}{2}\) weeks, the scientist found that the weight had decreased by 5\(\frac{1}{8}\) ounces. Find the average weight loss per week.
Answer:
Let the weight loss per week is x
A scientist measured the weight of some damp soil. After exposing the soil to the air for 4\(\frac{1}{2}\) weeks, the scientist found that the weight had decreased by 5\(\frac{1}{8}\) ounces.
4\(\frac{1}{2}\) weeks = 5\(\frac{1}{8}\)
1 week = x
x × 4\(\frac{1}{2}\) = 5\(\frac{1}{8}\)
x = 5\(\frac{1}{8}\) ÷ 4\(\frac{1}{2}\)
x = \(\frac{41}{8}\) ÷ \(\frac{9}{2}\)
x = 1 \(\frac{5}{36}\) ounces
Question 42.
A plank measures 4\(\frac{3}{4}\) feet. Elizabeth cuts off \(\frac{2}{5}\) of the plank. How long is the plank now?
Answer:
Given,
A plank measures 4\(\frac{3}{4}\) feet.
Elizabeth cuts off \(\frac{2}{5}\) of the plank.
4\(\frac{3}{4}\) – \(\frac{2}{5}\) = 4 \(\frac{7}{20}\)
Thus the plank is 4 \(\frac{7}{20}\) feet long now.