Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 6 Lesson 6.4 Comparing Two Functions to score better marks in the exam.
Math in Focus Grade 8 Course 3 A Chapter 6 Lesson 6.4 Answer Key Comparing Two Functions
Math in Focus Grade 8 Chapter 6 Lesson 6.4 Guided Practice Answer Key
Complete.
Question 1.
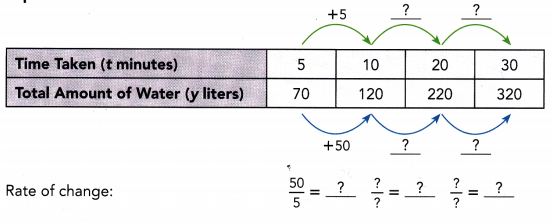
Water is pumped into two aquariums, P and Q. The tables show two functions relating the total amount of water, y liters, and the time taken, t minutes, to pump the water into each aquarium.
a) Use a verbal description to compare the two functions.
Aquarium P
Aquarium Q
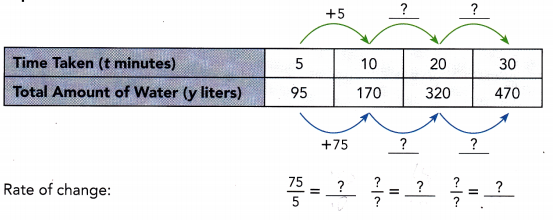
Both functions are 
and functions. The function for Aquarium has a greater rate of change than the function for Aquarium .
Answer:
Both functions are linear and increasing functions. The function for Aquarium Q has a greater rate of change than the function for Aquarium P.
b) Write an algebraic equation to represent each function. Then write the initial input and output values of each function.
Aquarium P
Use the ordered pair (5, 70) and the rate of change, , to find the value of the y-intercept, b.
Linear function:
So, the algebraic equation for Aquarium P is y = .
Answer:
Let the input be t and the output be y
y = mt + b
Substitute the values for m, t and y
70 = 10(5) + b
70 = 50 + b
b = 70 – 50
b = 20
Aquarium Q
Use the ordered pair (10, 170) and the rate of change, , to find the value of the y-intercept, b.
Linear function:
So, the algebraic equation for Aquarium Q is y = .
Both functions have an initial output value of corresponding to an initial input value of 0.
Answer:
Let the input be t and the output be y
y = mt + b
Substitute the values for m, t and y
170 = 10x + 20
170 – 20 = 10x
10x = 150
x = 150/10
x = 15
c) Which of the two aquariums, P and Q, is filled with water more quickly?
Comparing the rates of change for the two shops, Aquarium has a . rate of change. This means that Aquarium will be filled with water more quickly.
Answer:
Comparing the rates of change for the two shops, Aquarium Q has a greater. rate of change. This means that Aquarium Q will be filled with water more quickly.
Complete.
Question 2.
Two classes, A and B, compare the amount of donations they will raise for a charity by participating in a walkathon. The amount of donations they will raise, y dollars, is a function of the distance the students walk, x miles.
Class A
Class B
Amount of donations: y = 20x + 50
a) Write an algebraic equation to represent the table of values representing the amount of donations Class A will raise for the charity.
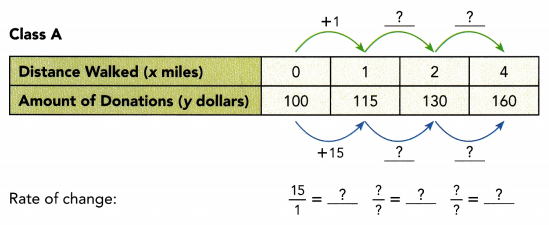
The algebraic equation is y = .
Answer:
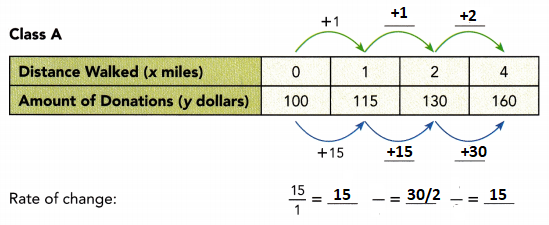
The algebraic equation is y = 15x + 100
b) Use a verbal description to compare the two functions.
Both functions are and functions. Comparing the two equations, because > 50, Class raises a greater amount of money at first.
Comparing the rates of change shows that Class A will raise $ for each mile the students walk, and Class B will raise $ for each mile the students walk. So, the amount of donations Class will raise increases more quickly than the amount of donations Class will raise.
Answer:
Both functions are linear and increasing functions. Comparing the two equations, because 100 > 50, Class A raises a greater amount of money at first.
Comparing the rates of change shows that Class A will raise $ 15 for each mile the students walk, and Class B will raise $ 20 for each mile the students walk. So, the amount of donations Class B will raise increases more quickly than the amount of donations Class A will raise.
Math in Focus Course 3A Practice 6.4 Answer Key
Tell whether the equation y = -2x + 3 can represent each of the following functions.
Question 1.
Answer: Yes
y = -2x + 3
y = -2(2) + 3
y = -4 + 3
y = -1
y = -2(3) + 3
y = -6 + 3
y = -3
y = -2x + 3
y = -2(-1) + 3
y = 2 + 3
y = 5
Question 2.
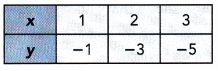
Answer: No
Question 3.
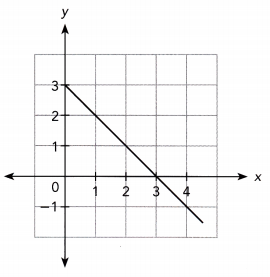
Answer: No
Tell whether each function can represent the table of values.
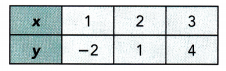
Question 4.
y = 3x – 4
Answer: No
Question 5.
y = 2x – 5
Answer: No
Question 6.
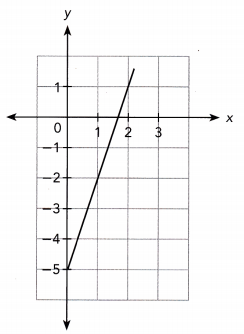
Answer: yes
Tell whether each function represents the verbal description.
Bryan has $30 in savings at first. He wants to save $5 per month beginning this month. y represents his total savings, in dollars, and x represents the number of months he saves.
Question 7.
Answer: No
Question 8.
y = 30 + 5x
Answer: Yes
Question 9.
y = 30 – 5x
Answer: No
Solve. Show your work.
Question 10.
Clara and Elaine have some savings. The functions that relate each girl’s total savings, y dollars, to the number of months, x, that each girl saves are as follows:
Clara: y = 380 + 20x
Elaine: y = 400 + 15x
a) Use a verbal description to compare the two functions.
Answer:
Clara has 380 dollars in her savings. She wants to save 20$ from this month.
Elaine has 400 dollars in her savings. She wants to save 15$ from this month.
b) Graph the two functions on the same coordinate plane. Use 1 unit on the horizontal axis to represent 1 month for the x interval from 0 to 8, and 1 unit on the vertical axis to represent $20 for the y interval from 380 to 540. For each function, draw a line through the points.
Answer:
We graph both functions:
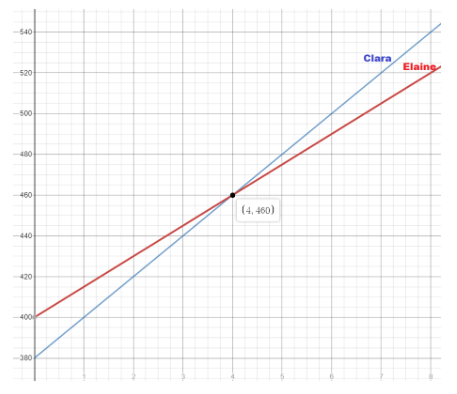
c) Who will save more over time? Explain.
Answer: Clara saves more money than Elaine.
Question 11.
The director of a theater group wants to rent a theater for an upcoming show. The director has two options for paying for the rental. Both options involve paying a deposit and then paying an additional charge for each ticket sold. For each function, the total amount the director would pay, y dollars, is a function of the number of tickets sold, x.
Option A
Option B
A deposit of $800 plus $6 per ticket sold.
a) Write an algebraic equation to represent each function.
Answer:
Option A: y = 1000 + 4x
Option B: y = 800 + 6x
b) Use a verbal description to compare the two functions.
Answer:
Both functions are a linear and increasing functions. Comparing the two equations, because 1000 > 800, Option A costs more at first. Comparing the rates of change shows that the total fee for option A increases by $4 for each ticket sold, and the total fee for option B increases by $6 for each ticket sold, and the total fee for the director will pay for Option B will increase more quickly than the total fee for Option A as the number of tickets sold increases.
c) Math Journal The theater seats up to 200 people. If the director expects to sell all the tickets, which of the two options, A or B, offers a better deal? Explain.
Answer:
The total fee for option A is lower than the total fee for Option B when all the tickets are sold.
Question 12.
A factory needs to grate at least 8,000 pounds of cheese each day.
The manager of the factory needs to buy a new cheese grating machine. She is trying to decide between Machine A and Machine B. The functions shown describe how many pounds of cheese, y, are left t minutes after each machine starts grating an initial batch of cheese.
Machine A
The function is y = 2,000 – 80t. The initial value of 2,000 pounds represents the weight of each batch of cheese to be grated. After one batch is grated, another batch can be added to the machine.
Machine B
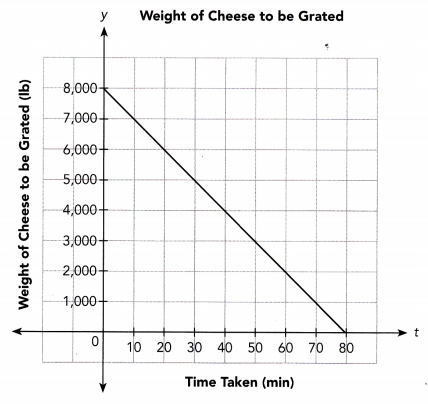
a) Write an algebraic equation to represent the function for Machine B.
Answer:
The graph of the function for Machine B passes through the points (0, 8000) and (80, 0) We determine the slope of the line using the slope formula:
m = \(\frac{0-8000}{80-0}\)
= \(\frac{-8000}{80}\)
= -100
The graph of the function for Machine B passes through the point (0, 8000), therefore the y-intercept is:
b = 8000
The equation for Machine B is:
y = -100t + 8000
b) Math Journal Assuming that the machines are of the same quality, which machine would you recommend that the manager buy? Explain.
Answer:
The equation for Machine A is:
y = -80t + 2000
We graph the two functions:
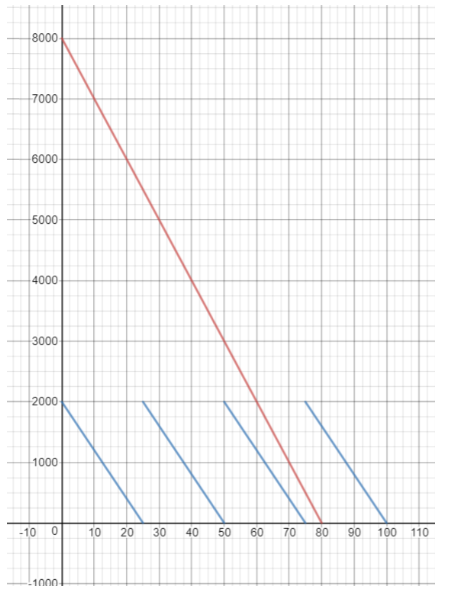
We notice that with the Machine from Option A the manager would grate 4 • 2000 = 8000 pounds of cheese in 100 minutes, while with the Machine from Option B he can grate 8000 pounds in only 80 minutes, so Option B is better.
Brain @ Work
Five teachers at a school brought a group of students to a museum exhibit.
For group tours involving any number of adults and at least 5 students, the museum offers three packages, A, B, and C. The functions shown below represent the total admission fee, y dollars, that five teachers and x students will pay to see the exhibit.
Package A
Each adult ticket costs $30 and each student ticket costs $15.
Package B
Package C
Each adult ticket costs $60 and each student ticket costs $12.
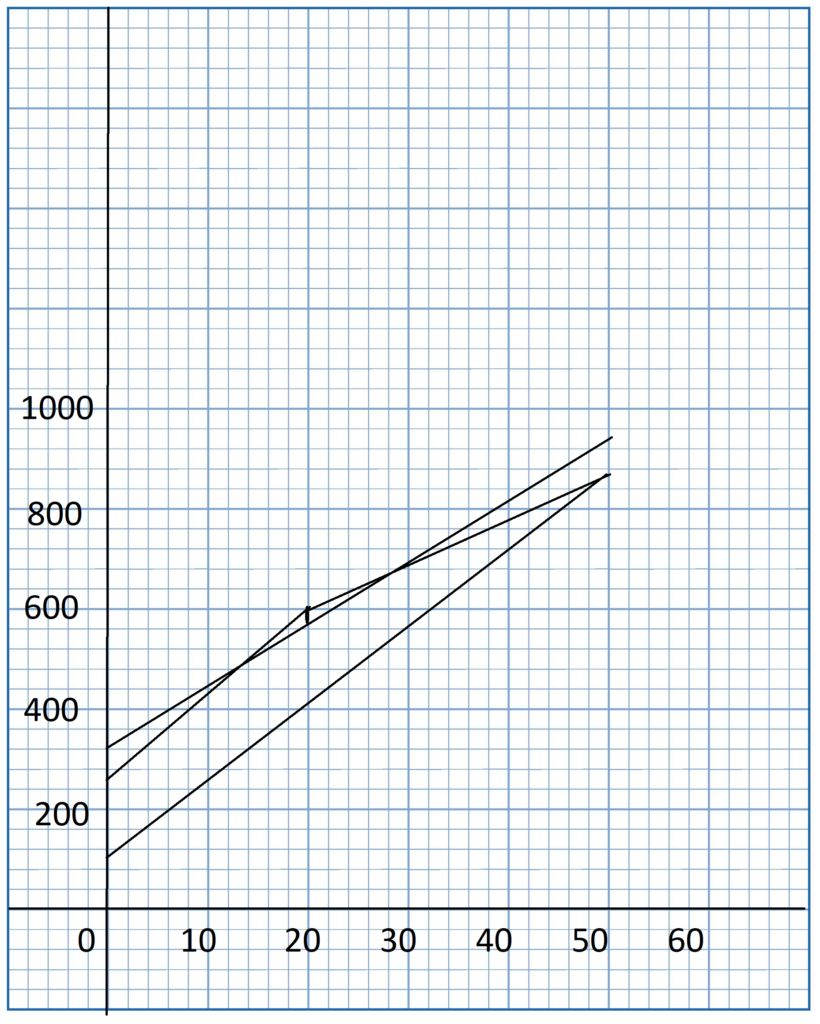
Question 1.
Use an algebraic equation to represent each of the three functions.
Answer:
Equation for Package A: y = 150 + 15x
Package B: y = 250 + 14x
Package C: y = 300 + 12x
Question 2.
Graph the three functions on the same coordinate plane. Use 1 unit on the horizontal axis to represent 5 students for the x interval from 0 to 50, and 1 unit on the vertical axis to represent $50 for the y interval from 150 to 950. For each function, draw a line through the points.
Answer:
