This handy Math in Focus Grade 5 Workbook Answer Key Cumulative Review Chapters 14 and 15 provides detailed solutions for the textbook questions.
Math in Focus Grade 5 Cumulative Review Answer Key for Chapters 14 and 15
Concepts and Skills
Name each solid. Then write the number of faces and vertices, and the shapes of the faces. (Lesson 14.1)
Question 1.
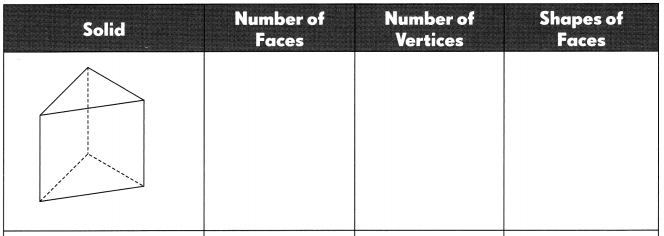
Answer:
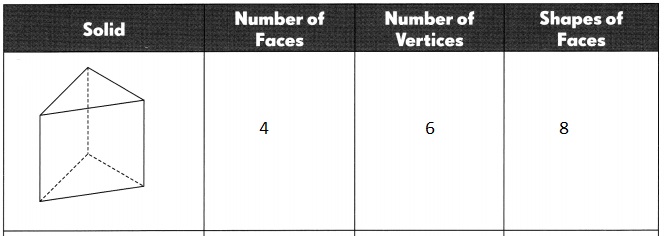
Explanation:
Given solid triangular prism shape has number of faces -4,
number of vertices-6 and shapes of faces- 8.
Question 2.
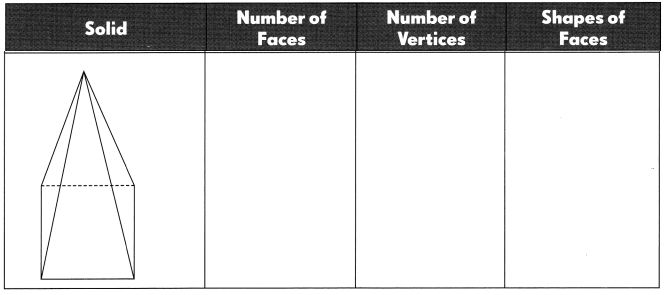
Answer:
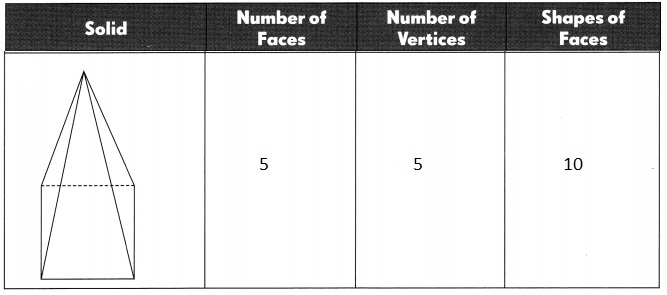
Explanation:
Given solid triangular prism shape has number of faces – 5,
number of vertices – 5 and shapes of faces – 10.
Name the solid formed from each net. (Lesson 14.1)
Question 3.
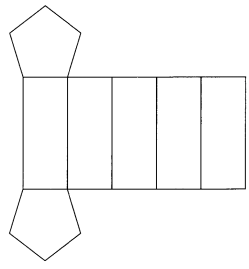
Answer:
Explanation:
Given solid formed with the net is pentagonal prism.
Question 4.
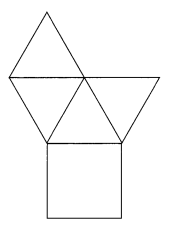
Answer:
Explanation:
Given solid formed with the net is square based pyramid.
Complete. (Lesson 14.2)
Question 5.
A ___ has two parallel and congruent bases that are joined by a curved surface.
Answer:
Cylinder,
Explanation:
A cylinder is formed by two parallel congurent circular bases and a curved surface that connects
the bases.
Question 6.
A ____ does not have any edges or vertices, and has the same distance
across any line through its center.
Answer:
Circle,
Explanation:
A circle does not have any edges or vertices, and has the same distance
across any line through its center.
Question 7.
A _____________ has one vertex, a circular base, and a curved surface.
Answer:
Cone,
Explanation:
A cone has one vertex, a circular base, and a curved surface.
Question 8.
A sphere has no ___ and________ surfaces.
Answer:
Faces, Edges, Vertices,
Explanation:
A sphere has no faces, edges, vertices and surfaces.
Find how many unit cubes are used to build each solid. (Lesson 15.1)
Question 9.
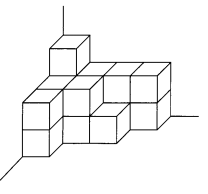
_____________ unit cubes
Answer:
16 unit cubes,
Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
we have 16 unit cubes,
So, the volume of a 16 unit cubes = 16 X (Side × Side × Side),
= 16 X (1 unit × 1 unit × 1 unit),
= 16 unit cubes.
Question 10.
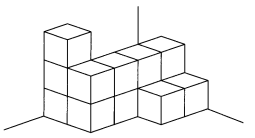
_____________ unit cubes
Answer:
13 unit cubes,
Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
we have 13 unit cubes,
So, the volume of a 13 unit cubes = 13 X (Side × Side × Side),
=13 X (1 unit × 1 unit × 1 unit),
= 13 unit cubes.
Draw a cube with edges 2 times as long as the edges of this unit cube. (Lesson 15.2)
Question 11.
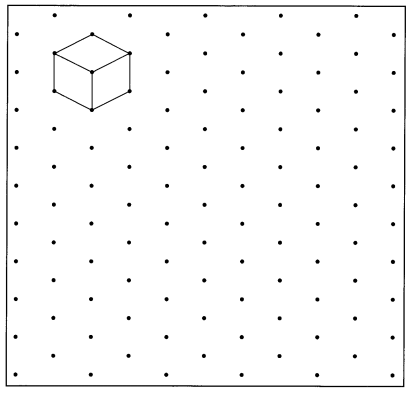
Answer:
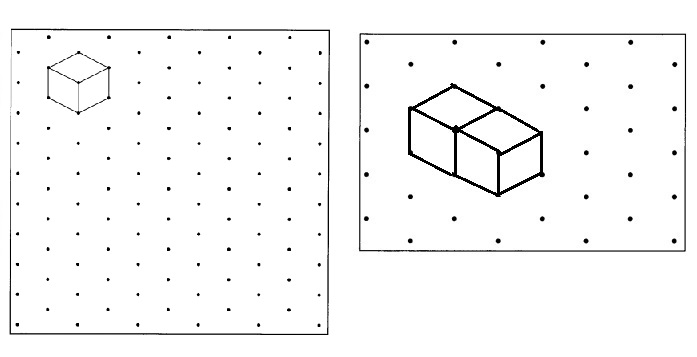
Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
Shown the volume of a unit cube = Side × Side × Side,
= 2 units × 1 unit × 1 unit,
= 2 units cubes.
Complete the drawing of this rectangular prism. (Lesson 15.2)
Question 12.
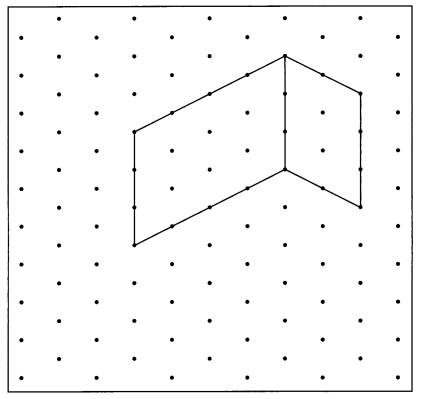
Answer:
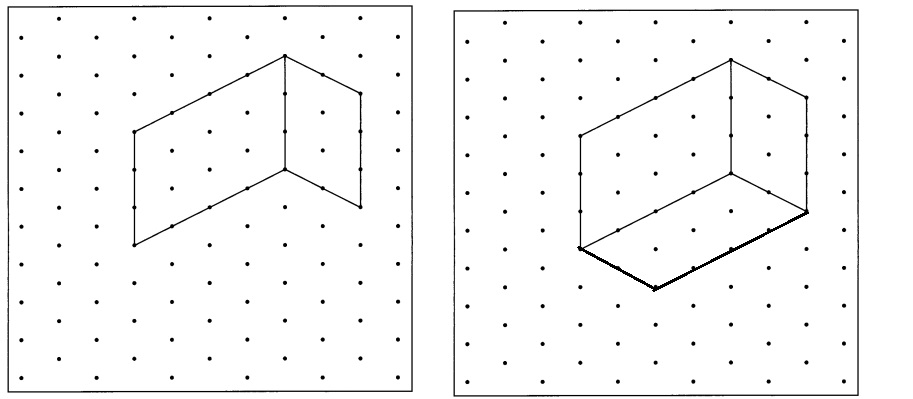
Explanation:
Drawn one rectangular prism on the dot paper,
As given rectangular prism has 4 units X 2 units X 3 units =
24 unit cubes rectangular prism.
Find the surface area of each prism. (Lesson 15.3)
Question 13.
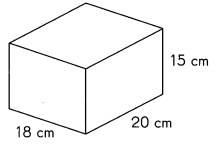
Answer:
The surface area of rectangular prism is 1860 cm2,
Explanation:
As the surface area of rectangular prism is
2 X [(width X length) + (height X length) + (height X width)],
= 2 X [(18 cm X 20 cm) + (20 cm X 15 m) + (15 cm X 18 cm)],
= 2 X [(360 cm2) + (300 cm2) + (270 cm2)]
= 2 X [ 930 cm2],
= 1860 cm2.
Question 14.
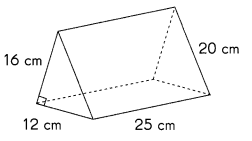
Answer:
Surface area of triangular prism = 1,392 cm2,
Explanation:
2 × \(\frac{1}{2}\) × 12 cm × 16 cm = 192 cm2,
12 cm × 25 cm = 300 cm.2
16 cm × 25 cm = 400 cm.2
20 cm × 25 cm = 500 cm.2
192 cm 2+ 300 cm2 + 400 cm2 + 500 cm.2 = 1,392 cm2,
Surface area of triangular prism = 1,392 cm2.
These solids are built using 1-inch cubes. Find and compare their volumes. (Lesson 15.4)
Question 15.
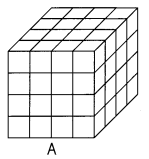
Length = _____4_______ in.
Width = _____4_______ in.
Height = _____4______ in.
Volume = _____64_____ in.3
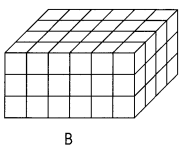
Length = ______6______ in.
Width = _______4_____ in.
Height = ______3_____ in.
Volume = _____72_____ in.3
Solid _______A____ has less volume than solid ____B______.
Answer:
Volume of given cube A has 64 cubic units,
Volume of given cube B has 72 cubic units,
Solid A has less volume than solid B,
Explanation:
As we know volume of solid is l X w X h,
Total surface area of A is 4 in X 4 in X 4 in = 64 cubic units.
Total surface area has 6 in X 4 in X 3 in = 72 cubic units.
Given cube contains 2 less small unit cubes so first we
calculate total surface and subtract missing cubic uints,
therefore, Solid A has less volume than solid B,
Find the volume of each rectangular prism. (Lesson 15.5)
Question 16.
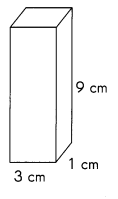
Answer:
Volume of given rectangular prism is 27 cm3,
Explanation:
Given Length = 3 cm, Width = 1 cm and Height = 9 cm,
Volume of the rectangular prism is lwh = 3 cm X 1 cm X 9 cm = 27 cm3.
Question 17.
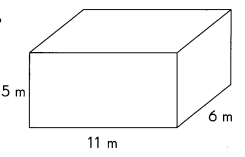
Answer:
Volume of given rectangular prism is 330 m3,
Explanation:
Given Length = 11 m, Width = 6 m and Height =5 m,
Volume of the rectangular prism is lwh = 11 cm X 6 m X 5 m = 330 m3.
Find the volume of water in each container in liters and milliliters. (Lesson 15.5)
Question 18.
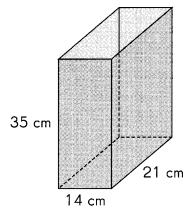
Answer:
Volume of given rectangular prism is 10,290 cm3 which is equal to 10,290 milliliters,
Explanation:
Given Length = 14 cm, Width = 21 cm and Height = 35 cm,
Volume of the rectangular prism is lwh = 14 cm X 21 cm X 35 cm = 10,290 cm3.
as 1 cubic centimeter is equal to 1 milliliters therefore volume of given
rectangular prism is 10,290 cm3 which is equal to 10,290 milliliters.
Question 19.
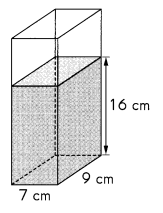
Answer:
Volume of given rectangular prism is 1,008 cm3 which is equal to 1,008 milliliters,
Explanation:
Given Length = 7 cm, Width = 9 cm and Height = 16 cm,
Volume of the rectangular prism is lwh = 7 cm X 9 cm X 16 cm = 1,008 cm3.
as 1 cubic centimeter is equal to 1 milliliters therefore volume of given
rectangular prism is 1,008 cm3 which is equal to 1,008 milliliters.
Problem Solving
Solve. Show your work.
Question 20.
The length of a rectangular block is 20 inches. Its width is half its length.
Its height is half its width. What is the surface area of the block?
Answer:
The surface area of a rectangular prism is 1860 cm2,
Explanation:
Given the length of a rectangular block is 20 inches. Its width is half its length.
So width is 10 inches, Its height is half its width is 5 inches
The surface area of the block is
2 X [(width X length) + (height X length) + (height X width)],
= 2 X [(10 in X 20 in) + (5 in X 20 in) + (5 in X 10 in)],
= 2 X [(200 in2) + (100 in2) + (50 in2)]
= 2 X [ 350 in2],
= 700 in2.
Solve. Show your work.
Question 21.
A rectangular piece of poster board measures 70 centimeters by 50 centimeters.
The net of a cube with 12-centimeter edges is cut from it.
What is the area of the poster board left?
Answer:
The area of the poster board left 2,636 cm2,
Explanation:
Given a rectangular piece of poster board measures 70 centimeters by 50 centimeters,
70 cm X 50 cm = 3,500 cm2, The net of a cube with 12-centimeter edges is cut from it.
Volume of cube is 6 X 12 cm X 12 cm = 864 cm2, therefore the area of the poster board
left is 3,500 cm2 – 864 cm2 = 2,636 cm2.
Question 22.
A rectangular prism is 15 inches long and 12 inches high.
Its width is \(\frac{3}{5}\) its length. Find its volume.
Answer:
Volume of a rectangular prism is 1,620 in3,
Explanation:
Given a rectangular prism is 15 inches long and 12 inches high.
Its width is \(\frac{3}{5}\) its length. So length is
\(\frac{3}{5}\) X 15 = \(\frac{3 X 15}{5}\) = 9 inches,
therefore volume is 15 inches X 12 inches X 9 inches = 1,620 in3.
Solve. Show your work.
Question 23.
Three cubes with edges measuring 5 inches are stacked on top of one another.
What is the total volume of the 3 cubes?
Answer:
The total volume of the 3 cubes is 375 in3,
Explanation:
Given three cubes with edges measuring 5 inches are stacked on top of one another.
3 X (5 inches X 5 inches X 5 inches) = 3 X (125 in3) = 375 in3.
Question 24.
The rectangular container shown contains 2 liters of water.
How much more water must be added to fill the container completely?
Give your answer in liters.
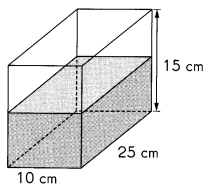
Answer:
1,750 cubic cm more water must be added to fill the container completely,
Explanation:
Given rectangular cuboid volume is 10 cm X 25 cm X 15 cm = 3,750 cubic cms as
the rectangular container shown contains 2 liters of water.
Equal to 2 X 1000 = 2,000 cubic cms so much more water must be
added to fill the container completely is 3,750 cubic cm – 2,000 cubic cm = 1,750 cubic cm.
Solve. Show your work.
Question 25.
A container is 28 centimeters long, 1 4 centimeters wide, and 10 centimeters high.
It is half-filled with juice. Kathy pours 500 milliliters of water into the
container to make a juice drink. Find the volume of juice drink in the container now.
Give your answer in liters and milliliters.
Answer:
Given a container is 28 centimeters long, 1 4 centimeters wide, and 10 centimeters high.
Volume of container is 28 cm X 14 cm X 10 cm = 3,920 cubic centimeters,
It is half-filled with juice. \(\frac{1}{2}\) X 3,920 = 1,960 cubic centimeters or
1,960 milliliters now Kathy pours 500 milliliters of water into the container
to make a juice drink. Therefore the volume of juice drink in the container now is
1,960 milliliters + 500 milliliters = 2,460 milliliters and 1,000 milliliters = 1 liter,
So 2 L 460 milliliters.
Question 26.
The fish tank shown is filled with 4 liters of water per minute from a faucet.
How long does it take to fill the tank completely?
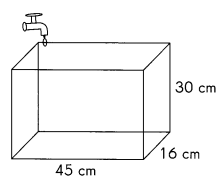
Answer:
Long does it will take to fill the tank completely is 6 minutes,
Explanation:
Given the tank has length is 45 cm, width is 16 cm and height is 30 cm,
volume = 45 cm X 16 cm X 30 cm = 2,16,00 cubic cms 21 liters 600 milliliters,
as fish tank shown is filled with 4 liters of water per minute from a faucet,
Long does it will take to fill the tank completely is 21,600 ÷ 4 = 5 minutes 400 ≈ 6 minutes.
Solve. Show your work.
Question 27.
A tank with a square base with edges measuring 20 centimeters and a
height of 36 centimeters is \(\frac{2}{3}\)-filled with water.
Each minute, 2 liters of water leak out of the tank through a crack in the bottom.
How long does it take for all the water to leak out?
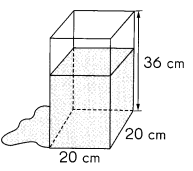
Answer:
It will be approximately 5 minutes long for water to leak out,
Explanation:
Given a tank with a square base with edges measuring 20 centimeters
and a height of 36 centimeters, So volume is
20 cm X 20 cm X 36 cm = 14,400 cubic centimeters ,
and tank is filled with \(\frac{2}{3}\)-filled with water means
\(\frac{2}{3}\) X 14,400 = 9,600 milliliters and each minute 2 liters of
water leak out of the tank through a crack in the bottom is
9,600 ÷ 2,000 = 4.8 ≈ 5minutes.
Read More: