Math in Focus Grade 5 Chapter 6 Practice 1 Answer Key Finding the Area of a Rectangle with Fractional Side Lengths

Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 6 Practice 1 Finding the Area of a Rectangle with Fractional Side Lengths to score better marks in the exam.

Math in Focus Grade 5 Chapter 6 Practice 1 Answer Key Finding the Area of a Rectangle with Fractional Side Lengths

Example

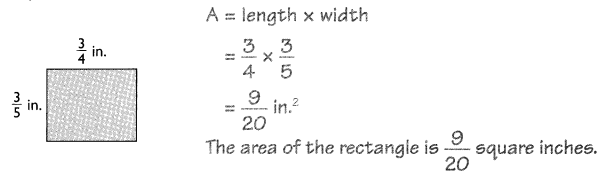
Question 1.

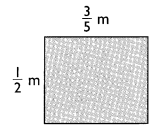
A = ____ × width
= ____ × \(\frac{1}{2}\)
= ___ m²
The area of the rectangle is ____ square meters.
Answer:
Area = length × width
A = 3/5 × 1/2
A = 3/10 m²
Explanation:
In the above image we can observe that length is 3/5 m and width is 1/2 m. The area of the rectangle is 3/10 square meters.

Question 2.

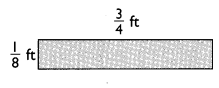
Answer:
Area = length × width
A = 3/4 × 1/8
A = 3/32 ft²
Explanation:
In the above image we can observe that length is 3/4 feet and width is 1/8 feet. The area of the rectangle is 3/32 square feet.

Find the area of each rectangle.

Question 3.

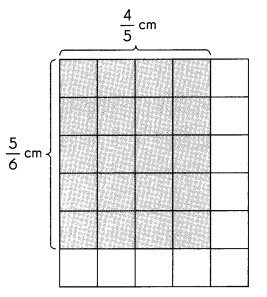
Answer:
Area = length × width
A = 4/5 × 5/6
A = 2/3 cm²
Explanation:
In the above image we can observe that length is 4/5 cm and width is 5/6 cm. The area of the rectangle is 2/3 square centimeters.

Question 4.

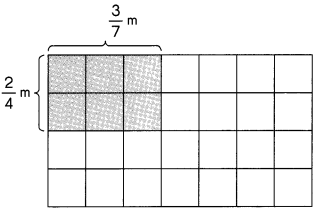
Answer:
Area = length × width
A = 3/7 × 2/4
A = 3/14 m²
Explanation:
In the above image we can observe that length is 3/7 m and width is 2/4 m. The area of the rectangle is 3/14 square meters.

Question 5.
A 1 -meter square plot of land is covered by a rectangular patch of grass that measures \(\frac{4}{7}\) meter by \(\frac{2}{3}\) meter. What is the area of the patch of grass?

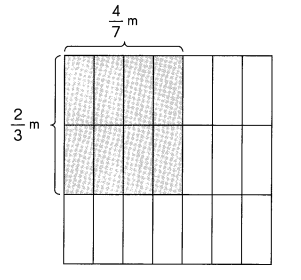
Answer:
Area = length × width
A = 4/7 × 2/3
A =8/21 m²
Explanation:
In the above image we can observe that length is 4/7 m and width is 2/3 m. The area of the rectangular patch of grass is 8/21 square meters.

Question 6.
Find the area of the top of a rectangle bedside table with a length of \(\frac{3}{4}\) yard and width that is \(\frac{1}{6}\) yard less than the length.
Answer:
Length = 3/4 yard
width = (3/4 – 1/6) yard
= 7/12 yard
Area = length × width
A = 3/4× 7/12
A = 7/16 yard²
Explanation:
The area of the top of a rectangle bedside table with a length of 3/4 yard and width of 7/12 yard is 7/16 square yards.

Find the area of each composite figure.

Question 7.

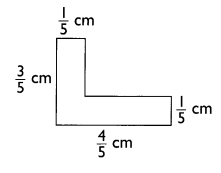
Answer:

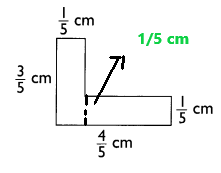
Area of the rectangle = length ×  width
A = (3/5 ×  1/5) + (3/5 ×  1/5)
A = 3/25 + 3/25
A = 6/25 cm²
Explanation:
To calculate the area we have divided the image into two rectangles.
Length and width of first rectangle are 3/5 cm and 1/5 cm.
So, Area of first rectangle = 3/5 × 1/5 = 3/25 cm²
Length of second rectangle is 3/5 cm (4/5 – 1/5 ) and width is 1/5 cm.
So, Area of second rectangle = 3/5 × 1/5 = 3/25 cm²
Hence, total area of the image = 3/25 + 3/25 = 6/25 cm²
Question 8.

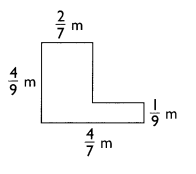
Answer:

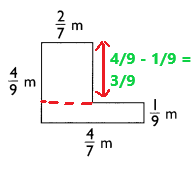
Explanation:
Area of the rectangle = length ×  width
A = (3/9 ×  2/7) + (4/7 ×  1/9)
A = 6/63 + 4/63
A = 10/63 m²
Explanation:
To calculate the area we have divided the image into two rectangles.
Length of first rectangle is 3/9 m (4/9 – 1/9 ) and width is 2/7 m.
So, Area of first rectangle = 3/9 × 2/7 = 6/63 m²
Length and width of second rectangle are 4/7 m and 1/9 m.
So, Area of second rectangle =4/7 × 1/9 = 4/63 m²
Hence, total area of the image = 6/63 + 4/63 = 10/63 m²

Question 9.

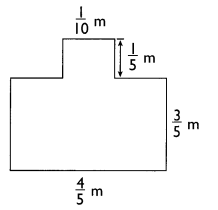
Answer:

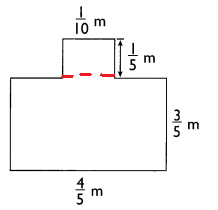
Area of the rectangle = length ×  width
A = (4/5 ×  3/5) + (1/10×  1/5)
A = 12/25 + 1/50
A = (24 + 1)/ 50
A = 1/2 m²
Explanation:
To calculate the area we have divided the image into two rectangles.
Length of first rectangle is 4/5 m and width is 3/5 m.
So, Area of first rectangle = 4/5 × 3/5 = 12/25 m²
Length and width of second rectangle are 1/10 m and 1/5 m.
So, Area of second rectangle = 1/10 × 1/5 = 1/50 m²
Hence, total area of the image = 12/25+ 1/50 = (24 + 1)/50 = 1/2 m²

Question 10.

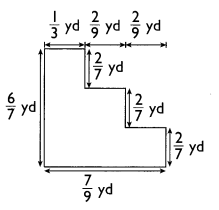
Answer:

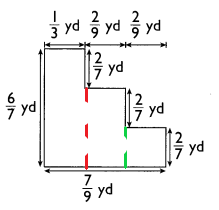
Area of the rectangle = length ×  width
A = (6/7 ×  1/3) + (4/7 ×  2/9) + (2/7 ×  2/9)
A = 2/7 + 8/63 + 4/63
A = (18 + 8 + 4)/63
A = 30/63 Yd²
Explanation:
To calculate the area we have divided the image into three rectangles.
Length and width of first rectangle are 6/7 yard and 1/3 yard.
So, Area of first rectangle =6/7 × 1/3 = 2/7 yd²
Length and width of second rectangle are 4/7 yard and 2/9 yard.
So, Area of second rectangle = 4/7 × 2/9 = 8/63 yd²
Length of third rectangle is 2/7 yard and width is 2/9 yard.
So, Area of third rectangle = 2/7 × 2/9 = 4/63 yd²
Hence, total area of the image = 2/7 + 8/63 + 4/63 = 30/63 yd²

Find the area of the shaded part.

Question 11.

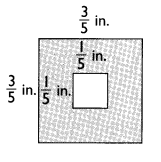
Answer:
Area of the square = length ×  width
A = (3/5 ×  3/5) – (1/5 × 1/5)
A = 9/25 – 1/25
A = 8/25 in²
Explanation:
To calculate the area we have subtract inner square from outer square.
Length and width of outer square are 3/5 in and 3/5 in.
So, Area of outer square = 3/5 × 3/5 = 9/25 in²
Length and width of inner square are 1/5 in and 1/5 in.
So, Area of inner square = 1/5 × 1/5 = 1/25 in²
Hence, area of the shaded part = 9/25 – 1/25 = 8/25 in²

Question 12.

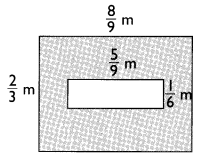
Answer:
Area of the rectangle = length ×  width
A = (8/9 × 2/3) – (5/9 × 1/6)
A = 16/27 – 5/54
A = (32 – 5)/54
A = 1/2 m²
Explanation:
To calculate the area we have subtract inner rectangle from outer rectangle.
Length and width of outer rectangle are 8/9 m and 2/3 m.
So, Area of outer rectangle =8/9 × 2/3 = 16/27 m²
Length and width of inner rectangle are 5/9 m and 1/6 m.
So, Area of inner rectangle = 5/9 × 1/6 = 5/54 m²
Hence, area of the shaded part = 16/27 – 5/54 = 27/54 = 1/2m²

Read More:

Easy Pivot Point Calculator