Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 4 Lesson 4.2 Solving Algebraic Equations to score better marks in the exam.
Math in Focus Grade 7 Course 2 A Chapter 4 Lesson 4.2 Answer Key Solving Algebraic Equations
Math in Focus Grade 7 Chapter 4 Lesson 4.2 Guided Practice Answer Key.
Solve.
Question 1.
6x + 2 = 8
6x + 2 = 8
6x + 2 – ![]() = 8 –
= 8 – ![]() Subtract
Subtract ![]() from both sides.
from both sides.
![]() =
= ![]() Simplify.
Simplify.
\(\frac{?}{?} x=\frac{?}{?}\) Divide both sides by ![]() .
.
x = ![]() Simplify.
Simplify.
Answer:
x =1
Explanation:
6x+2 =8
Subtract 2 on both sides.
6x + 2 – 2 = 8 -2
6x = 6
x =1
Let us consider second question, \(\frac{?}{?} x=\frac{?}{?}\)
Let us consider, a and b in the place of the “?” on both sides
(a/b)x = (a/b)
Divide (a/b) on both sides.
x =1
Question 2.
5 – 3x = 20
Answer:
x = -5
Explanation:
Let us consider the equation, 5 – 3x = 20
Subtract 5 both sides.
5 – 3x – 5 = 20 – 5
-3x = 15
put – on both sides to make x positive.
-(-3x) = -15
3x = -15
divide 3 on both sides to get the value of ‘x’
x = -5
Question 3.
4x – 3 + 0.5x = 1.5
Answer:
x = 1
Explanation:
4x – 3 + 0.5x = 1.5
Add all the variants of ‘x’
4.5x – 3 = 1.5
add 3 on both sides.
4.5x -3 + 3 = 1.5 + 3
4.5x = 4.5
divide 4.5 on both sides.
x= (4.5/4.5)
x = 1
Question 4.
\(\frac{9}{10}\)x – \(\frac{4}{5}\) = 1
Answer:
x = 2
Explanation:
(9/10)x – (4/5) = 1
Add (4/5) on both sides.
(9/10)x – (4/5) + (4/5) = 1 + (4/5)
(9/10)x = (9/5)
0.9x = 1.8
Divide (0.9) on both sides.
x = 1.8 ÷ 0.9
x = 2
Solve each equation. Check your solution.
Question 5.
11 – 4x = x + 16
11 – 4x = x + 16
11 – 4x – x = x + 16 – x Subtract x from both sides.
11 + ![]() = 16 Simplify.
= 16 Simplify.
11 + ![]() – 11 = 16 – 11 Subtract 11 from both sides
– 11 = 16 – 11 Subtract 11 from both sides
![]() = 5 Simplify.
= 5 Simplify.
\(\frac{?}{?} x=\frac{?}{?}\) Divide both sides by ![]() .
.
x = ![]() Simplify.
Simplify.
Answer:
-5x = 5
Explanation:
Given, 11 – 4x = x + 16
Subtract x from both sides.
11 – 4x – x = x + 16 – x
11 – 5x =16
Subtract 11 from both sides.
11 – 5x – 11=16 – 11
-5x = 5
x = -1
Let us consider second question, \(\frac{?}{?} x=\frac{?}{?}\)
Let us consider, a and b in the place of the “?” on both sides
(a/b)x = (a/b)
Substitute -1 in the place of x
(a/b)(-1) = (a/b)
Divide (a/b) on both sides.
= -1
Question 6.
3.4y – 5.2 = 3y + 2
Answer:
y = 18
Explanation:
Given, 3.4y – 5.2 = 3y + 2
(34/10)y – (52/10) = 3y + 2
Simplify (34/10) and (52/10), and bring 3y + 2 to another side.
(17/5)y – 26/5 – 3y – 2 = 0
get common divider to all.
17y – 26 – 5.(3y + 2) / 5 = 0
(17y – 26 – 15y – 10) / 5 = 0
(2y – 36 )/ 5 = 0
(2y – 36 ) = 0 × 5
2y – 36 = 0
2y = 36
y = 18
Question 7.
\(\frac{5}{9}\)y – \(\frac{1}{3}\) = \(\frac{2}{3}\)y + \(\frac{1}{3}\)
Answer:
y= -6
Explanation:
Given, (5/9)y – (1/3) = (2/3)y + (1/3)
Add (1/3) on both sides.
(5/9)y – (1/3) + (1/3)= (2/3)y + (1/3) + (1/3)
(5/9)y = (2/3)y + (2/3)
(5/9)y – (2/3)y = (2/3)
(5y – 3×2y)/9 = (2/3)
(5y – 6y)/9 = (2/3)
-y = (2/3) × 9
-y = 6
y= -6
Solve each equation. Check your solutions.
Question 8.
1.5(p + 3) = 18
Answer:
p = 9
Explanation:
Given, 1.5(p + 3) = 18
It can also be written as 1.5p + 4.5 = 18
Subtract 4.5 on both sides
1.5p + 4.5 – 4.5 = 18 -4.5
1.5p = 13.5
Divide 1.5 on both sides.
1.5p ÷ 1.5 = 13.5 ÷ 1.5
p = 9
Question 9.
\(\frac{1}{4}\)(q+ 1) = 9
Answer:
q = 35
Explanation:
Given, (1/4)(q + 1) = 9
multiply 4 on both sides.
(q + 1) = 36
Subtract 1 on both sides.
q +1 – 1 = 36 – 1
q = 35
Question 10.
2(x – 3) + 2 = 14
Answer:
x =9
Explanation:
Given, 2(x – 3) + 2 = 14
2x – 6 + 2 = 14
2x – 4 = 14
Add 4 on both sides
2x – 4 + 4 = 14 + 4
2x = 18
x =9
Question 11.
3(y – 1) + y = 1
Answer:
y =1
Explanation:
Given, 3(y – 1) + y = 1
3y – 3 + y = 1
4y – 3 = 1
Add 3 on the both sides
4y – 3 + 3 =1 + 3
4y = 4
y =1
Math in Focus Course 2A Practice 4.2 Answer Key
Solve each equation with variables on the same side.
Question 1.
4b – 2 = 6
Answer:
b = 2
Explanation:
Given, 4b – 2 = 6
Add 2 on the both sides.
4b – 2 + 2 = 6 + 2
4b = 8
b = 8 ÷ 4
b = 2
Question 2.
5x + 4 = 24
Answer:
x = 4
Explanation:
Given, 5x + 4 = 24
Subtract 4 on both sides.
5x + 4 – 4 = 24
5x = 20
Divide 5 on both sides
x = 20 ÷ 5
x = 4
Question 3.
7c – 11 = 17
Answer:
c = 4
Explanation:
Given, 7c – 11 = 17
Add 11 on both sides.
7c – 11 + 11 = 17 +11
7c = 28
Divide 7 on bot sides.
c = 28 ÷ 7
c = 4
Question 4.
18 = 3k – 3
Answer:
7 = k
Explanation:
Given, 18 = 3k – 3
Add 3 on both sides.
18 + 3 = 3k – 3 + 3
21 = 3K
Divide 3 on both sides.
21 ÷ 3 = 3k ÷ 3
7 = k
Question 5.
\(\frac{a}{4}\) – 1 = 3
Answer:
a = 16
Explanation:
Given, (a/4) -1 = 3
Add 1 on both sides.
(a/4) -1 + 1 = 3 + 1
(a/4) = 4
Multiply 4 on both sides.
(a/4) × 4 = 4 × 4
a = 16
Question 6.
\(\frac{2}{3}\)v = 2 – \(\frac{4}{3}\)
Answer:
v =1
Explanation:
Given, (2/3)v = 2 – (4/3)
(2/3)v = (2×3 -4)/3
(2/3)v = (6 – 4)/3
(2/3)v = (2/3)
Multiply (3/2) on both sides.
(2/3)v ×(3/2) = (2/3) ×(3/2)
v =1
Question 7.
\(\frac{5}{2}\)y + 8 =18
Answer:
y = 4
Explanation:
(5/2)y + 8 = 18
Subtract 8 on both sides.
(5/2)y + 8 – 8 = 18 – 8
(5/2)y = 10
Multiply 2 on both sides.
(5/2)y × 2 = 10 × 2
5y = 20
Divide 5 on both sides.
5y ÷ 5 = 20 ÷ 5
y = 4
Question 8.
\(\frac{3}{5}\)f – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Answer:
f = (5/3)
Explanation:
Given, (3/5)f – (1/2) = (1/2)
Add (1/2) on both sides.
(3/5)f – (1/2) + (1/2) = (1/2) + (1/2)
(3/5)f = 1
Multiply 5 on both sides.
(3/5)f × 5 = 1 × 5
3f = 5
Divide 3 on both sides.
f = (5/3)
Question 9.
4.5 + 0.2p = 6.1
Answer:
p = 8
Explanation:
Given, 4.5 + 0.2p = 6.1
Subtract 4.5 on both sides.
4.5 + 0.2p – 4.5 = 6.1 – 4.5
0.2p = 1.6
Divide 0.2 on both sides.
0.2p ÷ 0.2 = 1.6 ÷ 0.2
p = 8
Question 10.
1.5d + 3.2 = 9.2
Answer:
d = 4
Explanation:
Given, 1.5d + 3.2 = 9.2
Subtract 3.2 on both sides.
1.5d + 3.2 – 3.2 = 9.2 – 3.2
1.5d = 6
Divide 1.5 on both sides.
1.5d ÷ 1.5 = 6 ÷ 1.5
d = 4
Question 11.
0.8w – 4 = 4
Answer:
w = 10
Explanation:
Given, 0.8w – 4 = 4
Add 4 on both sides.
0.8w – 4 + 4 = 4 + 4
0.8w =8
Divide 0.8 on both sides.
0.8w ÷ 0.8 =8 ÷ 0.8
w = 10
Question 12.
1.4z – 0.5 = 3.7
Answer:
z = 3
Explanation:
Given, 1.4z – 0.5 = 3.7
Add 0.5 on both sides.
1.4z – 0.5 + 0.5 = 3.7 + 0.5
1.4z = 4.2
Divide 1.4 on both sides.
1.4z ÷ 1.4 = 4.2 ÷ 1.4
z = 3
Question 13.
Math Journal Priscilla was asked to solve the equation -4p + 5 = 7. Her solution is shown.
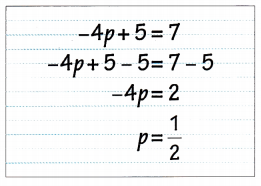
Priscilla concluded that p = \(\frac{1}{2}\) is the solution of the equation -4p + 5 = 7. Describe and correct the error Priscilla made.
Answer:
The answer priscilla got is wrong. P = – (1/2)
Explanation:
Given,-4p + 5 = 7
Subtract 5 on both sides.
-4p + 5 – 5= 7 – 5
-4p = 2
Divide 4 on both sides
-p = (2/4)
p = – (1/2)
Solve each equation with variables on both sides.
Question 14.
6a + 7 = 4a + 7
Answer:
a = 0
Explanation:
Given, 6a + 7 = 4a + 7
Subtract 7 on both sides.
6a + 7 – 7 = 4a + 7 – 7
6a = 4a
6a -4a = 0
2a = 0
a = 0
Question 15.
17g + 3 = 11g + 39
Answer:
g = 6
Explanation:
Given, 17g + 3 = 11g + 39
17g + 3 – 11g – 39 = 0
6 g – 36 = 0
6g = 36
Divide 6 on both sides.
6g ÷ 6 = 36 ÷ 6
g = 6
Question 16.
8h – 5 = 11h – 14
Answer:
h = 3
Explanation:
Given, 8h – 5 = 11h – 14
14 – 5 = 11h – 8h
9 = 3h
Divide 3 on both sides.
3h ÷ 3 = 9 ÷ 3
h = 3
Question 17.
9j + 4 = 13j – 6
Answer:
j = (5/2)
Explanation:
Given, 9j + 4 = 13j – 6
4 + 6 = 13j – 9j
10 = 4j
Divide 4 on both sides.
j = (10/4)
j = (5/2)
Question 18.
\(\frac{1}{2}\)f – 2 = \(\frac{1}{6}\)f
Answer:
f = 6
Explanation:
Given, (1/2)f – 2 = (1/6)f
(1/2)f – (1/6)f = 2
(3f – f)/6 = 2
Multiply 6 on both sides.
2f = 2 × 6
2f = 12
Divide 2 on both sides.
f = 12 ÷ 2
f = 6
Question 19.
25 + q = \(\frac{1}{2}\)q – 3
Answer:
q = -56
Explanation:
Given, 25 + q = (1/2)q – 3
25 + 3 = (1/2)q – q
28 = -(1/2)q
Multiply 2 on both sides.
28 × 2 = -(1/2)q × 2
-q = 56
q = -56
Question 20.
\(\frac{5}{9}\)v – \(\frac{1}{3}\) = \(\frac{2}{3}\)v + \(\frac{1}{3}\)
Answer:
v = -6
Explanation:
Given, (5/9)v – (1/3) = (2/3)v + (1/3)
Add (1/3) on both sides.
(5/9)v – (1/3) + (1/3) = (2/3)v + (1/3) + (1/3)
(5/9)v = (2/3)v + (2/3)
Subtract (2/3)v on both sides.
(5/9)v – (2/3)v = (2/3)v + (2/3) – (2/3)v
(5v – 6v)/9 = (2/3)
-v = (2/3) × 9
-v = 2 × 3
-v =6
v = -6
Question 21.
\(\frac{5}{4}\)e + \(\frac{1}{2}\) = 2e – \(\frac{1}{2}\)
Answer:
e = (4/3)
Explanation:
Given, (5/4)e + (1/2) = 2e – (1/2)
Add (1/2) on b1oth sides.
(5/4)e + (1/2) + (1/2) = 2e – (1/2) + (1/2)
(5/4)e + 1 = 2e
1 = 2e – (5/4)e
1 = ((2 × 4)e -5e)/4
(8e – 5e)/4 = 1
(3e/4) = 1
Multiply 4 on both sides.
(3e/4) × 4 = 1 × 4
3e = 4
e = (4/3)
Question 22.
7.5x – 4.1 = 6.7 – 4.5x
Answer:
x = 0.9
Explanation:
Given, 7.5x – 4.1 = 6.7 – 4.5x
Add 4.1 on both sides.
7.5x – 4.1 + 4.1 = 6.7 – 4.5x + 4.1
7.5x = 10.8 – 4.5x
Add 4.5x on both sides.
7.5x + 4.5x = 10.8 – 4.5x + 4.5x
12x =10.8
x = (10.8/12)
x = 0.9
Question 23.
3.4y – 5.2 = 3y + 2
Answer:
y = 18
Explanation:
Given, 3.4y – 5.2 = 3y + 2
Subtract 2 on both sides.
3.4y – 5.2 – 2 = 3y + 2 – 2
3.4y -7.2 = 3y
3.4y – 3y = 7.2
0.4y = 7.2
Divide 0.4 on both sides.
0.4y ÷ 0.4 = 7.2 ÷ 0.4
y = 18
Question 24.
b – 2.8 = 0.8b + 1.2
Answer:
b = 20
Explanation:
Given, b – 2.8 = 0.8b + 1.2
Subtract 1.2 on both sides.
b – 2.8 – 1.2 = 0.8b + 1.2 – 1.2
b – 4 = 0.8b
b – 0.8b = 4
0.2b = 4
Divide 0.2 on both sides.
0.2b ÷ 0.2 = 4 ÷ 0.2
b = 20
Question 25.
3.2s – 5 = 5 – 1.8s
Answer:
s =2
Explanation:
Given, 3.2s – 5 = 5 – 1.8s
Add 5 on both sides.
3.2s – 5 + 5 = 5 – 1.8s + 5
3.2s = 10 – 1.8s
Add 1.8s on both sides.
3.2s + 1.8s = 10 – 1.8s + 1.8s
5s = 10
Divide 5 on both sides.
5s ÷ 5 = 10 ÷ 5
s =2
Give your reasoning.
Question 26.
Math Journal How is the process of solving the equation \(\frac{3}{5}\)x – 1 = \(\frac{3}{10}\)x + \(\frac{1}{5}\) different from simplifying the expression \(\frac{3}{5}\)x – 1 + \(\frac{3}{10}\) x + \(\frac{1}{5}\)?
Answer:
x = 4, (9x -8)/10 Yes both are different from each other.
Explanation:
Given equations, (3/5)x – 1 = (3/10)x + (1/5)
(3/5)x -1 + (3/10)x + (1/5)
Let’s solve the first equation, (3/5)x – 1 = (3/10)x + (1/5)
Subtract (1/5) on both sides.
(3/5)x – 1 – (1/5) = (3/10)x + (1/5) – (1/5)
(3/5)x -(5 + 1)/5 = (3/10)x
(3/5)x – (6/5) = (3/10)x
(3/5)x – (3/10)x = (6/5)
(6 – 3)x/10 = (6/5)
Multiply 10 on both sides.
3x/10 × 10 = (6/5) × 10
3x = 12
Divide 3 on both sides
3x ÷ 3 = 12 ÷ 3
x = 4
Lets solve second equation, (3/5)x -1 + (3/10)x + (1/5)
(6 + 3)x/10 – 1 + (1/5)
9x/10 -(4/5)
(9x -8)/10
Solve each equation involving parentheses.
Question 27.
7(2z + 1) = 35
Answer:
z =2
Explanation:
Given, 7(2z + 1) = 35
Divide 7 on both sides.
7(2z + 1) ÷ 7 = 35 ÷ 7
2z + 1 = 5
Subtract 1 on both sides
2z + 1 – 1 = 5 – 1
2z = 4
z =2
Question 28.
18 = 6(5 – g)
Answer:
g = 2
Explanation:
Given, 18 = 6(5 – g)
18 = 30 – 6g
6g = 30 -18
6g = 12
Divide 6 on both sides.
6g ÷ 6 = 12 ÷ 6
g = 2
Question 29.
\(\frac{1}{5}\)(3r – 4) = \(\frac{2}{5}\)
Answer:
r = 2
Explanation:
(1/5)(3r – 4) = (2/5)
Multiply 5 on both sides.
(1/5)(3r – 4) × 5 = (2/5) × 5
(3r – 4) = 2
Add 4 on both sides.
3r – 4 + 4 = 2 + 4
3r = 6
Divide 3 on both sides.
3r ÷ 3 = 6 ÷ 3
r = 2
Question 30.
\(\frac{1}{5}\)(5x + 4) = \(\frac{3}{4}\)
Answer:
x = -(1/20)
Explanation:
(1/5)(5x + 4) = (3/4)
Multiply 5 on both sides.
(1/5)(5x + 4) = (3/4)
(1/5)(5x + 4) × 5 = (3/4) × 5
(5x + 4) = (15/4)
Multiply 4 on both sides.
(5x + 4) × 4 = (15/4) × 4
20x + 16 = 15
Subtract 16 on both sides.
20x + 16 – 16 = 15 -16
20x = -1
Divide 20 on both sides.
20x ÷ 20 = -1 ÷ 20
x = -(1/20)
Question 31.
0.6(d + 3) = 3d
Answer:
d = 0.75
Explanation:
Given, 0.6(d + 3) = 3d
0.6d + 1.8 = 3d
Subtract 1.8 on both sides.
0.6d + 1.8 – 1.8= 3d – 1.8
0.6d = 3d – 1.8
3d – 0.6d = 1.8
2.4d ÷ 2.4 = 1.8 ÷ 2.4
d = 0.75
Divide 2.4 on both sides.
2.4d = 1.8
Question 32.
0.3(k – 0.2) = 0.6
Answer:
k = 2.2
Explanation:
Given, 0.3(k – 0.2) = 0.6
Divide 0.3 on both sides.
0.3(k – 0.2) ÷ 0.3 = 0.6 ÷ 0.3
k – 0.2 = 2
Add 0.2 on both sides.
k – 0.2 + 0.2 = 2 + 0.2
k = 2.2
Question 33.
3(1.2b – 1) + 3.6 = 4.2
Answer:
b = 1
Explanation:
Given, 3(1.2b – 1) + 3.6 = 4.2
3.6b – 3 + 3.6 = 4.2
3.6b + 0.6 = 4.2
Subtract 0.6 on both sides.
3.6b + 0.6 – 0.6 = 4.2 -0.6
3.6b = 3.6
Divide 3.6 on both sides.
3.6b ÷ 3.6 = 3.6 ÷ 3.6
b = 1
Question 34.
0.7(h + 2) + 1.6 = 17
Answer:
h = 20
Explanation:
Given, 0.7(h + 2) + 1.6 = 17
0.7h + (0.7 × 2) + 1.6 = 17
0.7h + 1.4 + 1.6 = 17
0.7h + 3 = 17
Subtract 3 on both sides.
0.7h + 3 – 3 = 17 – 3
0.7h = 14
Divide 0.7 on both sides.
0.7h ÷ 0.7 = 14 ÷ 0.7
h = 20
Question 35.
2(a – 1) – 5a = 7
Answer:
Explanation:
Given, 2(a – 1) – 5a = 7
2a -2 -5a = 7
-3a – 2 = 7
Add 2 on the both sides.
-3a – 2+2 = 7 +2
-3a = 9
Divide -3 on both sides.
a = -(9/3)
a = -3
Question 36.
3(6 – 4x) – 27x = 10x – 31
Answer:
1 = x
Explanation:
Given, 3(6 – 4x) – 27x = 10x – 31
18 – 12x – 27x = 10x -31
18 -39x = 10x – 31
18 +31 = 10x + 39x
49 = 49x
Divide 49 on both sides.
49 ÷ 49 = 49x ÷ 49
1 = x
Question 37.
\(\frac{1}{4}\)(w – 4) – \(\frac{3}{4}\)w = 3
Answer:
w = -8
Explanation:
Given, (1/4)(w – 4) – (3/4)w =3
Multiply 4 on both sides.
4 ×( (1/4)(w – 4) – (3/4)w) = 3 × 4
(w – 4) – 3w = 12
w – 4 – 3w = 12
-2w – 4 = 12
Add 4 on both sides
-2w – 4 + 4 = 12 + 4
-2w = 16
-w = 8
w = -8
Question 38.
\(\frac{1}{6}\)s – \(\frac{1}{2}\)(s – 2) = \(\frac{45}{2}\)
Answer:
s = -(129/2)
Explanation:
(1/6)s – (1/2)(s – 2) = (45/2)
Multiply 2 on both sides.
2 × (1/6)s – 2 × (1/2)(s – 2) = (45/2) × 2
(1/3)s – (s-2) = 45
Multiply 3 on both sides.
3 × (1/3)s – 3 ×(s-2) = 45 × 3
s – 3s + 6 = 135
-2s + 6 = 135
Subtract 6 on both sides
-2s + 6 – 6 = 135 – 6
-2s = 129
Divide (-2) on both sides.
-2s ÷ (-2) = 129 ÷ (-2)
s = -(129/2)
Question 39.
5(y + 1) = 3(3y + 4)
Answer:
y = -(7/4)
Explanation:
Given, 5(y + 1) = 3(3y + 4)
5y + 5 = 9y + 12
Subtract 5 on both sides.
5y + 5 – 5 = 9y + 12 – 5
5y = 9y + 7
Subtract 5y on both sides.
5y – 5y = 9y + 7 – 5y
0 = 4y + 7
4y = -7
Divide 4 on both sides.
4y ÷ 4 = -7 ÷ 4
y = -(7/4)
Question 40.
2(b + 5) = 3(4 – b)
Answer:
b =(2/5)
Explanation:
Given, 2(b + 5) = 3(4 – b)
2b + 10 = 12 – 3b
Add 3b on both sides.
2b + 10 + 3b = 12 – 3b + 3b
5b + 10 = 12
Subtract 10 on both sides.
5b + 10 – 10 = 12 – 10
5b = 2
Divide 5 on both sides.
5b ÷ 5 = 2 ÷ 5
b =(2/5)
Question 41.
Math Journal Nelson solved the algebraic equation 3(2x + 5) = 17 as I shown below:
3(2x + 5) = 17
3(2x + 5) – 5 = 17 – 5
3(2x) = 12 6
x = 12
6x ÷ 6 = 12 ÷ 6
x = 2
Describe and correct the error Nelson made.
Answer:
x = (1/3)
Explanation:
Given, 3(2x + 5) = 17
3 × 2x + 3 × 5 = 17
6x + 15 = 17
Subtract 15 on both sides
6x + 15 – 15 = 17 – 15
6x = 2
Divide 6 on both sides.
6x ÷ 6 = 2 ÷ 6
x = (2/6)
x = (1/3)
Question 42.
Math Journal Describe the steps you could use to solve 2(b – 5) + 3(b – 2) = 8 + 7(b – 4). Solve and show your work.
Answer:
b = 2
Explanation:
Given, 2(b – 5) + 3(b – 2) = 8 + 7(b – 4)
2b – 10 +3b – 6 = 8 + 7b – 28
5b – 16 = 7b – 20
Add 16 on both sides.
5b – 10 + 16 = 7b – 20 + 16
5b = 7b – 4
7b – 5b = 4
2b = 4
Divide 2 on both sides.
2b ÷ 2 = 4 ÷ 2
b = 2