Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 7 Lesson 7.1 Writing Algebraic Expressions to score better marks in the exam.
Math in Focus Grade 6 Course 1 A Chapter 7 Lesson 7.1 Answer Key Writing Algebraic Expressions
Math in Focus Grade 6 Chapter 7 Lesson 7.1 Guided Practice Answer Key
Write an algebraic expression for each of the following.
Question 1.
The sum of x and 10
Answer:
x + 10
Explanation:
x + 10 is an algebraic expression in terms of x.
x and 10 are the terms of expression.
Question 2.
The difference “7 less than y”
Answer:
y – 7
Explanation:
y – 7 is an algebraic expression in terms of x.
y and 7 are the terms of expression.
Question 3.
Jim is now z years old.
a) His brother is 4 years older than Jim. Find his brother’s age in terms of z.
Answer:
Jim’s brothers age is = z+4
Explanation:
Jim brother is 4 years older than Jim.
His brother’s age in terms of z.
z + 4
b) His sister is 3 years younger than Jim. Find his sister’s age in terms of z.
Answer:
Jim’s sister’s are is = z – 3
Explanation:
Jim sister is 3 years younger than Jim.
His sister’s age in terms of z.
z – 3
Question 4.
The product of z and 6
Answer:
z x 6
Explanation:
x x 6 is an algebraic expression in terms of x.
x and 6 are the terms of expression.
Question 5.
The quotient of w and 8
Answer:
\(\frac{w}{8}\)
Explanation:
\(\frac{w}{8}\) is an algebraic expression in terms of x.
w and 8 are the terms of expression.
Question 6.
Mia bought a pair of shoes for p dollars. She also bought a dress that cost 5 times as much as the shoes, and a belt that cost \(\frac{1}{4}\) of the price of the shoes.
a) Find the cost of the dress in terms of p.
Answer:
5p
Explanation:
a pair of shoes for p dollars
a dress that cost 5 times shoes = 5p
b) Find the cost of the belt in terms of p.
Answer:
\(\frac{p}{4}\)
Explanation:
a belt that cost \(\frac{1}{4}\) of the price of the shoes.
the cost of the belt = \(\frac{p}{4}\)
Math in Focus Course 1A Practice 7.1 Answer Key
Write an algebraic expression for each of the following.
Question 1.
The sum of 4 and p
Answer:
p + 4
Explanation:
The sum of 4 and p is p + 4
p + 4 is an algebraic expression in terms of p.
p and 4 are the terms of expression.
Question 2.
The difference “8 less than q”
Answer:
q – 8
Explanation:
The difference “8 less than q” is q – 7
q – 7 is an algebraic expression in terms of q.
q and 7 are the terms of expression.
Question 3.
The product of 3 and r
Answer:
3 x r
Explanation:
The product of 3 and r is 3r
3 x r is an algebraic expression in terms of r.
r and 3 are the terms of expression.
Question 4.
The quotient of s and 5
Answer:
\(\frac{s}{5}\)
Explanation:
The quotient of s and 5 is \(\frac{s}{5}\)
\(\frac{s}{5}\) is an algebraic expression in terms of s.
s and 5 are the terms of expression.
Question 5.
Cheryl is now x years old.
a) Her father is 24 years older than Cheryl. Find her father’s age in terms of x.
Answer:
x + 24
Explanation:
Cheryl father is 24 years older than Cheryl.
Her father’s age in terms of x = x + 24
x + 24 is an algebraic expression.
b) Her brother is 2 years younger than Cheryl. Find her brother’s age in terms of x.
Answer:
x – 2
Explanation:
Cheryl brother is 2 years younger than Cheryl.
Her brother’s age in terms of x = x – 24
Here, x – 2 is the algebraic expression.
c) Her sister is twice as old as Cheryl. Find her sister’s age in terms of x.
Answer:
2x
Explanation:
Cheryl sister is twice as old as Cheryl.
Her sister’s age in terms of x = 2x
x = twice the age of her sister.
d) Her cousin is \(\frac{1}{3}\) Cheryl’s age. Find her cousin’s age in terms of x.
Answer:
\(\frac{x}{3}\)
Explanation:
Cheryl cousin is \(\frac{1}{3}\) Cheryl’s age.
Her cousin’s age in terms of x.
x\(\frac{1}{3}\) = \(\frac{x}{3}\)
Question 6.
Multiply k by 5, and then add 3 to the product.
Answer:
(k x 5) + 3
Explanation:
Multiply k by 5 = 5k
then add 3 to the product = (k x 5) + 3 = 5k + 3
Question 7.
Divide m by 7, and then subtract 4 from the quotient.
Answer:
\(\frac{m}{7}\) – 4
Explanation:
Divide m by 7 = \(\frac{m}{7}\)
then subtract 4 from the quotient.
\(\frac{m}{7}\) – 4
Question 8.
Divide j by 9, and then multiply the quotient by 2.
Answer:
\(\frac{j}{9}\) x 2
Explanation:
Divide j by 9 = \(\frac{j}{9}\)
then multiply the quotient by 2
\(\frac{j}{9}\) x 2
Question 9.
The sum of \(\frac{1}{3}\) of z and \(\frac{1}{5}\) of z
Answer:
\(\frac{z}{3}\) + \(\frac{z}{5}\)
Explanation:
\(\frac{1}{3}\) x z + \(\frac{1}{5}\) x z
= \(\frac{z}{3}\) + \(\frac{z}{5}\)
Solve.
Question 10.
Jeremy bought 5 pencils for w dollars. Each pen costs 35ct more than a Write an algebraic expression for each of the following in terms of w.

a) The cost, in dollars, of a pen
Answer:
\(\frac{w}{5}\) + 35
Explanation:
Jeremy bought 5 pencils for w dollars.
5 pencils = w dollars
Each pen costs 35ct more than a.
An algebraic expression for each of the following in terms of w.
\(\frac{w}{5}\) + 35
cost of one pen = \(\frac{w}{5}\) + 35 cents
b) The number of pencils that Jeremy can buy with $20
Answer:
\(\frac{100}{w}\)
Explanation:
Jeremy bought 5 pencils for w dollars.
5 pencils = w dollars
The number of pencils that Jeremy can buy with $20
\(\frac{20}{1}\)/ \(\frac{w}{5}\)
\(\frac{20}{1}\) x \(\frac{5}{w}\)
\(\frac{100}{w}\)
Question 11.
The figure shown is formed by a rectangle and a square. Express the area of the figure in terms of x.
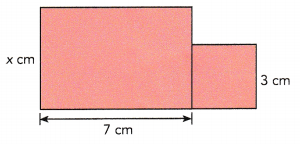
Answer:
x(7 + 9)
Explanation:
the area of the figure in terms of x
length of rectangle = 7cm
length of square = 3cm
x X 7 + 3 x 3
x X 7 + 9