Math in Focus Grade 7 Chapter 3 Lesson 3.6 Answer Key Writing Algebraic Expressions

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 3 Lesson 3.6 Writing Algebraic Expressions to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 3 Lesson 3.6 Answer Key Writing Algebraic Expressions

Math in Focus Grade 7 Chapter 3 Lesson 3.6 Guided Practice Answer Key

Complete.
Question 1.
The price of a ring was w dollars. Wendy bought it at a discount of 25%. Write an algebraic expression for the discounted price of the ring.

Answer:
Discounted price of ring = \(\frac{3}{4}\)w dollars.

Explanation:
Total cost price of ring = w dollars.
Discount price of ring = 25%.
Discounted price of ring = Total cost price of ring – (Discount price of ring  × Total cost price of ring)
= w – (25% × w)
= w – (25 ÷ 100 × w)
= w – \(\frac{1}{4}\)w
= (4w – w) ÷ 4
= 3w ÷ 4 or \(\frac{3}{4}\)w dollars.

 

Question 2.
6n blocks of clay are shared among 14 students. Write an algebraic expression for the number of blocks of clay that each student will get.

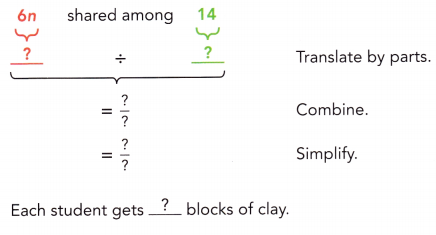
Answer:
Number of blocks of clay each student gets = 3n ÷ 7.

Explanation:
Total number of blocks of clay = 6n.
Number of students clays shared = 14.
Number of blocks of clay each student gets = Total number of blocks of clay  ÷ Number of students clays shared
= 6n ÷ 14
= 3n ÷ 7.

 

Question 3.
Desmond has w marbles and Mandy has \(\frac{1}{2}\)w marbles. Desmond gives one-tenth of his marbles and Mandy gives two-fifth of her marbles to their cousin Joel. Write an expression for the number of marbles Joel receives.

Joel receives marbles.
Answer:
Number of marbles Joel receives = \(\frac{3}{10}\)w.

Explanation:
Number of marbles Desmond has = w.
Number of marbles Mandy has = \(\frac{1}{2}\)w.
Desmond gives one-tenth of his marbles and Mandy gives two-fifth of her marbles to their cousin Joel.
=> Number of marbles Joel receives = (one-tenth × Number of marbles Desmond has) + (two-fifth × \(\frac{1}{2}\)w)
= (\(\frac{1}{10}\) × w) + (\(\frac{2}{5}\) × \(\frac{1}{2}\)w)
= \(\frac{1}{10}\)w + \(\frac{1}{5}\)w
LCD of 5 n 10 = 10.
= (1w + 2w) ÷ 10
= 3w ÷ 10 or \(\frac{3}{10}\)w.

 

Question 4.
After baking some bread, Janis has \(\frac{2}{3}\)b pounds of butter left. Then she uses \(\frac{3}{4}\) pound for white sauce. Write an algebraic expression for the amount of butter left.
Subtract \(\frac{3}{4}\) from \(\frac{2}{3}\)b.
There are pounds of butter left.

Caution
a subtracted from b is not a – b.
Answer:
Amount of butter left = (8b – 9) ÷ 12 pounds.

Explanation:
Amount of butter left Janis has = \(\frac{2}{3}\)b pounds.
Amount of butter Janis use for white sauce = \(\frac{3}{4}\) pound.
Amount of butter left = Amount of butter left Janis has – Amount of butter Janis use for white sauce
= \(\frac{2}{3}\)b – \(\frac{3}{4}\)
= LCD of 3 n 4 = 12.
= [(2b × 4) – (3 × 3)] ÷ 12
= (8b – 9) ÷ 12 pounds.

 

Complete.
Question 5.
Anne’s garden has a shape of an isosceles triangle with a base of length 2y feet arid sides of length \(\left(\frac{2}{5} y+3\right)\) feet each. Write an algebraic expression for the perimeter of Anne’s garden.
Perimeter of Annes garden:

Answer:
Perimeter of Anne’s garden = (14y + 12) ÷ 5 ft.

Explanation:
Length of the base of the triangle = 2y feet.
Length of other two sides = \(\left(\frac{2}{5} y+3\right)\) feet  each.
Perimeter of Anne’s garden = Length of the base of the triangle  + Length of other two sides
= 2y + 2( \(\left(\frac{2}{5} y+3\right)\))
= 2y + \(\left(\frac{4}{5} y+3\right)\)
= [(2y × 5) + 4(y + 3)] ÷ 5
= (10y + 4y + 12) ÷ 5
= (14y + 12) ÷ 5 ft.

 

Complete.
Question 6.
The price of a buffet lunch is $14.80 per adult and $12 per child. For a group of m adults and n children, how much does the lunch cost before tax and tips?

Total cost of lunch before tax and tips:

The total cost of lunch before tax and tips is dollars.
Answer:
Total cost of lunch before tax and tips = $14.80m + $12n.

Explanation:
Cost of buffet lunch for each adult = $14.80.
Number of adults = m.
Cost of buffet lunch for each child = $12.
Number of adults = n.
Total cost of lunch before tax and tips = (Cost of buffet lunch for each adult × Number of adults) + (Cost of buffet lunch for each child × Number of adults)
= ($14.80 × m) + ( $12 × n)
= $14.80m + $12n

 

Question 7.
Joshua had m quarters in his pocket. He also had one dime and n nickels. What was the total value of his coins?
Answer:
Total value of his coins = $0.4mn.

Explanation:
Number of quarters Joshua had in his pocket = m.
Number of dime Joshua had in his pocket = 1.
Number of nickels Joshua had in his pocket = n.
Conversion:
1 quarter = 0.25 dollar.
1 dime = 0.1 dollar.
1 nickel = 0.05 dollar.
Total value of his coins = Number of quarters Joshua had in his pocket + Number of dime Joshua had in his pocket + Number of nickels Joshua had in his pocket
= m + 1 + n
= ($0.25 × m) +($0.1) + (n × $0.05)
= $0.4mn.

 

Complete.
Question 8.
Anderson had b tennis balls. He gave 30 to his sister and divided the rest of the tennis balls equally among 5 friends. How many tennis balls did each friend receive?

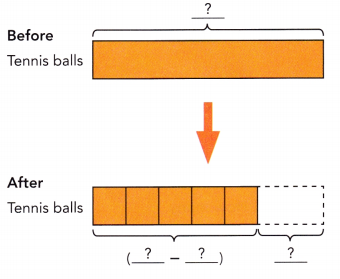
From the bar model, the number of tennis balls each friend received is:
Use the distributive property.
Each friend received tennis balls.
Answer:
Number of tennis balls he gave to each friend = (b – 30) ÷ 5.

Explanation:
Number of tennis balls Anderson had = b.
Number of tennis balls he gave to his sister = 30.
Number of friends he gave rest tennis balls = 5.
Number of tennis balls he gave to each friend = (Number of tennis balls Anderson had – Number of tennis balls he gave to his sister) ÷ Number of friends he gave rest tennis balls
= (b – 30) ÷ 5.

Technology Activity
Materials:

• spreadsheet software

Use Algebraic Expressions In real-world situations

Work in groups of three or four.
Translate verbal descriptions into algebraic expressions.

Maria used her smartphone for 4 days. Her average calling time was 130 minutes each day. Suppose that Maria used the phone for m minutes on the fifth day. Write an algebraic expression for the average number of minutes she spent on the phone over 5 days.

Step 1.
Complete.
Total number of minutes spent over five days:
Total number of minutes spent over four days +
Number of minutes spent on the fifth day

Use a spreadsheet to solve real-world problem involving algebraic expressions.

Step 2.
Label your spreadsheet and enter the values in column A as shown.

Step 3.
Enter the formula =130*4+A2 in cell B2 to find the total number of minutes she spent on her phone over five days. What is the value in cell B2 after you have entered the formula?

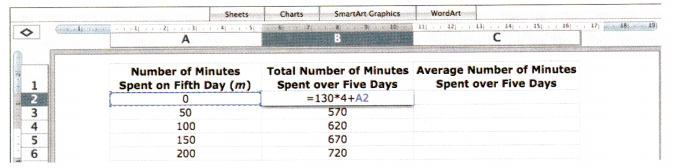
Step 4.
Complete cell C2 with a formula to find the average number of minutes she spent on her phone over five days.

Step 5.
Maria would like to have an average number of minutes she spent on her phone over five days to be 150 minutes. Determine the number of minutes she can spend on the fifth day by repeating Step 3 and Step 4 with different values in column A.

Math Journal Based on your activity, what is the relationship between the algebraic expressions of Step 1 and the formula used in the spreadsheet cell of Step 3 and Step 4? Explain how you can use technology to solve real-world problems.

Math in Focus Course 2A Practice 3.6 Answer Key

Translate each verbal description into an algebraic expression. Simplify the expression when you can.
Question 1.
Sum of one-sixth of x and 2.8
Answer:
Sum of one-sixth of x and 2.8 = \(\frac{x}{6}\)  + 28.

Explanation:
Sum of one-sixth of x and 2.8 = (one-sixth of x ) + 2.8
= (\(\frac{1}{6}\) × x) + 2.8
= \(\frac{x}{6}\)  + 28

 

Question 2.
One-half u subtracted from 3 times u
Answer:
One-half u subtracted from 3 times u = –\(\frac{5}{2}\)u.

Explanation:
One-half u subtracted from 3 times u = (\(\frac{1}{2}\)u) – (3 × u)
= \(\frac{1}{2}\)u – 3u
= (u – 6u) ÷ 2
= -5u ÷ 2 or –\(\frac{5}{2}\)u.

 

Question 3.
4.5 times q divided by 9
Answer:
4.5 times q divided by 9 = 0.5q.

Explanation:
4.5 times q divided by 9 = (4.5 × q) ÷ 9
= 0.5 × q
= 0.5q.

 

Question 4.
60% of one-half x
Answer:
60% of one-half x = \(\frac{3}{10}\)x.

Explanation:
60% of one-half x = 60% × \(\frac{1}{2}\)x
= (60 ÷ 100) × \(\frac{1}{2}\)x
= \(\frac{3}{5}\) × \(\frac{1}{2}\)x
= \(\frac{3}{10}\)x.

 

Question 5.
5x increased by 120%
Answer:
5x increased by 120% = 6x.

Explanation:
First, change the percentage to a number.
120(%) (120 ÷ 100) = 1.2
=> 5x increased by 120%:
5x × 1.2 = 6x.

 

Question 6.
7 times z reduced by a third of the product
Answer:
7 times z reduced by a third of the product = 14z.

Explanation:
7 times z reduced by a third of the product = (7 × z) – 3(7 × z)
= 7z – 21z
= -14z.

 

Question 7.
24% of w plus 50% of y
Answer:
24% of w plus 50% of y = \(\frac{6}{25}\)w + \(\frac{1}{2}\)y.

Explanation:
24% of w plus 50% of y = (24% × w) + (50% × y)
= [(24 ÷ 100) × w] + [(50 ÷ 100) × y]
= \(\frac{6}{25}\)w + \(\frac{1}{2}\)y.

 

Question 8.
Three-fourths of v subtracted from 6 times two-ninths y
Answer:
Three-fourths of v subtracted from 6 times two-ninths y = \(\frac{3}{4}\)v – \(\frac{4}{3}\)y.

Explanation:
Three-fourths of v subtracted from 6 times two-ninths y
= ( \(\frac{3}{4}\) × v) –  (6 × \(\frac{2}{9}\)y)
= \(\frac{3}{4}\)v – \(\frac{4}{3}\)y.

 

Question 9.
One-fourth of the sum of 2p and 11
Answer:
One-fourth of the sum of 2p and 11 = \(\frac{1}{2}\)p + \(\frac{11}{4}\).

Explanation:
One-fourth of the sum of 2p and 11
= \(\frac{1}{4}\) (2p + 11)
= ( \(\frac{1}{4}\)  × 2p) + (\(\frac{1}{4}\) × 11)
= \(\frac{1}{2}\)p + \(\frac{11}{4}\).

 

Question 10.
Sum of 2x, (\(\frac{2}{3}\)x + 5), and (11 – x)
Answer:
Sum of 2x, (\(\frac{2}{3}\)x + 5), and (11 – x) = (\(\frac{2}{3}\)x + 16.

Explanation:
Sum of 2x, (\(\frac{2}{3}\)x + 5), and (11 – x)
= 2x + (\(\frac{2}{3}\)x + 5) + (11 – x)
= 2x + \(\frac{2}{3}\)x + 5 + 11 – x
= (6x + 2x – 6x) ÷ 3 + 16
= 2x ÷ 3 + 16 or (\(\frac{2}{3}\)x + 16.

 

Solve. You may use a diagram, model, or table.
Question 11.
The length of \(\frac{2}{3}\) a rope is (4u – 5) inches. Express the total length of the rope in terms of u.
Answer:
Total length of the rope in terms of u = (8u – 10) ÷ 3 inches.

Explanation:
Length of a rope \(\frac{2}{3}\) = (4u – 5) inches
Total length of the rope in terms of u = \(\frac{2}{3}\) × (4u – 5)
= (8u – 10) ÷ 3 inches.

Question 12.
If 50 lb = 22.68 kg, what is \(\frac{15}{8}\)y pounds in kilograms?
Answer:
\(\frac{15}{8}\)y pounds = 0.84 kgs.

Explanation:
If 50 lb = 22.68 kg,
=> 1 pound = 22.68 ÷ 50 kg
=> 1 pound = 0.45 kg.
\(\frac{15}{8}\)y pounds = ?? kg
=> \(\frac{15}{8}\)y × 0.45
=> 6.75 ÷ 8
=> 0.84 kg.

 

Question 13.
The minute hand of a clock makes one complete round every 60 minutes. How many rounds does the minute hand make in 650x minutes?
Answer:
Number of rounds  the minute hand make in 650x minutes = 65x ÷ 6.

Explanation:
The minute hand of a clock makes one complete round every 60 minutes.
Number of rounds  the minute hand make in 650x minutes = 650x ÷ 60
= 65x ÷ 6.

 

Question 14.
Fifteen cards are added to n cards. 6 people then share the cards equally. Express the number of cards for each person in terms of n.
Answer:
Number of cards for each person in terms of n = (15 + n) ÷ 6.

Explanation:
Total number of cards = 15 + n.
Number of people the cards are shared = 6.
Number of cards for each person in terms of n = Total number of cards ÷ Number of people the cards are shared
= (15 + n) ÷ 6.

 

Question 15.
The pump price was g dollars per gallon of gasoline yesterday. The price increases by 10 cents per gallon today. If a driver pumps 12.4 gallons of gasoline today, how much does he have to pay?
Answer:
Cost he pays = $12.4g + $12.4.

Explanation:
Cost of pump per gallon of gasoline yesterday = g dollars.
Cost of price increased per gallon = 10 cents.
Conversion:
1 cent = 0.1 dollar.
10 cents = 0.1 × 10 = 1 dollar.
Number of gallons of gasoline today a driver pumps = 12.4.
Cost he pays = (Cost of pump per gallon of gasoline yesterday + Cost of price increased per gallon) × Number of gallons of gasoline today a driver pumps
= (g + 10cents)  × $12.4
= (g + $1) × 12.4
= $12.4g + $12.4.

 

Question 16.
Math Journal Each algebraic expression contains an error. Copy and complete.

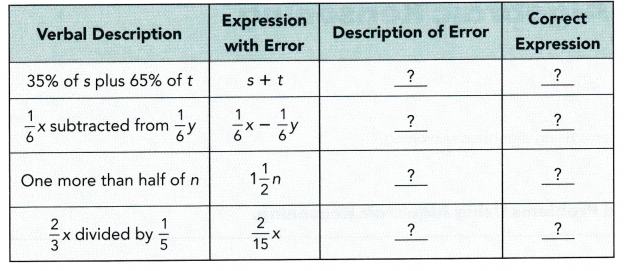
Answer:

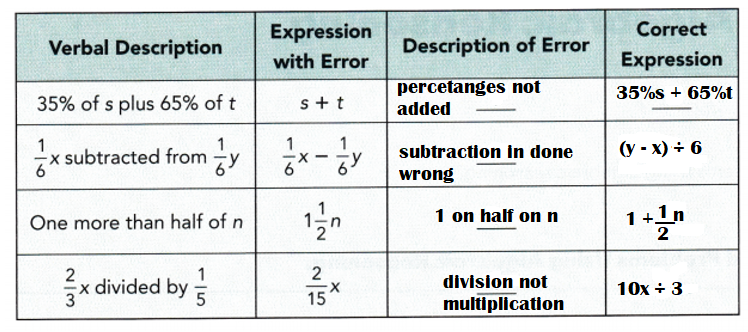
Explanation:
Correct Expressions:
35% of s plus 65% of t = (35% × s) + (65% × t)
= 35$s + 65%t.
\(\frac{1}{6}\)x subtracted from \(\frac{1}{6}\)y = \(\frac{1}{6}\)y – \(\frac{1}{6}\)x
= (y – x) ÷ 6.
One more than half on n = 1 + \(\frac{1}{2}\)n
= 1 + \(\frac{1}{2}\)n.
\(\frac{2}{3}\)x divided by \(\frac{1}{5}\) =  \(\frac{2}{3}\)x ÷ \(\frac{1}{5}\)
= \(\frac{2}{3}\)x × 5
= (2 × 5)x ÷ 3
= 10x ÷ 3.

 

Question 17.
The ratio of red counters to blue counters is 9 : 11. There are y blue counters. Express the number of red counters in terms of y.
Answer:
Number of red counters in terms of y = 11x ÷ 9 .

Explanation:
Ratio of red counters to blue counters = 9 : 11.
Number of blue counters = y.
Let Number of red counters = x.
Number of red counters in terms of y = x : y = 9:11
=> x = 9y ÷ 11.
=> 11x ÷ 9 = y.

 

Question 18.
When 18 boys joined a group of y students, the ratio of boys to girls in the group became 4 : 5. Write an algebraic expression for the number of girls in terms of y.
Answer:
Number of girls in terms of y = (4 ÷ 5g) – 18.

Explanation:
Total number of students = y + 18.
Ratio of boys to girls in the group became 4 : 5.
Number of girls in terms of y : y + 18 = 4:5g
=> y + 18 = 4 ÷ 5g.
=>y = (4 ÷ 5g) – 18.

 

Question 19.
Adrian is x years old. Benny is 7 years younger than Adrian. In 5 years’ time, Benny will be twice the age of Celine. How old is Celine now in terms of x?
Answer:
Age of Celine now = (x – 12) ÷ 2 years.

Explanation:
Age of Adrian = x years.
Benny is 7 years younger than Adrian.
Age of Benny = x – 7 years.
In 5 years’ time, Benny will be twice the age of Celine.
Let age of Celine be y years.
Age of Adrian now = x + 5 years.
Age of benny = 5 + (x – 7) years.
Age of Celine now =  5 + (x – 7)years = 2(5 + y)
=> x – 2 = 10 + 2y
=> x – 2 – 10 = 2y
=> x – 12 = 2y
=> (x – 12) ÷ 2 years = y.

 

Question 20.
A group has an equal number of adults and children. When n oranges are given to the group, each adult gets two oranges while each child gets one orange and there are still 5 oranges left. Write an algebraic expression for the number of oranges given to the adults.
Answer:
Total number of oranges  given to adults = (n + 4) ÷ 2

Explanation:
Number of oranges = n.
Let number of oranges given to the adults be x.
Number of oranges each adult gets = 2.
Number of oranges each child gets = 1.
Number of oranges are left = 5.
Total number of oranges = (Number of oranges each adult gets + Number of oranges each child gets) + Number of oranges are left
n = (2x + 1) – 5
=> n = 2x – 4
=> n + 4 = 2x.
=> (n + 4) ÷ 2 = x.

 

Question 21.
The list price of a camera was w dollars. Paul bought the camera for $35 less than the list price. If the sales tax was 8%, how much did Paul pay for the camera including the sales tax?

Answer:
Amount he pays for the camera = (21w ÷ 25) – 35 dollars.

Explanation:
List price of camera = w dollars.
Paul bought the camera for $35 less than the list price.
Cost of camera Paul bought  = (w – 35) dollars.
If the sales tax was 8%
Sales tax = 8% × w = 8%w dollars.
Amount he pays for the camera = Cost of camera Paul bought + Sales tax
= (w – 35) + 8%w
= (w – 35) + (4w ÷ 25)
= (25w – 4w) ÷ 25 – 35
= (21w ÷ 25) – 35 dollars.

 

Question 22.
There were m visitors in an exhibition on the first day and 1,200 fewer visitors on the second day. On the third day, the number of visitors was 30% greater than the number of visitors on the second day. What was the average number of visitors over the three days?
Answer:
Average number of visitors over the three days = \(\frac{5}{3}\)m – 520.

Explanation:
Number of visitors in an exhibition on the first day = m.
Number of visitors in an exhibition on the second day = Number of visitors in an exhibition on the first day  – 1200
= m – 1200.
On the third day, the number of visitors was 30% greater than the number of visitors on the second day.
=> Number of visitors in an exhibition on the third day = 30% Number of visitors in an exhibition on the second day
= 30% (m – 1200)
= 3÷10 (m – 1200)
= 3m – 360.
Average number of visitors over the three days = (Number of visitors in an exhibition on the first day + Number of visitors in an exhibition on the second day + Number of visitors in an exhibition on the third day) ÷ 3
= [m + (m – 1200) + (3m – 360)] ÷ 3
= (m + m – 1200 + 3m – 360) ÷ 3
= (5m – 1560) ÷ 3
= \(\frac{5}{3}\)m – 520.

 

Question 23.
A man drove x miles per hour for 3 hours and (2x – 60) miles per hour for the next 4.75 hours.
a) Express the total distance he traveled in terms of x.
Answer:
Total distance he traveled in terms of x = 12.5x – 285 miles.

Explanation:
Number of miles a man drove per hour = x.
Number of hours he drove x miles = 3.
Number of miles a man drove next per hour = 2x – 60.
Number of hours he drove (2x – 60) miles = 4.75 hours.
Number of miles a man drove 4.75 hours = (2x – 60) × 4.75
= 9.5x – 285.
Number of miles a man drove 3 hours = x × 3 = 3x.
Total distance he traveled in terms of x = Number of miles a man drove 3 hours + Number of miles a man drove 4.75 hours
= 3x + 9.5x – 285.
= 12.5x – 285 miles.

 

b) If x = 64, what is the total distance he traveled?
Answer:
Total distance he traveled in terms of x = 515 miles.

Explanation:
If x = 64,
Total distance he traveled in terms of x = 12.5x – 285
= 12.5(64) – 285
= 800 – 285
= 515 miles.