Math in Focus Grade 7 Chapter 3 Lesson 3.7 Answer Key Real-World Problems: Algebraic Reasoning

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 3 Lesson 3.7 Real-World Problems: Algebraic Reasoning to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 3 Lesson 3.7 Answer Key Real-World Problems: Algebraic Reasoning

Math in Focus Grade 7 Chapter 3 Lesson 3.7 Guided Practice Answer Key

Complete.
Question 1.
The area of a triangle is (u + 10) square centimeters. The ratio of the area of the unshaded region to the area of the shaded region is 1 : 3. Using algebraic reasoning, express the area of the shaded region in terms of u.

Area of shaded region:
Use the distributive property. Simplify.
The area of the shaded region of the triangle is square centimeters.
Answer:
The area of the shaded region of the triangle is \(\frac{3}{4}\) (u + 100) square centimeters.

Explanation:
The area of a triangle is (u + 10) square centimeters.
The ratio of the area of the unshaded region to the area of the shaded region is 1 : 3.
=> Shaded region = 3.
Unshaded region = 1.
Area of the shaded region of the triangle = \(\frac{3}{4}\) × Area of a triangle
= \(\frac{3}{4}\) ×(u + 10)
= \(\frac{3}{4}\) (u + 100) square centimeters.

Question 2.
There are 25 nickels and quarters, w coins are nickels and the rest are quarters.

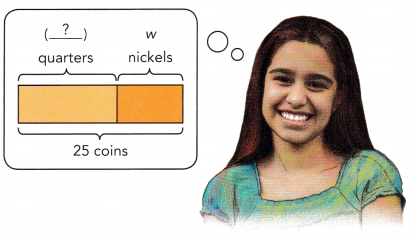
a) Write an algebraic expression for the number of coins that are quarters.
Number of quarters:

There are quarters.
Answer:
Number of quarters = 25 – w.

Explanation:
There are 25 nickels and quarters,
w coins are nickels and the rest are quarters.
=> Total number of coins = 25.
=> Number of nickels = w.
Number of quarters = Total number of coins – Number of nickels
= 25 – w.

b) Find the total value of the quarters.
Total value of quarters:

The total value of the quarters is dollars.
Answer:
Total value of quarters = (25 – w) dollars.

Explanation:
Number of quarters = 25 – w.
Total value of quarters = (25 – w) dollars.

Complete each ? with + or -, and with the correct value.
Question 3.
Amy has x comic books, Melvin has \(\left(\frac{2 x}{5}+1\right)\) comic books, and Joel has \(\frac{x}{10}\) fewer comic books than Melvin. Express the total number of comic books that Amy, Melvin, and Joel have in terms of x.

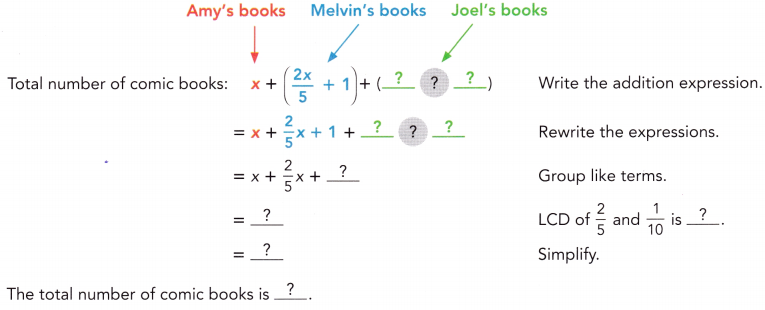
Answer:
Total number of comic books = \(\frac{17x}{10}\) + 2.

Explanation:
Amy has x comic books, Melvin has \(\left(\frac{2 x}{5}+1\right)\) comic books, and Joel has \(\frac{x}{10}\) fewer comic books than Melvin.
Number of Melvin has comic books = \(\left(\frac{2 x}{5}+1\right)\)
Number of Joel has comic books = Number of Melvin has comic books – \(\frac{x}{10}\)
=> \(\left(\frac{2 x}{5}+1\right)\) – \(\frac{x}{10}\)
=>\(\frac{2x}{5}\) – \(\frac{x}{10}\) + 1
LCD of 5 n 10 = 10.
=> (2x × 2) – x] ÷ 10 + 1
=> (4x -x) ÷ 10 + 1
=> \(\frac{3x}{10}\) + 1.
Total number of comic books = Number of  Amy has comic books + Number of Melvin has comic books + Number of Joel has comic books
= x + \(\left(\frac{2 x}{5}+1\right)\)  + \(\frac{3x}{10}\) + 1
= x + \(\frac{2x}{5}\) + \(\frac{3x}{10}\) + 1 + 1
LCD of 5 n 10 = 10.
= [10x + (2x × 2) + 3x] ÷ 10 + 2
= (10x + 4x + 3x) ÷ 10 + 2
= \(\frac{17x}{10}\) + 2.

Solve.
Question 4.
A shoe store stocks x pairs of sneakers and y pairs of sandals. During a promotion, a pair of sneakers is priced at $50 and a pair of sandals at $36. The shop manages to sell half the sneakers and 80% of the sandals. Write an expression for the total amount of sales the store makes.

Answer:
Total amount of sales the store makes = \(\frac{x}{2}\) + \(\frac{4}{5}\)y.

Explanation:
A shoe store stocks x pairs of sneakers and y pairs of sandals.
Total number of pair of sneakers a shoe store = x.
Total number of pair of sandals a shoe store = y.
a pair of sneakers is priced at $50 and a pair of sandals at $36.
=> Cost of pair of sneakers = $50.
Cost of pair of sandals = $36.
The shop manages to sell half the sneakers and 80% of the sandals.
Number of sneakers sold = Total number of pair of sneakers a shoe store ÷ 2.
= x ÷ 2 or \(\frac{x}{2}\)
Number of sandals sold = (80 ÷ 100) × y
= \(\frac{80}{100}\)y.
= \(\frac{4}{5}\)y
Total amount of sales the store makes = Number of sneakers sold + Number of sandals sold
= \(\frac{x}{2}\) + \(\frac{4}{5}\)y.

Math in Focus Course 2A Practice 3.7 Answer Key

Solve each question using algebraic reasoning.
Question 1.
40% of k liters of acid are added to 60% of w liters of water. Write an algebraic expression for the total volume of the solution.
Answer:
Total volume of the solution = (40% × k) + (60% × w).

Explanation:
40% of k liters of acid are added to 60% of w liters of water.
=> (40% × k) + (60% × w)
Total volume of the solution = (40% × k) + (60% × w).

Question 2.
Write an algebraic expression for the perimeter of the quadrilateral shown.

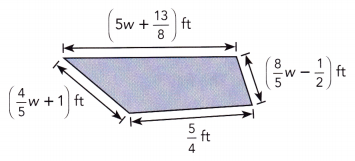
Answer:
Perimeter of the quadrilateral = \(\frac{37}{5}\)w + \(\frac{17}{8}\)

Explanation:
Perimeter of the quadrilateral = AB + BC + CD + AC
Perimeter of the quadrilateral = [5w + \(\frac{13}{8}\)] ft + [\(\frac{8}{5}\)w – \(\frac{1}{2}\)] ft +  \(\frac{5}{4}\) ft + [\(\frac{4}{5}\)w + 1] ft
= 5w + \(\frac{8}{5}\)w + \(\frac{4}{5}\)w + \(\frac{13}{8}\) – \(\frac{1}{2}\) + 1
LCD of 8 n 2 = 8.
= [(25w + 8w + 4w) ÷ 5] + [(13 – (1 × 4) + 8) ÷ 8]
= (33w + 4w) ÷ 5] + (13 – 4 + 8) ÷ 8
= (37w ÷ 5) + [(9 + 8) ÷ 8]
= (37w ÷ 5) + (17 ÷ 8) or \(\frac{37}{5}\)w + \(\frac{17}{8}\)

Question 3.
If the average daily sales amount for the past 5 days was (2.3q + 1.4) dollars, write an algebraic expression for the total sales amount for the past 5 days.
Answer:
Total sales amount for the past 5 days = 4.6q + 2.8.

Explanation:
If the average daily sales amount for the past 5 days was (2.3q + 1.4) dollars.
=> Let the sales be x.
Average daily sales for 5 days = (2.3q + 1.4)
Total sales amount for the past 5 days = Average daily sales for 5 days × 2
= (2.3q + 1.4) × 2
= (2.3q × 2) + (1.4 × 2)
= 4.6q + 2.8.

Question 4.
The weight of 2 science fiction books and 1 autobiography is \(\frac{5}{6}\) w pounds. What is the total weight of 4 of these science fiction books and 2 of these autobiographies?
Answer:
Total weight of 4 of these science fiction books and 2 of these autobiographies = \(\frac{5}{3}\) w pounds.

Explanation:
The weight of 2 science fiction books and 1 autobiography is \(\frac{5}{6}\) w pounds.
=> Weight of 2 science fiction books and 1 autobiography = \(\frac{5}{6}\) w pounds.
Total weight of 4 of these science fiction books and 2 of these autobiographies = 2 × Weight of 2 science fiction books and 1 autobiography
= 2 × \(\frac{5}{6}\) w pounds.
= \(\frac{5}{3}\) w pounds.

Question 5.
On her way to work, Ms. Bowman waited 20 minutes at a subway station. The train ride took her (x + 30) minutes to reach Grand Central Station. Then, she walked for another \(\frac{1}{3}\)x minutes before reaching her office. How much time, in minutes, did Ms. Bowman take to travel to her office?
Answer:
Number of minutes Ms. Bowman take to travel to her office = \(\frac{4}{3}\)x + 50.

Explanation:
Number of minutes Ms. Bowman waited  at a subway station = 20.
Number of minutes train ride took her to reach Grand Central Station = (x + 30)
Number of minutes train she walked before reaching her office = \(\frac{1}{3}\)x
Number of minutes Ms. Bowman take to travel to her office = Number of minutes Ms. Bowman waited  at a subway station + Number of minutes train ride took her to reach Grand Central Station + Number of minutes train she walked before reaching her office
= 20 + (x + 30) + \(\frac{1}{3}\)x
= x + 20 + 30 + \(\frac{1}{3}\)x
= x + \(\frac{1}{3}\)x + 50
= [(3x + x) ÷ 3] + 50
= \(\frac{4}{3}\)x + 50.

 

Question 6.
A ribbon measuring (v + 4) feet in length was cut into two pieces in the ratio 3 : 7. What was the length of the longer piece?
Answer:
Length of longer piece =  7x or 7(v+4)/10.

Explanation:
Total length of ribbon = (v + 4)
Ratio of the ribbon cut into two pieces = 3 : 7
=>let the two pieces be 3x and 7x , then
3x + 7x = v+4
10x = v+4
x = (v+4)/10
Length of the two pieces:
one piece = 3x or 3(v+4)/10.
Other piece =  7x or 7(v+4)/10.

 

Question 7.
When one-fifth of the boys left, there were still b boys and g girls who stayed to see a program. What was the total number of boys and girls at the beginning of the program?
Answer:
Total number of boys and girls at the beginning of the program = \(\frac{5}{4}\)b + g.

Explanation:
Number of girls = g.
Let the boys at the beginning be x.
Then, subtract one fifth from x to get b boys.
=> x – \(\frac{1}{5}\) = b.
=> (5x – x) ÷ 5 = b
=> 4x = b × 5
=> 4x = 5b
=> x = \(\frac{5}{4}\)b.
Total number of boys and girls at the beginning of the program = Number of boys at the beginning + Number of girls
= \(\frac{5}{4}\)b + g.
Question 8.
John is paid at an hourly-rate of $15 an hour and overtime time rate of 1.5 times his hourly-rate for his work. If John puts in w regular hours and y overtime hours in a week, what is his total wage for the week?
Answer:
Total wage for the week = $262.50.

Explanation:
Number of dollars John is paid at an hourly-rate for a day= 15.
overtime time rate of 1.5 times his hourly-rate for his work.
=> Number of dollars he gets for overtime for a day = 1.5 × Number of dollars John is paid at an hourly-rate for a day
= 1.5 × 15
= 22.5.
If John puts in w regular hours and y overtime hours in a week.
Number of days in a week = 7.
Total wage for the week = Number of days in a week × (Number of dollars John is paid at an hourly-rate for a day + Number of dollars he gets for overtime for a day)
= 7  × ( $15 + $22.5)
= 7 × $37.5
= $262.50.

Question 9.
Nathan is p years old now. In 10 years’ time, he will be 3 times as old as Martin. Express Martin’s age 10 years from now in terms of p.
Answer:
Martin’s age 10 years from now = (p – 20) ÷ 3 years.

Explanation:
Age of Nathan now = p years.
Let Martin age be m years now.
In 10 years’ time, he will be 3 times as old as Martin.
Age of Nathan 10 years later = (p + 10) = 3(m + 10)
=> p + 10 = 3m + 30
=> p = 3m + 30 – 10
=> p = 3m + 20.
=> p – 20 = 3m
=> (p – 20) ÷ 3 years = m.

Question 10.
Tom bought a computer for 15% off from the list price of p dollars. If the sales tax was 8%, how much did he pay for the computer including sales tax?
Answer:
Total price of computer he paid= 0.918p.

Explanation:
List price of computer Tom bought = p dollars.
Tom bought a computer for 15% off
=> Sales price of computer = p – (15% × p)
= (100p – 15p) ÷ 100
= 85p ÷ 100
= 0.85p.
Tax on Sales tax = (8% ) × Sales price of computer
= (8 ÷ 100) × 0.85p
= 0.08 × 0.85p
= 0.068p.
Total price of computer he paid = Sales price of computer  + Tax on Sales tax
= 0.85p + 0.068p
= 0.918p.

Question 11.
A farmer collected some eggs from his farm and found b eggs broken. He packed the remaining eggs in c egg cartons. Each egg carton can hold a dozen eggs and no eggs were leftover. Write an algebraic expression for the number of eggs he collected initially in terms of b and c.

Answer:
Number of eggs he collected initially = 12c + b.

Explanation:
Number of eggs broken = b.
Number of remaining eggs he packed in carton = c.
Number of eggs each canton can hold = 12 or dozen.
Number of eggs he collected initially = (Number of eggs each canton can hold × Number of remaining eggs he packed in carton) + Number of eggs broken
= (12 × c) + b
= 12c + b.

Question 12.
A teacher from Anderson Middle School printed k nametags in preparation for the science fair. Half of the nametags were given out to students and 100 nametags were given out to parents. Three-fifths of the remaining nametags were given out to teachers and contest judges. How many nametags were not given out?
Answer:
Number of nametags not given = \(\frac{1}{5}\)k –  40.

Explanation:
Total number of nametags teacher from Anderson Middle School printed in preparation for the science fair = k.
Number of nametags given to students = \(\frac{1}{2}\) × Total number of nametags teacher from Anderson Middle School printed in preparation for the science fair
= \(\frac{1}{2}\) × k
= \(\frac{1}{2}\)k.
Number of nametags given to parents = 100.
Total number of nametags given to parents and students = Number of nametags given to students + Number of nametags given to parents
= \(\frac{1}{2}\)k + 100
Remaining nametags = k – [\(\frac{1}{2}\)k + 100]
= (2k – k) ÷ 2 – 100
= \(\frac{1}{2}\)k – 100
Total number of nametags given to parents and students = \(\frac{3}{5}\) [Remaining nametags]
= \(\frac{3}{5}\) [\(\frac{1}{2}\)k – 100]
= \(\frac{3}{10}\)k – 60.
Number of nametags not given = \(\frac{2}{5}\) [\(\frac{1}{2}\)k – 100]
= \(\frac{1}{5}\)k –  40.

Question 13.
At the beginning of a journey, the fuel tank of a car was \(\frac{3}{4}\)-full. When the car reached its destination, it had consumed 60% of the gasoline in the tank. The full capacity of the fuel tank is w gallons.
a) Write an algebraic expression for the amount of gasoline left in the fuel tank.
Answer:
Amount of gasoline left in the fuel tank = 2w ÷ 5 gallons.

Explanation:
Total Capacity of fuel in the car = w gallons.
Capacity of the fuel tank of a car at the beginning of a journey = \(\frac{3}{4}\)w gallons.
Capacity of fuel the car consumed to reach its destination = 60% ×Total Capacity of fuel in the car
= 60% of w.
= \(\frac{6}{10}\)w
= \(\frac{3}{5}\) w gallons.
Amount of gasoline left in the fuel tank = Total Capacity of fuel in the car – Capacity of fuel the car consumed to reach its destination
= w – \(\frac{3}{5}\) w.
= (5w – 3w) ÷ 5
= 2w ÷ 5 gallons.

b) If w = 15.5, how much gasoline was left at the end of the journey?
Answer:
Amount of gasoline left at the end of the journey = 6.2 gallons.

Explanation:
Amount of gasoline left in the fuel tank = 2w ÷ 5 gallons.
If w = 15.5:
Amount of gasoline left at the end of the journey = 2w ÷ 5
= (2 × 15.5) ÷ 5
= 31 ÷ 5
= 6.2 gallons.

Bain @ work
Bryan and his father are from Singapore, where the temperature is measured in degrees Celsius. While visiting downtown Los Angeles, Bryan saw a temperature sign that read 72°F. He asked his father what the equivalent temperature was in °C.

His father could not recall the Fahrenheit-to-Celsius conversion formula, C = \(\frac{5}{9}\)(F – 32). However, he remembered that water freezes at 0°C or 32°F and boils at 100°C or 212°F.

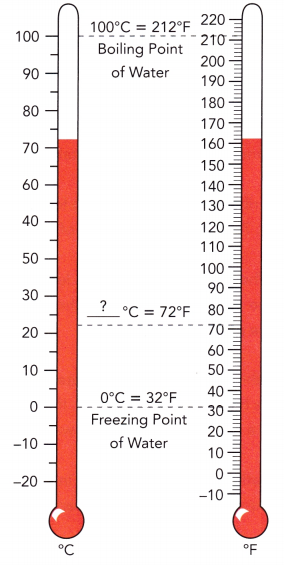
Using these two pieces of information, would you be able to help Bryan figure out the above conversion formula? Explain.
Answer:
Equivalent temperature of 72°F in Bryan asked his father = 22.22°C

Explanation:
Temperature Bryan saw While visiting downtown Los Angeles = 72°F
Fahrenheit-to-Celsius conversion formula:
(F – 32) ×\(\frac{5}{9}\)
= (72 – 32) × \(\frac{5}{9}\)
= 40 × \(\frac{5}{9}\)
= 200 ÷ 9
= 22.22 °C.