Math in Focus Grade 8 Chapter 4 Lesson 4.4 Answer Key Sketching Graphs of Linear Equations

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 4 Lesson 4.4 Sketching Graphs of Linear Equations to finish your assignments.

Math in Focus Grade 8 Course 3 A Chapter 4 Lesson 4.4 Answer Key Sketching Graphs of Linear Equations

Math in Focus Grade 8 Chapter 4 Lesson 4.4 Guided Practice Answer Key

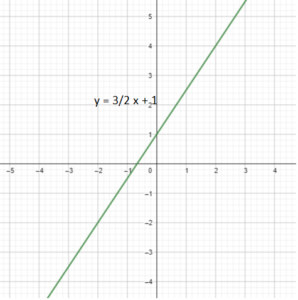
Use graph paper. Use 1 grid square to represent 1 unit for the x interval from -2 to 2, and the y interval from -2 to 4.

Question 1.
Graph the equation y = \(\frac{3}{2}\)x + 1.
Answer:

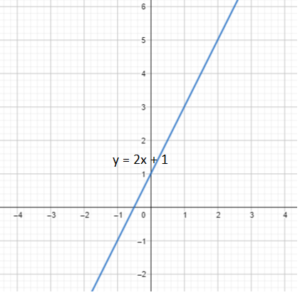
Use graph paper. Use 1 grid square to represent 1 unit on both axes for the x interval from 0 to 3, and the y Interval from -3 to 7.

Question 2.
Graph the equation y = 2x + 1.
Answer:

Question 3.
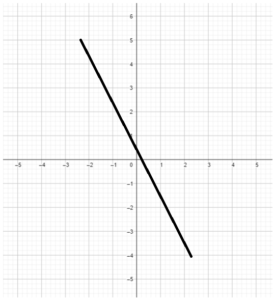
Graph the equation y = –\(\frac{1}{3}\)x – 2.
Answer:

Use graph paper. Use 1 grid square to represent 1 unit on both axes for the x interval from -2 to 2, and the y interval from 0 to 10.

Question 4.
Graph a line with slope -2 that passes through the point (2, 2).
Answer:

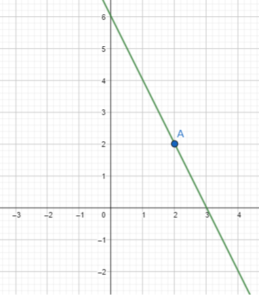
Question 5.
Graph a line with slope 2 that passes through the point (-2, 1).
Answer:

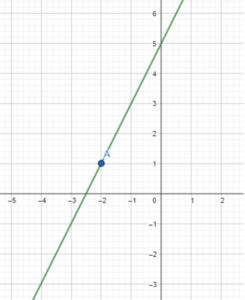
Math in Focus Course 3A Practice 4.4 Answer Key

For this practice, use 1 grid square to represent 1 unit on both axes for the interval from -6 to 6.

Graph each linear equation.

Question 1.
y = \(\frac{1}{3}\)x + 1
Answer:

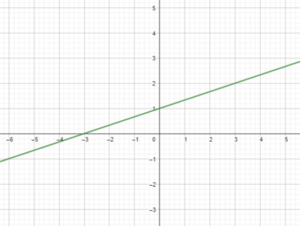
Question 2.
y = \(\frac{1}{6}\)x + 3
Answer:

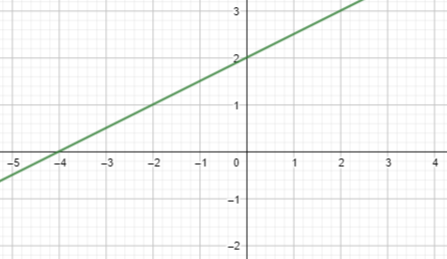
Question 3.
y = \(\frac{1}{2}\)x + 2
Answer:

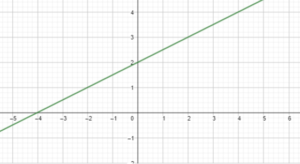
Question 4.
y = \(\frac{2}{3}\)x – 1
Answer:

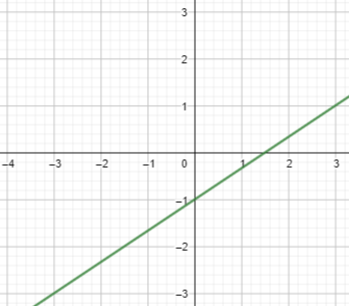
Question 5.
y = -x + 5
Answer:

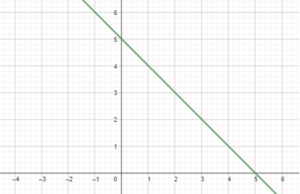
Question 6.
y = 3 – \(\frac{1}{4}\)x
Answer:

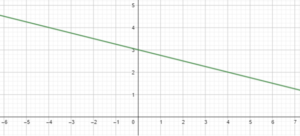
Question 7.
y = 1 – \(\frac{1}{2}\)x
Answer:

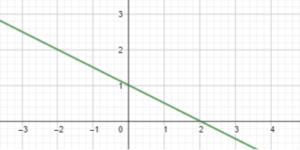
Question 8.
y = –\(\frac{1}{5}\)x – 2
Answer:

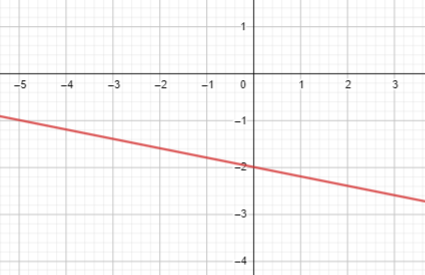
Question 9.
Math Journal Graph the equation y = 2 – \(\frac{2}{3}\)x. Explain how to use the graph to find other solutions of the equation.
Answer:

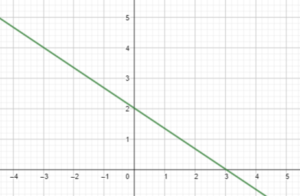
First select a value of the x-coordinate on the x-axis. Then trace it along the vertical grid lines until the gridline intersects with the graph.
Then trace horizontally from the graph to the y-axis to obtain the corresponding y-coordinate. This pair of x-coordinate and y-coordinate is one solution to the equation.

Question 10.
Math Journal Martha says that the point (4, -2) lies on the graph of the equation y = –\(\frac{1}{4}\)x – 1. Explain how you can find out if she is right without actually graphing the equation.
Answer:

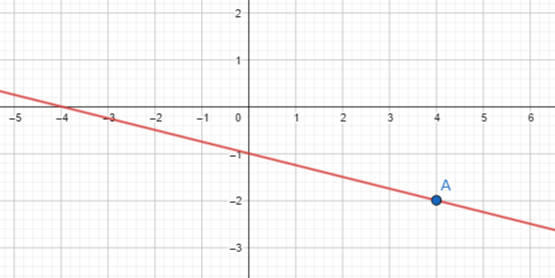
Graph each line with the given slope that passes through the given point.

Question 11.
Slope = \(\frac{2}{5}\); (5, 4)
Answer:
y = \(\frac{2}{5}\)x + 4

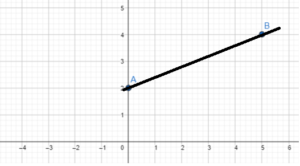
Question 12.
Slope = \(\frac{2}{3}\); (6, 1)
Answer:

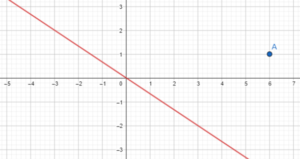
Question 13.
Slope = -3; (1, 0)
Answer:

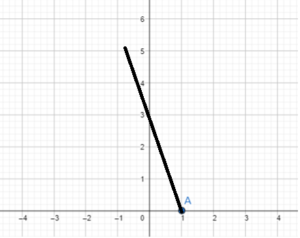
Question 14.
Slope = -2; (-1, -2)
Answer:

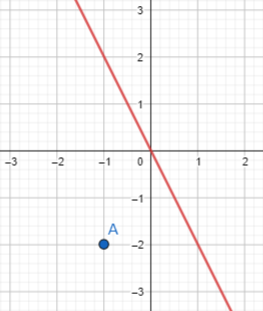
Question 15.
Math Journal Suppose that Emily shows you some of her homework:

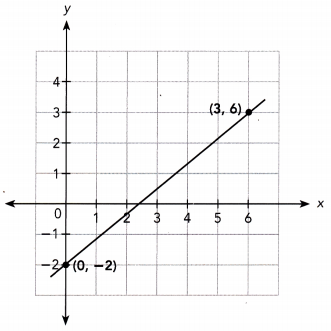
Graph the equation y = -2x + \(\frac{1}{2}\).
Describe Emily’s mistake. Graph the equation correctly.
Answer:
Emily made three mistakes. She labeled the coordinates (6, 3) incorrectly, drew the slope of the line incorrectly, and mistook the value for the slope as the y-intercept.