Math in Focus Grade 2 Mid Year Review Answer Key

Practice the problems of Math in Focus Grade 2 Workbook Answer Key Mid Year Review to score better marks in the exam.

Math in Focus Grade 2 Mid Year Review Answer Key

Multiple Choice

Fill in the circle next to the correct answer.

Question 1.
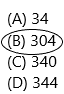
Which shows three hundred four?
(A) 34
(B) 304
(C) 340
(D) 344
Answer: Option  B is correct.

Explanation:
Follow the rules to write numbers in words:
The rules to write the numbers in words are discussed here. To write any number in the form of words, we have to check the place value. Let us learn this by observing the below steps.
1. The place value of one’s, a number from 1 to 9 is written in words as, one, two, three, four, five, six, seven, eight and nine.
2. The least number which is at tens place is 10, which is written in words as ten.
3. The numbers from 11 to 19 are written in words as, eleven, twelve, thirteen, fourteen, fifteen, sixteen, seventeen, eighteen and nineteen. And the next number is twenty.
4. After twenty, the numbers follow the pattern in such a way that they are written in words as thirty, forty, fifty, sixty, seventy, eighty, ninety and so on.
5. The preceding numbers are linked with these words and mentioned from one to nine. For example, twenty-one, twenty-two, etc.
Here 304 is given:
In number 304, one’s place is occupied with 4, so there are 4 ones, and tens place is also occupied with 0, so there are 0 tens, and hundred’s place is occupied with 3, so there are 3 hundred’s. So 3 hundred’s, 0 tens and 4 ones. Or we can write, 304 as ‘three hundred four’ in words.

 

Question 2.
Which number is shown in the chart?

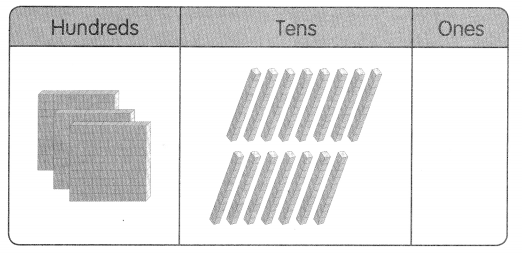
(A) 450
(B) 405
(C) 350
(D) 315
Answer: Option D is correct.

Explanation:
Observe the above picture, In the hundred’s place there are 3 stones. In ten’s place, there are 15 stones. In one’s place, there are no stones. By using this information, we can write the number.
The number is 315 and written in words are three hundred fifteen.

Question 3.
Continue the pattern.
540, 650, 760, 870, _____
(A) 890
(B) 950
(C) 980
(D) 1000
Answer: Option C is correct.

Explanation:
In Mathematics, number patterns are the patterns in which a list number follows a certain sequence. Generally, the patterns establish the relationship between two numbers. It is also known as the sequence of series in numbers. In order to solve the problems on the number pattern, first, we have to understand the rule being followed in the pattern.
The given numbers are 540, 650, 760, 870 and the next number is 980.
How it is 980, will be explained below:
The number starts with 540 and the next number is increased by 110.
If we add 110 to 540 then we get 540+110=650 and so on…870+110=980.
In another way we can think is by using places of digits.
540: 0 is in one’s place, 4 is in ten’s place, 5 is in hundred’s place. And coming to the next number, the number is in one’s place stays the same, the ten’s place is increased by 1 and the hundred’s place is increased by 1 and so on… the places of digits were increasing by 1.

Question 4.
Add the two numbers shown on the chart.

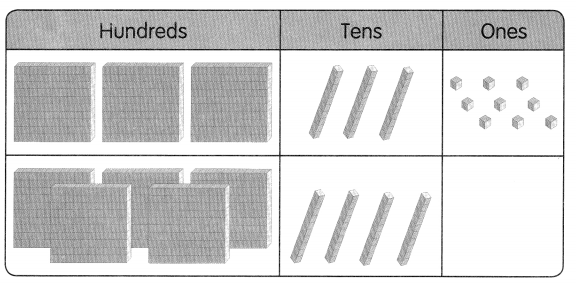
(A) 879
(B) 560
(C) 319
(D) 241
Answer: Option A is correct.

Explanation:
In the above picture, the first row has 3 stones are present in a hundred’s place, 3 stones are present in a ten’s place and 9 stones are present in one’s place.
The second row has 5 stones are present in a hundred’s place, 4 stones are present in a ten’s place and there are no stones present in one’s place.
By using the information of the first row we can write in words as three hundred thirty-nine and in number 339.
By using the information of the second row we can write in words as five hundred forty and in number 540.
Now add both the numbers:339+540=879.

Question 5.
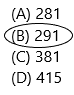
275 + 16 = _______
(A) 281
(B) 291
(C) 381
(D) 415
Answer: Option B is correct.

Explanation:
The addition is taking two or more numbers and adding them together, that is, it is the total sum of 2 or more numbers. The numbers with more than 2 digits can also be added vertically. We always start adding from the ones digit and move towards the digits at the highest place.
By adding 275 and 16 we get 291.

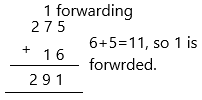
Question 6.
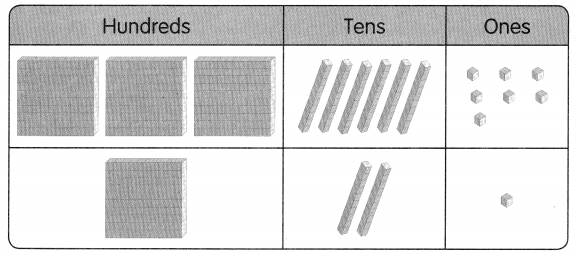
Subtract the two numbers shown on the chart.

(A) 488
(B) 367
(C) 246
(D) 121
Answer: Option C is correct.

Explanation:
In the above picture, the first row has 3 stones are present in a hundred’s place, 6 stones are present in a ten’s place and 7 stones are present in one’s place.
The second row has 1 stone is present in a hundred’s place, 2 stones are present in a ten’s place and there is 1 stone present in one’s place.
By using the information of the first row we can write in words as three hundred sixty-seven and in number 367.
By using the information of the second row we can write in words as one hundred twenty-one and in number 121.
Now add both the numbers:367-121=246.

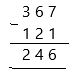
Question 7.
Subtract.

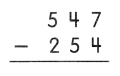
(A) 801
(B) 393
(C) 313
(D) 293
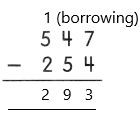
Answer: Option D is correct.

Explanation:
– In math, to subtract means to take away from a group or a number of things.
– When we subtract, the number of things in the group reduce or become less.
– The minuend, subtrahend and difference are parts of a subtraction problem.
– In the subtraction problem, 547 – 254 = 293, the number 547 is the minuend, the number 254 is the subtrahend and the number 293 is the difference.

Question 8.
Use these digits.

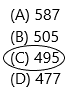
Make the greatest 3-digit number. Then make the least 3-digit number. Then subtract the two numbers.
(A) 587
(B) 505
(C) 495
(D) 477
Answer: Option c is correct.

Explanation:
The given number 2  7  5:
By using the above number we should make the greatest number:
– The digit at hundred’s place should be greatest of 2, 5, 7.
– So digit 7 should be there.
– Also no digit can repeat, so now we are left with digits 5 and 7.
– The digit at ten’s place should be greatest of 5 and 7 Hence digit 5 will be placed at ten’s place.
– Now, we are left with 2. The digit at one’s place is the remaining number.
– Therefore digit 2 will be placed at one’s place
– Hence the greatest three-digit number is 752.
By using the same numbers we should make the least number:
– The digit at hundred’s place should be the smallest of 2, 5, 7. So digit 2 should be there.
– Also no digit can repeat, so now we are left with digits 5 and 7.
– The digit at ten’s place should be the smallest of 5 and 7. Hence digit 5 will be placed at ten’s place.
– Now, we are left with 7. The digit at one’s place should be the remaining number.
– Therefore digit 7 will be placed at one’s place
– Hence the smallest three-digit number is 257.
Now subtract both the numbers:752-257=495.

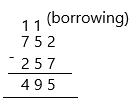
Question 9.
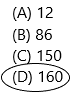
Darren has 86 marbles. Max has 74 marbles. How many marbles do they have in all?
(A) 12
(B) 86
(C) 150
(D) 160
Answer: Option D is correct.

The number of marbles Darren has=86
The number of marbles Max has=74
The total number of marbles =86+74=160.
Therefore, they both are having 160 marbles.

Question 10.
Felix has $125. He uses $70 to buy a pair of shoes. How much does he have left?
(A) $195
(B) $87
(C) $75
(D) $ 55
Answer: Option D is correct.

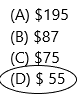
Explanation:
The amount Felix has is $125
The amount he uses to buy a pair of shoes is $70.
Now the amount he left with is assuming ‘X’.
To calculate the remaining amount we need to subtract the total amount-used amount. Then we get the answer.
X=125-70
X=55.

Question 11.
Look at the picture.

How many flowers are there?
(A) 7 + 5
(B) 7 × 5
(C) 5 × 2
(D) 5 × 10
Answer: Option B is correct.

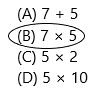
Explanation:

In the above picture, there are 7 sets. In each set, there are 5 flowers.
To calculate the number of flowers we have to multiply the number of sets and flowers present in the set.
The total number of flowers=X
X=7×5
X=35.

Question 12.
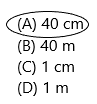
The length of a placemat is about ____
(A) 40 cm
(B) 40 m
(C) 1 cm
(D) 1 m
Answer: Option A is correct.

Explanation:
The standard or average size of the placemat is:
– Width: 12-14 inches
– Length: 16-20 inches
1 inch = 2.54 cm
Therefore, 16×2.54=40.64 cms.

Question 13.
Rosa has a ribbon 100 centimetres long. She uses 45 centimetres of it. What is the length of the ribbon left?
(A) 155 cm
(B) 100 cm
(C) 55 cm
(D) 65 cm
Answer: Option C is correct.

Explanation:
The number of centimetres she has ribbions=100
The number of cms she uses=45
The length of the remaining ribbon=X
To calculate the remaining ribbon we need to subtract total cms-used cms.
X=100-45
X=55.

Question 14.
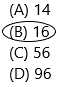
Letoya buys 35 books on Monday. She buys 21 books on Tuesday. She sells 40 of these books. How many books does she have left?
(A) 14
(B) 16
(C) 56
(D) 96
Answer: Option B is correct.

Explanation:
The number of books she buys on monday=35
The number of books she buys on tuesday=21
The total number of books she buys=35+21=56.
The number of books she sells in that 56 books=40.
The number of she has after selling 40 books=X
To calculate the value of X we need to subtract the total books-number of books sold.
X=56-40
X=16.

Question 15.
A carton of milk has a mass of 450 grams. Two cartons are put into a box with a mass of 37 grams. What is the total mass of the cartons and the box?
(A) 413 g
(B) 863 g
(C) 937 g
(D) 974 g
Answer: Option D is correct.

Explanation:
The mass of each carton of milk=450 grams.
The mass of each box to put cartons=37 grams.
The number of cartons of milk=2.
The total mass of carton of milk=450×2=900
The number of boxes=2
The total mass of 2 boxes=37×2=74.
The total mass of the cartons and the box=900+74=974.

Short Answer

Read the questions carefully.
Write your answers in the space provided.

Question 16.
Write 386 in words.
Answer: Three hundred eighty-six.
Follow the rules to write numbers in words:
The rules to write the numbers in words are discussed here. To write any number in the form of words, we have to check the place value. Let us learn this by observing the below steps.
1. The place value of one’s, a number from 1 to 9 is written in words as, one, two, three, four, five, six, seven, eight and nine.
2. The least number which is at tens place is 10, which is written in words as ten.
3. The numbers from 11 to 19 are written in words as, eleven, twelve, thirteen, fourteen, fifteen, sixteen, seventeen, eighteen and nineteen. And the next number is twenty.
4. After twenty, the numbers follow the pattern in such a way that they are written in words as thirty, forty, fifty, sixty, seventy, eighty, ninety and so on.
5. The preceding numbers are linked with these words and mentioned from one to nine. For example, twenty-one, twenty-two, etc.
Here 386 is given:
In number 386, one’s place is occupied with 6, so there are 6 ones, and tens place is also occupied with 8, so there are 8 tens, and hundred’s place is occupied with 3, so there are 3 hundred’s. So 3 hundred’s, 8 tens and 6 ones. Or we can write, 386 as ‘three hundred eighty-six’ in words.

Question 17.
Write 520 in expanded form.
Answer: 520 = (5 * 10²) + (2 * 10¹)
In mathematics, the expanded form of a number is defined as the notation. It is the way of writing the numbers to define the individual digit value. When the numbers are written using place value, it will create a new algebraic expression.

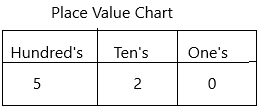
Here,
5 – Hundreds place, i.e. 500
2 – Tens place, i.e. 20
0 – one’s place, i.e. 0
520 = (5 * 10²) + (2 * 10¹)
520 = (5 * 100) + (2 * 10)
520 = 500 + 20.

Question 18.
Order the numbers from greatest to least.

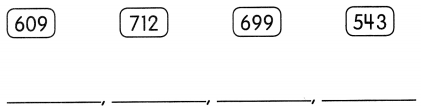
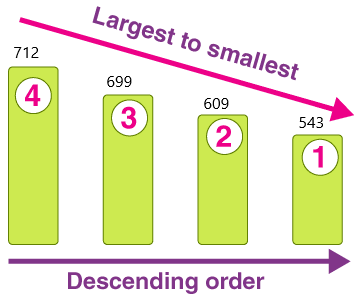
Answer: 712, 699, 609, 543.
In Mathematics, if a pattern of numbers is in the decreasing value, then the numbers are in descending order. It means that the numbers are arranged in the highest order to the lowest order. The symbol used to represent the order in descending form is ‘ > ‘. It shows the given sequence in increasing to decreasing order.
For example numbers from 1 to 10 can be represented in this form using the descending symbol. 10 > 9 > 8 > 7 > 6  > 5 > 4 > 3 > 2 >1.

Question 19.
Add 38 and 156. ________

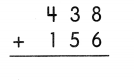
Answer: 594
Explanation:
The addition is taking two or more numbers and adding them together, that is, it is the total sum of 2 or more numbers. The numbers with more than 2 digits can also be added vertically. We always start adding from the ones digit and move towards the digits at the highest place.

Question 20.
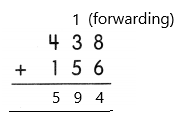
Subtract 17 from 831. _________
Answer: 814.
– In math, to subtract means to take away from a group or a number of things.
– When we subtract, the number of things in the group reduce or become less.
– The minuend, subtrahend and difference are parts of a subtraction problem.
– In the subtraction problem, 831 – 17 = 814, the number 831 is the minuend, the number 17 is the subtrahend and the number 814 is the difference.

Question 21.
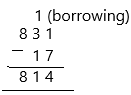
Subtract 284 from 861. ____
Answer: 577
– In math, to subtract means to take away from a group or a number of things.
– When we subtract, the number of things in the group reduce or become less.
– The minuend, subtrahend and difference are parts of a subtraction problem.
– In the subtraction problem, 861 – 284 = 577, the number 861 is the minuend, the number 284 is the subtrahend and the number 577 is the difference.

Question 22.
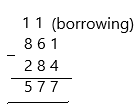
Fill in the blanks.
7 × 2 = ______ 2 × 7 = ___
_____ ÷2 = 7 _____ ÷ 7 = _____
Answer:
7 × 2 = 14  2 × 7= 14
– Multiplication is the process of calculating the product of two or more numbers. The multiplication of numbers say, ‘a’ and ‘b’, is stated as ‘a’ multiplied by ‘b’.
– In Maths, the basic explanation of multiplication is adding a number, with respect to another number, repeatedly.
– The symbol of multiplication is denoted by a cross sign (×) and also sometimes by a dot (.).
– The multiplication formula is given by:
Multiplier × Multiplicand = Product
1. The multiplicand is the total number of objects in each group
2. The multiplier is the number of equal groups
3. Product is the result of multiplication of multiplier and multiplicand
– If Multiplier = 7 and Multiplicand = 2, then the product is:
Product = 7 x 2 = 14.
Division:
14 ÷2 = 7  14 ÷ 7 = 2
– The division is a method of distributing a group of things into equal parts. It is one of the four basic operations of arithmetic, which gives a fair result of sharing.
– There are various signs which can be used to indicate division such as ÷, /.
– Each part involved in a division equation has a special name.
– Dividend ÷ divisor = quotient
Dividend: The dividend is the number that is being divided in the division process.
Divisor: The number by which dividend is being divided is called the divisor.
Quotient: A quotient is a result obtained in the division process.

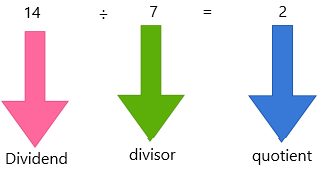
– The remainder is the portion of the dividend that is left over after division.
– The remainder is 0 for the above problem.
Special facts about division:
1. When dividing something by 1, the answer will always be the original number. It means if the divisor is 1, the quotient will always be equal to the dividend such as 10 ÷ 1= 10.
2. Division by 0 is undefined.
3. The division of the same dividend and divisor is always 1. For example: 4 ÷ 4 = 1.

Question 23.
What is the length of Drawing A? ________ cm
_____________ Drawing A
Answer:
The actual length of drawing A is 5 cm – 10 mm  1 cm – 2 mm.

Question 24.
What is the mass of the vegetables?

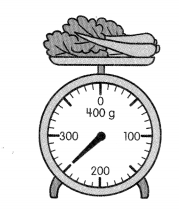
_________ g
Answer:250 grams.
Grams is a unit of measurement used to measure very light objects. For example, a small metal paperclip has a mass of around 1 gram. Other objects with a mass of about 1 gram are a stick of gum and a dollar bill. We can abbreviate the unit gram with the letter g.
In the clock show, the minute hand is after 200. Every minute is 10, 20, 30, 40, 50.
The minute hand is showing on 50. So, add 200+50=250 grams.

Question 25.
Fill in the blank with more than or less than.

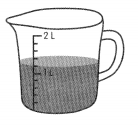
The container has ____________ 1 lifer of water.
Answer: more.
The container has more than 1 litre. Because in the above diagram, the liquid is above 1 litre. So it was more.

Question 26.
The Recycling Committee has $746. They raise $198 more. How much do they have now?
$__________
Answer: $944
Explanation:
The amount for the recycling committee=$746
The amount raised more=$198
The total amount of the committee=746+198=$944.

Question 27.
In a game, the Green Team scored 270 points. The Yellow Team scored 363 points. How many more points did the Yellow Team score than the Green Team?
_____ points
Answer: 93 points more.
Explanation:
The points scored green team=270
The points scored yellow team=363.
Now we have to calculate the points scored yellow team more than the green team.n Assume it as X.
X=363-270
X=93
Therefore, 93 points more for yellow team than green team.

Question 28.
Gina has 200 beads. 94 of the beads are red. The rest are yellow. How many yellow beads does Gina have? Complete the bar model. Then find the answer.

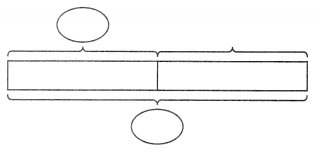
Gina has ___ yellow beads.
Answer:106 yellow beads.

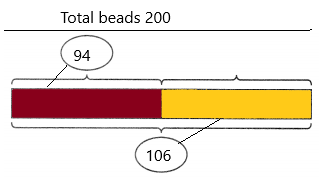
Explanation:
The number of total beads=200
The number of red beads=94.
The number of yellow beads=X
To calculate yellow beads subtract total beads – red beads. Then we get the remaining beads that are yellow beads.
X=200-94
X=106.

Question 29.
138 cars and 27 vans are in a parking lot. How many vehicles are there in all? Draw a bar model. Then find the answer.
There are ___ vehicles in all.
Answer: 165 vehicles.

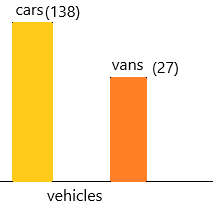
Explanation:
The total number of cars=138
The total number of vans=27
The total number of vehicles=138+27=165.

Question 30.
The mass of a bottle of oil is 2 kilograms. What is the mass of 9 such bottles? The mass is ___ kilograms.
Answer:18 kilograms.
Explanation:
The mass of each bottle of oil=2 kilograms.
We need to calculate for 9 bottles.
The mass of 9 bottles=9*2=18.
Therefore, the mass is 18 kilograms.

Question 31.
Eva has 40 crayons. She gives them to her friends to be shared equally. Each friend receives 5 crayons. How many friends are there?
There are ____ friends.
Answer:8 friends.
Explanation:
The number of crayons Eva has=40
The number of crayons she gives each friend=5
She shares it equally. Now we have to calculate the number of friends. Assume it as X.
X=40/5
X=8.
Therefore, 8 friends are there. She gives crayons equally to 8 friends..

Extended Response

Solve.

Show your work.

Question 32.
The Finch family drives 352 miles on vacation. The Perez family drives 168 miles more than the Finch family.

a. How far does the Perez family drive?

b. How many miles do they drive in all?

a. The Perez family drives _________ miles.

b. They drive _________ miles in all.
Answer: 520 miles.
Explanation:
(a). The number of miles Finch drives on vacation=352
The number of miles Perez drives more than Finch on vacation=168.
The total number of Perez drives more=352+168=520.
Therefore, he drives 520 miles.
(b). The total they drive in all is 520 miles. Add the miles they both drive then we get a total number of miles.
Therefore, 352+168=520.

Question 33.
Tasha has 249 cards. Tim has 53 fewer cards than Tasha. Lee has 79 more cards than Tim. How many cards does Lee have?

Lee has ___ cards.
Answer: 275 cards.
The number of cards Tasha has=249
The number of cards Tim has fewer than Tasha=53.
The total number of cards Tim has=249-53=196.
The total number of cards Lee has more than Tim=79.
The total number of cards Lee has=196+79=275.
Therefore, Lee has 275 cards.

Question 34.
Mikayla has 5 strings of beads. Each string has 4 beads on it. Mikayla divides her beads into 2 strings of beads.
a. How many beads does Mikayla have in all?

b. How many beads are there on each string in the end?

a. Mikayla has ___ beads in all.

b. There are ___ beads on each string in the end.
Answer:
a. Mikayla has 20 beads in all.
Explanation:
The number of strings she has=5
The total number of beads in each string=4
Later, the number of strings she divided her beads=2
The total number of beads=5*4=20.
Therefore, 20 beads are there.
b. There are 10 beads on each string in the end.
Explanation:
She divided beads into 2 strings. She has a total of 20 beads. Now we need to calculate the number of beads present in each string after the division of beads into 2 strings. Assume it as X.
X=20/2
X=10.
Therefore, 10 beads are present in each string after division.

Question 35.
The height of Kory’s desk is 58 centimeters. The height of Kory’s door is 239 centimeters.
a. What is the total height of Kory’s desk and door?

b. What is the difference in height between Kory’s desk and door?

a. The total height of Kory’s desk and door is ___ centimeters.

b. The difference in height between Kory’s desk and door is _________ centimeters.
Answer:
a. The total height of Kory’s desk and the door is 297 centimetres
Explanation:
Given:
The desk height=58 cms
The door height=239 cms
Now add both heights to get the total in between them. Assume it as X.
X=58+239
X=297.
b. The difference in height between Kory’s desk and the door is 181 centimetres.
Explanation:
To calculate difference between them we need to subtract both the cms.
239-58=181.
Therefore, the difference is 181 cms.

Question 36.
A barrel contains 60 litres of rainwater. Mrs. Potts uses 14 liters of rainwater to water her vegetable garden. She uses another 13 litres of rainwater to wash her car. How much rainwater is left in the barrel?
litres of rainwater is left in the barrel.
____ litres of rainwater is left in the barrel.
Answer: 33 litres.
Explanation:
The number of litres a barrel contains rainwater=60
The number litres she uses for vegetable garden=14
The number of litres she uses to wash her car=13.
The total number of litres used by her=14+13=27
The number of litres left after using=X.
X=60-27
X=33.
Therefore, 33 litres are left.

Question 37.
Ling mixes 120 cups of lemonade in the morning. She mixes 93 cups of lemonade in the afternoon.

a. How many cups of lemonade does she mix in all?

b. She sells 207 cups of lemonade. How many cups of lemonade does she have left?

a. She mixes ___ cups of lemonade in all.

b. She has ___ cups of lemonade left.
Answer:
a. She mixes 213 cups of lemonade in all.
Explanation:
The number of cups she mixes in the morning=120
The number of cups she mixes in the afternoon=93.
The total number of cups in all=120+93=213.
b. She has 6 cups of lemonade left.
Explanation:
Already we know the total number of cups is 213.
The number of cups she sold=207.
The number of cups she left=213-207=6.
Therefore, 6 cups are left.