Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 5 Lesson 5.1 Understanding Direct Proportion to score better marks in the exam.
Math in Focus Grade 7 Course 2 A Chapter 5 Lesson 5.1 Answer Key Understanding Direct Proportion
Hands-On Activity
Identify Direct Proportion In An Experiment
Work in pairs
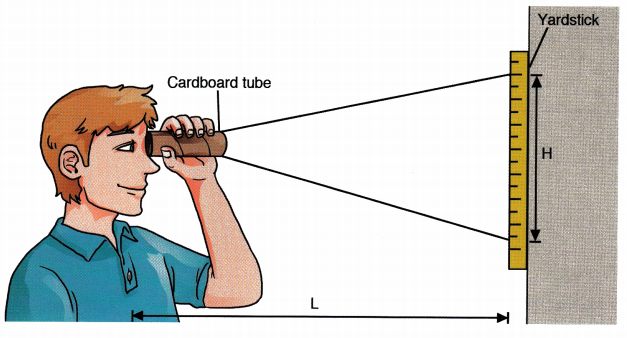
Step 1: Make a table like the one shown.
Step 2: Tape a yardstick to the
Step 3: Stand 1 foot away from the yardstick. Look at the yardstick through the cardboard tube. How many inches of the yardstick can you see? Record the number of inches in the table.
Step 4: Repeat Step 3 for the other values of L shown in the table. Then complete the table.
Math Journal What happens to H as L increases? Based on your observations, do you think H is directly proportional to L? Explain your thinking.
Math in Focus Grade 7 Chapter 5 Lesson 5.1 Guided Practice Answer Key
Copy and complete to determine whether y is directly proportional to x.
Question 1.
The table shows the distance traveled by a school bus, y miles, after x hours.
For each pair of values, x and y:
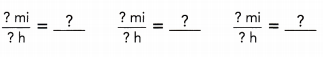
So, the distance traveled by the school bus is 
to the number of hours it has traveled.
The constant of proportionality is . and represents the speed of the bus.
The direct proportion equation is .
Answer:
The constant of proportionality is 50 miles per hour and represents the speed of the bus.
The direct proportion equation: Distance = speed × time.
Explanation:
Distance travelled in 2 hours = 100 miles.
Distance = speed × time
=> 100 = speed × 2
=> 100 ÷ 2 = Speed
=> Speed = 50 miles per hour.
Distance = speed × time
=> 150 = speed × 3
=> 150 ÷ 3 = Speed
=> Speed = 50 miles per hour.
Distance = speed × time
=> 200 = speed × 4
=> 200 ÷ 4 = Speed
=> Speed = 50 miles per hour.
Total distance travelled = 100 + 150 + 200 = 450 miles.
Question 2.
The table shows the number of pitches made, y, in x innings of a baseball game.
For each pair of values, x and y:
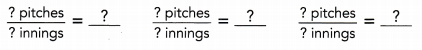
So, the number of pitches made is to the number of innings of a baseball game.
Answer:
The number of pitches made is 95 to the number of innings of a baseball game.
Explanation:
Number of pitches in 1st innings = 15.
Number of pitches in 2nd innings = 30.
Number of pitches in 3rd innings = 50.
Total number of pitches made = Number of pitches in 1st innings + Number of pitches in 2nd innings + Number of pitches in 3rd innings
= 15 + 30 + 50
= 45 + 50
= 95.
Tell whether each equation represents a direct proportion. If so, identify the constant of proportionality.
Question 3.
0.4y = x
0.4y = x
\( \frac{0.4 y}{?}=\frac{x}{?}\)
Divide both sides by .
y = Simplify.
Because the original equation 0.4y = x be rewritten as an equivalent equation in the form y = kx, it a direct proportion. The constant of proportionality is .
Answer:
Because the original equation 0.4y = x direct proportion be rewritten as an equivalent equation in the form y = kx, it y n x are a direct proportion. The constant of proportionality is k.
Explanation:
0.4y = x
Divide both sides by 0.4.
0.4y ÷ 0.4 = x ÷ 0.4
=> y = x ÷ 0.4.
Because the original equation 0.4y = x direct proportion be rewritten as an equivalent equation in the form y = kx, it yn x are a direct proportion. The constant of proportionality is k.
Tell whether each equation represents a direct proportion. If so, find the constant of proportionality.
Question 4.
x = 1 – 2y
x = 1 – 2y
x + 2y = 1 – 2y + 2y Add 2y to both sides.
x + 2y – = 1 – Subtract from both sides
2y = 1 – Simplify.
\(\frac{2 y}{?}=\frac{1}{?}-\frac{?}{?}\) . Divide both sides by .
y = Simplify.
Because the original equation x = 1 – 2y be rewritten as an equivalent equation in the form y = kx, it a direct proportion.
Answer:
Because the original equation x = 1 – 2y not a direct proportion be rewritten as an equivalent equation in the form y = kx, it not a direct proportion.
Explanation:
x = 1 – 2y
Add both sides 2y.
=> x + 2y = 1 – 2y + 2y
=> x + 2y = 1.
=> 2y = 1 – x.
Divide both sides by 2.
=>2y ÷ 2 = (1 – x) ÷ 2
=> y = (1 – x) ÷ 2.
Copy and complete.
Question 5.
The table shows the number of baseballs, y, made in x days. The number of baseballs made is directly proportional to the number of days of production. Find the constant of proportionality and tell what it represents in this situation. Then write a direct proportion equation.
Constant of proportionality:
The constant of proportionality is and represents .
The direct proportion equation is .
Answer:
Constant of proportionality: 56.
The constant of proportionality is 56 and represents baseballs produced.
The direct proportion equation: y = kx.
Explanation:
Number of baseballs produced on 1st day = 56.
=> y = kx
=> 56 = k × 1
=> 56 ÷ 1 = k
=> 56 = k.
Number of baseballs produced on 2nd day = 112.
y = kx
=> 112 = k × 2
=> 112 ÷ 2 = k
=> 56 = k.
Number of baseballs produced on 3rd day = 168.
y = kx
=> 168 = k × 3
=> 168 ÷ 3 = k
=> 56 = k.
Total number of baseballs produced = (Number of baseballs produced on 1st day + Number of baseballs produced on 2nd day + Number of baseballs produced on 3rd day)
= 56 + 112 + 168
= 336.
Question 6.
A cafeteria sells sandwiches for $4 each. The amount Jason pays for some sandwiches is directly proportional to the number he buys. Write an equation that represents the direct proportion.
Let be the number of sandwiches.
Let be the amount Jason pays.
Cost per sandwich: $ per sandwich
The direct proportion equation is = .
Answer:
Cost per sandwich: $4 per sandwich
The direct proportion equation: Cost of sandwiches a cafeteria sells × Number of sandwiches Jason buys = Total amount of sandwiches Jason buys.
Explanation:
Cost of sandwiches a cafeteria sells = $4 each.
Let,
Number of sandwiches Jason buys = 10.
Total amount of sandwiches Jason buys = Cost of sandwiches a cafeteria sells × Number of sandwiches Jason buys
= $4 × 10
= $40.
Question 7.
q is directly proportional to p, and p = 12 when q = 24. Find the constant of proportionality. Then write a direct proportion equation.
Constant of proportionality: \(\frac{q}{p}=\frac{?}{?}\)
= Write in simplest form.
The constant of proportionality is .
The direct proportion equation is .
Answer:
The constant of proportionality: 2.
The direct proportion equation: q = kp.
Explanation:
p = 12 when q = 24.
Direct proportion equation:
q = kp
=> 24 = k × 12
=> 24 ÷ 12 = k
=> 2 = k.
\(\frac{q}{p}=\frac{24}{12}\) = 2.
Solve.
Question 8.
w is directly proportional to h, and w = 18 when h = 3. Find the constant of proportionality. Then write a direct proportion equation.
Answer:
Constant of proportionality: 6.
Direct proportion equation: w = kh.
Explanation:
w = 18 when h = 3.
Direct proportion equation:
w = kh
=> 18 = k × 3
=> 18 ÷ 3 = k
=> 6 = k.
\(\frac{w}{h}=\frac{18}{3}\) = 6.
Math in Focus Course 2A Practice 5.1 Answer Key
Tell whether y is directly proportional to x. If so, find the constant of proportionality. Then write a direct proportion equation.
Question 1.
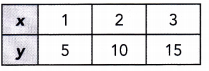
Answer:
Constant of proportionality: 5.
Explanation:
Direct proportion equation:
y = kx
=> 5 = k × 1
=> 5 ÷ 1 = k
=> 5 = k.
y = kx
=> 10 = k × 2
=> 10 ÷ 2 = k
=> 5 = k.
y = kx
=> 15 = k × 3
=> 15 ÷ 3 = k
=> 5 = k.
Question 2.
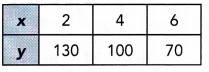
Answer:
Constant of proportionality: 65, 25, 11.67.
Explanation:
Direct proportion equation:
y = kx
=> 130 = k × 2
=> 130 ÷ 2 = k
=> 65 = k.
y = kx
=> 100 = k × 4
=> 100 ÷ 4 = k
=> 25 = k.
y = kx
=> 70 = k × 6
=> 70 ÷ 6 = k
=> 11.67 = k.
Question 3.
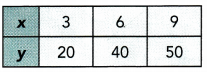
Answer:
Constant of proportionality: 6.67, 6.67, 5.56.
Explanation:
Direct proportion equation:
y = kx
=> 20 = k × 3
=> 20 ÷ 3 = k
=> 6.67 = k.
y = kx
=> 40 = k × 6
=> 40 ÷ 6 = k
=> 6.67 = k.
y = kx
=> 50 = k × 9
=> 50 ÷ 9 = k
=> 5.56 = k.
Question 4.
Answer:
Constant of proportionality: 25.
Explanation:
Direct proportion equation:
y = kx
=> 50 = k × 2
=> 50 ÷ 2 = k
=> 25 = k.
y = kx
=> 100 = k × 4
=> 100 ÷ 4 = k
=> 25 = k.
y = kx
=> 150 = k × 6
=> 150 ÷ 6 = k
=> 25 = k.
Tell whether each equation represents a direct proportion. If so, identify the constant of proportionality.
Question 5.
3y = \(\frac{1}{2}\) x
Answer:
Constant of proportionality: \(\frac{1}{6}\)
Explanation:
3y = \(\frac{1}{2}\) x
=>y = [\(\frac{1}{2}\) x] ÷ 3
=> y = \(\frac{1}{6}\) x
Question 6.
2y – 5 = x
Answer:
No, 2y – 5 = x is not direct proportion equation.
Explanation:
2y – 5 = x
=> 2y = x + 5
=> y = (x + 5) ÷ 2
Question 7.
p = 0.25q
Answer:
Constant of proportionality: 0.25
Explanation:
p = 0.25q
=> y = kx
Question 8.
4.5a = b + 12
Answer:
No, 4.5a = b + 12 is not direct proportion equation.
Explanation:
4.5a = b + 12
=> a = (b + 12) ÷ 4.5
Solve. Show your work.
Question 9.
The table shows the distance traveled, d miles, and the amount of gasoline used, n gallons. Tell whether d is directly proportional to n. If so, give the constant of proportionality and tell what it represents in this situation. Then write a direct proportion equation.
Answer:
Constant of proportionality = 20.
Direct proportion equation: d = kn.
Explanation:
y = kx
=> d = kn
=> 20 = k × 1
=> 20 ÷ 1 = k
=> 20 = k.
d = kn
=> 40 = k × 2
=> 40 ÷ 2 = k
=> 20 = k.
d = kn
=> 60 = k × 3
=> 60 ÷ 3 = k
=> 20 = k.
Question 10.
The table shows the number of points scored, y, in x basketball games. Tell whether y is directly proportional to x. If so, give the constant of proportionality and tell what it represents in this situation. Then write a direct proportion equation.
Answer:
Constant of proportionality: 24, 24, 26.67.
Direct proportion equation: y = kx.
Explanation:
y = kx
=> 24 = k × 1
=> 24 ÷ 1 = k
=> 24 = k.
y = kx
=> 48 = k × 2
=> 48 ÷ 2 = k
=> 24 = k.
y = kx
=> 80 = k × 3
=> 80 ÷ 3 = k
=> 26.67 = k.
Question 11.
The table shows the number of tennis balls produced, y, by x machines. Tell whether y is directly proportional to x. If so, give the constant of proportionality and tell what it represents in this situation. Then write a direct proportion equation.
Answer:
Constant of proportionality: 20.
Direct proportion equation: y = kx.
Explanation:
y = kx
=> 20 = k × 1
=> 20 ÷ 1 = k
=> 20 = k.
y = kx
=> 60 = k × 3
=> 60 ÷ 3 = k
=> 20 = k.
y = kx
=> 100 = k × 5
=> 100 ÷ 5 = k
=> 20 = k.
Question 12.
Math Journal Describe how can you tell whether two quantities are in direct proportion.
Answer:
Two quantities a and b are said to be in direct proportion if they increase or decrease together. In other words, the ratio of their corresponding values remains constant.
Explanation:
Two quantities a and b are said to be in direct proportion if they increase or decrease together. In other words, the ratio of their corresponding values remains constant. This means that,
a/ b = k where k is a positive number, then the quantities a and b are said to vary directly.
Question 13.
Math Journal An equilateral triangle with a side length of c inches has a perimeter of P inches. The perimeter of the equilateral triangle is described by the equation P = 3c. Tell whether P is directly proportional to c. Explain your reasoning.
Answer:
P is directly proportional to c having k = 3.
Explanation:
Length of equilateral triangle side = c inches.
Perimeter of equilateral triangle side = p inches.
Equation of perimeter of the equilateral triangle: P = 3c.
Direct proportion equation: y = kx.
=> P = 3c.
Question 14.
Jim rode his bike at a steady rate of 20 miles per hour. Given that his distance, d miles, is directly proportional to the time he rides, t hours, identify the constant of proportionality and write a direct proportion equation.
Answer:
Constant of proportionality: 20.
Direct proportion equation: d = 20t.
Explanation:
Speed of Jim rode his bike = 20 miles per hour.
Distance = d miles.
Time = t hours.
Distance = speed × time
= d = 20 × t
=> d = 20t miles.
Question 15.
Emily worked in a florist shop and earned $12 per hour. Given that the amount she earned, w dollars, is directly proportional to the time she worked, t hours, identify the constant of proportionality and write a direct proportion equation.
Answer:
Constant of proportionality: $12.
Direct proportion equation: w = S12t.
Explanation:
Amount of money Emily worked in a florist shop and earned = $12 per hour.
Number of hours = t.
Number of dollars she earned = w.
Amount of money she earned = Number of hours × Number of dollars
Number of dollars she earned = Number of hours × Amount of money Emily worked in a florist shop and earned
=>w = t × $12
=> w = S12t.
Question 16.
y is directly proportional to x, and y = 10 when x = 15. Write a direct proportion equation that relates x and y.
Answer:
Direct proportion equation: y = kx.
Explanation:
y = 10 when x = 15.
y = kx
=> 10 = k × 15
=> 10 × 15 = k
=> 2 ÷ 3 or \(\frac{2}{3}\) = k.
Question 17.
y is directly proportional to x, and y = 33 when x = 11. Write a direct proportion equation that relates x and y.
Answer:
Direct proportion equation: y = kx.
Explanation:
y = 33 when x = 11.
Direct proportion equation:
y = kx
=> 33 = k × 11
=> 33 ÷ 11 = k
=> 3 = k.
Question 18.
Karl hikes 3 miles in 45 minutes. Given that his distance is directly proportional to the time he walks, find the constant of proportionality and write an equation to represent the direct proportion.
Answer:
Constant of proportionality: speed = 0.67 miles per hour.
Direct proportion equation: Distance = speed × time.
Explanation:
Distance Karl hikes = 3 miles.
Time Karl hikes = 45 minutes.
Let speed be x.
Distance = speed × time
=> 3 = x × 45
=> 3 ÷ 45 = x.
=> 0.67 miles per hour = x.
Question 19.
Paul pays $20 to download 16 songs. Given that the amount he pays is directly proportional to the number of songs he downloads, find the constant of proportionality and write a direct proportion equation.
Answer:
Constant of proportionality: Cost of each song = $1.25.
Direct proportion equation: Total amount of songs = Number of songs download × Cost of each song.
Explanation:
Amount of money Paul pays = $20.
Number of songs download = 16.
Cost of each song =
Total amount of songs = Number of songs download × Cost of each song
=> $20 = 16 × Cost of each song
=> $20 ÷ 16 = Cost of each song
=> $1.25 = Cost of each song.
Question 20.
Math journal Each table shows the cost of placing an advertisement in a newspaper, C dollars, for t days. Describe how the two tables are alike, and how they are different. Be sure to discuss direct proportion in your answer.
Answer:
Constant of proportionality: Cost of placing an advertisement in a newspaper per day = 20 dollars.
Direct proportion equation: Total cost of advertisement ( c dollars) = Cost of placing an advertisement in a newspaper per day × Number of days.
Explanation:
Number of days of daily post = t = 5.
Total cost of advertisement ( c dollars) = 100.
Let Cost of placing an advertisement in a newspaper per day be x.
Total cost of advertisement ( c dollars) = Cost of placing an advertisement in a newspaper per day × Number of days of daily post
=> 100 = x × 5
=> 100 ÷ 5 = x
=> 20 dollars = x.
Number of days of evening star(t) = 5.
Total cost of advertisement (c dollars) = 80.
Let Cost of placing an advertisement in a newspaper per day be x.
Total cost of advertisement ( c dollars) = Cost of placing an advertisement in a newspaper per day × Number of days of evening star
=> 80 = x × 5
=> 80 ÷ 5 = x
=> 16 dollars = x.