Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 6 Lesson 6.1 Complementary, Supplementary, and Adjacent Angles to score better marks in the exam.
Math in Focus Grade 7 Course 2 B Chapter 6 Lesson 6.1 Answer Key Complementary, Supplementary, and Adjacent Angles
Math in Focus Grade 7 Chapter 6 Lesson 6.1 Guided Practice Answer Key
Technology Activity
Materials:
- geometry software
Explore The Relationship Of Complementary Angles Using Geometry Software
Work in pairs.
Step 1.
Construct \(\overline{\mathrm{AB}}\). Then construct a second line segment, \(\overline{\mathrm{BC}}\), that is perpendicular to \(\overline{\mathrm{AB}}\). Finally, construct line segment \(\overline{\mathrm{BD}}\).
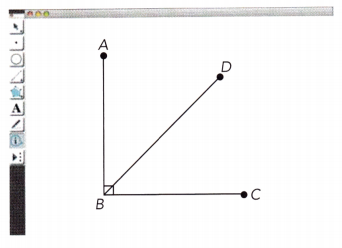
Step 2.
Select ∠ABC and find
Step 3.
Select ∠ABD and find its measure. Then select ∠DBC and find its measure.
Step 4.
Use the calculate function of the program to find the sum of the measures of ∠ABD and ∠DBC. What do you notice about the sum of their measures?
Step 5.
Select the point D and drag it so that you change the measures of ∠ABD and ∠DBC. Record your results in a table as shown below.

Step 6.
As the angle measures change, how does the sum of the angle measures change?
Math Journal
Describe what you notice about the sum of the measures of complementary angles.
Solve.
Question 1.
Name three pairs of complementary angles.
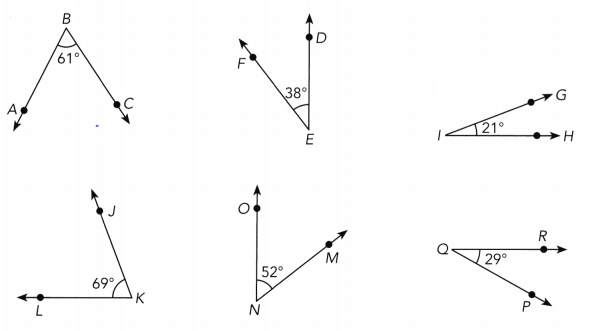
Answer:
m∠ABC = 61° We have:
m∠PQR = 29°
m∠ABC + m∠PQR = 61° + 29° = 90° we add the measures of the two angles:
Since the sum of their measures is 90° ∠ABC and ∠PQR are complementary angles
m∠DEF = 38° We have:
m∠MNO = 52°
m∠DEF + m∠MNO = 38° + 52° = 90° we add the measures of the two angles:
Since the sum of their measures is 90°, ∠DEF and ∠MNO are complementary angles
m∠GIH = 21° We have:
m∠JKL = 69°
m∠GIH + m∠JKL = 21° + 69° = 90° We add the measures of the two angles:
Since the sum of their measures is 90°, ∠GIH and ∠JKL are complementary angles
∠ABC and ∠PQR
∠DEF and ∠MNO
∠GIH and ∠JKL
Copy and complete the table.
Question 2.
Angles A and 8 are complementary. Find m∠B for each measure of ∠A.
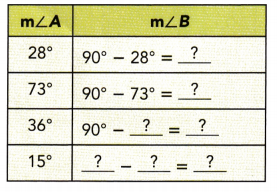
Answer:
m∠A + m∠B = 90° We are given:
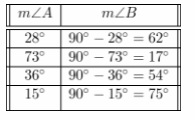
We determine each measure of ∠A:
62° ;17° ;54° ; 75°
Technology Activity
Materials:
- geometry software
Explore The Relationship Of Supplementary Angles Using Geometry Software
Work in pairs.
Step 1.
Construct \(\overline{P R}\). Then construct a second line segment, \(\overline{S Q}\), as shown below.
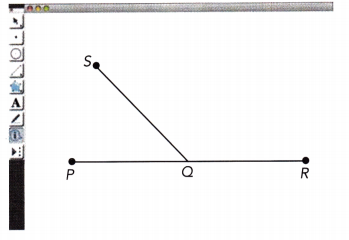
Step 2.
Select ∠PQR and find its measure.
Step 3.
Select ∠SQP and find its measure. Then select ∠SQR and find its measure.
Step 4.
Use the calculate function of the program to find the sum of the measures of ∠SQP and ∠SQR. What do you notice about the sum of their measures?
Step 5.
Select the point S and drag it so that you change the measures of ∠SQP and ∠SQR. Record your results in a table as shown below.

Step 6.
As the angle measures change, how does the sum of the angle measures change?
MathJournal
Describe what you notice about the sum of the measures of supplementary angles.
Solve.
Question 3.
Tell whether each pair of angles is supplementary.
a) m∠X = 32° and m∠Y = 108°
Answer:
m∠X = 32° a) We are given:
m∠Y = 108°
m∠X + m∠Y = 32° + 108° = 140° Add the measures of the two angles:
As m∠X + m∠Y ≠ 180°. ∠X and ∠Y are not supplementary
b) m∠A = 45° and m∠B = 45°
Answer:
m∠A = 45° b) We are given:
m∠B = 45°
m∠A + m∠B = 45° + 45° = 90° Add the measures of the two angles:
As m∠A + m∠B ≠ 180°, ∠A and ∠B are not supplementary.
c) m∠D = 12° and m∠E = 168°
Answer:
m∠D = 12° c) We are given:
m∠E = 168°
m∠D + m∠E = 12° + 168° = 180° Add the measures of the two angles:
As m∠D + m∠E = 180°, ∠D and ∠E are supplementary.
d) m∠V = 85° and m∠W = 95°
Answer:
m∠V = 85° d) We are given:
m∠W = 95°
m∠V + m∠W = 85° + 95° = 180° Add the measures of the two angles:
As m∠V + m∠W = 180°. ∠V and ∠W are supplementary.
Copy and complete the table.
Question 4.
Angles A and B are supplementary. Find m∠B for each measure of ∠A.

Answer:
m∠A + m∠B = 180° We are given:

We determine each measure of ∠A:
98°; 154°; 44°; 75°
Complete.
Question 5.
In the diagram, m∠ABC = 90°. Find the value of x.
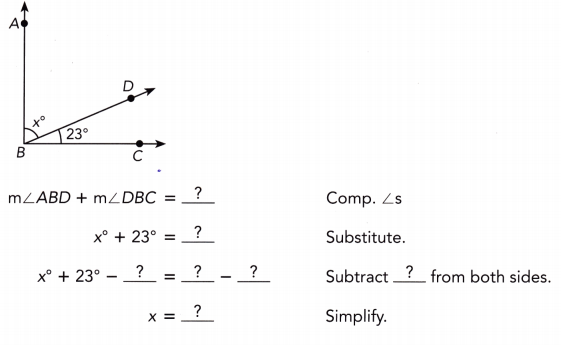
Answer:
We are given
m∠ABD + m∠DBC = 90° Complementary angles:
x° + 23° = 90° Substitute:
x + 23° – 23° = 90° — 23° Subtract 23° from bothsides:
x = 67 Simplify:
x = 67
Given that \(\overleftrightarrow{P Q}\) is a straight line, find the value of y.
Question 6.

Answer:
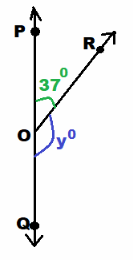
we are given
m∠PQR + m∠ROQ = 180° Adjacent angles on a straight line:
37° + y° = 180° Substitute:
37° + y° – 37° = 180° – 37° Subtract 37° from both sides:
y = 143 Simplify:
y = 143
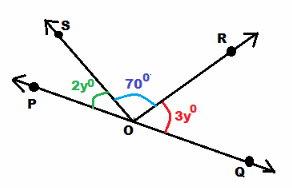
Question 7.
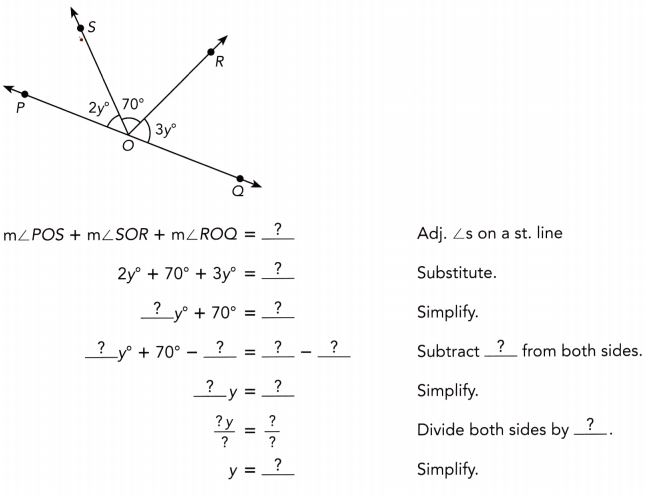
Answer:
we are given
m∠POS + m∠SQR + m∠ROQ = 180° Adjacent angles on a straight line:
2y° + 70° + 3y° = 180° substitute
5y° + 70° = 180° Simplify:
5y° + 70° – 70° = 180° — 70° Subtract 70° from both sides:
5g = 110 Simplify:
\(\frac{5 y}{5}\) = \(\frac{110}{5}\) Divide both sides by 5:
y = 22 Simplify:
y = 22
Complete.
Question 8.
In the diagram, m∠PQR = 90° and the ratio x : y = 1: 4. Find the values of x and y.
Method I
Use bar models.
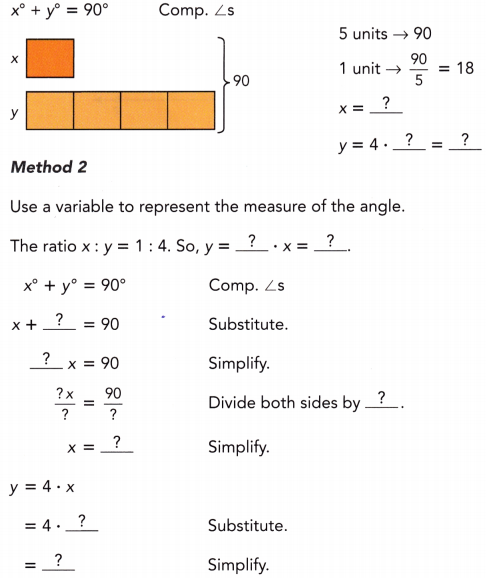
Answer:
m∠PQR = 90°
x : y = 1 : 4
we are given
x° + y° = 90° Method 1; use bar models
Complementary angles:

We use bar models:
5 units → 90 We have:
1 unit → \(\frac{90}{5}\) = 18
x = 18
y = 4 ∙ 18 = 72
Method 2; use a variable to represent the measure of the angle
y = 4 • x = 4x The ratio x : y = 1 : 4 So we have:
x° + y° = 90° Complementary angles
x + 4x = 90 Substitute:
5x = 90 Simplify:
\(\frac{5 x}{5}\) = \(\frac{90}{5}\) Divide both sides by 5:
x = 18 Simplify:
y = 4 • x Substitute:
= 4 • 18
= 72 Simptify:
x = 18; y = 72
Math in Focus Course 2B Practice 6.1 Answer Key
Tell whether each pair of angles is complementary.
Question 1.
m∠A = 25° and m∠B = 65°
Answer:
m∠A = 25° We are given:
m∠B = 65°
m∠A + m∠B = 25° + 65° = 90° We compute the sum:
Because the sum of the measures of the two angles is exactly 90°, the given angles are complementary.
Yes
Question 2.
m∠C = 105° and m∠D = 7°
Answer:
m∠C = 105° We are given:
m∠D = 7°
m∠C + m∠D = 105° + 7° = 112° We compute the sum:
Because the sum of the measures of the two angles is not exactly 90°, the given angles are not complementary.
No
Question 3.
m∠E = 112° and m∠F = 68°
Answer:
m∠E = 112° We are given:
m∠F = 68°
m∠E + m∠F = 112° + 68° = 180° We compute the sum:
Because the sum of the measures of the two angles is not exactly 90° the given angles are not complementary.
No
Question 4.
m∠G = 45° and m∠H = 45°
Answer:
m∠G = 45° We are given:
m∠H = 45°
m∠G + m∠H = 45° + 45° = 90° We compute the sum:
Because the sum of the measures of the two angles is exactly 90°, the given angles are complementary.
Yes
Tell whether each pair of angles is supplementary.
Question 5.
m∠A = 130° and m∠8 = 50°
Answer:
m∠A = 130° We are given:
m∠B = 50°
m∠A + m∠B = 130° + 50° = 180° We compute the sum:
Because the sum of the measures of the two angles is exactly 180°, the given angles are supplementary.
Yes
Question 6.
m∠C = 90° and m∠D = 80°
Answer:
m∠C = 90° We are given:
m∠D = 80°
m∠C + m∠D = 90° + 80° = 170° We compute the sum:
Because the sum of the measures of the two angles is exactly 180°, the given angles are not supplementary.
No
Question 7.
m∠E = 120° and m∠F = 60°
Answer:
m∠E = 120° We are given:
m∠F = 60°
m∠E + m∠F = 120° + 60° = 180° We compute the sum:
Because the sum of the measures of the two angles is exactly 180°, the given angles are supplementary.
yes
Question 8.
m∠G = 60° and m∠H = 30°
Answer:
m∠G = 60° We are given:
m∠H = 30°
m∠G + m∠H = 60° + 30° = 90° We compute the sum:
Because the sum of the measures of the two angles is exactly 180°, the given angles are not supplementary.
yes
Find the measure of the complement of the angle with the given measure.
Question 9.
19°
Answer:
m∠θ = 19° We are given:
90° – m∠θ = 90° – 19 = 71° We determine the measure of the complement of the angle with the given
measure:
71°
Question 10.
64°
Answer:
m∠θ = 64° We are given:
90° – m∠θ = 90° – 64° = 26° We determine the measure of the complement of the angle with the given
measure:
26°
Question 11.
7°
Answer:
m∠θ = 7° We are given:
90° – m∠θ = 90° – 7° = 83° We determine the measure of the complement of the angle with the given
measure:
83°
Question 12.
35°
Answer:
m∠θ = 35° We are given the angle:
90° – m∠θ = 90° – 35° = 55° We determine the measure of the complement of the angle with the given
measure:
55°
Find the measure of the supplement of the angle with the given measure.
Question 13.
78°
Answer:
m∠θ = 78° We are given the angle:
180° – m∠θ = 180° – 78° = 102° We determine the measure of the complement of the angle with the given measure:
102°
Question 14.
4°
Answer:
m∠θ = 4° We are given the angle:
180° – m∠θ = 180° – 78° = 102° We determine the measure of the complement of the angle with the given measure:
176°
Question 15.
153°
Answer:
m∠θ = 153° We are given the angle:
180° – m∠θ = 180° – 153° = 27° We determine the measure of the complement of the angle with the given measure:
27°
Question 16.
101°
Answer:
m∠θ = 101° We are given the angle:
180° – m∠θ = 180° – 101° = 79° We determine the measure of the complement of the angle with the given measure:
79°
∠ABD and ∠DBC are complementary angles. Find the value of x.
Question 17.
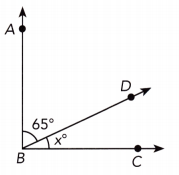
Answer:
m∠ABD + m∠DBC = 90° ∠ABD and ∠DBC complementary:
65 + x = 90 Substitute:
65 + x – 65 = 90 – 65 Subtract 65 from both sides:
x = 25 Simplify:
x = 25
Question 18.
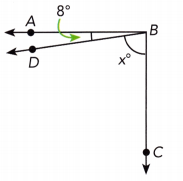
Answer:
m∠ABD + m∠DBC = 90° ∠ABD and ∠DBC complementary:
8 + x = 90 Substitute:
8 + x – 8 = 90 – 8 Subtract 8 from both sides:
x = 82 Simplify:
x = 82
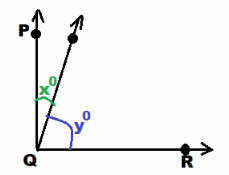
∠PQS and ∠SQR are complementary angles. Find the value of m.
Question 19.
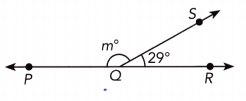
Answer:
m∠PQS + m∠SQR = 90° ∠PQS and ∠SQR supplementary:
m + 29 = 180 Substitute:
m + 29 – 29 = 180 – 29 Subtract 29 from both sides:
x = 151 Simplify:
x = 151
Question 20.
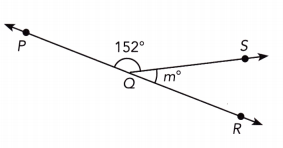
Answer:
m∠PQS + m∠SQR = 180° ∠PQS and ∠SQR supplementary:
152 + m = 180 Substitute:
152 + m – 152 = 180 – 152 Subtract 152 from both sides:
m = 28 Simplify:
m = 28
Answer each of the following.
Question 21.
The measure of an angle is 7°. Find the measure of its complement.
Answer:
m∠θ = 7° We are given the angle:
90° – m∠θ = 90° – 7° = 83° We determine the measure of the complement of the angle with the given measure:
83°
Question 22.
The measure of an angle is 84°. Find the measure of its supplement.
Answer:
m∠θ = 84° We are given the angle:
180° – m∠θ = 180° – 84° = 96° We determine the measure of the supplement of the angle with the given measure:
83°
Question 23.
Math Journal
a) Find the measures of the complement and the supplement of each of the following angles, where possible.
m∠W = 2° m∠X = 40° m∠Y = 32° m∠Z = 115°
Answer:
m∠W = 2° a) we are given the angle:
90° – m∠W = 90° – 2° = 88° We determine the complement of ∠W:
180° – m∠W = 180° – 2° = 178° We determine the supplement of ∠W:
m∠X = 40° We are given the angle:
90° — m∠X = 90° – 40° = 50° We determine the complement of ∠X:
180° — m∠X = 180° – 40° = 140° We determine the supplement of ∠X:
m∠Y = 32° We are given the angle:
90° — m∠Y = 90° — 32° = 58° We determine the complement of ∠Y:
180° — m∠Y = 180° — 32° = 148° We determine the supplement of ∠Y:
m∠Z = 115° We are given the angle:
As m∠Z > 90°: ∠Z has no complement
180° — m∠Z = 180 — 115° = 65° We determinethe supplement of ∠Z:
b) Which angle in a) does not have both a complement and a supplement?
Answer:
∠Z does not have both complement and supplement
c) In general, what must be true about the measure of an angle that has both a complement and a supplement?
Answer:
In order that an angle has both complement and supplement, its measure must be greater or equal than 0° and less or equal than 90°.
Question 24.
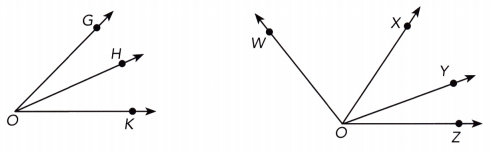
Math Journal Identify all the angles in each diagram. Tell which angles are adjacent. Explain your reasoning.
The measure of ∠ABC = 90°. Find the value of x.
Answer:
∠GOH We identify all the angles in the first diagram:
∠HOK
∠GOK
∠GOH and ∠HOK The adjacent angles in the diagram is the pair of angles which have a common side and a common vertex and don’t overlap:
∠WOX We identify all the angles in the second diagram:
∠XOY
∠YOZ
∠WOY
∠XOZ
∠WOZ
∠WOX and ∠XOY (common side OX, common vertex O) We identify the adjacent angles in the second diagram:
∠XOY and ∠YOZ (common side OY, common vertex O)
∠WOY and ∠YOZ (common side OY, common vertex O)
∠WOX and ∠XOZ (common side OX, common vertex O)
Question 25.
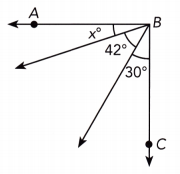
Answer:
m∠ABC = 90° We are given:
x° + 42° + 30° = 90° we have
x + 72° = 90°
x + 72 – 72 = 90 – 72 Subtract 72 from both sides
x = 18 simplify
x = 18
Question 26.
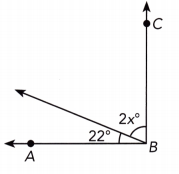
Answer:
m∠ABC = 90° We are given:
2x° + 22° = 90° we have
2x + 22 – 22 = 90 – 22 Subtract 22 from both sides
2x = 68 simplify
\(\frac{2 x}{2}\) = \(\frac{68}{2}\) Divide by 2:
x = 34 simplify:
x = 34
Question 27.
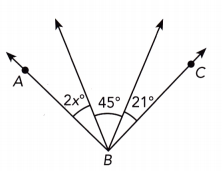
Answer:
m∠ABC = 90° We are given:
2x° + 45° + 21° = 90° we have
2x° + 66 = 90°
2x + 66 — 66 = 90 — 66 Subtract 66 from both sides:
2x = 24 Simplify:
\(\frac{2 x}{2}\) = \(\frac{24}{2}\) Divide by 2:
x = 12 Simplify:
x = 12
Question 28.
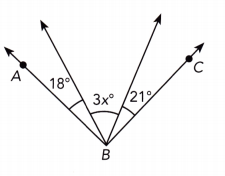
Answer:
m∠ABC = 90° We are given:
18° + 3x° + 21° = 90° we have
39° + 3x° = 90°
39 + 3x — 39 = 90 — 39 Subtract 39 from both sides:
3x = 51 Simplify:
\(\frac{3 x}{3}\) = \(\frac{51}{3}\) Divide by 3:
x = 17 Simplify:
x = 17
\(\overleftrightarrow{P R}\) is a straight line. Find the value of m.
Question 29.
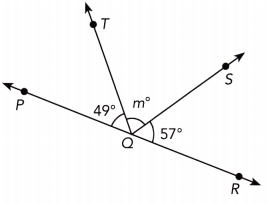
Answer:
m∠PQR = 90° Because \(\overline{P R}\) is a straight line, we have
m∠PQT + m∠TQS + m∠SQR = m∠PQR we have
49° + m° + 57° = 180° substitute
106° + m° = 180°
106 + m – 106 = 180 – 106 subtract 106 from both sides
m = 74
Question 30.
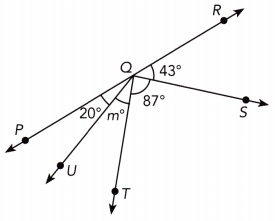
Answer:
m∠PQR = 180° Because \(\overline{P R}\) is a straight line, we have
m∠PQT + m∠TQS + m∠SQR = m∠PQR we have
20° + m° + 87° = 180° substitute
150° + m° = 180°
150 + m – 150 = 180 – 150 subtract 150 from both sides
m = 30 Simplify:
m = 30
In the diagram, the ratio a: b = 2: 3. Find the values of a and b.
Question 31.
Answer:
a : b = 2 : 3 we are given
\(\frac{a}{b}\) = \(\frac{2}{3}\) we rewrite the ratio
3a = 2b cross-multiply
\(\frac{3 a}{3}\) = \(\frac{2 b}{3}\) Divide both sides by 3
a = \(\frac{2 b}{3}\)
m∠RQS + m∠SQP = 90° ∠RQS and ∠SQP are complementary
b + a = 90
b + \(\frac{2 b}{3}\) = 90 substitute
\(\frac{3 b+2 b}{3}\) = 90 Determine b
\(\frac{5 b}{3}\) = 90
5b = 3 ∙ 90
5b = 270
\(\frac{5 b}{5}\) = \(\frac{270}{5}\)
b = 54
a = \(\frac{2 \cdot 54}{3}\) = 36 Determine a
a = 36
b = 54
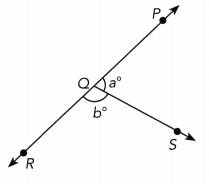
Question 32.
\(\overleftrightarrow{P R}\) is a straight line.
Answer:
a : b = 2 : 3 we are given
\(\frac{a}{b}\) = \(\frac{2}{3}\) we rewrite the ratio
3a = 2b cross-multiply
\(\frac{3 a}{3}\) = \(\frac{2 b}{3}\) Divide bothsides by 3
a = \(\frac{2 b}{3}\)
m∠RQS + m∠SQP = 180° ∠RQS and ∠SQP are supplementary
b + a = 180 substitute
b + \(\frac{2 b}{3}\) = 180
\(\frac{3 b+2 b}{3}\) = 180
\(\frac{5 b}{3}\) = 180
5b = 3 ∙ 180
5b = 540
\(\frac{5 b}{5}\) = \(\frac{540}{5}\)
b = 108
a = \(\frac{2 \cdot 108}{3}\) = 72
a = 72
b = 108
Solve.
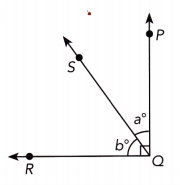
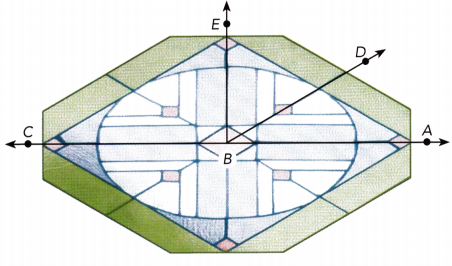
Question 33.
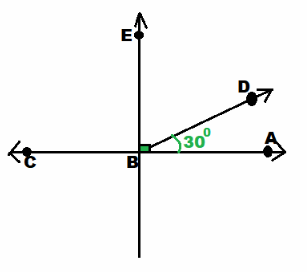
The diagram shows the pattern on a stained glass window. \(\overleftrightarrow{A C}\) is a straight line. ∠EBD and ∠DBA are complementary angles and m∠DBA = 30°. Find the measures of ∠EBD and ∠CBD.
Answer:
we are given
m∠EBD + m∠DBA = 90° ∠EBD and ∠DBA complementary:
m∠EBD + 30° = 90° Substitute:
m∠EBD + 30° — 30° = 90° – 30° Subtract 30° from both sides:
m∠EBD = 60° Simplify:
m∠CBD + m∠DBA = 180° \(\overline{A C}\) straight line:
m∠CBD + 30° = 180° Substitute
m∠CBD + 30° – 30° = 180° – 30° Subtract 30° from both sides
m∠CBD = 150° Simplify
m∠EBD = 60°
m∠CBD = 150°
Question 34.
The diagram shows a kite. The two diagonals \(\overline{M P}\) and \(\overline{Q T}\) are perpendicular to each other. Identify all pairs of complementary angles and all pairs of supplementary angles that are not pairs of right angles.
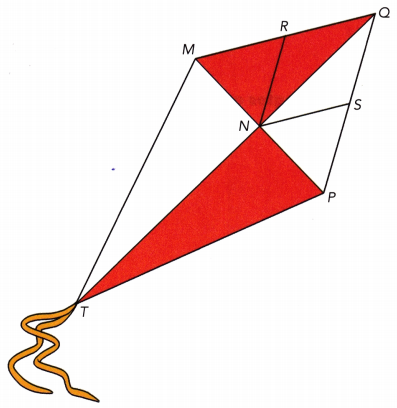
Answer:
\(\overline{M P}\) ⊥ \(\overline{Q T}\) We are given:
∠MNR and ∠RNQ We identify the pairs of complementary angles:
∠QNS and ∠SNP
∠NMQ and ∠MQN
∠NQP and ∠QPN
∠TMN and ∠MTN
∠NTP and ∠NPT
∠MNR and ∠RNQ We identify the pairs of supplementary angLes that are not pairs of right angles:
∠MNS and ∠SNP
Complementary angles: ∠MNR and ∠RNQ
∠QNS and ∠SNP
∠NMQ and ∠MQN
∠NQP and ∠QPN
∠TMN and ∠MTN
∠NTP and ∠NPT
Supplementary angles: ∠MNR and ∠RNP
∠MNS and ∠SNP