Math in Focus Grade 6 Chapter 10 Lesson 10.2 Answer Key Area of Parallelograms and Trapezoids

Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 10 Lesson 10.2 Area of Parallelograms and Trapezoids to score better marks in the exam.

Math in Focus Grade 6 Course 1 B Chapter 10 Lesson 10.2 Answer Key Area of Parallelograms and Trapezoids

Math in Focus Grade 6 Chapter 10 Lesson 10.2 Guided Practice Answer Key

Complete to find the sum of the bases, height, and area of each trapezoid. Each square measures 1 unit by 1 unit.

Question 1.

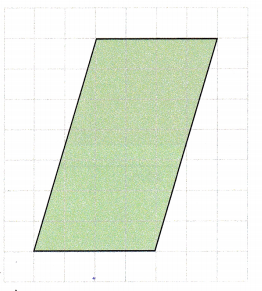
Base = units
Height = units
Area = bh
= ∙
= units²
Answer:
The base in the above figure is occupying 4 units, so it will measure 4 units and the height is occupying 7 units, so it will measure 7 units.
Base = 4 units
Height = 7 units
Area of rectangle = base×height
= 4×7
= 28 sq.units

Question 2.

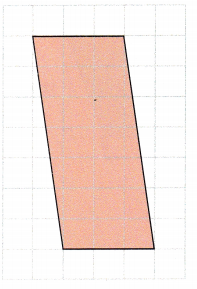
Base = units
Height = units
Area = bh
= ∙
= units²
Answer:
The base in the above figure is occupying 3 units, so it will measure 4 units and the height is occupying 7 units, so it will measure 7 units.
Base = 3 units
Height = 7 units
Area of rectangle = base×height
= 3×7
= 21 sq.units

Question 3.

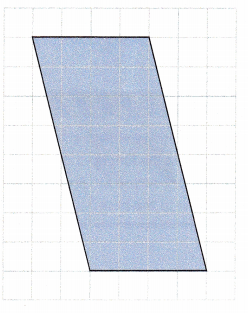
Base = units
Height = units
Area = bh
= ∙
= units²
Answer:
The base in the above figure is occupying 4 units, so it will measure 4 units and the height is occupying 8 units, so it will measure 7 units.
Base = 4 units
Height = 8 units
Area of rectangle = base×height
= 4×8
= 32 sq.units

Question 4.

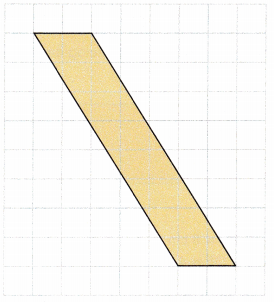
Base = units
Height = units
Area = bh
= ∙
= units²
Answer:
The base in the above figure is occupying 2 units, so it will measure 4 units and the height is occupying 8 units, so it will measure 7 units.
Base = 4 units
Height = 8 units
Area of rectangle = base×height
= 4×8
= 32 sq.units

Complete to find the area of each trapezoid.

Question 5.

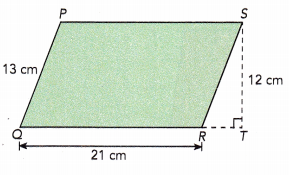
Base = units
Height = units
Area = bh
= ∙
= cm²
Answer:
In the given figure, base measures 21cm and the height measures 12cm.
Base = 21cm
Height = 12cm
Area = base × height
= 21 × 12
= 252 sq.cm

Question 6.

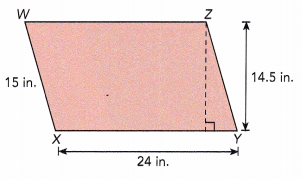
Base = in.
Height = in.
Area = bh
= ∙
= in²
Answer:
In the given figure, base measures 24 in and the height measures 14.5 in.
Base = 24 in
Height = 14.5 in
Area = base × height
= 24 × 14.5
= 348 sq.in

Complete to find the sum of the bases, height, and area of each trapezoid. Each square measures 1 unit by 1 unit.

Question 7.

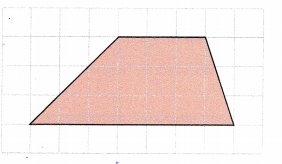
Height = units
Sum of bases = +
= units
Area = \(\frac{1}{2}\)h(sum of bases)
= ∙ ∙
= units²
Answer:
The lengths will be equal to the number of squares each occupies because each square has length of 1 unit.
Given figure has two bases measuring 7 units and 3 units each. The height is measuring 3 units.
Height = 3 units
Sum of bases = (7+3)
= 10 units
Area = \(\frac{1}{2}\)h(sum of bases)
= \(\frac{1}{2}\)×3×10
= \(\frac{1}{2}\)×30
= 30÷2
= 15 sq.units

Question 8.

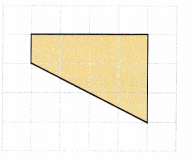
Height = units
Sum of bases = +
= units
Area = \(\frac{1}{2}\)h(sum of bases)
= ∙ ∙
= units²
Answer:
The lengths will be equal to the number of squares each occupies because each square has length of 1 unit.
Given figure has two vertical bases measuring 1 unit and 3 units each. The horizontal height is measuring 4 units.
Height = 4 units
Sum of bases = 1+3
= 4 units
Area = \(\frac{1}{2}\)h(sum of bases)
= \(\frac{1}{2}\)×4×4
= \(\frac{1}{2}\)×16
= 16÷2
= 8 sq.units

Question 9.

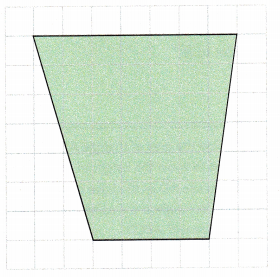
Height = units
Sum of bases = +
= units
Area = \(\frac{1}{2}\)h(sum of bases)
= ∙ ∙
= units²
Answer:
The lengths will be equal to the number of squares each occupies because each square has length of 1 unit.
Given figure has two vertical bases measuring 4 units and 7 units each. The horizontal height is measuring 7 units.
Height = 7 units
Sum of bases = 4+7
= 11 units
Area = \(\frac{1}{2}\)h(sum of bases)
= \(\frac{1}{2}\)×7×11
= \(\frac{1}{2}\)×77
= 77÷2
= 38.5 sq.units

Question 10.

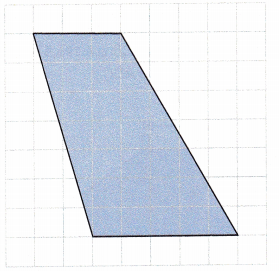
Height = units
Sum of bases = +
= units
Area = \(\frac{1}{2}\)h(sum of bases)
= ∙ ∙
= units²
Answer:
The lengths will be equal to the number of squares each occupies because each square has length of 1 unit.
Given figure has two vertical bases measuring 5 units and 3 units each. The horizontal height is measuring 7 units.
Height = 7 units
Sum of bases = 5+3
= 8 units
Area = \(\frac{1}{2}\)h(sum of bases)
= \(\frac{1}{2}\)×7×8
= \(\frac{1}{2}\)×56
= 56÷2
= 28 sq.units

Complete to find the area of each trapezoid.

Question 11.

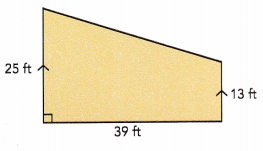
Height = ft
Sum of bases = +
= ft
Area = \(\frac{1}{2}\)h(sum of bases)
= ∙ ∙
= ft²
Answer:
Given figure has two vertical parallel sides measuring 25ft and 13ft each. The height of the trapezoid is 39ft.
Height = 39ft
Sum of bases = 25+13
= 38 ft
Area = \(\frac{1}{2}\)h(sum of bases)
= \(\frac{1}{2}\)×39×38
= 1482÷2
= 741 sq.ft

Question 12.

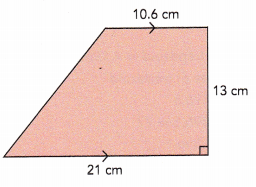
Height = cm
Sum of bases = +
= cm
Area = \(\frac{1}{2}\)h(sum of bases)
= ∙ ∙
= cm²
Answer:
Given figure has two horizontal parallel sides measuring 10.6cm and 21cm each. The height of the trapezoid is 13cm.
Height = 13cm
Sum of bases = 10.6+21
= 31.6 cm
Area = \(\frac{1}{2}\)h(sum of bases)
= \(\frac{1}{2}\)×31.6×13
= 410.8÷2
= 205.4 sq.cm

Complete to find the area of triangle ABD.

Question 13.
The area of trapezoid ABCD is 1,248 square centimeters.

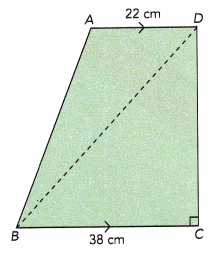
Area of trapezoid ABCD = \(\frac{1}{2}\)h(b₁ + b₂)
= \(\frac{1}{2}\) ∙ h ∙ ( + )
= \(\frac{1}{2}\) ∙ h ∙
= \(\frac{1}{2}\) ∙ ∙ h
= ∙ h
Since area of trapezoid = cm²
• h = area of trapezoid
• h =
h =
= cm
Height of trapezoid =
= cm
Area of triangle ABD = \(\frac{1}{2}\)bh
= \(\frac{1}{2}\) • •
= cm²
The area of triangle ABD is square centimeters.

Answer:
Given that the area of trapezoid ABCD is 1,248 sq.cm
From the figure, we can observe two horizontal parallel sides measuring 22 cm and 38 cm.
Sum of the sides = 22+38 = 60cm
Area of trapezoid ABCD = \(\frac{1}{2}\)×h×(b₁ + b₂)
= \(\frac{1}{2}\) × h × 60
= \(\frac{60}{2}\) × h
= 30×h
Since area of trapezoid = 1,248 cm²
30×h = 1248
(30×h)÷30 = 1248÷30
h = 41.6 cm
Height of trapezoid = 41.6 cm
Area of triangle ABD = \(\frac{1}{2}\)×b×h
Let us assume the base as AD measuring 22cm and the height is 41.6cm
= \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×22×41.6
= 915.2÷2
= 457.6 sq.cm
The area of triangle ABD is 457.6 square centimeters.

Math in Focus Course 1B Practice 10.2 Answer Key

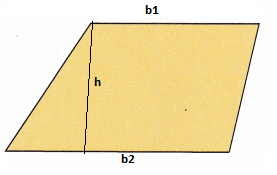
Copy each parallelogram. Label a base and a height for each. Use b and h.

Question 1.

Answer:

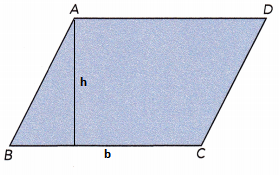
Explanation:
In parallelogram, any side can be the base of the paralleogram
But here, Let us assume the side BC as base of the paralleogram and label it as ‘b’.
The height of a parallelogram is the perpendicular distance between the base side and the parallel side opposite to it, the height is labelled as ‘h’.

Question 2.

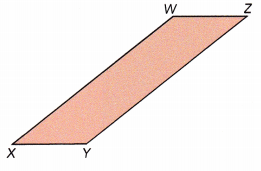
Answer:

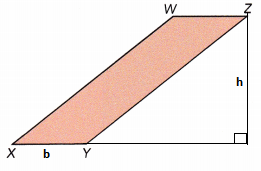
Explanation:
In parallelogram, any side can be the base of the paralleogram
But here, Let us assume the side XY as base of the paralleogram and label it as ‘b’.
The height of a parallelogram is the perpendicular distance between the base side and the parallel side opposite to it, the height is labelled as ‘h’.

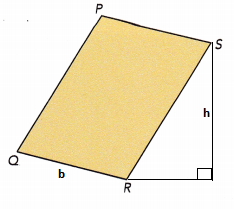
Question 3.

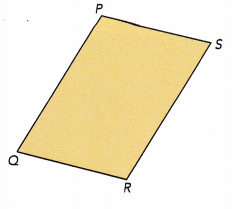
Answer:

Explanation:
In parallelogram, any side can be the base of the paralleogram
But here, Let us assume the side QR as the base of the paralleogram and label it as ‘b’.
The height of a parallelogram is the perpendicular distance between the base side and the parallel side opposite to it, the height is labelled as ‘h’.

Question 4.

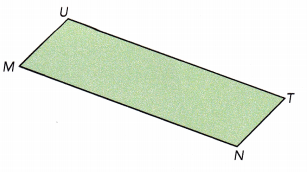
Answer:

Explanation:
In parallelogram, any side can be the base of the paralleogram
But here, Let us assume the side MN as the base of the paralleogram and label it as ‘b’.
The height of a parallelogram is the perpendicular distance between the base side and the parallel side opposite to it, the height is labelled as ‘h’.

Find the area of each parallelogram.

Question 5.

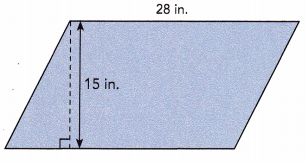
Answer:
From the given figure the base length is 28 in and the height is 15 in.
Base = 28 in
Height = 15 in
Area of the parallelogram = base × height
= 28×15
= 420 sq.in

Question 6.

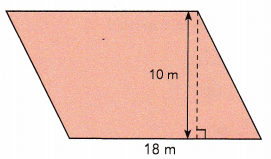
Answer:
From the given figure the base length is 18 in and the height is 10 in.
Base = 18 in
Height = 10 in
Area of the parallelogram = base × height
= 18×10
= 180 sq.in

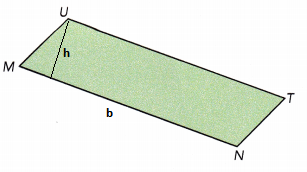
Copy each trapezoid. Label the height and bases. Use h₁, b₁ and b₂.

Question 7.

Answer:

Explanation:
The parallel sides are called the bases of the trapezium.
Let b1​ and b2​ be the lengths of these bases.
The distance between the bases is called the height of the trapezium. Let $h$ be this height.

Question 8.

Answer:

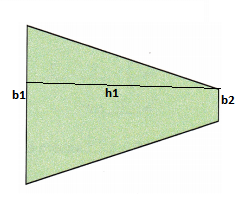
Explanation:
The parallel sides are called the bases of the trapezium.
Let b1​ and b2​ be the lengths of these bases.
The distance between the bases is called the height of the trapezium. Let $h$ be this height.

Question 9.

Answer:

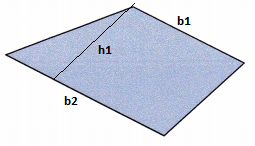
Explanation:
The parallel sides are called the bases of the trapezium.
Let b1​ and b2​ be the lengths of these bases.
The distance between the bases is called the height of the trapezium. Let $h$ be this height.

Question 10.

Answer:

Explanation:
The parallel sides are called the bases of the trapezium.
Let b1​ and b2​ be the lengths of these bases.
The distance between the bases is called the height of the trapezium. Let $h$ be this height.

Find the area of each trapezoid.

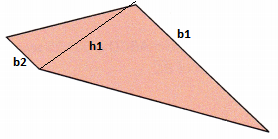
Question 11.

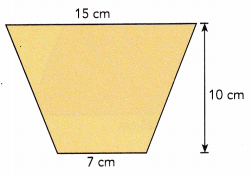
Answer:
Given figure has two horizontal bases measuring 15 cm and 7 cm each. The height is measuring 10 cm.
Height = 10 cm
Sum of bases = 15+ 7
= 22 cm
Area = \(\frac{1}{2}\)h(sum of bases)
= \(\frac{1}{2}\) × 10 × 22
= \(\frac{1}{2}\) × 220
= 220÷2
= 110 sq.cm

Question 12.

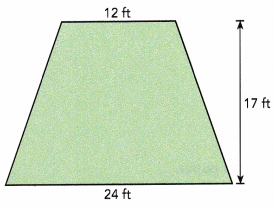
Answer:
Given figure has two horizontal bases measuring 12 ft and 24 ft each. The height is measuring 17 ft.
Height = 17 ft
Sum of bases = 12+ 24
= 36 ft
Area = \(\frac{1}{2}\)h(sum of bases)
= \(\frac{1}{2}\) × 17 × 36
= \(\frac{1}{2}\) × 612
= 612÷2
= 306 sq.ft

The area of each parallelogram is 64 square inches. Find the height. Round your answer to the nearest tenth of an inch.

Question 13.

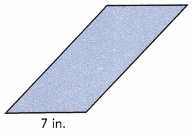
Answer:
Given that the area of parallelogram is 64 sq.in and the base is of 7 in length.
Area of parallelogram = base × height
64 = 7×height
64÷7 = (7×height)÷7
9.1 = height
Rounding off 9.1 to the nearest tenth of an inch
Height of the given parallelogram is 9 in.

Question 14.

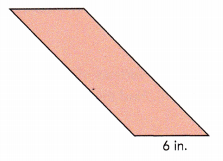
Answer:
Given that the area of parallelogram is 64 sq.in and the base is of 6 in length.
Area of parallelogram = base × height
64 = 6×height
64÷6 = (6×height)÷6
10.6 = height
Rounding off 10.6 to the nearest tenth of an inch
Height of the given parallelogram is 11 in.

The area of each trapezoid is 42 square centimeters. Find the height. Round your answer to the nearest tenth of a centimeter.

Question 15.

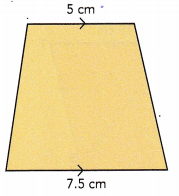
Answer:
Given that the area of trapezoid is 42 sq.cm. The two parallel sides are measuring 5 cm and 7.5 cm.
Sum of the sides = 5+7.5 = 12.5 cm
Area of trapezoid = \(\frac{1}{2}\)×h×(b₁ + b₂)
42 = \(\frac{1}{2}\) × h × 12.5
42 = 6.25 × h
42 ÷6.25 = (6.25 × h)÷6.25
6.7 = h
Rounding off 6.7 to the nearest tenth of an cm.
Height of the given trapezoid is 7 cm.

Question 16.

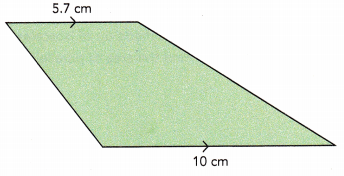
Answer:
Given that the area of trapezoid is 42 sq.cm. The two parallel sides are measuring 5 cm and 7.5 cm.
Sum of the sides = 5.7+10 = 15.7 cm
Area of trapezoid = \(\frac{1}{2}\)×h×(b₁ + b₂)
42 = \(\frac{1}{2}\) × h × 15.7
42 = 7.8 × h
42 ÷7.8 = (7.8 × h)÷7.8
5.3 = h
Rounding off 5.3 to the nearest tenth of an cm.
Height of the given trapezoid is 5 cm.

Solve.

Question 17.
The area of trapezoid ABCO is 503.25 square centimeters. Find the length of \(\overline{B C}\).

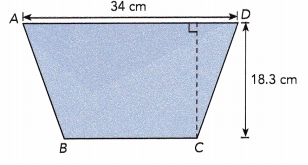
Answer:
Given that the area of trapezoid ABCD is 503.25 sq.cm
From the given figure, length of the height measures 18.3 cm and length of a side is 34 cm
Area of trapezoid = \(\frac{1}{2}\)×h×(b₁ + b₂)
503.25 = \(\frac{1}{2}\) × 18.3 × (34 + b₂)
503.25 = 9.1× (34 + b₂)
503.25÷9.1 = 9.1× (34 + b₂)÷9.1
55.3 = 34 + b₂
55.3 – 34 = 34 – 34 + b₂
21.3 = b₂
The length of second side BC will be 21.3 cm

Question 18.
The area of trapezoid EFGH is 273 square centimeters. Find the area of triangle EGH.

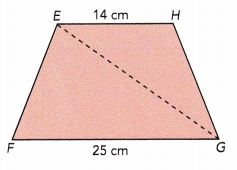
Answer:
Given that the area of trapezoid EFGH is 273 sq.cm. The length of two parallel bases will be 14 cm and 25 cm.
Area of trapezoid = \(\frac{1}{2}\)×h×(b₁ + b₂)
Sum of bases = 14+25 = 39cm
273 = \(\frac{1}{2}\)×h×39
273 = 19.5×h
273 ÷ 19.5 = (19.5×h)÷ 19.5
14 = h
The height of the trapezoid is 14 cm.
Area of triangle EGH = \(\frac{1}{2}\)×b×h
The length of base is 14cm
= \(\frac{1}{2}\)×14×14
= 196÷2
= 98 sq.cm

Solve. Use graph paper.

Question 19.
The coordinates of the vertices of a parallelogram are P (0, 5), Q (-3, 0), R (2, 0), and S (5, 5). Find the area of parallelogram PQRS.
Answer:

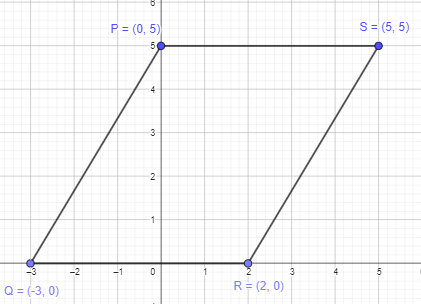
From the figure, we can get the height of the parallelogram which is 5 units.
Let us consider QR as base which measures 5 units.
Area of parallelogram = base×height
= 5×5
= 25 sq.units

Question 20.
Three out of the four coordinates of the vertices of parallelogram WXYZ are W(0, 1), X(-4, -4), and Y (-1, -4). Find the coordinates of Z. Then find the area of the parallelogram.
Answer:

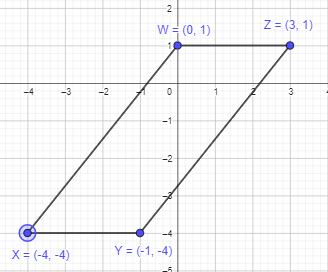
Given that three vertices of parallelogram WXYZ are W(0, 1), X(-4, -4), and Y (-1, -4).
Let XY be the base of parallelogram,since XY is measuring 3 units. The distance between W and Z will also be 3 units.
Thus, the point Z will be (3,1)
The height of the parallelogram is 5 units.
Area of parallelogram = base × height
= 3×5
= 15 sq.units

Question 21.
The coordinates of the vertices of trapezoid EFGH are E (-3, 3), F (-3, 0), G (1, -4), and H (1, 4). Find the area of the trapezoid.
Answer:

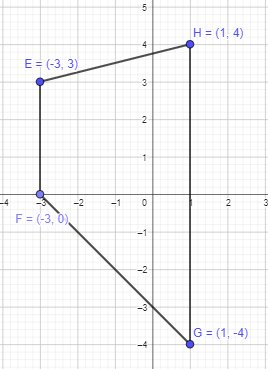
The two parallel sides EF and HG are measuring 3 units and 8 units respectively. The height is of 4 units length.
Sum of the sides = 3+8 = 11 units
Area of trapezoid = \(\frac{1}{2}\)×h×(b₁ + b₂)
= \(\frac{1}{2}\)×4×11
= 44 ÷2
= 22 sq.units

Question 22.
Three out of the four coordinates of the vertices of trapezoid ABCD are A (0, 1), B (-4, -4), and C(-1, -4). \(\overline{\mathrm{AD}}\) is parallel to \(\overline{\mathrm{BC}}\). AD is 6 units. The point D lies to the right of point A. Find the coordinates of point D. Then find the area of the trapezoid.
Answer:

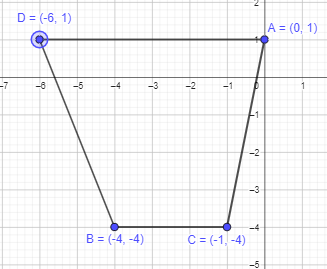
Given that the three vertices of trapezoid ABCD are A (0, 1), B (-4, -4), and C(-1, -4). AD is parallel to BC and length of AD is 6 units.
Therefore, the point D will be 6 units away from A which can be pointed at (-6,1)
The two parallel sides DA and BC are measuring 6 units and 3 units respectively. The height is of 5 units length.
Sum of the sides = 6+3 = 9 units
Area of trapezoid = \(\frac{1}{2}\)×h×(b₁ + b₂)
= \(\frac{1}{2}\)×5×9
= 45÷2
= 22.5 sq.units

Solve.

Question 23.
Parallelogram PQRT is made up of isosceles triangle PST and trapezoid PQRS. Find the area of parallelogram PQRT.

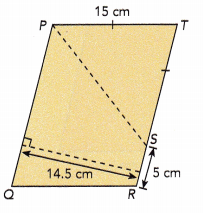
Answer:
Given that, PST is an isosceles triangle. Therefore the length of PT and TS will be 15cm.
Area of triangle = \(\frac{1}{2}\)×b×h
= \(\frac{1}{2}\)×15×15
= \(\frac{1}{2}\)×225
= 225÷2
= 112.5 sq.cm
Length of TR = Length of RS + Length of ST
Length of TR = 5+15 = 20 cm
Since PQRT is parallelogram, TR will be parallel to PQ. Thus, PQ = 20cm.
Area of trapezoid = \(\frac{1}{2}\)×h×(b₁ + b₂)
Sum of bases = SR + PQ
= 5 +15
= 20 cm
The height is of length 14.5 cm.
Area of trapezoid = \(\frac{1}{2}\)×14.5×20
= \(\frac{1}{2}\)×290
= 290÷2
= 145 sq.cm
Area of parallelogram PQRT = Area of isosceles triangle + Area of trapezoid
= 112.5 + 145
= 257.5 sq.cm