Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 1 Lesson 1.1 Representing Rational Numbers on the Number Line to finish your assignments.
Math in Focus Grade 7 Course 2 A Chapter 1 Lesson 1.1 Answer Key Representing Rational Numbers on the Number Line
Math in Focus Grade 7 Chapter 1 Lesson 1.1 Guided Practice Answer Key
Solve.
Question 1.
Find the absolute values of 3\(\frac{2}{7}\) and –\(\frac{18}{5}\)
Answer:
3(2/7) = (21+2)/7 = 23/7
The simplified form of 3(2/7) is 23/7
The absolute value of |3(2/7)| is 3(2/7)
The absolute value of |-(18/5)| is 18/5
Question 2.
Graph the two numbers on a number line and indicate their distances from 0. Which number is farther from 0?
Answer:
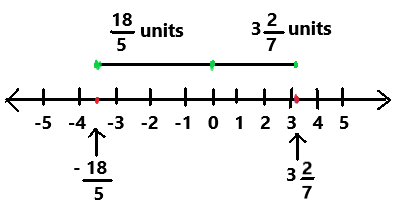
The number -18/5 is farther from 0.
Explanation:
In the above image we can observe a number line. On the number line the two numbers 3(2/7) and -18/5 are indicated. The two numbers distance from 0 are graphed. The number -18/5 is farther from 0.
Write each number in \(\frac{m}{n}\) form where m and n are integers.
Question 3.
11\(\frac{1}{6}\)
Answer:
11(1/6)
= (66 + 1)/6
= 67/6
The number 11(1/6) in m/n form is 67/6.
Here m = 67 and n= 6
Question 4.
48
Answer:
48 = 48/1
The number 48 in m/n form is 48/1.
Here m = 48 and n = 1
Question 5.
-5\(\frac{4}{12}\)
Answer:
-5(4/12)
= – (60 + 4)/12
= -64/12
= -16/3
The number -5(4/12) in m/n form is -16/3.
Here m = -16 and n = 3
Question 6.
–\(\frac{25}{10}\)
Answer:
-25/10 = -5/2
The given number -25/10 is already in m/n form.
Write each decimal as \(\frac{m}{n}\) where m and n are integers with n ≠ 0.
Question 7.
11.5
Answer:
11.5 = 23/2
The given decimal number 11.5 is represented in m/n form. The m/n form of 11.5 is 23/2.
Question 8.
-7.8
Answer:
-7.8 = -78/10
The given decimal number -7.8 is represented in m/n form. The m/n form of -7.8 is -78/10.
Question 9.
0.36
Answer:
0.36 = 36/100
The given decimal number 0.36 is represented in m/n form. The m/n form of 0.36 is 36/100.
Question 10.
-0.125
Answer:
-0.125 = – 125/1000
The given decimal number -0.125 is represented in m/n form. The m/n form of -0.125 is 125/1000.
Copy and complete.
Question 11.
Locate the rational numbers -1.5 and \(\frac{15}{4}\) on the number line.
STEP 1
Find the integers that the rational number lies between.
\(\frac{15}{4}\) can be written as a mixed number, 3\(\frac{3}{4}\), and 3\(\frac{3}{4}\) lies between 3 and 4. The negative decimal -1.5 lies between —2 and —1.
STEP 2
Graph a number line and label the integers.
Answer:

The integers are labeled on a number line.
STEP 3
Divide the distance between the integers into equal segments.
You divide the distance between —2 and —1 into ![]() segments and the distance between 3 and 4 into
segments and the distance between 3 and 4 into ![]() segments.
segments.

Answer:

Divide the distance between —2 and —1 into 1 segments and the distance between 3 and 4 into 3 segments.
STEP4
Use the segments to locate -1.5 and 3\(\frac{3}{4}\).

Answer:

Located the rational numbers -1.5 and 15/4 on the number line.
Locate the following rational numbers on the number line.
Question 12.
\(\frac{1}{6}\) and \(\frac{15}{3}\)
Answer:
1/6 and 15/3
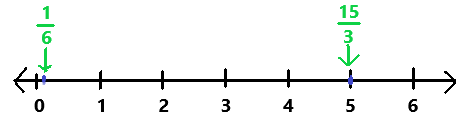
Explanation:
First we have to find the integers that where the rational number lies between on the number line.
The fraction 1/6 lies between 0 and 1. The simplified form of 15/3 is 5. The fraction 15/3 lies on number 5.
Next we have to label the integers and locate the rational numbers on a number line.
In the above image we can observe the rational numbers 1/6 and 15/3 are located on the number line.
Question 13.
-0.4 and \(\frac{11}{5}\)
Answer:
-0.4 and 11/5
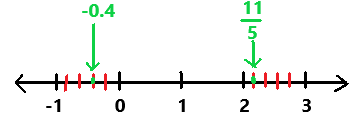
Explanation:
First we have to find the integers that where the rational number lies between on the number line.
The negative decimal -0.4 lies between —1 and 0.The fraction 11/5 lies between 2 and 3.
Next we have to label the integers and locate the rational numbers on a number line.
Divide the distance between —1 and 0 into 4 segments and the distance between 2 and 3 into 4 segments.
In the above image we can observe the rational numbers -0.4 and 11/5 are located on the number line.
Question 14.
\(\frac{12}{15}\) and -1.8
Answer:
12/15 and -1.8
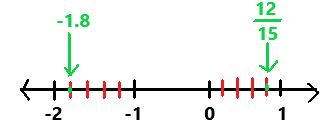
Explanation:
First we have to find the integers that where the rational number lies between on the number line.
The negative decimal -1.8 lies between —2 and -1.The fraction 12/15 lies between 0 and 1.
Next we have to label the integers and locate the rational numbers on a number line.
Divide the distance between —2 and -1 into 4 segments and the distance between 0 and 1 into 4 segments.
In the above image we can observe the rational numbers -1.8 and 12/15 are located on the number line.
Question 15.
\(-\frac{5}{15}\) and \(-\frac{25}{30}\)
Answer:
-5/15 and 25/30
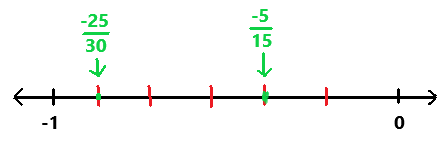
Explanation:
First we have to find the integers that where the rational number lies between on the number line.
The negative fractions -25/30 and -5/15 lies between —1 and 0.
Next we have to label the integers and locate the rational numbers on a number line.
In the above image we can observe the rational numbers -25/30 and -5/15 are located on the number line.
Math in Focus Course 2A Practice 1.1 Answer Key
Find the absolute value of each fraction. Use a number line to show how far the fraction is from 0. Write fractions in simplest form.
Question 1.
\(\frac{7}{10}\)
Answer:
7/10
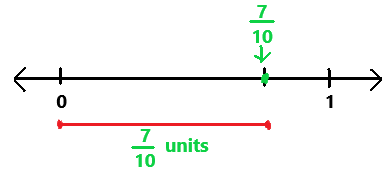
The absolute value of above fraction is 7/10.
Explanation:
First we have to find where the fraction lies between on the number line.
The fraction 7/10 lies between 0 and 1.
Next we have to label the fraction on a number line.
In the above image we can observe the fraction is 7/10 units far from the 0 on the number line.
Question 2.
\(\frac{18}{8}\)
Answer:
The absolute value of 18/8 is 18/8.
18/8 = 9/4
The simplest form of 18/8 is 9/4.
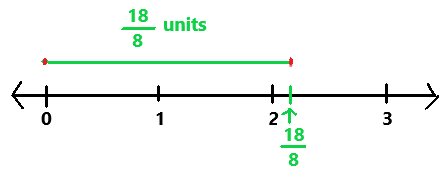
Explanation:
First we have to find where the fraction lies between on the number line.
The fraction 18/8 lies between 2 and 3.
Next we have to label the fraction on a number line.
In the above image we can observe the fraction is 18/8 units far from the 0 on the number line.
Question 3.
–\(\frac{5}{13}\)
Answer:
The absolute value of -5/13 is 5/13.
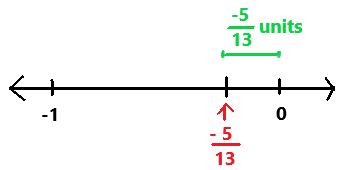
Explanation:
First we have to find where the fraction lies between on the number line.
The fraction -5/13 lies between -1 and 0.
Next we have to label the fraction on a number line.
In the above image we can observe the fraction is -5/13 units far from the 0 on the number line.
Question 4.
–\(\frac{48}{15}\)
Answer:
-48/15
The absolute value of -48/15 is 48/15.
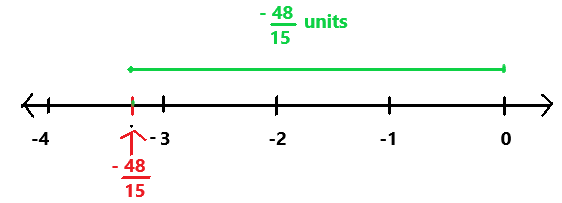
Explanation:
First we have to find where the fraction lies between on the number line.
The fraction -48/15 lies between -3 and 0.
Next we have to label the fraction on a number line.
In the above image we can observe the fraction is -48/15 units far from the 0 on the number line.
Write each integer or fraction as \(\frac{m}{n}\) in simplest form where m and n are integers.
Question 5.
67
Answer:
67
= 67/1
The number 67 in m/n form is 67/1.
Here m = 67 and n= 1
Question 6.
-345
Answer:
-345
= -345/1
The number -345 in m/n form is -345/1.
Here m = -345 and n= 1
Question 7.
\(\frac{25}{80}\)
Answer:
25/80
= 5/16
The simplest form of 25/80 is 5/16.
The fraction 25/80 in m/n form is 5/16.
Here m = 5 and n= 16
Question 8.
–\(\frac{264}{90}\)
Answer:
-264/90
= -44/15
The simplest form of -264/90 is -44/15.
The fraction -264/90 in m/n form is -44/15.
Here m = -44 and n= 15
Question 9.
–\(\frac{14}{70}\)
Answer:
-14/70
= -1/5
The simplest form of -14/70 is -1/5.
The fraction -14/70 in m/n form is -1/5.
Here m = -1 and n= 5
Question 10.
\(\frac{600}{480}\)
Answer:
600/480
= 50/40
= 5/4
The simplest form of 600/480 is 5/4.
The fraction 600/480 in m/n form is 5/4.
Here m =5 and n = 4
Write each mixed number or decimal \(\frac{m}{n}\) as in simplest form where m and n are integers.
Question 11.
7\(\frac{7}{9}\)
Answer:
7(7/9)
= (63 + 7)/9
= 70/9
The simplest form of the mixed number 7(7/9) is 70/9.
Here m = 70 and n = 9 both are integers.
Question 12.
-5\(\frac{1}{10}\)
Answer:
-5(1/10)
= -(50 + 1)/10
= -51/10
The simplest form of the mixed number -5(1/10) is -51/10.
Here m = -51 and n = 10 both are integers.
Question 13.
2\(\frac{5}{12}\)
Answer:
2(5/12)
= (24 + 5)/12
= 29/12
The simplest form of the mixed number 2(5/12) is 29/12.
Here m = 29 and n = 12 both are integers.
Question 14.
-10\(\frac{11}{36}\)
Answer:
-10(11/36)
=-(360 + 11)/36
= -371/36
The simplest form of the mixed number-10(11/36) is -371/36.
Here m =-371 and n = 36 both are integers.
Question 15.
0.4
Answer:
0.4
= 4/10
= 2/5
The simplest form of the decimal number 0.4 is 2/5.
Here m = 2 and n = 5 both are integers.
Question 16.
-0.625
Answer:
-0.625
= -625/1000
= -5/8
The simplest form of the decimal number -0.625 is -5/8.
Here m = -5 and n = 8 both are integers.
Question 17.
5.80
Answer:
5.80
= 29/5
The simplest form of the decimal number 5.80 is 29/5.
Here m = 29 and n = 5 both are integers.
Question 18.
9.001
Answer:
9.001
= 9001/1000
The simplest form of the decimal number 9.001 is 9001/1000.
Here m = 9001 and n =1000 both are integers.
Question 19.
-10.68
Answer:
-10.68
= -267/25
The simplest form of the decimal number -10.68 is -267/25.
Here m = -267 and n = 25 both are integers.
Copy and complete.
Question 20.
Locate the following rational numbers correctly on the number line.
–\(\frac{1}{4}\), -1.5, 0.8, \(\frac{5}{2}\)
Answer:
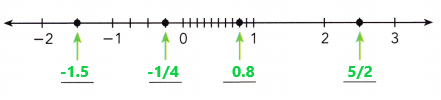
Explanation:
First we have to find where the given rational numbers lies between on the number line.
The negative decimal -1.5 lies between -2 and -1.
The negative fraction -1/4 lies between -1 and 0.
The decimal 0.8 lies between 0 and 1.
The fraction 5/2 lies between 2 and 3.
The above given rational numbers are located correctly on the number line.
Question 21.
Locate the following rational numbers correctly on the number line.
1\(\frac{7}{10}\), –\(\frac{13}{5}\), 2.25, -0.7

Answer:

Explanation:
First we have to find where the given rational numbers lies between on the number line.
The negative fraction -13/5 lies between -3 and -2
The negative decimal -0.7 lies between -1 and 0.
The mixed fraction 1(7/10) in fraction as 17/10 lies between 1 and 2.
The decimal 2.25 lies between 2 and 3.
The above given rational numbers are located correctly on the number line.
Graph each rational number on a separate number line.
Question 22.
67\(\frac{1}{8}\)
Answer:
67(1/8)
= (536 + 1)/8
= 537/8
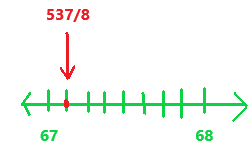
Explanation:
First we have to find where the given rational number lies between on the number line.
The mixed fraction 67(1/8) in fraction as 537/8 lies between 67 and 68.
The above given rational number is drawn correctly on the number line.
Question 23.
\(\frac{305}{20}\)
Answer:
305/20
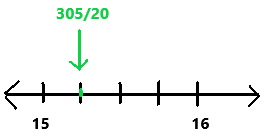
Explanation:
First we have to find where the given rational number lies between on the number line.
The fraction 305/20 lies between 15 and 16.
The above given rational number is drawn correctly on the number line.
Question 24.
\(\frac{98}{28}\)
Answer:
98/28
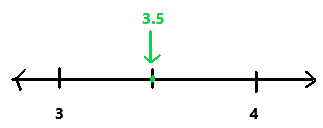
Explanation:
First we have to find where the given rational number lies between on the number line.
The fraction 98/28 lies between 3 and 4.
The above given rational number is drawn correctly on the number line.
Question 25.
–\(\frac{21}{12}\)
Answer:
-21/12
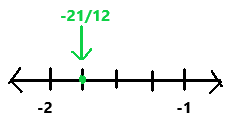
Explanation:
First we have to find where the given rational number lies between on the number line.
The fraction -21/12 lies between -2 and -1.
The above given rational number is correctly drawn on the number line.
Question 26.
-25.8
Answer:
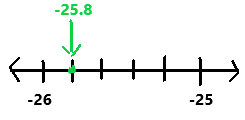
Explanation:
First we have to find where the given rational number lies between on the number line.
The decimal lies between -26 and -25.
The above given rational number is drawn correctly on the number line.
Question 27.
-45.3
Answer:
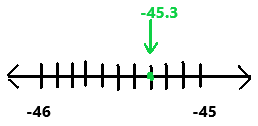
Explanation:
First we have to find where the given rational number lies between on the number line.
The decimal lies between -46 and -45.
The above given rational number is correctly drawn on the number line.
A video game gives you 10 minutes to find a treasure. The results of your first 8 games show the amount of time left unused when you have found the treasure. A negative time means you have gone beyond the 10 minutes allotted. Use these data for questions 28 to 35.
\(\frac{23}{8}\), 0, -7\(\frac{1}{5}\), 6, –\(\frac{17}{4}\), 8, 7.8, -9.1
Question 28.
Order the times left from most to least time using the symbol >.
Answer:
The time left from most to least are 8, 7.8, 6, 23/8, 0, -17/4, -7(1/5), -9.1.
Question 29.
Write the absolute value of each number.
Answer:
23/8, 0, -7(1/5), 6 , -17/4, 8, 7.8, -9.1
The absolute value of 23/8 is 23/8.
The absolute value of 0 is 0.
The absolute value of -7(1/5) is 7(1/5) or 36/5.
The absolute value of 6 is 6.
The absolute value of -17/4 is 17/4.
The absolute value of 8 is 8.
The absolute value of 7.8 is 7.8.
The absolute value of -9.1 is 9.1.
Question 30.
Which number has the greatest absolute value?
Answer:
The decimal number – 9.1 has the greatest absolute value.
Question 31.
Order the absolute values from least to greatest. Use the symbol <.
Answer:
The absolute values from least to greatest are 0 < 23/8 < 17/4 < 6 < 7(1/5) < 7.8 < 8 < 9.1.
Question 32.
Graph the original numbers on a number line.
Answer:
23/8, 0, -7(1/5), 6 , -17/4, 8, 7.8, -9.1

The original numbers on a number line is drawn on the graph.
Question 33.
Which negative number in the list is farthest from 0?
Answer:
The negative number –9.1 in the given list is farthest from 0.
Question 34.
Which positive number in the list is closest to 10?
Answer:
The positive number 8 in the given list is closest to 10.
Question 35.
Which time is closest to —5 minutes?
Answer:
The time -17/4 is closest to – 5 minutes.