Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 5 Review Test to score better marks in the exam.
Math in Focus Grade 7 Course 2 A Chapter 5 Review Test Answer Key
Concepts and Skills
Tell whether each table, graph, or equation represents a direct proportion, an inverse proportion, or neither.
Question 1.
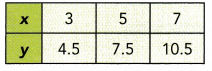
Answer:
![]()
Direct Proportion :
For each pair of values x and y →
\(\frac{y}{x}\) = \(\frac{4.5}{3}\) = 1.5
\(\frac{y}{x}\) = \(\frac{7.5}{5}\) = 1.5
\(\frac{y}{x}\) = \(\frac{10.5}{7}\) = 1.5
\(\frac{y}{x}\) is a constant so x and y is direct proportional
Inverse Proportion :
For each pair of values x and y →
xy = 3 ∙ 4.5 = 13.5
xy = 5 . 7.5 = 37.5
xy = 7 ∙ 10.5 = 73.5
xy is not a constant so y is not inversely proportional to x
NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten a. xy = k or y = \(\frac{k}{x}\)
Direct proportion
Question 2.

Answer:

Direct Proportion :
For each pair of valties x and y →
\(\frac{y}{x}\) = \(\frac{50}{2}\) = 25
\(\frac{y}{x}\) = \(\frac{25}{4}\) = 6.25
\(\frac{y}{x}\) = \(\frac{12.5}{8}\) = 1.56
\(\frac{y}{x}\) is not a constant so x and y does not represent direct proportion
Inverse Proportion :
For each pair of values x and y →
xy = 2 ∙ 50 = 100
xy = 4 ∙ 25 = 100
xy = 8 ∙ 12.5 = 100
The product of x and y is a constant so y is inversely proportional to x
NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Inverse Proportion
Question 3.
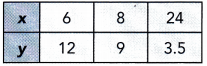
Answer:
![]()
Direct Proportion :
For each pair of values x and y →
\(\frac{y}{x}\) = \(\frac{12}{6}\) = 2
\(\frac{y}{x}\) = \(\frac{9}{8}\) = 1.125
\(\frac{y}{x}\) = \(\frac{3.5}{2.4}\) = 0.145
\(\frac{y}{x}\) is not a constant so x and y is not direct proportion.
Inverse Proportion :
For each pair of values x and y →
xy = 6 ∙ 12 = 72
xy = 8 ∙ 9 = 72
xy = 24 ∙ 3.5 = 84
The product of z and y is not a constant so y is not inversely proportional to z
NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Neither Direct Proportion nor Inverse Proportion
Question 4.
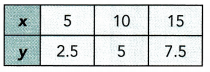
Answer:

Direct Proportion :
For each pair of values x and y →
\(\frac{y}{x}\) = \(\frac{5}{2.5}\) = 2
\(\frac{y}{x}\) = \(\frac{10}{5}\) = 2
\(\frac{y}{x}\) = \(\frac{15}{7.5}\) = 2
\(\frac{y}{x}\) is a constant so x and y is direct proportional
Inverse Proportion :
For each pair of values x and y →
xy = 2.5 ∙ 5 = 12.5
xy = 5 ∙ 10 = 50
xy = 7.5 ∙ 15 = 112.5
The product of x and y is not a constant so x is not inversely proportional to x
NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Direct Proportion
Question 5.
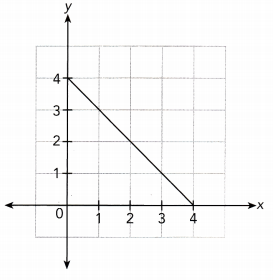
Answer:
Direct Proportion :
The given graph is a straight line that does not lie along
the x — axis or y — axis but does not pass through the origin.
So, the given graph does not represents a direct proportion.
Inverse Proportion :
$Use\graph\: $
x ∙ y = 3 ∙ 1 = 2
x ∙ y = 2 ∙ 2 = 4
x ∙ y = 1 ∙ 3 = 3
The product of x and y is not a constant so x and y does not represent a inverse proportion.
Neither direct proportion nor inverse proportion
Question 6.
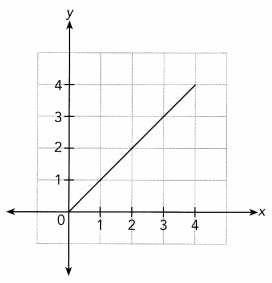
Answer:
Direct Proportion :
The given graph is a straight line that does not lie along the x — axis or y — axis and it pass through the origin.
So. the given graph represents a direct proportion.
Inverse Proportion :
$Use\graph\: $
x ∙ y = 1 ∙ 1 = 1
x ∙ y = 2 ∙ 2 = 4
x ∙ y = 3 ∙ 3 = 9
The product of x and y is not a constant so x and y does not ‘represent a inverse proportion.
Direct Proportion
Question 7.
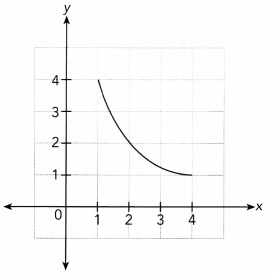
Answer:
Direct Proportion :
The given graph is not a straight line and it lie along the x — axis or y — axis and does not pass through the origin.
So. the given graph does not ‘represents a direct proportion.
Inverse Proportion:
$Use\ graph\: $
x ∙ y = 4 ∙ 1 = 4
x ∙ y = 2 ∙ 2 = 4
x ∙ y = 1 ∙ 4 = 4
The product of x and y is a constant so x and y represents a inverse proportion.
Inverse Proportion
Question 8.
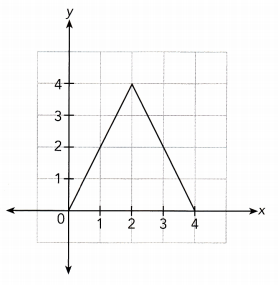
Answer:
Direct Proportion :
The given graph is not a straight line and it lie along the x — axis but it pass through the origin.
So, the given graph does not represents a direct proportion.
Inverse Proportion :
$Use\graph\: $
x ∙ y = 1 ∙ 2 = 2
x ∙ y = 2 ∙ 4 = 8
x ∙ y = 3 ∙ 2 = 6
The product of x and y is not a constant so x and y does not represent a inverse proportion.
Neither direct proportion nor inverse proportion
Question 9.
y = \(\frac{1}{2}\)x + 5
Answer:
y = \(\frac{1}{2} x\) + 5
Direct Proportion:
y = \(\frac{1}{2} x\) + 5
Because the original equation y = y = \(\frac{1}{2} x\) + 5 cannot be rewritten as an equivalent
equation in the form y = kx, it does not represent a direct proportion.
Inverse Proportion :
y = \(\frac{1}{2} x\) + 5
Because the original equation y = \(\frac{1}{2} x\) + 5 cannot be rewritten as an equivalent
equation in the form xy = k, it does not represent an inverse proportion.
NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten xy = k or y = \(\frac{k}{x}\)
Neither Direct Proportion nor Inverse Proportion
Question 10.
\(\frac{y}{4}\) = 7x
Answer:
\(\frac{y}{4}\) = 7x
4 ∙ \(\frac{y}{4}\) = 4 ∙ 7x
y = 28x
Because the original equation \(\frac{y}{4}\) = x can be rewritten as an equivalent equation in the form y = kx, it represent a direct proportion.
Inverse Proportion :
\(\frac{y}{4}\) = 7x
4 ∙ \(\frac{y}{4}\) = 4 ∙ 7x
y = 28x
Because the original equation \(\frac{y}{4}\) = x cannot be re’wrítten as an equivalent
equation in the form xy = k, it does not represent an inverse proportion.
NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k. and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k. and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Direct Proportion
Question 11.
-3 + x = y
Answer:
-3 + x = y
Direct Proportion :
-3 + x = y
-3 + x – x = y – x Subtract x from both sides
y – x = -3
Because the original equation -3 + x = y cannot be rewritten as an equivalent equation in the form y = kx, it does not represent a direct proportion.
Inverse Proportion :
-3 + x = y
-3 + x — x = y — x Subtract x from both sides
y – x = -3
Because the original equation — 3 + x = y cannot be rewritten as an equivalent equation in the form xy = k, it does not represent an inverse proportion.
NOTE :
Direct Proportion : y is directly proportional to z then they have a constant
of proportionality k, and it crin be rewritten as y = kz or \(\frac{y}{x}\) = k
Inverse Proportion : z and y are in inverse proportion thìen their product is a constant of proportionality k, and it can be rewritten as zy = k or y = \(\frac{k}{x}\)
Neither Direct Proportion nor inverse Proportion
Question 12.
\(\frac{y}{2}\) = \(\frac{3}{x}\)
Answer:
\(\frac{y}{2}\) = \(\frac{3}{x}\)
Direct Proportion :
\(\frac{y}{2}\) = \(\frac{3}{x}\)
x ∙ y = 3 ∙ 2 Cross Multiplication
xy = 6
Because the original equation \(\frac{y}{2}\) = \(\frac{3}{x}\) cannot be rewritten as an equivalent equation in the form y = kx, it does not represent a direct proportion.
Inverse Proportion :
\(\frac{y}{2}\) = \(\frac{3}{x}\)
x ∙ y = 3 ∙ 2 Cross Multiplication
xy = 6
Because the original equation \(\frac{y}{2}\) = \(\frac{3}{x}\) can be rewritten as an equivalent equation in the form xy = k, it does represent an inverse proportion.
NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it crin be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant
of proportionality k. and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Inverse proportion
In each table, y is directly proportional to x. Find the constant of proportionality. Then copy and complete the table.
Question 13.
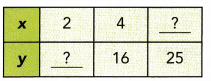
Answer:

y is directly proportional to z :
\(\frac{y}{x}\) = \(\frac{16}{4}\)
\(\frac{y}{x}\) = 4 Simplify
x ∙ \(\frac{y}{x}\) = 4 ∙ x Multiply both sides by x
y = 4x
Find missing value in the table.
When y = 25 find x.
y = 4x
25 = 4x Evaluate y = 25
\(\frac{25}{4}\) = \(\frac{4x}{4}\) Divide both sides by 4
x = 6.25 Simplify
When x = 2 find y,
y = 4x
y = 4 ∙ 2 Evaluate x = 2
y = 8 Simplify

The missing number are 8 and 6.25
Question 14.

Answer:

y is directly proportional to x :
\(\frac{y}{x}\) = \(\frac{2.5}{5}\)
\(\frac{y}{x}\) = \(\frac{1}{2}\) Simplify
x ∙ \(\frac{y}{x}\) = \(\frac{1}{2}\) ∙ x Multiply both sides by x
y = \(\frac{1}{2}\)x
Find missing value in the table.
When y = 3 find x,
y = \(\frac{1}{2}\)x
3 = \(\frac{1}{2}\)x Evaluate y = 3
2 ∙ 3 = 2 ∙ \(\frac{1}{2}\)x Multiply both sides by 2
x = 6 Simplify
When x = 3 find y,
y = \(\frac{1}{2}\)x
y = \(\frac{1}{2}\) ∙ 3 Evaluate x = 3
y = 1.5 simplify
![]()
The missing number are y = 1.5 and x = 6
In each table, y is inversely proportional to x. Find the constant of proportionality. Then copy and complete the table.
Question 15.

Answer:

y is inversely proportional to x :
xy = 2 ∙ 30
xy = 60 Simplify
Find missing value in the table.
When x = 4 find y.
xy = 60
4 ∙ y = 60 Evaluate x = 4
\(\frac{4 y}{4}\) = \(\frac{60}{4}\) Divide both sides by 4
y = 15 Simplify
When y = 10 find x.
x ∙ 10 = 60 Evaluate y = 10
\(\frac{10 x}{10}\) = \(\frac{60}{10}\) Divide both sides by 10
x = 6 Simplify

The missing number are y = 15 and x = 6
Question 16.

Answer:

y is inversely proportional to x :
xy = 5 ∙ 1.6
xy = 8 Simplify
Find missing value in the table.
When x = 2.5 find y.
xy = 8
2.5 ∙ y = 8 Evaluate x = 2.5
\(\frac{2.5 y}{2.5}\) = \(\frac{8}{2.5}\) Divide both sides by 2.5
y = 3.2 simplify
when y = 2 find x,
x ∙ 2 = 8 Evaluate y = 2
\(\frac{2 x}{2}\) = \(\frac{8}{2}\) Divide both sides by 2.
x = 4 simplify

The missing number are y = 3.2 and x = 4
Solve using proportionality reasoning.
Question 17.
y is directly proportional to x, and y = 56 when x = 7. Find the value of y when x = 4.
Answer:
x = 7 and y = 56
y is directly proportional to x:
\(\frac{y}{x}\) = \(\frac{56}{7}\)
\(\frac{y}{x}\) = 8
x ∙ \(\frac{y}{x}\) = 8 ∙ x Multiply both sides by x
y = 8x
Find the value of y when x = 4
We know y = 8x,
y = 8 ∙ 4 Evaluate y = 8x when x = 4
y = 32 Simplify
y = 32
Question 18.
y is inversely proportional to x, and y = 12 when x = 4. Find the value of x when y = 8.
Answer:
x = 4 and y = 12
y is inversely proportional to x :
xy = 4 ∙ 12
xy = 48
\(\frac{x y}{y}\) = \(\frac{48}{y}\) Divide both sides by y
x = \(\frac{48}{y}\)
Find the value of x when y = 8
We know x = \(\frac{48}{y}\),
x = \(\frac{48}{8}\) Evaluate x = \(\frac{48}{y}\) when y = 8
x = 6 simplify
x = 6
Problem Solving
Use a proportion to solve each question. Show your work.
Question 19.
The graph shows that the cost of gasoline, y dollars, is directly proportional to x gallons of gasoline.
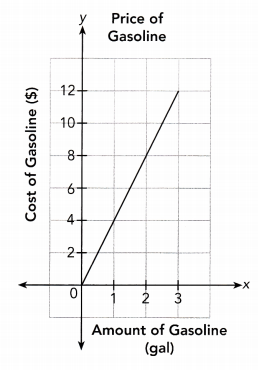
a) Find the constant of proportionality. What does this value represent in the context of the problem?
Answer:
y is directly proportional to x :
\(\frac{y}{x}\) = \(\frac{4}{1}\)
\(\frac{y}{x}\) = 4 simplify
Constant of Proportionality = 4
It represents the unit cost per gallons of gasoline.
b) Write a direct proportion equation.
Answer:
y is directly proportional to x :
\(\frac{y}{x}\) = \(\frac{4}{1}\) = 4 Simplify
\(\frac{y}{x}\) = \(\frac{8}{2}\) = 4 Simplify
\(\frac{y}{x}\) = \(\frac{12}{3}\) = 4 Simplify
x ∙ \(\frac{y}{x}\) = 4 ∙ x Multiply both sides by x
y = 4x
c) If Umberto spent $24 for gasoline, how many gallons of gasoline did he buy?
Answer:
y = 4x
24 = 4x Evaluate y = 24
\(\frac{24}{4}\) = \(\frac{4 x}{4}\) Divide both sides by 4
x = 6
Umberto will get 6 gallons of gasoline if he spent $24.
Question 20.
Out of every $100 that Judy earns at her part-time job, she saves $25 for college. The amount she saves is directly proportional to the amount she earns. If she earns $3,880 in one year, how much will she save for college?
Answer:
Amount of money she saves = y
Amount of money she earns = x
Find Direct Proportion Equation :
Amount of money she saves is directly proportional to Amount of money she earns :
\(\frac{y}{x}\) = \(\frac{25}{100}\)
\(\frac{y}{x}\) = \(\frac{1}{4}\) simplify
x ∙ \(\frac{y}{x}\) = x ∙ \(\frac{1}{4}\) Multiply both sides x
y = \(\frac{1}{4}\)x
If she earns $3880 in one year, how much she will save :
y = \(\frac{1}{4}\)x
y = \(\frac{1}{4}\) ∙ 3880 Evaluate x = 3880
y = 970
She will save $970 in one year if she earns $3880.
Question 21.
Harry made fruit punch using 2 parts orange juice to 3 parts soda water. The amount of soda water that Harry used is directly proportional to the amount of orange juice he used. How many cups of orange juice should Harry use with 18 cups of soda water?
Answer:
Amount of soda water = y
Amount of orange juice = x
Find Direct Proportion Equation :
Amount of soda water is directly proportional to Amount of orange juice :
\(\frac{y}{x}\) = \(\frac{3}{2}\)
\(\frac{y}{x}\) = 1.5 simplify
x ∙ \(\frac{y}{x}\) = x ∙ 1.5 Multiply both sides by x
y = 1.5x
How many cups of orange juice should Harry use with 18 cups of soda water :
y = 1.5z
18 = 1.5x Evaluate y = 18
\(\frac{18}{1.5}\) = \(\frac{1.5 x}{1.5}\) Divide both sides by 1.5
x = 12
Harry should ‘use 12 cups of orange juice with 18 cups of soda water.
12 cups
Use a graph paper. Solve.
Question 22.
An initial amount of money deposited in a bank account that earns interest is called the principal. In the table below, P stands for the principal, and l stands for the interest earned by that principal for a period of one year at a particular bank. P is directly proportional to l. Graph the direct proportion relationship between P and l. Use 1 unit on the horizontal axis to represent 1 dollar and 1 unit on the vertical axis to represent $50.

Answer:

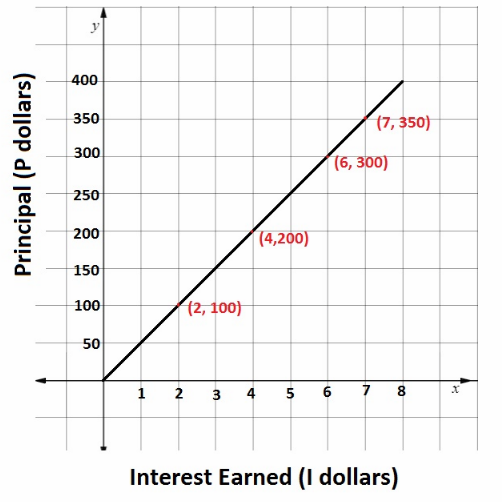
a) Using the graph, find the interest earned when the principal is $350.
Answer:
$From\ the\ graph,\ for\ $350\ Principal,\ Interest\ earned\ is\ $7 $
b) Write an equation relating P and I. Then find the principal when the interest earned is $15.
Answer:
P is directly proportional to I :
\(\frac{P}{I}\) = \(\frac{100}{2}\)
\(\frac{P}{I}\) = 50 Simplifying
I ∙ \(\frac{P}{I}\) = I ∙ 50 Multiplying both sides by I
P = 50I
Find the principal when the Interest earned is $15 :
P = 50I
P = 50 ∙ 15 Substituting I = 15
P = 750
Use a proportion to solve each question. Show your work.
Question 23.
The time taken by some students to deliver 500 flyers, t hours, is inversely proportional to the number of students, n. The graph shows the relationship between n and t.
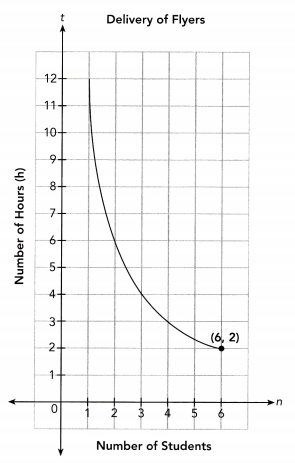
a) Find the constant of proportionality graphically.
Answer:
$Since,\ the\ line\ is\ passing\ through\ the\ point\ (6,\ 2) $
So, the constant of proportionality is 6 × 2 = 12
Constant of Proportionality = 12
b) Write an equation relating n and t.
Answer:
Number of hours (t) to delivers the flyers is inversely proportional to the ‘number of students
n ∙ t = 6 ∙ 2
nt = 12
c) Describe the relationship between the number of students and the time needed to deliver the flyers.
Answer:
Since t is inversely proportional to n
The number of students increases as the amount of time to deliver the flyers decreases.
d) Explain what the point (6, 2) represents in this situation.
Answer:
6 students take 2 hours to deliver 500 flyers.
Question 24.
Jerry has set aside a certain amount of money to download applications for his new smart phone. The number of applications he can afford to download is inversely proportional to the cost of each download. With his money, he can afford to download 12 applications that cost $2 each. How many applications can he afford to download if he finds less expensive applications that cost only $1.50 each?
Answer:
Number of application he can afford to download = x
Cost of each download = y
Find Inverse Proportion equation :
$He\ has\ the\ amount\ of\ money\ to\ download\ 12\ application\ which\ cost\ $2\ each\
Number of applications he can afford to download is inversely proportional to Cost of each download \ :
xy=12\cdot2
xy = 24 $
How many applications he can afford to download if cost of each application is $1.50 :
xy = 24
1.50 = 24 Substitute y = 1.50
\(\frac{1.50 x}{1.50}\) = \(\frac{24}{1.50}\) Divide both sides by 1.50
x = 16
$He\ can\ afford\ to\ download\ 16\ applications\ if\ each\ applications\ cost\ $1.50 $
16 application