Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 7 Practice 4 Ratios in Fraction Form to score better marks in the exam.
Math in Focus Grade 5 Chapter 7 Practice 4 Answer Key Ratios in Fraction Form
Write your answer in the box.
Question 1.
Which model correctly shows that A is \(\frac{7}{4}\) times B’?
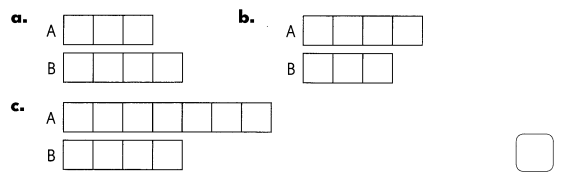
Answer: Option – C is the correct option
Complete.
The ratio of the lengths of Stick A and Stick B are as shown.
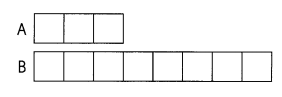
Question 2.
The ratio of the length of Stick A to the length of Stick B is 
Answer:
Given,
The length of Stick A is 3,
The length of Stick B is 8,
The ratio of the length of Stick A to the length of Stick B is 3 / 8.
Question 3.
The length of Stick A is 
times the length of Stick B.
Answer:
Given,
The length of Stick A is 3,
The length of Stick B is 8,
The ratio of the length of Stick A to the length of Stick B is 3 / 8
Question 4.
The ratio of the length of Stick B to the length of Stick A is .
Answer:
Given,
The length of Stick B is 8,
The length of Stick B is 3,
The ratio of the length of Stick A to the length of Stick B is 8 / 3.
Question 5.
The length of Stick B times the length of Stick A.
Answer:
Given,
The length of Stick B is 8,
The length of Stick A is 3,
The ratio of the length of Stick A to the length of Stick B is 8 / 3.
Complete.
The diagram shows the masses of two bags of rice, X and Y.
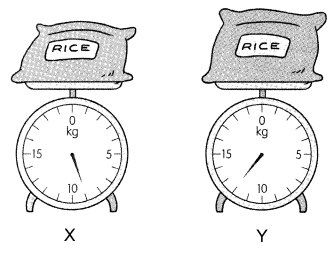
Question 6.
The mass of Y is times the mass of X.
Answer:
Given,
The mass of rice bag X is 9 kg,
The mass of rice bag Y is 12 kg,
So the mass of Y is 12 / 9 times the mass of X.
Question 7.
The moss of X is times the mass of Y.
Answer:
Given,
The mass of rice bag X is 9 kg,
The mass of rice bag Y is 12 kg,
So the mass of X is 9 / 12 times the mass of Y.
Question 8.
The ratio of the moss of X to the total mass of X and Y is ______________ : _______.
Answer:
9 : 21
Explanation:
Given,
The mass of rice bag X is 9 kg,
The mass of rice bag Y is 12 kg,
By adding 9 with 12 we get 21,
So the ratio of the mass of X to the total mass of Y is 9 : 21
Question 9.
The mass of X is times the total mass of X and Y.
Answer:
Given,
The mass of rice bag X is 9 kg,
The mass of rice bag X and mass of Y is by adding 9 with 12 we get 21 kg
To get into the simplest form 9 and 12 can divisible by 3 we get 3 / 7,
So the ratio of mass of X is 3 / 7 times the total mass of X and Y.
Question 10.
The mass of Y is times the total mass of X and Y.
Answer:
Given,
The mass of rice bag Y is 12 kg,
The mass of rice bag X and mass of Y is by adding 9 with 12 we get 21 kg
To get into the simplest form 12 and 21 can divisible by 3 we get 4 / 7,
So the ratio of mass of X is 4 / 7 times the total mass of X and Y.
Solve.
Question 11.
Pete played 1 8 tennis matches in a week. Jack played 6 fewer matches than Pete.
a. How many tennis matches did Jack play in that week?
Answer:12 matches
Explanation:
Given,
Pete played 18 matches in a week,
Jack played 6 fewer matches than Pete,
By subtracting 6 from 18 we get 12,
So Jack played 12 tennis matches in a week.
b. Find the ratio of the number of matches Pete played to the total number of matches both boys played. Give your answer in fraction form.
Answer:3 / 5
Explanation:
Given,
Pete played 18 number of matches in a week,
Total number of matches are by adding 18 with 12 we get 30,
Ratio of number of matches Pete played to the total number of matches both boys played is 18 / 30,
To get into the simplest form 18 / 30 can be divisible by six we get 3 / 5.
c. How many times the number of matches Pete played is the number of matches Jack played?
Solve. Draw a model to help you.
Answer:2 / 3
Explanation:
Given,
Pete played 12 number of matches,
Jack played 18 number of matches,
By dividing 12 / 18 with 6 we get 2 / 3 as the simplest form.
Question 12.
Kenny’s weight is \(\frac{6}{7}\) times Melvin’s weight.
a. What is the ratio of Kenny’s weight to Melvin’s weight? Give your answer in fraction form.
Answer:6 / 7
Explanation:
Given,
Kenny’s weight is considered as 6 times of Melvin’s weight,
Melvin’s weight is considered as 7 times of Kenny’s weight,
The ratio of Kenny’s weight to Melvin’s weight is 6 / 7.
b. What is the ratio of Melvin’s weight to the total weight of the two boys? Give your answer in fraction form.
Answer:7 / 13
Explanation:
Given,
Melvin’s weight is considered as 7,
Total weight of Kenny’s weight and Melvin’s weight is by adding 6 with 7 we get 13,
The ratio of Melvin’s weight to the total weight of two boys is 7 / 13.
c. How many times the total weight of the two boys is Kenny’s weight?
Answer:6 / 13
Explanation:
Given,
Kenny’s weight is considered as 6,
Total weight of Kenny’s weight and Melvin’s weight is by adding 6 with 7 we get 13,
The ratio of Kenny’s weight to the total weight of two boys is 6 / 13.
Solve.
Question 13.
Kimberly is 3 times as old as her sister, Halley.
a. Find the ratio of Kimberly’s age to Halley’s age. Give your answer in fraction form.
Answer:
Given,
Kimberly is 3 times as old as her sister,
Kimberly’s age as 3,
Halley’s age as 1,
The ratio of kimberly’s age to Halley’s age is 3 / 1.
b. Find the ratio of Halley’s age to their total age. Give your answer in fraction form.
Answer:
Given,
Halley’s age as 1,
Kimberly’s age as 3,
By adding 1 with 3 we get 4,
So the ratio of Halley’s age to their total age is 1 / 4.
c. How many times Kimberly’s age is Halley’s age?
Answer:
Given,
Kimberly’s age is 3 times as old as her sister,
Halley’s age can be considered as 1,
Halley’s age is 1 / 3 times Kimberly’s age.
d. How many times their total age is Kimberly’s age?
Answer:
Given,
Kimberly’s age is 3 times as old as her sister Halley,
Halley’s age is considered as 1,
By adding 3 with 1 we get 4,
Kimberly’s age is 3 / 4 times to their total age.
Solve.
Question 14.
In a college library, there are 4 times as many nonfiction books as fiction books.
a. Find the ratio of the number of nonfiction books to the number of fiction books. Give your answer in fraction form.
Answer:
Given,
Nonfiction books in the library is 4,
Fiction books in the library is 1,
The ratio of the number of nonfiction books to the number of fiction books is 4 / 1.
b. How many times the number of nonfiction books is the number of fiction books?
Answer:
Given,
The number of nonfiction books is 1 / 4 times the number of fiction books.
c. Suppose the number of fiction books is \(\frac{2}{7}\) times the number of nonfiction books. What would be the ratio of the number of nonfiction books to the total number of books? Give your answer in fraction form.
Answer:
Given,
The number of fiction books are 2,
The number of nonfiction books are 7,
Total number of books are by adding 2 with 7 we get 9,
The ratio of the number of nonfiction books to the total number of books are 7 / 9.