Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 6 Lesson 6.2 Representing Functions to score better marks in the exam.
Math in Focus Grade 8 Course 3 A Chapter 6 Lesson 6.2 Answer Key Representing Functions
Math in Focus Grade 8 Chapter 6 Lesson 6.2 Guided Practice Answer Key
Complete
Question 1.
A game shop rents out video games at a rate of $6 per game. The total amount of money the shop collects, y dollars, is a function of the number of games, x, that the shop rents out.
a) Write a verbal description of the function. Then write an algebraic equation for the function.
Total amount of money the shop collects equals the product of the rental rate and the ![]() .
.
![]() = 6 •
= 6 • ![]() Write an equation.
Write an equation.
![]() =
= ![]() Simplify.
Simplify.
Answer:
Given,
A game shop rents out video games at a rate of $6 per game.
The total amount of money the shop collects, y dollars, is a function of the number of games, x, that the shop rents out.
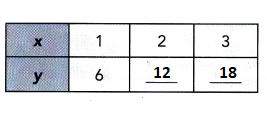
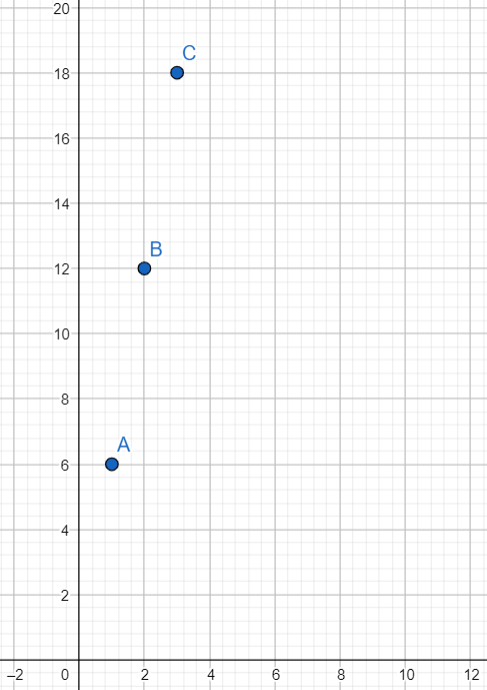
y = 6 • x
y = 6x
b) Construct a table of x- and y-values for the function. this situation,
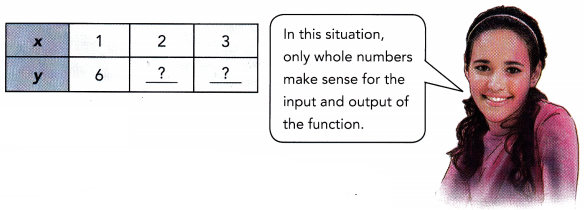
Answer:
c) Use the table of values in b) to graph the function. Use 1 unit on the horizontal axis to represent 1 game for the x interval, and 1 unit on the vertical axis to represent $6 for the y interval.
Answer:
Question 2.
A fire sprinkler sprays water at a rate of 8 gallons per minute. The total amount of water being sprayed, y gallons, is a function of the number of minutes, x, that the sprinkler sprays water.
a) Write a verbal description of the function. Then write an algebraic equation for the function.
Total amount of water being sprayed equals product of the rate of water flow and the ![]() .
.
![]() =
= ![]() •
• ![]() Write an equation.
Write an equation.
![]() =
= ![]() Simplify.
Simplify.
Answer:
Given,
A fire sprinkler sprays water at a rate of 8 gallons per minute.
The total amount of water being sprayed, y gallons, is a function of the number of minutes, x, that the sprinkler sprays water.
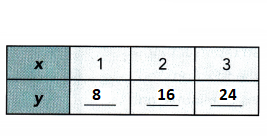
y = 8 • x
y = 8x
b) Construct a table of x- and y-values for the function.

Answer:
c) Use the table of values in b) to graph the function. Use 1 unit on the horizontal axis to represent 1 minute for the x interval, and 1 unit on the vertical axis to represent 8 gallons for the y interval.
Answer:
Question 3.
The table shows the total distance, y miles, indicated on the odometer of Jason’s car and the amount of gasoline used, x gallons, on a particular day.

a) Graph the function. Use 1 unit on the horizontal axis to represent 1 gallon for the x interval from 0 to 5, and 1 unit on the vertical axis to represent 30 miles for the y interval from 1,000 to 1,150.
Answer:
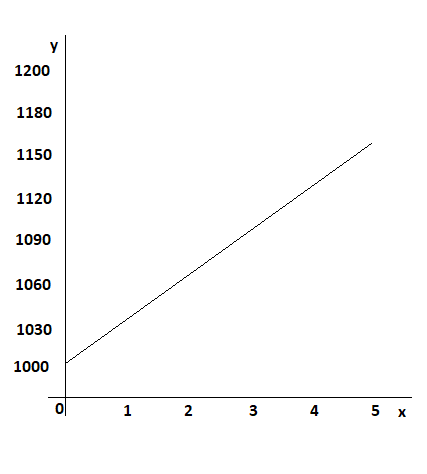
b) Write an algebraic equation for the function.
Answer: y = 30x + 1000
c) Describe how the slope and the y-intercept of the graph are related to the function.
Answer:
The y-intercept, 1000 means that the odometer of Jason’s car shows 1000 mi when he starts driving.
The shape 30, gives the rate at which the distance indicated on the odometer is changing. For every gallon of gasoline, the distance indicated on the odometer increases by 30 mi.
Math in Focus Course 3A Practice 6.2 Answer Key
Write a verbal description of each function. Then write an algebraic equation for the function.
Question 1.
Gordon is traveling at a constant speed of 80 kilometers per hour. The distance he travels, d kilometers, is a function of the amount of time he takes to travel, t hours.
Answer:
The distance Gordon travels equals 80km/h times the number of hours he takes to travel,
d = 80t
Question 2.
Mr. Henderson pays a monthly charge of $40 for a family cell phone plan. Each additional family member pays $10 every month. The total amount Mr. Henderson and his family members pay each month, y dollars, is a function of the number of the additional family members who use the plan, x.
Answer:
Given,
Mr. Henderson pays a monthly charge of $40 for a family cell phone plan.
Each additional family member pays $10 every month.
The total amount Mr. Henderson and his family members pay each month, y dollars, is a function of the number of the additional family members who use the plan, x.
y = 10x + 40
Question 3.
Math Journal In questions 1 and 2 tell whether all values for the input and output are meaningful for the functions. Explain.
Answer:
All the values for the input and output are meaningful because time and distance are continuous quantities.
Only whole numbers are meaningful for the input and output.
The input values which are the numbers of additional family members must be whole numbers.
So, the corresponding output values of the function
Write an algebraic equation for each function. Then construct a table of x- and y-values for the function.
Question 4.
The students from the Robotics Club are making model windmills for a workshop. Each windmill has three blades. The total number of blades needed, y, is a function of the number of windmills they make, x.
Answer:
Given,
Each windmill has three blades.
The total number of blades needed, y, is a function of the number of windmills they make, x.
y = 3x
Question 5.
A newly made glass vase has a temperature of 580°C. Its temperature then decreases at an average rate of 56°C per minute. The temperature of the glass vase, y°C, is a function of the number of minutes its temperature has been decreasing, x.
Answer: y = 580 – 56x
| X | -1 | 2 | 3 |
| y | 524 | 468 | 412 |
Each of the following graphs represents a function. Write an algebraic equation to represent the function.
Question 6.
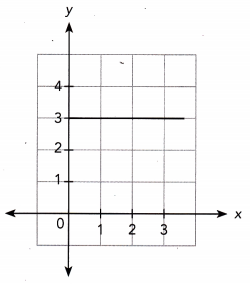
Answer: y = 3
Question 7.
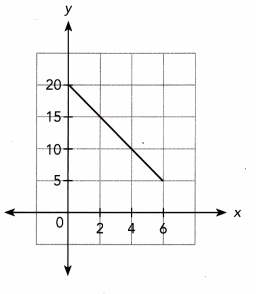
Answer: y -5/2 x + 20
Use the table of values to plot a graph to represent the function.
Question 8.
The table shows the number of chairs in a classroom, y, as a function of the number of students in the classroom. Use 1 unit on the horizontal axis to represent 1 student for the x interval, and 1 unit on the vertical axis to represent 4 chairs for the y interval.

Answer:
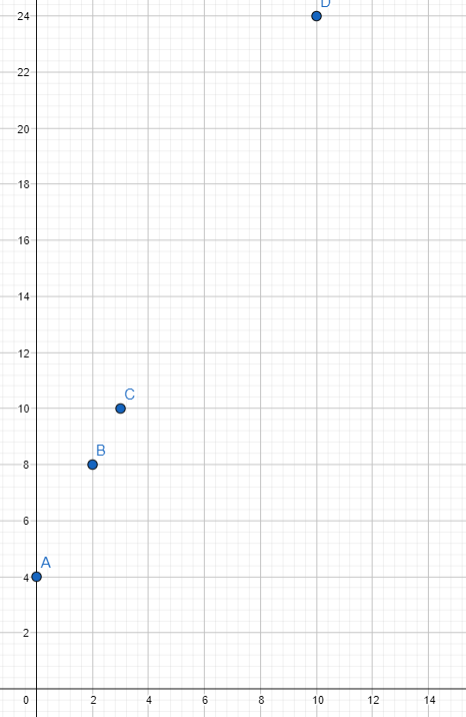
Use the table of values to plot a graph to represent the function. Then write an algebraic equation for the function.
Question 9.
A motorcyclist rode at a constant speed from City A to City B, which are 240 miles apart. The table shows his distance from City B, y miles, as a function of the number of hours he rode, x hours. Use 1 unit on the horizontal axis to represent 1 hour for the x interval, and 1 unit on the vertical axis to represent 40 miles for the y interval.

Answer:
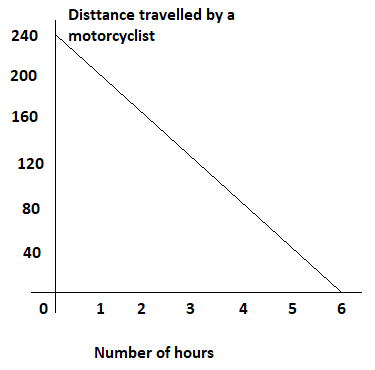
y = -40x + 240
Solve. Show your work.
Question 10.
The graph shows the temperature of a package of food, y°C, as a function of the time the food is in the freezer, x minutes.
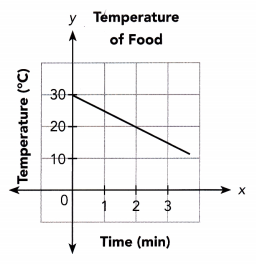
a) Write an equation in slope-intercept form to represent the function.
Answer:
The line passes through the points (0, 30) and (2, 20).
Use the slope formula:
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Substitute values:
= \(\frac{20-30}{2-0}\)
Subtract:
= \(\frac{-10}{2}\)
Simplify:
= -5
The line intersects the y-axis in point (0, 30). So the y-intercept is 30.
b = 30
Substitute the values of m and b. The slope-intercept form is:
y = -5x + 30
So an equation of the Line is y = -5x + 30.
b) What information do the values for slope and y-intercept give you about the function?
Answer:
The y-intercept shows that the initial temperature of the package was 30° C. The slope, -5, gives the rate at which the package’s temperature decreases each minute.
Question 11.
Hillary has $60 on her bus card. Every time she rides a bus, $1.50 is deducted from the value on her card. The amount of money she has on her card, y dollars, is a function of the number of times she rides a bus, x.
a) Write a verbal description of the function. Then write an algebraic equation for the function.
Answer:
The amount of money Hillary has on her bus card equals $60 minus $1.50 times the number if times she rides on a bus;
y = 60 – 1.5x
b) Construct a table of x- and y-values for the function in a). Use values of x from 0 to 6.
Answer:
| Number of bus rides | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Amount of money on Hillary’s Card (y) | 60 | 58.5 | 57 | 55.5 | 54 | 52.5 | 51 |
c) Use the table of values in b) to plot a graph to represent the function. Use 1 unit on the horizontal axis to represent 1 bus ride for the x interval from 0 to 6, and 2 units on the vertical axis to represent $3 for the y interval from 51 to 60.
Answer:
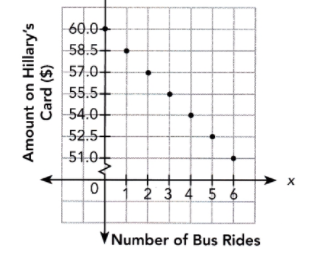
d) How many bus rides has Hillary taken if she has $51 left on her card?
Answer: 6