Math in Focus Grade 6 Chapter 6 Lesson 6.3 Answer Key Percent of a Quantity

Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 6 Lesson 6.3 Percent of a Quantity to score better marks in the exam.

Math in Focus Grade 6 Course 1 A Chapter 6 Lesson 6.3 Answer Key Percent of a Quantity

Math in Focus Grade 6 Chapter 6 Lesson 6.3 Guided Practice Answer Key

Complete. Use the models to help you.

Question 1.
What is 40% of 720 centimeters?
Method 1

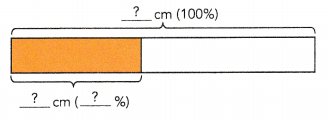
The model shows that:
100% → cm
1% → \(\frac{?}{?}\) = cm
40% → × = cm
40% of 720 centimeters is centimeters.

Method 2
40% of 720 cm = \(\frac{?}{100}\) × 720
= cm
40% of 720 centimeters is centimeters.
Answer:
288centimeters
Explanation:
Method 1
The model shows that:
100% → 720cm
1% → \(\frac{720}{100}\) = 7.2cm
40% → 7.2 × 40 = 288cm
40% of 720 centimeters is 288 centimeters.

Method 2
40% of 720 cm = \(\frac{40}{100}\) × 720
= 288 cm
40% of 720 centimeters is 288centimeters.

Question 2.
What is 75% of 800 kilograms?
Method 1

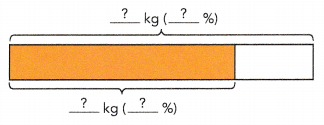
The model shows that:
100% → kg
1% → \(\frac{?}{?}\) = kg
75% → × = kg
75% of 800 kg is kg.

Method 2
75% of 800 kg = \(\frac{?}{?}\) × 800
= kg
75% of 800 kg is kg.
Answer:
600kg
Explanation:
The model shows that:
100% → 800kg
1% → \(\frac{800}{100}\) = 8kg
75% → 75 × 8 = 600kg
75% of 800 kg is 600kg.

Method 2
75% of 800 kg = \(\frac{75}{100}\) × 800
= 600kg
75% of 800 kg is 600kg.

Find the percent of each whole.

Question 3.
30% of 450
Answer: 135
Explanation:
30% of 450
= \(\frac{30}{100}\) × 450
= 135
30% of 450 is 135.

Question 4.
225% of $60
Answer: 135
Explanation:
225% of $60
= \(\frac{225}{100}\) × 60
= 135
225% of 60 is 135.

Question 5.
55% of 320
Answer: 176
Explanation:
55% of 320
= \(\frac{55}{100}\) × 320
= 176
55% of 320 is 176.

Question 6.
110% of $550
Answer: 605
Explanation:
110% of $550
= \(\frac{110}{100}\) × 550
= 605
110% of 550 is 605.

Solve. Use the model to help you.

Question 7.
27% of the students in a school are in grade 6. This is 540 students. How many students are there in the school?

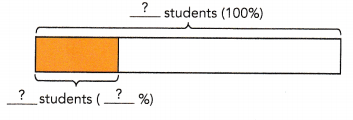
The model shows that:
% → students
1% → \(\frac{?}{?}\) = students
100% → 100 × = students
There are students in the school.
Answer:
2000 students.
Explanation:
The model shows that:
27% → 540 students
1% → \(\frac{540}{27}\) = 20 students
100% → 100 × 20 = 2000 students
There are 2000 students in the school.

Solve. You may draw a model to help you.

Question 8.
At an amusement park, 60% of the people were adults, and the rest were children. There were 720 adults. How many people were at the amusement park in all?
 % → people
1% → \(\frac{?}{?}\) = people
100% → × = people
There were people at the amusement park in all.
Answer:
1200 people
Explanation:
60% → 720people
1% → \(\frac{720}{60}\) = 12 people
100% → 100× 12 = 1200 people
There were 1200 people at the amusement park in all.

Find the missing value.

Question 9.
20% of is 163.
Answer: 185
Explanation:
20% of is 163.
\(\frac{20}{100}\) x = 163
x = (163 x 100)  ÷ 20
= 16300  ÷ 20
= 815

Question 10.
45% of is 150.
Answer: 333
Explanation:
45% of is 150.
\(\frac{45}{100}\) x = 150
x = (150 x 100)  ÷ 45
= 15000 ÷ 45
= 333

Math in Focus Course 1A Practice 6.3 Answer Key

Solve. Use the models to help you.

Question 1.
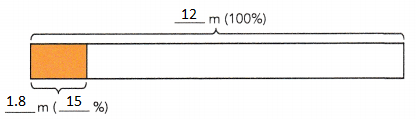
What is 15% of 12 meters?

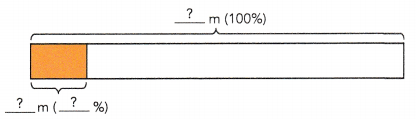
Answer: 1.8 m
Explanation:

Question 2.
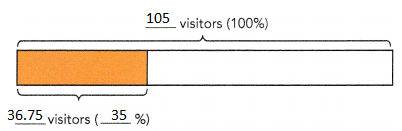
A park ranger finds that 35% of the park’s visitors stay at the campground. If 105 visitors stayed at the campground one day, how many visitors did the park have that day?

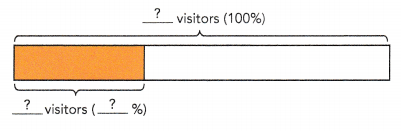
Answer: 36.75
Explanation:
A park ranger finds that 35% of the park’s visitors stay at the campground.
105 visitors stayed at the campground one day.
number of visitors did the park have that day

Find the quantity represented by each percent.

Question 3.
45% of $360
Answer:
$162
Explanation:
45% of $360
= \(\frac{45}{100}\) × 360
= 162
45% of 360 is 162.

Question 4.
66% of 740 kilometers
Answer:
488.4kg
Explanation:
66% of $740
= \(\frac{66}{100}\) × 740
= 488.4
66% of 740 is 488.4.

Solve. Show your work.

Question 5.
There are 1,500 students in a school. 65% of them are girls. How many girls are there in the school?
Answer:
975 girls.
Explanation:
There are 1,500 students in a school.
65% of them are girls.
Total girls in the school 65% of 1500
= \(\frac{65}{100}\) × 1500
= 975

Question 6.
A school raises $4,000 for its new library. 36% of the money is used to buy reference books. How much money is used to buy reference books?
Answer:
$1,440
Explanation:
A school raises $4,000 for its new library.
36% of the money is used to buy reference books.
Total money is used to buy reference books
36% of $4,000
= \(\frac{36}{100}\) × 4000
= 1440

Question 7.
Ms. Galan spent 55% of her savings on a television that cost $550. How much money did she have in her savings before she bought the television?
Answer:
$1,000
Explanation:
Ms. Galan spent 55% of her savings on a television that cost $550.
Money she have in her savings before she bought the television
550 = 55% of her savings
550 = \(\frac{55}{100}\) x
x = (550 x 100) ÷ 55
x = 1000

Question 8.
75% of a number is 354. Find the number.
Answer:
472 is the number
Explanation:
75% of x = 354
x = (354 x 100)  ÷ 75
x = 472

Question 9.
Ahyoka has 250 CDs. 10% are country, 70% are pop, and the rest are hip-hop. How many CDs are hip-hop?
Answer:
50 CDs
Explanation:
Ahyoka has 250 CDs.
10% are country, 70% are pop = 70 + 10 = 80%
the rest are hip-hop = 100 – 80 = 20%
Total hip-hop CDs = 20% of 250
= \(\frac{20}{100}\) × 250
= 50

Question 10.
There are 820 people at a stadium. 65% of them are adults, 20% of them are boys, and the rest are girls. How many girls are there at the stadium?
Answer:
123 girls
Explanation:
There are 820 people at a stadium.
65% of them are adults, 20% of them are boys = 65 + 20 = 55%
Rest of the girls = 100 – 85 = 15%
Number of girls at the stadium = 15% of 820
= \(\frac{15}{100}\) × 820
= 123

Question 11.
Ms. Stapleton had 2,600 hens, ducks, and goats on her farm. 35% of them were hens, and 25% of them were goats. How many ducks did she have on her farm?
Answer:
Ducks 790
Explanation:
total 2,600 hens, ducks, and goats in farm
Hens = 2,600 x 35%
= (2,600 x 35)/100
= 26 x 35
= 910

Goats = 25% of 2,600
= (2600 x 25)/100
= 26 x 25
= 900

Ducks = 2600 – (Hens + Goats)
Hens + Goats = 910 + 900 = 1,810
Ducks = 2,600 – 1,810
= 790

Question 12.
There are 1,505 fruits for sale at a farmer’s market. 39% of them are apples, 28% are oranges, 13% are honeydew melons, and the rest are watermelons. How many watermelons are there?
Answer:
301 watermelons
Explanation:
There are 1,505 fruits for sale at a farmer’s market.
39% of them are apples, 28% are oranges, 13% are honeydew melons,
Total apples, oranges and honeydew melons = 39 + 28 + 13 = 80
Number of watermelons = 100 – 80 = 20%
Number of watermelons 20% of 1505
= \(\frac{20}{100}\) × 1505
= 301

Question 13.
120% of a number is 45. Find the number.
Answer:
37.5
Explanation:
120% of x = 45
x = (45 x 100)  ÷ 120
x = 37.5

Question 14.
250% of a number is 60. Find the number.
Answer:
24 is the number
Explanation:
250% of x = 60
x = (60 x 100)  ÷ 250
x = 24

Question 15.
400% of a number is 45. Find the number.
Answer:
11.25 is the number
Explanation:
400% of x = 45
x = (45 x 100) ÷ 400
x = 11.25

Question 16.
Last month, Alex spent 40% of his salary on a laptop. He then spent 30% of it on his bills and saved the remaining $1,200. What was his salary?
Answer:
$4,000
Explanation:
He spent 70% of his salary and had $1200 left.
Let ‘x’ be his salary.
100% – 70% = 30% left.
30% of x = 1200
= \(\frac{30}{100}\) x = 1200
0.3x = 1200
x = 1200 ÷ 0.3
x = 4000

Question 17.
20% of the spectators at a tennis match are women. 10% of them are girls, 30% are boys, and the remaining 3,600 spectators are men. Find the total number of spectators at the match.
Answer:
9,000 spectators
Explanation:
20% of the spectators at a tennis match are women.
10% of them are girls, 30% are boys,
Total women, boys and girls = 20 + 10 + 30 = 60%
Men spectators = 3600
The total number of spectators at the match
40 % of x = 3600
\(\frac{40}{100}\) x = 3600
0.4x = 3600
x = 3600 ÷ 0.4
x = 9,000

Question 18.
Jovita made 300 greeting cards. She sold 40% of the cards, gave 85% of the remaining cards to her friends, and kept the rest of the cards for herself. How many greeting cards did she keep for herself?

Answer:
27 greeting cards
Explanation:
Jovita made 300 greeting cards.
She sold 40% of the cards = 300
\(\frac{40}{100}\) x 300 = 120
she sold 120 out of 300 = 300 – 120 = 180
she gave 85% of the remaining cards to her friends,
\(\frac{85}{100}\) x 180
Remaining cards = 180 – 153
Total greeting cards she kept for herself = 27

Question 19.
Patrick saved $500. He received 25% of the money for his birthday, saved 30% of the remainder from his allowance, and earned the rest of it by mowing lawns. How much of his savings did he earn by mowing lawns?
Answer:
$262.50
Explanation:
Patrick saved $500.
He received 25% of the money for his birthday,
saved 30% of the remainder from his allowance = 25 + 30 = 75%
75% of 500
= \(\frac{75}{100}\) x 500
= 75 x 5 = 375
Total savings he earn by mowing lawns
100 – 30 = 70%
70% of x = 375
0.7x = 375
x = 375 x 0.7
x = 262.50

Question 20.
Math Journal Michelle and Michael checked some books out of the library. 20% of the books Michelle checked out were fiction books, and 40% of the books Michael checked out were fiction books. Your friend thinks that Michael checked out more fiction books than Michelle. Explain the error in your friend’s thinking. Use an example to support your reasoning.
Answer:
The error in the assessment is that Michael checked more fiction books than Michelle.
Explanation:
We can determine who has more books only when we know how many books each person has checked out in total,
but not the proportion of fiction of books, (20% and 40%).
So, we can assume that Michael checked more fiction books than Michelle.