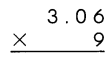
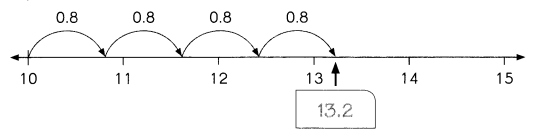
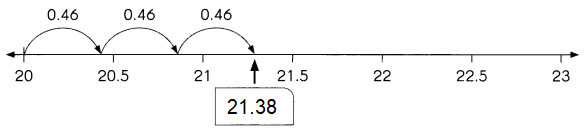
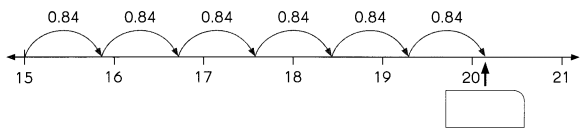
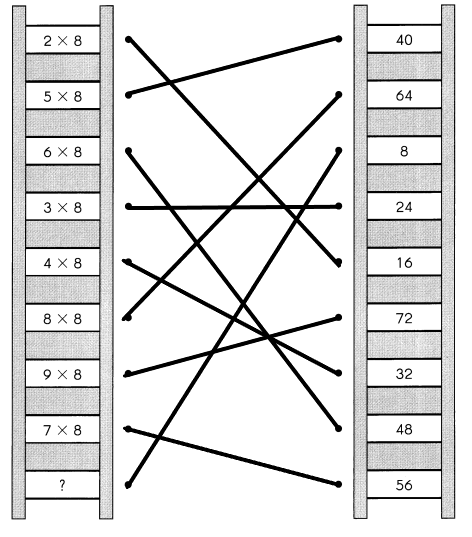
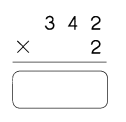
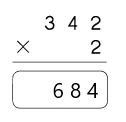
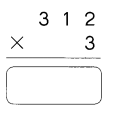
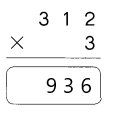
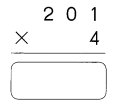
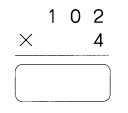
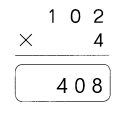
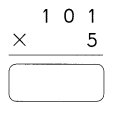
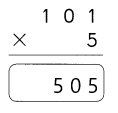
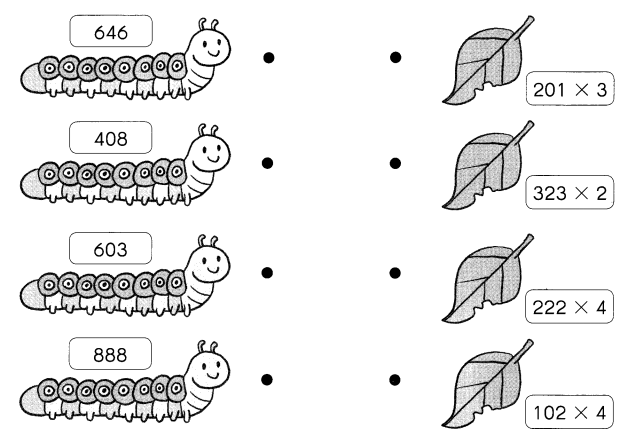
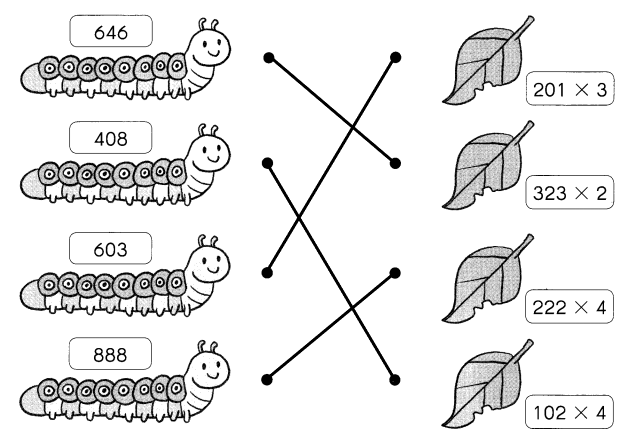
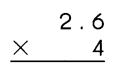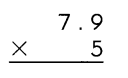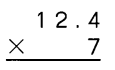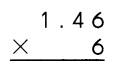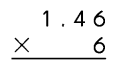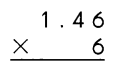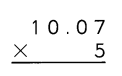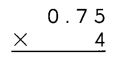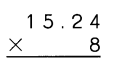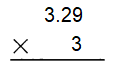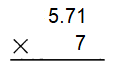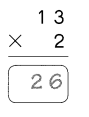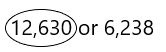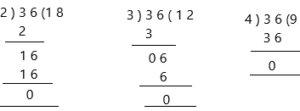Go through the Math in Focus Grade 4 Workbook Answer Key Cumulative Review Chapters 1 and 2 to finish your assignments.
Math in Focus Grade 4 Cumulative Review Chapters 1 and 2 Answer Key
Concepts and Skills
Write each number in standard form. (Lesson 1.1)
Question 1.
forty-eight thousand, six ____
Answer: 48,006
Explanation:
– A standard form of a number in Maths is basically mentioned for the representation of large numbers or small numbers. We use exponents to represent such numbers in standard form.
– The standard form of a number is introduced to avoid the difficulty of reading large numbers. Any number that can be written in the decimal form between 1.0 to 10.0 multiplied by the power of 10.
How to write a standard form of a number:
The steps to write the standard form of a number are as follows:
Step 1: Write the first number from the given number.
Step 2: Add the decimal point after the first number.
Step 3: Now, count the number of digits after the first number from the given number and write it in the power of 10.
By using the above steps we can write the number in standard form: 48,006
The above-given is word form, that we need to convert into the standard form:
Step 1:The first number is 4.
Step 2: Adding the decimal point after the number 4, it becomes “4.”
Step 3: The number of digits after 4 is 4
Hence, the standard form of 48,006 is 4.8006× 104.
Question 2.
one hundred thousand ____
Answer:100,000
Explanation:
– A standard form of a number in Maths is basically mentioned for the representation of large numbers or small numbers. We use exponents to represent such numbers in standard form.
– The standard form of a number is introduced to avoid the difficulty of reading the large numbers. Any number that can be written in the decimal form between 1.0 to 10.0 multiplied by the power of 10.
How to write a standard form of a number:
The steps to write the standard form of a number are as follows:
Step 1: Write the first number from the given number.
Step 2: Add the decimal point after the first number.
Step 3: Now, count the number of digits after the first number from the given number and write it in the power of 10.
By using the above steps we can write the number in standard form: 100,000
The above-given is word form, that we need to convert into the standard form:
Step 1:The first number is 1.
Step 2: Adding the decimal point after the number 1, it becomes “1.”
Step 3: The number of digits after 1 is 5
Hence, the standard form of 100,000 is 1× 105.
Question 3.
sixty-nine thousand, two hundred eleven ____
Answer:69,212
Explanation:
– A standard form of a number in Maths is basically mentioned for the representation of large numbers or small numbers. We use exponents to represent such numbers in standard form.
– The standard form of a number is introduced to avoid the difficulty of reading the large numbers. Any number that can be written in the decimal form between 1.0 to 10.0 multiplied by the power of 10.
How to write a standard form of a number:
The steps to write the standard form of a number are as follows:
Step 1: Write the first number from the given number.
Step 2: Add the decimal point after the first number.
Step 3: Now, count the number of digits after the first number from the given number and write it in the power of 10.
By using the above steps we can write the number in standard form: 69,212
The above-given is word form, that we need to convert into the standard form:
Step 1:The first number is 1.
Step 2: Adding the decimal point after the number 6, it becomes “6.”
Step 3: The number of digits after 6 is 4
Hence, the standard form of 69,212 is 6.9212× 104.
Write each number in word form. (Lesson 1.1)
Question 4.
53,900 _____
Answer: fifty-three thousand nine hundred
Explanation:
Numbers in words are written using the English alphabet. Numbers can be expressed both in words and figures. For example, 100,000 in words is written as One Lakh or One hundred thousand. Numbers in words can be written for all the natural numbers, based on the place value of digits, such as ones, tens, hundreds, thousands, and so on.
Likewise, 53,900 can be written in words by using the place value of digits.

1. On putting the commas, the number is represented by 53, 900.
2. The first digits places are ten thousand and thousands place, this can be written as fifty-three thousand.
3. The comma present on the rightmost side represents nine hundred.
4. Now write the overall word form: fifty-three thousand nine hundred.
Question 5.
16,658 ____
Answer: sixteen thousand, six hundred fifty-eight.
Explanation:
Numbers in words are written using the English alphabet. Numbers can be expressed both in words and figures. For example, 100,000 in words is written as One Lakh or One hundred thousand. Numbers in words can be written for all the natural numbers, based on the place value of digits, such as ones, tens, hundreds, thousands, and so on.
Likewise, 16,658 can be written in words by using the place value of digits.

1. On putting the commas, the number is represented by 16,658.
2. The first digits places are ten thousand and thousands place, this can be written as sixteen thousand.
3. The comma present on the rightmost side represents six hundred fifty-eight.
4. Now write the overall word form: sixteen thousand, six hundred fifty-eight.
Question 6.
20,306 _____
Answer: twenty thousand, three hundred six.
Explanation:
Numbers in words are written using the English alphabet. Numbers can be expressed both in words and figures. For example, 100,000 in words is written as One Lakh or One hundred thousand. Numbers in words can be written for all the natural numbers, based on the place value of digits, such as ones, tens, hundreds, thousands, and so on.
Likewise, 20,306 can be written in words by using the place value of digits.

1. On putting the commas, the number is represented by 20,306.
2. The first digits places are ten thousand and thousands place, this can be written as twenty thousand.
3. The comma present on the rightmost side represents three hundred six.
4. Now write the overall word form: twenty thousand, three hundred six.
Fill in the blank to write the number in expanded form. (Lesson 1.1)
Question 7.
13,901 = 10,000 + ___ + 900 + 1
Answer: 10,000+3000+900+0+1
Explanation:
The expanded form of the numbers helps to determine the place value of each digit in the given number. It means that the expansion of numbers is based on the place value. The expanded form splits the number, and it represents the number in units, tens, hundreds and thousands form.
How to write the numbers in expanded form:
Go through the below steps to write the numbers in expanded form:
Step 1: Get the standard form of the number.
Step 2:Identify the place value of the given number using the place value chart.
Step 3: Multiply the given digit by its place value and represent the number in the form of (digit × place value).
Step 4: Finally, represent all the numbers as the sum of (digit × place value) form, which is the expanded form of the number.

Now the expanded form of 13,901:
Step 1: The standard form of the number is 13901.
Step 2: The place value of the given number is:
1 – Ten thousand
3 – Thousands
9 – Hundreds
0 – Tens
1 – Ones
Step 3:Multiply the given number by its place value.
(i.e.,) 1×10, 000, 3×1000, 9×100, 0×10, 1×1
Step 4:Expanded form is 10,000+ 3000+900+0+1
Finally, the expanded form of the number 35713 is 10,000+ 3000+900+0+1.
Fill in the blanks. (Lesson 1.2)
Question 8.
100 more than 26,542 is ____
Answer:26,642
Explanation:
We are looking for a new number which is 100 more than 26542.
We will get the new number by adding 100 to 26542.
We write it down as:
26542+100=26642
And finally the solution for: What number is 100 more than 26542?
is 26642.
Question 9.
____ is 100 less than 79,023.
Answer:78,923
Explanation:
We are looking for a new number which is 100 less than 79,023
We will get the new number by subtracting 100 from 78,923.
We write it down as:
79,023-100=78,923.
And finally the solution for: What number is 100 less than 79,023?
is 78,923.
Circle the number that is greater. (Lesson 1.2)
Question 10.
12,630 or 6,238
Answer:
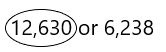
Explanation:
12,630 > 6,238
The greater than symbol in maths is placed between two values in which the first number is greater than the second number.
Now we need to compare the numbers:
Rules to compare the numbers:
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
Rule 1: Numbers with more digits
When we compare numbers, then check if both the numbers are having the same number of digits or not. If a number has more digits, then it is greater than the other number.
For example,
33 > 9 or else,
take the above-given numbers. Those are 12,630 and 6,238.
By comparing these two numbers the first number is having more digits than the second number.
So here rule 1 is applicable.
the first number is greater than the second number.
Therefore, 12,630 is greater than 6,238.
Question 11.
45,200 or 45,496
Answer:
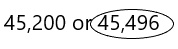
Explanation:
Now we need to compare the numbers:
Rules to compare the numbers:
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
– Numbers with more digits
– Numbers starting with a larger digit
Rule 1: Numbers with more digits
When we compare numbers, then check if both the numbers are having the same number of digits or not. If a number has more digits, then it is greater than the other number.
Rule 2: Numbers starting with a larger digit
This rule is applicable when two numbers are having the same number of digits. In such cases, we need to check the digit at the leftmost place, whichever is greater. Therefore, the number with a greater digit at the leftmost place of the number is greater than the other number.
the above-given numbers are having the same number of digits. So rule 2 is applicable here.
– 45,200 and 45,496 both the numbers have an equal number of digits, therefore, we will compare the left-most digit of both the numbers.
– As we can see the first two digits are the same for both the numbers, thus we need to compare the next left-most digit of both numbers.
– Now compare 2 and 4, here we need to circle the greatest number. So check out the number having 4 in the hundreds place, that could be the greatest number.
4 > 2
Therefore, the second number is having 4 in the hundreds place.
Thus, 45,496 > 45,200
Hence, the second number is greater than the first number.
45,496 is greater than 45,200.
Question 12.
62,529 or 69,522
Answer:
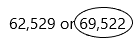
Explanation:
Rule 2 is applicable here because both numbers are having the same number of digits.
Now we compare the place value of digits in both numbers.
– 62,529 or 69,522 both the numbers have an equal number of digits, therefore, we will compare the left-most digit of both the numbers.
– As we can see the first digits are the same for both the numbers, thus we need to compare the next left-most digit of both numbers.
– Now compare 2 and 9, here we need to circle the greatest number. So check out the number 9 having in the thousands place, that could be the greatest number.
9 > 2
Therefore, the second number is having 4 in the hundreds place.
Thus, 69,522 > 62,529
Hence, the second number is greater than the first number.
69,522 is greater than 62,529.
Question 13.
90,236 or 87,415
Answer:
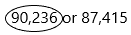
Explanation:
Rule 2 is applicable because both the numbers are having the same number of digits.
90,236 and 87,415 both the numbers have an equal number of digits, therefore, we will compare the left-most digit of both the numbers.
9 > 8
Therefore,
90,236 > 87,415
Hence, 90,236 is greater than 87,415.
Circle the number that is less. (Lesson 1.2)
Question 14.
6,563 or 48,200
Answer:
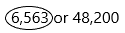
Explanation:
– Compare the numbers. The second number is having more digits than the first number. So rule 1 is applicable.
Rule 1: Number with more digits
When we compare numbers, then check if both the numbers are having the same number of digits or not. If a number has more digits, then it is greater than the other number.
According to rule 1, which number is having more digits is the greatest number. But here we need to circle the number which is less.
since 6,563 has 4 digits and 48,200 has 5 digits, therefore, according to rule 1, the number with more digits is greater than the number with fewer digits.
Here clearly shows that 6,563 is the less number than the second number. Because the second number is having more digits.
6,563 < 48,200
Hence, 6,563 is less than 48,200.
Question 15.
67,186 or 67,254
Answer:
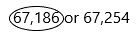
Explanation:
– Compare the numbers. Both numbers are having the same digits. So the rule 2 is applicable.
Rule 2: Number starting with a greater digit
This rule is applicable when two numbers are having the same number of digits. In such cases, we need to check the digit at the leftmost place, whichever is greater. Therefore, the number with a greater digit at the leftmost place of the number is greater than the other number.
– 67,186 and 67,254 both the numbers have an equal number of digits, therefore, we will compare the left-most digit of both the numbers.
– As we can see the first two digits are the same for both the numbers, thus we need to compare the next left-most digit of both numbers.
– 1 < 2
Therefore,
67,186 < 67,254
Hence, 67,186 is smaller than 67,254.
Question 16.
74,258 or 71,852
Answer:
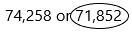
Explanation:
– 74,258 and 71,852 both the numbers have an equal number of digits, therefore, we will compare the left-most digit of both the numbers.
– But the left-most digit is also the same for both numbers, i.e.,7. So, we need to check the second left-most digit.
– Now compare 4 and 1. Here we need to circle the least number. So check the number having 1 in the thousands place and that number is the less number than the other number.
1 < 4
– The number 1 is having in the second number so the second number is less than the first number.
Therefore,
71,852 < 74,258
Hence, 71,852 is the smallest number than 74,258.
Question 17.
96,125 or 69,521
Answer:
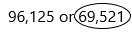
Explanation:
– 96,125 and 69,521 both the numbers have an equal number of digits, therefore, we will compare the first left-most digit of both the numbers.
– Compare 9 from the first number and 6 from the second number. Here we need to circle the less number so check the number which is having the least.
6 < 9
Therefore,
69,521 < 96,125
Hence, 69,521 is the smallest number than 96,125.
Write the set of numbers in order from least to greatest. (Lesson 1.2)
Question 18.

Answer:

Explanation:
– By applying rule 1 and rule 2 we can write the numbers from least to greatest.
– Here four numbers are given. Those are 8654, 56207, 56719, 68543.
– Three numbers are having the same digits and the first number is having 4 digits. So by applying rule 1, we can conclude that the first number is the least number that is 8,654.
– Now we need to compare the remaining three numbers. For these three numbers, we need to apply rule 2.
– 56207, 56719, 68543 the three numbers have an equal number of digits, therefore, we will compare the left-most digit of both the numbers.
– 56207 and 56719 As we can see the first two digits are the same for both the numbers, thus we need to compare the next left-most digit of both numbers.
– 2 < 7
Therefore,
56207 < 56719
Hence, 56207 is smaller than 56719.
– Now compare the 56207, 56719, 68543. As we already know, 56207 is smaller so let us check for 56719 and 68543.
– 5 < 6
Therefore,
56719 < 68543.
– hence, 56719 is smaller than 68543.
Now finally we can say:
8654 < 56207 < 56719 < 68543.
Continue or complete each number pattern. (Lesson 1.2)
Question 19.
11,500 11,000 10,500 _____ ____ ______
Answer: 10,000 9,500 9,000
Explanation:
Number patterns: A list of numbers that follow a certain sequence is known as patterns or number patterns.
– In Mathematics, a pattern is a repeated arrangement of numbers, shapes, colours and so on. The Pattern can be related to any type of event or object. If the set of numbers is related to each other in a specific rule, then the rule or manner is called a pattern. Sometimes, patterns are also known as a sequence. Patterns are finite or infinite in numbers.
Now the above-given pattern is an arithmetic pattern:
The arithmetic pattern is also known as the algebraic pattern. In an arithmetic pattern, the sequences are based on the addition or subtraction of the terms. If two or more terms in the sequence are given, we can use addition or subtraction to find the arithmetic pattern.
Here we need to find out the missing terms in the sequence.
– Here we can use the subtraction process to figure out the missing terms in the patterns.
In the pattern, the rule used is “ subtract 500 to the previous term to get the next term”.
The above-given numbers, take the second term (11,000). If we subtract “500” to the second term (11,000), we get the third term of 11,000-500=10,500
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 10,500. Therefore, 10,500-500 = 10,000.
Second missing term: The previous term is 10,000. So, 10,000-500 = 9,500
Third missing term: The previous term is 9,500. So, 9,500-500=9,000
hence, the complete arithmetic pattern is 11,500 11,000 10,500 10,000 9,500 9,000
Question 20.
63,800 64,100 64,400 ___ ___ _____
Answer: 64,700 65,000 65,300
Explanation:
Now the above-given pattern is an arithmetic pattern:
The arithmetic pattern is also known as the algebraic pattern. In an arithmetic pattern, the sequences are based on the addition or subtraction of the terms. If two or more terms in the sequence are given, we can use addition or subtraction to find the arithmetic pattern.
Here we need to find out the missing terms in the sequence.
– Here we can use the addition process to figure out the missing terms in the patterns.
In the pattern, the rule used is “ add 300 to the previous term to get the next term”.
The above-given numbers, take the second term (64,100). If we add “300” to the second term (64,100), we get the third term of 64,400.
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 64,400. Therefore, 64,400+300 = 64,700
Second missing term: The previous term is 64,700. So, 64,700+300 = 65,000
Third missing term: The previous term is 65,000. So, 65,000+300=65,300
hence, the complete arithmetic pattern is 63,800 64,100 64,400 64,700 65,000 65,300
Question 21.
27,852 29,853 ____ 33,855 35,856
Answer:31,854
Explanation:
Now the above-given pattern is an arithmetic pattern:
The arithmetic pattern is also known as the algebraic pattern. In an arithmetic pattern, the sequences are based on the addition or subtraction of the terms. If two or more terms in the sequence are given, we can use addition or subtraction to find the arithmetic pattern.
Here we need to find out the missing terms in the sequence.
– Here we can use the addition process to figure out the missing terms in the patterns.
In the pattern, the rule used is “ add 2001 to the previous term to get the next term”.
The above-given numbers, take the second term (29,853). If we add “2001” to the second term (29,853), we get the third term of 31,854.
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 29,853. Therefore, 29,853+2001 = 31,854
hence, the complete arithmetic pattern is 27,852 29,853 31,854 33,855 33,856
Find each sum or difference. Then use rounding to check that your answers are reasonable. (Lesson 2.1)
Question 22.
522 – 389
Answer:
522-389=133
The round off a number to 133 is 100.
Here we need to round off the numbers to get reasonable answers.
Rounding off means a number is made simpler by keeping its value intact but closer to the next number. It is done for whole numbers, and for decimals at various places of hundreds, tens, tenths, etc. Rounding off numbers is done to preserve the significant numbers. The number of significant figures in a result is simply the number of figures that are known with some degree of reliability.
– There are some rules for rounding off the number:
1. To get an accurate final result, always choose the smaller place value.
2. Look for the next smaller place which is towards the right of the number that is being rounded off to. For example, if you are rounding off a digit from hundreds place, look for a digit in the tens place.
3. If the digit in the smallest place is less than 5, then the digit is left untouched. Any number of digits after that number becomes zero and this is known as rounding down.
4. If the digit in the smallest place is greater than or equal to 5, then the digit is added with +1. Any digits after that number become zero and this is known as rounding up.
The above-given numbers are 522 and 389
Step 1: Round off the given number to the nearest 100

Step 2: subtract the numbers rounded off at step 1.
Estimated difference:500-400
Estimated difference=100.
Therefore, the answer is reasonable.
Question 23.
456 + 790
Answer: 1246
456+790=1246
The round off a number to 1246 is 1000
Here we need to round off the numbers to get reasonable answers.
Rounding off means a number is made simpler by keeping its value intact but closer to the next number. It is done for whole numbers, and for decimals at various places of hundreds, tens, tenths, etc. Rounding off numbers is done to preserve the significant numbers. The number of significant figures in a result is simply the number of figures that are known with some degree of reliability.
– There are some rules for rounding off the number:
1. To get an accurate final result, always choose the smaller place value.
2. Look for the next smaller place which is towards the right of the number that is being rounded off to. For example, if you are rounding off a digit from hundreds places, look for a digit in the tens place.
3. If the digit in the smallest place is less than 5, then the digit is left untouched. Any number of digits after that number becomes zero and this is known as rounding down.
4. If the digit in the smallest place is greater than or equal to 5, then the digit is added with +1. Any digits after that number become zero and this is known as rounding up.
The above-given numbers are 456 and 790
Step 1: Round off the given number to the nearest 100

Step 2: add the numbers rounded off at step 1.
Estimated difference:500+800
Estimated difference=1300.
1300 can be rounded off to the number 1000.
Therefore, the answer is reasonable.
Find each sum or difference. Then use front-end estimation to check that your answers are reasonable. (Lesson 2.1)
Question 24.
432 + 759
Answer:
Front-end estimation definition: It is a rounding technique used to get an approximate answer to a mathematical operation. It is the process of replacing the numbers in mathematical problems with numbers that are approximate (close to) to the original numbers.
432 can be rounded down to 400
– because the tens place is less than 5, so it rounded down.
759 can be rounded up to 800
– because the tens place is equal to 5, so the hundreds digit is added by ‘+1’ and the rest of the digits will become zero.
Now add the rounded off the numbers:
=400+800
=1200
Therefore, the front-end estimation is 1200.
Question 25.
816 – 532
Answer:
Front-end estimation definition: It is a rounding technique used to get an approximate answer to a mathematical operation. It is the process of replacing the numbers in mathematical problems with numbers that are approximate (close to) to the original numbers.
816 can be rounded down to 800
– because the tens place is less than 5, so it rounded down.
532 can be rounded up to 500
– because the tens place is less than 5, so it rounded down.
Now add the rounded off the numbers:
=800-500
=300
Therefore, the front-end estimation is 300.
Find each product. Then use rounding to check that your answers are reasonable. (Lesson 2.1)
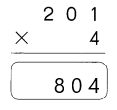
Question 26.
383 × 3
Answer: 1149
Explanation:
383 × 3=1149
The rounding of the number 1149 is 1000.
Explanation:
– 383 can be rounded as 400
– because the tens place is greater than 5 so the hundreds place value of a digit is added by ‘+1’ then it becomes 4 and the remaining digits become zero that is 400.
– Now multiply 400×3=1200
The number 1200 also rounded of t0 1000
– because if we round up by thousand or hundred the values are less than 5 s0 it becomes 1000.
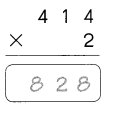
Question 27.
241 × 4
Answer:964
Explanation:
241 × 4=964
The rounding of the number 964 is 1000.
Explanation:
– 241 can be rounded as 200
– because the tens place is less than 5 s0 the hundreds place remains constant with the number 2 and the remaining places becomes zero that is 200.
– Now multiply 200×4=800
Therefore, the estimated value=800
Find each product. Then use front-end estimation to check that your answers are reasonable. (Lesson 2.1)
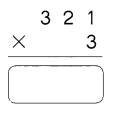
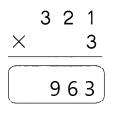
Question 28.
308 × 3
Answer:
The original product of 308 × 3=924
The round off value for 924 is 900
First, we need to find out the estimated values:
For the number 308, the round off value is 300
– because the tens place is less than 5 so the hundreds place remains constant that is 3 and the remaining place values will become zero then it becomes 300.
Now multiply 300 by 3
300×3=900
Thus, the front-end estimation value is 900
Therefore, the answer is reasonable.
Question 29.
126 × 5
Answer:
The original product of 126 × 5=630
The round off value for 630 is 600
First, we need to find out the estimated values:
For the number 126, the round off value is 100
– because the tens place is less than 5 so the hundreds place remains constant that is 1 and the remaining place values will become zero then it becomes 100.
Now multiply 100 by 5
100×5=500
Thus, the front-end estimation value is 500
Therefore, the answer is reasonable.
Find each quotient. Then use related multiplication facts to check that your answers are reasonable. (Lesson 2.1)
Question 30.
92 ÷ 4
Answer: 23
The division is a method of distributing a group of things into equal parts. It is one of the four basic operations of arithmetic, which gives a fair result of sharing.
Dividend ÷ divisor = quotient
quotient is 23
the remainder is 0.

Explanation:
here we need to write the multiplication facts:
The multiplication facts of 92 are:
1 × 92 = 92
2 x 46 = 92
4 x 23 = 92
therefore, the multiplication facts (1, 92) (1, 46) (4, 23).
Question 31.
78 ÷ 3
Answer:
The division is a method of distributing a group of things into equal parts. It is one of the four basic operations of arithmetic, which gives a fair result of sharing.
Dividend ÷ divisor = quotient
quotient is 26
the remainder is 0.
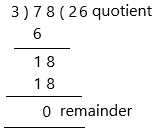
here we need to write the multiplication facts:
A multiplication fact is an answer to a multiplication calculation.
1 x 78 = 78
2 x 39 = 78
3 x 26 = 78
6 x 13 = 78.
therefore, the multiplication facts (1, 78) (2, 39) (3, 26) (6, 13).
Find the factors of each number. (Lesson 2.2)
Question 32.
36 ____________
Answer:1, 2, 3, 4, 6, 9, 12, 18, 36
Explanation:
– The factors of 36 are the numbers that divide 36 exactly without leaving the remainder. The factors of 36 can be positive as well as negative, but the factors of 36 cannot be decimal or fraction.
– The factors of 36 are the numbers, which are multiplied in pairs resulting in the original number 36. As the number 36 is a composite number, it has many factors other than one and the number itself. Thus, the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
– Likewise, we need to check and write the factors.
Question 33.
40 ____________
Answer: 1, 2, 4, 5, 8, 10, 20, 40
Explanation:
– Factors of 40 are the numbers that can divide the original number 40 and result in the whole number as a quotient. Basically, when we multiply any two factors in pairs we get the original number. Whereas multiples of 40 are the extended times of it, such as 40, 80, 120, 160, 200, 240 and so on. This is the difference between factors and multiples. 40 is a composite number same as 36, 24, 18, 60, 45, etc and have more than 2 factors.
– The numbers that divide 40 exactly without leaving a remainder are the factors of 40. In other words, the factors of 40 are the numbers that are multiplied in pairs resulting in an original number. As the number 40 is an even composite number, it has many factors other than 1 and 40. Therefore, the factors of 40 are 1, 2, 4, 5, 8, 10, 20 and 40.
Factors by division method:
The factors of 40 can be found using the division method. In the division method, we need to divide 40 by different consecutive integers. The integers that divide 40 exactly without leaving any remainder are the factors of 40. Now, let’s start dividing 40 by 1.
: 40/1 = 40 (Factor 1 and remainder 0)
: 40/2 = 20 (Factor 2 and remainder 0)
: 40/4 = 10 ( Factor 4 and remainder 0)
: 40/5 = 8 (Factor 5 and remainder 0)
: 40/8 = 5 (Factor 8 and remainder 0)
: 40/10 = 4 (Factor 10 and remainder 0)
: 40/20 = 2 (Factor 20 and remainder 0)
: 40/40 = 1 (Factor 40 and remainder 0)
Thus, the factors of 40 are 1, 2, 4, 5, 8, 10, 20 and 40.
Note:
If we divide 40 by any numbers other than 1, 2, 4, 5, 8, 10, 20 and 40, it leaves the remainder and hence, they are not the factors of 40.
Question 34.
96 ____________
Answer: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96.
Explanation:
-Factors of 96 are those numbers that can divide the original number evenly and leave no remainder. For example, if 2 is the factor of 96 then 96 divided by 2 is a whole number and not a fraction.
96 ÷ 2 = 48 [Remainder = 0]
– Since 96 is a composite number, therefore it will have factors more than two.
How to calculate the factors of 96:
-To find the factors of the natural number, 96, we need to check by which number 96 is evenly divisible and leaves no remainder.
– As we know, 1 and the number itself are the two common factors that all the integers will have apart from 1. Hence, 1 and 96 are the two factors of 96. By this, we can conclude that rest of the factors lies between 1 and 96.
: 96 ÷ 1 = 96 [Remainder = 0]
: 96 ÷ 2 = 48 [Remainder = 0]
: 96 ÷ 3 = 32 [Remainder = 0]
: 96 ÷ 4 = 24 [Remainder = 0]
: 96 ÷ 6 = 16 [Remainder = 0]
: 96 ÷ 8 = 12 [Remainder = 0]
: 96 ÷ 12 = 8 [Remainder = 0]
: 96 ÷ 16 = 6 [Remainder = 0]
: 96 ÷ 24 = 4 [Remainder = 0]
: 96 ÷ 32 = 3 [Remainder = 0]
: 96 ÷ 48 = 2 [Remainder = 0]
: 96 ÷ 96 = 1 [Remainder = 0]
therefore, the factors of 96 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96.
Find the common factors of each pair of numbers. (Lesson 2.2)
Question 35.
36 and 40
Answer:
FACTORS OF 36:
The factors of 36 are the numbers, which are multiplied in pairs resulting in the original number 36. As the number 36 is a composite number, it has many factors other than one and the number itself. Thus, the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
FACTORS OF 40:
The numbers that divide 40 exactly without leaving a remainder are the factors of 40. In other words, the factors of 40 are the numbers that are multiplied in pairs resulting in an original number. As the number 40 is an even composite number, it has many factors other than 1 and 40. Therefore, the factors of 40 are 1, 2, 4, 5, 8, 10, 20 and 40.
Then the common factors are those that are found in both lists:
The common factors are 1, 2, 4.
Question 36.
40 and 96
Answer:
FACTORS OF 40:
The numbers that divide 40 exactly without leaving a remainder are the factors of 40. In other words, the factors of 40 are the numbers that are multiplied in pairs resulting in an original number. As the number 40 is an even composite number, it has many factors other than 1 and 40. Therefore, the factors of 40 are 1, 2, 4, 5, 8, 10, 20 and 40.
FACTORS OF 96:
Factors of 96 are those numbers that can divide the original number evenly and leave no remainder.
Therefore, the factors of 96 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
Then the common factors are those that are found in both lists:
The common factors are 1, 2, 4, 8.
Find the greatest common factor of each pair of numbers. (Lesson 2.2)
Question 37.
30 and 16
_____
Answer:
The Greatest Common Factor (GCF) for 30 and 16, notation GCF(30,16), is 2.
The largest number, which is the factor of two or more numbers is called the Greatest Common Factor (GCF). It is the largest number (factor) that divide them resulting in a Natural number. Once all the factors of the number are found, there are few factors which are common in both. The largest number that is found in the common factors is called the greatest common factor. The GCF is also known as the Highest Common Factor (HCF)
Explanation:
– The factors of 30 are 1,2,3,5,6,10,15,30.
– The factors of 16 are 1,2,4,8,16.
So, as we can see, the Greatest Common Factor or Divisor is 2, because it is the greatest number that divides evenly into all of them.
Question 38.
48 and 18
______
Answer: 6
The Greatest Common Factor (GCF) for 48 and 18, notation CGF(48,18), is 6.
Explanation:
– The factors of 48 are 1,2,3,4,6,8,12,16,24,48;
– The factors of 18 are 1,2,3,6,9,18
So, as we can see, the Greatest Common Factor or Divisor is 6, because it is the greatest number that divides evenly into all of them.
Find the prime and composite numbers. (Lesson 2.2)

Question 39.
The prime numbers are ______
Answer: 31, 47
Definition: A prime number is a positive integer having exactly two factors. If p is a prime, then its only factors are necessarily 1 and p itself. Any number that does not follow this is termed a composite number, which can be factored into other positive integers. Another way of defining it is a positive number or integer, which is not a product of any other two positive integers other than 1 and the number itself.
Properties of prime numbers:
Some of the properties of prime numbers are listed below:
– Every number greater than 1 can be divided by at least one prime number.
– Every even positive integer greater than 2 can be expressed as the sum of two primes.
– Except for 2, all other prime numbers are odd. In other words, we can say that 2 is the only even prime number.
– Two prime numbers are always coprime to each other.
– Each composite number can be factored into prime factors and individually all of these are unique in nature.
Question 40.
The composite numbers are _____
Answer:
Definition 1: In Mathematics, composite numbers are numbers that have more than two factors.
Definition 2: The numbers which can be generated by multiplying the two smallest positive integers and containing at least one divisor other than the number ‘1’ and itself are known as composite numbers. These numbers always have more than two factors.
Fact: Any even number which is greater than 2 is a composite number.
Properties of composite numbers:
The properties of composite numbers are easy to remember.
– Composite numbers have more than two factors
– Composite numbers are evenly divisible by their factors
– Each composite number is a factor in itself
– The smallest composite number is 4
– Each composite number will include at least two prime numbers as its factors (Eg. 10 = 2 x 5, where 2 and 5 are prime numbers)
– Composite numbers are divisible by other composite numbers also
Composite number examples:
The examples of composite numbers are 6, 14, 25, 30, 52, etc, such that:
The factors of 6 are: 1, 2, 3, 6
The factors of 14 are: 1, 2, 7, 14
The factors of 25 are: 1, 5, 25
The factors of 30 are: 1, 2, 3, 5, 6, 10, 15, 30
The factors of 52 are: 1, 2, 4, 13, 26, 52
In all the above examples, we can see the composite numbers have more than two factors.
List the first eight multiples of each number. (Lesson 2.3)
Question 41.
4 ______
Answer:
Any number that can be expressed in the form of 4n where n is an integer, is a multiple of 4. As we know, if two values, p and q, are there, we say that q is a multiple of p if q = np for some integer n. In other words, the multiples of 4 are the numbers that leave no remainder (i.e. Remainder = 0), when it is divided by 4.
First 8 multiples of 4 are: 4, 8, 12, 16, 20, 24, 28, 32.
For example, 24, 28, 32 are said to be the multiples of 4 for the following reasons.
4 × 6 = 24; 4 multiplied by 6 to get 24
4 × 7 = 28; 4 multiplied by 7 to get 28
4 × 8 = 32; 4 multiplied by 8 to get 32
Also, we can say
24/4 = 6 and the remainder is 0
28/4 = 7 and the remainder is 0
32/4 = 8 and the remainder is 0.
Since the numbers are exactly divided by 4, the numbers 24, 28, 32 are multiples of 4.
Question 42.
6 ______
Answer:6, 12, 18, 24, 30, 36,42, 48
Multiples of 6 explanations:
The multiples for 6 are the numbers that are generated when 6 is multiplied by any natural number, such as 1, 2, 3, 4, 5, 6, 7, etc. That means any number that can be expressed in the form of 6n where n is an integer is a multiple of 6. As we know, if two values, p and q, are there, we say that q is a multiple of p if q = np for some integer n.
The first eight multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48.
6 × 1 = 6
6 × 2 = 12
6 × 3 = 18
6 × 4 = 24
6 × 5 = 30
6 × 6 = 36
6 × 7 = 42
6 × 8 = 48
– We can also find the multiples through the repeated addition of a number as many times as required. For example, to get the first five multiples of 6, we have to multiply 6 by 1, 2, 3, 4 and 5 or add the number of times as shown below:
: The first multiple of 6 is: 6 × 1 = 6
: The second multiple of 6 is: 6 × 2 = 12 Or 6 + 6 = 12 {here 6 is added for twice}
: The third multiple of 6 is: 6 × 3 = 18 Or 6 + 6 + 6 = 18 {here 6 is added for thrice}
: The fourth multiple of 6 is: 6 × 4 = 24 Or 6 + 6 + 6 + 6 = 24
: The fifth multiple of 6 is: 6 × 5 = 30 Or 6 + 6 + 6 + 6 + 6 = 30
Similarly, we write several multiples of the given numbers.
Question 43.
9 ______
Answer:9, 18, 27, 36, 45, 54, 63, 72
Multiples of 9 explanations:
Any number that can be denoted in the form 9n where n is a natural number, is a multiple of 9. So if two values p and q are there, we say that q is a multiple of p if q = np. In other words, the multiples of 9 are the numbers that leave no remainder (i.e. Remainder = 0), when it is divided by 9.
The first 8 multiples of 9 are:9, 18, 27, 36, 45, 54, 63, 72
For example, 54, 63, 72 are said to be the multiples of 4 for the following reasons.
9 × 6 = 54; 4 multiplied by 6 to get 54
9 × 7 = 63; 4 multiplied by 7 to get 63
9 × 8 = 72; 4 multiplied by 8 to get 72
Also, we can say
54/9 = 6 and the remainder is 0
63/9 = 7 and the remainder is 0
72/9 = 8 and the remainder is 0.
Since the numbers are exactly divided by 9, the numbers 54, 63, 72 are multiples of 9.
Find the first two common multiples of each pair of numbers. (Lesson 2.3)
Question 44.
4 and 6
______
Answer: 12, 24
Explanation:
– Common multiples of 4 and 6 are numbers that both 4 and 6 can be divided into evenly with no remainder.
– To find the common multiples of 4 and 6, we compare the list of multiples of 4 with the list of multiples of 6 to see what they have in common.
– To create a list of multiples of 4, we multiply 4 by 1, 4 by 2, and so on like this:
4 x 1 = 4
4 x 2 = 8
4 x 3 = 12
4 x 4 = 16…
– Similarly, to create a list of multiples of 6, we multiply 6 by 1, 6 by 2, and so on like this:
6 x 1 = 6
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24…
When we compare the two lists to see what they have in common, we get the answer to “What are the common multiples of 4 and 6?”
– 12, 24, 36, 48, etc.
Since 12 is the first number they have in common, 12 is the least common multiple of 4 and 6.
Therefore, the first two common multiples are 12 and 24.
Question 45.
6 and 9
______
Answer: 18 and 36
Explanation:
– Common multiples of 6 and 9 are numbers that both 6 and 9 can be divided into evenly with no remainder.
– To find the common multiples of 6 and 9, we compare the list of multiples of 6 with the list of multiples of 9 to see what they have in common.
– To create a list of multiples of 6, we multiply 6 by 1, 6 by 2, and so on like this:
6 x 1 = 6
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24…
– Similarly, to create a list of multiples of 9, we multiply 9 by 1, 9 by 2, and so on like this:
9 x 1 = 9
9 x 2 = 18
9 x 3 = 27
9 x 4 = 36
…
– When we compare the two lists to see what they have in common, we get the answer to “What are the common multiples of 6 and 9?”
– 18, 36, 54, 72, etc.
– Since 18 is the first number they have in common, 18 is the least common multiple of 6 and 9.
– Therefore, the first two common multiples of 6 and 9 are 18 and 36.
Find the least common multiple of each pair of numbers. (Lesson 2.3)
Question 46.
8 and 12
____________
Answer:
LCM is the method to find the smallest possible multiple of two or more numbers. LCM stands for Least common multiple. LCM of two numbers is divisible by both numbers.
We can find the LCM in two ways
– By listing the multiples
– By prime factorisation
LCM of 8 and 12:
First Method: Listing the multiples
– First, write the common multiples of all three numbers.
– Common Multiples of 8: 8,16,24,32,40,48,56,64,72,80….
– Common Multiples of 12: 12,24,36,48,60,72,………..
– Hence the Least common multiple of 8 and 12= 24
Question 47.
27 and 36
____________
Answer:
LCM is the method to find the smallest possible multiple of two or more numbers. LCM stands for Least common multiple. LCM of two numbers is divisible by both numbers.
We can find the LCM in two ways
– By listing the multiples
– By prime factorisation
LCM of 27 and 37:
Solution by using division method:
This method consists of grouping by separating the numbers that will be decomposed on the right side by commas while on the left side we put the prime numbers that divide any of the numbers on the right side. We start with the lowest prime numbers, divide all the rows of numbers by a prime number that is evenly divisible into ‘at least one of the numbers. We stop when it is no longer possible to divide (the last row of results is all 1’s). See below how it works step-by-step.
2 | 27, 36
2 | 27, 18
3 | 27, 9
3 | 9, 3
3 | 3, 1
1 | 1, 1
The LCM is the product of the prime numbers in the first column, so:
LCM = 2 . 2 . 3 . 3 . 3 = 108
Solution by listing multiples:
This method consists of listing the multiples of all the numbers that we want to find the LCM. Multiples of a number are calculated by multiplying that number by the natural numbers 2, 3, 4, …, etc. See below:
* The multiples of 27 are 27, 54, 81, 108
* The multiples of 36 are 36, 72, 108
Because 108 is the first number to appear on both lists of multiples, 108 is the LCM of 27 and 36.
Problem Solving
Solve. Show your work.
Question 48.
Make a 5-digit number using these clues.
The digit in the thousands place is 5.
The value of the digit in the ten thousand places is 20,000.
The digit in the tens place is 8.
One of the digits is a 0 and it is next to the digit 8.
The digit in the one’s place is 2 less than the digit in the tens place.

Answer:

Explanation:
2 is in the ten thousand place
5 is in the thousands place.
0 is in the hundreds place.
8 is in the tens place.
2 is in the one’s place.
Question 49.
3,219 millilitres of water and 185 millilitres of orange syrup are mixed to make orange juice. About how much orange juice will there be?
Answer: 3,404 millilitres.
Explanation:
The number of millilitres of water=3,219
The number of millilitres of orange syrup=185
When we mix both water and orange syrup to make orange juice. Now, how many millilitres of orange juice is there. Assume it as X.
Add both water and orange syrup
X=3219+185
X=3,404 millilitres.
Question 50.
An empty parking lot has 300 spaces. 215 cars and 89 SUVs drive into the parking lot. How many vehicles do not have parking spaces?
Answer:4 vehicles.
Explanation:
The number of spaces an empty parking has=300
The total number of spaces for cars and SUVs=215+89=304
We need to find out the number of vehicles that do not have parking spaces=X
The total number of spaces needed for vehicles=304
The number of spaces is there=300
To find out X we need to subtract the 304 and 300
X=304-300
X=4.
therefore, 4 vehicles do not have parking space.
Question 51.
Find a 2-digit number less than 50 using these clues. It can be divided by 4 exactly.
When 4 is added to it, it can be divided by 5 exactly.
The number is ____
Answer: 36
Explanation:
It is divisible by 4, but when 4 is added to it, it is divisible by 5 means that the number is a multiple of 4 and when 4 is added to it, it becomes a multiple of 5. Therefore, the number will be 4 less than a MULTIPLE of 4 & 5. Multiples of 4 & 5 that are less than 50 are: 20 and 40.
The number that’s 4 is less than 20: 16
The number that’s 4 is less than 40: 36.
Question 52.
Finch divides 12 peaches and 18 nectarines into the same number of equal groups. How many possible groups of each fruit can he make? How many are in each group?
Answer: 3 possible groups.
Explanation:
The number of peaches is there=12
the number of nectarines is there=18
She has to divide both groups into the same number of equal groups.
You need to find the common divisor of 12 and 18:
12 = 2*2*3
18 = 2*3*3
the common divisors of 12 and 18 are: 2, 3, and 6
he can make 3 possible groups:
group the fruits in 2 groups with 12/2 = 6 peaches and 18/2 = 9 nectarines in each.
group the fruits in 3 groups with 12/3 = 4 peaches and 18/3 = 6 nectarines in each.
group the fruits in 2 groups with 12/6 = 2 peaches and 18/6 = 3 nectarines in each.