Hillary

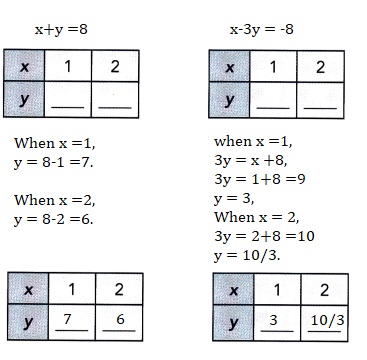
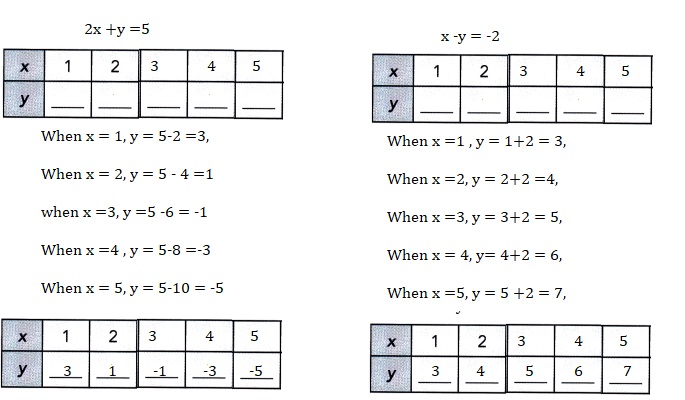
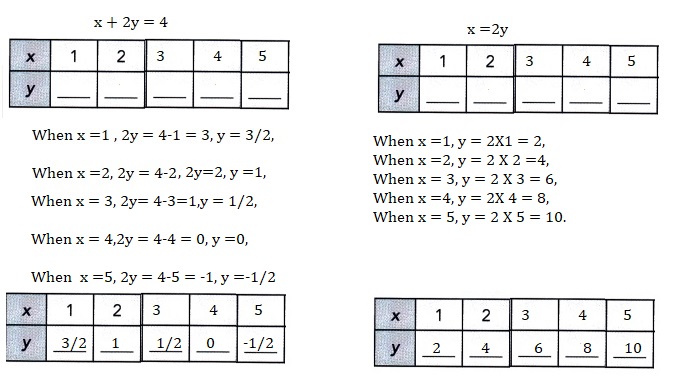
Go through the Math in Focus Grade 4 Workbook Answer Key Chapter 1 Place Value of Whole Numbers to finish your assignments.

Math in Focus Grade 4 Chapter 1 Answer Key Place Value of Whole Numbers

Math Journal

Question 1.
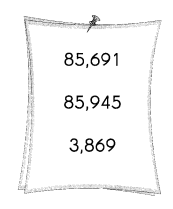
Kim wrote these statements about the three numbers shown here.
Do you agree? Explain why or why not.
3,869 is less than 85,945.
85,691 is greater than 85,945.

Answer:
The above-given statements are:
1. 3,869 is less than 85,945.
2. 85,691 is greater than 85,945.
The first statement is correct.
The second statement is wrong.
The first statement is correct because we are comparing numbers with their place values.
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.
Rules for comparing numbers:
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
* Numbers with more digits
* Numbers starting with a larger digit
Rule 1: Numbers with more digits
– When we compare numbers, then check if both the numbers are having the same number of digits or not. If a number has more digits, then it is greater than the other number.
Examples:
– 33 > 3
– 400 > 39
– 5555 > 555
– 10000 > 9999
Rule 2: Numbers starting with a larger digit
This rule is applicable when two numbers are having the same number of digits. In such cases, we need to check the digit at the leftmost place, whichever is greater. Therefore, the number with a greater digit at the leftmost place of the number is greater than the other number.
Examples:
* 323>232 [323 is greater than 232]
* 343<434 [343 is less than 434]
Thus, in the above examples, we can see that, when we compare the two numbers, though the number of digits is the same, one number is greater than/less than the other number.
Now according to the above rules, we check statement 1:
1. 3,869 is less than 85,945.
– In this statement, two numbers are given. The first number is having fewer digits than the second number so here rule 1 is applicable.
absolutely, 3,869 < 85,945
This can be written in another way:
85,945 > 3,869.
Now we check for statement 2:
2. 85,691 is greater than 85,945.
Here the same number of digits are having so rule 2 is applicable.
– 85,691 and 85,945 both the numbers have an equal number of digits, therefore, we will compare the left-most digit of both the numbers.
– As we can see the first two digits are the same for both the numbers, thus we need to compare the next left-most digit of both numbers.
6 < 9
Here it is a wrong statement because 6 is not greater than 9. So the second statement is wrong.

Question 2.
Sam continued this number pattern.
Do you agree? Explain why or why not.

Answer:

For number patterns there are certain rules:
To create a complete pattern, there are a set of rules to be considered. To apply the rule, we need to understand the nature of the sequence and the difference between the two successive numbers. It takes some amount of guesswork and checking to see whether the rule works throughout the whole series.
There are two basic divisions to find out the rules in number patterns:
* When the numbers in the given pattern get larger, they are said to be in ascending order. These patterns usually involve addition or multiplication.
* When the numbers in the given pattern get smaller, they are said to be in descending order. These patterns usually involve subtraction or division.
So the number pattern is correct.

Question 3.
Read the example. Then write your own 5-digit number and clues. Ask a friend or family member to solve your puzzle.

Example
45,870
1. The digit 5 is in the thousands place.
2. The value of the digit 7 is 70.
3. The digit in the hundreds place is 10 – 2.
4. The digit in the ten thousands place is 1 less than the digit in the thousands place.
5. The digit in the ones place is 0.

Number: _______
Clues: ______
Answer:
– According to the clues, the number is 15,870
– Now in line number 4, the digit in the ten thousand places is 1 less than hundreds of places. So, 1 < 5. 5 is in the thousand places so I placed 5 in the thousands place.
– In line 3 the hundreds place is 8. In the above-example 10-2 is given which is 8. So I placed 8 in the hundreds place.
– In line 2 the number 70 is given, 70 is nothing but 7 tens so I placed 7 in the tens place.
– In line 5 directly given that one’s place is 0.

Put on Your Thinking Cap!

Challenging Practice

Complete.

A 5-digit number is made up of different digits that are all odd numbers.

Question 1.
What is the greatest possible number? ______
Answer: 9,99,99
Explanation:
The largest 5 digit number that you can have when all digits are odd would be 99999.
that’s with no restrictions.
any other number you choose would have to be smaller.
the restrictions are:
the ten thousand digits are 3 times the one’s digit.
since the ten-thousands digit is fixed at 9, then the one’s digit has to be 3 because 3 * 3 = 9.
the thousands digit is 2 more than the hundreds digit.
since the thousands digit is fixed at 9, then the hundreds digit has to be 7 because 7 + 2 = 9.
that makes your number equal to 99793.
any other arrangement would force the ten-thousands digit to be something less than 9 or the thousands digit to be less than 9 which would result in a smaller number.

Question 2.
What is the value of the digit in the hundreds place? _____
Answer: 9
Explanation:
The largest 5 digit number that you can have when all digits are odd would be 99999.
The place values of 99999 are:
9 is in the hundred thousand place.
9 is in the ten thousand place
9 is in the thousand place
9 is in the hundreds place
9 is in the tens place
9 is in the one’s place.

Continue the pattern.

Question 3.

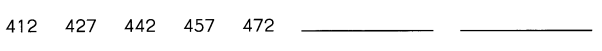
Answer: 487  502
Explanation:
A list of numbers that follow a certain sequence is known as patterns or number patterns. The different types of number patterns are algebraic or arithmetic patterns, geometric patterns, Fibonacci patterns and so on.
The above-given numbers are in the arithmetic pattern.
The arithmetic pattern is also known as the algebraic pattern. In an arithmetic pattern, the sequences are based on the addition or subtraction of the terms. If two or more terms in the sequence are given, we can use addition or subtraction to find the arithmetic pattern.
The numbers are 412  427  442  457  472  –  -. Now, we need to find the missing term in the sequence.
Here, we can use the addition process to figure out the missing terms in the patterns.
In the pattern, the rule used is “Add 15 to the previous term to get the next term”.
In the numbers given above, take the second term (427). If we add “15” to the second term (427), we get the third term 442.
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 472. Therefore, 472+15 = 487.
Second missing term: The previous term is 487. So, 487+15 = 502
Hence, the complete arithmetic pattern is 412  427   442   457   472   487   502.

Fill in the blanks.

Question 4.
What is 3 ten thousands + 14 tens + 16 ones? ______
Answer:30,156
Explanation:
In a number, the place (local) value of a non-zero digit is the value of this digit according to its position.
A number can have many digits, and each digit has a special place and value
ten thousand can be written as 10,000
tens can be written as 10
ones can be written as 1
3 x 10,000 = 30,000, 14 x 10 = 140 and 16 x 1 = 16
30 000 + 140 + 16 = 30 156.

Question 5.
7 thousands = _____ hundreds 10 tens
Answer:
7 thousand=7 hundreds 10 tens
This can be written as:
7000=700*10
7 thousands=70 hundreds
7 thousand=700 tens

Answer these questions.

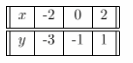
Question 6.
what is the value of the digit 5 in the ? ____
Answer: 5000
Explanation:
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.
According to the above solution, 5 is in the thousands place.
5 thousands is nothing but 5000
So it can be written as 5000.

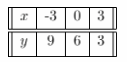
Question 7.
what is the value of the digit 5 in the ? ____
Answer:50
Explanation:
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.
According to the above solution, 5 is in the tens place.
5 tens are nothing but 50
So it can be written as 50.

Question 8.
what is the difference between the answers in Exercises 6 and 7? ____
Answer: Place values.
Explanation:
The place value is the position of each digit in a number. The place value of digits is determined as ones, tens, hundreds, thousands,ten-thousands and so on, based on their position in the number. For example, the place value of 1 in 1002 is thousands, i.e.1000.
The above-given number 75,859
7 is in the ten thousand place
5 is in the thousands of place
8 is in the hundreds place
5 is in the tens place
9 is in the one’s place.

Question 9.
, the difference between the values of the digits in the and the is 8,930. What is the digit in the ?
Answer:9
The above-given number 5 X,278
We need to find out the X.
The difference between and =8,930
Already we know the value in the square that is 7
X-7=8,930
If we subtract 59,278 and 50,348 then we get 8,930
so 9 is in the ten thousand places.
Check which number we subtract from the given number to get 8,930.
If we kept 9 in the X place and subtract with the assumed number that is 50,348 then we get the given number 8,930. Likewise we need to think and process the problem.

Put On Your Thinking cap!

Problem Solving

The button and the button do not work.
Justin wants to enter the number 82,365.
Explain what he can do to key in the number. Give two solutions.

Answer:
The above-given number is 82,365
But the 2 and 6 buttons are not working.
Here given clue we can add or subtract
First solution:
For example, if we add two 1’s means 1+1=2
if we add two 3’s or we can add 5+1=6 and 3+3=6.
Second solution:
If we subtract 5-3=2
if we subtract 7-1=6
These are the chances to enter the right values.

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 5 Systems of Linear Equations to score better marks in the exam.

Math in Focus Grade 8 Course 3 A Chapter 5 Answer Key Systems of Linear Equations

Math in Focus Grade 8 Chapter 5 Quick Check Answer Key

Complete the table of values and graph each linear equation.

Question 1.
y = 5x

Answer:
When x = 0, y=0,
x =1 , y = 5, x = 2, y = 10, when x = 3 y =15,

Explanation:

Question 2.
y = -x + 2

Answer:
x =0, y = 2, x= 1, y =1,
x= 2, y = 0, x =3,y =-1,

Explanation:

Solve. Show your work.

Question 3.
Samuel bought 30 books. The hardcover books cost $20 each while the rest,
which are paperbacks, cost $8 each. If he spent a total of $480, how many paperbacks did he buy?
Answer:
Number of paperbacks he buy are 10,

Let x be the no. of hard cover books and y be the no. of paper back books.
x + y = 30,
x = 30 – y,
20x + 8y = 480,
20(30 – y) + 8y = 480,
600 – 20y + 8y = 480,
-12y = – 120,
y = 120/12, y = 10,
x = 30-10 = 20,
No.of hard cover books = x = 20,
No.of paper back books = y = 10.

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 5 Lesson 5.1 Introduction to Systems of Linear Equations to score better marks in the exam.

Math in Focus Grade 7 Course 3 A Chapter 5 Lesson 5.1 Answer Key Introduction to Systems of Linear Equations

Math in Focus Grade 8 Chapter 5 Lesson 5.1 Guided Practice Answer Key

Solve the system of linear equations by copying and completing the tables of values.
The values x and y are positive integers.

Question 1.
A bottle of water and a taco cost $3. The cost of 3 bottles of water is $1 more than the cost of a taco.
Let x be the price of a bottle of water and y be the price of a taco in dollars.
The related system of equations and tables of values are:
3x – y = 1
x + y = 3

Answer:
The cost of a bottle of water is $2 and the cost of a taco is $1,

Explanation:

Solve each system of equations by making tables of values, x and y are positive integers.

Question 2.
x + y = 6
x + 2y = 8
Answer:

Explanation:
Solved each system of equations by making tables of values, x and y are positive integers.
For equation x+y = 6, when x =1 then y =5 and when x =2 then y=4,
For equation x +2y =8, when x =1 then y =7/2 and when x = 2 then x =3.

Question 3.
x + y = 8
x – 3y = -8
Answer:

Explanation:
Solved each system of equations by making tables of values, x and y are positive integers.
For equation x+y = 6, when x =1 then y =5 and when x =2 then y=4,
For equation x +2y =8, when x =1 then y =7/2 and when x = 2 then x =3.

For each linear equation, list in a table enough values for x and y to obtain a solution.
Remember that they must be positive integers.

Technology Activity

Materials:

• graphing calculator

Use Tables On A Graphing Calculator To Solve A System Of Equations

Work in pairs.

You can use a graphing calculator to create tables of values and solve systems of equations.
Use the steps below to solve this system:

8x + y = 38
x – 4y = 13

Step 1.
Solve each equation for y in terms of x. Input the two resulting expressions for y into the equation screen.

Caution
Use parentheses around fractional coefficients and the key for negative coefficients

Step 2.
Set the table function to use values of x starting at 0, with increments of 1.

Step 3.
Display the table. It will be in three columns as shown.

Step 4.
Find the row where the two y-values are the same. This y-value and the corresponding x-value will be the solutión to the equations.
The solution to the system of equations is given by x = and y = .

Math Journal How can you tell from the two columns of y-values that there is only one row where the y-values are the same?

Math in Focus Course 3A Practice 5.1 Answer Key

Solve each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.

Question 1.
2x + y = 5
x – y = -2
Answer:

Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.

Question 2.
x + 2y = 4
x = 2y
Answer:

Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.

Question 3.
3x + 2y = 10
5x – 2y = 6
Answer:

Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.

Question 4.
x – 2y = -5
x = y
Answer:

Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.

Question 5.
2y – x = -2
x + y = 2
Answer:

Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.

Question 6.
2x + y = 3
x + y = 1
Answer:

Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.

Question 7.
x + 2y = 1
x – 2y = 5
Answer:

Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.

Question 8.
2x – y = 5
2y + x = -1
Answer:

Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.

Question 9.
2x + y = -1
x + y = 1
Answer:

Explanation:
Solved each system of linear equations by making tables of values.
Each variable x is a positive integer less than 6.

Solve by making a table of values. The values x and y are integers.

Question 10.
A shop sells a party hat at x dollars and a mask at y dollars.
On a particular morning, 10 hats and 20 masks were sold for $30.
In the afternoon, 8 hats and 10 masks were sold for $18. The related system of linear equations is:
10x + 20y =30
8x + 10y = 18
Solve the system of linear equations. Then find the cost of each hat and each mask.
Answer:
The cost of each hat is $1 and each mask is$1,

Explanation:
Given A shop sells a party hat at x dollars and a mask at y dollars.
On a particular morning, 10 hats and 20 masks were sold for $30.
In the afternoon, 8 hats and 10 masks were sold for $18.
The related system of linear equations is:
10x + 20y =30—(1)
8x + 10y = 18—-(2) dividing equation 1 by 10 we get
x +2y = 3,
x = 3-2y substituting in equation 2 we get
8(3-2y) +10y =18,
24 – 16y+10y =18,
24 -6y =18,
6y = 24 -18,
6y =6, y =1 we have x = 3-2X 1 = 3-2 = 1.

Question 11.
Alicia is x years old and her cousin is y years old.
Alicia is 2 times as old as her cousin.
Three years later, their combined age will be 27 years.
The related system of linear equations is:
x = 2y
x + y = 27
Solve the system of linear equations. Then find Alicia’s age and her cousin’s age.
Answer:
Alicia’s age is 18 and her cousin’s age is 9 years old,

Explanation:
GivenAlicia is x years old and her cousin is y years old.
Alicia is 2 times as old as her cousin.
Three years later, their combined age will be 27 years.
The related system of linear equations is: x = 2y,
x + y = 27 solving the equations  2y + y = 27,
3y = 27, y = 27/3 =9, so x = 2X 9 = 18, Alicia’s age is 18 and her
cousin’s age is 9 years old.

Question 12.
Steve and Alex start driving at the same time from Boston to Paterson.
The journey is d kilometers. Steve drives at 100 kilometers per hour and
takes t hours to complete the journey. Alex, who drives at 80 kilometers per hour is
60 kilometers away from Paterson when Steve reaches Paterson.
The related system of linear equations is:
100t = d
80t = d – 60

Solve the system of linear equations by making tables of values.
Then find the distance between Boston and Paterson.
Answer:
300 kilometers is the distance between Boston and paterson,

Explanation:
Given Steve and Alex start driving at the same time from Boston to Paterson.
The journey is d kilometers. Steve drives at 100 kilometers per hour and
takes t hours to complete the journey. Alex, who drives at 80 kilometers per hour is
60 kilometers away from Paterson when Steve reaches Paterson.
The related system of linear equations is:
100t = d
80t = d – 60 substituting 80t = 100t -60,
100t-80t = 60,
20t = 60, t = 60/20, t =3 so distance is 100 X 3= 300 kilometers.

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 5 Lesson 5.2 Solving Systems of Linear Equations Using Algebraic Methods to score better marks in the exam.

Math in Focus Grade 7 Course 3 A Chapter 5 Lesson 5.2 Answer Key Solving Systems of Linear Equations Using Algebraic Methods

Math in Focus Grade 8 Chapter 5 Lesson 5.2 Guided Practice Answer Key

Solve each system of linear equations using the elimination method.

Question 1.
2a+ 3b= 29 —Equation 1
2a — b = 17 — Equation 2
Subtract Equation 2 from Equation 1:

Answer:
The solution to the system of linear equations is a = 23/2 and b =6,

Explanation:

Question 2.
2x – y = 2
3x + y = 13
Answer:
The solution to the system of linear equations is  x = 3 and y =4.

Explanation:
Given 2x -y =2 -Equation 1,
3x + y = 13- Equation 2 Adding Equation 2 and 1,
2x – y =2
3x + y =13
5x = 15,
x = 15/5 = 3, substituting x =3 in Equation 1
y = 2x -2= 2 X 3 -2 = 6-2 =4.

Question 3.
x + 6 = 1
x + y = 6
Answer:
The solution to the system of linear equations is x = -5 and y = 11,

Explanation:
Given x + 6 =1 means x = 1-6 = -5,
substituting x = -5 in Equation 2 – x + y  = 6 as x = -5,
-5 + y = 6, y = 6 +5 = 11.
Therefore x = -5 and y = 11.

Solve each system of linear equations using the elimination method.

Question 4.
7m + 2n = -8
2m = 3n – 13
Answer:
The solution to the system of linear equations is m = -2 and n =3,

Explanation:
Given 7m +2n = -8 – Equation 1 and 2m = 3n – 13- Equation 2,
to make elmination we need common values we multiply
Equation 1 by 3 and Equation 2 by 2 so that n becomes common,
3 X(7m +2n )= 3 X -8 = 21m + 6n = -24 and
2 X 2m = 2 X (3n – 13)= 4m = 6n – 26 means 6n = 4m + 26,
so 21m + 4m + 26 = -24, 25m = -24-26,
25m = -50,
m = -50/25 = -2, so substituting m= -2 in 2m = 3n -13,
2(-2)+13 = 3n,
-4+13 = 3n,
3n = 9, n = 9/3 = 3.

Question 5.
3x – 2y = 24
5x + 4y = -4
Answer:
The solution to the system of linear equations is x = 4 and y = -6,

Explanation:
Given Equation 1 as 3x -2y = 24 and Equation 2 as 5x +4y = -4,
to make elmination we need common values we multiply
Equation 1 by 2  so that y can be elminated,
2X(3x-2y =24)= 6x -4y = 48 adding with Equation 2
6x -4y =48
(+)5x +4y = -4
11x = 44,
x = 44/11 = 4, we substitute x = 4 in Equation 1 ,
3 X 4 – 2y = 24,
12- 2y = 24,
12-24 = 2y,
2y = -12, y = -12/2 = -6.

Question 6.
2x + 7y = -32
4x – 5y = 12
Answer:
The solution to the system of linear equations is y = -4 and x = -2,

Explanation:
Given 2x +7y = -32 Equation 1 and 4x -5y = 12 Equation 2,
to make elmination we need common values we multiply
Equation 1 by -2  so that x can be elminated,
-2 X(2x +7y=-32) = -4x – 14y = 64 now we add eqaution 1 with
equation 2 as -4x – 14y = 64
(+) 4x- 5y =12
                                 -19y = 76, y = -76/19 =-4, substituting y =-4
4x -5(-4)=12, 4x +20 = 12, 4x = 12-20 = -8, 4x = -8 , x =-8/4 = -2.

Solve each system of linear equations by using the substitution method.

Question 7.
2x + y = 5 — Equation 1
y = 4x – 7 — Equation 2
Substitute Equation 2 into Equation 1:

Answer:
The solution to the system of linear equations is x =2 and y =1,

Explanation:

Question 8.
4x + 3y = 23 — Equation 1
5x + y = 15 — Equation 2
Use Equation 2 to express y in terms of x:
5x + y = 15

Answer:
The solution to the system of linear equations is x =2 and y = 5,

Explanation:

Question 9.
3x – y = 8
2x + 3y = 9
Answer:
The solution to the system of linear equations is x = 3 and y = 1,

Explanation:
Given 3x – y =8 Equation 1 and 2x +3y = 9 Equation 2,
we can write Equation 1 as y = 3x -8,
substituting y in Equation 2 as
2x +3 (3x -8) = 9,
2x + 9x – 24 =9,
11x = 9+ 24 = 33, x = 33/11 = 3,so y = 3 X 3 – 8 = 9-8 = 1.

Question 10.
7m + 2n = -8
2m = 3n – 13
Answer:
The solution to the system of linear equations is m = -2 and n =3,

Explanation:
Given 7m +2n = -8  Equation 1 and 2m = 3n – 13 Equation 2,
to make elmination we need common values we multiply
Equation 1 by 3 and Equation 2 by 2 so that n can be elminated as
3(7m +2n =-8) = 21m +6n = -24 – equation 3and
2(2m = 3n -13) = 4m = 6n – 26 means 6n = 4m +26 substituting 6n in eqaution 3
21m +4m + 26 = -24,
25m = -24 -26 = -50 , m = -50/25 = -2, now
6n = 4(-2)+ 26 = -8 +26 = 18,
6n = 18, n = 18/6 = 3.

Solve each system of linear equations using elimination method or
substitution method. Explain why you choose each method.

Question 11.
2x + 3y = 29
2x – 17 = y
Answer:
The solution to the system of linear equations is x = 10 and y = 3,
used substitution method as already y is given in Equation 2,

Explanation:
Given 2x+3y = 29 as equation 1 and y already there ,
so we use substitution method as y = 2x -17  in equation 1
2x + 3(2x – 17) = 29,
2x + 6x – 51= 29,
8x = 29 +51= 80,
x = 80/8 = 10,
y = 2 X 10 -17 = 20 -17 = 3.

Question 12.
3a – 2b = 5
2a – 5b = 51
Answer:
The solution to the system of linear equations is a= -7 and b = -13,
Used elmination method because of no common values of a and b,

Explanation:
Given 3a- 2b =5 Equation 1 and 2a – 5b = 51 in Equation 2 in both
equations a or b is not common so we use elmination and we multiply
equation 1 by 2 2(3a-2b =5) = 6a – 4b = 10 and equation 2 by 3
3(2a -5b = 51) = 6a – 15b = 153 subtracting eqaution 2 from eqaution 1
6a-4b =10
(-) -6a +15b =-153
11 b = -143,
b = – 143/11 = -13, substituting in eqaution 1
3a -2(-13)=5,
3a +26 =5,
3a = 5 -26 = -21,
a = -21/3 = -7.

Math in Focus Course 3A Practice 5.2 Answer Key

Solve each system of linear equations using the elimination method.

Question 1.
2j + k = 6
j – k = 8
Answer:
The solution to the system of linear equations is j = 14/3 and k = -10/3,

Explanation:
Given 2j +k =6 equation 1,
j – k = 8 equation 2 adding 1 and 2
2j+j = 6 +8,
3j = 14,
j = 14/3,
k = j – 8 = 14/3 – 8 = 14- 24/3 = -10/3,.

Question 2.
2j + 3k = 11
2j – 5k = 3
Answer:
The solution to the system of linear equations is j =4 and k =1,

Explanation:
Given 2j +3k = 11 – Equation -1, 2j – 5k =3- Equation -2
subtracting eqaution 2 from 1
2j +3k =11
-2j +5k =  -3
8k = 8, k = 8/8 = 1, substuting k =1 in equtation 2
2j – 5 = 3, 2j = 3+5 = 8, j = 8/2 = 4.

Question 3.
3m + n = 30
2m – n = 20
Answer:
The solution to the system of linear equations is m = 10, n =0.

Explanation:
Given 3m + n = 30 Equation 1, 2m -n = 20 Equation 2
adding 1 and 2 we get
3m +n =30
2m – n =20
5m = 50, m = 50/5 = 10, substituting m = 10 in equation2
2 X 10 – n =20,
n = 20 – 20 = 0.

Question 4.
3x – y = 9
2x – y = 7
Answer:
The solution to the system of linear equations is x =2 and y = -3,

Explanation:
Given 3x -y = 9 Equation 1 and 2x -y =7 Equation 2,
subtracting eqaution 2 from 1
3x -y =9
-2x +y =-7
x = 2, substituting x =2 in 2(2)-y = 7,
y = 4 – 7 = -3,

Question 5.
5s – t = 12
3s + t = 12
Answer:
The solution to the system of linear equations is s = 3 and t =3,

Explanation:
Given 5s -t =12 as equation 1 and 3s +t = 12 equation 2 adding1 & 2
5s -t =12,
(+)3s+t =12
8s = 24, s = 24/8 = 3, substituting s = 3 in eqaution 2
t = 12 – 3s,
t = 12 – 3 X 3 = 12-9 = 3.

Question 6.
2b + c = 10
2b – c = 6
Answer:
The solution to the system of linear equations is b = 4 and c = 2,
Explanation:
Given 2b + c = 10 as equation 1 and
2b – c =6 as equation 2 adding euqtion 1 & 2
2b +c =10
(+) 2b -c =6
4b = 16, b = 16/4 = 4, substituting b = 4 in equation 2
2X4 -6 = c,
c = 8-6 = 2.

Question 7.
3m – n = 7
21m + 6n = -29
Answer:
The solution to the system of linear equations is m = 1/3 and n = -6,

Explanation:
Given 3m – n = 7 as equation 1 means n = 3m -7,
21m +6n = -29 is equation 2 substituting n = 3m -7 in  equation 2
21m +6(3m -7) = -29,
21m +18m – 42 = -29,
39m = -29+42,
39m = 13,
m = 13/39 = 1/3, substituting n = 3(1/3)-7 = 1-7 = -6.

Question 8.
7a + b = 10
2a + 3b = -8
Answer:
The solution to the system of linear equations is

Explanation:
Given 7a + b = 10 as equation 1 we get b = 10-7a,
we have 2a + 3b = -8 as equation 2 substituting b = 10-7a in
equation 2 –2a +3(10-7a) =-8,
2a + 30 – 21a = -8,
-19a = -8 -30
a = 38/19= 2, substituting a=2 in b = 10 -7 X2 = 10 – 14 = -4.

Question 9.
2p + 5q = 4
7p + 15q = 9
Answer:
The solution to the system of linear equations is p= -3 and q = 2,

Explanation:
Given 2p +5q = 4 as eqaution 1 and 7p +15 q = 9 as equation 2,
if we multiply eqauation 1 with 3 we get 15 q so that we can easily
subtract from equation 2 so
3 X (2p +5q = 4)= equation 1 becomes
6p + 15q = 12 now we subtract equation 2
(-) 7p -15q = -9
-p = 3, p = -3 substituting p =-3 in 2p+5q = 4,
2(-3)+5q = 4,
5q = 4+6 = 10, q = 10/5 = 2.

Solve each system of linear equations using the substitution method.

Question 10.
2j + k = 3
k = j – 9
Answer:
The solution to the system of linear equations is j = 4 and k = -5,

Explanation:
Given 2j +k = 3 as equation 1 and wehave k = j -9 substituting in
equation 1 2j+(j -9) = 3,
3j = 3 + 9 = 12,
j = 12/3 = 4, therefore k = 4 – 9 = -5.

Question 11.
2h + 3k = 13
h = 2k – 4
Answer:
The solution to the system of linear equations is h =2 and k = 3,

Explanation:
Given 2h +3k = 13 as equation 1 and h = 2k-4
substituting h in equation 1 as
2 (2k-4) +3k = 13,
4k – 8 +3k = 13,
7k = 13+8= 21,
k = 21/7 = 3,So h = 2 X 3 – 4 = 6-4 =2.

Question 12.
3m + b = 23
m – b = 5
Answer:
The solution to the system of linear equations is b = 2 and m =7,

Explanation:
Given 3m+ b = 23 as equation 1 and as m-b = 5 ,
b = m-5 substituting in equation 1  3m + m -5 = 23,
4m = 23+5, 4m = 28, m= 28/4 = 7,
b = 7 – 5= 2.

Question 13.
3h – k = 10
h – k = 2
Answer:
The solution to the system of linear equations is h =4 and k =2,

Explanation:
Given 3h – k =10 as equation 1 and h -k = 2 ,
k = h -2 substituting in eqaution 1 k,
3h -h +2 = 10,
2h = 10-2 = 8,
h = 8/2 = 4 therefore k = h -2 = 4-2 =2.

Question 14.
3s – t = 5
s + 2t = 4
Answer:
The solution to the system of linear equations is s =2 and t = 1,

Explanation:
Given 3s – t = 5 as equation 1 and s +2t = 4 means
s = 4-2t substituting s in equation 1 we get
3(4-2t)- t =5,
12 – 6t – t =5,
12 -7t =5,
7t = 12-5 = 7,
t =7/7 = 1, therefore s = 4 – 2X 1 = 4-2 =2.

Question 15.
2x + y = 20
3x + 4y = 40
Answer:
The solution to the system of linear equations is x = 8 and y = 4,

Explanation:
Given 2x +y = 20 as equation 1 and 3x +4y = 40 equation2,
Equation 1 can be written as  y = 20-2x and
sustituted in equation 2 as 3x +4 (20-2x) = 40,
3x + 80 – 8x = 40,
-5x = 40 -80= -40,
5x = 40,
x = 40/5 = 8, so y = 20 -2 X 8 = 20 -16 =4.

Question 16.
3x + 2y = 0
5x – 2y = 32
Answer:
The solution to the system of linear equations is x = 4 and y = -6,

Explanation:
Given 3x+ 2y = 0 as equation 1 and 5x -2y = 32 as equation 2,
adding equation 1 and 2 we get
3x +2y =0,
5x -2y = 32
8x = 32,
x = 32/8 = 4 substituting x = 4 in equation 1
3(4) +2y = 0,
2y = -12, y = -12/2 = -6.

Question 17.
5x – y = 20
4x + 3y = 16
Answer:
The solution to the system of linear equations is x = 4 and y =0,

Explanation:
Given 5x – y = 20 as equation 1 and 4x +3y = 16 as equation 2
From equation 1 we have y = 5x -20,
substituting y in equation 2
4x + 3(5x -20) = 16,
4x + 15x – 60 = 16,
19x = 16 +60,
19 x = 76,
x = 76/19 = 4, so y = 5 x 4 – 20 = 0.

Question 18.
3p + 4q = 3
\(\frac{1}{2}\) + q = 3p
Answer:
The solution to the system of linear equations is p =\(\frac{1}{3}\) and
q = \(\frac{1}{2}\),

Explanation:
Given 3p +4q = 3 as equation 1 and \(\frac{1}{2}\) + q = 3p as equation 2
q = 3p – (1/2) substituting in equation 1
3p+4(3p – 1/2) =3,
3p +12 p – 2 = 3,
15p = 3+2 = 5,
p = 5/15 = 1/3, now q = 3 X 1/3  -1/2 = 1 – 1/2 = 1/2,
so p =\(\frac{1}{3}\) and q = \(\frac{1}{2}\).

Solve each system of linear equations using the elimination method or
substitution method. Explain why you choose each method.

Question 19.
2x + 7y = 32
4x – 5y = -12
Answer:
The solution to the system of linear equations is x= 2 and y =4,
used elimination method to elminate x,

Explanation:
Given 2x +7y = 32 as equation 1 and we have
4x – 5y = -12 as equation 2 if we multiply equation 1 by 2 and
subtarct equation 2 we can eliminate x
2X(2x +7y) = 64,
4x +14 y = 64
-4x +5y = 12
19y = 76, y = 76/19 = 4, now 4x -5 X 4= -12,
4x – 20 = -12,
4x = 8, x = 8/4 = 2.

Question 20.
3x + 3y = 22
3x – 2y = 7
Answer:
The solution to the system of linear equations is x = 13/3 and
y =3 used elmination method to elminate x,

Explanation:
Given 3x +3y = 22 as equation 1 and 3x – 2y = 7 as
equation 2 subtracting equation 2 from 1 we can eliminate x
3x + 3y = 22,
-3x +2y = -7
5y = 15,  y = 15/5 = 3, substituting y =3 in eqaution 2
3x – 2 X 3 = 7,
3x = 7+6 = 13,
x = 13/3.

Question 21.
7m + 2n = 20
2m = 3n – 5
Answer:
The solution to the system of linear equations is m = 2 and n =3,
used subtitution method,

Explanation:
Given 7m + 2n = 20 as equation 1 and 2m = 3n -5,
so using substitution m = (3n-5)/2 in equation 1,
7 (3n- 5)/2 + 2n = 20
7 (3n -5) + 4n = 40,
21n – 35 + 4n = 40,
25n = 40 +35 = 75,
25n = 75, n = 75/25 = 3,
n = 3, so m = (3 X3 -5)/2 = (9-5)/2 = 4/2 = 2.

Question 22.
3h – 4k = 35
k = 2h – 20
Answer:
The solution to the system of linear equations is h = 15 and
k =10 used substitution method,

Explanation:
Given 3h – 4k = 35 as equation 1 and k =2h – 20,
substituting k in equation 1
3h – 4(2h – 20) = 35,
3h – 6h + 80  = 35,
– 3h + 80 = 35,
3h = 80-35 = 45,
3h = 45, h = 45/3 = 15, so k = 2 X 15 – 20 = 30-20 = 10.

Question 23.
2h + 7k = 32
3h – 2k = -2
Answer:
The solution to the system of linear equations is h = 2 and k = 4,
used elmination method,

Explanation:
Given 2h +7k = 32 as equation 1 and 3h – 2k = -2 as equation 2
multiplying equation 1 by 3 and eqaution 2 by 2 to elminate h,
3(2h+ 7k= 32) becomes 6h + 21 k = 96 and
2(3h – 2k=-2) becomes 6h – 4k = -4 substracting 2 from 1,
6h +21k = 96
-6h +4k = 4
25 k = 100,
k = 100/25 = 4, substituting k =4 in eqaution 2
3h – 2 X 4= -2,
3h = -2 + 8 = 6,
h = 6/3 = 2.

Question 24.
2m+4=3n
5m – 3n = -1
Answer:
The solution to the system of linear equations m = -11 and n -6,
used substitution method,

Explanation:
Given 2m+ 4 = 3n as equation 1 and 5m – 3n = -1 as equation 2,
substituting 3n in equation 2 as
5m -3(2m +4) =-1,
5m – 6m -12 = -1,
-m = -1 + 12 = 11, m = -11, therefore 3n = 2 (-11) + 4,
3n = -22 + 4 = -18,
n = -18/3 = -6.

Solve.

Question 25.
Math Journal Sam solves the following system of linear equations by the elimination method,
without using calculator.

He can multiply the first equation by 3 and the second equation by 2 in order to eliminate x.
Or he can eliminate y by multiplying the first equation by 17 and the second equation by 3.
Which way should Sam choose? Explain.
Answer:
Sam can either choose any of the methods by
using method 1 he can elminate x or
by using method 2 he can elminate y and find solutions,

Explanation:
Given in method 1 sam can multiply the first equation by 3 and the
second equation by 2 in order to eliminate x  and in method 2
he can eliminate y by multiplying the first equation by 17 and
the second equation by 3 therefore Sam can either choose any of the method by
using method 1 he can elminate x or
by using method 2 he can elminate y and find solutions,
Method 1 :
3 X (2x + 3y = 1) and 2 X (3x – 17 y =23)
6x + 9y =3  and
(-)6x – 34y = 46
43 y = -43, y = -43/43, y = -1, substuting y = -1 in 2x +3y = 1,
2x + 3X -1 = 1,
2x – 3 = 1,
2x = 1+3 = 4, x = 4/2 = 2.
Method 2:
17 X (2X +3y = 1) and 3 ( 3x – 17y =23),
34x + 51 y = 17
9x – 51 y = 69
43x = 86, x = 86/43 = 2, x = 2 substituting  2 X 2 + 3y = 1,
4 +3y = 1, 3y = 1-4 = -3, 3y = -3, y = -3/3 = -1,
therefore by both methods we got x =2 and y = -1 ,
Sam can either choose any of the methods.

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 5 Lesson 5.3 Real-World Problems: Systems of Linear Equations to score better marks in the exam.

Math in Focus Grade 7 Course 3 A Chapter 5 Lesson 5.3 Answer Key Real-World Problems: Systems of Linear Equations

Math in Focus Grade 8 Chapter 5 Lesson 5.3 Guided Practice Answer Key

Solve using systems of linear equations.

Question 1.
Two bowls and one cup have a mass of 800 grams. One bowl and two cups have a mass of 700 grams. Find the mass of a bowl and the mass of a cup.
Let the mass of a bowl be b grams and the mass of a cup be c grams.
Mass of two bowls and on cup:  =  – Equation 1

Mass of one bowl and two cups:  =  – Equation 2

Use Equation 1 to express c in terms of b:

The mass of a bowl grams and the mass of a cup is grams.
Answer:
The mass of a bowl is 300 grams and
the mass of a cup is 200 grams,

Explanation:

Solve using systems of linear equations.

Question 2.
Elizabeth is thinking of a two-digit number. When the tens digit is subtracted
from the ones digit, the difference is 2. One-fifth of the number is 1 less than
the sum of the digits. What is the number?
Answer:
Let the tens digit be c and the ones digit be d.
Tens digit subtracted from ones digit:

If the tens digit is c and the ones digit is d, then the value of the number is 10c + d.

Substitute 3 for c into Equation 3:
d = 5
=
The number is .
Answer:

Question 3.
Christopher is thinking of two positive integers.
The sum of the integers is 27. When twice the first integer is added to
half of the second integer, the sums 24. Find i the integers.

Answer:
The integers are x =7 and y = 20,

Explanation:
Given Christopher is thinking of two positive integers.
Let numbers be x and y , x+y = 27,
When twice the first integer is added to
half of the second integer, the sums 24,
2x +y/2 = 24,
x = 27-y,
2(27-y) + y/2 = 24,
4(27-y)+y = 48,
108-4y +y = 48,
108-3y = 48,
3y = 108-48,
3y = 60,
y = 60/3 = 20 and x = 27-20 = 7.

Math in Focus Course 3A Practice 5.3 Answer Key

Solve using systems of linear equations.

Question 1.
Jean stocked her aquarium with 36 fresh-water fish, which cost $212.
The male fish cost $5 each, while the female fish cost $7 each.
Find the number of male fish and the number of female fish.

Answer:
The number of male fish is 20 and the number of female fish is 16,

Explanation:
Given Jean stocked her aquarium with 36 fresh-water fish, which cost $212.
The male fish cost $5 each, while the female fish cost $7 each.
Lets take male fish as M and female fish as F,
M + F = 36, M = 36-F and 5M +7F = 212,
5(36-F) +7F = 212,
180- 5F +7F = 212,
2F = 212-180= 32,
F = 32/2 = 16, So M = 36 – 16 = 20.
The number of male fish is 20 and the number of female fish is 16.

Question 2.
Seventy concert tickets were sold for $550. Each adult ticket cost
$9 and each children’s ticket cost $5.
Find the number of adult tickets and the number of children’s tickets sold.
Answer:
50 is the number of adult tickets and 20 is the number of children’s tickets sold,

Explanation:
Given Seventy concert tickets were sold for $550. Each adult ticket cost
$9 and each children’s ticket cost $5. Let number of adult tickets be a and
number of children tickets is c, a + c = 70, a = 70 -c, 9a +5c = 550,
9(70-c) + 5c = 550,
630 – 9c +5c = 550,
630-550 = 4c,
80 = 4c,
c = 80/4 = 20,
so a= 70 – 20 = 50 tickets.
50 is the number of adult tickets and 20 is the number of children’s tickets sold.

Question 3.
George paid $2.75 for 4 granola bars and 1 apple.
Addison paid $2.25for 2 granola bars and 3 apples.
Find the cost of each granola bar and each apple.
Answer:
The cost of each granola is $0.6 and each apple is $0.35,

Explanation:
Given George paid $2.75 for 4 granola bars and 1 apple.
Addison paid $2.25 for 2 granola bars and 3 apples.
Lets take granola as g and apple as a
4g+ a = 2.75, a = 2.75 -4g
2g +3a = 2.25, substituting
2g +3 (2.75 -4g)= 2.25,
2g +8.25 – 12g = 2.25,
10g = 8.25-2.25,
10g = 6,
g = 6/10= $0.6,
a = 2.75 – 4 X 0.6 = 2.75 – 2.4 = $0.35,
The cost of each granola is $0.6 and each apple is $0.35.

Question 4.
4 thumb drives and 1 compact disk have a total capacity of 9 gigabytes.
5 thumb drives have 9 gigabytes more capacity than 1 compact disk.
Find the capacity of 1 thumb drive and the capacity of 1 compact disk.
Answer:
The capacity of 1 thumb drive is 2GB and
the capacity of 1 compact disk is 1 GB,

Question 5.
A book cover has the length and width (in inches) shown in the diagram.

a) Find the values of a and b.
Answer:
a=4in and b = 2in,

Explanation:
We have equations  (3a-b) = 2+a+2b,
3a – a = 2+2b +b,
2a = 2 + 3b,
2a – 3b = 2  equation 1
and 3b = 2+a means  2a -2-a =2,
a =4 so 3b = 2+4 = 6, b= 6/3 = 2. ,
therefore a = 4in and b = 2in.

b) Find the perimeter of the book cover.
Answer:
Peimeter of the book cover is 32in,

Explanation:
Given l = 3a-b = 3 x 4 – 2 = 12-2 = 10, width = 3 b = 3 X 2 = 6,
perimeter = 2(l+w) = 2(10+ 6)= 2(16)= 32 in.

Question 6.
Eileen saves dimes and quarters. She has 40 coins,
which totaled $6.55, in her bank. How many of each coin does she have?
Answer:
Eileen has 23 dimes and 17 quarters,

Aiden is a percussionist in his school band. One instrument he
plays is in the shape of an equilateral triangle shown below.
The side lengths are in inches. Find x and y.

Answer:
x = -1 and y = -5,
Explanation:
Given Aiden is a percussionist in his school band. One instrument he
plays is in the shape of an equilateral triangle so
3x – 2y = 7,
3x = 2y +7,
x = (2y +7)/3,
8x – 3y = 7 substituting x
8(2y +7)/3 = 7+3y,
16y +56 = 3(7 +3y)
16y +56 = 21 +9y
16y -9y = 21-56,
7y = -35, y = -35/7 = -5,x=(2X -5+7)/3 = (-10+7)/3 = -3/3 = -1.

Question 8.
Mrs. Green gave three riddles for her class to solve.

a) The sum of the digits of a two-digit number is 11.
Twice the tens digit plus 2 equals ten times the ones digit. What is the number?
Answer:
The number is 92,

Explanation:
Given the sum of the digits of a two-digit number is 11.
x + y = 11,y = 11-x
Twice the tens digit plus 2 equals ten times the ones digit
2x + 2 = 10y,
2x + 2 = 10(11-x),
2x +2 = 110 -10x,
2x +10x = 110-2,
12x = 108, x = 108/12 = 9, so y = 11-9 = 2,
the number is 92.

b) There are two numbers. The first number minus the second number is 15.
One-third of the sum of the numbers is one quarter of the first number.
What are the two numbers?
Answer:
The two numbers are 12 and -3,

Explanation:
Let x and y be the numbers ,
The first number minus the second number is 15. x – y = 15,
(x +y)/3 = x/4,
4x + 4y = 3x,
x = -4y, substituting  -4y – y = 15,
-5y = 15, y = -15/5 = -3,
x = – 4(-3) = 12.
The two numbers are 12 and -3.

c) A two-digit number is 1 more than eight times the sum of the digits.
The ones digit is 3 less than the tens digit. What is the number?
Answer:
The number is 41,

Explanation:
Given A two-digit number is 1 more than eight times the sum of the digits.
10x + y = 8(x+y)+1
The ones digit is 3 less than the tens digit means x = y +3,
10(y +3)+y = 8(y+3) +8y +1,
10 y + 30 +y = 8y + 24 +8y +1,
11y + 30 = 16 y +25,
16y – 11y = 30 -25,
5y = 5, y = 5/5 = 1, x = 1+ 3 = 4,
The number is 41.

Question 9.

On Saturday, $585 was collected from the sale of 55 tickets for a performance.
The table below shows the information about the sale of the tickets.
Find the number of adult tickets and the number of student’s tickets sold on that day.

Answer:
30 number of adult tickets and 25 number of student’s tickets sold on that day,

Explanation:
Given Students tickets cost 12 X .25 = 3, 12-3 =9 is the cost for student tickets,
Let a be the number of adult tickets and s the number of
student’s tickets sold on that day, a + s = 55 , s = 55-a and
12a +9s = 585,
12a+9(55 -a) = 585,
12a + 495 -9a = 585,
3a = 585- 495= 90,
a= 90/3 = 30, s = 55-30 = 25.
30 number of adult tickets and 25 number of student’s tickets sold on that day.

Question 10.
Eight years ago, Mr. Fontana was six times as old as his son.
In twelve years’ time, he will be twice as old as his son. How old are they now?

Answer:
Fathers age is 38 and sons age is 13 years old,
Explanation:
Let f be fathers age now and s be sons age now,
Eight years ago, Mr. Fontana was six times as old as his son.
f – 8 = 6(s -8), In twelve years’ time, he will be twice as old as his son,
f + 12 = 2(s+12),
f = 2s +24-12 = 2s+12,
2s +12 – 8 = 6s – 48,
2s +4 = 6s -48,
6s-2s = 48+4,
4s = 52,
s = 52/4 = 13, f = 2 X 13 +12 = 26 +12 = 38.
Fathers age is 38 and sons age is 13 years old.

Question 11.
A restaurant sells four combo meals. Jolly Meal, which cost $12.60,
consists of 2 yogurt cups and 1 sandwich. The $pecial Meal, which is
made up of 2 sandwiches and 1 yogurt cup, cost $13.50.
Calculate the cost of the following combo meals if the charge for
sandwiches and yogurt cups are the same for all combo meals.
a) Children’s Meal: 1 sandwich and 1 yogurt cup
Answer:
Children’s Meal: 1 sandwich and 1 yogurt cup is $8.7,

Explanation:
Given a restaurant sells four combo meals.
Jolly Meal, which cost $12.60, consists of 2 yogurt cups and 1 sandwich.
The $pecial Meal, which is made up of 2 sandwiches and 1 yogurt cup, cost $13.50.
Let sandwiches is s and yogurt is y
Jolly Meal 2y +s = $12.60, s = 12.60 – 2y,
2s +y = $13.50,
2 (12.60 -2y)+y =13.50,
25.2 – 4y +y = 13.50,
25.2-13.50 = 3y,
3y = 11.7,y = 11.7/3 = 3.9,
so s = 12.60 – 2(3.9) = 12.60 – 7.8 = 4.8,
therefore 1 sandwich and 1 yogurt cup is $4.8 + $3.9 = $8.7.

b) Family Meal: 2 sandwiches and 3 yogurt cups
Answer:
Family Meal: 2 sandwiches and 3 yogurt cups is $21.3,

Explanation:
We got sandwiches s = $4.8, yogurt y = $3.9,
so for 2 sandwiches and 3 yogurt cups it is
2X $4.8 and 3 X $3.9 = $9.6 + $11.7 = $21.3.

Question 12.
In a boat race, Jenny’s team rowed their boat from point A to point 8 and back to point A.
Points A and 8 are 30 miles apart. During the race,
there was a constant current flowing from A to 8.
She took 2 hours to travel from A to 8 and 2.5 hours to travel from 8 to A.

a) Calculate the speed of the boat from A to 6 and the speed from 8 to A.
Answer:
The effective speed of the boat downstream is 15 mph,
The effective speed of the boat upstream is 12 mph,
Explanation:
Given one way distance is 30 miles,
Down stream travel took 2 hours,
and Up stream travel took is 2.5 hours,
The effective speed downstream was 30/2 = 15 miles per hour,
The effective speed upstream was 30/2.5 = 12 miles per hour,
The effective speed downstream is u + v, where u is the speed of the
boat in the still water and v is the current speed,
The effective speed up stream is u – v,
u + v = 15, u – v = 12, v = u -12,
u + (u -12) = 15,
2u = 15+ 12 = 27, u = 27/2 = 13.5 mph,
v = 13.5 – 12 = 1.5 mph

b) Find the speed of the boat from A to B if there was no current.
Answer:
The speed of the boat in still water is 13.5 mph

c) Find the speed of the current.
Answer:
The speed of the current is 1.5 mph

Question 13.
Alex deposited $3,500 in two banks. The first bank paid 2% simple interest
per year while the second bank paid 3%. At the end of one year,
the difference in the interest amounts was $30. Find the amount Alex deposited in each bank.
Answer:
Alex deposited $2,700 in one bank and $800 in another bank,

Explanation:
Given Alex deposited $3,500 in two banks,
x + y = 3500,so y = 3500-x
The first bank paid 2% simple interest
per year while the second bank paid 3% and
At the end of one year,
the difference in the interest amounts was $30.
I = pRT interest of x is x X 0.02,
Interest of y is y X 0.03,
0.02x-0.03 y = 30 multiplying both sides by 100,
2x – 3y = 3000,substituting x
2x – 3(3500 – x) = 3000,
2x – 10,500  +3x = 3000,
5x = 10,500 + 3,000= 13,500,
x = 13,500/5 = $2700, y = 3500 – 2700 = $800,
Alex deposited $2,700 in one bank and $800 in another bank.

Question 14.
Greg’s favorite activities are bike riding and hip-hop dancing.
He wants to try to do these activities for 6 hours each week.
He would also like to try to burn off about 2,100 calories a week.
He finds that biking uses about 425 calories each hour and
hip-hop dancing uses about 325 calories each hour.
He wants to do bike riding for x hours and hip-hop dancing for y hours each week.

a) Copy and complete the following table.

Answer:

Explanation:
Copied and completed the table as shown above.

b) How much time should he spend doing each activity to accomplish his goal?
Answer:
Greg’s wants to do bike riding for 3/2 or 1.5 hours and
hip-hop dancing for 9/2 or 4.5 hours eqch week,

Explanation:
Given Greg’s favorite activities are bike riding and hip-hop dancing.
He wants to try to do these activities for 6 hours each week.
He would also like to try to burn off about 2,100 calories a week.
He finds that biking uses about 425 calories each hour and
hip-hop dancing uses about 325 calories each hour.
Let x hours is bike riding and y hours br hip hop dancing so
x + y = 6, y = 6 – x and 425x + 325y = 2,100 substituting y
425x +325(6-x) =2100,
425x + 1950 – 325x = 2100,
100x = 2100-1950=150,
x = 150/100 = 3/2, y = 6-3/2 = 9/2,
So Greg’s wants to do bike riding for 3/2 or 1.5 hours and
hip-hop dancing for 9/2 or 4.5 hours each week.

Question 15.
In an experiment, Matthew was given two saline (salt) solutions,
whose concentrations are shown below. He had to prepare 10 fluid ounces of
a new saline solution with a 27% concentration from the two solutions.
Calculate the volume of each solution used to prepare the new solution.

Answer:
The volume of each solution used to prepare the new solution is
x as 7.5 fl oz and y as 2.5 fl oz,

Explanation:
Given Matthew was given two saline (salt) solutions,
whose concentrations are 30 and 18. He had to prepare 10 fluid ounces of
a new saline solution with a 27% concentration from the two solutions.
The volume of each solution used to prepare the new solution is
30x +18 y = 270 and x + y = 10, y = 10 -x,
30 x+18(10-x)=270,
30x +180 – 18x = 270,
12 x = 270-180,
12x = 90, x= 90/12 = 7.5 and y= 10-7.5 = 2.5, therefore
the volume of each solution used to prepare the new solution is
x as 7.5 fl oz and y as 2.5 fl oz.

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 5 Lesson 5.4 Solve Systems of Linear Equations by Graphing to score better marks in the exam.

Math in Focus Grade 7 Course 3 A Chapter 5 Lesson 5.4 Answer Key Solve Systems of Linear Equations by Graphing

Math in Focus Grade 8 Chapter 5 Lesson 5.4 Guided Practice Answer Key

Technology Activity

Materials:

• graphing calculator

Explore The Graphical Method

Work in pairs.

Step 1.
Solve the system of linear equations using the elimination method or substitution method.
x + 2y = 4
x – y = 1

Step 2.
To solve this system of linear equations using a graphing calculator, solve each equation for y and enter each expression for y into the calculator.

Step 3.
Press the key. Use the function and select 5:lntersect to find
where the two graphs intersect.

Caution
Be sure to use parentheses around any fractional coefficients, and use the key if the coefficient is negative.

Step 4.
Repeat step 1 to step 3 for the system of linear equations
6x – 5y = -3,
x + y = 5.

Math Journal How is the solution you found in step 1 related to the coordinates of the point of intersection in step 3? Why do you think this happens?

Solve using the graphical method. Copy and complete the tables of values. Graph the system of linear equations on the same coordinate plane. Use 1 grid square on both axes to represent 1 unit for the x interval from -1 to 3 and the y interval from -1 to 5.

Question 1.
2x + y = 5
x – y = -2

2x + y = 5

x – y = -2

From the graph, the slope of 2x + y = 5 is and the y-intercept is . The slope of x – y = -2 is and its y-intercept is .
The point of intersection is (, ). Therefore, the solution to the system of equations is x = and y = .

Solve using the graphical method. Graph each system of linear equations on the same coordinate plane. Use 1 grid square on both axes to represent 1 unit for the Interval from -4 to 4.
Answer:
2x + y = 5
x – y = -2
We are given the system of equations:

For the equation 2x + y = 5 we build the table of values:

For the equation x – y = -2 we build the table of values:

We graph the two lines:
From the graph, the slope of 2x + y = 5 is -2 and the y-Intercept is 5.
The slope of x – y = -2 is 1 and the y-Intercept is 2.
The point of intersection is (1, 3). Therefore the solution of the system of equations is x = 1 and y = 3.
x = 1; y = 3

Question 2.
x + 2y = 5
x + y = 2
Answer:
x + 2y = 5
x + y = 2
We are given the system of equations:

For the equation x + 2y = 5 we build the table of values:

For the equation x + y = 2 we build the table of values:

We graph the two lines:
From the graph, the slope of x + 2y = 5 is -0.5 and the y-Intercept is 2.5. The slope of x + y = 2 is -1 and the y-Intercept is 2.
The point of intersection is (-1, 3). Therefore the solution of the system of equations is x = -1 and y = 3.
x = -1; y = 3

Question 3.
3x + 2y = 8
x – y = 1
Answer:
3x + 2y = 8
x – y = 1
We are given the system of equations:

For the equation 3x + 2y = 8 we build the table of values:

For the equation x – y = 1 we build the table of values:

We graph the two lines:
From the graph, the slope of 3x + 2y = 8 is -1.5 and the y-Intercept is 4. The slope of x – y = 1 is 1 and the y-Intercept is -1.
The point of intersection is (2, 1). Therefore the solution of the system of equations is x = 2 and y = 1.
x = 2; y = 1

Use graph paper. Use 1 grid square on both axis to represent 10 seconds for the t interval from 110 to 150 seconds, and 10°F for the T interval from 300 to 350°F.

Question 4.
Two ovens are being heated. Their temperatures are represented by the equations
Oven 1: T = t + 200
Oven 2: T = 2t + 80
where T is the temperature in °F of the oven and t is the time in seconds. Solve the system of linear equations graphically. When will the temperatures of the ovens be the same?
Answer:
T = t + 200
T = 2t + 80
We are given the system of equations:
For the equation T = t + 200 the slope is 1 and the y-intercept is 200.
For the equation T = 2t + 80 the slope is 2 and the y-intercept is 80.

We sketch the graph of the two equations using the slope and the y-irtercept values:
The point of intersection is (120, 320). Therefore the solution of the system of equations is t = 120 and T = 320.
t = 120 seconds; T = 320° F

Math in Focus Course 3A Practice 5.4 Answer Key

For this practice, unless otherwise stated, use 1 grid square to represent 1 unit on both axes for the interval from —8 to 8. Solve each system of linear equations using the graphical method.

Question 1.
x + y = 6
2x + y = 8
Answer:
x + y = 6
2x + y = 8
We are given the system of equations:

a) Copy and complete the tables of values for the system of linear equations, x + y = 6

Answer:
For the equation x + y = 6 we build the table of values:

For the equation 2x + y = 8 we build the table of values:

b) Graph x + y = 6 and 2x + y = 8 on the same coordinate plane. Find the point of intersection.
Answer:
We graph the two lines:
From the graph, the slope of x + y = 6 is -1 and the y-intercept is 6
The slope of 2x + y = 8 is -2 and the y-intercept is 8.
The point of intersection is (2, 4).

c) Use the graph in b) to solve the system of linear equations.
Answer:
Therefore the solution of the system or equations is x = 2 and y = 4.
x = 2; y = 4

Question 2.
x + y = 5
x – y = 2

a) Copy and complete the tables of values for the system of linear equations, x + y = 5

Answer:
x + y = 5
x – y = 2
We are given the system of equations:

For the equation x + y = 5 we build the table of values:

For the equation x – y = 2 we build the table of values:

We graph the two lines:

b) Graph x + y = 5 and x — y = 2 on the same coordinate plane. Find the point of intersection.
Answer:
From the graph, the slope of x + y = 5 is -1 and the y-intercept is 5
The slope of x – y = 2 is 1 and the y-intercept is -2.
The point of intersection is (3.5, 1.5)

c) Use the graph in b) to solve the system of linear equations.
Answer:
Therefore the solution oi me system or equations is x = 3.5 and y = 1.5.
x = 3.5; y = 1.5

Question 3.
x + 2y = 5
2x – 2y = 1
a) Graph x + 2y = 5 and 2x — 2y = 1 on the same coordinate plane. Find the point of intersection of the graphs.
Answer:
x + 2y = 5
2x – 2y = 1
We are given the system of equations:

For the equation x + 2y = 5 we build the table of values:

For the equation 2x — 2y = 1 we build the table of values:

We graph the two lines:

b) Use the graph in a) to solve the system of linear equations.
Answer:
From the graph, the slope of x + 2y = 5 is -0.5 and the y-intercept is 25.
The slope of 2x – 2y = 1 is 1 and the y-intercept is -0.5.
The point of intersection is (2, 1.5). Therefore the solution of the system of equations is x = 2 and y = 1.5.
x = 2; y = 1.5

Question 4.
2x + 3y= -1
x – 2y = 3

a) Graph 2x + 3y = -1 and x – 2y = 3 on the same coordinate plane. Find the point of intersection of the graphs.
Answer:
2x + 3y = -1
x – 2y = 3
We are given the system of equations:

For the equation 2x + 3y = -1 we build the table of values:

For the equation x — 2y = 3 we build the table of values:

We graph the two lines:

b) Use the graph in a) to solve the system of linear equations.
Answer:
From the graph, the slope of 2x + y = 5 is –\(\frac{2}{3}\) and the y-intercept is –\(\frac{1}{3}\)
The slope of x – 2y = 3 is 0.5 and the y-intercept is -1.5.
The point of intersection is (1, -1). Therefore the solution of the system of equations is x = 1 and y = -1.
x = 1: y = -1

Solve each system of equations using the graphical method.

Question 5.
x = 2y
y = x + 2
Answer:
x = 2y Equation 1
y = x + 2 Equation 2
We are given the system of equations:
y = 0.5x We rewrite Equation 1 in slope-intercept form:
y = x + 2 Equation 2 is written in slope-intercept form:

We graph the two equations: the first has slope 0.5 and y-intercept 0, while the second has slope 1 and y-intercept 2:
The point of intersection is (-4, -2). Therefore the soLution of the system of equations is x = -4 and y = -2.

Question 6.
y = 3
y = 2x + 1
Answer:
y = 3 Equation 1
y = 2x + 1 Equation 2
We are given the system of equations:
y = 3 Equation 1 is written in slope-intercept form:
y = 2x + 1 Equation 2 is written in slope-intercept form:

We graph the two equations: the first has slope 0 and y-intercept 3 (horizontal line), while the second has slope 2 and y-intercept 1:
The point of intersection is (1, 3). Therefore the solution of the system of equations is x = 1 and y = 3.
x = 1; y = 3

Question 7.
x = 2
y = 2x – 8
Answer:
x = 2 Equation 1
y = 2x — 8 Equation 2
We are given the system of equations:
x = 2 Equation 1 is the equation of a vertical line:
y = 2x – 8 Equation 2 is written in slope-intercept form:

We graph the two equations: the first is vertical passing through (2, 0), while the second slope 2 and y-intercept-8:
The point of intersection is (2, -4). Therefore the solution of the system of equations is x = 2 and y = -4.
x = 2 ; y = -4

Question 8.
3x – 2y = 19
3y = 2x – 21
Answer:
3x – 2y = 19 Equation 1
3y = 2x — 21 Equation 2
We are given the system of equations:
3x – 2y – 3x = 19 – 3x We rewrite Equation 1 in slope-intercept form:
-2y = -3x + 19
y = \(\frac{3}{2}\)x – \(\frac{19}{2}\)
y = \(\frac{3}{2}\)x – \(\frac{19}{2}\)
y = \(\frac{2}{3}\)x – 7
We rewrite Equation 2 in slope-intercept form:

We graph the two equations: the first has slope \(\frac{3}{2}\) and y-intercept –\(\frac{19}{2}\), while the second has slope \(\frac{1}{2}\) and y-intercept -7:
The point of intersection is (3, -5) Therefore the solution of the system of equations is x = 3 and y = -5.
x = 3; y = -5

Question 9.
2x + y = 11
x + 3y = 18
Answer:
2x + y = 11 Equation 1
x + 3y = 18 Equation 2
We are given the system of equations:
2x + y — 2x = 11 – 2x We rewrite Equation 1 in slope-intercept form:
y = 11 — 2x
x + 3y — x = 18 – x We rewrite Equation 2 in slope-intercept form:
3y = 18 – x
y = –\(\frac{1}{3}\)x + 6

We graph the two equations: the first has slope -2 and y-intercept 11, while the second has slope –\(\frac{1}{3}\) and y-intercept 6:
The point of intersection is (3, 5). Therefore the solution of the system of equations is x = 3 and y = 5
x = 3, y = 5

Question 10.
x + 2y = 1
4y – x = 17
Answer:
x + 2y = 1 Equation 1
4y — x = 17 Equation 2
We are given the system of equations:
x + 2y – x = 1 – x We rewrite Equation 1 in slope-intercept form:
2y = -x + 1
y = –\(\frac{1}{2}\)x + \(\frac{1}{2}\)
4y — x + x = 17 + x We rewrite Equation 2 in slope-intercept form:
4y = x + 17
y = \(\frac{1}{4}\)x + \(\frac{17}{4}\)

We graph the two equations: the first has slope –\(\frac{1}{2}\) and y-intercept \(\frac{1}{2}\), while the second has slope \(\frac{1}{4}\) and y-intercept \(\frac{17}{4}\)
The point of intersection is (-5, 3) Therefore the solution of the system of equations is x = -5 and y = 3.
x = -5; y = -3

Solve. Show your work.

Question 11.
Marianne jogged from point P to point Q while Walter jogged from point Q to point P. Point P and point Q are 7.5 kilometers apart. Marianne’s motion is represented by d = 8t and Walter’s motion is represented by 2d + 14t = 15, where t hours is the time and d kilometers is the distance from point P.

a) Solve the system of linear equations using the graphical method.
Answer:
We are given the system of equations:
d = 8t Equation 1
2d + 14t = 15 Equation 2
d = 8t a) Equation 1 is written in slope-intercept form:
2d + 14t — 14t = 15 — 14t We rewrite Equation 2 in slope-intercept form:
2d = -14t + 15
d = -7t + 7.5
img 36
We graph the two equations the first has slope 8 and y-intercept 0, while the second has sope -7 and y-
intercept 7.5:
The point of intersection is (0.5, 4). Therefore the solution of the system of equations is t = 0.5 and
d = 4.

b) When did Marianne and Walter meet? How far from point Q did they meet?
Answer:
t = 0.5 hours b) The t-coordinate of the intersection point s the time after which they met
d = 4 km The d-coordinate of the intersection point is the distance from point P when they met:
7.5 — 4 = 3.5 km The distance from point Q is
a) t = 0.5; d = 4
b) 0.5 hours; 3.5 km

Question 12.
Math Journal Explain when it is convenient to use each method of solving a system of linear equations: Elimination, substitution, and graphical. Give an example for each method.
Answer:
3x – 4y = 25
2x + 5y = 77
The elimination method is used when none of the variables has coefficient 1.
For example:
y = 2x + 3
3x – 2y = 7 The substitution method ¡s used when one of the variables has coefficient 1
For example:
y = 2x + 1
y = -x + 2
The graphical method is used when one of the variables has coefficient 1 in both equations.
For example:
The choice depends on the coefficients of the variables

Question 13.
Two cyclists are traveling along a track in the same direction. Their motions are described by the linear equations d = 10t and d – 8t = 2, where t hours is the time and d miles is the distance from point A on the-Track.
Answer:
d = 10t Equation 1
d – 8t = 2 Equation 2
We are given the system of equations:

a) Solve the system of linear equations using a graphing calculator.
Answer:
d = 8t a) Equation 1 is written in sLope-intercept form:
d — 8t + 8t = 2 + 8t We rewrite Equation 2 in slope-intercept form:
d = 8t + 2

We graph the two equations using a graphing calculator:
3d?
The point of intersection is (1,10). Therefore the solution of the system of equations is t = 1 and d = 10.

b) When will the cyclists meet?
Answer:
t = 1 hour b) The t-coordinate of the intersection point is the time after which they met
a) t = 1; d = 10
b) 1 hour

Question 14.
Dr. Murray is heating a beaker containing Liquid A and a beaker containing Liquid B. The temperature of Liquid A is represented by T = 2t + 140 and the temperature of Liquid B is represented by T = t + 160, where T°F is the temperature of the liquid after t seconds.
Answer:
T = 2t + 140 Equation 1
T = t + 160 Equation 2
We are given the system of equations:

a) Solve the system of linear equations using a graphing calculator.
Answer:
Equation 1 and Equation 2 are written in slope-intercept

We graph the two equations using a graphing calculator:
The point of intersection is (20, 180). Therefore the solution of the system of equations is t = 20 and T = 180.

b) When will the temperatures of the liquids be the same?
Answer:
t = 20 seconds b) The t-coordinate of the intersection point is the time after which the temperatures are
the same:
a) t = 20;T = 180;
b) 20 seconds

Question 15.
A carpenter is hammering an iron nail and another carpenter is hammering a copper nail. The temperatures of the nails increase during the hammering. The temperature of the iron nail is represented by T = 2t + 70 and the temperature of the copper nail is represented by T = 3t + 65, where T°F is the temperature of the nail after t seconds.
Answer:
T = 2t + 70 Equation 1
T = 3t + 65 Equation 2
We are given the system of equations:

a) Solve the system of linear equations using a graphing calculator.
Answer:
Equation 1 and Equation 2 are written in slope-intercept form.

We graph the two equations using a graphing calculator
The point of intersection is (5, 80). Therefore the solution of the system of equations is t = 5 and T = 80.

b) When will the temperatures of the nails be the same?
Answer:
t = 5 seconds b) The t-coordinate of the intersection point is the time after which the temperatures are
the same:

a) t = 5; T = 80;
b) 5 seconds

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 5 Lesson 5.5 Inconsistent and Dependent Systems of Linear Equations to score better marks in the exam.

Math in Focus Grade 7 Course 3 A Chapter 5 Lesson 5.5 Answer Key Inconsistent and Dependent Systems of Linear Equations

Math in Focus Grade 8 Chapter 5 Lesson 5.5 Guided Practice Answer Key

Identify whether each system of linear equations is inconsistent or has a unique solution. Justify your reasoning.

Question 1.
11x + y = 2 — Equation 1
22x + 2y = 3 —Equation 2
Rewrite each linear equations in slope-intercept form y = mx + b.
Equation 1
11x + y = 2
= Subtract 11x from both sides.
y = Simplify.
Equation 2
22x + 2y = 3
= Subtract 22x from both sides.
= Simplify.
= Divide both sides by 2.
y = Simplify.
The slope of the graph of the Equation 1 is and the y-intercept is .
The slope of the graph of the Equation 2 is and the y-intercept is .
The graphs of the linear equations have the same and different . The system of linear equations is , because the system of linear equations has no solution.
Answer:
11x + y = 2 Equation 1 We are given the system of equations:
22x + 2y = 3 Equation 2
11x + y = 2 Rewrite Equation 1 in slope-intercept form y = mx + b:
11x + y — 11x = 2 — 11x Subtract 11x from both sides:
y = —11x + 2 Simplify:
22x + 2y = 3 Rewrite Equation 2 in slope-intercept form y = mx + b
22x + 2y — 22x = 3 — 22x Subtract 22x from both sides
2y = —22x + 3 Simplify:
\(\frac{2 y}{2}\) = \(\frac{-22 x+3}{2}\) Divide both sides by 2:
y = -11x + \(\frac{3}{2}\) Simplify:
The slope of the graph of Equation 1 is -11 and the y-intercept is 2.
The slope of the graph of Equation 2 is -11 and the y-intercept is \(\frac{3}{2}\).
The graphs of the linear equations have the same slope and different y-intercept. The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent

Question 2.
13x + y = 23
26x + 2y = 21
Answer:
13x + y = 23 Equation 1 We are given the system of equations:
26x + 2y = 21 Equation 2
13x + y = 23 Rewrite Equation 1 in slope-intercept form y = mx + b:
13x + y — 13x = 23 — 13x Subtract 13x from both sides
y = —13x -i- 23 Simplify:
26x + 2y = 21 Rewrite Equation 2 in slope-intercept form y = mx + b:
26x + 2y — 26x = 21 — 26x Subtract 26x from both sides:
2y = -26x + 21 Simplify:
\(\frac{2 y}{2}\) = \(\frac{-26 x+21}{2}\) Divide both sides by 2:
y = —13x + \(\frac{21}{2}\) Simplify:
The slope of the graph of Equation 1 is -13 and the gj-intercept is 23.
The slope of the graph of Equation 2 is -13 and the y-intercept is \(\frac{21}{2}\).
The graphs of the linear equations have the same slope and different y-intercept The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent

Question 3.
\(\frac{1}{2}\)x + y = 4
3x + 8y = 16
Answer:
\(\frac{1}{4}\)x + y = 4 Equation 1
3x + 8y = 16 Equation 2
We are given the system of equations:
\(\frac{1}{2}\)x + y = 4 Rewrite Equation 1 in slope-intercept form y = mx + b:
\(\frac{1}{2}\)x + y – \(\frac{1}{2}\)x = 4 – \(\frac{1}{2}\)x Subtract 11x from both sides:
y = – \(\frac{1}{2}\)x + 4 Simplify:
3x + 8 = 16 Rewrite Equation 2 in slope-intercept form y = mx + b:
3x + 8y — 3x = 16 — 3x Subtract 3x from both sides:
8y = —3x + 16 Simplify:
\(\frac{8 y}{8}\) = \(\frac{-3 x+16}{8}\) Divide both sides by 8:
y = \(-\frac{3}{8}\)x + 2 simplify
The slope of the graph of Equation 1 is – \(\frac{1}{2}\) and the y-intercept is 4.
The slope of the graph of Equation 2 is – \(\frac{3}{8}\) and the y-intercept is 2.
– \(\frac{1}{2}\)x + 4 = — \(\frac{3}{8}\) + 2 The graphs of the linear equations have different slopes, therefore tne system of linear equations has a unique solution.
8 ∙ (-\(\frac{1}{2}\)x + 4) = 8 ∙ (-\(\frac{3}{8}\)x + 2
—4x + 32 = -3x + 16
-4x + 32 + 4x = -3x + 16 + 4x
32 = x + 16
32 — 16 = x + 16 — 16
x = 16
y = –\(\frac{3}{8}\)(16) + 2
= -6 + 2
= -4
Unique solution (x = 16; y = -4)

Question 4.
\(\frac{1}{3}\)x + y = 7
x + 3y = 6
Answer:
\(\frac{1}{3}\)x + y = 7 Equation 1
x + 3y = 6 Equation 2
We are given the system of equations:
\(\frac{1}{3}\)x + y = 7 Rewrite Equation lin slope-intercept form y = mx + b:
\(\frac{1}{3}\)x + y – \(\frac{1}{3}\)x = 7 – \(\frac{1}{3}\)x Subtract \(\frac{1}{3}\)x from both sides:
y = –\(\frac{1}{3}\)x + 7 Simplify:
x + 3y = 6 Rewrite Equation 2 in slope-intercept form y = mx + b:
x + 3y — x = 6 — x Subtract x from both sides:
3y = —x + 6 Simplify:
\(\frac{3 y}{3}\) = \(\frac{-x+6}{3}\) Divide both sides by 3:
y = \(\frac{1}{3}\)x + 2 Simplify:
The slope of the graph of Equation 1 is —\(\frac{1}{3}\) and the y-intercept is 7
The slope of the graph of Equation 2 is –\(\frac{1}{3}\) and the y-irtercept is 2.
The graphs of the linear equations have the same slope and different y-intercept The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent

Identify whether the system of linear equations is inconsistent or has a unique solution. Justify your reasoning.

Question 5.
5x + 2y = 4
20x + 8y = 30
Answer:
5x + 2y = 4 Equation 1
20x + 8y = 30 Equation 2
We are given the system of equations:
5x + 2 = Rewrite Equation 1 in slope-intercept form y = mx + b:
5x + 2y — 5x = 4 — 5x Subtract 5x from both sides and simplify:
\(\frac{2 y}{2}\) = \(\frac{-5 x+4}{2}\)
y = \(-\frac{5}{2}\)x + 2 Divide both sides by 2 and simplify:
20x + 8y = 30 Rewrite Equation 2 in slope-intercept form y = mx + b:
20x + 8y – 20x = 30 — 20x Subtract 20x from both sides and simplify:
8y = -20x + 30
\(\frac{8 y}{8}\) = \(\frac{-20 x+30}{8}\) Divide both sides by 8 and simplify:
y = –\(\frac{5}{2}\)x + \(\frac{15}{4}\)
The slope of the graph of Equation 1 is –\(\frac{5}{2}\) and the y-intercept is 2.
The slope of the graph of Equation 2 is —\(\frac{5}{2}\) and the y-intercept is \(\frac{15}{4}\).
The graphs of the linear equations have the same slope and different y-intercept The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent

Question 6.
7x + y = 14
10x + 4y = 32
Answer:
7x + y = 14 Equation 1 We are given the system of equations
10x + 4y = 32 Equation 2
7x + 4y = 14 Rewrite Equation 1 in slope-Intercept form y = mx + b
7x + y — 7x = 14 — 7x subtract 7x from both sides and simplify
y = —7x + 14 simplify
10x + 4y = 32 Rewrite Equation 2 in slope-intercept form y = mx + b
10x + 4y – 10x = 32 — 10x Subtract 10x from both sides and simplify:
4y = -10x + 32 simplify
\(\frac{4 y}{2}\) = \(\frac{-10 x+32}{4}\) Divide both sides by 4
y = –\(\frac{5}{2}\)x + 8 Simplify:
The slope of the graph of Equation 1 is -7 and the y-intercept is 14.
The slope of the graph of Equation 2 is –\(\frac{5}{2}\) and the y-intercept is 8.

—7x + 14 = —\(\frac{5}{2}\)x + 8 The graphs of the linear equations have different slopes, therefore the system of linear equations has an unique solution.
2 ∙ (-7x + 14) = 2(-\(\frac{5}{2}\)x + 8)
—14x + 28 = —5x + 16
—14x + 28 + 14x = —5x + 16 + 14x
28 = 9x + 16
28 — 16 = 9x + 16 — 16
12 = 9x
\(\frac{12}{9}\) = \(\frac{9 x}{9}\)
x = \(\frac{4}{3}\)
y = –\(\frac{5}{2}\) ∙ \(\frac{4}{3}\) + 8
= –\(\frac{10}{3}\) + 8
= \(\frac{14}{3}\)
Unique solution (x = \(\frac{4}{3}\); y = \(\frac{14}{3}\))

Question 7.
12x + 4y = 16
9x + 3y = 12
Answer:
12x + 4y = 16 Equation 1
9x + 3y = 12 Equation 2
we are given the system of equations:
12x + 4y = 16 Rewrite Equation 1 in slope-intercept form y = mx + b:
12x + 4y — 12x = 16 — 2x Subtract 12x from both sides and simplify:
4y = —12x + 16
\(\frac{4 y}{4}\) = \(\frac{-12 x+16}{4}\) Divide both sides by 4 and simplify:
y = —3x + 4
9x + 3y = 12 Rewrite Equation 2 in slope-intercept form y = mx + b:
9x + 3y — 9x = 12 — 9x Subtract 9x from both sides and simplify:
3y = —9x + 12
\(\frac{3 y}{4}\) = \(\frac{-9 x+12}{3}\) Divide both sides by 3 and simplify:
y = -3x + 4
Since Equation 1 and Equation 2 are equivalent, they have an infinite number of solutions. Therefore system of linear equations is dependent.
Dependent

Math in Focus Course 3A Practice 5.5 Answer Key

Graph each system of linear equations using a graphing calculator. State whether each system of equations is inconsistent or has a unique solution.

Question 1.
3x + y = 4
6x + 2y = 14
Answer:
3x + y = 4 Equation 1 We are given the system of equations:
6x + 2y = 14 Equation 2
3x + = 4 Rewrite Equation 1 in slope-intercept form y = mx + b:
3x + y — 3x = 4 — 3x Subtract 3x from both sides:
y = —3x + 4 Simplify:
6x + 2y = 14 Rewrite Equation 2 in slope-intercept form y = mx + b:
6x + 2y — 6x = 14 — 6x Subtract 6x from both sides:
2y = —6x + 14 Simplify:
\(\frac{2 y}{2}\) = \(\frac{-6 x+14}{2}\) Divide both sides by 2:
y = -3x + 7 Simplify:

We graph the two equations using a graphing calculator:
The graphs of the linear equations are parallel tines, so there is no point of intersection. Since there are no points that lie on both graphs, the system of linear equations is inconsistent
Inconsistent

Question 2.
10x + 5y = 15
x + y = 3
Answer:
10x + 5y = 15 Equation 1
x + y = 3 Equation 2
We are given the system of equations:
10x + 5y = 15 Rewrite Equation 1 in slope-intercept form y = mx + b:
10x + 5y — 10x = 15 — 10x Subtract 10x from both sides and simplify:
5y = 15 — 10x
\(\frac{5 y}{5}\) = \(\frac{-10 x+15}{5}\) Divide by 5 and simplify:
y = —2x + 3 Rewrite Equation 2 in slope-intercept form y = mx + b:
x + y — x = 3 — x Subtract x from both sides and simplify:

We graph the two equations:
x = 0
The graphs intersect in the point (0, 3). The system of linear equations has an unique solution:
y = 3
Unique solution (x = 0, y = 3)

Question 3.
x – 2y = 14
4y = 5 + 2x
Answer:
x — 2y = 14 Equation 1
4y = 5 + 2x Equation 2
We are given the system of equations:
x — 2y = 11 Rewrite Equation 1 in slope-intercept form y = mx + b:
x — 2y — x = 14 — x Subtract x from both sides and simplify:
-2y = 14 – x
\(\frac{-2 y}{-2}\) = \(\frac{14-x}{-2}\) Divide by -2 and simplify:
y = \(\frac{1}{2}\)x – 7
Divide by -2 and simplify:
4y = 5 + 2x Rewrite Equation 2 in slope-intercept form y = mx + b:
\(\frac{4 y}{4}\) = \(\frac{2 x+5}{4}\) Divide both sides by 4 and simplify:
y = \(\frac{1}{2}\)x + \(\frac{5}{4}\)

Graph both equations using a graphing calculator:
The graphs of the linear equations are parallel therefore there is no point to lie on both graphs, so the system has no solution, it is inconsistent.
Inconsistent

State whether each system of linear equations is inconsistent, dependent, or has a unique solution. Justify each answer. Solve each system of linear equations if possible.

Question 4.
x + y = 3
8x + 8y = 32
Answer:
x + y = 3 Equation 1
8x + 8y = 32 Equation 2
We are given the system of equations:
x + y = 3 Rewrite Equation 1 in slope-intercept form y = mx + b:
x + y — x = 3 — x Subtract x from both sides and simplify:
y = -x + 3
8x + 8y = 32 Rewrite Equation 2 in slope-intercept form y = mx + b:
8x + 8y — 8x = 32 — 8x Subtract 8x from both sides and simplify:
\(\frac{8 y}{8}\) = \(\frac{-8 x+32}{8}\) Divide both sides by 8 and simplify:
y = -x + 4
The linear equations have the same slope and different y-intercept The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent

Question 5.
6x + 2y = 12
3x + y = 21
Answer:
6x + 2y = 12 Equation 1
3x + y = 21 Equation 2
We are given the system of equations:
6x + 2y = 12 Rewrite Equation 1 in slope-intercept form y = mx + b:
6x + 2y — 6x = 12 — 6x Subtract 6x from both sides and simplify:
2y = —6x + 12
\(\frac{2 y}{2}\) = \(\frac{-6 x+12}{2}\) Divide both sides by 2 and simplify:
y = —3x + 6
3x + y = 21 Rewrite Equation 2 in slope-intercept form y = mx + b
3x + y – 3x = 21 – 3x Subtract 3x from both sides and simplify
y = -3x + 21
The linear equations have the same slope and different y-Intercept. The system of linear equations is Inconsistent because the system of linear equations has no solution.
Inconsistent

Question 6.
3x – 6y = 12
x – 2y = 4
Answer:
3x — 6y = 12 Equation 1
x — 2y = 4 Equation 2
We are given the system of equations:
3x – 6y = 12 Rewrite Equation 1 in slope-intercept form y = mx + b:
3x — 6y — 3x = 12 — 3x Subtract 3x from both sides and simplify:
—6y = —3x + 12
\(\frac{-6 y}{-6}\) = \(\frac{-3 x+12}{-6}\) Divide both sides by -6 and simplify:
y = \(\frac{1}{2}\)x – 2
x – 2y = 4 Rewrite Equation 2 in slope-intercept form y = mx + b:
x — 2y — x = 4 — x Subtract x from both sides and simplify:
—2y = —x + 4
\(\frac{-2 y}{-2}\) = \(\frac{-x+4}{-2}\) Divide both sides by -2 and simplify:
y = \(\frac{1}{2}\)x – 2
Since Equation 1 and Equation 2 are equivalent, they have an infinite number of solutions.
Therefore system of linear equations is dependent
Dependent

Question 7.
-15x + 3y = 3
-5x + y = 21
Answer:
—15x + 3y = 3 Equation 1
—5x + y = 21 Equation 2
We are given the system of equations:
-15x + 3y = 3 Rewrite Equation 1 in slope-intercept form y = mx + b:
—15x + 3y — 15x = 3 + 15x Add 15x to both sides and simplify
3y = 15x + 3
\(\frac{3 y}{3}\) = \(\frac{15 x+3}{3}\) Divide both sides by 3 and simplify:
y = 5x + 1
-5x + y = 21 Rewrite Equation 2 in slope-intercept form y = mx + b:
—5x + y + 5x = 21 + 5x Add 5x to both sides and simplify:
y = 5x + 21
The linear equations have the same slope and different y-intercept. The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent

Question 8.
2x + y = 8
4x – 2y = 24
Answer:
2x + y = 8 Equat ion 1
4x – 2y = 24 Equation 2
We are given the system of equations:
2x + y = 8 Rewrite Equation 1 in slope-intercept form y = mx + b:
2x + y — 2x = 8 — 2x Subtract 2x from both sides and simplify:
y = —2x + 8
4x — 2y = 24 Rewrite Equation 2 in slope-intercept form y = mx + b:
4x — 2y — 4x = 24 — 4x Subtract 4x from both sides and simplify:
—2y = —4x + 24
\(\frac{-2 y}{-2}\) = \(\frac{-4 x+24}{-2}\) Divide both sides by -2 and simplify:
y = 2x — 12
The slope of the graph of Equation 1 is -2 and the y-intercept is 8.
The slope of the graph of Equation 2 is 2 and the y-intercept is —12.
—2x + 8 = 2x — 12 The graphs of the linear equations have different slopes, therefore the system of linear equations has an unique solution.
—2x + 8 + 2x = 2x – 12 + 2x
8 = 4x — 12
8 + 12 = 4x — 12 + 12
4x = 20
x = \(\frac{20}{4}\)
x = 5
y = -2(5) + 8
= —10+8
= -2
Unique solution (x = 5; y = -2)

Question 9.
8x + 7y = 9
40x + 35y = 45
Answer:
8x + 7y = 9 Equation 1
40x + 35y = 45 Equation 2
We are given the system of equations:
8x + 7y = 9 Rewrite Equation 1 in slope-intercept form y = mx + b:
8x + 7y – 8x = 9 — 8x Subtract 8x from both sides and simplify:
7y = -8x + 9
\(\frac{7 y}{7}\) = \(\frac{-8 x+9}{7}\)
y = –\(\frac{8}{7}\)x + \(\frac{9}{7}\) Divide both sides by 7 and simplify:
40x + 35y = 45 Rewrite Equation 2 in slope-intercept form y = mx + b:
40x + 35y — 40x = 45 — 40x Subtract 40 from both sides and simplify:
35y = —40x + 45
\(\frac{35 y}{35}\) = \(\frac{-40 x+45}{35}\) Divide both sides by 35 and simpbfy:
y = –\(\frac{8}{7}\)x + \(\frac{9}{7}\)x
Since Equation 1 and Equation 2 are equivalent, they have an infinite number of solutions. Therefore system of linear equations is dependent
Dependent

Question 10.
x + 3y = 9
2x + 6y = 5
Answer:
x + 3y = 9 Equation 1
2x + 6y = 5 Equation 2
We are given the system of equations:
x + 3y = 9 Rewrite Equation 1 in slope-intercept form y = mx + b:
x + 3y — x = 9 — x Subtract x from both sides and simplify:
\(\frac{3 y}{3}\) = \(\frac{-x+9}{3}\) Divide both sides by 3 and simplify:
y = \(-\frac{1}{3} x\) + 3
2x + 6y = 6
Rewrite Equation 2 in slope-intercept form y = mx + b:
2x + 6y — 2x = 5 — 2x Subtract 2x from both sides and simplify:
6y = —2x + 5
\(\frac{6 y}{6}\) = \(\frac{-2 x+5}{6}\) Divide both sides by 6 and simplify:
y = –\(\frac{1}{3} x\) + \(\frac{5}{6}\)
The linear equations have the same slope and different y-intercept. The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent

Question 11.
9x + 21y = 27
6x + 14y = 18
Answer:
9x + 21y = 27 Equation 1
6x + 14y = 18 Equation 2
We are given the system of equations:
9x + 21y = 27 Rewrite Equation 1 in slope-intercept form y = mx + b:
9x + 21y – 9x = 27 — 9x Subtract 9x from both sides and simplify:
21y = —9x + 27
\(\frac{21 y}{21}\) = \(\frac{-9 x+27}{21}\) Divide both sides by 21 and simplify:
y = \(-\frac{3}{7}\)x + \(\frac{9}{7}\)
6x + 14y = 18 Rewrite Equation 2 in slope-intercept form y = mx + b
6x + 14y — 6x = 18 — 6x Subtract 6x from both sides and simplify:
14y = —6x + 18
\(\frac{14 y}{14}\) = \(\frac{-6 x+18}{14}\) Divide both sides by 14 and simplify:
y = \(-\frac{3}{7}\) + \(\frac{9}{7}\)
Since Equation 1 and Equation 2 are equivalent, they have an infinite number of solutions.
Therefore system of linear equations is dependent
Dependent

Question 12.
5x + 4y = 6
15x + 12y = 18
Answer:
5x + 4y = 6 Equation 1
15x + 12y = 18 Equation 2
We are given the system of equations:
5x + 4y = 6 Rewrite Equation 1 in slope-intercept form y = mx + b:
5x + 4y — 5x = 6 — 5x Subtract 4x from both sides and simplify:
4y = -5x + 6
\(\frac{4 y}{4}\) = \(\frac{-5 x+6}{4}\) Divide both sides by 5 and simplify:
y = \(-\frac{5}{4}\)x + \(\frac{3}{2}\)
15x + 12y = 18 Rewrite Equation 2 in slope-intercept form y = mx + b:
15x + 12y — 15x = 18 — 15x Subtract 15x from both sides and simplify:
12y = -15x + 18
\(\frac{12 y}{12}\) = \(\frac{-15 x+18}{12}\) Divide both sides by 12 and simplify:
y = \(-\frac{5}{4}\)x + \(\frac{3}{2}\)
Since Equation 1 and Equation 2 are equivalent, they have an infinite number of solutions.
Therefore system of linear equations is dependent
Dependent

Solve. Show your work.

Question 13.
David says he bought 9 apples and 6 apricots for $8.50 yesterday and bought 3 apples and 2 apricots for $7.40 today.

a) Write a system of equations to find the cost of an apple and an apricot.
Answer:
9x + 6y = 8.50 Equation 1
3x + 2y = 7.40 Equation 2
a) Lets note:
x = the cost of an apple
y = the cost of an apricot
We can write the system of equations:

b) State with reasons whether the system of equations has a unique solution, is inconsistent, or is dependent.
Answer:
9x + 6y = 8.50 b) Rewrite Equation 1 in slope-intercept form y = mx + b
9x + 6y — 9x = 8.50 – 9x Subtract 9x from both sides and simplify:
6y = -9x + 8.50
\(\frac{6 y}{6}\) = \(\frac{-9 x+8.50}{6}\) Divide both sides by 6 and simplify:
y = \(-\frac{3}{2}\)x + \(\frac{4.25}{3}\)
3x + 2y = 7.40 Rewrite Equation 2 in slope-intercept form y = mx + b:
3x + 2y — 3x = 7.40 — 3x Subtract 3x from both sides and simplify:
2y = 7.40 — 3x
\(\frac{2 y}{2}\) = \(\frac{-3 x+7.40}{2}\) Divide both sides by 2 and simplify:
y = –\(\frac{3}{2}\) + 3.70
The linear equations have the same slope and different y-intercept. The system of linear equations is inconsistent because the system of linear equations has no solution.

c) What does this tell you about the cost of apples and apricots on those two days?
Answer:
The cost of at least one type of fruits is different in the two days.

a) 9x + 6y = 8.50
3x + 2y = 7.40
b) Inconsistent system
c) The unit price changed

Question 14.
Ms. Cohen gave a riddle: A string is 2 meters longer than a rod. Half of the rod is 1 meter shorter than half of the string. Is this true or false?
a) Write a system of equations to find the length of the string and the length of the rod.
Answer:
s = r + 2 Equation 1
\(\frac{1}{2}\)r = \(\frac{1}{2}\)s – 1 Equation 2
(a) Let’s note:
s=the length of a string
r=the length of a rod
We can write the system of equations:

b) State with reasons whether the system of equations has a unique solution, is inconsistent, or is dependent.
Answer:
s = r + 2 b) Equation 1 is in slope-intercept form:
2 • \(\frac{1}{2}\)r = 2 • (\(\frac{1}{2}\)s – 1) We write Equation 2 in slope-intercept form:
r = s – 2
r + 2 = s – 2 + 2
s = r + 2
The two equations are equivalent therefore the system of equations is dependent and it has an infinity of solutions.

c) Comment on Ms. Cohen’s riddle.
Answer:
The answer ‘false’ to the question aims the situation in which the system is inconsistent while the answer ‘true’ reflects the cases in which the system either has a solution, or is dependent

a)
s = r + 2
\(\frac{1}{2}\)r = \(\frac{1}{2}\)s – 1
b) dependent system
c)The riddle is true as the system nas an infinity of solutions.

Question 15.
Math Journal Mr. Braunstein uses a cell phone plan that charges 2¢ per minute for local calls and 3.5¢ per minute for long distance calls. He made x minutes of local calls and y minutes of long distance calls in June. In July, he made 2x minutes of local calls and 2y minutes of long distance calls. His bill was $12 in June and $24 in July. Can he find how many minutes of each type of call he made each month? Explain.
Answer:
0.02x + 0.035y = 12 Equation 1
0.02(2x) + 0.035(2y) = 24 Equation 2
We write the system of equations:
All the coefficients of the two equations and the constants on the right are proportional, therefore the system is dependent which means the system has infinitely many solutions. This means he cannot find how many minutes of each type of call he made each month.
No (dependent system of equations)

Brain @ Work

Question 1.
Lorraine has $110 and Jane has $600 in their bank accounts. Lorraine’s account balance increases by $30 every year and her account balance will be C dollars in x years. Jane’s account balance reduces by $40 every year and her account balance will also be C dollars in x years.

a) Write two equations of C in terms of x.
Answer:
C = 110 + 30x
a) We write an equation for Lorraine account:
C = 600 — 40x We write an equation for Janes account:

b) Solve this system of linear equations to find the amount in the girls’ account balances when they are equal.
Answer:
C = 110 + 30x Equation 1 b) We write the system of equations:
C = 600 — 40x Equation 2
110 + 30x = 600 — 40x We substitute Equation 1 in Equation 2 and determine x:
110 + 30x + 40x = 600 — 40x + 40x
110 + 70x = 600
110 + 70x — 110 = 600— 110
70x = 490
x = \(\frac{490}{70}\)
x = 7
C = 110 + 30(7) Substitute 7 for c in Equation 1 to determine C:
= 110+ 210
= 320
a) C = 110 + 30x ; C = 110 + 30x
b) $320

Question 2.
The diagram below shows a 1-centimeter block of metals A and B.

Five blocks of A and two blocks of B have a total mass of 44 grams. Three blocks of A and five blocks of B have a total mass of 34 grams. An alloy is made by melting and mixing two blocks of metal A and one block of metal B.

Answer:
Lets note:
a = the mass of an A bIock
b = the mass of a B block
5a + 2b = 44 Equation 1
3a + 5b = 34 Equation 2
We write the system of equations:
5(5a + 2b) 5(44) Multiply Equation 1 by 5:
25a + 10b = 220 Equation 3
2(3a + 5b) = 2(34) Multiply Equation 2 by 2:
6a + 10b = 68 Equation 4 from Equation 3:
(25a + 10b) – (6a + 10b) = 220 — 68 we subtract Equation 4 from Equation 3:
25a + 10b — 6a — 1ob = 152 Simplify:
19a = 152
\(\frac{19 a}{19}\) = \(\frac{152}{19}\) We divide both sides by 19 and simplify:
a = 8
5(8) + 2b = 44 Substitute 8 for a in Equation 1 to determine b:
40 + 2b = 44
40 + 2b — 40 = 44 — 40
2b = 4
\(\frac{2 b}{2}\) = \(\frac{4}{2}\)
b = 2

we determine the density of the alloy
= \(\frac{2(8)+2}{3}\) = \(\frac{18}{3}\)
= 6 grams/cm³

Question 3.
The table shows Joseph’s phone usage and the total charges over three months.

Joseph suspects that there are errors in the charges. Use systems of linear equations to check whether the charges are correct.
Answer:
Let’s note:
x = the cost of a minute of a local voice call
y = the cost of one minute of an cut-of-state voice call
\(\frac{60}{40}\) = \(\frac{30}{20}\) ≠ \(\frac{45}{34}\) We notice that then coefficients of the variables for January and March are proportional, but the constants are not:
60x + 30y = 45 Equation 1
40x + 20y = 34 Equation 2
This means that the system of equations corresponding to these months is inconsistent
Therefore there is no solution, which is not correct: the charges for at least one of the months January and March is wrong
Incorrect

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 5 Review Test to score better marks in the exam.

Math in Focus Grade 8 Course 3 A Chapter 5 Review Test Answer Key

Concepts and Skills

Solve each system of linear equations using the elimination method.

Question 1.
3x + 2y = 18
2x + 3y = 22
Answer:
3x + 2y = 18 Equation 1
2x + 3y = 22 Equation 2
We are given the system of equations:
2 ∙ (3x + 2y) = 2 ∙ 18 We can eliminate first either x, or y.
6x + 4y = 36 Equation 3 We usually choose to eliminate the variable which has smaller coefficients, in this case both have the same coefficients. We choose to eliminate x.
Multiply Equation 1 by 2:
3 ∙ (2x + 3y) = 3 ∙ 22 Multiply Equation 2 by 3:
6x + 9y = 66 Equation 4
(6a + 9y — (6x + 4y) = 66 — 36 We subtract Equation 3 from Equation 4:
6x + 9y — 6x — 4y = 30 Use the distributive property:
5y = 30 Simplify, 6x is eliminated:
\(\frac{5 y}{5}\) = \(\frac{30}{5}\) Divide by 5 and simplify:
y = 6
3x + 2(6) = 18 Substitute 6 for y in Equation 1:
3x + 12 = 18 Simplify:
Subtract 12 from both sides:
3x + 12 — 12 = 18 — 12
3x = 6 Simplify:
\(\frac{3 x}{3}\) = \(\frac{6}{3}\) Divide by 3:
x = 2
y = 6 The solution to the system of linear equations is
x = 2
y = 6

Question 2.
5x + y = 8
x + 3y = 10
Answer:
5x + y = 8 Equation 1 We are given the system of equations:
x + 3y = 10 Equation 2
3 ∙ (5x + y) = 3 ∙ 8 We can eliminate first either x, or y.
15x + 3y = 24 Equation 3 We usually choose to eliminate the variable which has smaller coefficients, in this case y. Multiply Equation 1 by 3:
(15x + 3y) – (x + 3y) = 24 – 10 We subtract Equation 2 from Equation 3:
15x + 3y – x – 3y = 14 Use the distributive property:
14x = 14 Simplify, 3y is eliminated:
\(\frac{14 x}{14}\) = \(\frac{14}{14}\)
Divide by 14 and simplify:
x = 1
5(1) + y = 8 Substitute 1 for x in Equation 1:
5 + y = 8 Simplify:
5 + y – 5 = 8 – 5 Subtract 5 from both sides:
y = 3 Simplify:
x = 1
The solution to the system of linear equations is
y = 3
x = 1; y = 3

Question 3.
\(\frac{1}{2}\)a + b = 7
a + 3b = 19
Answer:
\(\frac{1}{2}\)a + b = 7 Equation 1
a + 3b = 19 Equation 2
We are given the system of equations:
2 ∙ (\(\frac{1}{2}\)a + b) = 7 We can eliminate rirst either a, or b
a + 2b = 14 Equation 3 We usually choose to etiminate the variable which has smaller coefficients, in this case a.
Multiply Equation 1 by 2:
(a + 3b) — (a + 2b) = 19 — 14 We subtract Equation 3 from Equation 2:
a + 3b — a — 2b = 5 Use the distributive property
b = 5 Simplify, a is eliminated:
a + 3(5) = 19 Substitute 5 for b in Equation 2:
a + 15 = 19 Simplify:
a + 15 — 15 = 19 — 15 Subtract 15 from both sides:
a = 4 Simplify:
a = 4 The solution to the system of linear equations is
b = 5
a = 4 ; b = 5

Solve each system of linear equations using the substitution method.

Question 4.
a + 2b = 1
2a + b = 8
Answer:
a + 2b = 1 Equation 1 We are given the system of equations:
2a + b = 8 Equation 2
2a + b = 8 Use Equation 2 to express b in terms of a:
2a + b — 2a = 8 — 2a Subtract 2a from both sides:
b = 8 — 2a Equation 3 Simplify:
a + 2(8 — 2a) = 1 Substitute Equation 3 into Equation 1:
a + 16 — 4a = 1 Use the distributive property:
—3a + 16 = 1 Simplify:
—3a + 16 — 16 = 1 — 16 Subtract 16 from both sides:
—3a = —15 Simplify:
\(\frac{-3 a}{-3}\) = \(\frac{-15}{-3}\) Divide by -3:
a = 5 Simplify:
b = 8 — 2(5) Substitute 5 for a in Equation 3:
= 8 — 10
= -2
a = 5 The solution of the system ¡S:
b = -2
a = 5; b = -2

Question 5.
2x + 11y = 15
x – y = 1
Answer:
2x + 11y = 15 Equation 1 We are given the system of equations:
x — y = 1 Equation 2
x — y = 1 Use Equation 2 to express x in terms of y:
x – y + y = 1 + y Add y to both sides:
x = y + 1 Equation 3 Simplify:
2(y + 1) + 11y = 15 Substitute Equation 3 into Equation 1:
2y + 2 + 11y = 15 Use the distributive property:
13y + 2 = 15 Simplify:
13y + 2 — 2 = 15 — 2 Subtract 2 from both sides:
13y = 13 Simplify:
\(\frac{13 y}{13}\) = \(\frac{13}{13}\) Divide by 13:
y = 1 Simplify:
x = 1 + 1
= 2 Substitute 1 for y in Equation 3:
x = 2 The solution of the system is:
y = 1
x = 2
y = 1

Question 6.
\(\frac{1}{2}\)x + \(\frac{1}{2}\)y = 7
3x – y = 22
Answer:
We are given the system of equations:
\(\frac{1}{2}\)x + \(\frac{1}{2}\)y = 7 Equation 1
3x — y = 22 Equation 2
3x — y = 22 use Equation 2 to express y is terms of x:
3x — y — 3x = 22 — 3x Subtract 3x from both sides:
—y = 22 — 3x Simplify:
y = 3x — 22 Equation 3
\(\frac{1}{2}\)x + \(\frac{1}{2}\)(3x – 22) Substitute Equation 3 into Equation 1:
2 • \(\frac{1}{2}\)x + 2 • \(\frac{1}{2}\)(3x —22) = 2 • 7 Multiply both sides by 2:
x + 3x — 22 = 14 Simplify:
4x — 22 = 14
4x — 22 + 22 = 14 + 22 Add 22 to both sides:
4x = 36 Simplify:
\(\frac{4 x}{4}\) = \(\frac{36}{4}\) Divide by 4
x = 9 Simplify:
y = 3(9) — 22 Substitute 9 for x in Equation 3:
= 27 — 22
= 5
x = 9 The solution of the system is:
y = 5
x = 9
y = 5

Solve each system of linear equations using the graphical method. Use 1 grid square to represent 1 unit on both axes for the interval -3 to 8.

Question 7.
2x + 3y = 24
2x + y = 12
Answer:
2x + 3y = 24 Equation 1
2x + y = 12 Equation 2
We are given the system of equations:
2x + 3y = 24 We rewrite Equation 1 in slope-intercept form:
2x + 3y – 2x = 24 — 2x
3y = —2x + 24
\(\frac{3 y}{3}\) = \(\frac{-2 x+24}{3}\)
y = –\(\frac{2}{3}\)x + 8
2x + y = 12 we rewrite Equation 2 in slope-intercept rorm:
2x + y – 2x = 12 — 2x
y = —2x + 12

We graph the two equations: the first has slope —\(\frac{2}{3}\) and y-intercept 8, while the second has slope -2 and y-intercept 12:
x = 3 The point of intersection is (3, 6). Therefore the solution of the system of equations is
y = 6
x = 3; y = 6

Question 8.
2x + 5y = 1
3x – y = – 7
Answer:
2x + 5y = 1 Equation 1
3x – y = —7 Equatiou 2
We are given the system of equations:
2x + 5y = 1 We rewrite Equation 1 in slope-intercept form:
2x + 5y — 2x = 1 — 2x
5y= —2x + 1
\(\frac{5 y}{5}\) = \(\frac{-2 x+1}{5}\)
y = –\(\frac{2}{5}\)x + \(\frac{1}{5}\)
3x — y = —7 We rewrite Equation 2 in slope-intercept form:
3x — y — 3x = —7 — 3x
—y = —3x — 7
y = 3x + 7

We graph the two equations: the first has slope —\(\frac{2}{5}\) and y-intercept \(\frac{1}{5}\), while the second has slope 3 and y-intercept 7:
x = -2 The point of intersection is (—2, 1). Therefore the solution of the system of equations is:
y = 1
x = —2; y = 1

Question 9.
x + 0.5y = 6
3x – y = 13
Answer:
x + 0.5y = 6 Equation 1
3x — y = 13 Equation 2
We are given the system of equations:
x + 0.5y = 6 We rewrite Equation 1 in stope-intercept form:
x + 0.5y — x = 6 — x
0.5y = —x + 6
\(\frac{0.5 y}{0.5}\) = \(\frac{-x+6}{0.5}\)
y = -2x + 12
3x — y = 13 We rewrite Equation 2 in slope-intercept form:
3x — y — 3x = 13 — 3x
—y = —3x + 13
y = 3x — 13

We graph the two equations: the first has slope -2 and y-intercept 12. while the second has slope 3 and y-intercept -13:
x = 5 The point of intersection is (5, 2). Therefore the solution of the system of equations is
y = 2
x = 5; y = 2

Solve each system of linear equations. Explain your choice of method.

Question 10.
x = 4y – 1
2x – 6y = – 1
Answer:
x = 4y — 1 Equation 1 We are given the system of equations:
2x — 6y = —1 Equation 2
5x + y = 15 As there is a variable with coefficient 1 (which is x in Equation 1), we can use the substitution method.
x = 4y — 1 Equation 1 expresses x is terms of y:
2(4y – 1) – 6y = —1 Substitute Equation 1 into Equation 2:
8y — 2 – 6y = —1 Use the distributive property
2y — 2 = —1 Simplify:
2y — 2 + 2 = —1 + 2 Add 2 to both sides:
2y = 1 Simplify:
\(\frac{2 y}{2}\) = \(\frac{1}{2}\) Divide by 2:
y = \(\frac{1}{2}\) simplify
x = 4(\(\frac{1}{2}\)) – 1 Substitute \(\frac{1}{2}\) for y in Equation 1:
= 2 – 1
= 1
x = 1 The solution of the system is
y = \(\frac{1}{2}\)
x = 1
y = \(\frac{1}{2}\)

Question 11.
3x – 14y = -49
5x + 2y = 45
Answer:
3x — 14y = -49 Equation 1
5x + 2y = 45 Equation 2
We are given the system of equations:
7 • (5x + 2y) = 7 . 45 The substitution method would lead to fractions as none of the variables has coefficient 1.
35x + 14y = 315 Equation 3
We use the elimination method.
We can eliminate first either z, or g.
We choose to eliminate the variable y because -14 is multiple of 2.
Multiply Equation 2 by 7:
(3x — 14y) + (35x + 14y) = —49 + 315 We add Equation 3 to Equation 1:
3x — 14y + 35x + 14y = 266 Simplify, 14y is eliminated:
38x = 266
\(\frac{38 x}{38}\) = \(\frac{266}{38}\) Divide by 38 and simplify
x = 7
5(7) + 2y = 45 Substitute 7 for x in Equation 2:
35 + 2y = 45 Simplify:
35 + 2y — 35 = 45 — 35 Subtract 35 from both sides:
2y = 10 Simplify:
\(\frac{2 y}{2}\) = \(\frac{10}{2}\) Divide by 2
y = 5 simplify
x = 7 The solution to the system of linear equations is
y = 5
x = 7
y = 5

Question 12.
x – \(\frac{1}{3}\)y = 6
2x + y = 2
Answer:
x – \(\frac{1}{3}\)y = 6 Equation 1
2x + y = 2 Equation 2
We are given the system of equations:
x – \(\frac{1}{3}\)y = 6 We can use substitution or graphical method as we have at least one variable with coefficient 1. We choose the graphical method
x – \(\frac{1}{3}\)y – x = 6 – x
–\(\frac{1}{3}\)y = -x + 6 We rewrite Equation 1 in slope-intercept form:
—3(\(\frac{1}{3}\)y) = —3(—x + 6)
y = 3x— 18
2x + y = 2 We rewrite Equation 2 in slope-intercept form:
2x + y — 2x = 2— 2x
y = —2x + 2

We graph the two equations: the first has slope 3 and y-intercept -18, while the second has slope -2 and y-intercept 2:
x = 5 The point of intersection is (5, 2). Therefore the solution of the system of equations is
y = 2
x = 5
y = 2

Identify whether each system of equations is inconsistent, dependent, or has a unique solution. Justify your answer. Solve the system of linear equations if it has a unique solution.

Question 13.
3x + 2y = 8
6x + 4y = 16
Answer:
3x + 2y = 8 Equation 1
6x + 4y = 16 Equation 2
we are given the system of equations
3x + 2y = 8 Rewrite Equation 1 in slope-intercept form y = mx + b
3x + 2y – 3x = 8 – 3x Subtract 3x from both sides and simplify
2y = -3x + 8
\(\frac{2 y}{2}\) = \(\frac{-3 x+8}{2}\) Divide both sides by 2 and simplify
y = \(-\frac{3}{2} x\) + 4
6x + 4y = 16 Rewrite Equation 2 in slope-intercept form y = mx + b:
6x + 4y — 6x = 16 — 6x Subtract 6x from both sides and simplify:
4y = —6x + 16
\(\frac{4 y}{4}\) = \(\frac{-6 x+16}{4}\) Divide both sides by 4 and simplify:
y = \(-\frac{3}{2} x\) + 4
Since Equation 1 and Equation 2 are equivalent, they have an infinite number of solutions.
Therefore system of linear equations is dependent
Dependent

Question 14.
\(\frac{x}{3}\) + y = 8
x + 3y = 10
Answer:
\(\frac{1}{3} x\) + y = 8 Equation 1
x + 3y = 10 Equation 2
We are given the system of equations:
\(\frac{1}{3} x\) + y = 8
Rewrite Equation 1 in slope-intercept form y = mx + b:
\(\frac{1}{3} x\) + y – \(\frac{1}{3} x\) = 8 – \(\frac{1}{3} x\) Subtract \(\frac{1}{3} x\) from both sides and simplify:
y = –\(\frac{1}{3} x\) + 8
x + 3y = 10 Rewrite Equation 2 in slope-intercept form y = mx + b
x + 3y — x = 10 — x Subtract x from both sides and simplify:
\(\frac{3 y}{3}\) = \(\frac{-x+10}{3}\) Divide both sides by 3 and simplify:
y = \(-\frac{1}{3} x\) + \(\frac{10}{3}\)
The linear equations have the same slope and different y-intercept. The system of linear equations is inconsistent because the system of Linear equations has no solution.
Inconsistent

Question 15.
\(\frac{1}{2}\)x + y = 7
x + 2y = 14
Answer:
\(\frac{1}{2}\)x + y = 7 Equation 1
x + 2y = 14 Equation 2
We are given the system of equations:
\(\frac{1}{2}\)x + y = 7 Rewrite Equation 1 in slope-intercept form y = mx + b:
\(\frac{1}{2}\)x + y — \(\frac{1}{2}\)x = 7 — \(\frac{1}{2}\)x Subtract \(\frac{1}{2}\)x from both sides and simplify:
y = –\(\frac{1}{2}\)x + 7
x + 2y = 14 Rewrite Equation 2 in slope-intercept form y = mx + b:
x + 2y — x = 14 — x Subtract x from both sides and simplify:
\(\frac{2 y}{2}\) = \(\frac{-x+14}{2}\) Divide both sides by 2 and simplify:
Since Equation 1 and Equation 2 are equivalent they have an infinite number of solutions.
Therefore system of linear equations is dependent.
Dependent

Question 16.
2x – \(\frac{1}{2}\)y = 10
y = 4x + 11
Answer:
2x — \(\frac{1}{2}\)y = 1o Equation 1
y = 4x + 11 Equation 2
We are given the system of equations:
2x – \(\frac{1}{2}\)y = 10 Rewrite Equation 1 in slope-intercept form y = mx + b:
2x – \(\frac{1}{2}\)y – 2x = 10 – 2x Subtract 2x from both sides and simplify:
–\(\frac{1}{2}\)y = -2x + 10
-2 ∙ (-\(\frac{1}{2}\)y) = -2(-2x + 10) Multiply both sides by -2 and simplify
y = 4x — 20
y = 4x + 11 Equation 2 is written in slope-intercept form y = mx + b
The linear equations have the same slope and different y-intercept The system of linear equations is inconsistent because the system of linear equations has no solution.
Inconsistent

Question 17.
2x – 5y = -21
4x + 3y = 23
Answer:
2x — 5y = —21 Equation 1
4x + 3y = 23 Equation 2
We are given the system of equations:
2(2x — 5y) = 2(—21) We use the elimination method.
4x — 10y = —42 Equation 3 Multiply Equation 1 by 2:
(4x + 3y) — (4x — 10y) = 23 — (—42) We subtract Equation 3 from Equation 2 and simplify:
4x + 3y — 4x + 10y = 65
13y = 65
\(\frac{13 y}{13}\) = \(\frac{65}{13}\) Divide by 13 and simplify:
y = 5
4x + 3(5) = 23 Substitute 5 for y in Equation 2:
4x + 15 = 23
4x + 15 — 15 = 23 — 15 Subtract 15 from both sides and simplify:
4x = 8
The system of linear equations has an unique solution:
\(\frac{4 x}{4}\) = \(\frac{8}{4}\) Divide by 4 and simplify:
x = 2
x = 2 The system of Linear equations has an unique solution:
y = 5
Unique solution (x = 2, y = 5)

Question 18.
6y – 12x = 60
4y – 40 = 8x
Answer:
6y — 12x = 60 Equation 1
4y — 40 = 8x Equation 2
We are given the system of equations:
6y — 12x = 60 Rewrite Equation 1 in slope-intercept form y = mx + b:
6y — 12x + 12x = 60 + 12x Add 12x to both sides and simplify
6y = 12x + 60
\(\frac{6 y}{6}\) = \(\frac{12 x+60}{6}\) Divide both sides by 6 and simplify:
y = 2x + 10
4y – 40 = 8x Rewrite Equation 2 in slope-intercept form y = mx + b
4y — 40 + 40 = 8x + 40 Add 40 to both sides and simplify:
4y = 8x + 40
\(\frac{4 y}{4}\) = \(\frac{8 x+40}{4}\) Divide both sides by 4 and simplify:
y = 2x + 10
Since Equation 1 and Equation 2 are equivalent, they have an infinite number of solutions. Therefore system of linear equations is dependent
Dependent

Problem Solving

Solve. Show your work.

Question 19.
Andy and Ben both worked a total of 88 hours one week. Ben worked 8 hours more than Andy. Find the number of hours each man had worked.
Answer:
Lets note:
a = the number of hours worked by Andy
b = the number of hours worked by Ben
a + b = 88 Equation 1 We write the system of equations:
b = a + 8 Equation 2
We use the substitution method.
b is expressed in terms of a in Equation 2:
a + (a + 8) = 88 Substitute Equation 2 into Equation 1:
a + a + 8 = 88 Simplify:
2a +8 = 88
2a + 8 – 8 = 88 — 8 Subtract 8 from both sides:
2a = 80 Simplify:
\(\frac{2 a}{2}\) = \(\frac{80}{2}\) Divide both sides by 2:
a = 40 simplify
b = 40 + 8 Substitute 40 for a in Equation 2:
= 48
So Andy worked 40 hours and Ben worked 48 hours
Andy: 40 hours
Ben: 48 hours

Question 20.
In three years’ time, Mr. Sullivan will be 3 times as old as his daughter. Six years ago, he was 6 times as old as she was. How old are they now?
Answer:
s + 3 = 3(d + 3) Equation 1
s — 6 = 6(d — 6) Equation 2
Lets note:
s = Mr Sullivans age now
d = the daughters age now
We can write the system of equations:
s — 6 = 6d — 36 We use the substitution method.
s — 6 + 6 = 6d — 36 + 6 Rewrite Equation 2 to express s in terms of d:
s = 6d — 30 Equation 3
(6d — 30) + 3 = 3(d + 3) Substitute Equation 3 in Equation 1 and simplify:
6d — 30 + 3 = 3d + 9
6d — 27 = 3d + 9
6d — 27 – 3d = 3d + 9 – 3d We subtract 3d from both sides:
3d — 27 = 9
3d — 27 + 27 = 9 + 27 Add 27 to both sides:
3d = 36
\(\frac{3 d}{3}\) = \(\frac{36}{3}\) Divide by 3 and simplify:
d = 12
s = 6(12) — 30 Substitute 12 for d in Equation 3:
= 72 – 30
= 42
d = 12 The solution to the system of linear equations is:
s = 42
Mr Sullivan’s age is 42 years, while his daughter’s is 12 years now
Mr Sullivan: 42 years
The daughter: 12 years

Question 21.
Samantha has a riddle for her sister: Find a pair of integers x and y that satisfy 7x + 3y = 64 and one of the integers is 3 times the other.
Answer:
7x + 3y = 64 Equation 1
x = 3y Equation 2
We write the systems of equations:
7x + 3y = 64 Equation 1
y = 3x Equation 2
x = 3y Equation 1 We solve the first system using substitution.
7(3y) + 3y = 64 Substitute Equation 2 into Equation 1:
21g + 3y = 64
24y = 64
\(\frac{24 y}{24}\) = \(\frac{64}{24}\) We determine y:
y = \(\frac{8}{3}\)
As y is not integer, this is not a solution.
y = 3x Equation 2 We solve the second system using substitution.
7x + 3(3x) = 64 Substitute Equation 2 into Equation 1:
7x + 9x = 64
16x = 64
\(\frac{16 x}{16}\) = \(\frac{64}{24}\) We determine x:
x = 4
y = 3(4) Substitute 4 for x in Equation 2:
= 12
x = 4 The two integers are 4 and 12.
y = 12
x = 4
y = 12

Question 22.
The shape ABC in the quilt block below is an isosceles triangle. In triangle ABC, AB = AC. The perimeter of triangle ABC is 27.3 inches. Find the values of x and y. Then find the length of each side of the triangle in inches.

Answer:
x + 5 = 6x — 2y Equation 1
2(x + 5) + y + 6.3 = 27.3 Equation 2 We can write the system of equations:

x + 5 – x = 6x — 2y — x Equation 1
2x + 10 + y + 6.3 = 27.3 Equation 2
we bring me system to the standard form:

5x — 2y = 5 Equation 1
2x + y + 16.3 = 27.3 Equation 2

5x — 2y = 5 Equation 1
2x + y + 16.3 — 16.3 = 27.3 — 16.3 Equation 2

5x — 2y = 5 Equation 1
2x + y = 11 Equation 2

2x + y = 11 We use the substitution method.
2x + y — 2x = 11 — 2x We express y in terms of x from Equation 2:
y = —2x + 11 Equation 3
5x — 2(—2x + 11) = 5 Substitute Equation 3 into Equation 1:
5x + 4x — 22 = 5
9x — 22 = 5
9x — 22 + 22 = 5 + 22 We determines x:
9x = 27
\(\frac{9 x}{9}\) = \(\frac{27}{9}\)
x = 3
y = —2(3) + 11 Substitute 3 for x in Equation 3:
= -6 + 11
= 5
x = 3 The system’s solution is:
y = 4
AB = AC = x + 5 = 3 + 5 = 8 We determine AB and AC:
BC = y + 6.3 = 5 + 6.3 = 11.3 We determine BC:
x = 3; y = 5
AB = 8 inches; AC = 8 inches BC = 11.3 inches

Question 23.
A bus company requires 4 buses and 8 vans to take 240 school children to the library. It requires 2 buses and 9 vans to take 170 children to the museum. Calculate the number of children a bus can carry and the number of children a van can carry.
Answer:
Let’s note:
b = the number of children in a bus
v = the number of children in a van
4b + 8v = 240 Equation 1
26 + 9v = 170 Equation 2
We write the system of equations:
2(2b + 9v) = 2(170) We use the elimination method.
4b + 18v = 340 Equation 3 Multiply Equation 2 by 2:
(4b + 18v) — (4b + 8v) = 340 — 240 Subtract Equation 1 from Equation 3:
4b + 18v — 4b — 8v = 100 Simplify:
10v = 100
\(\frac{10 v}{10}\) = \(\frac{100}{10}\) Divide by 10 and simplify:
v = 10
2b + 9(10) = 170 Substitute 10 for v in Equation 2:
2b + 90 = 170
2b + 90 — 90 = 170 — 90 Subtract 90 from both sides:
2b = 80
\(\frac{2 b}{2}\) = \(\frac{80}{2}\) Divide both sides by 2:
b = 40 Simplify:
A bus can carry 40 children, while a van can carry 10 children.
Bus: 40 children
Van : 10 children

Question 24.
At noon, Balloon M is 60 meters above ground, and Balloon N is 50 meters above ground. Balloon M is rising at the rate of 10 meters per second, while Balloon N is rising at the rate of 15 meters per second.

a) Write a system of two linear equations in which each equation gives the height, h meters, of a balloon t seconds after noon. Then solve the system using a graphing calculator.
Answer:
h = 60 + 10t Equation 1 a) We write a system of equations giving the height of each balloon:
h = 50 + 15t Equation 2

We use a graphing calculator to solve the system:
t = 2 The solution is:
h = 80

b) How many seconds after noon will the two balloons be at the same height?
How do you know?
Answer:
t = 2 seconds b) The two balloons will be at the same height when h = 80. We determined the time when this happens, which is the t-coordinate of the solution above:
a) t = 2, h = 80
b) 2 seconds

Question 25.
The water levels in two identical tanks rise at a rate of 4 inches per second. The water level, h inches, in Tank A is 3 inches at t = 0. The water level in Tank B is 16 inches at t = 3 seconds.

a) Write a system of equations for the water level h in the two tanks in terms of t.
Answer:
h = 3 + 4t Equation 1 a) we write system of equations for the water level in the two tanks
h = 16 + 4(t – 3) Equation 2

b) Graph the two equations on the same coordinate plane. Use 1 grid square on both axes to represent 1 unit for the interval 0 to 10.
Answer:
h = 4t + 3 Equation 1 b) We write the equations in slope-Intercept form
h = 16 + 4t – 12 Equation 2
h = 4t + 3 Equation 1
h = 4t + 4 Equation 2

We graph the two equations the first has slope 4 and y-Intercept 3, while the second has slope 4 and y-intercept 4.

c) When will the two tanks have the same water level? How do you know?
Answer:
The two tanks will never have the same level because the system of equations in part (a) is inconsistent because the slope is the same, but the y-intercept is not

a)
h = 3 + 4t
h = 16 + 4(t — 3)
b) See graph
c) Never

Question 26.
Natalie has x bags of onions and y bags of potatoes. There are a total of 8 bags. Each bag weighs 2 pounds. The total weight of the bags is 16 pounds. She wants to find the value of x and y.

a) Write a system of two linear equations.
Answer:
x + y = 8 Equation 1
2x + 2y = 16 Equation 2
a) We write a system of equations:

b) State with reasons whether the system of equations has a unique solution, is inconsistent, or is dependent.
Answer:
\(\frac{1}{2}\) = \(\frac{1}{2}\) = \(\frac{8}{16}\) b) We notice that the coefficients of the variables and the constants are proportional:
This means that the system is dependent

c) Can Natalie find the value of x and y? Why?
Answer:
She cannot find the value of x and y because there are an infinity of solutions.

a)
x + y = 8
2x + 2y = 16
b) Dependent system
c) No

This handy Math in Focus Grade 8 Workbook Answer Key Chapter 9 Congruence and Similarity detailed solutions for the textbook questions.

Math in Focus Grade 8 Course 3 B Chapter 9 Answer Key Congruence and Similarity

Math in Focus Grade 8 Chapter 9 Quick Check Answer Key

Complete.

Question 1.

Answer:

Explanation:
1. Scale factor: 2
2 × 8ft = 16 ft
2. Original length = 5
Scaled length = 5
Scale factor = 5/5 = 1
3. Original length = 8 m
Scaled length = 4 m
Scale factor = scale/actual = 4/8 = 1/2
4. Scale factor = 1/4
Original length = 4 inches
We know that
scale factor = scale/actual
1/4 = scale length/4
scaled length = 4/4
scaled length = 1 in.

Solve.

Question 2.
Shawn built a model of a ship whose length was 4,500 inches. His model was 15 inches long. Find the scale factor.
Answer:
Let the scale factor be x
Shawn built a model of a ship whose length was 4,500 inches.
His model was 15 inches long.
x × 15 = 4500
x = 4500/15
x = 300 inches

Question 3.
A line segment is 4 centimeters long. When projected on a screen, the line segment is 20 centimeters long. Find the scale factor.
Answer:
Let the scale factor be x
scale factor = scale/actual
Actual length = 4 cm
scaled length = 20 cm
scale factor = 20 cm/4 cm
scale factor = 5 cm
Thus the scale factor is 5 cm.

Question 4.
A model plane is built with a scale factor of \(\frac{1}{180}\). The actual length of the plane is 210 feet (2,520 inches). Find the length of the model.
Answer:
Given,
A model plane is built with a scale factor of \(\frac{1}{180}\).
The actual length of the plane is 210 feet (2,520 inches).
Scale/Actual = 1/180
1/180 = l/210 feet
210/180 = length
Length = 210/180
Length = 21/18
Length = 7/6
Length = 1.16 feet

Question 5.
The scale of a map is 2 inches : 3 kilometers. The length of a road on the map is 3 inches. Find the actual length of the road.
Answer:
Given,
The scale of a map is 2 inches : 3 kilometers.
The length of a road on the map is 3 inches
Let the actual length of the road be x.
2 in./ 3 km = 3 in / x km
x = (3 × 3)/2
x = 9/2 = 4.5 km
Thus the actual length of the road is 4.5 kilometers.

Question 6.
The diagram shows a plot of land ABCD drawn on a map.

a) On the map, \(\overline{C D}\) is 1\(\frac{3}{4}\) inches. Find the scale of the map.
Answer:

b) Find the area of ABCD on the map.
Answer:

The measures of two interior angles are given for each triangle. Find the measure of the third interior angle.

Question 7.
△ABC: 20°, 80°
Answer:
Given
△ABC: 20°, 80°
The sum of interior angles of the triangle = 180°
∠a + ∠b + ∠c = 180°
20°+ 80° + ∠c = 180°
100° + ∠c = 180°
∠c = 180° – 100°
∠c = 80°
Thus the measure of the third interior angle is 80°

Question 8.
△KLM: 37°, 76°
Answer:
Given,
△KLM: 37°, 76°
The sum of interior angles of the triangle = 180°
∠k + ∠l + ∠m = 180°
37°+ 76° + ∠m = 180°
113° + ∠m = 180°
∠m = 180° – 113°
∠m = 67°
Thus the measure of the third interior angle is 67°

Question 9.
△PQR: 15°, 103°
Answer:
Given,
△PQR: 15°, 103°
The sum of interior angles of the triangle = 180°
∠p + ∠q + ∠r = 180°
15°+ 103° + ∠r = 180°
∠r = 180° – 118°
∠r = 62°

Find the unknown angle measure.

Question 10.

Answer:

Let the unknown angle be y
The sum of three angles = 180°
20° + 27° + y = 180°
47° + y = 180°
y = 180° – 47°
y = 133°
x° + y° + 27° = 180°
x° + 133°  + 27° = 180°
x° = 180° – 133° – 27°
x° = 20°
Thus the unknown angle is 20°

Question 11.

Answer:
y° + y° = 120°
2y° = 120°
y = 120°/2
y =60°

Solve for each variable.

Question 12.

Answer:
a° + 2b° = 180
b° = 40° (alternate angles)
2b° = 80°
a° + 2b° = 180
a° + 80° = 180°
a° = 180° – 80°
a° = 100°

Question 13.

Answer:
c° + 28° = 180°
c° = 180° – 28°
c° = 152°

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 8 Review Test to score better marks in the exam.

Math in Focus Grade 8 Course 3 B Chapter 8 Review Test Answer Key

Concepts and Skills

State whether a rotation, translation, or a combination of both is involved in each activity.

Question 1.
A turning blade of a windmill
Answer:
A turning blade of a windmill is rotation. Because the blade of a windmill rotates in a horizontal axis.

Question 2.
Pressing the keys on a computer keyboard
Answer:
Pressing the keys on a computer keyboard is a translation. Because the keyboard translates the number into binary data.

Question 3.
A printer head moving left and right
Answer:
A printer head moving left and right is a translation. Because it is moving from left to right and right to left it means translating from left to right and right to left.

Question 4.
Wheels on a moving bicycle
Answer:
Wheels on a moving bicycle is a rotation. Because the bicycle wheel is rotated in clockwise and anticlockwise.

Describe the translations.

Question 5.
Climbing up 8 steps of a staircase (assume horizontal and vertical distances of each step are the same)
Answer:
The translation is a type of transformation that moves each point in a figure with the same distance in the same direction. Climbing up 8 steps of a staircase is a translation.

Question 6.
Taking an elevator from level 2 to level 5 of a building
Answer: Taking an elevator from level 2 to level 5 of a building is translation. Because the elevator is a device that moves up and down.

Write an equation of the line(s) of reflection.

Question 7.

Answer:
Reflection in x axis is (x,y) = (x,-y)
Reflection in y axis is (x,y) = (-x,y)
In the above figure consider the left image as ABCD and right image as PQRS
The reflection in y axis is
P(1,1) reflection is A(-1,1)
Q(3,1) reflection is B(-3,1)
R(4,-1) reflection is C(-4,-1)
S(2,-1) reflection is D(-2,-1)

Question 8.

Answer:
Reflection in x axis is (x,y) = (x,-y)
Reflection in y axis is (x,y) = (-x,y)
Consider the image below the x axis is OAB and above the x axis is OPQ
O(0,0) reflection is O(0,0)
A(0,-1) reflection in x axis is P(0,-(-1)) = P(0,1)
B(-1,0) reflection in y axis is Q(-(-1),0) = B(1,0)

Question 9.

Answer:
Reflection in x axis is (x,y) = (x,-y)
Reflection in y axis is (x,y) = (-x,y)
Consider the image below the x axis is ABC and above the x axis is PQR
A(1,1) reflection to x axis is P(1,-1)
B(0,3) reflection to x axis is Q(0,-3)
C(-2,1) reflection to x axis is R(-2,-1)

Question 10.

Answer:

Each diagram shows a figure and its line of reflection. On a copy of the graph, draw the image.

Question 11.

Answer:
Reflection in x axis is (x,y) = (x,-y)
Reflection in y axis is (x,y) = (-x,y)
Consider the image below the x axis is ABCD.
A(-3,-3) reflection to the x axis is (-3,3)
B(0,-3) reflection to the x axis is (0,3)
C(-1,-4) reflection to the x axis is (-1,4)
D(-2,-4) reflection to the x axis is (-2,4)

Question 12.

Answer:

Solve on graph paper. Show your work.

Question 13.
\(\overline{\mathrm{AB}}\) is dilated with center at the origin and scale factor 2. Draw \(\overline{\mathrm{AB}}\) and its image \(\overline{A^{\prime} B^{\prime}}\). Use 1 grid square on the horizontal axis to represent 1 unit for x interval from -4 to 10, and 1 grid square on the vertical axis to represent 1 unit for the y interval from -2 to 4.
a) A (2, 1) and B (5, 2)
Answer:

b) A (1, -1) and B (-2, 2)
Answer:

Question 14.
The table shows the coordinates for ∆XYZ and its images using two transformation. Use 1 grid square on both axes to represent 1 unit for the interval from -3 to 9.

a) ∆XYZ is mapped onto ∆X’Y’Z’ and ∆X”Y”Z” by a dilation. Draw each triangle and its image on the same coordinate plane. Then mark and label D as the center of dilation.
Answer:

In the drawn graph ABC = XYZ, DEF = X’Y’Z’, GHI = X”Y”Z”

b) ∆XYZ is mapped onto ∆ABC by a rotation 90° counterclockwise about the origin. Draw ∆ABC on the coordinate plane.
Answer:

In the drawn map XYZ = ABC and ABC = DEF
90⁰ counterclockwise rotation = (-y,x)
X(1,3) = X(-3,1)
Y(1,1) = Y(-1,1)
Z(2,1) = Z(-1,2)

c) ∆XYZ is mapped onto ∆PQR by a translation 3 units to the left and 4 units up. Draw ∆PQR on the coordinate plane.
Answer:

In the drawn graph XYZ = ABC and PQR = DEF.
In the graph ∆DEF is the translation.

d) Compare the transformations that mapped ∆XYZ onto ∆ABC and ∆PQR in terms of preservation of the shape and size of ∆XYZ.
Answer:
The transformations ∆XYZ onto ∆ABC is rotation it means the figure turns in the clockwise or counter clockwise but it doesn’t change the shape and size.∆PQR onto ∆XYZ is a translation it means moving the figure on the coordinate plane without changing the shape and size.

Problem Solving

Solve. Show your work.

Question 15.
Jane had lunch with her friends from 1 P.M. to 2 P.M. Describe the geometric transformation of the hour hand of the clock.
Answer:

Question 16.
A scientist used a sensor to track the movement of a mouse. It moved from the point (-2, 3) to the point (8, 6). State the new coordinates of any point (x, y) under this translation.
Answer:
Given that,
The mouse moved from the point (-2,3) to the point (8,6)
(x1,y1) = (-2,3)
(x2,y2) = (8,6)
New coordinates are (x,y)
x coordinate = x2 – x1 = 8 – (-2) = 8 + 2 = 10.
y coordinate = y2 – y1 = (6-3) = 3.
Therefore, New coordinates are (x+10, y+3).

Question 17.
Mrs. Morales outlined a clover with four identical leaflets, as shown, on a coordinate plane. The center of the clover is at (1, 0).

a) How many lines of symmetry does the clover have? Sketch them on a copy of the clover leaf.
Answer:

b) Find an equation of each line of reflection.
Answer:
The equation of each line of reflection is x = 0, y = 0, y = -x and y = x
Therefore there are four symmetry.

Question 18.
A circular mold in a Petri dish had a diameter of \(\frac{1}{2}\) inch. The diameter grew by 32% in a day.

a) What is the scale factor of dilation?
Answer:
Given that the circular in a Petri dish has a diameter of ½ inch.
The diameter grew in a day = 32%
The formula for the scale factor of dilation is = dimensions of a new shape/dimensions of a old shape
= 32%/1/2 = 0.32/0.5 = 0.64

b) Find the diameter of the mold after a day.
Answer:
The circular mold in a Petri dish has a diameter of 1/2
The diameter grew in a day = 32%
= 2 × 0.32 = 0.64
Therefore the diameter of the mold after a day = 0.64.

Question 19.
A figurine of the Statue of Liberty is 10 inches tall. The height of the Statue of Liberty is 150 feet. What is the scale factor of the dilation if the figurine is the image of the statue?
Answer:
Given that,
Figurine of the statue of Liberty is 10 inches tall
The height of the statue of Liberty is 150 feet.
The scalar factor of the dilation if the figurine is the image of the statue = figurine of the statue of Liberty/height of the statue of Liberty
Here 1 feet = 12 inches
150 inches = 150 × 12 = 1800
= 10/1800
= 1/180
= 0.005
Therefore, the scale factor of the dilation is 0.005 inches.

Question 20.
A spotlight is placed 2 feet from a 1-foot tall vase. A shadow 5 feet tall is cast on a wall as shown in the diagram. Find the distance of the vase from the wall.

Answer:
Given that,
The spotlight is placed 2 feets away from a 1 foot tall vase.
A shadow 5 feet tall is cast on a Wall.
Consider the distance from the vase to the wall is d.
The distance of a vase from the wall = distance of shadow from the spot light/distance of vase from the spotlight
= 2+d/2 = 5
= 2+d = 10
d = 10 – 2
d = 8
Therefore the distance from the vase to the wall is 8 feet.