Hillary

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 6 Review Test to score better marks in the exam.

Math in Focus Grade 8 Course 3 A Chapter 6 Review Test Answer Key

Concepts and Skills

Given the relation described, identify the input and the output.

Question 1.
Daphne wants to find the area of a circle given its radius.
Answer:
Input: Radius
Output: Area of Circle

Question 2.
Mr. Reynard wants to find the total cost of the number of items he bought at a store where everything costs one dollar.
Answer:
Input: one dollar
Output: total cost of the number of items

Question 3.
The head of the English department wants to see how each student in Grade 8 does on an English test.
Answer:
Input: Each student’s name
Output: Grades for the English test

Based on the mapping diagrams, state the type of relation. Tell whether each relation is a function.

Question 4.

Answer: Many to one relation, it is a function

Question 5.

Answer: One to many relation, it is not a function

Tell whether each relation is a function.

Question 6.

Answer: One to one relation, it is a function

Question 7.

Answer: Many tone relation, it is a function

Question 8.

Answer: No

Use graph paper. Show your work.

Question 9.
Represent the function y = -4x + 6 as a table and as a graph. Use 1 grid square on the horizontal axis to represent 1 unit for the x interval from -3 to 3, and 1 grid square on the vertical axis to represent 2 units for the y interval from -6 to 18.
Answer:
Given,
y = -4x + 6

Tell whether each function is linear or nonlinear. Then tell whether the function is increasing or decreasing.

Question 10.

Answer: Non-Linear and decreasing function

Question 11.
The area of a square, A square centimeters, is a function of its side length, s centimeters, where A = s².
Answer:
Non-linear and increasing function

Problem Solving

Describe the function. Sketch a graph for the function.

Question 12.
A large region has experienced heavy rains. Government officials decide to open a floodgate to release water from the reservoir at a constant rate of 1 cubic kilometer per hour. Before they open the gate, there are 29 cubic kilometers of water in the reservoir. The amount of water in the reservoir, y cubic kilometers, is a function of the number of hours the floodgate has been opened, x hours.
a) Give the least possible input value and the corresponding output value. Tell whether the function is linear or nonlinear. Then tell whether the function is increasing or decreasing. Explain.
Answer:
The least possible input value is the smallest value of x which is obtained at the initial moment:
x = 0
The corresponding output value y is the amount of water in the reservoir in the initial moment:
y = 29

b) Sketch a graph for the function. Identify the y-intercept of the graph.
Answer:
The graph passes through the point (0, 29), therefore the y-intercept is:
b = 29
In order to sketch a graph of the function, we use the slope m = -1 and the y-intercept 29:

Solve. Show your work.

Question 13.
The student council orders T-shirts with the school logo from an online company. The cost for each T-shirt is $2, and the shipping charge for all the shirts is $25. The student council wants to find out the total amount of money they pay, y dollars, for the number of T-shirts they order, x.
a) Write an algebraic equation to represent the function.
Answer: y = 25 + 2x

b) Use graph paper. Graph the relationship between x and y. Use 1 unit on the horizontal axis to represent 1 T-shirt for the x interval from 0 to 10, and 1 unit on the vertical axis to represent $2 for the y interval from 25 to 45.
Answer:

c) Identify whether the function is linear or nonlinear.
Answer: It is linear

d) Identify whether the function is increasing or decreasing. Explain.
Answer: It is increasing because as the values of x increase, the corresponding values of y also increase.

Question 14.
A scientist is checking to see whether pollutants are causing a decrease in oxygen levels in a river near a pipe that drains into the river. She notices that the distance downstream from the pipe, in meters, and the concentration of oxygen in the water, in milligrams per liter, can be described by the function y = 2 + 0.1x, where y is the concentration of oxygen and x is the distance from the pipe. The scientist also tested oxygen levels upstream from the pipe. The graph shows a function that represents this upstream oxygen level concentration.

a) Copy the graph shown. Then graph the function y = 2 + 0.1x on the same coordinate plane.
Answer:
We are given the downstream function:
y = 2 + 0.1x
We graph both functions:

b) Use a verbal description to compare the two functions. Give a possible reason for the difference in oxygen levels upstream and downstream from the pipe.
Answer:
The oxygen level upstream from the pipe is always at 12mg/L regardless of the distance from the pipe.
However, the oxygen level in the river downstream from the pipe is 2mg/L when the distance from the pipe is 0 m and it increases as the distance from the pipe increases. Because the concentration of oxygen increases at a rate of 0.1mg/L, the rate of change of the function is constant. So, it is an increasing linear function; One possible reason is that the river is polluted downstream from the pipe.

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 6 Lesson 6.4 Comparing Two Functions to score better marks in the exam.

Math in Focus Grade 8 Course 3 A Chapter 6 Lesson 6.4 Answer Key Comparing Two Functions

Math in Focus Grade 8 Chapter 6 Lesson 6.4 Guided Practice Answer Key

Complete.

Question 1.
Water is pumped into two aquariums, P and Q. The tables show two functions relating the total amount of water, y liters, and the time taken, t minutes, to pump the water into each aquarium.

a) Use a verbal description to compare the two functions.
Aquarium P

Aquarium Q

Both functions are and functions. The function for Aquarium has a greater rate of change than the function for Aquarium .
Answer:

Both functions are linear and increasing functions. The function for Aquarium Q has a greater rate of change than the function for Aquarium P.

b) Write an algebraic equation to represent each function. Then write the initial input and output values of each function.
Aquarium P
Use the ordered pair (5, 70) and the rate of change, , to find the value of the y-intercept, b.
Linear function:

So, the algebraic equation for Aquarium P is y = .
Answer:
Let the input be t and the output be y
y = mt + b
Substitute the values for m, t and y
70 = 10(5) + b
70 = 50 + b
b = 70 – 50
b = 20

Aquarium Q
Use the ordered pair (10, 170) and the rate of change, , to find the value of the y-intercept, b.
Linear function:

So, the algebraic equation for Aquarium Q is y = .
Both functions have an initial output value of corresponding to an initial input value of 0.
Answer:
Let the input be t and the output be y
y = mt + b
Substitute the values for m, t and y
170 = 10x + 20
170 – 20 = 10x
10x = 150
x = 150/10
x = 15

c) Which of the two aquariums, P and Q, is filled with water more quickly?
Comparing the rates of change for the two shops, Aquarium has a . rate of change. This means that Aquarium will be filled with water more quickly.
Answer:
Comparing the rates of change for the two shops, Aquarium Q has a greater. rate of change. This means that Aquarium Q will be filled with water more quickly.

Complete.

Question 2.
Two classes, A and B, compare the amount of donations they will raise for a charity by participating in a walkathon. The amount of donations they will raise, y dollars, is a function of the distance the students walk, x miles.
Class A

Class B
Amount of donations: y = 20x + 50

a) Write an algebraic equation to represent the table of values representing the amount of donations Class A will raise for the charity.

The algebraic equation is y = .
Answer:

The algebraic equation is y = 15x + 100

b) Use a verbal description to compare the two functions.
Both functions are and functions. Comparing the two equations, because > 50, Class raises a greater amount of money at first.
Comparing the rates of change shows that Class A will raise $ for each mile the students walk, and Class B will raise $ for each mile the students walk. So, the amount of donations Class will raise increases more quickly than the amount of donations Class will raise.
Answer:
Both functions are linear and increasing functions. Comparing the two equations, because 100 > 50, Class A raises a greater amount of money at first.
Comparing the rates of change shows that Class A will raise $ 15 for each mile the students walk, and Class B will raise $ 20 for each mile the students walk. So, the amount of donations Class B will raise increases more quickly than the amount of donations Class A will raise.

Math in Focus Course 3A Practice 6.4 Answer Key

Tell whether the equation y = -2x + 3 can represent each of the following functions.

Question 1.

Answer: Yes
y = -2x + 3
y = -2(2) + 3
y = -4 + 3
y = -1
y = -2(3) + 3
y = -6 + 3
y = -3
y = -2x + 3
y = -2(-1) + 3
y = 2 + 3
y = 5

Question 2.

Answer: No

Question 3.

Answer: No

Tell whether each function can represent the table of values.

Question 4.
y = 3x – 4
Answer: No

Question 5.
y = 2x – 5
Answer: No

Question 6.

Answer: yes

Tell whether each function represents the verbal description.

Bryan has $30 in savings at first. He wants to save $5 per month beginning this month. y represents his total savings, in dollars, and x represents the number of months he saves.
Question 7.

Answer: No

Question 8.
y = 30 + 5x
Answer: Yes

Question 9.
y = 30 – 5x
Answer: No

Solve. Show your work.

Question 10.
Clara and Elaine have some savings. The functions that relate each girl’s total savings, y dollars, to the number of months, x, that each girl saves are as follows:
Clara: y = 380 + 20x
Elaine: y = 400 + 15x
a) Use a verbal description to compare the two functions.
Answer:
Clara has 380 dollars in her savings. She wants to save 20$ from this month.
Elaine has 400 dollars in her savings. She wants to save 15$ from this month.

b) Graph the two functions on the same coordinate plane. Use 1 unit on the horizontal axis to represent 1 month for the x interval from 0 to 8, and 1 unit on the vertical axis to represent $20 for the y interval from 380 to 540. For each function, draw a line through the points.
Answer:
We graph both functions:

c) Who will save more over time? Explain.
Answer: Clara saves more money than Elaine.

Question 11.
The director of a theater group wants to rent a theater for an upcoming show. The director has two options for paying for the rental. Both options involve paying a deposit and then paying an additional charge for each ticket sold. For each function, the total amount the director would pay, y dollars, is a function of the number of tickets sold, x.
Option A

Option B
A deposit of $800 plus $6 per ticket sold.
a) Write an algebraic equation to represent each function.
Answer:
Option A: y = 1000 + 4x
Option B: y = 800 + 6x

b) Use a verbal description to compare the two functions.
Answer:
Both functions are a linear and increasing functions. Comparing the two equations, because 1000 > 800, Option A costs more at first. Comparing the rates of change shows that the total fee for option A increases by $4 for each ticket sold, and the total fee for option B increases by $6 for each ticket sold, and the total fee for the director will pay for Option B will increase more quickly than the total fee for Option A as the number of tickets sold increases.

c) Math Journal The theater seats up to 200 people. If the director expects to sell all the tickets, which of the two options, A or B, offers a better deal? Explain.
Answer:
The total fee for option A is lower than the total fee for Option B when all the tickets are sold.

Question 12.
A factory needs to grate at least 8,000 pounds of cheese each day.

The manager of the factory needs to buy a new cheese grating machine. She is trying to decide between Machine A and Machine B. The functions shown describe how many pounds of cheese, y, are left t minutes after each machine starts grating an initial batch of cheese.
Machine A
The function is y = 2,000 – 80t. The initial value of 2,000 pounds represents the weight of each batch of cheese to be grated. After one batch is grated, another batch can be added to the machine.

Machine B

a) Write an algebraic equation to represent the function for Machine B.
Answer:
The graph of the function for Machine B passes through the points (0, 8000) and (80, 0) We determine the slope of the line using the slope formula:
m = \(\frac{0-8000}{80-0}\)
= \(\frac{-8000}{80}\)
= -100
The graph of the function for Machine B passes through the point (0, 8000), therefore the y-intercept is:
b = 8000
The equation for Machine B is:
y = -100t + 8000

b) Math Journal Assuming that the machines are of the same quality, which machine would you recommend that the manager buy? Explain.
Answer:
The equation for Machine A is:
y = -80t + 2000
We graph the two functions:

We notice that with the Machine from Option A the manager would grate 4 • 2000 = 8000 pounds of cheese in 100 minutes, while with the Machine from Option B he can grate 8000 pounds in only 80 minutes, so Option B is better.

Brain @ Work

Five teachers at a school brought a group of students to a museum exhibit.

For group tours involving any number of adults and at least 5 students, the museum offers three packages, A, B, and C. The functions shown below represent the total admission fee, y dollars, that five teachers and x students will pay to see the exhibit.
Package A
Each adult ticket costs $30 and each student ticket costs $15.

Package B

Package C
Each adult ticket costs $60 and each student ticket costs $12.

Question 1.
Use an algebraic equation to represent each of the three functions.
Answer:
Equation for Package A: y = 150 + 15x
Package B: y = 250 + 14x
Package C: y = 300 + 12x

Question 2.
Graph the three functions on the same coordinate plane. Use 1 unit on the horizontal axis to represent 5 students for the x interval from 0 to 50, and 1 unit on the vertical axis to represent $50 for the y interval from 150 to 950. For each function, draw a line through the points.
Answer:

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 6 Lesson 6.3 Understanding Linear and Nonlinear Functions to score better marks in the exam.

Math in Focus Grade 8 Course 3 A Chapter 6 Lesson 6.3 Answer Key Understanding Linear and Nonlinear Functions

Math in Focus Grade 8 Chapter 6 Lesson 6.3 Guided Practice Answer Key

Tell whether each table of values represents a linear or nonlinear function. Explain.

Question 1.

Because the rate of change for the function is , the table represents a function.
Answer:

Because the rate of change for the function is constant, the table represents a linear function.

Question 2.

Because the rate of change for the function is , the table represents a function.
Answer:
Because the rate of change for the function is non-constant, the table represents a non-linear function.

Tell whether each graph represents a linear function. If so, find the rate of change.

Question 3.

Because the graph is a , it represents a function.
The line passes through (, ) and (, ).
Rate of change = \(\frac{?-?}{?-?}\)
=
So, the rate of change of the graph is .
Answer:
Because the graph is a straight line, it represents a linear function.
The line passes through (0, 3) and (6, 8).
Rate of change = \(\frac{8-3}{6-0}\)
= 5/6
So, the rate of change of the graph is constant.

Question 4.

Because the graph is a , it represents a function.
Answer:
Because the graph is a curve, it represents a non-linear function.

Describe the function. Sketch a graph for the function.

Question 5.
A cruise ship traveling at a constant speed consumes 4,000 gallons of gasoline per hour. When fully filled, it has a fuel capacity of 330,000 gallons. The amount of gasoline consumed, y gallons, is a function of the total traveling time, x hours.
a) Give the least possible input value and the corresponding output value. Tell whether the function is linear or nonlinear. Then tell whether the function is increasing or decreasing. Explain.
Answer:
At the beginning of the trip, the cruise ship has 330,000 gallons of gasoline.
So, the least possible input value is 0 and the corresponding output value is 330,000.
For every hour of traveling time, the cruise ship consumes 4,000 gallons of gasoline.
So, the rate of change of the function is constant.
As the total traveling time increases, the amount of gasoline left decreases.
Thus the function is a linear and decreasing function.

b) Sketch a graph for the function.
Answer:

Hands-On Activity

Materials:
number cards (from -5 to 5)

SKETCH LINEAR FUNCTIONS

Work in pairs.

STEP 1: Shuffle the cards and place them face down on the table.

STEP 2: Each player draws two cards. Use your cards to write an equation in slope-intercept form. Use one of the cards for the slope and one for the y-intercept of the equation.
For example:

Slope-intercept form: y = -2x + 3

STEP 3: Graph the equation you wrote.

STEP 4: Copy and complete the table. For each equation that you and your partner write, record the slope, the y-intercept, and whether the function is increasing or decreasing.

STEP 5: Repeat STEP 2 to STEP 4 until a player has written two equations that represent increasing functions and two equations that represent decreasing functions. If no player has done this, reshuffle the cards and repeat STEP 2 to STEP 4. The player who reaches this goal first wins the game.

Math Journal What can you conclude about the slope of the graph of an increasing function and the slope of the graph of a decreasing function? Explain.
Answer:

Math in Focus Course 3A Practice 6.3 Answer Key

Tell whether each table of values represents a linear or nonlinear function.

Question 1.

Answer: Linear function

Question 2.

Answer:

Linear Function

Question 3.

Answer:

Non-linear function

Question 4.

Answer:

Tell whether each graph represents a linear function. If so, find the rate of change.

Question 5.

Answer:
Yes, 1/2

Question 6.

Answer: Non-linear and decreasing

Tell whether each function is linear or nonlinear. Then tell whether the function is increasing or decreasing.

Question 7.

Answer:
Non-linear and increasing function

Question 8.

Answer: straight line and linear function

Question 9.

Answer: Non-linear and decreasing function

Question 10.

Answer: Straight line and linear function

Describe the function. Sketch a graph for the function.

Question 11.
A machine at a factory pours juice into bottles at a constant rate of 6 liters per minute. The total amount of juice poured, y liters is a function of the number of minutes that the juice is poured, x.
a) Give the least possible input value and the corresponding output value. Tell whether the function is linear or nonlinear. Then tell whether the function is increasing or decreasing. Explain.
Answer:
If the time taken for the machine to pour juice into bottles is 0 min, the amount of juice poured will be 0L.
So, the least possible input value is 0 and the corresponding output value is 0.
Because the machine pours juice at 6L/min, the rate of change of the function is constant. As the time taken for the machine to pour juice into bottles increases, the amount of juice poured also increases.
Hence the function is a linear and increasing function.

b) Sketch a graph for the function.
Answer:

Question 12.
Aidan was 100 miles from Town P. He traveled to Town P by car at a constant speed. The distance from Town P, y miles, is a function of the traveling time, x hours.
a) Give the least possible input value and the corresponding output value. Tell whether the function is linear or nonlinear. Then tell whether the function is increasing or decreasing. Explain.
Answer:
When Aidan [eaves to Town P, the corresponding distance from his position to Town P is 100, therefore the least possible input value is 0 and the corresponding output is 100.

Because each hour he is driving by the same speed, the rate of change of the function is constant.

As time passes (the input increases), the distance to Town P (the output) decreases, so the function is decreasing.
Therefore the function is linear and decreasing.

b) Sketch a graph for the function.
Answer:
The distance to Town P starts at (0, 100) and falls from left to right The slope of the line, which is constant, is the distance traveLed each hour (the speed):

Solve. Use graph paper.

Question 13.
The table shows the number of students, y, as a function of the number of teachers, x.

a) Tell whether the function is linear or nonlinear. Then tell whether the function is increasing or decreasing. Explain.
Answer:
The function has a constant rate of change, 25.
Thus it is a linear and increasing function.
As the number of students increases, the number of teachers also increases.

b) Graph the table of values and draw a line through the points. Use 1 unit on the horizontal axis to represent 1 teacher for the x interval, and 1 unit on the vertical axis to represent 25 students for the y interval from 100 to 250. Do the coordinates of every point on the line make sense for the function? Explain.
Answer:

No, because the number of teachers and students must be whole numbers.

Question 14.
A cyclist starts riding from home to another town. His cycling speed, y miles per hour, is a function of the amount of time he takes to cycle, x hours.

a) Tell whether the function is linear or nonlinear. Then tell whether the function is increasing or decreasing. Explain.
Answer:
Non-linear function and decreasing

b) Graph the table of values and draw a curve through the points. Use 1 unit on the horizontal axis to represent 1 hour for the x interval, and 1 unit on the vertical axis to represent 1 mile per hour for the y interval. Do the coordinates of every point on the curve make sense for the function? Explain.
Answer:

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 6 Lesson 6.2 Representing Functions to score better marks in the exam.

Math in Focus Grade 8 Course 3 A Chapter 6 Lesson 6.2 Answer Key Representing Functions

Math in Focus Grade 8 Chapter 6 Lesson 6.2 Guided Practice Answer Key

Complete

Question 1.
A game shop rents out video games at a rate of $6 per game. The total amount of money the shop collects, y dollars, is a function of the number of games, x, that the shop rents out.
a) Write a verbal description of the function. Then write an algebraic equation for the function.
Total amount of money the shop collects equals the product of the rental rate and the .
= 6 • Write an equation.
= Simplify.
Answer:
Given,
A game shop rents out video games at a rate of $6 per game.
The total amount of money the shop collects, y dollars, is a function of the number of games, x, that the shop rents out.
y = 6 • x
y = 6x

b) Construct a table of x- and y-values for the function. this situation,

Answer:

c) Use the table of values in b) to graph the function. Use 1 unit on the horizontal axis to represent 1 game for the x interval, and 1 unit on the vertical axis to represent $6 for the y interval.
Answer:

Question 2.
A fire sprinkler sprays water at a rate of 8 gallons per minute. The total amount of water being sprayed, y gallons, is a function of the number of minutes, x, that the sprinkler sprays water.
a) Write a verbal description of the function. Then write an algebraic equation for the function.
Total amount of water being sprayed equals product of the rate of water flow and the .
= • Write an equation.
= Simplify.
Answer:
Given,
A fire sprinkler sprays water at a rate of 8 gallons per minute.
The total amount of water being sprayed, y gallons, is a function of the number of minutes, x, that the sprinkler sprays water.
y = 8 • x
y = 8x

b) Construct a table of x- and y-values for the function.

Answer:

c) Use the table of values in b) to graph the function. Use 1 unit on the horizontal axis to represent 1 minute for the x interval, and 1 unit on the vertical axis to represent 8 gallons for the y interval.
Answer:

Question 3.
The table shows the total distance, y miles, indicated on the odometer of Jason’s car and the amount of gasoline used, x gallons, on a particular day.

a) Graph the function. Use 1 unit on the horizontal axis to represent 1 gallon for the x interval from 0 to 5, and 1 unit on the vertical axis to represent 30 miles for the y interval from 1,000 to 1,150.
Answer:

b) Write an algebraic equation for the function.
Answer: y = 30x + 1000

c) Describe how the slope and the y-intercept of the graph are related to the function.
Answer:
The y-intercept, 1000 means that the odometer of Jason’s car shows 1000 mi when he starts driving.
The shape 30, gives the rate at which the distance indicated on the odometer is changing. For every gallon of gasoline, the distance indicated on the odometer increases by 30 mi.

Math in Focus Course 3A Practice 6.2 Answer Key

Write a verbal description of each function. Then write an algebraic equation for the function.

Question 1.
Gordon is traveling at a constant speed of 80 kilometers per hour. The distance he travels, d kilometers, is a function of the amount of time he takes to travel, t hours.
Answer:
The distance Gordon travels equals 80km/h times the number of hours he takes to travel,
d = 80t

Question 2.
Mr. Henderson pays a monthly charge of $40 for a family cell phone plan. Each additional family member pays $10 every month. The total amount Mr. Henderson and his family members pay each month, y dollars, is a function of the number of the additional family members who use the plan, x.
Answer:
Given,
Mr. Henderson pays a monthly charge of $40 for a family cell phone plan.
Each additional family member pays $10 every month.
The total amount Mr. Henderson and his family members pay each month, y dollars, is a function of the number of the additional family members who use the plan, x.
y = 10x + 40

Question 3.
Math Journal In questions 1 and 2 tell whether all values for the input and output are meaningful for the functions. Explain.
Answer:
All the values for the input and output are meaningful because time and distance are continuous quantities.
Only whole numbers are meaningful for the input and output.
The input values which are the numbers of additional family members must be whole numbers.
So, the corresponding output values of the function

Write an algebraic equation for each function. Then construct a table of x- and y-values for the function.

Question 4.
The students from the Robotics Club are making model windmills for a workshop. Each windmill has three blades. The total number of blades needed, y, is a function of the number of windmills they make, x.
Answer:
Given,
Each windmill has three blades.
The total number of blades needed, y, is a function of the number of windmills they make, x.
y = 3x

Question 5.
A newly made glass vase has a temperature of 580°C. Its temperature then decreases at an average rate of 56°C per minute. The temperature of the glass vase, y°C, is a function of the number of minutes its temperature has been decreasing, x.
Answer: y = 580 – 56x

Each of the following graphs represents a function. Write an algebraic equation to represent the function.

Question 6.

Answer: y = 3

Question 7.

Answer: y -5/2 x + 20

Use the table of values to plot a graph to represent the function.

Question 8.
The table shows the number of chairs in a classroom, y, as a function of the number of students in the classroom. Use 1 unit on the horizontal axis to represent 1 student for the x interval, and 1 unit on the vertical axis to represent 4 chairs for the y interval.

Answer:

Use the table of values to plot a graph to represent the function. Then write an algebraic equation for the function.

Question 9.
A motorcyclist rode at a constant speed from City A to City B, which are 240 miles apart. The table shows his distance from City B, y miles, as a function of the number of hours he rode, x hours. Use 1 unit on the horizontal axis to represent 1 hour for the x interval, and 1 unit on the vertical axis to represent 40 miles for the y interval.

Answer:

y = -40x + 240

Solve. Show your work.

Question 10.
The graph shows the temperature of a package of food, y°C, as a function of the time the food is in the freezer, x minutes.

a) Write an equation in slope-intercept form to represent the function.
Answer:
The line passes through the points (0, 30) and (2, 20).
Use the slope formula:
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Substitute values:
= \(\frac{20-30}{2-0}\)
Subtract:
= \(\frac{-10}{2}\)
Simplify:
= -5
The line intersects the y-axis in point (0, 30). So the y-intercept is 30.
b = 30
Substitute the values of m and b. The slope-intercept form is:
y = -5x + 30
So an equation of the Line is y = -5x + 30.

b) What information do the values for slope and y-intercept give you about the function?
Answer:
The y-intercept shows that the initial temperature of the package was 30° C. The slope, -5, gives the rate at which the package’s temperature decreases each minute.

Question 11.
Hillary has $60 on her bus card. Every time she rides a bus, $1.50 is deducted from the value on her card. The amount of money she has on her card, y dollars, is a function of the number of times she rides a bus, x.
a) Write a verbal description of the function. Then write an algebraic equation for the function.
Answer:
The amount of money Hillary has on her bus card equals $60 minus $1.50 times the number if times she rides on a bus;
y = 60 – 1.5x

b) Construct a table of x- and y-values for the function in a). Use values of x from 0 to 6.
Answer:

c) Use the table of values in b) to plot a graph to represent the function. Use 1 unit on the horizontal axis to represent 1 bus ride for the x interval from 0 to 6, and 2 units on the vertical axis to represent $3 for the y interval from 51 to 60.
Answer:

d) How many bus rides has Hillary taken if she has $51 left on her card?
Answer: 6

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 6 Lesson 6.1 Understanding Relations and Functions to score better marks in the exam.

Math in Focus Grade 8 Course 3 A Chapter 6 Lesson 6.1 Answer Key Understanding Relations and Functions

Math in Focus Grade 8 Chapter 6 Lesson 6.1 Guided Practice Answer Key

Complete.

Question 1.
Describe the relation between the inputs and the outputs.

The relation between the inputs and the outputs is a -to- relation.
Answer:
The relation between the inputs and the outputs is a many to one relation.
Because all the inputs are connected to the single output.

Question 2.
Describe the relation between the inputs and the outputs.

The relation between the inputs and the outputs is a -to- relation.
Answer:
The relation between the inputs and the outputs is a many to many relation.

Question 3.
The table shows the relation between the heights of five statues and their weights.

Copy and complete the mapping diagram to show the relation between the heights of the five statues and their weights. Then identify the type of relation between the heights and the weights.

The relation between the heights and the weights is a -to- relation.
Answer:
The relation between the heights and the weights is a one -to- one relation.

Tell whether each relation is a function. Explain.

Question 4.

Because the mapping diagram shows a -to- relation, it a function.
Answer:
Because the mapping diagram shows a one to many relation, it is a one to many function.

Question 5.

Because the mapping diagram shows a -to- relation, it a function.
Answer:
Because the mapping diagram shows a one to many relation, it is a one to many function.

Question 6.

Because the table shows a -to- relation, it a function.
Answer:
Because the table shows a one to one relation, it is a one to one function.

Tell whether the relation represented by each graph is a function. Explain.

Question 7.

Answer:
You can graph relation by writing and graphing orders pairs.
ordered pairs (1, 2), (2, 2), (3, 5), (4, 2)

From the above graph, we can say that it is a many to one relation and it is a many to one function.
The above graph is not a function.

Question 8.

Answer:
The ordered pairs are (1,5), (2,4), (3,1), (3,3), (4,2)

It is a many to one relation.
By seeing the above graph we can say that the relation is not a function.

Question 9.

Answer: The above graph is a function.

Question 10.

Answer: The above graph is not a function.

Math in Focus Course 3A Practice 6.1 Answer Key

Given the relation described, identify the input and the output.

Question 1.
Mrs. Thomas wants to find out the price charged for the same stereo speaker at different stores.
Answer:
Given
Mrs. Thomas wants to find out the price charged for the same stereo speaker at different stores.
the price of the stereo speaker is input and stores is the output.

Question 2.
Five students, Jessie, Patrick, Wayne, Colin, and Susie, have different heights. Their teacher wants to know their heights.
Answer:
the number of students is input and heights is the output.

Question 3.
Ginny wants to know what after-school activities each of her friends signed up for so she knows whether she shares the same interests.
Answer:
Ginny wants to know what after-school activities each of her friends signed up for so she knows whether she shares the same interests.
Friends is input and after-school activities is output.

Based on the mapping diagram, state the type of relation.

Question 4.

Answer:
It is a many to many relation.

Question 5.

Answer:
It is a one to many relation.

Question 6.

Answer:
It is a one to one relation.

Draw a mapping diagram to represent each relation. Then identify each type of relation.

Question 7.
The table shows the numbers of various types of fruit sold in a supermarket. Draw a mapping diagram to represent the relation between each fruit and the number sold by the supermarket. Identify the type of relation between the fruit and the number sold.

Answer:

Its is Many to one relation.

Question 8.
The table shows the scores of a soccer team playing in eight different games. Each game is represented by a number.

Draw a mapping diagram to represent the relation between the score for each game and the game number. Identify the type of relation between the score and the game number.
Answer:

One to many relation

Tell whether each statement is True or False. Explain.

Question 9.
A function is a type of relation.
Answer: true

Explanation: A function is a correspondence between two sets called domain and range.

Question 10.
All relations are functions.
Answer: False

Question 11.
Only a many-to-one relation is a function.
Answer: False

Question 12.
A one-to-many relation is a function.
Answer: True

Identify the type of relation in each mapping diagram. Then tell whether the relation is a function. Explain.

Question 13.

Answer: It is one to one relation. Thus the relation is a one to one function.

Question 14.

Answer: It is one to many relation. The relation is not a function.

Question 15.

Answer: It is a many to one relation.

Tell whether the relation represented by each graph is a function. Explain.

Question 16.

Answer: It is a many to one relation and it is not a function.

Question 17.

Answer: It is a one to many relation, it is not a function.

Question 18.

Answer: The above graph is a many to function.

Question 19.

Answer: The above graph is a many to function.

Tell whether the relation described is a function. Use a graph to support your answer.

Question 20.
The cost, y dollars, of some cheese that costs $3 per pound varies directly with the weight, x pounds, of the cheese. Use 1 unit on the horizontal axis to represent 1 pound for the x interval from 0 to 6, and 1 unit on the vertical axis to represent $3 for the y interval from 0 to 18.
Answer:

We build a table of values

We draw the graph

We apply the vertical test: as any vertical line intersects the graph in exactly one point, the relation is a function
Function

Question 21.
A tank contains 3 liters of water. The water in the tank is draining out at a rate of 0.5 liter per hour. Use 1 unit on the horizontal axis to represent 1 hour for the x interval from 0 to 6, and 1 unit on the vertical axis to represent 0.5 liter for the y interval from 0 to 3.0.
Answer:

We build a table of values

We draw the graph

We apply the vertical test: as any vertical line intersects the graph in exactly one point, the relation is a function.
Function

Question 22.
A veterinarian weighed some puppies to see if weight depends on age. The table shows the ages, x months, and the weights, y pounds, of the puppies. Use 1 unit on the horizontal axis to represent 1 month for the x interval, and 1 unit on the vertical axis to represent 1 pound for the y interval.

Answer:

we are given the table of values

we draw the graph

We apply the vertical test: as there is a vertical line which intersects the graph in more than one point, the relation is not a function.
Not a function

Solve. Show your work.

Question 23.
The table shows the number of computers the students have and the number of students in eight schools.

a) Draw a mapping diagram to represent the relation between the number of computers and the number of students.
Answer:
We draw a mapping diagram to represent the relation between the number of computers and the number of students:

b) From the mapping diagram, identify the relation between the number of computers and the number of students.
Answer: One to many relation

c) Tell whether the relation represented by the mapping diagram is a function. Explain.
Answer: No, because two inputs have more than one output each, it is not a function.

Question 24.
Math Journal Is the relationship between the side length of a square and the area of the square an example of a function? Explain.
Answer:
The relation between the side length x of a square and the area of the square x² is a one-to-one relation because to each value of x corresponds only one value of x².
Therefore the relation is a function.
Function

The table below shows the number of books sold by each of six bookstores and the sales made by each store in a week. Use the table to answer questions 25 to 27.

Question 25.
Draw a mapping diagram to represent a relation between the bookstores and the number of books they sold in the week. Identify the type of relation between the bookstores and the number of books sold. Then tell whether the relation represented by the mapping diagram is a function. Explain.
Answer:
Many to one relation, it is a function, each input has only one output.

Question 26.
Draw a mapping diagram to represent the relation between the sales made by the bookstores and the number of books sold in the week. Identify the type of relation between the sales made by the bookstores and the number of books sold. Then tell whether the relation represented by the mapping diagram is a function. Explain.
Answer:
We draw a mapping diagram to represent a relation between the sales made by bookstores and the number of books sold each week:

From the diagram we notice that the relation is one-to-many. Therefore the relation is not a function.
Not a function

Question 27.
Math Journal The store owners want to know if the relation between the number of books sold and the sales made by the bookstores is a function.
a) Draw a mapping diagram, with the number of books sold as the input, and the sales made by each bookstore as the output. Is the relation a function? Explain.
Answer:
No, One input, 523, more than one output, 2,317 and 2,569.

b) Why might one bookstore get more money for selling the same number of books as another bookstore?
Answer:
One bookstore could be selling books that are more expensive.

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 6 Functions to score better marks in the exam.

Math in Focus Grade 8 Course 3 A Chapter 6 Answer Key Functions

Math in Focus Grade 8 Chapter 6 Quick Check Answer Key

Write an algebraic expression for each of the following.

Question 1.
Benedict has 7 packs of cards. Each pack has x cards. He gives 3 cards to his sister. Write an algebraic expression for the number of cards that he has left.
Answer:
Given,
Benedict has 7 packs of cards.
Each pack has x cards.
He gives 3 cards to his sister.
7x – 3
Thus the algebraic expression for the number of cards that he has left is 7x – 3.

Question 2.
y highlighters are shared equally among 9 students. One of the students, Jessie, then buys another 3 highlighters. Write an algebraic expression for the number of highlighters she has in total.
Answer:
Given,
y highlighters are shared equally among 9 students.
One of the students, Jessie, then buys another 3 highlighters.
y/9 + 3

Evaluate each expression for the given value of the variable.

Question 3.
5x + 7 when x = -3
Answer:
Given the expression 5x + 7
when x = -3
5(-3) + 7
= -15 + 7
= -8

Question 4.
-4x – 1 when x = 3
Answer:
Given the expression -4x – 1
when x = 3
-4(3) – 1
-12 – 1 = -13

Question 5.
3 – \(\frac{1}{2}\)x when x = -5
Answer:
Given the expression 3 – \(\frac{1}{2}\)x
when x = -5
3 – \(\frac{1}{2}\)(-5)
3 + \(\frac{5}{2}\)

Question 6.
\(\frac{3}{4}\)x – 2 when x = 7
Answer:
Given the expression \(\frac{3}{4}\)x – 2
when x = 7
\(\frac{3}{4}\)(7) – 2
\(\frac{21}{4}\) – 2

This handy Math in Focus Grade 8 Workbook Answer Key Chapter 10 Review Test detailed solutions for the textbook questions.

Math in Focus Grade 8 Course 3 B Chapter 10 Review Test Answer Key

Concepts and Skills

Draw scatter plot for each of the given table of bivariate data.

Question 1.
Use 2 centimeters on the horizontal axis to represent 1 unit. Use 1 centimeter on the vertical axis to represent 5 units for the y interval from 50 to 110.

Answer:

Question 2.
Use 2 centimeters on the horizontal axis to represent 10 units for the x interval from 90 to 120. Use 1 centimeter on the vertical axis to represent 5 units for the y interval from 60 to 100.

Answer:

Describe the association between the bivariate data shown in each scatter plot.

Question 3.

Answer:
The association between the bivariate data shown in the above scatter plot is strong, linear and negative.

Question 4.

Answer: The association between the bivariate data shown in the above scatter plot is strong, non-linear, and negative.

State the line that represents the line of best fit for each scatter plot.

Question 5.

Answer: The best line fit from the above scatter plot is line B.

Question 6.

Answer: The best line fit from the above scatter plot is line B.

Identify the outlier(s) in each scatter plot.

Question 7.

Answer: (4, 2) is the outlier.

Question 8.

Answer: (4, 1) is the outlier

Construct each scatter plot and draw a line of best fit for the given table of bivariate data.

Question 9.
Use 1 centimeter on the horizontal axis to represent a score of 10. Use 1 centimeter on the vertical axis to represent a score of 5.

Answer:

Question 10.
Use 1 centimeter on the horizontal axis to represent 1,000 products. Use 1 centimeter on the vertical axis to represent $50.

Answer:

Question 11.
Use 2 centimeters on the horizontal axis to represent 5 inches. Use 1 centimeter on the vertical axis to represent 5 inches for the y interval from 35 to 90.

Answer:

Identify whether the given data is categorical or quantitative.

Question 12.
Brown, green, blue
Answer: categorical

Question 13.
$1, $2, $3, $4
Answer: quantitative

Question 13.
1 A.M., 2 A.M., 3 A.M.
Answer: categorical

Use the two-way table to answer questions 15 to 18.

Question 15.
Copy and complete the two-way table.
Answer:

Question 16.
Describe the association between the two categorical data.
Answer: The association between the two categorial data describes number of people like and do not like jogging and the number of people like swimming and do not like swimming.

Question 17.
Find the relative frequencies among the rows, and interpret their meanings. Round your answer to the nearest hundredth where necessary.
Answer:
Jogging:
156/196 = 0.80
40/196 = 0.20
72/204 = 0.35
132/204 = 0.65

Question 18.
Find the relative frequencies among the columns, and interpret their meanings. Round your answer to the nearest hundredth where necessary.
Answer:
156/228 = 0.68
72/228 = 0.32
40/172 = 0.23
132/172 = 0.77

Question 19.
Construct a two-way table using the data below.

M represents participarted in a marathon
NM represents not participarted in a marathon
F represents member of a fitness club
NF represents non-member of a fitness club
Answer:

Problem Solving

Refer to the scenario below to answer questions 20 to 27.

A bank wants to reduce the number of hours that its tellers work per month. To do this, more Automated Teller Machines (ATMs) are installed in the branch offices. The table below shows the number of ATMs, x, in the branch offices and the corresponding number of hours per month, y, that its tellers work.

Question 20.
Use graph paper to construct the scatter plot for the above bivariate data. Use 1 centimeter on the horizontal axis to represent 1 ATM. Use 1 centimeter on the vertical axis to represent 10 hours for the y interval from 80 to 230.
Answer:

Question 21.
Describe the association between the number of hours that tellers work and the number of ATMs.
Answer: By seeing the above graph we can say that as the number of ATMs increases, the number of hours that tellers work decreases.

Question 22.
Identify the outlier(s).
Answer:(10,110)

Question 23.
Draw a line of best fit.
Answer:

Question 24.
Write an equation for the line of best fit.
Answer:
The target of this task is to give the equation of the Line of best fit for the scatter pLot of the number of ATMs to the number of hours teller works.

For the equation of the line of best fit, use points that the best fit Une passes through, (7, 156) and (12, 88), to solve for the slope of the line. The slope of the line equates the difference of y₂ to y₁ over the difference of x₂ to x₁. Then, let m be the slope, (7, 156) be (x₁, y₁) and(12. 88) be (x₂, y₂) so
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)   Slope Formula
= \(\frac{88-156}{12-7}\)  Subtraction
= \(\frac{-68}{5}\)  Subtract
= -13.6   Simplify
Next, use the slope-intercept form to determine the equation of the straight Line given by y = mx ± b, where m is the slope, b is the y-intercept, and (7, 156) be (x, y) then
y = mx + b     Slope-intercept Form.
156 = -13.6(7) + b     Substitution.
156 = -95.2 + b     Multiply.
156 + 95.2 = -95.2 + b + 95.2    Add 95.2 to both sides.
251.2 = b    Simplify.
Lastly, using the slope-intercept form again, [et rn be the sLope equals to -13.6 and b equals to 251.2. thus
y = mx + b   Slope-intercept Form.
y = -13.6x + 251.2 Substitution.
Therefore, the equation of the line of best fit is y = -13.6x + 251.2.

Question 25.
Using the equation in 24, predict the number of teller hours required per month when there are 2 ATMs.
Answer:
The goal of this task is to give the approximate hours the tellers wiLl work per month using the graph if there are 2 Automated Teller Machines.

To estimate the hours tellers work y given the number of ATMs x, study the graph then note at what point does x equals to 2 meets y. The point is on (2, 224). Therefore, if there only exist 2 Automated Teller Machines in the branch office, then telLers would have to work around 224 hours per month.

Question 26.
Using the equation in 24, predict the number of teller hours required per month when there are 15 ATMs.
Answer:
The objective of this task is to calculated using the equation of the Line y = -13.6x + 251.2 the total hours the tellers will work per month if there are 15 Automated Teller Machines.

To compute the tellers hours per month if there exist 15 ATMs in the office branch, note that the teller hours is denoted as y and the number of ATMs is denoted as x. Then when x is 15.
y = -13.6x + 251.2    Equation of the line.
= -13.6(15) + 251.2    Substitution.
= -204 + 251.2    Multiply.
= 47.2    Simplify.
Therefore, when using the equation y = -13.6z + 251.2. the total hours the tellers work would be 47.2 if there are 15 ATMs.

Question 27.
Math Journal Explain why the equation is 24 cannot be used to predict the number of teller hours required per month for more than 30 ATMs. Discuss the accuracy of the prediction.
Answer:
The goal of this task ¡sto prove that the equation y = -13.6x + 251.2 to make a prediction for the length of working hours when there are 20 Automated Teller Machines, then describe how accurate this kind of prediction is. If 20 is to be substituted to the equation,
y = -13.6(20) + 251.2 = -20.8
The negative value of time that the equation provided makes it impossible to utilize the equation. Next rote that the association of number of ATMs to the number of hours teller works is weak, negative and linear The weak association makes it hard to tell a relationship or pattern of the two variables. Therefore, the prediction is not very right.

Refer to the scenario below to answer questions 28 to 32.

A survey is conducted to find out if providing nutrition information on the menu affects whether patrons recommend the restaurant to others.

P represents provide nutritional information
NP represents do not provide nutritional information
R represents recommend
NR represents do not recommend

Question 28.
Construct a two-way table using the above data.
Answer:
The objective of this task ¡s to make a two-way table of the survey about being aware of the nutrition of the foods and the customer recommendation.

Since there are two categories in the survey, the information about the nutrients of the food and the customer recommendation, then the two-way table will. be divided into these categories. Observe that there are 6 who are provided with information and recommended the restaurant, S was not given an information about the nutrition but still recommends it, 2 who were provided with this info but did not recommend the place, and 1 are not given information and did not recommended the restaurant.

Question 29.
Are there greater or fewer people that are informed of the nutrition of the food they eat?
Answer:
The goal is to determine if there are bigger or smaller population of people who are aware of the nutrition of the food they consume. Notice that the total number of people who answered no” when asked whether they have the nutritional information is greater than those who answered ‘yes’ Therefore, the are lesser number of people who are conscious of the nutrition of food they are taking.

Question 30.
Find the relative frequencies among the rows, and interpret their meanings. Round your answer to the nearest hundredth where necessary.
Answer:
The objective is to solve for the relative frequencies from the survey about preferred sports among the girls and boys.

To determine the relative frequency, divide each of the frequency of those who are aware of the nutritional information to the total number of those who recommend and do not recommend the restaurant Also, divide the frequency of those who are not provided with the nutritional information to the total number of those who recommend and do not recommend the restaurant.

From the table, observe that the highest reLative frequency obtained is the one where nutritional facts are not provided so the customers did not recommend the shop.
Therefore, when the owners refuse to give the nutritional information, the number of people who do not recommend the restaurant increases.

Question 31.
Find the relative frequencies among the columns, and interpret their meanings. Round your answer to the nearest hundredth where necessary.
Answer:
The objective is to solve for the relative frequencies from the survey about preferred sports among the girLs and boys.

To determine the relative frequency, divide each of the frequency of those who recommend the restaurant to the total number of those who are provided by nutritional information and to the total number of those who are not given the nutritional information. Also, divide the frequency of those who does not recommend the restaurant to the total number of those who are aware of nutritionaL information and to the total number of those who are not aware of the nutritional information.

Observe that the highest relative frequency is obtained is the one where nutritional facts are provided so the customers recommend the shop. Therefore, as the nutritional information is lay out by the restaurant owner, the number people who recommend the restaurant increases.

Question 32.
Math Journal Would you recommend that restaurant owners provide nutrition information for the menu items to their customers? Explain.
Answer:
The objective of this task is to make a recommendation on whether owners of restaurant lay out the nutritional facts of the food they serve. Since when the nutritional information is given by the restaurant owner, the number people who recommend the restaurant increases. On the other hand, when the owners refuse to give the nutritional information, the number of people who do not recommend the restaurant increases. Therefore, it is a good suggestion to the owners to give information about the food they serve for their customers to also recommend their shop to others.

This handy Math in Focus Grade 8 Workbook Answer Key Chapter 10 Lesson 10.3 Two-Way Tables detailed solutions for the textbook questions.

Math in Focus Grade 8 Course 3 B Chapter 10 Lesson 10.3 Answer Key Two-Way Tables

Math in Focus Grade 8 Chapter 10 Lesson 10.3 Guided Practice Answer Key

Solve.

Question 1.
A survey asked 1,000 gym members what type of exercises they do when they visit the gym. The results are recorded in a two-way table as shown.

a) Find the total number of male gym members surveyed.
Total number of males = Total surveyed – Total number of females
= –
=
The total number of male gym members surveyed is .
Answer:
Total number of males = Total surveyed – Total number of females
= 1000 – 481
= 519
The total number of male gym members surveyed is 519.

b) Find the number of male gym members who chose both types of exercises.
Number of males who chose both
= Total number of males – Number of males who chose cardios – Number of males who chose weights
= – –
=
The number of male gym members who chose both types of exercises is .
Answer:
Number of males who chose both
= Total number of males – Number of males who chose cardios – Number of males who chose weights
= 519 – 125 – 279
= 115
The number of male gym members who chose both types of exercises is 115.

c) Find the total number of gym members who chose cardio exercises.
Total number of members who chose cardios
= Number of males who chose cardios + Number of female who chose cardios
= ___ +____
= __
The total number of gym members who chose cardio exercises is ___.
Answer:
Total number of members who chose cardios
= Number of males who chose cardios + Number of female who chose cardios
= 125 +295
= 420
The total number of gym members who chose cardio exercises is 420.

Question 2.
An athletic club owner wants to know which cardio exercise is most popular: cycling, running, or swimming. The owner is also interested in whether athletic club members read sports magazines. He surveys 20 randomly selected athletic club members. Results are shown below.

C represents cycling
R represents running
S represents swimming
Y represents read sports magazines
N represents do not read sports magazines

a) Summarize the data into a two-way table.
Answer:

b) Which cardio exercise do club members prefer?
The total number of members who chose cycling, running, and swimming is , , and respectively. So members prefer .
Answer:
By seeing the above table we can know how many members prefer cardio exercise.
The total number of members who chose cycling, running, and swimming is 6, 9, and 5 respectively. So members prefer running.

c) What percent of club members read sports magazines?
The total number of club members surveyed is .
The number of people that read sports magazines is .
Percent of participants that read sports magazines is .
Answer:
The total number of club members surveyed is 20.
The number of people that read sports magazines is 10.
Percent of participants that read sports magazines is 50%.

d) Describe any association between the type of cardio exercise that the club members prefer and whether the members read sports magazines.
The number of cyclists, runners, and swimmers that read sports magazines is , , and . So, more prefer to read sports magazines.
There is association between the type of cardio exercise that the club members prefer and whether the members read sports magazines.
Answer:
The number of cyclists, runners, and swimmers that read sports magazines is 5, 2, and 3. So, more cyclists prefer to read sports magazines.
There is no association between the type of cardio exercise that the club members prefer and whether the members read sports magazines.

Copy the table. Solve. Round your answer to the nearest hundredth where necessary.

Question 3.
A survey asked 1,000 gym members what type of exercises they do when they visit the gym. The results are recorded into a two-way table as shown.

a) Find the relative frequencies to compare the distribution of genders among each type of exercises.

Answer:

b) Describe the distribution of male and female gym members for each type of exercises.
More members do cardio exercises than members.
More members do weight exercises than members. Among those who do both types of exercises, it is distributed between male and female gym members, with slightly more  members.
Answer:
More female members do cardio exercises than male members.
More male members do weight exercises than female members. Among those who do both types of exercises, it is almost evenly distributed between male and female gym members, with slightly more female members.

c) Find the relative frequencies to compare the distribution of the type of exercises among each gender.

Answer:

d) Describe the distribution of male and of female gym members for each type of exercises.
Among male members, most do exercises and least do exercises.
Among female members, most do exercises and least do exercises.
Answer:
Among male members, most do weight exercises and least do both exercises.
Among female members, most do cardio exercises and least do weight exercises.

Math in Focus Course 3B Practice 10.3 Answer Key

Identify the categorical data.

Question 1.
Temperature, Weight, Color
Answer: Color

Question 2.
Street name, Number of boxes. Time
Answer: Street name

Identify whether the given data is categorical or quantitative.

Question 3.
Large, medium, small
Answer: categorical

Question 4.
20 mi/h, 40 mi/h, 50 mi/h
Answer: quantitative

Use the two-way table to answer questions 5 to 9.

In some states, all passengers in a vehicle are required to wear a seat belt when the vehicle is on a public road. A poll of 275 randomly selected vehicle passengers was conducted in a state that has the seat belt law to determine the association between passengers who know the seat belt law and passengers who obey this law.

Question 5.
Find the number of passengers who wear seat belts.
Answer:
Number of passengers = Total randomly selected vehicle passengers – Number of passengers not wearing seat belts.
275 – 50 = 225

Question 6.
Find the number of passengers who wear seat belts and do not know the seat belt law.
Answer:

Question 7.
Find the number of passengers who do not wear seat belts and know the seat belt law.
Answer: 50 – 15 = 35

Question 8.
Describe what you can see in the data from the row totals and column totals.
Answer: From the table, we observe the number of passengers who wear seat belts and the number of passengers who know seat belt law.

Question 9.
Is there any association between the passengers who know the seat belt law and passengers who obey the seat belt law?
Answer: From the table, we observe the number of passengers who know the seat belt law and passengers who obey the seat belt law.

Use the data below to answer questions 10 to 12.

A survey of 24 households shows whether they save a portion of their income regularly and whether they have life insurance.

S represents save regularly
NS represents do not save regularly
L represents have life insurance
NL represents do not have life insurance

Question 10.
Arrange the above data into a two-way table.
Answer:
The objective of this task is to make a two-way table of the survey about whether the household has a life insurance and if they regularly save a part of their salary.

Since there are two categories in the survey, whether they save regularly a portion of their earnings and if they have life insurance, then the two-way table will be divided into this categories. Observe that there are 8 homes that has savings and insurance, 3 homes do not have savings but they have life insurance and another 3 have savings but do not have life insurance. Lastly, there are 10 households that do not have both savings and life insurance.

Question 11.
Do more or fewer households have life insurance than not? Support your answer with the given data.
Answer:
The target of this task is to compare the number of household that has a life insurance and to does who does not have.

Observe the two-way table. Notice that there are 11 houses that have life insurance and 13 who does not have. Therefore, there are fewer households that acquire life insurance than do not have.

Question 12.
Is there any association between households that save regularly and households that have life insurances? Justify your answer from the data.
Answer:
The goal is to verify the relation of the households that regularly save a portion of their income to the homes with life insurance.

Households with savings tend to have life insurance compared to households who do not save since there are 8 households who have savings and insurance, but only 3 households who do not have savings and possess a life insurance.

Use the table to answer questions 13 to 15.

The table below shows whether the sales target of salesperson are met and whether they are paid on commission.

Question 13.
Find the relative frequencies among the rows, and interpret their,L meanings. Round your answer to the nearest hundredth where necessary.
Answer:
245/330 = 0.74
85/330 = 0.26
12/76 = 0.16
64/76 = 0.84

Question 14.
Find the relative frequencies among the columns, and interpret their meanings. Round your answer to the nearest hundredth where necessary.
Answer:
245/257 = 0.95
12/257 = 0.04
85/149 = 0.57
64/149 = 0.43

Question 15.
Describe the association between a salesperson meeting the sales target and whether the salesperson is paid on commission.
Answer:
Salesperson those who are not paid on commission tend not to meet the sales target, while salesperson who are paid on commission tend to meet the sales target.

Brain @Work

Question 1.
Mindy was shown two scatter plots.
a) The diagram below shows the first scatter plot.

Mindy concluded that there is a linear association between the bivariate data. But her teacher told her she is wrong. Explain why her teacher says so.
Answer: We can see some data missing points in the above graph between the interval that has no data points, it may not be necessary to follow linear trend.

b) The diagram below shows the second scatter plot.

Mindy concluded that there is a linear association between the bivariate data. Her teacher disagree with her. Explain why.
Answer:
There are only 3 data points and that is an insufficient amount of data to conclude the association between the bivariate data.

Question 2.
A school principal conducted research to find out about students learning a second language and students learning music. He surveyed 500 students, and the relative frequencies of the data are shown below.

a) The total number of students who are learning second language is 200. Find the total number of students who are and who are not learning music.
Answer: 200 × 90/100 = 180
200 × 10/100 = 20
500 – 200 = 300
300 × 45/100 = 135
300 × 55/100 = 165
total number of students who are not learning music = 20 + 165 = 185
total number of students who are learning music = 180 + 135 = 315

b) Represent the actual data in a two-way table.
Answer:

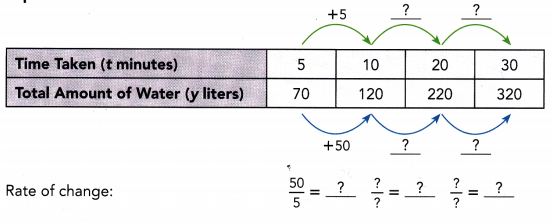
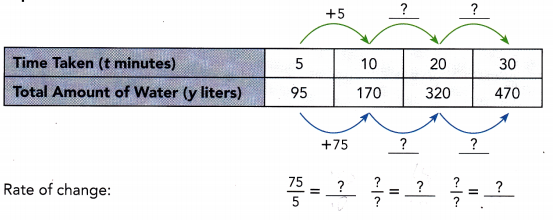
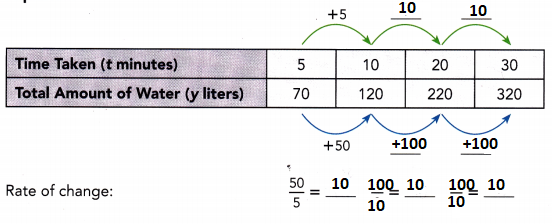
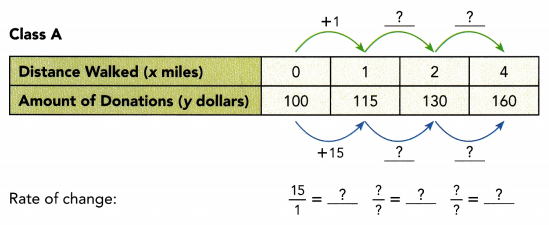
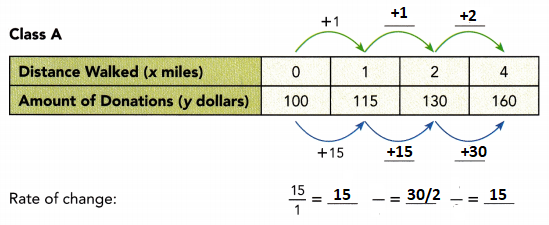
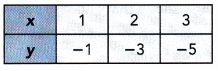
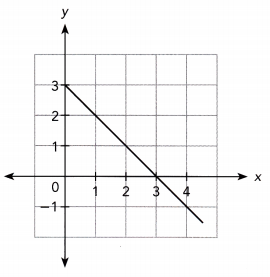
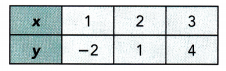
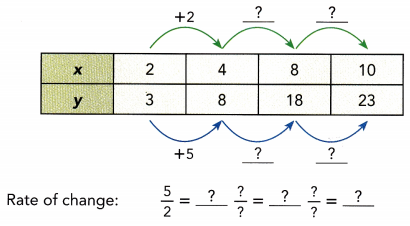
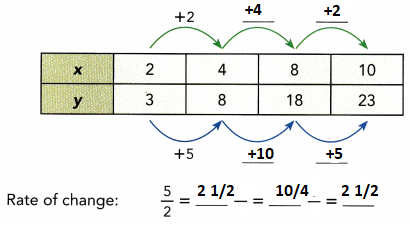
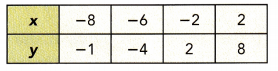
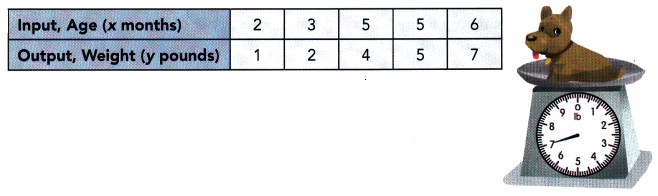
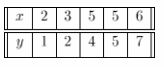
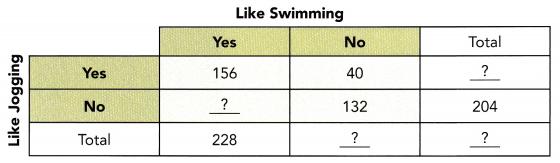
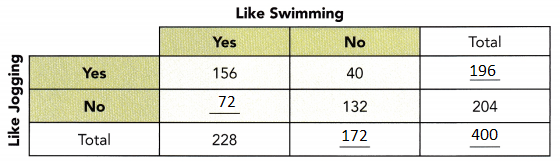
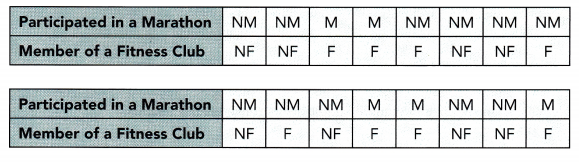
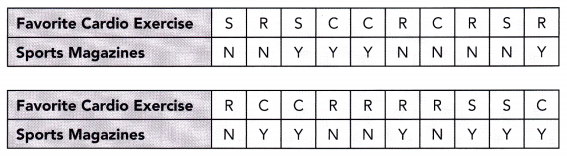
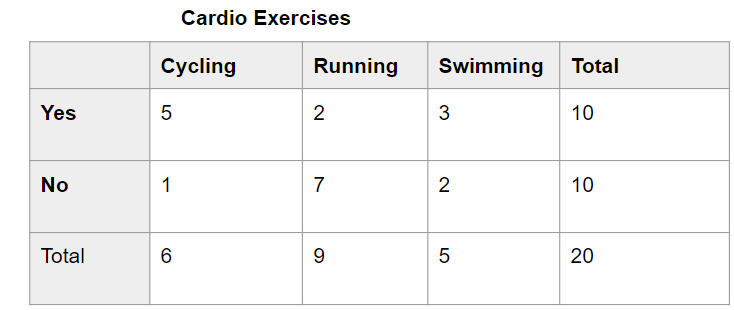
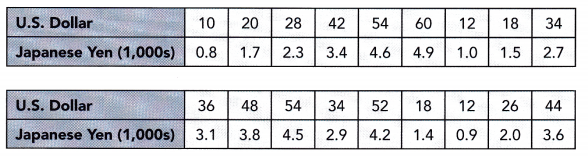
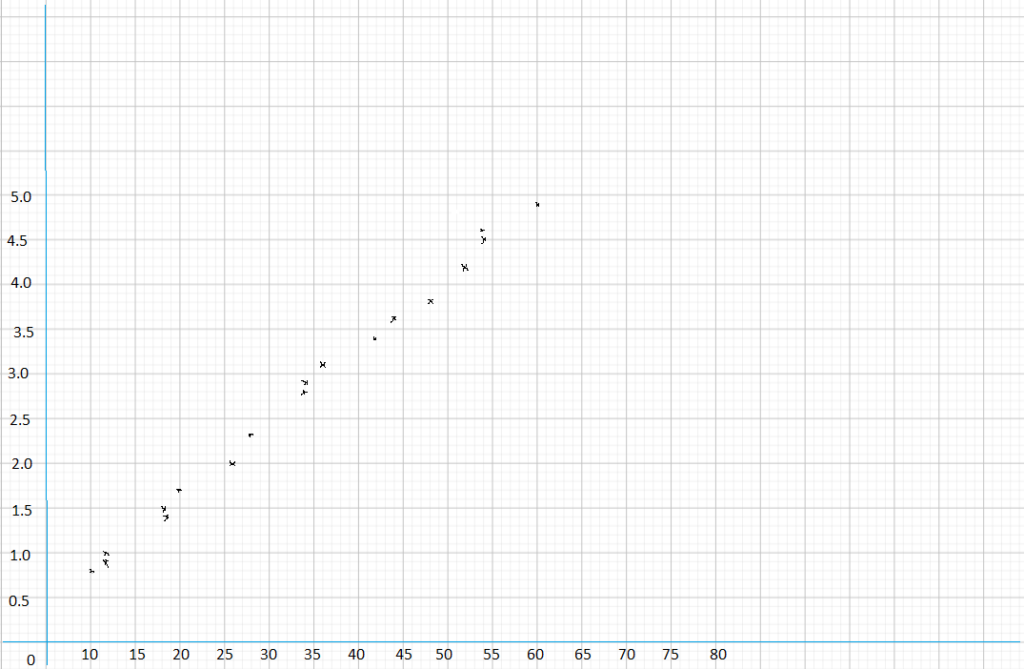
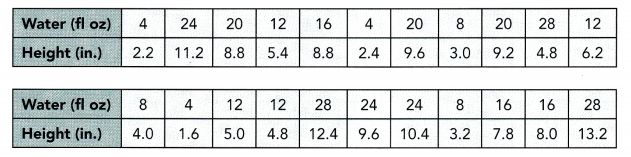
This handy Math in Focus Grade 8 Workbook Answer Key Chapter 10 Lesson 10.2 Modeling Linear Associations detailed solutions for the textbook questions.

Math in Focus Grade 8 Course 3 B Chapter 10 Lesson 10.2 Answer Key Modeling Linear Associations

Hands-On Activity

Materials:
measuring tape

CONSTRUCT AND INTERPRET SCATTER PLOTS

Work in groups of 5.

Background
A person’s height is closely associated with their arm span. In a medical context, this association can be used to estimate realistic lengths for prosthetic limbs. In this activity, you will collect data on the heights and arm spans of classmates.

STEP 1: Measure the arm span of one group member while he or she is standing straight up against a wall with arms stretched out from the body and with all the fingers extended fully. Measure the arm span from the tip of the middle finger of one hand all the way to the other middle finger on the other hand.

STEP 2: While in the same position, use a ruler to mark the member’s height on the wall. While holding the ruler, ask the member to step away so you can measure the height.

STEP 3: Repeat STEP 1 and STEP 2 with the other group members.

STEP 4: Organize the data in a table like the one shown below.

STEP 5: Collect data from all the groups. Construct a scatter plot with the collected data.

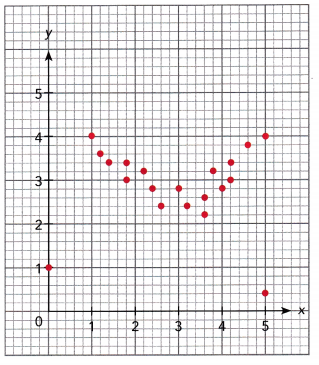
Math Journal From the scatter plot drawn, describe any association you see between the height and arms span.
Using the collected data, obtain a measure for the arm span of a schoolmate. Use the scatter plot to predict his or her height. Compare your estimations with the actual measurements to find how accurate the estimate is.
Answer:

Math in Focus Grade 8 Chapter 10 Lesson 10.2 Guided Practice Answer Key

Use graph paper. Solve.

Question 1.
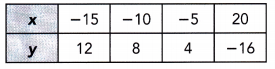
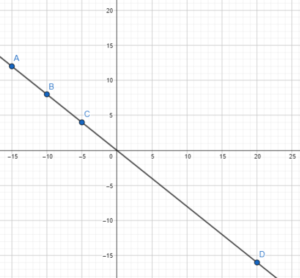
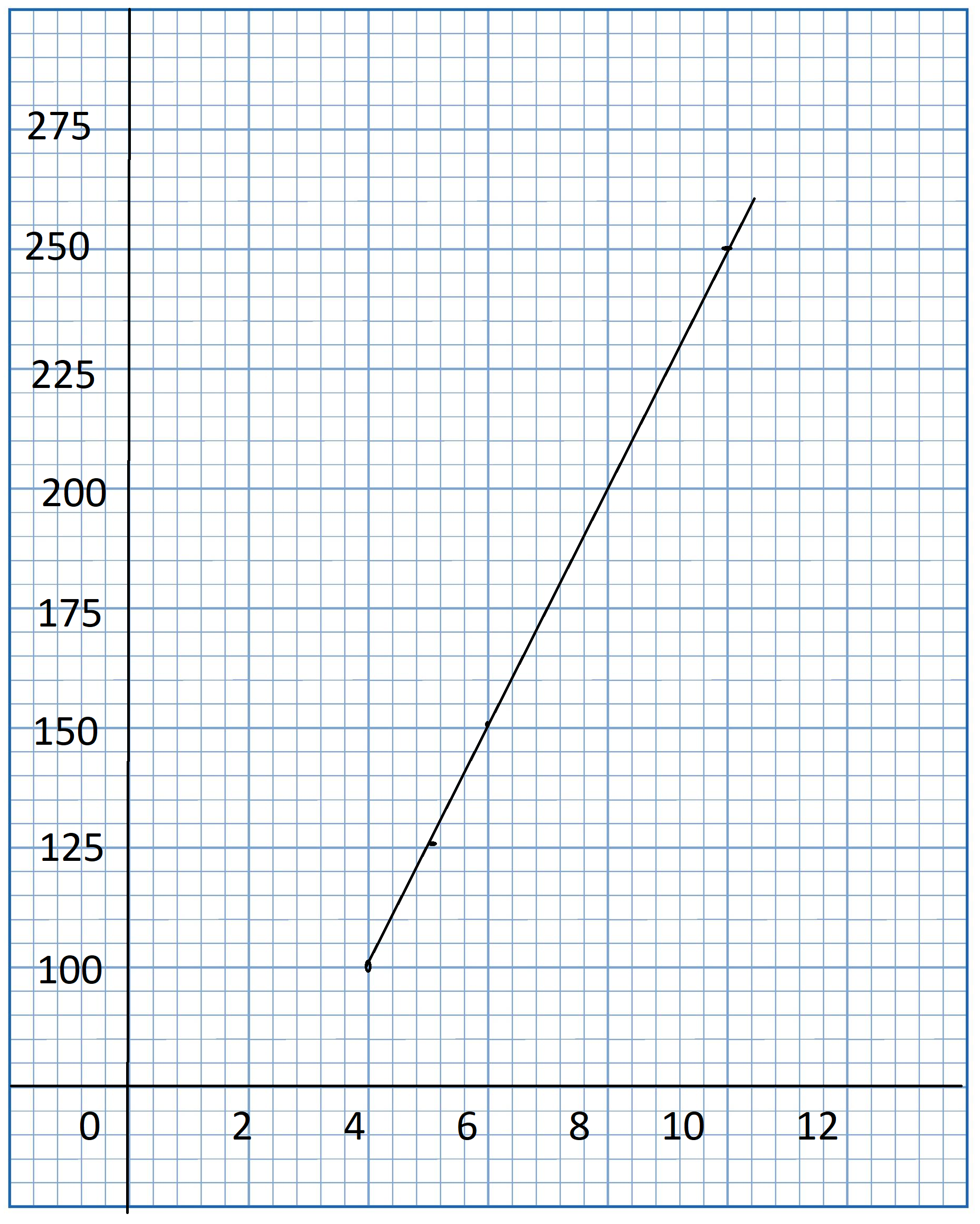
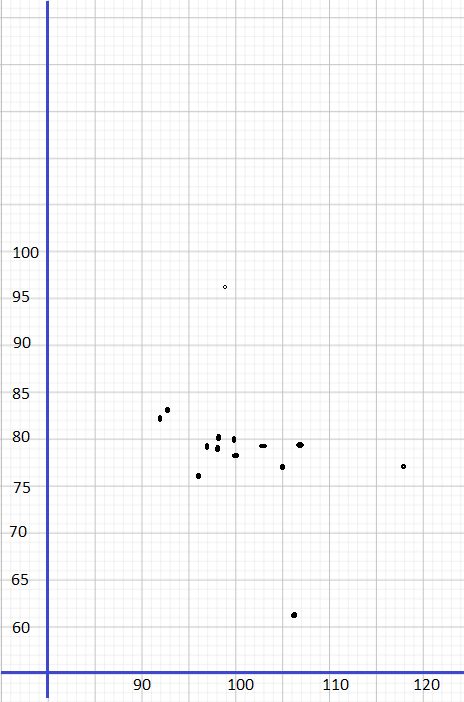
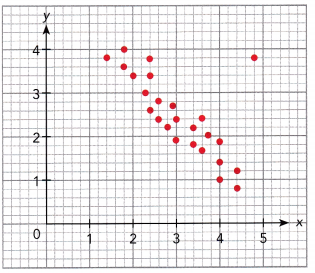
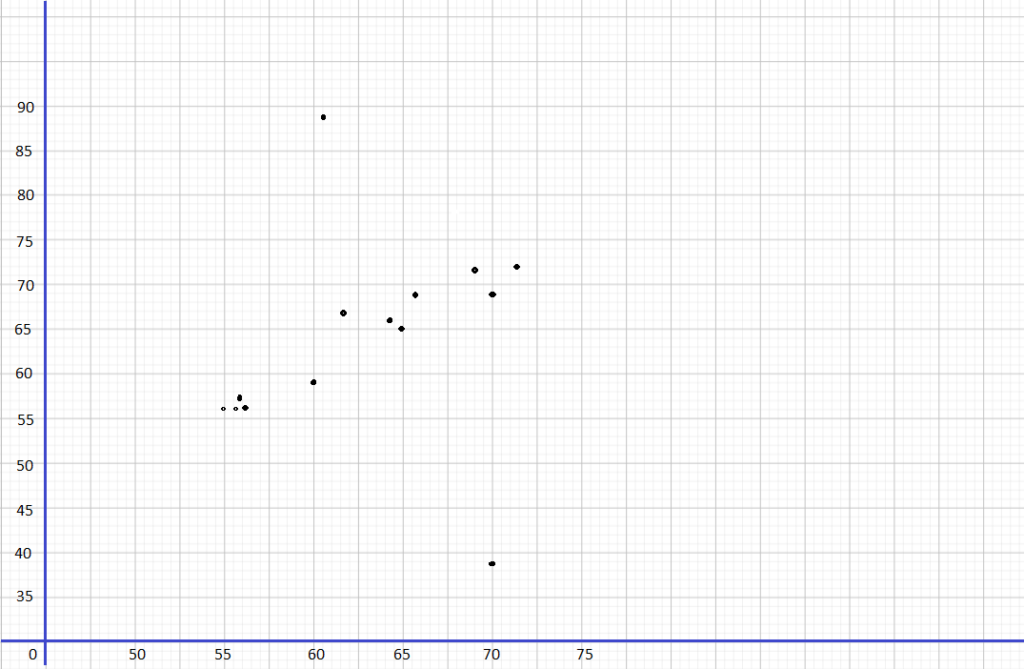
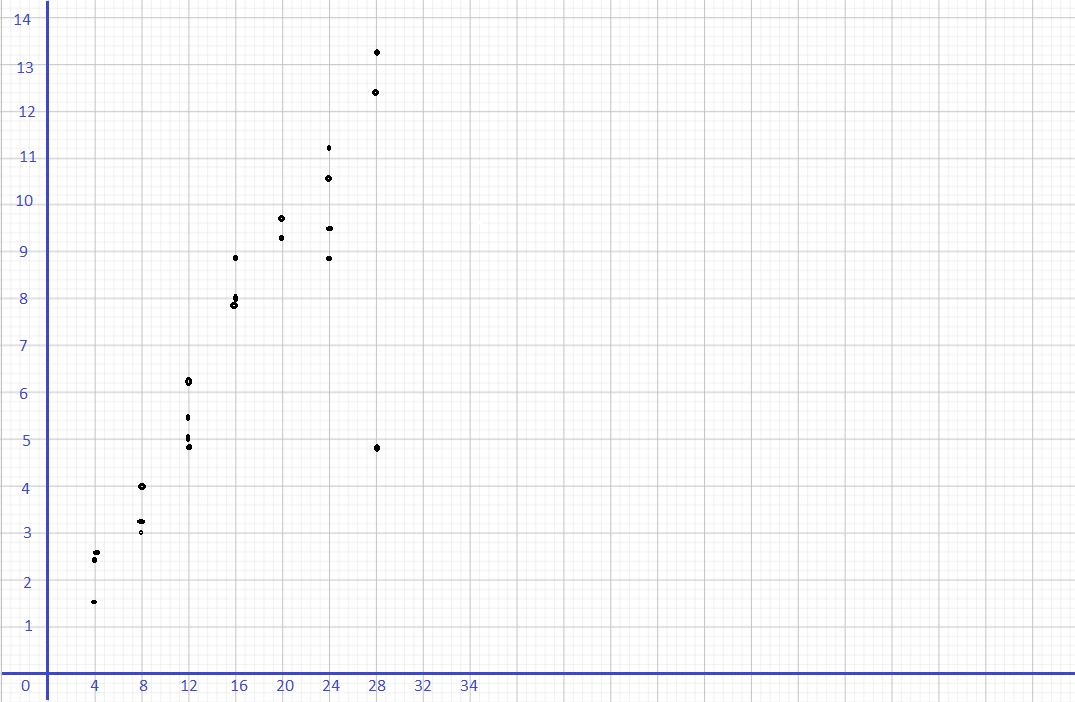
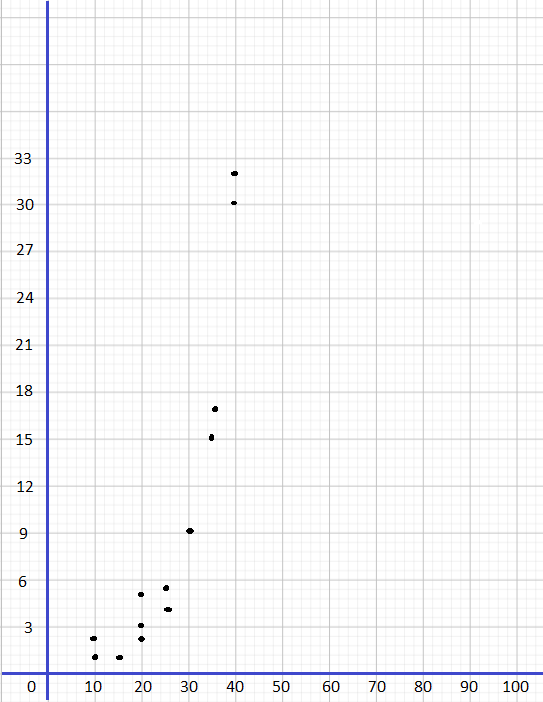
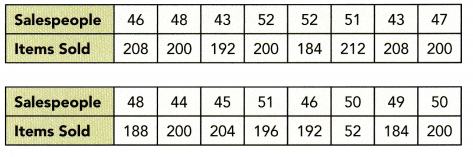
A city collected data over the course of a week to find the association between the number of waste bins per acre, x, in their parks and the pounds of litter collected, y pounds, in each bin. The data is shown below.

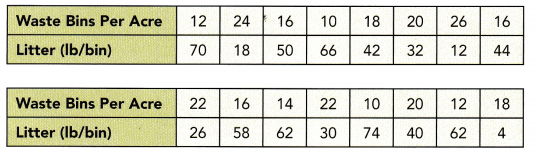
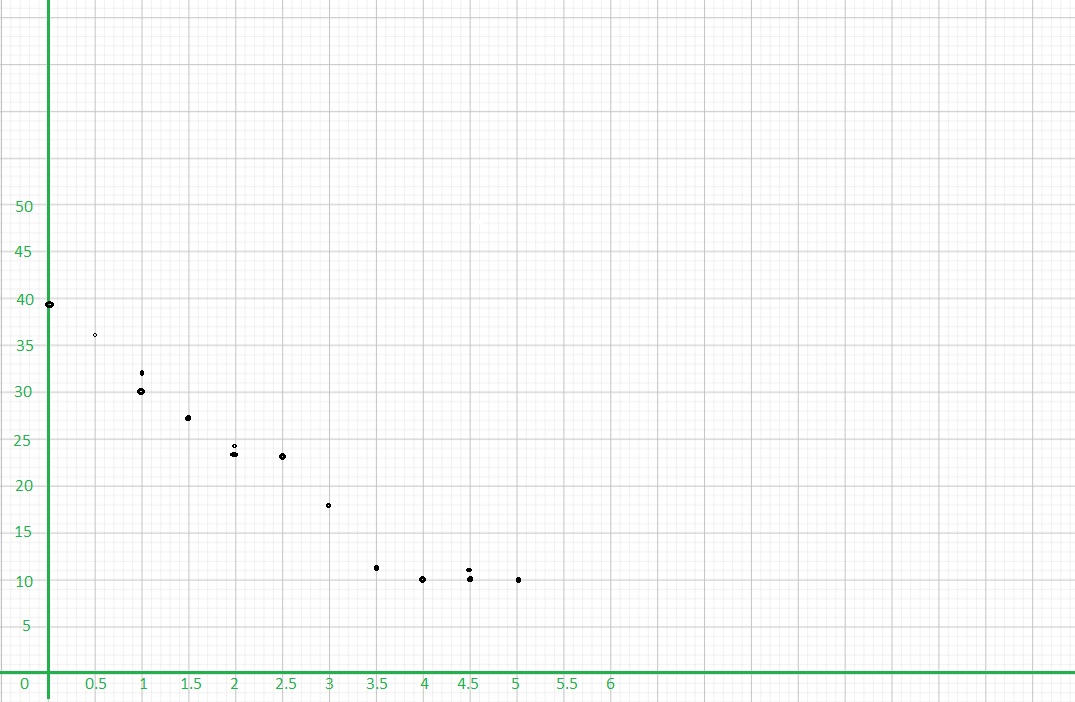
a) Construct a scatter plot for this data. Use 1 centimeter on the horizontal axis to represent 2 waste bins per acre for x interval from 8 to 26. Use 1 centimeter on the vertical axis to represent 5 pounds of litter per week. Sketch a line of best fit for the given table of data.
Answer:
Observe that

• 12 bins per acre corresponds to 70 lbs of litter,
• 24 waste bins has 18 pounds of trash,
• 16 waste bins per acre means 50 Lbs. of garbage,
• 10 bins per acre, 66 pounds of litter are coLlected,
• 18 bins per acre corresponds to 42 lbs. of Litter,
• 20 waste bins has 32 pounds of trash,
• 26 waste bins per acre means 12 lbs. of garbage,
• 16 bins per acre, 44 pounds of litter are collected,
• 22 bins per acre corresponds to 26 lbs. of Litter,
• 16 waste bins has 58 pounds of trash,
• 14 waste bins per acre means 62 Lbs. of garbage,
• 22 bins per acre, 30 pounds of litter are collected,
• 10 bins per acre corresponds to 74 lbs. of litter,
• 20 waste bins has 40 pounds of trash,
• 12 waste bins per acre means 62 Lbs. of garbage, and
• 18 bins per acre, 4 pounds of Utter are coLLected.

Note that the Line of best fit is a straight line that best shows the data on a scatter plot Therefore, the scatter plot would be as depicted below.

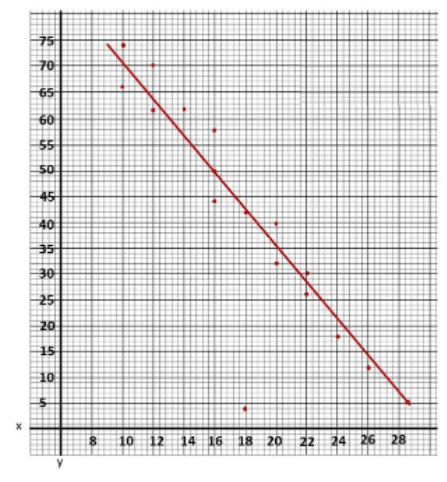
b) Identify the association and describe the meaning of the association in context.
There is a , , and association between the number of waste bins per acre and the pounds of litter collected per bin.
Answer:
The scatter plot shows a strong, negative and linear association which indicates that the more waste bins per acre in the city the lesser the pounds of litter collected.

c) Identify the outlier and describe the outlier in context.
The data point (, ) is an outlier representing only pounds of litter collected per bin when there are waste bins per acre in the park.
Answer:
The outlier is the data that is very different from the rest in a set Notice the outlier is the point that is away from then line, in this case, observe the best-fit line, then the point isolated to it is at (18, 4). The outlier represents 18 waste bins per acre and a litter of 4 pounds.

Question 2.
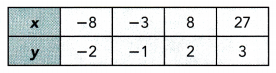
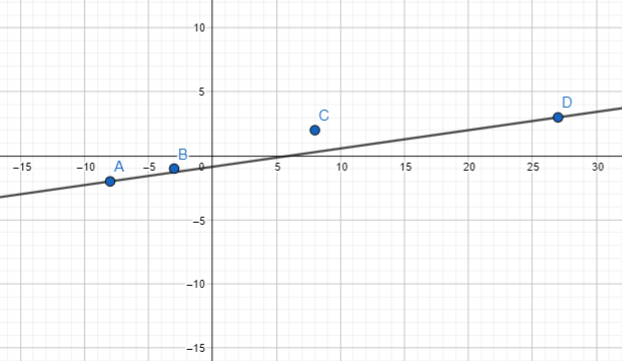
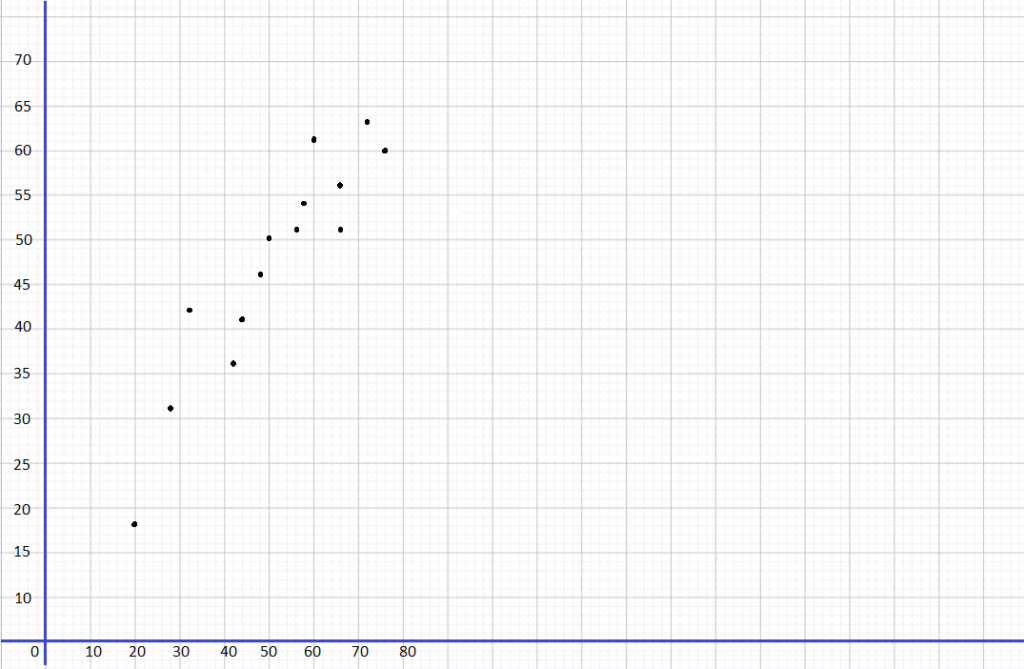
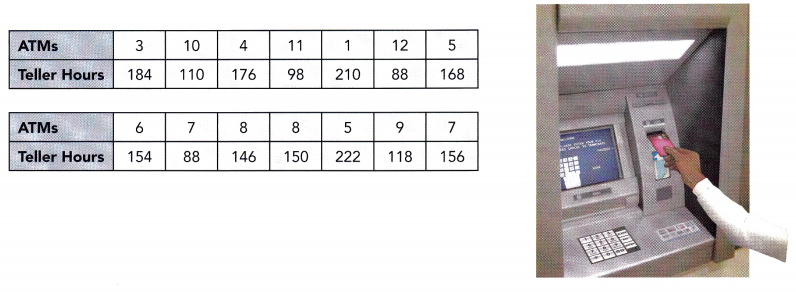
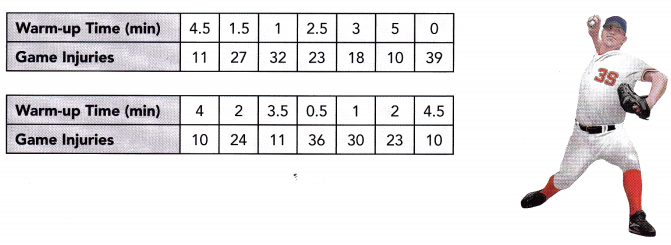
A city collected data to find the association between the daily high temperature, x °F, and the number of pool visitors, y, that day. The data is shown below.

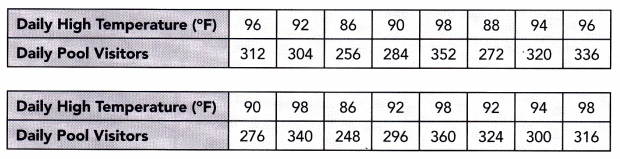
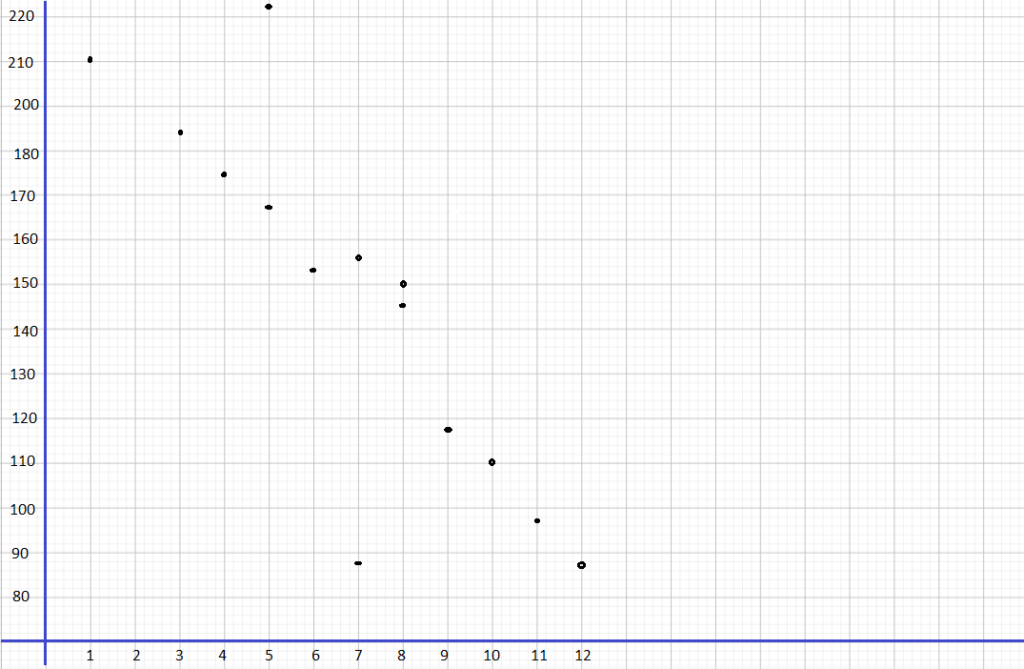
Construct a scatter plot for this data. Use 1 centimeter on the horizontal axis to represent 2°F on the x interval from 84 to 98. Use 1 centimeter on the vertical axis to represent 10 pool visitors on the y interval from 220 to 360. Sketch a line that appears to best fit the data and write its equation.
Answer:
The objective is to make a scatter plot daily high temperature and daily pool visitor, give the line of best fit for the scatter plot and the equation for it

Observe that when the temperature is 96 F the pool visitors are 312. a 92° F temperature in the city makes 304 visitors, the city has 256 pool visitors when the temperature is at 86°F, when the temperature is 90° the pool visitors are 284, a 98°F temperature in the city makes 332 visitors, the city has 88 pool visitors when the temperature is at 272°F, when the temperature is 94°F the pool visitors are 320. a 96°F temperature in the city makes 336 visitors, the city has 276 pool visitors when The temperature is at 90°F, when the temperature is 98°F the pool visitors are 340, a 86 F temperature in the city makes 248 visitors, the city has 296 pool visitors when The temperature is at 92°F, when the temperature is 98°F the pool visitors are 360, a 92°F temperature in the city makes 324 visitors, the city has 300 pool visitors when The temperature is at 94°F, and when the temperature is 9W F the pool visitors are 316. Also, note that the line of best fit is the most possibLe straight line that best shows The data on a scatter plot Thus, the scatter plot will be as depicted below.

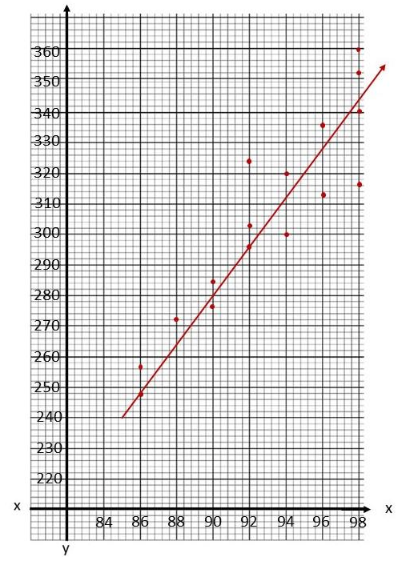
For the equation of the Line of best fit, first, use points that the best fit line passes through, (86, 248) and (92, 296), to solve for the slope of the line. The slope of the line equates the difference of y₂ to y₁ over the difference of x₂ to x₁. Then, Let in be the slope, (86, 248) be (x₁, y₁) and (92, 296) be (x₂, y₂) so
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)      Slope Formula.
= \(\frac{296-248}{92-86}\)  Substitution.
= \(\frac{48}{6}\)    Subtract.
= 8     Simplify.
Next, use the slope-intercept form to determine the equation of the straight line given by y = mx + b, where in is the slope, b is the y-intercept, and (86, 248) be (x, y) then
y = mx + b     Slope-intercept Form.
248 = 8(86) + b     Substitution.
248 = 688 + b      Multiply.
248 – 688 = 688 + b – 688    Subtract both sides by 688
-440 = b Simplify.
Lastly, using the slope-intercept form again, let m be the sLope equals to 8 and b equals to -440, thus
y = mx + b   Slope-intercept Form.
y = 8x – 440     Substitution.
Therefore, the equation of the line of best fit is y = 8x – 440.

Question 3.
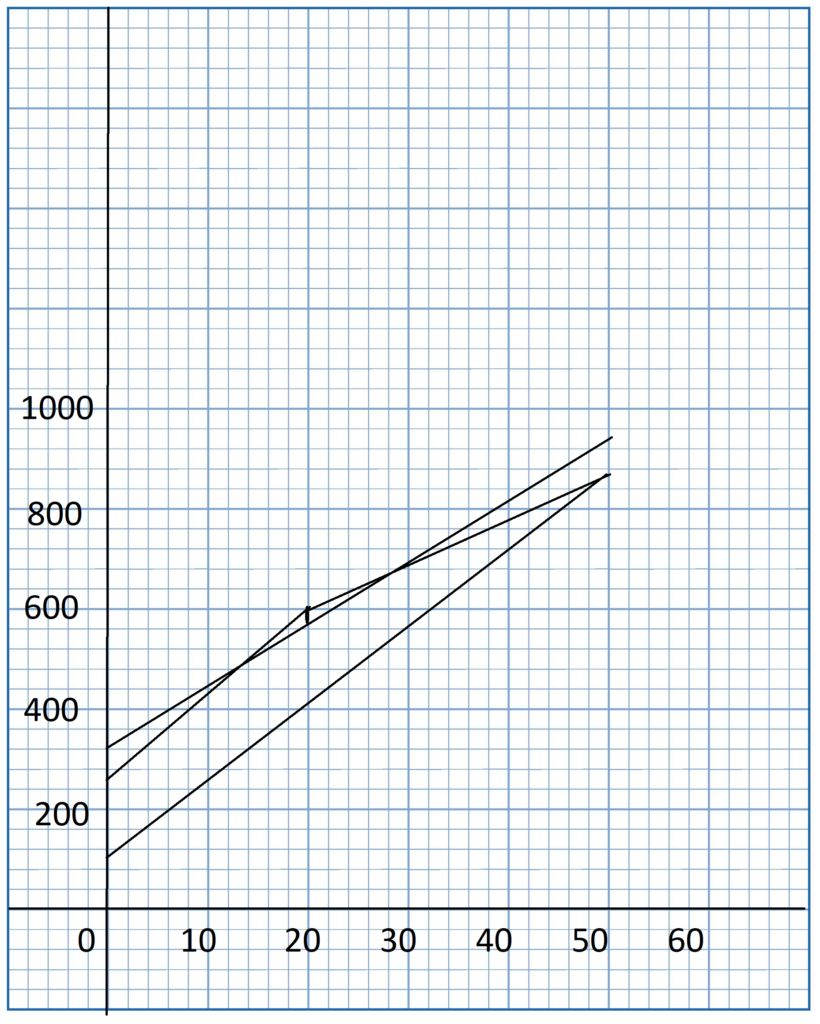
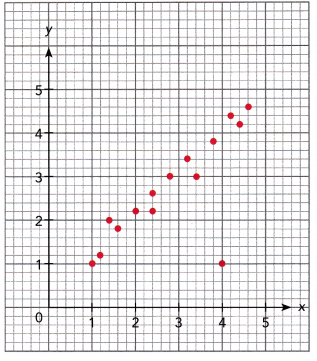
The scatter plot below shows the number of eggs hatched, y, per 100 eggs in an incubator with varying temperatures, x°F.

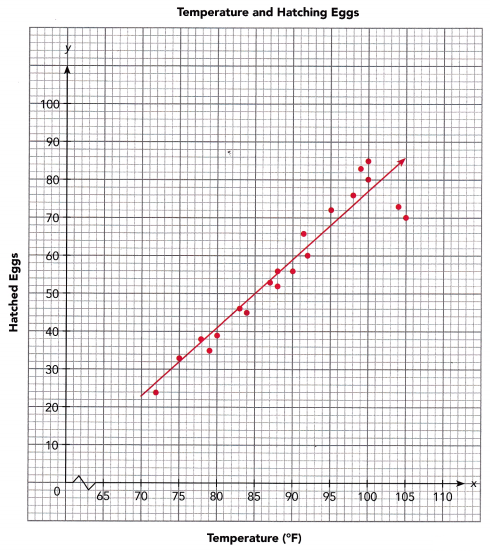
a) Given that the line of best fit passes through (80, 41) and (95, 68), find the equation of the line of best fit.
First find the slope of the line of best fit that passes through the points (80, 41) and (95, 68).
m = \(\frac{?-?}{?-?}\) = \(\frac{?}{?}\) =
Next find the y-intercept using the equation in slope-intercept form

Finally, write an equation,
y = mx + b
y = x + Substitute for m and for b.
The equation of the line of best fit is .
Answer:
a. To find the equation of the Line, compute for the slope of the Line then substitute it in the slope-intercept form together with one of the points that the line of best fit passes through. From here, b wilL be solved then use the slope-intercept form again substituting only the slope m and y-intercept b.
Determining the slope of the line, let (80. 41) be x₁ and y₁ while (95, 68) be x₂ and y₂. Then,
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)      Formula.
= \(\frac{68-41}{95-80}\)  Substitution.
= \(\frac{27}{15}\)    Subtract.
= 1.8     Simplify.
Now, let (80, 41) be (x, y), and since the slope is equal to 1.8, then,
y = mx + b    Formula.
41 = 1.8(80) + b    Substitution.
41 = 144 + b    Multiply.
41 – 144 = 144 – 144 + b    Subtract 144 From Both Sides.
103 = b    Evaluate.
Since m is equal to 1.8 and b is equal to -103, then
y = mx + b   Slope-Intercept Form.
y = 1.8x + (-103)    Substitution.
y = 1.8x – 103    Simplify.
Therefore, the equation of the line is y = 1.8x – 103.

b) Use the graph to estimate the number of eggs that would hatch per 100 eggs if the temperature of the incubator is kept at 86°F.
About eggs could be predicated to hatch if the incubator is kept at a temperature of .
Answer:
To estimate the number of hatched eggs x and the temperature of the incubator y, study the graph then note at what point does y at 86°F meets x. The point is on (52, 86). Therefore, there are 52 eggs wilt be hatched at 81°F

c) Use the equation to estimate the number of eggs that would hatch per 100 eggs if the temperature of the incubator is kept at 65°F.
Using the equation , substitute for x.
y = • – =
About eggs could be expeced to hatch when the temperature of the incubator is kept at 65°F.
Answer:
To compute the number of eggs hatched at 65°F, note that the equation of the line is y = 1.8x + b, the number of hatched eggs is denoted as y, and temperature of The incubator denoted as x. So let x be 65°F.
y = 1.8x – 103    Formula.
y = 1.8(65) – 103    Substitution.
y = 117 – 103    Multiply.
y = 14     Subtract.
Therefore, there will be 14 hatched eggs at 65°F.

Technology Activity

Materials:
graphing calculator

USE A GRAPHING CALCULATOR TO GRAPH A LINE OF BEST FIT FOR A SCATTER PLOT

Background
In the Hands-On Activity on page 186, you drew a scatter plot for the data on the heights and arm spans of all the groups. In this activity, you will learn how to construct a scatter plot and graph the line of best fit using a graphing calculator.

STEP 1: Press and select 1 : Edit to choose the edit function. Input the data for arm spans in column L1 and the data for heights in column L2. You should have at least 20 data points to interpret the data accurately.

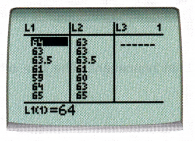
STEP 2: Press , and select 1 to go to the scatter plot setting screen. Under Type, select the scatter plot options as shown.

STEP 3: Press to see the scatter plot.

STEP 4: Press and select CALC, 4: LinReg(ax+b). Press select Y-VARS, 1 : Function and 1 :Y1. Press This step is to find the values of m and b for the line of best fit. In the graphing calculator, the value of m is denoted by a.

STEP 5: Press to see the scatter plot and the line of best fit. Press and select 9: ZoomStat to zoom in the graph.

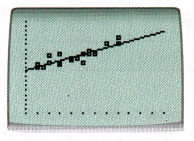
Math Journal Compare the hand drawn scatter plot and the one drawn using graphing calculator. Is there any difference between the line of best fit drawn by hand and by the graphing calculator? Compare both sets of m and b values. Discuss how you can plot a better line of best fit based on the m and b values obtained using the graphing calculator.
Answer:

Math in Focus Course 3B Practice 10.2 Answer Key

State the line that represents the line of best fit for each scatter plot.

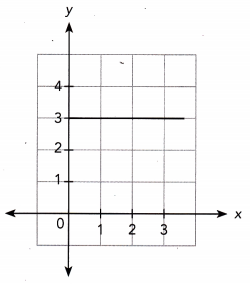
Question 1.

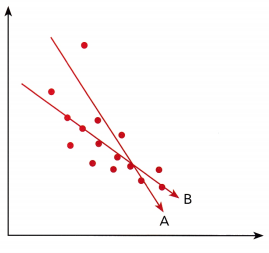
Answer:
The goal of this task is to determine the Line of best fit for the scatter plot.

Line B best fits the scatter plot It is the more possible straight line that best shows the data on a scatter plot compared to Line .4.

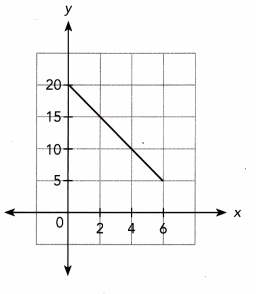
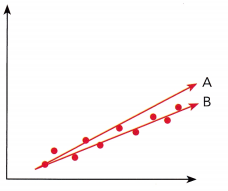
Question 2.

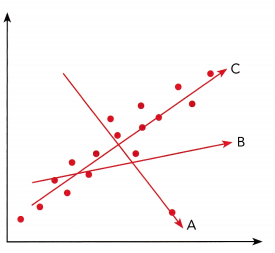
Answer:
The objective of this task is to determine the tine of best fit for the scatter plot.

Line C best fits the given scatter plot It is the most possible straight line that best shows the data on a scatter plot in comparison to line 4 and line B.

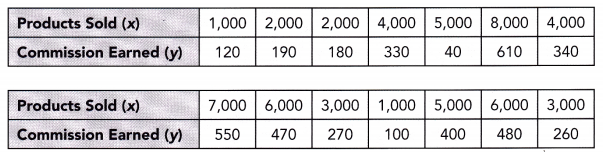
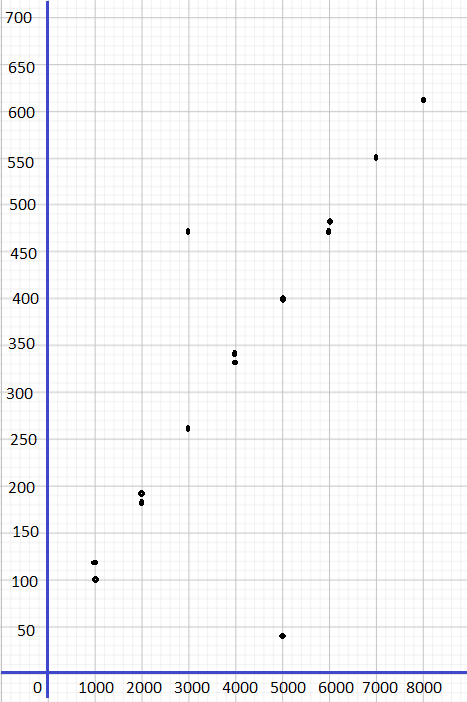
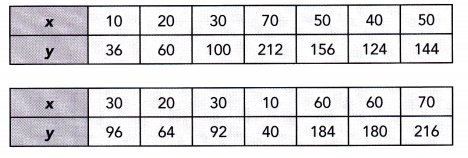
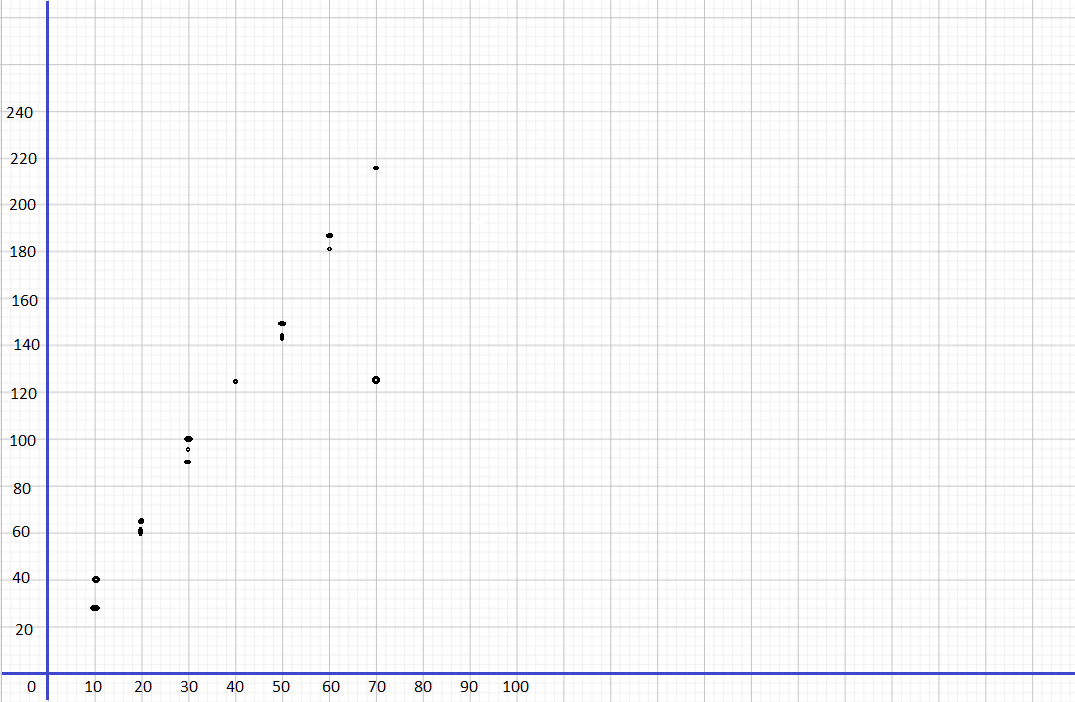
Construct each scatter plot and draw a line of best fit for each table of bivariate data.

Question 3.
Use 1 centimeter on the horizontal axis to represent 1 unit. Use 1 centimeter on the vertical axis to represent 20 units.

Answer:
The target of this task ¡s to make a scatter plot from the given values of r and y and the tine of best fit for the scatter plot.

Notice that when x is 4 y is 72, if x is equal to 1 y is equal to 12, when is equal to 2 y is 32, if z is 3 y is equal to 164, the value of y is 88 when z is 5. when z is 6 y is 112, if z is equal to 3 y is equal to 52, when z is equal to 6 y is 88, if z is 2 y is equal to 40, and the vaLue of y is 136 when z is 7. Also, the line of best fit is the most a possible straight line that best shows the data on a scatter plot Thus, the scatter plot will be as depicted below.

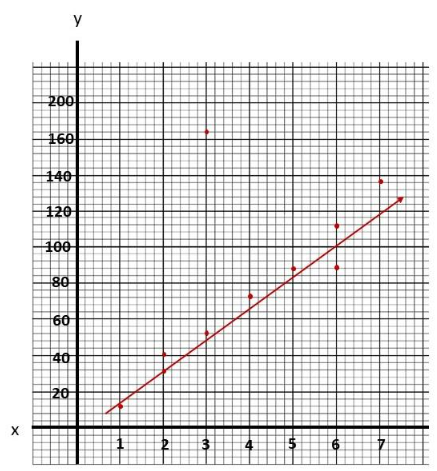
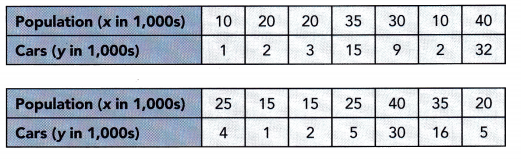
Question 4.
Use 1 centimeter on the horizontal axis to represent 1 unit for the x interval from 80 to 87. Use 1 centimeter on the vertical axis to represent 10 units for the y interval from 200 to 300.

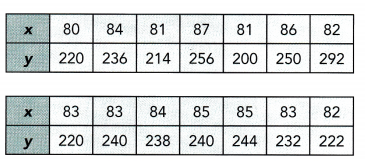
Answer:
The goal is to make a scatter plot from the given values of z and y and the line of best fit for the scatter plot.

Notice that when z is 80 y is 220, if z is equal to 84 y is equal to 236, when z is equal to 81 y is 214, if z is 87 y is equal to 256, the value of y is 200 when z is 81, when z is 86 y is 250, if z is equal to 82 y is equal to 292, when z is equal to 83 y is 220, if z is 83 y is equal to 240, the value of y is 238 when z is 84. when z is 85 y is 240, x is equal to 85 y is equal to 244, when z is equal to 83 y is 232 and if z is equal to 82 y is equal to 222. Also, the line of best fit is the most possible straight line that best shows the data on a scatter plot Thus, the scatter plot wilt be as depicted below.

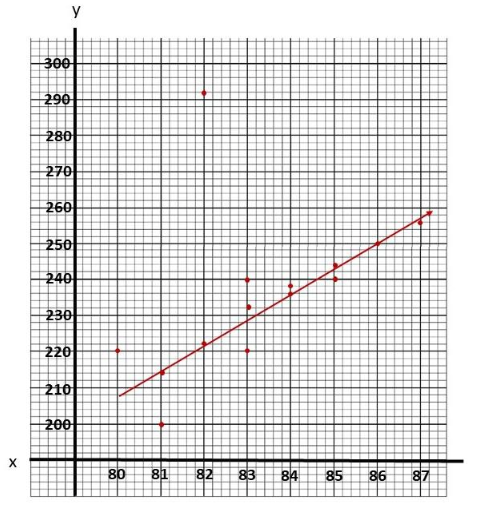
Question 5.
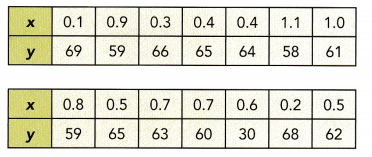
Use 1 centimeter on the horizontal axis to represent 0.1 unit. Use 1 centimeter on the vertical axis to represent 5 units for the y interval from 20 to 70.

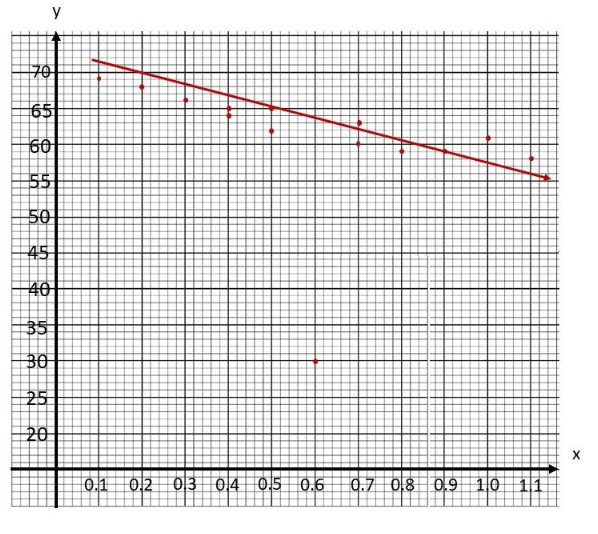
Answer:
The objective is to make a scatter plot from the given values of x and y and the line of best fît for the scatter plot

Notice that when r is 0.1 y is 69, if x is equal to 0.9 y is equal to 59, when x is equal to 0.3 y is 66, if x is 0.4 y is equal to 65, the value of y is 64 when x is 0.4, when x is 1.1 y is 58, if z is equal to 1.0 y is equal to 61, when x is equal.to 0.8 y is 59, if x is 0.5 y is equal to 65, the value of y is 63 when x is 0.7, when x is 0.7 y is 60, if x is equal to 0.6 y is equal to 30, when x is equal to 0.2 y is 68 and if x is equal to 0.5 y is equal to 62. Also, the line of best fit is the most possible straight line that best shows the data on a scatter plot Thus, the scatter plot will be as depicted below.

Construct a scatter plot and draw a line of best fit for each table of bivariate data. Find an equation of the line of best fit.

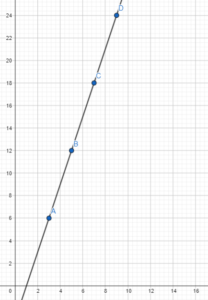
Question 6.
Use 2 centimeters on the horizontal axis to represent 1 tree for the x interval from 13 to 18. Use 1 centimeter on the vertical axis to represent 20 squirrels for the y interval from 260 to 480.

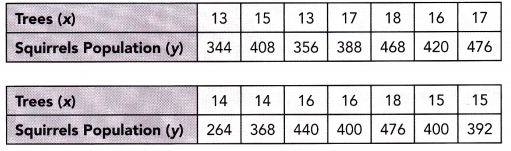
Answer:
The task is to make a scatter plot and give the tine of best fit for the number of trees and the population of squirrels then determine the equation of the line.

For the scatter plot determine at which point does the number of trees x meets its corresponding population of the squirrel y according to the table. For the tine of best fit, note that it is the most possible straight line that best shows the data on a scatter plot Thus, the scatter plot will be as depicted below.

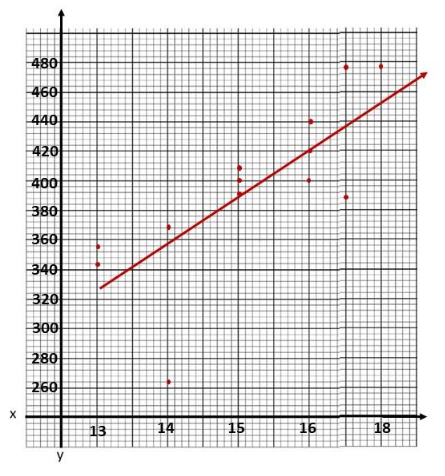
For the equation of the line of best fit, use points that the best fit Une passes through, (15. 392) and (16, 420). to solve for the slope of the line. The slope of the line equates the difference of y₂ to y₁ over the difference of x₂ to x₁. Then, let m be the slope, (15, 392) be (x₁, y₁) and (16, 420) be (x₂, y₂) so
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)       Formula.
= \(\frac{420-392}{16-15}\)    Substitution.
= \(\frac{28}{1}\)      Subtract.
= 28    Simplify.
Next use the slope-intercept form to determine the equation of the straight line given by y = mx + b, where ni is the slope, b is the y-intercept, and (15, 392) be (x, y) then
y = mx + b     Slope-intercept Form.
392 = 28(15) + b    Substitution.
392 = 420 + b    Multiply.
392 – 420 = 420 + b – 420     Subtract both sides by 420
-28 = b      Simplify.
Lastly, using the slope-intercept form again, let rn be the slope equals to 28 and b equals to -28. thus
y = mx + b      Slope-intercept Form.
y = 28x – 28    Substitution.
Therefore, the equation of the Une of best fit is y = 28x – 28.

Question 7.
Use 1 centimeter on the horizontal axis to represent 5 kilometers. Use 1 centimeter on the vertical axis to represent 1 liter for the y interval from 5 to 16.

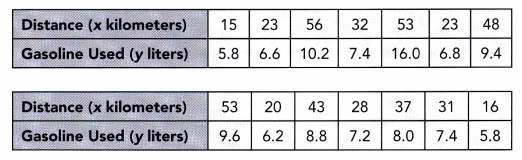
Answer:
The task is to make a scatter plot and give the line of best fit for the distance traveLled and the gasoline used then to determine the equation of the line.

For the scatter plot, determine at which point does the distance x meets the corresponding gasoline used y according to the table. For the tine of best fit, note that it is the most possible straight line that best shows the data on a scatter plot Thus, the scatter plot will be as depicted below.

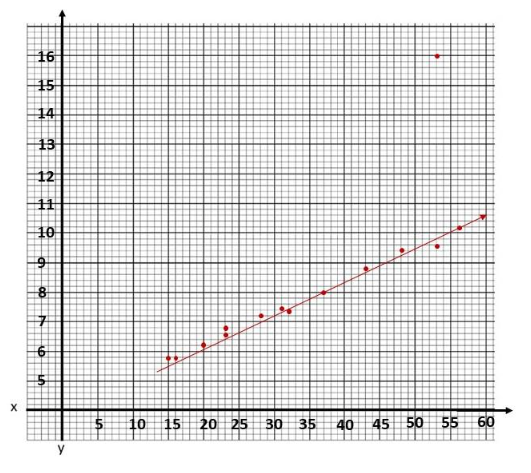
For the equation of the line of best fit, use points that the best fit line passes through, (37, 8) and (56, 10.2), to solve for the slope of the Line. The slope of the line equates the difference of y₂ to y₁ over the difference of x₂ to x₁. Then, let m be the sLope, (37, 8) be (x₁, y₁) and (56, 10.2) be (x₂. y₂) so
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)       Formula.
= \(\frac{10.2-8}{56-37}\)    Substitution.
= \(\frac{2.2}{19}\)      Subtract.
Next, use the slope-intercept form to determine the equation of the straight line given by y = mx + b, where m is the sLope, b is the y-intercept, and (37, 8) be (x, y) then
y = mx + b      Slope-intercept Form.
8 = (\(\frac{2.2}{19}\))37 + b    Substitution.
8 = (\(\frac{407}{95}\)) + b    Multiply.
(\(\frac{353}{95}\)) = b     Subtract (\(\frac{407}{95}\)) to both sides.
Lastly, using the slope-intercept form again, let m be the slope equals to (\(\frac{2.2}{19}\)) and b equals to (\(\frac{353}{95}\)), thus
y = mx + b    Slope-intercept Form.
y = \(\frac{2.2 x}{19}\) – \(\frac{353}{95}\)      Substitution.
Therefore, the equation of the tine of best fit is y = \(\frac{2.2 x}{19}\) – \(\frac{353}{95}\).

Use the scatter plot below to answer questions 8 to 13.

Snow density is an important factor affecting the speed and control in snow boarding. To understand the relationship between snow density, y grams per cubic centimeters, and air temperature, x°C, data are collected and shown below.

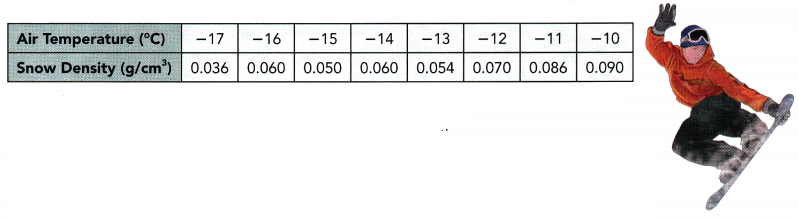
Question 8.
Use graph paper to construct the scatter plot. Use 1 centimeter on the horizontal axis to represent 1°C for the x interval from -17 to -9. Use 1 centimeter on the vertical axis to represent 0.010 grams per cubic centimeter.
Answer:
The objective is to make a scatter plot for the snow density and air temperature.

Observe that when the air temperature is at -17°C the snow density is 0.036g/cm³, at -16° the density is 0.060g/cm³, the air temperature is at -15°C the snow density is 0.050g/cm3, at -14° the density is 0.60g/cm³, the air temperature is at -13°C the snow density is 0.054g/cm³, at -12° the density is 0.070g/cm³. the air temperature is at -11°C the snow density is 0.086g/cm³, and at -10° the density is 0.090g/cm³. Thus, the scatter plot will be as depicted below.

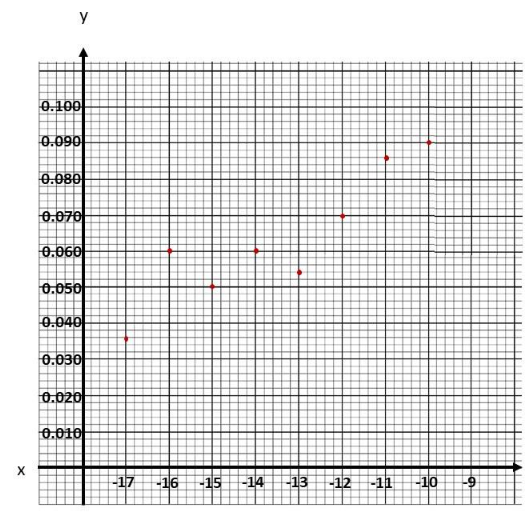
Question 9.
Describe the association between air temperature and snow density.
Answer:
The target is to determine the association in bivariate data then explain the relationship between the two.

The scatter plot shows a weak, positive and linear association. This relationship indicates that the greater the temperature, the higher the snow density.

Question 10.
Sketch a line of best fit.
Answer:
The goal of this task is to determine the line of best fit in the scatter plot of the snow density and air temperature.

Observe that when the air temperature is at -17°C the snow density is 0.036g/cm³, at 16 the density is 0.060g/cm³. the air temperature is at -15°C the snow density is 0.050g/cm³, at -14° the density is 0.060g/cm³, the air temperature is at -13°C the snow density is 0.054g/cm³, at -12° the density is 0.070g/cm³. the air temperature is at -11°C the snow density is 0.086g/cm³, and at -10° the density is 0.090g/cm³. Also, the line of best fit is the most possible straight line that best shows the data on a scatter plot Thus, the line of best fit for scatter plot will be as depicted below.

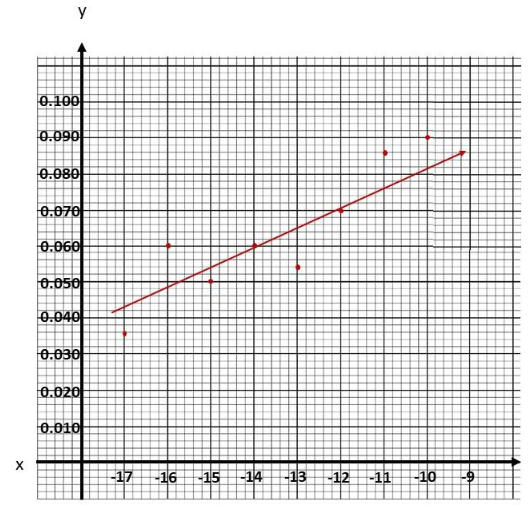
Question 11.
Find an equation for the line of best fit.
Answer:
The objective of this task is to determine the equation of the Line of best fit for the air temperature and snow density.

Notice that the best fit Une passes through (-14, 0.060) and (- 12.0.070). Use these points to solve for the slope of the line which equates the difference of y₂ to y₁ over the difference of x₂ to x₁. Then, let m be the slope, (-14,0.060) be (x₁, y₁) and (-12,0.070) be (x₂. y₂) so
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)    Slope Formula.
= \(\frac{0.070-0.060}{(-12)-(-14)}\)    Substitution.
= \(\frac{0.01}{2}\) Subtract.
= 0.005 Simplify.
Next use the slope-intercept form to determine the equation of the straight line given by y = mx + b, where w is the slope, b is the y-intercept, and (-14,0.060) be (x, y) then
y = mx + b    Slope-intercept Form.
0.060 = (0.005)(-14) + b    Substitution.
0.060 = -0.07 + b   Multiply.
0.060 + 0.07 = -0.07 + b + 0.07    Add 0.07 to both sides.
b = 0.13 Simplify.
Lastly, using the slope-intercept form again, let w be the slope equals to 0.005 and b equals to 0.13. thus
y = mx + b     Slope-intercept Form.
y = 0.005x + 0.13   Substitution
Therefore, the equation of the line of best fit is y = 0.005x + 0.13.

Question 12.
Predict the density when the temperature is at -14.5°C.
Answer:
The target of this task is to give the approximate snow density using the graph if the temperature is at -14.6°C.

To estimate the snow density x given the air temperature y, study the graph and the tine of best fit then note at what point does y at -14°C meets x. The point is on (-14.6, 0.062).

Therefore, at an air temperature of -14°C, the snow density is around 0.062g/cm³.

Question 13.
Predict the density when the temperature is at -9°C.
Answer:
The goal is to calculate using the equation of the Line y = 0.005x + 0.13 the snow density if the air temperature is at -9°C.

To compute the snow density at -9°C, note that snow density is denoted as y and the air temperature is denoted as x. Then when x is -9,
y = 0.005x + 0.13    Equation of the line.
= 0.005(-9) + 0.13     Substitution.
= -0.045 + 0.13    Multiply.
= 0.085   Simplify.

Therefore, when using the equation y = 0.005x + 0.13 the snow density is about 0.085 at a temperature of -9°C.

This handy Math in Focus Grade 8 Workbook Answer Key Chapter 10 Lesson 10.1 Scatter Plots detailed solutions for the textbook questions.

Math in Focus Grade 8 Course 3 B Chapter 10 Lesson 10.1 Answer Key Scatter Plots

Math in Focus Grade 8 Chapter 10 Lesson 10.1 Guided Practice Answer Key

Use graph paper. Solve.

Question 1.
The table shows some monetary exchanges between U.S. dollars, x dollars, and Japanese yen, y yen, over a time period of 4 months at a major airport.

Construct a scatter plot for this data. Use 2 centimeters on the horizontal axis to represent $10. Use 2 centimeters on the vertical axis to represent 500 yen.
Answer:

Complete.

Question 2.
Describe the association between the bivariate data shown in each scatter plot.

Graph E: and association
Graph F: , , and association
Graph G: association
Answer:
Graph E: strong and non-linear association
Graph F: Strong, Positive, and linear association
Graph G: No association

Use graph paper. Solve.

Question 3.
Dan is investigating the effect of the amount of water, x, given to tomato seedlings on their growth. He waters each of the 22 plants with a given amount of water daily. He records their height, y, at the end of two weeks. His data is shown below.

a) Construct a scatter plot for this data. Use 1 centimeter on the horizontal axis to represent 4 fluid ounce. Use 1 centimeter on the vertical axis to represent 1 inch. Identify any outlier(s).
An outlier appears to be located at (, ).
Answer:

An outlier appears to be located at (28, 4.8).

b) Explain what the outlier(s) likely represent(s) in this context.
The outlier represents and after two weeks.
Answer: The outlier represents 28 fluid ounces of water daily and a growth of 4.8 inches after two weeks.

c) Describe the meaning in context of the association between the two data sets. Validate the outliers as being very different from the rest of the data points.
The , , and association indicates that tomato seedlings that are given more water daily experience growth over the two weeks. The general trend shows that seedlings that are given 28 fluid ounces of water daily generally grew about inches, but the outlier represents a seedling that grew only inches with fluid ounces of water daily.
Answer:
The strong, positive, and linear association indicates that tomato seedlings that are given more water daily experience more growth over the two weeks. The general trend shows that seedlings that are given 28 fluid ounces of water daily generally grew about 12 inches to 13 inches, but the outlier represents a seedling that grew only 4.8 inches with 28 fluid ounces of water daily.

Math in Focus Course 3B Practice 10.1 Answer Key

Draw scatter plot for each of the given table of bivariate data.

Question 1.
Use 1 centimeter on the horizontal axis to represent 10 units. Use 1 centimeter on the vertical axis to represent 20 units.

Answer:

Question 2.
Use 1 centimeter on the horizontal axis to represent 5,000 people. Use 2 centimeters on the vertical axis to represent 5,000 cars.

Answer:

Question 3.
Use 1 centimeter on the horizontal axis to represent 1 hour. Use 1 centimeter on the vertical axis to represent a score of 10.

Answer:

Describe the association between the bivariate data shown in each scatter plot.

Question 4.

Answer: Strong, linear and positive

Question 5.

Answer: Strong, linear and negative

Describe the association between the bivariate data shown in each scatter plot.

Question 6.

Answer: strong, nonlinear and positive

Question 7.

Answer: Strong, negative and nonlinear

Identify the outlier(s) in each scatter plot.

Question 8.

Answer: (1, 1) and (4, 1)

Question 9.

Answer: (0, 1) and (5, 0.4)

Use the table of bivariate data below to answer questions 10 to 13.

A retailer wanted to know the association between the number of items sold, y, and the number of salespeople, x, in a store. So she recorded the number of salesperson and items sold over 16 days in the table below.

Question 10.
Use graph paper to construct the scatter plot. Use 1 centimeter on the horizontal axis to represent 1 salesperson for the x interval from 43 to 52. Use 1 centimeter on the vertical axis to represent 20 items.
Answer:

Question 11.
Identify the outlier. Give a likely explanation for the occurrence of the outlier.
Answer: (50, 52) because there could have been an accident or construction that blocked the access to the store for a long time that day.

Question 12.
Describe the association between the number of items sold and the number of salespeople in the store. Explain your answer.
Answer: The wide range of sampling values might be important when investigating the association between bivariate data

Question 13.
Math Journal If the data collected for the number of salespeople ranged from 0 to 100, do you think the answer to 12 would be different? Explain why a wide range of sampling values might be important when investigating the association between bivariate data.
Answer: If the association occurs over a greater range of values, then the narrow range if value might not be enough to identify the data.

Use the table of data below to answer questions 14 to 17.

To investigate the benefits of warming up before playing a baseball game, 14 amateur baseball players were surveyed. The number of game injuries, x, in a year and the time the player spent warming up for each game, y minutes, are recorded below.

Question 14.
Use graph paper to construct the scatter plot. Use 2 centimeters on the horizontal axis to represent 1 minute. Use 1 centimeter on the vertical axis to represent 5 game injuries.
Answer:

Question 15.
Identify any outliers.
Answer: no

Question 16.
Math journal Is there a linear association between the number of game injuries and the time spent warming up before each game? Explain.
Answer:
The task is to verify if there exist a linear association in the scatter plot for the number of game injuries and the time spent in warming up. If the scatter plot follows a straight line then it is linear, otherwise, it has a nonlinear association. Observe that there is a liner association in the scatter plot because as the time spent in warming up increases, the number of game injuries increases and thus the marks of these variables have a negative linear association

Question 17.
Math Journal From the results shown, can you recommend minimum : warm-up time for baseball players before they start a game? How does
analyzing association of data sets help to provide useful information?
Answer:
The target of this task is to give a suggestion about how long should the players warm-up, and then make a conclusion about the importance of studying the relationship of a group of data. Observe the scatter plot of the number of minutes players warm-up and the number of injuries. From 1 – 3 minutes, the behavior of data shows that as the time increases, the recorded injuries decreases. When the Length of warming up enters 4 the number of injuries are almost the same even at Longer warming-up time. Therefore, the shortest warming-up time is 4 minutes. A good analyzation of a group of data helps in making a good prediction.