Math in Focus

This handy Math in Focus Grade 7 Workbook Answer Key Chapter 9 Statistics detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Chapter 9 Answer Key Statistics

Math in Focus Grade 7 Chapter 9 Quick Check Answer Key

Find the mean of each set of data. Round your answer to 2 decimal places if it is not exact.

Question 1.
9, 11, 6, 29, 5
Answer:
Definition of mean: The most common measure of central tendency is the arithmetic mean. In layman’s terms, the mean of data indicates an average of the given collection of data.  It is equal to the sum of all the values in the group of data divided by the total number of values.
For n values in a set of data namely as x₁, x_2, x_{3, …} x_n, the mean of data is given as:

It can also be denoted as:

The above-given data: 9, 11, 6, 29, 5
Mean=9+11+6+29+5/5
Mean=60/5
Mean=12.

Question 2.
43, 88, 39, 10, 26, 17, 35
Answer:
Definition of mean: The most common measure of central tendency is the arithmetic mean. In layman’s terms, the mean of data indicates an average of the given collection of data.  It is equal to the sum of all the values in the group of data divided by the total number of values.
For n values in a set of data namely as x₁, x_2, x_{3, …} x_n, the mean of data is given as:

It can also be denoted as:

The above-given data: 43, 88, 39, 10, 26, 17, 35
Mean=43+88+39+10+26+17+35/7
Mean=258/7
Mean=36.85 (round to nearest number)
Mean=37.

Question 3.
53.6, 36.7, 88.5, 90.6
Answer:
Definition of mean: The most common measure of central tendency is the arithmetic mean. In layman’s terms, the mean of data indicates an average of the given collection of data.  It is equal to the sum of all the values in the group of data divided by the total number of values.
For n values in a set of data namely as x₁, x_2, x_{3, …} x_n, the mean of data is given as:

It can also be denoted as:

The above-given data: 53.6, 36.7, 88.5, 90.6
Mean=53.6+36.7+88.5+90.6/4
Mean=269.4/4
Mean=67.35
Mean=67 (rounded to nearest number)

Question 4.
0.14, 1.05, 3.1, 7.18, 4.3, 8
Answer:
Definition of mean: The most common measure of central tendency is the arithmetic mean. In layman’s terms, the mean of data indicates an average of the given collection of data.  It is equal to the sum of all the values in the group of data divided by the total number of values.
For n values in a set of data namely as x₁, x_2, x_{3, …} x_n, the mean of data is given as:

It can also be denoted as:

The above-given data: 0.14, 1.05, 3.1, 7.18, 4.3, 8
Mean=0.14+1.05+3.1+7.18+4.3+8/6
Mean=23.77/6
Mean=3.96
Mean=4

Solve. Show your work.

Question 5.
The heights, in inches, of 10 children are
54, 66, 52, 60.5, 61.25, 55, 58.75, 51.5, 53, 50.
Find the mean height of the children.
Answer:
Definition of mean: The most common measure of central tendency is the arithmetic mean. In layman’s terms, the mean of data indicates an average of the given collection of data.  It is equal to the sum of all the values in the group of data divided by the total number of values.
For n values in a set of data namely as x₁, x_2, x_{3, …} x_n, the mean of data is given as:

It can also be denoted as:

the above-given data: 54, 66, 52, 60.5, 61.25, 55, 58.75, 51.5, 53, 50.
Mean=54+66+52+60.5+61.25+55+58.75+51.5+53+50/10
Mean=562/10
Mean height of children=56.2

Find the median of each set of numbers.

Question 6.
41,29, 78, 12, 56, 30, 22
Answer: 30
Explanation:
The median of a set of data is the middlemost number or centre value in the set. The median is also the number that is halfway into the set.
To find the median, the data should be arranged, first, in order of least to greatest or greatest to the least value. A median is a number that is separated by the higher half of a data sample, a population or a probability distribution, from the lower half. The median is different for different types of distribution.
Median formula:
The formula to calculate the median of the finite number of data set is given here. The median formula is different for even and odd numbers of observations. Therefore, it is necessary to recognise first if we have an odd number of values or an even number of values in a given data set.
The formula to calculate the median of the data set is given as follow.
An odd number of observations:
If the total number of observations given is odd, then the formula to calculate the median is:
Median = {(n+1)/2}^thterm
where n is the number of observations
Even number of observations:
If the total number of observations is even, then the median formula is:
Median  = [(n/2)^th term + {(n/2)+1}^th]/2
where n is the number of observations
How to  calculate Median:
To find the median, place all the numbers in the ascending order and find the middle.
Put them in ascending order: 12, 22, 29, 30, 41, 56, 78
The middle number is 30, so the median is 30.

Question 7.
193, 121.5, 162.3, 125, 103.8, 149.6
Answer:
The median of a set of data is the middlemost number or centre value in the set. The median is also the number that is halfway into the set.
To find the median, the data should be arranged, first, in order of least to greatest or greatest to the least value. A median is a number that is separated by the higher half of a data sample, a population or a probability distribution, from the lower half. The median is different for different types of distribution.
Median formula:
The formula to calculate the median of the finite number of data set is given here. The median formula is different for even and odd numbers of observations. Therefore, it is necessary to recognise first if we have an odd number of values or an even number of values in a given data set.
Sorted data set: 103.8, 121.5, 125, 149.6, 162.3, 193
Meadian=125+149.6/2
Median=274.6/2
Median=137.3
Thus, the median is 137.3

Question 8.
9, 2, 2, 4, 4, 4, 1, 3, 6, 5, 3, 6
Answer: 4
Explanation:
The median of a set of data is the middlemost number or centre value in the set. The median is also the number that is halfway into the set.
To find the median, the data should be arranged, first, in order of least to greatest or greatest to the least value. A median is a number that is separated by the higher half of a data sample, a population or a probability distribution, from the lower half. The median is different for different types of distribution.
Median formula:
The formula to calculate the median of the finite number of data set is given here. The median formula is different for even and odd numbers of observations. Therefore, it is necessary to recognise first if we have an odd number of values or an even number of values in a given data set.
Sorted data set: 1, 2, 2, 3, 3, 4, 4, 4, 5, 6, 6, 9
Median=4+4/2
Median=8/2
Median=4
Thus, the median is 4.

Question 9.
1,011, 1,100, 1,001, 1,010, 1,110, 1,000, 1,011, 100
Answer:
Explanation:
The median of a set of data is the middlemost number or centre value in the set. The median is also the number that is halfway into the set.
To find the median, the data should be arranged, first, in order of least to greatest or greatest to the least value. A median is a number that is separated by the higher half of a data sample, a population or a probability distribution, from the lower half. The median is different for different types of distribution.
Median formula:
The formula to calculate the median of the finite number of data set is given here. The median formula is different for even and odd numbers of observations. Therefore, it is necessary to recognise first if we have an odd number of values or an even number of values in a given data set.
Sorted data set: 100, 1000, 1001, 1010, 1011, 1011, 1100, 1110
Median=2021/2
Median=1010.5
Thus, the median is 1010.5

Solve. Show your work.

Question 10.
The daily low temperatures for the past 10 days were
30.6°F, 32.1 °F, 29.5°F, 30.2°F, 26.4°F, 34.3°F, 31.6°F, 32°F, 25.9°F, and 26.4°F.
What was the median daily low temperature?
Answer:
The statistical concept of the median is a value that divides a data sample, population, or probability distribution into two halves. Finding the median essentially involves finding the value in a data sample that has a physical location between the rest of the numbers. Note that when calculating the median of a finite list of numbers, the order of the data samples is important. Conventionally, the values are listed in ascending order, but there is no real reason that listing the values in descending order would provide different results. In the case where the total number of values in a data sample is odd, the median is simply the number in the middle of the list of all values. When the data sample contains an even number of values, the median is the mean of the two middle values. While this can be confusing, simply remember that even though the median sometimes involves the computation of a mean, when this case arises, it will involve only the two middle values, while a mean involves all the values in the data sample. In the odd cases where there are only two data samples or there is an even number of samples where all the values are the same, the mean and median will be the same. Given the same data set as before, the median would be acquired in the following manner:
30.6°F, 32.1 °F, 29.5°F, 30.2°F, 26.4°F, 34.3°F, 31.6°F, 32°F, 25.9°F, and 26.4°F.
The formula to calculate the median of the finite number of data set is given here. The median formula is different for even and odd numbers of observations. Therefore, it is necessary to recognise first if we have an odd number of values or an even number of values in a given data set.
Sorted data set: 25.9, 26.4, 26.4, 29.5, 30.2, 30.6, 31.6, 32, 32.1, 34.3
Median=30.2+30.6/2
Median=60.8/2
Median=30.4
Thus, the median is 30.4

Summarize each of the following data sets in a frequency table and draw a dot plot.

Question 11.
The data show the number of misspelled words found in 15 essays.

Answer:
Definition of frequency: Frequency means the number of times a value appears in the data. A table can quickly show us how many times each value appears. If the data has many different values, it is easier to use intervals of values to present them in a table.

A dot chart or dot plot is a statistical chart consisting of data points plotted on a fairly simple scale, typically using filled in circles.

Question 12.
In a game, each child is given 10 balls to hit at moving targets. The data show the number of hits scored by 20 children.

Answer:
Definition of frequency: Frequency means the number of times a value appears in the data. A table can quickly show us how many times each value appears. If the data has many different values, it is easier to use intervals of values to present them in a table.

A dot chart or dot plot is a statistical chart consisting of data points plotted on a fairly simple scale, typically using filled in circles.

This handy Math in Focus Grade 7 Workbook Answer Key Cumulative Review Chapters 6-8 detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Cumulative Review Chapters 6-8 Answer Key

Concepts and Skills

Tell whether each pair of angles is supplementary, complementary, or neither. (Lesson 6.1)

Question 1.
m∠1 = 18° and m∠2 = 82°
Answer:
Given each pair of angles are complementary angles.

Explanation:
The sum of two angles is equal to 90° is called complementary angles. In the given figure if we sum up both the angles that is 18°+ 82°we get a 90° angle.

Question 2.
m∠3 = 103° and m∠4 = 77°
Answer:
Given each pair of angles are supplementary angles.

Explanation:
Supplementary angles are those angles that sum up to 180°.

Question 3.
m∠5 = 95° and m∠6 = 85°
Answer:
Given each pair of angles are supplementary angles.

Explanation:
Supplementary angles are those angles that sum up to 180°. Therefore add 95° and 85° then we get 180°.

Question 4.
m∠7 = 21° and m∠8 = 69°
Answer:
Given each pair of angles are complementary angles.

Explanation:
The sum of two angles is equal to 90° is called complementary angles. In the given figure if we sum up both the angles that are 21°+ 69°we get a 90° angle.

Find the measure of each numbered angle. (Lessons 6.1, 6.2)

Question 5.
\(\overleftrightarrow{P R}\) is a straight line.

Answer:
54°

Explanation:
Given, ∠SQR = 126°
∠QPR = 180°
∠PQS = 1
Here we need to calculate the numbered angle.
To find that we need to subtract ∠QPR from ∠SQR
∠1 = 180°-126°
∠1   = 54°
Hence the numbered angle is 54°

Question 6.
\(\overleftrightarrow{P R}\) is a straight line.

Answer:
88°

Explanation:
The straight-line QPR has 180°.
Given, ∠PQS = 54°
∠QTR = 38°
∠SQT is numbered angle that is ∠2
Now we need to calculate the numbered angle
Therefore QPR = ∠PQS + ∠QTR + ∠2
180°= 54°+38°+ ∠2
180°= 92°+ ∠2
180°-92° = ∠2
∠2 = 88°

Question 7.

Answer:
The numbered angle 3 is 94°

Explanation:
The sum of angles around a point is 360°
40°+125°+101°+3=360°
3= 360°-40°-125°-101°
3= 360° – 266°
3 = 94°
Hence the numbered angle 3 is 94°

Question 8.

Answer:
36°

Explanation:

The sum of angles around a point is 360°
When two lines cross the angles are opposite to each other. Therefore opposite angles are equal to each other.
The angle ∠ABC and ∠DBE are opposite to each other. So ∠ABC = ∠DBE
Given, ∠ABC = 162°, ∠DBE means the numbered angle 4 is also 162°
Now we need to calculate the numbered angle 5
To calculate the angle 5 we need to add ∠ABC + ∠DBE+ 5 = 360°
162°+162°+∠5 = 360°
324°+ ∠5 =360°
∠5 = 360°-324°
∠5 = 36°

\(\overleftrightarrow{M N}\) is parallel to \(\overleftrightarrow{P Q}\). Find the measure of each numbered angle. (Lesson 6.3)

Question 9.

Answer:
m∠1 = 81°
Vertical ∠s

Question 10.

Answer:
m∠3 = 49°
Alternate interior ∠s

Find the measures of ∠1 and ∠2 in each diagram. (lesson 6.4)

Question 11.
Triangle ABC is an isosceles triangle.

Answer:
32°

Explanation:

1+32°+x =180°
1+x° = 180°-32°
1+x°= 148°
1+x°+2 = 180°
148° +2 = 180°
2 = 180°-148°
2 = 32°
1+x°= 148°
32°+x°= 148°
x°=148°-32°
x°=  116°
1=148-116
1=32°

Question 12.
\(\overleftrightarrow{P R}\) is a straight line.

Answer:
110°+1 = 180°
1 = 180°-110°
1 = 70°

Use the given Information to construct each polygon.

Construct triangle ABC with sides AB = 5.8 cm, BC = 6.6 cm, and AC = 4.5 cm. (Lessons 7.1, 7.2, 7.3)

Step 1:
we are given
AB = 5.8
BC = 6.6
AC = 4.5

Step 2:
Use a ruler to draw the segment 66 cm long. LabeL its endpoints by B and C.

Step 3:
Because AB = 5.8 cm, use the ruLer to set the compass to a radius of 5.8 cm Then using A as center draw an arc of radius 5.8 cm above \(\overline{B C}\).

Step 4:
Because AC = 4.5 cm, use the ruler to set the compass to a radius of 4.5 cm. Then using G as center draw an arc of radius 4.5 cm that intersects the first arc. Label the intersection as A.

Step 5:
Use the ruler to draw \(\overline{A B}\) and \(\overline{A C}\)

a) Measure the angles of the triangle.
Answer:
m∠A ≈ 79°
m∠B ≈ 42°
m∠C ≈ 59°

b) Use a compass and straightedge to bisect angle B.
Answer:

c) Use a compass and straightedge to construct the perpendicular bisector of AB.
Answer:

d) The two bisectors intersect at a point D, label D in your construction.
Answer:

e) Measure the distances BD and CD.
Answer:
BD ≈ 3.2 cm
CD ≈ 3.8 cm

Question 14.
Construct quadrilateral PQRS with PQ = PR = 7.8 cm, PQ ||SR, m∠PQR = 73°, and RS = 4 cm. (Lessons 7.1, 7.2, 7.4)

Step 1:
We are given
PQ = PR = 7.8
PQ || SR
m∠PQR = 73°
RS = 4

Step 2:
Sketch the quadrilateral

Step 3:
First we construct △PRQ using the side-side-angle method.

Step 4:
Determine m∠RPQ
m∠RPQ + 2.73° = 180°
m∠RPQ = 180° – 146°
m∠RPQ = 34°

Step 5:
As PQ || SR, we have
m∠SRP = m∠RPQ = 34°

Step 6:
We construct △PRS, using the side-angle-side method.

a) Measure the length of PS.
Answer:
PS ≈ 5 cm

b) Use a compass and straightedge to construct the angle bisector of ∠S.
Answer:

c) Use a compass and straightedge to construct the perpendicular bisector of \(\overline{P Q}\).
Answer:

d) Label the point where the angle bisector and perpendicular bisector intersect as W.
Answer:

Solve. Show your work. (Lesson 7.5)

Question 15.
Jacob builds a model plane that is 800 millimeters long. If the actual plane is 40 meters, what is the scale of the model? (10 mm = 1 cm)
Answer:
We are given
Length on the plane: 800 mm
Actual length: 40 m

Determine the scale of the model:
\(\frac{\text { Length on the plane }}{\text { Actual length }}=\frac{800 \mathrm{~mm}}{40 \mathrm{~m}}=\frac{80 \mathrm{~cm}}{4,000 \mathrm{~cm}}=\frac{1}{50}\)
= \(\frac{1}{50}\)

Question 16.
The scale of a map is 1 : 1,500. If a square piece of land measures 4 inches on each side on the map, find the actual area of this piece of land to the nearest tenth of an acre. (1 acre = 43,560 ft²)
Answer:

We have:
Step 1:
Map length : Actual length = 1 in. : 1,500 in.
Map area: ActuaL area = 1 in.² : 1, 5002 in²

Step 2:
Let y represent the actual area of the piece of land in square inches.

Step 3:
Write a proportion: \(\frac{\text { Piece area on map }}{\text { Actual area of piece }}=\frac{1}{2,250,000}\)

Step 4:
Substitute:
\(\frac{4^{2}}{y}=\frac{1}{2,250,000}\)

Step 5:
Write the cross products:
y = 16.2,250,000

Step 6:
Simplify
y = 36,000,000 in²

Step 7:
Convert to acres:
1 acre = 43,560 ft = 43. 560. 12² = 6. 272, 640 in²
\(\frac{36,000,000}{6,272,640}\) ≈ 5.7 acres
= 5.7 acres

Match each solid with its net. (Lesson 8.1)

Question 17.

Answer:
The net of a cone consists of a circle and a sector of a circle.
The net b) does not consists a sector of circle, so we eliminate it
The net a) also doesn’t contain a sector of circle, therefore we eliminate it
The net d) is an ellipse sector, not a circle sector, so we eliminate it

The correct answer is (c)

Question 18.

Answer:

The net of a trianguLar prism contains 4 triangles.

The net b) contains 3 triangles and a rectangle, not 4 triangles, so we eliminate it
The net c) contains 4 triangles and a rectangle, not 4 triangles, so we eliminate it
The net d) contains 3 triangles, not 4 triangles, so we eliminate it

The correct answer is (a)

For each solid, sketch and describe the shape of the cross section formed when a plane slices the solid in the direction indicated. (Lesson 8.1)

Question 19.
A cube of length 6 centimeters perpendicular to a base and parallel to two opposite faces.

Answer:

A cross-section perpendicular to a base and parallel to two opposite faces can be drawn starting with a point for example on one of the edges of the top face. We draw a parallel line to two of the edges on the top face other than the one opposite to the one containing the initial point From the ends of the line we draw two vertical lines to the vertical edges. We join the ends of these two paralLels.

Question 20.
A cylinder of radius 3 centimeters parallel to its bases.

Answer:

A cross section parallel to its bases has the shape of a circle of radius 3:

Question 21.
A right triangle base prism parallel to its bases.

Answer:

A cross-section paralleL to its bases can be drawn starting with a point for example on one of the edges other than the bases We draw a parallel line to each of the corresponding edges on the bases. We join the ends of these two parallels.

Question 22.
Copy and complete the table. Use 3.14 as an approximation for π. (Lesson 8.2)

Answer:
Step 1:
We are given the cylinder:
V = 942
h = 12

Step 2:
Determine the radius r:
V = πr²h
942 ≈ 3.14 · r² · 12
942 = 37.68 r²
r² = \(\frac{942}{36.68}\)
r² = 25
r = \(\sqrt{25}\)
r = 5 ft

Step 3:
Determine the diameter:
d = 2 · r = 2 · 5 = 10 ft

Step 4:
Determine the total surface area:
S = 2πr² + 2πrh
= 2π · 5² + 2π · 5 · 12
= 50π + 120π
= 170π
≈170 · 3.14
= 533.8 ft²

Step 5:
We are given the cylinder:
V = 879.2
d = 10

Step 6:
Determine the radius:
r= \(\frac{d}{2}\) = \(\frac{10}{2}\) = 5 cm

Step 7:
Determine the height:
V = πr²h
879.2 ≈ 3.14 · 5² · h 
879.2 = 78.5h
h = \(\frac{879.2}{78.5}\) = 11.2cm

Step 8:
Determine the total surface area:
S = 2πr² -1- 2πrh
= 2π · 5² + 2π · 5 · 11.2
= 50π + 112π
= 162π
≈ 162 · 3.14
= 508.7cm²

Step 9:
We are given the cylinder:
r = 4
S = 251.2

Step 10:
Determine the height:
S = 2πr² + 2πrh
251.2 ≈ 2 · 3.14 · 4² + 2 · 3.14 · 4 · h
251.2 = 100.48 + 25.12h
251.2 – 100.18 = 100.48 + 25.12h – 100.48
150.72 = 25.12h
h = \(\frac{150.72}{25.12}\)
h = 6 m

Step 11:
Determine the volume:
V = πr²h ≈ 3.14 · 4^{2 ·} 6 ≈ 301.4 m³

Step 12:
Determine the diameter:
d = 2r = 2 · 4 = 8 m

Step 13:
Complete the table

Find the exact surface area of each solid cone. (Lesson 8.3)

Question 23.
A cone with radius of 8.7 meters and a slant height of 12.8 meters.
Answer:
We are given the cone:
r = 8.7
l = 12.8
Use the formula for the cone’s surface area:
S = πr² + πrl
Substitute r, l to find the exact surface area:
= π · 8.7² + π · 8.7 · 12.8
= 75.69π + 111.36π
= 187.05 π m²

Question 24.
A cone of diameter 16.8 centimeters and slant height 20.6 centimeters.
Answer:
We are given the cone:
d = 16.8
l = 20.6
First we determine the radius:
r = \(\frac{d}{2}\) = \(\frac{16.8}{2}\) = 8.4
Use the formuLa for the cones surface area:
S = πr² + πrl
Substitute r, ito find the exact surface area:
= π · 8.42 + π · 8.4 · 20.6
= 70.56π + 173.04π
= 243.6π cm²

Find the volume of each solid. Use 3.14 as an approximation for π. Round your answers to the nearest tenth when you can. (Lessons 8.3, 8.4)

Question 25.
A square pyramid with a height of 13 centimeters and a base that is 8 centimeters on each edge.
Answer:
Use the formula:
V = \(\frac{1}{3}\) Bh
Substitute for B and h.
= \(\frac{1}{3}\) · (8²) · 13
Multiply and round:
≈ 277.3 cm³

= 277.3 cm³

Question 26.
An octagonal pyramid with a height of 8.2 inches and a base area of 34.5 square inches.
Answer:
Use the formula:
V = \(\frac{1}{3}\) Bh
Substitute for B and h.
= \(\frac{1}{3}\) · 34.5 · 8.2
Multiply and round:
= 94.3 in³

Question 27.
A cone with a radius of 6.5 centimeters and a height of 14 centimeters.
Answer:
We are given the cone:
r = 6.5
h = 14
Use the formula for the cone’s volume to find the volume:
V = \(\frac{1}{3}\)πr²h
≈ \(\frac{1}{3}\) · 3.14 · 6.5² · 14
≈ 619.1 cm³
= 619.1 cm³

Question 28.
A cone with a diameter of 24.6 feet and a height of 18.5 feet.
Answer:
We are given the cone:
d = 24.6
h = 18.5
Determine the radius:
r = \(\frac{d}{2\) = \(\frac{24.6}{2}\) = 12.3 ft
Use the formula for the cone’s volume to find the volume:
V = \(\frac{1}{3}\)πr²h
≈ \(\frac{1}{3}\) · 3.14 · 12.3² · 18.5
≈ 2,929.5 ft³
= 2,929.5 ft³

Question 29.
A sphere with a radius of 9.6 feet.
Answer:
We are given the sphere:
r = 9.6
Use the formula for the volume of a sphere:
V = \(\frac{4}{3}\)πr³ ≈ \(\frac{4}{3}\) · 3.14 · 9.6³
Multiply:
= 3,704.094…
Round to the nearest tenth:
≈ 3,704.1 ft³
= 3,704.1 ft³

Question 30.
A sphere with a diameter of 39.8 centimeters.
Answer:
We are given the sphere:
d = 39.8
Determine the radius of the sphere:
r = \(\frac{d}{2}\) = \(\frac{39.8}{2}\) = 19.9 cm
Use the formula for the volume of a sphere:
V = \(\frac{4}{3}\)πr³ ≈ \(\frac{4}{3}\) · 3.14 · 19.9³
Multiply:
= 32,993.4411….
Round to the nearest tenth:
≈ 32,993.4 cm³
= 32,993.4 cm³

Problem Solving

Find the value of each variable. (Chapter 6)

Question 31.

Answer:
x°=37°
2x=74°

Explanation:

A 360-degree angle is a complete angle of a point.
∠ABC = 360°-291°
∠ABC = 69°
∠ABC+BCA+CAB = 180°
69°+x°+2x°=180°
3x°+69=180°
3x°=180-69
3x°=111
x°=111÷3
x°=37°
2x°=74°

Question 32.

Answer:

Explanation:

∠DFE = 180°-112°
∠DFE = 68°
y°+3y°+ 68°= 180°
4y°+68° = 180°
4y°= 180°- 68°
4y°=112
y°=112÷4
y°= 28°
3y°= 84°

Question 33.

Answer:
Alternate exterior ∠s:
m∠HIN = 132°
VerticaL ∠
m∠HIN = 3b° + b°
Substitute and simplify:
132 = 4b
Divide by 4:
\(\frac{132}{4}\) = \(\frac{4b}{4}\)
Simplify
b = 33
Straight ∠:
3a° + 3b° + b° = 180°
Substitute and simplify:
3a ° + 4b° = 180°
3a + 4 · 33 = 180
3a + 132 = 180
Subtract 132 from both sides:
3a + 132 – 132 = 180 – 132
Simplify
3a = 48
Divide by 3
\(\frac{3a}{3}\) = \(\frac{48}{3}\)
Simplify
a = 16

a = 16; b = 33

Question 34.

Answer:
35°

Explanation:

∠PTU = c°
∠PRS = 80°
∠PUR = 2c°
∠TPS = 5c°
The sum of angles around the point is 360°
Sum of ∠PTU+ ∠PRS + ∠PUR + ∠TPS = 360°
c°+80°+2c°+5c° = 360°
8c° + 80° = 360°
8c° = 360°- 80°
8c° = 280°
c° = 280÷8
c°= 35°
2c°= 70°
5c°= 175°

Solve. Show your Work.

Question 35.
Segment AB is parallel to segments CD and EF. Segment BC is parallel to segment ED. Find the measure of ∠ABC. (Chapter 6)
Answer:

Question 36.
The diagram shows a triangular pin. Triangle ABC is an isosceles triangle. Line BD is parallel to line EF. m∠AEF = 40° and m∠DBC = 27°.
Find the measures of ∠EBD and ∠BAC. (Chapter 6)

Answer:
We are given:

Corresponding ∠s:
m∠EBD = 40°
Determine m∠ABC:
m∠ABC – m∠EBD + m∠DBC
= 40° – 27°
= 67°
△ABC isosceles:
m∠ACB = m∠ABC = 67°
Sum of ∠s in a triangle:
m∠BAC + m∠ACB + m∠ABC = 180°
Substitute:
m∠BAC + 67° + 67° = 180°
Simplify:
m∠BAC + 134° = 180°
We subtract 134° from both sides:
m∠BAC + 134° – 134° = 180° – 134°
Simplify:
m∠BAC = 46°

m∠EBD = 40°
m∠BAC = 46°

Question 37.
X, Y, and Zare the location of three manufacturing factories linked by three straight roads as shown in the diagram. A water pipe will go from Factory Y, and will be equidistant from the two roads linking Factory X and Factory Z to Factory Y. (Chapter 7)
a) Construct triangle XYZ to represent the locations of the three factories using a scale of 1 centimeter to 100 meters.
Answer:

b) Using a compass and straightedge only, construct the path of the water pipe.
Answer:
The Line whose points are equidistant from \(\overline{Y^{\prime} X^{\prime}}\) and \(\overline{Y^{\prime} Z^{\prime}}\) is the angle bisector of ∠Y’. We construct it:

c) The water department needs to build a temporary construction worksite that must be equidistant from Factory Y and Factory Z and at a distance of 400 meters from Factory X. Label the position of the construction worksite to be set up in your diagram as point W.

Answer:
The tine whose points are equidistant from Y’ and Z’ is the perpendicular bisector of \(\overline{Y^{\prime} Z^{\prime}}\). We construct it and label by W its intersection with the angle bisector from part b):

Question 38.
A model of a gym uses a scale of 1 : 12. The actual gym will be a rectangular prism. It will be 69.6 feet long, 54 feet wide, and 22.8 feet high. Find, in cubic feet, the volume of the model of the gym. (Chapters 7, 8)
Answer:
85691 cubic feet

Explanation:
The actual gym is a rectangular prism.
Given the length of a rectangular prism is 69.6 feet
Width = 54 feet
Height = 22.8 feet
The voulme of a rectangular prism is = Length × Width × Height
Volume = 69.6 × 54 × 22.8
Volume = 85691 cubic feet

Question 39.
Mrs. Sullivan buys a 5-liter bottle of apple juice. She can either use cylindrical glass A or cylindrical glass B to serve the apple juice. Use 3.14 as an approximation for π. (1,000 cm³ = 1 L) (Chapter 8)

We are given:
d_A = 6
h_A = 9
d_B = 5
h_B = 12

a) What is the volume of glass A?
Answer:
Determine the radius of glass A:
r_A = \(\frac{d_{A}}{2}\) = \(\frac{6}{2}\) = 3 cm
Determine the volume of glass A
V_A = πr_A²h_A ≈ 3.14 · 3² · 9 = 254.34 cm³

b) How many glasses of apple juice can she serve if she uses glass A?
Answer:
Determine the number of glasses A:
\(\frac{5 \cdot 1,000}{254.34}\) = \(\frac{5,000}{254.34}\) ≈ 19 glasses

c) What is the volume of glass B?
Answer:
Determine the radius of glass B:
r_B = \(\frac{d_{B}}{2}\) = \(\frac{5}{2}\) = 2.5 cm
Determine the volume of glass B
V_B = πr_B²h_B ≈ 3.14 · 2.5² · 12 = 235.5 cm³

d) How many glasses of apple juice can she serve if she uses glass B?
Answer:
Determine the number of glasses B:
\(\frac{5 \cdot 1,000}{235.5}\) = \(\frac{5,000}{235.5}\) ≈ 21 glasses

e) If Mrs. Sullivan sells one glass of apple juice for $1.80, what is the maximum amount of money she can collect?
Answer:
21 · 1.80 = 37.80

This handy Math in Focus Grade 7 Workbook Answer Key Chapter 8 Review Test detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Chapter 8 Review Test Answer Key

Concepts and Skills

For this review, r represents radius and h represents height. You may use a calculator and use 3.14 as an approximation for π. Round your answers to the nearest tenth unless otherwise stated.

Question 1.
Find the volume of each cylinder to the nearest unit. Use the given dimensions,
a) r = 4.2 inches; h = 14 inches
Answer:
775 cubic units

Explanation:
The volume of the cylinder is =π r² h
π = 3.14, r = 4.2, h= 14 inches
volume of the cylinder = 3.14×4.2×4.2×14 = 775 cubic units

b) r = 7 centimeters; h = 12 centimeters
Answer:
1846 cubic units

Explanation:|
The volume of the cylinder is =π r² h
π = 3.14, r = 7, h= 12 centimeters
volume of the cylinder = 3.14×7×7×12 = 1846 cubic units

Question 2.
Find the volume of each cone to the nearest unit. Use the given dimensions.
a) r = 3 centimeters; h = 8 centimeters
Answer:
75 cm³.

Explanation:
The volume of each cone is 1/3hπr²
r = 3 centimeters; h = 8 centimeters
Therefore the volume of each cone is = 1/3×8×3.14×3×3 = 75 cm³.

b) r = 8 inches; h = 15 inches
Answer:
1004 cm³.

Explanation:
The volume of each cone is 1/3hπr².
Given r = 8 inches; h = 15 inches and π=3.14
Therefore the volume of each cone is = 1/3×8×3.14×15 ×15 = 1004 cm³.

Question 3.
Find the volume of each pyramid. Use the given dimensions.

a) A square base with an edge length of 6 centimeters; h = 4 centimeters.
Answer:
We are given the cone:
l = 6
h = 4
Use the formula for the volume of a pyramid:
V = \(\frac{1}{3}\)Bh = \(\frac{1}{3}\)l²h
Substitute for l, h:
= \(\frac{1}{3}\) · 6² · 4
Multiply:
= 48 cm³

b) A rectangular base with length of 6 inches and width = 3.3 inches; h = 7 inches.
Answer:
We are given the cone:
l = 6
w = 3.3
h = 7
Use the formula for the volume of a pyramid:
V = \(\frac{1}{3}\)Bh = \(\frac{1}{3}\)lwh
Substitute for l, w, h:
= \(\frac{1}{3}\) · 6 · 3.3 · 7
Multiply:
= 46.2 in³

Question 4.
Find the volume of each sphere to the nearest unit. Use the given dimensions,
a) r = 9.6 centimeters
Answer:
3705 cm³

Explanation:
The volume of each sphere is = 4/3 πr³
Given r = 9.6 centimeters
Volume of the sphere is = 4/3×3.14×9.6×9.6×9.6 = 3705 cm³.

b) d = 26 centimeters
Answer:
9202 cm³.

Explanation:
The volume of each sphere is = 4/3 πr³
Given diameter is = 13 cm
Here we need a radius to calculate the volume of the sphere hence r = d/2 = 26/2 = 13 cm
Volume of the sphere is = 4/3×3.14×13×13×13=9202 cm³.

Question 5.
Find the exact surface area of each solid.

Answer:
a) We are given the cylinder:
r = 3
h = 6
Use the formula for the surface area of a cylinder.
S = 2πr² + 2πrh
Substitute for r, h:
= 2π · 3² + 2π · 3 · 6
Multiply:
= 18π + 36π
Add:
= 54π ft²

b) We are given the sphere:
d = 28
Determine the radius of the sphere:
r = \(\frac{d}{2}\) = \(\frac{28}{2}\) = 14
Use the formula for the surface area of a sphere:
S = 4πr²
Substitute for r:
= 4π · 14²
Multiply:
= 784π m²

c) We are given the cone:
r = 6
l = 10
Use the formula for the surface area of a cone:
S = πr² + πrl
Substitute for r, l:
= π · 6² + π · 6 · 10
Multiply:
= 36π + 60π
Add:
= 96π in²

Question 6.
Find the volume and surface area of each solid. Round to the nearest tenth.
a) A solid cone with a diameter of 5 feet, a slant height of 7 feet, and a height of 6.5 feet.
Answer:
We are given the cone.
d = 5
l = 7
h = 6.5
Find the radius:
r = \(\frac{d}{2}\) = \(\frac{5}{2}\) = 2.5
Use the formula for the volume of the cone:
V = \(\frac{1}{3}\) πr²h
≈ \(\frac{1}{3}\) · 3.14 · 2.5² · 6.5
≈ 42.5 ft³
Use the formula for the surface area of the cone:
S = πr² + πrl
= π · 2.5² + π · 2.5 · 7
= 6.25π + 17.5π
= 23.75π
≈ 23.75 · 3.14
≈ 74.6 ft²

b) A sphere with a radius of 28 millimeters.
Answer:
We are given the sphere:
r = 28
Use the formula for the volume of the sphere:
V = \(\frac{4}{3}\) πr³ = \(\frac{4}{3}\) · 3.14 · 28³
≈ 91,905.7 mm³
Use the formula for the surface area of the sphere:
S = 4πr² ≈ 4 · 3.14 · 28²
≈ 9,487 mm²

c) A solid cylinder with a radius of 1.4 inches and a height of 4.2 inches.
Answer:
We are given the cylinder:
r = 1.4
h = 4.2
Use the formula for the volume of the cylinder:
V = πr²h ≈ 3.14 · 1.4² · 4.2
≈ 25.8 in³
Use the formula for the surface area of the cylinder:
S = 2πr² + 2πrh
= 2π · 1.4² + 2π · 1.4 · 4.2
= 3.92π + 11.76π
= 15.68π
≈ 15.68 · 3.14
≈ 49.2 in²

Problem Solving

Solve. Show your work.

Question 7.
The volume of a cone is 450 cubic centimeters and the radius of the base is 5 centimeters. What is the height of the cone to the nearest tenth?
Answer:
We are given:
V = 450
r = 5
Use the formula for the volume of the sphere:
V = \(\frac{1}{3}\) · πr² · h
Substitute for V, πn r:
450 = \(\frac{1}{3}\) · 3.14 · 5² · h
Multiply:
450 = \(\frac{78.5}{3}\) · h
Multiply:
450 = \(\frac{78.5}{3}\) · h
Multiply both sides by 3:
3 · 450 = 3 · \(\frac{78.5}{3}\) · h
Multiply:
1,350 = 78.5h
Divide both sides by 78.5
\(\frac{1,350}{78.5}\) = \(\frac{78.5h}{78.5}\)
Simplify
h ≈ 17.2 cm

Question 8.
The surface area of a sphere is 498.96 square centimeters. What is the radius of the sphere to the nearest tenth?
Answer:
We are given the sphere:
S = 498.96
Use the formula for the surface area of a sphere:
S = 4πr²
Substitute S and π:
498.96 = 4 · 3.14 · r²
Multiply:
498.96 = 12.56 · r²
Divide each side by 12.56
\(\frac{498.96}{12.56}=\frac{12.56 r^{2}}{12.56}{78.5}\)
Evaluate:
39.7261 ≈ r²
Find the square root of each side:
\(\sqrt[2]{39.7261}\) ≈ r²
Round to the nearest tenth:
r ≈ 6.3 cm

Question 9.
A cone with a height of 6 inches and a slant height of 7.5 inches has a lateral surface with an area of approximately 106 square inches.

a) What is the radius? Round to the nearest tenth.
Answer:
We are given:
h = 6
l = 7.5
A = 106
Use the formula for the cone’s lateral surface area:
A = πrl
Substitute A, l, π to find r:
106 = 3.14 · r · 7.5
Multiply:
106 = 23.55r
Divide both sides by 23.55
\(\frac{106}{23.55}=\frac{23.55 r}{23.55}\)
r ≈ 4.5 in

b) What is the volume of the cone? Round to the nearest tenth.
Answer:
Use the formula for the cone’s volume:
V = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) · 3.14 · 4.5² · 6
≈ 127.2 in³

Question 10.
A cylinder, a cone, and a sphere are shown below. Each solid has a radius of 1 inch and a height of 2 inches. Which of them has the greatest volume? Justify your answer.

Answer:
We are given:
r = 1
h = 2
Determine the cylinder’s volume:
V_cylinder = πr²h = π · 1² · 2 = 2π
Determine the cone’s volume:
V_cone = \(\frac{1}{3}\) πr²h = \(\frac{1}{3}\) · π · 1² · 2
= \(\frac{2 \pi}{3}\)
Determine the sphere’s volume:
V_sphere = \(\frac{4}{3}\) πr³ = \(\frac{4}{3}\) · π · 1³
= \(\frac{4 \pi}{3}\)
We have:
\(\frac{2 \pi}{3}\) < \(\frac{4 \pi}{3}\) < 2π
V_cone < V_sphere < V_cylinder
The greatest volume is the cylinder’s

Question 11.
Two metal cubes each have an edge length of 4 centimeters. They are melted and recast into a square pyramid with a height of 5 centimeters. Find the area of the base of the pyramid.
Answer:
Determine the volume of the two cubes:
V = 2 · 4³ = 2 · 64 = 128 cm³
Use the formula of a pyramids volume:
V = \(\frac{1}{3}\) Bh
Substitute for V, h:
128 = \(\frac{1}{3}\) · B · 5
Multiply both sides by 3:
3 · 128 = 3 · \(\frac{5B}{3}\)
384 = 5B
Divide by 5:
\(\frac{384}{5}\) = \(\frac{5B}{5}\)
B = 76.8 cm²

Question 12.
A conical party hat has a diameter of 7 centimeters and a slant height of 14.5 centimeters. Paul wants to wrap the lateral surface of the party hat with plastic wrap. How much plastic wrap will he use? Round to the nearest square centimeter.
Answer:
We are given the cone:
d = 7
l = 14.5
Determine the radius of the cone:
r = \(\frac{d}{2}\) = \(\frac{7}{2}\) = 3.5
Determine the lateral surface of the cone:
A = πrl ≈ 3.14 · 3.5 · 14.5 ≈ 159 cm²
= 159 cm²

Question 13.
The composite solid shown is made up of a hemisphere attached to the top of a cube. The diameter of the hemisphere is the same as the edge length of the cube. Find the volume of the composite solid. Round to the nearest tenth.
Answer:

Determine the radius of the hemisphere:
r = \(\frac{9}{2}\) = 4.5
Determine the volume of the hemisphere:
V_hemisphere = \(\frac{1}{2}\) · \(\frac{4}{3}\) πr³
≈ \(\frac{2}{3}\) · 3.14 · 4.5³
≈ 190.8 cm³
Determine the volume of the cube:
V_cube = 9³ = 729 cm³
Determine the volume of the composite solid:
V_solid = V_hemisphere + V_cube
= 190.8 + 729
= 919.8 cm³

Question 14.
The circumference of a fully inflated beach ball is 12π, or about 37.68 inches. What is the radius of the beach ball? What is the volume of
the beach ball? Round to the nearest tenth if necessary.
Answer:
The radius of the beach ball is 6 inches.
The volume of the beach ball is 151 inches.

Explanation:
The circumference of a fully inflated beach ball is 12π.
Circumference of a circle = 2πr
12π=2πr
r=6
Hence radius of the beach ball is 6 inches.
Now we need to calculate the volume of a beach ball
The volume of the sphere is 4/3 πr³
Volume = 4/3×3.14×6×6×6
The volume of the beach ball = 904 inches.

Question 15.
A pyramid made of clay has a square base of length 8 inches and a height of 12 inches. The pyramid is reshaped into a cylinder with a radius of 8 inches. What is the height of the cylinder? Round to the nearest inch
Answer:
The height of the cylinder is 1.27 inches

Explanation:
Given: The base(b) of the square pyramid as 8 inches length and height(h) of the square pyramid as 12 inches.
Now we need to calculate Volume of square pyramid to know the height of cylinder.
The volume of the square pyramid is given by = 1/3(b)²h
Volume = 1/3 (8×8)²×12
Volume = 1/3 (64)×12
Volume = 256 inches
Now pyramid is reshaped into a cylinder with a radius = 8 inches
Volume of cylinder is π r² h
Volume = 3.14×8×8×h
Volume is 256 inches
256 = 3.14×8×8×h
h = 1.27 inches

This handy Math in Focus Grade 7 Workbook Answer Key Chapter 8 Lesson 8.4 Finding Volume and Surface Area of Spheres detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Chapter 8 Lesson 8.4 Answer Key Finding Volume and Surface Area of Spheres

Math in Focus Grade 7 Chapter 8 Lesson 8.4 Guided Practice Answer Key

Solve.

Question 1.
The diameter of a sphere is 8.8 meters. What is the volume of the sphere? Round your answer to the nearest hundredth. Use 3.14 as an approximation for π.

Radius of the sphere:
8.8 ÷ = m The radius is half the diameter.
Volume of the sphere:
\(\frac{4}{3}\)πr³ ≈ \(\frac{4}{3}\) ∙ ∙ ∙ ∙ Use the formula for the volume of a sphere.
= Multiply.
≈ m³ Round to the nearest hundredth.
The volume of the sphere is about cubic meters.
Answer: The volume of the sphere is about 356.63 cubic meters.

Explanation:
Given, diameter of a sphere is 8.8 meters.
Then r = 4.4 m
We know that the volume of the sphere is V =  \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\) × 3.14 × 4.4 × 4.4 × 4.4
V = \(\frac{1069.9}{3}\)
V = 356.63 m³
So, The volume of the sphere is about 356.63 cubic meters.

Question 2.
Diane bought a spherical ball made of quartz at a garage sale. The volume of the ball is 1,450 cubic centimeters. What is the radius of the ball to the nearest centimeter? Use 3.14 as an approximation for π.

The radius of the spherical ball is about centimeters.
Answer: The radius of the sphere is  7 meters.

Explanation:
Given, The volume of the sphere is about 1450 cubic meters.
Then r = ?
We know that the volume of the sphere is V =  \(\frac{4}{3}\)πr³
1450 = \(\frac{4}{3}\) × 3.14 ×r³
r³ = \(\frac{1450 × 3}{3.14 × 4}\)
r³ = \(\frac{4350}{12.56}\)
r³= 346.33
r = 7
So, The radius of the sphere is  7 meters.

Hands-On Activity

Materials:

• string
• hemisphere
• cylinder that has the same radius and height twice the radius of the hemisphere

Work in pairs.

STEP 1: Wrap the string tightly around the hemisphere as shown in the diagram. Measure the length of the string used, and then use the same length of string to wrap around the curved surface of the cylinder.

STEP 2: How much of the curved surface of the cylinder does the string cover? If you wrap the whole sphere with string, how much of the curved surface of the cylinder would the same string cover?

STEP 3: How is the surface area of the sphere related to the area of the curved surface of the cylinder?

STEP 4: Copy and complete the following to write a formula for the surface area of a sphere. (Hint: The height of a cylinder is twice the radius of a sphere.)
Surface area of a sphere = Area of cylinder’s curved surface

Solve.

Question 3.
What is the surface area of a sphere with a radius of 6 centimeters? Use 3.14 as an approximation for π.
Answer: The surface area of a sphere is  452.16 cm²

Explanation:
Given, r = 6 cm,
The surface area of a sphere is A = 4πr²
= 4 × 3.14 × 6 × 6
= 452.16 cm²
So, The surface area of a sphere is  452.16 cm²

Question 4.
A spherical rubber ball has a surface area of 3,215.36 square centimeters. What is the radius of the rubber ball to the nearest centimeter? Use 3.14 as an approximation for π.

The radius of the rubber ball is about centimeters.
Answer: The radius of a sphere is 16 cm.

Explanation:
rubber ball has a surface area of 3,215.36 square centimeters.
Given, A = 3,215.36 cm²,
The surface area of a sphere is A = 4πr²
3,215.36 = 4 × 3.14 × r²
r² = \(\frac{3,215.36}{3.14 × 4}\)
r² = 256
r = 16
So, The radius of a sphere is 16 cm.

Math in Focus Course 2B Practice 8.4 Answer Key

For this practice, you may use a calculator and use 3.14 as an approximation for π. Round your answers to the nearest tenth when you can.

Solve.

Question 1.
What is the volume of a sphere with a radius of 5 centimeters?
Answer: The volume of the sphere is about 523.33 cm³.

Explanation:
Given,  r = 5 cm
We know that the volume of the sphere is V =  \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\) × 3.14 × 5 × 5 × 5
V = \(\frac{1570}{3}\)
V = 523.33 cm³
So, The volume of the sphere is about 523.33 cm³.

Question 2.
What is the surface area of a sphere with a radius of 4.4 centimeters?
Answer: The surface area of a sphere is  243.16 cm²

Explanation:
Given, r = 4.4 cm,
The surface area of a sphere is A = 4πr²
= 4 × 3.14 × 4.4 × 4.4
= 243.16 cm²
So, The surface area of a sphere is  243.16 cm²

Question 3.
A fully inflated beach ball has a radius of 10 inches.
a) What is the surface area of the beach ball?
Answer: The surface area of a sphere is  1256 in²

Explanation:
Given, r = 10 in,
The surface area of a sphere is A = 4πr²
= 4 × 3.14 ×10 × 10
= 1256 in²
So, The surface area of a sphere is  1256 in²

b) What is the volume of air inside the beach ball?
Answer:  The volume of the air inside the ball is about 4186.6 in³.

Explanation:
Given,  r = 10 in
We know that the volume of the sphere is V =  \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\) × 3.14 × 10 × 10 × 10
V = 4186.6 in³
So, The volume of the air inside the ball is about 4186.6 in³.

Question 4.
What is the surface area of a sphere.
a) with a diameter of 28.6 centimeters?
Answer: The surface area of a sphere is  2,568 cm²

Explanation:
Given, d = 28.6
Then, r = 14.3 cm,
The surface area of a sphere is A = 4πr²
= 4 × 3.14 × 14.3 × 14.3
= 2,568 cm²
So, The surface area of a sphere is  2,568 cm²

b) with a volume of 3,680 cubic centimeters?
Answer:  The surface area of a sphere is  1133.54 cm²

Explanation:
Given, The volume of the sphere is about 3680 cubic meters.
Then r = ?
We know that the volume of the sphere is V =  \(\frac{4}{3}\)πr³
3680 = \(\frac{4}{3}\) × 3.14 ×r³
r³ = \(\frac{3680× 3}{3.14 × 4}\)
r³ = \(\frac{11040}{12.56}\)
r³= 878.9
r = 9.5
So, The radius of the sphere is  9.5 cm.

Then, r = 9.5 cm,
The surface area of a sphere is A = 4πr²
= 4 × 3.14 × 9.5 × 9.5
= 1133.54 cm²
So, The surface area of a sphere is  1133.54 cm²

Question 5.
A billiard ball has a surface area of 84 square centimeters. What is the radius of the billiard ball?
Answer: The radius of a billiard ball is 2..5 cm.v

Explanation:
billiard ball has a surface area of 84 square centimeters.
Given, A = 84 cm²,
The surface area of a sphere is A = 4πr²
84 = 4 × 3.14 × r²
r² = \(\frac{84}{3.14 × 4}\)
r² = 6.68
r = 2.5
So, The radius of a billiard ball is 2..5 cm.

Question 6.
A bowl is in the shape of a hemisphere. The radius of the bowl is 10 centimeters. How many liters of water can the bowl hold? (1,000 cm³ = 1 liter)

Answer: the bowl can hold 0.020 liters of water

Explanation:
Volume of the hemisphere  V = \(\frac{2}{3}\)πr
Given, r = 10 cm
V = \(\frac{2}{3}\) × 3.14 × 10
V = 20.9 cm³
The volume of the hemisphere is 20.9 cm³

Then, Given that 1000 cm = 1 liter, and
we want to know how many liters the bowl can hold.
= \(\frac{20.93}{1000}\)
= 0.020 liters
So, the bowl can hold 0.020 liters of water

Question 7.
Math Journal
a) What dimension of a sphere do you need to find its surface area and volume?
Answer: We need the dimension of radius of a sphere to find the surface area and its volume

b) Suppose a sphere has a radius greater than 1 unit. If you double the radius, which value will increase by a greater amount, the volume or the surface area of the sphere? Explain your thinking.
Answer: The surface area increases. with the square of the radius.
If you double the radius you quadruple the surface area

Explanation:
If r is the radius of a sphere its surface area = 4πr².
If the radius is doubled then its surface area = 4π(2r)² = 4 × 4πr².
So the surface area becomes 4-fold or the increase in surface area is 300%.

Question 8.
A basketball is shipped in a cube-shaped box. The basketball just touches the sides of the box, as shown.

a) What is the radius of the basketball?
Answer: the radius of the basketball is  4.8 in.

Explanation:
Given, diameter of a sphere is 9.6 in.
r = \(\frac{d}{2}\)
= \(\frac{9.6}{2}\)
= 4.8 in.
Then r = 4.8 in.
So, the radius of the basketball is  4.8 in.

b) What is the volume of the basketball?
Answer: The volume of the basketball is about 463 in³.

Explanation:
Given,  r = 4.8 in
We know that the volume of the sphere is V =  \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\) × 3.14 × 4.8 × 4.8 × 4.8
V = \(\frac{1389}{3}\)
V = 463 in³
So, The volume of the basketball is about 463 in³.

c) About what percent of the space in the cube is occupied by the basketball?
Answer: 52.3 % of the cube is occupied by the baseball

Explanation:
Given, the cube side a = 9.6 in
The volume of a cube  V = a³
V = 9.6 × 9.6 × 9.6
V = 884.73 in³
The volume of a cube is 884.73 in³

The volume of the basketball is about 463 in³.
So, around 52.3 % of the cube is occupied by the baseball

Question 9.
A solid metal ball with a radius of 10 inches is melted and made into smaller spherical metal balls with a radius of 2 inches each. How many smaller spherical balls can be made?
Answer: total of 125 smaller spherical metal balls can be made

Explanation:
r = 10 in
Volume of the metal ball  V =  \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\) × 3.14 × 10 × 10 × 10
V = 4186.6 in³
So, The volume of the sphere is about 4186.6 in³

Volume of the smaller spherical metal balls , with r = 2 in.
V =  \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\) × 3.14 × 2 × 2 × 2
V = 33.49 in³

So, divide the volumes, we get
= \(\frac{4186.6}{33.49}\)
= 125
Hence,  total of 125 smaller spherical metal balls can be made

Question 10.
Nathan cuts a clay sphere in half to get two hemispheres. He measures the circumference of the hemispheres to be 175.84 centimeters.

a) What is the radius of each hemisphere?
Answer: The radius of each hemisphere is 28 cm

Explanation:
Given, C = 175.84 cm
The circumference of the hemisphere is C = 2πr
175.84 = 2 × 3.14 × r
r = \(\frac{175.84}{6.28}\)
r = 28 cm
So, The radius of each hemisphere is 28 cm

b) What is the total surface area of each solid hemisphere?
Answer: The  total surface area of each hemisphere is  7,385.28 cm²

Explanation:
the total surface area of each hemisphere is A = 3πr²
= 3 × 3.14 × 28 × 28
= 7,385.28 cm²
So, The  total surface area of each hemisphere is  7,385.28 cm²

Question 11.
The volume of a sphere is 3,052.08 cubic meters.
a) What is the radius of the sphere?
Answer: The radius of the sphere is  9 cm.

Explanation:
Given, The volume of the sphere is about 3,052.08 cubic meters.
Then r = ?
We know that the volume of the sphere is V =  \(\frac{4}{3}\)πr³
3,052.08 = \(\frac{4}{3}\) × 3.14 ×r³
r³ = \(\frac{3,052.08× 3}{3.14 × 4}\)
r³ = \(\frac{91529}{12.56}\)
r³= 729
r = 9
So, The radius of the sphere is  9 cm.

b) What is the surface area of the sphere?
Answer: The surface area of a sphere is  1017.36 cm²

Explanation:
Then, r = 9 cm,
The surface area of a sphere is A = 4πr²
= 4 × 3.14 × 9 × 9
= 1017.36 cm²
So, The surface area of a sphere is  1017.36 cm²

Question 12.
Once you know how to find the surface area of a sphere, you can use the surface area formula to see why the volume formula works.
Think of a sphere as being divided up into hundreds of “pyramids” that have a common vertex at the center of the sphere. The surface of the sphere is made up of the bases of all these pyramids. The height of each pyramid is r, and you can call the areas of the bases B₁, B₂, B₃, and so on. To find the surface area of the sphere, you can find the sum of the areas of all the bases.

Show why the volume formula works by supplying a reason for each step below.

Answer:
Add the volumes of the pyramids to get the volume of the sphere:
V = \(\frac{1}{3}\) · r · B₁ + \(\frac{1}{3}\) · r · B₂ + \(\frac{1}{3}\) · r · B₃ + ………..
Factor out \(\frac{1}{3}\)r:
= \(\frac{1}{3}\)r(B₁ + B₂ + B₃)
The sum of the pyramids bases form the surface area of the sphere:
= \(\frac{1}{3}\)r(4πr²)
Use the commutative property of multiplication:
= \(\frac{4}{3}\) πr³

This handy Math in Focus Grade 7 Workbook Answer Key Chapter 8 Lesson 8.5 Real-World Problems: Composite Solids detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Chapter 8 Lesson 8.5 Answer Key Real-World Problems: Composite Solids

Math in Focus Grade 7 Chapter 8 Lesson 8.5 Guided Practice Answer Key

Solve.

Question 1.
A composite solid is made up of a cone and a cylinder. The slant height of the cone is 25 centimeters. The height of the cylinder is 15 centimeters and its radius is 12 centimeters. The height of the solid is 37 centimeters. Use 3.14 as an approximation for π.

a) Find the volume of the composite solid to the nearest cubic centimeter.
Volume of the cylinder:
πr²h = ∙ ∙ Use the formula for volume of a cylinder.
= cm³ Evaluate .

Volume of the cone:
Height of cone = –
= cm
\(\frac{1}{3}\) πr²h = \(\frac{1}{3}\) ∙ ∙ ∙ ∙ Use the formula for the volume of a cone.
= cm³ Multiply.
Volume of the composite solid:
+ = Add the volumes of the cylinder and the cone.
≈ cm³ Multiply and round.
The volume of the composite solid is about cubic centimeters.
Answer:  The volume of the composite solid is about 10,098 cm³
We are given:
l = 25
h_cylinder = 15
H = 37
r = 12
Use the formula for the volume of a cylinder:
V_cylinder = πr²h_cylinder
= π · 12² · 15
Evaluate:
= 2,160π cm³
The height of the cone:
h_cone = H – h_cylinder
= 37 – 15
= 22 cm
Use the formula for the volume of a cone:
V_cone = \(\frac{1}{3}\)πr²h_cone
= \(\frac{1}{3}\) · π · 12² · 22
Multiply:
= 1,056π cm³
Find the volume of the composite solid by adding the volumes of the cylinder and the cone:
V = V_cylinder + V_cone
= 2,160π + 1,056π
= 3,216π cm³
Multiply and round:
≈ 10,098 cm³

b) Find the surface area of the composite solid to the nearest square centimeter.

The surface area of the composite solid is about square centimeters.
Answer: The surface area of the composite solid is about  2,525 cm^2.
Use the formuLas for the surface areas:
S = πrl + 2πrh_cylinder + πr²
Substitute for r, l, h_cylinder
= π · 12 · 25 + 2π · 12 · 15 + π · 12²
Evaluate each term:
= 300π + 360π + 144π
Add:
= 804π
Multiply and round:
≈ 804 · 3.14 ≈ 2,525 cm²

Question 2.
A birdhouse looks like a cube with a square pyramid on top. As shown, the birdhouse has a circular entrance with a diameter of 4 inches. Find the exterior surface area of the birdhouse.

Answer: The exterior surface area of the birdhouse is 647.4 in²
Determine the Lateral surface area of the pyramid:
S₁ = 4 · \(\frac{1}{2}\) · 10 · 13 = 260 in²
Determine the radius of the entrance:
r = \(\frac{4}{2}\) = 2
Determine the lateral surface area of the house:
S₂ = 4 · 10 · 10 – π · 2² ≈ 387.4 in²
Compute the exterior surface area of the house:
S = S₁ + S₂ = 260 + 387.4 = 647.4 in²
= 647.4 in²

Question 3.
The solid shown is a cylinder with a cone-shaped hole. The diameter of the cylinder is 22 centimeters. Its height is 15 centimeters. The radius of the cone-shaped hole is 7 centimeters and the height is 10 centimeters. Find the volume of the solid. Use 3.14 as an approximation for π. Round your answer to the nearest cubic centimeter.

Answer: The volume of the solid is  5. 187 cm³
Determine the radius R of the cylinder:
R = \(\frac{22}{2}\) = 11 cm
Determine the volume of the cylinder
V_cylinder = πR²h = π · 11² ·  15 = 1, 815π cm²
Determine the volume of the cone:
V_cone = \(\frac{1}{3}\)πR²h = \(\frac{1}{3}\) · π · 7² · 10 ≈ 163π cm³
Determine the volume of the solid:
V = V_cylinder – V_cone
= 1,815π – 163π
= 1,652π
≈ 3.14 · 1,652
≈ 5. 187 cm³

Math in Focus Course 2B Practice 8.5 Answer Key

For this practice, you may use a calculator and use 3.14 as an approximation for π. Round your answers to the nearest tenth when you can.

Solve.

Question 1.
Jack has a cylindrical block that has a radius of 0.6 cm and is 22 centimeters long. He puts together 8 such blocks to form the composite solid shown. What is the volume of the composite solid?

Answer: The volume of the composite solid is 199 cm³
We are given the cylinder:
r = 0.6
h = 22
Determine the volume of one cylinder:
V_cylinder = πr²h ≈ 3.14 · 0.6² · 22
≈ 24.87 cm³
Determine the volume of the composite solid:
V_solid = 8V_cylinder = 8 · 24.87 ≈ 199 cm³

Question 2.
The trophy for a basketball tournament is made up of a miniature basketball attached to a rectangular prism. The radius of the basketball is 5 centimeters. The prism measures 8 centimeters by 5 centimeters by 15 centimeters. What is the volume of the trophy to the nearest cubic centimeter?

Answer: The volume of the trophy is 1,123 cm³
We are given:
r = 5
l = 8
w = 5
h = 15
Determine the volume of the sphere:
V_sphere = \(\frac{4}{3}\)πr³
≈ \(\frac{4}{3}\) · 3.14 · 5³
≈ 523 cm³
Determine the volume of the prism:
V_prism = lwh = 8 · 5 · 15 = 600 cm³
Determine the volume of the trophy:
V_trophy = V_sphere + V_prism
= 523 + 600
= 1,123 cm³

Question 3.
A necklace is made up of 50 spherical beads. Each bead has a radius of 8 millimeters.
a) What is the volume of the necklace?
Answer: The volume of the necklace is 107, 178.7 mm³
We are given the sphere:
r = 8
Determine the volume of a spherical bead:
V_bead = \(\frac{4}{3}\)πr³
≈ \(\frac{4}{3}\) · 3.14 · 8³
≈ 2,143.573
Determine the volume of the necklace:
V_necklace = 50 · V_bead
≈ 50 – 2. 143.573 ≈ 107, 178.7 mm³

b) What is the surface area of the necklace?
Answer: The surface area of the necklace is 40,192 mm²
Determine the surface area of a spherical bead:
S_bead = 4πr² ≈ 4 · 3.14 · 8²
≈ 803.84 mm²
Determine the surface area of the necklace:
S_necklace = 50 · S_bead
= 50 · 803.84
≈ 40,192 mm²

Question 4.
A crystal trophy is made up of a rectangular pyramid whose base is attached to the top of a rectangular prism. The base of the pyramid and the top of the prism are each 4 inches long and 3 inches wide. The height of the pyramid is 2.5 inches and the height of the prism is 9.5 inches. What is the volume of the crystal trophy?
Answer: The volume of the crystal trophy is 124 in³
We are given:
l = 4
w = 3
h_pyramid = 2.5
h_prism = 9.5
Determine the volume of the pyramid:
V_pyramid =\(\frac{1}{3}\) · lwh_pyramid 
= \(\frac{1}{3}\) · 4 · 3 · 2.5
= 10 in³
Determine the volume of the prism:
V_prism = lwh_prism = 4 · 3 · 9.5
= 114 in³
Determine the volume of the trophy:
V_trophy = V_pyramid + V_prism
= 10 + 114
= 124 in³

Question 5.
At a food stand, you can buy a paper cone filled with slush made of frozen juice. The slush forms a hemisphere on top of the cone, as shown. What is the volume of the cone of slush?

Answer: The volume of the cone of slush is 314.9 cm³
We are given:
d = 8
h = 10.8
Determine the radius:
r = \(\frac{d}{2}\) = \(\frac{8}{2}\) = 4
Determine the volume of the hemisphere:
V_hemisphere = \(\frac{1}{2}\) · \(\frac{4}{3}\) πr³
≈ \(\frac{2}{3}\) · 3.14 · 4³
≈ 134 cm³
Determine the volume of the cone:
V_cone = \(\frac{1}{3}\) πr²h
≈ \(\frac{1}{3}\) · 3.14 · 4² · 10.8
≈ 180.9 cm³
Determine the volume of the cone of slush:
V = V_hemisphere + V_cone
= 134 + 180.9
= 314.9 cm³

Question 6.
A wooden paper towel holder is composed of two cylinders. The diameter of the base is 12 .centimeters and its height is 2 centimeters. The combined height of the two cylinders is 30 centimeters. What is the volume of the paper towel holder?

Answer: The volume of the paper towel holder is 438 cm³
We are given:
d₁ = 3
h₁ = 30
d₂ = 12
h₂ = 2
Determine the radius of the upper cylinder:
r₁ = \(\frac{d_{1}}{2}\) = \(\frac{3}{2}\) = 1.5
Determine the volume of the upper cylinder:
V₁ = πr₁²h₁ = π · 1 5² · 30 = 67.5π cm³
Determine the radius of the lower cylinder:
r₂ = \(\frac{d_{2}}{2}\) = \(\frac{12}{2}\) = 6
Determine the volume of the lower cylinder:
V₂ = πr₂²h₂ = π · 6² · 2 = 72π cm³
Determine the volume of the paper tower holder:
V = V₁ + V₂ = 67.5π + 72π
≈ 139.5π
≈ 139.5 · 3.14
≈ 438 cm³

Question 7.
The edge of the base of a square pyramid is 11 inches. The pyramid has a height of 14 inches. What is the volume of the composite solid formed when two such pyramids are joined at the base, as shown in the diagram?

Answer: The volume of the composite solid is  1,129.3 in³
We are given:
L = 11
h = 14
Determine the volume of one pyramid:
V₁ = V₂ = \(\frac{1}{3}\)l²h = \(\frac{1}{3}\) · 11² · 14 ≈ 564.67 in³
Determine the volume of the composite solid:
V = V₁ + V₂ = 2V₁ = 2 · 564.67
≈ 1,129.3 in³

Question 8.
A clock in the shape of an hour glass is made up of two identical cones connected at their vertices. The radius of each cone is 7 centimeters. The combined height of the two cones is 11.8 centimeters. What is the volume of the clock?

Answer: The volume of the clock is 605.2 cm³
We are given:
r = 7
H = 11.8
Determine the height of each cone:
h = \(\frac{H}{2}\) = \(\frac{11.8}{2}\) = 5.9
Determine the volume of one cone:
V₁ = V₂ = \(\frac{1}{3}\)πr²h =  \(\frac{1}{3}\) · π · 7² · 59
≈ 96.3677π
Determine the volume of the clock:
V = V₁ + V₂ = 2V₁ = 2 · 96.367π
≈ 192.734 · 3.14
≈ 605.2 cm³

Question 9.
Jason made a long pole by joining three different lengths of cylindrical poles together. Each pole has the same diameter of 18 cm. The diagram below is not drawn to scale.

a) What is the volume of the long pole?
Answer: The volume of the long pole is 8,393.2 cm³
We are given:
d = 18
h₁ = 7
h₂ = 11
h₃ = 15
Determine the radius
r = \(\frac{d}{2}\) = \(\frac{18}{2}\) = 9
Determine the volume of the tong pole:
V = V₁ + V₂ + V₃
= πr²h₁ + πr²h₂ + πr² h3
= πr²(h₁ + h₂ + h₃)
≈ 3.14 · 9² · (7 + 11 + 15)
≈ 8,393.2 cm³

b) What is the surface area of the long pole?
Answer: The surface area of the long pole is  2,373.8 cm²
Determine the surface area of the long pole
= 2πr² + 2πr(h₁ + h₂ + h₃)
= 2πr(r + h₁ + h₂ + h₃)
≈ 2 · 3.14 · 9(9 + 7 + 11 + 15)
≈ 2,373.8 cm²

Brain @ Work

How can you make the following cross-sections by slicing a cube? Use a computer drawing program or pencil and paper to show your answers for a) and b).
a) An isosceles triangle
Answer:
We take a point on one edge, then take two congruent segments from one of the vertices on the same edge on the other two edges
We draw the cross-section in the cube in the shape of an isosceles triangle:

b) A regular hexagon
Answer:
To get a hexagon, we slice the cube with a plane going through alt six faces of the cube.
We draw the cross-section in the cube in the shape of a regular hexagon:

c) What other polygons can be cross-sections of a cube?
Answer:
The cross-section can be a quadrilateral when a plane crosses 4 faces of the cube:

The cross-section can also be a pentagon when a plane crosses 5 faces of the cube:

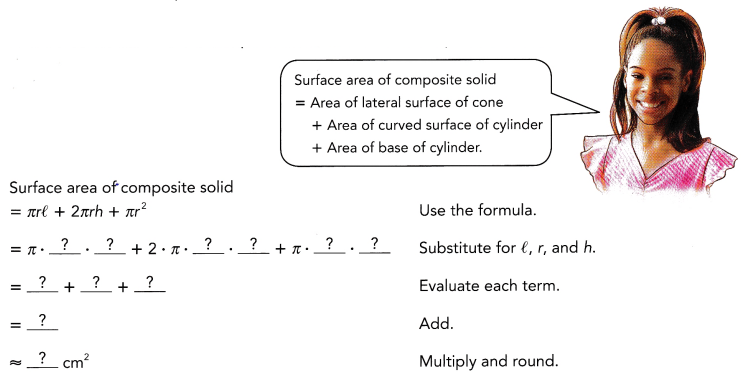
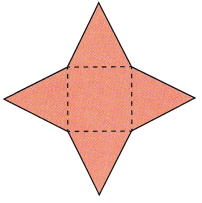
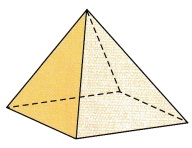
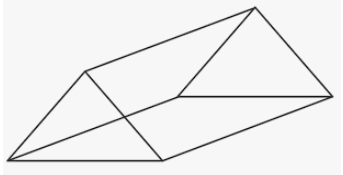
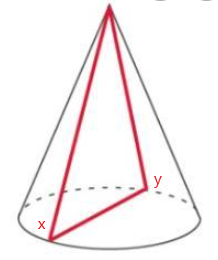
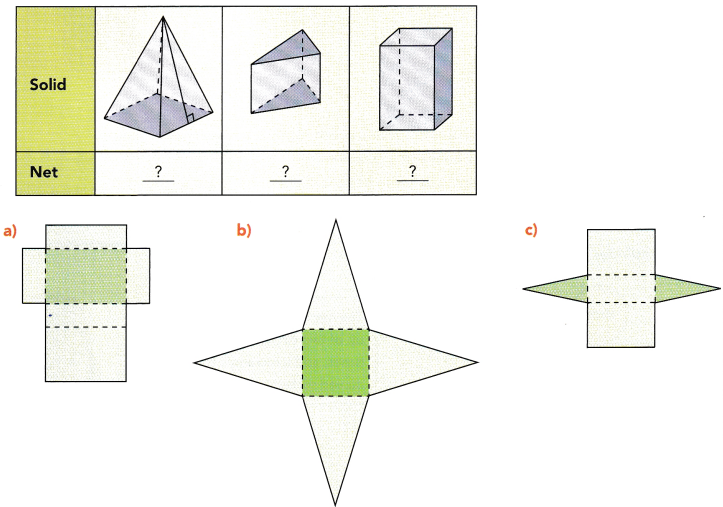
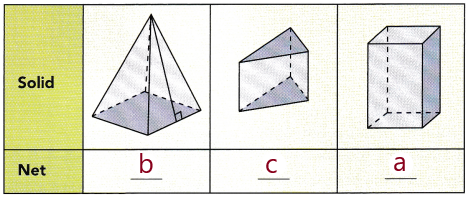
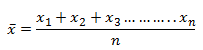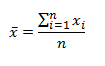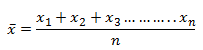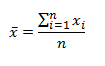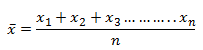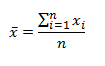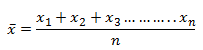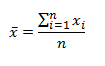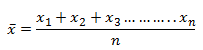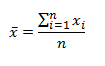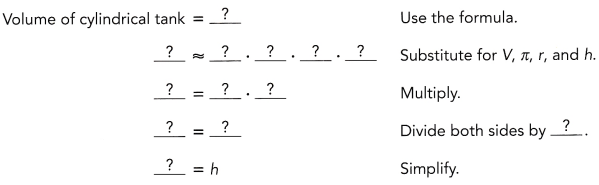This handy Math in Focus Grade 7 Workbook Answer Key Chapter 8 Lesson 8.3 Finding Volume and Surface Area of Pyramids and Cones detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Chapter 8 Lesson 8.3 Answer Key Finding Volume and Surface Area of Pyramids and Cones

Hands-On Activity

Materials:

• nets for a pyramid, a triangular prism, a cylinder, and a cone
• scissors
• ruler
• tape
• rice grains

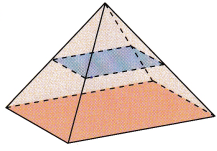
EXPLORE VOLUME RELATIONSHIPS BETWEEN A PYRAMID AND A PRISM, AND BETWEEN A CONE AND A CYLINDER

Work in pairs.

STEP 1: Cut out the nets for a triangular pyramid and triangular prism.

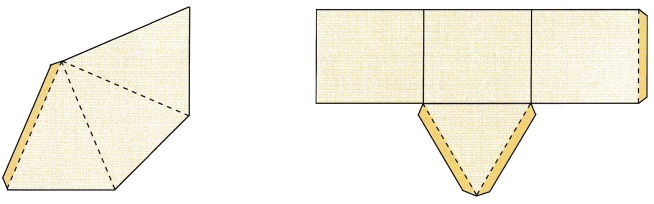
STEP 2: Fold the nets to make a triangular pyramid and triangular prism. Each solid will be open at one end. Tape the edges to hold them in place.

STEP 3: Do the pyramid and prism have the same height? Do the base of the pyramid and the base of the prism have about the same area?

STEP 4: Fill the pyramid completely with rice grains and pour them into the prism. Keep doing this until the prism is filled with rice grains. Flow many pyramids of rice grains are needed to fill the prism?

Math Journal What is the relationship between the volume of a triangular pyramid and the volume of a triangular prism with the same base and height? Suggest a formula for the volume of a pyramid.

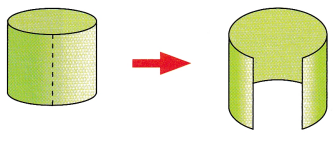
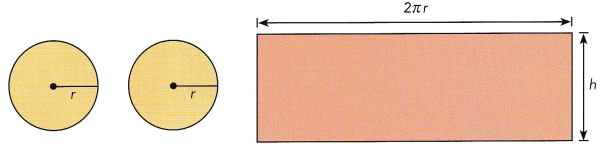
STEP 5: Cut out the nets for a cylinder and cone.

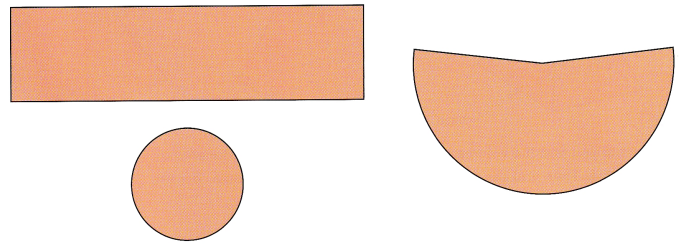
STEP 6: Use the cutouts of the rectangle and circle to make a cylinder. Tape the edges to hold them in place. The cylinder will be open at one end.

STEP 7: Fold the cutout of the sector of the circle to make a cone. Tape the edges to hold them in place. The cone will be open at its wide end.

STEP 8: Are the cylinder and the cone about the same height? Do the base of the cylinder and the base of the cone have about the same area?

STEP 9: Fill the cone completely with rice grains and pour them into the cylinder. Keep doing this until the cylinder is filled with rice grains. How many cones of rice grains are needed to fill the cylinder?

Math Journal What is the relationship between the volume of a cone and the volume of a cylinder with the same base and height? Suggest a formula for the volume of a cone.
Answer: The relationship between the volume of a cone and the volume of a cylinder with the same base and height is the volume of the cone is one-third the volume of the cylinder.

Explanation:
We know that the volume of the cylinder is  V = πr²h
the volume of the cone V=1/3hπr².
Then, The relationship between the volume of a cone and the volume of a cylinder,
with the same base and height is the volume of the cone is one-third the volume of the cylinder.
And, \(\frac{1}{3}\) πr²h = \(\frac{1}{3}\) πr²h
Hence, The volume of the cone and the volume of the cylinder is equal when their respective base and height are equal.

Math in Focus Grade 7 Chapter 8 Lesson 8.3 Guided Practice Answer Key

Solve.

Question 1.
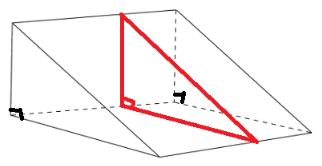
The base of a pyramid is a right triangle. The triangle has a base of 5 centimeters and a height of 3 centimeters. The pyramid has a height of 6 centimeters. What is the volume of the pyramid?

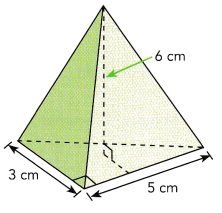
Use the formula for the volume of a pyramid.
Volume of pyramid
= \(\frac{1}{3}\) Bh Use the formula.
= \(\frac{1}{3}\) ∙ ( ∙ ∙ ) ∙     Substitute for B and h.
= cm³ Multiply.
The volume of the pyramid is cubic centimeters.
Answer:  The volume of the pyramid is 10 cm³

Explanation:
The volume of the pyramid is \(\frac{1}{3}\) bh
Here b = 5 cm, h = 6 cm
V = \(\frac{1}{3}\) (\(\frac{1}{2}\) × 3 × 5) 6
V = 15 cm³
So, The volume of the pyramid is 15 cm³.

Question 2.
A square pyramid has a height of 12 meters. If a side of the base measures 5.5 meters, what is the volume of the pyramid?
Answer: The volume of the Square pyramid is 121 cm³.

Explanation:
The volume of the Square pyramid is \(\frac{1}{3}\) a²h
Here a = 5.5 m, h = 12 m
V = \(\frac{1}{3}\) (5.5 × 5.5 × 12)
= 30.25 × 4
V = 121 m³
So, The volume of the Square pyramid is 121 cm³.

Question 3.
A square pyramid has a volume of 400 cubic centimeters. The length of the base is 10 centimeters. What is the height of the pyramid?
Let the height of the pyramid be h centimeters.
Volume of pyramid = \(\frac{1}{3}\) Bh Use the formula.
= \(\frac{1}{3}\) ∙ ( ∙ ) ∙ h Substitute for the volume and dimensions of the base.
= ∙ h Multiply both sides by .
= Divide both sides by
= h Simplify.
The height of the pyramid is centimeters.
Answer: The height of the Square pyramid is 12 cm.

Explanation:
The volume of the Square pyramid is 400 cm³
Here a = 10 cm, h = ?
V = \(\frac{1}{3}\) a²h
400 = \(\frac{1}{3}\) 10 × 10 × h
h = \(\frac{400 × 3}{10 × 10}\)
= 12 cm
So, The height of the Square pyramid is 12 cm.

Question 4.
A rectangular pyramid has a volume of 58 cubic meters. If the sides of the base measure 3 meters by 5 meters, what is the height of the pyramid?
Answer: The height of the Rectangular pyramid is 11.6 m.

Explanation:
The volume of the Rectangular pyramid is 58 m³
Here l = 5 m, b = 3 m , h = ?
V = \(\frac{1}{3}\) lbh
58 = \(\frac{1}{3}\) 5 × 3 × h
h = \(\frac{58 × 3}{5 × 3}\)
= 11.6 m
So, The height of the Rectangular pyramid is 11.6 m.

Question 5.
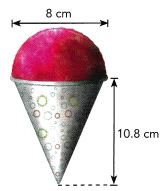
A party hat is in the shape of a cone. Find the exact volume of the party hat. Use 3.14 as an approximation for π to find the approximate volume of the cone. Round your answer to the nearest tenth.

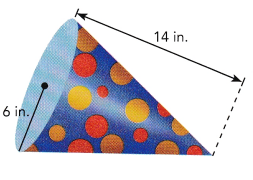
Use the formula for the volume of a cone, V = \(\frac{1}{3}\)Bh
Volume of the party hat = \(\frac{1}{3}\) ∙ πr² ∙ h Use the formula.
= \(\frac{1}{3}\) ∙ ∙ ∙ Substitute for π, r, and h.
= Multiply.
≈ in³ Round to the nearest tenth.
The exact volume of the party hat is cubic inches.
An approximate volume is cubic inches.
Answer: The volume of the party hat is 504 in³.

Explanation:
the volume of the cone V=1/3hπr².
Here r = 6 in. , h = 14 in.
V = \(\frac{1}{3}\) 14 × 6 × 6 × 3.14
V = 504 in³.
So, The volume of the party hat is 504 in³.

Question 6.
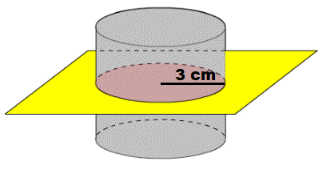
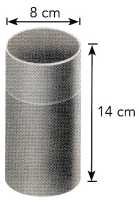
The diagram shows a cone-shaped container. Find the exact volume of the container. Use 3.14 as an approximation for π to find the approximate volume of the container. Round your answer to the nearest tenth.

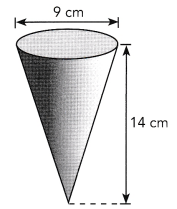
Answer: The volume of the container is 283 cm³.

Explanation:
the volume of the cone V=1/3hπr².
Here d= 9 cm , then
r = 4.5 cm , h = 14 cm.
V = \(\frac{1}{3}\) 14 × 4.5 × 4.5 × 3.14
V = 283.5 cm³.
So, The volume of the container is 283 cm³.

Question 7.
A cone has a height of 57 centimeters and a volume of 2,923.34 cubic centimeters. What is the radius of the cone? Use 3.14 as an approximation for π.
Let the height of the cone be h centimeters.

The radius of the cone is about centimeters.
Answer: The radius of the cone  is 7.16 cm.

Explanation:
the volume of the cone V=1/3hπr².
Here V = 2923.34 cm³
r = ? , h = 57 cm.
2923.34 = \(\frac{1}{3}\) 57 × r² × 3.14
r² = \(\frac{2923.34 × 3}{57 × 3.14}\)
r² =51.28 cm.
r = 7.16 cm
So, The radius of the cone  is 7.16 cm.

Question 8.
A cone has a height of 7.2 inches and a volume of 188.4 cubic inches. What is the radius of the cone? Use 3.14 as an approximation for π.
Answer: The radius of the cone  is 5.11 in.

Explanation:
the volume of the cone V=1/3hπr².
Here V = 188.4 in³
r = ? , h =7.2 in.
188.4 = \(\frac{1}{3}\) 7.2 × r² × 3.14
r² = \(\frac{188.4 × 3}{7.2 × 3.14}\)
r² =26.16 in.
r = 5.11 in
So, The radius of the cone  is 5.11 in.

Question 9.
Jean wants to sell lemonade in cone-shaped paper cups. Each cup has a diameter of 4 centimeters and a height of 8 centimeters. She wants to make enough lemonade for 50 cups. How much lemonade does Jean need to make? Round your answer to the nearest tenth. Use 3.14 as an approximation for π.

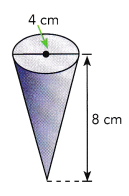
Answer: The lemonade jean needs to made is 1600 ml

Explanation:
the volume of the cone V=1/3hπr².
Here d= 4 cm , then
r = 2 cm , h = 8 cm.
V = \(\frac{1}{3}\) 8 × 2 × 2 × 3.14
V = 32 cm³.
So, The volume of the cup is 32 cm³.

Given, She wants to make enough lemonade for 50 cups.
= 50 × 32
= 1600 ml
So, The lemonade jean needs to made is 1600 ml

Hands-On Activity

FIND A FORMULA FOR THE AREA OF THE CURVED SURFACE OF A CONE

Work in pairs.

STEP 1: Copy and complete the table. For each pyramid, the base has edges of length b. The slant height is h.

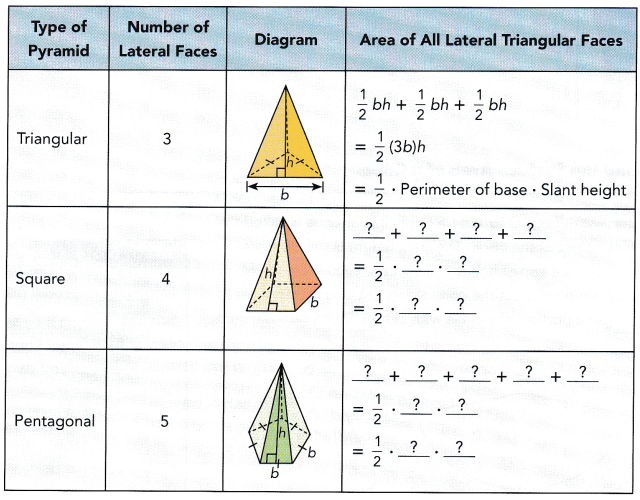
STEP 2: In general, what is the formula for the area of all the lateral triangular faces of a pyramid?

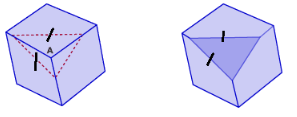
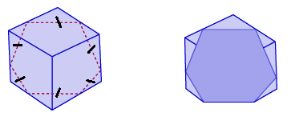
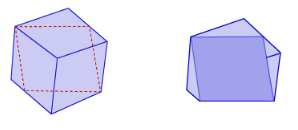
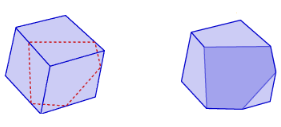
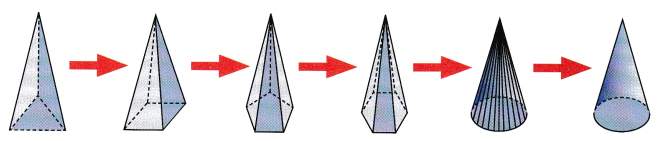
STEP 3: Suppose the number of sides of the base of the pyramid increases as shown below. Name the solid that is eventually formed.

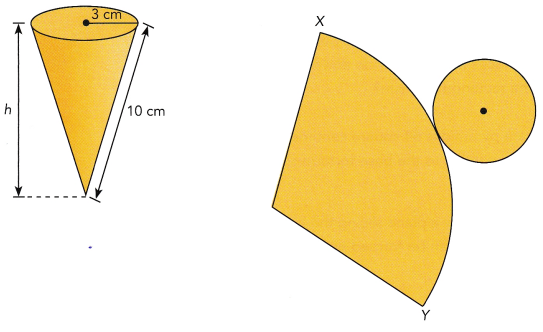
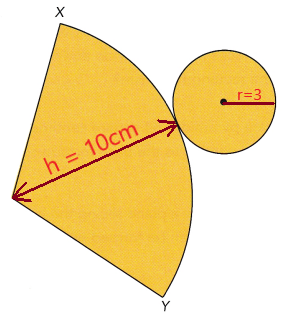
STEP 4: The formula for the curved surface area of a cone is related to the formula for the surface area of the triangular faces of a pyramid. Copy and complete the formula for the curved surface area of a cone. Let r represent the radius of the base of a cone. Let € represent the slant height of the cone.

Question 10.
A solid cone has a radius of 7 inches and a slant height of 14 inches.

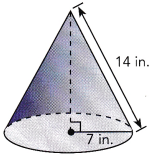
a) What is the exact area of the cone’s curved surface?
πrl = ∙ ∙ Use the formula for the lateral surface area of a cone.
= in² Multiply.
The exact area of the cone’s curved surface is square inches.
Answer: The exact area of the cone’s curved surface is 307.72 in²

Explanation:
The curved surface area of a cone  S =  πrl
Here r = 7 in, l = 14 in
S = 3.14 × 7 × 14
S = 307.72 in²
So, The exact area of the cone’s curved surface is 307.72 in²

b) What is the total surface area of the cone? Find both the exact value and an approximate value. Use \(\frac{22}{7}\) an approximation for π.
Total surface area of the cone:
Area of base + Area of curved surface = πr² + The lateral surface area is .
= ∙ ∙ + Substitute for r.
= Multiply.
= Add.
= in² Substitute for π.
The total surface area of the cone is exactly square inches, and approximately square inches.
Answer: The total surface area of the cone is exactly 462 in²

Explanation:
The total surface area of the cone is T = πr(r +l)
Here r = 7 in, l = 14 in
T = \(\frac{22}{7}\) × 7 ( 7 + 14 )
= 21 × 22
T = 462 in²
So, The total surface area of the cone is exactly 462 in²

Question 11.
The radius of a cone is 3 inches, and the slant height is 12 inches.

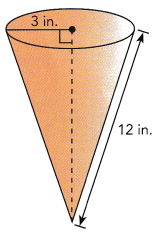
a) What is the exact area of the cone’s curved surface?
Answer: The exact area of the cone’s curved surface is 113.04 in²

Explanation:
The curved surface area of a cone  S =  πrl
Here r = 3 in, l = 12 in
S = 3.14 × 3 × 12
S = 113.04 in²
So, The exact area of the cone’s curved surface is 113.04 in²

b) What is the total surface area of the cone? Find both the exact value and an approximate value. Use 3.14 as an approximation for π.
Answer: The total surface area of the cone is exactly 141.3 in²

Explanation:
The total surface area of the cone is T = πr(r +l)
Here r = 3 in, l = 12 in
T = 3.14 × 3 ( 3 + 12 )
= 3.14 × 45
T = 141.3 in²
So, The total surface area of the cone is exactly 141.3 in²

Question 12.
A conical straw hat has a diameter of 16 inches and a lateral surface area of 251.2 square inches. Find the approximate slant height of the straw hat. Use 3.14 as an approximation for π.

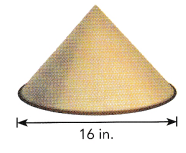
Let the lateral height of the hat be l inches.
Area of lateral surface of hat = πrl Use the formula for the lateral surface area of a cone.

The slant height of the hat is about inches.
Answer: The slant height of the hat is about 10 in.

Explanation:
Area of lateral surface of hat = πrl
Here, d = 16 in , S = 251.2 in²
Then r = 8 in
251.2 = 3.14 × 8 × l
l = \(\frac{251.2}{3.14 × 8}\)
l = 10 in
So, The slant height of the hat is about 10 in.

Question 13.
Jessica makes a cone-shaped paper filter to line a cone-shaped funnel. The funnel has a radius of 5 inches and a slant height of 10 inches. Suppose Jessica wants to make cone-shaped filters for 25 such funnels. About how many square inches of filter paper will she need? Use 3.14 as an approximation for π.
Answer: The filter paper she needs is  3925 in²

Explanation:
The lateral surface area of the funnel S = πrl
Here r = 5 in, l = 10 in
S = 3.14 × 5 × 10
S = 157 in²
Given, Jessica wants to make cone-shaped filters for 25 such funnels.
157 × 25 = 3925 in²
So, The filter paper she needs is  3925 in²

Math in Focus Course 2B Practice 8.3 Answer Key

For this practice, you may use a calculator and use 3.14 as an approximation for π. Round your answers to the nearest tenth when you can.

Find the volume of each pyramid.

Question 1.

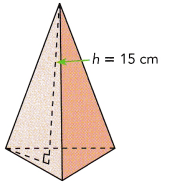
Base area = 72 cm²
Answer:  The volume of the pyramid is 48 cm²

Explanation:
The volume of a pyramid is V = \(\frac{1}{3}\)bh
Given, h = 15 cm, A = 72 cm²
A = \(\frac{1}{2}\)bh
b = \(\frac{72 × 2}{15}\)
b = 9.6 cm

V = \(\frac{1}{3}\) 9.6 × 15
V = 48cm²
So, The volume of the pyramid is 48 cm²

Question 2.

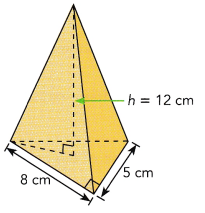
Answer: The volume of the pyramid is 32 cm³.

Explanation:
The volume of the pyramid is \(\frac{1}{3}\)bh
Here b = 8 cm, h = 12 cm
V = \(\frac{1}{3}\) 8 × 12
= 8 × 4
V = 32 cm³
So, The volume of the pyramid is 32 cm³.

Question 3.
A rectangular pyramid with a height of 10 inches and a base that measures 9 inches by 7 inches.
Answer: The volume of the rectangular  pyramid is 210 in³.

Explanation:
The volume of the rectangular pyramid is \(\frac{1}{3}\)lbh
Here b = 7 in, h = 10 in, l = 9 in
V = \(\frac{1}{3}\) 9 × 7 × 10
= 30 × 7
V = 210 in³
So, The volume of the rectangular  pyramid is 210 in³.

Question 4.
A square pyramid with a height of 18 feet and a base that is 12 feet on each edge.
Answer: The volume of the square  pyramid is 864 ft³.

Explanation:
The volume of the square pyramid is \(\frac{1}{3}\)a²h
Here h = 18 ft, l = 12 ft
V = \(\frac{1}{3}\) 12 × 12 × 18
= 144 × 6
V =864 ft³
So, The volume of the square  pyramid is 864 ft³.

Find the exact and approximate volume for each cone.

Question 5.

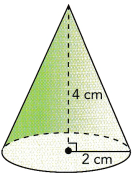
Answer: The exact volume of the cone is 16.74 cm³.
The approximate volume of the cone is 16 cm³

Explanation:
the volume of the cone V=1/3hπr².
Here r = 2 cm. , h = 4 cm.
V = \(\frac{1}{3}\) 4 × 2 × 2 × 3.14
V = 16.74 cm³.
So, The exact volume of the cone is 16.74 cm³.
The approximate volume of the cone is 16 cm³

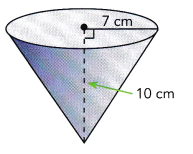
Question 6.

Answer: The exact volume of the cone is 512.86 cm³.
The approximate volume of the cone is 512 cm³

Explanation:
the volume of the cone V=1/3hπr².
Here r = 7 cm. , h = 10 cm.
V = \(\frac{1}{3}\) 10 × 7 × 7 × 3.14
V = 512.86 cm³.
So, The exact volume of the cone is 512.86 cm³.
The approximate volume of the cone is 512 cm³

Question 7.
A solid cone with a diameter of 10 centimeters and a height of 8 centimeters.
Answer: The exact volume of the cone is 209.33 cm³.
The approximate volume of the cone is 209 cm³

Explanation:
the volume of the cone V=1/3hπr².
Here, d = 10 cm,
r = 5 cm. , h = 8 cm.
V = \(\frac{1}{3}\) 8 × 5 × 5 × 3.14
V = 209.33 cm³.
So, The exact volume of the cone is 209.33 cm³.
The approximate volume of the cone is 209 cm³

Question 8.
A cone with a radius of 4.9 centimeters and a height of 6.9 centimeters.
Answer:  The exact volume of the cone is 173.4 cm³.
The approximate volume of the cone is 173 cm³

Explanation:
the volume of the cone V=1/3hπr².
Here r = 4.9 cm. , h = 6.9 cm.
V = \(\frac{1}{3}\) 6.9 × 4.9 × 4.9 × 3.14
V = 173.4 cm³.
So, The exact volume of the cone is 173.4 cm³.
The approximate volume of the cone is 173 cm³

Find the exact and an approximate surface area for each solid cone. Round your approximation to the nearest square unit.

Question 9.
A cone with a radius of 2.5 centimeters and a slant height of 5.6 centimeters.
Answer:  The exact area of the cone’s curved surface is 43.96 cm²
The  approximate area of the cone’s curved surface is 44 cm²

Explanation:
The curved surface area of a cone  S =  πrl
Here r = 2.5 cm , l = 5.6 cm
S = 3.14 × 2.5 × 5.6
S = 43.96 cm²
So, The exact area of the cone’s curved surface is 43.96 cm²
The  approximate area of the cone’s curved surface is 44 cm²

Question 10.
A cone with a diameter of 72 centimeters and a slant height of 48 centimeters.
Answer:  The exact area of the cone’s curved surface is 5425.92 cm²
The  approximate area of the cone’s curved surface is 5426 cm²

Explanation:
The curved surface area of a cone  S =  πrl
Here, d = 72 cm then,
r = 36 cm , l = 48 cm
S = 3.14 × 36 × 48
S = 5425.92 cm²
So, The exact area of the cone’s curved surface is 5425.92 cm²
The  approximate area of the cone’s curved surface is 5426 cm²

Question 11.
A cone with a diameter of 18 meters and a slant height of 22 meters.
Answer:  The exact area of the cone’s curved surface is 621.72 m²
The  approximate area of the cone’s curved surface is 622 m²

Explanation:
The curved surface area of a cone  S =  πrl
Here, d = 18 m then,
r = 9 m , l =  22 m
S = 3.14 × 9 × 22
S = 621.72 m²
So, The exact area of the cone’s curved surface is 621.72 m²
The  approximate area of the cone’s curved surface is 622 m²

Solve.

Question 12.
A square pyramid has a volume of 605 cubic centimeters and a height of 15 centimeters.
a) What is the area of the base of the pyramid?
Answer: the area of the base of the Square pyramid is 121 cm².

Explanation:
the area of the base of the Square pyramid A = a²
Given, V = 605 cm³ , h = 15 cm
The volume of the Square pyramid is \(\frac{1}{3}\) a²h
605 = \(\frac{1}{3}\)  × 15 × a²
a² = \(\frac{605}{5}\)
a²= 121 cm
a = 11 cm

Then, A = 11 × 11 = 121 cm²
So, the area of the base of the Square pyramid is 121 cm².

b) What is the length of an edge of the base?
Answer:  the length of an edge of the base is 11 cm

Explanation:
Given, V = 605 cm³ , h = 15 cm
The volume of the Square pyramid is \(\frac{1}{3}\) a²h
605 = \(\frac{1}{3}\)  × 15 × a²
a² = \(\frac{605}{5}\)
a²= 121 cm
a = 11 cm
So, the length of an edge of the base is 11 cm

Question 13.
The volume of a square pyramid is 333 cubic centimeters. The length of an edge of the base of the pyramid is 10 centimeters. What is the height of the pyramid rounded to the nearest centimeter?
Answer: The height of the Square pyramid is 10 cm.

Explanation:
The volume of the Square pyramid is \(\frac{1}{3}\) a²h
Here V = 333 cm³, a = 10 cm
h = \(\frac{V × 3}{a²}\)
= \(\frac{333 × 3}{10 × 10}\)
h =9.99 cm = 10 cm.
So, The height of the Square pyramid is 10 cm.

Question 14.
A candle in the shape of a cone has a radius of 5 centimeters. The slant height is 15 centimeters.
a) What is the area of the base of the candle?
Answer: the area of the base of the candle is 78.5 cm²

Explanation:
the area of the base of the cone is A =πr²
Here , r = 5 cm,
A =3.14 × 5 × 5
A = 78.5 cm²
So, the area of the base of the candle is 78.5 cm²

b) What is the area of the curved surface of the candle?
Answer: The area of the curved surface of the candle  is 235.5 cm²

Explanation:
The curved surface area of a cone  S =  πrl
Here r = 5 cm, l = 15 cm
S = 3.14 × 5 × 15
S = 235.5 cm²
So, The area of the curved surface of the candle  is 235.5 cm²

c) Suppose the candle is wrapped in plastic. If there is no overlap, how much plastic is needed?
Answer: The area of the surface of the cone and the wrapped plastic area without overlapping will be equal

Explanation:
The curved surface area of a cone  S =  πrl
Here r = 5 cm, l = 15 cm
S = 3.14 × 5 × 15
S = 235.5 cm²
So, The area of the curved surface of the candle  is 235.5 cm²
Hence, The area of the surface of the cone and the wrapped plastic area without overlapping will be equal

Question 15.
A cone has a slant height of 8.5 centimeters. The height of the cone is 7.5 centimeters and the radius is 4 centimeters.
a) What is the area of the lateral surface?
Answer: the area of the lateral surface is 94.2 cm²

Explanation:
Area of lateral surface of hat = πrl
Here, r= 4 cm , l = 7.5 cm
S = 3.14 × 4 × 7.5
S = 94.2 cm²
So, the area of the lateral surface is 94.2 cm²

b) What is the volume of the cone?
Answer: The volume of the cone is125.6 cm³.

Explanation:
the volume of the cone V=1/3hπr².
Here , r = 4 cm , h = 7.5 cm.
V = \(\frac{1}{3}\) 7.5 × 4 × 4 × 3.14
V = 125.6  cm³.
So, The volume of the cone is125.6 cm³.

Question 16.
One of the entrances to the Louvre Museum in France is in the shape of a pyramid. The entrance has a height of about 70 feet and a volume of about 233,330 cubic feet. What is the area of the base of the pyramid to the nearest foot?

Answer: the area of the base of the Square pyramid is 10,000 ft².

Explanation:

the area of the base of the Square pyramid A = a²
Given, V = 233,330 ft³ , h = 70 ft
The volume of the Square pyramid is \(\frac{1}{3}\) a²h
233,330 = \(\frac{1}{3}\)  × 70 × a²
a² = \(\frac{233,330 × 3}{70}\)
a²= 9999.85 ft = 10,000
a = 100 ft

Then, A = 100 × 100 = 10,000 ft²
So, the area of the base of the Square pyramid is 10,000 ft².

Question 17.
Math Journal Cylinder P and cone Q have the same radius and height. The volume of cylinder P is 393 cubic centimeters. Joseph says that the volume of cone Q is 131 cubic centimeters. Explain how Joseph arrived at his answer.

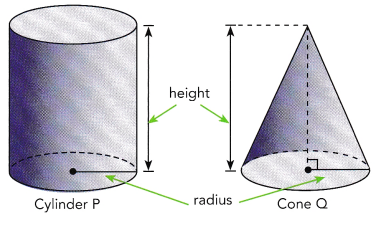
Answer:  The volume of the cone and the volume of the cylinder is equal when their respective base and height are equal.

Explanation:
We know that the volume of the cylinder is  V = πr²h
the volume of the cone V=1/3hπr².
Then, The relationship between the volume of a cone and the volume of a cylinder,
with the same base and height is the volume of the cone is one-third the volume of the cylinder.
And, \(\frac{1}{3}\) πr²h = \(\frac{1}{3}\) πr²h
Hence, The volume of the cone and the volume of the cylinder is equal when their respective base and height are equal.

Question 18.
A circle has a radius of 61 millimeters. Three-quarters of the circle is used to form a net for the curved part of a cone. The net is taped together to form the cone without any overlap. The height of the finished cone is 40 millimeters.

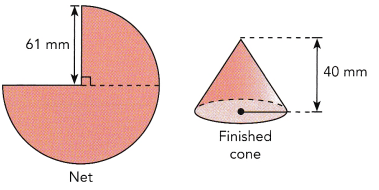
a) What is the circumference of the base of the cone?
Answer: The circumference of the base of the cone is  383.08 mm

Explanation:
The circumference of the cone is 2πr
Here d = 61 mm,
Then r = 30.5 mm
C = 2 × 3.14 × 30.5
= 191.54 mm
So, The circumference of the base of the cone is  191.54 mm

b) What is the radius of the cone?
Answer: r = 30.5 mm

Explanation:
The circumference of the cone is 2πr
Here d = 61 mm,
Then r = 30.5 mm

c) What is the volume of the cone?
Answer: The volume of the cone is 38,946 mm³

Explanation:
the volume of the cone V=1/3hπr².
Here , r = 30.5 mm , h = 40 mm.
V = \(\frac{1}{3}\) 40 × 30.5 × 30.5 × 3.14
V = 38,946 mm³.
So, The volume of the cone is 38,946 mm³

d) What is the area of the curved surface of the cone?
Answer: The area of the cone’s curved surface is 3,830 mm²

Explanation:
The curved surface area of a cone  S =  πrl
Here r =  30.5 mm , l = 40 mm
S = 3.14 × 30.5 × 40
S = 3,830 mm²
So, The area of the cone’s curved surface is 3,830 mm²

Question 19.
Martha used a filter in the shape of a cone to filter sand from a liquid. The volume of liquid that the filter can hold is 66 cubic centimeters. The height of the filter is 6 centimeters. What is the diameter of the filter? Round your answer to the nearest tenth.
Answer: The diameter of the filter is  7 cm.

Explanation:
Given, V = 66 cm³
the volume of the cone V=1/3hπr².
r = ? , h = 6 cm.
66 = \(\frac{1}{3}\) 6 × r² × 3.14
r² = \(\frac{66 × 3}{6 × 3.14}\)
r² =10.5 cm
r = 3.24 cm
The radius of the filter  is 3.24 cm

Then, the diameter d = 2r = 2 × 3.24 = 6.48 cm = 7 cm
So, The diameter of the filter is  7 cm.

This handy Math in Focus Grade 7 Workbook Answer Key Chapter 8 Lesson 8.2 Finding Volume and Surface Area of Cylinders detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Chapter 8 Lesson 8.2 Answer Key Finding Volume and Surface Area of Cylinders

Math in Focus Grade 7 Chapter 8 Lesson 8.2 Guided Practice Answer Key

Use the given dimensions to find the volume of each cylinder. Use 3.14 as an approximation for π. Round your answer to the nearest tenth.

Question 1.
Radius = 5 cm, Height = 7.5 cm
Answer: The volume of the cylinder is 588.75 cm³

Explanation:
We know that , the volume of the cylinder V = πr²h
Here r = 5 cm , h = 7.5 cm,
V = πr²h
= 3.14 × (5)² × 7.5
= 5.8875 cm³
So, The volume of the cylinder is 588.75 cm³

Question 2.
Diameter = 7 in., Height = 5 in.
Answer: The volume of the cylinder is 192.3 in³

Explanation:
We know that , the volume of the cylinder V = πr²h
Here d = 7 in , h = 5 in,
then, r = 3.5
V = πr²h
= 3.14 × (3.5)² × 5
= 192.3 cm³
So, The volume of the cylinder is 192.3 cm³

Complete. Use 3.14 as an approximation for π.

Question 3.
The volume of a cylindrical tank of water is 1,808.64 cubic meters. The radius is 12 meters. What is the height of the cylindrical tank?
Use the formula for volume to find the height, h, of the cylinder.

The height of the cylindrical tank is about meters.
Answer:  The height of the cylindrical tank is about 4 meters.

Explanation:
Given, the volume of the tank V = 1,808.64 cubic meters, radius r = 12 meters
We know that , the volume of the cylinder V = πr²h
here π = 3.14
V = πr²h
h = \(\frac{V}{πr²}\)
= \(\frac{1808.64}{3.14 × 12 × 12}\)
= \(\frac{1808.64}{452.16}\)
= 4
So, The height of the cylindrical tank is about 4 meters.

Hands-On Activity

Materials:

• a tin can or any other cylindrical object
• paper
• scissors

Work in pairs.

STEP 1: What is the shape of the bases of your cylinder?
Write an expression for the area of one base in terms of r.

STEP 2: Cut a piece of paper to cover the curved surface of the cylinder. One end of the paper should meet the other end without overlapping.

STEP 3: Lay the paper flat on the table to form a rectangle. Use the information below to write expressions for its length and width in terms of r and h.
Length of rectangle = Circumference of the base =
Width of rectangle = Height of cylinder =
Now write an expression for the area of the curved surface in terms of rand h.

STEP 4: Use the expressions written in STEP 1 and STEP 3 to write an expression for the surface area of a cylinder.
Surface area = Area of bases + Area of curved surface

Solve. Use 3.14 as an approximation for π. Round to the nearest tenth.

Question 4.
A cylinder has a radius of 4 inches and a height of 7 inches. Find the surface area of the cylinder.
Answer: The surface area of the cylinder is 276 in².

Explanation:
The formula for the surface area of the cylinder A = 2πrh + 2πr²
Here r = 4 in. , h = 7 in. ,
A = (2 × 3.14 × 4 × 7) + ( 2 × 3.14 × 4 × 4)
= 175.84 + 100.48
= 276.32 in²
≈ 276 in²
So, The surface area of the cylinder is 276 in².

Solve.

Question 5.
The area of the curved surface of a cylindrical can is l62π square centimeters and its height is 9 centimeters. What is the diameter of the can?
Area of curved surface = 2πrh Use the formula for the area of the curved surface.
= 2πr • Substitute the surface area and height.
= 2 • • πr Multiply 2 by
= Simplify.
\(\frac{?}{?}=\frac{?}{?}\) Divide both sides by .
= r Simplify.
The diameter of the can is centimeters.
Answer: The diameter of the can is 18 cm

Explanation:
Given, The area of the curved surface of a cylindrical can is l62π square centimeters and h = 9 cm,
We know that Area of curved surface = 2πrh
Now equate the given data to the area formula we get,
2πrh = l62π
2 × r × 9 = 162
r = \(\frac{162}{18}\)
r = 9 cm
Then, d = 2r = 2 × 9 = 18cm,
So, The diameter of the can is 18cm

Math in Focus Course 2B Practice 8.2 Answer Key

For this practice, you may use a calculator. Use 3.14 as an approximation for π. Round your answers to the nearest tenth when you can.

Find the volume of each cylinder.

Question 1.

Answer: The volume of the cylinder is 263 cm³

Explanation:
We know that , the volume of the cylinder V = πr²h
Here r = 3.8 cm , h = 5.8 cm,
V = πr²h
= 3.14 × (3.8)² × 5.8
= 3.14 × 83.75
= 262.98 cm³
≈ 263 cm³
So, The volume of the cylinder is 263 cm³

Question 2.

Answer: The volume of the cylinder is 12 m³

Explanation:
We know that , the volume of the cylinder V = πr²h
Here d = 1.2 m , h = 10.6 m,
then, r = 0.6 m
Because r = \(\frac{d}{2}\):
V = πr²h
= 3.14 × (0.6)² × 10.6
= 3.14 × 3.816
= 11.98 m³
≈ 12 m³
So, The volume of the cylinder is 12 m³

Solve.

Question 3.
A cylinder has a radius of 6 centimeters and a height of 28 centimeters. What is the volume?
Answer: The volume of the cylinder is 3165 cm³

Explanation:
We know that , the volume of the cylinder V = πr²h
Here r = 6 cm , h = 28 cm,
V = πr²h
= 3.14 × (6)² × 28
= 3.14 × 1008
= 3165.12 cm³
≈ 3165 cm³
So, The volume of the cylinder is 3165 cm³

Question 4.
A cylinder has a volume of 239 cubic centimeters and a height of 6 centimeters. What is the radius?
Answer:  The radius of the cylinder is 3.5cm

Explanation:
We know that , the volume of the cylinder V = πr²h
Here v = 239 cm³ , h = 6 cm,
V = πr²h
r² = \(\frac{V}{πh}\)
= \(\frac{239}{3.14 × 6}\)
r²= 12.68
r = 3.56
≈ 3.5 cm
So, The radius of the cylinder is 3.5cm

Question 5.
Jenny is making a cylindrical pencil holder in shop class. It will be 14 centimeters high and 8 centimeters across. The bottom and sides of the container will be made of metal.

a) What is the area of the base?
Answer: The area of the base is  100.48 cm²

Explanation:
The area of the base = 2πr²
Given, d = 8cm,
Then r = 4 cm
2πr² = 2 × 3.14 × 4 × 4
= 100.48 cm²
So, The area of the base is  100.48 cm²

b) What is the area of the curved surface of the pencil holder?
Answer: The Area of curved surface is 351.68 cm²

Explanation:
We know that Area of curved surface = 2πrh
Here, h = 14 cm , r = 4 cm
2πrh  =  2 × 3.14 × 4 × 14
= 351.68 cm²
So, The Area of curved surface is 351.68 cm²

c) What is the total surface area of the pencil holder?
Answer: The total surface area of the pencil holder is 452 cm².

Explanation:
The formula for the total surface area of the cylinder A = 2πrh + 2πr²
Here r = 4 cm, h = 14 cm ,
A = (2 × 3.14 × 4 × 14) + ( 2 × 3.14 × 4 × 4)
= 351.68 + 100.48
= 452.16 cm²
≈ 452 cm²
So, The total surface area of the pencil holder is 452 cm².

Question 6.
You want to make a tube with a height of 8 inches and a radius of 5 inches out of cardboard. The tube will be open at both ends. How much cardboard will you need to make the tube?
Answer: The cardboard needed  to make the tube will be 753 in.

Explanation:
Given, h = 8 in. , r = 5 in.
cardboard needed  to make the tube will be the curved surface area of the tube,
The  Area of curved surface = 2πrh
2πrh  =  2 × 3.14 × 8 × 15
= 753.6 in²
So, The Area of curved surface is 753 in².

Question 7.
The volume of a soup can is 125.6 cubic inches. The diameter of the can is 8 inches. What is the height of the soup can?

Answer: The height of the can is about 2.5inches .

Explanation:
Given, the volume of a soup can V = 125.6 cubic in., diameter of the can is 8 in.
Then, r = 4 in.,
We know that , the volume of the cylinder V = πr²h
here π = 3.14
V = πr²h
h = \(\frac{V}{πr²}\)
= \(\frac{125.6}{3.14 × 4 × 4}\)
= \(\frac{125.6}{50.24}\)
= 2.5 in.
So, The height of the can is about 2.5inches .

Question 8.
Mrs. Lavender bought a cylindrical lampshade with height 14 inches and diameter-10 inches. As shown in the diagram, the lampshade is open at the top and bottom. Find the surface area of the lampshade.
Answer:  the surface area of the lampshade is  439 in²

Explanation:
We know that Area of curved surface = 2πrh
Here, h = 14 in , d = 10 in.,
Then r = 5 in,
2πrh  =  2 × 3.14 × 5 × 14
= 439.6 in²
So, The Area of curved surface is 439 in².

Question 9.
The volume of a cylinder is 121 π cubic inches and its height is 4 inches.

a) What is the radius of the cylinder?
Answer: The radius of the cylinder is 5 in.

Explanation:
We know that , the volume of the cylinder V = πr²h
Here v = 121 π cubic inches , h = 4 inches.
V = πr²h
r² = \(\frac{V}{πh}\)
= \(\frac{121 × 3.14}{3.14 × 4}\)
r²= 30.25
r = 5.5
≈ 5 in
So, The radius of the cylinder is 5 in.

b) What is the surface area of the cylinder? Give your answer in terms of π.
Answer: the surface area of the cylinder is  40π in².

Explanation:
We know that Area of curved surface = 2πrh
Here, h = 4 in , r = 5 in
2πrh  =  2 × π × 4 × 5
= 40π in²
So, The Area of curved surface is 40π in².

Question 10.
The diagram shows a mallet made by attaching two solid cylinders together. What is the volume of the mallet?

Answer: The volume of the mallet is V = 8024 cm³.

Explanation:
We know that , the volume of the cylinder V = πr²h
The volume of first cylinder is
Here d = 22 cm  , h = 18cm,
then, r = 11 cm
V = πr²h
= 3.14 × (11)² × 18
= 6838.92 cm³
So, The volume of the first cylinder is 6838 cm³

The volume of second cylinder is
Here d = 6 cm  , h = 42 cm,
then, r = 3 cm
V = πr²h
= 3.14 × (3)² × 42
= 1186.92 cm³
So, The volume of the second cylinder is 1186 cm³

Then, The volume of the mallet is  volume of first cylinder + volume of second cylinder
= 6836 + 1186
V = 8024 cm³.
So, The volume of the mallet is V = 8024 cm³.

Question 11.
A company makes cylindrical cans for peaches. Each can has a radius of 4 centimeters and a height of 12 centimeters. The company plans to increase the volume of each can by 25%.
a) What will be the height of the new can if the radius remains the same?
Answer: The height of the new can is about 15 cm

Explanation:
We know that , the volume of the cylinder V = πr²h
Here r = 4 cm , h =12 cm,
V = πr²h
= 3.14 × (4)² × 12
= 602.88 cm³
So, The volume of the cylinder is 602 cm³

Given, increase the volume of each can by 25%.
The 25% of 602 = 150
Then V = 602 + 150 = 752 cm³

The new volume of the can is 752 cm³,
the height of the new can if the radius remains the same will be
V = πr²h
h = \(\frac{V}{πr²}\)
= \(\frac{752}{3.14 × 4 × 4}\)
= \(\frac{752}{50.24}\)
= 14.9 cm.
So, The height of the new can is about 15 cm .

b) What will be the radius of the new can if the height remains the same?
Answer: The radius of the new can is 4 cm.

Explanation:
The new volume of the can is 752 cm³,
the radius of the new can if the height remains the same will be
V = πr²h
r² = \(\frac{V}{πh}\)
= \(\frac{752}{3.14 × 12}\)
r²= 19.95
r = 4.4
≈ 4 cm
So, The radius of the new can is 4 cm

Question 12.
A cylindrical water tank has a radius of 5 feet and a height of 10 feet. The volume of water in the tank is 565.2 cubic feet.
a) What is the height of the water in the tank?
Answer: The height of the water in the tank is 7.2 feet.

Explanation:
Given, V = 565.2 cubic feet, r = 5 feet
We know that , the volume of the cylinder V = πr²h
here π = 3.14
V = πr²h
h = \(\frac{V}{πr²}\)
= \(\frac{565.2}{3.14 × 5 × 5}\)
= \(\frac{565.2}{78.5}\)
= 7.2 feet.
So, The height of the water in the tank is 7.2 feet.

b) What percent of the tank’s volume is filled with water?
Answer: The percent of the tank’s volume is filled with water is 72%

Explanation:
The height of the tank is 10 feet and
the height of the water in the tank is 7.2 feet
Then, 7.2 is 72% of 10
So, The percent of the tank’s volume is filled with water is 72%

Question 13.
Eric is painting 8 wooden cylinders. Each cylinder has a radius of 6.2 inches and a height of 12.4 inches. Eric can paint 50 square inches of wood using one pint of paint. How much paint will Eric need to paint all the wooden cylinders?
Answer:  The paint will Eric need to paint all the wooden cylinders is 4 liters

Explanation:
Given, Eric is painting 8 wooden cylinders.
Each cylinder has a radius of 6.2 inches and a height of 12.4 inches.
Eric can paint 50 square inches of wood using one pint of paint.
= 8 × 50
= 400 in²
The paint will Eric need to paint all the wooden cylinders is 4 liters

Question 14.
The area of the curved surface of a cylindrical jar is 1,584 square centimeters. The height of the jar is 28 centimeters.
a) What is the circumference of the jar?
Answer: The circumference of the jar is 175 cm

Explanation:
Given, The area of the curved surface of a cylindrical jar is1 584 square centimeters and h = 28 cm,
We know that Area of curved surface = 2πrh
Now equate the given data to the area formula we get,
2πrh = 1584
2 × r × 28 = 1584
r = \(\frac{1584}{2 × 28}\)
r =28.28 cm
Then, d = 2r = 2 × 28 = 56 cm,
So, The diameter of the jar is 56cm

Circumference of the jar is C = πd
C = 3.14 × 56 = 175.84 cm
So, The circumference of the jar is 175 cm

b) What is the radius of the jar?
Answer:  The radius of the jar is 28.28 cm

Explanation:
Given, The area of the curved surface of a cylindrical jar is1 584 square centimeters and h = 28 cm,
We know that Area of curved surface = 2πrh
Now equate the given data to the area formula we get,
2πrh = 1584
2 × r × 28 = 1584
r = \(\frac{1584}{2 × 28}\)
r =28.28 cm
So, The radius of the jar is 28.28 cm.

Question 15.
Math journal Joyce uses the formula 5 = 2πr(r + h) to find the surface area of a cylinder. Assuming she uses the correct values for r and h, will she get the correct volume? Explain your thinking.
Answer: Yes, she will get the correct volume.

Explanation:
We know that , Surface area = Area of bases + Area of curved surface
She used the formulas 2πrh + 2πr²
the volume of the cylinder V = πr²h
she uses the correct values for r and h
So, yes she will get the correct volume.

This handy Math in Focus Grade 7 Workbook Answer Key Chapter 8 Lesson 8.1 Recognizing Cylinders, Cones, Spheres, and Pyramids detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Chapter 8 Lesson 8.1 Answer Key Recognizing Cylinders, Cones, Spheres, and Pyramids

Hands-On Activity

Materials:

• clay
• string

FIND THE SHAPE OF CROSS SECTIONS OF SOLIDS

Work in pairs.

STEP 1: Make three clay cubes. Use the string to slice a cube vertically so that the cross section is parallel to one face, as shown. Sketch the cross section and describe its shape.

STEP 2: Use a string to slice another cube diagonally, as shown. Sketch the cross section and describe its shape.

STEP 3: Use a string to slice the last cube through the midpoints of each of three edges that share a common vertex, as shown. Sketch the cross section and describe its shape.

Math Journal Are you able to slice a cube in other ways to form the cross-section in STEP 1 to STEP 3?
Answer:

Math in Focus Grade 7 Chapter 8 Lesson 8.1 Guided Practice Answer Key

For each solid, name the shape of the cross-section formed when the solid is sliced by the plane shown.

Question 1.

Answer: Rectangle

Explanation:

The shape of the cross-section formed when the solid is sliced by the plane is a  Rectangle.
Because, It  forms a closed figure having four sides of which two of the opposite sides are equal.
So, it forms a Rectangle.

Question 2.

Answer: Rectangle

Explanation:

The shape of the cross-section formed when the solid is sliced by the plane is a  Rectangle.
Because, It  forms a closed figure having four sides of which two of the opposite sides are equal.
So, it forms a Rectangle.

Question 3.

Answer: Square

Explanation:

The shape of the cross-section formed when the solid is sliced by the plane is a  Square.
Because, It  forms a closed figure having four sides of which all the sides are equal.
So, it forms a Square

Question 4.

Answer: Triangle

Explanation:

The shape of the cross-section formed when the solid is sliced by the plane is a  Triangle.
Because, It  forms a closed figure having three sides .
So, it forms a Triangle.

Math in Focus Course 2B Practice 8.1 Answer Key

Match each set to its net.

Answer: The combinations of the figures are
1- f
2- c
3- d
4- e
5- b
6- a

Name the solid that can be formed from each net.

Question 7.

Answer: The closed figure formed is a cylinder

Explanation:

It forms a cylinder

Question 8.

Answer: The closed figure formed is a cylinder

Explanation:

It is a cylinder.

Question 9.

Answer: The closed figure formed is a Square pyramid

Explanation:

It is a square pyramid

Question 10.

Answer: The closed figure formed is a Triangular prism

Explanation:

It is a triangular prism.

Solve. Show your work.

Question 11.
Tell what cross-section is formed when a plane slices a square pyramid as described.
a) Perpendicular to its base and passes through its vertex.
Answer: The figure Perpendicular to its base and passes through its vertex is a triangle

Explanation:
Thee square pyramid is


So, The figure Perpendicular to its base and passes through its vertex is a triangle

b) Parallel to its base.
Answer: The figure parallel to its base is a square

Explanation:

The square pyramid is


So, The figure parallel to its base is a square.

Question 12.
The diagram shows a cone and its net.

a) Copy the net of the cone and label these dimensions on the net.
Answer:

b) How is the circumference of the base of the cone related to the curve XV?
Answer: The  closed figure  of the net forms a cone and its is a circle

Explanation:

Given,, the radius of a circle is 3 cm
From that the circumference of a circle is 2πr
C = 2 (3.14)(3) =  18.84 cm
So,  The xy becomes the circumference of a circle .

Question 13.
The diagram shows the net of a cylinder. Which sides of the rectangle have the same length as the circumference of the circular base?

Answer: The sides of the rectangle have the same length as the circumference of the circular base are  AB and DC

Explanation:
The closed figure of this  net becomes a cylinder

So, The sides of the rectangle have the same length as the circumference of the circular base are  AB and DC.

Question 14.
A base of each of the following prism is shaded. Name the shape of the cross section formed when each prism is sliced by a plane parallel to each base. Copy each prism. Sketch the cross sections and label them with the dimensions.
a)

Answer:

b)

Answer:

Question 15.
A cross-section that is parallel to one of the bases of a rectangular prism is 3 inches wide and 6 inches long. A cross-section that is perpendicular to its bases and parallel to two other faces is 4 inches wide and 6 inches long. What are the dimensions of the rectangular prism?
Answer: The dimensions of a rectangular prism are

Question 16.
The area of the base of a square pyramid is 64 square centimeters. Several planes slice through the pyramid parallel to the base to form square cross-sections.
a) Besides the cross-section formed by a plane slicing the base, how many cross-sections parallel to the base can be formed with areas that are perfect squares?
Answer: There can be 7 perfect squares after the multiple cross section.

Explanation:
The area of the base of a square pyramid is 64 square centimeters
That is a = 8 , Area a² = 8 × 8 = 64
So, cross-sections parallel to the base can be formed with areas that are perfect squares are
If a = 7 ,  a² = 7 × 7 = 49,
If a = 6 ,  a² = 6 × 6 = 36,
If a = 5 ,  a² = 5 × 5 = 25,
If a = 4 ,  a² = 4 × 4 = 16,
If a = 3 ,  a² = 3 × 3 = 9,
If a = 2 ,  a² = 2 × 2 = 4,
If a =  ,  a² = 1 × 1 = 1,
There can be 7 perfect squares after the multiple cross section.

b) Find the sum of the area of the base and the areas of the cross-sections found in a).
Answer: The sum of the area of the base is 28 cm²
The sum of the area of the cross-sections is  140 cm²

This handy Math in Focus Grade 7 Workbook Answer Key Chapter 8 Volume and Surface Area of Solids detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Chapter 8 Answer Key Volume and Surface Area of Solids

Math in Focus Grade 7 Chapter 8 Quick Check Answer Key

Solve.

Question 1.
A cube has edges measuring 6 centimeters each.
a) Find its volume.
Answer: The volume of the cube V  is 216 cm³

Explanation:
Given, the edge of a cube a = 6 cm each
Formula for volume of a cube V  is  a³
Here, a = 6
V = a³ = 6³
V = 6 × 6 × 6 = 216
So, The volume of the cube V  is 216 cm³.

b) Find its surface area.
Answer: The surface area of the cube A is 216 cm²

Explanation:
Given, the edge of a cube a = 6 cm each
Formula for surface area of a cube  A  is  6a²
Here, a = 6
A = 6a² = 6 × 6²
A = 6 × 6 × 6 = 216 cm²
So, The surface area of the cube A  is  216 cm².

Question 2.
The volume of a cube is 512 cubic centimeters. Find the length of each edge of the cube.
Answer: The length of each edge of the cube a is 8 cm

Explanation:
Given, the volume of a cube is 512 cubic centimeters.
Here, V = a³ = 512 cm³
a³ = 8× 8 × 8 = 512 cm³
Then, a = 8.
So, the length of each edge of the cube a is 8 cm

Question 3.
A pyramid has a square base measuring 10 inches on each side. It has four faces that are congruent isosceles triangles. The height of each triangle is 13 inches. Find the surface area of the pyramid.

Answer: The total surface area of the pyramid is 360 in²

Explanation:
Given, The height of each triangle is 13 inches.
The pyramid has a square base measuring 10 inches on each side.
The area of each triangle is \(\frac{1}{2}\) × bh ,
Here, base b = 10 in. and height h = 13 in.
Area of each triangle = \(\frac{1}{2}\) × 10 × 13
Area of each triangle  = 65 in²
There are total 4 triangles in the pyramid , so the area of 4 triangles are 4 × 65 = 260 in².
The area of a square is a² = 10² = 10 × 10 = 100 in²
So, The total surface area of a pyramid is 260 + 100 = 360 in².

Use 3.14 as an approximation for π.

Question 4.
Shawn makes waffles for breakfast. Each waffle is a circle with a diameter of 6 inches.
a) Find the circumference of a waffle.
Answer: The circumference of a waffle is  18.85 in.

Explanation:
Given, Each waffle is a circle with a diameter of 6 inches
We know that radius r = \(\frac{d}{2}\)
Here, d = 6
then, r = \(\frac{6}{2}\) = 3,
The circumference of a circle  is C = 2πr
C = 2 × π  × 3  , let us take π = 3.14,
C = 6.28 × 3  = 18.85
So, The circumference of a waffle is C = 18.85 in.

b) Find the area of the waffle.
Answer: The area of the waffle is 28.27 in²

Explanation:
Here r = 3 in.
The area of a circle is A =  πr²,  let us take π = 3.14,
A = 3.14  × 3 × 3 = 28.27
So, The area of the waffle is 28.27 in²

Question 5.
The circumference of a wheel is 320.28 centimeters.
a) Find the radius of the wheel.
Answer: The radius of the wheel is 51 cm

Explanation:
Given, The circumference of a wheel is 320.28 centimeters.
We know that the circumference of a circle is  π d
Where d is the diameter of the circle
then,  π d = 320.28
d = \(\frac{320.28}{ π}\) , take  π = 3.14
= \(\frac{320.28}{ 3.14}\)
d = 102,
d = 2r or r = \(\frac{d}{2}\)
r = \(\frac{102}{2}\)
r = 51 cm.
So, The radius of the wheel is 51 cm

b) Find the area of the wheel.
Answer: The area of the wheel is 8167.14 cm²

Explanation:
Here r = 51 cm
The area of a circle is A =  πr²,  let us take π = 3.14,
A = 3.14  × 51 × 51
= 3.14 × 2601
A = 8167.14
So, The area of the wheel is 8167.14 cm²

Match each solid to its net.

Question 6.

Answer:

Explanation:
1. The first solid represents a pyramid with a square base and four triangles having a height perpendicular to the base.
2. The second solid represents a triangular prism .
3. The third solid represents a cuboid.

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 7 Review Test to score better marks in the exam.

Math in Focus Grade 7 Course 2 B Chapter 7 Review Test Answer Key

Concepts and Skills

Construct the angle bisector of ∠ABC on a copy of each figure using a compass and straightedge.

Question 1.

Answer:

Question 2.

Answer:

Use a protractor to draw an angle with the given measure. Then use a compass and straightedge to construct its angle bisector.

Question 3.
m∠XYZ = 37°
Answer:

Question 4.
m∠PQR = 72°
Answer:

Question 5.
m∠KLM = 128°
Answer:

On a copy of each angle, construct the angle with the given measure by constructing the angle bisector. Use only a compass and straightedge.

Question 6.
Construct a 65° angle whose vertex is point X.

Answer:

Question 7.
Construct a 66° angle whose vertex is point Y.

Answer:

Draw a line segment with the given length. Then construct the perpendicular bisector of the segment using a compass and straightedge.

Question 8.
AB = 6.5 cm
Answer:

Question 9.
CD = 4.5 cm
Answer:

Question 10.
AD = 10.8 cm
Answer:

On a copy of the figure shown, using only a compass and straightedge, draw the perpendicular bisectors of \(\overline{\mathbf{P Q}}\) and \(\overline{\mathbf{P R}}\). Label the point where the two perpendicular bisectors intersect as W.

Question 11.

Answer:

Question 12.

Answer:

Use the given information to find the number of triangles that can be constructed. Try constructing the triangles to make your decision.

Question 13.
Triangle WXY: WX = 4.5 cm, m∠XWY = 60°, and m∠WXY = 40°.
Answer:

Question 14.
Triangle ABC: AB = 5 cm, AC = 4.5 cm, and m∠CAB = 60°.
Answer:

Question 15.
Triangle DEF: DE = 4 cm, EF = 3 cm, and DF = 8 cm.
Answer:

Use the given information to construct each quadrilateral.

Question 16.
Rhombus DEFG with diagonal DF = 4.2 cm and DE = 5 cm.
Answer:

Question 17.
Parallelogram ABCD with AB = 7 cm, DA = 4.5 cm, and m∠ABC = 50°.
Answer:

Question 18.
Quadrilateral ABCD such that AB = 5 cm, AD = 3.5 cm, BC = 4 cm, m∠BAD = 60°, and m∠ABC = 90°.
Answer:

Solve. Show your work.

Question 19.
A rectangular garden is 15 meters long and 9 meters wide. Use a scale of 1 centimeter to 3 meters, make a scale drawing of the garden.
Answer:
length of the garden is = 45 m
width of the garden is = 27 m

Explanation:
Given the length of the rectangle = 15m
Breadth of the rectangle = 9 m
given scale as 1 centimeter = 3 m
The new length of the garden is = 15 × 3 = 45 m
New breadth of the garden is = 9 × 3 = 27 m

Question 20.
The scale of the floor plan of a room is 1 inch: 6.5 feet. On the floor plan, the room is 8 inches long and 6 inches wide. What are the actual dimensions of the room?
Answer:
1 inch : 6.5 feet means 1 inch on the map represents 6.5 feet on the ground.
Let’s note:
x cm = the actuaL Length
y cm = the actual width.
We have:
1 in. : 6.5 ft = 8 in. : x ft = 6 in. : y ft
Write ratios in fraction form:
\(\frac{1 \mathrm{in} .}{6.5 \mathrm{ft}}=\frac{8 \mathrm{in} .}{x \mathrm{ft}}=\frac{6 \mathrm{in} .}{y \mathrm{ft}}\)
Write without units:
\(\frac{1}{6.5}\) = \(\frac{8}{x}\) = \(\frac{6}{y}\)
Write cross products:
x = 8 · 6.5
y = 6 · 6.5
Simplify
x = 52 ft
y = 39 ft
The actual dimensions of the room are 52 ft and 39 ft.

Question 21.
A model of a car is made using the scale 1 : 25. The actual length of the car is 4.8 meters. Calculate the length of the model of the car in centimeters.

Answer:
1 : 25 means 1 cm on the map represents 25 cm on the ground.
Let x inches be the Length of the car on the map.
We have:
4.8 cm = 4.8 · 100 cm = 480 cm
1 cm : 25 cm = x cm : 480 cm
Write ratios in fraction form:
\(\frac{1 \mathrm{~cm}}{25 \mathrm{~cm}}\) = \(\frac{x \mathrm{~cm}}{480 \mathrm{~cm}}\)
Write without units:
\(\frac{1}{25}\) = \(\frac{x}{480}\)
Write cross products:
25x = 480
Divide both sides by 25:
\(\frac{25x}{25}\) = \(\frac{480}{25}\)
Simplify:
x = 19.2
On the map, the car’s length is 19.2 cm.

Question 22.
The scale on a map is 1 inch : 120 miles. On the map, a highway is 5 inches long. Find the actual length of the highway in miles.
Answer:
Length = 24 miles

Explanation:
Scale on a map is 1 inch: 120 miles
The highway is 5 inches.
The actual length of the highway in miles is 1 × \(\frac{120}{5}\)
length of the highway is 24 miles.

Problem Solving

Solve.

Question 23.
Joe constructed an isosceles triangle WXY such that VVX = WY = 5 cm and XY = 4 cm. Construct another isosceles triangle ABC such that AB = AC = 10 cm and BC = 8 cm. Is triangle ABC an enlargement or a reduction of triangle WXY? Explain your answer and give the scale factor. Justify your answer.
Answer:
We are given △WXY and △ABC:
WX = WY = 5
XY = 4
AB = AC = 10
BC = 8
We construct △WXY:

We construct △ABC:

The sides of △ABC have twice the lengths of the sides of △WXY. Therefore △ABC is an enlargement of △WXY. The scale factor is 2.

Question 24.
James was asked to design a square decorative tile with a side length of 90 millimeters. Construct the square on which James will draw his design.
Answer:
We have to construct the square:
AB = 90 mm
Sketch the square:

Use a ruler to draw \(\overline{A B}\) so that is 90 mm long:

Using a protractor, draw ∠A and ∠B with a measure of 90°.

Because AD = BC = 90 mm, set the compass to a radius of 90 mm. Then using A and B as the center, draw two arcs intersecting the rays drawn in the previous step. Label these points of intersection as D and C.

Draw \(\overline{C D}\).

Question 25.
Harry is designing a theater platform in the shape of a rhombus using a blueprint. The lengths of the diagonals on his blueprint are 4 centimeters and 9 centimeters. Construct the rhombus. Then measure a side length. If the scale of the drawing is 1 centimeter: 2 meters, about what length of skirting does Harry need to go around all four edges of the platform?
Answer:
We are given the rhombus:
AC = 9
BD = 4
We draw the segment of length 20 and label it BD:

We bisect the segment \(\overline{A C}\).
Place the compass point at A. Then draw an arc on each side of \(\overline{A C}\) with a radius greater than half of the length of \(\overline{A C}\).
Using the same radius, set the compass point in C. Draw one arc on each side of \(\overline{A C}\).
Label the points where the arcs intersect as E and F.

Use a straightedge to draw a line through E and F. Label the intersection point of \(\overline{E F}\) and \(\overline{A C}\) by O.

As rhombus diagonals bisect each other, point O is the middle point of \(\overline{B D}\). Place the compass point at O.Then draw an arc on each side of \(\overline{A C}\) with a radius \(\frac{4}{2}\) = 2cm. Label the intersections of these arcs with \(\overline{E F}\) by B and D.

Use a ruler to draw AB, BC, CD, DA.

Measure a side of the rhombus:
AB ≈ 4.9 cm
We are given the scale:
1 cm : 2 m
Let’s note by r the actual length of one side of the rhombus.
\(\frac{1}{2}\) = \(\frac{4.9}{x}\)
We determine x:
x = 2 49
x = 9.8 m
Calculate the perimeter of the rhombus:
4 · 9.8 = 39.2 m

Question 26.
Michael wants to make some kites out of a plastic sheet for a family picnic. Before making the kites he wants to make a \(\frac{1}{4}\) scale model to find the lengths and angles needed for each kite. The diagram shows the measurements of the actual kite. He knows that \(\overline{A C}\) is the perpendicular bisector of \(\overline{B D}\), and that \(\overline{A N}\) should be 6 inches long. Construct the model he will use and find the measures of ∠ABC and the lengths AB and BC in the actual kite.

Answer:
We are given the actual kite dimensions:
AC = 24
BD = 20
AN = 6
Determine the dimensions of the model kite:
\(\frac{1}{4}=\frac{A^{\prime} C^{\prime}}{A C}=\frac{B^{\prime} D^{\prime}}{B D}=\frac{A^{\prime} N^{\prime}}{A N}\)
\(\frac{1}{4}=\frac{A^{\prime} C^{\prime}}{24}=\frac{B^{\prime} D^{\prime}}{20}=\frac{A^{\prime} N^{\prime}}{6}\)
4A’C” = 24 ⇒ A’C” = 6
4B’D’ = 20 ⇒ B’D’ = 5
4A’N’ = 6 ⇒ A’N’ = 1.5
We draw the segment of length 5 and label it B’D’:

We bisect the segment \(\overline{B^{\prime} D^{\prime}}\).
Place the compass point at B’. Then draw an arc on each side of \(\overline{B^{\prime} D^{\prime}}\) with a radius greater than half of the length of \(\overline{B^{\prime} D^{\prime}}\).
Using the same radius, set the compass point in D’. Draw one arc on each side of \(\overline{B^{\prime} D^{\prime}}\).
Label the points where the arcs intersect as E and F
Use a straightedge to draw a line through E and F. Label the intersection point of \(\overline{E F}\)
and \(\overline{B^{\prime} D^{\prime}}\) by N’.

Place the compass point at N’. With a radius of 1.5 in. draw an arc above \(\overline{B^{\prime} D^{\prime}}\). Label the intersection of this arc with \(\overline{E F}\) by A’.
Place the compass point at N’. With a radius of 6 – 1.5 = 4.5 in. draw an arc below \(\overline{B^{\prime} D^{\prime}}\). Label the intersection of this arc with \(\overline{E F}\) by C”.

Use a ruler to draw A’B’, B’C”, C”D’, D’A’.
Measure a side of the rhombus:

Measure ∠ABC:
m∠ABC ≈ 93°
Measure the length5 A’B’ and B’C” in the model kite:
A’B’ ≈ 2.9 in.
B’C” ≈ 5.1 in.
Determine the Lengths AB and BC in the actual kite:
\(\frac{1}{4}=\frac{A^{\prime} B^{\prime}}{A B}=\frac{B^{\prime} C^{\prime}}{B C}\)
\(\frac{1}{4}=\frac{2.9}{A B}=\frac{5.1}{B C}\)
AB = 4 · 2.9 = 11.6 in.
BC = 4 · 5.1 = 20.4 in.

Question 27.
The scale of a map is 1 inch to 5 feet. Find the area of a rectangular region on the map if the area of the actual region is 95 square feet.
Answer:
The area of a rectangular region is 19 square inches.

Explanation:
The scale of a map is 1 inch to 5 feet.
The area of the actual region is 95 square feet.
The area of a rectangular region is = 95 × \(\frac{1}{5}\)
Area of rectangle is = 19 sqaure inches.

Question 28.
The floor plan of a building has a scale of \(\frac{1}{4}\) inch to 1 foot. A room has an area of 40 square inches on the floor plan. What is the actual room area in square feet?
Answer:
10 square feet.

Explanation:
The floor plan of a building has a scale of \(\frac{1}{4}\) inch to 1 foot.
A room has an area of 40 square inches.
The actual room area in square feet is 1× \(\frac{40}{4}\)
= 10 sqaure feet.

Question 29.
The scale of a map is 1 : 2,400. If a rectangular piece of property measures 2 inches by 3 inches on the map, what is the actual area of this piece of property to the nearest tenth of an acre? (1 acre = 43,560 ft²)
Answer:
1: 2,400 means 1 inch on the map represents 2,400 inches on the ground.
Map length : Actual length = 1 in. : 2,400 in.
Map area: Actual area = 1 in.² : 2. 400² in.²
Let y represent the actual area of the rectangle in square inches.
Write a proportion:
\(\frac{\text { Area of rectangle on map }}{\text { Actual area of rectangle }}=\frac{1}{5,760,000}\)
Substitute:
\(\frac{2 \cdot 3}{y}\) = \(\frac{1}{5,760,000}\)
Write the cross products:
y = 6 · 5.760,000
Simplify:
y = 34,560,000 in.²
We convert the actual area to acres:
1 acre = 43,560 ft² = 43,460 · 12² in.²
= 6,258,240 in.²
\(\frac{34,560,000}{6,258,240}\) ≈ 5.52 acres