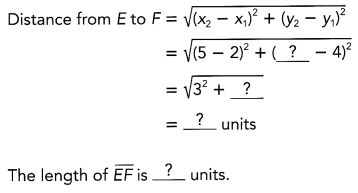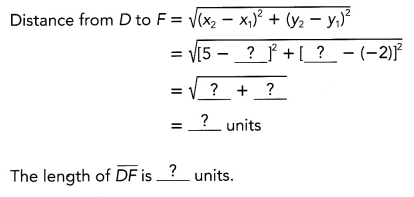Hillary

This handy Math in Focus Grade 7 Workbook Answer Key Chapter 9 Lesson 9.5 Making Inferences About Populations detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Chapter 9 Lesson 9.5 Answer Key Making Inferences About Populations

Math in Focus Grade 7 Chapter 9 Lesson 9.5 Guided Practice Answer Key

Solve.

Question 1.
A random sample of ages {15, 5, 8, 7, 18, 6, 15, 17, 6, 15} of 10 children was collected from a population of 100 children.
a) Calculate the sample mean age of the children and use it to estimate the population mean age.
Answer:
Mean is the average of the given numbers and is calculated by dividing the sum of given numbers by the total number of numbers.
Mean=Sum of observations/total number of observations
Mean=15+5+8+7+18+6+15+17+6+15/10
Mean=112/10
Mean=11.2 years.

b) Calculate the MAD of the sample.
Answer:
Now we got mean in the above question:
Mean=11.2 years. So calculate MAD.
The ratio of the sum of all absolute values of deviation from central measure to the total number of observations.
M.A. D = (Σ Absolute Values of Deviation from Central Measure) / (Total Number of Observations)
How to calculate MAD:
Steps to find the mean deviation from mean:
(i)Find the mean of the given observations.
(ii)Calculate the difference between each observation and the calculated mean
(iii)Evaluate the mean of the differences obtained in the second step.
This gives you the mean deviation from the mean.
Mean=11.2
The given data set: 15, 5, 8, 7, 18, 6, 15, 17, 6, 15
|15-11.2|=3.8
|5-11.2|=6.2
|8-11.2|=3.2
|7-11.2|=4.2
|18-11.2|=6.8
|6-11.2|=5.2
|15-11.2|=3.8
|17-11.2|=5.8
|6-11.2|=5.2
|15-11.2|=3.8
Now calculate MAD:
MAD=3.8+6.2+3.2+4.2+6.8+5.2+3.8+5.8+5.2+3.8/10
MAD=48/10
MAD=4.8 years

c) Calculate the MAD to mean ratio.
Answer:
About 43%
To calculate MAD to mean:
4.8 is what percent of 11.2
4.8/11.2*100%
After calculating the above equation we get:
=42.857
=43 (rounded to the nearest number).

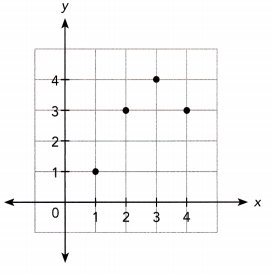
d) Draw a dot plot for the ages and the mean age.
Answer:
A dot plot visually groups the number of data points in a data set based on the value of each point. This gives a visual depiction of the distribution of the data, similar to a histogram or probability distribution function. Dot plots allow a quick visual analysis of the data to detect the central tendency, dispersion, skewness, and modality of the data.
The given data set: 15, 5, 8, 7, 18, 6, 15, 17, 6, 15

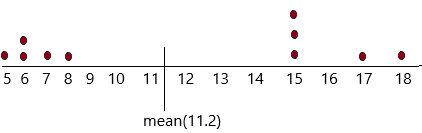
e) Using the MAD to mean ratio and the dot plot, describe informally how varied the population ages are.
Answer:
Since the MAD to mean ratio is about 43%, the data vary from the mean significantly. The dot plot confirms that the data are spread far away from the mean.

Hands-On Activity

Materials
a novel with 200 to 300 pages

USE STATISTICS FROM A SAMPLE TO DESCRIBE THE VARIABILITY OF A POPULATION

Work in pairs.

The activity can be a collaborative effort for the whole class.

Background
The population is made up of all the words in a book. The length of a word is defined by the number of letters in it. The population characteristic is the mean word length.

STEP 1: Determine which sampling method you intend to use.

STEP 2: Generate five random samples. Each sample consists of 20 words.

STEP 3: For the 20 words in each sample, record each word and its length in a table like the one shown. Then calculate the mean and the mean absolute deviation for each sample.

STEP 4: When you have completed STEP 1 to STEP 3 for all 20 samples, calculate the mean of the sample means.

Math journal What is the estimate of the population mean word length? By observing the mean absolute deviations of the five samples, describe informally whether the words in the book vary greatly in length.
Answer:

Solve.

Question 2.
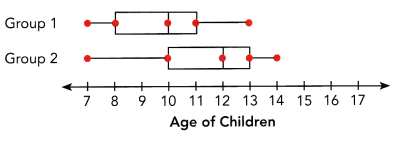
The ages of two groups of children are summarized in the box plots.

a) Show that the two groups have the same measure of variation (that is, the difference between quartiles) and the same interquartile range.
Answer:
The above box plot gives the data:
Group 1 data:
lowest number=7
Q1=8; Q2=10; Q3=11
Highest number=13
Group 2 data:
lowest number=7
Q1=10; Q2=12; Q3=13
Highest number=14
To show the same measure of variation
Group 1: Q2-Q1=10-8=2
Q3-Q2=1
Interquartile range=Q3-Q1
Interquartile range=11-8
Interquartile range=3
Group 2 calculation:
Q2-Q1=12-10=2
Q3-Q2=13-12=1
Interquartile range=Q3-Q1
Interquartile range=13-10
Interquartile range=3

b) Express the difference in median age in terms of the interquartile range.
Answer:
The above box plot gives the data:
Group 1 data:
lowest number=7
Q1=8; Q2=10; Q3=11
Highest number=13
Group 2 data:
lowest number=7
Q1=10; Q2=12; Q3=13
Highest number=14
We got the interquartile range for group 1 and group 2 is 3
The difference in median age in terms of IQR=X
X= Q2 of group1 – Q2 of group 2 /IQR
X=12-10/3
X=2/3 yr

c) What inference can you draw about the age distributions of the children in the two groups?
Answer:
The above box plot gives the data:
Group 1 data:
lowest number=7
Q1=8; Q2=10; Q3=11
Highest number=13
Group 2 data:
lowest number=7
Q1=10; Q2=12; Q3=13
Highest number=14
Since Q1 of group 2 is the same as the Q2 of group 1, it means that 75% of children in group 2 are older than 50% of children in group 1. Also, the median of group 2 is greater than the median of group 1. So the children in group 2 are generally older than group 1.

Question 3.
Two classes took a math test. The results are summarized in the box plots.

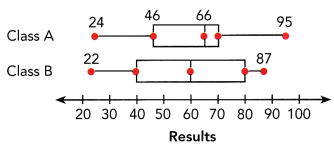
a) For which class are the data more spread out? Explain.
Answer: Class B
Class A data set:
Lowest number=24
Q1=46; Q2=66; Q3=70
Highest number=95
Class B data set:
Lowest number=22
Q1=40; Q2=60; Q3=80
Highest number=87
Now calculate the interquartile range:
IQR of class A=Q3-Q1
IQR of class A=70-46
IQR of class A=24
IQR of class B=Q3-Q1
IQR of class B=80-40
IQR of class B=40
Therefore, class B data are more spread out than class A because the interquartile range of class B is greater.

b) Comment on the performance of the two classes.
Answer:
Class A data set:
Lowest number=24
Q1=46; Q2=66; Q3=70
Highest number=95
Class B data set:
Lowest number=22
Q1=40; Q2=60; Q3=80
Highest number=87
Now here we need to check the performance according to the value of the median.
The median value of class A is 66
The median value of class B is 60
Thus, class A performed moderately better than class B because the median of class A is slightly higher at 66 and class B is 60.

Question 4.
The numbers of questions that two groups of students answered correctly in a recent mathematics test are shown in the table.

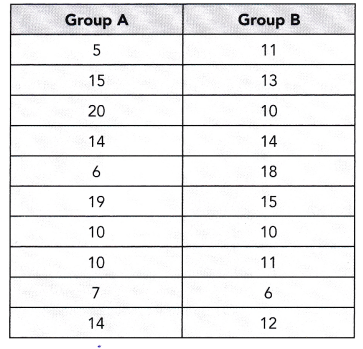
a) Find the mean number of correct questions for each of the two groups.
Answer:
Mean is the average of the given numbers and is calculated by dividing the sum of given numbers by the total number of numbers.
Mean=Sum of observations/total number of observations
Mean of group A=5+15+20+14+6+19+10+10+7+14/10
Mean of group A=120/10
Mean of group A=12
Now calculate the mean for group B:
Mean of group B=11+13+10+14+18+15+10+11+6+12/10
Mean of group B=120/10
Mean of group B=12

b) Calculate the mean absolute deviation of each of the two groups.
Answer:
Now we got mean in the above question:
Mean of group A=12
Mean of group B=12. So calculate MAD.
The ratio of the sum of all absolute values of deviation from central measure to the total number of observations.
M.A. D = (Σ Absolute Values of Deviation from Central Measure) / (Total Number of Observations)
How to calculate MAD:
Steps to find the mean deviation from mean:
(i)Find the mean of the given observations.
(ii)Calculate the difference between each observation and the calculated mean
(iii)Evaluate the mean of the differences obtained in the second step.
This gives you the mean deviation from the mean.
The MAD of group A:
Data set of group A=5, 15, 20, 14, 6, 19, 10, 10, 7, 14
Mean=12
|5-12|=7
|15-12|=5
|20-12|=8
|14-12|=2
|6-12|=6
|19-12|=7
|10-12|=2
|10-12|=2
|7-12|=5
|14-12|=2
Now find the mean of the obtained differences:
MAD of group A=7+5+8+2+6+7+2+2+5+2/10
MAD of group A=46/10
MAD of group A=4.6
Now calculate the MAD of group B
Mean=12
data set of group B=11, 13, 10, 14, 18, 15, 10, 11, 6, 12
|11-12|=1
|13-12|=1
|10-12|=2
|14-12|=2
|18-12|=6
|15-12|=3
|10-12|=2
|11-12|=1
|6-12|=6
|12-12|=0
Now find the mean of the obtained differences:
MAD of group B=1+1+2+2+6+3+2+1+6+0/10
MAD of group B=24/10
MAD of group B=2.4

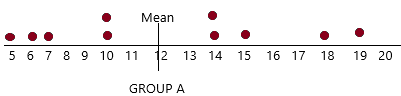
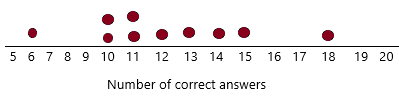
c) Draw separate dot plots for the two groups.
Answer:
A dot plot visually groups the number of data points in a data set based on the value of each point. This gives a visual depiction of the distribution of the data, similar to a histogram or probability distribution function. Dot plots allow a quick visual analysis of the data to detect the central tendency, dispersion, skewness, and modality of the data.
Dot plot for group A:

Dot plot for group B:

d) Interpret the above statistics and the dot plots.
Answer:
from the two-dot plots in above question (C), group A’s data are more scattered away from the mean and group B’s data cluster more closely around the mean. This explains why the MAD of group A is greater then that of group B.

e) What conclusion can you make about the performance of the two groups of students on the test?
Answer:
Group A’s performance is more varied whereas group B’s performance is more uniform.

Math in Focus Course 2B Practice 9.5 Answer Key

Solve. Show your work.

Question 1.
A random sample of a certain type of ball bearing produces a mean weight of 28 grams and a mean absolute deviation of 2.1 grams. What can be inferred from the sample about the population mean weight of this type of ball bearing?
Answer:
The above-given question:
The mean weight of ball bearing produces=28 grams
The mean absolute deviation=2.1 grams.
this can be calculated as:
2.1/28*100%
After calculating the above equation we get
=7.5%
Therefore, the estimated population mean weight is 28 grams with a MAD to mean ratio of 7.5%

Question 2.
You interviewed a random sample of 25 marathon runners and compiled the following statistics.
Mean time to complete the race = 220 minutes and MAD = 50 minutes What can you infer about the time to complete the race among the population of runners represented by your sample?
Answer:
The mean time to complete the race=220
The given MAD=50 min
This can be calculated as:
50/220*100%
After calculating the above equation we get
=22.72%
Therefore, the time to complete the race among the population of runners represented by your sample is 22.72%

Refer to the random sample below to answer the following. Round your answers to the nearest tenth.

The table shows a random sample of the volume, in milliliters, of 15 servings of orange juice from a vending machine.

Question 3.
Use the sample mean volume to estimate the population mean volume of a serving of orange juice.
Answer:
The above-given data: 251, 254, 254, 249, 250, 248, 250, 252, 251, 253, 247, 245, 255, 254, 251
Mean is the average of the given numbers and is calculated by dividing the sum of given numbers by the total number of numbers.
Mean=Sum of observations/total number of observations
Mean=251+254+254+249+250+248+250+252+252+253+247+245+255+254+251/15
Mean=3764/15
Mean=250.93 ml
therefore, the sample means volume to estimate the population mean volume of a serving of orange juice is 250.93ml.

Question 4.
Calculate the MAD and the MAD to mean ratio.
Answer:
The ratio of the sum of all absolute values of deviation from central measure to the total number of observations.
M.A. D = (Σ Absolute Values of Deviation from Central Measure) / (Total Number of Observations)
How to calculate MAD:
Steps to find the mean deviation from mean:
(i)Find the mean of the given observations.
(ii)Calculate the difference between each observation and the calculated mean
(iii)Evaluate the mean of the differences obtained in the second step.
This gives you the mean deviation from the mean.
The above-given data: 251, 254, 254, 249, 250, 248, 250, 252, 251, 253, 247, 245, 255, 254, 251
Mean=250.9
Now subtract:
|251-250.9|=0.1
|254-250.9|=3.1
|254-250.9|=3.1
|249-250.9|=1.9
|250-250.9|=0.9
|248-250.9|=2.9
|250-250.9|=0.9
|252-250.9|=1.1
|251-250.9|=0.1
|253-250.9|=2.1
|247-250.9|=3.9
|245-250.9|=5.9
|255-250.9|=4.1
|254-250.9|=3.1
|251-250.9|=0.1
Now calculate the mean of obtained differences.
MAD=0.1+3.1+3.1+1.9+0.9+2.9+0.9+1.1+0.1+2.1+3.9+5.9+4.1+3.1+0.1/15
MAD=33.3/15
MAD=2.22
Now we know mean and MAD from this we can calculate ratio.
Ratio=2.22/250.9*100%
Ratio=0.88%

Question 5.
Use the MAD to informally infer whether the volume of orange juice in a serving varies greatly.
Answer:
The mean=250.9
The mean deviation=2.22
As the average deviation from the mean is less than 1%, the volume of orange juice per serving does not vary significantly.

Refer to the box plots at the right to answer the following.

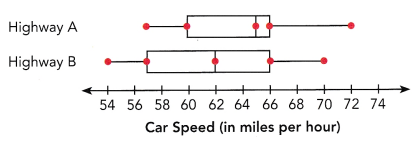
Two large random samples of car speeds on two highways from 4 P.M. to 6 P.M. were collected. The data were summarized in two box plots.

Question 6.
By comparing the interquartile ranges of the two box plots, what can you infer about car speeds on the two highways for the middle 50% of the cars?
Answer:
The above-given data:
The highway A data:
Lower value=57
Q1=60; Q2=65; Q3=66
Highest value=72
The Highway B data:
Lower value=54
Q1=57; Q2=62; Q3=66
Highest value=70
From this we can calculate the Interquartile range:
IQR=Q3-Q1
IQR of highway A=66-60
IQR of highway A=6
now calculate the interquartile range of highway B:
IQR of highway B=Q3-Q1
IQR of highway B= 66-57
IQR of highway B=9
By comparing the interquartile ranges of the two box plots, the highway B car speeds are more for 50% of the middle cars. Because the interquartile range of highway B is greater than that of highway A.

Question 7.
By comparing the medians of the two plots, what inference can you make?
Answer:
The above-given data:
The highway A data:
Lower value=57
Q1=60; Q2=65; Q3=66
Highest value=72
The Highway B data:
Lower value=54
Q1=57; Q2=62; Q3=66
Highest value=70
the median of highway A=65
the median of highway B=62
Therefore, the median car speeds on highway A is higher than that of highway B.

Question 8.
Suppose the speed limit on the two highways is 65 miles per hour. What per cent of the cars drove faster than the speed limit on the two highways?
Answer:
the above-given question:
The speed limit on the two highways=65 miles per hour.
The per cent of the cars drove faster than the speed limit on the two highways=X
X% of cars 65 we need to calcularte:
X/100*65
X/100=1/65
X=1/65*100
X=1.53
Therefore, 1.53% of the cars drove faster.

Question 9.
What can you infer about the overall car speeds on the two highways?
Answer:
50% of the cars on highway A go faster than the speed limit but less than 50% of the cars on highway B go faster than the speed limit.

Refer to the scenario below to answer the following.

Henry and Carl go jogging every morning for several weeks. The following are the mean and the MAD of the distances they jog.

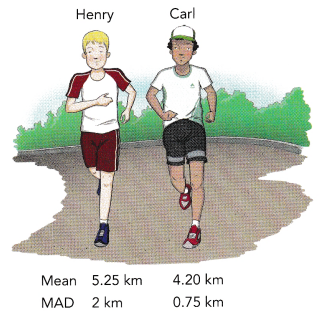
Question 10.
What would you infer about the distances they jog if you only compare their mean distances?
Answer:
the mean distance of henry=5.25km
The mean distance of Carl=4.20km
Henry jogs more than Carl
5.25-4.20=1.05
Henry jogs 1.05 km more than carl.

Question 11.
What can you conclude if you take into account both the mean and the MAD for your comparison?
Answer:
the mean distance of henry=5.25km
The mean distance of Carl=4.20km
the MAD distance of henry=2 kms
The MAD distance of Carl=0.75kms
By comparing all those distances, we can say Henry’s jogging distance is more varied than Carls jogging distance.

Refer to the random samples below to answer the following. Round your answers to the nearest tenth.

3 random samples of time taken, in seconds, to solve a crossword puzzle during a competition were collected.
S₁ = {100, 87, 95, 103, 110, 90, 84, 88}
S₂ = {75, 98, 120, 106, 70, 79, 100, 90}
S₃ = {60, 68, 110, 88, 78, 90, 104, 73}

Question 12.
Calculate the mean time of each of the 3 samples.
Answer:
Mean is the average of the given numbers and is calculated by dividing the sum of given numbers by the total number of numbers.
Mean=Sum of observations/total number of observations
Mean of S1=100+87+95+103+110+90+84+88/8
Mean of S1=757/8
Mean of S1=94.625
Now calculate for S2
Mean of S2=75+98+120+106+70+79+100+90/8
Mean of S2=738/8
Mean os S2=92.25
Now calculate for S3
Mean of S3=60+68+110+88+78+90+104+73/8
Mean of S3=671/8
Mean of S3=83.875

Question 13.
Estimate the population mean time of the competition using the mean of the 3 sample means.
Answer:
Now we got 3 samples:
S1=94.625; S2=92.25; S3=83.875
Now we have to calculate for these 3 samples
Mean time=94.625+92.25+83.875/3
Mean time=270.75/3
Mean time=90.25
Mean time=90.3 (rounded to nearest number)
Therefore, the estimated population mean time f the competition using the mean of the 3 sample means is 90.3s

Question 14.
Combine S₁, S₂, and S₃ into one sample and use the mean in question 13 to calculate the MAD of the combined sample.
Answer:
The ratio of the sum of all absolute values of deviation from central measure to the total number of observations.
M.A. D = (Σ Absolute Values of Deviation from Central Measure) / (Total Number of Observations)
How to calculate MAD:
Steps to find the mean deviation from mean:
(i)Find the mean of the given observations.
(ii)Calculate the difference between each observation and the calculated mean
(iii)Evaluate the mean of the differences obtained in the second step.
This gives you the mean deviation from the mean.
Mean=90.3
Now we got 3 samples:
S1=94.625; S2=92.25; S3=83.875
|94.625-90.3|=4.325
|92.25-90.3|=1.95
|83.875-90.3|=6.425
Now calculate the mean for obtained differences:
MAD=4.325+1.95+6.425/3
MAD=12.7/3
MAD=4.23

Question 15.
If you use the MAD found in question 14 to gauge the time variation among competitors, what can you infer?
Answer:
On average, time variation is from the mean is about 13.3% of the value of the meantime.

Refer to the random samples below to answer the following. Hound your answers to the nearest hundredth when you can.

Below are the history test scores of two classes of 20 students each.

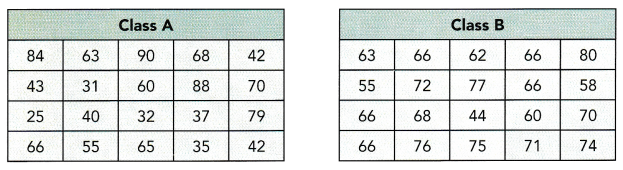
Question 16.
Find the range of scores for each class.
Answer:
The range in statistics for a given data set is the difference between the highest and lowest values.
Range=highest observation-lowest observation
The given data set of class A is 84, 63, 90, 68, 42, 43, 31, 60, 88, 70, 25, 40, 32, 37, 79, 66, 55, 65, 35, 42
The given data set of class B is 63, 66, 62, 66, 80, 55, 72, 77, 66, 58, 66, 68, 44, 60, 70, 66, 76, 75, 71, 74
range of class A:
Maximum value=90
Minimum value=25
range=90-25
range of class A=65
Range of class B:
Maximum value=80
minimum value=44
Range=80-44
range of class B=36

Question 17.
Calculate the mean scores for each class.
Answer:
Mean is the average of the given numbers and is calculated by dividing the sum of given numbers by the total number of numbers.
Mean=Sum of observations/total number of observations
The given data set of class A is 84, 63, 90, 68, 42, 43, 31, 60, 88, 70, 25, 40, 32, 37, 79, 66, 55, 65, 35, 42
The given data set of class B is 63, 66, 62, 66, 80, 55, 72, 77, 66, 58, 66, 68, 44, 60, 70, 66, 76, 75, 71, 74
Mean=84+63+90+68+42+43+31+60+88+70+25+40+32+37+79+66+55+65+35+42/20
Mean of class A=1115/20
Mean of claa A=55.75
Now calculate mean of class B
Mean of class B=63+66+62+66+80+55+72+77+66+58+66+68+44+60+70+66+76+75+71+74/20
Mean of class B=1335/20
Mean of class B=66.75

Question 18.
Calculate the MAD for each class.
Answer:
The ratio of the sum of all absolute values of deviation from central measure to the total number of observations.
M.A. D = (Σ Absolute Values of Deviation from Central Measure) / (Total Number of Observations)
How to calculate MAD:
Steps to find the mean deviation from mean:
(i)Find the mean of the given observations.
(ii)Calculate the difference between each observation and the calculated mean
(iii)Evaluate the mean of the differences obtained in the second step.
This gives you the mean deviation from the mean.
The given data set of class A is 84, 63, 90, 68, 42, 43, 31, 60, 88, 70, 25, 40, 32, 37, 79, 66, 55, 65, 35, 42
Mean of class A=55.75
|84-55.75|=28.25
|63-55.75|=7.25
|90-55.75|=34.25
|68-55.75|=12.25
|42-55.75|=13.75
|43-55.75|=12.75
|31-55.75|=24.75
|60-55.75|=4.25
|88-55.75|=32.25
|70-55.75|=14.25
|25-55.75|=30.75
|40-55.75|=15.75
|32-55.75|=23.75
|37-55.75|=18.75
|79-55.75|=23.25
|66-55.75|=10.25
|55-55.75|=0.75
|65-55.75|=9.25
|35-55.75|=20.75
|42-55.75|=13.75
Now calculate the mean for obtained differences
MAD of class A=351/20
MAD of class A=17.55
Now likewise calculate for class B
Mean of class B=66.75
The given data set of class B is 63, 66, 62, 66, 80, 55, 72, 77, 66, 58, 66, 68, 44, 60, 70, 66, 76, 75, 71, 74
|63-66.75|=3.75
|66-66.75|=0.75
|62-66.75|=4.75
|66-66.75|=0.75
|80-66.75|=13.25
|55-66.75|=11.75
|72-66.75|=5.25
|77-66.75|=10.25
|66-66.75|=0.75
|68-66.75|=1.25
|44-66.75|=22.75
|60-66.75|=6.75
|70-66.75|=3.25
|66-66.75|=0.7
|76-66.75|=9.25
|75-66.75|=8.25
|71-66.75|=4.25
|74-66.75|=7.25
Now calculate the mean for obtained differences
MAD of class B=115/20
MAD of class B=5.75

Question 19.
By comparing the mean scores and the MADs of the two classes, what can you infer about the performance of the two classes?
Answer:
Mean of class A=55.75
Mean of class B=66.75
MAD of class A=17.55
MAD of class B=5.75
the mean score of class B is greater than the mean score of class A. In other words, class B’s performance on average is better than class A’s performance. In addition, the MAD shows that class B’s scores is less varied than class A’s scores.

Brain @ Work

The bar graph displays monthly rainfall, in milliliters, from April to August.

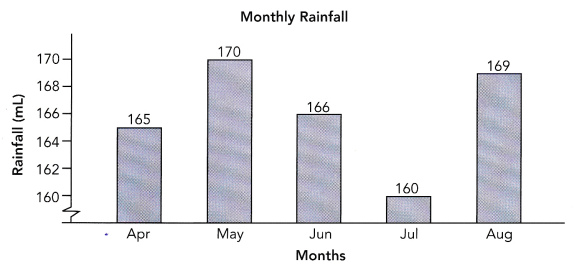
Alex draws the conclusion that rainfall varies greatly from April to August.

a) Find the mean rainfall.
Answer:
The given data: 165, 170, 166, 160, 169
Mean is the average of the given numbers and is calculated by dividing the sum of given numbers by the total number of numbers.
Mean=Sum of observations/total number of observations
Mean=165+170+166+160+169/5
Mean=830/5
Mean=166 ml

b) Calculate the mean absolute deviation.
Answer:
The ratio of the sum of all absolute values of deviation from central measure to the total number of observations.
M.A. D = (Σ Absolute Values of Deviation from Central Measure) / (Total Number of Observations)
How to calculate MAD:
Steps to find the mean deviation from mean:
(i)Find the mean of the given observations.
(ii)Calculate the difference between each observation and the calculated mean
(iii)Evaluate the mean of the differences obtained in the second step.
This gives you the mean deviation from the mean.
Mean=166
The given data: 165, 170, 166, 160, 169
|165-166|=1
|170-166|=4
|166-166|=0
|160-166|=6
|169-166|=3
Now calculate the mean for obtained differences:
MAD=1+4+0+6+3/5
MAD=14/5
MAD=2.8 ml

c) Based on your mean absolute deviation, do you agree with Alex’s conclusion? Explain why you agree or disagree.
Answer:
No, I disagree with Alex’s conclusion.
MAD to mean ratio:
2.8/166*100%
=1.69%
The MAD to mean ratio is 1.69%. It means that the average deviation from the mean is very insignificant. The vertical axis of the bar graph is not drawn to scale. As such, it creates a visual distortion of the differences in heights of the vertical bar.

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 7 Lesson 7.1 Constructing Angle Bisectors to score better marks in the exam.

Math in Focus Grade 7 Course 2 B Chapter 7 Lesson 7.1 Answer Key Constructing Angle Bisectors

Math in Focus Grade 7 Chapter 7 Lesson 7.1 Guided Practice Answer Key

Hands-On Activity

Materials

• ruler

Explore The Distance Between Points On The Sides Of An Ancle And Points On The Angle Bisector

Work in pairs.

\(\overrightarrow{Q S}\) is the angle bisector of ∠YQX. Points X and Y are equidistant from point Q.

Points S₁, S₂, S₃, and S₄ lie on \(\overrightarrow{Q S}\), the angle bisector of ∠YQX.

Step 1.
Measure and record each length to the nearest tenth of a centimeter.

Answer:
S₁X = 5 cm            S₁Y = 5 cm
S₂X = 4 cm           S₂Y = 4 cm
S₃x  = 3 cm           S₃Y = 3 cm
S₄x = 2 cm           S₄Y = 2 cm

Step 2.
Compare the lengths of \(\overline{S_{1} X}\) and \(\overline{S_{1} Y}\). Then compare the lengths of the two segments in each of the following pairs: \(\overline{S_{2} X}\) and \(\overline{S_{2} Y}\), \(\overline{S_{3} X}\) and \(\overline{S_{3} Y}\), and \(\overline{S_{4} X}\) and \(\overline{S_{4} Y}\). What do you observe about each pair of segment lengths?

Math Journal
Suppose you choose any point on the angle bisector. Do you think you will observe the same relationship between the lengths of the segments that connect the point to points X and V? What conclusion can you make?.

From the activity, any two points on the sides of an angle that are the same distance from the vertex are also the same distance from any point on the angle bisector.

Trace or copy ∠PQR. Then draw the angle bisector of ∠PQR.

Question 1.

Answer:

Complete.

Question 2.
Two walls intersect to form a right angle. In gym class, the students use the two walls to play a game in which the players line up so that each player is equidistant from the two walls.
a) Copy the diagram and draw a line to show where students should line up.
Answer:
We are given the angle:

The players are equidistant from the two walls if they are placed on the angles bisector. We buiLd the bisector.
First, with the compass point at the vertex, draw an arc that intersects \(\overrightarrow{Q P}\) and \(\overrightarrow{Q R}\).
Label the intersection points as A and B.

Using the same radius, draw an arc with A as the center.

Using B as the center, draw another arc with the same radius. Label the point where the two arcs intersect as C.

Use a straightedge to draw \(\overline{Q C}\).

b) What is the measure of the angle formed by the students and Wall 1 ? How do you know?

Answer:
Because the measure of the angle PQR is 90° and the bisector divides it in two congruent parts, the measure of the angle formed by the students and each of the walls is:
\(\frac{90^{\circ}}{2}\) = 45°

Trace or copy the diagram. Then complete.

Question 3.
Use ∠X to construct a 15° angle whose vertex is point X.

Answer:

Math in Focus Course 2B Practice 7.1 Answer Key

Construct the angle bisector of ∠ABC on a copy of each figure.

Question 1.

Answer:

Question 2.

Answer:

Draw each angle with a protractor. Then construct its angle bisector.

Question 3.
m∠POR = 75°
Answer:

Question 4.
m∠ADE = 122°
Answer:

Copy the angle shown. Then perform the indicated construction.

Question 5.
Construct a 25° angle at point X.

Answer:

Question 6.
Construct a 108° angle at point Y.

Answer:

Solve.

Question 7.
Justin wants to construct the angle bisector of ∠XYZ. Trace or copy the diagram. Using only a compass and a straightedge, construct the angle bisector and describe each step clearly.

Answer:

Explanation:
1. With ‘Y’ as center draw an arc of any radius to cut the rays of the angle at X and Z.
2. With ‘Z’ as center draw an arc of radius more than half of XZ, in the interior of the given angle.
3. With ‘X’ as center draw an arc of same radius to cut the previous arc at ‘o’.
4. Join YO. YO is the angle bisector of the given angle.

Question 8.
Draw two straight lines intersecting at an angle of 108°. Find the points that are equidistant from the two sides of each 108° angle formed by the intersecting lines.
Answer:
We are given:

The points equidistant from the two sides of each 108° angle formed by the intersection of the two Unes are placed on the 108° angles bisector.
We construct the bisector of the angle NOQ.

With the compass point at the vertex O, draw an arc that intersects \(\overrightarrow{O N}\) and \(\overrightarrow{O Q}\).
Label the intersection points as A and B.

Using the same radius, draw an arc with B as the center.

Using A as the center, draw another arc with the same radius Label the point where the two arcs intersect as C.

Use a straightedge to draw \(\overline{O C}\), which is the bisector of both vertical angles NOQ and POM.

Question 9.
Draw an obtuse angle of any measure and label it as ∠XYZ. Construct an angle that is one-fourth the measure of ∠XYZ, describing briefly the steps involved.
Answer:
We are given the obtuse angle:

In order to divide the angle in 4 congruent parts, first we construct the bisector \(\overrightarrow{Y V}\) of
the angle XYZ:

We have:
m∠XYV = m∠VYZ = \(\frac{m \angle X Y Z}{2}\)
Then we construct the bisector \(\overrightarrow{Y W}\) of the angle XYV:

We have:
m∠XYW = m∠WYV = \(\frac{m \angle X Y V}{2}\)
= \(\frac{\frac{X Y X}{2}}{2}\) = \(\frac{m \angle X Y Z}{4}\)
Divide the angle twice, constructing angle bisectors.

Question 10.
The diagram shows ∠ABC with \(\overrightarrow{B D}\) being its angle bisector and BF = BG E is a point on \(\overrightarrow{B D}\) and m∠ABD = 26°. Copy and complete.
m∠DBC =
Length of \(\overline{E G}\) = Length of

Answer:
\(\overline{B D}\) is angle bisector:
m∠DBC = m∠ABD
Substitute:
m∠DBC = 26°
△BEF ≅ △BEG (side-angle-side)
BF = BG
m∠DBC = m∠ABD
BE = BE
Congruent triangles:
Length of \(\overline{E G}\)  = Length of \(\overline{E F}\)

Question 11.
Officials are planning to build a new airport to serve three major cities in one region. The cities are located at W, X, and V, which are represented by the vertices of the triangle shown. The officials want to place the airport at the intersection of the angle bisectors of ∠XWY and ∠XYW. Copy or trace the triangle. Find the possible location of the airport and label it point Q.

Answer:
We construct the bisector of ∠XWY:

We construct the bisector of ∠XYW:

The intersection Q of the two bisectors is the possible location for the airport.

Question 12.
Joshua used a square piece of paper to make a paper airplane. As a first step, he made several folds in the paper, as shown in the diagram. First he folded along diagonal \(\overline{\mathrm{QS}}\), then he unfolded the paper. Next he folded along \(\overline{\mathrm{QT}}\) so that \(\overline{\mathrm{PQ}}\) lined up with \(\overline{\mathrm{QS}}\). Then he unfolded the paper again. In the diagram, what is the measure of ∠PQT? Give a brief explanation for your answer.

Answer:
In order to Line up \(\overline{P Q}\) with \(\overline{Q S}\) folding along \(\overline{Q T}\), the points of \(\overline{Q T}\) should be equidistant to \(\overline{P Q}\) and \(\overline{Q S}\), therefore on the bisector of ∠PQS.
we aetermine m∠PQT:
m∠PQT = \(\frac{m \angle P Q S}{2}\)
= \(\frac{\frac{90^{\circ}}{2}}{2}\) = \(\frac{45^{\circ}}{2}\)
= 22.5°

Question 13.
Kimberly wants to bisect the straight angle shown, and then bisect one of the resulting angles. She then wants to continue this process until she obtains an angle of measure 11.25°. How many times does she need to construct an angle bisector to produce an angle with this measure? Explain.

Answer:
Given the Angle measure of 11.25°.
Here we need to find out the angle which after bisecting gives an angle of 11.25°.
We know that when an angle is bisected it is divided into two equal angles.
Therefore, the double of the angle obtained after bisecting we will get the angle that was bisected
Hence, the angle is
= 2 × 11.25°
= 22.5°

Question 14.
Max designed a support for a bridge. In his design, five spokes are attached to a metal beam. The angles formed by the spokes all have the same measure. Explain how Max can use geometric construction to accurately draw his design.

Answer:
Take an arbitrary point outside the line:

Draw an arc with the point in A. Label the intersections with the Line by B and C:

Join A to B and C:

Construct the bisector of ∠BAC:

Construct the bisectors of ∠BAD and ∠DAC:

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 7 Geometric Construction to score better marks in the exam.

Math in Focus Grade 7 Course 2 B Chapter 7 Answer Key Geometric Construction

Math in Focus Grade 7 Chapter 7 Quick Check Answer Key

Copy and complete the table by classifying the triangles.

Question 1.

Answer:
Figure A is an Equilateral Triangle.
Figure B is an Isosceles Triangle.
Figure E is a Right Triangle.
Figure F is an Acute angle Triangle.
Figure C is an Obtuse angle Triangle

Explanation:

1. Equilateral triangle: In an equilateral triangle each angle is 60°. All sides and lengths of an equilateral triangle are equal. From the given figure we can classify that figure A is an Equilateral triangle.
2. Isosceles triangle: In the isosceles triangle only two sides are equal, the number of vertices and the number of edges are 3. By observing the given diagram figure B is called an Isosceles triangle
3. Right Triangle: A right-angled triangle is a triangle in which one of the angles is 90 degrees. Figure E is called a right-angled triangle.
4. Acute triangle: An acute angle is an angle that is less than 90. Since all the three angles are less than 90° then it is called an acute angle. Figure F is an acute angle from the above diagram.
5. Obtuse triangle: Obtuse angle is an angle that has greater than 90°. The figure C is called an obtuse triangle.

Copy and complete the table.

Question 2.

Answer:
1. Square: All sides are equal.
2. Rectangle: Rectangle is a quadrilateral with four right angles. The area of a rectangle is length width.
3.Trapezium: Trapezium has four vertices and four sides.
4. Parallelogram: In a parallelogram, both sides are parallel and equal.
5. Square parallelogram: The diagonals have equal length.

Explanation:

Measure ∠ABC.

Question 3.

Answer:
∠ABC has 60° which is an acute angle triangle.

Explanation:
An acute angle is an angle that has less than 90°. The figure given here has less than 90° and the measure of that angle is 60°.

Question 4.

Answer:
The measurement of  ∠ABC is 80°. And it is an acute angle triangle.

Explanation:
An acute angle is an angle that has less than 90°. The figure given here has less than 90° and the measure of that angle is 80°.

Question 5.

Answer:
The measurement of ∠ABC is 110°.

Explanation:
An obtuse angle is an angle that has greater than 90°. From the given figure we can measure the angle ∠ABC has 110°

Question 6.

Answer:
The measurement of ∠ABC is 120°which is an obtuse angle triangle.

Explanation:
An obtuse angle is an angle that has greater than 90°. From the given figure we can measure the angle ∠ABC has 120°

Use a protractor to draw each angle.

Question 7.
m∠DEF = 39°
Answer:
Angle DEF is an acute angle and the angle between 90° to 180°.

Explanation:

Question 8.
m∠XYZ = 92°
Answer:
Angle XYZ has a right angle and it is 92°.

Explanation:

Question 9.
m∠PQR = 146°
Answer:
Angle PQR is 146°.

Explanation:

Copy \(\overleftrightarrow{\mathbf{A B}}\), \(\overleftrightarrow{\mathbf{C D}}\), and \(\overleftrightarrow{\mathbf{X Y}}\) on a sheet of paper. Draw a perpendicular line to each given line.

Question 10.

Answer:
We take the straight line AB  They insect at each at a right angle.

Explanation:

Question 11.

Answer:
We take a straight line CD, then draw a perpendicular line XY between the line CD. They insect each at a right angle.

Explanation:

Question 12.

Answer:
We take the straight line XY, then draw a perpendicular line AB between the line XY. The angle insects are at a right angle.

Explanation:

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 6 Review Test to score better marks in the exam.

Math in Focus Grade 7 Course 2 B Chapter 6 Review Test Answer Key

Concepts and Skills

Tell whether each pair of angles are supplementary, complementary or neither.

Question 1.
m∠1 = 23° and m∠2 = 157°
Answer:

Explanation:

Question 2.
m∠3 = 65° and m∠4 = 25°
Answer:

Explanation:

Question 3.
m∠5 = 43° and m∠6 = 57°
Answer:

Explanation:

Question 4.
m∠7 = 82° and m∠8 = 8°
Answer:

Explanation:

Question 5.
m∠9 = 110° and m∠10 = 80°
Answer:

Explanation:

Question 6.
m∠11 = 18° and m∠12 = 62°
Answer:

Explanation:

Tell whether the following list of angle measures are complementary or supplementary.

m∠A = 67°, m∠B = 80°, m∠C = 131°, m∠D = 21°,
m∠E = 51°, m∠F = 46°, m∠G = 10°, m∠H = 120°,
m∠J = 69°, m∠K = 60°, m∠P = 49°, m∠Q = 113°,
m∠R = 44°, m∠S = 41°

Question 7.
Name two pairs of complementary angles.
Answer:
m∠B = 80°, m∠G = 10°
m∠F = 46°, m∠R = 44°

Explanation:
Two angles are called complementary when the measures of their angles add to 90 degrees. The two pairs of complementary angles are m∠B = 80°, m∠G = 10°. If we add both angles the sum adds up to 90°.

Question 8.
Name two pairs of supplementary angles.
Answer:
m∠A = 67°, m∠Q = 113°
m∠H = 120°, m∠K = 60°

Explanation:
Two angles are called supplementary when the measures of their angles add to 180 degrees. The two pairs of supplementary angles are m∠A = 67°, m∠Q = 113°. If we add both angles the sum adds up to 180°.

Copy and complete.

Question 9.
Name two pairs of angles for each type of angle pair.

Answer:
∠TBC = 60°, ∠ABR = 30° are complementary angles.
∠RBT = 120°, ∠TBC = 60°are supplementary angles.

Explanation:

The two pairs of angles for complementary angles are ∠TBC = 60°, ∠ABR = 30°.
The two pairs of angles for supplementary angles are ∠RBT = 120°, ∠TBC = 60°

Find the measure of each numbered angle.

Question 10.
\(\overleftrightarrow{\mathrm{AB}}\) is a straight line.

Answer:
The measurement of numbered angle 1 is 43°.

Explanation:

∠AOC + ∠BOC = 180°
1 + 137° = 180°
1 = 180° – 137°
1 = 43°

Question 11.
\(\overleftrightarrow{\mathrm{AB}}\) is a straight line.

Answer:
The measurement of numbered angle 2 is 120°.

Explanation:

∠AOD + ∠DOC + ∠COB = 180°
38° + 2 + 22° = 180°
2 + 60° = 180°
2 = 180° – 60°
2 = 120°

Find the measure of each numbered angle.

Question 12.

Answer:
The measurement of numbered angle 3 is 195°

Explanation:

∠AOB + ∠COB + ∠AOC = 360°
3 + 120°+ 45° = 360°
3 + 165° = 360°
3 = 360° – 165°
3 = 195°

Question 13.
\(\overleftrightarrow{\mathrm{AB}}\) is a straight line.

Answer:
The measurement of  numbered angle 4 is 73°

Explanation:

∠AOD + ∠DOC + ∠COB = 180°
4 + 17° + 90° = 180°
4 + 107° = 180°
4 = 180° – 107°
4 = 73°

Use an equation to find the value of each variable.

Question 14.
\(\overleftrightarrow{\mathrm{AB}}\) is a straight line.

Answer:
s°= 45°, 3s°= 135°

Explanation:

∠AOC + ∠COB = 180°
3s° + s° = 180°
4s° = 180°
s° = 180 ÷ 4
s° = 45°
3s°= 135°

Question 15.
\(\overleftrightarrow{\mathrm{AB}}\) is a straight line.

Answer:
w° = 28°, 2w° =56°, 3w°=140°

Explanation:

∠AOD + ∠DOC + ∠COB = 180°
3w° + 40° + 2w° = 180°
5w° + 40° = 180°
5w° = 180° – 40°
5w° = 140°
w° = 28°
3w°= 3 × 28 = 84°
2w°= 2° × 28 = 56°

Question 16.
\(\overleftrightarrow{\mathrm{AB}}\) is a straight line.

Answer:
t° = 30°, 2t° = 30°

Explanation:

∠BOC + ∠AOD + ∠DOC = 180°
t° + 2t° + 90° = 180°
3t° + 90° = 180°
3t° = 180° – 90°
3t° = 90°
t° = 90° ÷ 3
t° = 30°

Question 17.

Answer:
v°=17°, u°=73°

Explanation:
∠AOB + ∠BOC = 90°
53° + v° = 90°
v° = 90° – 53°
v° = 17°
∠BOC + ∠COD = 90°
v° + u° = 90°
17° + u° = 90°
u° = 90° – 17°
u° = 73°

Question 18.
\(\overleftrightarrow{\mathrm{AB}}\), \(\overleftrightarrow{\mathrm{CD}}\), and \(\overleftrightarrow{\mathrm{EF}}\) are a straight line.

Answer:
r°= 22°, 4r°= 88°

Explanation:
∠COA = ∠BOD = r° (vertically opposite angles)
∠EOB + ∠BOD + ∠FOD = 180°
4r° + r° + 70° = 180°
5r° + 70° = 180°
5r° = 180° – 70°
5r° = 110°
r° = 110 ÷ 5
r° = 22°
4r° = 4 × 22 = 88°

Question 19.

Answer:
x° = 36°, 2x° = 72°, 3x° = 108°, 4x° = 144°

Explanation:

3x° + 2x° = 180°
5x° = 180°
x° = 180÷5
x° = 36°
2x° = 36 × 2 = 72°
3x° = 3 × 36 = 108°
4x° = 4 × 36 = 144°

\(\overline{M N}\) is parallel to \(\overline{P Q}\). Find the measure of each numbered angle.

Question 20.

Answer:
∠1 = 25°, ∠2 = 65°, x° = 65°

Explanation:
Let ∠QPS = x°
∠NPM + ∠NPQ + ∠QPS = 180°
90° + 25° + x° = 180°
115° + x° = 180°
x° = 180 -115°
x° = 65°
∠2 = ∠x = 65° Corresponding angles are equal
∠NMP + ∠PNM = 90°
∠2 + ∠1 = 90°
65° + ∠1 = 90°
∠1 = 90° – 65°
∠1 = 25°

Question 21.

Answer:
∠1 = 52°, ∠2 = 52°, ∠3 = 66°

Explanation:
Let ∠SOQ = x°
114°+ x° = 180°
x° = 180° – 114°
x° = 66°
x° = ∠3 = 66° (vertically opposite angles)
∠3 + ∠TSQ + ∠QSN = 180°
∠3 + 62° + ∠2 = 180°
66° + 62° + ∠2 = 180°
∠2 = 180° – 128°
∠2 = 52°
∠1 = ∠2 (vertically opposite angles)
∠1 = 52°

Problem Solving

Solve. Show your work.

Find the value of x.

Question 22.
Find the value of x.

Answer:
x° + 2x° = 330°
3x°= 330°
x° = 330 ÷ 3
x° = 110°

Question 23.
ABCD is a rhombus. Find the measures of ∠1 and ∠2.

Answer:
∠1 = 70°, ∠2 = 120°

Explanation:
Opposite angles in a rhombus are equal.
∠1 = 70°
∠1 + ∠2 + 70° = 360°
70° + ∠2 + 70° = 360°
∠2 + 140° = 360°
∠2 = 360° – 140°
∠2 = 120°

Question 24.
ABCD is a rectangle. \(\overline{\mathrm{AE}}\) and \(\overline{\mathrm{DC}}\) are straight lines. ∠FBG is a right angle, m

ABF = 74°, and m∠BEG = 42°. Find the measures of ∠EBG and ∠BGC.

Answer:
x=∠EBG =16°, ∠BGC = 122°
Explanation:
74° + 90° + x° = 180°
x° = 180° – 164°
x° = 16°
16° + 42° + ∠BGC = 180°
∠BGC = 180° – 58°
∠BGC = 122°

Question 25.
The diagram shows the flag of the United Kingdom. m∠MNR = 90°. Name two pairs of complementary and supplementary angles.

Answer:
∠MNQ, ∠SNP, ∠QNS are complementary angles.
∠MNR, ∠MNQ, ∠SNP are supplementary angles.

Explanation:
The two pairs of angles for complementary angles are ∠MNQ, ∠SNP, ∠QNS.
The two pairs of angles for supplementary angles are ∠MNR, ∠MNQ, ∠SNP.

Question 26.
m∠1 = 15° and m∠2 = 131°. \(\overleftrightarrow{\mathrm{AB}}\) is a straight line. Find the measure of ∠3.

Answer:
∠3 = 34°

Explanation:
m∠1 + m∠2 + m∠3 = 180°
15° + 131° + m∠3 = 180°
m∠3 + 146° = 180°
m∠3 = 180° – 146°
m∠3 = 34°

Question 27.
The diagram shows ∠1 and ∠2, which are formed by \(\overleftrightarrow{M N}\) intersecting \(\overleftrightarrow{P Q}\) and \(\overleftrightarrow{R S}\). In the diagram, m∠1 = (12x + 7)°, m∠2 = (10x + 15)°, and x = 4. Explain how you know that \(\overleftrightarrow{P Q}\) is parallel to \(\overleftrightarrow{R S}\).

Answer:
Parllel lines are lines that are always the same distance apart and will never intersect. Hence in the given figure the lines \(\overleftrightarrow{P Q}\) is parallel to \(\overleftrightarrow{R S}\).
And iif two lines are parllel the corresponding angles are equal. Therefore ∠1 = ∠2

Explanation:
m∠1 = m∠2  are corresponding angles
(12x + 7)° = (10x + 15)°
12x – 10x = 15 – 7
2x = 8
x° = 8 ÷ 2
x° = 4°
(12x + 7)° = 12 × 4 + 7 = 48 + 7 = 55°
(10x +15)° = 10 × 4 + 15 = 40 + 15 = 55°

Question 28.
In the diagram, m∠1 = (5x – 20)°, m∠2 = (2x + 14)°, and m∠3 = 18°. Use an equation to find the measures of ∠1 and ∠2.

Answer:
∠1 = 100°, ∠2 = 62°, ∠3 = 24°

Explanation:
m∠1 + m∠2 + m∠3 = 180°
(5x – 20)° + (2x + 14)° + 18° =180°
7x – 6 + 18° = 180°
7x +12 = 180°
7x = 180° – 12°
7x = 168°
x°= 24°
5x – 20 = 5 × 24 – 20 = 120 – 20 =100°
2x + 14 = 2 × 24 + 14 = 62°
∠1 = 100°, ∠2 = 62°, ∠3 = 24°

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 7 Lesson 7.4 Identifying Volumes of Composite Solids to score better marks in the exam.

Math in Focus Grade 7 Course 3 B Chapter 7 Lesson 7.4 Answer Key Identifying Volumes of Composite Solids

Math in Focus Grade 8 Chapter 7 Lesson 7.4 Guided Practice Answer Key

Solve.

Question 1.
A solid metal trophy is made up of a cylinder and a cone. The radius of the cylinder is equal to the radius of the cone. Find the volume of metal used to make the trophy. Round your answer to the nearest tenth. Use 3.14 as an approximation for π.

First find the height of the cone.
Let h represent the height of the cone in centimeters.

Then find the volume of the cone.
Volume = \(\frac{1}{3}\) • Area of base • Height
= Use the exact value of the height of the cone.
≈ cm³
Next find the volume of the cylinder.
Volume = Area of base• Height
=
≈ cm³
Finally, find the volume of metal used.
Volume of metal used = Volume of cone + Volume of cylinder
≈ +
= cm³
So, the volume of metal used is approximately cubic centimeters.

Answer:
The volume of metal used is approximately 957 cubic centimeters,

Explanation:

Now the volume of cone
Volume = \(\frac{1}{3}\) • Area of base • Height,
Area of base is πr² = 3.14 × 6 cm × 6 cm = 113.04 cm²,
V = Volume of cone = \(\frac{1}{3}\) • 113.04 • 10.39 = 391.495 cm²,
Given the radius of the cylinder is equal to the radius of the cone.
The volume of the cylinder =
Volume of cylinder = Area of base X height = 113.04 cm² × 5 cm = 565.2 cm³,
Volume of metal used = Volume of cone + Volume of cylinder,
Volume of metal used = 391.495 cm³ + 565.2 cm³ = 956.695 cm³,
therefore the volume of metal used is approximately 957 cubic centimeters.

Math in Focus Course 3B Practice 7.4 Answer Key

For this practice, you may use a calculator. Use 3.14 as an approximation for n. Round your answer to the nearest tenth if necessary.

Question 1.
Find the volume of each of the following composite solids.

a) A triangular prism with a cylindrical hole cut out of it.

Answer:
Volume of triangular prism with a cylindrical hole cut out of it is 1089.12 cm³,

Explanation:
Volume of rectangular prism is width X height X length,
we have width 14.1 cm, height = 12 cm and length = 10 cm,
Volume of rectangular prism = 14.1 × 12 × 10 = 1,692 cm³,
Volume of cylinder =πr²h= 3.14 × 4 × 4 × 12 = 602.88 cm³,
therefore volume of triangular prism with a cylindrical hole cut out of it is
Volume of rectangular prism – Volume of  cylinder =
1,692 cm³ – 602.88 cm³ = 1089.12 cm³.

b) A sphere connected to a cone that sits on top of a hemisphere.

Answer:
Volume of sphere connected to a cone that sits on top of a hemisphere is 41.866 cm³,

Explanation:
First we calculate the volume of cone,
we calculate height of cone h² + 3² = 5²,
h² = 25 – 9 = 16, so height of cone is square root of 16 which is 4,
Now volume of cone =  \(\frac{1}{3}\) • 3.14 × 3 × 3 • 4,
Volume of cone = 37.68 cm³,
Volume of sphere = \(\frac{4}{3}\) • 3.14 × r³,
= \(\frac{4}{3}\) • 3.14 × 1 cm × 1 cm × 1 cm = 4.186 cm³,
therefore volume of sphere connected to a cone that sits on top of a hemisphere
= Volume of cone + Volume of sphere
= 37.68 cm³ + 4.186 cm³ = 41.866 cm³.

Question 2.
A ceramic candle holder in the shape of a cylinder has a radius of 2.40 inches. A hemisphere of radius 1.75 inches is removed from the center of the cylinder. Find the volume of ceramic in the candle holder.

Answer:
The volume of ceramic in the candle holder is 27.104 in³,

Explanation:
Given a ceramic candle holder in the shape of a cylinder has a radius of 2.40 inches.
Now we caluculate height of cylinder using pythagorean theroem
2.40² + h² = 4²,
h² = 16 – 5.76 = 10.24, the height is square root of 10.24 is 3.2 in
h = 3.2 in now volume of cylinder is 3.14 × r^{2 ×} h = 3.14 × 2.4 × 2.4 × 3.2 = Volume of cylinder is 57.876 in³,
As a hemisphere of radius 1.75 inches is removed from the center of the cylinder, the volume removed is 3.14 × 1.75 × 1.75 × 3.2 = 30.772 in³,
therefore the volume of ceramic in the candle holder is
volume of cylinder – volume of removed
= 57.876 in³ – 30.772 in³ = 27.104 in³.

Question 3.
A tent has a conical roof and a cylindrical wall as shown. The cylindrical wall and the conical roof are of the same height. The radius of the tent is 9 meters. Ropes are used to tie the tent to the ground.
a) Find the height of the wall.
Answer:
The height of the wall is 1.5 m,

Explanation:
Using pythogorean theorem the height h of the wall =
h² + 0.8² = 1.7²,
h² = 2.89 – 0.64 = 2.25
so height is square root of 2.25 is 1.5 m.

b) Find the volume of space inside the tent.
Answer:

The volume of space inside the tent is  508.68 m³,

Explanation:
First we calculate the volume cylindrical walls as
3.14 × r² × h = 3.14 × 9 × 9 × 1.5 = 381.51 m³,
Now volume conical roof is \(\frac{1}{3}\) • 3.14 × r × r • h,
\(\frac{1}{3}\) • 3.14 × 9 × 9 • 1.5 = 127.17 m³,
therefore the volume of space inside the tent is
381.51 m³ + 127.17 m³ = 508.68 m³.

Question 4.
A traffic cone is made up of a cone fixed on top of a square prism base with a height of 1 inch. Find the volume of the traffic cone.

Answer:
The volume of the traffic cone is 1561.75 in³,

Explanation:
Given a traffic cone is made up of a cone fixed on top of a square prism base with a height of 1 inch with radius 7.3 in and height 28 in,
So volume of the traffic cone is \(\frac{1}{3}\) • 3.14 × r × r • h =
\(\frac{1}{3}\) • 3.14 × 7.3 × 7.3 × 28 = 1561.75 in³.

Question 5.
A sculpture is made out of a cone resting on top of a hemisphere. The hemisphere has a radius of 1 meter. Use the information in the diagram below to find the volume of the sculpture.

Answer:
Volume of sculpture is 37.68 m³,

Explanation:
Given a sculpture is made out of a cone resting on top of a hemisphere.
The hemisphere has a radius of 1 meter. Radius of cone is 2 m+ 1 m = 3 m,
applying phthagorean theorem to find height of cone
h² + 3² = 5²,
h² = 25 – 9 = 16, h is square root of 16 is 4 m now volume of sculputure is
\(\frac{1}{3}\) • 3.14 × r × r • h
= \(\frac{1}{3}\) • 3.14 × 3 m × 3 m × 4 m
= 37.68 m³.

Question 6.
A trophy is made of a glass triangular prism attached to a 0.5 inch high wooden block shaped like a square prism. The height of the trophy is 6 inches. The volume of the wooden base is 4.5 cubic inches. Find the volume of the entire trophy, including the base.

Answer:

Explanation:
Given a trophy is made of a glass triangular prism attached to a 0.5 inch high wooden block shaped like a square prism.
The height of the trophy is 6 inches.
The volume of the wooden base is 4.5 cubic inches.
Let x be the equal length of each side of the square ,
then the volume of the block will be 0.5 × x² = 4.5,
x² = 9 , so x is square root of 9 is 3,
The area of each triangular face of the prism will be 1/2 × 3 × 6 = 9.
The volume of the triangular prism will be 9 × 3 = 27 cubic inches.
The total volume will be 4.5 + 27 = 31.5 cubic inches.

Question 7.
A swimming pool is 12 feet long and 10 feet wide. At its deepest, it is 7 feet deep. A slope 5 feet long links the deep end to the shallow end. Jonathan wants to fill the pool with 800 cubic feet of water. Is this possible? Explain.

Answer:
Yes, it is possible that the volume of the pool is exactly 800 cubic feet which will allow the 800 cubic feet of water to completely fill it,

Explanation:
The minimum volume of the pool is 12 × 10 × 2 = 240 cubic feet and
the maximum volume of the pool is 12 × 10 × 7 = 840 cubic feet.
since 800 cubic feet is somewhere between 240 and 840 cubic feet than 800 cubic feet of water could fill the pool.
To fill the pool with exactly 800 cubic feet of water, the sloped section would have to have a cross section of a
right triangle where the vertical leg would have to be .4206601574 feet and the horizontal leg would have to be 4.982273079 feet and the hypotenuse would have to be 5 feet.
The slope of 5 feet in length that links the deep end of the pool to the shallow end of the pool if the hypotenuse of this right triangle.
The formula for the volume of the pool would be
10 × 12 × (7 – .4206601574) + 10 × 1/2 × .420601574 × 4.982273079 = 800 cubic feet.
So, if the minimum depth of the pool is 6.579339843 feet and the sloped section of the pool is 5 feet and the horizontal distance of the sloped section of the pool is 4.982273079 feet, and the maximum depth of the pool is 7 feet, then the volume of the pool will be exactly 800 cubic feet.
The area of this vertical cross section will be 80 square feet.
The volume of the pool will be 10 × the area of the vertical cross section, making the volume equal to 800 cubic feet.
Yes it is possible that the volume of the pool is exactly 800 cubic feet which will allow the 800 cubic feet of water to completely fill it.

Question 8.
A crystal paperweight is shaped like a cylinder with a star-shaped hole. The top of the star-shaped hole is shaped like a square with four points that are identical equilateral triangles. The height of the cylinder is 3 centimeters. Find the volume of the paperweight.

Answer:
There is far too little information given. In addition to the height of the cylinder, we need to know its radius, along with the lengths of the sides of the square and equilateral triangles.

Question 9.
Math Journal The solid shown below is made of a cylinder with two identical cones at the ends of the cylinder. Linda says that if the radius of the cylinder is doubled, the volume of the solid will also be doubled. Is she correct? Why?

Answer:
Linda is not correct,

Explanation:
Let radius of cylinder = r ,
Then, volume of cylinder is given by V = πr²h,
According to the question, now Radius of the cylinder = 2r
Then, volume of cylinder is given by V’ = π(2r)²h = 4πr²h =4 (πr²h) = 4V ⇒ V’ = 4V ,
Thus, volume will be four times more if the radius of a cylinder is doubled.
Linda is not correct because it becomes four times more.

Brain @ Work

Question 1.
An architect designs a staircase for a new house. There will be 14 steps, and each step will be 17 centimeters high and 25 centimeters wide. The architect will build a railing on both sides of the steps. Find the total length needed for the two railings, not including any vertical support posts.

Answer:
The goal is to find the measure of the railings for the both sides of the staircase if the stairs have 14 steps and the steps are 17 centimeters in height and 25 centimeters in width.

Observe that the width, height and the railings of the staircase forms a right triangle. To determine the height and the width of the stairs, multiply the 14 steps to the measure of the riser and the measure of the width of the steps. For the height, 14 multiplied by 17 is 238 whiLe the product of 14 and 25 is 350 will be the width. Then appLying the Pythagorean Theorem which equates the square of the hypotenuse to the sum of the squares of the legs, the length of the railings can be computed represented by y which serves as the hypotenuse.
238² + 350² = y²   Use Pythagorean Theorem.
56, 644 + 122, 500 = y²    Multiply.
179, 144 = y²     Add.
y = \(\sqrt{179,144}\)      Find positive square root.
y ≈ 423.3 Simplify.
Therefore, the measure of the two railings are 423.3 centimeters.

Question 2.
The Colorado river is about 210 meters wide. Brad and John start swimming from the same bank. Brad swims 215 meters against the current to reach a point on the opposite bank. Brad’s swimming speed is greater than the speed of the current. John swims 220 meters with the current to reach another point on the opposite bank. Find the distance between the two points.
Answer:
First, for better understanding, illustrate the situation of John and Brad Let A be the starting point of Brad and John, B be the corresponding point of A in the opposite side of the river, C be the position of Brad on the other side of the river after he swims, and D be John’s position after swimming Since Brad swims opposite the current while John swims along with the current, then they went on the opposite side of one another to reach the other side of the river.

Notice that, the distance of the John and Brad can be computed by adding the distance of \(\overline{C B}\) and \(\overline{D B}\). Also, the measure of \(\overline{C B}\) and \(\overline{D B}\) can be solved by applying Pythagorean Theorem since \(\overline{A B}\), \(\overline{A C}\), and \(\overline{C B}\) creates a right triangle and \(\overline{A B}\), \(\overline{A D}\), and \(\overline{D B}\) form another right triangle.

For \(\overline{A B}\), \(\overline{A C}\), and \(\overline{C B}\)  Let \(\overline{A C}\) be the hypotenuse and the other lines be the Legs. Note that Pythagorean Theorem states that the square of the hypotenuse is equal to the sum of the squares of the legs of a right triangle then
\(\overline{A B}^{2}+\overline{C B}^{2}=\overline{A C}^{2}\)      Use the Pythagorean Theorem.
210² + \(\overline{C B}^{2}\) = 215²   Substitution.
44. 100 + \(\overline{C B}^{2}\) = 46,225   Multiply.
\(\overline{C B}^{2}\) = 2, 125     Subtract 44.100 to both sides.
\(\overline{C B}\) = \(\sqrt{2,125}\)   Find the positive square root.
\(\overline{C B}\) ≈  46.1   Simplify.
Therefore, \(\overline{C B}\) measures about 46.1 meters.

Next, for \(\overline{A B}\), \(\overline{A D}\), and \(\overline{D B}\), let \(\overline{A D}\) be the hypotenuse and the remaining sides are the [egs then apply the Pythagorean Theorem again.
\(\overline{A B}^{2}+\overline{D B}^{2}=\overline{A D}^{2}\)     Use the Pythagorean Theorem.
210² + \(\overline{D B}^{2}\) = 220²   Substitution
44, 100 + \(\overline{D B}^{2}\) = 48, 400 Multiply.
\(\overline{D B}^{2}\) = 4,300   Subtract 44,100 to both sides.
\(\overline{D B}\) = \(\sqrt{4,300}\) Find the positive square root.
\(\overline{D B}\) ≈  65.6      Simplify.
Therefore, \(\overline{D B}\) measures around 65.6 meters.

Lastly, add the two distances to determine the distance of John and Brad to one another.
46.1 + 65.6 = 111.7
Therefore, Brad and John are 111.7 meters away from one another.

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 7 Lesson 7.3 Understanding the Pythagorean Theorem and Solids to score better marks in the exam.

Math in Focus Grade 7 Course 3 B Chapter 7 Lesson 7.3 Answer Key Understanding the Pythagorean Theorem and Solids

Math in Focus Grade 8 Chapter 7 Lesson 7.3 Guided Practice Answer Key

Solve.

Question 1.
The radius of a cone-shaped hat is 5 centimeters. The slant length of the hat is 8 centimeters. What is the height of the hat? Round your answer to the nearest tenth.

Let the height be x centimeters.

So, the height of the hat is approximately centimeters.
Answer:
The height of the hat is approximately 6 centimeters,

Explanation:

Solve.

Question 2.
Given the diagonal length, XY, of the end wall of the King’s Chamber of the Great Pyramid and the length, XZ, of the chamber, find the length, YZ, of the central diagonal. Find both the exact value and the approximate value to the nearest tenth.

+ = YZ² Use the Pythagorean Theorem.
+ = YZ² Substitute values for \(\overline{X Y}\) and \(\overline{X Z}\).
+ = YZ² Multiply.
= Add.
= YZ Find the positive square root.
YZ ≈ m Round to the nearest tenth.
So, the length of the central diagonal is exactly meters and approximately meters.
Answer:

Explanation:
Given the diagonal length, XY, of the end wall of the King’s Chamber of the
Great Pyramid and the length, XZ, of the chamber, find the length, YZ, of the central diagonal is
xy² + xz²  = yz² (using pythagorean theorem)
(7.8)² + (10.5)² = yz²,
yz² = 60.84 +110.25,
yz² = 171.09, square root of 171.09 is 13.08,
yz = 13.08,
So, the length of the cenetral diagonal is exactly 13.08 meters
and approximately 13 meters.

Math in Focus Course 3B Practice 7.3 Answer Key

For this practice, you may use a calculator. Use 3.14 as an approximation for π.
Round your answer to the nearest tenth where necessary.

For each solid, find the value of the variable.

Question 1.

Answer:
The value of variable w is 8 in,

Explanation:
We solid cube have w² + 6 ² = 10² (using pythagorean theorem)
w² = 100 -36,
w² = 64, the value of w is square root of 64 which is 8,
therefore w is 8 in.

Question 2.

Answer:
The value of variable x is 5,

Explanation:
We have x² = 3² + 4² (using pythagorean theorem)
x² = 9 + 16 = 25, the value of x is square root of  25 is 5.

Question 3.

Answer:
The value of variable y is 16 in,

Explanation:
We have 20² = y² + 12² (using pythagorean theorem)
400 = y² + 144,
y² = 400-144 = 256,
so the value of y is sqaure root of 256 is 16,  y = 16 in.

Question 4.

Answer:
The value of variable z is 20 in,

Explanation:
The value of variable z = 2 X 10in = 20 in.

Solve. Show your work. Round your answer to the nearest tenth.

Question 5.
Find the lateral surface area.

Answer:
The lateral surface area is 272 cm²,

Explanation:
Given square pyramid, the lateral surface area(L.A) is 2bh,
where b is base and h is slant height so L.A = 2 × 8cm × 17 cm = 272 cm².

Question 6.
The area of the lateral surface is πrl, where l is the slant height of the cone.
Find the lateral surface area of the cone.

Answer:
The lateral surface of cone is 137.375 cm²,

Explanation:
Given height as 12 cm and slant height l of cone as 12.5 cm so radius of cone is
r ² + 12² = 12.5² (using pythagorean theorem)
r² = 156.25 -144 = 12.25, radius r is square root of 12.25 is 3.5 cm,
now the lateral surface area (L.A) of the cone is  πrl,
L.A = 3.14 × 3.5 × 12.5 = 137.375 cm².

Question 7.
A straw that is 16 centimeters long fits inside the glass shown.
The height of the glass is 14 centimeters. Find the radius of the glass.

Answer:
The radius of the glass is 7.745 approximately 8,

Explanation:
Given a straw that is 16 centimeters long fits inside the glass shown.
The height of the glass is 14 centimeters.
The radius of the glass is 16² = 14² + r² (using pythagorean theorem)
r² = 256- 196 = 60, so r is square root of 60 is 7.745 approximately 8.

Question 8.
A spider sits in a corner of a tank shaped like a rectangular prism. The tank is 13 inches long, 6 inches wide, and 8 inches high. The spider starts to make a web by spinning a length of silk that stretches tightly from one corner along a central diagonal to the opposite corner.

a) Find the length of the diagonal of the rectangular floor of the tank.
Answer:
14.318 is the length of the diagonal of the rectangular floor of the tank,

Explanation:
Given a spider sits in a corner of a tank shaped like a rectangular prism.
The tank is 13 inches long, 6 inches wide, and 8 inches high.
The length of the diagonal of the rectangular floor of the tank is
d² = 13² + 6² = 169 + 36 = 205 so d is square root of 205 is 14.318 in.

b) Find the length of the silk the spider spins from one corner of the tank to the other corner.
Answer:
16.401 in is the length of the silk the spider spins from one corner of the tank to the other corner,

Explanation:
Now the length l of the silk the spider spins from one corner of the tank to the other corner is
l² = 14.318² + 8 ² =  205 + 64 = 269,
so l is square root of 269 is 16.401 in.

Question 9.
A conical party hat ¡s made from a piece of paper as shown. Given that its radius is 3 inches, find the height of the party hat.

Answer:
The height of the party hat is 4 in,

Explanation:
Given a conical party hat ¡s made from a piece of paper is shown with hypotenues 5 in and  its radius is 3 inches,  let the height of the party hat be h so
5² = 3² + h² (using pythagorean theorem)
h² = 25 – 9 = 16, so h is square root of 16 is 4 in.

Question 10.
Mindy wants to make a metal paperweight in the shape of a square pyramid. The paperweight will have the dimensions shown.
a) Find the length of a diagonal of the square base.
Answer:

The length of a diagonal of the square base is 4.24 in,

Explanation:
The length of a diagonal of the square base is
l² = 3² + 3² = 9 + 9 = 18,
so the length is square root of 18 is 4.24 in.

b) Find the height of the paperweight.
Answer:
4 in is the height of the paperweight,

Explanation:
Let h be the height of the paperweight so applying
h² + 3² = 5² (using pythagorean theorem),
h² = 25 – 9 = 16, so h is square root of 16 is 4 in.

Question 11.
Math Journal A box shaped like a rectangular prism is 14.5 centimeters long, 4 centimeters wide, and 3.5 centimeters high. You have a ruler that is 15 centimeters long and 3 centimeters wide. Can it fit inside this box? Explain.
Answer:
No, the ruler cannot fit inside the box,

Explanation:
Given a box shaped like a rectangular prism is 14.5 centimeters long,
4 centimeters wide, and 3.5 centimeters high and I have a ruler that is
15 centimeters long and 3 centimeters wide so by seeing the
length of the ruler is 15 cm which is 15-14.5 = 0.5 more than the rectangular prism,
therefore the ruler cannot fit inside the box.

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 7 Lesson 7.2 Understanding the Distance Formula to score better marks in the exam.

Math in Focus Grade 7 Course 3 B Chapter 7 Lesson 7.2 Answer Key Understanding the Distance Formula

Math in Focus Grade 8 Chapter 7 Lesson 7.2 Guided Practice Answer Key

Solve.

Question 1.
Points P (-5, 3) and Q (3, -6) are plotted on a coordinate plane. Find the distance between points P and Q. Find both the exact value and an approximate value. Round your answer to the nearest tenth.


So, the distance between points P and Q is exactly units and approximately units.
Answer:
The task is to determine the distance between the points P and Q. compute for the exact vaLue, and then calculate the approximate value.

Note that P is on point (-5, 3) and Q is on point (3, -6), to determine the third vertex R, make a right triangle where Line P and line Q will meet Notice that the vertex wilL be either on (-5, -6) or (3, 3). Say, the third vertex is (-5, -6), then to find the lengths of side \(\overline{P R}\) and \(\overline{Q R}\), determine the absolute value of the y-coordinates of point P and point R, and point Q and point R.
PR = |3 – (-6)|
= |9|
= 9 units
\(\overline{Q R}\) = |3 – (-5)|
= |8|
= 8 units
Apply the Pythagorean Theorem which states that the sum of the squares of the two legs of a right triangle is equal to the square of the hypotenuse. Note that \(\overline{P R}\) and \(\overline{Q R}\) are the legs of the triangle ∆PQR and Let \(\overline{P Q}\) be the hypotenuse.
PR² + QR² = \(\overline{P Q}^{2}\)   Apply Pythagorean Theorem.
9² + 8^{2 =}  \(\overline{P Q}^{2}\)    Substitution.
81 + 64 = \(\overline{P Q}^{2}\)  Evaluate the Squares.
145 = \(\overline{P Q}^{2}\)   Add.
\(\sqrt{145}=\sqrt{\overline{P Q}^{2}}\) Use Square Root Property.
\(\overline{P Q}\) ≈ 12 Simplify.
Therefore, point P is exactly \(\sqrt{145}\) units away from point Q or around 12 units.

Solve.

Question 2.
Mrs. Smith gives the class the coordinates D (-1, -2), E (2, 4), and F (5, -1) and asks them to join the three points to form triangle DEF.

a) Find the length of \(\overline{\mathrm{DE}}\), \(\overline{\mathrm{EF}}\), and \(\overline{\mathrm{DF}}\).

First find the length of \(\overline{\mathrm{DE}}\).
Let D (-1, -2) be (x₁, y₁) and E(2, 4) be (x₂, y₂).

Answer:
The goal of this task is to analyze the graph of ∆DEF where the coordinates of points D, E, and F are (-1, -2), (2, 4), and (5, -1) respectively then
a. Determine the Length of Line \(\overline{D E}\), \(\overline{E F}\) and \(\overline{D F}\), and
b. Verify if ∆DEF is an isosceles triangle

a) The length of the sides of the triangle can be obtained by applying the distance formula which is the formula used in determining the distance between two points. For the measure of \(\overline{D E}\), let D(-1, -2) be (x₁, y₁) and E(2, 4) be (x₂, y₂).
\(\overline{D E}\) = \(\sqrt{\left(x_{2}-x_{1}\right)+\left(y_{2}-y_{1}\right)}\)   Formula.
= \(\sqrt{(2-(-1))^{2}+(4-(-2))^{2}}\)    Substitution.
= \(\sqrt{3^{2}+6^{2}}\)     Subtract.
= \(\sqrt{9+36}\)     Multiply.
= \(\sqrt{45}\)    Add.
≈ 6.7 Simplify
Therefore,  measures exactly \(\sqrt{45}\) units or approximately 6.7 units.

Next find the length of \(\overline{\mathrm{EF}}\)
Let E (2, 4) be (x₁, y₁) and F(5, -1) be (x₂, y₂).

Answer:
Next, the length of \(\overline{E F}\) can be obtained by applying the distance formula which is the formula used in determining the distance between two points Forthe measure of \(\overline{E F}\), let E (2, 4) be (x₁, y₁) and F(5, -1) be (x₂, y₂)
\(\overline{E F}\) = \(\sqrt{\left(x_{2}-x_{1}\right)+\left(y_{2}-y_{1}\right)}\)   Formula.
= \(\sqrt{(5-2)^{2}+(5-4)^{2}}\)   Substitution.
= \(\sqrt{3^{2}+1^{2}}\)    Subtract.
= \(\sqrt{9+1}\)   Multiply.
= \(\sqrt{10}\)    Add.
≈ 3.2 Simplify
Therefore, \(\overline{E F}\) measures exactly \(\sqrt{10}\) units or approximately 3.2 units.

If two of the three sides of a triangle are of the same length, the triangle is an isosceles triangle.

Then find the length of \(\overline{\mathrm{DF}}\).
Let D (-1, -2) be (x₁, y₁) and F(5, -1) be (x₂, y₂).

Answer:
Lastly, the length of \(\overline{D F}\) can be obtained by applying the distance formula which is the formula used in determining the distance between two points For the measure of \(\overline{D E}\), let D(-1, -2) be (x₁, y₁) and F(5, -1) be (x₂, y₂).
\(\overline{D F}\) = \(\sqrt{\left(x_{2}-x_{1}\right)+\left(y_{2}-y_{1}\right)}\) Formula.
= \(\sqrt{(5-(-1))^{2}+((-1)-(-2))^{2}}\)     Substitution.
= \(\sqrt{6^{2}+1^{2}}\)     Subtract.
= \(\sqrt{36+1}\)     Multiply.
= \(\sqrt{37}\)     Add.
≈ 6.1 Simplify
Therefore, \(\overline{D F}\) measures exactly \(\sqrt{37}\)  units or approximateLy 6.1 units.

b) Is triangle DEF an isosceles triangle? Explain.
Because , triangle DEF is .
Answer:
Note that an isosceles triangle is a triangle whose 2 sides are equal. Since no two sides have the same length, the triangle is not an isosceles triangle.

Solve

Question 3.
Mr. Jacobs gives his students the coordinates R (-3, 3), S(-1, -3), and T(-5, -4) and asks them to join the three points to form triangle RST.

a) Find the lengths of \(\overline{R T}\), \(\overline{S T}\) and \(\overline{R S}\).
First find the length of \(\overline{R T}\).
Let R (-3, 3) be (x₁, y₁) and T(-5, -4) be (x₂, y₂).


The length of \(\overline{R S}\) is units.
Answer:
The task is to analyze the graph of ∆RST where the coordinates of points R, S, and T are (-3, 3), (-1, -2), and (-5, -4) respectively then complete the solution to a. Determine the Length of Line \(\overline{R T}\), \(\overline{S T}\) and \(\overline{R S}\), and b. Verify if ∆DEF is an isosceles triangle.

a) The length of the sides of the triangle can be obtained by applying the distance formula which is the formula used in determining the distance between two points. For the measure of \(\overline{R T}\) substitute R(-3, 3) to (x₁, y₁) while T(-5, -4) to (x₂, y₂). Then,

Since there is no negative magnitude(distance), take only the positive vaLue in ±7.3. Therefore, \(\overline{R T}\) is around 7.3 units.

Next, to determine the Length of \(\overline{S T}\), substitute S(-1, -2) to (x₁, y₁) whiLe T(-5, -4) to (x₂, y₂). Then, applying the distance formula,

Since there is no negative magnitude(distance), take only the positive value in ±4.1 Therefore, \(\overline{S T}\) is approximately 4.1 units.

Lastly, to determine the length of \(\overline{R S}\), substitute R(-3, 3) to (x₁, y₁) while T(-1, -2) to (x₂, y₂). Then, applying the distance formula,

Since there is no negative magnitude(distance), take only the positive value in ±6.3. Therefore, \(\overline{R S}\) is approximately 6.3 units.

b) Is triangle RST an isosceles triangle? Explain.
Because , triangle RST is .
Answer:
Note that an isosceles triangle is a triangle whose 2 sides are equal. Since no two sides have the same length, the triangle is not an isosceles triangle.

Math in Focus Course 3B Practice 7.2 Answer Key

For this practice, you may use a calculator. Round your answers to the nearest tenth if necessary.

Question 1.
Points M (-3, -2) and N (4, 5) are plotted on a coordinate plane. Find the exact distance between points M and N.

Answer:
The goal of this task is to give the exact distance of point M to point N if M has a coordinates (-3, -2) and N is on point (4, 5).

First identify the third vertex forming a right triangle where \(\overline{M N}\) is the hypotenuse. Say Point P is the Last vertex and it is on the point (-3, 5) then find the Lengths of \(\overline{P M}\)and \(\overline{P N}\)
\(\overline{P M}\) = |5 – (-2)|
= 7 units
\(\overline{P N}\) = |-3 – 4|
= 7 units
Apply the Pythagorean Theorem which states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the two sides then
\(\overline{P M}^{2}+\overline{P N}^{2}=\overline{M N}^{2}\)    Use the Pythagorean Theorem.
7² + 7² = \(\overline{M N}^{2}\)   Substitute values for \(\overline{P M}\) and \(\overline{P N}\)
49 + 49 = \(\overline{M N}^{2}\)    Multiply
98 = \(\overline{M N}^{2}\)   Add.
\(\overline{M N}\) = \(\sqrt{98}\)    Find the positive square root.
\(\overline{M N}\) ≈ 9.9 units   Round to the nearest tenth.
Therefore, the exact distance of point M to point N is \(\sqrt{98}\).

Question 2.
Find the distance between each pair of points. Which pair of points are the greatest distance apart?
a) A(1, 4), B(6, 6)
Answer:
To find the distance of two points, use the distance formula which is the formula used in determining the distance between two points. Then, let A(1, 4) be (x₁, y₁) while B(6, 6) be (x₂, y₁) and g be the distance of A to B.
g = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Distance Formula.
= \(\sqrt{(6-1)^{2}+(6-4)^{2}}\)       Substitution.
= \(\sqrt{5^{2}+2^{2}}\)       Subtract.
= \(\sqrt{25+4}\)      Evaluate the squares.
= \(\sqrt{29}\)     Add.
≈ ±5.4    Evaluate.
Note that there is no negative magnitude (distance), thus take only the positive value of g. Therefore, A is 5.4 units away from B.

b) C(-4, 7), D(3, 2)
Answer:
Apply the distance formula then let C(-4, 7) be (x₁, y₁) while D(3, 2) be (x₂, y₂) and h be the distance of C to D.
h = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)   Distance Formula.
= \(\sqrt{(3-(-4))^{2}+(2-7)^{2}}\)    Substitution.
= \(\sqrt{7^{2}+(-5)^{2}}\)   Subtract.
= \(\sqrt{49+25}\)   Evaluate the squares.
= \(\sqrt{74}\)   Add.
≈ ±8.6     Evaluate.
Since there is no negative magnitude(distance), take only the positive value of h. Therefore, the distance of C to D is 8.6 units.

c) L(2, -5), N(-3, -1)
Answer:
Use the distance formuLa then let L(2, -5) be (x₁, y₁) while N(-3, -1) be (x₂, y₂) and o be the distance of L to N.
o = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)   Distance Formula.
= \(\sqrt{((-3)-2)^{2}+((-1)-(-5))^{2}}\)    Substitution.
= \(\sqrt{(-5)^{2}+4^{2}}\)   Subtract.
= \(\sqrt{25+16}\)   Evaluate the squares.
= \(\sqrt{41}\)   Add.
≈ ±6.4      Evaluate.
No magnitude(distance) is negative so take only the positive value of o. Therefore, L is 6.4 units away from N.

d) Y(-6, -4), Z(0, 5)
Answer:
Let Y(-6, -4) be (x₁, y₁) white Z(0. 5) be (x₂, y₂) and p be the distance of Y to Z then apply the distance formula.
p = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)   Distance Formula.
= \(\sqrt{(0-(-6))^{2}+(5-(-4))^{2}}\)    Substitution.
= \(\sqrt{6^{2}+9^{2}}\)   Subtract.
= \(\sqrt{36+81}\)   Evaluate the squares.
= \(\sqrt{117}\)   Add.
≈ ±10.8     Evaluate.
Take only the positive value of p since there is no negative magnitude(distance). Therefore, Y is 10.8 units away from Z.

Question 3.
Zack plots the points R(1, -4), S(-5, 0), and T(5, 2) on a coordinate plane. He joins the three points to form triangle RST. Is the triangle an isosceles triangle? Explain.

Answer:
The target of this task is to verify if ∆RST is an isosceles triangle when points R, S, and T have coordinates (1, -4), (-5, 0) and (5, 2) respectively.

An isosce[es triangLe is a triangle where two of its sides are equal. Calculate the length of \(\overline{R S}\), \(\overline{S T}\), and \(\overline{R T}\) to determine if there exist two sides that are equal by applying the distance formula which is the formula used in determining the distance between two points. For \(\overline{R S}\) let R(1, -4) be (x₁, y₁) while S(-5, 0) be (x₂, y₂) and n be the distance of R to S.
n = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)   Distance Formula.
= \(\sqrt{((-5)-1)^{2}+(0-(-4))^{2}}\)    Substitution.
= \(\sqrt{(-6)^{2}+(-4)^{2}}\)   Subtract.
= \(\sqrt{36+16}\)   Evaluate the squares.
= \(\sqrt{52}\)   Add.
≈ ±7.2     Evaluate.
Note that there is no negative magnitude(distance), thus take only the positive value of n. Therefore, R is 7.2 units away from S.

For \(\overline{S T}\) let S(-5, 0) be (x₁, y₁) while T(5, 2) be (x₂, y₂) and a be the distance of S to T.
a = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)   Distance Formula.
= \(\sqrt{(5-(-5))^{2}+(2-0)^{2}}\)    Substitution.
= \(\sqrt{10^{2}+2^{2}}\)   Subtract.
= \(\sqrt{100+4}\)   Evaluate the squares.
= \(\sqrt{104}\)   Add.
≈ ±10.2     Evaluate.
Since there is no negative magnitude(distance), take only the positive value of a. Therefore, the distance of S to T is 10.2 units.

Then for \(\overline{R T}\) let R(1, -4) be (x₁, y₁) whiLe T(5, 2) be (x₂, y₂) and k be the distance of Sto T.
k = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)   Distance Formula.
= \(\sqrt{(5-1)^{2}+(2-(-4))^{2}}\)    Substitution.
= \(\sqrt{4^{2}+6^{2}}\)   Subtract.
= \(\sqrt{16+36}\)   Evaluate the squares.
= \(\sqrt{52}\)   Add.
≈ ±7.2     Evaluate.
No magnitude(distance) is negative so take only the positive value of k. Therefore, R is 7.2 units away from T.

Notice that \(\overline{R S}\) is 7.2 units, \(\overline{S T}\) is 10.2 units and \(\overline{R T}\) is also 7.2 units. Two sides of ∆RST is equal which is a property of an isosceles triangle. Therefore the triangle is an isosceles triangle.

Use the data in the diagram for questions 4 to 6. Each unit on the grid equals 1 kilometer.

Question 4.
Find the approximate distance from the school to each of the following locations.
a) Zoo
b) Park
c) Swimming pool
d) Library
Answer:
The goal is to determine the estimated distance of school at point A(-2, 1) to the a. Zoo at B(-4, 4), b. Park at C(2, 3), c. Swimming Pool at D(0, -2), and d. Library at E(-5, -3). Note that every unit is equal to 1 kilometer.

a) Calculate for the distance two points A and B to determine the distance of the school and the zoo. Apply the distance formula which is the formula used in determining the distance between two points. Let e be the distance of A to B, and A(-2, 1) be (x₁, y₁) while B(-4, 4) be (x₂, y₂).
e = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Distance Formula.
= \(\sqrt{((-4)-(-2))^{2}+(4-1)^{2}}\)      Substitution.
= \(\sqrt{(-2)^{2}+(3)^{2}}\)     Subtract.
= \(\sqrt{4+9}\)    Evaluate the squares.
= \(\sqrt{13}\)    Add.
≈ ±3.6    Evaluate.
Because that there is no negative magnitude(distance), take only the positive value of e. Therefore, the zoo is around 3.6 kilometers away from the school.

b) Compute for the distance of points A and C to know the distance of school to park by applying the distance formula describe in (a). Then Let f be the distance of A to C, and A(-2, 1)) be (x₁, y₁) whiLe C(2, 3) be (x₂, y₂).
f = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Distance Formula.
= \(\sqrt{(2-(-2))^{2}+(3-1)^{2}}\)      Substitution.
= \(\sqrt{4^{2}+2^{2}}\)     Subtract.
= \(\sqrt{16+4}\)    Evaluate the squares.
= \(\sqrt{20}\)    Add.
≈ ±4.5    Evaluate.
Since there is no negative magnitude(distance), take only the positive value of f. Therefore, the distance of school to the park is approximately 4.5 kiLometers.

c) Solve for the distance of two points A and D to identify the distance of the school and the swimming pool using the distance formula as mentioned above. Next, Let g be the distance of A to D, and A(-2, 1)) be (x₁, y₁) while D(0, -2) be (x₂, y₂).
g = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Distance Formula.
= \(\sqrt{(0-(-2))^{2}+((-2)-1)^{2}}\)      Substitution.
= \(\sqrt{2^{2}+(-3)^{2}}\)     Subtract.
= \(\sqrt{4+9}\)    Evaluate the squares.
= \(\sqrt{13}\)    Add.
≈ ±3.6      Evaluate.
No magnitude(distance) is negative thus take only the positive value of g. Therefore, the swimming pool is around 3.6 kilometers away from the school.

d) Calculate for the distance of point A and point E to determine the distance ci me school and the library by applying the distance formula Let h be the distance of A to E, and A(-2, 1)) be (x₁, y₁) while E(-5, -3) be (x₂, y₂).
h = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Distance Formula.
= \(\sqrt{((-5)-(-2))^{2}+((-3)-1)^{2}}\)      Substitution.
= \(\sqrt{(-3)^{2}+(-4)^{2}}\)     Subtract.
= \(\sqrt{9+16}\)    Evaluate the squares.
= \(\sqrt{25}\)    Add.
≈ ±5      Evaluate.
There is no negative magnitude(distance) so take only the positive value of h. Therefore, the library is 5 kilometers away from the school.

Question 5.
Which two locations are the same distance from the school?
Answer:
The objective of this task is to determine the locations that are equal in distance from the school.

Note that by applying the distance formula which is the formula used in determining the distance between two points. The distance of A(school) to B(park) is computed by substituting A(-2, 1) to (x₁, y₁) while B(-4, 4) to (x₂, y₂) and letting e be the distance.
e = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Distance Formula.
= \(\sqrt{((-4)-(-2))^{2}+(4-1)^{2}}\)      Substitution.
= \(\sqrt{(-2)^{2}+(3)^{2}}\)     Subtract.
= \(\sqrt{4+9}\)    Evaluate the squares.
= \(\sqrt{13}\)    Add.
≈ ±3.6     Evaluate.
Thus, the park is 3.6 kilometers from the school.

Also, A(-2, 1) is substituted to (x₁, y₁) whiLe D(0, -2) to (x₂, y₂) to calculate for the distance of the school to the swimming pool.
g = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Distance Formula.
= \(\sqrt{(0-(-2))^{2}+((-2)-1)^{2}}\)      Substitution.
= \(\sqrt{2^{2}+(-3)^{2}}\)     Subtract.
= \(\sqrt{4+9}\)    Evaluate the squares.
= \(\sqrt{13}\)    Add.
≈ ±3.6       Evaluate.
Thus, the swimming pool is 3.6 kilometers from the school.
Therefore, the swimming pool and the park is have the same distance from the schooL

Question 6.
Which location is farthest from the school?
Answer:
The task is to identify the location with the largest distance from the school at point A(-2, 1) if the zoo is at B( -4, 4), park at C(2, 3), swimming pool at D(0, -2), and Library at E(-5, -3).

First calculate for the distance of points A and B to determine the distance of the school and the zoo. Apply the distance formula which is the formula used in determining the distance between two points. Let h be the distance of A to B, and A(-2, 1) be (x₁, y₁) while B(-4, 4) be (x₂, y₂).
h = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Distance Formula.
= \(\sqrt{((-4)-(-2))^{2}+(4-1)^{2}}\)      Substitution.
= \(\sqrt{(-2)^{2}+(3)^{2}}\)     Subtract.
= \(\sqrt{4+9}\)    Evaluate the squares.
= \(\sqrt{13}\)    Add.
≈ ±3.6       Evaluate.
Because that there is no negative magnitude(distance), take only the positive vaLue of h. Therefore, the zoo is around 3.6 kilometers away from the school.

Next, compute for the distance of points A and C to know the distance of school to park by app[ying the distance formula describe in (a). Then let j be the distance of A to C, and A(-2, 1) be (x₁, y₁) while C(2, 3) be (x₂, y(x₁, y₁)).
j = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Distance Formula.
= \(\sqrt{(2-(-2))^{2}+(3-1)^{2}}\)      Substitution.
= \(\sqrt{4^{2}+2^{2}}\)     Subtract.
= \(\sqrt{16+4}\)    Evaluate the squares.
= \(\sqrt{20}\)    Add.
≈ ±4.5       Evaluate.
Since there is no negative magnitude(distance), take only the positive vaLue of j Therefore, the distance of the school to the park is approximately 4.5 kiLometers.

Now, solve for the distance of two points A and D to identify the distance of schooL and the swimming pool using the distance formula as mentioned above. Let k be the distance of A to D, and A(-2, 1) be (x₁, y₁) while D(0, -2) be (x₂, y₂).
k = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Distance Formula.
= \(\sqrt{(0-(-2))^{2}+((-2)-1)^{2}}\)      Substitution.
= \(\sqrt{2^{2}+(-3)^{2}}\)     Subtract.
= \(\sqrt{4+9}\)    Evaluate the squares.
= \(\sqrt{13}\)    Add.
≈ ±3.6      Evaluate.
No magnitude(distance is negative thus take only the positive value of k. Therefore, the swimming pool is around 3.6 kilometers away from the school.

Lastly, calculate for the distance of point A and point E to determine the distance of the schooL and the library by applying the distance formula Let l be the distance of A to E, and A(-2, 1) be (x₁, y₁) whiLe E(-5, -3) be (x₂, y₂).
l = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Distance Formula.
= \(\sqrt{((-5)-(-2))^{2}+((-3)-1)^{2}}\)      Substitution.
= \(\sqrt{(-3)^{2}+(-4)^{2}}\)     Subtract.
= \(\sqrt{9+16}\)    Evaluate the squares.
= \(\sqrt{25}\)    Add.
= ±5    Evaluate.
There is no negative magnitude(distance) so take only the positive value of l. Therefore, the library is 5 kilometers away from the school.
Since the school has a distance of 3.6 kilometers for both the zoo and swimming pool, has a distance of 4.5 kilometers to the park and 5 kilometers to the Library. Therefore, library has the farthest distance from the school.

Solve. Show your work.

Question 7.
A ship is located at the point shown in the diagram. The ship needs to stop at a port for refueling on its way to the lighthouse. It can either stop at Port A or Port B. If the captain wants the journey to be as short as possible, which port should the ship stop at?

Answer:
The goal is to find which port the captain should pass for a shorter journey to the Lighthouse at (4, 4) if the ship is on point (-4, -2) and the two possible port to stop are Port A(-3, 3) and Port B(3, 1)

First, calculate the distance or me ship to Port A to the from Port A to the Lighthouse. Afterward, add the computed distances to determine the total distance the ship will travel if it will pass through Port A. Applying the distance formula which is the formula used in determining the distance between two points. Let the position of the ship (-4, -2) be (x₁, y₁) whiLe Port A(-3, 3) be (x₂, y₂) and u denoted their distance.
u = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Distance Formula.
= \(\sqrt{((-3)-(-4))^{2}+(3-(-2))^{2}}\)      Substitution.
= \(\sqrt{1^{2}+5^{2}}\)     Subtract.
= \(\sqrt{1+25}\)    Evaluate the squares.
= \(\sqrt{26}\)    Add.
≈ ±5.1    Evaluate.
Note that there is no negative magnitude(distance) so only take u equals to 5.1. Thus, the ship is 5.1 units away from Port A.
For the distance of Port A to the [ighthouse, let Port A(-3. 3) be substituted to (x₁, y₁) while the position (4, 4) of the Lighthouse to (x₂, y₂) and let w be their distance then
w = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Distance Formula.
= \(\sqrt{(4-(-3))^{2}+(4-3)^{2}}\)      Substitution.
= \(\sqrt{7^{2}+1^{2}}\)     Subtract.
= \(\sqrt{49+1}\)    Evaluate the squares.
= \(\sqrt{50}\)    Add.
≈ ±7.1    Evaluate.
Hence, Port A and the Lighthouse has a distance of 7.1 units. Now add the two distances u and w,
u + w = 5.1 – 7.1
= 12.2 units
Thus, the total distance that the ship will travel if it stops to Port A then proceed to the Lighthouse is 12.2 units.

Next, calculate the distance of the ship to Port B then from Port B to the Lighthouse. Then, add the computed distances to determine the total distance the ship will travel if it will pass through Port B. Apply the distance formula to compute for the distance of the ship to the Port B. Let the position of the ship (-4, -2) be (x₁, y₁) while Port B(3, 1) be (x₂, y₂) and y denoted their distance.
y = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Distance Formula.
= \(\sqrt{(3-(-4))^{2}+(1-(-2))^{2}}\)      Substitution.
= \(\sqrt{7^{2}+3^{2}}\)     Subtract.
= \(\sqrt{49+9}\)    Evaluate the squares.
= \(\sqrt{58}\)    Add.
≈ ±7.6      Evaluate.
Thus, the ship is 7.6 units away from Port B.

For the distance of Port B to the [ighthouse, [et Port B(3, 1) be substituted to (x₁, y₁) white the position (4, 4) of the lighthouse to (x₂, y₂) and let z be their distance then
z = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)    Distance Formula.
= \(\sqrt{(4-3)^{2}+(4-1)^{2}}\)      Substitution.
= \(\sqrt{1^{2}+3^{2}}\)     Subtract.
= \(\sqrt{1+9}\)    Evaluate the squares.
= \(\sqrt{10}\)    Add.
≈ ±3.2       Evaluate.
Hence, Port B and the lighthouse has a distance of 3.2 units. Now add the two distances y and z,
y + z = 7.6 + 3.2
= 10.8 units
Thus, the total distance that the ship will travel if it stop to Port B then proceed to the lighthouse is 10.8 units.
Therefore, the ship should take the route passing to Port B to the lighthouse for a shorter journey.

Question 8.
Blair drew two triangles on a coordinate plane.
a) Find the lengths of the sides of triangle XYZ Classify the triangle by its side lengths.
Answer:

b) Blair thinks that triangle RST is a right triangle. Do you agree? Why or why not?
Answer:
Determine the sides of the triangle by applying the distance formula. Afterwards, use the Converse of Pythagorean Theorem which states that if the square of the length of the hypotenuse of a triangle is equal to the sum of the squares of the lengths of the two legs, then the triangle is a right triangle. If the hypotenuse of ∆RST is equal to the sum of the square of its legs then ∆RST is indeed a right triangle. To calculate side \(\overline{S R}\), substitute S(1, 4) to (x₁, y₁) while R(4, 5) to (x₂, y₂)


Thus, \(\overline{R T}\) is 5.1 units Long. Since \(\overline{R T}\) has the largest length use it as the hypotenuse then
(5.1)² = (45)² + (3.2)²  Use the Converse Pythagorean Theorem.
26.01 = 20.25 + 10.24    Evaluate the squares.
26.01 ≠ 30.49   Add.
Since, the square of \(\overline{R T}\) is not equal to the sum of the squares of ST and SR, then ∆RST is not a right triangle.

Question 9.
The engine on a cruise ship has broken down and the passengers are waiting for a patrol ship to rescue them. The positions of the two ships are shown on the right. Each unit on the grid equals 6 miles.

a) How far is the patrol ship from the cruise ship?
Answer:

The objective of this task is to analyze the positions of the cruise ship and the patrol ship then a. Find the distance of the two ships to each other, and b. Determine how long will it takes the patrol ship to reach the boat if its traveling at the speed of 50 miles per hour.

Observe that position of the patrol ship denoted by point S is on (-4, 5) while the coordinates of the cruise ship represented by point H is (2, -3) Say vertex P is on (2, 5) and forms a right triangle with the other two points then,
\(\overline{S P}\) = |-4 – 2|
= |-6|
= 6 units
\(\overline{H P}\) = |-3 – 5|
= |-8|
= 8 units
Apply the Pythagorean Theorem which states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the two other sides then
\(\overline{S P}^{2}+\overline{H P}^{2}=\overline{S H}^{2}\)    Use the Pythagorean Theorem.
6² + 8² = \(\overline{S H}^{2}\)    Substitute values for \(\overline{S P}\) and \(\overline{H P}\)
36 + 64 = \(\overline{S H}^{2}\)    Multiply.
100 = \(\overline{S H}^{2}\)      Add.
\(\overline{S H}\) = \(\sqrt{100}\)    Find the positive square root.
\(\overline{S H}\) = 10 units.    Simplify.
Since each unit is equal to 6 miles then multiply 10 units to 6. Therefore, the patrol ship is 60 miles away from the other ship.

b) If the patrol ship travels at a speed of 50 miles per hour, how long will it take to reach the boat?
Answer:
Since the patrol ship is 60 miles away from the cruise ship and it is travelling at the speed of 5Omi[es per hour, then divide this speed to the distance of the ships to each other to know how long will it takes the patrol ship to reach the boat.
= \(\frac{60 \text { miles }}{50 \text { miles } / \text { hour }}\)
1.2 hour
Therefore, the patrol ship will meet the other ship in 1.2 hours or in 1 hour and 12 minutes.

Question 10.
Math Journal Point P (1,2) is the center of a circle. Three of the following points lie on the circle. Tell which point is not on the circle. Explain your reasoning. A (-1, 4), B (4, 4), C (3, 0), and D (3, 4)
Answer:
The goal of this task is to find out which point among D(3, 4), C(3, 0), B(4, 4), and A(-1, 4) does not belong on circle P whose center is at (1, 2).

To determine which points does note belong to the circle, solve for the distance between the center of the circle and each of the points by applying the distance formula. This states that distance is equal to the square root of the sum of the x-coordinate of the second point minus the x-coordinate of the first point and the y-coordinate of the second point minus the y-coordinate of the first point. Let (1, 2) be (x₁, y₁) and (3, 4) be (x₂, y₂) and p be the distance of the center from point D, then
p = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)   Formula.
= \(\sqrt{(3-1)^{2}+(4-2)^{2}}\)       Substitution.
= \(\sqrt{2^{2}+2^{2}}\)       Subtract.
= \(\sqrt{4+4}\)       Evaluate the squares.
= \(\sqrt{8}\)       Add.
≈ ±2.8          Evaluate.
Therefore, the center of the circle is approximateLy 2.8 units from point D.

Applying the distance formula, let (1, 2) be (x₁, y₁) and (3, 0) be (x₂, y₂) and q be the distance of the center from point C, then
q = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)   Formula.
= \(\sqrt{(3-1)^{2}+(0-2)^{2}}\)       Substitution.
= \(\sqrt{2^{2}+(-2)^{2}}\)       Subtract.
= \(\sqrt{4+4}\)       Evaluate the squares.
= \(\sqrt{8}\)       Add.
≈ ±2.8 Evaluate.
Therefore, the center of the circle is around 2.8 units from point C.

Next, using the distance formula, let (1, 2) be (x₁, y₁) and (4, 4) be (x₂, y₂) and r be the distance of the center from point B, then
r = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)   Formula.
= \(\sqrt{(4-1)^{2}+(4-2)^{2}}\)       Substitution.
= \(\sqrt{3^{2}+2^{2}}\)       Subtract.
= \(\sqrt{9+4}\)       Evaluate the squares.
= \(\sqrt{13}\)       Add.
≈ ±3.6         Evaluate.
Therefore, the center of the circle is about 3.6 units from point B.

Applying the distance formula for the last time, let (1, 2) be (x₁, y₁) and (-1, 4) be (x₂, y₂) and s be the distance of the center from point A, then
s = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)   Formula.
= \(\sqrt{(-1)-1)^{2}+(4-2)^{2}}\)       Substitution.
= \(\sqrt{(-2)^{2}+2^{2}}\)       Subtract.
= \(\sqrt{4+4}\)       Evaluate the squares.
= \(\sqrt{8}\)       Add.
≈ ±2.8     Evaluate.
Therefore, the center of the circle is approximateLy 2.8 units from point A. Notice that points A, C and D has the same distance from the center of the circle. Thus point B does not belong on circle P.

Question 11.
Math Journal Jose found the distance between points X and Y by first counting grids to find the horizontal and vertical distances. Then he used the Pythagorean Theorem. How is his method different from using the distance formula? How is it the same?
Answer:
The task is to state the similarity and difference of the Pythagorean Theorem and the distance formula.

Both the Pythagorean Theorem and the Distance Formula is utilized to determine the measure of a Line segment The Pythagorean Theorem is used most of the time when the Length of a diagonal Line is unknown The method includes generating Line segments that will serve as the legs of the hypotenuse. This legs must have known measurements so the method will work. The distance formula on the other hand only needs the coordinates of the endpoints of the line so the measure of the length of the segment can be computed.

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 7 Lesson 7.1 Understanding the Pythagorean Theorem and Plane Figures to score better marks in the exam.

Math in Focus Grade 7 Course 3 B Chapter 7 Lesson 7.1 Answer Key Understanding the Pythagorean Theorem and Plane Figures

Math in Focus Grade 8 Chapter 7 Lesson 7.1 Guided Practice Answer Key

Hands-On Activity

Materials:

• scissors

Use Rearrangementto Prove The Pythagorean Theorem

In a right triangle, the longest side is known as the hypotenuse. The two shorter sides are called legs.

Step 1.
Draw four identical right triangles, with side lengths a, b, and c, on a a piece of paper and cut them out. Make one leg shorter than the other.

Step 2.
Arrange the triangles to form a square with side length c.

Step 3.
What is the area of the square whose sides are c units long? Label the large square with its area.

Step 4.
Draw two squares on a different piece of paper. One square should have side lengths of b units, and the other should have side lengths of a units. You can use one of the triangles as a guide to mark off a units and b units. Cut out these square and arrange the four triangles and the two new squares to form a large square like the one shown.

Step 5.
Write an algebraic expression in terms of a and b for the combined area of the two small squares.

Math Journal Compare the areas of the squares found in Step 3 and Step 5. Write an equation that relates the area of one square to the sum of the areas of the other two squares.

In the activity, you explored the relationship among the sides of a right triangle. This relationship is true for all right triangles and is described by the Pythagorean Theorem.

In the activity, you observed the following:

Pythagorean Theorem
The square of the length of the hypotenuse of a right triangle is equal to the sum of the squares of the two legs. For the triangle shown, you can write this equation: a² + b² = c².

Complete.

Question 1.
Merlin wants to put a fence around a right triangular garden.
He measures two sides. Find the length of the unknown side.

Answer:
The length of the unknown side is 15 ft,

Explanation:

Complete.

Question 2.
Find the values of x and y. Round your answer to the nearest tenth.

Notice that there are two right triangles.
One has a hypotenuse that is 2.5 inches long, and the other has a hypotenuse that is y inches long.
First find the value of x.

Answer:
The value of x is approximately 2 and
the value of y is approximately 4

Hands-On Activity

Materials

• graph paper
• ruler

Explore Pythagorean Triples
A Pythagorean triple is any set of three whole numbers that satisfy the
Pythagorean Theorem equation c² = a² + b². The table shows several sets of Pythagorean triples.

Step 1.
Select one Pythagorean triple from the table. Draw a triangle with legs a units and b units long on a piece of graph paper.

Step 2.
Using a strip of graph paper as a measuring tool, measure the hypotenuse of the triangle. Is it equal to the greatest value in the Pythagorean triple?

Step 3.
Repeat Step 1 and Step 2 using the other Pythagorean triples in the table.

Step 4.
The converse of the Pythagorean Theorem says that if the sum of the squares of the lengths of the two legs of a triangle equals the square of the length of the hypotenuse, then the triangle is a right triangle. Do your triangle measurements support this statement? Explain.

Copy and complete each with a value and each with = or ≠.

Question 3.
A triangle has side lengths 13 centimeters, 15 centimeters, and 18 centimeter Is it a right triangle?

Answer:
The triangle is a not a right triangle,

Explanation:

Complete.

Question 4.
A ladder 18 feet long is leaning against a wall. The base of the ladder is 9 feet away from the wall. Find the distance from the top of the ladder to the ground. Round your answer to the nearest tenth.
Let the distance from the top of the ladder to the ground be x feet.

The distance from the top of the ladder to the ground is approximately feet.
Answer:
The distance from the top of the ladder to the ground is approximately 16 feet,

Explanation:

Complete.

Question 5.
A tree has a shadow length of approximately 9 feet. The distance from the tip of the tree to the tip of the shadow is about 15 feet. How tall is the tree?

Let the height of the tree be x feet.

Answer:
The height of the tree is 12  feet,

Explanation:

Question 6.
The support pole of the tent shown forms one leg of a right triangle. One side of the tent forms the hypotenuse of the right triangle. Find the length of the base of the tent.

So, the length of the base of the tent is inches.
Answer:
The length of the base of the tent is 48 in,

Explanation:

Math in Focus Course 3B Practice 7.1 Answer Key

For this practice, you may use a calculator.

Copy the road signs shown below, identify a right triangle in each sign,
and label the hypotenuse with an arrow.

Question 1.

Answer:

Explanation:
Identified a right triangle in the sign,
and labeled the hypotenuse with an arrow.

Question 2.

Answer:

Explanation:
Identified a right triangle in the sign,
and labeled the hypotenuse with an arrow.

Find the value of x.

Question 3.

Answer:
x = 15 cm,

Explanation:
Using pythagorean x ² = 9²  + 12² = 81 + 144 =225,
x is equal to square root of 225 which is 15 cm.

Question 4.

Answer:
x = 3.96 approximately 4 cm,

Explanation:
Using pythagorean x ² + 4.5²  = 6² ,
x ² + 20.25 = 36,
x ² = 36 – 20.25 = 15.75,
x is equal to square root of 15.75 which is 3.96 approximately 4 cm.

Question 5.

Answer:
4 cm

Explanation:
Using pythagorean x ² + 10²  = 12.5² ,
x ² + 100 = 156.25,
x ² = 156.25 – 100 = 15.75,
x is equal to square root of 15.75 which is 3.96 approximately 4 cm.

Question 6.

Answer:

Using pythagorean x² + 4.5²  = 6² ,
x ² + 20.25 = 36,
x ² = 36 – 20.25 = 15.75,
x is equal to square root of 15.75 which is 3.96 approximately 4 cm.

Calculate each unknown side length. Round your answer to the nearest tenth.

Question 7.

Answer:
x is 3 inches and y is 12.64 approximately 13,

Explanation:
First we calculate the given right angled triangle using
phythagorean theorem x² + 4² = 5² ,
x² = 25- 16 = 9 squareroot of 9 is 3 therefore
x is 3 inches, Now
3² + y ² = 13² ,
y² = 169- 9 = 160,so y is square root of 160 is 12.64 approximately 13.

Question 8.

Answer:
the unknown side length is 20 in,

Explanation:
We take x as y +z inches,
First right angle triangle as base z and height 16 in and hypotenuse as 20,
so z² + 16² = 20²,
z² = 400 – 256 = 144     z is square root of 144 is 12 inches,
Now anthe triangle base y height 16 in and hypotenuse is 18
so y² + 16² = 18²,
y² = 324- 256 = 68 so y is square root of 68 is 8.24 in,
so x = y + z = 8.24 in + 12 in = 20.24 approximately 20.

Question 9.

Answer:
x is 6 in and y is 12in,

Explanation:
Given smaller right andle triangle and bigger right traingle,
First smaller using pythogorean theorem
x² + 4² = 7² ,
x² = 49-16= 33, x is square root of 33 is 5.744 approximately 6,
Now 10² + 6² = y² ,
y² = 100 + 36 = 136, so y is square root of 136 is 11.66 approximately 12,
So x = 6 in and y = 12 in respectively.

Question 10.

Answer:
x = 4in and y = 9 in,

Explanation:
Given right angled triangle applying pythagorean theorem we have
x² + 8² = 9²,
x² = 81 – 64 = 17, so square root of 17 is 4.123 approximately 4
x = 4 in  and y= 9 in.

Solve. Show your work. Round your answer to the nearest tenth.

Question 11.
Daniel had two pieces of wire. He bent each piece of wire into the shape of a triangle. Determine which triangle is a right triangle.

Answer:
Triangle B is a right triangle,
Explanation:
Given Triangle A  applying pythagorean theorem
26² + 18² = 36² ,
676 + 324 = 1296,
1000 ≠ 1296,
For Triangle B applying pythagorean theorem
20² + 15² = 25²,
400 +  225 = 625,
625 = 625,
The converse of the Pythagorean Theorem says that if the sum of the squares of the lengths of the two legs of a triangle equals the square of the length of the hypotenuse, then the triangle is a right triangle so triangle B is right triangle.

Question 12.
Kendrick wants to build a slide for his son in the backyard. He buys a slide that is 8 feet long. The height of the stairs is 5 feet. Find the distance from the bottom of the stairs to the base of the slide.

Answer:
The distance from the bottom of the stairs to the base of the slide is
approximately 6 ft,

Explanation:
Given
Kendrick wants to build a slide for his son in the backyard.
He buys a slide that is 8 feet long. The height of the stairs is 5 feet.
To find the distance from the bottom of the stairs to the base b of the slide applying pythagorean theorem as 5² + b² = 8²,
b² = 64 – 25 = 39, square root of b is 6.244 approximately 6 ft.

Question 13.
Mrs. Hanson uses a wheelchair. Her husband decides to build a ramp to make it easier for her to enter and leave the house. Find the length of the ramp.

Answer:
The length of the ramp is approximately 71 in,

Explanation:
Given Mrs. Hanson uses a wheelchair. Her husband decides to build a ramp of r inches to make it easier for her to enter and leave the house.
As triangle is right triangle applying pythagorean theorem
r² = 12² + 70²,
r² = 144 + 4900 =5044, r is square root of 5044 is 71.02 in,
So the length of the ramp is approximately 71 in.

Question 14.
A sign is hung outside a shop on the wall of a building. One end of the brace that holds the sign is connected to the wall. The other end of the brace is connected to the wall by a wire. Use the dimensions in the diagram to find the length of the wire.

Answer:
The length of wire is approximately 4 ft,

Explanation:
Given a sign is hung outside a shop on the wall of a building.
One end of the brace that holds the sign is connected to the wall.
The other end of the brace is connected to the wall by a wire.
the length l of the wire is l² = 3² + 3²,
l² = 9 + 9 = 18, l is square root of 18 is 4.24 ,
so the length of wire is approximately 4 ft.

Question 15.
Kelly is flying a kite. When the string, which is 34 feet long, becomes taut, the distance along the ground from the kite to Kelly’s hand is 6.5 feet. Find the vertical height of the kite above her hand.

Answer:
Vertical height of the kite above her hand is 33.37 approximately 34 feet,

Explanation:
Given Kelly is flying a kite. When the string, which is 34 feet long,
becomes taut, the distance along the ground from the kite to Kelly’s hand is 6.5 feet.
Let the vertical height v of the kite above her hand. As it is right triangle applying pythogorean theorem
34² = 6.5² + v²,
v² = 1156 – 42.25 = 1113.75,
so vertical height is square root of 1113.75 is 33.37 approximately 34 feet.

Question 16.
In a movie scene, an actor runs up a ramp that leads from the top of one building to the top of another building. The horizontal distance between the two buildings is 8.6 meters. The height of the shorter building is 18 meters while the height of the taller building is 24 meters. Find the length of the ramp.

Answer:
The length of ramp is is 6.16 approximately 6 m,

Explanation:
Given in a movie scene, an actor runs up a ramp that leads from the top of one building to the top of another building.
The horizontal distance between the two buildings is 8.6 meters.
The height of the shorter building is 18 meters while the height of the taller building is 24 meters. The length of ramp is l and it is right triangle so
l² = 8.6² -(24-18)²,
l² =  73.96 – (6)²,
l² = 73.96 – 36 = 37.96 , so l is square root of 37.96 is 6.16 approximately 6 m.

Question 17.
The size of a rectangular television screen is given as the length of the diagonal of the screen. Find the size of a television screen that has a height of 38.4 inches and width of 28.8 inches.
Answer:
the length of the diagonal of the screen is 48 inches,

Explanation:
Given the size of a rectangular television screen is given as the length l of the diagonal of the screen.
The size of a television screen that has a height of 38.4 inches and width of 28.8 inches is
l² = 38.4² + 28.8²,
l² = 1474.56 + 829.44= 2304, l is the square root of 2304 is 48 inches.

Question 18.
A ship sailed from Port X to Port Y. It traveled 20 kilometers due north and then 25 kilometers due west. Find the shortest distance between the two ports.
Answer:
The shortest distance between the two ports is 32.01 approximately 32 kilometers,

Explanation:
Given a ship sailed from Port X to Port Y. It traveled 20 kilometers due north and then 25 kilometers due west. Let s be the shortest distance between the two ports its right triangle applying pythagorean theorem
s² = 20² + 25²
= 400+ 625
= 1025, s is the square root of 1025 is 32.01
approximately 32 kilometers.

Question 19.
Mike wants to build a sailboat. The scale drawing is shown on the right. Find the values of x and y.

Answer:
The value of x is 7.07 approximately 7 and
y is 14.21 approximately 14,

Explanation:
Given both right traingles 1st triangle applying
pythagorean theorem x² + x² = 10²,
2x² = 100,
x² = 100/2 = 50 so x is square root of 50 is 7.07 approximately 7,
and 2nd triangle applying pythogorean theorem
y² = 11² +( 7+2)²,
y² = 121 + 81 = 202, y is squareroot of 202 is 14.21 approximately 14.

Question 20.
The diagonal length of a square window is 40 centimeters. Find the area of the window.
Answer:
The area of window is 800 cm²,

Explanation:

Question 21.
Triangles ABC and ACD are right triangles. AB is 28 meters long. AC is 21 meters long. Find the lengths of \(\overline{B C}\) and \(\overline{A D}\).

Answer:

Explanation:
Given Triangles ABC and ACD are right triangles. AB is 28 meters long.
AC is 21 meters long.
so BC² = 21² + 28²,
Bc ² = 441 + 784 = 1225, so Bc is square root of 1225 is 35 m.

Question 22.
The infield of a baseball diamond is a square. Barry measures the distance from home plate to second base and finds that it is about 38.7 meters.

a) Find the approximate distance from home plate to first base.
Answer:
The approximate distance from home plate to first base is 27.4 m

Explanation:
The 38.7 meters is the diagonal of a square; the distance from home plate to first base is a side of the square. The length of the side of the square is the length of the diagonal, divided by the square root of 2.
=38.7/ 1.414 =  27.4 meters.

b) Find the area of the infield.
Answer:
The area of the infield is 750.76 square meters,

Explanation:
Given the side of a baseball diamond is a square and side distance is 27.4 m
so the area of the infield is side × side = 27.4 × 27.4 = 750.76 square meters.

Question 23.
The road sign shown is in the shape of an equilateral triangle. The height of the road sign is 15 inches.

a) Find the length of each side.
Answer:
The length of each side is 17 in,

Explanation:
As we know in an equilateral triangle h = (1/2) × √3 × a.
Angles of Equilateral Triangle: A = B = C = 60° ,
Sides of Equilateral Triangle: a = b = c.
So 15 = 1/2 × √3 × a,
30 = 1.732 × a,
a = 30/1.732 = 17.32 approximately 17 in.

b) Find the area of the sign.
Answer:
The area of the sign is 127.5 in²,

Explanation:
As we know area of triangle is 1/2 × base ×  height,
1/2 × 17 in × 15 in = 127.5 in².

Question 24.
Math Journal A salesman selling windows says that a window frame J that is 8 feet long and 6.5 feet wide is rectangular. He also says that it has a diagonal length of 12 feet. Danielle thinks that the salesman is wrong in saying that the window is rectangular. Who is right and why?
Answer:
Yes, Danielle thinks that the salesman is wrong in saying that the window is rectangular,

Explanation:
Given a salesman selling windows says that a window frame J that is 8 feet long and 6.5 feet wide is rectangular.
He also says that it has a diagonal length of 12 feet.
But if we calculate the diagonal length we get

d = 10 not 12 so sales man is wrong.

Question 25.
Math Journal Fiona buys a triangular table. The sides of the table top are 29.4 inches, 39.2 inches, and 49 inches long. She wants to place the table in a corner of a rectangular room. Will the table fit snugly in the corner? Explain.
Answer:
Yes the table fit snugly in the corner,

Explanation:
Given Fiona buys a triangular table.
The sides of the table top are 29.4 inches, 39.2 inches, and 49 inches long.
She wants to place the table in a corner of a rectangular room.
The table fit snugly in the corner.

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Chapter 7 The Pythagorean Theorem to score better marks in the exam.

Math in Focus Grade 8 Course 3 A Chapter 7 Answer Key The Pythagorean Theorem

Math in Focus Grade 8 Chapter 7 Quick Check Answer Key

Find the square of each number.

Question 1.
3
Answer:
9,

Explanation:
Given number is 3 the square is 3² = 3 X 3 = 9.

Question 2.
\(\frac{1}{4}\)
Answer:
\(\frac{1}{16}\),

Explanation:
Given number is \(\frac{1}{4}\) the sqaure is
(\(\frac{1}{4}\))² = \(\frac{1}{4}\) X \(\frac{1}{4}\) =
\(\frac{1 X 1}{4 X 4}\) = \(\frac{1}{16}\).

Question 3.
-7
Answer:
49,

Explanation:
Given number is -7 the square is (-7)² = -7 X -7 = 49.

Find the square roots of each number.

Question 4.
16
Answer:
4,

Explanation:

Question 5.
64
Answer:
8,

Explanation:

Question 6.
400
Answer:
20,

Explanation:

Find the cube of each number.

Question 7.
\(\frac{1}{2}\)
Answer:
\(\frac{1}{8}\),

Explanation:
Given \(\frac{1}{2}\) the cube is (\(\frac{1}{2}\))³ =
\(\frac{1}{2}\) X \(\frac{1}{2}\) X \(\frac{1}{2}\) =
\(\frac{1 X 1 x 1}{2X 2 X 2}\) =\(\frac{1}{8}\).

Question 8.
7
Answer:
343

Explanation:
Given 7 the cube is (7)³ = 7 X 7 X 7 = 343.

Question 9.
11
Answer:
1331,

Explanation:
Given 11 the cube is (11)³ = 11 X 11 X 11 = 1331.

Find the cube root of each number.

Question 10.
8
Answer:
2

Explanation:

Question 11.
27
Answer:
3

Explanation:

Question 12.
125
Answer:
5

Explanation:

Use graph paper. Plot each pair of points on a coordinate plane. Connect the points to form a line segment and find its length.

Question 13.
(3, 5) and (3, 9)
Answer:
The objective is to plot and connect point (-3, 1) and point(-3, -3) on a coordinate plane, then identify the length of the line that the two points create.

Note that to represent point (-3, 1), point out in which part of the graph does -3 and 1 meet. -3 is 3 units to the left of 0 and 1 is 1 unit up. Likewise, for point (-3, -3), point out in which part of the graph does -3 and -3 meet. The first -3 is 3 units to the left of 0 and the other -3 is 3 units down. Then, let O be the point (-3, 1), and P be the point (-3, -3).

To find the length of the line segment \(\overline{O P}\), get the absolute value of the difference of y-coordinate of point O  to the y-coordinate of P since points O and P have the same x-coordinate which is -3. Then
length of \(\overline{O P}\) = |1 – (-3)|
= |1 + 3|
= 4
Therefore, the length of \(\overline{O P}\) is 4 units.

Question 14.
(3, -6) and (3, -9)
Answer:
The goal of this task is to plot and connect point (1, 2) and point (1, -1) on a coordinate plane, then identify the length of the line that the two points create.

Notice that to show point (1, 2), specify in which part of the graph does 1 and 2 meet. 1 is 1 unit to the right of 0 and 2 is 2 units up. Likewise, for point (1, -1), specify in which part of the graph does 1 and -1 meet 1 is 1 unit to the right of 0 and -1 is 1 unit down. Then, Let Q be the point (1, 2), and R be the point (1, -1).

To find the length of the line segment \(\overline{Q R}\), get the absolute value of the difference of y-coordinate of point Q  to the y-coordinate of R since points Q and R have the same x-coordinate which is 1. Then
length of \(\overline{Q R}\) = |2 – (-1)|
= |2 + 1|
= 3
Therefore, the length of \(\overline{Q R}\) is 3 units.

Question 15.
(-4, 9) and (-8, 9)
Answer:
The target of this task is to plot and connect point (1, -3) and point (5, -3) on a coordinate plane, then identify the length of the line that the two points create.

Observe that to represent point (1, -3), point out in which part of the graph does 1 and -3 meet 1 is 1 unit to the right of 0 and -3 is 3 units down. Likewise, for point (5, -3), point out in which part of the graph does 5 and -3 meet 5 is 5 units to the right of 0 and -3 is 3 units down Then, let S be the point (1, -3), and T be the point (5, -3).

Now, to find the length of the line segment \(\overline{S T}\), get the absolute value of the difference of x-coordinate 1 of point S to the x-coordinate of T since points S and T have the same y-coordinate which is -3. Then
length of \(\overline{S T}\) = |1 – 5|
= |-4|
= 4
Therefore, the length of \(\overline{S T}\) is 4 units.

Question 16.
(-2, 5) and (8, 5)
Answer:
The objective of this task is to plot and connect point (-5, 3) and point (5, 3) on a coordinate plane, then identify the
length of the line that the two points create.

Note that to show point (-5, 3), specify in which part of the graph does -5 and 3 meet -5 is 5 units to the left of 0 and 3 is 3 units up. Likewise, for point (5, 3), specify in which part of the graph does 5 and 3 meet 5 is 5 units to the right of 0 and 3 is 3 units up. Then, let U be the point (-5, 3), and V be the point (5, 3).

Next, to determine the length of the Line segment \(\overline{U V}\), get the absolute value of the difference of x-coordinate of point U to the x-coordinate of V since points U and V have the same y-coordinate 3. Then
length of \(\overline{U V}\) = |-5 – (5)|
= |-5 + -5|
= |-10|
= 10
Therefore, the length of \(\overline{U V}\) is 10 units.

Find the volume of each solid. Use 3.14 as an approximation for π. Round your answers to the nearest tenth if necessary.

Question 17.

Answer:
Volume of cone ≈ 1206.37 cm³ ,

Explanation:

Question 18.

Answer:
The volume of cylinder ≈1206.37 cm³ ,

Question 19.

Answer:
Volume of sphere is ≈33.51 cm³,

Explanation:

Question 20.

Answer:
Volume of triangular prism is 35 cm³ ,

Explanation:
Volume of triangular prism = area of cross-section X length,
5 cm²  × 7 cm = 35 cm³.

Question 21.

Answer:
Volume of Pyramid is 15 cm³,

Explanation:

Practice the problems of Math in Focus Grade 8 Workbook Answer Key Cumulative Review Chapters 5-6 to score better marks in the exam.

Math in Focus Grade 8 Course 3 A Cumulative Review Chapters 5-6 Answer Key

Concepts and Skills

Solve each system of linear equations by making tables of values. Each variable x is a positive integer less than 7. (Lesson 5.1)

Question 1.
4x + 3y = 23
y – 2x = 1
Answer:
Given the linear equations,
4x + 3y = 23
y – 2x = 1
4(y – 2x = 1)
2y – 4x = 2
4x + 3y = 23
-4x + 2y= 2
5y = 25
y = 5
substitute the value of x in the above equation.
(5) – 2x = 1
5 – 2x = 1
-2x = 1 – 5
-2x = -4
x = 2
Thus the value of x is 2 and y is 5

Question 2.
4y + 3x = 19
x + y = 5
Answer:
Given,
4y + 3x = 19
x + y = 5
Rewrite them as
3x + 4y = 19
3x + 3y = 15
–     –          –
0x + y = 4
y = 4
substitute the value of y in the above equation
x + 4 = 5
x = 5 – 4
x = 1

Solve each system of linear equations by using the elimination or substitution method. Explain your choice of method. (Lesson 5.2)

Question 3.
3a – 2b = 1
2a + 3b = 18
Answer:
Given,
3a – 2b = 1—- (×2)
2a + 3b = 18–(×3)
6a – 4b = 2
6a + 6b = 36
–    –          –
0a – 10b = -34
10b = 34
b = 3.4
substitution the value of b in the equation
3a – 2(3.4) = 1
3a – 6.8 = 1
3a = 1 + 6.8
3a = 7.8
a = 2.6
substitution method

Question 4.
0.7x – 1.2y = -11.5
0.5x + 3.5y = 31
Answer:
Given,
0.7x – 1.2y = -11.5
0.5x + 3.5y = 31
5 (0.7x – 1.2y = -11.5)
0.35x – 6y = -57.5
7(0.5x + 3.5y = 31)

0.35x + 24.5y = 217
0.35x – 6y = -57.5
–          +        +
0x + 30.5y = 274.5
30.5y = 274.5
y = 274.5/30.5
y = 9
Now substitute the value of y in the above equation.
0.5x + 3.5(9) = 31
0.5x = 31 – 31.5
0.5x = -0.5
x = -0.5/0.5
x = -1
Substitution method is used to solve the given equations.

Question 5.
\(\frac{1}{4}\)h + \(\frac{2}{3}\)k = 5
\(\frac{3}{4}\)h + k = 6
Answer:
Given,
\(\frac{1}{4}\)h + \(\frac{2}{3}\)k = 5
\(\frac{3}{4}\)h + k = 6
\(\frac{2}{3}\) \(\frac{3}{4}\)h + \(\frac{2}{3}\)k = 6 . \(\frac{2}{3}\)
Now solve both the equations
\(\frac{1}{4}\)h + \(\frac{2}{3}\)k = 5
\(\frac{1}{2}\)h + \(\frac{2}{3}\)k = 4
\(\frac{1}{4}\)h + 0 = 1
h = 1/\(\frac{1}{4}\)
h = 4
Now substitute the value of h in the above equation
\(\frac{3}{4}\)(4) + k = 6
3 + k = 6
k = 6 – 3
k = 3
The substitution method is used to solve the given equations.

Solve each system of linear equations by using the graphical method. Use 1 grid square on both axes to represent 1 unit for the interval from -5 to 10. (Lesson 5.4)

Question 6.
3x + y = 3
4x – 2y = 14
Answer:
Given,
3x + y = 3
4x – 2y = 14
3x + y = 3— × (2)
6x + 2y = 6 —- (eq. 3)
Solving eq. 3 and 2
6x + 2y = 6
4x – 2y = 14
10x = 20
x = 20/10
x = 2
3(2) + y = 3
6 + y = 3
y = 3 – 6
y = -3
3x + y = 3

4x – 2y = 14

Question 7.
2x – y = 3
x + y = 9
Answer:
Given,
2x – y = 3
x + y = 9
3x = 12
x = 4
4 + y = 9
y = 9 – 4
y = 5

x + y = 9

Question 8.
2x + y = 25
3x – 4y = – 1
Answer:
Given,
2x + y = 25— eq. 1
3x – 4y = – 1—- eq. 2
Solve the equations 1 & 2
2x + y = 25 —× 4
8x + 4y = 100—(eq. 3)
3x – 4y = – 1
Solving equations 3 and 2
8x + 4y = 100
3x – 4y = – 1
11x = 99
x = 99/11
x = 9
Substitute the value of 9 in eq. 1
2(9) + y = 25
y = 25 – 18
y = 7

Identify whether each system of linear equations is inconsistent or dependent. Justify your answer. (Lesson 5.5)

Question 9.
3x + 4y = 12
\(\frac{3}{4}\)x + y = 3
Answer:
Given,
3x + 4y = 12
\(\frac{3}{4}\)x + y = 3
3x + 4y = 12
Dependent
After multiplying equation 2 by 4, the equations are 3x + 4y = 12
Thus the equations are equivalent

Question 10.
0.2x + 1.2 = y
x + 8 = 5y
Answer:
Given,
0.2x + 1.2 = y
x + 8 = 5y
0.2x – y = 1.2 — × 5
x – 5y = 6
x – 5y = -8
0
Inconsistent

Question 11.
3x + 2y = \(\frac{1}{3}\)
9x + 6y = 1
Answer:
Given,
3x + 2y = \(\frac{1}{3}\)
9x + 6y = 1
9x + 6y = 1
Dependent
Thus the equations are equivalent

Tell whether the relation in each mapping diagram, table, or graph is a function. Explain. (Lesson 6.1)

Question 12.

Answer:
No, because the output has more than one value.

Question 13.

Answer:
Yes because each input has exactly one output, it is a function.

Question 14.

Answer:
Yes because each input has exactly one output, it is a function.

Question 15.

Answer:
No because, at least one vertical line intersects the graph at more than one point, it is not a function.

Write an algebraic equation for each function. (Lesson 6.2)

Question 16.
A chef makes 100 hot dog buns each morning. In the afternoons, he makes 40 hot dog buns per hour. The total number of hot dog buns he makes each day, y, is a function of the time he takes to make the buns in the afternoons, x hours.
Answer:
40x
Th number of hot dog buns made in the afternoons is the product between number of hours x and the rate of 40 hot dog buns per hour:

y = 100 + 40x
The total number of hot dogs buns per day is the sum between the number of hot dogs buns made in the morning and the number of hot dogs buns made in the afternoon:

Question 17.
Gina walks 2 kilometers from home to a park. She then jogs at an average speed of 7 kilometers per hour. The total distance she traveled, d kilometers, ¡s a function of the time she takes to jog, t hours.
Answer:
Given,
Gina walks 2 kilometers from home to a park. She then jogs at an average speed of 7 kilometers per hour.
The total distance she traveled, d kilometers, is a function of the time she takes to jog, t hours.
d = 2 + 7t

Question 18.

Answer:
The graph being a line, the function is Linear. Its slope-intercept equation S:
y = mx + b
We determine the slope m using the sLope formula and the points (0, 4) and (4, 16):
m = \(\frac{16-4}{4-0}\)
= \(\frac{12}{4}\)
= 3
The graph intersects the y-axis in (0, 4), so the y-intercept is 4:
b = 4
The line’s equation is:
y = 3x + 4

Question 19.

Answer: y = -10x + 40

Tell whether each table, equation, or graph represents a linear function. If so, find the rate of change. Then tell whether the function is increasing or decreasing. (Lesson 6.3)

Question 20.

Answer: Yes, It is increasing

Question 21.

Answer:
No; it is decreasing

Question 22.
3y + 2x = 10
Answer:
No, it is decreasing

Question 23.
V = l³, l > 0
Answer: no; increasing

Question 24.

Answer: Yes, it is decreasing

Question 25.

Answer:
Yes; decreasing

Problem Solving

Solve. Show your work.

Question 26.
A school librarian keeps track of the number of students in the library at any one time, and the number of computers being used. The table shows the data she collected for one day. (Chapter 6)

Draw a mapping diagram to represent the relation between the number of students in the library and the number of computers being used. Is this relation a function? Explain.
Answer:

It is a one to many relation.

Question 27.
Find two numbers whose sum is 60, such that twice the lesser number is equal to half of the greater number. (Chapter 5)
Answer:
Let the two numbers be x and 4x
x + 4x = 60
5x = 60
x = 60/5
x = 12
4x = 4(12) = 48

Question 28.
The diagram shows a parallelogram with side lengths in inches. (Chapter 5)

a) Find the values of a and b.
Answer:
3b – 4 + 2b + 3
5b – 1
b = 1/5 inch.
(3a – b) + (2a + b)
5a

b) Find the perimeter of the parallelogram.
Answer:
perimeter of the parallelogram = 2(a + b)
p = 2 (5b – 1 + 5a)
p = 10a + 10b – 2

Question 29.
Glenn donates $50 to a charity. In addition, he pledges to donate $2 per month beginning this month. The total amount he donates, y dollars, is a function of the number of months he donates, x months. (Chapter 6)
a) Write an algebraic equation for the function.
Answer: y = 50 + 2x

b) Graph the function and draw a line through the points. Use 1 unit on the horizontal axis to represent 1 month for the x interval from 0 to 6, and 1 unit on the vertical axis to represent $2 for the y interval from 50 to 62. Do the coordinates of every point on the line make sense for the function? Explain.
Answer:

No, only whole numbers are meaningful for the input and output. The input values, which are the number of months must be whole numbers. Hence, the corresponding output values of the function are also whole numbers.

c) Describe how the slope and y-intercept of the graph are related to the function.
Answer:
The y-intercept, 50 means that Glenn donated $50 to the charity at first. The slope 2, gives the rate that he donates per month. For every month that passes, the total amount that he donated increases by $2.

Question 30.
In a stationery store, 15 pencils and 20 rulers are sold for $20.50. Jennifer buys 7 pencils and 2 rulers for $5.90. Find the price of each item. (Chapter 5)
Answer:
Let the cost of the pencil be x
Let the cost of rulers be y
15x + 20y = 50
7x + 2y = 5.90—- × 10
70x + 20y = 59—Eq.3
Solving and eq. 3 – 1
70x + 20y = 59
15x + 20y = 50
55x = 9
x = 9/55
x = 0.16
Thus the cost of each pencil is $0.16
7(0.16) + 2y = 5.90
1.12 + 2y = 5.90
2y = 5.90 – 1.12
2y = 4.78
y = 2.39
Thus the cost of the rulers is $2.39

Question 31.
A group of 70 students and teachers visited a theme park. The teachers were charged a regular price of $50 per ticket. A 30% count of the regular ticket price was given to each student. The total ticket price for the whole group cost $2,600. Find the number of students and teachers in the group. (Chapter 5)
Answer:
Let’s note:
t = the number of teachers
s = the number of students
The total number of persons in the group:
t + s = 70   Equation 1
The cost of all tickets:
50t + (1 – 0.30)50s = 2600
50t + 35s = 2600    Equation 2
We write the system:
t + s = 70   Equation 1
50t + 35s = 2600   Equation 2
We use the substitution method
t + s = 70
We express t in terms of s from Equation 1:
t + s – s = 70 – s
t = 70 – s   Equation 3
Substitute Equation 3 in Equation 2 and determine s:
50(70 – s) + 35s = 2600
3500 – 50s + 35s = 2600
3500 – 15s = 2600
3500 – 15s – 3500 = 2600 – 3500
-15s = -900
\(\frac{-15 s}{-15}\) = \(\frac{-900}{-15}\)
s = 60
Substitute s in Equation 1 to determine t:
t = 70 – 60
= 10
The number of students is 60 and the number of teachers is 10.

Question 32.
The fuel tank in Tasha’s car can hold up to 8 gallons of gasoline. She can drive a distance of 40 miles for each galIf gasoline. The total amount of gasoline in her fuel tank, y gallons, is a function of the distance she drives, x miles. (Chapter 6)
a) Give the least possible input value and the corresponding output value. Tell whether the function is linear or nonlinear. Then tell whether the function is increasing or decreasing. Explain.
Answer:
At the initial moment the tank is full, therefore it has 8 gallons. As the car moves, the amount of gasoline decreases by 1 gallon for each 40 miles, therefore it is linear and decreasing. The Least possible input value is 0 (the initial distance). The corresponding output value is 8 gallons.
x = 0 miles
y = 8 gallons

b) Sketch a graph for the function. Identify the y-intercept of the graph.
Answer:
The graph starts at (0; 8) and falls to the right with the slope \(\frac{1}{40}\).
y = mx + b
y = –\(\frac{1}{40}\)x + 8
We graph the function.

The y-intercept is b = 8.

Question 33.
The pressure in two tanks increases at a constant rate of 2 bars per minute. The initial pressure in Tank A is 3 bars. The pressure in Tank B is 14 bars after 3 minutes. (Chapter 5)
a) Write a system of two linear equations for the pressure p in the two tanks in terms of the time t.
Answer:
The pressure in two tanks increases at a constant rate of 2 bars per minute.
The initial pressure in Tank A is 3 bars.
Tank A: p = 2t + 3
The pressure in Tank B is 14 bars after 3 minutes.
Tank B: p = 2t + 8

b) Graph the two equations on a coordinate plane. Use 1 grid square on both axes to represent 1 unit for the interval from 0 to 5.
Answer:
We graph the two functions on a coordinate plane:

c) When will the pressure in both tanks be the same? How do you know?
Answer:
The pressure in both tanks will not be the same.
The two lines are parallel.

Question 34.
Mr. Johannsen wants to compare how fast water evaporates from two inflatable swimming pools, A and B, placed at different locations. The height of the water level in each pool, h inches, is a function of the time it takes for the water to evaporate, t days. (Chapter 6)
Pool A

Pool B
An initial water level of 24 inches where water evaporates at a rate of 0.4 inch per day
a) Write an algebraic equation to represent each function.
Answer:
We are given the function for pool A:

We have:

The rate of change is:
\(\frac{-2.5}{5}\) = -0.5
\(\frac{-2.5}{5}\) = -0.5
\(\frac{-2.5}{5}\) = -0.5
\(\frac{-2.5}{5}\) = -0.5
Because the rate of change for the function is constant the table represents a linear function. Its slope is:
m = -0.5
We determine the y-intercept using the fact that the graph passes through the point (0.25):
b = 25
Substitute m, b to determine the equation:
h = -0.5t + 25
We determine the equation for Pool B, using the y-intercept 24 and the slope -0.4:
h = -0.4t + 24

b) Graph the two functions on the same coordinate grid. Use 1 unit on the horizontal axis to represent 5 days for the t interval from 0 to 20, and 1 unit on the vertical axis to represent 1 inch for the h interval from 15 to 25.
Answer:
We graph the two functions:

c) Use a verbal description to compare the two functions.
Answer:
Both functions are linear and decreasing.

The initial height of the water in Pool A is greater than that of Pool B, but the rate of water evaporation is higher for Pool A. After 10 days the height of the water in Pool A is smaller than that of Pool B.