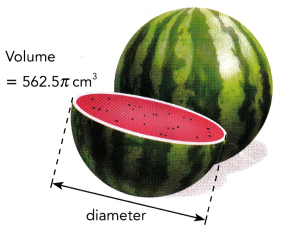
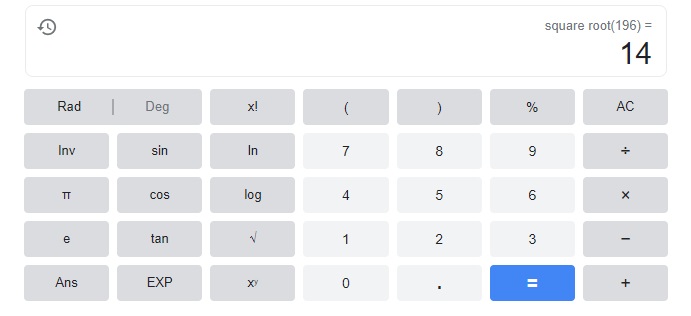
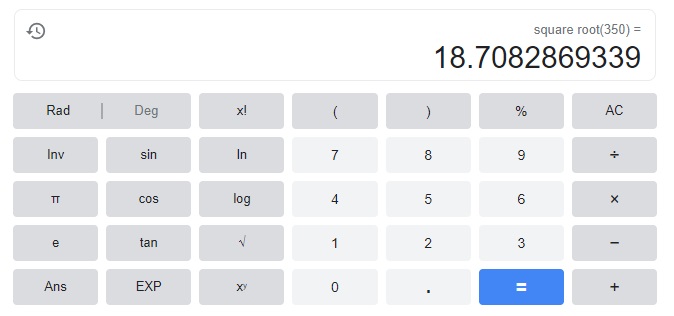
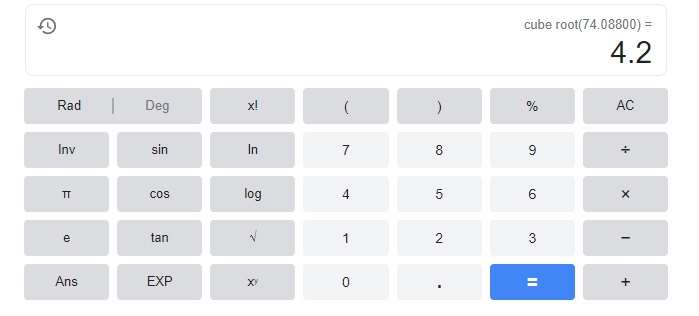
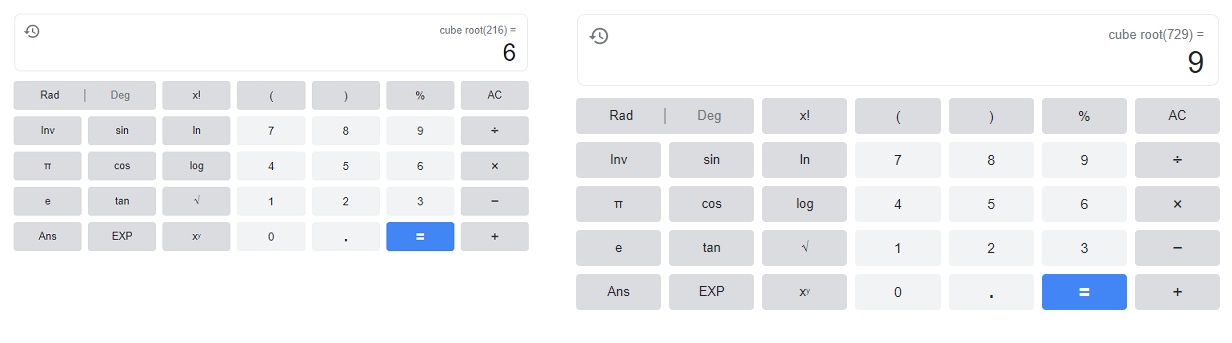
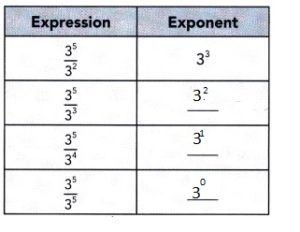
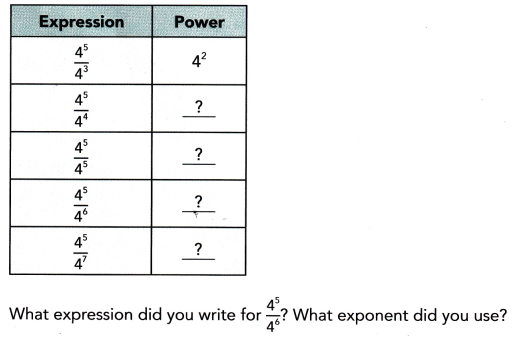
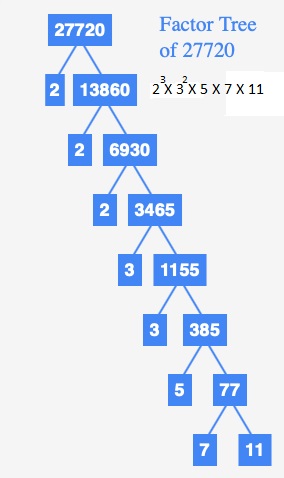
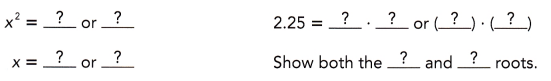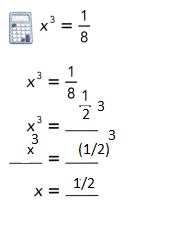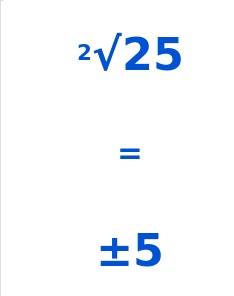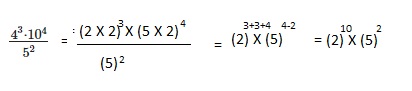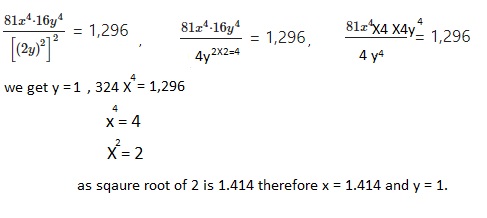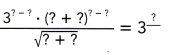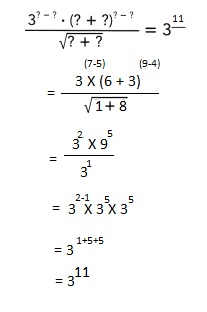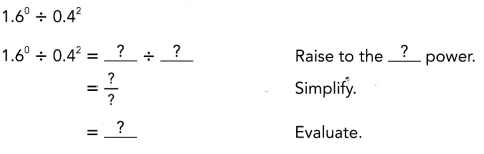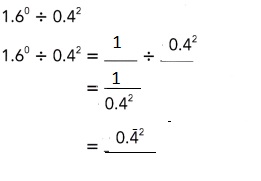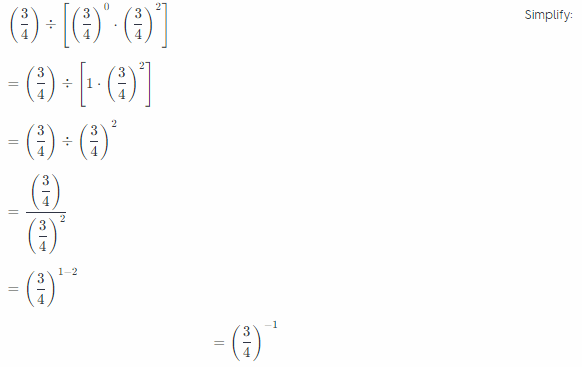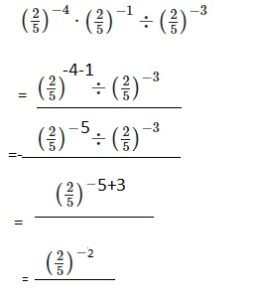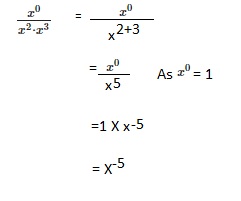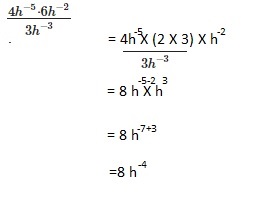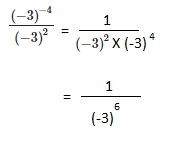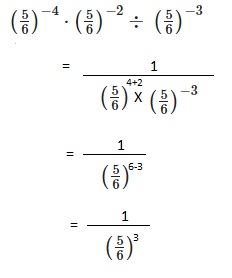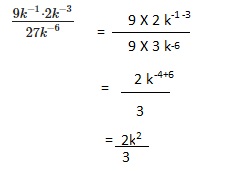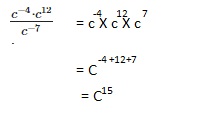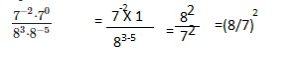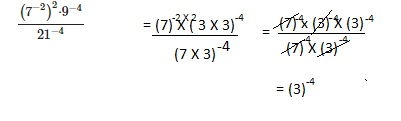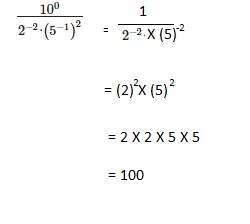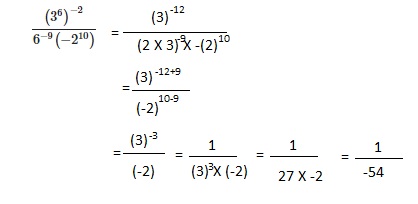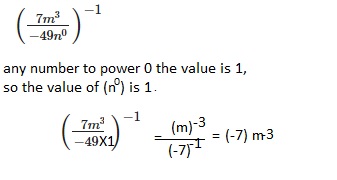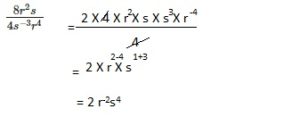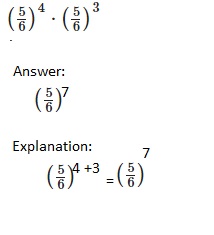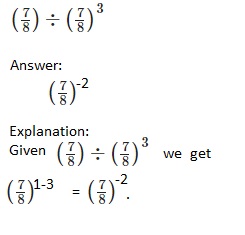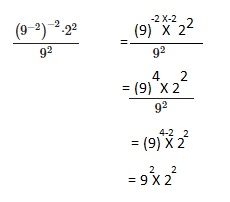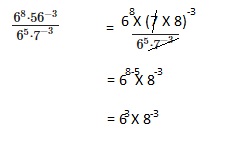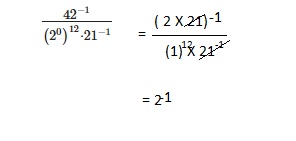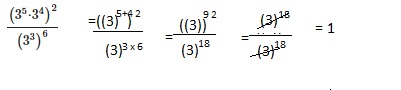Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 1 Lesson 1.1 Exponential Notation to finish your assignments.
Math in Focus Grade 7 Course 3 A Chapter 1 Lesson 1.1 Answer Key Exponential Notation
Math in Focus Grade 8 Chapter 1 Lesson 1.1 Guided Practice Answer Key
Identify the base and exponent in each expression.
Question 1.
23
Answer:
Base is 2 and exponent is 3,
Explanation:
23 = 2 • 2 • 2,
Here base is 2 and exponent is 3.
Question 2.
(-5)4
Answer:
Base is -5 and exponent is 4.
Explanation:
(-5)4 = -5 • -5 • -5 • -5,
Here base is -5 and exponent is 4.
Tell whether each statement is correct. If it is incorrect, state the reason.
Question 3.
63 = 6 • 6 • 6
Answer:
Statement 63 = 6 • 6 • 6 is correct,
Explanation:
Given 63 = 6 • 6 • 6 is correct statement .
Question 4.
5 • 5 = 25
Answer:
Statement 5 • 5 =25 is incorrect,
Explanation:
Given Statement 5 • 5 =25 is incorrect reason is
5 • 5 is 52 not 25.
Write in exponential notation.
Question 5.

Answer:

Explanation:
Given 2 • 2 • 2 • 2 • 2 • 2 so exponential notation is
2 times 6 equals to 26 the base is 2 and the exponent is 6.
Question 6.

Answer:

Explanation:
Given (-4) • (-4) • (-4) so exponential notation is
(-4) times 3 equals to (-4)3 the base is (-4) and the exponent is 3.
Question 7.

Answer:

Explanation:
Given (2/3)y • (2/3)y • (2/3)y • (2/3)y so exponential notation is
(2/3)y times 4 equals to ((2/3)y)4 the base is (2/3)y and the exponent is 4.
Expand and evaluate each expression.
Question 8.

Answer:

Explanation:
Given 34 evaluating as 3 • 3 • 3 • 3, therefore the base 3 is used as a factor of four times
and evaluated as 81.
Question 9.

Answer:

Explanation:
Given (-5)3 evaluating as -5 • -5 • -5, therefore the base -5 is used as a factor of three times
and evaluated as -125.
Question 10.

Answer:
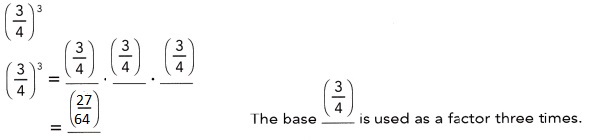
Explanation:
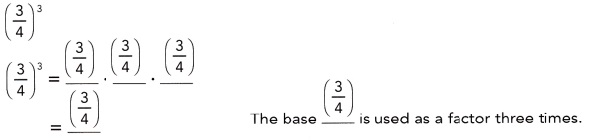
Given (3/4)3 evaluating as (3/4) • (3/4) • (3/4),
therefore the base (3/4) is used as a factor of three times
and evaluated as (27/64).
Write the prime factorization of each number in exponential notation.
Question 11.
625

Answer:

Explanation:
Given to find the prime factorization of 625 in exponential notation,
So 625 has last digit 5 and 5 itself is prime 5 has factors 1 and 5 only,
When divided 625 with 5 we get remainder 125,
In 125 the last digit is 5 again the factors of 5 are 1,5,
Now dividing 125 with 5 we get remainder 25 and also
25 has last digit 5 factors of 25 are 1,5 leaving remainder of 5,
5 itself is prime so the last digit is 5,
So 625 = 5 • 125,
= 5 • 5 • 25,
= 5 • 5 • 5 • 5
= (5)4
Solving 625 using prime factorization method we got
the exponential notation as (5)4.
Question 12.

Answer:

Explanation:
Given to find the prime factorization of 630 in exponential notation,
So 630 has last digit as 0 as 0 is not prime and next
numbers are 21 when divided by 3 we get remainder 70,
Now 70 is divisible by 7 we will get remainder 10,
10 is not a prime number,
so 630 = 3 • 210,
630 = 3 • 3 • 70,
630 = 3 • 3 • 7 • 10,
630 = (3)2 • 7 • 10,
Solving 625 using prime factorization method we got the
exponential notation as (3)2 • 7 • 10.
Solve. Show your work.
Question 13.
Karen ate at a restaurant. One day later, Karen told three friends about the restaurant.
The day after that, each of the friends Karen had told about the restaurant told
three more friends about the restaurant.
If this pattern continued, how many friends were told about
the restaurant five days after Karen ate there?
Answer:
81 friends were told about
the restaurant five days after Karen ate there,
Explanation:
Karen ate at a restaurant, One day later Karen told three friends about the restaurant.
The day after that each of the friends Karen had told about
the restaurant told three more friends about the restaurant.
If this pattern continued friends that were told about
the restaurant five days after Karen ate there at a restaurant
Explanation:
Number of friends who were told about the restaurant five days after
Karen ate there = Initial number of people who knew about the restaurant •
Rate of word-of-mouth referrals over 5 days
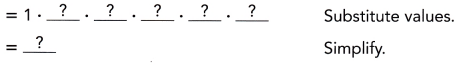
![]() people were told about the restaurant 5 days after Karen ate there.
people were told about the restaurant 5 days after Karen ate there.
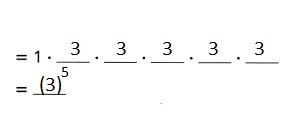
Question 14.
Dewin, at age 25, invests $2,000 in his retirement account.
It will earn 6% interest, compounded yearly.
How much will be in his account when he retires at age 65?
Answer:
A = $21,914.91
A = P + I where
P (principal) = $2,000.00
I (Interest) = $19,914.91
Explanation:

Math in Focus Course 3A Practice 1.1 Answer Key
Identify the base and exponent in each expression.
Question 1.
105
Answer:
Base is 10 and exponent is 5,
Explanation:
(10)5 = 10 • 10 • 10 • 10 • 10,
Here base is 10 and exponent is 5.
Question 2.
(-7)5
Answer:
Base is -7 and exponent is 5.
Explanation:
-7 • -7 • -7 • -7 • -7,
Here base is -7 and exponent is 5.
Question 3.
(0.2)4
Answer:
Base is 0.2 and exponent is 4.
Explanation:
0.2 • 0.2 • 0.2 • 0.2,
Here base is 0.2 and exponent is 4.
Tell whether each statement is correct. If it is incorrect, state the reason.
Question 4.
243 = 2 • 4 • 4 • 4
Answer:
Statement is incorrect,
Explanation:
Statement 243 is incorrect,
As base is 24 and exponent is 3
243 = 24 • 24 • 24 not 243 ≠ 2 • 4 • 4 • 4.
Question 5.
(-2)4 = -2 • -2 • -2 • -2
Answer:
Statement is correct,
Explanation:
Given (-2)4 here base is -2 and exponent is 4,
so (-2)4 = -2 • -2 • -2 • -2.
Question 6.
\(\left(\frac{4}{5}\right)^{5}\) = \(\frac{4}{5}\) • \(\frac{4}{5}\)
• \(\frac{4}{5}\) • \(\frac{4}{5}\) • \(\frac{4}{5}\)
Answer:
Statement is correct,
Explanation:
Given \(\left(\frac{4}{5}\right)^{5}\) here base is
\(\left(\frac{4}{5}\right)^{5}\) and exponent is 5.
Write in exponential notation.
Question 7.
243 = 2 • 4 • 4 • 4
Answer:
Statement is incorrect,
Explanation:
Statement 243 is incorrect,
As base is 24 and exponent is 3
243 = 24 • 24 • 24 not 243 ≠ 2 • 4 • 4 • 4.
Question 8.
(-2)4 = -2 • -2 • -2 • -2
Answer:
Statement is correct,
Explanation:
Given (-2)4 here base is -2 and exponent is 4,
so (-2)4 = -2 • -2 • -2 • -2.
Write in exponential notation.
Question 9.
\(\frac{1}{3}\) • \(\frac{1}{3}\)
Answer:
\(\left(\frac{1}{3}\right)^{2}\),
Explanation:
Given \(\frac{1}{3}\) • \(\frac{1}{3}\) exponential
notation is equal to \(\left(\frac{1}{3}\right)^{2}\).
Question 10.
5 • 5 • 5 • 5
Answer:
5 • 5 • 5 • 5 = 54,
Explanation:
Given 5 • 5 • 5 • 5 exponential notation is equal to 54,
base is 5 and exponent is 4.
Question 11.
(-2) • (-2) • (-2)
Answer:
(-2) • (-2) • (-2) = (-2)3,
Explanation:
Given (-2) • (-2) • (-2) exponential notation is equal to (-2)3
base is (-2) and exponent is 3.
Question 12.
0.12 • 0.12 • 0.12 • 0.12 • 0.12
Answer:
0.12 • 0.12 • 0.12 • 0.12 • 0.12 = (0.12)5,
Explanation:
Given 0.12 • 0.12 • 0.12 • 0.12 • 0.12 exponential notation is equal to (0.12)5
base is 0.12 and exponent is 5.
Question 13.
a • a • a
Answer:
a • a • a = (a)3,
Explanation:
Given a • a • a exponential notation is equal to (a)3
base is a and exponent is 3.
Question 14.
mn • mn • mn • mn • mn
Answer:
mn • mn • mn • mn • mn = (mn)5,
Explanation:
Given mn • mn • mn • mn • mn exponential notation is equal to (mn)5
base is mn and exponent is 5.
Expand and evaluate each expression.
Question 15.
23
Answer:
23 = 2 • 2 • 2,
Explanation:
Given expression 23 upon evaluating we get 2 • 2 • 2.
Question 16.
\(\left(\frac{3}{8}\right)^{4}\)
Answer:
Given expression \(\left(\frac{3}{8}\right)^{4}\) upon evaluting
we get \(\frac{3}{8}\) • \(\frac{3}{8}\)
• \(\frac{3}{8}\) • \(\frac{3}{8}\).
Question 17.
104
Answer:
104 = 10 • 10 • 10 • 10,
Explanation:
Given expression 104 upon evaluating we get 10 • 10 • 10 • 10.
Question 18.
-3.44
Answer:
-3.44 = -3.4 • -3.4 • -3.4 • -3.4,
Explanation:
Given expression -3.44 upon evaluating we get -3.4 • -3.4 • -3.4 • -3.4.
Write the prime factorization of each number ¡n exponential notation.
Question 19.
125
Answer:

Explanation:
Given to find the prime factorization of 125 in exponential notation,
So 125 has last digit 5 and 5 itself is prime 5 has factors 1 and 5 only,
When divided 125 with 5 we get remainder 125,
In 125 the last digit is 5 again the factors of 5 are 1,5,
Now dividing 125 with 5 we get remainder 25 and also
25 has last digit 5 factors of 25 are 1,5 leaving remainder of 5,
5 itself is prime so the last digit is 5,
So 125 = 5 • 25,
= 5 • 5 • 5,
= 5 • 5 • 5
= (5)3
Solving 125 using prime factorization method we got
the exponential notation as (5)3.
Question 20.
4,802
Answer:
4802 We are given the number:
4802 = 2 ∙ 2401 The last digit is 2, therefore the number is divisible by 2:
= 2 ∙ 7 ∙ 343 The last digit doubled 2, subtracted from 240 leads to 238, which is divisible by 7.
Therefore 2401 is divisible by 7:
= 2 ∙ 7 ∙ 7 ∙ 49
The last digit doubled 6, subtracted from 34 leads to 28, which is divisible by 7.
Therefore 343 is divisible by 7:
= 2 • 7 • 7 • 7 • 7 49 is divisible by 7:
4802 = 2 • 74 we simplify
4802 = 2 • 74
Question 21.
91,125
Answer:

Order the following expressions from least to greatest.
Question 22.
-52, (-5)2, and -25
Answer:
Least to greatest -25, (-5)2, and -52,
Explanation:
According to the order (Brackets, Order, Division, Multiplication,
Addition, Subtraction) the following given expressions from
least to greatest -25, (-5)2, and -52.
Question 23.
-43, -34, and (-3)4
Answer:
Least to greatest -34, (-3)4, and -43,
Explanation:
According to the order (Brackets, Order, Division, Multiplication,
Addition, Subtraction) the following given expressions from
least to greatest -43, (-3)4, and -34.
Solve. Show your work.
Question 24.
Barnard’s Star is approximately 10,000,000,000,000,000 meters from the Sun.
Epsilon Eridani is at a distance of about 100,000,000,000,000,000 meters from the Sun.
Write each distance as 10 raised to a power.
Answer:
Barnard’s Star is approximately 1016 meters from the Sun.
Epsilon Eridani is at a distance of about 1017 meters from the Sun,
Explanation:
Given Barnard’s Star ¡s approximately 10,000,000,000,000,000 meters from the Sun.
Epsilon Eridani is at a distance of about 100,000,000,000,000,000 meters from the Sun.
Each distance as 10 raised to power is Barnard’s Star ¡s approximately 1016 meters from the Sun.
Epsilon Eridani is at a distance of about 1017 meters from the Sun.
Question 25.
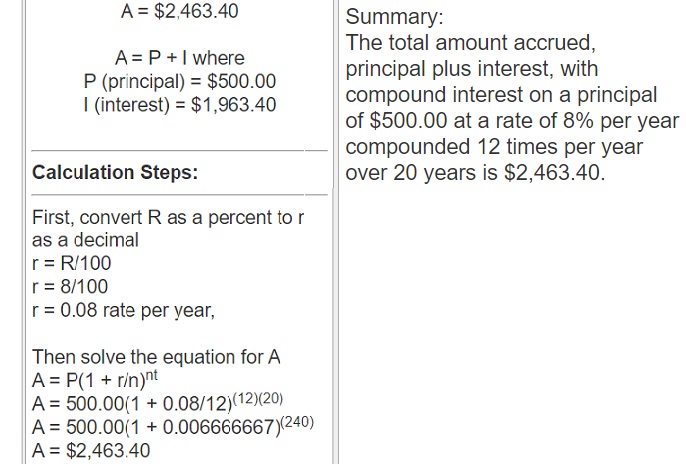
Use the formula A = P(1 + r)n to find out how much $500 would be worth in
20 years if it increases by 8% each year.
Answer:
The amount increases in 20 years is $2,463.40,
Explanation:
Question 26.
Jen cut a piece of paper in half and threw away one half.
She cut the remaining paper in half and threw away one half.
She continued doing this until she had a piece of paper whose area was \(\frac{1}{32}\) as
great as the area of the original piece of paper. How many cuts did she make?
Answer:
Jen made 5 cuts of the original piece of paper,
Explanation:
Given Jen cut a piece of paper in half and threw away one half.
She cut the remaining paper in half and threw away one half.
She continued doing this until she had a piece of paper whose area was
\(\frac{1}{32}\) as great as the area of the original piece of paper.
Number of cuts and many cuts she made are
Since Jen cut a piece of paper in half and threw away one half it becomes
\(\frac{1}{2}\) and \(\frac{1}{2}\) then
She cut the remaining paper in half and threw away one half so
again \(\frac{1}{2}\) and \(\frac{1}{2}\) and so on
till she got \(\frac{1}{32}\) as denominator is 32

So \(\left(\frac{1}{2}\right)^{5}\),
therefore, Jen made 5 cuts of the original piece of paper.







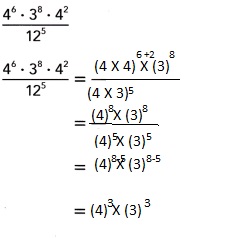
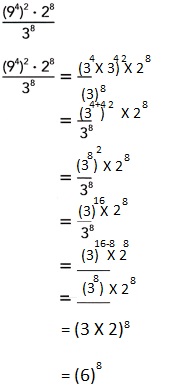
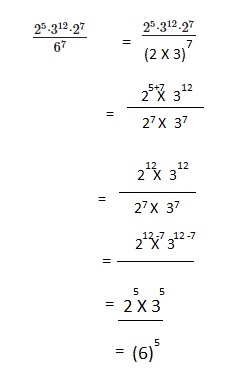
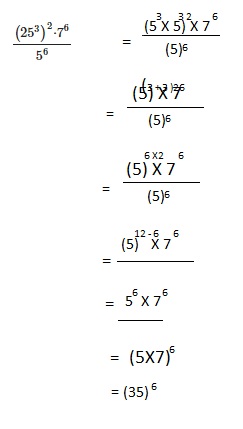
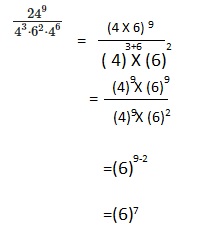
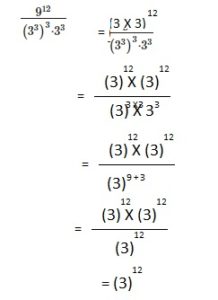
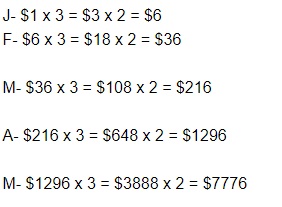
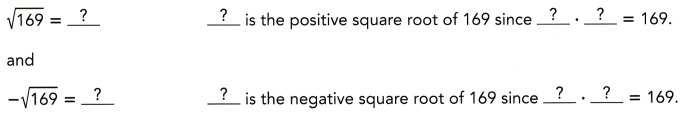
 Explanation:
Explanation: we get for 169 it is 13 and for – 169 it is -13
we get for 169 it is 13 and for – 169 it is -13