Math in Focus

Go through the Math in Focus Grade 1 Workbook Answer Key Chapter 15 Practice 3 Telling Time to the Half Hour to finish your assignments.

Math in Focus Grade 1 Chapter 15 Practice 3 Answer Key Telling Time to the Half Hour

Match the clock to the correct time.

Question 1.

Answer:

Color the clock faces that show the correct time.

Question 2.

Answer:

Question 3.

Answer:

Question 4.

Answer:

Question 5.

Answer:

Question 6.

Answer:

The children go to the zoo with their parents. Look at the pictures. Write the correct times.

Answer: The children go to the zoo with their parents at ten o’clock

Question 7.
They visit the bird and butterfly area at ___________

Answer:

Question 8.
They look at the bears at ___________
Answer: They look at the bears at half past eleven

The pictures show what each child does on a Sunday. Look at the pictures. Then fill in the blanks.

Example

Question

Answer: At half past twelve (12:30) joe’s had her dinner

Question 9.
At ____ Ashley enjoys lunch with her mother.

Answer: At 3 o’clock (03:00) Ashley enjoys lunch with her mother.

Question 10.
Pedro goes to the bowling alley with his Grandpa at ____
Answer:

Question 11.
John walks his dog at
_____.
Answer: John walks his dog at half past five
05:30

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 4 Review Test to score better marks in the exam.

Math in Focus Grade 7 Course 2 A Chapter 4 Review Test Answer Key

Concepts and Skills

Solve each equation.

Question 1.
8x – 7 = 17
Answer:
x = 3

Explanation:
Given, 8x – 7 = 17

Add 7 on both sides.

8x – 7 + 7 = 17 + 7

8x = 24

Divide 8 on both sides.

8x ÷ 8 = 24 ÷ 8

x = 3

Question 2.
4 – 6x = 8
Answer:
x = -(2/3)

Explanation:
Given, 4 – 6x = 8

Subtract 4 on both sides.

4 – 6x – 4 = 8 – 4

-6x = 4

Divide -6 on both sides.

-6x ÷ -6 = 4 ÷ -6

x = -(2/3)

Question 3.
6 – \(\frac{y}{3}\) = 0
Answer:
y = 18

Explanation:
Give, 6 – (y/3) = 0

Subtract 6 on both sides.

6 – (y/3) – 6= 0 – 6

-(y/3) = -6

(y/3) = 6

Multiply 3 on both sides.

(y/3) × 3 = 6 × 3

y = 18

Question 4.
3 – 3.6x = 4.2
Answer:
x = -0.333

Explanation:
Given, 3 – 3.6x = 4.2

Subtract 3 on both sides.

3 – 3.6x – 3  = 4.2 – 3

-3.6x = 1.2

Divide  -3.6 on both sides.

-3.6x ÷ -3.6 = 1.2 ÷ -3.6

x = -0.333

Question 5.
7x – 5 = 3x + 4
Answer:
x = (3/2)

Explanation:
Given, 7x – 5 = 3x + 4

Add 5 on both sides.

7x – 5 + 5 = 3x + 4 + 5

7x = 3x + 9

Subtract 3x on both sides.

7x – 3x = 3x + 9 – 3x

4x  = 9

Divide 4  on both sides.

4x ÷ 4 = 9 ÷ 4

x = (9/4)

x = (3/2)

Question 6.
\(\frac{7}{10}\)y – \(\frac{1}{5}\) = \(\frac{3}{5}\)y + \(\frac{6}{5}\)
Answer:
y = 14

Explanation:
(7/10)y – (1/5) = (3/5)y + (6/5)

Add (1/5) on the both sides.

(7/10)y – (1/5) + (1/5) = (3/5)y + (6/5) + (1/5)

(7/10)y = (3/5)y + (7/5)

Subtract (3/5)y on both sides.

(7/10)y – (3/5)y = (3/5)y +(7/5) – (3/5)y

(7/10)y – ((3×2)/10)y =(7/5)

(7/10)y – (6/10)y =(7/5)

(y/10) = (7/5)

Multiply 1y = 140 on both sides.

(y/10) × 10 = (7/5) × 10

y = 14

Question 7.
3.4y – 5.2 – 3y = 2
Answer:
y = 18

Explanation:
Given, 3.4y – 5.2 – 3y = 2

0.4y – 5.2 = 2

Add 5.2 on both sides.

0.4y – 5.2 + 5.2 = 2 + 5.2

0.4y = 7.2

Divide 0.4 on both sides.

0.4y ÷ 0.4 = 7.2 ÷ 0.4

y = 18

Question 8.
15y – 4(2y – 3) = -2
Answer:
y = -2

Explanation:
Given, 15y – 4(2y – 3) = -2

15y – 8y + 12 = -2

7y + 12 = -2

Subtract 12 on both sides.

7y + 12 – 12= -2 – 12

7y = -14

Divide 7 on both sides.

7y ÷ 7= -14 ÷ 7

y = -2

Question 9.
\(\frac{1}{4}\)(x + 3) + \(\frac{3}{8}\)x = \(\frac{13}{4}\)
Answer:
x = 4

Explanation:
Given, (1/4)(x + 3) + (3/8)x = (13/4)

(1/4)x + (3/4) + (3/8)x = (13/4)

Subtract (3/4) on both sides.

(1/4)x + (3/4) + (3/8)x – (3/4) = (13/4) – (3/4)

(1/4)x + (3/8)x =(13-3)/4

(2 + 3)x/8 = 10/4

(5/8)x = (10/4)

Multiply 8 on both sides.

(5/8)x × 8 = (10/4) × 8

5x = 20

Divide 5 on both sides.

5x ÷ 5 = 20 ÷ 5

x = 4

Question 10.
0.4(x + 0.7) = 0.6x – 4.2
Answer:
x = 22.4

Explanation:
Given, 0.4(x + 0.7) = 0.6x – 4.2

0.4x + 0.28 =0.6x – 4.2

Add 4.2 on the both sides.

0.4x +0.28 + 4.2 =0.6x – 4.2 + 4.2

0.4x + 4.48 = 0.6x

Subtract 0.4x on the both sides.

0.4x + 4.48 – 0.4x = 0.6x – 0.4x

4.48 = 0.2x

0.2x = 4.48

Divide o.2 on both sides.

0.2x ÷ 0.2 = 4.48 ÷ 0.2

x = 22.4

Solve each inequality. Graph each solution set.

Question 11.
4x – 3 > 1
Answer:
x > 1

Explanation:
Given, 4x – 3 > 1

Add 3 on both sides.

4x – 3 + 3 > 1 + 3

4x > 4

x > 1

Question 12.
6 ≤ 1 – 5x
Answer:
-1 ≤ x

Explanation:
Given, 6 ≤ 1 – 5x

Subtract 6 on both sides.

6 – 6 ≤ 1 – 5x – 6

0 ≤ -5x – 5

0 ≤ -5 (x + 1)

Divide -5 on both sides.

0 ÷ -5  ≤ -5 (x + 1) ÷ -5

0 ≤ (x + 1)

-1 ≤ x

Question 13.
\(\frac{2}{3}\) – \(\frac{x}{6}\) ≥ –\(\frac{1}{2}\)
Answer:
x ≤ 1

Explanation:
(2/3) – (x/6) ≥ (1/2)

Subtract (2/3) on both sides.

(2/3) – (x/6) – (2/3) ≥ (1/2) – (2/3)

-(x/6) ≥ (3 – 4/6)

-(x/6) ≥ -(1/6)

Multiply -6 on both sides.

-(x/6) × (-6) ≥ -(1/6) × (-6)

x ≤ 1

Question 14.
-6.9 < 8.1 – 1.5x
Answer:
x > 10

Explanation:
Given, -6.9 < 8.1 – 1.5x

Subtract 8.1 on both sides.

-6.9 – 8.1 < 8.1 – 1.5x – 8.1

-15 < -1.5x

1.5x > 15

Divide 1.5 on both sides.

1.5x ÷ 1.5 > 15 ÷ 1.5

x > 10

Question 15.
9y – 5 ≤ 4y + 15
Answer:
y ≤  4

Explanation:
Given, 9y – 5 ≤ 4y + 15

Subtract 4y on both sides.

9y – 5 – 4y ≤ 4y + 15 – 4y

5y – 5 ≤ 15

Add 5 on both sides.

5y – 5 + 5 ≤ 15 + 5

5y ≤ 20

Divide 5 on both sides.

5y ÷ 5 ≤ 20 ÷ 5

y ≤  4

Question 16.
\(\frac{7}{9}\)x – \(\frac{2}{3}\) > \(\frac{1}{6}\)x + 3
Answer:
x > 6

Explanation:
Given, (7/9)x – (2/3) > (1/6)x + 3

Subtract (1/6)x on both sides.

(7/9)x – (2/3) – (1/6)x > (1/6)x + 3 – (1/6)x

(14 – 3)/18x – (2/3) > 3

11/18x – (2/3) > 3

Add (2/3) on both sides.

11/18x- (2/3) + (2/3) > 3 + (2/3)

11/18x > (11/3)

Divide 11 on both sides.

11/18x ÷ 11 > (11/3) ÷ 11

(1/18)x > (1/3)

Multiply 3 on both sides.

(1/18)x × 3  > (1/3) × 3

(1/6)x > 1

Multiply 6 on both sides.

(1/6)x × 6 > 1 × 6

x > 6

Question 17.
12.9 < 0.3(5.3 – x)
Answer:

Question 18.
3(x + 1) > 5x + 7
Answer:

Question 19.
\(\frac{1}{5}\)(4x – 1) ≥ \(\frac{2}{3}\)x + \(\frac{3}{5}\)
Answer:
x ≥ 6

Explanation:
Given, (1/5)(4x – 1) ≥ (2/3)x + (3/5)

Multiply 5 on both sides

(1/5)(4x – 1) × 5  ≥ ((2/3)x + (3/5)) × 5

(4x – 1) ≥  (10/3)x + 3

Add 1 on both sides.

(4x – 1) + 1 ≥  (10/3)x + 3 + 1

4x ≥  (10/3)x + 4

Subtract (10/3)x on both sides.

4x – (10/3)x ≥  (10/3)x + 4 – (10/3)x

(12 – 10)x/3 ≥ 4

(2/3)x ≥ 4

Multiply 3 on both sides.

(2/3)x × 3 ≥ 4 × 3

2x ≥ 12

Divide 2 on both sides.

2x ÷ 2  ≥ 12 ÷ 2

x ≥ 6

Question 20.
4(3 – 0.1x) ≤ 15 – 0.6x
Answer:
x ≤ 15

Explanation:
Given, 4(3 – 0.1x) ≤ 15 – 0.6x

12 -0.4x ≤ 15 – 0.6x

Subtract 12 on both sides.

12 -0.4x – 12 ≤ 15 – 0.6x – 12

-0.4x ≤ 3 -0.6x

Add 0.6x on both sides.

-0.4x + 0.6x ≤ 3 -0.6x + 0.6x

0.2x ≤ 3

Divide 0.2 on both sides.

0.2x ÷ 0.2 ≤ 3 ÷ 0.2

x ≤ 15

Problem Solving

Write an equation for questions 21 to 25. Solve and show your work.

Question 21.
Aiden wrote a riddle: Five less than \(\frac{1}{5}\) times a number is the same as the sum of the number and \(\frac{1}{3}\). Find the number.
Answer:
x = -(20/3)

Explanation:
Let us consider the number be ‘x’.

(1/5)x – 5 = x + (1/3)

Add 5 on both sides.

(1/5)x – 5 + 5 = x + (1/3) + 5

(1/5)x = x + (16/3)

Subtract (1/5)x on both sides.

(1/5)x – (1/5)x  = x + (16/3) – (1/5)x

0 = (4/5)x + (16/3)

(4/5)x = (- 16/3)

Multiply 5 on both sides.

(4/5)x × 5 = (- 16/3) × 5

4x = – 80/3

Divide 4 on both sides.

4x ÷ 4 = (- 80/3) ÷ 4

x = -(20/3)

Question 22.
Mary is 6 years older than her sister Kelly. The sum of their ages is 48. How old is Kelly?
Answer:
Kelly’s age, x = 21

Explanation:
Let us consider the age of the Kelly be ‘x’.

Age of Mary is  x +6

Sum of their ages = 48

x +x + 6 = 48

2x + 6 = 48

Subtract 6 on both sides.

2x + 6 – 6 = 48 – 6

2x = 42

Divide 2 on  both sides.

2x ÷ 2 = 42 ÷ 2

x = 21

Question 23.
The sum of the page numbers of two facing pages in a book is 145. What are the page numbers?
Answer:
x = 72; x + 1 = 73.

72, 73 are the page numbers.

Explanation:
Let us consider the numbers be x and x+1.

x + x +1 = 145

2x + 1 = 145

Subtract 1 on both sides.

2x + 1 – 1 = 145 – 1

2x = 144

Divide 2 on both sides.

2x ÷ 2 = 144 ÷ 2

x = 72

x + 1 = 73

The sum of numbers of two facing pages in a book = 145

Question 24.
The perimeter of an equilateral triangle is 6\(\frac{3}{4}\) inches. Find the length of each side of the equilateral triangle.
Answer:
Length of each side, a = (3/2)

Explanation:
Given, The perimeter of an equilateral triangle is 6(3/4).

3a = 6(3/4)

Divide 3 on both sides.

3a ÷ 3 = 6(3/4) ÷ 3

a = (6/4)

a = (3/2)

Question 25.
The sum of the interior angle measures of a quadrilateral is 360°. The measure of angle A is three times the measure of angle D. The measure of angle 6 is four times that of angle D. The measure of angle C is 24° more than angle B. Find the measure of each angle of the quadrilateral.

Answer:

Write an inequality for each question. Solve and show your work.

Question 26.
Laura wants the average amount of money she spends each day on her four-day vacation to be no more than $64. On the first three days, she spends $71, $62, and $59. What is the greatest amount of money she can spend on the fourth day?
Answer:
64

Explanation:
Given, Mean = ax=n(Mean)−(a1+...+an)

= 4(64) – (71 + 62 + 59)

= 256 – 192

= 64

Question 27.
Kevin plans to sign up for p hours of training at a culinary school. The school offers two payment options as shown below.

For how many hours of training is Option B less expensive than Option A?
Answer:
x < 20, 20 hours.

Explanation:
Let us consider number of hours be ‘x’.

18x + 0 < 8x +200

18x < 8x + 200

Subtract 8x on both sides.

18x – 8x < 8x + 200 – 8x

10x < 200

Divide 10 on both sides.

10x ÷ 10 < 200 ÷ 10

x < 20

Question 28.
Peter has found a job in a computer store. As shown below, he has two options for how he will be paid. The commission he makes for Option B is based on his weekly sales. For example, if his sales total $1,000 a week, he receives his base salary of $250 plus 8% of $1,000.

Peter is thinking about Option B. What would his weekly sales need to be for him to make at least as much as he would for Option A?
Answer:
The sales should be nearly above 4000$ per week to get more than Option A. Option A is better than Option B.

Explanation:

Let us consider ‘x’ be the number of sales.

600 ≥ 250 + 0.08x

Subtract 250 on both sides.

600 – 250 ≥ 250 + (0.08×1000)x – 250

350 ≥ 80x

Divide 80 on both sides.

350 ÷ 80 ≥ 80x ÷ 80

4 ≥ x

The sales should be nearly above 4000$ per week to get more than Option A.

so Option A is better than Option B.

Question 29.
The school events committee is planning to buy a banner and some helium balloons for graduation night. A store charges them $35 for the banner and $3.50 for each helium balloon. If the committee has at most $125 to spend, how many helium balloons can they buy?
Answer:
x ≤ 25

Explanation:
Let us consider number of helium balloons be ‘x’.

35 + 3.5x ≤ 125

Subtract 35 on both sides.

35 + 3.5x – 35 ≤ 125 – 35

3.5x ÷ 3.5  ≤ 90 ÷ 3.5

Divide 3.5 on both sides.

3.5x ≤ 90

x ≤ 25

Question 30.
The coach of the field hockey team can spend at most $475 on new team uniforms. The coach will order the uniforms online and pay a mailing cost of $6.50. If each uniform costs $29, how many uniforms can the coach order?
Answer:
x ≤ 16, 16 uniforms.

Explanation:
Let us consider the number of uniforms be ‘x’.

6.5 + 29x ≤ 475

Subtract 6.5 on both sides.

6.5 + 29x – 6.5 ≤ 475 – 6.5

29x ≤ 468.5

Divide 29 on both sides.

29x ÷ 29 ≤ 468.5 ÷ 29

x ≤ 16

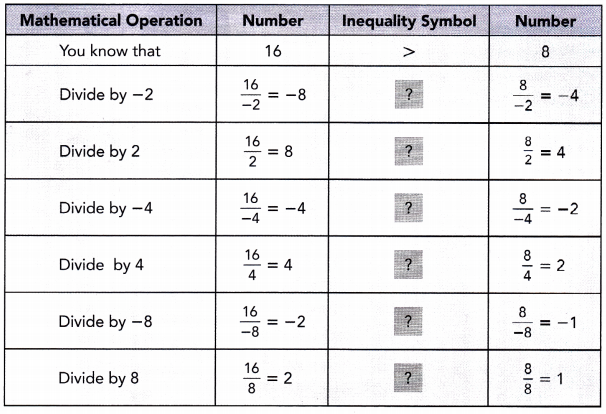
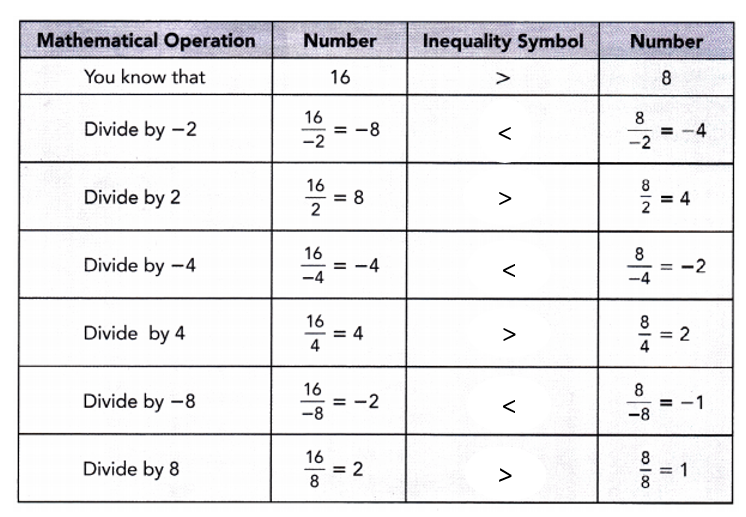
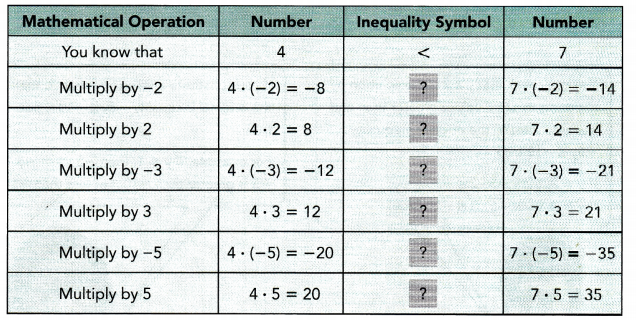
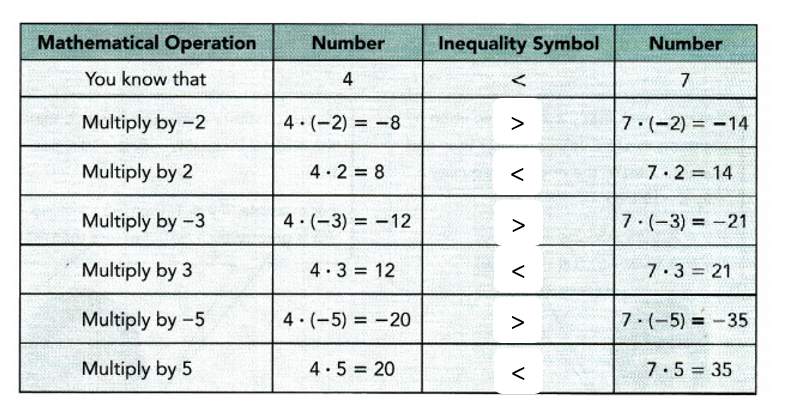
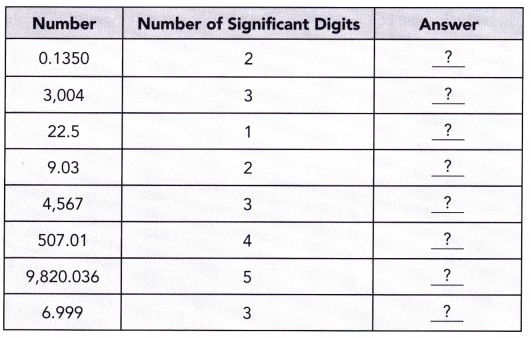
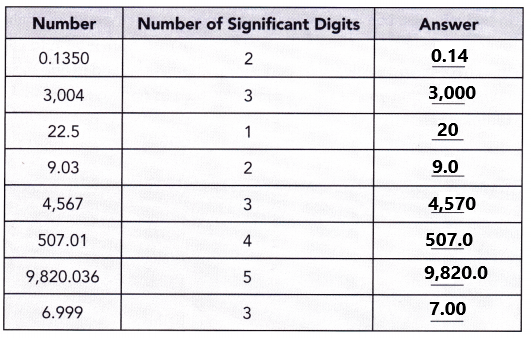
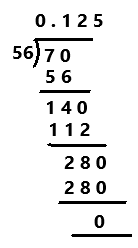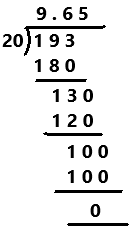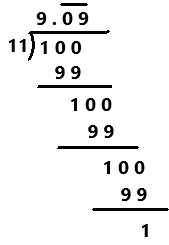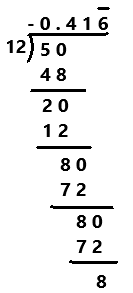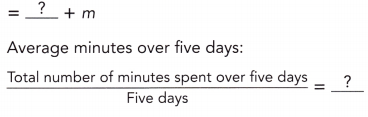Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 4 Lesson 4.5 Real-World Problems: Algebraic Inequalities to score better marks in the exam.

Math in Focus Grade 7 Course 2 A Chapter 4 Lesson 4.5 Answer Key Real-World Problems: Algebraic Inequalities

Math in Focus Grade 7 Chapter 4 Lesson 4.5 Guided Practice Answer Key

Solve.

Question 1.
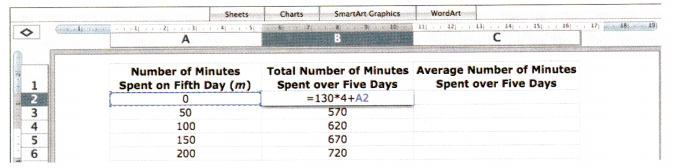
The average of 87, 90, 89, and a fourth number is at least 90. Describe the value of the fourth number.
Answer:
x = 94

Explanation:
The average of the 4 number is 90.

The sum of the numbers = 4 × 90

= 360

Let us  consider the fourth number be ‘x’

The sum of the numbers = 360

87 +90 + 89 + x = 360

266 + x = 360

x = 360 – 266

x = 94

Copy and complete.

Question 2.
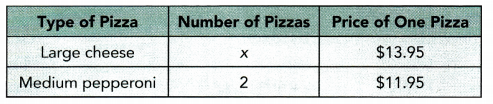
Grace is at the bookstore with $75 to spend. She plans to buy a reference book that costs $18 and some novels that cost $12 each. Find how many novels Grace can buy along with the reference book.
Let x be the number of novels Grace can buy. Define the variable.
+ 12x ≤ Write an inequality.
+ 12x – ≤ – Subtract from both sides.
12x ≤ Simplify.
12 ÷ ≤ ÷ Divide both sides by .
x ≤ Simplify.
Grace can buy at most novels.
Answer:
x ≤ 4.75

Explanation:
The equation is 12x+18 ≤ 75

Subtract 18 on both sides.

12x+18 – 18 ≤ 75 – 18

12x ≤ 57

Divide 12 on both sides.

12x ÷ 12 ≤ 57 ÷ 12

x ≤ 4.75

Question 3.
While Cheryl is on vacation, she wants to put her dog Cocoa in a kennel that offers an obedience class. She calls two boarding kennels to find their fees for their services.

After how many days will Best Dog Kennel be the cheaper option?
Let x be the number of days.

For Best Dog Kennel to be the cheaper option,
80 + > 100 + Write an inequality.
80 + – > 100 + – Subtract from both sides.
80 + > 100 Simplify.
80 + – 80 > 100 – 80 Subtract 80 from both sides.
> 20 Simplify.
÷ > 20 ÷ Divide both sides by .
x > Simplify.
Anytime after days, Best Dog Kennel will be the cheaper option.
Answer:
x > 4

Anytime after 4 days, Best Dog Kennel will be the cheaper option.

Explanation:
Happy dogs kernel costs 80 + 20x

Best dogs kernel costs  100 + 15x

80 + 20x > 100 + 15x

Subtract 15x on both sides.

80 + 20x – 15x > 100 + 15x – 15x

80 + 5x > 100

Subtract 80 on both sides.

80 + 5x – 80 > 100 – 80

5x > 20

Divide 5 on both sides.

5x ÷ 5 > 20 ÷ 5

x > 4

Anytime after 4 days, Best Dog Kennel will be the cheaper option.

Math in Focus Course 2A Practice 4.5 Answer Key

Solve. Show your work.

Question 1.
The perimeter of an equilateral triangle is at most 45 centimeters. Find the possible length of each side.
Answer:
The length of each side, a = 15

Explanation:
Perimeter of an equilateral triangle = 45 cms

Perimeter = 3a = 45cms

3a = 45

Divide 3 on both sides.

3a ÷ 3 = 45 ÷ 3

a = 15

Question 2.
Roger scored 1,800 points in four rounds of a debate competition. His opponent, Sawyer, scored 324 points in the first round, 530 points in the second round, and 619 points in the third round. How many points must Sawyer score in the final round to surpass Roger’s score?
Answer:
Sawyer should score more than 327 in the fourth round to surpass Roger’s score.

Explanation:
Roger scored 1800 points in four rounds.

Sawyer scored 324 + 530 + 619 + x in four rounds

‘x’ be the points sawyer scored in the fourth round.

Sawyer score in the final round to surpass Roger’s score:
324 + 530 + 619 + x > 1800

1473 + x > 1800

Subtract 1473 on both sides.

1473 + x – 1473 > 1800 – 1473

x > 327

Sawyer should score more than 327 in the fourth round.

Question 3.
Ben plans to sign up for a language class that will cost at least $195. His father gives him $75 and he earns $28 from mowing the lawn for his neighbors. Write and solve an inequality to find out how much more money he needs to save before he can sign up for the class.
Answer:
x + 75 + 28 ≥ 195; Ben needs to save, x ≥ 92 

Explanation:
The equation for the above problem is, x + 75 + 28 ≥ 195

x + 103 ≥ 195

Subtract 103 on both sides.

x + 103 -103 ≥ 195 -103

x ≥ 92

Question 4.
In her last basketball game, Casey scored 46 points. In the current game, she has scored 24 points so far. How many more two-point baskets must she make if she wants her total score in her current game to be at least as great as her score in the last game?
Answer:
11 two-point baskets Casey should make to want her total score in the current game to be at least as great as the score in the last game.

Explanation:
Casey scored in the last basket ball game = 46

Casey scored in the current basket ball game = 24

Number of baskets she must make be ‘x’.

Let the equation be 24 + 2x ≥ 46

Subtract 24 on both sides.

24 + 2x – 24 ≥ 46 – 24

2x ≥ 22

Divide 2 on both sides.

2x ÷ 2 ≥ 22 ÷ 2

x ≥ 11

Question 5.
At Middleton Middle School, Marianne must score an average of at least 80 points on 4 tests before she can apply for the scholarship. If she scored 79, 81, and 77 for the first three tests, what must she score on her last test?
Answer:
The score of Marianne in her last test, x = 83

Explanation:
The average Marianne scored in the 4 tests = 80

The three tests scores are 79, 81 and 77

Let us consider the fourth test be ‘x’.

The total score =  the no of tests × average of Marianne scores

= 4 × 80

= 320

79 + 81 + 77 + x = 320

237 + x = 320

Subtract 237 on both sides.

237 + x – 237 = 320 – 237

x = 83

Question 6.
At the movies, a bag of popcorn costs $3.50 and a bottle of mineral water costs $2.75. If Madeline has $18 and bought only 2 bottles of water, how many bags of popcorn can she buy at most?

Answer:
3.5 > x, Madeline can buy more than 3 bags.

Explanation:
Let the number of popcorn bags be  x’

Given,   18 > 2 × 2.75 + 3.50x

18 > 5.5 +3.50x

Subtract 5.5 on both sides.

18 – 5.5 > 5.5 +3.50x – 5.5

12.5 > 3.50x

Divide 3.50 on both sides.

12.5 ÷ 3.50 > 3.50x ÷ 3.50

3.5 > x

Question 7.
Party favors are on sale for $2.40 each. You have $380 to spend on the decorations and gifts, and you have already spent $270 on decorations. Write and solve an inequality to find the number of party favors you can buy.
Answer:
approximately, we can buy 45 party favors.

Explanation:
Money you have to spend on decorations and gifts = 380

Money already spent = 270

Remaining money = Money you have to spend on decorations and gifts – Money already spent

= 380 – 270

=110

Party favors are on sale for $2.40 each.

Number of party favor = 2.40x

‘x’ be the number of party favors.

2.40x < 110

Divide 2.40 on both sides.

2.40x ÷ 2.40 < 110 ÷ 2.40

x < 45.8

So approximately, we can buy 45 party favors.

Question 8.
Charlie wants to join a golf club. He finds two clubs that have fees as shown in the table.

After how many months will Golf Club B be less expensive than Golf Club A?
Answer:
2 months.

Explanation:
Let us consider the number of months be ‘x’

80 + 45x > 110 + 30x

Subtract 30x on both sides.

80 + 45x – 30x > 110 + 30x – 30x

80 + 15x > 110

Subtract 80 on both sides.

80 + 15x – 80 > 110 – 80

15x > 30

Divide 15 on both sides.

15x ÷ 15 > 30 ÷ 15

x > 2

Question 9.
Molly can either take her lunch or buy it at school, It costs $1 .95 to buy lunch. If she wants to spend no more than $30 each month, how many lunches can she buy at most?
Answer:
15 days

Explanation:
Let us consider the number of days ‘x’

1.95x ≤ 30

Divide 1.95 on both sides.

1.95x ÷ 1.95 ≤ 30 ÷ 1.95

x ≤ 15.38

Approximately, 15 days

Question 10.
Tyson always likes to have at least $150 in his savings account. Currently he has $800 in the account. If he withdraws $35 each week, after how many weeks will the amount n his savings account be less than $150?
Answer:
18.5 weeks

Explanation:
Let us consider the number if weeks be ‘x’.

800 + 35x < 150

Subtract 150 on both sides.

800 + 35x – 150 < 150 – 150

35x < – 650

Divide 35 on both sides.

35x ÷ 35 < – 650 ÷ 35

x > 18.5

Question 11.
A cab company charges $0.80 per mile plus $2 for tolls. Melissa has at most $16 to spend on her cab fare. Write and solve an inequality for the maximum distance she can travel if she has at most $16 for cab fare. Can she afford to take a cab from her home to an airport that is 25 miles away?
Answer:
The maximum distance Melissa can travel is 17.5 miles. she cannot afford to travel to airport as 25 miles id greater than 17.5

Explanation:
Given, A cab company charges $0.80 per mile plus $2 for tolls.

Melissa has at most $16 to spend on her cab fare.

Let us consider the miles travelled e ‘x’.

0.8x + 2 ≤ 16

Subtract 2 on both sides.

0.8x + 2 – 2 ≤ 16 – 2

0.8x ≤ 14

Divide 0.8 on both sides.

0.8x ÷ 0.8 ≤ 14 ÷ 0.8

x ≤ 17.5

Question 12.
Nine subtracted from four times a number is less than or equal to fifteen. Write an inequality and solve it.
Answer:
4x-9≤15; x ≤ 6 

Explanation:
Give, Nine subtracted from four times a number is less than or equal to fifteen

i.e; 4x-9≤15

Add 9 on both sides.

4x-9 + 9 ≤ 15 + 9

4x ≤ 24

Divide 4 on both sides.

4x ÷ 4 ≤ 24 ÷ 4

x ≤ 6

Question 13.
Sixteen plus five times a number is more than the number minus eight. Write an inequality and solve it.
Answer:
16 + 5x > x – 8 ; x > -6

Explanation:
Given, Sixteen plus five times a number is more than the number minus eight.

i.e; 16 + 5x > x – 8

Add 8 on both sides.

16 + 5x + 8 > x – 8 + 8

24 + 5x > x

Subtract x on both sides.

24 + 5x – x > x -x

24 +4x > 0

4x > -24

Divide 4 on both sides.

4x ÷ 4 > -24 ÷ 4

x > -6

Question 14.
Math Journal Write a word problem that can be solved using an inequality. Write the inequality that represents your problem. Then solve it.
Answer:
x = 2

Explanation:
Problem: four less than three times a number is equal to the same number.

3x – 4 = x

Subtract x on both sides.

3x – 4 – x = x – x

2x -4 = 0

Add 4 on both sides.

2x -4 + 4 = 0 + 4

2x = 4

Divide 2 on both sides.

2x ÷ 2 = 4 ÷ 2

x = 2

Brain @ Work

A father said, “My son is five times as old as my daughter. My wife is five times as old as my son and I am twice as old as my wife. Grandmother here, who is as old as all of us put together, is celebrating her 81st birthday today.” What ¡s the age of the man’s son?

Answer:

The age of man’s son is 5  years old.

Explanation:
Let us consider daughter’s age be ‘x’.

So, the son’s age is 5x

The wife’s age is “5 times old as son”, so 5 × 5x = 25x

His age is twice of this wife’s age, 2 × 25x = 50x

The sum of all  the ages  = 81

x + 5x + 25x + 50x = 81

81x = 81

Divide 81 on both sides.

81x ÷ 81 = 81 ÷ 81

x = 1

The age of man’s son is 5  years old.

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 4 Lesson 4.4 Solving Algebraic Inequalities to score better marks in the exam.

Math in Focus Grade 7 Course 2 A Chapter 4 Lesson 4.4 Answer Key Solving Algebraic Inequalities

Math in Focus Grade 7 Chapter 4 Lesson 4.4 Guided Practice Answer Key

Copy and complete. Solve each inequality and graph the solution set on a number line.

Question 1.
0.2x + 3 + 0.8x ≤ 4
0.2x + 3 + 0.8x ≤ 4
+ 3 ≤ 4 Add the like terms.
+ 3 ≤ 4 – Subtract from both sides.
≤ Simplify.
Answer:
x ≤ 1

Explanation:
Given, 0.2x + 3 + 0.8x ≤ 4
x + 3 ≤ 4

Subtract 3 on both sides.

x + 3 – 3 ≤ 4 – 3

x ≤ 1

Question 2.
\(\frac{1}{4}\)x – 1 + \(\frac{3}{4}\)x > 0
\(\frac{1}{4}\)x – 1 + \(\frac{3}{4}\)x > 0
– 1 > 0 Add the like terms.
– 1 + > 0 + Add to both sides.
> Simplify.
Answer:
x > 1

Explanation:
Given, (1/4)x – 1 + (3/4)x >0

x – 1 > 0

Add 1 on both sides.

x – 1 + 1 > 0 + 1

x > 1

Solve each inequality and graph the solution set on a number line.

Question 3.
2x + 3 < 13 + x
Answer:
x < 10

Explanation:
Given, 2x + 3 < 13 + x

Subtract x and 3 on both sides.

2x + 3 – x – 3 < 13 + x – x – 3

x < 10

Question 4.
1.5x – 3 ≥ 4 + 0.5x
Answer:
x ≥ 7

Explanation:
Given, 1.5x – 3 ≥ 4 + 0.5x

Subtract 0.5x o both sides.

1.5x – 3 – 0.5x ≥ 4 + 0.5x – 0.5x

1x – 3 ≥ 4

Add 3 on both sides.

x – 3 + 3 ≥ 4 + 3

x ≥ 7

Question 5.
4 + \(\frac{1}{3}\)x > 8 + \(\frac{4}{3}\)x
Answer:
x < 4

Explanation:
Given, 4 + (1/3)x > 8 + (4/3)x

Subtract (1/3)x on both sides.

4 + (1/3)x – (1/3)x > 8 + (4/3)x – (1/3)x

4 > 8 -x

Subtract 8 on both sides.

4 – 8 > 8 -x – 8

-x < -4

x < 4

Hands-On Activity

EXPLORE DIVISION AND MULTIPLICATIVE PROPERTIES OF AN INEQUALITY

Work individually.

Step 1: Use a copy of this table. Complete each using the symbols > or <.

Math Journal What happens to the direction of the inequality symbol when you divide by a positive number? Based on your observation, write a rule for dividing both sides of an inequality by a positive number.

Math Journal What happens to the direction of the inequality symbol when you divide by a negative number? Based on your observation, write a rule for dividing both sides of an inequality by a negative number.

Step 2: Use a copy of this table. Complete each using the symbols > or <.

Math Journal What happens to the direction of the inequality symbol when you multiply by a positive number? Based on your observation, write a rule for multiplying both sides of an inequality by a positive number.

Math Journal What happens to the direction of the inequality symbol when you multiply by a negative number? Based on your observation, write a rule for multiplying both sides of an inequality by a negative number.

Solve each inequality and graph the solution set on a number line.

Question 6.
–\(\frac{1}{5}\)w ≤ 2
Answer:
x ≥ -10

Explanation:
Given, -(1/5)x ≤ 2

Multiply 5 on both sides

-(1/5)x × 5  ≤ 2 × 5

-x ≤ 10

x ≥ -10

Question 7.
-7m > 21
Answer:
m < -3

Explanation:
Given, -7m > 21

Divide 7 on both sides.

-7m ÷ 7 > 21 ÷ 7

-m > 3

m < -3

Question 8.
6 > -0.3y
Answer:
y > -20

Explanation:
Given, 6 > -0.3y

Divide 0.3 on both sides.

6 ÷ 0.3 > -0.3y ÷ 0.3

20 > -y

y > -20

Solve each inequality and graph the solution set on a number line.

Question 9.
4y + 7 < 27
4y + 7 < 27
4y + 7 – < 27 – Subtract from both sides.
4y < Simplify.
4y ÷ < ÷ Divide both sides by .
y < Simplify.
Answer:
y < 5

Explanation:
Given,  4y + 7 < 27

Subtract 7 on  both sides.

4y + 7 – 7 < 27 – 7

4y < 20

Divide 4 on both sides

4y ÷ 4 < 20 ÷ 4

y < 5

Question 10.
-5y – 9 > 21
-5y – 9 > 21
-5y – 9 + ≥ 21 + Add to both sides.
-5y ≥ Simplify.
– 5y ÷ ≤ ÷ Divide both sides by and reverse the inequality symbol.
y ≤ Simplify.
Answer:
y ≤ -6

Explanation:
Given, -5y – 9 > 21

Add 9 on both sides.

-5y – 9 + 9 > 21 + 9

– 5y > 30

Divide 5 on both sides.

– 5y ÷ 5 > 30 ÷ 5

-y < 6

y ≤-6

Question 11.
\(\frac{1}{2}\)x + \(\frac{3}{4}\) ≥ 5
Answer:
x ≥  (17/2)

Explanation:
Given, (1/2)x  + (3/4) ≥ 5

Subtract (3/4) on both sides.

(1/2)x  + (3/4) – (3/4) ≥ 5 – (3/4)

(1/2)x ≥  (20 – 3)/4

(1/2)x ≥  (17/4)

Multiply 2 on both sides

(1/2)x × 2 ≥  (17/4) × 2

x ≥  (17/2)

Question 12.
1.5 – 0.3y > 3.6
Answer:
y < -7

Explanation:
Given, 1.5 – 0.3y > 3.6

Subtract 1.5 on both sides.

1.5 – 0.3y – 1.5 > 3.6 – 1.5

-0.3y > 2.1

Divide -0.3 on both sides

-0.3y ÷ (-0.3) > 2.1 ÷ (-0.3)

y < -7

Question 13.
-8y + 32 ≤ -17 – y
Answer:
y ≥ 7

Explanation:
Given, -8y + 32 ≤ -17 – y

Add y on both sides

-8y + 32 + y ≤ -17 – y + y

-7y +32 ≤ -17

Subtract 32 on both sides.

-7y +32 – 32 ≤ -17 -32

-7y ≤ -49

Divide -7 on both sides.

-7y ÷ (-7) ≤ -49 ÷ (-7)

y ≥ 7

Question 14.
4(2 – y) ≥ 20
Answer:
y ≤ -3

Explanation:
Given, 4(2 – y) ≥ 20

8 – 4y ≥ 20

Subtract  8 on both sides

8 – 4y – 8 ≥ 20 – 8

-4y ≥ 12

Divide -4 on both sides

-4y ÷ (-4) ≥ 12 ÷ (-4)

y ≤ -3

Math in Focus Course 2A Practice 4.4 Answer Key

Solve each inequality using addition and subtraction. Then graph each solution set on a number line.

Question 1.
x + 8 > 14
Answer:
x > 6

Explanation:
Given, x + 8 > 14

Subtract 8 on both sides.

x + 8 – 8 > 14 – 8

x > 6

Question 2.
2 ≥ x – 12
Answer:
x ≤14

Explanation:
Given, 2 ≥ x – 12

Add 12 on both sides.

2 + 12 ≥ x – 12 + 12

14 ≥ x

x ≤14

Question 3.
-7x + 5 + 8x > 3
Answer:
x > -2

Explanation:
Given, -7x + 5 + 8x > 3

x + 5 > 3

Subtract 5 on both sides.

x + 5 – 5 > 3 – 5

x > -2

Question 4.
– 2x – 3 + 3x ≥ 12
Answer:
x ≥ 15

Explanation:
Given, -2x – 3 + 3x ≥ 12

x – 3 ≥ 12

Add 3 on both sides.

x – 3 + 3 ≥ 12 + 3

x ≥ 15

Question 5.
29 < \(\frac{2}{3}\)x + 14 + \(\frac{1}{3}\)x
Answer:
x>15

Explanation:
29 < (2/3)x + 14 + (1/3)x

Subtract 14 on both sides.

29 – 14 < (2/3)x + 14 + (1/3)x – 14

15 < x

x>15

Question 6.
\(\frac{1}{5}\)x + 9 + \(\frac{4}{5}\)x > -11
Answer:
x > -20

Explanation:
Given, (1/5)x + 9 + (4/5)x > -11

Subtract 9 on both sides.

(1/5)x + 9 + (4/5)x – 9 > -11 – 9

x > -20

Question 7.
0.7x + 4 + 0.3x ≤ 10
Answer:
x ≤ 6

Explanation:
Given, 0.7x + 4 + 0.3x ≤ 10

Subtract 4 on both sides.

0.7x + 4 + 0.3x – 4 ≤ 10 – 4

x ≤ 6

Question 8.
0.4x – 6 + 0.6x ≥ 19
Answer:
x ≥ 25

Explanation:
Given , 0.4x – 6 + 0.6x ≥ 19

x – 6 ≥ 19

Add 6 on both sides.

x – 6 + 6 ≥ 19 + 6

x ≥ 25

Question 9.
3x + 4 < 2x + 9
Answer:
x < 5

Explanation:
Given, 3x + 4 < 2x + 9

Subtract 4 on both sides.

3x + 4 – 4 < 2x + 9 – 4

3x < 2x + 5

Subtract 2x on both sides

3x – 2x < 2x + 5 – 2x

x < 5

Question 10.
8 – 4x > 12 – 3x
Answer:
x < -4

Explanation:
Given, 8 – 4x > 12 – 3x

Add 3x on both sides

8 – 4x + 3x > 12 – 3x +3x

8 -x > 12

Subtract 8 on both sides.

8 -x – 8 > 12 – 8

-x > 4

x < -4

Question 11.
\(\frac{2}{3}\)x + 2 ≥ 9 – \(\frac{1}{3}\)x
Answer:
x ≥ 7

Explanation:
Given, (2/3)x + 2 ≥ 9 – (1/3)x

Add (1/3)x on both sides

(2/3)x + 2 + (1/3)x ≥ 9 – (1/3)x + (1/3)x

x +2 ≥ 9

Subtract 2 on both sides.

x +2 – 2 ≥ 9 – 2

x ≥ 7

Question 12.
13 + 1\(\frac{3}{5}\)x ≥ 18 + \(\frac{3}{5}\)x
Answer:
x ≥ 5

Explanation:
Given, 13 + 1(3/5)x ≥ 18 + (3/5)x

13 + (8/5)x ≥ 18 + (3/5)x

Subtract (3/5)x on both sides.

13 + (8/5)x – (3/5)x ≥ 18 + (3/5)x – (3/5)x

13 + x ≥ 18

Subtract 13 on both sides.

13 + x – 13 ≥ 18 – 13

x ≥ 5

Question 13.
1.7x + 5 < 16 + 0.7x
Answer:
x < 11

Explanation:
Given, 1.7x + 5 < 16 + 0.7x

Subtract 0.7x on both sides.

1.7x + 5 – 0.7x < 16 + 0.7x – 0.7x

5  + x < 16

Subtract 5 on both sides.

5  + x – 5 < 16 – 5

x < 11

Question 14.
8.5 – 0.9x > 9.8 – 1.9x
Answer:
x < 1.3

Explanation:
Given, 8.5 – 0.9x > 9.8 – 1.9x

Add 0.9x on both sides.

8.5 – 0.9x + 0.9x > 9.8 – 1.9x + 0.9x

8.5 > 9.8 – x

Subtract 9.8 on both sides.

8.5  – 9.8 > 9.8 – x – 9.8

-1 .3 > – x

x < 1.3

Question 15.
Math Journal Solve the inequality 8 + 2x ≥ 12 and show your work. What value is a solution of 8 + 2x ≥ 12 but is not a solution of 8 + 2x > 12?
Answer:
x ≥ 2, x > 2 Both  the solutions are not same.

Explanation:
Given, two equations: 8 + 2x ≥ 12

8 + 2x > 12

Let us solve 1st equation: 8 + 2x ≥ 12

Subtract 8 on both sides.

8 + 2x – 8 ≥ 12 – 8

2x ≥ 4

Divide 2 on both sides

2x ÷ 2 ≥ 4 ÷ 2

x ≥ 2

Let us solve 2nd equation:
8 + 2x > 12

Subtract 8 on both sides.

8 + 2x – 8 > 12 – 8

2x > 4

Divide 2 on both sides

2x ÷ 2 > 4 ÷ 2

x > 2

Question 16.
Math Journal Eric solved the inequality 6y ≤ -18 as shown below:
6y ≤ -18
6y ÷ 6 ≥ -18 ÷ 6
y ≥ -3
Describe and correct the error that Eric made.
Answer:
y ≥ 3

Explanation:
Given, 6y ≤ -18

Divide 6 on both sides.

6y ÷ 6 ≥ -18 ÷ 6

y ≥ 3

Solve each inequality using division and multiplication. Then graph the solution set on a number line.

Question 17.
3 ≥ -3x
Answer:
x ≥ -1

Explanation:
Given, 3 ≥ -3x

Divide 3 on both sides.

3 ÷ 3 ≥ -3x ÷ 3

1 ≥ -x

x ≥ -1

Question 18.
-4x > 12
Answer:
x < -3

Explanation:
Given, -4x > 12

Divide -4 on both sides.

-4x ÷ – 4 > 12 ÷ – 4

x < -3

Question 19.
–\(\frac{x}{5}\) ≤ 2
Answer:
x ≥ -10

Explanation:
Given, -(x/5) ≤ 2

Multiply -5 on both sides.

-(x/5)  ≤ 2

-(x/5) × -5 ≤ 2 × -5

x ≥ -10

Question 20.
–\(\frac{2}{3}\)x > 8
Answer:
x < -12

Explanation:
Given, -(2/3)x > 8

Multiply 3 on both sides.

-(2/3)x × 3 > 8 × 3

-2x > 24

Divide -2 on both sides.

-2x ÷ -2 > 24 ÷ -2

x < -12

Question 21.
-0.2x ≥ 6
Answer:
x ≤ -30

Explanation:
Given, -0.2x ≥ 6

Divide -0.2 on both sides.

-0.2x ÷ -0.2 ≥ 6 ÷ -0.2

x ≤ -30

Question 22.
9 > -0.5x
Answer:
x > – 18

Explanation:
Given, 9 > -0.5x

Divide – 0.5 on both sides.

9 ÷ -0.5 > -0.5x ÷ -0.5

-18 >x

x > – 18

Solve each inequality using the four operations. Then graph each solution set on a number line.

Question 23.
7y – 3 > 11
Answer:
y > 2

Explanation:
Given, 7y – 3 > 11

Add 3 on both sides.

7y – 3 + 3 > 11 + 3

7y > 14

Divide 7 on both sides.

7y ÷ 7 > 14 ÷ 7

y > 2

Question 24.
-3a + 5 < -7
Answer:
a > 4

Explanation:
Given, -3a + 5 < -7

Subtract 5 on both sides.

-3a + 5 – 5 < -7 – 5

-3a < -12

Divide -3 on both sides.

-3a ÷ -3 < -12 ÷ -3

a > 4

Question 25.
\(\frac{x}{4}\) + \(\frac{3}{16}\) ≥ 1
Answer:
x ≥ (13/4)

Explanation:
(x/4) + (3/16) ≥ 1

multiply 4 on both sides.

((x/4) + (3/16) ) ×  4 ≥ 1 ×  4

x + (3/4) ≥ 4

Subtract (3/4) on both sides.

x + (3/4) – (3/4) ≥ 4 –  (3/4)

x ≥ (13/4)

Question 26.
\(\frac{3}{5}\)a – \(\frac{4}{5}\) < \(\frac{7}{10}\)
Answer:
a < (5/2)

Explanation:
Given, (3/5)a – (4/5) < (7/10)

Add (4/5) on both sides.

(3/5)a – (4/5) + (4/5) < (7/10) + (4/5)

(3/5)a < ((7+(4 × 2))/10)

(3/5)a < (7+8)/10

(3/5)a < 15/10

Divide 3 on both sides.

(3/5)a ÷ 3 < 15/10 ÷ 3

(a/5) < (5/10)

(a/5) < (1/2)

Multiply 5 on both sides.

(a/5) × 5 < (1/2) × 5

a < (5/2)

Question 27.

7 – 0.3x > 4
Answer:
x < 10

Explanation:
Given, 7 – 0.3x > 4

Subtract 7 on both sides.

7 – 0.3x – 7 > 4 – 7

-0.3x > -3

Divide -0.3 on both sides.

-0.3x ÷ -0.3 > -3 ÷ -0.3

x < 10

Question 28.
2.4y + 5 < 29
Answer:
y < 10

Explanation:
Given, 2.4y + 5 < 29

Subtract 5 on both sides.

2.4y + 5 – 5 < 29 – 5

2.4y < 24

Divide 2.4 on both sidea.

2.4y ÷ 2.4 < 24 ÷ 2.4

y < 10

Question 29.
5x + 3 < 7 + 7x
Answer:
x > -2

Explanation:
Given, 5x + 3 < 7 + 7x

Subtract 3 on both sides.

5x + 3 – 3 < 7 + 7x – 3

5x < 4 + 7x

subtract 5x on both sides.

5x -5x < 4 + 7x – 5x

0 < 4 + 2x

-4 < 2x

2x > -4

Divide 2 on both sides.

2x ÷ 2 > -4 ÷ 2

x > -2

Question 30.
11 – 7x ≤ 20 – 8x
Answer:
x ≤ 9

Explanation:
Given, 11 – 7x ≤ 20 – 8x

Subtract 11 on both sides.

11 – 7x – 11 ≤ 20 – 8x – 11

-7x ≤ 9 – 8x

8x – 7x ≤ 9

x ≤ 9

Question 31.
\(\frac{4}{3}\) – \(\frac{5}{6}\)x ≥ –\(\frac{1}{6}\) – \(\frac{2}{3}\)x
Answer:
x ≤ 7

Explanation:
Given, (4/3) – (5/6)x ≥ -(1/6) – (2/3)x

Add (2/3)x on both sides.

(4/3) – (5/6)x + (2/3)x ≥ -(1/6) – (2/3)x + (2/3)x

(4/3) – ((5x – 4x)/6) ≥ -(1/6)

(4/3) -(x/6) ≥ -(1/6)

Add (1/6) on both sides.

(4/3) -(x/6) + (1/6) ≥ -(1/6) + (1/6)

((6 + 1)/6) – x/6 ≥  0

(7/6) – x/6 ≥  0

7 – x ≥  0

7 ≥  x

x ≤ 7

Question 32.
\(\frac{2}{5}\)x + 4 ≤ \(\frac{7}{10}\)x – 8
Answer:
x ≥ 40

Explanation:
Given, (2/5)x + 4 ≤ (7/10)x – 8

Subtract 4 on both sides.

(2/5)x + 4 – 4 ≤ (7/10)x – 8 – 4

(2/5)x ≤ (7/10)x – 12

12 ≤ (7/10)x  – (2/5)x

12 ≤  (7 – 4)x/10

12 ≤ 3x/10

Multiply 10 on both sides.

12 × 10 ≤ 3x/10 × 10

120 ≤ 3x

Divide 3 on both sides.

120 ÷ 3 ≤ 3x ÷ 3

40 ≤ x

x ≥ 40

Question 33.
5.4x + 4.2 – 3.8x > 9
Answer:
x > 3

Explanation:
Given, 5.4x + 4.2 – 3.8x > 9

1.6x + 4.2 > 9

Subtract 4.2 on both sides.

1.6x + 4.2 – 4.2 > 9 – 4.2

1.6x > 4.8

Divide 1.6 on both sides.

1.6x > 4.8

1.6x ÷ 1.6 > 4.8 ÷ 1.6

x > 3

Question 34.
6.6 + 1.3x – 5.2x ≤ 14
Answer:

Explanation:
Given, 6.6 + 1.3x – 5.2x ≤ 14

Subtract 6.6 on both sides.

6.6 + 1.3x – 5.2x – 6.6 ≤ 14 – 6.6

-3.9x ≤ 7.4

Divide -3.9 on both sides.

-3.9x ÷ -3.9 ≤ 7.4 ÷ -3.9

x ≥ -(74/39)

Solve each inequality with parentheses using the four operations.

Question 35.
3(y + 2) ≤ 18
Answer:
y ≤ 4

Explanation:
Given, 3(y + 2) ≤ 18
Divide 3 on the both sides.

3(y + 2) ÷ 3 ≤ 18 ÷ 3

(y + 2) ≤ 6

Subtract 2 on both sides.

y + 2 – 2 ≤ 6 – 2

y ≤ 4

Question 36.
8(y – 1) > 24
Answer:
y > 4

Explanation:
Given, 8(y – 1) > 24

Divide 8 on both sides.

8(y – 1) ÷ 8 > 24 ÷ 8

y – 1 > 3

Add 1 on both sides.

y – 1 + 1 > 3 + 1

y > 4

Question 37.
\(\frac{1}{2}\)(a + 1) ≤ 4
Answer:
a ≤ 7

Explanation:
Given, (1/2) (a + 1) ≤ 4

Multiply 2 on both sides.

(1/2) (a + 1) × 2 ≤ 4 × 2

a +1 ≤ 8

Subtract 1 on both sides.

a +1 -1 ≤ 8 – 1

a ≤ 7

Question 38.
\(\frac{2}{3}\)(3 – a) < 3
Answer:
a > -(3/2)

Explanation:
Given, (2/3)(3 – a) < 3

Divide (2/3) on both sides.

(2/3)(3 – a) ÷ (2/3) < 3 ÷ (2/3)

(3 – a) < (9/2)

Subtract  3 on both sides.

3 – a – 3 < (9/2) – 3

-a  < (9-6)/2

a > -(3/2)

Question 39.
1.3(2 – x) > 3.9
Answer:
x < -1

Explanation:
Given, 1.3(2 – x) > 3.9

Divide 1.3 on both sides.

1.3(2 – x) ÷ 1.3 > 3.9 ÷ 1.3

2 – x > 3

Subtract 2 on both sides.

2 – x – 2 > 3 – 2

-x > 1

x < -1

Question 40.
3.6(5x – 1) < 5.4
Answer:
x < (1/2)

Explanation:
Given, 3.6(5x – 1) < 5.4

Divide 3.6 on both sides.

3.6(5x – 1) ÷ 3.6 < 5.4 ÷ 3.6

5x -1 < 1.5

Add 1 on both sides.

5x -1 + 1 < 1.5 + 1

5x < 2.5

Divide 5 on both sides.

5x ÷ 5 < 2.5 ÷ 5

x < (1/2)

Question 41.
4 + 2(1 – 3y) < 36
Answer:
y > -5

Explanation:
Given, 4 + 2(1 – 3y) < 36

Subtract 4 on both sides.

4 + 2(1 – 3y) – 4 < 36 – 4

2(1 – 3y) < 32

Divide 2 on both sides.

2(1 – 3y) ÷ 2 < 32 ÷ 2

1 – 3y < 16

Subtract 1 on both sides.

1 – 3y – 1 < 16 – 1

-3y < 15

Divide -3 on both sides.

-3y ÷ -3 < 15 ÷ -3

y > -5

Question 42.
2(3 – x) > 5x – 1
Answer:
x < 1

Explanation:
Given, 2(3 – x) > 5x – 1

6 – 2x > 5x – 1

Add 1 on both sides.

6 – 2x + 1 > 5x – 1 + 1

7 -2x > 5x

Add 2x on both sides.

7 -2x + 2x > 5x + 2x

7 > 7x

Divide 7 on both sides.

7 ÷ 7 > 7x ÷ 7

1 > x

x < 1

Question 43.
\(\frac{5}{9}\)(x + 1) ≥ \(\frac{2}{3}\)
Answer:
x ≥ (1/5)

Explanation:
Given, (5/9)(x + 1) ≥ (2/3)

Multiply 9 on both sides.

(5/9)(x + 1) × 9 ≥ (2/3) × 9

5 (x + 1) ≥  2 × 3

5 (x + 1) ≥ 6

Divide 5 on both sides.

5 (x + 1) ÷ 5  ≥ 6 ÷ 5

x + 1 ≥ (6/5)

Subtract 1 on both sides.

x + 1 – 1 ≥ (6/5) – 1

x ≥ (6-5)/5

x ≥ (1/5)

Question 44.
\(\frac{2}{3}\)(1 – 3x) > \(\frac{1}{6}\)
Answer:
x < (1/4)

Explanation:
Given,  (2/3) (1 – 3x) > (1/6)

Multiply 3 on both sides.

(2/3) (1 – 3x) × 3 > (1/6) × 3

2 (1 – 3x) > (1/2)

Divide 2 on both sides.

2 (1 – 3x) ÷ 2 > (1/2) ÷ 2

1 – 3x > (1/4)

Subtract 1 on both sides.

1 – 3x – 1 > (1/4) – 1

-3x > -(3/4)

Divide  -3 on both sides.

-3x ÷ -3 > -(3/4) ÷ -3

x < (1/4)

Question 45.
1.7 + 0.2(1 – x) ≥ 2.7
Answer:
x ≤ -4

Explanation:
Given, 1.7 + 0.2(1 – x) ≥ 2.7

1.7 + 0.2 -0.2x ≥ 2.7

1.9 – 0.2x ≥ 2.7

Subtract 1.9 on both sides.

1.9 – 0.2x – 1.9 ≥ 2.7 – 1.9

-0.2x ≥ 0.8

Divide -0.2 on both sides.

-0.2x ÷ -0.2 ≥ 0.8 ÷ -0.2

x ≤ -4

Question 46.
2.5(3 – 2x) + 1 ≥ 29
Answer:
x ≤ 4.1

Explanation:
Given, 2.5(3 – 2x) + 1 ≥ 29

7.5 – 5x + 1 ≥ 29

8.5 -5x ≥ 29

Subtract 8.5 on both sides.

8.5 -5x – 8.5 ≥ 29 – 8.5

-5x ≥ 20.5

Divide -5 on both sides.

-5x ÷ -5  ≥ 20.5 ÷ -5

x ≤ 4.1

Question 47.
Math Journal Compare solving the inequality -5(x + 6) < 10 with solving the equation -5(x + 6) = 10. Describe the similarities and differences between solving the inequality and solving the equation. Explain how the solution set of the inequality -5(x + 6) < 10 is different from the solution of the equation -5(x + 6) = 10.
Answer:
The solution of the equation -5(x + 6) < 10 is  x > -8, which represents the number x can be any number greater than -8.

The solution of the equation -5(x + 6) = 10 is x = -8, here the number x will be only -8 not any other number.

Explanation:
Given two equations are, -5(x + 6) < 10 and  -5(x + 6) = 10

Let us consider -5(x + 6) < 10

Divide -5 on both sides.

-5(x + 6) ÷ -5 < 10 ÷ -5

(x + 6) > -2

Subtract 6 on both sides.

x + 6 – 6 > -2 – 6

x > -8

Let us consider the second equation -5(x + 6) = 10

Divide -5 on both sides.

-5(x + 6) ÷ -5 = 10 ÷ -5

(x + 6) = -2

Subtract 6 on both sides.

x + 6 – 6 = -2 – 6

x = -8

Solve each inequality using the four operations.

Question 48.
10 – 3(4a – 3) < 2(3a – 4) – 9.2
Answer:
a > 2.01

Explanation:
Given, 10 – 3(4a – 3) < 2(3a – 4) – 9.2

10 – 12a + 9 < 6a – 8 – 9.2

19 – 12a < 6a – 17.2

Subtract  6a on both sides.

19 – 12a – 6a < 6a – 17.2 – 6a

19 – 18a < -17.2

Subtract 19 on both sides.

19 – 18a – 19 < -17.2 – 19

-18a <-36.2

Divide -18 on both sides.

-18a ÷ -18 <-36.2 ÷ -18

a > 2.01

Question 49.

7(2a – 3) ≤ 5 – 2(3a – 1)
Answer:
a ≤  (7/5)

Explanation:
Given, 7(2a – 3) ≤ 5 – 2(3a – 1)

14a – 21 ≤ 5 – 6a + 2

14a -21 ≤ 7 – 6a

Subtract 7 on both sides.

14a -21 – 7 ≤ 7 – 6a – 7

14a -28 ≤ -6a

Add 6a on both sides.

14a -28 + 6a ≤ -6a + 6a

20a ≤ 28

Divide 20 on both sides.

20a ÷ 20 ≤ 28 ÷ 20

a ≤  (7/5)

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 4 Lesson 4.3 Real-World Problems: Algebraic Equations to score better marks in the exam.

Math in Focus Grade 7 Course 2 A Chapter 4 Lesson 4.3 Answer Key Real-World Problems: Algebraic Equations

Math in Focus Grade 7 Chapter 4 Lesson 4.3 Guided Practice Answer Key

Solve. Copy and complete.

Question 1.
Mark wrote a riddle: A negative number is \(\frac{2}{5}\) of another negative number. If the sum of the two negative numbers is -35, find the two negative numbers.
Method 1
Use bar models.

The two negative numbers are and .

Method 2
Use algebraic reasoning.
Let one of the numbers be x.
Then the other number is \(\frac{2}{5}\)x.

+ = -35 Write an equation.
x = -35 Add the like terms.
x ÷ = ÷ Divide both sides by
x = Simplify.
The other number: \(\frac{2}{5}\)x = \(\frac{2}{5}\) ∙ Evaluate \(\frac{2}{5}\)x when x = .
=
The two negative numbers are and .
Answer:
x = -25, (2/5)x = -10

Explanation:
Let one of the numbers be x.
Then the other number is (2/5)x.

x + (2/5)x = -35

(5x + 2x)/5 = -35

7x/5 = -35

Divide both sides by 7

7x/5 ÷ 7 = -(35) ÷ 7

(x/5) = -5

Multiply both sides by 5

(x/5) × 5 = -5 × 5

x = -25

(2/5)x = (2/5) × (-25)

= 2 × -5

= -10

Solve.

Question 2.
At an auditorium, tickets are sold for “circle seats” and “row seats.” There are 220 circle seats, and the rest of the seats are row seats. Each circle seat ticket costs $100 and each row seat ticket costs $60.
a) Write an expression for the total amount collected from the sale of all the seats at the auditorium.
Answer:
100(220) + 60(y – 220) = x

Explanation:
Let us consider the amount collected from the sale be ‘x’

Number of seats be ‘y’

Number of circle seats =220

Number of row seats = y – 220

Cost of each circle seat = $100

Cost of each row seat = $60

100(220) + 60(y – 220) = x

b) The total amount collected when all the tickets are sold is $68,800. How many row seat tickets are sold?
Answer:
x = 780

Explanation:
Number of row tickets be ‘x’

The total amount collected when all the tickets are sold = $68,800

With the above given details

100(220) + 60(x) = 68800

22000 + 60x =68800

subtract 22000 on both sides.

22000 + 60x – 22000 =68800 – 22000

60x = 46800

Divide 6 on both sides.

60x ÷ 60 = 46800 ÷ 60

x = 780

Copy and complete each with a value and each with +, -, ×, or ÷.

Question 3.
James has 16 more game cards than Fay. If they have 48 game cards altogether, find the number of game cards James has.

Let the number of cards that Fay has be x.
Then the number of cards that James has is x 16.
Because they have 48 cards altogether,
x (x 16) =
x 16 –
x 16 =
x =
x =
x =
Number of cards that James has:
x 16 16
=
James has game cards.
Answer:
James has 32 game cards

Explanation:
Let the number of cards that Fay has be x.

Then the number of cards that James has is x + 16

Because they have 48 cards altogether,

x + x+ 16 = 48

2x + 16 = 48

Subtract 16 on both sides.

2x + 16 – 16 = 48 -16

2x = 32

Divide 2 on both sides

2x ÷ 2 = 32 ÷ 2

x = 16

number of cards that Fay, x = 16

the number of game cards James has x + 16 = 16 + 16

 

Math in Focus Course 2A Practice 4.3 Answer Key

Solve. Show your work.

Question 1.
Two sections of a garden are shaped like identical isosceles triangles. The base of each triangle is 50 feet, and the other two sides are each x feet long. If the combined perimeter of both gardens is 242 feet, find the value of x.

Answer:
a = 35.5

Explanation:
Let us consider the sides be x

The perimeter of both the gardens = 242

2 × garden areas = 242

one garden are perimeter = 242 ÷ 2

one garden are perimeter = 121

Perimeter of a isosceles triangle = 2a +b

b =50

2a + 50 =121

Subtract 50 on both sides.

2a +50 – 50= 121 -50

2a = 71

Divide 2 on both sides

2a ÷ 2 = 71 ÷ 2

a = 35.5

Question 2.
Richard has a rectangular plot of land that is 525 feet long and y feet wide. He decides to build a fence around the plot. If the perimeter of the plot is 1,504 feet, find the value of y.
Answer:
y = 227

Explanation:
Given, perimeter of the plot = 1504

Length of the plot, l = 525

Breadth of the plot, b = y

Perimeter of the plot = 2(l + b)

1504 = 2 (525 + y)

Divide 2 on the both sides

1504 ÷ 2 = 2 (525 + y)÷ 2

752 = 525 + y

Subtract 525 on both sides.

752 – 525 = 525 + y -525

y = 227

Question 3.
The diagram shows an artificial lake. When Amanda jogged twice around the lake, she jogged a distance of 2,700 meters. Find the value of x.

Answer:
x = 120

Explanation:

As Amanda jogged twice around the lake.

2(x + 140 + x + x+ 250+x +x + 3x) = 2700

2 (8x + 390) = 2700

Divide 2 on both sides

2 (8x + 390) ÷ 2 = 2700 ÷ 2

8x + 390 = 1350

Subtract 390 on both sides.

8x + 390 – 390 = 1350 -390

8x = 960

Divide 8 on both sides

8x ÷ 8= 960 ÷ 8

x = 120

Question 4.
Olivia wants to trim a lampshade with braid. The lampshade is shaped like a rectangular prism. The length of the base of the lampshade is 4 inches greater than its width. If the perimeter of the base is 54 inches, find the length of the base.

Answer:

Explanation:
Given, perimeter of the base = 54 inches

Consider length of the lamp, l = (x +4)

x = (l – 4)

Consider breadth of the lamp, b = l

perimeter of the base = 54

2 (l + b) = 54

2 ((l – 4) + l) = 54

Divide 2 on both sides.

2 ((l – 4) + l) ÷ 2 = 54 ÷ 2

2l – 4 =  27

add 4 on both sides.

2l – 4 + 4 =  27 + 4

2l = 31

Divide 2 on both sides

2l ÷ 2 = 31 ÷ 2

l = 15.5

breadth, l = 15.5

Length, x = l -4 = 15.5 – 4 = 11.5

Verification:
2(l + b ) = 54

2(11.5 + 15.5)

2 (27)

54

Hence proved

Question 5.
Daphne was given a riddle to solve: The sum of two consecutive positive integers is 71. Find the two positive integers.
Answer:

Explanation:
Consider the two consecutive positive numbers be x, x +1

Given, The sum of two consecutive positive integers = 71

x + x +1 = 71

2x +1 = 71

Subtract 1 on both sides.

2x +1 -1 = 71 – 1

2x = 70

Divide 2 on both sides.

2x ÷ 2 = 70 ÷ 2

x = 35

since, x =35  ==>  x + 1 = 35 + 1 = 36

Verification:
x + x +1 = 71

35 + 36 = 71

Hence proved.

Question 6.
The sum of a negative number, \(\frac{1}{4}\) of the negative number, and \(\frac{7}{16}\) of the negative number is -13 \(\frac{1}{2}\). What is the negative number?
Answer:
-x = -9 (5/11)

Explanation:
-x(1/4) – x(7/16) =  -13 (1/2)

-11x/16 = -13(1/2)

Multiply 2 on both sides.

(-11x/16) × 2 = -13(1/2) × 2

(-11x/8) = -13

Multiply 8 on both sides.

(-11x/8) × 8 =-13 × 8

x = 9 (5/11)

Question 7.
3.5 times a positive number is equal to the sum of the positive number and 0.5. What is the positive number?
Answer:
x = 0.2

Explanation:
Let us consider the positive number be ‘x’

3.5x = x + 0.5

Subtract x on both sides.

3.5x – x = x + 0.5 – x

2.5x = 0.5

Divide 2.5 on both sides.

2.5x ÷ 2.5 = 0.5 ÷ 2.5

x = 0.2

Verification:

Positive Number x = 0.2

3.5x = x + 0.5

Substitute 0.2 in the equation.

3.5(0.2) = 0.2 + 0.5

0.7 = 0.7

Hence Proved.

Question 8.
Eugene wrote a riddle: A positive number is 5 less than another positive number. Six times the lesser number minus 3 times the greater number is 3. Find the two positive numbers.
Answer:
x = 11

Explanation:
Let us consider the two positive numbers be  ‘x’ and  ‘x -5’

Given, Six times the lesser number minus 3 times the greater number is 3

6 (x – 5) – 3(x) = 3

6x – 30 -3x = 3

3x – 30 = 3

Add 30 on both sides.

3x – 30 + 30 = 3 + 30

3x = 33

Divide 3 on both sides.

3x ÷ 3 = 33 ÷ 3

x = 11

Verification:
6 (x – 5) – 3(x) = 3

Substitute x = 11

6 (11 – 5) – 3(11)

= 6 × 6 – 33

= 36 – 33

= 3

Hence proved.

Question 9.
At a charity basketball game, 450 tickets were sold to students at a school. The remaining x tickets were sold to the public. The prices of the two types of tickets are shown. When all the tickets were sold, $10,500 was collected. How many tickets were sold to the public?

Answer:
x = 150

Explanation:
Consider the number of tickets sold to public be ‘x’

The cost of each ticket sold to the student = 15$

Number of students at school the tickets were sold = 450

Cost of ticket to the public = 25$

Total amount collected when all the tickets were sold = $10,500

25(x) + 15(450) = 10500

25x + 6750 = 10500

Subtract 6750 on both sides.

25x + 6750 – 6750 = 10500 – 6750

25x = 3750

Divide 25 on both sides.

25x ÷ 25 = 3750 ÷ 25

x = 150

Verification:
25(x) + 15(450) = 10500

Substitute x = 150

25(x) + 15(450)

= 25(150) + 15(450)

= 3750 + 6750

= 10,500

Hence proved.

Question 10.
Henry ordered pizzas for a party and organized the information into a table. If Henry paid a total of $93.65, how many large cheese pizzas did he order?

Answer:

Explanation:
Total amount Henry paid = 93.65$

Number of medium pepperoni pizza = 2

Price of one medium pepperoni pizza = $11.95

Number of large cheese be ‘x’

Price of one large cheese = $13.95

2(11.95) + x(13.95) = 93.65

23.9 + 13.95x = 93.65

Subtract 23.9 on both sides.

23.9 + 13.95x – 23.9 = 93.65 – 23.9

13.95x = 69.75

Divide 13.95 on both sides.

13.95x ÷ 13.95 = 69.75 ÷ 13.95

x = 5

Verification:
2(11.95) + x(13.95) = 93.65

23.9 + 13.95x

Substitute x = 5

23.9 + 13.95(5)

= 23.9 + 69.75

= 93.65

Hence proved.

Question 11.
Marvin saved dimes and quarters in his piggy bank to buy a gift for his mother. He counted his savings and organized the information in a table.

If he saved $11, how many dimes and quarters did Marvin have?
Answer:
Dime, x = 40 ; Quarter, x- 12 = 28

Explanation:
Given, Number of dime coins = x

Number of quarter coins = x – 12

Value of one dime coin = 0.10$

Value of one quarter coin = 0.25$

0.10x + 0.25(x – 12) =11

0.10x + 0.25x – 3 =11

Add 3 on both sides.

0.10x + 0.25x – 3 + 3 =11 + 3

0.35x =14

Divide 0.35 on both sides.

0.35x ÷ 0.35 =14 ÷ 0.35

x = 40

x – 12 = 40 -12 = 28

Verification:
0.10x + 0.25(x – 12) =11

Substitute x = 40

0.10(40)+ 0.25(40- 12)

= 4 + 7

= 11

Question 12.
A bike shop charges x dollars to rent a bike for half a day. It charges (x + 40) dollars to rent a bike for a full day. The table shows the shop’s bike rentals for one day. On that day, the shop made a total of $600 from bike rentals.

How much does it cost to rent a bike for a full day?
Answer:
Amount for full day = x + 40 =  60 + 40 = 100$

Explanation:
Given, Amount for half day = x

Number of bikes taken for rental for half day = 5

Amount for full day = x + 40

Number of bikes taken for rental for full day = 3

Total number of amount the bike shop made on rental on that day = $600

5(x) + 3(x +40) = 600

5x + 3x +120 = 600

Subtract 120 on both sides.

5x + 3x +120 – 120 = 600 – 120

8x = 480

Divide 8 on both sides.

8x ÷ 8 = 480 ÷ 8

x = 60

Amount for full day = x + 40 = 60 + 40 = 100

Verification:
5(x) + 3(x +40) = 600

= 5x + 3x +120

= 8x + 120

Substitute x = 60

8 (60) +120

= 480 + 120

= 600

Hence proved

Question 13.
An artist is weaving a rectangular wall hanging. The wall hanging is already 18 inches long, and the artist plans to weave an additional 2 inches each day. The finished wall hanging will be 60 inches long. How many days will it take the artist to finish the wall hanging?

Answer:
x = 21 days

Explanation:
Given, total length of the wall hanging = 60 inches

Artist finished 18 inches, so the remaining would be 60 – 18 = 42

the artist plans to weave an additional 2 inches each day

i.e; 2 inches – 1 day

42 inches – ?

Let us consider the no. of days for weaving 42 inches be ‘x’

2 inches – 1 day

42 inches – x days

Let us cross multiply

2 × (x) = 42 × 1

2x = 42

Divide 2 on both sides.

2x ÷ 2 = 42 ÷ 2

x = 21 days

Question 14.
Ms. Kendrick plans to buy a laptop for $1,345 in 12 weeks. $he has already saved $145. How much should she save each week so she can buy the laptop?
Answer:
Amount she should save each week, x = 100

Explanation:
Given, Ms. Kendrick plans to buy a laptop for $1,345 in 12 weeks

she already saved $145.

Let us consider the amount per week in the 12 weeks = x

12x + 145 = 1345

Subtract 145 in both sides.

12x + 145 – 145 = 1345 – 145

12x = 1200

Divide 12 on both sides.

12x ÷ 12 = 1200 ÷ 12

x = 100

Question 15.
A plant grows at a rate of 4.5 centimeters per week. It is now 12 centimeters tall. 5uppose that the plant continues to grow at the same rate. In how many weeks will it reach a height of 48 centimeters?
Answer:
x = 8 weeks

Explanation:
We can apply the formula, y = mx + b

y = 48

m = 4.5

b= 12

48 = 4.5x + 12

Subtract 12 on both sides.

48 – 12 = 4.5x + 12 – 12

4.5x = 36

Divide 4.5 on both sides.

4.5x  ÷ 4.5  = 36 ÷ 4.5

x = 8

Question 16.
Mr. Johnson is currently four times as old as his son, David. If Mr. Johnson was 46 years old two years ago, how old is David now?
Answer:
David age, x = 12

Explanation:
Let us consider, David’s age be ‘x’

Mr. Johnson is currently four times as old as his son, s0 4x

As Mr. Johnson was 46 years old two years ago, at present his age is 46 +2 = 48

4x = 48

Divide 4 on both sides

4x ÷ 4 = 48 ÷ 4

x = 12

Question 17.
Mr. Warren drove from Townsville to Villaville and back again at the speeds shown. His total driving time was 12 hours. How far apart are the two towns?

Answer:
Distance, x = 350 miles

Explanation:
Distance from townsville to villaville = x/70 miles per hour

Distance from villavile to townsville = x/50 miles per hour

it takes 12 hours

x/70 + x/50 = 12

(7x + 5x)/350 = 12

12x/350 = 12

Divide 12 on both sides.

12x/350 ÷ 12 = 12 ÷ 12

x/350 = 1

x = 350 miles

Question 18.
A factory made 845 pairs of shoes in January. These shoes were sent to three shoe stores and one outlet mall. The number of pairs of shoes sent to each store was four times the number sent to the outlet mall. How many pairs of shoes were sent to the outlet mall in January?
Answer:
Pairs of shoes were sent to the outlet mall in January, x = 65

Explanation:
Consider the number of pairs shoes sent to outlet mall be ‘x’

Number of pairs shoes sent to each store = 4x + 4x +4x

4x + 4x +4x +x = 845

13x =845

Divide 13 on both sides

13x ÷ 13 =845 ÷ 13

x = 65

Question 19.
The cost of seeing a weekday show is \(\frac{2}{3}\) the cost of a weekend show. In one month, Andy spent $42.50 for 4 weekday shows and 3 weekend shows. Find the price of a weekday show and the price of a weekend show.
Answer:
The cost of seeing a weekday show, x = 5

The cost of seeing weekend show, y = 7.5

Explanation:
Let us consider, x be the cost of week day show

y be the cost of weekend show

x = (2/3)y

In one month, Andy spent $42.50 for 4 weekday shows and 3 weekend shows

4x + 3y = 42.50

4(2/3)y + 3y = 42.50

Multiply 3 on both sides

4(2/3)y × 3+ 3y × 3 = 42.50 × 3

8y + 9y = 127.5

17y = 127.5

Divide 17 on both sides

17y ÷ 17 = 127.5 ÷ 17

y = 7.5

x = (2/3)y = (2/3) × 7.5

= 5

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 4 Lesson 4.2 Solving Algebraic Equations to score better marks in the exam.

Math in Focus Grade 7 Course 2 A Chapter 4 Lesson 4.2 Answer Key Solving Algebraic Equations

Math in Focus Grade 7 Chapter 4 Lesson 4.2 Guided Practice Answer Key.

Solve.

Question 1.
6x + 2 = 8
6x + 2 = 8
6x + 2 – = 8 – Subtract from both sides.
= Simplify.
\(\frac{?}{?} x=\frac{?}{?}\) Divide both sides by .
x = Simplify.
Answer:
x =1

Explanation:
6x+2 =8

Subtract 2 on both sides.

6x + 2 – 2 = 8 -2

6x = 6

x =1

Let us consider second question, \(\frac{?}{?} x=\frac{?}{?}\)

Let us consider, a and b in the place of the “?” on both sides

(a/b)x = (a/b)

Divide (a/b) on both sides.

x =1

Question 2.
5 – 3x = 20
Answer:
x = -5

Explanation:
Let us consider the equation,   5 – 3x = 20

Subtract 5 both sides.

5 – 3x – 5 = 20 – 5

-3x = 15

put  – on both sides to make x positive.

-(-3x) = -15

3x = -15

divide 3 on both sides to get the value of ‘x’

x = -5

Question 3.
4x – 3 + 0.5x = 1.5
Answer:
x = 1

Explanation:
4x – 3 + 0.5x = 1.5

Add all the variants of ‘x’

4.5x – 3 = 1.5

add 3 on both sides.

4.5x -3 + 3 = 1.5 + 3

4.5x = 4.5

divide 4.5 on both sides.

x= (4.5/4.5)

x = 1

Question 4.
\(\frac{9}{10}\)x – \(\frac{4}{5}\) = 1
Answer:
x = 2

Explanation:
(9/10)x – (4/5) = 1

Add (4/5) on both sides.

(9/10)x – (4/5) + (4/5) = 1 + (4/5)

(9/10)x = (9/5)

0.9x =  1.8

Divide (0.9) on both sides.

x = 1.8 ÷ 0.9

x = 2

Solve each equation. Check your solution.

Question 5.
11 – 4x = x + 16
11 – 4x = x + 16
11 – 4x – x = x + 16 – x Subtract x from both sides.
11 + = 16 Simplify.
11 + – 11 = 16 – 11 Subtract 11 from both sides
= 5 Simplify.
\(\frac{?}{?} x=\frac{?}{?}\) Divide both sides by .
x = Simplify.
Answer:
-5x = 5

Explanation:
Given, 11 – 4x = x + 16

Subtract x from both sides.

11 – 4x – x = x + 16 – x

11 – 5x =16

Subtract 11 from both sides.

11 – 5x – 11=16 – 11

-5x = 5

x = -1

Let us consider second question, \(\frac{?}{?} x=\frac{?}{?}\)

Let us consider, a and b in the place of the “?” on both sides

(a/b)x = (a/b)

Substitute -1 in the place of  x

(a/b)(-1) = (a/b)

Divide (a/b) on both sides.

= -1

Question 6.
3.4y – 5.2 = 3y + 2
Answer:
y = 18

Explanation:
Given, 3.4y – 5.2 = 3y + 2

(34/10)y – (52/10) = 3y + 2

Simplify (34/10) and (52/10), and bring 3y + 2 to another side.

(17/5)y – 26/5 – 3y – 2 = 0

get common divider to all.

17y – 26 – 5.(3y + 2) / 5 = 0

(17y – 26 – 15y – 10) / 5  = 0

(2y – 36 )/ 5 = 0

(2y – 36 ) = 0 × 5

2y – 36 = 0

2y = 36

y = 18

Question 7.
\(\frac{5}{9}\)y – \(\frac{1}{3}\) = \(\frac{2}{3}\)y + \(\frac{1}{3}\)
Answer:
y= -6

Explanation:
Given, (5/9)y – (1/3) = (2/3)y + (1/3)

Add (1/3) on both sides.

(5/9)y – (1/3) + (1/3)= (2/3)y + (1/3) + (1/3)

(5/9)y = (2/3)y + (2/3)

(5/9)y – (2/3)y = (2/3)

(5y – 3×2y)/9 = (2/3)

(5y – 6y)/9 = (2/3)

-y = (2/3) × 9

-y = 6

y= -6

Solve each equation. Check your solutions.

Question 8.
1.5(p + 3) = 18
Answer:
p = 9

Explanation:
Given, 1.5(p + 3) = 18

It can also be written as 1.5p + 4.5 = 18

Subtract 4.5 on both sides

1.5p + 4.5 – 4.5 = 18 -4.5

1.5p = 13.5

Divide 1.5 on both sides.

1.5p ÷ 1.5 =  13.5 ÷ 1.5

p = 9

Question 9.
\(\frac{1}{4}\)(q+ 1) = 9
Answer:
q = 35

Explanation:
Given, (1/4)(q + 1) = 9

multiply 4 on both sides.

(q + 1) = 36

Subtract 1 on both sides.

q +1 – 1 = 36 – 1

q = 35

Question 10.
2(x – 3) + 2 = 14
Answer:
x =9

Explanation:
Given, 2(x – 3) + 2 = 14

2x – 6 + 2 = 14

2x – 4 = 14

Add 4 on both sides

2x – 4 + 4 = 14 + 4

2x = 18

x =9

Question 11.
3(y – 1) + y = 1
Answer:
y =1

Explanation:
Given, 3(y – 1) + y = 1

3y – 3 + y = 1

4y – 3 = 1

Add 3 on the both sides

4y – 3 + 3 =1 + 3

4y = 4

y =1

Math in Focus Course 2A Practice 4.2 Answer Key

Solve each equation with variables on the same side.

Question 1.
4b – 2 = 6
Answer:
b = 2

Explanation:
Given, 4b – 2 = 6

Add 2 on the both sides.

4b – 2 + 2 = 6 + 2

4b = 8

b = 8 ÷ 4

b = 2

Question 2.
5x + 4 = 24
Answer:
x = 4

Explanation:
Given, 5x + 4 = 24

Subtract 4 on both sides.

5x + 4 – 4 = 24

5x = 20

Divide 5 on both sides

x = 20 ÷ 5

x = 4

Question 3.
7c – 11 = 17
Answer:
c = 4

Explanation:
Given, 7c – 11 = 17

Add 11 on both sides.

7c – 11 + 11 = 17 +11

7c = 28

Divide 7 on bot sides.

c =  28 ÷ 7

c = 4

Question 4.
18 = 3k – 3
Answer:
7 = k

Explanation:
Given, 18 = 3k – 3

Add 3 on both sides.

18 + 3 = 3k – 3 + 3

21 = 3K

Divide 3 on both sides.

21 ÷ 3 = 3k ÷ 3

7 = k

Question 5.
\(\frac{a}{4}\) – 1 = 3
Answer:
a = 16

Explanation:
Given, (a/4) -1 = 3

Add 1 on both sides.

(a/4) -1 + 1 = 3 + 1

(a/4) = 4

Multiply 4 on both sides.

(a/4) × 4 = 4 × 4

a = 16

Question 6.
\(\frac{2}{3}\)v = 2 – \(\frac{4}{3}\)
Answer:
v =1

Explanation:
Given, (2/3)v = 2 – (4/3)

(2/3)v = (2×3 -4)/3

(2/3)v = (6 – 4)/3

(2/3)v = (2/3)

Multiply (3/2) on both sides.

(2/3)v ×(3/2) = (2/3) ×(3/2)

v =1

Question 7.
\(\frac{5}{2}\)y + 8 =18
Answer:
y = 4

Explanation:
(5/2)y + 8 = 18

Subtract 8 on both sides.

(5/2)y + 8 – 8 = 18 – 8

(5/2)y = 10

Multiply 2 on both sides.

(5/2)y × 2 = 10 × 2

5y = 20

Divide 5 on both sides.

5y ÷ 5 = 20 ÷ 5

y = 4

Question 8.

\(\frac{3}{5}\)f – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Answer:
f = (5/3)

Explanation:
Given, (3/5)f – (1/2) = (1/2)

Add (1/2) on both sides.

(3/5)f – (1/2) + (1/2) = (1/2) + (1/2)

(3/5)f = 1

Multiply 5 on both sides.

(3/5)f  × 5 = 1 × 5

3f = 5

Divide 3 on both sides.

f = (5/3)

Question 9.
4.5 + 0.2p = 6.1
Answer:
p = 8

Explanation:
Given, 4.5 + 0.2p = 6.1

Subtract 4.5 on both sides.

4.5 + 0.2p – 4.5 = 6.1 – 4.5

0.2p = 1.6

Divide 0.2 on both sides.

0.2p ÷ 0.2 = 1.6 ÷ 0.2

p = 8

Question 10.
1.5d + 3.2 = 9.2
Answer:
d = 4

Explanation:
Given, 1.5d + 3.2 = 9.2

Subtract 3.2 on both sides.

1.5d + 3.2 – 3.2  = 9.2 – 3.2

1.5d = 6

Divide 1.5 on both sides.

1.5d  ÷ 1.5 = 6 ÷ 1.5

d = 4

Question 11.
0.8w – 4 = 4
Answer:
w = 10

Explanation:
Given, 0.8w – 4 = 4

Add 4 on both sides.

0.8w – 4 + 4 = 4 + 4

0.8w =8

Divide 0.8 on both sides.

0.8w ÷ 0.8 =8 ÷ 0.8

w = 10

Question 12.
1.4z – 0.5 = 3.7
Answer:
z = 3

Explanation:
Given, 1.4z – 0.5 = 3.7

Add 0.5 on both sides.

1.4z – 0.5 + 0.5 = 3.7 + 0.5

1.4z = 4.2

Divide 1.4 on both sides.

1.4z ÷ 1.4 = 4.2 ÷ 1.4

z = 3

Question 13.
Math Journal Priscilla was asked to solve the equation -4p + 5 = 7. Her solution is shown.

Priscilla concluded that p = \(\frac{1}{2}\) is the solution of the equation -4p + 5 = 7. Describe and correct the error Priscilla made.
Answer:
The answer priscilla got is wrong. P = – (1/2)

Explanation:
Given,-4p + 5 = 7

Subtract 5 on both sides.

-4p + 5 – 5= 7 – 5

-4p = 2

Divide 4 on both sides

-p = (2/4)

p = – (1/2)

Solve each equation with variables on both sides.

Question 14.
6a + 7 = 4a + 7
Answer:
a = 0 

Explanation:
Given, 6a + 7 = 4a + 7

Subtract 7 on both sides.

6a + 7 – 7 = 4a + 7 – 7

6a = 4a

6a -4a = 0

2a = 0

a = 0

Question 15.
17g + 3 = 11g + 39
Answer:
g = 6

Explanation:
Given, 17g + 3 = 11g + 39

17g + 3 – 11g – 39 = 0

6 g – 36 = 0

6g = 36

Divide 6 on both sides.

6g ÷ 6 = 36 ÷ 6

g = 6

Question 16.
8h – 5 = 11h – 14
Answer:
h = 3

Explanation:
Given, 8h – 5 = 11h – 14

14 – 5 = 11h – 8h

9 = 3h

Divide 3 on both sides.

3h ÷ 3 = 9 ÷ 3

h = 3

Question 17.
9j + 4 = 13j – 6
Answer:
j = (5/2)

Explanation:
Given, 9j + 4 = 13j – 6

4 + 6 = 13j – 9j

10 =  4j

Divide 4 on both sides.

j = (10/4)

j = (5/2)

Question 18.
\(\frac{1}{2}\)f – 2 = \(\frac{1}{6}\)f
Answer:
f = 6

Explanation:
Given, (1/2)f – 2 = (1/6)f

(1/2)f – (1/6)f = 2

(3f – f)/6 = 2

Multiply  6 on both sides.

2f = 2 × 6

2f = 12

Divide 2 on both sides.

f = 12 ÷ 2

f = 6

Question 19.
25 + q = \(\frac{1}{2}\)q – 3
Answer:
q = -56

Explanation:
Given, 25 + q = (1/2)q – 3

25 + 3 = (1/2)q – q

28 = -(1/2)q

Multiply 2 on both sides.

28 × 2 = -(1/2)q × 2

-q = 56

q = -56

Question 20.
\(\frac{5}{9}\)v – \(\frac{1}{3}\) = \(\frac{2}{3}\)v + \(\frac{1}{3}\)
Answer:
v = -6

Explanation:
Given, (5/9)v – (1/3) = (2/3)v + (1/3)

Add (1/3) on both sides.

(5/9)v – (1/3) + (1/3) = (2/3)v + (1/3) + (1/3)

(5/9)v = (2/3)v + (2/3)

Subtract (2/3)v on both sides.

(5/9)v – (2/3)v = (2/3)v + (2/3) – (2/3)v

(5v – 6v)/9 = (2/3)

-v = (2/3) × 9

-v = 2 × 3

-v =6

v = -6

Question 21.
\(\frac{5}{4}\)e + \(\frac{1}{2}\) = 2e – \(\frac{1}{2}\)
Answer:
e = (4/3)

Explanation:
Given, (5/4)e + (1/2) = 2e – (1/2)

Add (1/2) on b1oth sides.

(5/4)e + (1/2) + (1/2) = 2e – (1/2) + (1/2)

(5/4)e + 1 = 2e

1 = 2e – (5/4)e

1 = ((2 × 4)e -5e)/4

(8e – 5e)/4 = 1

(3e/4) = 1

Multiply 4 on both sides.

(3e/4) × 4 = 1 × 4

3e = 4

e = (4/3)

Question 22.
7.5x – 4.1 = 6.7 – 4.5x
Answer:
x = 0.9

Explanation:
Given, 7.5x – 4.1 = 6.7 – 4.5x

Add 4.1 on both sides.

7.5x – 4.1 + 4.1 = 6.7 – 4.5x + 4.1

7.5x = 10.8 – 4.5x

Add 4.5x on both sides.

7.5x + 4.5x = 10.8 – 4.5x + 4.5x

12x =10.8

x = (10.8/12)

x = 0.9

Question 23.
3.4y – 5.2 = 3y + 2
Answer:
y = 18

Explanation:
Given, 3.4y – 5.2 = 3y + 2

Subtract 2 on both sides.

3.4y – 5.2  – 2 = 3y + 2 – 2

3.4y -7.2 = 3y

3.4y – 3y = 7.2

0.4y = 7.2

Divide 0.4 on both sides.

0.4y ÷ 0.4 = 7.2 ÷ 0.4

y = 18

Question 24.
b – 2.8 = 0.8b + 1.2
Answer:
b = 20

Explanation:
Given, b – 2.8 = 0.8b + 1.2

Subtract 1.2 on both sides.

b – 2.8 – 1.2 = 0.8b + 1.2 – 1.2

b – 4 = 0.8b

b – 0.8b = 4

0.2b = 4

Divide 0.2 on both sides.

0.2b ÷ 0.2 = 4 ÷ 0.2

b = 20

Question 25.
3.2s – 5 = 5 – 1.8s
Answer:
s =2

Explanation:
Given, 3.2s – 5 = 5 – 1.8s

Add 5 on both sides.

3.2s – 5 + 5 = 5 – 1.8s + 5

3.2s = 10 – 1.8s

Add 1.8s on both sides.

3.2s + 1.8s = 10 – 1.8s + 1.8s

5s = 10

Divide 5 on both sides.

5s ÷ 5 = 10 ÷ 5

s =2

Give your reasoning.

Question 26.
Math Journal How is the process of solving the equation \(\frac{3}{5}\)x – 1 = \(\frac{3}{10}\)x + \(\frac{1}{5}\) different from simplifying the expression \(\frac{3}{5}\)x – 1 + \(\frac{3}{10}\) x + \(\frac{1}{5}\)?
Answer:
x = 4, (9x -8)/10  Yes both are different from each other.

Explanation:
Given equations, (3/5)x – 1 = (3/10)x + (1/5)

(3/5)x -1 + (3/10)x + (1/5)

Let’s solve the first equation, (3/5)x – 1 = (3/10)x + (1/5)

Subtract (1/5) on both sides.

(3/5)x – 1 – (1/5) = (3/10)x + (1/5) – (1/5)

(3/5)x -(5 + 1)/5 = (3/10)x

(3/5)x – (6/5) = (3/10)x

(3/5)x – (3/10)x = (6/5)

(6 – 3)x/10 = (6/5)

Multiply 10 on both sides.

3x/10 × 10 = (6/5) × 10

3x = 12

Divide 3 on both sides

3x ÷ 3 = 12 ÷ 3

x = 4

Lets solve second equation, (3/5)x -1 + (3/10)x + (1/5)

(6 + 3)x/10 – 1 + (1/5)

9x/10 -(4/5)

(9x -8)/10

Solve each equation involving parentheses.

Question 27.
7(2z + 1) = 35
Answer:
z =2

Explanation:
Given, 7(2z + 1) = 35

Divide 7 on both sides.

7(2z + 1) ÷  7 = 35 ÷ 7

2z + 1 = 5

Subtract 1 on both sides

2z + 1 – 1 = 5 – 1

2z = 4

z =2

Question 28.
18 = 6(5 – g)
Answer:
g = 2

Explanation:
Given, 18 = 6(5 – g)

18 = 30 – 6g

6g = 30 -18

6g = 12

Divide 6 on both sides.

6g ÷ 6 = 12 ÷ 6

g = 2

Question 29.
\(\frac{1}{5}\)(3r – 4) = \(\frac{2}{5}\)
Answer:
r = 2

Explanation:
(1/5)(3r – 4) = (2/5)

Multiply 5 on both sides.

(1/5)(3r – 4)  × 5 = (2/5) × 5

(3r – 4) = 2

Add 4 on both sides.

3r – 4 + 4 = 2 + 4

3r = 6

Divide 3 on both sides.

3r ÷ 3 = 6 ÷ 3

r = 2

Question 30.
\(\frac{1}{5}\)(5x + 4) = \(\frac{3}{4}\)
Answer:
x = -(1/20)

Explanation:
(1/5)(5x + 4) = (3/4)

Multiply 5 on both sides.

(1/5)(5x + 4) = (3/4)

(1/5)(5x + 4) × 5 = (3/4) × 5

(5x + 4) = (15/4)

Multiply 4 on both sides.

(5x + 4) × 4 = (15/4) × 4

20x + 16 = 15

Subtract 16 on both sides.

20x + 16 – 16 = 15 -16

20x = -1

Divide 20 on both sides.

20x ÷ 20 = -1 ÷ 20

x = -(1/20)

Question 31.
0.6(d + 3) = 3d
Answer:
d = 0.75

Explanation:
Given, 0.6(d + 3) = 3d

0.6d + 1.8 = 3d

Subtract 1.8 on both sides.

0.6d + 1.8 – 1.8= 3d – 1.8

0.6d = 3d – 1.8

3d – 0.6d = 1.8

2.4d ÷  2.4 = 1.8 ÷ 2.4

d = 0.75

Divide 2.4 on both sides.

2.4d = 1.8

Question 32.
0.3(k – 0.2) = 0.6
Answer:
k = 2.2

Explanation:
Given, 0.3(k – 0.2) = 0.6

Divide 0.3 on both sides.

0.3(k – 0.2) ÷ 0.3 = 0.6 ÷ 0.3

k – 0.2 = 2

Add 0.2 on both sides.

k – 0.2 + 0.2 = 2 + 0.2

k = 2.2

Question 33.
3(1.2b – 1) + 3.6 = 4.2
Answer:
b = 1

Explanation:
Given, 3(1.2b – 1) + 3.6 = 4.2

3.6b – 3 + 3.6 = 4.2

3.6b + 0.6 = 4.2

Subtract 0.6 on both sides.

3.6b + 0.6 – 0.6 = 4.2 -0.6

3.6b = 3.6

Divide 3.6 on both sides.

3.6b ÷ 3.6 = 3.6 ÷ 3.6

b = 1

Question 34.
0.7(h + 2) + 1.6 = 17
Answer:
h = 20

Explanation:
Given, 0.7(h + 2) + 1.6 = 17

0.7h + (0.7 × 2) + 1.6 = 17

0.7h + 1.4 + 1.6 = 17

0.7h + 3 = 17

Subtract 3 on both sides.

0.7h + 3 – 3 = 17 – 3

0.7h = 14

Divide 0.7 on both sides.

0.7h ÷ 0.7 = 14 ÷ 0.7

h = 20

Question 35.
2(a – 1) – 5a = 7
Answer:

Explanation:
Given, 2(a – 1) – 5a = 7

2a -2 -5a = 7

-3a – 2 = 7

Add 2 on the both sides.

-3a – 2+2 = 7 +2

-3a = 9

Divide -3 on both sides.

a = -(9/3)

a = -3

Question 36.
3(6 – 4x) – 27x = 10x – 31
Answer:
1 = x

Explanation:
Given, 3(6 – 4x) – 27x = 10x – 31

18 – 12x – 27x = 10x -31

18 -39x = 10x – 31

18 +31 = 10x + 39x

49 = 49x

Divide 49 on both sides.

49 ÷ 49 = 49x ÷ 49

1 = x

Question 37.
\(\frac{1}{4}\)(w – 4) – \(\frac{3}{4}\)w = 3
Answer:
w = -8

Explanation:
Given, (1/4)(w – 4) – (3/4)w =3

Multiply 4 on both sides.

4 ×( (1/4)(w – 4) – (3/4)w) = 3 × 4

(w – 4) – 3w = 12

w – 4 – 3w = 12

-2w – 4 = 12

Add 4 on both sides

-2w – 4 + 4 = 12 + 4

-2w = 16

-w = 8

w = -8

Question 38.
\(\frac{1}{6}\)s – \(\frac{1}{2}\)(s – 2) = \(\frac{45}{2}\)
Answer:
s = -(129/2)

Explanation:
(1/6)s – (1/2)(s – 2) = (45/2)

Multiply 2 on both sides.

2 × (1/6)s – 2 × (1/2)(s – 2) = (45/2) × 2

(1/3)s – (s-2) = 45

Multiply 3 on both sides.

3 × (1/3)s – 3 ×(s-2) = 45 × 3

s – 3s + 6 = 135

-2s + 6 = 135

Subtract 6 on both sides

-2s + 6 – 6 = 135 – 6

-2s = 129

Divide (-2) on both sides.

-2s ÷ (-2) = 129 ÷ (-2)

s = -(129/2)

Question 39.
5(y + 1) = 3(3y + 4)
Answer:
y = -(7/4)

Explanation:
Given, 5(y + 1) = 3(3y + 4)

5y + 5 = 9y + 12

Subtract 5 on both sides.

5y + 5 – 5 = 9y + 12 – 5

5y = 9y + 7

Subtract 5y on both sides.

5y – 5y = 9y + 7 – 5y

0 = 4y + 7

4y = -7

Divide 4 on both sides.

4y ÷ 4 = -7 ÷ 4

y = -(7/4)

Question 40.
2(b + 5) = 3(4 – b)
Answer:
b =(2/5)

Explanation:
Given, 2(b + 5) = 3(4 – b)

2b + 10 = 12 – 3b

Add 3b on both sides.

2b + 10 + 3b = 12 – 3b + 3b

5b + 10 = 12

Subtract 10 on both sides.

5b + 10 – 10 = 12 – 10

5b = 2

Divide 5 on both sides.

5b ÷ 5 = 2 ÷ 5

b =(2/5)

Question 41.

Math Journal Nelson solved the algebraic equation 3(2x + 5) = 17 as I shown below:
3(2x + 5) = 17
3(2x + 5) – 5 = 17 – 5
3(2x) = 12 6
x = 12
6x ÷ 6 = 12 ÷ 6
x = 2
Describe and correct the error Nelson made.
Answer:
x = (1/3)

Explanation:
Given, 3(2x + 5) = 17

3 × 2x + 3 × 5 = 17

6x + 15 = 17

Subtract 15 on both sides

6x + 15 – 15 = 17 – 15

6x = 2

Divide 6 on both sides.

6x ÷ 6 = 2 ÷ 6

x = (2/6)

x = (1/3)

Question 42.
Math Journal Describe the steps you could use to solve 2(b – 5) + 3(b – 2) = 8 + 7(b – 4). Solve and show your work.
Answer:
b = 2

Explanation:
Given, 2(b – 5) + 3(b – 2) = 8 + 7(b – 4)

2b – 10 +3b – 6 = 8 + 7b – 28

5b – 16 = 7b – 20

Add 16 on both sides.

5b – 10 + 16 = 7b – 20 + 16

5b = 7b – 4

7b – 5b = 4

2b = 4

Divide 2 on both sides.

2b ÷ 2 = 4 ÷ 2

b = 2

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 2 Rational Number Operations to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 2 Answer Key Rational Number Operations

Math in Focus Grade 7 Chapter 2 Quick Check Answer Key

Complete each ? with > or <.

Question 1.
-3 ? 5
Answer:
-3 < 5
Explanation:
Compare the above two numbers. The number -3 is less than 5.

Question 2.
-7 ? -12
Answer:
-7 > -12
Explanation:
Compare the above two numbers. The number -7 is greater than -12.

Question 3.
10 ? -16
Answer:
10 > -16
Explanation:
Compare the above two numbers. The number 10 is greater than -16.

Question 4.
-28 ? 0
Answer:
-28 < 0
Explanation:
Compare the above two numbers. The number -28 is less than 0.

Question 5.
\(\frac{1}{2}\) ? \(\frac{3}{4}\)
Answer:
1/2 < 3/4
Explanation:
Compare above two fractions. The fraction 1/2 is less than 3/4.

Question 6.
-1\(\frac{1}{4}\) ? 2\(\frac{2}{3}\)
Answer:
The mixed fraction -1(1/4) in fraction form as -5/4.
The mixed fraction 2(2/3) in fraction form as 8/3.
-1(1/4) < 2(2/3)
Explanation:
Compare above two mixed fractions. The mixed fraction -1(1/4) is less than 2(2/3).

Question 7.
0.15 ? 0.13
Answer:
0.15 > 0.13
Explanation:
Compare the above decimal numbers. The decimal number 0.15 is greater than 0.13.

Question 8.
-1.23 ? -1.25
Answer:
-1.23 > -1.25
Explanation:
Compare the above decimal numbers. The decimal number -1.23 is greater than -1.25.

Evaluate each expression.

Question 9.
75 – (18 + 2) ∙ 3
Answer:
75 – (18 + 2) ∙ 3 Given
= 75 – 20 ∙ 3 Perform operation in parentheses
= 75 – 60 Multiply
= 15 subtract

Question 10.
15 ∙ (40 ÷ 8) + 72
Answer:
15 ∙ (40 ÷ 8) + 72 Given
= 15 ∙ 5 + 72 Perform operation in parentheses
= 75 + 72 Multiply
= 147 Add
= 147

Express each improper fraction as a mixed number.

Question 11.
\(\frac{12}{17}\)
Answer:

Question 12.
\(\frac{19}{3}\)
Answer:
19/3 = 6(1/3)
Explanation:
The mixed number for the improper fraction 19/3 is 6(1/3).

Express each mixed number as an improper fraction.

Question 13.
4\(\frac{3}{5}\)
Answer:
4(3/5) =(20 + 3)/5 = 23/5
Explanation:
The improper fraction for the mixed number 4(3/5) is 23/5.

Question 14.
6\(\frac{7}{9}\)
Answer:
6(7/9) = (54 + 7)/9 = 61/9
Explanation:
The improper fraction for the mixed number 6(7/9) is 61/9.

Add or subtract. Express your answer in simplest form.

Question 15.
\(\frac{2}{3}\) + \(\frac{5}{4}\)
Answer:
2/3 + 5/4
= (8 + 15)/12
= 23/12
The simplest form of 2/3 + 5/4 is 23/12.
Explanation:
Perform addition operation on above two fractions. Add 2/3 with 5/4 the sum is 23/12.

Question 16.
\(\frac{7}{8}\) – \(\frac{2}{3}\)
Answer:
7/8 – 2/3
= (21 – 16)/24
= 5/24
The simplest form of 7/8 – 2/3 is 5/24.
Explanation:
Perform subtraction operation on above two fractions. Subtract 2/3 from 7/8 the difference is 5/24.

Question 17.
1\(\frac{1}{4}\) + 3\(\frac{2}{5}\)
Answer:
The mixed fraction 1(1/4) in fraction form as 5/4.
The mixed fraction 3(2/5) in fraction form as 17/5.
1(1/4) + 3(2/5)
= 5/4 + 17/5
= (25 + 68)/20
= 93/20
The simplest form of 1(1/4) + 3(2/5) is 93/20.
Explanation:
Perform addition operation on above two fractions. Add 1(1/4) with 3(2/5) the sum is 93/20.

Multiply or divide. Express your answer in simplest form.

Question 18.
\(\frac{2}{9}\) • \(\frac{3}{4}\)
Answer:
2/9 • 3/4
= 6/36
= 1/6
The simplest form of 2/9 • 3/4 is 1/6.
Explanation:
Perform multiplication operation on above two numbers. Multiply 2/9 with 3/4 the product is 1/6.

Question 19.
1\(\frac{2}{9}\) • \(\frac{3}{4}\)
Answer:
1(2/9) • 3/4
= 11/9 • 3/4
= 33/36
The simplest form of 1(2/9) • 3/4 is 33/36.
Explanation:
Perform multiplication operation on above two numbers. Multiply 1(2/9) with 3/4 the product is 33/36.

Question 20.
\(\frac{5}{8}\) ÷ \(\frac{21}{4}\)
Answer:
5/8 ÷ 21/4
= 5/8 • 4/21
= 5/2 • 1/21
= 5/42
The simplest form of 5/8 ÷ 21/4 is 5/42.
Explanation:
Perform division operation on above two numbers. Divide 5/8 by 21/4 the result is 5/42.

Question 21.
\(\frac{3}{4}\) ÷ 1\(\frac{1}{2}\)
Answer:
3/4 ÷ 1(1/2)
= 3/4 ÷ 3/2
= 3/4 • 2/3
= 1/2
The simplest form of 3/4 ÷ 1(1/2) is 1/2.
Explanation:
Perform division operation on above two numbers. Divide 3/4 by 1(1/2) the result is 1/2.

Multiply or divide.

Question 22.
15.8 • 2.7
Answer:
15.8 • 2.7
= 42.66
Explanation:
Perform multiplication operation on above two numbers. Multiply 15.8 with 2.7 the product is 42.66.

Question 23.
8.82 ÷ 0.6
Answer:
8.82 ÷ 0.6
= 14.7
Explanation:
Perform division operation on above two numbers. Divide 8.82 by 0.6 the result is 14.7.

Question 24.
25% of $420
Answer:
25% of $420
= 25/100 • $420
= 1/4 • $420
= $420/4
= $105
Explanation:
Perform multiplication operation. Multiply 25/100 with $420 the product is $105.

Question 25.
115 is what percent of 345?
Answer:
X% of 345 = 115
x/100 • 345 = 115
x = 115/345 • 100
x = 1/3 • 100
x = 33.33%
115 is 33.33% of 345.

Question 26.
24 boys out of 64 classmates is what percent?
Answer:
24/64 • 100
= 3/8 • 100
= 75/2
= 37.5%
24 boys out of 64 classmates is 37.5%.

Solve.

Question 27.
A seedling that Jeffrey planted in 2009 was 50 centimeters tall. In 2010, it was 120 centimeters tall.
a) Find the increase in the height of the seedling Jeffrey planted.
Answer:
A seedling that Jeffrey planted in 2009 was 50 centimeters tall.
In 2010, it was 120 centimeters tall.
120 – 50 = 70 centimeters.
The height of the seedling Jeffrey planted is increased by 70 centimeters.

b) Find the percent increase in the height of the seedling.
Answer:
Percent in the increase in height :
\(\frac{70}{50}\) × 100%
= 1.4 × 100%
= 140%
70 centimeters ; 140%

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 1 Review Test to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 1 Review Test Answer Key

Concepts and Skills

Write each number in \(\frac{m}{n}\) form where m and n are integers with n ≠ 0. Simplify your answers.

Question 1.
20.75
Answer:
20.75 = 83/4
Explanation:
The given decimal number 20.75 is represented in m/n form. The m/n form of 20.75 is 83/4.

Question 2.
-0.48
Answer:
-0.48 = -12/25
Explanation:
The given decimal number -0.48 is represented in m/n form. The m/n form of -0.48 is -12/25.

Question 3.
4\(\frac{6}{13}\)
Answer:
4(6/13)
= (52 + 6)/13
= 58/13
Explanation:
The given mixed fraction is 4(6/13). The simplified mixed fraction is represented in m/n form. The m/n form of 4(6/13) is 58/13.

Question 4.
–\(\frac{39}{56}\)
Answer:
-39/56
Explanation:
The given number -39/56 is already in m/n form.

Question 5.
1.34
Answer:
1.34 = 134/100 = 67/50
Explanation:
The given decimal number 1.34 is represented in m/n form. The m/n form of 1.34 is 134/100 or 67/50.

Question 6.
60%
Answer:
60% = 60/100
Explanation:
The given number 60% is represented in m/n form. The m/n form of 60% is 60/100.

For each pair of numbers, find the absolute value of each number. Then, determine which number is farther from 0 on the number line.

Question 7.
—16 and —18
Answer:
The absolute value of the number|-16| is 16.
The absolute value of the number |-18| is 18. 

Explanation:
In the above image we can observe a number line.
The absolute value of |-16| is 16. So the number -16 is 16 units from 0.
The absolute value of |-18| is 18. So the number -18 is 18 units from 0.
So, the number -18 is farther from 0 on the number line.

Question 8.
–\(\frac{15}{4}\) and \(\frac{18}{7}\)
Answer:
-15/4 and 18/7
The absolute value of |-15/4| is 15/4.
The absolute value of |18/7| is 18/7.

Explanation:
In the above image we can observe a number line.
The absolute value of |-15/4| is 15/4. So the number -15/4 is 15/4 units from 0.
The absolute value of |18/7| is 18/7. So the number 18/7 is 18/7 units from 0.
So, the number -15/4 is farther from 0 on the number line.

Question 9.
2.36 and -2.7
Answer:
2.36 and -2.7
The absolute value of |2.36| is 2.36.
The absolute value of |-2.7| is 2.7. 

Explanation:
In the above image we can observe a number line.
The absolute value of |2.36| is 2.36. So the number 2.36 is 2.36 units from 0.
The absolute value of |-2.7| is 2.7. So the number -2.7 is 2.7 units from 0.
So, the number -2.7 is farther from 0 on the number line.

Question 10.
\(\frac{31}{3}\) and \(\frac{40}{6}\)
Answer:
31/3 and 40/6
The absolute value of |31/3| is 31/3.
The absolute value of |40/6| is 40/6. 

Explanation:
In the above image we can observe a number line.
The absolute value of |31/3| is 31/3. So the number 31/3 is 31/3 units from 0.
The absolute value of |40/6| is 40/6. So the number 40/6 is 40/6 units from 0.
So, the number 31/3 is farther from 0 on the number line.

Using long division, write each rational number as a decimal. Use the bar notation if the rational number is a repeating decimal.

Question 11.
\(\frac{7}{56}\)
Answer:
7/56

Explanation:
A Decimal Number that contains a finite number of digits next to the decimal point is called a Terminating Decimal. Perform division operation on given rational number. By using long division method, divide 56 by 7 the quotient is 0.125 which is a terminating decimal.

Question 12.
9\(\frac{13}{20}\)
Answer:
9(13/20)
= (180 + 13)/20
= 193/20

Explanation:
Perform division operation on given rational number. The mixed fraction 9(13/20) in fraction form is 193/20. By using long division method, divide 193 by 20 the quotient is 9.65 which is a terminating decimal.

Question 13.
\(\frac{100}{11}\)
Answer:
100/11

Explanation:
A repeating decimal is decimal representation of a number whose digits are periodic and the infinitely repeated portion is not zero.
Perform division operation on given rational number. By using long division method, divide 100 by 11 the quotient is 9.0909… which is a repeating decimal. The repeating decimals are denoted by the bar notation as we can observe in the above image.

Question 14.
–\(\frac{5}{12}\)
Answer:
-5/12

Explanation:
Perform division operation on given rational number. By using long division method, divide -5 by 12 the quotient is -0.41666… which is a repeating decimal. The repeating decimals are denoted by the bar notation as we can observe in the above image.

Question 15.
-2\(\frac{9}{55}\)
Answer:
-2(9/55)
= -(110 + 9)/55
= -119/55

Explanation:
Perform division operation on given rational number. The mixed fraction of -2(9/55) in fraction form as -119/55. By using long division method, divide -119 by 55 the quotient is -2. 16363… which is a repeating decimal. The repeating decimals are denoted by the bar notation as we can observe in the above image.

Question 16.
47%
Answer:
47%
= 47/100

Explanation:
Perform division operation on given rational number. The 47% in fraction form is 47/100. By using long division method, divide 47 by 100 the quotient is 0.47 which is a terminating decimal.

Problem Solving

Use the irrational numbers below for questions 17 to 20.

Question 17.
Using rational numbers, find a segment with a distance of not more than 0.1 to locate each irrational number approximately on the real number line.
Answer:
The irrational number \(\sqrt{31}\) lies between the rational numbers with a distance of not more than 0.1 are 5.5 and 5.6.
5.5 < \(\sqrt{31}\) < 5.6
The irrational number –\(\sqrt{112}\) lies between the rational numbers with a distance of not more than 0.1 are -10.6 and -10.5.
-10.6 < –\(\sqrt{112}\) < -10.5
The irrational number ∛142 lies between the rational numbers with a distance of not more than 0.1 are 5.2 and 5.3.
5.2 <  ∛142 < 5.3
The irrational number -(1/4) π³ lies between the rational numbers with a distance of not more than 0.1 are -7.8 and -7.7.
-7.8 < -(1/4) π³ < -7.7

Question 18.
Write a rational approximation of each irrational number correct to 2 decimal places.
Answer:
\(\sqrt{31}\) = 5.5776
The rational approximation of irrational number \(\sqrt{31}\) is 5.58.
–\(\sqrt{112}\) = – 10.58300
The rational approximation of irrational number –\(\sqrt{112}\) is -10.58.
∛142 = 5.21710
The rational approximation of irrational number ∛142 is 5.22.
-(1/4) π³ = – 7.75156
The rational approximation of irrational number -(1/4) π³ is -7.75.

Question 19.
Graph on a real number line the interval and the approximate location of each irrational number.
Answer:

The given irrational numbers on the number lines as we can observe in the above image.

Question 20.
Order the irrational numbers from greatest to least using the symbol >.
Answer:
The given irrational numbers from greatest to least are \(\sqrt{31}\) > ∛142 > -(1/4) π³ > –\(\sqrt{112}\)

Use the real numbers below for questions 21 to 24.

-12\(\frac{3}{8}\), \(\frac{90}{7}\), –\(\sqrt{49}\), \(\sqrt{164}\), -8.207

Question 21.
Find the absolute value of each real number in decimal form, correct to three decimal places.
Answer:
-12(3/8)
= -(96 + 3)/8
= – 99/8
The absolute value of |-99/8| is 99/8.
The decimal form of 99/8 is 12.375.
90/7
The absolute value of |90/7| is 90/7.
The decimal form of 90/7 is 12.8571.
The decimal value 12.8571 is corrected to three decimal places is 12.857.
–\(\sqrt{49}\)
The absolute value of |-\(\sqrt{49}\)| is \(\sqrt{49}\).
The decimal form of \(\sqrt{49}\) is 7.000.
\(\sqrt{164}\)
The absolute value of |\(\sqrt{164}\)| is \(\sqrt{164}\).
The decimal form of \(\sqrt{164}\) is 12.8062.
The decimal value 12.8062 is corrected to three decimal places is 12.806.
-8.207
The absolute value of |-8.207| is 8.207.

Question 22.
Graph each real number on a real number line.
Answer:

questions 23.
Order the numbers from least to greatest using the symbol <.
Answer:
The given real numbers from least to greatest are -12\(\frac{3}{8}\) < -8.207 <  –\(\sqrt{49}\) < \(\sqrt{164}\) < \(\frac{90}{7}\).

Question 24.
Math Journal Explain why the product of a nonzero rational number and an irrational number is irrational.
Answer:
The product of a non- zero rational and an irrational number is irrational because if we add any rational value to an irrational number it remains irrational.

Solve.

Question 25.
Round each number to the given number of significant digits.

Answer:

Question 26.
The distance between New York City, New York, and Sydney, Australia, is about 15,989 kilometers. What is this distance when rounded to 2 significant digits?
Answer:
The distance between New York City, New York, and Sydney, Australia, is 15,989 kilometers. After rounding to 2 significant digits the distance is 16,000 kilometers.

Question 27.
A dime has a mass of 2.268 grams. Round the mass of the dime to 3 significant digits.
Answer:
The dime has a mass of 2.268 grams. After rounding the mass of the dime to 3 significant digits the mass is 2.27 grams.

Question 28.
In 2009, the population of New York City was estimated at 8,391,881. Round this population estimation to the given number of significant digits.
a) 2 significant digits
Answer:
The given population 8,391,881 is rounded to 2 significant digits as 8.3 million.

b) 3 significant digits
Answer:
The given population 8,391,881 is rounded to 3 significant digits as 8.39 million.

c) 4 significant digits
Answer:
The given population 8,391,881 is rounded to 4 significant digits as 8,392 thousands.

Question 29.
A square has an area of 72 square inches. What is the length of a side of the square correct to 2 significant digits?
Answer:
A square has an area of 72 square inches.
Length of square = ?
Area of the square = side x side
72 = s²
\(\sqrt{72}\) = s
8.485 = s
8.5 inches = length of a side
The length of a side of the square is corrected to 2 significant digits as 8.5 inches.

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 1 Lesson 1.4 Introducing the Real Number System to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 1 Lesson 1.4 Answer Key Introducing the Real Number System

Math in Focus Grade 7 Chapter 1 Lesson 1.4 Guided Practice Answer Key

Represent each real number as a decimal rounded to 2 decimal places.

Question 1.
208\(\frac{12}{19}\)
Answer:
208(12/19)
= (3,952 + 12)/19
= 3,964/19
=208.6315
= 208.63
Explanation:
The mixed fraction 208(12/19) in fraction form as 3,964/19. Divide 3,964 by 19 the quotient is 208.6315. The given real number as a decimal rounded to 2 decimal places is 208.63.

Question 2.
–\(\frac{456}{37}\)
Answer:
-456/37
= -12.3243
= -12.32
Explanation:
Perform division operation on given real number. Divide -456 by 37 the quotient is -12.3243. The given real number as a decimal rounded to 2 decimal places is -12.32.

Question 3.
4π
Answer:
4π
= 12.56637
= 12.57
Explanation:
Perform multiplication operation on given real number. Multiply 4 with π the product is 12.56637. The given real number as a decimal rounded to 2 decimal places is 12.57.

Represent each real number below as a decimal rounded to 4 decimal places when necessary. Locate each number on a real number line.

Question 4.
–\(\frac{199}{23}\), -12.054, π³, \(\frac{\pi}{2}\), \(\sqrt{200}\), –\(\sqrt{289}\)
Answer:

–\(\frac{199}{23}\) = -8.65217
The real number above as a decimal rounded to 4 decimal places as -8.6522.
π³ = 31.00627 
The real number above as a decimal rounded to 4 decimal places as 31.0063.
\(\frac{\pi}{2}\) = 1.570796
The real number above as a decimal rounded to 4 decimal places as 1.5708.
\(\sqrt{200}\) = 14.14213
The real number above as a decimal rounded to 4 decimal places as 14.1421.
–\(\sqrt{289}\) = -17
Located each number on a real number line as we can observe in the above image.

Math in Focus Course 2A Practice 1.4 Answer Key

Use a calculator. Compare each pair of real numbers using either < or >.

Question 1.
\(\sqrt{18}\) and \(\sqrt{19}\)
Answer:
\(\sqrt{18}\) = 4.242
\(\sqrt{19}\) = 4.358
\(\sqrt{18}\) < \(\sqrt{19}\)
Explanation:
By using calculator the given real numbers are compared. The real number \(\sqrt{18}\) is less than \(\sqrt{19}\).

Question 2.
-2.23 and –\(\sqrt{5}\)
Answer:
-2.23
–\(\sqrt{5}\) = -2.24
-2.23 > –\(\sqrt{5}\)
Explanation:
By using calculator the given real numbers are compared. The real number -2.23 is greater than –\(\sqrt{5}\).

Question 3.
6.61640 and \(\sqrt{38}\)
Answer:
6.61640
\(\sqrt{38}\) = 6.16441
6.61640 > \(\sqrt{38}\)
Explanation:
By using calculator the given real numbers are compared. The real number 6.61640 is greater than \(\sqrt{38}\).

Question 4.
-87.09812 and -87.098126…
Answer:
-87.09812 > -87.09813
Explanation:
By using calculator the given real numbers are compared. The real number -87.09812 is greater than -87.09813.

Use the irrational numbers below for questions 5 to 7.

Question 5.
Find the absolute value of each irrational number with 3 decimal places.
Answer:
The absolute value of each irrational number with 3 decimal places are 5.099, 6.775, 3.142, 1.772.

Question 6.
Graph each irrational number on a real number line.
Answer:

In the above image we can observe the given irrational numbers on a real number line.

Question 7.
Order the irrational numbers from greatest to least using the symbol >.
Answer:
The irrational numbers from greatest to least are as below.

Use the real numbers below for questions 8 and 9.

Question 8.
Copy and complete the table using the real numbers above.

Answer:

In the above table we can observe the given real number as rational numbers and irrational numbers.

Question 9.
Order the real numbers from least to greatest using the symbol <.
Answer:
The real numbers from least to greatest are as below.

Solve.

Question 10.
Using a formula from physics, a sky diver knows that she can free fall \(\sqrt{875}\) seconds before opening her parachute.
a) About how many seconds (to the nearest 0.01 second) can she free fall?
Answer:
A skydiver knows she can free fall for \(\sqrt{875}\) seconds before opening lier parachute.
\(\sqrt{875}\) = 29.58 seconds
She can free fall for 29.58 seconds before opening her parachute.

b) For her next jump, she can free fall for 29.55 seconds. Does she have more time on her first or second jump? Explain using a number line.
Answer:

For first jump she can free fall for 29.58 seconds
For second jump she can free fall for 29.55 seconds
Graph 29.55 and 29.58 on a number line :

Since, 29.55 is on the left of 29.58
So, 29.55 < 29.58
Thus, She have more time on her first jump.

29.58; First Jump

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 3 Lesson 3.7 Real-World Problems: Algebraic Reasoning to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 3 Lesson 3.7 Answer Key Real-World Problems: Algebraic Reasoning

Math in Focus Grade 7 Chapter 3 Lesson 3.7 Guided Practice Answer Key

Complete.
Question 1.
The area of a triangle is (u + 10) square centimeters. The ratio of the area of the unshaded region to the area of the shaded region is 1 : 3. Using algebraic reasoning, express the area of the shaded region in terms of u.

Area of shaded region:
Use the distributive property. Simplify.
The area of the shaded region of the triangle is square centimeters.
Answer:
The area of the shaded region of the triangle is \(\frac{3}{4}\) (u + 100) square centimeters.

Explanation:
The area of a triangle is (u + 10) square centimeters.
The ratio of the area of the unshaded region to the area of the shaded region is 1 : 3.
=> Shaded region = 3.
Unshaded region = 1.
Area of the shaded region of the triangle = \(\frac{3}{4}\) × Area of a triangle
= \(\frac{3}{4}\) ×(u + 10)
= \(\frac{3}{4}\) (u + 100) square centimeters.

Question 2.
There are 25 nickels and quarters, w coins are nickels and the rest are quarters.

a) Write an algebraic expression for the number of coins that are quarters.
Number of quarters:

There are quarters.
Answer:
Number of quarters = 25 – w.

Explanation:
There are 25 nickels and quarters,
w coins are nickels and the rest are quarters.
=> Total number of coins = 25.
=> Number of nickels = w.
Number of quarters = Total number of coins – Number of nickels
= 25 – w.

b) Find the total value of the quarters.
Total value of quarters:

The total value of the quarters is dollars.
Answer:
Total value of quarters = (25 – w) dollars.

Explanation:
Number of quarters = 25 – w.
Total value of quarters = (25 – w) dollars.

Complete each ? with + or -, and with the correct value.
Question 3.
Amy has x comic books, Melvin has \(\left(\frac{2 x}{5}+1\right)\) comic books, and Joel has \(\frac{x}{10}\) fewer comic books than Melvin. Express the total number of comic books that Amy, Melvin, and Joel have in terms of x.

Answer:
Total number of comic books = \(\frac{17x}{10}\) + 2.

Explanation:
Amy has x comic books, Melvin has \(\left(\frac{2 x}{5}+1\right)\) comic books, and Joel has \(\frac{x}{10}\) fewer comic books than Melvin.
Number of Melvin has comic books = \(\left(\frac{2 x}{5}+1\right)\)
Number of Joel has comic books = Number of Melvin has comic books – \(\frac{x}{10}\)
=> \(\left(\frac{2 x}{5}+1\right)\) – \(\frac{x}{10}\)
=>\(\frac{2x}{5}\) – \(\frac{x}{10}\) + 1
LCD of 5 n 10 = 10.
=> (2x × 2) – x] ÷ 10 + 1
=> (4x -x) ÷ 10 + 1
=> \(\frac{3x}{10}\) + 1.
Total number of comic books = Number of  Amy has comic books + Number of Melvin has comic books + Number of Joel has comic books
= x + \(\left(\frac{2 x}{5}+1\right)\)  + \(\frac{3x}{10}\) + 1
= x + \(\frac{2x}{5}\) + \(\frac{3x}{10}\) + 1 + 1
LCD of 5 n 10 = 10.
= [10x + (2x × 2) + 3x] ÷ 10 + 2
= (10x + 4x + 3x) ÷ 10 + 2
= \(\frac{17x}{10}\) + 2.

Solve.
Question 4.
A shoe store stocks x pairs of sneakers and y pairs of sandals. During a promotion, a pair of sneakers is priced at $50 and a pair of sandals at $36. The shop manages to sell half the sneakers and 80% of the sandals. Write an expression for the total amount of sales the store makes.

Answer:
Total amount of sales the store makes = \(\frac{x}{2}\) + \(\frac{4}{5}\)y.

Explanation:
A shoe store stocks x pairs of sneakers and y pairs of sandals.
Total number of pair of sneakers a shoe store = x.
Total number of pair of sandals a shoe store = y.
a pair of sneakers is priced at $50 and a pair of sandals at $36.
=> Cost of pair of sneakers = $50.
Cost of pair of sandals = $36.
The shop manages to sell half the sneakers and 80% of the sandals.
Number of sneakers sold = Total number of pair of sneakers a shoe store ÷ 2.
= x ÷ 2 or \(\frac{x}{2}\)
Number of sandals sold = (80 ÷ 100) × y
= \(\frac{80}{100}\)y.
= \(\frac{4}{5}\)y
Total amount of sales the store makes = Number of sneakers sold + Number of sandals sold
= \(\frac{x}{2}\) + \(\frac{4}{5}\)y.

Math in Focus Course 2A Practice 3.7 Answer Key

Solve each question using algebraic reasoning.
Question 1.
40% of k liters of acid are added to 60% of w liters of water. Write an algebraic expression for the total volume of the solution.
Answer:
Total volume of the solution = (40% × k) + (60% × w).

Explanation:
40% of k liters of acid are added to 60% of w liters of water.
=> (40% × k) + (60% × w)
Total volume of the solution = (40% × k) + (60% × w).

Question 2.
Write an algebraic expression for the perimeter of the quadrilateral shown.

Answer:
Perimeter of the quadrilateral = \(\frac{37}{5}\)w + \(\frac{17}{8}\)

Explanation:
Perimeter of the quadrilateral = AB + BC + CD + AC
Perimeter of the quadrilateral = [5w + \(\frac{13}{8}\)] ft + [\(\frac{8}{5}\)w – \(\frac{1}{2}\)] ft +  \(\frac{5}{4}\) ft + [\(\frac{4}{5}\)w + 1] ft
= 5w + \(\frac{8}{5}\)w + \(\frac{4}{5}\)w + \(\frac{13}{8}\) – \(\frac{1}{2}\) + 1
LCD of 8 n 2 = 8.
= [(25w + 8w + 4w) ÷ 5] + [(13 – (1 × 4) + 8) ÷ 8]
= (33w + 4w) ÷ 5] + (13 – 4 + 8) ÷ 8
= (37w ÷ 5) + [(9 + 8) ÷ 8]
= (37w ÷ 5) + (17 ÷ 8) or \(\frac{37}{5}\)w + \(\frac{17}{8}\)

Question 3.
If the average daily sales amount for the past 5 days was (2.3q + 1.4) dollars, write an algebraic expression for the total sales amount for the past 5 days.
Answer:
Total sales amount for the past 5 days = 4.6q + 2.8.

Explanation:
If the average daily sales amount for the past 5 days was (2.3q + 1.4) dollars.
=> Let the sales be x.
Average daily sales for 5 days = (2.3q + 1.4)
Total sales amount for the past 5 days = Average daily sales for 5 days × 2
= (2.3q + 1.4) × 2
= (2.3q × 2) + (1.4 × 2)
= 4.6q + 2.8.

Question 4.
The weight of 2 science fiction books and 1 autobiography is \(\frac{5}{6}\) w pounds. What is the total weight of 4 of these science fiction books and 2 of these autobiographies?
Answer:
Total weight of 4 of these science fiction books and 2 of these autobiographies = \(\frac{5}{3}\) w pounds.

Explanation:
The weight of 2 science fiction books and 1 autobiography is \(\frac{5}{6}\) w pounds.
=> Weight of 2 science fiction books and 1 autobiography = \(\frac{5}{6}\) w pounds.
Total weight of 4 of these science fiction books and 2 of these autobiographies = 2 × Weight of 2 science fiction books and 1 autobiography
= 2 × \(\frac{5}{6}\) w pounds.
= \(\frac{5}{3}\) w pounds.

Question 5.
On her way to work, Ms. Bowman waited 20 minutes at a subway station. The train ride took her (x + 30) minutes to reach Grand Central Station. Then, she walked for another \(\frac{1}{3}\)x minutes before reaching her office. How much time, in minutes, did Ms. Bowman take to travel to her office?
Answer:
Number of minutes Ms. Bowman take to travel to her office = \(\frac{4}{3}\)x + 50.

Explanation:
Number of minutes Ms. Bowman waited  at a subway station = 20.
Number of minutes train ride took her to reach Grand Central Station = (x + 30)
Number of minutes train she walked before reaching her office = \(\frac{1}{3}\)x
Number of minutes Ms. Bowman take to travel to her office = Number of minutes Ms. Bowman waited  at a subway station + Number of minutes train ride took her to reach Grand Central Station + Number of minutes train she walked before reaching her office
= 20 + (x + 30) + \(\frac{1}{3}\)x
= x + 20 + 30 + \(\frac{1}{3}\)x
= x + \(\frac{1}{3}\)x + 50
= [(3x + x) ÷ 3] + 50
= \(\frac{4}{3}\)x + 50.

 

Question 6.
A ribbon measuring (v + 4) feet in length was cut into two pieces in the ratio 3 : 7. What was the length of the longer piece?
Answer:
Length of longer piece =  7x or 7(v+4)/10.

Explanation:
Total length of ribbon = (v + 4)
Ratio of the ribbon cut into two pieces = 3 : 7
=>let the two pieces be 3x and 7x , then
3x + 7x = v+4
10x = v+4
x = (v+4)/10
Length of the two pieces:
one piece = 3x or 3(v+4)/10.
Other piece =  7x or 7(v+4)/10.

 

Question 7.
When one-fifth of the boys left, there were still b boys and g girls who stayed to see a program. What was the total number of boys and girls at the beginning of the program?
Answer:
Total number of boys and girls at the beginning of the program = \(\frac{5}{4}\)b + g.

Explanation:
Number of girls = g.
Let the boys at the beginning be x.
Then, subtract one fifth from x to get b boys.
=> x – \(\frac{1}{5}\) = b.
=> (5x – x) ÷ 5 = b
=> 4x = b × 5
=> 4x = 5b
=> x = \(\frac{5}{4}\)b.
Total number of boys and girls at the beginning of the program = Number of boys at the beginning + Number of girls
= \(\frac{5}{4}\)b + g.
Question 8.
John is paid at an hourly-rate of $15 an hour and overtime time rate of 1.5 times his hourly-rate for his work. If John puts in w regular hours and y overtime hours in a week, what is his total wage for the week?
Answer:
Total wage for the week = $262.50.

Explanation:
Number of dollars John is paid at an hourly-rate for a day= 15.
overtime time rate of 1.5 times his hourly-rate for his work.
=> Number of dollars he gets for overtime for a day = 1.5 × Number of dollars John is paid at an hourly-rate for a day
= 1.5 × 15
= 22.5.
If John puts in w regular hours and y overtime hours in a week.
Number of days in a week = 7.
Total wage for the week = Number of days in a week × (Number of dollars John is paid at an hourly-rate for a day + Number of dollars he gets for overtime for a day)
= 7  × ( $15 + $22.5)
= 7 × $37.5
= $262.50.

Question 9.
Nathan is p years old now. In 10 years’ time, he will be 3 times as old as Martin. Express Martin’s age 10 years from now in terms of p.
Answer:
Martin’s age 10 years from now = (p – 20) ÷ 3 years.

Explanation:
Age of Nathan now = p years.
Let Martin age be m years now.
In 10 years’ time, he will be 3 times as old as Martin.
Age of Nathan 10 years later = (p + 10) = 3(m + 10)
=> p + 10 = 3m + 30
=> p = 3m + 30 – 10
=> p = 3m + 20.
=> p – 20 = 3m
=> (p – 20) ÷ 3 years = m.

Question 10.
Tom bought a computer for 15% off from the list price of p dollars. If the sales tax was 8%, how much did he pay for the computer including sales tax?
Answer:
Total price of computer he paid= 0.918p.

Explanation:
List price of computer Tom bought = p dollars.
Tom bought a computer for 15% off
=> Sales price of computer = p – (15% × p)
= (100p – 15p) ÷ 100
= 85p ÷ 100
= 0.85p.
Tax on Sales tax = (8% ) × Sales price of computer
= (8 ÷ 100) × 0.85p
= 0.08 × 0.85p
= 0.068p.
Total price of computer he paid = Sales price of computer  + Tax on Sales tax
= 0.85p + 0.068p
= 0.918p.

Question 11.
A farmer collected some eggs from his farm and found b eggs broken. He packed the remaining eggs in c egg cartons. Each egg carton can hold a dozen eggs and no eggs were leftover. Write an algebraic expression for the number of eggs he collected initially in terms of b and c.

Answer:
Number of eggs he collected initially = 12c + b.

Explanation:
Number of eggs broken = b.
Number of remaining eggs he packed in carton = c.
Number of eggs each canton can hold = 12 or dozen.
Number of eggs he collected initially = (Number of eggs each canton can hold × Number of remaining eggs he packed in carton) + Number of eggs broken
= (12 × c) + b
= 12c + b.

Question 12.
A teacher from Anderson Middle School printed k nametags in preparation for the science fair. Half of the nametags were given out to students and 100 nametags were given out to parents. Three-fifths of the remaining nametags were given out to teachers and contest judges. How many nametags were not given out?
Answer:
Number of nametags not given = \(\frac{1}{5}\)k –  40.

Explanation:
Total number of nametags teacher from Anderson Middle School printed in preparation for the science fair = k.
Number of nametags given to students = \(\frac{1}{2}\) × Total number of nametags teacher from Anderson Middle School printed in preparation for the science fair
= \(\frac{1}{2}\) × k
= \(\frac{1}{2}\)k.
Number of nametags given to parents = 100.
Total number of nametags given to parents and students = Number of nametags given to students + Number of nametags given to parents
= \(\frac{1}{2}\)k + 100
Remaining nametags = k – [\(\frac{1}{2}\)k + 100]
= (2k – k) ÷ 2 – 100
= \(\frac{1}{2}\)k – 100
Total number of nametags given to parents and students = \(\frac{3}{5}\) [Remaining nametags]
= \(\frac{3}{5}\) [\(\frac{1}{2}\)k – 100]
= \(\frac{3}{10}\)k – 60.
Number of nametags not given = \(\frac{2}{5}\) [\(\frac{1}{2}\)k – 100]
= \(\frac{1}{5}\)k –  40.

Question 13.
At the beginning of a journey, the fuel tank of a car was \(\frac{3}{4}\)-full. When the car reached its destination, it had consumed 60% of the gasoline in the tank. The full capacity of the fuel tank is w gallons.
a) Write an algebraic expression for the amount of gasoline left in the fuel tank.
Answer:
Amount of gasoline left in the fuel tank = 2w ÷ 5 gallons.

Explanation:
Total Capacity of fuel in the car = w gallons.
Capacity of the fuel tank of a car at the beginning of a journey = \(\frac{3}{4}\)w gallons.
Capacity of fuel the car consumed to reach its destination = 60% ×Total Capacity of fuel in the car
= 60% of w.
= \(\frac{6}{10}\)w
= \(\frac{3}{5}\) w gallons.
Amount of gasoline left in the fuel tank = Total Capacity of fuel in the car – Capacity of fuel the car consumed to reach its destination
= w – \(\frac{3}{5}\) w.
= (5w – 3w) ÷ 5
= 2w ÷ 5 gallons.

b) If w = 15.5, how much gasoline was left at the end of the journey?
Answer:
Amount of gasoline left at the end of the journey = 6.2 gallons.

Explanation:
Amount of gasoline left in the fuel tank = 2w ÷ 5 gallons.
If w = 15.5:
Amount of gasoline left at the end of the journey = 2w ÷ 5
= (2 × 15.5) ÷ 5
= 31 ÷ 5
= 6.2 gallons.

Bain @ work
Bryan and his father are from Singapore, where the temperature is measured in degrees Celsius. While visiting downtown Los Angeles, Bryan saw a temperature sign that read 72°F. He asked his father what the equivalent temperature was in °C.

His father could not recall the Fahrenheit-to-Celsius conversion formula, C = \(\frac{5}{9}\)(F – 32). However, he remembered that water freezes at 0°C or 32°F and boils at 100°C or 212°F.

Using these two pieces of information, would you be able to help Bryan figure out the above conversion formula? Explain.
Answer:
Equivalent temperature of 72°F in Bryan asked his father = 22.22°C

Explanation:
Temperature Bryan saw While visiting downtown Los Angeles = 72°F
Fahrenheit-to-Celsius conversion formula:
(F – 32) ×\(\frac{5}{9}\)
= (72 – 32) × \(\frac{5}{9}\)
= 40 × \(\frac{5}{9}\)
= 200 ÷ 9
= 22.22 °C.