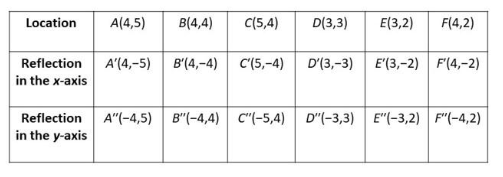
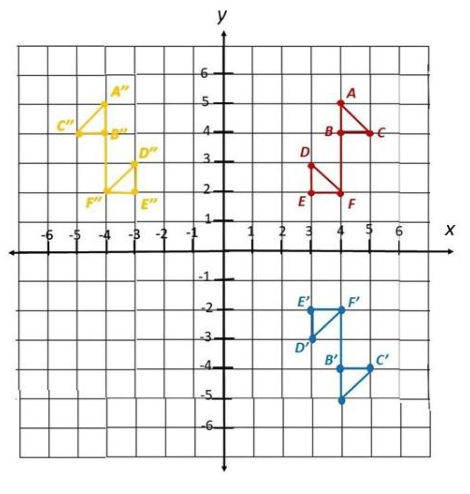
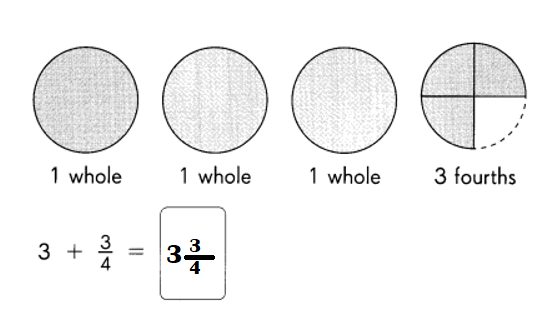
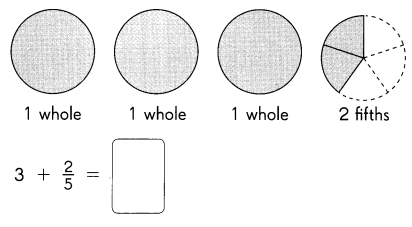
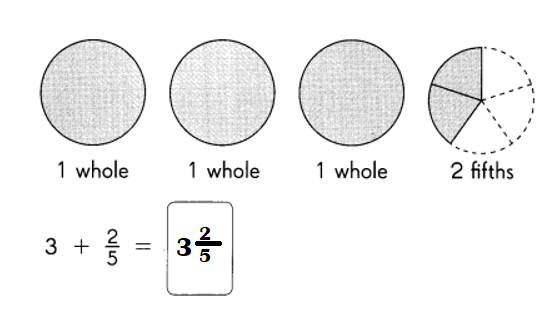
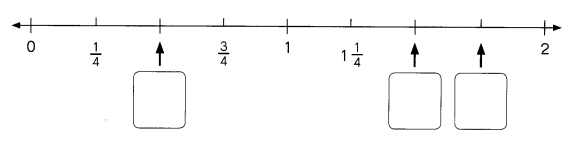
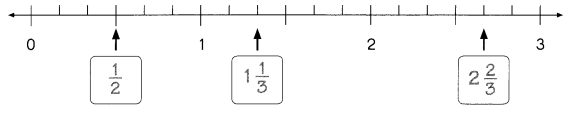
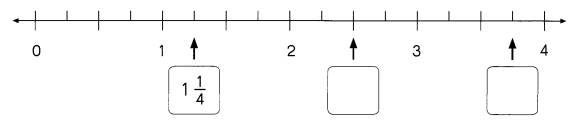
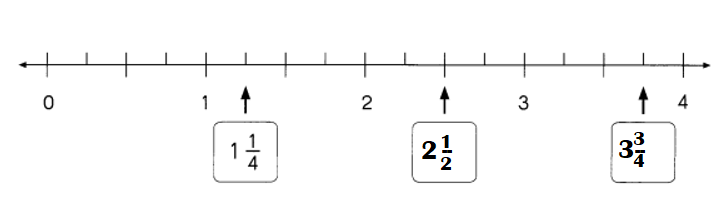
Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 2 Review Test to finish your assignments.
Math in Focus Grade 8 Course 3 A Chapter 2 Review Test Answer Key
Concepts and Skills
Tell whether each number is written correctly in scientific notation. If incorrectly written, state the reason.
Question 1.
10 • 102
Answer:
10 • 102 is correct in scientific notation, because the given notation is equal to 10.
Question 2.
0.99 • 1012
Answer:
The 0.99 • 1012 is incorrect in scientific notation.
The coefficient is less than 1
Question 3.
1.4 • 102
Answer:
1.4 • 102 is Correct in scientific notation, because the given notation is in between 1 to 10.
Question 4.
0.4 • 1025
Answer:
0.4 • 1025 is incorrect in scientific notation.
Because the coefficient is less than 1.
Write each number in scientific notation.
Question 5.
714,000
Answer:
714,000 in the scientific notation is
7.14 •10⁵
Question 6.
0.00087
Answer:
0.00087 in the scientific notation is 0.87 • 10-3
Write each number in standard form.
Question 7.
3.46 • 102
Answer:
3.46 • 10²
10² = 100
3.46 × 100 = 346.
Question 8.
5.4 • 104
Answer:
5.4 • 10⁴
5.4 × 10,000
= 54,000
Identify the greater number in each pair of numbers.
Question 9.
7.8 • 10-5 and 5.4 • 10-7
Answer:
7.8 • 10-5 is greater than the 5.4 • 10-7
Because 7.8 • 10-5 has a big exponent.
Question 10.
1.4 • 10-5 and 6 • 10-4
Answer:
6 • 10-4 is greater than the 1.4 • 10-5
Because 6 • 10-4 has a big exponent.
Question 11.
6.5 • 10-15 and 9.3 • 10-12
Answer:
9.3 • 10-12 is greater than the 6.5 • 10-15
Because 9.3 • 10-12 has a big exponent.
Question 12.
3.5 • 10-2 and 4 • 10-3
Answer:
3.5 • 10-2 is greater than the 4 • 10-3
Because 3.5 • 10-2 has a big exponent.
Evaluate. Write your answer in scientific notation. Round the coefficient to the nearest tenth.
Question 13.
2.44 • 103 + 1.9 • 105
Answer:
2.44 • 103 + 1.9 • 105
Rewrite the numbers to have the same power of 10
0.0244 • 10⁵ + 1.9 • 10⁵
Now add the numbers
0.0244 + 1.9 = 1.9244
Rewrite the number in scientific notation is
1.9244 • 10⁵
1.9244 rounded to the nearest tenth is 1.9
Question 14.
3.12 • 10-3 – 3 • 10-3
Answer:
3.12 • 10-3 – 3 • 10-3
Now subtract the numbers
(3.12 – 3) • 10-3
Rewrite the number in scientific notation is
0.12 • 10-3
Question 15.
2.4 • 10-2 • 5 • 10-1
Answer:
2.4 • 10-2 • 5 • 10-1
Here bases are equal powers should be added.
2.4 • 5 • 10-3
12 • 10-3
Question 16.
3.2 • 108 ÷ (1.6 • 104)
Answer:
3.2 • 108 ÷ (1.6 • 104)
3.2/1.6 × 10⁸/10⁴
3.2/1.6 × 10⁴
2 • 10⁴
Express each of the following in prefix form. Choose the most appropriate unit.
Question 17.
2.8 • 103 meters
Answer:
2.8 • 103 meters
We have to using the prefix form
2.8 • 10¹ • 10²
2.8 • 10¹ centimeters
28 centimeters
Question 18.
1.5 • 10-6 meter
Answer:
1.5 • 10-6 meter
We have to use the prefix form
1.5 • 10-6 meter
1.5 micrometers
Question 19.
6.4 • 109 bytes
Answer:
6.4 • 109 bytes
We have to use the prefix form
64 • 108 bytes
Question 20.
4.8 • 10-9 gram
Answer:
4.8 • 10-9 gram
We have to use the prefix form
4.8 • 10-6 •10-3 gram
4.8 •10-3 micrograms
0.0048 micrograms
Problem Solving
The table shows the length of two organisms. Use the table to answer questions 21 to 23.

Question 21.
Which organism is longer?
Answer:
Given that the length of eriophyid mite = 250 micrometers
The length of patiriella parvivipara = 5 millimeter.
1 micrometer = 0.001 millimeters
250 micrometers = 0.001 • 25 = 0.025 millimetres
Therefore, The length of patiriella parvivipara is longer.
Question 22.
Express the length of the eriophyid mite in millimeters.
Answer:
Given that the length of the eriophyid mite 250 micrometers
1 micrometer = 0.001 millimeters
250 micrometers = 0.001 • 25 = 0.025 millimeters
Therefore the length of the eriophyid mite in millimeters is 0.025
Question 23.
Write each length in scientific notation using the basic unit.
Answer:
Given that the length of eriophyid mite = 250 micrometers
0.025 • 104
The length of patiriella parvivipara = 5 millimeter.
5 millimetres = 0.5 • 10¹
The top five materials used in the automotive industry in the United States in 2000 are as shown in the table. Use the table to answer questions 24 to 26. Write your answers in scientific notation. Round coefficients to the nearest tenth.
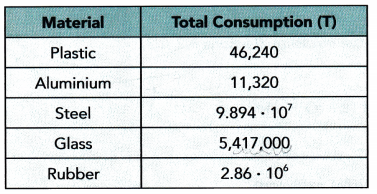
Question 24.
How much more plastic was used than aluminum?
Answer:
Given that the plastic material used in the automotive industry is 46240 = 46.240 • 10³
The aluminum Material used in the automotive industry is 11,320 = 11.320 • 10³
Plastic material – aluminium material = 46.240 • 10³ – 11.320 • 10³ = 34.92 = 3.492 • 10¹
Plastic material is 3.492 • 10¹ consumption is used more than aluminum.
34920 rounded to the nearest tenth is 34920
Question 25.
How much more steel was used than glass?
Answer:
Given that the steel material used in the automotive industry is 9.894 • 10⁷
9.894 • 10⁷
The glass material used in the automotive industry is 54,17,000 = 0.5417000 • 10⁷
Steel material – glass material = 9.894 • 10⁷ – 0.5417000 • 10⁷ = 9.3523 = 93.523 • 10-1
93.523 • 10-1 rounded to the nearest tenth is 93.5 • 10-1
Question 26.
Find the total consumption of these materials used by the automotive industry in 2000.
Answer:
Given that the plastic material used in the automotive industry is 46,240 = 46.240 • 10³
The aluminum material used in the automotive industry is 11,320 = 11.320 • 10³
The steel material used in the automotive industry is 9.894 • 10⁷
The glass material used in the automotive industry is 54,17,000 = 0.5417000 • 10⁷
The rubber material used in the automotive industry is 2.86 • 10⁶
Total consumption = 46.240 • 10³ + 11.320 • 10³ + 9.894 • 10⁷ + 0.5417000 • 10⁷ + 2.86 • 10⁶ = 70.8547 • 10²⁶
70.8547 • 10²⁶ rounded to the nearest tenth is 70.85 • 10²⁶
Question 27.
The table shows the weights of some animals. Round your answers to the nearest tenth.
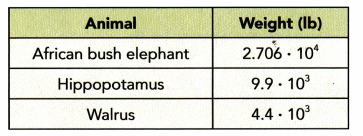
a) About how many times greater than the weight of a walrus is the weight of a hippopotamus?
Answer:
Given that the weight of a walrus = 4.4 • 10³
And the weight of a hippopotamus = 9.9 • 10³
weight of hippopotamus – weight of walrus = 9.9 • 10³ – 4.4 • 10³ = 5.5
Weight of a hippopotamus is 5.5 times greater than that of a walrus.
5.5 rounded to the nearest tenth is 5.5
b) About how many times greater than the weight of a hippopotamus is the weight of an African bush elephant?
Answer:
Given that the weight of a hippopotamus = 9.9 • 10³
The weight of a African bush elephant = 2.706 • 10⁴ = 27.06 • 10³
Weight of African bush elephant – weight of a hippopotamus = 27.06;• 10³ – 9.9 • 10³ = 17.16
The weight of an African bush elephant is 17.16 times greater than the hippopotamus.
17.16 rounded to the nearest tenth is 17.2
Question 28.
The floor of the Palace of the Parliament in Romania measures 8.9 • 102 feet by 7.9• 102 feet. The building reaches 2.82 • 102 feet above ground, and 3.02 • 102 feet below ground. Use the formula for the volume of a rectangular prism to estimate the volume inside the palace.
Answer:
Length: 8.9 • 102 feet We are given the dimensions of the rectangular prism:
Width: 7.9 • 102 feet
Above height: 2.82 • 102 feet
Below height: 3.02 • 102 feet
Length • Width • (Above height + Below height) We determine the volume of the prism:
= 8.9 • 102 • 7.9 • 102 • (2.82 • 102 + 3.02 • 102)
= 8.9 • 102 7.9 • 102 • [(2.82 + 3.02) • 102]
= 8.9 • 102 • 7.9 • 102 • 5.84 • 102
= 8.9 • 7.9 • 5.84 • 102 • 102 • 102
= 410.6104 • 102+2+2
= 410.6104 • 106
= 4.106104 • 108
≈ 4.1 • 108 cube feet
Question 29.
The Stockholm Globe Arena in Sweden resembles a hemisphere. It has an inner diameter of about 1.1 • 102 meters. Find the approximate volume of the building. Use 3.14 as an approximation for π.
Answer:
Given that the inner diameter of a hemisphere is 1.1 • 10².
Assume that the building is in the shape of a hemisphere.
D = 2r
1.1 • 10² = 2r
r = 1.1 • 10²/2 = 110/2 = 55
Volume of a hemisphere = ⅔ πr³ cubic units
= ⅔ • 3.14 • (55)³
= 348,278.33