Math in Focus

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 4 Lesson 4.2 Understanding Slope-Intercept Form to finish your assignments.

Math in Focus Grade 8 Course 3 A Chapter 4 Lesson 4.2 Answer Key Understanding Slope-Intercept Form

Technology Activity

Materials
graphing calculator

EXPLORE THE RELATIONSHIP BETWEEN y = mx AND y = mx + b

Work in pairs

Answer:

Math Journal The equation of another line is given by 2y = 5x – 4. It can also be written as y = 2.5x – 2. Predict the y-intercept. Use the graphing calculator to check your prediction. Is your prediction correct?
Answer:
Slope m = 2.5
y-intercept = -2

Math in Focus Grade 8 Chapter 4 Lesson 4.2 Guided Practice Answer Key

Write an equation for each line.

Question 1.
The line passes through the points (, ) and (, ).
Slope m = \(\frac{?-?}{?-?}\)
= \(\frac{?}{?}\)
=

The line intersects the y-axis at the point (, ).
So, the y-intercept is .
So, the equation of the line is .
Answer:
The line passes through the points (6, 3) and (-4, -2).
Slope m = \(\frac{6-(-4)}{3-(-2)}\)
= \(\frac{10}{5}\)
= 2
The line passes through the y-axis at the point (0, 0).
Thus m = 2 and y-intercept b is 0.
y = 2x

Question 2.
The line passes through the points (, ) and (, ).
Slope m = \(\frac{?-?}{?-?}\)
= \(\frac{?}{?}\)
=

The line intersects the y-axis at the point (, ).
So, the y-intercept is .
So, the equation of the line is .
Answer:
The line passes through the points (1, -6) and (-4, 9).
Slope m = \(\frac{9-(-6)}{-4-1}\)
= \(\frac{15}{-5}\)
= -3
The line intersects the y-axis at the point (0, -3).
So, the y-intercept is -3.
So, the equation of the line is y = -3x -3.

Question 3.

Answer:
The line passes through the points (-5, -2) and (1, -2).
Slope m = \(\frac{-2-(-2)}{1+5}\)
= \(\frac{0}{6}\)
= 0
The line intersects the y-axis at the point (0, -2).
So, the y-intercept is -2.
So, the equation of the line is y = 0x -2.

Question 4.

Answer:
The line passes through the points (0, 2) and (2, 4).
Slope m = \(\frac{4-2)}{2-0}\)
= \(\frac{2}{2}\)
= 1
The line intersects the y-axis at the point (0, 0).
So, the y-intercept is 0.
So, the equation of the line is y = -2x + 2

Math in Focus Course 3A Practice 4.2 Answer Key

Identify the y-Intercept. Then calculate the slope using the points indicated.

Question 1.

Answer:
The line passes through the points (-2, -2) and (3, 3).
Slope m = \(\frac{3-(-2)}{3-(-2)}\)
= \(\frac{5}{5}\)
= 1
The line intersects the y-axis at the point (0, 0).
So, the y-intercept is 0.
So, the equation of the line is y = x.

Question 2.

Answer:
The line passes through the points (0, -1) and (2, -3).
Slope m = \(\frac{-3-(-1)}{2-0}\)
= \(\frac{-2}{2}\)
= -1
The line intersects the y-axis at the point (0, -1).
So, the y-intercept is -1.
So, the equation of the line is y = -1x -1.

Question 3.

Answer:
The line passes through the points (0, 3) and (8, -6).
Slope m = \(\frac{-6-3}{8-0}\)
= \(\frac{-9}{8}\)
m = \(\frac{-9}{8}\)
The line intersects the y-axis at the point (0, 3).
So, the y-intercept is 3.

Question 4.

Answer:
The line passes through the points (0, 2) and (4, 6).
Slope m = \(\frac{6-2}{4-0}\)
= \(\frac{4}{4}\)
m = 1
The line intersects the y-axis at the point (0, -2).
So, the y-intercept is -2.

Write an equation in the form y = mx or y = mx + b for each line.

Question 5.

Answer:
The line passes through the points (4, 3) and (-4, -3).
Slope m = \(\frac{-3-3}{-4-4}\)
= \(\frac{-6}{-8}\)
= \(\frac{3}{4}\)
The line intersects the y-axis at the point (0, 0).
So, the y-intercept is 0.
So, the equation of the line is y = \(\frac{3}{4}\)x

Question 6.

Answer:
The line passes through the points (-2, 4) and (2, -2).
Slope m = \(\frac{-2-4}{2+2}\)
= \(\frac{-6}{4}\)
= \(\frac{-3}{2}\)
The line intersects the y-axis at the point (0, 1).
So, the y-intercept is 1.
So, the equation of the line is y = \(\frac{-3}{2}\)x +1.

Question 7.

Answer:
The line passes through the points (-8, 3) and (0, -2).
Slope m = \(\frac{-2-3}{0+8}\)
= \(\frac{-5}{8}\)
The line intersects the y-axis at the point (0, -2).
So, the y-intercept is -2.
So, the equation of the line is y = \(\frac{-5}{8}\)x -2.

Question 8.

Answer:
The line passes through the points (0, 4) and (-3, -2).
Slope m = \(\frac{-2-4}{-3-0}\)
= \(\frac{-6}{-3}\)
= 2
The line intersects the y-axis at the point (0, 4).
So, the y-intercept is 4.
So, the equation of the line is y = 2x + 4

Graph each line using 1 grid square to represent 1 unit on both axes for the interval from -4 to 4. Then write the equation for each line.

Question 9.
The line passes through the points (-4, 3) and (-4, -2).
Answer:

Question 10.
The line passes through the points (-3, 4) and (1, 4).
Answer:

Question 11.
Math Journal Line A passes through the origin and has a negative slope. Line B has a positive y-intercept and a positive slope. Line C has a negative slope and a negative y-intercept. Give a possible equation for each line. Justify your answer.
Answer:
Possible equations: Line A: y = -3x; Line B: y = 5x + 2; Line C: y = -2x – 7.
For line A, the value of m in the equation y = mx + b is negative and the value of b is 0.
For line B, both m and b have positive values. For line C, both m and b have negative values.

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 4 Lesson 4.1 Finding and Interpreting Slopes of Lines to finish your assignments.

Math in Focus Grade 8 Course 3 A Chapter 4 Lesson 4.1 Answer Key Finding and Interpreting Slopes of Lines

Hands-On Activity

Materials:
graph paper

USE TRIANGLES TO FIND THE SLOPE OF A LINE

Work in pairs.

You can find the slope of any nonvertical line, not just. a line that represents a direct proportion, by finding the ratio of the rise to the run.

STEP 1: Graph the line below on graph paper. The line should pass through the points (0, 1) and (6, 4). Then draw and label three right triangles on the line as shown. The triangles should be the same shape but different sizes. Make sure that each right angle lies on the intersection of two grid lines.

STEP 2: Copy and complete the table.

STEP 3: What do you observe about the ratios in the last column of the table?

Math Journal As you have learned, the slope of a line is the ratio of the rise to the run. Which side of each triangle has a length equal to the rise? Which has a length equal to the run? For each line you drew, what did you notice about the three ratios you calculated?
Answer:

Hands-On Activity

Materials
graph paper

USE POINTS TO FIND THE SLOPE OF A LINE

STEP 1: Graph the line that passes through each pair of points, using 1 grid square to represent 1 unit on both axes for the interval from 0 to 7.
a) Line 1: (0, 1) and (4, 2)
b) Line 2: (0, 1) and (4, 5)
c) Line 3: (0, 1) and (4, 7)

STEP 2: For each line you drew, draw a right triangle. The segment connecting the two points should be the longest side. Find the length of the vertical side, the length of horizontal side, and the ratio \(\frac{\text { Length of vertical side }}{\text { Length of horizontal side }}\).

Math Journal Of the three lines drawn in STEP 1, which line has the greatest slope? Which line has the least slope? How can you tell by looking at the lines? How can you tell from the ratios you calculated?

Math in Focus Grade 8 Chapter 4 Lesson 4.1 Guided Practice Answer Key

Complete.

Question 1.
The graphs give information about the distance, d miles, traveled over time, t hours, by cars and trucks on a California highway. Which speed is slower?

Speed for cars:
Unit rate = \(\frac{\text { Rise }}{\text { Run }}\)
= \(\frac{?}{?}\)
= mi/h
Speed for trucks:
Unit rate = \(\frac{\text { Rise }}{\text { Run }}\)
= \(\frac{?}{?}\)
= mi/h
The slope for the car speed graph is , so the unit rate is miles per hour.
The slope for the truck speed graph is , so the unit rate is miles per hour.
The speed for is slower than the speed for .
Answer:
Speed for cars:
= \(\frac{100}{1.5}\)
= 66.6 mi/h
Speed for trucks:
= \(\frac{100}{2}\)
= 50 mi/h
The slope for the car speed graph is 66.6, so the unit rate is 67 miles per hour.
The slope for the truck speed graph is 50, so the unit rate is 50 miles per hour.
The speed for trucks is slower than the speed for car.

Question 2.
The graph passes through the points (, ) and (, )

Slope = \(\frac{\text { Rise }}{\text { Run }}\)
= \(\frac{?}{?}\)
= \(\frac{?}{?}\)
= \(\frac{?}{?}\)
The slope is .
Answer:
The graph passes through the points (-2, 4) and (2, -2)
Slope = \(\frac{\text { Rise }}{\text { Run }}\)
m = \(\frac{4+2}{-2-2}\)
= \(\frac{6}{-4}\)
= \(\frac{-3}{2}\)
The slope is \(\frac{-3}{2}\)

Question 3.
The graph passes through the points (, ) and (, )

Slope = \(\frac{\text { Rise }}{\text { Run }}\)
= \(\frac{?}{?}\)
= \(\frac{?}{?}\)
= \(\frac{?}{?}\)
The slope is .
Answer:
The graph passes through the points (4, 3) and (-2, -1)
Slope = \(\frac{\text { Rise }}{\text { Run }}\)
= \(\frac{-1-3}{-2-4}\)
= \(\frac{-4}{-6}\)
= \(\frac{2}{3}\)
The slope is 2/3.

Solve. Show your work.

Question 4.
The graphs represent the amount of water, w gallons, in Pool A over time, t hours, and the amount of water, w gallons, left in Pool B over time, t hours.

a) Find the slope of the line graph for Pool A. What does it represent?
Answer:
slope = 180/4
slope = 45

b) Find the slope of the line graph for Pool B. What does it represent?
Answer:
Slope = \(\frac{\text { Rise }}{\text { Run }}\)
= \(\frac{150}{4-0}\)
= 37.5

Complete.

Question 5.

Use the points (, ) and (, ):
Slope = \(\frac{\text { Rise }}{\text { Run }}\)
= \(\frac{?}{?}\)
= \(\frac{?}{?}\)
=
The slope is .
Answer:
Use the points (3, 4) and (3, 0):
Slope = \(\frac{\text { Rise }}{\text { Run }}\)
= \(\frac{0-4}{0}\)
= undefined
The slope is undefined.

Find the slope of the line passing through each pair of points.

Question 6.
M(-2, 0) and N(0, 4)
Let M (-2, 0) be (x₁, y₁) and N (0, 4) be (x₂, y₂).
Method 1
Slope = \(\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\)
= \(\frac{?}{?}\)
= \(\frac{?}{?}\)
=

Method 2
Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{?}{?}\)
= \(\frac{?}{?}\)
=
The slope is .
Answer:
Method 1
Slope = \(\frac{0-4}{-2-0}\)
= \(\frac{-4}{-2}\)
= 2
Slope = 2
Method 2
Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{4-0}{0+2}\)
= \(\frac{4}{2}\)
= 2
The slope is 2.

Question 7.
S(-5, 8) and T(-2, 2)
Let S (-5, 8) be (x₁, y₁) and T(-2, 2) be (x₂, y₂).

Method 1
Slope = \(\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\)
= \(\frac{?}{?}\)
= \(\frac{?}{?}\)
=

Method 2
Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{?}{?}\)
= \(\frac{?}{?}\)
=
The slope is .
Answer:
Let S (-5, 8) be (x₁, y₁) and T(-2, 2) be (x₂, y₂).
Method 1
Slope = \(\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\)
= \(\frac{8-2}{-5+2}\)
= \(\frac{6}{-3}\)
= -2

Method 2
Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{2-8}{-2+5}\)
= \(\frac{-6}{3}\)
= -2
The slope is -2.

Math in Focus Course 3A Practice 4.1 Answer Key

Find the slope of each line using the points indicated.

Question 1.

Answer:
Let the points be (-1,4) and (-4, -1)
Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{-1-4}{-4+1}\)
= \(\frac{-5}{-3}\)
= \(\frac{5}{3}\)
The slope is \(\frac{5}{3}\).

Question 2.

Answer:
Let the points be (-5,10) and (-1, 0)
Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{0-10}{-1+5}\)
= \(\frac{-10}{4}\)
= \(\frac{-5}{2}\)
The slope is \(\frac{-5}{2}\).

Question 3.

Answer:
Let the points be (-10,3) and (2, 3)
Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{3-3}{2-10}\)
= 0
The slope is 0.

Question 4.

Answer:
Let the points be (4,2) and (4, 0)
Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{0-2}{4-4}\)
= undefined
The slope is undefined.

Question 5.
Math Journal Jason says that the line in Graph B has a greater slope than the line in Graph A because it is steeper. What error is Jason making? Justify your answer.

Answer:
Jason compared the two lines visually. Because the two graphs have different scales for the vertical aces, the slopes cannot be accurately compared by their steepness.

Question 6.
Math Journal Andy graphs a vertical line through the points (5, 2) and (5, 5). He says the slope of the line is \(\frac{3}{0}\). What error is he making?
Answer:
Let the points be (5, 2) and (5, 5)
Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{5-2}{5-5}\)
= undefined
The slope is undefined.

Find the slope of the line passing through each pair of points.

Question 7.
A (-10, 3), B (0, 3)
Answer:
Let the points be A (-10, 3), B (0, 3)
Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{3-3}{0+10}\)
= 0
The slope is 0.

Question 8.
S(5, -2), T(2, -5)
Answer:
Let the points be S(5, -2), T(2, -5)
Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{-5+2}{2-5}\)
= \(\frac{-3}{-3}\)
= 1
The slope is 1.

Question 9.
P(0, -7), Q(-3, 5)
Answer:
Let the points be P(0, -7), Q(-3, 5)
Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{5+7}{-3-0}\)
= \(\frac{12}{-3}\)
= -4
The slope is -4.

Question 10.
X(4, 4), V(4, -2)
Answer:
Let the points be X(4, 4), V(4, -2)
Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{-2-4}{4-4}\)
= undefined
The slope is undefined.

Question 11.
Math Journal Two points have the same x-coordinates but different y-coordinates. Make a prediction about the slope of a line drawn through the points. Justify your prediction.
Answer:
Two points have the same x-coordinates but different y-coordinates. A vertical line graph is drawn. Because slope = rise/run and the run is 0, the slope is undefined. Any number divided by zero is undefined.

Question 12.
MathJournal Two points have the same y-coordinates but different x-coordinates. Make a prediction about the slope of a line drawn through the points. Justify your prediction.
Answer:
It is a line parallel to the x-axis. No matter what the value of x is, y stays the same.

Solve. Show your work.

Question 13.
In the Fahrenheit system, water freezes at 32°F and boils at 212°F. In the Celsius system, water freezes at 0°C and boils at 100°C.
a) Translate the verbal description into a pair of points in the form (temperature in °C, temperature in °F).
Answer: (0, 32); (100, 212)

b) Find the slope of the line passing through the pair of points in a).
Answer: 9/5

c) Suppose the temperature in a room goes up by 5°C. By how much does the temperature go up in degrees Fahrenheit? Explain.
Answer: By 9° F; The slope of the line is 9/5,
so a horizontal change of 5 corresponds to a vertical change of 9.

Question 14.
The table shows how much a certain amount of gasoline costs at two gasoline stations on a particular day.

a) At which station is each additional gallon of gasoline more expensive? Explain.
Answer:
The cost at station A is more expensive.
(1, 3) a) We consider the points:
(3, 11)
Slope_B = \(\frac{11-3}{3-1}\) The cost of an additional gallon is the slope of the line representing the cost
= \(\frac{8}{2}\)
= 4
We determine the slope of the tine representing the cost at Station A:
= 4
(1,4) We consider the points:
(3, 10)
slope_B = \(\frac{10-4}{3-1}\)
= \(\frac{6}{2}\)
= 3
As Slope_A > Slope_B, each additional gallon is more expensive at Station A.

b) Graph the relationship between cost and gallons of gasoline purchased for each station. Use 1 unit on the horizontal axis to represent 1 gallon for the x interval from 0 to 5, and 1 unit on the vertical axis to represent $2 for the y interval from 0 to 20.
Answer:
b) We graph the cost of gasoline at Station A and Station B:

c) Which graph is steeper?
Answer:
We notice that Graph A is steeper than Graph B.

a) Station A
b) See graphs
C) Graph A

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 4 Lines and Linear Equations to finish your assignments.

Math in Focus Grade 8 Course 3 A Chapter 4 Answer Key Lines and Linear Equations

Math in Focus Grade 8 Chapter 4 Quick Check Answer Key

Tell whether each graph represents a direct proportion. If so, find the constant of proportionality. Then write a direct proportion equation.

Question 1.

Answer:
If y = kx then y is said to be directly proportional to x.
y = 10x
y/10 = x
Thus the above graph is said to be constant of proportionality.

Question 2.

Answer: y = 1/10 x
The above graph is not direct proportion.

Go through the Math in Focus Grade 8 Workbook Answer Key Cumulative Review Chapters 3-4 to finish your assignments.

Math in Focus Grade 8 Course 3 A Cumulative Review Chapters 3-4 Answer Key

Concepts and Skills

Solve each equation. Show your work. (Lesson 3.1)

Question 1.
0.2(x + 2) – 2 = 0.4
Answer:
0.2x + 0.4 – 2 = 0.4
0.2x = 2
x = 2/0.2
x = 10

Question 2.
2(x – 5) – 3(3 – x) = \(\frac{1}{2}\) (x – 2)
Answer:
2x – 10 – 9 + 3x = \(\frac{1}{2}\)x – 1
5x – 18 = \(\frac{1}{2}\)x
4 \(\frac{1}{2}\)x = 18
4x = 36
x = 36/4 = 9

Question 3.
\(\frac{x}{3}\) + \(\frac{3+x}{6}\) = 3
Answer:
\(\frac{x}{3}\) + \(\frac{3+x}{6}\) = 3
2x + 3 + x = 18
3x = 18 – 3
3x = 15
x = 15/3
x = 5

Question 4.
\(\frac{2(x+3)}{5}\) – \(\frac{x-1}{2}\) = 2
Answer:
\(\frac{2(x+3)}{5}\) – \(\frac{x-1}{2}\) = 2
\(\frac{2x+6}{5}\) – \(\frac{x-1}{2}\) = 2
4x + 12 – 5x + 5 = 10
-x + 17 = 10
-x = 10 – 17
-x = -7
x = 7

Express each decimal as a fraction, without the use of calculator. (Lesson 3.1)

Question 5.
\(0 . \overline{5}\)
Answer:
\(\frac{5}{9}\)

Question 6.
\(0 . \overline{8}\)
Answer: \(\frac{8}{9}\)

Question 7.
\(0.2 \overline{7}\)
Answer: \(\frac{5}{18}\)

Question 8.
\(0 . \overline{09}\)
Answer: \(\frac{90}{999}\)

Tell whether each equation has one solution, no solution, or an infinite number of solutions. Show your work. (Lesson 3.2)

Question 9.
3x – 2 = -3(\(\frac{2}{3}\) – x)
Answer:
3x – 2 = -3(\(\frac{2}{3}\) – x)
3x – = -2 + 3x
3x – 3x + 2 = 0
2
Infinite solutions

Question 10.
3x + 6 = -2(\(\frac{3}{2}\) – x)
Answer:
3x + 6 = -2(\(\frac{3}{2}\) – x)
3x + 6 = -3 + 2x
3x – 2x = -3 – 6
x = -9
One solution

Question 11.
5(6a – 6) + 40 = 3(10a – 7) + 31
Answer:
5(6a – 6) + 40 = 3(10a – 7) + 31
30a – 30 + 40 = 30a – 21 + 31
Infinte solution

Question 12.
3x + 7 = -8(\(\frac{3}{4}\) – x)
Answer:
3x + 7 = -8(\(\frac{3}{4}\) – x)
3x + 7 = -6 + 8x
3x – 8x = -6 – 7
-5x = -13
x = 13/5
One solution

Question 13.
\(\frac{1}{4}\)(2x – 1) = \(\frac{1}{2}\)x + \(\frac{3}{8}\)
Answer:
Given,
\(\frac{1}{4}\)(2x – 1) = \(\frac{1}{2}\)x + \(\frac{3}{8}\)
\(\frac{1}{4}\)x – \(\frac{1}{4}\) = \(\frac{1}{2}\)x + \(\frac{3}{8}\)
\(\frac{1}{4}\)x – \(\frac{1}{2}\)x = \(\frac{1}{4}\) + \(\frac{3}{8}\)
–\(\frac{1}{4}\)x = \(\frac{5}{8}\)
x = –\(\frac{5}{2}\)
No solution

Question 14.
\(\frac{1}{8}\)x + 6 = \(\frac{1}{16}\)(2x – 96)
Answer:
Given,
\(\frac{1}{8}\)x + 6 = \(\frac{1}{16}\)(2x – 96)
\(\frac{1}{8}\)x + 6 = \(\frac{1}{8}\)x – 6
No solution

Find the value of y when x = 4. (Lesson 3.3)

Question 15.
2x – 1 = \(\frac{1}{2}\) + y
Answer:
2x – 1 = \(\frac{1}{2}\) + y
x = 4
2(4) – 1 = \(\frac{1}{2}\) + y
7 = \(\frac{1}{2}\) + y
y = 7 – \(\frac{1}{2}\)
y = 6 \(\frac{1}{2}\) or 6.5

Question 16.
\(\frac{1}{4}\)(2y – 1) = 0.6 + \(\frac{5x}{8}\)
Answer:
Given,
\(\frac{1}{4}\)(2y – 1) = 0.6 + \(\frac{5x}{8}\)
X = 4
\(\frac{1}{4}\)(2y – 1) = 0.6 + \(\frac{5(4)}{8}\)
\(\frac{1}{4}\)(2y – 1) = 0.6 + \(\frac{20}{8}\)
0.25 (2y – 1) = 0.6 + 2.5
0.5y – 0.25 = 3.1
0.5y = 3.1 + 0.25
0.5y = 3.35
y = 6.7

Express y in terms of x. Find the value of y when x = 4. (Lesson 3.4)

Question 17.
6(3x + y) = 3
Answer:
Given equation
6(3x + y) = 3
18x + 6y = 3
Substitute the value of x in the given equation
x = 4
18(4) + 6y = 3
72 + 6y = 3
24 + 2y = 1
2y = -23
y = -23/2
y = -11 1/2

Question 18.
\(\frac{2 x-1}{4}\) = 3y
Answer:
Given,
\(\frac{2 x-1}{4}\) = 3y
Substitute the value of x in the given equation
3y = \(\frac{2 x-1}{4}\)
3y = (2(4) – 1)4
3y = 7/4
y = 7/12

Express x in terms of y. Find the value of x when y = -2. (Lesson 3.4)

Question 19.
(\(\frac{2x-y}{5}\)) = 9
Answer:
Given,
(\(\frac{2x-y}{5}\)) = 9
2x – y = 9 × 5
2x – y = 45
Substitute the value of y in the given equation
y = -2
2x – (-2) = 45
2x + 2 = 45
2x = 45 – 2
2x = 43
x = 43/2
x = 21.5

Question 20.
0.75(x + y) = 12
Answer:
Given,
0.75(x + y) = 12
0.75x + 0.75y = 12
Substitute the value of y in the given equation
y = -2
0.75x + 0.75 (-2) = 12
0.75x – 1.5 = 12
0.75x = 12 – 1.5
0.75x = 10.5
x = 14

Find the slope of the line passing through each pair of points. (Lesson 4.1)

Question 21.
A (1, 2), B (4, 8)
Answer:
The line passes through the points (1, 2) and (4, 8).
Slope m = \(\frac{8-2}{4-1}\)
= \(\frac{6}{3}\)
= 2
Thus the slope, m = 2

Question 22.
C(1, 4), D(2, 7)
Answer:
The line passes through the points (1, 4) and (2, 7).
Slope m = \(\frac{7-4}{2-1}\)
= \(\frac{3}{1}\)
= 3
Thus the slope, m = 3

Question 23.
E (0, 0), F (-7, 7)
Answer:
The line passes through the points (0, 0) and (-7, 7).
Slope m = \(\frac{7-0}{-7-0}\)
= \(\frac{7}{-7}\)
= -1
Thus the slope, m =-1

Question 24.
G (-3, 0), F (0, -6)
Answer:
The line passes through the points (-3, 0) and (0, -6).
Slope m = \(\frac{-6-0}{0+3}\)
= \(\frac{-6}{3}\)
= -2
Thus the slope, m = -2

Identify the y-intercept. Then calculate the slope using the points indicated. (Lessons 4.1, 4.2)

Question 25.

Answer:
The line passes through the points (0, 10) and (2.5, 30).
Slope m = \(\frac{30-10}{2.5-0}\)
= \(\frac{20}{2.5}\)
= 8
Thus the slope, m = 8
y-intercept = 10

Question 26.

Answer:
The line passes through the points (0, 3) and (0, 14).
m = 14/3
y-intercept = 14

For each equation, find the slope and the y-intercept of the graph of the equation. (Lesson 4.3)

Question 27.
y = 7x + 1
Answer:
Given,
y = 7x + 1
slope, m = 7
y-intercept, b = 1

Question 28.
y = -2x – 5
Answer:
Given,
y = -2x – 5
slope, m = -2
y-intercept, b = -5

Question 29.
2y = 4x + 6
Answer:
Given,
2y = 4x + 6
y = 2x + 3
slope, m = 2
y-intercept, b = 3

Question 30.
4y + 3x = 8
Answer:
Given,
4y + 3x = 8
4y = -3x + 8
y = 3/4 x + 2
slope, m = 3/4
y-intercept, b = 2

Use the given slope and y-intercept of a line to write an equation in slope-intercept form. (Lesson 4.3)

Question 31.
Slope, m = 3
y-intercept, b = 2
Answer:
Slope, m = 3
y-intercept, b = 2
The equation in slope-intercept is y = mx + b
y = 3x + 2

Question 32.
Slope, m = -1
y-intercept, b = 4
Answer:
Slope, m = -1
y-intercept, b = 4
The equation in slope-intercept is y = mx + b
y = -1x + 4

Question 33.
Slope, m = 5
y-intercept, b = -2
Answer:
Slope, m = 5
y-intercept, b = -2
The equation in slope-intercept is y = mx + b
y = 5x – 2

Question 34.
Slope, m = –\(\frac{3}{2}\)
y-intercept, b = -5
Answer:
Slope, m = –\(\frac{3}{2}\)
y-intercept, b = -5
The equation in slope-intercept is y = mx + b
y = –\(\frac{3}{2}\)x – 5

Solve. Show your work. (Lesson 4.3)

Question 35.
Write an equation of the line parallel to 2y = 4x + 3 that has a y-intercept of 4.
Answer: y = 2x + 4

Question 36.
A line has slope -4 and passes through the point (\(\frac{3}{4}\), 3). Write an equation of the line.
Answer:
y = -4x + 6

Question 37.
Write an equation of the line that passes through the point (2, 3) and is parallel to 3y + 2x = 7.
Answer:
y = –\(\frac{2}{3}\)x + \(\frac{13}{3}\)

Use graph paper. Graph each linear equation. Use 1 grid scale to represent 1 unit on both axes for the interval -5 to 5. (Lesson 4.4)

Question 38.
y = -2x + 8
Answer:

Question 39.
y = -2 – 3x
Answer:

Question 40.
y = \(\frac{1}{2}\)x – 3
Answer:

Solve. Show your work. (Lesson 4.5)

Question 41.
Bobby and Chloe each have a bank account. The balance, y dollars, in each account for x weeks, is shown in the graph.

a) Who saved money and who withdrew money during the 10 weeks?
Answer: Bobby’s savings increased, so he saved money. Chloe’s savings decreased, so she withdrew money.

b) Whose balance changed more over 10 weeks?
Answer:
Bobby changed by $100, Chloe’s changed by -$50; Bobby’s changed more.

c) Explain what information the coordinates of P give about the situation.
Answer:
After 5 weeks, Bobby and Chloe have the same amount of money, which is $75.

Problem Solving

Solve. Show your work.

Question 42.
The diagram shows a sheet of metal of width y inches. It is bent into a U-shaped gutter that is used to channel rain from a roof. The horizontal section of the gutter shown on the right is 10 inches wide and the heights are in the ratio of 2 : 3. (Chapter 3).

a) Let x represents the longer height of the gutter, in inches. Write a linear equation for the width of the sheet of metal, y inches-, in terms of the longer height of the gutter, x inches.
Answer: y = 5/3 x + 10

b) The width of the sheet of metal is 30 inches. Calculate the longer height of the gutter.
Answer: 12 in

Question 43.
In a grocery store, each apple costs $0.50, each orange costs $0.40, and each pear costs $0.30. Mrs. Fortney bought y apples, three times as many oranges as apples, and 7 fewer pears than apples. $he spent a total of $19.90 on the fruits. (Chapter 3)
a) Write a linear equation to find the amount spent on each fruit.
Answer: 50y + 120y + 30y – 210 = 1990
200y = 2200

b) Find the total cost spent on apples and pears.
Answer: $6.70

Question 44.
Jack traveled from his home to Denver at an average speed of x miles per hour. He arrived in \(\frac{3}{4}\) hour and took a 15-minute break. From Denver, he traveled at an average speed of (x + 2) miles per hour and reached his grandmother’s place in 1.5 hours. (Chapter 3)
a) Write a linear equation for the total distance traveled, D miles, in terms of average speed, x miles per hour.
Answer:
D = \(\frac{3}{4}\)x + \(\frac{3}{2}\)
D = \(\frac{3}{4}\)x + 1.5
D = \(\frac{9}{4}\)x + 3

b) The total distance traveled for the whole journey was 120 miles. Find the average speed for both parts of the journey.
Answer:
First part: 52 mi/h
Second part: 54 mi/h

Use graph paper. Solve.

Question 45.
Xavier walks into an elevator in the basement of a building. Its control panel displays “0” for the floor number. As Xavier goes up, the numbers increase one by one on the display. The table shows the floor numbers and the distance from ground level. (Chapter 4)

a) Graph the relationship between the distance of the elevator from ground level at different floor numbers. Use 1 grid square to represent 1 unit on the horizontal axis for the x interval 0 to 4, and 1 grid square for 10 units on the vertical axis for the y interval -10 to 30.
Answer:

b) Find the vertical intercept of the graph and explain what information it gives about the situation.
Answer: -10
It is the distance of the elevator from ground level, 10 ft below ground level when it is at the basement level.

c) Find the slope of the graph and explain what information it gives about the situation.
Answer: 10
The slope represents the increase in distance, in ft, of the elevator from ground level for every increase of the 1-floor number

d) Write an equation relating the distance of the elevator from ground level and the floor number on the display.
Answer: y = 10x – 10

e) What is the distance of the elevator from the ground level of the highest floor that is less than 165 feet? Is there a floor number with a distance from the ground level of exactly 165 feet?
Answer: 160 ft
There is no floor number with distance from ground level for exactly 165 ft.

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 3 Lesson 3.4 Solving for a Variable in a Two-Variable Linear Equation to finish your assignments.

Math in Focus Grade 7 Course 3 A Chapter 3 Lesson 3.4 Answer Key Solving for a Variable in a Two-Variable Linear Equation

Math in Focus Grade 8 Chapter 3 Lesson 3.4 Guided Practice Answer Key

Solve. Show your work.

Question 1.
Express x in terms of y for the equation 2(x – 3) =3y -1. Find the value of x when y = 3.

Answer:
x = 7,

Explanation:

Question 2.
Express x in terms of y for the equation y = \(\frac{2 x+3}{2}\). Find the value of x when y = -13.
Answer:
x = -29/2,

Explanation:

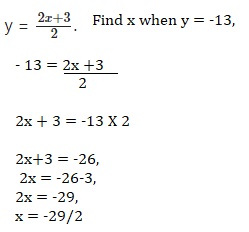
Solve. Show your work.

Question 3.
The mean (or average) of three numbers x, x\(\sqrt{3}\) and 2 is M.

a) Express x in terms of M.

Answer:
x = 3M-2/2.732
Explanation:

b) Create a table of values for M and x when M = 0, 1, 2, and 3.
Round each x-value to the nearest hundredth.
Substitute 0, 1, 2, and 3 for M into the equation x = .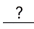

Answer :
When M = 0, X = -0.732,
M= 1, x =0.366, M=2 , x = 1.464 and M = 3 , x= 2.562,
Explanation:

Math in Focus Course 3A Practice 3.4 Answer Key

Express y in terms of x. Find the value of y when x = -1.

Question 1.
5 – y = 3x
Answer:
y = 5 – 3x,y = 8

Explanation:
Given 5 -y = 3x, x=-1,
Expressing y in terms of x as y = 5-3x and as x = -1
y = 5 – 3(-1)= 5 +3 = 8.

Question 2.
-3(x + 2) = 5y
Answer:
y =-3/5(x+2), y = -3/5,

Explanation:
Given -3(x+2) = 5y and x = -1
Expressing y in terms of x as y = -3/5(x +2),
y = -3/5(-1+2),
y= -3/5(1),
y = -3/5.

Question 3.
6(x – y) = 19
Answer:
y= x -19/6, y = -25/6,

Explanation:
Given 6(x-y)=19,
6x – 19 =  6y,
y = x – 19/6,when x = -1,
y = -1 -19/6 = -25/6.

Question 4.
4x – 3 = 0.4x – 2y
Answer:
y= 1.5 – 1.8 x, y = 3.3,

Explanation:
Given 4x – 3 =0.4x -2y,
4x – 3-0.4x = -2y
3.6x -3 =-2y
y = -3.6x/2 + 3/2
y = 1.5 – 1.8x, when x = -1
y = 1.5 -1.8(-1)= 1.5+1.8 = 3.3.

Question 5.
\(\frac{1}{6}\)x + \(\frac{3}{4}\)y = 4
Answer:
y = (96-4x)/18,y = 5.5

Explanation:
Given\(\frac{1}{6}\)x + \(\frac{3}{4}\)y = 4 multiplying both sides with 24,
4x +18 y =96,
18 y = 96-4x
y = (96- 4x)/18,when x = -1,
y = (96-4(-1))/18 = 96+4/18 = 100/18 = 5.5.

Question 6.
0.5y – 2 = 0.25x
Answer:
y = 4+0.5x, y = 3.5,

Explanation:
Given 0.5y – 2 = 0.25x,
0.5 y = 2 +0.25x
y = 4 +0.5 x, when x = -1,
y = 4 +0.5(-1) = 4 -0.5 = 3.5.

Express x in terms of y. Find the value of x when y = 5.

Question 7.
5x – y = 3(x + y)
Answer:
x = 2y, x = 10,

Explanation:
Given 5x – y = 3(x+y),
5x – y = 3x +3y,
5x -3x = 3y+y,
2x = 4y,
x = 2y,when y = 5,
x = 2 X 5 = 10.

Question 8.
3(x + 2y) = 2x + 5y
Answer:
x = -y, x = -5,

Explanation:
Given 3(x+2y)=2x +5y,
3x +6y = 2x +5y,
3x – 2x = 5y-6y,
x = -y,when y =5, x = -5.

Question 9.
1.5(x – y) = 1
Answer:
x= 0.66 +y, x = 5.66,

Explanation:
Given 1.5(x-y)=1,
1.5x = 1+ 1.5 y,
x = 0.66 + y,when y = 5, x = 0.66 + 5,
x = 5.66.

Question 10.

2y + 8 = \(\frac{1}{4} x\)
Answer:
x =(8y+32), x = 72,

Explanation:
Given 2y+ 8 = \(\frac{1}{4} x\),
4(2y+8)= x,
x = 8y + 32, when y = 5,
x = 8 X 5+ 32= 40 +32 = 72.

Question 11.
\(\frac{2(x-3)}{y}\) = 5
Answer:
x = (5y+6)/2, x = 31/2,

Explanation:
Given \(\frac{2(x-3)}{y}\) = 5,
2(x -3)=5y,
2x – 6 = 5y,
2x = 5y +6,
x =(5y +6)/2,when y = 5,
x = (5 X 5 +6)/2,
x = 31/2.

Question 12.
\(\frac{1}{3}(6 x-1)\) = \(\frac{6 y}{5}\)
Answer:
x= (18y+5)/30, x =95/30,

Explanation:
Given\(\frac{1}{3}(6 x-1)\) = \(\frac{6 y}{5}\),
5(6x-1) = 18y,
30 x- 5 = 18y,
30x = 18y +5,
x=(18y+ 5 )/30, when y =5,
x = (18X 5+5)/30= 95/30.

Solve. Show your work.

Question 13.
The perimeter, P inches, of a semicircle of diameter, d inches, is represented by P = 0.5πd+ d.

a) Express d in terms of P.
Answer:
p = d(0.5π +1) inches,

Explanation:
Given the perimeter, P inches, of a semicircle of diameter,
d inches, is represented by P = 0.5πd+ d so p= d(0.5π +1) inches.

b) Find the diameter if the perimeter is 36 inches.
Use \(\frac{22}{7}\) as an approximation for π.
Answer:
The diameter is 14.007 inches,

Explanation:
Given to find the diameter if the perimeter is 36 inches.
Using \(\frac{22}{7}\) as an approximation for π= 3.14,
we have p = d(0.5π +1) inches,
36 = d(0.5 X 3.14 +1),
36 = d(1.57 +1),
36 = d (2.57),
d = 36/2.57= 14.007 inches.

Question 14.
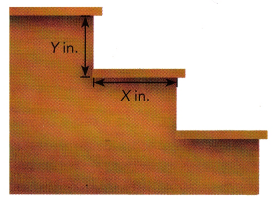
The horizontal distance, X inches, and vertical distance,
Y inches, of each step of a staircase are related by the linear equation
X = \(\frac{1}{2}\)(20 + Y).

a) Express Y in terms of X.
Answer:

Y = 2X – 20,

Explanation:
Given X = \(\frac{1}{2}\)(20 + Y),
2 X = 20 + Y,
Y = 2X – 20.

b) Complete the table below.

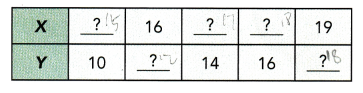
Answer:

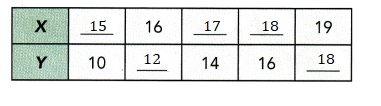
Explanation:
We have Y = 2X – 20,
when Y = 10, 2X = Y + 20 = 2X = 30, X =15,
When X = 16, Y = (2x-20) = 2X 16 – 20 = 32 – 20 =12,
When Y = 14, 2X = Y +20 ,2 X = 14 + 20 = 34 , X =17,
When Y =16, 2X = 16+20 = 36, X = 36/2 = 18,
When X = 19,Y =(2x -20)= 2X 19 – 20 = 38 – 20 = 18,
Completed the table above.

c) Find the value of X and Y if X = Y.
Answer:
If X = Y then Y = 20,

Explanation:
We have Y =2X – 20,
Y = 2 Y -20,
2Y -Y =20,
Y = 20.

Question 15.
Use the isosceles triangle.

a) Write an equation for y in terms of x.

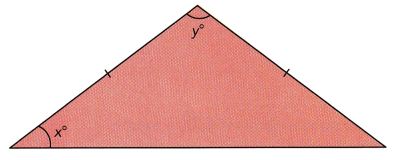
Answer:
x + y = 90,

Explanation:
Given the triangle is isosceles is 2(x +y)+ 90 = 180,
2(x+y) = 180-90= 90,
x + y = 90/2 = 45.

b) Find the value of y when x = 24.5.
Answer:
y = 65.5,

Explanation:
We have x +y = 90, when x = 24.5 ,
y = 90-24.5 = 65.5.

Question 16.
At a travel agency, the cost of a trip to Mexico is $350 for an adult and $200 for a child.
One month, the agency sold 50 trips. Of these trips, y trips were for children.
The travel agency collected C dollars from selling all 50 trips.

a) Write a linear equation for C in terms of y.
Answer:
C =350(50 -y)+ 200 y,

Explanation:
Given at a travel agency, the cost of a trip to Mexico is $350 for an adult and $200 for a child.
One month, the agency sold 50 trips. Of these trips, y trips were for children.
The travel agency collected C dollars from selling all 50 trips. is
C =350(50 -y)+ 200 y.

b) Express y in terms of C.
Answer:
y = (17,500 – C)/150,

Explanation:
We have C =350(50 -y)+ 200 y,
C = 17,500 – 350y + 200y,
C = 17,500 – 150y,
150 y = 17,500 -C
y = (17,500 – C)/150.

c) If $15,250 was collected, find the number of children going on the trip.
Answer:
The number of children going on the trip is 15,

Explanation:
If $15,250 is collected the number of children going on the trip,
we have y= (17,500-c)/150,
y= (17,500-15,250)/150,
y= 2,250/150= 15.

Question 17.
A trash disposal company charges accordinq to the weight of trash it disposes.
The charge, y dollars, for x pounds of trash is represented by the equation
y = 2(\(\frac{1}{4}\)x – 10).

a) Write an equation for x in terms of y.
Answer:
x = 2x +40,

Explanation:
y = 2(\(\frac{1}{4}\)x – 10),
y = 1/2 x – 20,
1/2 x = y +20,
x = 2y +40.

b) Create a table of x- and y-values for y = 60, 80, 100, 120, and 140.
Answer:

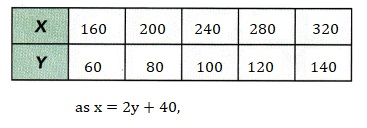
Explanation:
We have x = 2y + 40,
when y =60, x = 2X 60+ 40 =120 + 40 = 160,
when y = 80, x = 2 X 80 + 40 = 160 + 40 = 200,
when y = 100, x = 2 X 100+ 40 = 200 + 40 = 240,
when y = 120 , x = 2 X 120 + 40 = 240 + 40 = 280,
when y = 140, x = 2 X 140 + 40 = 280 + 40 = 320,
Created a table of x and y values above.

Question 18.
The mean, or average, of three numbers 17.4, 23.8, and x is M.

a) Write an equation for x in terms of M.
Answer:
x = 3M – 41.2,

Explanation:
Given the mean or average of three numbers 17.4, 23.8, and x is M so
M = (17.4 + 23.8 +x)/3,
3 M = x + 41.2,
x = 3M – 41.2.

b) Create a table of values for M = 15, 17, 19, 21, and 23.
Answer:

Explanation:
Created the tables of values M = 15,17,19,21 and 23,
so x = 3.8,9.8,15.8,21.8,27.8 respectively.

Question 19.
A rectangle has a width of w units and a length of 5 units.
Its perimeter is given by P = 2(w + 5). Solve for w in terms of P.
Create a table of values for P = 12, 14, 16, and 18.
Answer:

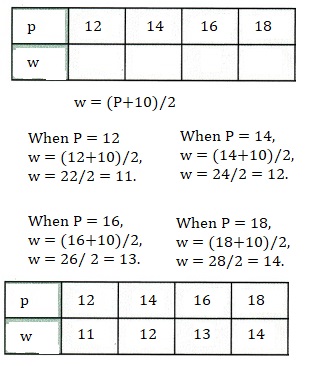
Explanation:
Given P = 2(w+5),
2w +10 = P,
2w = P + 10,
w = (p+10)/2,
Craeted a table of values for P=12,14,16 and 18 as shown above.

Question 20.
In the number pattern 3, 7, 11, 15, 19, …, each new number is
4 greater than the previous number. To find the number L in the nth position,
use the formula L = 3 + 4(n – 1).

a) What number is in the tenth position?
Answer:
39 is in the tenth position,

Explanation:
Given the number pattern 3, 7, 11, 15, 19, …, each new number is
4 greater than the previous number. To find the number L in the nth position,
we use the formula L = 3 + 4(n – 1) when n = tenth position,
L = 3 +4(10-1),
L = 3 + 4(9),
L = 3 + 36= 39.

b) In which position is the number 63?
Answer:
In 16th position is the number 63.

Explanation:
We have L= 3+4(n -1)  where L is the number and n will be position
if the number is 63 the position is 63 = 3+4(n-1),
63 -3 = 4(n-1),
60 = 4(n-1),
n -1 = 60/4,
n -1 = 15,
n = 15+1 = 16.

Brain @ Work

Question 1.
Lynnette runs a private tutoring business. She rents a room for $500 a month, which is her only expense. She charges $50 an hour per student, and gives each student two lessons per month. Each lesson lasts 1.5 hours.

a) Write an equation for her monthly profit, P, in terms of s, the number of students she has.
Answer:
P = $50s – $500,

Explanation:
Given Lynnette runs a private tutoring business.
She rents a room for $500 a month, which is her only expense.
She charges $50 an hour per student, equation for her monthly profit P
in terms of s, the number of students she has is P = $50s – $500.

b) Find her monthly profit if she has 40 students.
Answer:
If she has 40 students her montly profit is $1,500,

Explanation:
We have P = $50s – $500, if Lynnette has 40 students
P = $50 X 40 – $500,
P = $2,000 – $500 = $1500.

c) Find the minimum number of students she needs if she wants to make a monthly profit of at least $4,600.

Answer:
102 minimum number of students she needs if she wants to make a monthly profit of at least $4,600,

Explanation:
We have P = $50s – $500 if Lynnette wants to make a monthly profit of at least $4,600,
the number of students s is $4,600 = $50s – $500,
$50s = $4,600+ $500,
$50s = $5,100,
s = $5,100/50 = 102.

Question 2.
Stefanie’s train will leave her train station in 24 minutes and
she is y miles from the station. To catch the train, she walks at a speed of
4 miles per hour and later runs at a speed of 8 miles per hour.
a) Write an equation in terms of y for the distance she has to walk, w,
to reach the station in 24 minutes.
Answer:
w = (16-5y)/5 or  (3.2-y)

Explanation:
Given Stefanie’s train will leave her train station in 24 minutes and
she is y miles from the station. To catch the train, she walks at a speed of
4 miles per hour and later runs at a speed of 8 miles per hour.
Walk is w/4 and run (y-w)/8,
so w/4+(y -w)/ 8 = 24/60,
2w+y -w = 24 X 8/60,
w + y = 16/5,
w = (16-5y)/5 or 3.2 -y,

b) Solve for y in terms of w. How far is she from the station if she has to
walk 1 mile to reach the station on time?
Answer:
y =2.2,

Explanation:
As we have w = (16-5y)/5 or 3.2 -y if she is from the station if she has to
walk 1 mile to reach the station on time then y = 3.2 – 1= 2.2.

c) Why do the values of y have to be between 1.6 and 3.2?
Answer:
As walk cannot not zero or less than 4 miles,

Explanation:
If y values are not to be between 1.6 and 3.2 As walk cannot not zero or less than
4 miles if y = 3.2 then w = 3.2 – 3.2 = 0.

Question 3.
A polygon has n sides. The sum of the measures of a polygon’s
interior angles is equal to the sum of the measures of r right angles.
A table of r- and n-values is shown below.
Explain how you would find a linear equation involving r and n.

Answer:
The sum of the measures of interior angles of a polygon of n sides is equal to
$\Rightarrow 2(n-2)$ right angles,

Explanation:
If a polygon has $n$ sides, then it is divided into $(n-2)$ triangles.
As we know that the sum of the angles of triangle = 180∘.
Therefore, the sum of the angles of $(n-2)$ triangles = 180 $\times$ (n−2),
$\Rightarrow$ 2$\times$right angles$\times$(n−2),
The sum of the measures of interior angles of a polygon of n sides is equal to
$\Rightarrow 2(n-2)$ right angles.

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 3 Review Test to finish your assignments.

Math in Focus Grade 8 Course 3 A Chapter 3 Review Test Answer Key

Concepts and Skills

Solve each linear equation. Show your work.

Question 1.
2(x – 5) – 8 = 20
Answer:
Given,
2(x – 5) – 8 = 20
2x – 10 – 8 = 20
2x – 18 = 20
2x = 20 + 18
2x = 38
x = 38/2
x = 19

Question 2.
2x – (5 – x) = \(\frac{5}{2}\)
Answer:
Given,
2x – (5 – x) = \(\frac{5}{2}\)
2x – 5 + x = \(\frac{5}{2}\)
3x – 5 = \(\frac{5}{2}\)
3x = \(\frac{5}{2}\) + 5

Question 3.
\(\frac{1}{4}\)(x + 2) – 2 = 0.5
Answer:
Given,
\(\frac{1}{4}\)(x + 2) – 2 = 0.5
\(\frac{1}{4}\)x + \(\frac{1}{2}\) – 2 – \(\frac{1}{2}\) = 0
\(\frac{1}{4}\)x – 2 = 0
\(\frac{1}{4}\)x = 2
x = 2 × 4
x = 8

Question 4.
4x – \(\frac{5-2x}{5}\) = \(\frac{3}{5}\)
Answer:
4x – \(\frac{5-2x}{5}\) = \(\frac{3}{5}\)
20x – (5 – 2x) = 3
20x – 5 + 2x = 3
22x – 5 = 3
22x = 3 + 5
22x = 8
x = 8/22 or 4/11

Write each repeating decimal as a fraction. Show your work.

Question 5.
\(0 . \overline{2}\)
Answer: \(\frac{2}{9}\)

Question 6.
\(0.9 \overline{3}\)
Answer:
\(\frac{14}{15}\)

Question 7.
\(0.2 \overline{6}\)
Answer: \(\frac{4}{15}\)

Question 8.
\(0.3 \overline{16}\)
Answer: \(\frac{313}{990}\)

Tell whether each equation has one solution, no solution, or an infinite number of solutions. Show your work.

Question 9.
2x + 4 = -2(\(\frac{1}{2}\) – x)
Answer:
Given,
2x + 4 = -2(\(\frac{1}{2}\) – x)
2x + 4 = -1 + 2x
2x – 2x + 4 = -1
4 = -1
No solution

Question 10.
6y + (16 – 2y) = 4(4 + y)
Answer:
Given,
6y + (16 – 2y) = 4(4 + y)
6y + 16 – 2y = 16 + 4y
4y + 16 = 16 + 4y
It has solution or Identity

Question 11.
4x + 5 = 2x – 7
Answer:
Given,
4x + 5 = 2x – 7
4x – 2x = -7 – 5
2x = -12
x = -6
One solutions

Question 12.
2x + 5 = -4(-\(\frac{5}{4}\) – \(\frac{1}{2}\)x)
Answer:
Given,
2x + 5 = -4(-\(\frac{5}{4}\) – \(\frac{1}{2}\)x)
2x + 5 = 5 + 2x
Identity

Find the value of y when x = 4.

Question 13.
4x – 2 = y + 5
Answer:
Given,
4x – 2 = y + 5
4(4) – 2 = y + 5
16 – 2 = y + 5
14 – 5 = y
y = 9

Question 14.
x – 4y = 2
Answer:
Given,
x – 4y = 2
4 – 4y = 2
4 – 2 = 4y
2 = 4y
y = 2/4
y = 1/2 or 0.5

Question 15.
y – x = \(\frac{1}{3}\)(x + 14)
Answer:
Given,
y – x = \(\frac{1}{3}\)(x + 14)
y – 4 = \(\frac{1}{3}\)(4 + 14)
y – 4 = \(\frac{18}{3}\)
y = \(\frac{18}{3}\) + 4
y = 6 + 4
y = 10

Question 16.
\(\frac{3x-7}{y}\) = \(\frac{1}{3}\)
Answer:
Given,
\(\frac{3x-7}{y}\) = \(\frac{1}{3}\)
x = 4
\(\frac{3(4)-7}{y}\) = \(\frac{1}{3}\)
\(\frac{5}{y}\) = \(\frac{1}{3}\)
5 × 3 = 1 × y
y = 15

Question 17.
\(\frac{1}{7}\)(3x + y) = x
Answer:
Given,
\(\frac{1}{7}\)(3x + y) = x
x = 4
\(\frac{1}{7}\)(3(4) + y) = 4
12 + y = 4 – \(\frac{1}{7}\)
y = 4 – \(\frac{1}{7}\) – 12
y = -8 – \(\frac{1}{7}\)
y = -8.14

Question 18.
\(\frac{3y+1}{4}\) = 2x
Answer:
Given,
\(\frac{3y+1}{4}\) = 2x
x = 4
\(\frac{3y+1}{4}\) = 2 × 4
\(\frac{3y+1}{4}\) = 8
3y + 1 = 8 × 4
3y + 1 = 32
3y = 31
y = \(\frac{31}{3}\)

Express x in terms of y. Find the value of x when y = -2.

Question 19.
4x + y = 2(x + 3y)
Answer:
Given,
4x + y = 2(x + 3y)
4x + y = 2x + 6y
4x – 2x = 6y – y
2x =  5y
y = -2
2x = 5(-2)
2x = -10
x = -10/2
x = -5

Question 20.
3(x – 2y) = 4x + 5y
Answer:
Given,
3(x – 2y) = 4x + 5y
3x – 6y = 4x + 5y
3x – 4x = 5y + 6y
-x = 11y
y = -2
x = -11(-2)
x = 22

Question 21.
\(\frac{1}{3}\)x + \(\frac{5}{6}\)y = 2
Answer:
Given,
\(\frac{1}{3}\)x + \(\frac{5}{6}\)y = 2
y = -2
\(\frac{1}{3}\)x + \(\frac{5}{6}\)(-2) = 2
\(\frac{1}{3}\)x – \(\frac{10}{6}\) = 2
2x – 10 = 12
2x = 12 + 10
2x = 22
x = 11

Question 22.
\(\frac{0.5(x-3)}{y}\) = 10
Answer:
Given,
\(\frac{0.5(x-3)}{y}\) = 10
y = -2
\(\frac{0.5(x-3)}{-2}\) = 10
0.5(x – 3) = 10 × -2
0.5x – 1.5 = -20
0.5x = -20 + 1.5
0.5x = -18.5
x = -12.33

Question 23.
0.25(x + y) = 15 – x
Answer:
Given,
0.25(x + y) = 15 – x
0.25x + 0.25y = 15 – x
0.25x + 0.25(-2) = 15 – x
0.25x + x = 15 – 0.25(-2)
1.25x = 15 + 0.50
1.25x = 15.50
x = 15.50/1.25
x = 12.4

Question 24.
\(\frac{y}{2}\) – \(\frac{2 x+y}{5}\) = 7
Answer:
Given,
\(\frac{y}{2}\) – \(\frac{2 x+y}{5}\) = 7
y = -2
\(\frac{-2}{2}\) – \(\frac{2 x – 2}{5}\) = 7
-1 – \(\frac{2 x – 2}{5}\) = 7
– \(\frac{2 x – 2}{5}\) = 7 + 1
– \(\frac{2 x – 2}{5}\) = 8
-(2x – 2) = 8 × 5
-2x + 2 = 40
-2x = 40 – 2
-2x = 38
x = -19

Problem Solving

Solve. Show your work.

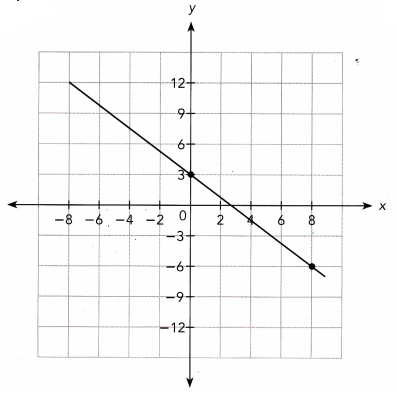
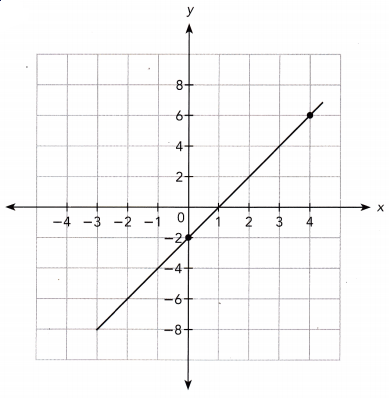
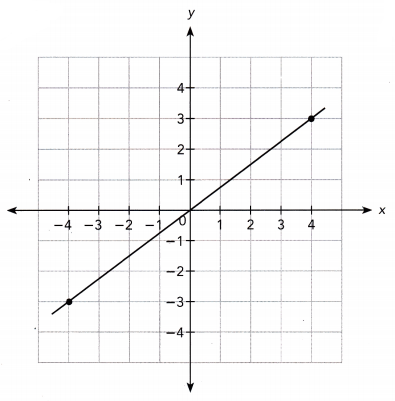
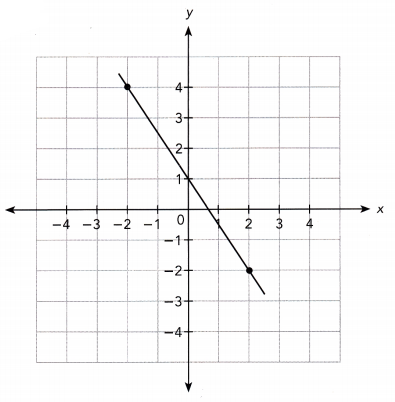
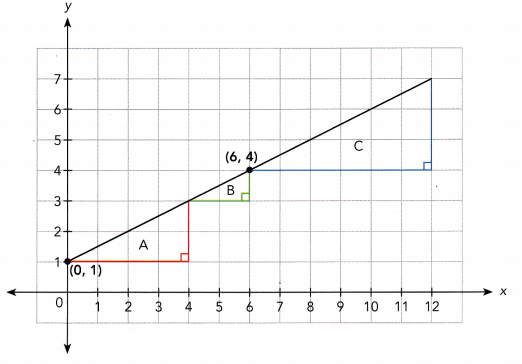
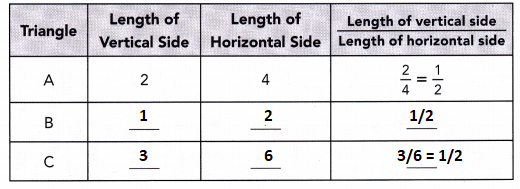
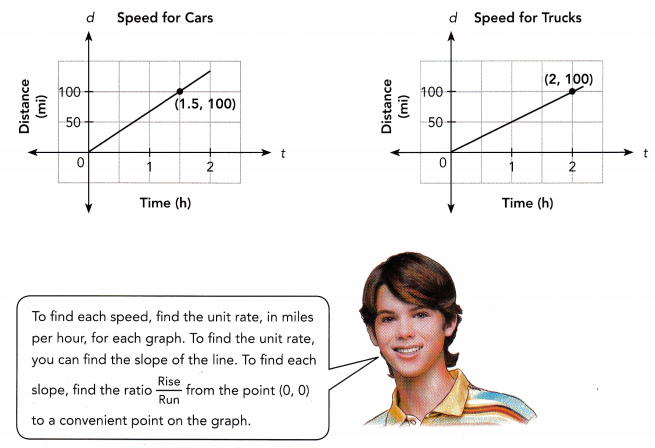
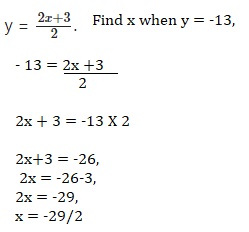
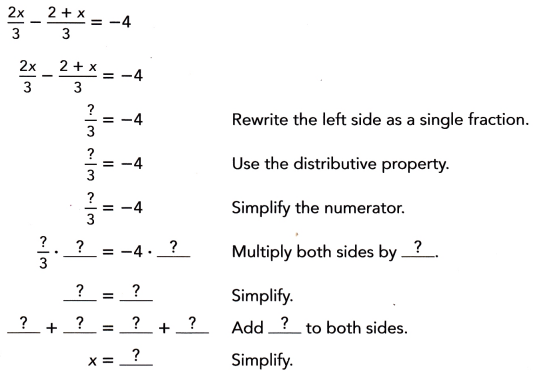
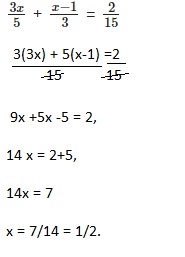
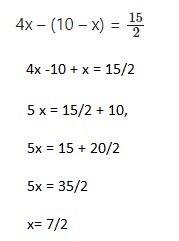
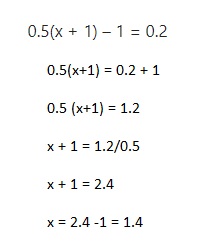
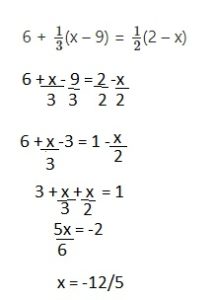
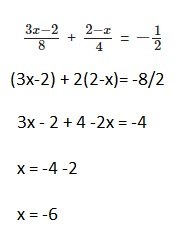
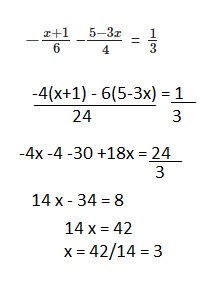
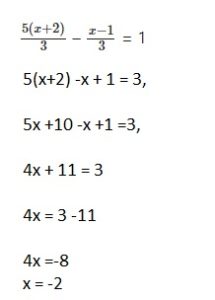
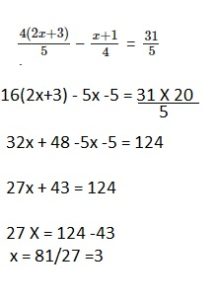
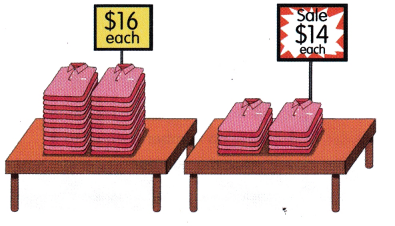
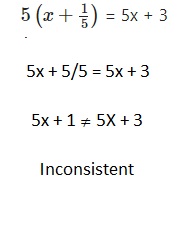
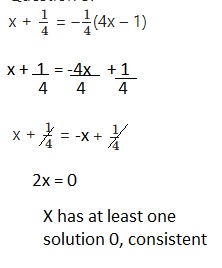
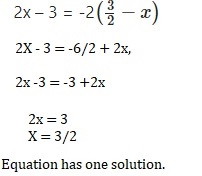
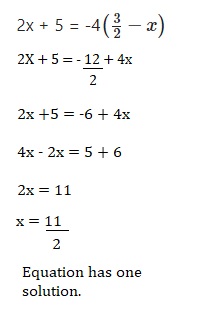
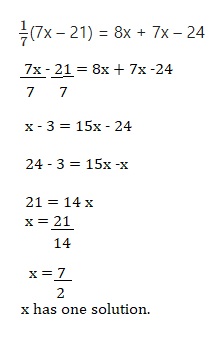
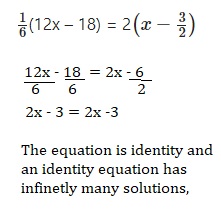
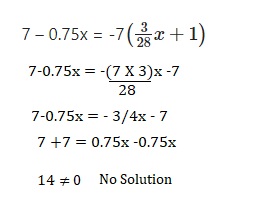
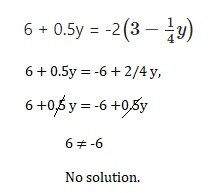
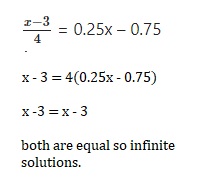
Question 25.
A circular pizza with a radius of 7 inches is cut into four quadrants. The perimeter Q of each quadrant can be found using the formula Q = d(1 + \(\frac{\pi}{4}\)), where d is the diameter of the pizza. Find the perimeter of each quadrant of the pizza. Use \(\frac{22}{7}\) as an approximation for π.

Answer:
Given,
A circular pizza with a radius of 7 inches is cut into four quadrants.
The perimeter Q of each quadrant can be found using the formula Q = d(1 + \(\frac{\pi}{4}\)), where d is the diameter of the pizza.
pi = \(\frac{22}{7}\)
Q = d(1 + \(\frac{\pi}{4}\))
Q = d(1 + \(\frac{\pi}{4}\))
Q = d(1 + 0.785)
Q = 2(7)(1.785)
Q = 24.99 or 25 approx
Thus the perimeter of each quadrant of the pizza is 25 inches.

Question 26.
Some students painted a design on the wall of the cafeteria using the school colors. The middle section of the design is 4.2 feet tall and is painted white. The top section is red, and the bottom section is blue. The ratio of the height of the blue section to the height of the red section is 1: 2. The total height of the design is 10.5 feet. Find the height of the red section of the design.
Answer:
Given,
The middle section of the design is 4.2 feet tall and is painted white.
The top section is red, and the bottom section is blue.
The ratio of the height of the blue section to the height of the red section is 1: 2.
The total height of the design is 10.5 feet.
x + 4.2 + 2x = 10.5
3x + 4.2 = 10.5
3x = 10.5 – 4.2
3x = 6.3
x = 2.1
2x = 4.2

Question 27.
In a grocery store, each pound of green beans costs one and a quarter times the price of each pound of potatoes. Mrs. Gomez bought 4 pounds of green beans and 5 pounds of potatoes. Miss Jacobs bought 10 pounds of potatoes. They paid the same amount.
a) Write a linear equation to find the cost of each pound of potatoes, p dollars.
Answer: 4 . \(\frac{5}{4}\)p + 5p = 10p

b) Tell whether the equation has one solution, is inconsistent, or is an identity. Explain your reasoning.
Answer:
Since 0 = 0 is always true, the linear equation is true for any value of p.
So, this equation has infinitely many solutions and it is an identity.

Question 28.
A department store is offering a percent discount on the original price of a watch. The original price of the watch is $80.
a) Let r represent the percent discount, written as a decimal. Write an equation to find the discounted price, y dollars, of the watch.
Answer: y = 80 – 80r

b) The store gave discounts of 5%, 10%, and 15% during this sale in the three previous years. Create a table of r- and y-values for the equation.
Answer:

Question 29.
The company Jake uses for Internet service charges $25 each month plus $0.04 for each minute of usage time.
a) Write a linear equation for the monthly charge, M dollars, in terms of usage time, t minutes.
Answer: M = 25 + 0.04t

b) Express t in terms of M.
Answer: t = 25(M – 25)

c) Calculate his usage time in hours if he paid $49 for his Internet bill in November.
Answer: 10h

Math in Focus Grade 7 Course 3 A Chapter 3 Lesson 3.1 Answer Key Solving Linear Equations with One Variable

Math in Focus Grade 8 Chapter 3 Lesson 3.1 Guided Practice Answer Key

Solve each linear equation.

Question 1.

Answer:
x = –\(\frac{2}{15}\)

Explanation:
(2x/3) -(2+x)/3 = -4,
2x/3 -2/3 + x /3 = -4,
(2x/3+ x/3) = -4 +(2/3),
(2x+x)/3 = (-12+ 2)/3,
x = -10/3

Question 2.
00.6(1 – x) + 0.2(x – 5) = 10
Answer:
x = -26

Explanation:
Given 00.6(1 – x) + 0.2(x – 5) = 10 upon solving
0.6 – 0.6x + 0.2 x – (0.2 X 5) = 10,
0.6 – 0.4x -1.0 = 10,
0.6 – o.4x =  11,
-0.4 x = 11 – 0.6,
-0.4x = 10.4
x = -10.4 ÷ 0.4
x = -26

Question 3.
\(\frac{3 x}{5}\) + \(\frac{x-1}{3}\) = \(\frac{2}{15}\)
Answer:
\(\frac{1}{2}\),

Explanation:

Write each repeating decimal as a fraction. Show your work.

Question 4.
\(0 . \overline{09}\)
Answer:
9/100,

Explanation:

Question 5.
\(0 . \overline{8}\)
Answer:
8/10,

Explanation:

Question 6.
\(0.0 \overline{6}\)
Answer:
6/100,

Explanation:

Write an equation and solve. Show your work.

Question 7.
Mr. Johnson wants to add a circular pond to his backyard. The backyard is 20\(\frac{1}{2}\) yards long, and the pond wilt be
6\(\frac{1}{4}\) yards across. He wants the pond set back from the house, so that the distance from the pond to the back
fence is half the distance from the pond to the back of the house. How far should the pond be from the back of the house?

Let the distance from the pond to the house be x yards.
So, the distance from the pond to the fence is \(\frac{1}{2}\)x yards.

The length of the backyard is about yards and the width of the pond is about yards. So the total distance of the pond to the house and of the pond to the gate is around yards. of yards is about yards. So, the answer is reasonable.

Answer:
The distance from the pond to the house is 13.666 yards,

Explanation:
Given let the distance from the pond to the house be x yards.
So, the distance from the pond to the fence is \(\frac{1}{2}\)x yards,

The length of the backyard is about 20 1/2 yards and
the width of the pond is about 6 1/4 yards.
So the total distance of the pond to the house and of the pond to the gate is around 201/2yards.
13.66 yards and 6 1/4  yards is about  20 1/2 yards. So, the answer is reasonable.

Question 8.
A packager of tea leaves blends 3.5 pounds of Tea Leaf A with 1.5 pounds of
Tea Leaf B to make a special blend. One pound of Tea Leaf B costs $2 less than
one pound of Tea Leaf A. The packager finds that the
cost of making the blend is $3 per pound, Find the cost of one pound of Tea Leaf B.
Answer:
$3 is the cost of one pound of tea Leaf B,

Explanation:
Given A packager of tea leaves blends 3.5 pounds of Tea ,
Leaf A with 1.5 pounds of Tea,
Leaf B to make a special blend.
One pound of Tea Leaf B costs $2 less than one pound of Tea Leaf A.
The packager finds that the cost of making the blend is $3 per pound,
So the packager has 3.5 pounds means
Leaf A + Leaf B = 3.5 pound,
1.5 pound + Leaf B = 3.5 Pound,
Leaf B = 2 Pounds to make blend,
Given the packager finds that the cost of making the blend is $3 per pound,
therefore $3 is the cost of one pound of tea Leaf B.

Math in Focus Course 3A Practice 3.1 Answer Key

Solve each linear equation. Show your work.

Question 1.
4x – (10 – x) = \(\frac{15}{2}\)
Answer:
x= 7/2,

Explanation:

Question 2.
0.5(x + 1) – 1 = 0.2
Answer:
x= 1.4,

Explanation:

Question 3.
2(x – 1) – 6 = 101(1 – x) + 6
Answer:
x = \(\frac{1}{2}\)

Explanation:
Given 2(x-1)-6 = 101(1-x) + 6,
2x -2 -6 = 101 -101x +6,
2x -8 = 107-101x,
2x +101 x = 107+8,
103 x = 115,
x = 115/103.

Question 4.
8(x – 3) – (x – 3) = 0.7
Answer:
x = 3.1,

Explanation:
Given 8(x – 3) – (x – 3) = 0.7,
8x – 24 – x +3 = 0.7,
7x – 21 = 0.7,
7x = 0.7 + 21,
7x = 21.7,
x = 21.7 ÷ 7,
x = 3.1.

Question 5.
2(x – 4) + 0.5(2 + 8x) = 0
Answer:
x = 7/6,

Explanation:
Given 2(x – 4) + 0.5(2 + 8x) = 0,
2x – 8 + 1.0 + 4x = 0,
6x -7 = 0,
x = 7/6.

Question 6.
5 – 3(x -7 ) = 2(2 – x) – 8
Answer:
x = 30,

Explanation:
Given 5-3(x-7)= 2(2-x)-8,
5 – 3x +21 = 4 -2x -8,
-3x +26 = -2x -4,
26+4 = -2x +3x
30 = x.

Question 7.
3x – 0.4(5 – 2x) = 5.6
Answer:
x = 2,

Explanation:
Given 3x – 0.4(5 – 2x) = 5.6,
3x – 2 + 0.8 x = 5.6,
3x + 0.8 x = 5.6 + 2,
3.8 x = 7.6,
x = 7.6 ÷ 3.8,
x = 2.

Question 8.
6 + \(\frac{1}{3}\)(x – 9) = \(\frac{1}{2}\)(2 – x)
Answer:
x = -12/5,

Explanation:

Question 9.
\(\frac{3 x-2}{8}\) + \(\frac{2-x}{4}\) = \(-\frac{1}{2}\)
Answer:
x = -6,

Explanation:

Question 10.
\(-\frac{x+1}{6}\) -\(\) = \(\frac{1}{3}\)
Answer:
x = 3,

Explanation:

Question 11.
\(\frac{5(x+2)}{3}\) – \(\frac{x-1}{3}\) = 1
Answer:
x = -2,

Explanation:

Question 12.
\(\frac{4(2 x+3)}{5}\) – \(\frac{x+1}{4}\) = \(\frac{31}{5}\)
Answer:
x = 3,

Explanation:

Express each repeating decimal as a fraction. Show your work.

Question 13.
\(0.8 \overline{3}\)
Answer:
5/6,

Explanation:

Question 14.
\(0.0 \overline{8}\)
Answer:
8/99,

Explanation:

Question 15.
\(0 . \overline{1}\)
Answer:
1/9,

Explanation:

Question 16.
\(0.08 \overline{3}\)
Answer:
1/12

Explanation:

Question 17.
\(0.0 \overline{5}\)
Answer:
1/20,

Explanation:

Question 18.
\(0.0 \overline{45}\)
Answer:
9/200,

Explanation:

Solve each problem algebraically. Show your work.

Question 19.
Logan saves $5.50 in dimes and quarters over a week.
He has 20 more dimes than quarters.
Find the number of dimes and quarters he saves.
Answer:
Logan saves 10 quarters and  30 dimes each week,

Explanation:

Question 20.
Maggie makes some fruit punch. She mixes 2\(\frac{1}{2}\) quarts of grape juice with 1\(\frac{1}{2}\) quarts of orange juice. One quart of grape juice costs $1 less than one quart of orange juice. She finds that the total cost of making the fruit punch is $12.50. Calculate the cost of each quart of grape juice and each quart of orange juice.
Answer:
The cost of each quart of orange juice=$3.75,
The cost of each quart of grape juice=$2.75,

Explanation:
The expression for the total cost of making fruit punch is as follows;
Total cost of making fruit punch=
total cost of making grape juice + total cost of making orange juice where;
Total cost of making fruit punch=$12.50,
Total cost of making grape juice=Cost per unit of grape juice×total quantity of grape juice,
Total cost making grape juice=(2 1/2)×g=2.5 g,
Total cost of making orange juice=Cost per unit of orange juice×total quantity of orange juice,
Total cost of making orange juice=(1 1/2)×o=1.5 o,replacing;
12.50=2.5 g+1.5 o…equation 1,
But price per unit of grape juice is one dollars less that the price per unit  of orange juice;
Price per unit of orange juice=o,
Price per unit of grape juice=(o-1), g=o-1
replace the value of g=o-1 in equation 1;
12.50=2.5 g+1.5 o…equation 1
12.50=2.5(o-1)+1.5 o,
12.50=2.5 o-2.5+1.5 o,
2.5 o+1.5 o=12.50+2.50,
4 o=15,
o=15/4=3.75,
g=o-1=3.75-1=2.75,
The cost of each quart of orange juice=o=$3.75,
The cost of each quart of grape juice=g=$2.75.

Question 21.
Ms. Handler walks to work at an average speed of 5 kilometers per hour.
If she increases her speed to 6 kilometers per hour, she will save 10 minutes.

a) Complete the table.

Answer:

Explanation:
Completed the table as shown above,

b) Find the distance she walks.
Answer:
Ms.Hadler walks 5 km,

Explanation:
I assume that the increase in speed is for the whole distance and
that we want to know far she has to walk.
Let X be the distance,
60min/5Km * X km = 12X minutes,
60min/6km * X km = 10X minutes,
10X +10 = 12X
10 = 2X
X = 5km,

Question 22.
Jane is x years old today. Her brother Kenny is 4 years older.
After seven years, their total combined age will be 24 years.
a) Write a linear equation for their total combined age after 7 years.
Answer:
Linear equation for their total combined age after 7 years is 2x+ 18 =24,

Explanation:
Given Jane is x years old today. Her brother Kenny is 4 years older.,
x and x+4,After seven years, their total combined age will be 24 years,
x +7 +x+4+7 =24,
2x + 18 = 24,
so linear equation for their total combined age after 7 years is 2x +18 = 24.

b) Find Jane’s age today.
Answer:
Janes age today is 3,

Explanation:
Equation is 2x + 18 = 24,
2x = 24-18 = 6,
x = 6/2 = 3 years.

Question 23.
Casper bought some pencils at 50¢ each. He had $3 left after the purchase.
If he wanted to buy the same number of note pads at 80.
Answer:
.50p+3 = .80p-1.50,

Explanation:
.50p+3 = .80p-1.50,
.3p = 4.50,
p = 15,
so, 15 pencils cost $7.50, meaning he started out with $10.50
15 notepads cost $12.00, so he’d be $1.50 short.

Question 24.
Alexis earns 2\(\frac{1}{2}\) times as much as Gary in a day.
James earns $18 more than Gary in a day. If the total daily salary of all three people is $306,
find Alexis’s salary.
Answer:
Alexis salary is $160,

Answer:
Number of shirts sold are 40,

Explanation:
Given a store has y shirts. It sold most of them for $16 each, and the last dozen
were sold on sale for $14 each. If it sold all the shirts for $616,
y=(616-(14 X 12))/16 + 12,
y = (616-168)/16 + 12,
y = 448/16 +12,
y = 28 +12 = 40,
therefore number of shirts sold are 40.

Question 26.
There are 40 questions on a class test. Six points are given for each
correct answer and three points are deducted for each wrong or missing answer.
Find the number of correct answers for a test score of 105.
Answer:
The number of correct answers are 25,

Explanation:
Given there are 40 questions on a class test. Six points are given for each
correct answer and three points are deducted for each wrong or missing answer.
Let x be correct answers incorrect are 40 – x,
so 6x -3(40-x)=105,
6x -120 +3x = 105,
9x= 105+120,
9x = 225,
x = 225 ÷ 9,
x = 25, therefore correct answers are 25 and wrong answers are (40-25)= 15.

Question 27.
Math Journal Georgina was given that the length of a rectangle was
2.5 inches longer than its width, and that the perimeter of the rectangle was 75.4 inches.
She found the length and width algebraically.
How could she use estimation to check if her answers were reasonable?
Answer:
length is 20.1 inches and width is 17.6 inches,

Explanation:
Given Georgina was given that the length of a rectangle was
2.5 inches longer than its width, and that the perimeter of the rectangle was 75.4 inches.
Let length is and width is w so
perimeter = 2(l+w),
75.4 = 2(2.5 +w + w),
75.4 =2(2.5+2w),
37.7 = 2.5 +2w,
2w = 37.7-2.5,
2w = 35.2,
w = 35.2 ÷ 2,
w = 17.6, therfore width is 1
so length = 17.6 + 2.5 = 20.1 inches.

Question 28.
Math Journal Consider the decimal \(0 . \overline{9}\).
a) Find the fraction equivalent of \(0 . \overline{9}\).
Answer:
The fraction eqivalent is 9/10,

Explanation:
0.9 is a decimal fraction, 1 place means tenths,
0.9 is 9/10.

b) The decimal \(0 . \overline{9}\) can be thought of as being equal to the following sum, in which the pattern shown continues forever.
0.9 + 0.09 + 0.009 + 0.0009 + …
How can thinking about this sum help you explain the result you saw in a)?
Answer:
Thinking about this sum helped in explaining the result in tenths place,

Explanation:
Every place value after the decimal point can be expressed as a fraction
with $10$ to some power in the denominator.
The first place after the decimal point is called the “tenths place” If I had $0.9$,
I would have $9$ tenths, or as a fraction $\frac{\mathrm{9/}}{10}$.
The second place after the decimal is called the “hundredths place”.
The question above asks for $0.09$. This would be $9$ hundredths, or as a fraction $\frac{\mathrm{9/}}{\mathrm{100\; and\; so\; on\; thinking\; about\; this\; sum\; helped\; in\; explaining\; the\; result\; in\; tenths\; place.}}$

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 3 Lesson 3.1 Solving Linear Equations with One Variable to finish your assignments.

Math in Focus Grade 7 Course 3 A Chapter 3 Lesson 3.2 Answer Key Identifying the Number of Solutions to a Linear Equation

Math in Focus Grade 8 Chapter 3 Lesson 3.2 Guided Practice Answer Key

Tell whether each equation is consistent or inconsistent. Justify your answer by simplifying each equation. Write +, ×, or ÷ for each ?

Question 1.
7(x – 3) – 7x – 21 = 0

Answer:
The equation has a solution,
the equation is consistent.

Explanation:
Given 7(x-3)-7x – 21 ≠ 0,
7x – 21 – 7x -21 ≠ 0 (using the distributive property),
-42 ≠ 0 because -42 ≠ 0 the equation has a solution,
the equation is consistent.

Question 2.
\(5\left(x+\frac{1}{5}\right)\) = 5x + 3
Answer:
Inconsistent,

Explanation:

Question 3.
x + \(\frac{1}{4}\) = –\(\frac{1}{4}\)(4x – 1)
Answer:
The equation has a solution,
the equation is consistent.

Equation:

Tell whether each equation is an identity. Justify your answer by simplifying each equation.
Write +, -, ×, or ÷ for each Write = or ≠ for each

Question 4.

Answer:
Left side is equal to right side,
Equation has an identity,

Explanation:

Question 5.

Answer:
Left side is not equal to right side,
Equation has no identity,

Explanation:

Try substituting some values of x into the equation. If you find that the left side is always equal to the right side, the equation is an identity.

Math in Focus Course 3A Practice 3.2 Answer Key

Tell whether each equation has one solution, no solution, or an infinite number of solutions. Justify your answer.

Question 1.
2x – 3 = -2\(\left(\frac{3}{2}-x\right)\)
Answer:
Equation has one solution,

Explanation:

Question 2.
2x + 5 = -4\(\left(\frac{3}{2}-x\right)\)
Answer:
Equation has one solution,

Explanation:

Question 3.
3x + 5 = 2x – 7
Answer:
x = -12, Equation has one solution,

Explanation:
Given 3x + 5 = 2x -7,
3x – 2x = -7 -5,
x = -12,
Equation has one solution.

Question 4.
5y + (86 – y) = 86 + 4y
Answer:
The equation is identity and
an identity equation has infinetly many solutions,

Explanation:
Given 5y + (86 – y) = 86 + 4y upon solving
5y +86 -y = 86 + 4y,
4y + 86 = 86 + 4y ,the equation is identity and
an identity equation has infinetly many solutions.

Question 5.
0.5(6x – 3) = 3(1 + x)
Answer:
No solution,

Explanation:
Given 0.5(6x -3) = 3(1 + x),
(0.5 X  6x) – (0.5 X 3) = 3 +3x,
3x -1.5 = 3 + 3x
-1.5 ≠ 3, So the equation has no solution,

Question 6.
4(18a — 7) + 40 = 3(4 + 24a)
Answer:
The equation is identity and
an identity equation has infinetly many solutions,

Explanation:
4 X 18a – 4 X 7 + 40 = 12 + 72a
72 a – 28 +40 = 72a+ 12
72a + 12 = 72a+12,
both are equal so infinite solutions.

Question 7.
\(\frac{1}{7}\)(7x – 21) = 8x + 7x – 24
Answer:
Equation has one solution,

Explanation:
Given \(\frac{1}{7}\)(7x – 21) = 8x + 7x – 24,

Question 8.
\(\frac{1}{6}\)(12x – 18) = 2\(\left(x-\frac{3}{2}\right)\)
Answer:
The equation is identity and
an identity equation has infinetly many solutions,

Question 9.
7 – 0.75x = -7\(\left(\frac{3}{28} x+1\right)\)
Answer:
No solution,

Explanation:

Question 10.
6 + 0.5y = -2\(\left(3-\frac{1}{4} y\right)\)
Answer:
No solution,

Explanation:

Question 11.
\(\frac{x-3}{4}\) = 0.25x – 0.75
Answer:
The equation is identity and
an identity equation has infinetly many solutions,

Explanation:

Question 12.
\(\frac{1}{3}\)x + 5 = \(\frac{1}{6}\)(2x – 5)
Answer:
No solution,

Explanation:

Solve. Show your work.

Question 13.
Cabinet A is 5 inches taller than Cabinet B. Cabinet C is 3 inches taller than Cabinet B whose height is x inches.

a) Write algebraic expressions for the heights of cabinets A and C.
Answer:
Cabinet A = 5 + x,
Cabinet C = 3 + x,

Explanation:
Given Cabinet B height is x inches as Cabinet A is 5 inches taller than Cabinet B
Cabinet A = 5 + x and Cabinet C is 3 inches taller than Cabinet B so Cabinet C = 3 + x.

b) If the total height of the three cabinets is (3x + 8) inches, can you solve for the height of Cabinet B? Explain.
Answer:
We cannot solve for the height of Cabinet B
we need numbers.

Explanation:
Given the total height of the three cabinets is (3x + 8) inches,
we have Cabinet A = 5 + x, Cabinet B = x and Cabinet C = 3 + x,
5 + x + x +3 + x = 3x +8, We cannot solve for the height of Cabinet B
we need numbers.

Question 14.
A room’s floor is y meters long. Its width is 5 meters shorter.
If the perimeter of the floor is (4y + 1) meters, can you solve for its length? Explain.
Answer:
There is not answer. Or, the problem needs more definition,

Explanation:
Room Floor Length(L) = y m.Width(W) y – 5 m.
Perimeter = 4y + 1,Find: Length(L),
Using perimeter formula P = 2L + 2W to get an equation to solve.
P = 4y + 1 = 2(y) + 2(y – 5),
4y + 1 = 2y + 2y – 10 => 1 = -10,
There is not answer. Or, the problem needs more definition.

Question 15.
Math Journal
Grace gave her sister a riddle: I have a number x. I add 15 to twice x to get result A.
I subtract 4 from x to get result B. I multiply result B by 3 to get result C.
Result A is equal to result C. Grace’s sister said the riddle cannot be solved,
but Grace thought otherwise. Who is right? Explain.
Answer:
Grace is right she solved the riddle,

Explanation:
Given Grace gave her sister a riddle: I have a number x. I add 15 to twice x to get result A.
A= 15 + 2x, I subtract 4 from x to get result B. B = x -4,
I multiply result B by 3 to get result C. 3B = C ,
Result A is equal to result C, 15 + 2x = C = 3(x-4)
15 + 2x = 3x – 12,
15 + 12 = 3x -2x,
27 = x.
Grace is right she solved the riddle.

Question 16.

Math Journal Look at this “proof” that 2 = 0.

What is wrong with this proof? How can a true statement lead to an inconsistent equation?
Answer:
Substituting values of a and b and a true statement lead to an inconsistent equation,
Inconsistent equations is defined as two or more equations that are
impossible to solve based on using one set of values for the variables.

Explanation:
As when a =1 and b= 1 then (a-b)(a+b) = 0 means
(1-1)(1+1) = 0,0=0 true statement,
0= 0 but if (a-b)(a+b) =0  dividing both sides by (a-b) we get
a + b = 0 substitute for a and b we get 1 + 1 = 0 and 2 = 0 which is inconsistent.

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 3 Algebraic Linear Equations to finish your assignments.

Math in Focus Grade 8 Course 3 A Chapter 3 Answer Key Algebraic Linear Equations

Math in Focus Grade 8 Chapter 3 Quick Check Answer Key

Explain why each pair of equations is equivalent or not equivalent.

Question 1.
x + 4 = 10 and x – 1 = 3
Answer:
Not equivalent,

Explanation:
Given x + 4 = 10 and x-1 =3 means x = 3+1 =4,
if we substitute x = 4 in x + 4 = 4 + 4 = 8 ≠ 10,
so equations are not equivalent.

Question 2.
\(\frac{1}{5}\)x = 4 and x = 20
Answer:
Equivalent,

Explanation:
Given \(\frac{1}{5}\)x = 4 and x = 20 upon solving
\(\frac{1}{5}\)x = 4 we get x = 4 X 5 = 20 therefore
pair is equivalent as x = 20.

Question 3.
0.5x + 1 = 1.5x and 2x = 2
Answer:
Equivalent,

Explanation:
Given 0.5x +1 = 1.5x and 2x =2 means x= 2/2 equal to 1,
so 0.5 (1) + 1 = 1.5 X 1 is 0.5 +1 = 1.5 , So 1.5 = 1.5,therefore
both equations are equivalent.

Question 4.
2(x + 9) = 14 and 2(x – 7) = -18
Answer:
Equivalent,

Explanation:
Given 2(x -7) = -18 upon solving
2x – 14 = -18,
2x = -18+14,
2x = -4 therfore x = -4/2 = -2 now substituting
2(-2 -7) = – 4 -14 = -18 which is equal to – 18
So both equations are equivalent.

Write a linear equation for each situation. State the independent and dependent variables for each equation.

Question 5.
A manufacturer produces beverages in small and large bottles.
Each small bottle contains s liters of beverages.
Each large bottle contains t liters, which is 1 more liter than the
quantity in the small bottle. Express t in terms of s.
Answer:
t = (s + (sX1)) liters,

Explanation:
Given A manufacturer produces beverages in small and large bottles.
Each small bottle contains s liters of beverages.
Each large bottle contains t liters, which is 1 more liter than the
quantity in the small bottle. Expressing t in terms of s as t = (s + (sX1))  liters.

Question 6.
Hazel is 4 years younger than Alphonso. Express Alphonso’s age, a, in terms of Hazel’s age, h.
Answer:
h=(a-4),

Explanation:
Given Hazel is 4 years younger than Alphonso.
Expressing Alphonso’s age, a, in terms of Hazel’s age, h.
h=(a-4).

Question 7.
A bouquet of lavender costs $12. Find the cost, C, of n bouquets of lavender.
Answer:
C = $12n

Explanation:
Given a bouquet of lavender costs $12, the cost, C, of n bouquets of lavender is
c = $12 X n = $12n.

Question 8.
The distance, d miles, traveled by a bus is 40 times the time,t hours,
used for the journey. Find d in terms of t.
Answer:
d = 40t,

Explanation:
Given the distance, d miles, traveled by a bus is 40 times the time,t hours,
used for the journey is d = 40t.

Solve each equation.

Question 9.
4x = 14 + 2x
Answer:
x =7,

Explanation:
Given 4x = 14 + 2x, upon solving
4x – 2x = 14,
2x = 14,
x = 14/2 = 7.

Question 10.
\(\frac{1}{3}\)v = 2 – \(\frac{2}{9}\)v
Answer:
v = \(\frac{18}{5}\),

Explanation:
Given \(\frac{1}{3}\)v = 2 – \(\frac{2}{9}\)v,
\(\frac{1}{3}\)v = \(\frac{18 -2v}{9}\),
\(\frac{9}{3}\)v = 18 -2v,
3 v = 18 -2v,
5v = 18, therefore v = \(\frac{18}{5}\).

Question 11.
c + 2(1 – c) = 10 – 3c
Answer:
c = 4,

Explanation:
Given c + 2(1 – c) = 10 – 3c,
c + 2 – 2c = 10 -3c,
2 – c = 10 – 3c,
3c-c = 10-2,
2c = 8,
c = 4.

Question 12.
3(2 + 3x) = 13(x + 2)
Answer:
x = -5,

Explanation:
Given 3(2+3x) = 13(x +2) upon solving
6 + 9x = 13x + 26,
6-26 = 13x – 9x,
-20 = 4 x,
x = -5.

Write the decimal for each fraction. Use bar notation.

Question 13.
\(\frac{3}{18}\)
Answer:

Explanation:
A bar notation, which is a way to show repeating numbers after a decimal point,
here when 3 divides by 18 we get 0.166666 where 6 is repeating so we keep a bar on 6
as shown above.

Question 14.
\(\frac{14}{99}\)
Answer:

Explanation:
When 14 divides by 99 we get 0.14141414 where 14 is repeating so we keep a bar on 14
as shown above.

Question 15.
\(\frac{13}{12}\)
Answer:

Explanation:
When 13 divides by 12 we get 1.083333 where 3 is repeating so we keep a bar on 3
as shown above.

Question 16.
\(\frac{5}{27}\)
Answer:

Explanation:
When 5 divides by 27 we get 0.185185 where 185 is repeating so we keep a bar on 185
as shown above.

Go through the Math in Focus Grade 8 Workbook Answer Key Cumulative Review Chapters 1-2 to finish your assignments.

Math in Focus Grade 8 Course 3 A Cumulative Review Chapters 1-2 Answer Key

Concepts and Skills

Write the prime factorization of each number in exponential notation. (Lesson 1.1)

Question 1.
16,807
Answer:
Prime factorization of 16,807 is 7×7×7×7×7×7
The number in the exponential notation is 7⁶.

Question 2.
25,920
Answer:
Prime factorization of 25,920 is 2×2×2×2×2×2×3×3×3×3×5.
The number in the exponential form is 2⁶ × 3⁴ × 5.

Simplify each expression. Write your answer in exponential notation. (Lessons 1.2, 1.3)

Question 3.
\(\frac{\left[\left(\frac{3}{5}\right) \cdot\left(\frac{3}{5}\right)^{3}\right]^{4}}{\left[\left(\frac{3}{5}\right)^{2}\right]^{2}}\)
Answer:
((3/5) • (3/5)³)⁴/((3/5)²)²
⅗ • ( ⅗)³)⁴ • ((⅗)²)²
⅗ • (⅗)¹² • (⅗)⁴
Bases are equal powers should be added.
⅗ • (⅗)¹⁶
(⅗)¹⁷

Question 4.
(a⁶ • a⁷)³ ÷ (4a³)²
Answer:
Given (a6 • a7)3 ÷ (4a3)2
(a⁶)³ • (a⁷)³ ÷ (4a)⁶
a¹⁸ • a²¹ ÷ 4a⁶
Bases are equal powers should be added.
a³⁹/4a⁶
¼ × a³⁹/a⁶
¼ × a³³

Simplify each expression. Write your answer using a positive exponent. (Lessons 1.2, 1.3, 1.4, 1.5)

Question 5.
\(\frac{6^{3} \cdot 15^{3}}{\left(7^{0}\right)^{3}}\)
Answer:
6³ • 15³/(7⁰)³
= 90³/7⁰
= 90³/1
= 90³

Question 6.
\(\frac{2^{8} \cdot(-3)^{8} \cdot 3^{0}}{5^{-8}}\)
Answer:
Given 2⁸ • (-3)⁸ • 3⁰/5^-8
= -6⁸ • 1/5^-8
= -6⁸/5^-8

Question 7.
[12² • 3²]³ ÷ 3⁶
Answer:
Given [122 • 32]3 ÷ 36
12⁶ • 3⁶ ÷ 3⁶
36⁶/3⁶
12⁶/1⁶

Question 8.
(16⁷ ÷ 16⁴) • \(\frac{\left(5^{0}\right)^{3}}{2^{3} \cdot 4^{3}}\)
Answer:
Given (167 ÷ 164) • (5⁰)³/2³ • 4³
16⁷/16⁴ • 5⁰/2³ • 4³
16³ • 1/2³ • 4³
64³ • (½)³

Question 9.
8^-2 • \(\frac{3^{0} \cdot 8^{-3}}{4^{-5}}\) .
Answer:
Given 8-2 • 3⁰ • 8-3/4^-5
8-2 • 1 • 8-3/4^-5
8-2 • 8-3/4^-5
8-5/4^-5
2-5/1^-5

Question 10.
6^-4 • (5⁰)^-4 • (\(\frac{1}{3}\))^-4 ÷ 3^-4
Answer:
6^-4 (5⁰)^-4 ∙ (\(\frac{1}{3}\))^-4 ÷ 3^-4 We are given the expression:
6^-4 ∙ (5⁰)^-4 ∙ (\(\frac{1}{3}\))^-4 ÷ 3^-4 Simplify:
= 6^-4 ∙ \(\frac{1}{3^{-4}} \cdot \frac{1}{3^{-4}}\)
= \(\frac{6^{-4}}{3^{-4}} \cdot \frac{1}{\frac{1}{3^{4}}}\)
= \(\left(\frac{6}{3}\right)^{-4} \cdot 3^{4}\)
= 2^-4 ∙ 3⁴
= \(\frac{3^{4}}{2^{4}}\)
= \(\left(\frac{3}{2}\right)^{4}\)

Evaluate the square roots of each number. Round your answer to the nearest tenth when you can. (Lesson 1.6)

Question 11.
576
Answer:
576 = (24)²
Square of 576 is 24
24 rounded to the nearest tenth is 20

Question 12.
1,003.4
Answer:
1,003.4 = (31.6764897046)²
Square of 1,003.4 is 31.6764897046
31.6764897046 rounded to the nearest tenth is 30

Evaluate the cube root of each number. Round your answer to the nearest tenth when you can. (Lesson 1.6)

Question 13.
\(\frac{27}{216}\)
Answer:
27/216
0.125
0.125 = (0.5)³
Cubic root of 27/216 is 0.5

Question 14.
-629.5
Answer:
-629.5 = (-8.57035039349)³
Cubic root of -629.5 is -8.57035039349

Evaluate each expression and write your answer in scientific notation. Identify the greater number. (Lessons 2.1, 2.2, 2.3)

Question 15.
3.27 • 10¹¹ + 3.13 • 10¹¹ and 9.28 • 10¹¹ – 4.15 • 10¹¹
Answer:
3.27 • 1011 + 3.13 • 1011
3.27 + 3.13 • 10¹¹
6.4 • 10¹¹
And 9.28 • 1011 – 4.15 • 1011
9.28 – 4.15 • 10¹¹
5.13 • 10¹¹
6.4 • 10¹¹ is the greater number

Question 16.
9.1 • 10^-5 – 8.2 • 10^-6 and 1.2 • 10^-6 – 5.5 • 10^-7
Answer:
9.1 • 10^-5 – 8.2 • 10^-6
9.1 • 10^-5 – 0.82 • 10^-5
9.1 – 0.82 • 10^-5
8.28 • 10^-5
And 1.2 • 10-6 – 5.5 • 10^-7
1.2 • 10-6 – 0.55 • 10^-6
1.2 – 0.55 • 10^-6
0.65 • 10^-6
8.28 • 10^-5 is the greater number.

Question 17.
8.4 • 10⁵ • 2 • 10⁵ and 3.2 • 10^-7 • 2 • 10^-5
Answer:
8.4 • 10⁵ • 2 • 10⁵
8.4 • 10⁵ • 2 • 10⁵
16.8 • 10¹⁰
And 3.2 • 10^-7 • 2 • 10^-5
6.4 • 10^-12
16.8 • 10¹⁰ is the greater number.

Question 18.
9.1 • 10³ ÷ (7 • 10⁵) and 7.2 • 10^-4 ÷ (1.2 • 10^-4)
Answer:
9.1 • 10³ ÷ (7 • 10⁵)
9.1/7 • 10³/10⁵
1.3 • 1/10²
1.3 • 10-2
And 7.2 • 10^-4 ÷ (1.2 • 10^-4)
7.2/1.2 • 10^-4/10^-4
6 • 1
6 = 0.6 • 10¹
0.6 • 10¹ is the greater number.

Write each measurement in the appropriate unit in prefix form. (Lesson 2.2)

Question 19.
0.000020 meter
Answer:
0.02 • 10³ meter
0.02 millimeter

Question 20.
0.070 gram
Answer:
Given 0.070 gram
0.07 •10^-3 gram

Question 21.
35,000,000 bytes
Answer:
Given 35000000 bytes
35 • 10⁶ bytes
0.035 kilobytes

Question 22.
42,000 volts
Answer:
Given 42,000 volts
42 • 10³ volts
42 millivolts.

Problem Solving

Solve. Show your work.

Question 23.
The total surface area of a cube is 4,704 square inches. What is the length of each side? (Chapter 1)

Answer:
From the given question
Total surface area = 4,704 in².
We know that
The total surface area of a cube is 6a²
Where a = side of the cube
6a² = 4704
a² = 4704/6
a² = 784
a = √784
a = 28 in

Question 24.
The volume of a spherical balloon is 12.348π cubic feet. (Chapter 1)
a) Find its radius. Round to the nearest tenth.
Answer:
Given that the volume of a spherical balloon is 12.348π cubic feet.
We know that
The volume of the spherical balloon is 4/3 × πr³
4/3 × πr³ = 12.348π cubic feet.
r³ = 12.348π/4/3× π
r³ = 12.348/ 1.33
r³ = 9.261
r = 2.1
2.1 rounded to the nearest tenth is 2.1

b) Air is pumped into the balloon, so that its radius doubles every 10 seconds. Using 3.14 as an approximation for n, find its surface area after 30 seconds. Round to the nearest tenth.
Answer:
Let r be the radius of the balloon
The radius of the balloon doubles for every 10 seconds.
For 10 seconds radius = r²
For 20 seconds radius = r³
For 30 seconds radius = r⁴
Therefore r⁴ = 30
r = ± 2.340
2.340 rounded to the nearest tenth is 2.3

Question 25.
An oxygen atom has a total of 8 protons. If the mass of one proton is 1.67 • 10^-24 gram, find the total mass of the protons in the oxygen atom. Write your answer in scientific notation. Round the coefficient to 3 significant digits. (Chapters 1, 2)
Answer:
Given that the oxygen atom has a total of 8 protons
Mass of one proton = 1.67 • 10-24
Mass of 8 protons = 8
Total mass of a protons = 8 × 1.67 • 10-24
= 13.36• 10-24
13.36• 10-24 Round the coefficient to 3 significant digits is 13.4

Question 26.
The table lists the energy in Calories contained in 100 grams of fruits. (Chapter 2)

a) Calculate the total energy of the three fruits. Write your answer in scientific notation.
Answer:
Given that the energy in calories contained in 100 grams of apples = 4.9 • 10⁴
The energy in calories contained in 100 grams of oranges = 6.2 • 10⁴
The energy in calories contained in 100 grams of pear = 3.5 • 10⁴
Total energy in all the three fruits = 4.9 • 10⁴ + 6.2 • 10⁴ + 3.5 • 10⁴
= 4.9 + 6.2 + 3.5 • 10⁴
= 14.6 • 10⁴

b) Find the difference in energy contained between 100 grams of apple and 100 grams of pear.
Answer:
Given that the energy in calories contained in 100 grams of apples = 4.9 • 10⁴
The energy in calories contained in 100 grams of pear = 3.5 • 10⁴
Difference = 4.9 • 10⁴ – 3.5 • 10⁴
= 1.4 • 10⁴
The difference in the energy contained between 100 grams of apple and 100 grams of pear is 1.4 • 10⁴

c) How many times more energy does 100 grams .of orange have compared to 100 grams of apple? Round to the nearest tenth.
Answer:
Given that the energy in calories contained in 100 grams of oranges = 6.2 • 10⁴
The energy in calories contained in 100 grams of apples = 4.9 • 10⁴
6.2 • 10⁴ – 4.9 • 10⁴
6.2 – 4.9 • 10⁴
1.3 • 10⁴
The energy in calories contained in 100 grams of oranges is 1.3 • 10⁴ times more than the 100 grams of apple

Question 27.
Jim deposits $2,000 in a bank, which gives 6% interest, compounded yearly. Use the formula A = P (1 + r )ⁿ to find the amount of money in his account after 15 years. A represents the final amount of investment, P is the original principal, r is the interest rate, and n is the number of years it was invested. (Chapter 1)
Answer:
Given that
Jim deposits $2,000 in a bank
It gives 6% interest
Using the formula A = P (1 + r )n
P is the original principal
r is the interest rate
n is the number of years
A = 2000(1+6)¹⁵
A = 2000(7)¹⁵
A = 2000 • 7¹⁵