This handy Math in Focus Grade 8 Workbook Answer Key Chapter 11 Lesson 11.3 Independent Events detailed solutions for the textbook questions.
Math in Focus Grade 8 Course 3 B Chapter 11 Lesson 11.3 Answer Key Independent Events
Math in Focus Grade 8 Chapter 11 Lesson 11.3 Guided Practice Answer Key
Solve. Show your work.
Question 1.
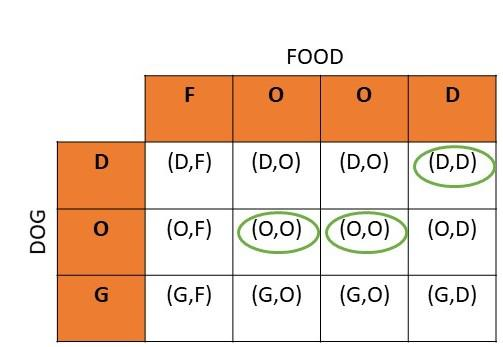
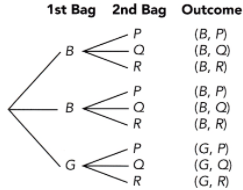
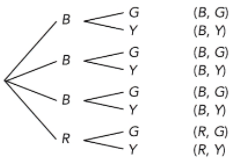
A game is played with a bag of 6 color tokens and a bag of 6 letter tiles. The 6 tokens consist of 2 green tokens, 1 yellow token, and 3 red tokens. The 6 letter tiles consist of 4 tiles of letter A and 2 tiles of letter B. To win the game, you need to randomly get a yellow token and a tile of letter B from a random selection in each bag.
a) Copy and complete the tree diagram.
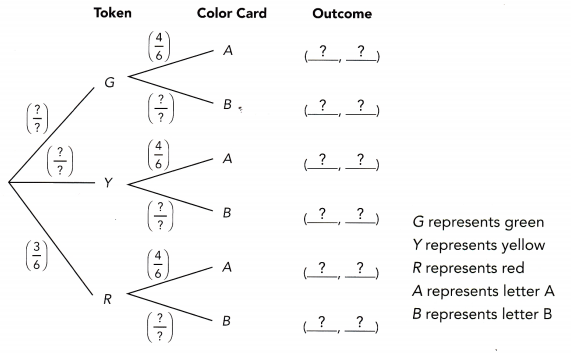
Answer:
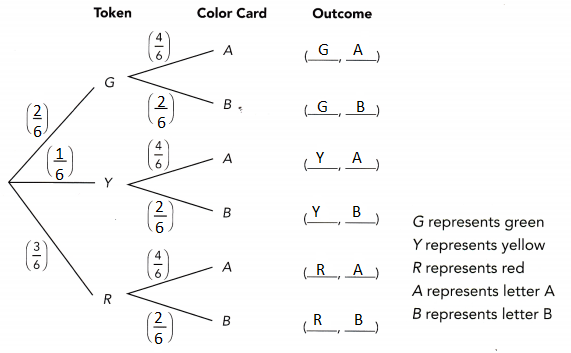
b) Use the multiplication rule of probability to find the probability of winning the game in one try.
P(winning the game) = P(Y, B)
= P(Y) • P(B)
= ![]() •
• ![]()
= ![]()
The probability of winning the game is ![]() .
.
Answer:
P(winning the game) = P(Y, B)
= P(Y) • P(B)
P(Y) = 1/6 and P(B) = 2/6
= 1/6 • 2/6
= 2/36
= 1/18
The probability of winning the game is 1/18.
Technology Activity
Materials:
spreadsheet software
SIMULATE RANDOMNESS
Work in pairs.
Background
Two fair six-sided number dice are thrown. Using a spreadsheet, data will be generated to investigate how frequently the outcome of doubles (1 and 1, 2 and 2, … , 6 and 6) occurs.
STEP 1: Label your spreadsheet as shown.

STEP 2: To generate a random integer between 1 and 6, in cell A2, enter the formula = INT(RAND()*6 + 1) to simulate rolling a die. A random number from 1 to 6 should appear in the cell.

STEP 3: To model 100 rolls, select cells A2 to A101 and choose Fill Down from the Edit menu.
STEP 4: Repeat STEP 2 and STEP 3 for cells B2 to B101.

STEP 5: In cell C2, enter the formula = A2 – B2. Select cells C2 to C101 and choose Fill Down from the Edit menu. This column serves as a check to see if the random numbers generated in columns A and B are the same. If the numbers are the same, their difference is 0. A zero difference indicates doubles outcome.
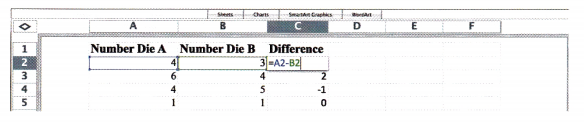
STEP 6: To see how many times the data shows double occurring, in cell E1, enter the formula = COUNTIF(C2:C101,0).
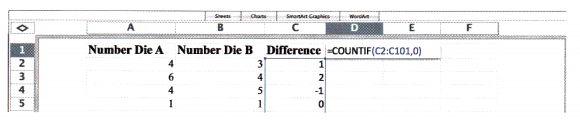
STEP 7: Find the experimental probability of the occurrence of two number dice showing the same number by dividing the number you get in cell E1 by the total, 100 rolls.
Math Journal Find the theoretical probability of rolling doubles with 2 fair number dice. Compare this theoretical probability with the experimental probability you obtained in the spreadsheet simulation. Are these two values the same?

Answer:
Question 2.
In a bag, there are 9 magenta balls and 1 orange ball. Two balls are randomly drawn, one at a time with replacement.
a) Find the probability of drawing two magenta balls.
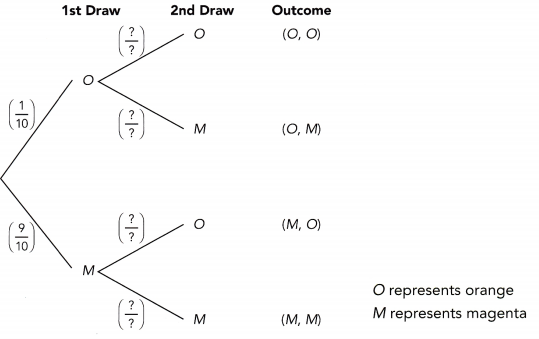
P(M, M) = P(M) • P(M)
= ![]() •
• ![]()
= ![]()
The probability drawing two magenta balls is ![]() .
.
Answer:
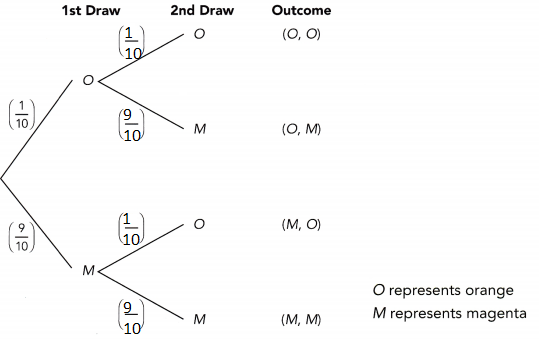
P(M) = 9/10
P(M, M) = P(M) • P(M)
= 9/10 • 9/10
= 81/100
The probability drawing two magenta balls is 81/100.
b) Find the probability of drawing an orange ball followed by a magenta ball.
P(O, M) = P(O) • P(M)
= ![]() •
• ![]()
= ![]()
The probability drawing an orange ball followed by a magenta ball is ![]() .
.
Answer:
P(O) = 1/10
P(M) = 9/10
P(O, M) = P(O) • P(M)
= 1/10 • 9/10
= 9/100
The probability drawing an orange ball followed by a magenta ball is ![]() .
.
c) Find the probability of drawing both orange balls.
P(O, O) = P(O) • P(O)
= ![]() •
• ![]()
= ![]()
The probability drawing both orange balls is ![]() .
.
Answer:
P(O) = 1/10
P(O, O) = P(O) • P(O)
= 1/10 • 1/10
= 1/100
The probability drawing both orange balls is 1/100.
Question 3.
On weekends, Carli either jogs (J) or plays tennis (T) each day, but never both. The probability of her playing tennis is 0.75.
a) Find the probability that Carli jogs on both days.
Because J and T are complementary,
P(J) = 1 – P(T)
= 1 – ![]()
= ![]()
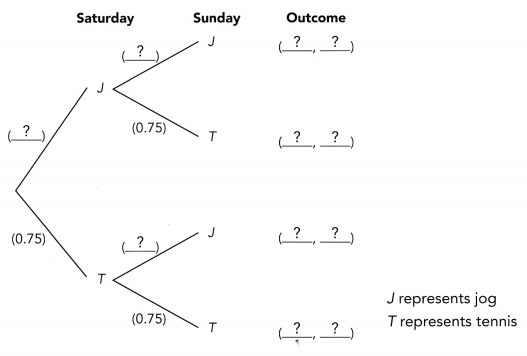
P(J, J) = P(J) • P(J)
P(J, J) = ![]() •
• ![]()
= ![]()
The probability that Carli jogs both days is ![]() .
.
Answer:
P(J) = 1 – P(T)
= 1 – 0.75
= 0.25
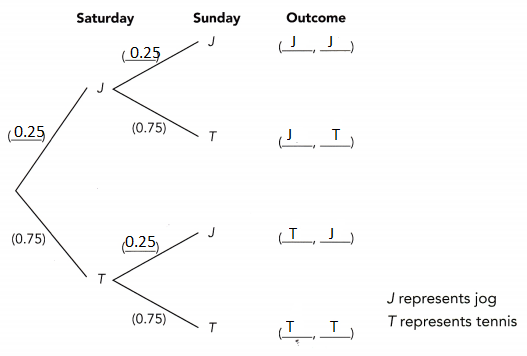
P(J, J) = P(J) • P(J)
P(J, J) = 0.25 • 0.25
= 0.0625
The probability that Carli jogs both days is 0.0625.
b) Find the probability that Carli jogs on exactly one of the days.
Using the addition rule of probability:
P(J, J) + P(T, J) = P(J) • P(T) + P(T) • P(J)
= ![]() •
• ![]() +
+ ![]() •
• ![]()
= ![]()
The probability that Carli jogs on exactly one of the days is ![]() .
.
Answer:
Using the addition rule of probability:
P(J, J) + P(T, J) = P(J) • P(T) + P(T) • P(J)
= 0.25 • 0.75 + 0.75 • 0.25
= 0.125 + 0.125
= 0.25
The probability that Carli jogs on exactly one of the days is 0.25.
Math in Focus Course 3B Practice 11.3 Answer Key
Draw a tree diagram to represent each compound event.
Question 1.
Tossing a fair coin followed by drawing a marble from a bag of 3 marbles:
1 yellow, 1 green, and 1 blue.
Answer:
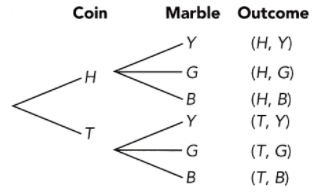
H represents heads
T represents tails
Y represents yellow
G represents green
B represents blue
Question 2.
Drawing two balls randomly with replacement from a bag with 1 green ball and 1 purple ball.
Answer:
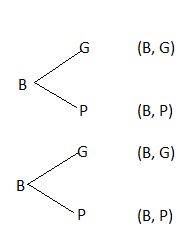
B represents ball
G represents green ball
P represents purple ball
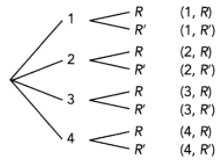
Question 3.
Drawing a ball randomly from a bag containing 1 red ball and 1 blue ball, followed by tossing a fair six-sided number die.
Answer:
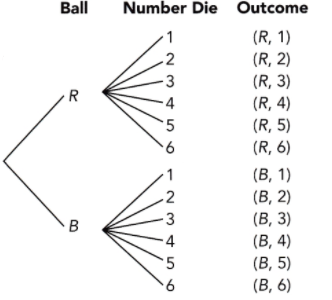
R represents red ball
B represents blue ball
Question 4.
Tossing a fair coin twice.
Answer:
If we toss a fair coin twice, we have the following possible outcomes, or events: {(H,H), (H,T),(T,H), (T,T). The total number of possible outcomes is therefore 4 and the number of outcomes where the result is two heads is 1. The probability of getting two heads in tossing a fair coin twice is therefore 1/4.
Question 5.
Reading or playing on each day of a weekend.
Answer:
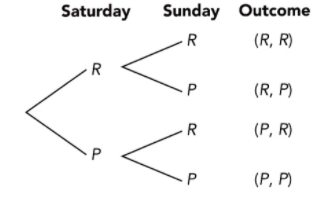
R represents reading
P represents playing
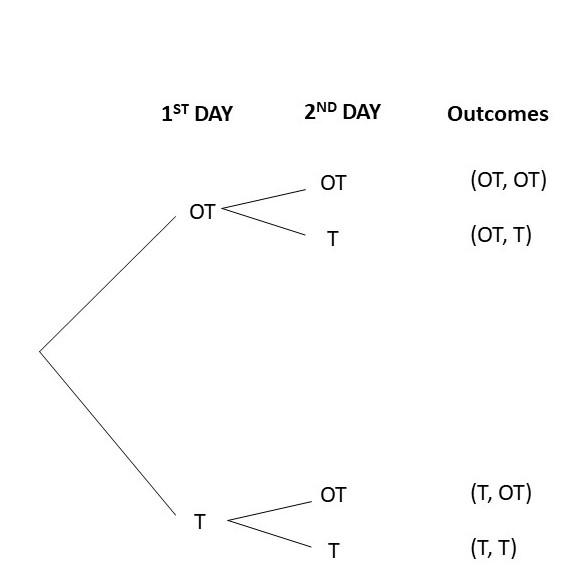
Question 6.
On time or tardy for school for two consecutive days.
Answer:
Solve. Show your work.
Question 7.
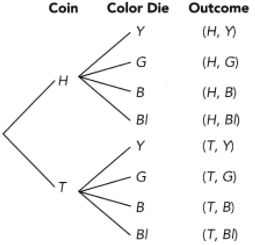
Mindy is playing a game that uses the spinner shown below and a fair coin. An outcome of 3 on the spinner and heads on the coin wins the game.

a) Draw a tree diagram to represent the possible outcomes of this game.
Answer:
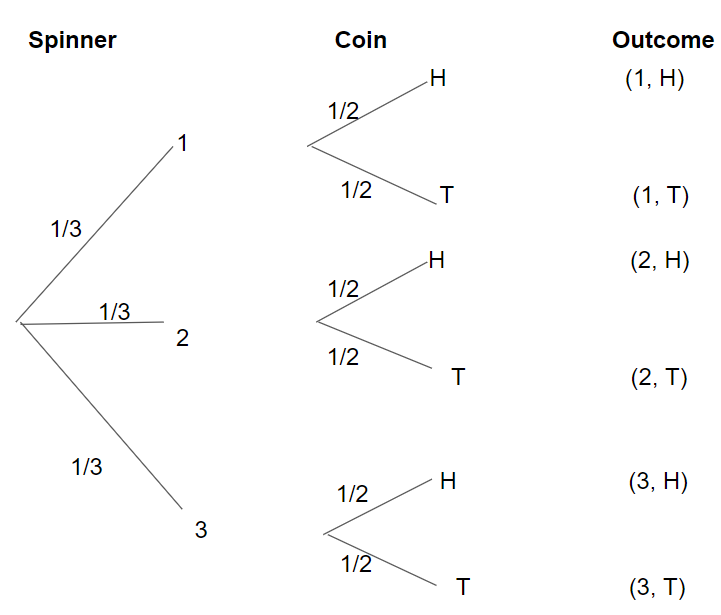
H represents Heads
T represents Tails
b) Find the probability of winning the game in one try.
Answer:
1/2 × 1/3 = 1/6
Thus the probability of winning the game in one try is 1/6.
c) Find the probability of losing the game in one try.
Answer:
1/2 + 1/3
= 3/6 + 2/6
= 5/6
Thus the probability of losing the game in one try is 5/6.
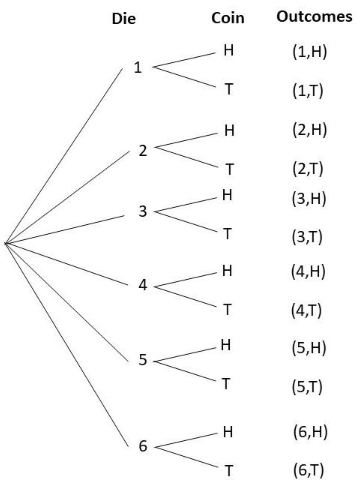
Question 8.
There are 2 blue balls and 4 yellow balls in a bag. A ball is randomly drawn from the bag, and it is replaced before a second ball is randomly drawn.
a) Draw a tree diagram to represent the possible outcomes.
Answer:
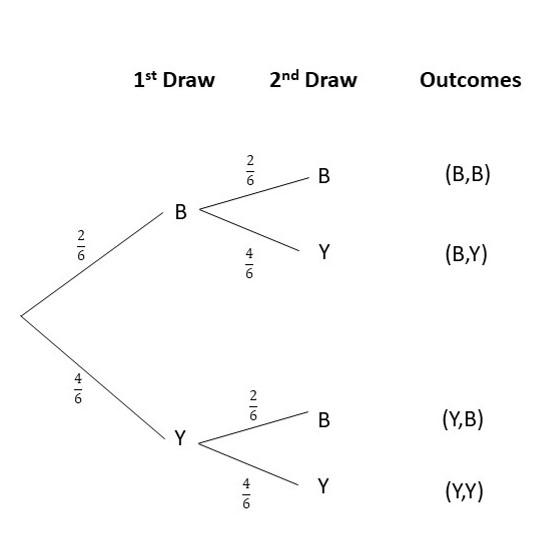
b) Find the probability that a yellow ball is drawn first, followed by another yellow ball.
Answer:
The probability of obtaining 2 yellow balls is 4/9.
Explanation:
P(Y,Y) = P(Y) x P(Y)
= 4/6 x 4/6
= 16/36
= 4/9
c) Find the probability that a yellow ball is drawn after a blue ball is drawn first.
Answer:
The probability of picking a blue than a yellow ball is 2/9.
Explanation:
P(B,Y) = P(B) x P(Y)
= 2/6 x 4/6
= 8/36
= 2/9
Question 9.
Jasmine has 3 blue pens and 2 green pens in her pencil case. She randomly selects a pen from her pencil case, and replaces it before she randomly selects again.
a) Draw a tree diagram to represent the possible outcomes.
Answer:
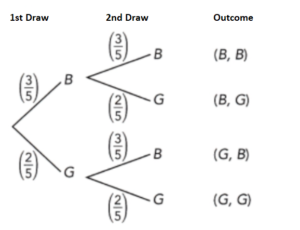
B represents blue
G represents green
b) Find the probability that she selects 2 blue pens.
Answer:
P(B) =3/5
P(B) × P(B) = 3/5 × 3/5 = 9/25
c) Find the probability that she selects 2 green pens.
Answer:
P(G) = 2/5
P(G) × P(G) = 2/5 × 2/5 = 4/25
Thus the probability that she selects 2 green pens is 4/25
d) Find the probability that she selects 2 pens of the same color.
Answer:
P(B, B) + P(G, G) = 9/25 + 4/25 = 13/25
Therefore the probability that she selects 2 pens of the same color is 13/25
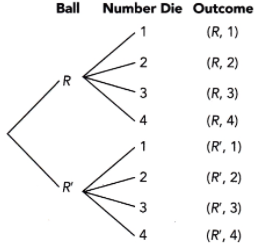
Question 10.
Henry has 4 fiction books, 6 non-fiction books, and 1 Spanish book on his bookshelf. He randomly selects two books with replacement.

a) Draw a tree diagram to represent the possible outcomes.
Answer:
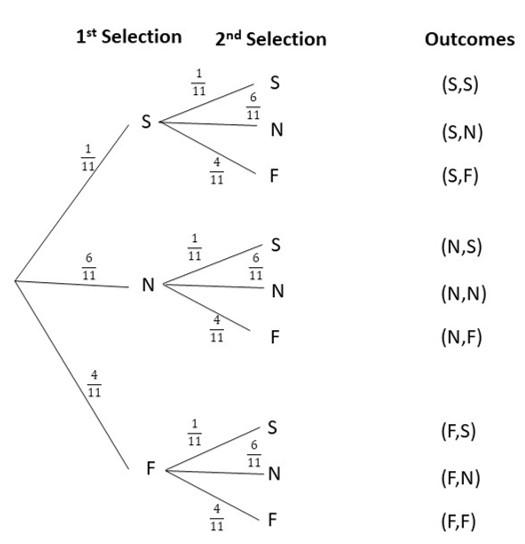
b) Find the probability that he selects a fiction book twice.
Answer:
The probability of obtaining 2 fictional books is 16/121 or around 0.13
Explanation:
P(F,F) = P(F) x P(F)
= 4/11 x 4/11
= 16/121
~ 0.13
c) Find the probability that he first selects a non-fiction book, and then a Spanish book.
Answer:
The probability of obtaining a non-fiction book and a spanish book is 6/121 or around 0.05
Explanation:
P(N,S) = P(N) x P(S)
= 6/11 x 1/11
= 6/121
~ 0.05
d) Find the probability that he first selects a fiction book, and then a non-fiction book.
Answer:
The probability of obtaining a fiction book and a non-fiction book is 24/121 or around 0.20
P(F,N) = P(F) x P(N)
= 4/11 x 6/11
= 24/121
~ 0.20
Question 11.
Andy tosses a fair six-sided number die twice. What is the probability of tossing an even number on the first toss and a prime number on the second toss?

Answer:
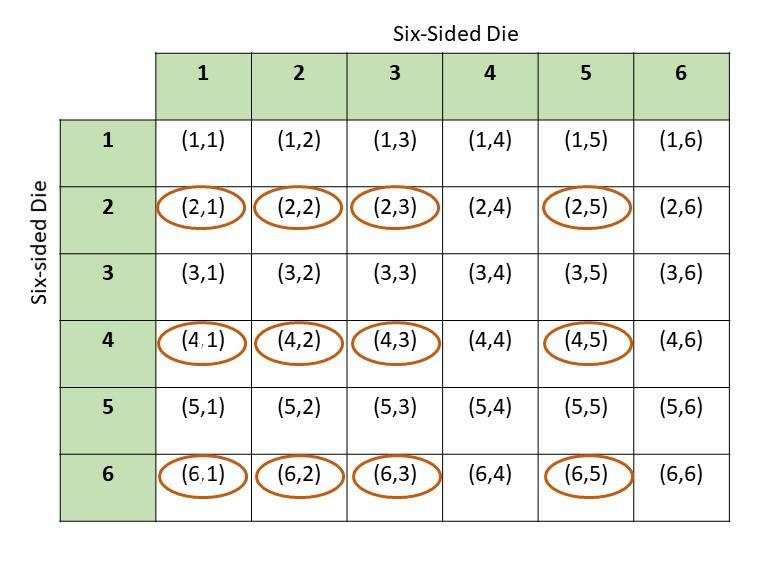
There are 36 total possible outcomes and 12 of them are favorable outcomes
P(E,P) = favorable outcomes/total outcomes
= 12/36
=1/3
Therefore, the probability of obtaining an even number and a prime number on the 2 tosses is 1/3.
Question 12.
The probability that Fiona wakes up before 8 A.M. when she does not need to set her alarm is \(\frac{4}{10}\). On any two consecutive days that Fiona does not need to set her alarm, what is the probability of her waking up before 8 A.M. for at least one of the days?
Answer:
The probability of waking up earlier than 8 AM at least once is 0.64.
Explanation:
P(E) + P(L) = 1
P(L) = 1 – P(E)
P(L) = 1 – 2/5
P(L) = 3/5
Therefore, the probability of that she will wakeup late is 3/5.
The probability of Fiona waking up late two days consecutively is 0.36
P(L,L) = P(L) x P(L)
= 3/5 x 3/5
= 9/25
= 0.36
The probability of waking up earlier than 8 AM at least once
A = 1 – P(L,L)
A = 1 – 0.36
A = 0.64
Question 13.
A globe is spinning on a globe stand. The globe surface is painted with 30% yellow, 10% green, and the rest is painted blue. Two times Danny randomly points to a spot on the globe while it spins. The color he points to each time is recorded.
a) What is the probability that he points to the same color on both spins?
Answer:
The probability of getting to the same color on both spins is 0.46
Explanation:
P(M) = P(Y,Y) + P(G,G) + P(B,B)
= P(Y) x P(Y) + P(G) x P(G) + P(B) x P(B)
= 0.3 x 0.3 + 0.1 x 0.1 + 0.6 x 0.6
= 0.09 + 0.01 + 0.36
= 0.46
b) What is the probability that he points to yellow at least one time?

Answer:
The probability of selecting yellow at least once is 0.51
Explanation:
P(NY) + P(Y) = 1
P(NY) = 1 – P(Y)
P(NY) = 1 – 0.3
P(NY) = 0.7
Therefore, the probability of not selecting yellow is 0.7
P(NY,NY) = P(NY) x P(NY)
P(NY,NY) = 0.7 x 0.7
P(NY,NY) = 0.49
Therefore, the probability of selecting twice is 0.49
P(A) + P(NY, NY) = 1
P(A) = 1 – 0.49
P(A) = 0.51
Therefore, the probability of selecting yellow at least once is 0.51.
Question 14.
Math Journal Sally thinks that for two independent events, because the occurrence of one event will not have any impact on the probability of the other event, they are also mutually exclusive. Do you agree with her? Explain your reasoning using an example.
Answer:
In an independent event, the existence of one does not affect the others. For example, eating chocolates and watching TV as they both are not mutually exclusive. Mutually exclusive events are two (or more) events that cannot be done at the same time. Thus independent events are not mutually exclusive.
Question 15.
A game is designed so that a player wins when the game piece lands on the letter A. The game piece begins on letter G. A fair six-sided number die is tossed. If the number tossed is odd, the game piece moves one step counterclockwise. If the number tossed is even, the game piece moves one step clockwise.
a) What is the probability that a player will win after tossing the number die once?
Answer:
Winning with one roll of die means getting an even number, say P(E). A number die has 6 possible results and 3 of these are even so the probability of getting even number die is the same as the probability of winning in one roll of the number die, which is 3/6 or 1/2.
b) What is the probability that a player will win after tossing the number die twice?
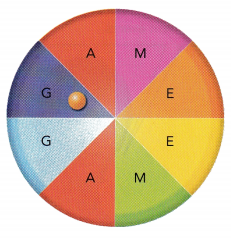
Answer:
The probability of arriving on A with two rolls of the dice is 1/4.
Explanation:
P(O,O) = P(O) x P(O)
P(O,O) = 1/2 x 1/2
P(O,O) = 1/4
Therefore, the probability of arriving on A with two rolls of the dice is 1/4.
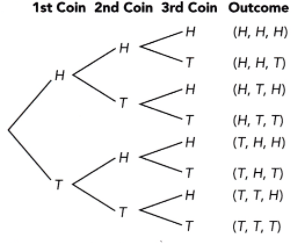













 and
and  =8,930
=8,930