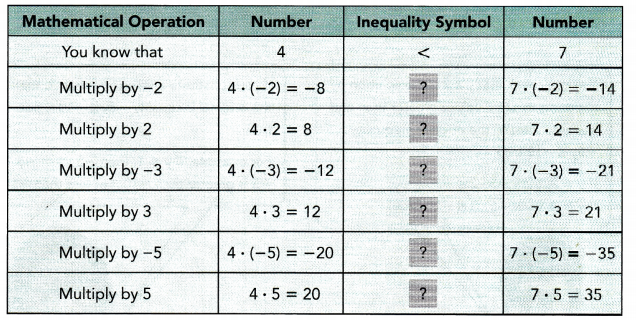
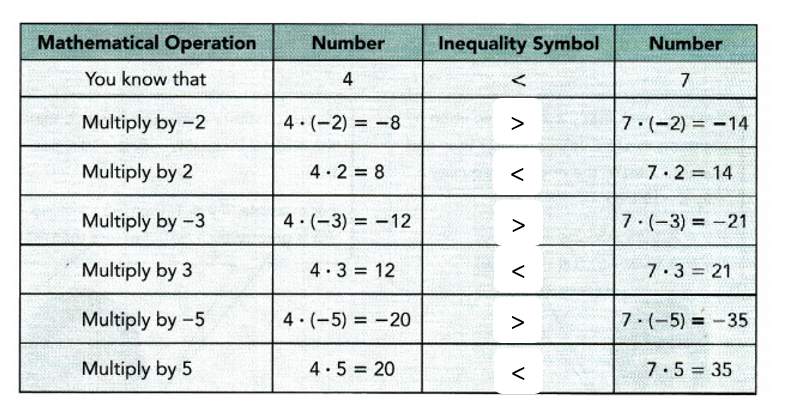
Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 5 Lesson 5.4 Understanding Inverse Proportion to score better marks in the exam.
Math in Focus Grade 7 Course 2 A Chapter 5 Lesson 5.4 Answer Key Understanding Inverse Proportion
Hands-On Activity
Materials
- algebra tiles
RECOGNIZE INVERSE PROPORTION
Work in pairs.
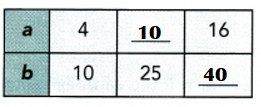
There are 6 ways of forming a rectangle with 12 algebra tiles. The diagram shows two possible ways.
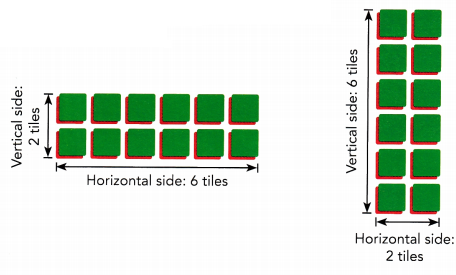
Step 1: Form a different rectangle by rearranging the 12 algebra tiles. Record your results in a table like the one shown.

Step 2: Complete the table by repeating Step 1:
Math Journal Write down your observations about the values of v • h. Describe the relationship between v and h.
Answer:
Math in Focus Grade 7 Chapter 5 Lesson 5.4 Guided Practice Answer Key
Copy and complete.
Question 1.
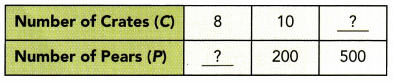
Some friends want to share the cost of buying a present. The table shows the amount of money that each person has to contribute, y dollars, and the number of people sharing the cost, x. Tell whether y is inversely proportional to x. If so, find the constant of proportionality.

For each pair of values, x and y:
1 • 180 = ![]()
![]() • 90 =
• 90 = ![]() .
. ![]() •
• ![]() =
= ![]()
The value of x increases as the value of y decreases, and the product of x and y is a ![]() value. So, y is inversely proportional to x.
value. So, y is inversely proportional to x.
The constant of proportionality is ![]() .
.
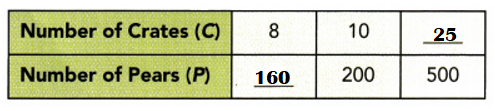
Answer:

For each pair of values, x and y ;
1. 180 = 180
2. 90 = 180
3. 60 = 180
The va1te of increases as the value of y decreases, and the product of x and y is a constant value.
So y is inversely proportional to x.
constant of proportionality = 180
Yes, y is proportional to x
Constant of proportionality = 180
Question 2.
Henry drove from Town A to Town B. The table shows the time he took, y hours, if he traveled at various speeds, x miles per hour. Tell whether x and y are in inverse proportion. If so, find the constant of proportionality.

For each pair of values, x and y:
40 • 9 = ![]() 50 •
50 • ![]() =
= ![]()
![]() •
• ![]() =
= ![]()
The value of x increases as the value of y decreases, but the product of x and y is ![]() value. So, y is
value. So, y is ![]() inversely proportional to x.
inversely proportional to x.
Answer:

For each pair of values, x and y :
40 ∙ 9 = 360
50 ∙ 7\(\frac{1}{3}\) = 366.66
60 ∙ 6 = 360
The value of x increases as the value of y decreases, but the product of x and y is not a constant value.
So y is not inversely proportional to z.
No, y is not proportional to x
Tell whether the equation represents an inverse proportion. If so, find the constant of proportionality.
Question 3.
\(\frac{3}{5}\)y = \(\frac{6}{x}\)
\(\frac{3}{5}\)y = \(\frac{6}{x}\)
\(\frac{3}{5}\) ∙ ![]() = \(\frac{6}{x}\) ∙
= \(\frac{6}{x}\) ∙ ![]() Multiply both sides by
Multiply both sides by ![]() .
.
y = \(\frac{?}{x}\) Simplify
y ∙ x = \(\frac{?}{x}\) ∙ x Multiply both sides by x.
xy = ![]() Simplify
Simplify
The original equation ![]() be rewritten as two equivalent equations in the form y = \(\frac{k}{x}\) and xy = k. So, the equation
be rewritten as two equivalent equations in the form y = \(\frac{k}{x}\) and xy = k. So, the equation ![]() an inverse proportion. The constant of proportionality is
an inverse proportion. The constant of proportionality is ![]() .
.
Answer:
\(\frac{3}{5}\)y = \(\frac{6}{x}\)
\(\frac{3}{5}\)y ∙ \(\frac{5}{3}\) = \(\frac{6}{x}\) ∙ \(\frac{5}{3}\). Multiply both sides by \(\frac{5}{3}\)
y = \(\frac{10}{x}\) Simplify
y ∙ x = \(\frac{10}{x}\) ∙ x Multiply both sides by x
xy = 10 Simplify
The original equation can be rewritten as two equivalent equations in the form
y = \(\frac{k}{x}\) and xy = k. So, the equation represents an inverse proportion.
The constant of proportionality is 10
Yes, the equation represents an inverse proportion.
Constant of proportionality is 10
Question 4.
y – 3x = 5
y – 3x = 5
y – 3x + ![]() = 5 +
= 5 + ![]() Add
Add ![]() to both sides.
to both sides.
![]() =
= ![]() Simplify.
Simplify.
The original equation ![]() be rewritten as two equivalent equations in the form y = \(\frac{k}{x}\) and xy = k. So, the equation
be rewritten as two equivalent equations in the form y = \(\frac{k}{x}\) and xy = k. So, the equation ![]() an inverse proportion.
an inverse proportion.
Answer:
y – 3x = 5
y – 3x + 3x = 5 + 3x Add 3x to both sides
y = 5 + 3x Simplify
The original equation cannot be rewritten as two equivalent equations in the form
y = \(\frac{k}{x}\) and xy = k. So, the equation cannot represents an inverse proportion.
No, the equation cannot represents an inverse proportion.
Solve an inverse proportion problem graphically.
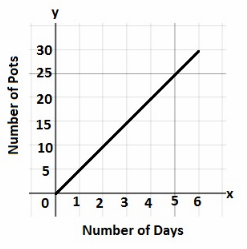
Question 5.
The amount of time needed for volunteers to pick up trash on a beach is inversely proportional to the number of volunteers. The graph shows the amount of time, y hours, needed by x volunteers.
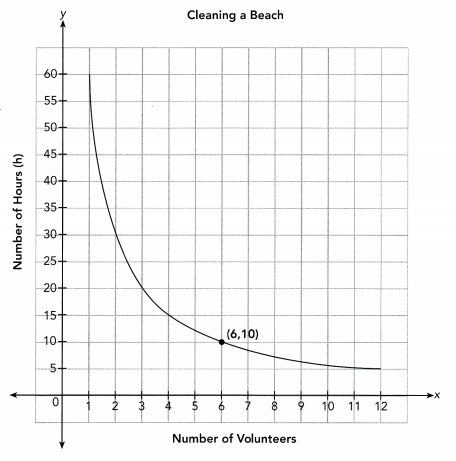
a) Find the constant of proportionality graphically. Then write an inverse proportion equation.
Use the point (![]() ,
, ![]() ) from the graph to find the constant of proportionality:
) from the graph to find the constant of proportionality:
x • y = ![]() •
• ![]() Choose the point (
Choose the point (![]() ,
, ![]() ).
).
xy = ![]() Multiply.
Multiply.
The constant of proportionality is ![]() .
.
The inverse proportion equation is ![]() .
.
Answer:
Use the point (6, 10) from the graph to find the constant of proportionality.
x ∙ y = 6 10 Choose the point (6, 10)
xy = 60 Multiply
The constant of proportionality is 60
The inverse proportion equation is xy = 60
b) Explain what the point (6, 10) represents in this situation.
It means that ![]() volunteers can clean the beach in
volunteers can clean the beach in ![]() hours.
hours.
Answer:
It means that 6 volunteers can beach in 10 hours.
Copy and complete.
Question 6.
y is inversely proportional to x, and y = 3 when x = 5.
Answer:
y = 3 when x = 5
a) Find the value of the constant
Constant of proportionality:
x ∙ y = ![]() ∙
∙ ![]()
The constant of proportionality is ![]() .
.
Answer:
Constant of proportionality :
x ∙ y = 5 ∙ 3 = 15
b) Write an inverse proportion equation that relates x and y.
Inverse proportion equation:
![]() =
= ![]() or
or ![]() =
= ![]()
The inverse proportion equation is ![]() =
= ![]() or
or ![]() =
= ![]() .
.
Answer:
Inverse proportion equation :
xy = 15 or y = \(\frac{15}{x}\)
c) Find the value of x when y = 10.
When x = 10 and y = \(\frac{?}{x}\), y = \(\frac{?}{?}\) Evaluate y = \(\frac{?}{x}\) when x = 10.
y = ![]() . Simplify.
. Simplify.
The value of y is ![]() .
.
Answer:
When x = 10 and y = \(\frac{15}{x}\),
y = \(\frac{15}{10}\)
y = 1.5
Solve.
Question 7.
Trucks are used to paint dividing lines on a long highway. The number of hours, y, the trucks take to paint the lines is inversely proportional to the number of trucks, x. 15 trucks can paint the highway in 28 hours. How many trucks are needed to paint the same highway in 20 hours?
Let x be the number of trucks.
Let y be the number of hours.
Constant of proportionality:
x ∙ y = ![]() ∙
∙ ![]()
= ![]()
Inverse proportion equation:
xy = ![]() Write an inverse equation.
Write an inverse equation.
When y = 20 and xy = ![]() ,
,
20 ∙ x = ![]()
20x = ![]()
\(\frac{20 x}{?}=\frac{?}{?}\)
x = ![]()
![]() trucks are needed to paint the highway in 20 hours.
trucks are needed to paint the highway in 20 hours.
Answer:
Let x be the number of trucks.
Let y be the number of hours.
Constant of proportionality :
x ∙ y = 15 ∙ 28
xy = 420
Inverse proportion equation :
xy = 420 Write an inverse equat ion
When y = 20 and xy = 420 :
20 ∙ x = 420 Evaluate y = 420 when y = 20
20x = 420 Simplify
\(\frac{20 x}{20}\) = \(\frac{420}{20}\) Divide both sides by 20
x = 21 simplify
21 trucks are needed to paint the
xy = 420
x = 21
Math in Focus Course 2A Practice 5.4 Answer Key
Tell whether two quantities are in inverse proportion. If so, find the constant of proportionality.
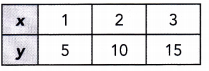
Question 1.
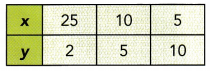
Answer:
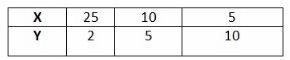
For each pair of values, x and y :
25 . 2 = 50
10 . 5 = 50
5 . 10 = 50
The value of x decreases as the value of y increases and the product of x and y is a constant value.
So y is inversely proportional to x.
Constant of Proportionality = 50
Yes, y is proportional to x
Constant of proportionality = 50
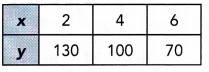
Question 2.
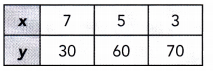
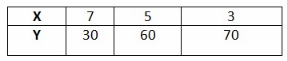
Answer:
For each pair of values, x and y :
7 . 30 = 210
5 . 60 = 300
3 . 70 = 210
The value of x decreases as the value of y increases, but the product of x and y is not a constant value.
So y is not inversely proportional to x.
No, y is not proportional to x
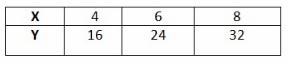
Question 3.

Answer:
For each pair of values, x and y :
4 ∙ 16 = 64
6 ∙ 24 = 144
8 ∙ 32 = 236
The value of x increases as well as the value of y increases, and the product of x and y is also not a constant value.
So y is not inversely proportional to x.
No, y is not proportional to x
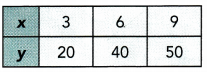
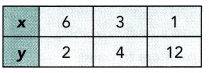
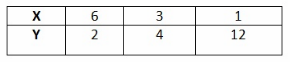
Question 4.
Answer:
For each pair of values, x and y :
6 ∙ 2 = 12
3 ∙ 4 = 12
1 ∙ 12 = 12
The value of decreases as the value of y increases, and the product of x and y is a constant value.
So y is inversely proportional to x.
Constant of Proportionality = 12
Yes, y is proportional to x
Constant of proportionality = 12
Tell whether each equation represents an inverse proportion. If so, give the constant of proportionality.
Question 5.
10x = \(\frac{5}{y}\)
Answer:
10x = \(\frac{5}{y}\)
\(\frac{y}{10}\) ∙ 10x = \(\frac{y}{10}\) ∙ \(\frac{5}{y}\) Multiply both sides by \(\frac{5}{y}\)
xy = \(\frac{1}{2}\) Simplify
The original equation can be rewritten as two qui valent equations in the form
y = \(\frac{k}{x}\) and xy = k. So, the equation represents an inverse proportion.
The constant of proportionality is \(\frac{1}{2}\)
Yes, the equation represents an inverse proportion.
Constant of proportionality is \(\frac{1}{2}\)
Question 6.
\(\frac{y}{20}\) = x
Answer:
\(\frac{y}{20}\) = x
\(\frac{1}{y}\) ∙ \(\frac{y}{20}\) = \(\frac{1}{y}\) ∙ x Multiply both sides by \(\frac{1}{y}\)
\(\frac{1}{20}\) = \(\frac{x}{y}\) Simplify
The original equation cannot be rewritten as two equivalent equations in the form
y = \(\frac{k}{x}\) and xy = k. So. the equation cannot represents an inverse proportion.
No, the equation represents an inverse proportion.
Question 7.
y + \(\frac{1}{7}\)x = \(\frac{1}{2}\)
Answer:
y + \(\frac{1}{7}\)x = \(\frac{1}{2}\)
y + \(\frac{1}{7}\)x – \(\frac{1}{7}\)x = \(\frac{1}{2}\) – \(\frac{1}{7}\)x Subtract \(\frac{1}{7}\)x to both sides
y = \(\frac{1}{2}\) – \(\frac{1}{7}\)x Simplify
The original equation cannot be rewritten as two equivalent equations in the form
y = \(\frac{k}{x}\) and xy = k. So, the equation cannot represents an inverse proportion.
No, the equation cannot represents an inverse proportion.
Question 8.
0.1x = \(\frac{5}{y}\)
Answer:
0.1x = \(\frac{5}{y}\)
y ∙ 0.1x = \(\frac{5}{y}\) ∙ y Multiply both sides by y
0.1xy = 5 Simplify
\(\frac{0.1 x y}{0.1}\) = \(\frac{5}{0.1}\) Divide both sides by 0.1
xy = 50 Simplify
The original equation can be rewritten as two equivalent equations in the form
y = \(\frac{k}{x}\) and xy = k. So, the equation represents an inverse proportion.
The constant of proportionality is 50
Yes, the equation represents an inverse proportion.
Constant of proportionality is 50
Each graph represents an inverse proportion. Find the constant of proportionality.
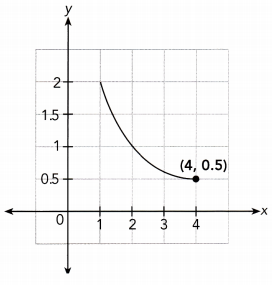
Question 9.
Answer:
Find the constant of proportionality graphically. Then write an inverse proportion equation.
Use the point (4, 0.5) f rom the graph to find the constant of proportionality.
x ∙ y = 4 ∙ 0.5 Choose the point (4, 0.5)
xy = 2 Multiply
The constant of proportionality is 2
The inverse proportion eqnation is xy = 2
Constant proportionality = 2; xy = 2
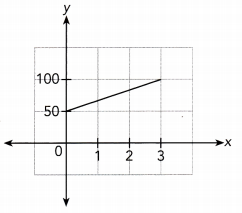
Question 10.
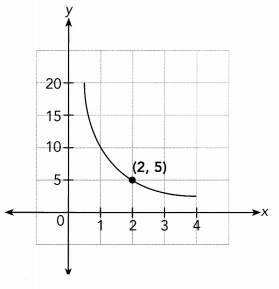
Answer:
Find the constant of proportionality graphically. Then write an inverse proportion equation.
Use the paint (2, 5) from the graph to find the constant of proportionality.
x ∙ y = 2 ∙ 5 Choose the point (2, 5)
xy = 10 Multiply
The constant of proportionality is 10
The inverse proportion equation is xy = 10
Constant of proportionality = 10; xy = 10
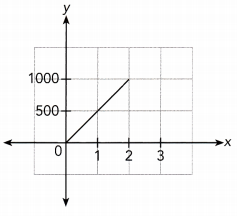
Question 11.
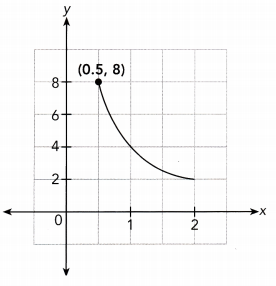
Answer:
Find the constant of proportionality graphically. Then write an inverse proportion equation.
Use the point (0.5, 8) from the graph to find the constant of proportionality.
x ∙ y = 0.5 ∙ 8 Choose the point (0.5, 8)
xy = 4 Multiply
The constant of proportionality is 4
The inverse proportion equation is xy = 4
Constant of proportionality = 4 ; xy = 4
Question 12.
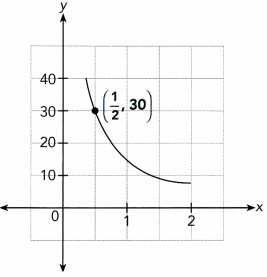
Answer:
Find the constant of proportionality graphically. Then write an inverse proportion equal ion.
Use the point (\(\frac{1}{2}\), 30) from the graph to find the constant of proportionality.
x ∙ y = \(\frac{1}{2}\) ∙ 30 Choosethe point (\(\frac{1}{2}\), 3o)
xy = 15 Multiply
The constant of proportionality is 15
The inverse proportion equation is xy = 15
Constant of proportionality = 15; xy = 15
Solve. Show your work.
Question 13.
Math Journal Describe how can you tell whether two quantities are in inverse proportion.
Answer:
The two quantities are in inverse proportion when :
1 → When x increases and y decreases or when y increases and x decreases.
2 → The product of both the quantities should remain constant.
When one quantity increases and other quantity decreases.
The product of two quantity should be constant.
Question 14.
The workers at a bakery must mix 12 batches of bagel dough every hour to meet the needs of customers. The number of batches of bagel dough, b, that each worker needs to mix in one hour is inversely proportional to the number of workers, n. The graph shows the relationship between b and n.
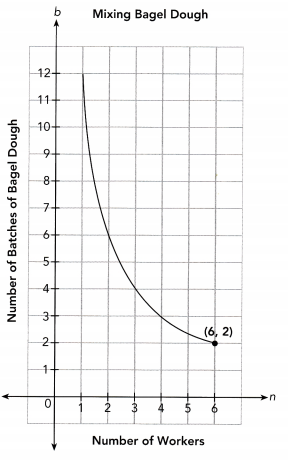
a) Find the constant of proportionality from the graph. Then write an inverse proportion equation.
Answer:
Use the point (6, 2) from the graph to find the on stunt of proportionality.
n ∙ b = 6 ∙ 2 Choose the point (6, 2)
bn = 12 Multiply
The constant of proportionality is 12
The inverse proportion equation is bn = 12
b) Explain what the constant of proportionality represents in this situation.
Answer:
It means that the workers should mix 12 bagel dough in every hours.
c) Explain what the point (6, 2) represents in this situation.
Answer:
It means that 6 workers should mix 2 batches of bagel dough.
Question 15.
A rectangle has a fixed area that does not change. The length, l, of the rectangle is inversely proportional to its width, w. The graph shows the relationship between l and w.
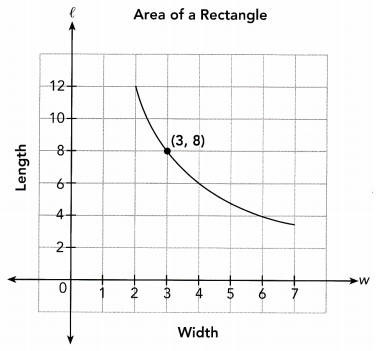
a) Find the constant of proportionality from the graph. Then write an inverse proportion equation.
Answer:
Use the point (3, 8) from the graph to find the constant of proportionality.
w ∙ l = 3 ∙ 8 Choose the point (3, 8)
lw = 24 Multiply
The constant of proportionality is 24
The inverse proportion equation is lw = 24
b) Explain what the constant of proportionality represents in this situation.
Answer:
It represent the Area of rectangle.
c) Explain what the point (3, 8) represents in this situation.
Answer:
It ‘means that 3 represents the width and 8 represent the length.
Question 16.
y is inversely proportional to x, and y = 2 when x = 5.
Answer:
y = 2 when x = 5
a) Find the constant of proportionality.
Answer:
Constant of proportionality :
x ∙ y = 5 ∙ 2 = 10
b) Write an inverse equation relating x and y.
Answer:
inverse proportion equation :
xy = 10 or y = \(\frac{10}{x}\)
c) Find the value of x when y = 4.
Answer:
When y = 4 and y = \(\frac{15}{x}\),
4 = \(\frac{15}{x}\)
\(\frac{x}{4}\) ∙ 4 = \(\frac{x}{4}\) ∙ \(\frac{15}{x}\)
x = \(\frac{15}{4}\)
x = 3.75
Question 17.
y is inversely proportional to x, and y = \(\frac{1}{3}\) when x = \(\frac{1}{2}\).
Answer:
y = \(\frac{1}{3}\) when x = \(\frac{1}{2}\)
a) Find the constant of proportionality.
Answer:
Constant of proportionality :
x ∙ y = \(\frac{1}{3}\) ∙ \(\frac{1}{2}\) = \(\frac{1}{6}\)
b) Write an inverse proportion equation relating x and y.
Answer:
Inverse proportion equation :
xy = \(\frac{1}{6}\) or y = \(\frac{1}{6 x}\)
c) Find the value of y when x = \(\frac{1}{5}\).
Answer:
when x = \(\frac{1}{5}\) and y = \(\frac{1}{6 x}\),
y = \(\frac{1}{6 \cdot \frac{1}{5}}\)
y = \(\frac{1}{6}\) ∙ 5
y = \(\frac{5}{6}\)
Question 18.
Math Journal y is inversely proportional to x. Describe how the value of y changes if the value of x is halved.
Answer:
Since y is proportional to x so the product of x and y will always be constant.
So, when the value of x is halved then the value of y will be doubted.
The value of y will be doubled.
Question 19.
The number of hours it takes to mow nine lawns is inversely proportional to the number of gardeners. It takes three gardeners four hours to mow nine lawns. How many hours would it take one gardener to mow the same nine lawns?

Answer:
Let x be the number of hours.
Let y be the number of gardeners.
The numbers of hours to mow nine lawns is inversely proportional to the number of gardeners.
Constant of proportionality :
x ∙ y = 4 ∙ 3
xy = 12
Inverse proportion equation :
xy = 12 write an inverse equation
When y = 1 and xy = 12 :
1 ∙ x = 12 Evaluate xy = 12 ‘when y = 1
x = 12 Simplify
It takes one gardeners 12 hours to mow nine lawns..
xy = 12 Write an inverse equation
12 hours
Question 20.
The number of minutes it takes to download a file is inversely proportional to the download speed. It takes Jolene 12 minutes to download a file when the download speed is 256 kilobytes per second. How long will it take her to download the same file if the download speed is 512 kilobytes per second?
Answer:
Let x be the number of minutes.
Let y be the download speed.
Number of minutes to download a file is inversely proportional to the download speed.
Constant of proportionality :
x ∙ y = 12 ∙ 256
xy = 3072
Inverse proportion equation :
xy = 3072 Write an inverse equation
When y = 512 and xy = 3072 :
512 ∙ x = 3072 Evaltate xy = 3072 when y = 512
512x = 3072 Simplify
\(\frac{512 x}{512}\) = \(\frac{3072}{512}\) Divide both sides by 512
x = 6 Simplify
It will take 6 minutes to download the same file if the download speed is 512 kilobytes per second.
6 minutes
Question 21.
Math journal Each table shows the price, y dollars, that x people have to pay to rent a guest house for one day. Describe how the two tables are alike, and how they are different. Be sure to discuss inverse proportion.

Answer:

For each pair of values, x and y ;
1 ∙ 240 = 240
2 ∙ 120 = 240
3 ∙ 80 = 240
4 ∙ 60 = 240
The value of x increases as the value of y decreases, and the product of x and y is a constant value.
So y is inversely proportional to x.
Constant of Proportionality = 240

For each pair of values, x and y ;
1 ∙ 240 = 240
2 ∙ 120 = 240
3 ∙ 85 = 255
4 ∙ 65 = 260
The value of x increases as the value of y decreases, but the product of x and y is not a constant value.
So y is not inversely proportional to x.
Alike : The two guest house are alike when the number of people are 1 and 2
Different : The two guest house are different because guest house A is inversely proportional whereas the guest house B is ‘not inversely proportional.
Guest house A: Number of people is Inversely proportional to the price of guest house.
Guest house B : Number of people is not Inversely proportional to the price of guest house.
Math Journal In questions 22 to 25, tell whether each relationship represents a direct or inverse proportion. Explain your answer.
Question 22.
A rectangle with length x inches and width y inches has an area of 50 square inches. The area is given by the equation xy = 50.
Answer:
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in Inverse proportion then their product is a constant of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
The given equation is inverse Proportion because it is written as xy = k
Inverse proportion
Question 23.
The density of a substance is the mass of the substance per unit of volume. A particular substance with a mass of m grams and a volume of v cubic centimeters has a density of 3 grams per cubic centimeter. An equation for the density of the substance is 3 = \(\frac{m}{v}\).
Answer:
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it. can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k. and it cain be rewritten as xy = k or y = \(\frac{k}{x}\)
3 = \(\frac{m}{v}\) The given equation is Direct Proportion because it is written as \(\frac{y}{x}\) = k
Direct Proportion
Question 24.
The music director at a school wants students to sell 200 tickets to the spring musical. The 200 tickets are distributed to the students in equal amounts so that each student gets y tickets to sell. The number of tickets each student gets is given by the equation y = \(\frac{200}{x}\).
Answer:
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten as y = k or y = \(\frac{k}{x}\)
y = \(\frac{200}{x}\)
xy = 200
The given equation is Inverse Proportion because it is written us xy = k
Inverse proportion
Question 25.
The sales tax you pay when you buy a new shirt is based on the amount the store charges for the shirt.
Answer:
The amount of sale tax depends on the number of shirt purchased.
Sale tax = Shirt price ∙ sale tax rate
Since sale tax is directly proportional to number of shirts
So, the equation is Directly Proportional
Directly Proportional
Brain @ Work
Question 1.
Tom is French, but lives in United States. On a visit to Germany, he saw a book that cost 25.99 euros plus 7% VAT (value-added tax). At that time, one euro was approximately equal to 0.726 U.S. dollars. In the United States, Tom could have bought the same book for 23.99 U.S. dollars plus 6% tax. Should Tom have bought the book in Germany? Explain your answer.
Answer:
Cost of book In Germany:
Price of book = 25.99 euros
VAT = 7%
Cost of book after VAT
= 25.99 + 25.99 ∙ 7%
= 25.99 + 25.99 ∙ \(\frac{7}{100}\)
= 25.99 + 1.81
= 27.80 euros
= 27.80 ∙ 0.726 Convert euros to dollars
= $20.18
Cost of book in United States:
Price of book = 23.99 dollars
Tax = 6%
Cost of book after VAT
= 23.99 + 23.99 ∙ 6%
= 23.99 + 23.99 ∙ \(\frac{6}{100}\)
= 23.99 + 1.43
= $25.09
Tom should bought the book from Germany because it was cheaper in Germany.
Germany
Question 2.
Johnny leaves Town P to drive to Town Q, a distance of 350 miles. He hopes to use only 12 gallons of gasoline. After traveling 150 miles, he checks his gauge and estimates that he has used 5 gallons of gasoline. At this rate, will he be able to reach Town Q before stopping for gasoline? Justify your answer.

Answer:
Distance between Town P and Town Q = 350 miles
Estimated gasoline he wili requin =12 galions
After traveling 150 miles he used 5 gallons of gasoline
Gasoline requires per miles = \(\frac{5}{150}\) = \(\frac{1}{30}\) gallons
Distance left to travel = 350 – 150 = 200 miles
Gasoline required for remaining distance
= 200 • \(\frac{1}{30}\)
= 6\(\frac{2}{3}\) gallons