Hillary

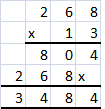
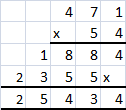
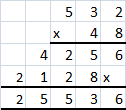
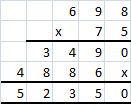
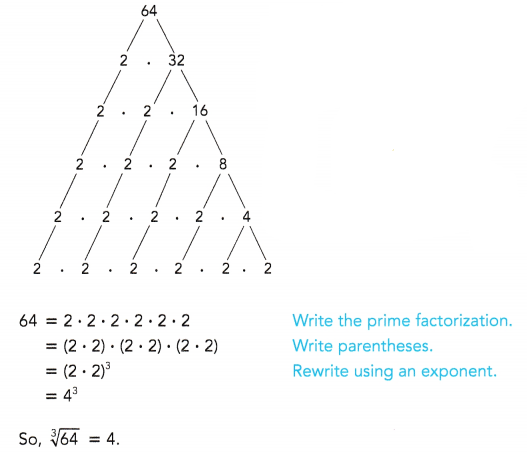
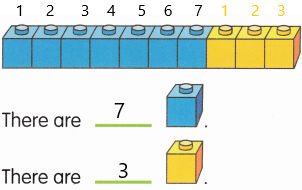
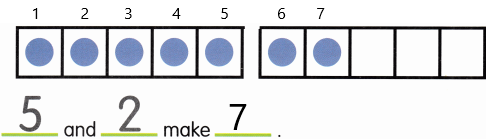
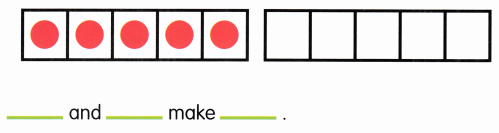
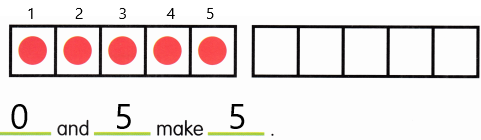
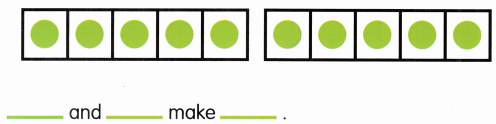
Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 4 Review Test to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 4 Review Test Answer Key

Concepts and Skills

Write each ratio in simplest form.

Question 1.
8 : 24
Answer:
1 : 3
Explanation:
The simplest form of 8 : 24 is 1 : 3
Divide each side by the highest common factor.
That is the highest number which divides evenly into both numbers.
G.C.M for 8 and 24 is 8

Question 2.
6 : 20
Answer:
3 : 10
Explanation:
The simplest form of 6 : 20 is 3 : 10
Divide each side by the highest common factor.
That is the highest number which divides evenly into both numbers.
G.C.M for 6 and 20 is 2

Question 3.
14 : 49
Answer:
2 : 7
Explanation:
The simplest form of 14 : 49 is 2 : 7
Divide each side by the highest common factor.
That is the highest number which divides evenly into both numbers.
G.C.M for 14 and 49 is 7

Question 4.
27 : 72
Answer:
3 : 8
Explanation:
The simplest form of 27 : 72 is 3 : 8
Divide each side by the highest common factor.
That is the highest number which divides evenly into both numbers.
G.C.M for 27 and 72 is 9

Question 5.
14 : 49
Answer:
2 : 7
Explanation:
The simplest form of 14 : 49 is 2 : 7
Divide each side by the highest common factor.
That is the highest number which divides evenly into both numbers.
G.C.M for 14 and 49 is 7

Question 6.
45 : 30
Answer:
3 : 2
Explanation:
The simplest form of 45 : 30 is 3 : 2
Divide each side by the highest common factor.
That is the highest number which divides evenly into both numbers.
G.C.M for 45 and 30 is 15

Question 7.
27 : 72
Answer:
3 : 8
Explanation:
The simplest form of 27 : 72 is 3 : 8
Divide each side by the highest common factor.
That is the highest number which divides evenly into both numbers.
G.C.M for 27 and 72 is 9

Question 8.
64 : 56
Answer:
8 : 7
Explanation:
The simplest form of 64 : 56 is 8 : 7
Divide each side by the highest common factor.
That is the highest number which divides evenly into both numbers.
G.C.M for 64 and 56 is 8

Find the missing term in each pair of equivalent ratios.

Question 9.
1 : 3 = 6 :
Answer: 18
Explanation:
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a = 1, b = 3, c = 6, d = x
1 x x = 3 x 6
x = 18

Question 10.
4 : 7 = : 21
Answer: 12
Explanation:
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a = 4, b = 7, c = x, d = 21
4 x 21 = 7 x x
84 = 7x
x = \(\frac{84}{7}\)
x = 12

Question 11.
25 : 15 = : 3
Answer: 5
Explanation:
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a = 25, b = 15, c = x, d = 3
25 x 3 = 15 x x
15x = 75
x = \(\frac{75}{15}\)
x = 5
Question 12.
54 : 36 = 18 :
Answer: 12
Explanation:
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a = 54, b = 36, c = 18, d = x
54 x x = 36 x 18
54x = 648
x = \(\frac{648}{54}\)
x = 12

Question 13.
4 : = 20 : 25
Answer: 5
Explanation:
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a = 4, b = x, c = 20, d = 25
4 x 25 = x x 20
100 = 20x
x = \(\frac{100}{20}\)
x = 5

Question 14.
: 9 = 48 : 72
Answer: 6
Explanation:
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a = x, b = 9, c = 48, d = 72
x x 72 = 9 x 48
72x = 432
x = \(\frac{432}{72}\)
x = 6

Question 15.
28 : = 4 : 6
Answer: 42
Explanation:
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a = 28, b = x, c = 4, d = 6
28 x 6 = x x 4
168 = 4x
x = \(\frac{168}{4}\)
x = 42

Question 16.
: 36 = 21 : 12
Answer: 63
Explanation:
product of extremes = product of means
a:b = c:d
\(\frac{a}{b}\) = \(\frac{c}{d}\)
ad = bc
a = x, b = 36, c = 21, d = 12
x x 12 = 36 x 21
12x = 756
x = \(\frac{756}{12}\)
x = 63

Problem Solving

Solve. Show your work.

Question 17.
The city has 28 fire engines and 36 fire trucks. Find the ratio of the number of fire engines to the number of fire trucks in simplest form.
Answer:
7 : 9
Explanation:
The city has 28 fire engines and 36 fire trucks.
Ratio is 28 : 36
The ratio of the number of fire engines to the number of fire trucks in simplest form.
7 : 9

Question 18.
Of the 80 students who signed up for after school clubs, 16 students signed up for the art club, and the rest signed up for other clubs. Find the ratio of the number of students who signed up for the art club to the number of students who signed up for other dubs. Give your answer in simplest form.
Answer:
1 : 4
Explanation:
80 students who signed up for after school clubs,
16 students signed up for the art club,
the rest signed up for other clubs = 80 – 16 = 64
The ratio of the number of students who signed up for the art club to the number of students who signed up for other dubs are 16 : 64
simplest form of ratio is 1 : 4

Question 19.
On Saturday, Alison used her cell phone for 36 minutes. On Sunday, she used her cell phone for 18 minutes more than on Saturday. Find the ratio of the number of minutes Alison used on Saturday to the total number of minutes on Saturday and Sunday. Give your answer in simplest form.
Answer:
2 : 5
Explanation:
On Saturday 36 min
On Sunday 36 + 18 = 54 min
the number of minutes Alison used on Saturday to the total number of minutes on Saturday and Sunday is
36 + 54 =90 min
the ratio is 36 : 90 = 2 : 5

Question 20.
Daniel is 12 years old. Elliot is 15 years older than Daniel. Frank is 3 years younger than Elliot. Find the ratio of Daniel’s age to Frank’s age. Give your answer in simplest form.
Answer:
1: 2
Explanation:
Daniel’s age is 12 years
Elliots age is 15 + 12 = 27 years
Franks age is 27 -3 = 24 years
the ratio of Daniel’s age to Frank’s age
12 : 24
1 : 2

Question 21.
The ratio of the number of left-handed batters to the number of right-handed batters is 5 : 8. There are 45 left-handed batters.
a) How many right-handed batters are there?
Answer: 72
Explanation:
45 : 5  = x : 8
x =(45 x 8) /5 = 72

b) Find the ratio of the number of left-handed batters to the total number of batters. Give your answer in simplest form.
Answer:
5 : 13
Explanation:
45 + 72 = 117 total number of batters
45 : 117
5 : 13

Question 22.
Mrs. Johnson gave a sum of money to her son and daughter in the ratio 5 : 6. Her daughter received $2,400. How much did Mrs. Johnson give away in all?
Answer:
$2000
Explanation:
son and daughter in the ratio 5 : 6
6 : x = 5 x 2400
x = (5x 2400)/6 = 2000

Question 23.
The ratio of the number of boys to the number of girls in a school is 5 : 7. If there are 600 students in the school, how many girls are there?
Answer:
350 girls
Explanation:
ratio of boys and girls = 5 + 7 = 12
total students = 600
number of girls =7 x 600/12 = 50 x 7 = 350

Question 24.
The murals in a school are painted by its grade 6 and grade 7 students. The number of mural painters from grade 6 and the number of mural painters from grade 7 is the same for each mural in the school. Copy and complete the table.

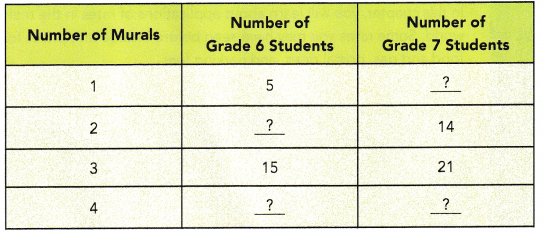
Answer:

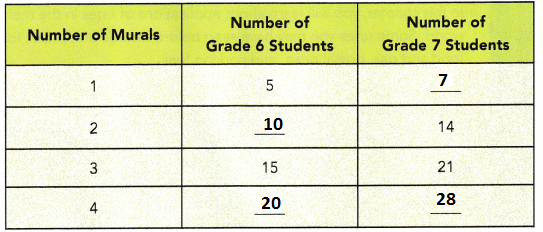
Explanation:
The number of mural painters from grade 6 and the number of mural painters from grade 7 is the same for each mural in the school
Each time the number of Murals in Garde 6 increased with 5 multiple.
At the same time in Grade 7 also increased with 7 multiple.

Question 25.
A sum of money was shared among Aaron, Ben, and Charles in the ratio 2 : 5 : 7. If Charles’s share was $1,180 more than Aaron’s share, what was the original sum of money shared?
Answer:
Explanation:
Aaron, Ben, and Charles in the ratio 2 : 5 : 7
2+5+7= 14

Aaron: 2x
Ben: 5x
Charles:7x

7x = 2x + 1180
5x = 1180
x = 236

2x + 5x + 7x = 14x
14x = 14*236 = $3304

Question 26.
The ratio of the number of beads Karen had to the number of beads Patricia had was 2 : 5. After Patricia bought another 75 beads, the ratio became 4 : 15. How many beads did each girl have at first?
Answer:
36 : 90 beads
Explanation
2:5
2x : 5x
2x : 5x+75 = 4:15
2x X 15 = 4 ( 5x + 75)
30x = 20x + 180
30x-20x = 180
10x=180
x=180/10 = 18
2x:5x
18 x2 : 5×18
36 : 90

Question 27.
Mr. Young had some bottles of apple juice and orange juice. The ratio of the number of bottles of apple juice to the number of bottles of orange juice was 3 : 2. After he sold 64 bottles of apple juice, the ratio became 1 : 6. How many bottles of apple juice and orange juice did Mr. Young have altogether in the end?
Answer:
56 bottles
Explanation:
A : O = 3 : 2
Apple  = 3 x 3 = 9
Orange = 2 x 3 = 6 =>6
64/8 = 8
8 x 6 = 48
48 + 8 = 56 bottles left out juice

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 4 Ratio to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 4 Answer Key Ratio

Math in Focus Grade 6 Chapter 4 Quick Check Answer Key

Express each fraction as two equivalent fractions using division.

Question 1.
\(\frac{3}{4}\)

Answer:
\(\frac{6}{8}\) and \(\frac{9}{12}\)

Explanation:
To find equivalent fractions,
just multiply the numerator and denominator of that reduced fraction (3/4) by any integer number, i.e., multiply by 2, 3, 4 and so on.

\(\frac{3×2}{4×2}\) = \(\frac{6}{8}\)

\(\frac{3×3}{4×3}\) = \(\frac{9}{12}\)

Question 2.
\(\frac{7}{9}\)

Answer:
\(\frac{14}{18}\) and \(\frac{21}{27}\)

Explanation:
To find equivalent fractions,
just multiply the numerator and denominator of that reduced fraction (7/9) by any integer number, i.e., multiply by 2, 3, 10, 30 and so on.

\(\frac{7×2}{9×2}\) = \(\frac{14}{18}\)

\(\frac{7×3}{9×3}\) = \(\frac{21}{27}\)

Question 3.
\(\frac{6}{11}\)

Answer:
\(\frac{12}{22}\) and \(\frac{18}{33}\)

Explanation:
To find equivalent fractions,
just multiply the numerator and denominator of that reduced fraction (6/11) by any integer number, i.e., multiply by 2, 3, 10, 30 and so on.

\(\frac{6×2}{11×2}\) = \(\frac{12}{22}\)

\(\frac{6×3}{11×3}\) = \(\frac{18}{33}\)

Question 4.
\(\frac{16}{56}\)

Answer:
\(\frac{4}{14}\) and \(\frac{2}{7}\)

Explanation:
To find equivalent fractions,
Divide the numerator and denominator to reduce fraction (16/56) by 4 and 2.

\(\frac{16}{56}\) ÷ 4

= \(\frac{4}{14}\) ÷ 2

= \(\frac{2}{7}\)

Question 5.
\(\frac{21}{63}\)

Answer:
\(\frac{1}{3}\) and \(\frac{2}{6}\)

Explanation:
To find equivalent fractions,
Divide the numerator and denominator to reduce fraction \(\frac{21}{63}\) by 21.

\(\frac{21}{63}\) ÷ 1

= \(\frac{1}{3}\)

Multiply with integer 2
\(\frac{1×2}{3×2}\)

= \(\frac{2}{6}\)

Question 6.
\(\frac{35}{140}\)

Answer:
\(\frac{1}{4}\) and \(\frac{2}{8}\)

Explanation:
To find equivalent fractions,
Divide the numerator and denominator to reduce fraction \(\frac{35}{140}\) by 35.

\(\frac{35}{140}\) ÷ 35

= \(\frac{1}{4}\)

Multiply with integer 2
\(\frac{1×2}{4×2}\)

= \(\frac{2}{8}\)

Find the unknown numerator or denominator in each pair of equivalent fractions.

Question 7.
\(\frac{3}{8}\) = \(\frac{?}{56}\)

Answer: 21
Explanation:
Use cross multiplication to calculate the unknown variable x or fraction.

\(\frac{3}{8}\) = \(\frac{?}{56}\)

\(\frac{3×56}{8}\) = \(\frac{168}{8}\) = 21

Question 8.
\(\frac{7}{9}\) = \(\frac{21}{?}\)

Answer: 27
Explanation:
Use cross multiplication to calculate the unknown variable x or fraction.

\(\frac{7}{9}\) = \(\frac{21}{?}\)

\(\frac{9×21}{7}\) = \(\frac{189}{7}\) = 27

Question 9.
\(\frac{?}{11}\) = \(\frac{30}{55}\)

Answer: 6
Explanation:
Use cross multiplication to calculate the unknown variable x or fraction.

\(\frac{?}{11}\) = \(\frac{30}{55}\)

\(\frac{30×11}{55}\) = \(\frac{330}{55}\) = 6

Question 10.
\(\frac{6}{?}\) = \(\frac{42}{84}\)

Answer: 12
Explanation:
Use cross multiplication to calculate the unknown variable x or fraction.

\(\frac{6}{?}\) = \(\frac{42}{84}\)

\(\frac{6×84}{42}\) = \(\frac{504}{42}\) = 12

Writing fractions in simplest form

Question 11.
\(\frac{5}{45}\)

Answer:
\(\frac{1}{9}\)

Explanation:
If the numerator and denominator can be divided by the same number,
which is called a common factor a simple form of fraction.
See if at least one number in the fraction is a prime number.

Question 12.
\(\frac{18}{63}\)

Answer:
\(\frac{2}{7}\)

Explanation:
If the numerator and denominator can be divided by the same number,
which is called a common factor a simple form of fraction.
See if at least one number in the fraction is a prime number.

Question 13.
\(\frac{22}{55}\)

Answer:
\(\frac{2}{5}\)

Explanation:
If the numerator and denominator can be divided by the same number,
which is called a common factor a simple form of fraction.
See if at least one number in the fraction is a prime number.

Find the unknown measurement.

Question 14.
cm = 4 m
Answer:
400 cm
Explanation:
1m = 100 cm
4 m = 4 x 100
= 400 cm

Question 15.
9.8 kg = g
Answer:
9800 g
Explanation:
1 kg = 1000 g
9.8 kg = 1000 x 9.8
= 9800 g

Question 16.
6 ft = yd
Answer:
2 yards
Explanation:
1 feet = 0.33 yards
6 feet = 0.333 x 6
= 2 yards

Question 17.
10 L = mL
Answer:
10000 mL
Explanation:
1 L = 1000 mL
10 L = 1000 x 10
= 10000 mL

Question 18.
yd = 72 in.
Answer:
2 yards
Explanation:
1 yd = 36 in
72 in = 72/36 = 2

Question 19.
5 lb = oz
Answer:
80 oz
Explanation:
1 lb = 16 oz
5 lb = 16 x 5 = 80

Find the values of P and Q.

Question 20.

Answer:
P = 24 and Q = 6
Explanation:
Each block  is of 6 units, as shown below picture

P is of four blocks 6 x 4 = 24 and
Q is 6

Question 21.

Answer:
P = 12 and Q = 16
Explanation:

Each bock is of 4 units
P is 4 x 3 =12 and Q is 4 x 4 = 16

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 5 Rates to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 5 Answer Key Rates

Math in Focus Grade 6 Chapter 5 Quick Check Answer Key

Multiply

Question 1.
268 × 13
Answer:
3,484
Explanation:

Question 2.
54 × 471
Answer:
25,434
Explanation:

Question 3.
532 × 48
Answer:
25,536
Explanation:

Question 4.
75 × 698
Answer:
52,350
Explanation:

Find each product. Express the product in simplest form.

Question 5.
4 × \(\frac{5}{32}\)
Answer:
\(\frac{5}{8}\)
Explanation:
The first step when multiplying fractions is to multiply the two numerators.
The second step is to multiply the two denominators.
Finally, simplify the new fractions.
= 4 × \(\frac{5}{32}\)
= 4 x 5 ÷ 32
= \(\frac{20}{32}\)
= \(\frac{5}{8}\)

Question 6.
\(\frac{7}{12}\) × 36
Answer: 21
Explanation:
The first step when multiplying fractions is to multiply the two numerators.
The second step is to multiply the two denominators.
Finally, simplify the new fractions.
\(\frac{7}{12}\) x 36
= \(\frac{(7)(36)}{12}\)
= \(\frac{252}{12}\) = 21

Question 7.
3\(\frac{2}{7}\) × 5
Answer:
\(\frac{115}{7}\)
Explanation:
The first step when multiplying fractions is to multiply the two numerators.
The second step is to multiply the two denominators.
Finally, simplify the new fractions.
3\(\frac{2}{7}\) x 5
= \(\frac{23}{7}\) x 5
= \(\frac{115}{7}\)

Question 8.
9\(\frac{1}{2}\) × 8
Answer: 76
Explanation:
The first step when multiplying fractions is to multiply the two numerators.
The second step is to multiply the two denominators.
Finally, simplify the new fractions.
9\(\frac{1}{2}\) x 8
= \(\frac{19}{2}\) x 8
= \(\frac{152}{2}\) = 76

Find each product. Express the product in simplest form.

Question 9.
\(\frac{2}{7}\) × \(\frac{63}{84}\)
Answer:
\(\frac{3}{14}\)
Explanation:
The first step when multiplying fractions is to multiply the two numerators.
The second step is to multiply the two denominators.
Finally, simplify the new fractions.
\(\frac{2}{7}\) x \(\frac{63}{84}\)
= \(\frac{(2)(63)}{(7)(84)}\)
= \(\frac{126}{588}\)
= \(\frac{3}{14}\)

Question 10.
\(\frac{11}{18}\) × \(\frac{3}{44}\)
Answer: 24
Explanation:
The first step when multiplying fractions is to multiply the two numerators.
The second step is to multiply the two denominators.
Finally, simplify the new fractions.
\(\frac{11}{18}\) x \(\frac{3}{44}\)
= \(\frac{11 X3}{18 x 44}\)
= \(\frac{33}{792}\) = 24

Find each quotient. Express the quotient in simplest form.

Question 11.
\(\frac{6}{7}\) ÷ 30
Answer:
\(\frac{1}{35}\)
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction.
A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
\(\frac{6}{7}\) ÷ 30
= \(\frac{6}{7}\) ÷ \(\frac{30}{1}\)
= \(\frac{6}{7 X 30}\)
= \(\frac{6}{210}\)
= \(\frac{2}{70}\)
= \(\frac{1}{35}\)

Question 12.
72 ÷ \(\frac{9}{10}\)
Answer:
\(\frac{1}{80}\)
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction.
A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
\(\frac{9}{10}\) ÷ 72
= \(\frac{9}{10}\) ÷ \(\frac{72}{1}\)
= \(\frac{9}{10 X 72}\)
= \(\frac{9}{720}\)
= \(\frac{1}{80}\)

Question 13.
\(\frac{7}{9}\) ÷ 49
Answer:
\(\frac{1}{63}\)
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction.
A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
\(\frac{7}{9}\) ÷ 49
= \(\frac{7}{9}\) ÷ \(\frac{49}{1}\)
= \(\frac{7}{9 X 49}\)
= \(\frac{7}{441}\)
= \(\frac{1}{63}\)

Question 14.
56 ÷ \(\frac{8}{11}\)
Answer:
\(\frac{1}{77}\)
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction.
A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
\(\frac{8}{11}\) ÷ 56
= \(\frac{8}{11}\) ÷ \(\frac{56}{1}\)
= \(\frac{8}{11 X 56}\)
= \(\frac{8}{616}\)
= \(\frac{1}{77}\)

Question 15.
\(\frac{4}{9}\) ÷ \(\frac{36}{135}\)
Answer:
\(\frac{5}{3}\)
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction.
A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
= \(\frac{4}{9}\) ÷ \(\frac{36}{135}\)
= \(\frac{4}{9}\) x \(\frac{135}{36}\)
= \(\frac{4 X 135}{9 X 36}\)
= \(\frac{540}{324}\)
= \(\frac{5}{3}\)

Question 16.
\(\frac{77}{92}\) ÷ \(\frac{11}{42}\)
Answer:
\(\frac{5467}{56}\) OR 97\(\frac{35}{56}\)
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction.
A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.
= \(\frac{77}{92}\) ÷ \(\frac{11}{142}\)
= \(\frac{77}{92}\) x \(\frac{142}{11}\)
= \(\frac{77 X 142}{92 X 11}\)
= \(\frac{10,934}{1,012}\)
= \(\frac{5467}{56}\)

Find the value of each set.

Question 17.
If 7 units represent 98 liters, find the value of 15 units.
Answer:
210 liters
Explanation:
First, find out the value of 1 unit,
98 ÷ 7 = 14 liters.
Then, multiply 14 by 15 which is 210 liters.

Question 18.
If 13 units represent 143 square meters, find the value of 24 units.
Answer:
264 square meters
Explanation:
First, find out the value of 1 unit,
143 ÷ 13 = 11 liters.
Then, multiply 11 by 24 which is 264 liters.

Express each ratio in simplest form.

Question 19.
4 km : 370 m
Answer:
400m : 37m
Explanation:
The simplest form of the ratio is when the numbers are expressed as natural numbers with no common factors.
convert km in m
1km = 1000m
4 km : 370 m
4000m : 370
The common factor in the above equation is 2, 5.

Question 20.
66 L : 120 mL
Answer:
550mL : 1mL
Explanation:
The simplest form of the ratio is when the numbers are expressed as natural numbers with no common factors.
Convert liter into milliliters
1 L = 1000mL
66 L : 120 mL
66000 : 120mL
550mL : 1mL
The common factor in the above equation is 2, 3, 5.

Question 21.
15 in. : 5 ft
Answer:
12ft : 1ft
Explanation:
The simplest form of the ratio is when the numbers are expressed as natural numbers with no common factors.
Convert inches to feet
1 feet = 12 inches
15 in. : 5 ft
= 15 x 12 : 5
= 60 : 5
= 12 : 1
The common factor in the above equation is 5.

Question 22.
270 qt: 105 gal
Answer:
Explanation:
The simplest form of the ratio is when the numbers are expressed as natural numbers with no common factors.
Convert quarter to gallon
1gal = 4 qt
270 qt : 105 gal
= 270 : 105 x 4
= 270 : 420
= 9 : 14
The common factor in the above equation is 30.

Find two ratios equivalent to each ratio.

Question 23.
4 : 9
Answer:
8 : 18
Explanation:
Equivalent ratios are ratios that make the same comparison of numbers.
Two ratios are equivalent if one can be expressed as a multiple of the other.
multiples of 4 (4, 8, 12, 16, 20, 24, 28, . . . ) and 9 (9, 18, 27, 36, . . . . )

Question 24.
5 : 13
Answer:
10 : 26
Explanation:
Equivalent ratios are ratios that make the same comparison of numbers.
Two ratios are equivalent if one can be expressed as a multiple of the other.
multiples of 5 (5, 10, 15, 20, . . . ) and 13 (13, 26, 39, 52, 65, 78, 91, . . . . )

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 3 Lesson 3.4 Real-World Problems: Fractions and Decimals to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 3 Lesson 3.4 Answer Key Real-World Problems: Fractions and Decimals

Math in Focus Grade 6 Chapter 3 Lesson 3.4 Guided Practice Answer Key

Solve.

Question 1.
The cost of carpeting a square yard is $8.60. How carpet 9.7 square yards?

9.7 × $ = $
It costs $ to carpet 9.7 square yards.
Answer:
9.7 × $8.60 = $83.42
It costs $83.42 to carpet 9.7 square yards.
Explanation:
The cost of carpeting a square yard is $8.60.
Cost of carpet 9.7 square yards
9.7 × $8.60 = $83.42
It costs $83.42 to carpet 9.7 square yards.

Question 2.
A roll of cloth 12 meters long is cut into smaller pieces of the same size. Each piece is 0.75 meter long. How many small pieces of cloth can be cut from the 12-meter roll?

12 =
small pieces of cloth can be cut from the 12-meter roll.
Answer:
12 ÷ 0.75 = 16
16 small pieces of cloth can be cut from the 12-meter roll.
Explanation:
A roll of cloth 12 meters long is cut into smaller pieces of the same size.
Each piece is 0.75 meter long.
Number of small pieces of cloth can be cut from the 12-meter roll
12 ÷ 0.75 = 16

Question 3.
Rosie buys 2.24 pounds of sliced ham to make sandwiches. She uses 0.16 pound for a sandwich. How many sandwiches can Rosie make?
÷ =
Rosie can make sandwiches.
Answer:
2.24÷ 0.16 = 14
Rosie can make 14 sandwiches.
Explanation:
Rosie buys 2.24 pounds of sliced ham to make sandwiches.
She uses 0.16 pound for a sandwich.
Number of sandwiches can Rosie make
2.24 ÷ 0.16 = 14

Question 4.
Bryce has $12.75. She wants to buy gifts for friends at a souvenir shop. If each souvenir costs $0.85, how many souvenirs can Bryce buy?
$ $ =
Bryce can buy souvenirs.
Answer:
$12.75 ÷ $0.85 = 15
Bryce can buy 15 souvenirs.
Explanation:
Bryce has $12.75.
She wants to buy gifts for friends at a souvenir shop.
Each souvenir costs $0.85,
Number of souvenirs can Bryce buy
$12.75 ÷ $0.85 = 15

Question 5.
A paper artist uses 18 paper rectangles for a collage. He uses 6 of them for the border of the artwork. He then cuts the remaining paper rectangles into equal strips, each \(\frac{1}{4}\) of a paper rectangle. How many strips of paper does he cut?

Answer:
48 strips of paper
Explanation:

A paper artist uses 18 paper rectangles for a collage.
He uses 6 of them for the border of the artwork.
He then cuts the remaining paper rectangles into equal strips, each \(\frac{1}{4}\) of a paper rectangle
Total strips of paper he cut
18 – 6 = 12
12 ÷ \(\frac{1}{4}\)
=48

Question 6.
Sophie buys a roll of string that is 20 meters long. She uses 3 meters of string to tie a parcel. She then cuts the remaining string into equal pieces, each \(\frac{1}{2}\) meter long. How many pieces does Sophie cut?
÷ \(\frac{?}{?}\) = ×
=
Sophie cuts pieces.
Answer:
Sophie cuts 34 pieces.
Explanation:
Sophie buys a roll of string that is 20 meters long.
She uses 3 meters of string to tie a parcel.
20 – 3 = 17 mtrs
the roll of string after use 3 mtrs is 17 mtrs
17 ÷ \(\frac{1}{2}\) = 17 × 2
= 34
Sophie cuts 34 pieces.

Question 7.
Andrea buys 75 cups of cranberry-apple juice for a party. She uses \(\frac{2}{5}\) of the juice to make punch. She then uses the remaining juice to pour single servings that are \(\frac{5}{6}\) cup each. How many single servings does Andrea pour?



The remaining juice is poured into single servings that are \(\frac{5}{6}\) cup each.
÷ \(\frac{?}{?}\) = × \(\frac{?}{?}\)
=
Andrea pours single servings.
Answer:
The remaining juice is poured into single servings that are \(\frac{5}{6}\) cup each.

45 ÷ \(\frac{5}{6}\) = 45 × \(\frac{6}{5}\)
= 54
Andrea pours 54 single servings.
Explanation:
Andrea buys 75 cups of cranberry-apple juice for a party.
She uses \(\frac{2}{5}\) of the juice to make punch.
She then uses the remaining juice to pour single servings that are \(\frac{5}{6}\) cup each.
Number of single servings does Andrea pour

Andrea pours 54 single servings.

Question 8.
Meredith bakes 5 pumpkin pies. She cuts the pies into quarters and distributes the pieces equally among her neighbors. Each neighbor receives \(\frac{3}{4}\) of a pie.
a) How many neighbors does Meredith distribute the pies to?
5 ÷ \(\frac{3}{4}\) = × \(\frac{?}{?}\)
=
Meredith distributes the pies to neighbors.

How many neighbors does Meredith distribute the pies to?
Answer:
6\(\frac{2}{3}\)
Explanation:
5 ÷ \(\frac{3}{4}\) = 5 × \(\frac{4}{3}\)

= \(\frac{20}{3}\)

= 6\(\frac{2}{3}\)

Meredith distributes the pies to 6 neighbors.

b) What fraction of a pie is left?
× \(\frac{3}{4}\) =
5 – =
of a pie is left.
Answer:
\(\frac{1}{2}\) pie is left over.
Explanation:
\(\frac{1}{2}\) ÷ 6

= \(\frac{1}{2}\) x \(\frac{1}{6}\)

= \(\frac{1}{12}\)

c) What is the total amount of pie each neighbor will receive if the remainder is divided evenly and distributed to each neighbor?
5 ÷ =
Each neighbor will receive of a pie in total.
Answer:
Each neighbor will receive \(\frac{5}{6}\) of each pie.
Explanation:
Meredith bakes 5 pumpkin pies.
She cuts the pies into quarters and distributes the pieces equally among her neighbors.\(\frac{3}{4}\) + \(\frac{1}{12}\)

= \(\frac{9}{12}\) + \(\frac{1}{12}\)

= \(\frac{10}{12}\)

= \(\frac{5}{6}\)

Question 9.
Some bottles containing \(\frac{2}{5}\) gallon of water each are used to fill a 7-gallon container. How many of these bottles are needed to fill the container with water to its brim?

7 ÷ \(\frac{2}{5}\) = × \(\frac{?}{?}\)
=
bottles are needed to fill the container with water to its brim.
Answer:
7 ÷ \(\frac{2}{5}\) = 7 × \(\frac{5}{2}\)

= \(\frac{35}{2}\)

17 \(\frac{1}{2}\) bottles are needed to fill the container with water to its brim.

Explanation:
Bottles containing \(\frac{2}{5}\) gallon of water used to fill a 7-gallon container.
Number of bottles are needed to fill the container with water to its brim
7 ÷ \(\frac{2}{5}\) = 7 × \(\frac{5}{2}\)

= \(\frac{35}{2}\)

= 17 \(\frac{1}{2}\)

Question 10.
Lilian has a part-time job. Each month, she spends \(\frac{1}{3}\) of her earnings on clothes, saves \(\frac{3}{8}\) of the remainder, and spends the rest of her earnings on food.
a) What fraction of her earnings does she spend on food?
b) If she earns $540, how much does she spend on food each month?
Method 1
a)

The model shows that:
She spends \(\frac{?}{?}\) of her earnings on food.
Answer:
She spends \(\frac{5}{8}\) of her earnings on food.

b) units → $540
1 unit → $ ÷ = $
units → × $ = $
She spends $ on food each month.
Answer:
She spends $225 on food each month.
Explanation:
12 units → $540
1 unit → $540 ÷ 12 = $45
5 units → 5 × $45 = $225
She spends $225 on food each month.
Method 2
a)

Answer:
She spends \(\frac{5}{8}\)
Explanation:

b) \(\frac{?}{?}\) × $540 = $
She spends $ on food each month.
Answer:
$225
Explanation:
540 x (1/3) = 180 for cloths
540 – 180 = 360
\(\frac{5}{8}\) × $360 = $225
She spends $225 on food each month.

Question 11.
\(\frac{2}{3}\) of a square is colored green. Asha cuts this green part into a number of pieces so that each piece is \(\frac{1}{9}\) of the whole square.
a) Find the number of pieces Asha has.
\(\frac{?}{?}\) ÷ \(\frac{?}{?}\) = \(\frac{?}{?}\) ×
=
Asha has pieces.
Answer:
Asha has 6 pieces.
Explanation:
\(\frac{2}{3}\) ÷ \(\frac{1}{9}\) = \(\frac{2}{3}\) × 9
= 6
Asha has 6 pieces.

b) If the area of the square is 45 square inches, what is the area of each piece?
Area of green part = \(\frac{?}{?}\) × 45 = in.²
Area of each piece = ÷ = in.²
The area of each piece is square inches.
Answer:
The area of each piece is 5 square inches.
Explanation:
Area of green part = \(\frac{1}{9}\) × 45 = 5 in.²
Area of each piece = 45 ÷ 9 = 5 in.²
The area of each piece is 5 square inches.

Question 12.
\(\frac{3}{5}\) of the students in a class were boys. The teacher divided the boys equally into groups so that each group of boys had \(\frac{1}{10}\) of the number of students in the class. The teacher then divided the girls equally into groups such that each group of girls had \(\frac{1}{5}\) of the number of students in the class.
a) Find the number of groups of boys and the number of groups of girls.

There were groups of boys and groups of girls.
Answer:
There were 6 groups of boys and 2 groups of girls.
Explanation:

b) If there were 16 girls in the class, how many boys were there ¡n each group?
\(\frac{2}{5}\) of the class → 16 students
\(\frac{1}{5}\) of the class → students
\(\frac{3}{5}\) of the class → students
÷ 6 =
There were boys in each group.
Answer:
There were 4 boys in each group.
Explanation:
\(\frac{2}{5}\) of the class → 16 students
\(\frac{1}{5}\) of the class → 8 students
\(\frac{3}{5}\) of the class → 24 students
24 ÷ 6 =
There were 4 boys in each group.

Math in Focus Course 1A Practice 3.4 Answer Key

Solve. Show your work.

Question 1.
An ounce of pine nuts costs $1.40. If Ellen buys 2.5 ounces of pine nuts, how much will she have to pay?
Answer:
$3.50
Explanation:
One ounce cost $1.40,
she needed 2 and a half ounces
so, 1.40 x 2.5 = $3.50

Question 2.
25 pints of apple juice are poured into \(\frac{1}{2}\) pint bottles. How many bottles can be filled with apple juice?
Answer:
50 bottles can be filled with apple juice
Explanation:
25 pints of apple juice are poured into \(\frac{1}{2}\) pint bottles.
25 ÷ \(\frac{1}{2}\)
= 25 x 2 = 50 bottles

Question 3.
40 pounds of sugar are repackaged into packets of \(\frac{1}{16}\) pound each. How many packets of sugar are there?
Answer:
640 packets of sugar
Explanation:
40 pounds of sugar are repackaged into packets of \(\frac{1}{16}\) pound each.
Total packets of sugar 40 ÷ \(\frac{1}{16}\)
= 40 x 16 = 640

Question 4.
Tom used \(\frac{5}{8}\) yard of ribbon to tie weights on the tail of his kite. He cut the length of ribbon into equal pieces that were \(\frac{1}{12}\) yard long. How many pieces, each \(\frac{1}{12}\) yard long, did Tom cut from the \(\frac{5}{8}\) yard ribbon?

Answer:
7 \(\frac{2}{4}\) pieces
Explanation:
Tom used \(\frac{5}{8}\) yard of ribbon to tie weights on the tail of his kite.
He cut the length of ribbon into equal pieces that were \(\frac{1}{12}\) yard long.
Number of pieces = \(\frac{5}{8}\)÷ \(\frac{1}{12}\)
= 5 x \(\frac{12}{8}\)
= \(\frac{60}{8}\)
= 7 \(\frac{2}{4}\)

Question 5.
A carpenter has a 6-foot long board. He wants to cut the board into pieces that are \(\frac{4}{5}\) foot long.
a) How many pieces of length \(\frac{4}{5}\) foot can the carpenter cut from the board?
Answer:
7 \(\frac{2}{4}\) pieces
Explanation:
A carpenter has a 6-foot long board.
He wants to cut the board into pieces that are \(\frac{4}{5}\) foot long.
Number of pieces he get from the length \(\frac{4}{5}\)
6 ÷ \(\frac{4}{5}\)
= \(\frac{30}{4}\)
= 7 \(\frac{2}{4}\)

b) What length of the original board will be left after the carpenter has cut all the pieces that are \(\frac{4}{5}\) foot long?
Answer:
\(\frac{2}{4}\) pieces
Explanation:
A carpenter has a 6-foot long board.
He wants to cut the board into pieces that are \(\frac{4}{5}\) foot long.
Number of pieces he get from the length \(\frac{4}{5}\)
6 ÷ \(\frac{4}{5}\)
= \(\frac{30}{4}\)
= 7 \(\frac{2}{4}\)
Carpenter will cut 7 equal pieces of \(\frac{4}{5}\)
\(\frac{2}{4}\) is remaining.

Question 6.
A candle maker has 4\(\frac{1}{2}\) pounds of clear wax. He wants to cut the wax into pieces that are \(\frac{2}{3}\) pound each.
a) How many \(\frac{2}{3}\)-pound pieces can he divide the wax into?
Answer:
6 pieces

b) How much wax is left over?
Answer:
\(\frac{3}{4}\)
Explanation:
A candle maker has 4\(\frac{1}{2}\) pounds of clear wax.
He wants to cut the wax into pieces that are \(\frac{2}{3}\) pound each.
4\(\frac{1}{2}\) ÷ \(\frac{2}{3}\)
= \(\frac{9}{2}\) ÷ \(\frac{2}{3}\)
= \(\frac{9}{3}\) x \(\frac{2}{2}\)
= \(\frac{27}{4}\)
= 6 \(\frac{3}{4}\)

Question 7.
A roll of ribbon was 9 meters long. Kevin cut 8 pieces of ribbon, each of length 0.8 meter, to tie some presents. He then cut the remaining ribbon into some pieces, each of length 0.4 meter.
a) How many pieces of ribbon, each 0.4 meter in length, did Kevin have?
Answer:
6 pieces of 0.4 length

b) What was the length of ribbon left over?
Answer:
\(\frac{2}{4}\)
Explanation:
A roll of ribbon was 9 meters long.
Kevin cut 8 pieces of ribbon, each of length 0.8 meter, to tie some presents.
8 x 0.8 = 6.4 meters are used out of 6
So, 6 – 6.4 = 2.6
He then cut the remaining ribbon into some pieces, each of length 0.4 meter.
2.6 ÷ 0.4 = 6\(\frac{2}{4}\)

Question 8.
Mike has a large tropical fish collection. He gives \(\frac{2}{3}\) of his fish to a local high school. Then he gives \(\frac{2}{5}\) of the remaining fish to an elementary school. In the end, he has 30 fish left. How many fish did Mike have at first?
Answer:
150 fishes at first
Explanation:
Let, number of fishes = x
He gives \(\frac{2}{3}\) of his fish to a local high school.
That means \(\frac{1}{3}\) of his fish left.
Then he gives \(\frac{2}{5}\) of the remaining fish to an elementary school.
\(\frac{2}{3}\) x \(\frac{1}{3}\) x X = 30
\(\frac{3}{15}\)x X = 30
\(\frac{1}{5}\) x X = 30
X = 30 x 5 = 150

Question 9.
A costume designer has 40 yards of red fabric to make costumes for a musical in which 8 performers will wear red dresses and 14 people will wear red scarves. The costume maker uses 3\(\frac{1}{2}\) yards for each dress, and \(\frac{3}{4}\) yard for a scarf.
a) After making the dresses and scarves, the costume designer uses the leftover fabric to make some sashes for the dresses. If each sash uses \(\frac{1}{4}\) yard of fabric, how many sashes can be made?
Answer:
6 sashes

b) The costume designer decides to make the sashes a little smaller, so that each of the 8 dresses can have a sash. What fraction of a yard of fabric should the costume maker use to make each sash?
Answer:
\(\frac{1}{4}\) yard of fabric
Explanation:
Total fabric used for dresses= 8×3.5= 28 yards
Total fabric used for scarfs=14×0.75= 10.5 yards
Remaining fabric=40-28-10.5= 1.5 yards
Sashes made=1.5/0.25= 6 sashes.

Question 10.
Jack read \(\frac{1}{6}\) of a book on Monday and another \(\frac{1}{3}\) of it on Tuesday. He took another 4 days to finish reading the book. He read the same number of pages on each of the 4 days.
a) What fraction of the book did he read on each of the 4 days?
Answer:
Jack read \(\frac{1}{4}\)

b) If he read 40 pages on each of these 4 days, find the number of pages in the book.
Answer:
160 pages
Explanation:
Jack read \(\frac{1}{6}\) of a book on Monday and
another \(\frac{1}{3}\) of it on Tuesday
Total pages on both days \(\frac{1}{6}\) + \(\frac{1}{3}\)
= \(\frac{3}{6}\) = \(\frac{1}{2}\)
If he read 40 pages on each of these 4 days
Total number of pages in a book
40 x 4 = 160
fraction of the book he read on each of the 4 days
\(\frac{40}{160}\)
= \(\frac{1}{4}\)

Question 11.
The school librarian has $100 to spend on some books for the school. She wants to order many copies of the same book so an entire classroom can read the book. Each copy costs $3.95, Shipping for the books will be $6.95.
a) How many copies can the librarian order?
Answer:
23 books
Explanation:
100 – 6.95 = 93.05
93.05/3.95 =23.5
23.5 is rounded to 23 books

b) Describe how you can use estimation to decide if your answer to part a) is reasonable.
Answer:
23 books at cost of $4 is reasonable.
Explanation
25 book at cost $4 = $100
estimated cost of each book is $4
23 book cost is $92
$8 is for Shipping chargers
23 books  at $4 is reasonable

Question 12.
Jason cycled for 3 hours. He cycled 7\(\frac{1}{2}\) miles each hour for the first two hours and the distance he cycled for the third hour was \(\frac{1}{4}\) of the total distance he cycled in 3 hours. What was the total distance Jason cycled in 3 hours?
Answer:
8\(\frac{2}{4}\) miles
Explanation:
Jason cycled 7\(\frac{1}{2}\) miles each hour for the first two hours and
the distance he cycled for the third hour was \(\frac{1}{4}\)
The total distance he cycled in 3 hours,
7\(\frac{1}{2}\) + \(\frac{1}{4}\)
= \(\frac{15}{4}\) + \(\frac{1}{4}\)
= \(\frac{34}{4}\)
= 8\(\frac{2}{4}\)

Question 13.
The length of a field was 20 yards. Mr. Matsumoto planted a row of peas every \(\frac{3}{4}\) yard.
a) How many rows of peas did Mr. Matsumoto plant?
Answer:
15 rows planted

b) What was the remaining length of field?
Answer:
5 yards
Explanation:
The length of a field was 20 yards.
Mr. Matsumoto planted a row of peas every \(\frac{3}{4}\) yard
20x \(\frac{3}{4}\) yard
= \(\frac{60}{4}\) = 15
Remaining length of the field 20 – 15 = 5 yards

Question 14.
A sign in an elevator says the elevator can lift up to 450 kilograms. John has 10 boxes that weigh 13.75 kilograms each, and a number of additional boxes that weigh 15.5 kilograms each. If he puts the 10 boxes on the elevator, how many of the additional boxes can be lifted in the same load?
Answer:
20 additional boxes
Explanation:
Weight of each box = 13.75 kg
Weight of 10 boxes = 13.75 x 10 = 137.5 kg
Space left in the box can be adjusted = 450 – 137.5 = 312.5 kg
Weight of additional boxes = 15.5 kg
Additional boxes can be lifted in the same load = 312.5 + 15.5 = 20.1 kg

Question 15.
Ken had a number of colored marbles in a bag. \(\frac{1}{4}\) of the marbles were red, \(\frac{2}{3}\) of the remaining marbles were blue, and the rest were yellow. Given that there were 120 red and yellow marbles altogether, how many marbles were there in the bag?

Answer:
240 marbles
Explanation
\(\frac{1}{4}\) = 0.25 of the marbles were red,
\(\frac{2}{3}\) x 0.75 = 0.5 of the remaining marbles were blue,
rest are yellow
1 – [0.25 + 0.5] = 0.25 [yellow]
0.25 + 0.25 = 0.5
RED + YELLOW = 120
total
RED + YELLOW+ BLUE = 120 + 120 = 240

Question 16.
Rachel used \(\frac{3}{8}\) of her money to buy some blouses and \(\frac{2}{5}\) of the remainder to buy 2 pairs of pants. A pair of pants costs 3 times as much as a blouse. How many blouses did she buy?
Answer:
9 blouses
Explanation:
Rachel used \(\frac{3}{8}\) of her money to buy some blouses,
If total cloth is 8 parts, out of which 3 parts are used.
So, \(\frac{5}{8}\) left.
She used \(\frac{2}{5}\) of the remainder to buy 2 pairs of pants.
\(\frac{2}{5}\) x \(\frac{5}{8}\)

= \(\frac{10}{40}\)
= \(\frac{1}{4}\) used for 2 pairs of pants \(\frac{1}{8}\) each.
A pair of pants costs 3 times as much as a blouse.
So, each blouse cost \(\frac{1}{24}\)
Number of blouses she buy are
\(\frac{3}{8}\) x \(\frac{24}{1}\)
= \(\frac{72}{8}\)
= 9

Question 17.
Sheila went shopping and spent $120 on a coat. She then used \(\frac{2}{3}\) of the remaining money to buy a dress. She was left with \(\frac{1}{5}\) of her original amount of money. How much did Sheila have at first?
Answer:
let Sheila has  $M first
Explanation:
Let M = original amount of money
M – 120 – [(2/5)(M-120)] = M/5
M – 120 – 2M/5 + 48 = M/5
M – 2M/5 – M/5 = 120 – 48
5M/5 – 2M/5 – M/5 = 72
2M/5 = 72
M = 72(5/2)
M = 36(5)
M = $180
Sheila started with $180
180 – 120 = 60
60 – (2/5)(60) = 36
180(1/5) = 36
She has $36 left and that is indeed 1/5 of the original $180.

Brain @ Work

Question 1.
Alex, Beth and Carol share a sum of money. Alex receives 0.7 of the sum of money. Beth and Carol receive the rest of the money. If Beth receives \(\frac{5}{12}\) of the money shared by both her and Carol, and Carol receives $847, how much money does Alex get?
Answer:
Alex’s share = $3,388
Explanation:
Let the total money be X ,
Alex = 0.70 or \(\frac{7}{10}\) of total amount

Share of Beth + Carol = 1 – share of Alex
= 1 – \(\frac{7}{10}\)
=\(\frac{3}{10}\)
Beth and Carol = \(\frac{3}{10}\) of total amount
Beth = \(\frac{5}{12}\) of the \(\frac{3}{10}\) of total amount
Carol = \(\frac{7}{12}\) of the \(\frac{3}{10}\) of total amount

Since Carol receives $847,
Share of Beth + Carol = share of Carol ÷ \(\frac{7}{12}\)
= 847 ÷ \(\frac{7}{12}\)
= 847 x \(\frac{12}{7}\)
= $1425

Total amount = Alex +Beth + Carol
we know,
Beth + Carol = \(\frac{3}{10}\)  x total amount = $1425
total amount = 1452 ÷ \(\frac{3}{10}\)
= $1,452 x \(\frac{10}{3}\)
= 4,840

Total amount = Alex + Beth + Carol
4840 = Alex + 1452
Alex = 4840  – 1452
Alex = 3388
Alex’s share = $3,388 

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 2 Review Test to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 2 Review Test Answer Key

Concepts and Skills

Write the opposite of each number.

Question 1.
-47
Answer:
The opposite number of -47 is 47.

Question 2.
56
Answer:
The opposite number of 56 is -56.

Question 3.
-78
Answer:
The opposite number of -78 is 78.

Draw a horizontal number line to represent each set of numbers.

Question 4.
-41, -37, -34, -30, -28, -25, -22
Answer:

The given numbers -41, -37, -34, -30, -28, -25, -22 are represented in the above horizontal number line. On a horizontal number line, the numbers become greater as you move to the right, and less as you move to the left.

Question 5.
-133, -129, -126, -122, -119
Answer:

The given numbers -133, -129, -126, -122, -119 are represented in the above horizontal number line. On a horizontal number line, the numbers become greater as you move to the right, and less as you move to the left.

Draw a vertical number line to represent each set of numbers.

Question 6.
-8, -6, -2, 1, 3, 4
Answer:

The given numbers -8, -6, -2, 1, 3, 4 are represented in the above vertical number line. On a vertical number line, the numbers become greater as you move up, and lesser as you move down.

Question 7.
Odd numbers greater than -40 but less than -28.
Answer:
Odd numbers greater than -40 but less than -28 are -39, -37, -35, -33, -31, -29.

The odd numbers greater than -40 but less than -28 are -39, -37, -35, -33, -31, -29 are represented in the above vertical number line. On a vertical number line, the numbers become greater as you move up, and lesser as you move down.

Write a positive or negative number to represent each situation.

Question 8.
A deposit of $94
Answer:
$94
Explanation:
The given situation is a deposit of $94. The situation is represented with positive number $94.

Question 9.
181°F below zero.
Answer:
-181°F
Explanation:
The given situation is 181°F below zero. Below represents negative number and above represents positive number. So the situation is represented with negative number -181°F.

Question 10.
The plane’s altitude is 23,920 feet
Answer:
23,920 feet
Explanation:
The given situation is the plane’s altitude is 23,920 feet. The situation is represented with positive number 23,920 feet.

Question 11.
The elevation of a sunken ship that is 11 meters beneath the ocean’s surface
Answer:
-11 meters
Explanation:
The given situation is the elevation of a sunken ship that is 11 meters beneath the ocean’s surface. Here the word beneath represents negative sign. So the situation is represented with negative number -11 meters.

Question 12.
A gain of 35 yards
Answer:
35 yards
Explanation:
The given situation is a gain of 35 yards. The word gain represents a positive sign. The situation is represented with positive number 35 yards.

Copy and complete each Inequality using > or <.

Question 13.
-14  -18
Answer:
-14 -18
Explanation:
The given numbers are -14 and -18. Here we have to compare both the numbers. By comparing the above given numbers the number -14 is greater than -18.

Question 14.
17  -11
Answer:
17 -11
Explanation:
The given numbers are 17 and -11. Here we have to compare both the numbers. By comparing the above given numbers the number 17 is greater than -11.

Question 15.
-34  23
Answer:
-34  23
Explanation:
The given numbers are -34 and 23. Here we have to compare both the numbers. By comparing the above given numbers the number -34 is less than 23.

Question 16.
-157  -145
Answer:
-157 -145
Explanation:
The given numbers are -157 and -145. Here we have to compare both the numbers. By comparing the above given numbers the number -157 is less than -145.

Order the numbers in each set.

Question 17.
Order the numbers from greatest to least:
15, -14, 7, 2, -5, -6, -9
Answer:
The number from greatest to least: 15, 7, 2, -5, -6, -9, -14.

Question 18.
Order the numbers from least to greatest: 112, -140, -50, 51, -122, 175, -182
Answer:
The numbers from least to greatest: -182, -140, -122, -50, 51, 112, 175.

Write an Inequality for each of the following statements using > or <.

Question 19.
-112°C is warmer than -143°C.
Answer:
-112°C > -143°C
Explanation:
The given situation is -112°C is warmer than -143°C. Here we have to compare both the temperatures. After comparing the temperatures -112°C is greater than -143°C.

Question 20.
The lowest recorded temperature yesterday was -4°C, which is colder than today’s lowest recorded temperature of 4°C.
Answer:
-4°C < 4°C
Explanation:
After comparing the above given temperatures and situation -4°C is less than 4°C.

Write the absolute value of each number.

Question 21.
|79|
Answer:
The absolute value of the number |79| is 79.

Question 22.
|-88|
Answer:
The absolute value of the number |-88| is 88.

Question 23.
|-102|
Answer:
The absolute value of the number |-102| is 102.

Copy and complete each inequality using > or <.

Question 24.
|-65|  |-57|
Answer:
|-65| |-57|
Explanation:
The absolute value of the number |-65| is 65.
The absolute value of the number |-57| is 57.
So, the number |-65| is greater than |-57|.

Question 25.
|111|  |-124|
Answer:
|111|  |-124|
Explanation:
The absolute value of the number |111| is 111.
The absolute value of the number |-124| is 124.
So, the number |111| is less than |-124|.

Question 26.
|-153|  |135|
Answer:
|-153|  |135|
Explanation:
The absolute value of the number |-153| is 153.
The absolute value of the number |135| is 135.
So, the number |-153| is greater than |135|.

Question 27.
|-209|  |-278|
Answer:
|-209|  |-278|
Explanation:
The absolute value of the number |-209| is 209.
The absolute value of the number |-278| is 278.
So, the number |-209| is less than |-278|.

Problem Solving

Answer the questions.

Question 28.
The Afar Depression is a land formation in Africa. At one location in the Afar Depression, the elevation is -75 meters. At another location, the elevation is -125 meters. Write an inequality to compare the elevations. Which elevation is farther from sea level?
Answer:
-75 meters > -125 meters
The elevation -125 meters is farther from sea level.
Explanation:
At one location in the Afar Depression, the elevation is -75 meters.
At another location, the elevation is -125 meters.
After comparing the above elevations -75 meters is greater than -125 meters.

Question 29.
The table shows temperature readings taken at the same location at three different times.

a) At what time was the location the coldest?
Answer:
At 12:30 A.M. the location is coldest.

b) Between 12:30 A.M. and 8:30 A.M., the temperature was always rising. Between what two times shown in the table did the temperature reach 0°C?
Answer:
Between 4:30 A.M. and 8:30 A.M. the temperature reaches to 0°C as we can observe in the above table.

Question 30.
Clarence owes his brother Joe $240, and his best friend Tristan $166. His sister Chloe owes Clarence $275, and his friend Luke owes Clarence $150.
a) Clarence writes the number -240 to represent the amount he owes his brother Joe. What numbers should Clarence use to represent the other amounts given above?
Answer:
-166 to represent the amount Clarence owes to his best friend Tristan.
275 to represent the amount Chloe  owes to Clarence.
150 to represent the amount Luke owes to Clarence.

b) Who owes the most money?
Answer:
Clarence owes the most money($240 + $166 = $406).

c) How much does Clarence owe in total?
Answer:
Clarence owes $406 in total.

d) Which is greater, the amount of money Clarence owes, or the amount of money that people owe him?
Answer:
The amount of money that people owe to Clarence is greater.
Explanation:
The total amount that people owes to Clarence is $275 + $150 = $475
The total amount that Clarence owes to others is $240 + $166 = $406

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 2 Lesson 2.2 Absolute Value to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 2 Lesson 2.2 Answer Key Absolute Value

Math in Focus Grade 6 Chapter 2 Lesson 2.2 Guided Practice Answer Key

Use the number line to find the absolute value of each of the following numbers.

Question 1.
|-10|
Answer:

The absolute value of the number |-10| is 10.
-10 is 10 units from 0.

Question 2.
|3|
Answer:

The absolute value of the number |3| is 3.
3 is 3 units from 0.

Question 3.
|-8|
Answer:

The absolute value of the number |-8| is 8.
-8 is 8 units from 0.

Question 4.
|1|
Answer:

The absolute value of the number |1| is 1.
1 is 1 units from 0.

Question 5.
|-7|
Answer:

The absolute value of the number |-7| is 7.
-7 is 7 units from 0.

Question 6.
|0|
Answer:

The absolute value of the number |0| is 0.

Write the absolute value of each number.

Question 7.
|-23|
Answer:
The absolute value of the number |-23| is 23.

Question 8.
|41|
Answer:
The absolute value of the number |41| is 41.

Question 9.
|-38|
Answer:
The absolute value of the number |-38| is 38.

Question 10.
|114|
Answer:
The absolute value of the number |114| is 114.

Question 11.
|-132|
Answer:
The absolute value of the number |-132| is 132.

Question 12.
|506|
Answer:
The absolute value of the number |506| is 506.

Use absolute values to interpret real-world situations.

a) The figure shows a section from Keith’s bank account statement.

As of May 31, Keith had $280 ¡n his bank account. On June 24, after he withdrew $490, he had -$170 in his bank account.
|-170| = 170
This means that Keith had overdrawn $170.

b) A dog is standing on a cliff, 35 feet above sea level. A dolphin is swimming 6 feet below sea level. An octopus is moving along the seabed, 40 feet below sea level.
You can use positive and negative numbers to show the elevation of the animals relative to sea level.

Dog’s elevation = 35 ft
Dolphin’s elevation = -6 ft
Octopus’s elevation = -40 ft
To decide which animal ¡s farthest from sea level, you do not need to think about whether the animals are above or below sea level. You can use absolute values to compare distances.
Distance of dog from sea level = |35|
= 35 ft
Distance of dolphin from sea level = |-6|
= 6 ft
Distance of octopus from sea level = |-40|
= 40 ft
The octopus is farthest from sea level.

Answer the questions.

Question 13.
Joe owes his sister Lisa $12, and his sister Kelly $18. His brother David owes Joe $20.

a) Joe writes the number -12 to represent the amount he owes Lisa. What numbers should Joe use to represent the other amounts given above?
Answer:
-18 to represent the amount he owes Kelly.
20 to represent the amount his brother David owes Joe.

b) Which person owes the most money?
Answer:
Joe owes the most money($12 + $18 = $30)

Question 14.
At a parking garage, you can park underground or above ground. The lowest part of the underground parking is 40 feet below ground level. The highest part of the parking garage is 20 feet above ground level. The limousine parking area is 23 feet below ground level.
a) Use positive and negative numbers to represent the locations, with respect to ground level, of the three different parts of the parking
garage.
Answer:
The lowest part of the underground parking is 40 feet below ground level which represents -40 feet.
The highest part of the parking garage is 20 feet above ground level which represents 20 feet.
The limousine parking area is 23 feet below ground level which represents -23 feet.

b) Which part of the parking garage is closest to ground level?
Answer:
The highest part of the parking garage is 20 feet above ground level which is closest among all levels of parking.

Math in Focus Course 1A Practice 2.2 Answer Key

Use the number line to find the absolute value of each of the following numbers.

Question 1.
|-11|
Answer:

The absolute value of the number |-11| is 11.
-11 is 11 units from 0.

Question 2.
|4|
Answer:

The absolute value of the number |4| is 4.
4 is 4 units from 0.

Question 3.
|-6|
Answer:

The absolute value of the number |-6| is 8.
-6 is 6 units from 0.

Write the absolute value of each number.

Question 4.
|35|
Answer:
The absolute value of the number |35| is 35.

Question 5.
|-46|
Answer:
The absolute value of the number |-46| is 46.

Question 6.
|-77|
Answer:
The absolute value of the number |-77| is 77.

Copy and complete each inequality using > or <.

Question 7.
|-26| |30|
Answer:
|-26|  |30|
Explanation:
The absolute value of the number |-26| is 26.
The absolute value of the number |30| is 30.
So, the number |-26| is less than |30|.

Question 8.
|-92| |-114|
Answer:
|-92|  |-114|
Explanation:
The absolute value of the number |-92| is 92.
The absolute value of the number |-114| is 114.
So, the number |-92| is less than |-114|.

Question 9.
|511| |-500|
Answer:
|511|  |-500|
Explanation:
The absolute value of the number |511| is 511.
The absolute value of the number |-500| is 500.
So, the number |511| is greater than |-500|.

Question 10.
|-707| |-628|
Answer:
|-707|  |-628|
Explanation:
The absolute value of the number |-707| is 707.
The absolute value of the number |-628| is 628.
So, the number |-707| is greater than |-628|.

Answer the questions.

Question 11.
Two numbers have an absolute value of 16. Which of the two numbers is greater than 12?
Answer:
The absolute value of -16 is 16 and the absolute value of 16 is 16. So we know that 16 is greater than 12 but -16 is not.

Question 12.
Math Journal Jesse graphed a point to represent the absolute value of a number on a number line. If the original number is less than -10, describe all the possible values for the point Jesse graphed on the number line. Explain
your thinking.
Answer:
The possible values for the point Jesse graphed on the number line will be the values which are less than or equal to -11
Explanation:
Jessie pointed a number less than -10 on the number line. So the possible values will start from -11 and will decrease further.

Question 13.
The table shows a monthly bank account statement for the period March to July.

a) For which months is the account overdrawn?
Answer:
The account overdrawn in March, April and July months.

b) How much was the bank owed in March?
Answer:
The bank owed $450 in March.

c) In which month was the account overdrawn by the greatest amount?
Answer:
In March month the account overdrawn by the greatest amount with $450.

d) In which month was the account overdrawn by the least amount?
Answer:
In April month the account overdrawn by the least amount with $180.

e) How much was the bank owed ¡n total?
Answer:
$450 + $180 + $240 = $870
In total the bank owed is $870.

Question 14.
The table shows some locations with their elevations.

a) Which location is the closest to sea level?
Answer:
The location closest to sea level is Laguna Salada.

b) Which locations are within 200 feet of sea level?
Answer:
The locations within 200 feet of sea level are Salton City and Laguna Salada.

c) How much farther from sea level is Desert Shores than Salton City?
Answer:
-75.4 farther from sea level is Desert Shores than Salton City.

d) Write the locations ¡r, order from the location that is farthest from sea level to the location that is closest to sea level.
Answer:
The location that is farthest from sea level to the location that is closest to sea level are Bombay Beach, Desert Shores, Salton City, Laguna Salada.

Question 15.
The table shows the average surface temperature of some planets.

a) Which planet has the highest average surface temperature?
Answer:
Earth has the highest average surface temperature.

b) Which planet has the lowest average surface temperature?
Answer:
Uranus has the lowest average surface temperature.

c) On Earth, the boiling temperature of water at sea level is 100°C. Which planet has an average surface temperature that is closest to this temperature?
Answer:
Earth has an average surface temperature that is closet to the temperature 100°C.

d) Order the temperatures from lowest to highest.
Answer:
The temperature from lowest to highest are -218, -108, -53, 14.

Brain @ Work

Question 1.
You can interpret a negative sign in front of a number as meaning “the opposite of.” So, -3 means the opposite of 3.

a) What number is -(-3) the opposite of?
Answer:
The opposite number of -(-3) is -3.

b) What number is -(-3) equal to?
Answer:
The number -(-3) is equal to 3.

Question 2.
On a certain day, the maximum recorded temperature was 15°C and the minimum recorded temperature was -8°C. How many degrees Celsius was the difference between the recorded maximum and recorded minimum temperatures?
Answer:
The maximum recorded temperature was 15°C.
The minimum recorded temperature was -8°C.
The difference between the recorded maximum temperature and recorded minimum temperature is 15°C + 8°C = 23°C
Explanation:
On a number line 15°C is 15 units after 0.
-8°C on a number line 8 units before 0.
So, the total difference is 15°C + 8°C = 23°C

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 1 Lesson 1.5 Cubes and Cube Roots to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 1 Lesson 1.5 Answer Key Cubes and Cube Roots

Math in Focus Grade 6 Chapter 1 Lesson 1.5 Guided Practice Answer Key

Find a cube of a whole number.

a) A cube has edges 2 centimeters long. Find its volume.

Volume of cube = 2 × 2 × 2 = 8 cm³
2 × 2 × 2 is called the cube of 2.
You can write 2 × 2 × 2 as 2³.
So, 2³ = 8.

The number 3 in 2³ is the exponent. The number 2 is the base.
The cube of a whole number is called a perfect cube.
Since 8 = 2 × 2 × 2, 8 is a perfect cube.

b) Find the cube of 7.
7³ = 7 × 7 × 7
= 343
The cube of 7 is 343.

I can relate this to finding the volume of a cube with edges of length 7 units.

Find the cube of each number.

Question 1.
5
Answer:
125

Explanation:
I can relate this to finding the volume of a cube with edges of length 5 units.
^{5³ = 5 x 5 x 5}
= 125
The cube of 5 is 125.

Question 2.
6
Answer:
216

Explanation:
I can relate this to finding the volume of a cube with edges of length 7 units.
^{7³ = 7 x 7 x 7}
= 216
The cube of 6 is 216.

Question 3.
9
Answer:
729

Explanation:
I can relate this to finding the volume of a cube with edges of length 9 units.
^{9³ = 9 x 9 x 9}
= 729
The cube of 5 is 729.

Find a cube root of a perfect cube.

a) A cube has a volume of 27 cubic meters. Find the length of each edge of the cube.

You know that
Volume of cube = edge × edge × edge.
To find the length of the edge of the cube, you need to find a number whose cube is 27.
You know that 3 × 3 × 3 = 27.
So, the length of each edge of the cube is 3 meters. 3 is called the cube root of 27. This can be written as
\(\sqrt[3]{27}\) = 3
Finding the cube root of a number is the inverse of finding the cube of a number.

b) Find the cube root of 64.
By prime factorization,

I can relate this to finding the length of an edge of a cube, when I know it has a volume of 64 units³.

Find the cube root of each number.

Question 4.
216
Answer:
6

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 216 = 2 x 2 x 2 x 3 x 3 x 3
= (2.3)³
=6³
so, cube root of 216 is 6.

Question 5.
343
Answer:
7

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 343 = 7 x 7 x 7
=7³
so, cube root of 343 is 7.

Question 6.
1,000
Answer:
10

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 1000 = 2 x 2 x 2 x 5 x 5 x 5
= (2.5)³
=10³
so, cube root of 1000 is 10.

Complete.

Question 7.
Find the values of 5² + 5³ and 5 • 5 • 5 • 5 • 5.

Answer:

Find the value of each of the following.

Question 8.
6³ + 4²
Answer:
232

Explanation:
6³ = 6 x 6 x 6= 216
4² = 4 x 4 = 16
6³ + 4² =  216 + 16 = 232
6³ + 4²  = 232

Question 9.
7³ – 4³
Answer:
279

Explanation:
7³ = 7 x 7 x 7 = 343
4³ = 4 x 4 x 4 = 64
7³ – 4³ = 343 – 64 = 279
7³ – 4³ = 279

Question 10.
3² × 5³ + 9²
Answer:
215

Explanation:
3² = 3 x 3 = 9
5³ = 5 x 5 x 5 = 125
9² = 9 x 9 = 81
3² x 5³ x 9² = 9+125+81 = 215.
3² x 5³ x 9²  = 215.

Question 11.
8³ ÷ 4² – 5²
Answer:
7

Explanation:
8³ = 8 x 8 x 8 = 512
4² = 4 x 4 = 16
5² = 5 x 5 = 25
8³ ÷ 4² – 5² = 512 ÷ 16 – (25)
= 32 – 25
= 7

8³ ÷ 4² – 5² = 7

Question 12.
7² + 6³ ÷ 2³
Answer:
76

Explanation:
7²  = 7 x 7 = 49
6³ = 6 x 6 x 6 = 216
2³ = 2 x 2 x 2 = 8
7² + 6³ ÷ 2³ = 49 + (216 ÷ 8)
= 49 + 27
= 76
7² + 6³ ÷ 2³ = 76

Question 13.
9³ – 4² × 3³
Answer:
297

Explanation:
9³ = 9 x 9 x 9 = 729
4² = 4 x 4 = 16
3³ = 3 x 3 x 3 = 27
9³ – 4² + 3³ = 729 – (16 x 27)
= 729 – 432
= 279
9³ – 4² + 3³ = 279.

Math in Focus Course 1A Practice 1.5 Answer Key

Find the cube of each number.

Question 1.
8
Answer:
512

Explanation:
I can relate this to finding the volume of a cube with edges of length 8 units.
^{8³ = 8 x 8 x 8}
= 64 x 8
= 512
The cube of 8 is 512.

Question 2.
3
Answer:
27

Explanation:
I can relate this to finding the volume of a cube with edges of length 3 units.
^{3³ = 3 x 3 x 3}
9 x 3
= 27
The cube of 3 is 27.

Question 3.
10
Answer:
1000

Explanation:
I can relate this to finding the volume of a cube with edges of length 10 units.
^{10³ = 10 x 10 x 10}
=100 x 10
= 1000
The cube of 10 is 1000.

Find the cube root of each number.

Question 4.
125
Answer:
5

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 125 = 5 x 5 x 5
=5³
so, cube root of 125 is 5.

Question 5.
512
Answer:
8

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 512 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
= (2.2.2)³
=8³
so, cube root of 512 is 8.

Question 6.
729
Answer:
9

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 729 = 3 x 3 x 3 x 3 x 3 x 3
= (3.3)³
=9³
so, cube root of 729 is 9.

Solve.

Question 7.
List the perfect cubes that are between 100 and 600.
Answer:
125, 216, 343 and 512.

Explanation:
125, 216, 343 and 512 are the perfect cubes between 100 and 600.

Question 8.
Math Journal Find the value of each expression. Then describe any patterns you see.
a) 2² – 1²
Answer:
3

Explanation:
2² = 2 x 2 = 4
1² = 1 x 1 = 1
2² – 1² = 4 – 1
= 3
2² – 1² = 3.

b) 3² – 2²
Answer:
5

Explanation:
3² = 3 x 3 = 9
2² = 2 x 2 = 4
3² – 2² = 9 – 4
= 5
3² – 2² = 5.

c) 4² – 3²
Answer:
7

Explanation:
4² = 4 x 4 = 16
3² = 3 x 3 = 9
4² – 3² = 16 – 9
= 7
4² – 3² = 7.

d) 5² – 4²
Answer:
9

Explanation:
5² = 5 x 5 = 25
4² = 4 x 4 = 16
5² – 4² = 25 – 16
= 9
5² – 4² = 9.

Question 9.
Find two consecutive numbers whose squares differ by 17.
Answer:
8 and 9

Explanation:
The square of 8 is 64
The square of 9 is 81
81 – 64 = 17
So, 8 and 9 are two consecutive numbers whose squares differ by 17.

Find the value of each of the following.

Question 10.
8³ + 5²
Answer:
537

Explanation:
8³ = 8 x 8 x 8 = 512
5² = 5 x 5 = 25
8³ + 5² = 512 + 25
= 537
8³ + 5² = 537.

Question 11.
10³ – 6²
Answer:
964

Explanation:
10³ = 10 x 10 x 10 = 1000
6² = 6 x 6 = 36
10³ – 6² = 1000 – 36
= 964
10³ – 6² = 964.

Question 12.
3³ × 9²
Answer:
2187

Explanation:
3³ = 3 x 3 x 3 = 27
9² = 9 x 9 = 81
3³ x 9² = 27 x 81
= 2187
3³ x 9² = 2187

Question 13.
9³ – 5² + 6²
Answer:
740

Explanation:
9³ = 9 x 9 x 9 = 729
5² = 5 x 5 = 25
6² = 6 x 6 = 36
9³ –  5² + 6² = 729 – 25 + 36
= 740
9³ – 5² + 6² = 740.

Question 14.
7² + 8³ – 4²
Answer:
545

Explanation:
7² = 7 x 7 = 49
8³ = 8 x 8 x 8 = 512
4² = 4 x 4 = 16
7² + 8³ – 4² = 49 + 512 – 16
= 545
7² + 8³ – 4² = 545

Question 15.
9³ – 5² + 6²
Answer:
740

Explanation:
9³ = 9 x 9 x 9 = 729
5² = 5 x 5 = 25
6² = 6 x 6 = 36
9³ – 5² + 6² = 729 – 25  + 36
= 740
9³ – 5² + 6² = 740

Question 16.
8³ × 5³ ÷ 5²
Answer:
2560

Explanation:
8³ = 8 x 8 x 8 = 512
5³ = 5 x 5 x 5 = 125
5² = 5 x 5 = 25
8³ × 5³ ÷ 5² = 512 x 125 ÷ 25
= 2560
8³ × 5³ ÷ 5² = 2560

Question 17.
10³ ÷ 8² × 4²
Answer:
250

Explanation:
10³ = 10 x 10 x 10 = 1000
8² = 8 x 8 = 64
4² = 4 x 4 = 16
10³ ÷ 8² x 4² = 1000 ÷ 64 x 16
= 250
10³ ÷ 8² x 4² = 250.

Question 18.
7³ – 10² ÷ 2²
Answer:
318

Explanation:
7³ = 7 x 7 x 7 = 343
10² = 10 x 10 = 100
2² = 2 x 2 = 4
7³ – 10² ÷ 2² = 343 – (100 ÷ 4 )
= 343 – 25
= 318
7³ – 10² ÷ 2² = 318

Question 19.
3³ + 4³ × 6²
Answer:
2331

Explanation:
3³ = 3 x 3 x 3= 27
4³ = 4 x 4 x 4 = 64
6² = 6 x 6 = 36
3³ + 4³ × 6² = 27 + (64 x 36 )
= 27 + 2304
= 2331
3³ + 4³ × 6² = 2331.

Find the value of each of the following.

Question 20.
17³
Answer:
4913

Explanation:
I can relate this to finding the volume of a cube with edges of length 17 units.
17³ = 17 x 17 x 17
= 289 x 17
= 4913
The cube of 17 is 4913.

Question 21.
16³
Answer:
4096

Explanation:
I can relate this to finding the volume of a cube with edges of length 16 units.
16³ = 16 x 16 x 16
= 256 x 16
= 4096
The cube of 16 is 4096.

Question 22.
18³
Answer:
5832

Explanation:
I can relate this to finding the volume of a cube with edges of length 18 units.
18³ = 18 x 18 x 18
= 324 x 18
= 5832
The cube of 18 is 5832.

Question 23.

Answer:
12

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 1728 = 2 x 2x 2 x 2 x 2 x 2 x 3 x 3 x 3
= (2.2.3)³
=12³
So, cube root of 1728 is 12.

Question 24.

Answer:
20

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 8000 = 2 x 2 x 2 x 2 x 2 x 2 x 5 x 5 x 5
= (2.2.5)³
=20³
So, cube root of 8000 is 20.

Question 25.

Answer:
15

Explanation:
Finding the cube root of a number is the inverse of finding the cube of a number
prime factorization of 3375 = 3 x 3 x 3 x 5 x 5 x 5
= (3.5)³
=15³
So, cube root of 3375 is 15.

Solve.

Question 26.
Given that 11³ = 1,331, find the cube of 110.
Answer:
1,331,000

Explanation:
If 11³ = 1,331 then 110³ will be 1,331,000.

Question 27.
Given that 14³ = 2,744, find the cube root of 2,744,000.
Answer:
140³

Explanation:
If 14³ = 2,744 then cube root of 2,744,000 is 140³.

Question 28.
Given that = 16, evaluate 160³.
Answer:
4,096,000

Explanation:
If cube root 4096 is 16 then 160³ will be 4,906,000.

Question 29.
Evaluate 13² + 20³ – 18².
Answer:
7845

Explanation:
13² = 13 x 13 = 169
20³ = 20 x 20 x 20 = 8000
18² = 18 x 18 = 324
13² + 20³ – 18² = 169 + 8000 – 324
= 7845
13² + 20³ – 18² = 7845.

Question 30.
Evaluate the cube root of 12³ × 5³ + 8³.
Answer:
68

Explanation:
Cube root of 12³ × 5³ + 8³ will be the number itself
So, 12 x 5 + 8 = 68 is cube root of 12³ × 5³ + 8³.

Question 31.
Find three consecutive numbers whose cubes have a sum of 2,241.
Answer:
8, 9, 10

Explanation:
8³ = 512
9³ = 729
10³ = 1000
512 + 729 + 1000 = 2241
So, the three consecutive numbers whose cubes have a sum of 2241 are 8, 9 and 10.

Question 32.
A cubic crate with an edge length of 16 feet will be used to contain cubic wooden boxes. Each wooden box has an edge length of 4 feet. How many wooden boxes can the crate contain?
Answer:
4 wooden boxes

Explanation:
A cubic crate with an edge length of 16 feet will be used to contain cubic wooden boxes.
Each wooden box has an edge length of 4 feet
4 x 4 = 16
S0, the wooden crate can contain 4 wooden boxes.

Brain @ Work

Mr. Henderson wants to tile his patio that is rectangular in shape. His patio measures 108 inches by 144 inches. Find the fewest square tiles he can use without cutting any of them. (Hint: First find the largest size tile he can use.)

Answer:
21 tiles of 12 inches square tile

Explanation:
Mr. Henderson wants to tile his patio that is rectangular in shape.
His patio measures 108 inches by 144 inches
The largest size tile he can use is 12 inches
12 in x 12 tiles = 144 in
12 in x 9 tiles = 108 in
So, Mr. Henderson wants 21 tiles of 12 inches to tile his patio in rectangular shape without cutting any square tile.

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 1 Lesson 1.1 The Number Line to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 1 Lesson 1.1 Answer Key The Number Line

Math in Focus Grade 6 Chapter 1 Lesson 1.1 Guided Practice Answer Key

Draw a horizontal number line to represent each set of whole numbers.

Question 1.
Positive whole numbers less than 5
Answer:
0, 1, 2, 3 and 4 are the positive whole numbers less than 5.

Question 2.
Whole numbers greater than 9 but less than 14
Answer:
10, 11, 12, 13 are the whole numbers greater than 9 but less than 14.

Draw a vertical number line to represent each set of whole numbers.

Question 3.
Odd numbers between 1 and 10
Answer:
1, 3, 5, 7 and 9 are the odd numbers between 1 and 10.

Question 4.
Positive odd numbers < 15
Answer:
1, 3, 5, 7, 9, 11, 13  are the positive odd numbers < 15.

Represent fractions, mixed numbers, and decimals on a horizontal number line.

a) Represent the fractions \(\frac{1}{4}\), \(\frac{2}{4}\), and \(\frac{3}{4}\) on a number line.

To represent \(\frac{1}{4}\)s, subdivide each interval between two consecutive whole numbers into four equal intervals using three tick marks.

Answer:

b) Represent the decimals from 0.1 to 0.9 on a horizontal number line. Use an interval of 0.1 between each decimal.

To represent decimals in tenths, subdivide each interval between two consecutive whole numbers into ten equal intervals.

Answer:

Complete each with the correct value, and each with > or <.

Question 5.
Fill in the missing fractions and mixed numbers on the number line. Then complete the statements of inequality.

Answer:

Draw a horizontal number line to represent each set of numbers.

Question 6.
Mixed numbers greater than 10 but less than 11 Use an interval of \(\frac{1}{4}\) between each pair of mixed numbers.
Answer:

Question 7.
Mixed numbers from 3 to 4, with an interval of \(\frac{1}{10}\) between each pair of mixed numbers.
Answer:

Question 8.
Decimals between 0 and 1, with an interval of 0.25 between each pair of decimals
Answer:

Question 9.
Decimals greater than 8.0 but less than 12.0
Use an interval of 0.8 between each pair of decimals.
Answer:

Represent fractions1 mixed numbers, and decimals on a vertical number line.

a) Represent the fractions \(\frac{1}{5}\), \(\frac{2}{5}\), \(\frac{3}{5}\), \(\frac{4}{5}\) on a vertical number line.
To represent these fractions on the number line, subdivide the interval between 0 and 1 into five smaller intervals.

Answer:

b) Represent the decimals 2.0, 2.2, 2.4, 2.6, …, 4.0 on a vertical number line.
To represent these decimals, subdivide the interval from 2.0 to 4.0 into ten equal intervals of 0.2.

To decide how many tick marks to show on the number line, you can 3.6 count up by 0.2s, marking them as you go:
2.0, 2.2, 2.4, 2.6, 2.8, 3.0, 3.2, 3.4, 3.2, 3.6, 3.8, 4.0.

Answer:

Write statements of inequality comparing two fractions or two decimals using the symbols > and <.

You can use a number line to compare fractions and decimals.

a) Compare the two fractions, \(\frac{2}{3}\) and \(\frac{5}{6}\).
Use a number line to compare \(\frac{2}{3}\) and \(\frac{5}{6}\).

The numbers \(\frac{2}{3}\) and \(\frac{4}{6}\) are equivalent and are represented by the same point on a number line.

The fraction \(\frac{5}{6}\) lies to the right of \(\frac{2}{3}\). This means that \(\frac{5}{6}\) is greater than \(\frac{2}{3}\).
This can be represented as:
\(\frac{5}{6}\) > \(\frac{2}{3}\).

b) Compare the two decimals, 1.3 and 1.15. Use a number line to help you.

The decimal 1.15 lies to the left of 1.3. This means that 1.15 is less than 1.3. This can be represented by:
1.15 < 1.3.
Answer:

Complete each with the correct value, and each with > or <.

Question 10.
a) Fill in the missing decimals on the number line.

Answer:

b) Compare each pair of decimals using < or >. Use the number line in a) to help you.
0.1 0.05 0.02 0.07
Answer:

Draw a vertical number line to represent each set of numbers.

Question 11.
Mixed numbers greater than 6 but less than 7
Use an interval of \(\frac{1}{6}\) between each pair of mixed numbers.
Answer:

Question 12.
Positive fractions less than 1, with an interval of \(\frac{1}{12}\) between each pair of fractions.
Answer:

Question 13.
Decimals between 11.4 and 15.0, with an interval of 0.4 between each pair of decimals
Answer:

Question 14.
Decimals greater than 7.2 but less than 9.6
Use an interval of 0.3 between each pair of decimals.
Answer:

Question 15.
Positive decimals less than 7.5, with an interval of 0.75 between each pair of decimals
Answer:

Compare each pair of numbers using > or <. Use a number line to help you.

Question 16.
3\(\frac{9}{10}\) 3\(\frac{3}{10}\)
Answer:

Question 17.
2.17 2.71
Answer:

Question 18.
14.4 13.38
Answer:

Question 19.
8\(\frac{5}{12}\) \(\frac{100}{12}\)
Answer:

Compare numbers in different forms.

Look at these number lines.

Every whole number, fraction, and decimal can be represented on the number line. A given point on a number line can be written ¡n different forms. For example,
\(\frac{1}{2}\) = 0.5 and \(\frac{3}{4}\) = 0.75.

You can see that \(\frac{1}{4}\) = 0.25, \(\frac{1}{2}\) = 0.5, and \(\frac{3}{4}\) = 0.75.
You can also see that \(\frac{1}{5}\) = 0.2, \(\frac{2}{5}\) = 0.4, \(\frac{3}{5}\) = 0.6, and \(\frac{4}{5}\) = 0.8.

a) Which is greater, \(\frac{1}{4}\) or 0.3?
\(\frac{1}{4}\) = 0.25
0.25 lies to the left of 0.3
So, 0.3 > \(\frac{1}{4}\)
Answer:

b) Which is lesser, 0.62 or \(\frac{3}{5}\)?

Answer:

Complete.

Question 20.
Which is greater, \(\frac{1}{2}\) or 0.55?

Answer:

Compare each using > or <. Use a number line to help you.

Question 21.
0.2 \(\frac{1}{4}\)
Answer:

Question 22.
\(\frac{3}{4}\) 0.7
Answer:

Question 23.
0.89 \(\frac{4}{5}\)
Answer:

Question 24.
0.25 \(\frac{1}{5}\)
Answer:

Question 25.
\(\frac{2}{5}\) 0.3
Answer:

Question 26.
3.26 3\(\frac{5}{8}\)
Answer:

Math in Focus Course 1A Practice 1.1 Answer Key

Copy and complete each number line by filling in the missing values.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

Draw a horizontal number line to represent each set of numbers.

Question 4.
Odd numbers from 11 to 21
Answer:

Question 5.
Positive whole numbers less than 9
Answer:

Question 6.
Whole numbers greater than 12 but less than 18
Answer:

Question 7.
Mixed numbers between 0 and 2, with an interval of \(\frac{1}{3}\) between each pair of mixed numbers
Answer:

Question 8.
Decimals from 7.0 to 8.4, with an interval of 0.2 between each pair of decimals
Answer:

Draw a vertical number line to represent each set of numbers.

Question 9.
Even numbers between 20 and 32
Answer:

Question 10.
Positive whole numbers less than 13
Answer:

Question 11.
Whole numbers greater than 6 but less than 16
Answer:

Question 12.
Positive fractions less than 1, with an interval of \(\frac{1}{8}\) between each pair of fractions
Answer:

Question 13.
Decimals between 10 and 15, with an interval of 0.75 between each pair of decimals
Answer:

Compare each pair of numbers using > or <. Use a number line to help you.

Question 14.
2\(\frac{3}{7}\) 1\(\frac{9}{7}\)
Answer:

Question 15.
\(\frac{17}{25}\) 1\(\frac{7}{25}\)
Answer:

Question 16.
1\(\frac{4}{5}\) 1\(\frac{2}{3}\)
Answer:

Question 17.
33.61 36.13
Answer:

Question 18.
59.05 59.5
Answer:

Question 19.
98.072 98.027
Answer:

Draw a horizontal number line from 2 to 3 to represent each set of numbers.

Question 20.
2\(\frac{4}{5}\), 2\(\frac{3}{20}\), 2\(\frac{1}{2}\), 2\(\frac{11}{20}\), and 2\(\frac{9}{20}\)
Answer:

Question 21.
2.5, 2.125, 2.375, and 2.875
Answer:

Draw a horizontal number line from 0 to 1 to represent each set of numbers.

Question 22.
\(\frac{1}{3}\), \(\frac{1}{4}\), \(\frac{3}{8}\), \(\frac{3}{4}\), \(\frac{7}{8}\) and \(\frac{5}{6}\)
Answer:

Question 23.
0.1, 0.25, 0.05, 0.8, 0.75, and 0.95
Answer:

Compare each pair of numbers using > or <. Use a number line to help you.

Question 24.
0.8 \(\frac{1}{10}\)
Answer:

Question 25.
\(\frac{1}{5}\) 0.25
Answer:

Question 26.
\(\frac{3}{5}\) 0.35
Answer:

Question 27.
0.14 \(\frac{1}{4}\)
Answer:

Question 28.
\(\frac{2}{5}\) 0.3
Answer:

Question 29.
0.64 \(\frac{9}{10}\)
Answer:

Question 30.
0.2 \(\frac{1}{6}\)
Answer:

Question 31.
\(\frac{7}{8}\) 0.87
Answer:

Solve.

Question 32.
The wingspan of one butterfly is 1\(\frac{9}{16}\) inches. The wingspan of another butterfly is 1\(\frac{5}{8}\) inches. Write an inequality comparing the two wingspans.
Answer:

Question 33.
For a class project, Jina made a model of the Empire State Building that was 23.7 centimeters tall. Her friend Caleb made a model that was 23\(\frac{3}{5}\) centimeters tall. Whose model was taller? How much taller was it?
Answer:

Go through the Math in Focus Grade K Workbook Answer Key Chapter 16 Classifying and Sorting to finish your assignments.

Math in Focus Kindergarten Chapter 16 Answer Key Classifying and Sorting

Lesson 1 Classifying Things by One Attribute

Sort and match.

Question 1.


Answer:

Explanation:
Here are 2 things one is circle and the other is circle
so matched with one attribute

Question 2.


Answer:

Explanation:
Here are pictures with colors matched with the correct color
so matched with one attribute

Question 3.


Answer:

Explanation:
Here are pictures with colors matched with the correct color
so matched with one attribute

Question 4.


Answer:

Explanation:
Here are pictures with colors matched with the correct pattern
so matched with one attribute

Make an X on the item that does not belong.

Question 1.

Answer:

Explanation:
The both are in red green is odd
so, crossed out the green

Question 2.

Answer:

Explanation:
The orange is not in the above attributes

Question 3.

Answer:

Explanation:
The blue color is crossed because the bird and baby is in yellow color

Question 4.

Answer:

Explanation:
Cap and quilt in same pattern so crossed the shirt

Lesson 2 Classifying and Sorting Things by Two Attributes

Match.

Answer:

Explanation:
Matched with two attributes for the shapes.

Make an X on the wrong common attribute.

Question 1.

Answer:

Explanation:
Both are triangle and red in color so crossed the small

Question 2.

Answer:

Explanation:
The above shapes are green and small
so, crossed the square

Question 3.

Answer:

Explanation:
The above are all circles and big
so, crossed the purple.

Go through the Math in Focus Grade K Workbook Answer Key Chapter 15 Length and Height to finish your assignments.

Math in Focus Kindergarten Chapter 15 Answer Key Length and Height

Lesson 1 Comparing Lengths

Draw a long tail.

Answer:

The question asked was to draw a long tail.

Draw a short tail.

Answer:

The question asked was to draw a short tail.

Draw a longer object.

Question 1.

Answer:

Question 2.

Answer:

Draw a shorter object.

Question 1.

Answer:

Question 2.

Answer:

Make an X on the kite with the longest tail. Circle the kite with the shortest tail.

Answer:

Lesson 2 Comparing Lengths Using Nonstandard Units

Measure, count and write.

Question 1.

The pencil is about ___________ cubes long.
Answer:
The long and short scales are two of several naming systems for integer powers of ten which use some of the same terms for different magnitudes.

The pencil is 2 cubes long.

Question 2.

The spoon is about ___________ cubes long.
Answer:
The long and short scales are two of several naming systems for integer powers of ten which use some of the same terms for different magnitudes

The spoon is 3 cubes long.

Question 3.

The toothbrush is about ____________ cubes long.
Answer:
The long and short scales are two of several naming systems for integer powers of ten which use some of the same terms for different magnitudes

The tooth brush is about 5 cubes long.

Question 4.

The comb is about ____________ cubes long.
Answer:
The long and short scales are two of several naming systems for integer powers of ten which use some of the same terms for different magnitudes

The comb is about 3 cubes long.

Question 5.

The tube is about ____________ cubes long.
Answer:
The long and short scales are two of several naming systems for integer powers of ten which use some of the same terms for different magnitudes.

The tube is about 2 cubes long.

Question 6.

The paintbrush is about ____________ cubes long.
Answer:
The long and short scales are two of several naming systems for integer powers of ten which use some of the same terms for different magnitudes.

The paint brush is about 7 cubes long.

Count and write.

Question 1.

The pencil is about __________ long.

The crayon is about ____________ long.
The pencil is about ____________ longer than the crayon.
Answer:
The pencil is about 7 cubes long.
The crayon is about 4 cubes long.
The pencil is about ‘X’ longer than the crayon.
X=7-4
X=3
The pencil is about 3 cubes longer than a crayon.

Question 2.

The leaf is about ___________ long.

The carrot is about __________ long.
The leaf is about ____________ shorter than the carrot.
Answer:
The leaf is about 6 long
The carrot is about 9 long.
The leaf is about ‘X’ shorter than the carrot.
X=9-6
X=3
The leaf is about 3 shorter than the carrot.

Lesson 3 Comparing Heights Using Nonstandard Units

Count and write. Make an X on the taller vase.

Answer:
I crossed vase A because it is a taller one.


Count the circles present in vase A.

Answer:
Count the circles in vase B.

Count and write. Circle the shorter flower.

Answer:

Answer:
Count the circles in the flower B.