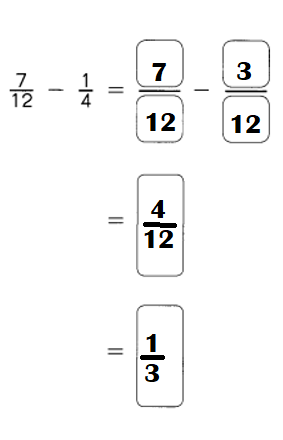
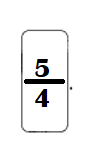
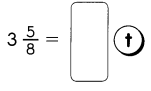
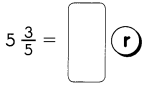
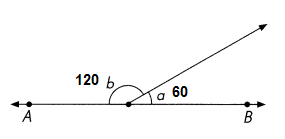
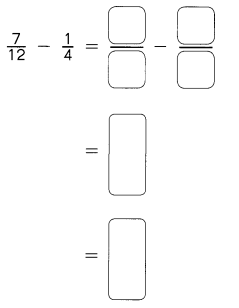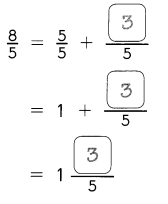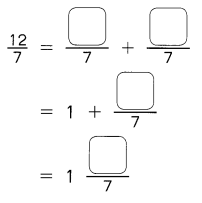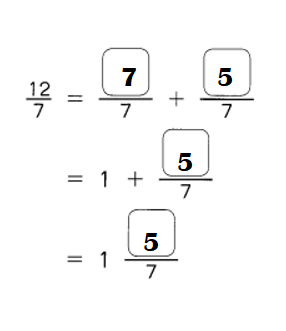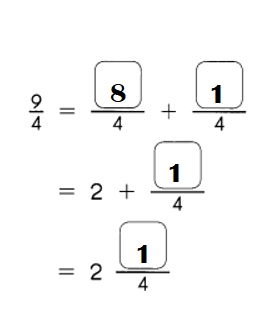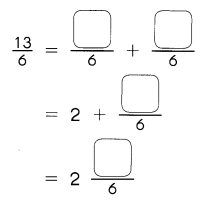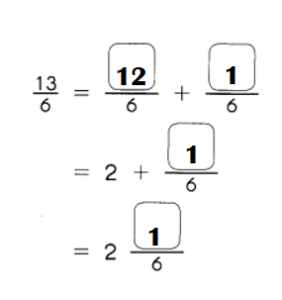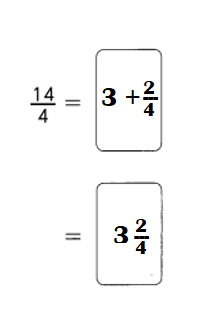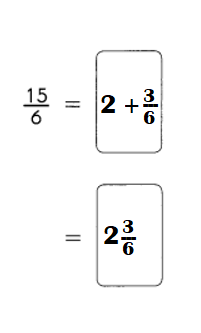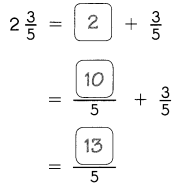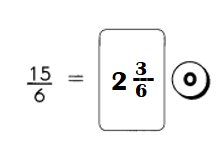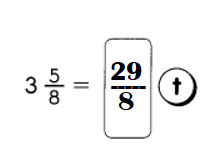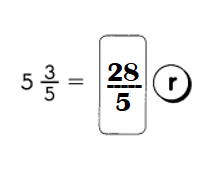Go through the Math in Focus Grade 4 Workbook Answer Key Chapter 2 Practice 2 Factors to finish your assignments.
Math in Focus Grade 4 Chapter 2 Practice 2 Answer Key Factors
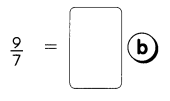
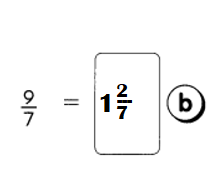
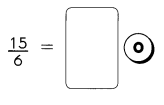
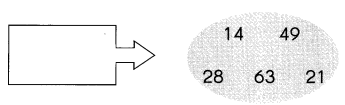
Find the missing factors.
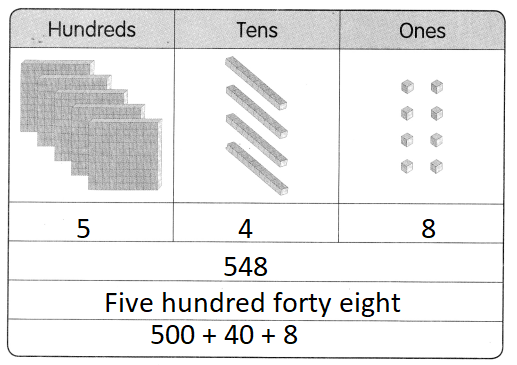
Example 12 1 × 12 = 12
2 × 6 = 12
3 × 4 = 12
The factors of 12 are
1, 2, 3, 4, 6, and 12.
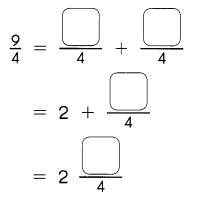
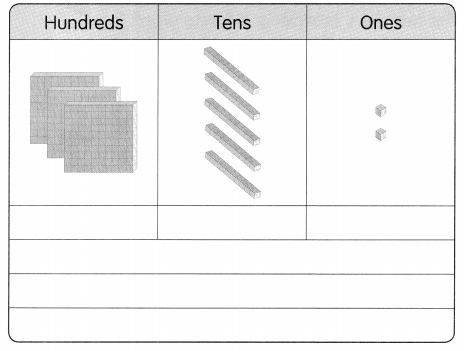
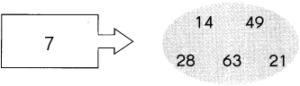
Question 1.
70
1 × ____ = 70
2 × ____ = 70
3 × ____ = 70
4 × ____ = 70
The factors of 70 are 1, 2, 5, 7, ___, ____
___ and ___
Answer:
Factor definition:
When a number is said to be a factor of any other second number, then the first number must divide the second number completely without leaving any remainder. In simple words, if a number (dividend) is exactly divisible by any number (divisor), then the divisor is a factor of that dividend. Every number has a common factor that is one and the number itself.
1 × 70= 70
2 × 35= 70
3 × 23.3= 70
4 × 17.5= 70
Point to remember: Fractions cannot be considered as factors for any number.
The numbers that divide 70 exactly without leaving a remainder are the factors of 70. As 70 is an even composite number, it has many factors other than 1 and 70. Hence, the factors of 70 are 1, 2, 5, 7, 10, 14, 35, and 70. Similarly, the negative factors of 70 are -1, -2, -5, -7, -10, -14, -35, and -70.
1 × 70= 70
2 × 35= 70
5 × 14=70
7 × 10=70
Factors of 70: 1, 2, 5, 7, 10, 14, 35, and 70.
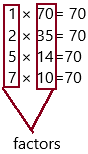
Find the factors of each number.
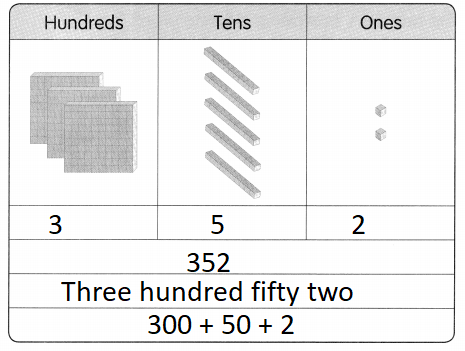
Question 2.
40
The factors of 40 are
_________
Answer: 1, 2, 4, 5, 8, 10, 20, and 40.
Explanation:
The Factors of 40 are all the integers (positive and negative whole numbers) that you can evenly divide into 40. 40 divided by a factor of 40 will equal another Factor of 40.
How to find the factors of 40:
Since the Factors of 40 are all the numbers that you can evenly divide into 40, we simply need to divide 40 by all numbers up to 40 to see which ones result in an even quotient. When we did that, we found that these calculations resulted in an even quotient:
40 ÷ 1 = 40
40 ÷ 2 = 20
40 ÷ 4 = 10
40 ÷ 5 = 8
40 ÷ 8 = 5
40 ÷ 10 = 4
40 ÷ 20 = 2
40 ÷ 40 = 1
The Positive Factors of 40 are therefore all the numbers we used to divide (divisors) above to get an even number. Here is the list of all Positive Factors of 40 in numerical order:
1, 2, 4, 5, 8, 10, 20, and 40.
Question 3.
63
The factors of 63 are
___________
Answer:
Explanation:
The Factors of 63 are all the integers (positive and negative whole numbers) that you can evenly divide into 63. 63 divided by a factor of 63 will equal another Factor of 63.
How to find the factors of 63:
Since the Factors of 63 are all the numbers that you can evenly divide into 63, we simply need to divide 63 by all numbers up to 63 to see which ones result in an even quotient. When we did that, we found that these calculations resulted in an even quotient:
63 ÷ 1 = 63
63 ÷ 3 = 21
63 ÷ 7 = 9
63 ÷ 9 = 7
63 ÷ 21 = 3
63 ÷ 63 = 1
The Positive Factors of 63 are therefore all the numbers we used to divide (divisors) above to get an even number. Here is the list of all Positive Factors of 63 in numerical order:
1, 3, 7, 9, 21, and 63.
Divide. Then answer each question.
Question 4.
65 ÷ 5 = ____
Answer:13
There are four important terms used in division. These are dividend, divisor, quotient and remainder.
– Dividend: The number to be divided by another number is called the dividend.
– Divisor: The number by which we divide another number (dividend) into equal parts is called the divisor.
– Quotient: The result of division is called a quotient.
– Reminder: The leftover number after division is called the remainder.
– The pictorial representation of the above terminology is given below.

Division formula:
Dividend=Divisor×Quotient+Remainder.
After division, we can put all the values in the formula to verify or check whether our division is correct or not.
the above-given question is 65 ÷ 5 = 13
Here, dividend =65, Divisor =5, quotient =13 and remainder =0
Let us put all the above values in the formula,
Dividend=Divisor×Quotient+Remainder
⇒65 = 5 × 13 + 0
⇒ 65 ÷ 5 = 13
Hence, our division is correct.
Question 5.
46 ÷ 4 = ___
Is 5 a factor of 65?
Answer:
Explanation:
There are four important terms used in division. These are dividend, divisor, quotient and remainder.
– Dividend: The number to be divided by another number is called the dividend.
– Divisor: The number by which we divide another number (dividend) into equal parts is called the divisor.
– Quotient: The result of division is called a quotient.
– Reminder: The leftover number after division is called the remainder.
– The pictorial representation of the above terminology is given below.

Division formula:
Dividend=Divisor×Quotient+Remainder.
After division, we can put all the values in the formula to verify or check whether our division is correct or not.
the above-given question is 46 ÷ 4 = 11.5
Here, dividend =46, Divisor =4, quotient =11.5 and remainder =0
Let us put all the above values in the formula,
Dividend=Divisor×Quotient+Remainder
⇒46 = 4 × 11.5 + 0
⇒ 65 ÷ 5 = 11.5
Hence, our division is correct.
Another question is there, is 5 is a factor of 65:
Yes, 5 is a factor of 65.
– The 4 factors of 65 are:
1, 5, 13, 65
– The factor pairs of 65 are:
1 × 65 = 65
5 × 13 = 65
Question 5.
46 ÷ 4 = ___
Is 4 a factor of 46? ____
Answer: 11.5
Explanation:
There are four important terms used in division. These are dividend, divisor, quotient and remainder.
– Dividend: The number to be divided by another number is called the dividend.
– Divisor: The number by which we divide another number (dividend) into equal parts is called the divisor.
– Quotient: The result of division is called a quotient.
– Reminder: The leftover number after division is called the remainder.
– The pictorial representation of the above terminology is given below.

Another question is there is 4 a factor of 46:
No 4 is not a factor of 46
Therefore, the 4 factors of 46 are:
1, 2, 23, 46.
– The factor pairs of 46 are:
1 × 46 = 46
2 × 23 = 46
Find the common factors of each pair of numbers.
Question 6.

Answer:

Explanation:
– To find common factors of two numbers, first, list out all the factors of two numbers separately and then compare them. Now write the factors which are common to both the numbers. These factors are called common factors of given two numbers.
– As we know, the factors are the numbers that divide the original number completely. But how to check if two or more numbers have common factors between them.
Follow the below steps to find the common factors.
* Write the factors of the given numbers.
* Find the common factor present in them.
Let us check the factors of the two numbers, i.e., 10 and 15.
Factors of 10 = 1, 2, 5, 10
Factors of 15 = 1, 3, 5, 15
Clearly, we can see, the common factors between 10 and 15 are 1, 5.
Question 7.

Answer:

Explanation:
– To find common factors of two numbers, first, list out all the factors of two numbers separately and then compare them. Now write the factors which are common to both the numbers. These factors are called common factors of given two numbers.
– As we know, the factors are the numbers that divide the original number completely. But how to check if two or more numbers have common factors between them.
Follow the below steps to find the common factors.
* Write the factors of the given numbers.
* Find the common factor present in them.
Let us check the factors of the two numbers, i.e., 24 and 36.
Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
Clearly, we can see, the common factors between 24 and 36 are 1, 2, 3, 4, 6, 12.
Divide. Then answer each question.
Question 8.
18 ÷ 4 = ___ 16 ÷ 4 = ____
Is 4 a common factor of 18 and 16? ____
Answer:
18 ÷ 4 = 4.5
16 ÷ 4 = 4
Explanation:
There are four important terms used in division. These are dividend, divisor, quotient and remainder.
– Dividend: The number to be divided by another number is called the dividend.
– Divisor: The number by which we divide another number (dividend) into equal parts is called the divisor.
– Quotient: The result of division is called a quotient.
– Reminder: The leftover number after division is called the remainder.
– The pictorial representation of the above terminology is given below.

Another question is there is 4 a common factor of 18 and 16:
No 4 is not a factor of 46
Therefore, the factors of 18 and 16 are:
factors of 18: 1, 2, 3, 6, 9, 18
factors of 16: 1, 2, 4, 8, 16.
The common factors are 1, 2
Question 9.
42 ÷ 3 = ____ 84 ÷ 3 = ____
Is 3 a common factor of 42 and 84? ____
Answer:
42 ÷ 3 = 14
84 ÷ 3 = 28
Yes, 3 is a common factor for both the numbers.
Explanation:
There are four important terms used in division. These are dividend, divisor, quotient and remainder.
– Dividend: The number to be divided by another number is called the dividend.
– Divisor: The number by which we divide another number (dividend) into equal parts is called the divisor.
– Quotient: The result of division is called a quotient.
– Reminder: The leftover number after division is called the remainder.
– The pictorial representation of the above terminology is given below.
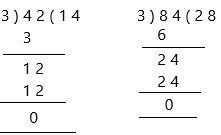
Another question is there is 3 a common factor of 42 and 84:
Therefore, the factors of 42 and 84 are:
factors of 42: 1, 2, 3, 6, 7, 14, 21, 42
factors of 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
The common factors are 1, 2, 3, 6, 7, 14, 21, 42
Therefore, 3 is a common factor for 42 and 84.
Look at the numbers 80, 27, 40, 62, 36, and 55. Then fill in the blanks.
Question 10.
Which of the numbers have 2 as a factor? _________
Answer:80, 40, 62, 36
The above-given numbers are 80, 27, 40, 62, 36, and 55.
we have to find out the numbers having 2 as a factor.
80, 40, 62, 36 are the factors of 2.
80/40 = 2
40/20 = 2
62/32 = 2
36/18 = 2
Factors are the numbers, that can divide a number exactly. Hence, after division, there is no remainder left. Factors are the numbers you multiply together to get another number. Thus, a factor is the divisor of another number.
Question 11.
Which of the numbers have 5 as a factor? ______
Answer: 80, 40, 55
Factors can be calculated by using multiplication and division.
– Since multiplication of two numbers results in a product such that the two numbers become the factors of the product. Thus, to find the factors we need to follow the below steps:
* If we need to find the factors of a number say N, then write the multiplication of two numbers in different ways, such that the resulting value is equal to N
* All the individual numbers, that results in the product equal to N are the factors
5 × 12 = 80
5 × 8 = 40
5 × 11 = 55
Factors are the numbers, that can divide a number exactly. Hence, after division, there is no remainder left. Factors are the numbers you multiply together to get another number. Thus, a factor is the divisor of another number.
Question 12.
Which of the numbers have both 2 and 5 as factors? ______
Answer:
The numbers 80, 40 have 2 and 5
40 × 2 =80
5 × 8 = 40
5 × 16 = 80
Factors are the numbers, that can divide a number exactly. Hence, after division, there is no remainder left. Factors are the numbers you multiply together to get another number. Thus, a factor is the divisor of another number.
Each set of numbers is all the factors of a number. Find each number.
Question 13.

Answer:

Explanation:
– The factors of a number are defined as the numbers which when multiplied will give the original number, by multiplying the two factors we get the result as the original number. The factors can be either positive or negative integers.
– Factors of 8 are all the integers that can evenly divide the given number 8. Now let us study how to calculate all factors of 8.
– According to the definition of factors of 8, we know that factors of 8 are all the positive or negative integers that divide the number 8 completely. So let us simply divide the number 8 by every number which completely divides 8 in ascending order till 8.
8 ÷ 1 = 8
8 ÷ 2 = 4
8 ÷ 3 = not divides completely
8 ÷ 4 = 2
8 ÷ 5 = not divides completely
8 ÷ 6 = not divides completely
8 ÷ 7 = not divides completely
8 ÷ 8 = 1
So all factors of 8: 1, 2, 4, and 8.
Question 14.

Answer:

Explanation:
– When we divide every number with 12 up to that number itself, the numbers that evenly divide with 12 are the factors of 12.
– This is a very simple and straightforward method. The entire process takes only 5 steps.
– To start off here is step number 1:
Step 1: Consider the number 12
Step 2: Divide it with all the numbers starting from 1 to 12
Step 3: Capture the results
: 12/1 = 12
: 12/2 = 6
: 12/3 = 4
: 12/4 = 3
: 12/5 = 2.4
: 12/6 = 2
: 12/7 = 1.7
: 12/8 = 1.5
: 12/9 = 1.3
: 12/10 = 1.2
: 12/11 = 1.09
: 12/12 = 1
Step 4: Filter out the positive integer quotient for the above, rejecting the decimals.
Step 5: The factors of 12 are 1, 2, 3, 4, 6, 12.
Question 15.

Answer:

Explanation:
The factors of 6 are the numbers that divide 6 exactly without leaving the remainder. In other words, the factors of 6 are the numbers that are multiplied in pairs resulting in an original number 6. As 6 is an even composite number, it has many factors other than 1 and 6. Thus, the factors of 6 are 1, 2, 3 and 6. Similarly, the negative pair factors of 6 are -1, -2, -3 and -6.
Factors of 6: 1, 2, 3 and 6.
Factors of 6 by division method:
– In the division method, the factors of 6 can be found by dividing 6 by different integers. If the integers divide 6 exactly and leave the remainder 0, then those integers are the factors of 6. Now, let us discuss how to find the factors of 6 using the division method.
* 6/1 = 6 (Factor is 1 and Remainder is 0)
* 6/2 = 3 (Factor is 2 and Remainder is 0)
* 6/3 = 2 (Factor is 3 and Remainder is 0)
* 6/6 = 1 (Factor is 6 and Remainder is 0)
– If we divide the number 6 by any numbers other than 1, 2, 3 and 6, then it leaves the remainder. Hence, the factors of 6 are 1, 2, 3 and 6.
Question 16.

Answer:

Explanation:
The factors of 16 are the numbers that divide the number 16 completely without leaving any remainder. As the number 16 is a composite number, it has more than one factor. The factors of 16 are 1, 2, 4, 8 and 16. Similarly, the negative factors of 16 are -1, -2, -4, -8 and -16.
– Factors of 16: 1, 2, 4, 8 and 16.
How to calculate factors of 16:
Go through the following steps to calculate the factors of 16.
* First, write the number 16.
* Find the two numbers, which gives the result as 16 under the multiplication, say 2 and 8, such as 2 × 8 = 16.
* We know that 2 is a prime number that has only two factors, i.e., 1 and the number itself (1 and 2). So, it cannot be further factorized.
* Look at the number 8, which is a composite number but not a prime number. So it can be further factorized.
* 8 can be factored as 2 x 2 x 2 x 1.
* Therefore, the factorization of 16 is written as, 16 = 2 × 2 × 2 × 2 x 1.
Find the greatest common factor of each pair of numbers.
Example
12 and 28
Method 1
The factors of 12 are 1, 2, 3, 4, 6, and 12.
The factors of 28 are 1, 2, 4, 7, 14, and 28.
The common factors of 12 and 28 are 1, 2, and 4.
The greatest common factor of 12 and 28 is 4.
Method 2
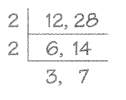
2 × 2 = 4
The greatest common factor of 12 and 28 is 4.
3 and 7 have no common factor other than 1.

Question 17.
16 and 30
_________
Answer: GCF of 16 and 30 is 2.
Explanation:
GCF of 16 and 30 is the largest possible number that divides 16 and 30 exactly without any remainder. The factors of 16 and 30 are 1, 2, 4, 8, 16 and 1, 2, 3, 5, 6, 10, 15, 30 respectively. There are 3 commonly used methods to find the GCF of 16 and 30 – long division, prime factorization, and Euclidean algorithm.
– The GCF of two non-zero integers, x(16) and y(30) is the greatest positive integer m(2) that divides both x(16) and y(30) without any remainder.
Methods to find GCF of 16 and 30:
– The methods to find the GCF of 16 and 30 are explained below.
* Long Division Method
* Using Euclid’s Algorithm
* Listing Common Factors
# GCF of 16 and 30 by long division method:
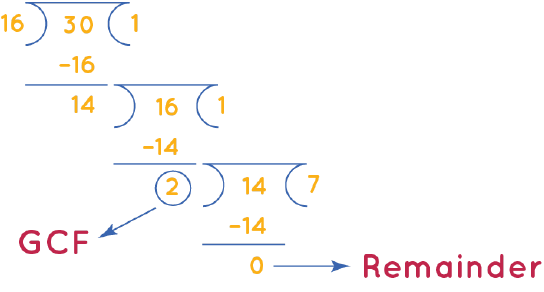
GCF of 16 and 30 is the divisor that we get when the remainder becomes 0 after doing long division repeatedly.
Step 1: Divide 30 (larger number) by 16 (smaller number).
Step 2: Since the remainder ≠ 0, we will divide the divisor of step 1 (16) by the remainder (14).
Step 3: Repeat this process until the remainder = 0.
The corresponding divisor (2) is the GCF of 16 and 30.
# GCF of 16 and 30 by listing common factors:
Factors of 16: 1, 2, 4, 8, 16
Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30.
There are 2 common factors of 16 and 30, which are 1 and 2. Therefore, the greatest common factor of 16 and 30 is 2.
Find the greatest common factor of the numbers.
Question 18.
21 and 54
___________
Answer: 3
The Greatest Common Factor (GCF) for 21 and 54, notation GCF(21,54), is 3.
Explanation:
To find the GCF of 21 and 54, we first need to find the factors of 21 and 54 and then choose the greatest common factor that is dividable by both 21 and 54.
– The factors of 21 are 1,3,7,21;
– The factors of 54 are 1,2,3,6,9,18,27,54.
So, as we can see, the Greatest Common Factor or Divisor is 3, because it is the greatest number that divides evenly into all of them.
Find all the factors. Then list the prime numbers.
Example
13
The factor of 13 are 1 and 13. 13 is a prime number.
A prime number has only 2 factors, 1 and itself.

Question 19.
12 ____
Answer:
The factors of 12 are the numbers that divide 12 exactly without leaving any remainder. As 12 is an even composite number, it has many factors other than 1 and 12. The factors of 12 can be positive or negative. Hence, the factors of 12 are 1, 2, 3, 4, 6 and 12. Similarly, the negative factors of 12 are -1, -2, -3, -4, -6 and -12.
Factors of 12: 1, 2, 3, 4, 6 and 12.
Now we need to write the prime numbers in the factors of 12.
prime numbers: A prime number is a positive integer having exactly two factors. If p is a prime, then its only factors are necessarily 1 and p itself. Any number that does not follow this is termed a composite number, which can be factored into other positive integers. Another way of defining it is a positive number or integer, which is not a product of any other two positive integers other than 1 and the number itself.
Therefore, the prime numbers are 2 and 3.
Question 20.
7 ______
Answer:
The factors of 20 are the numbers that divide 20 exactly without leaving a remainder. In other words, the numbers are multiplied in pairs resulting in the number 20 being the factor of 20. As 20 is an even composite number, it has many factors other than 1 and 20. Thus, the factors of 20 are 1, 2, 4, 5, 10 and 20. Similarly, the negative factors of 20 are -1, -2, -4, -5, -10 and -20.
Factors of 20: 1, 2, 4, 5, 10 and 20.
Now we need to write the prime numbers in the factors of 20.
prime numbers: A prime number is a positive integer having exactly two factors. If p is a prime, then its only factors are necessarily 1 and p itself. Any number that does not follow this is termed a composite number, which can be factored into other positive integers. Another way of defining it is a positive number or integer, which is not a product of any other two positive integers other than 1 and the number itself.
Therefore, the prime numbers are 2 and 5.
Question 21.
19 ____
Answer:
The numbers that divide 19 completely without leaving a remainder are the factors of 19. In other words, the numbers which are multiplied in pairs, resulting in an original number, are the factors of 19. As number 19 is a prime number, it has only two factors: one and the number itself. Hence, the factors of 19 are 1 and 19, and its negative factors are -1 and -19.
Factors of 19: 1 and 19.
Now we need to write the prime numbers in the factors of 19.
prime numbers: A prime number is a positive integer having exactly two factors. If p is a prime, then its only factors are necessarily 1 and p itself. Any number that does not follow this is termed a composite number, which can be factored into other positive integers. Another way of defining it is a positive number or integer, which is not a product of any other two positive integers other than 1 and the number itself.
Therefore, the prime number is 19.
Question 22.
24 ______
Answer:
By the definition of factors, we know, a factor can divide a given number into an equal number of parts. Therefore, factors of 24 are such whole numbers that can divide 24 into an equal number of parts. These factors cannot be a fraction.
Factors of 24: 1, 2, 3, 4, 6, 8, 12 and 24.
Now we need to write the prime numbers in the factors of 24.
prime numbers: A prime number is a positive integer having exactly two factors. If p is a prime, then its only factors are necessarily 1 and p itself. Any number that does not follow this is termed a composite number, which can be factored into other positive integers. Another way of defining it is a positive number or integer, which is not a product of any other two positive integers other than 1 and the number itself.
Therefore, the prime numbers are 2, 3.
Question 23.
11 ____
Answer:
In Mathematics, the numbers that divide 11 completely without leaving any remainder are the factors of 11. In other words, the factors of 11 are the numbers that are multiplied in pairs and result in the original number 11. As 11 is a prime number, it has only two factors, such as one and the number itself. Hence, the factors of 11 are 1 and 11, and the negative factors of 11 are -1 and -11.
Factors of 11: 1 and 11.
Now we need to write the prime numbers in the factors of 11.
prime numbers: A prime number is a positive integer having exactly two factors. If p is a prime, then its only factors are necessarily 1 and p itself. Any number that does not follow this is termed a composite number, which can be factored into other positive integers. Another way of defining it is a positive number or integer, which is not a product of any other two positive integers other than 1 and the number itself.
Therefore, the prime number is 11.
Question 24.
63 ______
Answer:
The factors of 63 are the numbers that divide the number 63 exactly without leaving any remainder. In other words, the pair factors of 63 are the numbers that are multiplied in pairs resulting in the original number 63. Since the number 63 is a composite number, 63 has more than two factors. Thus, the factors of 63 are 1, 3, 7, 9, 21 and 63.
Now we need to write the prime numbers in the factors of 63.
prime numbers: A prime number is a positive integer having exactly two factors. If p is a prime, then its only factors are necessarily 1 and p itself. Any number that does not follow this is termed a composite number, which can be factored into other positive integers. Another way of defining it is a positive number or integer, which is not a product of any other two positive integers other than 1 and the number itself.
Therefore, the prime numbers are 3, 7.
Question 25.
Look at the given numbers in Exercises 19-24.
The prime numbers are _____
Explain your reasoning. _________
Answer:
The above-given numbers are 12, 7, 19, 24, 11, 63.
To that we need to write the prime numbers:
Definition: A prime number is a positive integer having exactly two factors. If p is a prime, then its only factors are necessarily 1 and p itself. Any number that does not follow this is termed a composite number, which can be factored into other positive integers. Another way of defining it is a positive number or integer, which is not a product of any other two positive integers other than 1 and the number itself.
Properties of prime numbers:
Some of the properties of prime numbers are listed below:
– Every number greater than 1 can be divided by at least one prime number.
– Every even positive integer greater than 2 can be expressed as the sum of two primes.
– Except for 2, all other prime numbers are odd. In other words, we can say that 2 is the only even prime number.
– Two prime numbers are always coprime to each other.
– Each composite number can be factored into prime factors and individually all of these are unique in nature.
Now from the above definition and properties, we can write the prime numbers:
The prime numbers are:7, 11, 19
Find all the factors. Then list the composite numbers.
Example
18
The factors of 18 are 1, 2, 3, 6,
9 and 18
18 is a composite number.
18 has factors other than 1 and itself, so it is a composite number.

Question 26.
20 _______________
Answer:
The factors of 20 are the numbers that divide 20 exactly without leaving a remainder. In other words, the numbers are multiplied in pairs resulting in the number 20 being the factor of 20. As 20 is an even composite number, it has many factors other than 1 and 20. Thus, the factors of 20 are 1, 2, 4, 5, 10 and 20. Similarly, the negative factors of 20 are -1, -2, -4, -5, -10 and -20.
Now we need to write the composite numbers:
Definition: In Mathematics, composite numbers are numbers that have more than two factors.
therefore, the composite numbers are 4, 10, and 20.
Hence, these numbers are having more than two factors.
Question 27.
15 ______
Answer:
Factors of 15 divide the original number, wholly. A number or an integer that divides 15 evenly without leaving a remainder, then the number is a factor of 15. As the number 15 is an odd composite number, it has more than two factors. Thus, the factors of 15 are 1, 3, 5 and 15.
Now we need to write the composite numbers:
Definition: In Mathematics, composite numbers are numbers that have more than two factors.
therefore, 15 is the composite number.
Hence, this number is having more than two factors.
Question 28.
5 _______________
Answer:
Factors of 5 are the real numbers that can divide the original number, uniformly. If ‘x’ is the factor of 5, then ‘x’ divides 5 into equal parts and there is no remainder left.
The factors of 5 are 1 and 5.
Now we need to write the composite numbers:
Definition: In Mathematics, composite numbers are numbers that have more than two factors.
therefore, there is no composite number.
Question 29.
17 _____
Answer:
The numbers that divide 17 completely and leave the remainder 0, then the numbers are the factors of 17. In other words, if two numbers are multiplied together and result in 17, then the numbers are the factors of 17. As 17 is a prime number, it has only two factors, such as 1 and the number itself. Hence, the factors of 17 are 1 and 17.
Now we need to write the composite numbers:
Definition: In Mathematics, composite numbers are numbers that have more than two factors.
therefore, there is no composite number.
Question 30.
33 _________________
Answer:
Go through the steps given below to learn how to find the factors of 33.
Step 1: First, write the number 33 in your notebook.
Step 2: Find the two numbers, which on multiplication gives 33, suppose 3 and 11, such as 3 × 11 = 33.
Step 3: We know that 3 is a prime number that has only two factors, i.e. 1 and the number itself. So, we cannot factorize it further.
3 = 1 × 3
Step 4:Also, 11 is a prime number and cannot be factored further.
11 = 1 × 11
Step 5: Therefore, the factorization of 33 gives us 1 × 3 × 11.
The unique numbers which are obtained from the above expression are 1, 3, 11, and 33.
Now we need to write the composite numbers:
Definition: In Mathematics, composite numbers are numbers that have more than two factors.
therefore, 33 is the composite number.
Hence, this number is having more than two factors.
Question 31.
27 _____
Answer:
The steps to find the factors are:
1. First, write the number 27 in your notebook.
2. Find the two numbers, which on multiplication gives 27, say 3 and 9, such as 3 × 9 = 27.
3. We know 3 is a prime number that has only two factors, i.e. 1 and the number itself. So, we cannot further factorize it. (i.e.) 3 = 1 × 3
4. But 9 is not a prime number and can be further factorized. (i.e.) 9 = 3 × 3 × 1
5. Therefore, the factorization of 27 gives us, 1 × 3 × 3 × 3.
6. Write down all the unique numbers which are obtained here.
7. Factors of 27: 1, 3, 9 and 27.
Now we need to write the composite numbers:
Definition: In Mathematics, composite numbers are numbers that have more than two factors.
therefore, 9 and 27 are the composite number.
Hence, these numbers are having more than two factors.
Question 32.
Look at the given numbers in Exercises 26-31.
The composite numbers are ____
Explain your reasoning. _____
Answer:
The above-given numbers are 20, 15, 5, 17, 33, 27
To that we need to write the composite numbers:
Def 1: In Mathematics, composite numbers are numbers that have more than two factors.
Def 2: The numbers which can be generated by multiplying the two smallest positive integers and contain at least one divisor other than the number ‘1’ and itself are known as composite numbers. These numbers always have more than two factors.
properties of composite numbers:
The properties of composite numbers are easy to remember.
– Composite numbers have more than two factors
– Composite numbers are evenly divisible by their factors
– Each composite number is a factor in itself
– The smallest composite number is 4
– Each composite number will include at least two prime numbers as its factors (Eg. 10 = 2 x 5, where 2 and 5 are prime numbers)
– Composite numbers are divisible by other composite numbers also
From the above definition and properties we can write the composite numbers:
Therefore, the composite numbers are 20, 15, 27, 33
Use the method given below to find prime numbers.
Question 33.
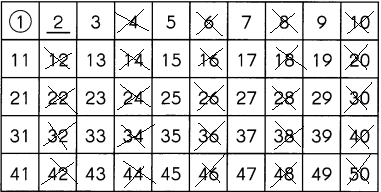
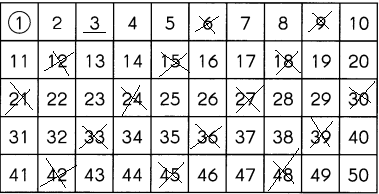
Find the prime numbers between 1 and 50.
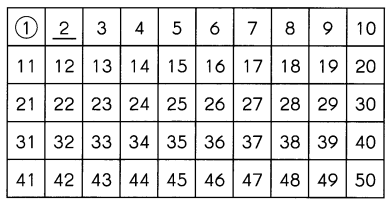
Step 1
1 is neither prime nor composite. So, 1 has been circled. As 2 is the first prime number, it has been underlined. Next, cross out all the numbers that can be divided by 2.
Step 2
3 is the next prime number. Underline it.
Then, cross out all the numbers that can be divided by 3.
Keep underlining the prime numbers and crossing out the numbers that can be divided by the prime numbers until you reach 50.
The prime numbers are ____
Answer:
A prime number is a positive integer having exactly two factors. If p is a prime, then its only factors are necessarily 1 and p itself. Any number that does not follow this is termed a composite number, which can be factored into other positive integers. Another way of defining it is a positive number or integer, which is not a product of any other two positive integers other than 1 and the number itself.
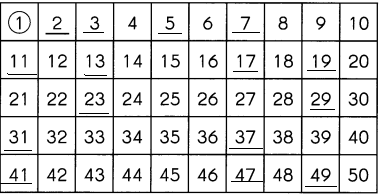
The prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.
Question 34.
Find two prime numbers between 60 and 90. ____
Answer:
First of all the prime numbers between 60 and 90 are 61, 67, 71, 73, 79, 83, 89.
Question 35.
Find two composite numbers between 60 and 90. ____
Answer:
The composite numbers between 0 and 90 are: 60, 62, 63, 64, 65, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90.
The two composite numbers: 70 and 80
Two composite numbers between 60 and 90 are 70 and 80. All numbers which end in a zero are evenly divisible by 10.
Question 36.
Are there more prime numbers from 1 to 25 or from 26 to 50?
Answer:
YES. There are 9 prime numbers from 1 to 25. There are only 6 prime numbers from 26 to 50.
The prime numbers between 1 to 25 are: 2, 3, 5, 7, 11, 13, 17, 19, 23.
The prime numbers between 26 to 50: 29, 31, 37, 41, 43, 47, 53, 59.
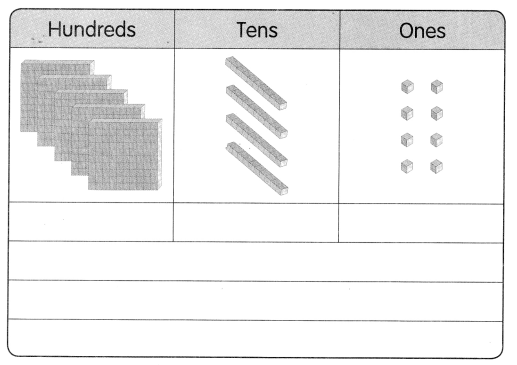
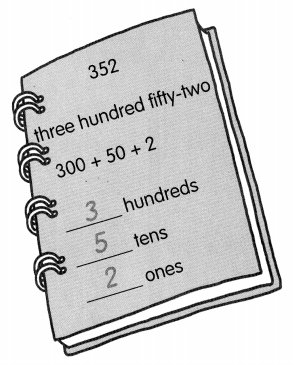
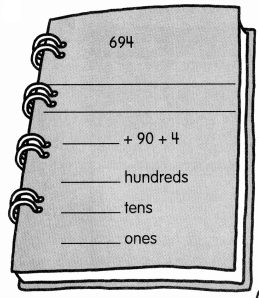
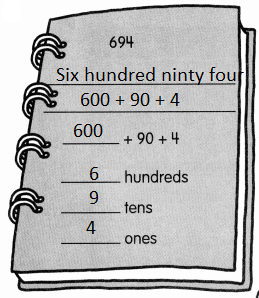
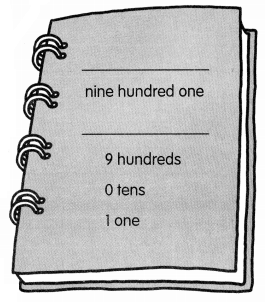
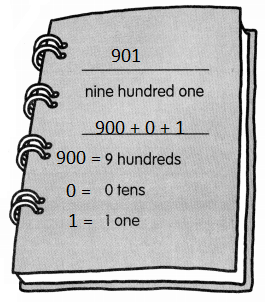

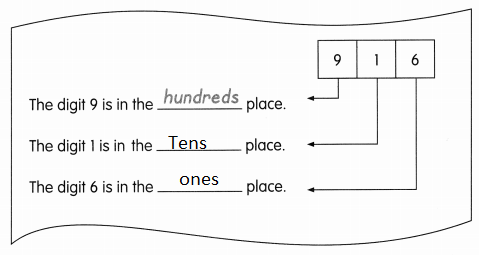
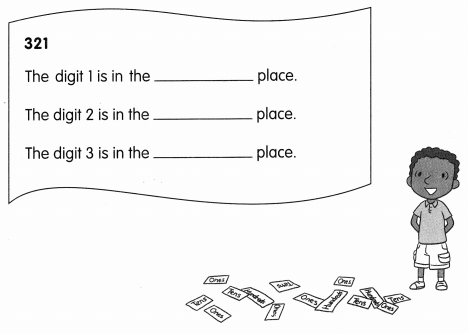
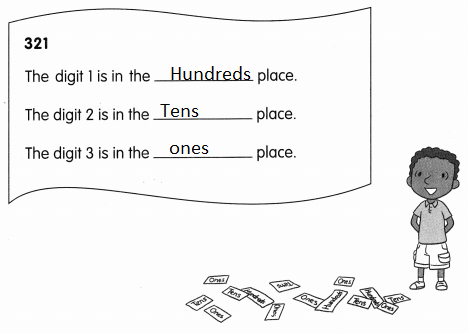


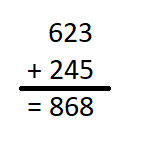
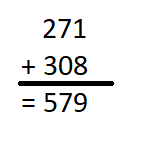

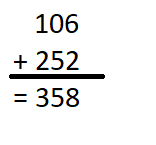
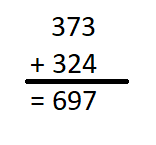

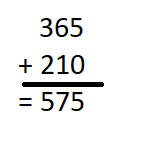
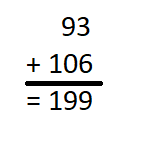
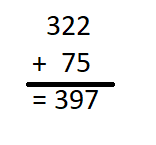







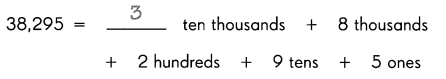











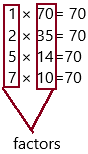







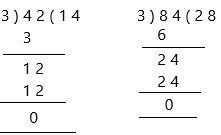





















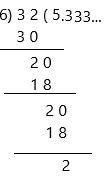



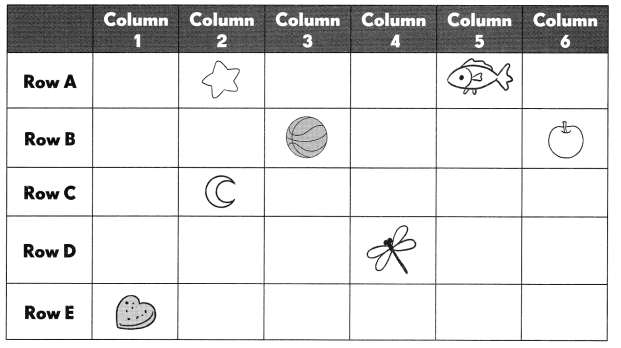

 is in Row __________ and Column __________
is in Row __________ and Column __________