Go through the Math in Focus Grade 4 Workbook Answer Key Chapter 1 Practice 3 Comparing Numbers to 10,000 to finish your assignments.
Math in Focus Grade 4 Chapter 1 Practice 3 Answer Key Comparing Numbers to 10,000
Write > or < in each ![]() Example 15,408
Example 15,408 ![]() 12,508 > means greater than.
12,508 > means greater than.
< means less than.

Question 1.
63,809 ![]() 36,908
36,908
Answer: >
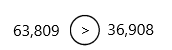
Explanation:
– The three comparison symbols are less than (<), greater than (>) and equal to (=).
– The less than and greater than symbols are used based on two numbers given to compare.
– A bigger number greater than a smaller number is represented as:
– Bigger Number > Smaller Number
– A smaller number less than a greater number is represented as:
– Smaller Number < Greater Number
Rules to compare numbers:
There are certain rules, based on which it becomes easier to compare numbers. These rules are:
* Numbers with more digits
* Numbers starting with a larger digit
Rule 1: Numbers with more digits
When we compare numbers, then check if both the numbers are having the same number of digits or not. If a number has more digits, then it is greater than the other number.
Examples:
– 33 > 3
– 400 > 39
– 5555 > 555
– 10000 > 9999
Rule 2:Numbers starting with a larger digit
This rule is applicable when two numbers are having the same number of digits. In such cases, we need to check the digit at the leftmost place, whichever is greater. Therefore, the number with a greater digit at the leftmost place of the number is greater than the other number.
Examples:
– 323>232 [323 is greater than 232]
– 343<434 [343 is less than 434]
Thus, in the above examples, we can see that, when we compare the two numbers, though the number of digits is the same, one number is greater than/less than the other number.
The above-given numbers: 63,809 and 36,908
63,809 and 36,908 both the numbers have an equal number of digits, therefore, we will compare the left-most digit of both the numbers. Thus we will compare the left-most digit of both numbers.
6 > 3
Therefore,
63,809 > 36,908
Hence, 63,809 is greater than 36,908.
Question 2.
86,415 ![]() 86,591
86,591
Answer: <
![]()
Explanation:
Check the rules in question 1.
The above-given numbers are 86,451 and 86,591
86,451 and 86,591 both the numbers have an equal number of digits, therefore, we will compare the left-most digit of both the numbers. So here rule 2 is applicable.
But the left-most digit is also the same for both numbers, i.e.,8. So, we need to check the second left-most digit.
4 < 5
Therefore,
86,415 < 86,591
Hence, 86,415 is smaller than 86,591.
Question 3.
45,638 ![]() 8,594
8,594
Answer: >
![]()
Explanation:
The above-given numbers are 45,638 and 8,594
45,638 and 8,594
Since 45,638 has 5 digits and 8,594 has four digits, therefore, according to rule 1, the number with more digits is greater than the number with fewer digits.
Hence, 45,638 is greater than 8,594.
Question 4.
60,960 ![]() 69,999
69,999
Answer: <
![]()
Explanation:
60,960 and 69,999 both the numbers have an equal number of digits, therefore, we will compare the left-most digit of both the numbers.
But the left-most digit is also the same for both numbers, i.e.,6. So, we need to check the second left-most digit.
0 < 9
60,960 < 69,999
Hence, 60,960 is smaller than 69,999.
Compare the eight numbers in Exercises 1 to 4.
Question 5.
Which number is the greatest? ________________
Answer:86,591
The above-given numbers are 63,809, 36,908, 86,415, 86,591, 45,638, 8,594, 60,960, 69,999.
The greatest number is 86,591
Now compare all the numbers according to the rules.
Question 6.
Which number is the least? ________________
Answer:8,594
The above-given numbers are 63,809, 36,908, 86,415, 86,591, 45,638, 8,594, 60,960, 69,999.
The least number is 8,594
Now compare all the numbers according to the rules.
Order these numbers.
Example
Order these numbers.
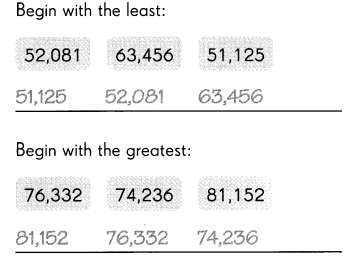
Question 7.
Begin with the least:

Answer: 79,631 96,137 97,136
Explanation:
Now compare all the numbers
79,631 96,137 and 97,136 all the numbers have an equal number of digits, therefore, we will compare the left-most digit of both the numbers.
Therefore,
7 < 9
Now easily we can say 79,631 is the least.
Question 8.
Begin with the greatest:

Answer: 81,074 80,000 9,469
Explanation:
Apply rule 1:
When we compare numbers, then check if both the numbers are having the same number of digits or not. If a number has more digits, then it is greater than the other number.
So that we can easily say 9,469 is the least number.
Now compare 80,000 and 81,074 both the numbers have an equal number of digits, therefore, we will compare the left-most digit of both the numbers. Here applying rule 2.
But the left-most digit is also the same for both numbers, i.e.,8. So, we need to check the second left-most digit.
0 < 1
Therefore,
80,000 < 81,074
Hence, 80,000 is smaller than 81,074
The numbers from greatest to least:
81,074 80,000 9,469
Write the missing numbers.
Example
1,000 more than 82,586 is ____
17,312 is 40,000 less than 57,312.
Question 9.
10,000 more than 56,821 is ________________
Answer: 66,821
Explanation:
We are looking for a new number which is 10,000 more than 56,821.
We will get the new number by adding 10,000 to 56,821.
We write it down as:
56,821+10,000=66,821
And finally the solution for: What number is 10,000 more than 56,821?
is 66,821.
Question 10.
____ is 50,000 less than 79,895.
Answer:29,895
Explanation:
We are looking for a new number which is 50000 less than 79895.
We will get the new number by subtracting 50000 from 79895.
We write it down as:
79,895-50,000=29,895
And finally the solution for: What number is 50000 less than 79895?
is 29,895.
Question 11.
2,000 less than 18,563 is ________________
Answer:16,563
Explanation:
We are looking for a new number which is 2,000 less than 18,563.
We will get the new number by subtracting 2,000 from 18,563.
We write it down as:
18,563-2,000=16,563
And finally the solution for: What number is 2000 less than 18563?
is 16,563
Question 12.
_____ is 3,000 more than 48,200.
Answer:51,200
Explanation:
We are looking for a new number which is 3,000 more than 48,200.
We will get the new number by adding 3,000 to 48,200.
We write it down as:
48,200+3,000=51,200
And finally the solution for: What number is 3000 more than 48200?
is 51200.
Use the number line to count on or back.
Count on in steps of 4,000 from 20,000. Then write the number that you land on. The first one has been done for you.

Question 13.

Answer:

Question 14.

Answer: 36,000

Explanation:
– A number line is a pictorial representation of numbers on a straight line. It’s a reference for comparing and ordering numbers. It can be used to represent any real number that includes every whole number and natural number. Just to recollect, the whole number is a set of numbers that include all counting numbers (1, 2, 3,4,5,6 …….) and zero (0), whereas the natural number is the set of all counting numbers i.e. 1, 2, 3, 4, 5, 6……..
– Starting point at 2000 and ending point is 50,000
– We count by 1’s here.
– In question 13, step 1 is done and from there 3 steps are forwarded.
– from 24,000 we need forward 3 steps by using counting in steps of 4000
– After 3 steps then we get 36,000
– 24,000+4,000=28,000
– 28,000+4,000=32,000
– 32,000+4,000=36,000
Count back in steps of 3,000 from 50,000. Then write the number that you land on.
Question 15.
6 steps 
Answer:32,000

Explanation:
– A number line can be used to record the stages.
– Count back, you need to subtract from the larger number to the smaller number in stages.
– When you use a number line to subtract, you’ll move to the left, instead of the right, on the line.
– 50,000-3000=47,000
– 47,000-3000=44,000
– 44,000-3,000=41,000
– 41,000-3000=38,000
– 38,000-3,000=35,000
– 35,000-3,000=32,000
Question 16.
8 steps 
Answer:26,000

Explanation:
– A number line can be used to record the stages.
– Count back, you need to subtract from the larger number to the smaller number in stages.
– When you use a number line to subtract, you’ll move to the left, instead of the right, on the line.
– 50,000-3000=47,000
– 47,000-3000=44,000
– 44,000-3,000=41,000
– 41,000-3000=38,000
– 38,000-3,000=35,000
– 35,000-3,000=32,000
– 32,000-3000=29,000
– 29,000-3000=26,000
Continue or complete the number patterns. Then write the rule for each pattern.
Example
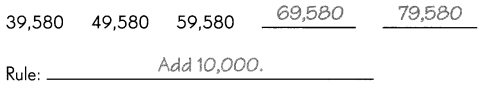
Question 17.
![]()
Rule: ____
Answer:
A Number Pattern refers to a sequence of numbers that follow a certain order in mathematics. Patterns typically describe the inverse relationship between numbers. The sequences of numbers can also be called patterns.
Types of number patterns:
1. Arithmetic Sequences
2. Geometric Sequences
The above-given numbers are in the arithmetic pattern.
Arithmetic sequence:
Arithmetic sequences are sequences of numbers with constant differences between consecutive terms in mathematics. Common differences between consecutive terms are called common differences.
Here are some examples of arithmetic numbers:
1, 4, 7, 10, 13, 16, …… is an arithmetic sequence because the difference between consecutive terms is 3.
1, 4, 8, 11, 15, 18, …… is not an arithmetic sequence because the difference between consecutive terms is not a constant.
The above-given numbers are 96,500 86,500 76,500 – –
Now, we need to find the missing term in the sequence.
Here, we can use the subtraction process to figure out the missing terms in the patterns.
In the pattern, the rule used is “subtracting 10,000 to the previous term to get the next term”.
In the given above, take the second term (86,500). If we subtract “10,000” to the second term (86,500), we get the third term of 76,500.
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 76,500. Therefore, 76,500-10,000 = 66,500
Second missing term: The previous term is 66,500. So, 66,500-10,000 = 56,500
Hence, the complete arithmetic pattern is 96,500 86,500 76,500 66,500 56,500
Question 18.
39,860 ____ 41,860 ____ 43,860
Rule: ________________
Answer:
The above-given numbers are 39,860 – 41,860 – 43,860
Now, we need to find the missing term in the sequence.
Here, we can use the addition process to figure out the missing terms in the patterns.
In the pattern, the rule used is “adding 1000 to the previous term to get the next term”.
In the given above, take the first term (39,860). If we add “1000” to the first term (86,500), we get the second term.
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 39,860. Therefore, 39,860+1,000 = 40,860
The previous term is 40,860. So, 40,860+1,000 = 41,860 (already given)
Second missing term: The previous term is 41,860. Therefore, 41,860+1000=42,860
Hence, the complete arithmetic pattern is 39,860 40,860 41,860 42,860
Question 19.
![]()
Rule: ___________
Answer:
The above-given numbers are 25,000 20,000 15,000 – –
Now, we need to find the missing term in the sequence.
Here, we can use the subtraction process to figure out the missing terms in the patterns.
In the pattern, the rule used is “subtracting 5000 to the previous term to get the next term”.
In the given above, take the second term (20,000). If we subtract “5000” to the second term (20,000), we get the third term of 15,000
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 15,000. Therefore, 15,000-5,000 = 10,000
Second missing term: The previous term is 10,000. Therefore, 10,000-5000=5,000
Hence, the complete arithmetic pattern is 25,000 20,000 15,000 10,000 5,000
Question 20.
![]()
Rule: ________________
Answer: subtract 500 from backwards.
Explanation:
The above-given numbers are – 10,349 10,849 – – 12,349
Now, we need to find the missing term in the sequence.
Here, we can use the addition process to figure out the missing terms in the patterns.
In the pattern, the rule used is “adding 500 to the previous term to get the next term”.
Here we don’t know the first term but given the second and third term. By using these 2 terms we can write the number pattern. First of all, check the difference between the 2nd and 3rd numbers. The difference is 500
If we subtract 500 from 10,349 we get 9,849. Therefore, the first term is 9,849. From there we can add 500 to every next number (or) another solution is by using the given terms we got the difference 500. We can calculate from the backwards means the last number is 12,349. We start from 12,349-500=11,849
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 12,349. Therefore, 12,349-500 = 11,849
Second missing term: The previous term is 11,849 Therefore, 11,849-500=11,349
Hence, the complete arithmetic pattern is 9,849 10,349 10,849 11,849 11,349
Question 21.
![]()
Rule: ________________
Answer:
The above-given numbers are 93,308 94,313 95,318 – –
Now, we need to find the missing term in the sequence.
Here, we can use the addition process to figure out the missing terms in the patterns.
In the pattern, the rule used is “adding 1005 to the previous term to get the next term”.
In the given above, take the second term (94,313). If we add “1005” to the second term (94,313), we get the third term of 95,318
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 95,318. Therefore, 95,318+1005 = 96,323
Second missing term: The previous term is 96,323. Therefore, 96,323+1005=97,328
Hence, the complete arithmetic pattern is 93,308 94,313 95,318 96,323 97,328
Question 22.
![]()
Rule: ________________
Answer:
The above-given numbers are 85,765 87,775 89,985 91,995 – –
Now, we need to find the missing term in the sequence.
Here, we can use the addition process to figure out the missing terms in the patterns.
In the pattern, the rule used is “adding 2010 to the previous term to get the next term”.
In the given above, take the third term (89,985). If we add “2010” to the third term (89,989), we get the fourth term of 91,995
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 91,995. Therefore, 91,995+2010 = 94,005
Second missing term: The previous term is 96,323. Therefore, 94,005+2010=96,015
Hence, the complete arithmetic pattern is 85,765 87,775 89,985 91,995 94,005 96,015