Go through the Math in Focus Grade 4 Workbook Answer Key Chapter 2 Practice 3 Multiples to finish your assignments.
Math in Focus Grade 4 Chapter 2 Practice 3 Answer Key Multiples
Fill in the table with the multiples of each given number.
Example

Question 1.

Answer: 7, 14, 21, 28, 35
![]()
Explanation:
– A multiple is a numerical value that is generated when a natural number is multiplied by another natural number or counting number.
– Multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, … and so on. How do we get to know a number is multiple of another number? If a number is multiple of another number, then it is evenly divisible by the original number. For example, 14 divided by 7 is equal to 2, thus it is a multiple of 7.
– Any number that can be denoted in the form 7n where n is a natural number is a multiple of 7. So if two values p and q are there, we say that q is a multiple of p if q = np for some natural number n.
7 x 1=7
7 x 2=14
7 x 3=15
7 x 4=28
7 x 5=35
If a number is multiple of 7, then it is evenly divisible by 7.
14 is a multiple of 7 because 14/7 = 2
21 is a multiple of 7 because 21/7= 3
28 is a multiple of 7 because 28/7=4
35 is a multiple of 7 because 35/7=5.
Therefore, the first five multiples of 7 are 7, 14, 21, 28, 35.
Question 2.

Answer:8, 16, 24, 32, 40
![]()
Explanation:
The multiples of 8 are 8, 16, 24, 32, 40, 48, 56, 64, 72, 80… and so on. It is a sequence where the difference between each next number and the preceding number, i.e. two consecutive results, is 8. Multiples are the numbers that give products of any number multiplied by other natural numbers.
The multiples of 8 are the numbers that are generated when 8 is multiplied by any natural number. That means any number that can be expressed in the form of 8n where n is an integer is a multiple of 8. As we know, if two values, p and q, are there, we say that q is a multiple of p if q = np for some integer n.
Thus, as per the definition given above, the multiple of 8 is obtained by multiplying some integer with 8.
Take the first five multiples of 8: 8, 16, 24, 32, 40.
8 × 1 = 8; 8 multiplied by 1 to get 8
8 × 2 = 16; 8 multiplied by 2 to get 16
8 × 3 = 24; 8 multiplied by 3 to get 24
8 × 4 = 32; 8 multiplied by 4 to get 32
8 × 5 = 40; 8 multiplied by 5 to get 40
Question 3.

Answer: 9, 18, 27, 36, 45.
![]()
Explanation:
Any number that can be denoted in the form 9n where n is a natural number, is a multiple of 9. So if two values p and q are there, we say that q is a multiple of p if q = np. In other words, the multiples of 9 are the numbers that leave no remainder (i.e. Remainder = 0), when it is divided by 9.
Thus, as per the definition given above, the multiple of 9 is obtained by multiplying some integer with 9.
Take the first five multiples of 9: 9, 18, 27, 36, 45.
9 × 1 = 9; 9 multiplied by 1 to get 9
9 × 2 = 18; 9 multiplied by 2 to get 18
9 × 3 = 27; 9 multiplied by 3 to get 27
9 × 4 = 36; 9 multiplied by 4 to get 36
9 × 5 = 45; 9 multiplied by 5 to get 45
Therefore, the first five multiples of 9 are 9, 18, 27, 36, 45.
Fill in the blanks.
Question 4.
The first multiple of 9 is ____
Answer: 9
Explanation:
Any number that can be denoted in the form 9n where n is a natural number, is a multiple of 9. So if two values p and q are there, we say that q is a multiple of p if q = np. In other words, the multiples of 9 are the numbers that leave no remainder (i.e. Remainder = 0), when it is divided by 9.
Thus, as per the definition given above, the multiple of 9 is obtained by multiplying some integer with 9.
Take the first five multiples of 9: 9, 18, 27, 36, 45.
9 × 1 = 9; 9 multiplied by 1 to get 9
9 × 2 = 18; 9 multiplied by 2 to get 18
9 × 3 = 27; 9 multiplied by 3 to get 27
9 × 4 = 36; 9 multiplied by 4 to get 36
9 × 5 = 45; 9 multiplied by 5 to get 45
Therefore, the first multiple of 9 are 9.
Question 5.
The second multiple of 8 is ____
Answer: 16
The multiples of 8 are 8, 16, 24, 32, 40, 48, 56, 64, 72, 80… and so on. It is a sequence where the difference between each next number and the preceding number, i.e. two consecutive results, is 8. Multiples are the numbers that give products of any number multiplied by other natural numbers.
The multiples of 8 are the numbers that are generated when 8 is multiplied by any natural number. That means any number that can be expressed in the form of 8n where n is an integer is a multiple of 8. As we know, if two values, p and q, are there, we say that q is a multiple of p if q = np for some integer n.
Thus, as per the definition given above, the multiple of 8 is obtained by multiplying some integer with 8.
Take the first five multiples of 8: 8, 16, 24, 32, 40.
8 × 1 = 8; 8 multiplied by 1 to get 8
8 × 2 = 16; 8 multiplied by 2 to get 16
8 × 3 = 24; 8 multiplied by 3 to get 24
8 × 4 = 32; 8 multiplied by 4 to get 32
8 × 5 = 40; 8 multiplied by 5 to get 40
Therefore, the second multiple of 8 is 16.
Question 6.
The first twelve multiples of 7 are ____
Answer: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84.
![]()
Explanation:
– A multiple is a numerical value that is generated when a natural number is multiplied by another natural number or counting number.
– Multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, … and so on. How do we get to know a number is multiple of another number? If a number is multiple of another number, then it is evenly divisible by the original number. For example, 14 divided by 7 is equal to 2, thus it is a multiple of 7.
– Any number that can be denoted in the form 7n where n is a natural number is a multiple of 7. So if two values p and q are there, we say that q is a multiple of p if q = np for some natural number n.
7 x 1=7
7 x 2=14
7 x 3=15
7 x 4=28
7 x 5=35
If a number is multiple of 7, then it is evenly divisible by 7.
14 is a multiple of 7 because 14/7 = 2
21 is a multiple of 7 because 21/7= 3
28 is a multiple of 7 because 28/7=4
35 is a multiple of 7 because 35/7=5.
Therefore, the first twelve multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84.
Question 7.
The seventh multiple of 7 is ____
Answer: 49
Explanation:
– A multiple is a numerical value that is generated when a natural number is multiplied by another natural number or counting number.
– Multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, … and so on. How do we get to know a number is multiple of another number? If a number is multiple of another number, then it is evenly divisible by the original number. For example, 14 divided by 7 is equal to 2, thus it is a multiple of 7.
– Any number that can be denoted in the form 7n where n is a natural number is a multiple of 7. So if two values p and q are there, we say that q is a multiple of p if q = np for some natural number n.
7 x 1=7
7 x 2=14
7 x 3=15
7 x 4=28
7 x 5=35
7 x 6=42
7 x 7=49
If a number is multiple of 7, then it is evenly divisible by 7.
14 is a multiple of 7 because 14/7 = 2
21 is a multiple of 7 because 21/7= 3
28 is a multiple of 7 because 28/7=4
35 is a multiple of 7 because 35/7=5.
42 is a multiple of 7 because 42/7=6
49 is a multiple of 7 because 49/7=9
Therefore, the first seven multiples of 7 are 7, 14, 21, 28, 35, 42, 49
Hence, the seventh multiple is 49.
Question 8.
The twelfth multiple of 7 is ____.
Answer: 84.
Explanation:
– A multiple is a numerical value that is generated when a natural number is multiplied by another natural number or counting number.
– Multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, … and so on. How do we get to know a number is multiple of another number? If a number is multiple of another number, then it is evenly divisible by the original number. For example, 14 divided by 7 is equal to 2, thus it is a multiple of 7.
– Any number that can be denoted in the form 7n where n is a natural number is a multiple of 7. So if two values p and q are there, we say that q is a multiple of p if q = np for some natural number n.
7 x 1=7
7 x 2=14
7 x 3=15
7 x 4=28
7 x 5=35
7 x 6=42
7 x 7=49
7 x 8=56
7 x 9=63
7 x 10=70
7 x 11=77
7 x 12=84
If a number is multiple of 7, then it is evenly divisible by 7.
14 is a multiple of 7 because 14/7 = 2
21 is a multiple of 7 because 21/7= 3
28 is a multiple of 7 because 28/7=4
35 is a multiple of 7 because 35/7=5.
42 is a multiple of 7 because 42/7=6.
49 is a multiple of 7 because 49/7=7.
56 is a multiple of 7 because 56/7=8.
63 is a multiple of 7 because 63/7=9.
70 is a multiple of 7 because 70/7=10.
77 is a multiple of 7 because 77/7=11.
84 is a multiple of 7 because 84/7=12.
Therefore, the first twelve multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84.
Hence, the twelfth multiple is 84.
Check (✓) the correct box and fill in the blank when necessary.
Question 9.
Is 32 a multiple of 6?
![]() Yes, it is the ___ multiple of 6.
Yes, it is the ___ multiple of 6.
![]() No, it is not a multiple of 6.
No, it is not a multiple of 6.
Answer:
32 is not a multiple of 6
Explanation:
If we divide 32 and 6 then we get 5.333
![]() no, it is not a multiple of 6.
no, it is not a multiple of 6.
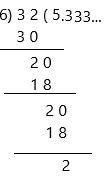
When we divide any multiple with 6 then it should leave the remainder 0 then that number is the multiple of 6.
Question 10.
Is 63 a multiple of 9?
![]() Yes, it is the ___ multiple of 9.
Yes, it is the ___ multiple of 9.
![]() No, it is not a multiple of 9.
No, it is not a multiple of 9.
Answer: yes, 63 is the multiple of 9.
Explanation:
![]()
63 is a multiple of 9 because 63/9=7
Any number that can be denoted in the form 9n where n is a natural number, is a multiple of 9. So if two values p and q are there, we say that q is a multiple of p if q = np. In other words, the multiples of 9 are the numbers that leave no remainder (i.e. Remainder = 0), when it is divided by 9.
Thus, as per the definition given above, the multiple of 9 is obtained by multiplying some integer with 9.
Take the first ten multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90
9 × 1 = 9; 9 multiplied by 1 to get 9
9 × 2 = 18; 9 multiplied by 2 to get 18
9 × 3 = 27; 9 multiplied by 3 to get 27
9 × 4 = 36; 9 multiplied by 4 to get 36
9 × 5 = 45; 9 multiplied by 5 to get 45
9 × 6 = 54; 9 multiplied by 6 to get 54
9 × 7 = 63; 9 multiplied by 7 to get 63
9 × 8 = 72; 9 multiplied by 8 to get 72
9 × 9 = 81; 9 multiplied by 9 to get 81
9 × 10 = 90; 9 multiplied by 10 to get 90
Therefore, 63 is a multiple of 9.
Use the numbers in the boxes to make your lists.

Question 11.
Multiples of 3 ____
Answer: 15, 24, 30, 63, 84
Explanation:
Any number that can be denoted in the form 3n where n is an integer is the multiples of 3. So if two values p and q are there, we say that q is a multiple of p if q = np for some integer n. In other words, the multiples of 3 are the numbers that leave no remainder (i.e. Remainder = 0), when it is divided by 3.
The above-given numbers are 30, 84, 15, 63, 56, 24.
To know which number is multiple of 3, we need to divide the given numbers by 3.
30 is the multiple of 3 because 30/3=10
84 is the multiple of 3 because 84/3=28
15 is the multiple of 3 because 15/3=5
63 is the multiple o 3 because 63/3=21
24 is the multiple of 3 because 24/3=8
56 is not the multiple of 3 because 56/3=18.6667
It is in decimals and the remainder does not leave with zero so 56 is not a multiple of 3.
Therefore, the multiples of 3 are 15, 24, 30, 63, 84.
Question 12.
Multiples of 8 _____
Answer: 24, 56
Explanation:
The multiples of 8 are the numbers that are generated when 8 is multiplied by any natural number. That means any number that can be expressed in the form of 8n where n is an integer is a multiple of 8. As we know, if two values, p and q, are there, we say that q is a multiple of p if q = np for some integer n.
The above-given numbers are 30, 84, 15, 63, 56, 24.
To know which number is multiple of 3, we need to divide the given numbers by 8.
30 is not the multiple of 8 because 30/8=3.75
84 is not the multiple of 8 because 84/8=10.5
15 is not the multiple of 8 because 15/8=1.875
63 is not the multiple of 8 because 63/8=7.875
It is in decimals and the remainder does not leave with zero. so these are all not the multiples of 8.
24 is the multiple of 8 because 24/8=3
56 is the multiple of 8 because 56/8=7
Therefore, the multiples of 8 are 24, 56.
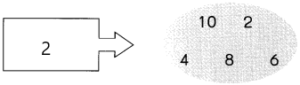
Each shaded area shows some of the multiples of a number. Write the number in the box to the left of each shaded area.
Question 13.
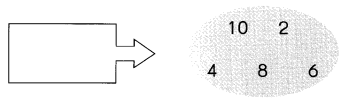
Answer:
Explanation:
In simple words, the multiples of 2 are the numbers that leave no remainder (i.e. Remainder = 0), when it is divided by 2. It means the numbers that are exactly divided by 2 are the multiples of 2.
First 10 Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20.
In math sentences, we can write as:
2/2=1; remainder 0.
4/2=2; remainder 0.
6/2=3; remainder 0.
8/2=4; remainder 0.
10/2=5; remainder 0.
Since the numbers are exactly divided by 2, the numbers 2, 4, 6, 8, 10 are the multiples of 2.
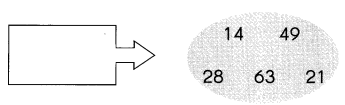
Question 14.
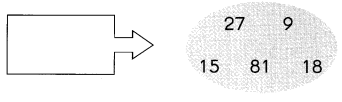
Answer:
Explanation:
Any number that can be denoted in the form 3n where n is an integer is the multiples of 3. So if two values p and q are there, we say that q is a multiple of p if q = np for some integer n. In other words, the multiples of 3 are the numbers that leave no remainder (i.e. Remainder = 0), when it is divided by 3.
First 10 Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30.
9/3=3; remainder 0.
15/3=5; remainder 0.
18/3=6; remainder 0.
27/3=9; remainder 0.
81/3=27; remainder 0.
Since the above-given numbers are exactly divided by 3, the numbers 9, 15, 18, 27, 81 are the multiples of 3.
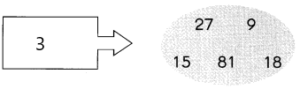
Question 15.
Answer:
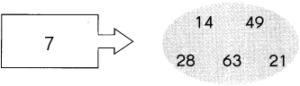
Explanation:
Multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, … and so on. How do we get to know a number is multiple of another number? If a number is multiple of another number, then it is evenly divisible by the original number. For example, 14 divided by 7 is equal to 2, thus it is a multiple of 7.
14/7=2; remainder 0.
21/7=3; remainder 0.
28/7=4; remainder 0.
63/7=9; remainder 0.
49/7=7; remainder 0.
Since the above-given numbers are exactly divided by 7, the numbers 14, 21, 28, 63, 49 are the multiples of 7.
Find the common multiples and the least common multiple.
1 × 2 = 2
2 × 2 = 4
3 × 2 = 6
4 × 2 = 8
5 × 2 = 10
6 × 2 = 12
7 × 2 = 14
8 × 2 = 16
9 × 2 = 18
1 × 3 = 3
2 × 3 = 6
3 × 3 = 9
4 × 3 = 12
5 × 3 = 15
6 × 3 = 18
A common multiple is shared by two or more numbers.

A common multiple that is less than all the others is called the least common multiple.

The first three common multiples of 2 and 3 are 6, 12, and 18
The least common multiple of 2 and 3 is 6.
Question 16.
The first 14 multiples of 5 are 5, 10, 15, 20, 25, 30, 35, ____
The first 10 multiples of? are 7, 14, 21, 28, 35, 42, _____
The first two common multiples of 5 and 7 are _____________
The least common multiple of 5 and 7 is __________
Answer: 35, 70
Explanation:
– The common multiples of 5 and 7 include 35, 70, 105, 140, 175, 210, 245, 280, and so on. The least common multiple is 35. A multiple is a result of multiplying a number by an integer.
– Multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 125, 130, 135, 140, and so on.
– Multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140, and so on.
– The quantities of 35, 70, 105, 140 are some of the common multiples of 7 and 5.
– A common multiple is defined as a quantity into which each of two or more quantities may be divided with zero remainders.
But in the question asked only the first two common multiples of 5 and 7:
The first two common multiples are 35, 70
The least common multiple of 5 and 7 is 35.
Question 17.
The first 1 5 multiples of 4 are ____________________________
The first 1 2 multiples of 5 are ____________________________
The first three common multiples of 4 and 5 are ____
The least common multiple of 4 and 5 is ____.
Answer:
Multiples of 4:
The multiples of 4 are: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80.
we can say that the multiples of 4 are the results in the multiplication table of 4, as both are the same.
The multiples of 5 are: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100.
All numbers which can be divided or are a product of 5 are multiples of 5.
From the above numbers we need to write common multiples and least common multiple:
The first three common multiples of 4 and 5 are: 20, 40, 60
The least common multiple of 4 and 5 is 20.
Write the first ten multiples of each number. Then find the least common multiple.
Question 18.
8 and 5
8 ________
5 ________
The least common multiple of 8 and 5 is _____
Answer:
Multiples of 8:
The multiples of 8 are the numbers that are generated when 8 is multiplied by any natural number. That means any number that can be expressed in the form of 8n where n is an integer is a multiple of 8. As we know, if two values, p and q, are there, we say that q is a multiple of p if q = np for some integer n.
– Thus, as per the definition given above, the multiple of 8 is obtained by multiplying some integer with 8.
– The first ten multiples of 8 are: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80
Multiples of 5:
The multiples of 5 are the numbers that are generated when 5 is multiplied by any natural number. That means any number that can be expressed in the form of 5n where n is an integer is a multiple of 5. As we know, if two values, p and q, are there, we say that q is a multiple of p if q = np for some integer n.
– As per the definition given above, the multiple of 5 is a number obtained by multiplying some integer with 5.
– The first ten multiples of 5 are: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
For example, 10, 20, 25 and 30 are all multiples of 5 for the following reasons.
5 × 2 = 10; 5 multiplied by 2 to get 10
5 × 4 = 20; 5 multiplied by 4 to get 20
5 × 5 = 25; 5 multiplied by 5 to get 25
5 × 6 = 30; 5 multiplied by 6 to get 30
From the above multiples we need to write the least common multiple:
The least common multiple of 8 and 5 are: 40
Since 40 is the first number they have in common, 40 is the least common multiple of 8 and 5.
Question 19.
6 and 9
6 _________
9 ________
The least common multiple of 6 and 9 is _____
Answer:
Multiples of 6:
The multiples for 6 are the numbers that are generated when 6 is multiplied by any natural number, such as 1, 2, 3, 4, 5, 6, 7, etc. That means any number that can be expressed in the form of 6n where n is an integer is a multiple of 6. As we know, if two values, p and q, are there, we say that q is a multiple of p if q = np for some integer n.
– As per the definition given above, the multiple of 6 is obtained by multiplying some integer with 6.
– The multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60.
Multiples of 9:
Any number that can be denoted in the form 9n where n is a natural number, is a multiple of 9. So if two values p and q are there, we say that q is a multiple of p if q = np. In other words, the multiples of 9 are the numbers that leave no remainder (i.e. Remainder = 0), when it is divided by 9.
First 10 Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90.
From the above multiples we need to write the least common multiple:
The least common multiple of 6 and 9 are: 18
Since 18 is the first number they have in common, 18 is the least common multiple of 6 and 9.
Question 20.
12 and 15
12 _____
15 ________
The least common multiple of 12 and 15 is ____
Answer:
Multiples of 12:
The multiples of 12 are the numbers that are generated when 12 is multiplied by any natural number. That means any number that can be expressed in the form of 12n where n is an integer is a multiple of 12. As we know, if two values, p and q, are there, we say that q is a multiple of p if q = np for some integer n.
– Thus, as per the definition given above, the multiple of 12 is obtained by multiplying some integer with 12.
– The multiples of 12 are 12, 24, 36, 48, 60, 72, 84, 96, 120
Multiples of 15:
Any number that can be denoted in form 15n where n is an integer is a multiple of 15. So if two values p and q, we say that q is a multiple of p if q = np for some integer n.
– The multiples of 15 are: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150.
From the above multiples we need to write the least common multiple:
The least common multiple of 12 and 15 are: 60
Since 60 is the first number they have in common, 60 is the least common multiple of 12 and 15.
Fill in the blanks. More than one answer is possible.
Question 21.
12 is the least common multiple of 3 and ____
Answer: 4
Explanation:
The multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30.
The multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 26, 40.
– When we compare the two lists to see what they have in common, we get the answer to “What are the common multiples of 3 and 4?”
– 12, 24, 36, 48, etc.
– Since 12 is the first number they have in common, 12 is the least common multiple of 3 and 4.
Question 22.
32 is the least common multiple of 8 and ___
Answer: 32
Explanation:
– Common multiples of 8 and 32 are numbers that both 8 and 32 can be divided into evenly with no remainder.
– To find the common multiples of 8 and 32, we compare the list of multiples of 8 with the list of multiples of 32 to see what they have in common.
– To create a list of multiples of 8, we multiply 8 by 1, 8 by 2, and so on like this:
8 x 1 = 8
8 x 2 = 16
8 x 3 = 24
8 x 4 = 32
…
– Similarly, to create a list of multiples of 32, we multiply 32 by 1, 32 by 2, and so on like this:
32 x 1 = 32
32 x 2 = 64
32 x 3 = 96
32 x 4 = 128
…
– When we compare the two lists to see what they have in common, we get the answer to “What are the common multiples of 8 and 32?”
32, 64, 96, 128, etc.
– Since 32 is the first number they have in common, 32 is the least common multiple of 8 and 32.
Question 23.
24 is the least common multiple of 6 and ____
Answer: 8
Explanation:
– Common multiples of 6 and 8 are numbers that both 6 and 8 can be divided into evenly with no remainder.
– To find the common multiples of 6 and 8, we compare the list of multiples of 6 with the list of multiples of 8 to see what they have in common.
– To create a list of multiples of 6, we multiply 6 by 1, 6 by 2, and so on like this:
6 x 1 = 6
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24
…
– Similarly, to create a list of multiples of 8, we multiply 8 by 1, 8 by 2, and so on like this:
8 x 1 = 8
8 x 2 = 16
8 x 3 = 24
8 x 4 = 32
…
– When we compare the two lists to see what they have in common, we get the answer to “What are the common multiples of 6 and 8?”
24, 48, 72, 96 etc.
– Since 24 is the first number they have in common, 24 is the least common multiple of 6 and 8.
Question 24.
15 is the least common multiple of 3 and ____
Answer:5
Explanation:
– Common multiples of 3 and 5 are numbers that both 3 and 5 can be divided into evenly with no remainder.
– To find the common multiples of 3 and 5, we compare the list of multiples of 3 with the list of multiples of 5 to see what they have in common.
– To create a list of multiples of 3, we multiply 3 by 1, 3 by 2, and so on like this:
3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
…
– Similarly, to create a list of multiples of 5, we multiply 5 by 1, 5 by 2, and so on like this:
5 x 1 = 5
5 x 2 = 10
5 x 3 = 15
5 x 4 = 20
…
– When we compare the two lists to see what they have in common, we get the answer to “What are the common multiples of 3 and 5?”
15, 30, 45, 60, etc.
– Since 15 is the first number they have in common, 15 is the least common multiple of 3 and 5.
Question 25.
60 is the least common multiple of 15 and ___.
Answer: 20
Explanation:
– Common multiples of 15 and 20 are numbers that both 15 and 20 can be divided into evenly with no remainder.
– To find the common multiples of 15 and 20, we compare the list of multiples of 15 with the list of multiples of 20 to see what they have in common.
– To create a list of multiples of 15, we multiply 15 by 1, 15 by 2, and so on like this:
15 x 1 = 15
15 x 2 = 30
15 x 3 = 45
15 x 4 = 60
…
– Similarly, to create a list of multiples of 20, we multiply 20 by 1, 20 by 2, and so on like this:
20 x 1 = 20
20 x 2 = 40
20 x 3 = 60
20 x 4 = 80
…
-When we compare the two lists to see what they have in common, we get the answer to “What are the common multiples of 15 and 20?”
60, 120, 180, 240, etc.
– Since 60 is the first number they have in common, 60 is the least common multiple of 15 and 20.