Math in Focus

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 3 Lesson 3.6 Writing Algebraic Expressions to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 3 Lesson 3.6 Answer Key Writing Algebraic Expressions

Math in Focus Grade 7 Chapter 3 Lesson 3.6 Guided Practice Answer Key

Complete.
Question 1.
The price of a ring was w dollars. Wendy bought it at a discount of 25%. Write an algebraic expression for the discounted price of the ring.

Answer:
Discounted price of ring = \(\frac{3}{4}\)w dollars.

Explanation:
Total cost price of ring = w dollars.
Discount price of ring = 25%.
Discounted price of ring = Total cost price of ring – (Discount price of ring  × Total cost price of ring)
= w – (25% × w)
= w – (25 ÷ 100 × w)
= w – \(\frac{1}{4}\)w
= (4w – w) ÷ 4
= 3w ÷ 4 or \(\frac{3}{4}\)w dollars.

 

Question 2.
6n blocks of clay are shared among 14 students. Write an algebraic expression for the number of blocks of clay that each student will get.

Answer:
Number of blocks of clay each student gets = 3n ÷ 7.

Explanation:
Total number of blocks of clay = 6n.
Number of students clays shared = 14.
Number of blocks of clay each student gets = Total number of blocks of clay  ÷ Number of students clays shared
= 6n ÷ 14
= 3n ÷ 7.

 

Question 3.
Desmond has w marbles and Mandy has \(\frac{1}{2}\)w marbles. Desmond gives one-tenth of his marbles and Mandy gives two-fifth of her marbles to their cousin Joel. Write an expression for the number of marbles Joel receives.

Joel receives marbles.
Answer:
Number of marbles Joel receives = \(\frac{3}{10}\)w.

Explanation:
Number of marbles Desmond has = w.
Number of marbles Mandy has = \(\frac{1}{2}\)w.
Desmond gives one-tenth of his marbles and Mandy gives two-fifth of her marbles to their cousin Joel.
=> Number of marbles Joel receives = (one-tenth × Number of marbles Desmond has) + (two-fifth × \(\frac{1}{2}\)w)
= (\(\frac{1}{10}\) × w) + (\(\frac{2}{5}\) × \(\frac{1}{2}\)w)
= \(\frac{1}{10}\)w + \(\frac{1}{5}\)w
LCD of 5 n 10 = 10.
= (1w + 2w) ÷ 10
= 3w ÷ 10 or \(\frac{3}{10}\)w.

 

Question 4.
After baking some bread, Janis has \(\frac{2}{3}\)b pounds of butter left. Then she uses \(\frac{3}{4}\) pound for white sauce. Write an algebraic expression for the amount of butter left.
Subtract \(\frac{3}{4}\) from \(\frac{2}{3}\)b.
There are pounds of butter left.

Caution
a subtracted from b is not a – b.
Answer:
Amount of butter left = (8b – 9) ÷ 12 pounds.

Explanation:
Amount of butter left Janis has = \(\frac{2}{3}\)b pounds.
Amount of butter Janis use for white sauce = \(\frac{3}{4}\) pound.
Amount of butter left = Amount of butter left Janis has – Amount of butter Janis use for white sauce
= \(\frac{2}{3}\)b – \(\frac{3}{4}\)
= LCD of 3 n 4 = 12.
= [(2b × 4) – (3 × 3)] ÷ 12
= (8b – 9) ÷ 12 pounds.

 

Complete.
Question 5.
Anne’s garden has a shape of an isosceles triangle with a base of length 2y feet arid sides of length \(\left(\frac{2}{5} y+3\right)\) feet each. Write an algebraic expression for the perimeter of Anne’s garden.
Perimeter of Annes garden:

Answer:
Perimeter of Anne’s garden = (14y + 12) ÷ 5 ft.

Explanation:
Length of the base of the triangle = 2y feet.
Length of other two sides = \(\left(\frac{2}{5} y+3\right)\) feet  each.
Perimeter of Anne’s garden = Length of the base of the triangle  + Length of other two sides
= 2y + 2( \(\left(\frac{2}{5} y+3\right)\))
= 2y + \(\left(\frac{4}{5} y+3\right)\)
= [(2y × 5) + 4(y + 3)] ÷ 5
= (10y + 4y + 12) ÷ 5
= (14y + 12) ÷ 5 ft.

 

Complete.
Question 6.
The price of a buffet lunch is $14.80 per adult and $12 per child. For a group of m adults and n children, how much does the lunch cost before tax and tips?

Total cost of lunch before tax and tips:

The total cost of lunch before tax and tips is dollars.
Answer:
Total cost of lunch before tax and tips = $14.80m + $12n.

Explanation:
Cost of buffet lunch for each adult = $14.80.
Number of adults = m.
Cost of buffet lunch for each child = $12.
Number of adults = n.
Total cost of lunch before tax and tips = (Cost of buffet lunch for each adult × Number of adults) + (Cost of buffet lunch for each child × Number of adults)
= ($14.80 × m) + ( $12 × n)
= $14.80m + $12n

 

Question 7.
Joshua had m quarters in his pocket. He also had one dime and n nickels. What was the total value of his coins?
Answer:
Total value of his coins = $0.4mn.

Explanation:
Number of quarters Joshua had in his pocket = m.
Number of dime Joshua had in his pocket = 1.
Number of nickels Joshua had in his pocket = n.
Conversion:
1 quarter = 0.25 dollar.
1 dime = 0.1 dollar.
1 nickel = 0.05 dollar.
Total value of his coins = Number of quarters Joshua had in his pocket + Number of dime Joshua had in his pocket + Number of nickels Joshua had in his pocket
= m + 1 + n
= ($0.25 × m) +($0.1) + (n × $0.05)
= $0.4mn.

 

Complete.
Question 8.
Anderson had b tennis balls. He gave 30 to his sister and divided the rest of the tennis balls equally among 5 friends. How many tennis balls did each friend receive?

From the bar model, the number of tennis balls each friend received is:
Use the distributive property.
Each friend received tennis balls.
Answer:
Number of tennis balls he gave to each friend = (b – 30) ÷ 5.

Explanation:
Number of tennis balls Anderson had = b.
Number of tennis balls he gave to his sister = 30.
Number of friends he gave rest tennis balls = 5.
Number of tennis balls he gave to each friend = (Number of tennis balls Anderson had – Number of tennis balls he gave to his sister) ÷ Number of friends he gave rest tennis balls
= (b – 30) ÷ 5.

Technology Activity
Materials:

• spreadsheet software

Use Algebraic Expressions In real-world situations

Work in groups of three or four.
Translate verbal descriptions into algebraic expressions.

Maria used her smartphone for 4 days. Her average calling time was 130 minutes each day. Suppose that Maria used the phone for m minutes on the fifth day. Write an algebraic expression for the average number of minutes she spent on the phone over 5 days.

Step 1.
Complete.
Total number of minutes spent over five days:
Total number of minutes spent over four days +
Number of minutes spent on the fifth day

Use a spreadsheet to solve real-world problem involving algebraic expressions.

Step 2.
Label your spreadsheet and enter the values in column A as shown.

Step 3.
Enter the formula =130*4+A2 in cell B2 to find the total number of minutes she spent on her phone over five days. What is the value in cell B2 after you have entered the formula?

Step 4.
Complete cell C2 with a formula to find the average number of minutes she spent on her phone over five days.

Step 5.
Maria would like to have an average number of minutes she spent on her phone over five days to be 150 minutes. Determine the number of minutes she can spend on the fifth day by repeating Step 3 and Step 4 with different values in column A.

Math Journal Based on your activity, what is the relationship between the algebraic expressions of Step 1 and the formula used in the spreadsheet cell of Step 3 and Step 4? Explain how you can use technology to solve real-world problems.

Math in Focus Course 2A Practice 3.6 Answer Key

Translate each verbal description into an algebraic expression. Simplify the expression when you can.
Question 1.
Sum of one-sixth of x and 2.8
Answer:
Sum of one-sixth of x and 2.8 = \(\frac{x}{6}\)  + 28.

Explanation:
Sum of one-sixth of x and 2.8 = (one-sixth of x ) + 2.8
= (\(\frac{1}{6}\) × x) + 2.8
= \(\frac{x}{6}\)  + 28

 

Question 2.
One-half u subtracted from 3 times u
Answer:
One-half u subtracted from 3 times u = –\(\frac{5}{2}\)u.

Explanation:
One-half u subtracted from 3 times u = (\(\frac{1}{2}\)u) – (3 × u)
= \(\frac{1}{2}\)u – 3u
= (u – 6u) ÷ 2
= -5u ÷ 2 or –\(\frac{5}{2}\)u.

 

Question 3.
4.5 times q divided by 9
Answer:
4.5 times q divided by 9 = 0.5q.

Explanation:
4.5 times q divided by 9 = (4.5 × q) ÷ 9
= 0.5 × q
= 0.5q.

 

Question 4.
60% of one-half x
Answer:
60% of one-half x = \(\frac{3}{10}\)x.

Explanation:
60% of one-half x = 60% × \(\frac{1}{2}\)x
= (60 ÷ 100) × \(\frac{1}{2}\)x
= \(\frac{3}{5}\) × \(\frac{1}{2}\)x
= \(\frac{3}{10}\)x.

 

Question 5.
5x increased by 120%
Answer:
5x increased by 120% = 6x.

Explanation:
First, change the percentage to a number.
120(%) (120 ÷ 100) = 1.2
=> 5x increased by 120%:
5x × 1.2 = 6x.

 

Question 6.
7 times z reduced by a third of the product
Answer:
7 times z reduced by a third of the product = 14z.

Explanation:
7 times z reduced by a third of the product = (7 × z) – 3(7 × z)
= 7z – 21z
= -14z.

 

Question 7.
24% of w plus 50% of y
Answer:
24% of w plus 50% of y = \(\frac{6}{25}\)w + \(\frac{1}{2}\)y.

Explanation:
24% of w plus 50% of y = (24% × w) + (50% × y)
= [(24 ÷ 100) × w] + [(50 ÷ 100) × y]
= \(\frac{6}{25}\)w + \(\frac{1}{2}\)y.

 

Question 8.
Three-fourths of v subtracted from 6 times two-ninths y
Answer:
Three-fourths of v subtracted from 6 times two-ninths y = \(\frac{3}{4}\)v – \(\frac{4}{3}\)y.

Explanation:
Three-fourths of v subtracted from 6 times two-ninths y
= ( \(\frac{3}{4}\) × v) –  (6 × \(\frac{2}{9}\)y)
= \(\frac{3}{4}\)v – \(\frac{4}{3}\)y.

 

Question 9.
One-fourth of the sum of 2p and 11
Answer:
One-fourth of the sum of 2p and 11 = \(\frac{1}{2}\)p + \(\frac{11}{4}\).

Explanation:
One-fourth of the sum of 2p and 11
= \(\frac{1}{4}\) (2p + 11)
= ( \(\frac{1}{4}\)  × 2p) + (\(\frac{1}{4}\) × 11)
= \(\frac{1}{2}\)p + \(\frac{11}{4}\).

 

Question 10.
Sum of 2x, (\(\frac{2}{3}\)x + 5), and (11 – x)
Answer:
Sum of 2x, (\(\frac{2}{3}\)x + 5), and (11 – x) = (\(\frac{2}{3}\)x + 16.

Explanation:
Sum of 2x, (\(\frac{2}{3}\)x + 5), and (11 – x)
= 2x + (\(\frac{2}{3}\)x + 5) + (11 – x)
= 2x + \(\frac{2}{3}\)x + 5 + 11 – x
= (6x + 2x – 6x) ÷ 3 + 16
= 2x ÷ 3 + 16 or (\(\frac{2}{3}\)x + 16.

 

Solve. You may use a diagram, model, or table.
Question 11.
The length of \(\frac{2}{3}\) a rope is (4u – 5) inches. Express the total length of the rope in terms of u.
Answer:
Total length of the rope in terms of u = (8u – 10) ÷ 3 inches.

Explanation:
Length of a rope \(\frac{2}{3}\) = (4u – 5) inches
Total length of the rope in terms of u = \(\frac{2}{3}\) × (4u – 5)
= (8u – 10) ÷ 3 inches.

Question 12.
If 50 lb = 22.68 kg, what is \(\frac{15}{8}\)y pounds in kilograms?
Answer:
\(\frac{15}{8}\)y pounds = 0.84 kgs.

Explanation:
If 50 lb = 22.68 kg,
=> 1 pound = 22.68 ÷ 50 kg
=> 1 pound = 0.45 kg.
\(\frac{15}{8}\)y pounds = ?? kg
=> \(\frac{15}{8}\)y × 0.45
=> 6.75 ÷ 8
=> 0.84 kg.

 

Question 13.
The minute hand of a clock makes one complete round every 60 minutes. How many rounds does the minute hand make in 650x minutes?
Answer:
Number of rounds  the minute hand make in 650x minutes = 65x ÷ 6.

Explanation:
The minute hand of a clock makes one complete round every 60 minutes.
Number of rounds  the minute hand make in 650x minutes = 650x ÷ 60
= 65x ÷ 6.

 

Question 14.
Fifteen cards are added to n cards. 6 people then share the cards equally. Express the number of cards for each person in terms of n.
Answer:
Number of cards for each person in terms of n = (15 + n) ÷ 6.

Explanation:
Total number of cards = 15 + n.
Number of people the cards are shared = 6.
Number of cards for each person in terms of n = Total number of cards ÷ Number of people the cards are shared
= (15 + n) ÷ 6.

 

Question 15.
The pump price was g dollars per gallon of gasoline yesterday. The price increases by 10 cents per gallon today. If a driver pumps 12.4 gallons of gasoline today, how much does he have to pay?
Answer:
Cost he pays = $12.4g + $12.4.

Explanation:
Cost of pump per gallon of gasoline yesterday = g dollars.
Cost of price increased per gallon = 10 cents.
Conversion:
1 cent = 0.1 dollar.
10 cents = 0.1 × 10 = 1 dollar.
Number of gallons of gasoline today a driver pumps = 12.4.
Cost he pays = (Cost of pump per gallon of gasoline yesterday + Cost of price increased per gallon) × Number of gallons of gasoline today a driver pumps
= (g + 10cents)  × $12.4
= (g + $1) × 12.4
= $12.4g + $12.4.

 

Question 16.
Math Journal Each algebraic expression contains an error. Copy and complete.

Answer:

Explanation:
Correct Expressions:
35% of s plus 65% of t = (35% × s) + (65% × t)
= 35$s + 65%t.
\(\frac{1}{6}\)x subtracted from \(\frac{1}{6}\)y = \(\frac{1}{6}\)y – \(\frac{1}{6}\)x
= (y – x) ÷ 6.
One more than half on n = 1 + \(\frac{1}{2}\)n
= 1 + \(\frac{1}{2}\)n.
\(\frac{2}{3}\)x divided by \(\frac{1}{5}\) =  \(\frac{2}{3}\)x ÷ \(\frac{1}{5}\)
= \(\frac{2}{3}\)x × 5
= (2 × 5)x ÷ 3
= 10x ÷ 3.

 

Question 17.
The ratio of red counters to blue counters is 9 : 11. There are y blue counters. Express the number of red counters in terms of y.
Answer:
Number of red counters in terms of y = 11x ÷ 9 .

Explanation:
Ratio of red counters to blue counters = 9 : 11.
Number of blue counters = y.
Let Number of red counters = x.
Number of red counters in terms of y = x : y = 9:11
=> x = 9y ÷ 11.
=> 11x ÷ 9 = y.

 

Question 18.
When 18 boys joined a group of y students, the ratio of boys to girls in the group became 4 : 5. Write an algebraic expression for the number of girls in terms of y.
Answer:
Number of girls in terms of y = (4 ÷ 5g) – 18.

Explanation:
Total number of students = y + 18.
Ratio of boys to girls in the group became 4 : 5.
Number of girls in terms of y : y + 18 = 4:5g
=> y + 18 = 4 ÷ 5g.
=>y = (4 ÷ 5g) – 18.

 

Question 19.
Adrian is x years old. Benny is 7 years younger than Adrian. In 5 years’ time, Benny will be twice the age of Celine. How old is Celine now in terms of x?
Answer:
Age of Celine now = (x – 12) ÷ 2 years.

Explanation:
Age of Adrian = x years.
Benny is 7 years younger than Adrian.
Age of Benny = x – 7 years.
In 5 years’ time, Benny will be twice the age of Celine.
Let age of Celine be y years.
Age of Adrian now = x + 5 years.
Age of benny = 5 + (x – 7) years.
Age of Celine now =  5 + (x – 7)years = 2(5 + y)
=> x – 2 = 10 + 2y
=> x – 2 – 10 = 2y
=> x – 12 = 2y
=> (x – 12) ÷ 2 years = y.

 

Question 20.
A group has an equal number of adults and children. When n oranges are given to the group, each adult gets two oranges while each child gets one orange and there are still 5 oranges left. Write an algebraic expression for the number of oranges given to the adults.
Answer:
Total number of oranges  given to adults = (n + 4) ÷ 2

Explanation:
Number of oranges = n.
Let number of oranges given to the adults be x.
Number of oranges each adult gets = 2.
Number of oranges each child gets = 1.
Number of oranges are left = 5.
Total number of oranges = (Number of oranges each adult gets + Number of oranges each child gets) + Number of oranges are left
n = (2x + 1) – 5
=> n = 2x – 4
=> n + 4 = 2x.
=> (n + 4) ÷ 2 = x.

 

Question 21.
The list price of a camera was w dollars. Paul bought the camera for $35 less than the list price. If the sales tax was 8%, how much did Paul pay for the camera including the sales tax?

Answer:
Amount he pays for the camera = (21w ÷ 25) – 35 dollars.

Explanation:
List price of camera = w dollars.
Paul bought the camera for $35 less than the list price.
Cost of camera Paul bought  = (w – 35) dollars.
If the sales tax was 8%
Sales tax = 8% × w = 8%w dollars.
Amount he pays for the camera = Cost of camera Paul bought + Sales tax
= (w – 35) + 8%w
= (w – 35) + (4w ÷ 25)
= (25w – 4w) ÷ 25 – 35
= (21w ÷ 25) – 35 dollars.

 

Question 22.
There were m visitors in an exhibition on the first day and 1,200 fewer visitors on the second day. On the third day, the number of visitors was 30% greater than the number of visitors on the second day. What was the average number of visitors over the three days?
Answer:
Average number of visitors over the three days = \(\frac{5}{3}\)m – 520.

Explanation:
Number of visitors in an exhibition on the first day = m.
Number of visitors in an exhibition on the second day = Number of visitors in an exhibition on the first day  – 1200
= m – 1200.
On the third day, the number of visitors was 30% greater than the number of visitors on the second day.
=> Number of visitors in an exhibition on the third day = 30% Number of visitors in an exhibition on the second day
= 30% (m – 1200)
= 3÷10 (m – 1200)
= 3m – 360.
Average number of visitors over the three days = (Number of visitors in an exhibition on the first day + Number of visitors in an exhibition on the second day + Number of visitors in an exhibition on the third day) ÷ 3
= [m + (m – 1200) + (3m – 360)] ÷ 3
= (m + m – 1200 + 3m – 360) ÷ 3
= (5m – 1560) ÷ 3
= \(\frac{5}{3}\)m – 520.

 

Question 23.
A man drove x miles per hour for 3 hours and (2x – 60) miles per hour for the next 4.75 hours.
a) Express the total distance he traveled in terms of x.
Answer:
Total distance he traveled in terms of x = 12.5x – 285 miles.

Explanation:
Number of miles a man drove per hour = x.
Number of hours he drove x miles = 3.
Number of miles a man drove next per hour = 2x – 60.
Number of hours he drove (2x – 60) miles = 4.75 hours.
Number of miles a man drove 4.75 hours = (2x – 60) × 4.75
= 9.5x – 285.
Number of miles a man drove 3 hours = x × 3 = 3x.
Total distance he traveled in terms of x = Number of miles a man drove 3 hours + Number of miles a man drove 4.75 hours
= 3x + 9.5x – 285.
= 12.5x – 285 miles.

 

b) If x = 64, what is the total distance he traveled?
Answer:
Total distance he traveled in terms of x = 515 miles.

Explanation:
If x = 64,
Total distance he traveled in terms of x = 12.5x – 285
= 12.5(64) – 285
= 800 – 285
= 515 miles.

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 3 Lesson 3.5 Factoring Algebraic Expressions to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 3 Lesson 3.5 Answer Key Factoring Algebraic Expressions

Math in Focus Grade 7 Chapter 3 Lesson 3.5 Guided Practice Answer Key

Copy and complete to factor the expression.
Question 1.
2j – 10 k
2j – 10k = + ()    Rewrite the expression.
= () + ()   The GCF of 2j and -10k is 2.
=      Factor 2 from each term.
Answer:
2j – 10 k = 2 (-5k + j) or 2 (j – 5k).

Explanation:
2j – 10 k = -10k + 2j
= 2 (-5k) + 2 (j)
= 2 (-5k + j) or 2 (j – 5k)

Factor each expression.
Question 2.
6a – 18b
Answer:
6a – 18b =  3 (2a – 6b).

Explanation:
6a – 18b =  3 (2a) + 3 (-6b)
= 3 (2a – 6b).

Question 3.
8p – 12q
Answer:
8p – 12q = 4 (2p – 3q).

Explanation:
8p – 12q = 4 (2p) + 4 (-3q)
= 4 (2p – 3q).

Question 4.
-5x – 3
Answer:
-5x – 3 = -1 (5x + 3).

Explanation:
-5x – 3 = -1 (5x) -1 (3)
= -1 (5x + 3).

Question 5.
-3f – 6
Answer:
-3f – 6 = -3 (f + 2).

Explanation:
-3f – 6 = -3 (f) – 3 (2)
= -3 (f + 2).

Question 6.
-8p – 10q
Answer:
-8p – 10q = -2 (4p + 5q).

Explanation:
-8p – 10q = -2 (4p) – 2 (5q)
= -2 (4p + 5q)

Math in Focus Course 2A Practice 3.5 Answer Key

Factor each expression with two terms.
Question 1.
2x + 8
Answer:
2x + 8 = 2 (x + 4).

Explanation:
2x + 8 = 2 (x) + 2 (4)
= 2 (x + 4).

Question 2.
5a + 5
Answer:
5a + 5 = 5 (a + 1).

Explanation:
5a + 5 = 5 (a) + 5 (1)
= 5 (a + 1).

Question 3.
3x – 12
Answer:
3x – 12 = 3 (x – 4).

Explanation:
3x – 12 = 3 (x) + 3 (-4)
= 3 (x – 4).

Question 4.
4x – 16
Answer:
4x – 16 = 4 (x – 4).

Explanation:
4x – 16 = 4 (x) + 4 (-4)
= 4 (x – 4).

Question 5.
2x + 8y
Answer:
2x + 8y = 2 (x + 4y).

Explanation:
2x + 8y = 2 (x) + 2 (4y)
= 2 (x + 4y).

Question 6.
7a + 7b
Answer:
7a + 7b = 7 (a + b).

Explanation:
7a + 7b = 7 (a) + 7 (b)
= 7 (a + b).

Question 7.
5p + 15q
Answer:
5p + 15q = 5 (p + 3q).

Explanation:
5p + 15q = 5 (p) + 5 (3q)
= 5 (p + 3q).

Question 8.
14w + 49m
Answer:
14w + 49m = 7 (2w + 7m).

Explanation:
14w + 49m = 7 (2w) + 7 (7m)
= 7 (2w + 7m).

Question 9.
4j – 16 k
Answer:
4j – 16 k = 4 (j – 4k).

Explanation:
4j – 16 k = 4(j) + 4(-4k)
= 4 (j – 4k).

Question 10.
8t – 32u
Answer:
8t – 32u = 8 (t – 4u).

Explanation:
8t – 32u = 8(t) + 8 (-4u)
= 8 (t – 4u).

Question 11.
2a – 10p
Answer:
2a – 10p = 2 (a – 5p).

Explanation:
2a – 10p = 2 (a) + 2 (-5p)
= 2(a – 5p).

Question 12.
9h – 45f
Answer:
9h – 45f = 9 (h – 5f).

Explanation:
9h – 45f = 9 (h) + 9 (-5f)
= 9(h – 5f).

Factor each expression with negative terms.
Question 13.
-p – 2
Answer:
-p – 2 = -1 (p + 2).

Explanation:
-p – 2 = -1 (p) – 1(2)
= -1 (p + 2).

Question 14.
-x – 5
Answer:
-x – 5 = -1 (x + 5).

Explanation:
-x – 5 = -1 (x) -1 (5)
= -1 (x + 5).

Question 15.
-2d – 7
Answer:
-2d – 7 = -1 (2d + 7).

Explanation:
-2d – 7 = -1 (2d) – 1(7)
= -1 (2d + 7).

Question 16.
– 4y – 11
Answer:
– 4y – 11 = -1 (4y + 11).

Explanation:
– 4y – 11 = -1 (4y) – 1(11)
= -1 (4y + 11).

Question 17.
-3a – 6
Answer:
-3a – 6 = -3 ( a + 2).

Explanation:
-3a – 6 = -3 (a) – 3 (2)
= -3 ( a + 2).

Question 18.
-4x – 20
Answer:
-4x – 20 = -4 (x + 5).

Explanation:
-4x – 20 = -4(x) – 4 (5)
= -4 (x + 5).

Question 19.
-5k – 25
Answer:
-5k – 25 = -5 (k + 5).

Explanation:
-5k – 25 = -5 (k) – 5( 5)
= -5 (k + 5).

Question 20.
-7u – 49
Answer:
-7u – 49 = -7 (u + 7).

Explanation:
-7u – 49 = -7 (u) – 7 (7)
= -7 (u + 7).

Question 21.
-1 – 4n
Answer:
-1 – 4n = -1 (1 + 4n).

Explanation:
-1 – 4n = -1 (1) – 1(4n)
= -1 (1 + 4n).

Question 22.
-3 – 6a
Answer:
-3 – 6a = -3 (1 + 2a).

Explanation:
-3 – 6a = -3 (1) – 3( 2a)
= -3 (1 + 2a).

Question 23.
-12x – 16y
Answer:
-12x – 16y = -4 (3x + 4y).

Explanation:
-12x – 16y = -4 (3x) – 4(4y)
= -4 (3x + 4y).

Question 24.
-25m – 10n
Answer:
-25m – 10n = -5 (5m + 2n).

Explanation:
-25m – 10n = -5 (5m) – 5(2n)
= -5 (5m + 2n).

Factor each expression with three terms.
Question 25.
4x + 4y + 8
Answer:
4x + 4y + 8 = 4 (x + y + 2).

Explanation:
4x + 4y + 8 = 4(x) + 4(y) + 4(2)
= 4 (x + y + 2).

Question 26.
2a + 6b + 4
Answer:
2a + 6b + 4 = 2( a + 3b + 2).

Explanation:
2a + 6b + 4 = 2(a) + 2(3b) + 2(2)
= 2( a + 3b + 2).

Question 27.
5p + 10q + 10
Answer:
5p + 10q + 10 = 5(p + 2q + 2).

Explanation:
5p + 10q + 10 = 5(p) + 5(2q) + 5(2)
= 5(p + 2q + 2).

Question 28.
12d + 6e + 18
Answer:
12d + 6e + 18 = 6(2d + e + 3).

Explanation:
12d + 6e + 18 = 6(2d) + 6(e) + 6(3)
= 6(2d + e + 3).

Question 29.
3s – 9t – 15
Answer:
3s – 9t – 15 = 3(s – 3t – 5).

Explanation:
3s – 9t – 15 = 3(s) + 3(-3t) + 3(-5)
= 3(s – 3t – 5).

Question 30.
4a – 6b – 12
Answer:
4a – 6b – 12 = 2(2a – 3b – 6).

Explanation:
4a – 6b – 12 = 2(2a) + 2(-3b) + 2(-6)
= 2(2a – 3b – 6).

Question 31.
12a – 9b – 6
Answer:
12a – 9b – 6 = 3(4a – 3b – 2).

Explanation:
12a – 9b – 6 = 3(4a) + 3(-3b) + 3(-2)
= 3(4a – 3b – 2).

Question 32.
24g – 12h – 36
Answer:
24g – 12h – 36 = 6(4g – 2h – 6).

Explanation:
24g – 12h – 36 = 6(4g) + 6(-2h) + 6(-6)
= 6(4g – 2h – 6).

Solve. Show your work.
Question 33.
A rectangle has an area of (12m – 30n) square units. Its width is 6 units. Factor the expression for the area to find an expression for the length of the rectangle.

Answer:
Length of the rectangle = 2m – 5n units .

Explanation:
Given Area of rectangle  = (12m – 30n) square units.
Width = 6 units.
Formula: Area of rectangle = Length × Width
=> (12m – 30n) square units = Length × 6units.
=> (12m – 30n) ÷ 6 = Length
=> [6(2m – 5n) ] ÷ 6 = Length
=> 2m – 5n units = Length.

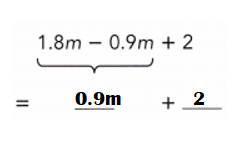
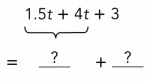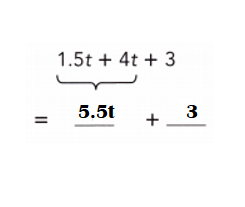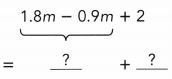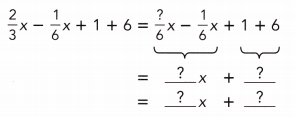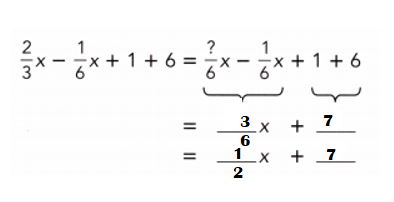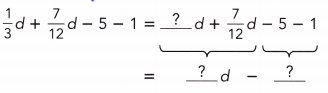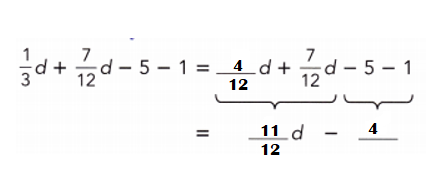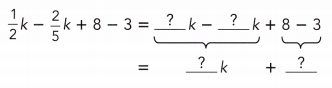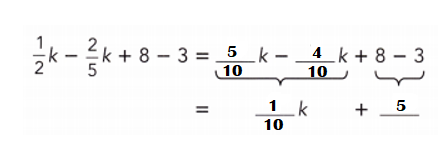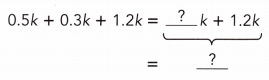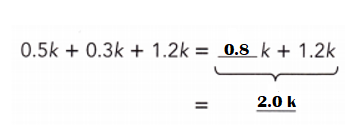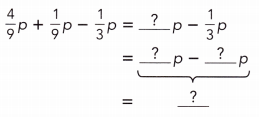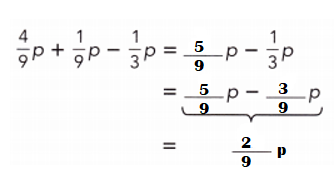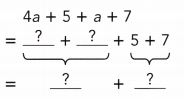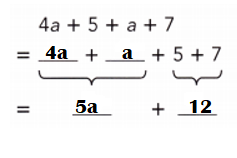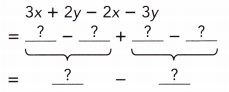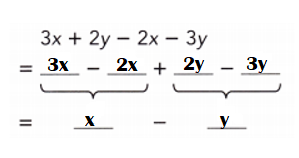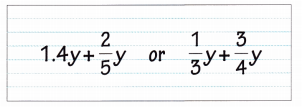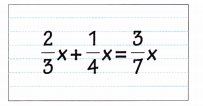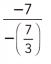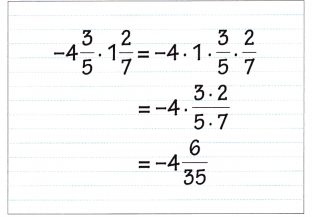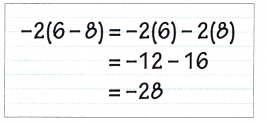Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 3 Lesson 3.4 Expanding Algebraic Expressions to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 3 Lesson 3.4 Answer Key Expanding Algebraic Expressions

Math in Focus Grade 7 Chapter 3 Lesson 3.4 Guided Practice Answer Key

Copy and complete to expand the expression.
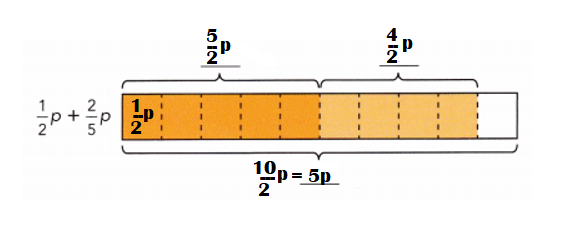
Question 1.
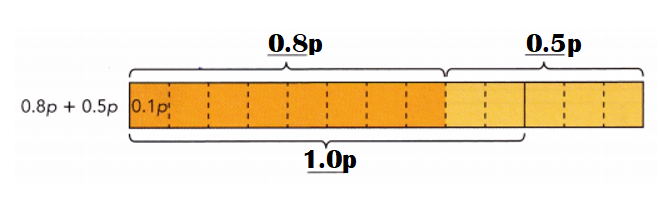
\(\frac{1}{4}\) (8x + 12)
Method 1
Use a bar model.

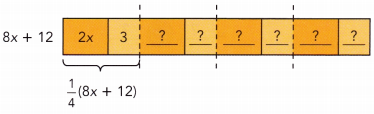
From the bar model, \(\frac{1}{4}\)(8x +12) =
Method 2
Use the distributive property.

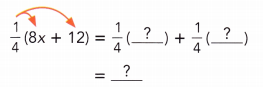
Answer:
\(\frac{1}{4}\) (8x + 12) = 2x + 3.

Explanation:
Method 1:
\(\frac{1}{4}\) (8x + 12)
= (\(\frac{1}{4}\)  × 8x) + (\(\frac{1}{4}\)  × 12)
= 2x + 3.
\(\frac{1}{4}\) (8x + 12) = (2x + 3) + (2x + 3) +  (2x + 3) +  (2x + 3)

Method 2:
\(\frac{1}{4}\) (8x + 12)
= (\(\frac{1}{4}\)  × 8x) + (\(\frac{1}{4}\)  × 12)
= 2x + 3.

Expand each expression.
Question 2.
\(\frac{1}{3}\)(9x + 6)
Answer:
\(\frac{1}{3}\)(9x + 6) = 3x + 2.

Explanation:
\(\frac{1}{3}\)(9x + 6)
= (\(\frac{1}{3}\) × 9x) + (\(\frac{1}{3}\) × 6)
= 3x + 2

Question 3.
\(\frac{1}{5}\)(25x + 15)
Answer:
\(\frac{1}{5}\)(25x + 15) = 5x + 3.

Explanation:
\(\frac{1}{5}\)(25x + 15)
= (\(\frac{1}{5}\) × 25x) + (\(\frac{1}{5}\) × 15)
= 5x + 3.

Copy and complete to expand each expression. Write + or – in each .
Question 4.
0.3(2x + 5)
0.3(2x + 5) = 0.3() + 0.3()
= +
Answer:
0.3(2x + 5) = (0.3 × 2x) + (0.3 × 5) = 0.6x + 1.5.

Explanation:
0.3(2x + 5) = (0.3 × 2x) + (0.3 × 5)
= 0.6x + 1.5.

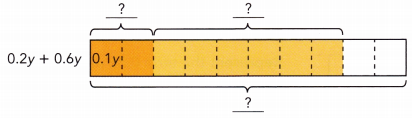
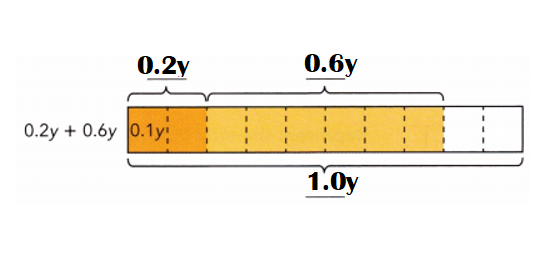
Question 5.
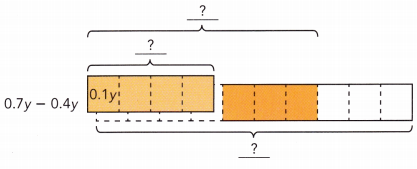
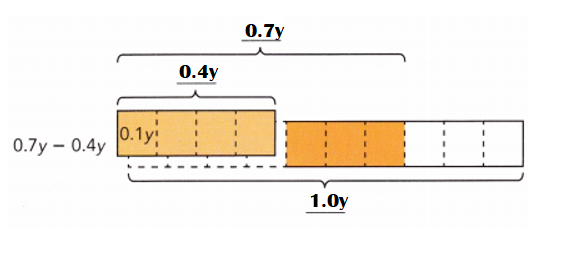
0.5(1.4y – 2.1)
0.5(1.4y – 2.1) = 0.5 () 0.5(- )
= (- )
=
Answer:
0.5(1.4y – 2.1) = (0.5 × 1.4y) + (0.5 × -2.1) = 0.7y – 1.05.

Explanation:
0.5(1.4y – 2.1) = (0.5 × 1.4y) + (0.5 × -2.1)
= 0.7y + (-1.05)
= 0.7y – 1.05.

 

Expand each expression.
Question 6.
0.4(3y + 2)
Answer:
0.4(3y + 2) = 1.2y + 0.8.

Explanation:
0.4(3y + 2) = (0.4 × 3y) + (0.4 × 2)
= 1.2y + 0.8.

Question 7.
0.2(4x – 3.1)
Answer:
0.2(4x – 3.1) = 0.8x – 6.2.

Explanation:
0.2(4x – 3.1) = (0.2 × 4x) + (0.2 × -3.1)
= 0.8x + (-6.2)
= 0.8x – 6.2.

 

Expand each expression.
Question 8.
-4(3d – 2)
Answer:
-4(3d – 2) = -12d + 8.

Explanation:
-4(3d – 2) = (-4 × 3d) + (-4 × -2)
= -12d + 8.

 

Question 9.
-7(5k + e)
Answer:
-7(5k + e) = -35k – 7e.

Explanation:
-7(5k + e) = (-7 × 5k) + (-7 × e)
= -35k + (-7e)
= -35k – 7e.

Question 10.
-4(0.6x – 4)
Answer:
-4(0.6x – 4) = -2.4x + 16.

Explanation:
-4(0.6x – 4) = (-4 × 0.6x) + (-4 × -4)
= -2.4x + (16)
= -2.4x + 16.

Question 11.
–\(\frac{1}{4}\)(-3y + \(\frac{1}{2}\))
Answer:
–\(\frac{1}{4}\)(-3y + \(\frac{1}{2}\)) = \(\frac{3}{4}\)y –\(\frac{1}{8}\)

Explanation:
–\(\frac{1}{4}\)(-3y + \(\frac{1}{2}\))
= (-\(\frac{1}{4}\) × -3y) + (-\(\frac{1}{4}\) × \(\frac{1}{2}\)))
= \(\frac{3}{4}\)y +(-\(\frac{1}{8}\))
= \(\frac{3}{4}\)y –\(\frac{1}{8}\)

Copy and complete to expand and simplify the expression.
Question 12.
2(2a + 3b) + 5b .
2(2a + 3b) + 5b = 2(2 a) + 2 () +
= + +
=
Answer:
2(2a + 3b) + 5b = 4a + 11b.

Explanation:
2(2a + 3b) + 5b = (2 × 2a) + (2 × 3b) + 5b.
= 4a + 6b + 5b
= 4a + 11b.

Expand and simplify each expression.
Question 13.
-3(\(\frac{1}{2}\)k – 4) – 2k
Answer:
-3(\(\frac{1}{2}\)k – 4) – 2k = –\(\frac{5}{2}\)k + 12.

Explanation:
-3(\(\frac{1}{2}\)k – 4) – 2k
= ( -3 × \(\frac{1}{2}\)k) + (-3 × -4) – 2k
= –\(\frac{3}{2}\)k + 12 – 2k
= (-3k – 2k) ÷ 2 + 12
= –\(\frac{5}{2}\)k + 12.

Question 14.
5(2h – 3) – (2k – 1)
Answer:
5(2h – 3) – (2k – 1) = 10h – 2k – 14.

Explanation:
5(2h – 3) – (2k – 1) = (5 × 2h) + (5 × -3) -2k + 1.
= 10h – 15 – 2k + 1
= 10h – 2k – 14.

Math in Focus Course 2A Practice 3.4 Answer Key

Expand each expression.
Question 1.
\(\frac{1}{4}\) (4x + 8)
Answer:
\(\frac{1}{4}\) (4x + 8) = x + 2.

Explanation:
\(\frac{1}{4}\) (4x + 8)
= (\(\frac{1}{4}\) × 4x) + (\(\frac{1}{4}\) × 8)
= x + 2.

Question 2.
\(\frac{1}{3}\) (6b + 9)
Answer:
\(\frac{1}{3}\) (6b + 9) = 2b + 3.

Explanation:
\(\frac{1}{3}\) (6b + 9)
= (\(\frac{1}{3}\)  × 6b) + (\(\frac{1}{3}\) × 9)
= 2b + 3.

Question 3.
\(\frac{1}{2}\) (p + 2)
Answer:
\(\frac{1}{2}\) (p + 2) = \(\frac{1}{2}\)p + \(\frac{1}{4}\)

Explanation:
\(\frac{1}{2}\) (p + 2)
= (\(\frac{1}{2}\) × p) + (\(\frac{1}{2}\) × 2)
= \(\frac{1}{2}\)p + \(\frac{1}{4}\)

Question 4.
\(\frac{1}{5}\) (4a + 3)
Answer:
\(\frac{1}{5}\) (4a + 3) = \(\frac{4}{5}\)a + \(\frac{3}{5}\)

Explanation:
\(\frac{1}{5}\) (4a + 3)
= (\(\frac{1}{5}\)  × 4a) + (\(\frac{1}{5}\) × 3)
= \(\frac{4}{5}\)a + \(\frac{3}{5}\)

Question 5.
\(\frac{1}{2}\)(4k – 6)
Answer:
\(\frac{1}{2}\)(4k – 6) = 2k – 3.

Explanation:
\(\frac{1}{2}\)(4k – 6)
= (\(\frac{1}{2}\) × 4k) + ( \(\frac{1}{2}\) × -6)
= (2k) + (-3)
= 2k – 3.

Question 6.
\(\frac{1}{3}\) (16a – 8)
Answer:
\(\frac{1}{3}\) (16a – 8) = \(\frac{16}{3}\)a – \(\frac{8}{3}\).

Explanation:
\(\frac{1}{3}\) (16a – 8)
= (\(\frac{1}{3}\)  × 16a) + ( \(\frac{1}{3}\)  × -8)
= (\(\frac{16}{3}\)a) + (- \(\frac{8}{3}\))
= \(\frac{16}{3}\)a – \(\frac{8}{3}\)

Question 7.
\(\frac{1}{3}\) (5b – 1)
Answer:
\(\frac{1}{3}\) (5b – 1) = \(\frac{5}{3}\)b – \(\frac{1}{3}\)

Explanation:
\(\frac{1}{3}\) (5b – 1)
= ( \(\frac{1}{3}\) × 5b) + ( \(\frac{1}{3}\) × -1)
= (\(\frac{5}{3}\)b) + (- \(\frac{1}{3}\))
= \(\frac{5}{3}\)b – \(\frac{1}{3}\)

Question 8.
\(\frac{2}{5}\) (k – 10)
Answer:
\(\frac{2}{5}\) (k – 10) = \(\frac{2}{5}\)k – 4.

Explanation:
\(\frac{2}{5}\) (k – 10)
= (\(\frac{2}{5}\) × k) + ( \(\frac{2}{5}\)  × -10)
= (\(\frac{2}{5}\)k) + (-4)
= \(\frac{2}{5}\)k – 4.

Question 9.
3(4x + 0.2)
Answer:
3(4x + 0.2) = 12x + 0.6.

Explanation:
3(4x + 0.2)
= (3 × 4x) + (3 × 0.2)
= 12x + 0.6.

Question 10.
4(0.1y + 5)
Answer:
4(0.1y + 5) = 0.4y + 20.

Explanation:
4(0.1y + 5)
= (4 × 0.1y) + ( 4 × 5)
= 0.4y + 20.

Question 11.
0.2(3x + 4)
Answer:
0.2(3x + 4) = 0.6x + 0.8.

Explanation:
0.2(3x + 4)
= (0.2 × 3x) + (0.2 × 4)
= 0.6x + 0.8.

Question 12.
0.6(3h + 5)
Answer:
0.6(3h + 5) = 1.8h + 3.0.

Explanation:
0.6(3h + 5)
= (0.6 × 3h) + (0.6 × 5)
= 1.8h + 3.0.

Question 13.
0.2(m – 3)
Answer:
0.2(m – 3) = 0.2m – 0.6.

Explanation:
0.2(m – 3) = (0.2 × m) + ( 0.2 × -3)
= (0.2m) + (-0.6)
= 0.2m – 0.6.

Question 14.
0.3(p – 3)
Answer:
0.3(p – 3) = 0.3p – 0.9.

Explanation:
0.3(p – 3)
= (0.3 × p) + (0.3 × -3)
= (0.3p) + (-0.9)
= 0.3p – 0.9.

Question 15.
0.4(1.5d + 0.5)
Answer:
0.4(1.5d + 0.5) = 0.6d + 0.20.

Explanation:
0.4(1.5d + 0.5) = (0.4 × 1.5d) + (0.4 × 0.5)
= (0.6d) + (0.20)
= 0.6d + 0.20.

Question 16.
1.2(0.3x – 1.4)
Answer:
1.2(0.3x – 1.4) = 0.36x – 1.68.

Explanation:
1.2(0.3x – 1.4)
= (1.2 × 0.3x) + (1.2 × -1.4)
= (0.36x) + (-1.68)
= 0.36x – 1.68.

 

Expand each expression with a negative factor.
Question 17.
-2(x + 1)
Answer:
-2(x + 1) = -2x – 2.

Explanation:
-2(x + 1) = (-2 × x) + (-2 × 1)
= (-2x) + (-2)
= -2x – 2.

Question 18.
-3(2x + 5)
Answer:
-3(2x + 5) = -6x – 15.

Explanation:
-3(2x + 5)
= (-3 × 2x) + (-3 × 5)
= (-6x) + (-15)
= -6x – 15.

Question 19.
-3(4a + 9b)
Answer:
-3(4a + 9b) = -12a – 27b.

Explanation:
-3(4a + 9b)
= (-3 × 4a) + (-3 × 9b)
= (-12a) + (-27b)
= -12a – 27b.

Question 20.
-7(2k – h)
Answer:
-7(2k – h) = -14k + 7h.

Explanation:
-7(2k – h)
= (-7 × 2k) + (-7 × -h)
= (-14k) + (7h)
= -14k + 7h.

Question 21.
-4(p + \(\frac{1}{2}\))
Answer:
-4(p + \(\frac{1}{2}\)) = -4p – 2.

Explanation:
-4(p + \(\frac{1}{2}\)) = (-4 × p) + (-4 × \(\frac{1}{2}\))
= (-4p) + × (-2)
= -4p – 2.

Question 22.
–\(\frac{1}{2}\) (6x – \(\frac{1}{3}\))
Answer:
–\(\frac{1}{2}\) (6x – \(\frac{1}{3}\)) = -3x + \(\frac{1}{6}\).

Explanation:
–\(\frac{1}{2}\) (6x – \(\frac{1}{3}\))
= (-\(\frac{1}{2}\)  × 6x) + (-\(\frac{1}{2}\) × – \(\frac{1}{3}\))
= (-3x) + (\(\frac{1}{6}\))
= -3x + \(\frac{1}{6}\).

Question 23.
-2(5k + 1.7)
Answer:
-2(5k + 1.7) = -10k – 3.4.

Explanation:
-2(5k + 1.7) = (-2 × 5k) + (-2 × 1.7)
= (-10k) + (-3.4)
= -10k – 3.4.

Question 24.
-3(0.2m + 5)
Answer:
-3(0.2m + 5) = -0.6m – 15.

Explanation:
-3(0.2m + 5)
= (-3 × 0.2m) + (-3 × 5)
= (-0.6m) + (-15)
= -0.6m – 15.

Question 25.
-5(q – 0.3)
Answer:
-5(q – 0.3) = -5q + 1.5.

Explanation:
-5(q – 0.3)
= (-5 × q) + (-5 × -0.3)
= (-5q) + (1.5)
= -5q + 1.5.

Question 26.
-0.6(0.4y – 1)
Answer:
-0.6(0.4y – 1) = -0.24y + 0.6.

Explanation:
-0.6(0.4y – 1)
= (-0.6 × 0.4y) + (-0.6 × -1)
= (-0.24y) + (0.6)
= -0.24y + 0.6.

Expand and simplify each expression.
Question 27.
3(2y + 1) + 4
Answer:
3(2y + 1) + 4 = 6y + 7.

Explanation:
3(2y + 1) + 4
= (3 × 2y) + (3 × 1) + 4
= 6y + 3 + 4
= 6y + 7.

Question 28.
3(2a + 5) – 8
Answer:
3(2a + 5) – 8 = 6a + 7.

Explanation:
3(2a + 5) – 8
= (3 × 2a) + (3 × 5) – 8
= 6a + 15 – 8
= 6a + 7.

Question 29.
2(x + 2) + 3x
Answer:
2(x + 2) + 3x = 5x + 4.

Explanation:
2(x + 2) + 3x
= (2 × x) + (2 × 2) + 3x
= 2x + 4 + 3x
= 5x + 4.

Question 30.
6(b + 3) – 2b
Answer:
6(b + 3) – 2b = 4b + 18.

Explanation:
6(b + 3) – 2b
= (6 × b) + (6 × 3) – 2b.
= 6b + 18 – 2b
= 4b + 18.

Question 31.
5(\(\frac{1}{6}\)a + 1) + 3
Answer:
5(\(\frac{1}{6}\)a + 1) + 3 = \(\frac{5}{6}\)a  + 8.

Explanation:
5(\(\frac{1}{6}\)a + 1) + 3
= (5 × \(\frac{1}{6}\)a) + (5 × 1) + 3
= (\(\frac{5}{6}\)a) + 5 + 3.
= \(\frac{5}{6}\)a + 5 + 3
= \(\frac{5}{6}\)a  + 8.

Question 32.
4(\(\frac{1}{8}\)a – 3) – \(\frac{1}{2}\)a
Answer:
4(\(\frac{1}{8}\)a – 3) – \(\frac{1}{2}\)a = -12.

Explanation:
4(\(\frac{1}{8}\)a – 3) – \(\frac{1}{2}\)a
= (4 × \(\frac{1}{8}\)a) + (4 × -3) – \(\frac{1}{2}\)a
= \(\frac{1}{2}\)a – 12 – \(\frac{1}{2}\)a
= -12.

 

Expand and simplify each expression.
Question 33.
0.2(x + 1) + 0.7x.
Answer:
0.2(x + 1) + 0.7x. = 0.9x + 0.2.

Explanation:
0.2(x + 1) + 0.7x
= (0.2 × x) + (0.2 × 1) + 0.7x
= 0.2x + 0.2 + 0.7x
= 0.9x + 0.2.

Question 34.
0.5(y + 2) – 0.3y
Answer:
0.5(y + 2) – 0.3y = 0.2y + 1.0.

Explanation:
0.5(y + 2) – 0.3y
= (0.5 × y) + ( 0.5 × 2) – 0.3y.
= 0.5y + 1.0 – 0.3y
= 0.2y + 1.0.

Question 35.
-2(4 m + 1) – m
Answer:
-2(4 m + 1) – m = -9m – 2.

Explanation:
-2(4 m + 1) – m
= (-2 × 4m) + (-2 × 1) -m
= -8m – 2 – m
= -9m – 2.

Question 36.
10 – 3(2n – 1)
Answer:
10 – 3(2n – 1) = 13 – 6n.

Explanation:
10 – 3(2n – 1)
= 10 + (-3 × 2n) + (-3 × -1)
= 10 – 6n + 3
= 13 – 6n.

Question 37.
-0.8(r + 3) + 2.2r
Answer:
-0.8(r + 3) + 2.2r = 1.4r – 2.4.

Explanation:
-0.8(r + 3) + 2.2r
= (-0.8 × r) + (-0.8 × 3) + 2.2r
= -0.8r – 2.4 + 2.2r
= 1.4r – 2.4.

Question 38.
-(1.2x + 7) + 1.5x
Answer:
-(1.2x + 7) + 1.5x = -7 + 0.3x.

Explanation:
-(1.2x + 7) + 1.5x
= (-1 × 1.2x) + (-1 × 7) + 1.5x
= -1.2x – 7 + 1.5x
= -7 + 0.3x.

 

Expand and simplify each expression with two variables.
Question 39.
4x + 6(3y + x)
Answer:
4x + 6(3y + x) = 10x + 18y.

Explanation:
4x + 6(3y + x)
= 4x + (6 × 3y) + (6 × x)
= 4x + 18y + 6x
= 10x + 18y.

Question 40.
7a + 5(3a – b)
Answer:
7a + 5(3a – b) = 22a – 5b.

Explanation:
7a + 5(3a – b)
= 7a + (5 × 3a) + (5 × -b)
= 7a + 15a – 5b
= 22a – 5b.

Question 41.
8g + 5(v – g)
Answer:
8g + 5(v – g) = 3g + 5v.

Explanation:
8g + 5(v – g)
= 8g + (5 × v) + (5 × -g)
= 8g + 5v – 5g
= 3g + 5v.

Question 42.
4q + 6(p – 2q)
Answer:
4q + 6(p – 2q) = 6p – 8q.

Explanation:
4q + 6(p – 2q) = 4q + (6 × p) + (6 × -2q)
= 4q + 6p – 12q
= 6p – 8q.

Question 43.
2(a + 2b) + (a + 3b)
Answer:
2(a + 2b) + (a + 3b) = 3a + 7b.

Explanation:
2(a + 2b) + (a + 3b)
= (2 × a) + (2 × 2b) + a + 3b
= 2a + 4b + a + 3b
= 3a + 7b.

Question 44.
3(m – 2n) + 6(n – 2m)
Answer:
3(m – 2n) + 6(n – 2m) = -9m.

Explanation:
3(m – 2n) + 6(n – 2m) = (3 × m) + (3 × -2n) + (6 ×n) + (6 × -2m)
= 3m – 6n + 6n – 12m
= -9m.

Question 45.
4(d + e) – 3(d – 2e)
Answer:
4(d + e) – 3(d – 2e) = d + 10e.

Explanation:
4(d + e) – 3(d – 2e)
= (4 × d) + (4 × e) + (-3 × d) + (-3 × -2e)
= 4d + 4e – 3d + 6e
= d + 10e.

Question 46.
3(3q – p) – (q – 6p)
Answer:
3(3q – p) – (q – 6p) = 8q + 3p.

Explanation:
3(3q – p) – (q – 6p)
= (3 × 3q) + (3 × -p) + (-1 × q) + (-1 × -6p)
= 9q – 3p – q + 6p
= 8q + 3p.

Question 47.
-4(x + 3y) + 3(2x – 5y)
Answer:
-4(x + 3y) + 3(2x – 5y) = 2x – 27y.

Explanation:
-4(x + 3y) + 3(2x – 5y)
= (-4 × x) + (-4 × 3y) + (3 × 2x) + (3 × -5y)
= -4x – 12y + 6x – 15y
= 2x – 27y.

Question 48.
-7(y + 2t) – 3(y – t)
Answer:
-7(y + 2t) – 3(y – t) = -10y – 11t.

Explanation:
-7(y + 2t) – 3(y – t)
= (-7 × y) + (-7 × 2t) + (-3 5 y) + (-3 × -t)
= -7y – 14t -3y + 3t
= -10y – 11t.

 

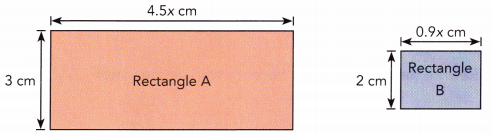
Write an expression for the missing dimension of each shaded figure and a multiplication expression for its area. Then expand and simplify the multiplication expression.
Question 49.

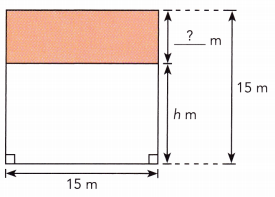
Answer:
Area of the ABCD square figure = 225 square m.

Explanation:

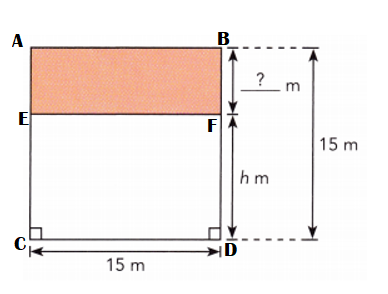
Length of BF shaded figure = BD – BF
= 15 m – h m
= (15 – h) m.
Area of the ABCD square figure = CD × BD
= 15 m × 15 m
= 225 square m.

 

Question 50.

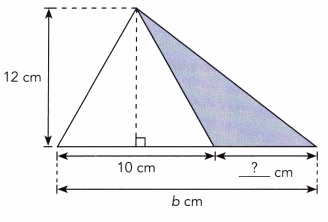
Answer:
Area of triangle ADE = 6b square cm.

Explanation:

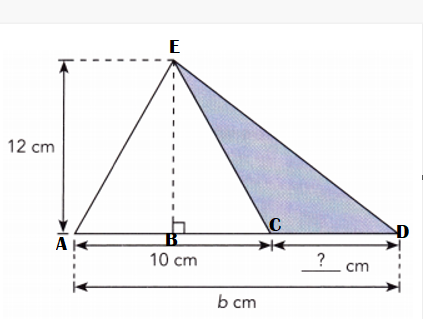
Length of the CD shaded figure :
AD = AC + CD
= b cm = 10 cm + ?? cm
= b cm – 10cm = ?? cm.
Area of triangle ADE = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × b cm × 12 cm
= 6cm × b cm
= 6b square cm.

Write an expression for the area of the figure. Expand and simplify.
Question 51.

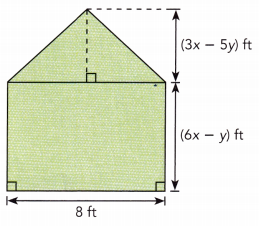
Answer:
Total area of ABCDE figure = (60x – 28y) ft.

Explanation:

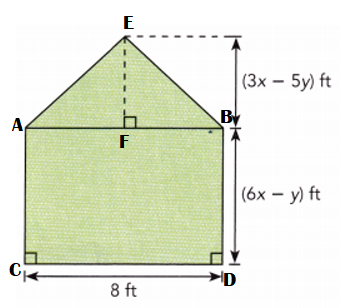
Area of the triangle ABE = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\)  × 8 ft × (3x – 5y) ft
= 4 ft × (3x – 5y) ft
= (4 × 3x) + (4 × -5y) ft
= (12x – 20y) ft
Area of rectangle ABCD = Length × Width
= 8 ft × ((6x – y) ft
= [(8 × 6x) + (8 × -y)] ft
= (48x – 8y) ft
Total area of ABCDE = Area of the triangle ABE + Area of rectangle ABCD
= (12x – 20y) ft + (48x – 8y) ft
= (12x – 20y + 48x – 8y) ft
= (60x – 28y) ft.

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 3 Lesson 3.3 Simplifying Algebraic Expressions to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 3 Lesson 3.3 Answer Key Simplifying Algebraic Expressions

Math in Focus Grade 7 Chapter 3 Lesson 3.3 Guided Practice Answer Key

Complete.
Question 1.
1.5t + 4t+ 3

Answer:

Explanation:
1.5t + 4t+ 3
= 5.5t + 3.

 

Question 2.
1.8m – 0.9m + 2

Answer:

Explanation:
1.8m – 0.9m + 2
= 0.9m + 2.

 

Copy and complete to simplify each expression.
Question 3.
\(\frac{2}{3}\)x – \(\frac{1}{6}\)x + 1 + 6

Answer:
\(\frac{2}{3}\)x – \(\frac{1}{6}\)x + 1 + 6 = \(\frac{1}{2}\)x + 7.

Explanation:
\(\frac{2}{3}\)x – \(\frac{1}{6}\)x + 1 + 6
= \(\frac{2}{3}\)x – \(\frac{1}{6}\)x  + 7
LCD of 3 n 6 = 6.
= [(2 × 2)x – (1 × 1)x] ÷ 6 + 7
= (4x – x) ÷ 6 + 7
= 3x ÷ 6 + 7
= x ÷ 2 + 7.

 

Question 4.
\(\frac{1}{3}\)d + \(\frac{7}{12}\)d – 5 – 1

Answer:
\(\frac{1}{3}\)d + \(\frac{7}{12}\)d – 5 – 1 = \(\frac{11}{12}\)d – 4.

Explanation:
\(\frac{1}{3}\)d + \(\frac{7}{12}\)d – 5 – 1
= \(\frac{1}{3}\)d + \(\frac{7}{12}\)d – 4
LCD of 3 n 12 = 12.
= [(1 × 4)d + (7 × 1)d] ÷ 12 – 4
= (4d + 7d) ÷ 12 – 4
= 11d ÷ 12 – 4 or \(\frac{11}{12}\)d – 4.

Question 5.
\(\frac{1}{2}\)k – \(\frac{2}{5}\)k + 8 – 3

Answer:
\(\frac{1}{2}\)k – \(\frac{2}{5}\)k + 8 – 3 = \(\frac{1}{10}\)k + 5.

Explanation:
\(\frac{1}{2}\)k – \(\frac{2}{5}\)k + 8 – 3
= \(\frac{1}{2}\)k – \(\frac{2}{5}\)k + 5
LCD of 2 n 5 = 10.
= [(1 × 5)k – (2 × 2) k] ÷ 10 + 5
= (5k – 4k) ÷ 10 + 5
= k ÷ 10 + 5 or \(\frac{1}{10}\)k + 5.

 

Copy and complete to simplify each expression.
Question 6.
0.5k + 0.3k + 1.2k

Answer:

Explanation:
0.5k + 0.3k + 1.2k
= 0.8k + 1.2k
= 2.0k.

 

Question 7.
\(\frac{1}{2}\)p + \(\frac{1}{2}\)p – \(\frac{1}{2}\)p

Answer:

Explanation:
\(\frac{1}{2}\)p + \(\frac{1}{2}\)p – \(\frac{1}{2}\)p
= (1 + 1)p ÷ 2 – \(\frac{1}{2}\)p
= 2p ÷ 2 –  \(\frac{1}{2}\)p
= p ÷ 1 – \(\frac{1}{2}\)p
= (2p – p) ÷ 2
= p ÷ 2 or – \(\frac{1}{2}\)p.

 

Complete to simplify each expression.
Question 8.
4a + 5 + a + 7

Answer:

Explanation:
4a + 5 + a + 7
= 4a + a + 7 + 5
= 5a + 7 + 5
= 5a + 12.

 

Question 9.
\(\frac{3}{7}\)x + \(\frac{3}{5}\) – \(\frac{2}{7}\)x – \(\frac{2}{5}\)

Answer:

Explanation:
\(\frac{3}{7}\)x + \(\frac{3}{5}\) – \(\frac{2}{7}\)x – \(\frac{2}{5}\)
= \(\frac{3}{7}\)x  – \(\frac{2}{7}\)x  + \(\frac{3}{5}\) – \(\frac{2}{5}\)
= [(3 – 2)x ÷ 7] + \(\frac{3}{5}\) – \(\frac{2}{5}\)
= \(\frac{1}{7}\)x + \(\frac{3}{5}\) – \(\frac{2}{5}\)
= \(\frac{1}{7}\)x + [(3 – 2) ÷ 5]
= \(\frac{1}{7}\)x + \(\frac{1}{5}\).

 

Copy and complete to simplify each expression.
Question 10.
6a + 9b + a + b

Answer:

Explanation:
6a + 9b + a + b
= 6a + a + 9b + b
= 7a + 9b + b
= 7a + 10b.

 

Question 11.
3x + 2y – 2x – 3y

Answer:

Explanation:
3x + 2y – 2x – 3y
= 3x – 2x – 3y + 2y
= x – 3y + 2y
= x – y.

 

Math in Focus Course 2A Practice 3.3 Answer Key

Simplify each expression with one variable.
Question 1.
0.3x + 0.6x + 3
Answer:
0.3x + 0.6x + 3 = 0.9x + 3.

Explanation:
0.3x + 0.6x + 3
= 0.9x + 3.

 

Question 2.
\(\frac{2}{7}\)x + \(\frac{3}{7}\)x + 4
Answer:
\(\frac{2}{7}\)x + \(\frac{3}{7}\)x + 4 = \(\frac{5}{7}\)x + 4.

Explanation:
\(\frac{2}{7}\)x + \(\frac{3}{7}\)x + 4
= (2 + 3)x ÷ 7 + 4
= 5x ÷ 7 + 4
= \(\frac{5}{7}\)x + 4.

 

Question 3.
0.8x – 0.2x – 5
Answer:
0.8x – 0.2x – 5 = 0.6x – 5.

Explanation:
0.8x – 0.2x – 5
= 0.6x – 5.

 

Question 4.
\(\frac{7}{8}\)x – \(\frac{1}{8}\)x – 5
Answer:
\(\frac{7}{8}\)x – \(\frac{1}{8}\)x – 5 = \(\frac{3}{4}\)x – 5.

Explanation:
\(\frac{7}{8}\)x – \(\frac{1}{8}\)x – 5
= (7 – 1)x ÷ 8 – 5
= 6x ÷ 8 – 5
= 3x ÷ 4 – 5  or \(\frac{3}{4}\)x – 5.

 

Simplify each expression with three algebraic terms.
Question 5.
0.3p + 0.2p + 0.4p
Answer:
0.3p + 0.2p + 0.4p = 0.9p.

Explanation:
0.3p + 0.2p + 0.4p
= 0.5p + 0.4p
= 0.9p.

 

Question 6.
0.2 + o.8p – 0.6p
Answer:
0.2 + o.8p – 0.6p = 0.2(1 + p).

Explanation:
0.2 + o.8p – 0.6p
= 0.2 + 0.2p.
= 0.2(1 + p).

 

Question 7.
\(\frac{1}{3}\)y + \(\frac{1}{6}\)y + \(\frac{5}{12}\)y
Answer:
\(\frac{1}{3}\)y + \(\frac{1}{6}\)y + \(\frac{5}{12}\)y = \(\frac{2}{3}\)y.

Explanation:
\(\frac{1}{3}\)y + \(\frac{1}{6}\)y + \(\frac{5}{12}\)y
= LCD of 3 n 6 = 6.
= [(2 + 1)y ÷ 6] + \(\frac{5}{12}\)y
= 3y ÷ 6 + \(\frac{5}{12}\)y
= y ÷ 6 + \(\frac{5}{12}\)y
= \(\frac{1}{6}\)y + \(\frac{5}{12}\)y
LCD of 6 n 12 = 12.
= [(1 × 2) + 5]y ÷ 12
= (3 + 5)y ÷ 12
= 8y ÷ 12
= 2y ÷ 3 or \(\frac{2}{3}\)y.

 

Question 8.
\(\frac{1}{2}\)a + \(\frac{2}{3}\)a – \(\frac{1}{6}\)a
Answer:
\(\frac{1}{2}\)a + \(\frac{2}{3}\)a – \(\frac{1}{6}\)a = a.

Explanation:
\(\frac{1}{2}\)a + \(\frac{2}{3}\)a – \(\frac{1}{6}\)a
= LCD of 2 n 3 = 6.
= [(1 × 3) + (2 × 2)]a ÷ 6 – \(\frac{1}{6}\)a
= (3 + 4)a ÷ 6 – \(\frac{1}{6}\)a
= \(\frac{7}{6}\)a –  \(\frac{1}{6}\)a
= (7 – 1)a ÷ 6
= 6a ÷ 6
= a ÷ 1 or a.

 

Simplify each expression with one variable.
Question 9.
7x + 6 + 4x
Answer:
7x + 6 + 4x = 11x + 6.

Explanation:
7x + 6 + 4x
= 7x + 4x + 6
= 11x + 6.

 

Question 10.
8y – 4 – 6y
Answer:
8y – 4 – 6y = 2y – 4.

Explanation:
8y – 4 – 6y
= 8y – 6y – 4
= 2y – 4.

 

Question 11.
1.8x – 0.6 – 0.7x
Answer:
1.8x – 0.6 – 0.7x = 1.1x – 0.6.

Explanation:
1.8x – 0.6 – 0.7x
= 1.8x – 0.7x – 0.6
= 1.1x – 0.6.

Question 12.
\(\frac{4}{7}\)x + \(\frac{1}{5}\) + \(\frac{2}{7}\)x
Answer:
\(\frac{4}{7}\)x + \(\frac{1}{5}\) + \(\frac{2}{7}\)x = \(\frac{6}{7}\)x + \(\frac{1}{5}\).

Explanation:
\(\frac{4}{7}\)x + \(\frac{1}{5}\) + \(\frac{2}{7}\)x
= \(\frac{4}{7}\)x  + \(\frac{2}{7}\)x + \(\frac{1}{5}\)
= (4 + 2)x ÷ 7 + \(\frac{1}{5}\)
= 6x ÷ 7 + \(\frac{1}{5}\)
= \(\frac{6}{7}\)x + \(\frac{1}{5}\)

 

Simplify each expression with two variables.
Question 13.
2x + 4x + 7y
Answer:
2x + 4x + 7y = 6x + 7y.

Explanation:
2x + 4x + 7y
= 6x + 7y.

 

Question 14.
5x + x + 3y
Answer:
5x + x + 3y = 6x + 3y.

Explanation:
5x + x + 3y
= 6x + 3y.

 

Question 15.
9x + 7x + 3y
Answer:
9x + 7x + 3y = 16x + 3y.

Explanation:
9x + 7x + 3y
= 16x + 3y.

 

Question 16.
8m – 7m – 6n
Answer:
8m – 7m – 6n = m – 6n.

Explanation:
8m – 7m – 6n
= m – 6n.

 

Question 17.
2.3a – 1.8a + 3.5b – 2.7b
Answer:
2.3a – 1.8a + 3.5b – 2.7b = 0.5a + 0.8b.

Explanation:
2.3a – 1.8a + 3.5b – 2.7b
= 0.5a + 3.5b – 2.7b
= 0.5a + 0.8b.

 

Question 18.
2.5x + 1.8z + 1.6x + 0.9z
Answer:
2.5x + 1.8z + 1.6x + 0.9z = 4.1x + 2.7z.

Explanation:
2.5x + 1.8z + 1.6x + 0.9z
= 2.5x + 1.6x + 1.8z + 0.9z
= 4.1x + 2.7z.

 

Question 19.
\(\frac{3}{5}\)a + \(\frac{2}{5}\)a + \(\frac{1}{6}\)b + \(\frac{1}{6}\)b
Answer:
\(\frac{3}{5}\)a + \(\frac{2}{5}\)a + \(\frac{1}{6}\)b + \(\frac{1}{6}\)b = a + \(\frac{1}{3}\)b.

Explanation:
\(\frac{3}{5}\)a + \(\frac{2}{5}\)a + \(\frac{1}{6}\)b + \(\frac{1}{6}\)b
= [(3 + 2)a ÷ 5] + \(\frac{1}{6}\)b + \(\frac{1}{6}\)b
= [5a ÷ 5] + \(\frac{1}{6}\)b + \(\frac{1}{6}\)b
= a +  \(\frac{1}{6}\)b + \(\frac{1}{6}\)b
= a + [(1 + 1)b ÷ 6]
= a + [2b ÷ 6]
= a + \(\frac{1}{3}\)b.

 

Question 20.
\(\frac{2}{3}\)a – \(\frac{1}{6}\)a + \(\frac{3}{5}\)b – \(\frac{3}{10}\)b
Answer:
\(\frac{2}{3}\)a – \(\frac{1}{6}\)a + \(\frac{3}{5}\)b – \(\frac{3}{10}\)b = \(\frac{1}{2}\)a  + \(\frac{3}{10}\)b.

Explanation:
\(\frac{2}{3}\)a – \(\frac{1}{6}\)a + \(\frac{3}{5}\)b – \(\frac{3}{10}\)b
LCD of 3 n 6 = 6.
= [[(2 × 2) – (1 × 1)]a ÷ 6] + \(\frac{3}{5}\)b – \(\frac{3}{10}\)b
= [(4 – 1)a ÷ 6] + \(\frac{3}{5}\)b – \(\frac{3}{10}\)b
= (3a ÷ 6) + \(\frac{3}{5}\)b – \(\frac{3}{10}\)b
= \(\frac{1}{2}\)a + \(\frac{3}{5}\)b – \(\frac{3}{10}\)b
LCD of 5 n 10 = 10.
= \(\frac{1}{2}\)a  + [[(3 × 2) – (3 × 1)]b ÷ 10]
= \(\frac{1}{2}\)a + [(6 – 3)b ÷ 10]
= \(\frac{1}{2}\)a + (3b ÷ 10)
= \(\frac{1}{2}\)a  + \(\frac{3}{10}\)b.

 

Find the perimeter of each figure.
Question 21.

Answer:
Perimeter of triangle = 18cm.

Explanation:
Perimeter of triangle = Side + side + side
= 4.8cm + 4.8cm + 8.4cm
= 9.6cm + 8.4cm
= 18cm.

 

Question 22.

Answer:
Perimeter of rectangle = 8m.

Explanation:
Perimeter of rectangle = 2(Length + Width)
= 2( \(\frac{5}{2}\)m + \(\frac{3}{2}\)m)
= 2[(5 + 3)÷2]m
= 2 (8 ÷ 2)m
= 2 × 4m
= 8m.

Question 23.
Math journal When adding or subtracting algebraic expressions, how do you identify the like terms?
Answer:
We identity the like terms if they have the same variable (or variables) with the same exponent and later do the addition or subtraction process required to solve the problem.

Explanation:
Two or more like terms are like if they have the same variable (or variables) with the same exponent. To combine like terms, we add or subtract the coefficients. The variable factors remain the same.

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 3 Lesson 3.2 Subtracting Algebraic Terms to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 3 Lesson 3.2 Answer Key Subtracting Algebraic Terms

Math in Focus Grade 7 Chapter 3 Lesson 3.2 Guided Practice Answer Key

Copy and complete to simplify each expression.

Question 1.
0.7y – 0.4y

0.7y – 0.4y =
Answer:

Explanation:
0.7y – 0.4y
= 0.3y.

 

Question 2.
1.1a – 0.2a

1.1a – 0.2a =
Answer:

Explanation:
1.1a – 0.2a
=0.9a

 

Question 3.
1.2y – y
1.2y – y =
Answer:
1.2y – y = 0.2y.

Explanation:
1.2y – y
= 0.2y.

 

Copy and complete to simplify each expression.
Question 4.
\(\frac{4}{9}\)x – \(\frac{1}{3}\)x

The LCD of \(\frac{4}{9}\) and \(\frac{1}{3}\) is .
So, x is divided into x sections.
\(\frac{4}{9}\)x – \(\frac{1}{3}\)x =
Answer:
\(\frac{4}{9}\)x – \(\frac{1}{3}\)x = \(\frac{1}{9}\)x.

Explanation:
The LCD of \(\frac{4}{9}\) and \(\frac{1}{3}\) is 9.
So, x is divided into 9  x sections.
\(\frac{4}{9}\)x – \(\frac{1}{3}\)x
= [4 – (1 × 3)]x ÷ 9
= (4 – 3)x ÷ 9
= x ÷ 9 or \(\frac{1}{9}\)x

 

Question 5.
\(\frac{3}{4}\)p – \(\frac{1}{6}\)p
\(\frac{3}{4}\)p – \(\frac{1}{6}\)p =
=
Rewrite the coefficients as fractions with denominator .
Answer:
\(\frac{3}{4}\)p – \(\frac{1}{6}\)p = \(\frac{7}{12}\)p.

Explanation:
\(\frac{3}{4}\)p – \(\frac{1}{6}\)p
LCD of 4 n 6 = 12.
= [(3 × 3) – (1 × 2)]p ÷ 12
= (9 – 2)p ÷ 12
= 7p ÷ 12 or \(\frac{7}{12}\)p

Math in Focus Course 2A Practice 3.2 Answer Key

Simplify each expression with decimal coefficients.
Question 1.
0.8y – 0.7y
Answer:
0.8y – 0.7y = 0.1y.

Explanation:
0.8y – 0.7y = 0.1y.

Question 2.
0.9x – 0.6x
Answer:
0.9x – 0.6x = 0.3x.

Explanation:
0.9x – 0.6x = 0.3x.

Question 3.
1.7p – 0.4p
Answer:
1.7p – 0.4p = 1.3p.

Explanation:
1.7p – 0.4p = 1.3p.

Question 4.
1.9h – 0.9h
Answer:
1.9h – 0.9h = 1.0h.

Explanation:
1.9h – 0.9h = 1.0h.

Question 5.
1.3m – 0.5m
Answer:
1.3m – 0.5m = 0.8m.

Explanation:
1.3m – 0.5m = 0.8m.

Question 6.
1.6n – 0.8n
Answer:
1.6n – 0.8n = 0.8n.

Explanation:
1.6n – 0.8n = 0.8n.

 

Simplify each expression with fractional coefficients.
Question 7.
\(\frac{5}{6}\)x – \(\frac{1}{6}\)x
Answer:
\(\frac{5}{6}\)x – \(\frac{1}{6}\)x = \(\frac{2}{3}\)x

Explanation:
\(\frac{5}{6}\)x – \(\frac{1}{6}\)x
= (5 – 1)x ÷ 6
= 4x ÷ 6
= 2x ÷ 3 or \(\frac{2}{3}\)x

 

Question 8.
\(\frac{7}{8}\)x – \(\frac{5}{8}\)x
Answer:
\(\frac{7}{8}\)x – \(\frac{5}{8}\)x = \(\frac{1}{4}\)x.

Explanation:
\(\frac{7}{8}\)x – \(\frac{5}{8}\)x
= (7 – 5)x ÷ 8
= 2x ÷ 8
= x ÷ 4 or \(\frac{1}{4}\)x

 

Question 9.
\(\frac{9}{5}\)x – \(\frac{1}{5}\)x
Answer:
\(\frac{9}{5}\)x – \(\frac{1}{5}\)x = \(\frac{8}{5}\)x.

Explanation:
\(\frac{9}{5}\)x – \(\frac{1}{5}\)x
= (9 – 1)x ÷ 5
= 8x ÷ 5 or \(\frac{8}{5}\)x.

 

Question 10.
\(\frac{8}{3}\)p – \(\frac{1}{3}\)p
Answer:
\(\frac{8}{3}\)p – \(\frac{1}{3}\)p = \(\frac{7}{3}\)p.

Explanation:
\(\frac{8}{3}\)p – \(\frac{1}{3}\)p
= (8 – 1)p ÷ 3
= 7p ÷ 3 or \(\frac{7}{3}\)p.

 

Simplify each expression with fractional coefficients by rewriting the fractions.
Question 11.
\(\frac{1}{4}\)a – \(\frac{1}{8}\)a
Answer:
\(\frac{1}{4}\)a – \(\frac{1}{8}\)a = \(\frac{1}{8}\)a.

Explanation:
\(\frac{1}{4}\)a – \(\frac{1}{8}\)a
= LCD of 4 n 8 = 8.
= (2 – 1)a ÷ 8
= a ÷ 8 or \(\frac{1}{8}\)a

 

Question 12.
\(\frac{5}{6}\)m – \(\frac{2}{3}\)m
Answer:
\(\frac{5}{6}\)m – \(\frac{2}{3}\)m = \(\frac{1}{6}\)m

Explanation:
\(\frac{5}{6}\)m – \(\frac{2}{3}\)m
= LCD of 6 n 3 = 6.
= [5 – (2 × 2)]m ÷ 6
= (5 – 4)m ÷ 6
= m ÷ 6 or \(\frac{1}{6}\)m

 

Question 13.
\(\frac{5}{3}\)b – \(\frac{1}{6}\)b
Answer:
\(\frac{5}{3}\)b – \(\frac{1}{6}\)b = \(\frac{1}{2}\)b.

Explanation:
\(\frac{5}{3}\)b – \(\frac{1}{6}\)b
= LCD of 3 n 6 = 6.
= [(5× 2) – 1]b ÷ 6
= (10 – 1)b ÷ 6
= 9b ÷ 6
= 3b ÷ 6
= b ÷ 2 or \(\frac{1}{2}\)b.

 

Question 14.
\(\frac{7}{4}\)x – \(\frac{1}{8}\)x
Answer:
\(\frac{7}{4}\)x – \(\frac{1}{8}\)x = \(\frac{13}{8}\)x.

Explanation:
\(\frac{7}{4}\)x – \(\frac{1}{8}\)x
LCD of 4 n 8 = 8.
= [(7 × 2) – 1]x ÷ 8
= (14 – 1)x ÷ 8
= 13x ÷ 8 or \(\frac{13}{8}\)x.

 

Question 15.
\(\frac{4}{5}\)p – \(\frac{1}{3}\)p
Answer:
\(\frac{4}{5}\)p – \(\frac{1}{3}\)p = \(\frac{2}{3}\)p.

Explanation:
\(\frac{4}{5}\)p – \(\frac{1}{3}\)p
LCD of 5 n 3 = 15.
= [(4 × 3) – (1 × 5)]p ÷ 15
= (15 – 5)p ÷ 15
= 10p ÷ 15
= 2p ÷ 3 or \(\frac{2}{3}\)p.

 

Question 16.
\(\frac{3}{4}\)r – \(\frac{2}{3}\)r
Answer:
\(\frac{3}{4}\)r – \(\frac{2}{3}\)r = \(\frac{1}{12}\)r.

Explanation:
\(\frac{3}{4}\)r – \(\frac{2}{3}\)r
LCD of 4 n 3 = 12.
= [(3 × 3) – (2 × 4)]r ÷ 12
= (9 – 8)r ÷ 12
= r ÷ 12 or \(\frac{1}{12}\)r.

 

Question 17.
\(\frac{11}{7}\)k – \(\frac{1}{2}\)k
Answer:
\(\frac{11}{7}\)k – \(\frac{1}{2}\)k = \(\frac{15}{14}\)k.

Explanation:
\(\frac{11}{7}\)k – \(\frac{1}{2}\)k
LCD of 7 n 2 = 14.
= [(11 × 2) – (1 × 7)]k ÷ 14
= (22 – 7)k ÷ 14
= 15k ÷ 14 or \(\frac{15}{14}\)k.

 

Question 18.
\(\frac{7}{4}\)d – \(\frac{3}{5}\)d
Answer:
\(\frac{7}{4}\)d – \(\frac{3}{5}\)d = \(\frac{23}{20}\)d.

Explanation:
\(\frac{7}{4}\)d – \(\frac{3}{5}\)d
LCD of 4 n 5 = 20.
= [(7 × 5) – (3 × 4)]d ÷ 20
= (35 – 12)d ÷ 20
= 23d ÷ 20 or \(\frac{23}{20}\)d.

 

Solve. Show your work.
Question 19.
Math Journal Matthew simplified the algebraic expression \(\frac{3}{2}\)x – \(\frac{1}{3}\)x as shown below.
\(\frac{3}{2}\)x – \(\frac{1}{4}\)x = \(\frac{18}{12}\)x – \(\frac{4}{12}\)x
= \(\frac{14}{12}\)x
Is Matthew’s simplification correct? Why or why not?
Answer:
Matthew’s simplification is incorrect because \(\frac{3}{2}\)x – \(\frac{1}{4}\)x  is not equal to \(\frac{18}{12}\)x – \(\frac{4}{12}\)x.

Explanation:
\(\frac{3}{2}\)x – \(\frac{1}{4}\)x
LCD of 2 n 4 = 4.
= [(3 × 2) – (1 × 1)]x ÷ 4
= (6 – 1)x ÷ 4
= 5x ÷ 4 or \(\frac{5}{4}\)x.

\(\frac{18}{12}\)x – \(\frac{4}{12}\)x
= (18 – 4)x ÷ 12
= 14x ÷ 12
= 7x ÷ 6 or \(\frac{7}{6}\)x.

\(\frac{14}{12}\)x = \(\frac{7}{6}\)x

 

Question 20.
Rectangle A, shown below, is larger than rectangle B. Write and simplify an algebraic expression that represents the difference in the areas of the two rectangles.

Answer:
Difference in the Area of rectangle A and Area of rectangle B = 11.7 square cm.

Explanation:
Area of rectangle A = Length × Width
= 4.5cm  × 3cm
= 13.5 square cm.
Area of rectangle B = Length × Width
= 0.9cm  × 2cm
= 1.8 square cm.
Difference in the Area of rectangle A and Area of rectangle B:
= 13.5 square cm – 1.8 square cm
= 11.7 square cm.

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 3 Lesson 3.1 Adding Algebraic Terms to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 3 Lesson 3.1 Answer Key Adding Algebraic Terms

Math in Focus Grade 7 Chapter 3 Lesson 3.1 Guided Practice Answer Key
Copy and complete to simplify each expression.

Question 1.
0.2y + 0.6y

0.2y + 0.6y =
Answer:
0.2y + 0.6y = 0.8y.

Explanation:

 

Question 2.
0.8p + 0.5p

0.8 p + 0.5p =
Answer:
0.8 p + 0.5p = 1.3p.

Explanation:

Question 3.
1.3g + 0.9g
1.3g + 0.9g =
Answer:
1.3g + 0.9g =  2.2g.

Explanation:
1.3g + 0.9g =  2.2g.

Copy and complete to simplify each expression.
Question 4.
x + \(\frac{3}{4}\)x

x + \(\frac{3}{4}\)x =
Answer:

Explanation:
x + \(\frac{3}{4}\)x = (4x + 3x) ÷ 4
= 7x ÷ 4 or \(\frac{7}{4}\)x

 

Question 5.
\(\frac{1}{2}\)p + \(\frac{2}{5}\)p

The LCD of \(\frac{1}{2}\) and \(\frac{2}{5}\) is .
So, p is divided into p sections.
\(\frac{1}{2}\)p + \(\frac{2}{5}\)p =
Answer:
\(\frac{1}{2}\)p + \(\frac{2}{5}\)p = \(\frac{15}{10}\)p

Explanation:
The LCD of \(\frac{1}{2}\) and \(\frac{2}{5}\) is 10.
So, p is divided into 10 p sections.
\(\frac{1}{2}\)p + \(\frac{2}{5}\)p
= [(1 ×5)p + (2 × 5)p] ÷ 10
= (5p + 10p) ÷ 10
= 15p ÷ 10 or \(\frac{15}{10}\)p

 

Simplify each expression.
Question 6.
m + \(\frac{5}{6}\)m
Answer:
m + \(\frac{5}{6}\)m = \(\frac{11}{6}\)m

Explanation:
m + \(\frac{5}{6}\)m
= (6m + 5m) ÷ 6
= 11m ÷ 6 or \(\frac{11}{6}\)m.

 

Question 7.
\(\frac{1}{4}\)x + \(\frac{2}{3}\)x
Answer:
\(\frac{1}{4}\)x + \(\frac{2}{3}\)x = \(\frac{7}{12}\)x

Explanation:
\(\frac{1}{4}\)x + \(\frac{2}{3}\)x
= LCM of 4 n 3 = 12.
\(\frac{1}{4}\)x + \(\frac{2}{3}\)x
= [(1 × 3) + (2 × 4)]x ÷ 12
= (3 + 4)x ÷ 12
= 7x ÷ 12 or \(\frac{7}{12}\)x

 

Question 8.
Math Journal In questions 5 and 7 you can multiply the two denominators to get the LCD. Does this always work? Explain.
Answer:
You can multiply the two denominators to get the LCD because there is no common factors between the denominators, so you can multiply the numbers to simplify the problem.

Explanation:
Question5:
\(\frac{1}{2}\)p + \(\frac{2}{5}\)p
LCD of 2 n 5 = 2 × 5 = 10.
Question7:
\(\frac{1}{4}\)x + \(\frac{2}{3}\)x
LCD of 4 n 3 = 4 × 3 = 12.

 

Math in Focus Course 2A Practice 3.1 Answer Key

Simplify each expression with decimal coefficients.

Question 1.
0.5y + 0.2y
Answer:
0.5y + 0.2y = 0.7y.

Explanation:
0.5y + 0.2y = 0.7y.

Question 2.
0.2x + 0.8x
Answer:
0.2x + 0.8x = 1.0x.

Explanation:
0.2x + 0.8x = 1.0x.

Question 3.
x + 0.6x
Answer:
x + 0.6x = 1.6x.

Explanation:
x + 0.6x
= 1x + 0.6x
= 1.6x.

 

Question 4.
0.4a + 1.2a
Answer:
0.4a + 1.2a = 1.6a.

Explanation:
0.4a + 1.2a = 1.6a.

Question 5.
0.7b + 0.9b
Answer:
0.7b + 0.9b = 1.6b.

Explanation:
0.7b + 0.9b = 1.6b

Question 6.
0.6m + 0.8m
Answer:
0.6m + 0.8m = 1.4m.

Explanation:
0.6m + 0.8m = 1.4m.

Question 7.
0.5k + 1.6k
Answer:
0.5k + 1.6k = 2.1k.

Explanation:
0.5k + 1.6k = 2.1k.

Question 8.
0.8a + 1.8a
Answer:
0.8a + 1.8a = 2.6a.

Explanation:
0.8a + 1.8a = 2.6a.

Simplify each expression with fractional coefficients.
Question 9.
\(\frac{1}{5}\)x + \(\frac{2}{5}\)x
Answer:
\(\frac{1}{5}\)x + \(\frac{2}{5}\)x = \(\frac{3}{5}\)x

Explanation:
\(\frac{1}{5}\)x + \(\frac{2}{5}\)x
= [(1 + 2)x] ÷ 5
= 3x ÷ 5
= \(\frac{3}{5}\)x

Question 10.
\(\frac{3}{7}\)p + \(\frac{2}{7}\)p
Answer:
\(\frac{3}{7}\)p + \(\frac{2}{7}\)p = \(\frac{5}{7}\)p

Explanation:
\(\frac{3}{7}\)p + \(\frac{2}{7}\)p
= [(3 + 2)p] ÷ 7
= 5p ÷ 7
= \(\frac{5}{7}\)p

Question 11.
\(\frac{5}{8}\)m + \(\frac{7}{8}\)m
Answer:
\(\frac{5}{8}\)m + \(\frac{7}{8}\)m = \(\frac{3}{2}\)m

Explanation:
\(\frac{5}{8}\)m + \(\frac{7}{8}\)m
= (5 + 7)m ÷ 8
= 12m ÷ 8
= 6m ÷ 4
= 3m ÷ 2
= \(\frac{3}{2}\)m

Question 12.
\(\frac{4}{9}\)n + \(\frac{7}{9}\)n
Answer:
\(\frac{4}{9}\)n + \(\frac{7}{9}\)n = \(\frac{13}{9}\)n.

Explanation:
\(\frac{4}{9}\)n + \(\frac{7}{9}\)n
= (4 + 9)n ÷ 9
= 13n ÷ 9
= \(\frac{13}{9}\)n

Simplify each expression with fractional coefficients by rewriting the fractions.
Question 13.
\(\frac{1}{6}\)a + \(\frac{1}{3}\)a
Answer:
\(\frac{1}{6}\)a + \(\frac{1}{3}\)a = \(\frac{1}{2}\)a

Explanation:
\(\frac{1}{6}\)a + \(\frac{1}{3}\)a
= LCD of 6 n 3 = 3.
= (1 + 2)a ÷ 6
= 3a ÷ 6
= a ÷ 2 or \(\frac{1}{2}\)a

 

Question 14.
\(\frac{1}{2}\)k + \(\frac{3}{8}\)k
Answer:
\(\frac{1}{2}\)k + \(\frac{3}{8}\)k =

Explanation:
\(\frac{1}{2}\)k + \(\frac{3}{8}\)k
= LCD of 2 n 8 = 8.
= (4 + 3)k ÷ 8
= 7k ÷ 8 or  \(\frac{7}{8}\)k

 

Question 15.
\(\frac{2}{5}\)p + \(\frac{7}{10}\)p
Answer:
\(\frac{2}{5}\)p + \(\frac{7}{10}\)p = \(\frac{11}{10}\)p

Explanation:
\(\frac{2}{5}\)p + \(\frac{7}{10}\)p
= LCD of 5 n 10 = 10.
= [(2 ×2) + 7]p ÷ 10
= (4 + 7)p ÷ 10
= 11p ÷ 10 or \(\frac{11}{10}\)p

 

Question 16.
\(\frac{7}{9}\)r + \(\frac{2}{3}\)r
Answer:
\(\frac{7}{9}\)r + \(\frac{2}{3}\)r = \(\frac{13}{9}\)r

Explanation:
\(\frac{7}{9}\)r + \(\frac{2}{3}\)r
= LCD of 9 n 3 = 9.
= [7 + (2 × 3)]r ÷ 9
= (7 + 6)r ÷ 9
= 13r ÷ 9 or \(\frac{13}{9}\)r

 

Question 17.
\(\frac{1}{4}\)a + \(\frac{1}{3}\)a
Answer:
\(\frac{1}{4}\)a + \(\frac{1}{3}\)a = \(\frac{7}{12}\)a

Explanation:
\(\frac{1}{4}\)a + \(\frac{1}{3}\)a
= LCD of 4 n 3 = 12.
= [(1 × 3) + (1 × 4)]a ÷12
= (3 + 4)a ÷ 12
= 7a ÷ 12 or \(\frac{7}{12}\)a

 

Question 18.
\(\frac{1}{2}\)x + \(\frac{2}{5}\)x
Answer:
\(\frac{1}{2}\)x + \(\frac{2}{5}\)x = \(\frac{9}{10}\)x

Explanation:
\(\frac{1}{2}\)x + \(\frac{2}{5}\)x
= LCD of 2 n 5 = 10.
= [(1 × 5) + (2 × 2)]x ÷ 10
= (5 + 4)x ÷ 10
= 9x ÷ 10 or \(\frac{9}{10}\)x

 

Question 19.
\(\frac{3}{5}\)p + \(\frac{3}{4}\)p
Answer:
\(\frac{3}{5}\)p + \(\frac{3}{4}\)p = \(\frac{27}{20}\)p

Explanation:
\(\frac{3}{5}\)p + \(\frac{3}{4}\)p
= LCD of 5 n 4 = 20.
= [(3 × 4) + (3 × 5)]p ÷ 20
= (12 + 15)p ÷ 20
= 27p ÷ 20 or \(\frac{27}{20}\)p

 

Question 20.
\(\frac{4}{5}\)y + \(\frac{1}{3}\)y
Answer:
\(\frac{4}{5}\)y + \(\frac{1}{3}\)y = \(\frac{17}{15}\)y

Explanation:
\(\frac{4}{5}\)y + \(\frac{1}{3}\)y
= LCD of 5 n 3 = 15.
= [(4 × 3) + (1 × 5)]y ÷ 15
= (12 + 5)y ÷ 15
= 17y ÷ 15 or \(\frac{17}{15}\)y

 

Solve. Show your work.
Question 21.
The figures show rectangle A and rectangle B. Write and simplify an algebraic expression for each of the following.
a) The perimeter of rectangle A.
Answer:
Perimeter of rectangle A = \(\frac{28}{3}\)m

Explanation:

Perimeter of rectangle A = 2(Length + Width)
= 2(\(\frac{2}{3}\)m + 4m)
= 2[(2 + 12)m ÷ 3]
= 2(14m ÷ 3)
= 28m ÷ 3 or \(\frac{28}{3}\)m

 

b) The perimeter of rectangle B.
Answer:
Perimeter of rectangle B = \(\frac{35}{9}\)m

Explanation:

Perimeter of rectangle B = 2(Length + Width)
= 2(1.5m + \(\frac{4}{9}\)m)
= 2[(1.5 × 9) + 4)m ÷ 9]
= 2[(13.5 + 4) ÷ 9]m
= 2(17.5m ÷ 9)
= 35m ÷ 9 or \(\frac{35}{9}\)m

 

c) The sum of the perimeters of the two rectangles.

Answer:
Sum of the perimeters of the two rectangles = \(\frac{119}{9}\)m.

Explanation:
Perimeter of rectangle A = \(\frac{28}{3}\)m
Perimeter of rectangle B = \(\frac{35}{9}\)m
Sum of Perimeter of rectangle A n Perimeter of rectangle B
= \(\frac{28}{3}\)m + \(\frac{35}{9}\)m
LCD of 3 n 9 = 9.
= [(28 × 3) + (35 × 1)]m ÷ 9
= (84 + 35)m ÷ 9
= 119m ÷ 9 or \(\frac{119}{9}\)m

 

Question 22.
The length and width of two rectangular gardens are shown. Find the sum of the areas of the two gardens in simplest form.

Answer:
Sum of the areas of the two gardens = 13.1y ft.

Explanation:
Area of rectangular garden 1 = Length × Width
= 2y ft × 3.3 ft
= 6.6y square ft.
Area of rectangular garden 2 = Length × Width
= 5y ft × 1.3y ft
= 6.5y square ft.
Sum of Area of rectangular garden 1 and Area of rectangular garden 2
= 6.6y square ft + 6.5y square ft
= 13.1y square ft.

 

Question 23.
Math Journal James and Evan simplified the same algebraic expression. Their work is shown.

Describe a method each person might have used to get his answer. Which method do you prefer? Why?
Answer:
Both the method are easy to solve. I would like to prefer to simplified method.

Explanation:
James algebraic expression: Simplified method
\(\frac{1}{5}\)x + 0.3x = \(\frac{1}{2}\)x.
Evan algebraic expression: Fractional method
\(\frac{1}{5}\)x + 0.3x = 0.5x.

 

Question 24.
Which of the following expressions has a greater value if y is a positive number? Explain your reasoning.

Answer:
1.4y + \(\frac{2}{5}\)y has a greater value if y is a positive number.

Explanation:
Expression 1:
1.4y + \(\frac{2}{5}\)y
If y = 1.
= (1.4 × 1) + \(\frac{2}{5}\) × 1
= 1.4 + \(\frac{2}{5}\)
= [(1.4 × 5) + 2] ÷ 5
= (7 + 2) ÷ 5
= 9 ÷ 5 or \(\frac{9}{5}\)
= 1.8.
Expression 2:
\(\frac{1}{3}\)y + \(\frac{3}{4}\)y
If  y = 1.
= [\(\frac{1}{3}\) × 1] + \(\frac{3}{4}\) × 1
=  \(\frac{1}{3}\) + \(\frac{3}{4}\)
LCD of 3 n 4 = 12.
= [(1 × 4) + (3 × 3)] ÷ 12
= (4 + 9) ÷ 12
= 13 ÷ 12 or \(\frac{13}{12}\)
= 1.08.

Question 25.
A restaurant serves x meals of chicken quarters daily and makes soup each day using \(\frac{1}{2}\) of a chicken. The chef expresses the number of chickens she uses each 1 1 day as \(\frac{1}{4}\)x + \(\frac{1}{2}\). How many chickens does she use in three days?
Answer:
Amount of chicken used in 3 days = 9x ÷ 4. or \(\frac{9}{4}\)x

Explanation:
A restaurant serves x meals of chicken quarters daily.
makes soup each day using \(\frac{1}{2}\) of a chicken.
=> Amount of soup each day used  = \(\frac{1}{2}\)  × x = \(\frac{1}{2}\).
Amount of chicken used daily = \(\frac{1}{4}\)x + \(\frac{1}{2}\).
Number of days = 3.
Amount of chicken used in 3 days = Amount of chicken used daily × Number of days
= [\(\frac{1}{4}\)x + \(\frac{1}{2}\)] × 3
= LCD of 4 n 2 = 4.
= [[(1 × 1)x + (1 × 2)] ÷ 4 ] × 3
= [(1x + 2x) ÷ 4]× 3
= (3x ÷ 4) × 3
= 9x ÷ 4.

 

Question 26.
Mary simplified the algebraic expression \(\frac{2}{3}\)x + \(\frac{1}{4}\)x as shown below.

Describe and correct the error Mary made.
Answer:
Mary did not take the LCD and solved the problem, that is her error.
\(\frac{2}{3}\)x + \(\frac{1}{4}\)x = \(\frac{11}{12}\)x.

Explanation:
\(\frac{2}{3}\)x + \(\frac{1}{4}\)x
= LCD of 3 n 4 = 12.
= [(2 ×4)x + (1 × 3)x] ÷ 12
= (8x + 3x) ÷ 12
= 11x ÷ 12 or \(\frac{11}{12}\)x

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 3 Algebraic Expressions to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 3 Answer Key Algebraic Expressions

Math in Focus Grade 7 Chapter 3 Quick Check Answer Key

Consider the algebraic expression 3x + 4. State the following.

Question 1.
How many terms are there?
Answer:
Two terms are there.

Explanation:
Algebraic expression : 3x + 4

Question 2.
State the coefficient of the algebraic term.
Answer:
3 is coefficient of the algebraic term.

Explanation:
A coefficient is an integer that is written along with a variable or it is multiplied by the variable. In other words, a coefficient is the numerical factor of a term containing constant and variables.
In the term 3x + 4, 3 is the coefficient.

Question 3.
What is the constant term?
Answer:
4 is the constant term in 3x + 4.

Explanation:
A constant term is a term in an algebraic expression that does not contain any variables and therefore is constant.

Question 4.
Write the operation symbol.
Answer:
Addition (+) is the operation symbol in 3x + 4.

Explanation:
The symbol indicating a math operation is an operator symbol.

 

Question 5.
Complete the table.

Answer:

Explanation:
When x = 0:
7x = 7 × 0 = 0.
5x – 2 = 5(0) – 2 = 0 – 2 = – 2.

When x = 2:
x + 9 = 2 + 9 = 11.
7x = 7 × 2 = 14.
5x – 2 = 5(2) – 2 = 10 – 2 = 8.

When x = -1:
x + 9 = -1 + 9 = 8.
7x = 7 × -1 = -7.
5x – 2 = 5(-1) – 2 = -5 – 2 = -7.

When x = 7:
x + 9 = 7 + 9 = 16.
7x = 7 × 7 = 49.
5x – 2 = 5(7) – 2 = 35 – 2 = 33.

 

State whether each expression can be simplified. Explain your reasoning.
Question 6.
2k – 3 + k
Answer:
2k – 3 + k = 3(k – 1).

Explanation:
2k – 3 + k
= 3k – 3
= 3(k – 1)

Question 7.
7x + 3 – 3y
Answer:
7x + 3 – 3y = 7x + 3(1 – y).

Explanation:
7x + 3 – 3y
= 7x + 3(1 – 1y)
= 7x + 3(1 – y)

Question 8.
6u + 5w – 1
Answer:
6u + 5w – 1 cannot be simplified further as there is no common terms.

Explanation:
6u + 5w – 1
= 6u + 5w – 1.

Question 9.
4g – 3g – g
Answer:
4g – 3g – g = 0.

Explanation:
4g – 3g – g
= g(4 – 3 – 1)
= g(1 – 1)
= g (0)
= 0.

Simplify each expression.
Question 10.
4t + 1 + 6
Answer:
4t + 1 + 6 = 4t + 7.

Explanation:
4t + 1 + 6
= 4t + 7.

Question 11.
5p – 5p
Answer:
5p – 5p = 0.

Explanation:
5p – 5p
= 5p(1 – 1)
= 5p(0)
= 0.

Question 12.
4y + 5y + 3
Answer:
4y + 5y + 3 = 7y + 3.

Explanation:
4y + 5y + 3
= y(4 + 3) + 3
= y(7) + 3
= 7y + 3.

Question 13.
4m – 3m – 3
Answer:
4m – 3m – 3 = m – 3.

Explanation:
4m – 3m – 3
= m(4 – 3) – 3
= m(1) – 3
= m – 3.

Expand each expression.
Question 14.
4(h + 2)
Answer:
4(h + 2) = 4h + 8.

Explanation:
4(h + 2)
= 4h + 8.

Question 15.
5(4 + 5c)
Answer:
5(4 + 5c) = 20 + 25c.

Explanation:
5(4 + 5c)
= 20 + 25c.

Question 16.
3(4x – 11)
Answer:
3(4x – 11) = 12x – 33.

Explanation:
3(4x – 11)
= 12x – 33.

Question 17.
7(3 – 5p)
Answer:
7(3 – 5p) = 21 – 35p.

Explanation:
7(3 – 5p)
= 21 – 35p.

Factor each expression.
Question 18.
6m + 3
Answer:
6m + 3 = 3(2m + 1).

Explanation:
6m + 3
= 3(2m + 1)

Question 19.
4v + 14
Answer:
4v + 14 = 2(2v + 7).

Explanation:
4v + 14
= 2(2v + 7)

Question 20.
10p – 2
Answer:
10p – 2 = 2(5p – 1).

Explanation:
10p – 2
= 2(5p – 1)

Question 21.
6 – 18c
Answer:
6 – 18c = 6(1 – 3c).

Explanation:
6 – 18c
= 6(1 – 3c).

Choose an equivalent expression.
Question 22.
6y – 3 is equivalent to
a) 3(3y – 1)
b) 3(2y – 1)
c) 3(2y – 3)
d) 6(3y – 1)
Answer:
6y – 3 is equivalent to 3(2y – 1).
b) 3(2y – 1).

Explanation:
a. 3(3y – 1) = 9y – 3.
b. 3(2y – 1) = 6y – 3.
c. 3(2y – 3) = 6y – 9.
d. 6(3y – 1) = 18y – 6.

 

x is an unknown number. Write an expression for each of the following.
Question 23.
7 more than the number
Answer:
Expression = x + 7.

Explanation:
x is an unknown number.
7 more than the number
=> x + 7.

Question 24.
Product of 8 and the number
Answer:
Expression = 8x.

Explanation:
Product of 8 and the number.
=> 8 × x= 8x.

Question 25.
5 less than twice the number
Answer:
Expression = 2x – 5.

Explanation:
5 less than twice the number.
=> 2x – 5.

Question 26.
3 more than half the number
Answer:
Expression = 3 + (x ÷ 2).

Explanation:
3 more than half the number.
=> 3 + (x ÷ 2)

Go through the Math in Focus Grade 7 Workbook Answer Key Cumulative Review Chapters 1-2 to finish your assignments.

Math in Focus Grade 7 Course 2 A Cumulative Review Chapters 1-2 Answer Key

Concepts and Skills

Write each number as \(\frac{m}{n}\) in simplest form, where m and n are integers with n ≠ 0. (Lesson 1.1)

Question 1.
-0.87
Answer:
0.87 can be written in the \(\frac{m}{n}\) form as –\(\frac{87}{100}\)

Question 2.
12.8
Answer:
12.8 can be written in the \(\frac{m}{n}\) form as \(\frac{128}{10}\) or \(\frac{64}{5}\)

Question 3.
-1.9
Answer:
-1.9 can be written in the \(\frac{m}{n}\) form as \(\frac{-19}{10}\)

Using long division, write each rational number as a terminating or a repeating decimal. Identify a pattern of repeating digits using bar notation. (Lesson 1.2)

Question 4.
\(\frac{9}{5}\)
Answer: \(1 . \overline{8}\)

Question 5.
\(\frac{23}{16}\)
Answer: 1.4375 it is a terminating decimal

Question 6.
–\(\frac{51}{110}\)
Answer: \(0 . 46\overline{36}\)

Use a calculator. Locate each irrational number to 2 decimal places on the number line using rational approximations. (Lesson 1.3)

Question 7.
\(\sqrt{44}\)
Answer: 6.63

Question 8.
\(\sqrt{132}\)
Answer: 11.48

Question 9.
–\(\sqrt{162}\)
Answer: 12.72

Question 10.

Answer: 4.64

Question 11.
\(\frac{\pi}{7}\)
Answer: 0.44

Question 12.
π³
Answer: 30.95

Order the real numbers below from greatest to least using the symbol >. (Lesson 1.4)

Question 13.
\(\sqrt{345}\), \(\frac{244}{7}\), , –\(\frac{86}{3}\), 33.9
Answer:\(\frac{244}{7}\) > 33.9> \(\sqrt{345}\)>>-\(\frac{86}{3}\)

Round each number to the given number of significant digits. (Lesson 1.5)

Question 14.
349,950 (to 4 significant digits)
Answer: 350000

Question 15.
0.09608 (to 3 significant digits)
Answer: 0.0961

Evaluate each expression. (Lessons 2.1, 2.2)

Question 16.
7 + (-12)
Answer:
7 – 12 = -5

Question 17.
-15 + (-20)
Answer:
-15 – 20 = -35

Question 18.
-8 + 6 – 4
Answer:
– 8 – 4 + 6
-12 + 6 = -6

Question 19.
11 – (-14)
Answer:
11 – (-14)
– × – = +
11 + 14 = 25

Question 20.
32 – (-17)
Answer:
32 – (-17)
– × – = +
32 + 17 = 39

Question 21.
-7 – 5 – (-6)
Answer:
-7 – 5 – (-6)
-7 – 5 + 6
-12 + 6 = -6

Question 22.
-250 + 480
Answer:
-250 + 480
480 – 250 = 230
The greatest value has a positive sign so put a positive sign to the obtained answer.
-250 + 480 = 230

Question 23.
-109 – (-121)
Answer:
-109 – (-121)
-109 + 121
The greatest value has a positive sign so put a positive sign to the obtained answer.
121 – 109 = 12

Question 24.
43 + (-95) – (-16)
Answer:
43 + (-95) – (-16)
43 – 95 + 16
43 + 16 – 95 = -36

Evaluate each product or quotient. As needed, give your answer in simplest form. (Lessons 2.3, 2.5)

Question 25.
-12.8
Answer:
– × + = –
12 × 8 = 96
Put negative sign to the obtained answer.
We get -96

Question 26.
\(\frac{2}{15} \cdot\left(-\frac{5}{8}\right)\)
Answer:
– × + = –
\(\frac{2}{15}\) × –\(\frac{5}{8}\) = –\(\frac{10}{120}\) = \(\frac{1}{12}\)

Question 27.
\(2 \frac{2}{5} \cdot\left(-1 \frac{1}{4}\right)\)
Answer:
– × + = –
2\(\frac{2}{5}\) × -1\(\frac{1}{4}\)
\(\frac{12}{5}\) × –\(\frac{5}{4}\)
= –\(\frac{60}{20}\)
= -3

Question 28.
-9 ÷ (-7)
Answer:
Cancel – by –
9 ÷ 7 = 1.28

Question 29.
\(-\frac{7}{16} \div\left(-\frac{21}{6}\right)\)
Answer:
Given,
\(\frac{7}{16}\) × –\(\frac{21}{6}\)
= \(\frac{7}{16}\) × –\(\frac{7}{2}\)
= –\(\frac{49}{32}\)

Question 30.

Answer:
–\(\frac{3}{4}\) × 2\(\frac{1}{4}\)
= –\(\frac{3}{4}\) × \(\frac{9}{4}\)
= – \(\frac{27}{16}\)

Evaluate each expression. (Lessons 2.3, 2.4, 2.5, 2.6)

Question 31.
-3 • 12 – (-6) + 2(-7) ÷ 7
Answer:
-3 • 12 – (-6) + 2(-7) ÷ 7
((-3) 12) – (-6) + ((2 * (-7)/7))
= -32

Question 32.
\(\frac{2}{3}\) • \(\frac{1}{6}\) + 1\(\frac{5}{9}\) + 2\(\left(-\frac{7}{18}\right)\)
Answer:
Given,
\(\frac{2}{3}\) • \(\frac{1}{6}\) + 1\(\frac{5}{9}\) + 2\(\left(-\frac{7}{18}\right)\)
\(\frac{2}{18}\) + \(\frac{14}{9}\) – \(\frac{43}{18}\)
– \(\frac{41}{18}\) + \(\frac{14}{9}\)
= – \(\frac{41}{18}\) + \(\frac{28}{18}\)
= –\(\frac{13}{18}\)

Question 33.
-4 • 5.2 – 0.5• (-7.8) + 2 • 1.3
Answer: -14.3

Question 34.
–\(\frac{1}{5}\) [-20 + 1.2(-3)] + 1\(\frac{2}{5}\)
Answer:
Given,
–\(\frac{1}{5}\) [-20 + 1.2(-3)] + 1\(\frac{2}{5}\)
–\(\frac{1}{5}\) [-20 – 3.6] + 1\(\frac{2}{5}\)
–\(\frac{1}{5}\) [-23.6] + 1\(\frac{2}{5}\)
4.72 + \(\frac{7}{5}\)
4.72 + 1.4
= 6.12

Problem Solving

Solve. Show your work.

Question 35.
An athlete completes a 400-meter dash in 46.3 seconds. What is his speed in meters per second correct to 3 significant digits? (Chapter 1)
Answer:
An athlete completes a 400-meter dash in 46.3 seconds.
400/46.3
8.639
8.64 m/s

Question 36.
The greatest and least temperatures ever recorded in Tim’s hometown are 101°F and -36°F. Find the difference between these two temperatures. (Chapter 2)
Answer:
Given,
The greatest and least temperatures ever recorded in Tim’s hometown are 101°F and -36°F.
101°F – (-36°F)
= 101°F + 36°F
= 137°F

Question 37.
On a math quiz consisting of 100 questions, the teacher gives 2 points for a correct answer, -1 point for an incorrect answer, and -2 points for not answering a question at all. (Chapter 2)
a) Emily answered 75 questions correctly, 18 incorrectly, and did not answer 7 questions. What is her score?
Answer:
75 × 2 = 150
18 × -1 = -18
7 × -2 = -14
150 -18 – 14
150 – 32 = 118
Thus the score of Emily is 118

b) Amy answered 30 questions correctly and 62 incorrectly. What is her score?
Answer:
30 × 2 = 60
62 × – 1 = -62
60 – 62 = -2
Amy score is -2

Question 38.
Justin dug a hole that was 9\(\frac{1}{2}\) inches deep. His sister Jean built a sand castle next to the hole that was 12\(\frac{3}{4}\) inches high. Show how you could use subtraction to find the vertical distance from the top of the castle to the bottom of the hole. (Chapter 2)
Answer:
Justin dug a hole that was 9\(\frac{1}{2}\) inches deep.
His sister Jean built a sand castle next to the hole that was 12\(\frac{3}{4}\) inches high.
12\(\frac{3}{4}\) – 9\(\frac{1}{2}\)
12 – 9 = 3
\(\frac{3}{4}\) – \(\frac{1}{2}\)  = \(\frac{1}{4}\)
= 3\(\frac{1}{4}\) inches

Question 39.
Rick started his hike at an elevation of 8,975 feet. He descended at a constant rate of 8.5 feet per minute for 45 minutes. Find Rick’s elevation after 45 minutes. Give your answer to 4 significant digits. (Chapters 1, 2)
Answer:
Given,
Rick started his hike at an elevation of 8,975 feet.
He descended at a constant rate of 8.5 feet per minute for 45 minutes.
8.5 × 45 = 382.5 feet
8975 feet – 382.5 feet = 8592.5 feet
8593 feet

Question 40.
A car travels’at 68\(\frac{2}{3}\) miles per hour for 2\(\frac{1}{12}\) hours. Find the distance that the car has traveled correct to 3 significant digits. (Chapters 1, 2)
Answer: 68\(\frac{2}{3}\) × 2\(\frac{1}{12}\)
= 143 \(\frac{1}{18}\)
= 143.055

Question 41.
In a particular town, the temperature at midnight is -2°C. It rises at a steady rate for 12 hours to reach a temperature of 22°C at noon. (Chapter 2)
a) Find the difference between the temperature at noon and at midnight.
Answer: 24°C

b) Find the temperature at 7 A.M.
Answer: 12°C

c) Find the time when the temperature is 4°C.
Answer: 3 A.M.

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 2 Review Test to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 2 Review Test Answer Key

Concepts and Skills

Evaluate each sum or difference.

Question 1.
-6 + 14
Answer:
If the signs are different we have to subtract the numbers.
14 – 6 = 8
Thus -6 + 14 = 8

Question 2.
-25 + (-9)
Answer:
If the signs are same then you have to add the numbers.
-25 – 9 = -34

Question 3.
52 + (-52)
Answer:
52 – 52 = 0

Question 4.
46 + (-17) + 38
Answer:
46 + 38 – 17
84 – 17 = 67

Question 5.
-80 + 63 + (-24)
Answer:
First, arrange all the negative signs in one place
-80 – 24 + 63
Here greatest value has a negative sign so the results will be negative.
-124 + 63 = -61

Question 6.
35 – 140
Answer:
Given,
35 – 140
140 – 35 = 105
Here greatest value has a negative sign so the results will be negative i.e., -105.

Question 7.
-61 – 28
Answer:
Given,
-61 – 28
If the signs are the same then you have to add the numbers.
61 + 28 = 89
-61 – 28 = -89

Question 8.
128 – (-73)
Answer:
Given,
128 – (-73)
128 + 73 = 201

Question 9.
-8 – (-50)
Answer:
Given,
-8 – (-50)
-8 + 50
50 – 8 = 42

Question 10.
\(\frac{1}{4}\) – \(\frac{7}{8}\)
Answer:
Given,
\(\frac{1}{4}\) – \(\frac{7}{8}\)
Here the denominators of both the fractions are not same.
The LCM of 4 and 8 is 8.
\(\frac{2}{8}\) – \(\frac{7}{8}\)
(2-7)/8 = – \(\frac{5}{8}\)

Question 11.
14\(\frac{2}{3}\) – 8\(\frac{4}{5}\)
Answer:
Given,
14\(\frac{2}{3}\) – 8\(\frac{4}{5}\)
14 – 8 = 6
Now subtract the fractions
\(\frac{2}{3}\) – \(\frac{4}{5}\)
Here the denominators of both the fractions are not same.
LCM of 3 and 5 is 15.
\(\frac{10}{15}\) – \(\frac{12}{15}\) = – \(\frac{2}{15}\)

Question 12.
-6\(\frac{1}{7}\) + 3\(\frac{5}{14}\)
Answer:
Given,
-6\(\frac{1}{7}\) + 3\(\frac{5}{14}\)
– 6 + 3 = -3
\(\frac{5}{14}\) – \(\frac{1}{7}\)
Here the denominators of both the fractions are not same.
LCM of 14 and 7 is 14.
\(\frac{5}{14}\) – \(\frac{2}{14}\) = \(\frac{3}{14}\)
-3 + \(\frac{3}{14}\) = -2\(\frac{11}{14}\)

Evaluate each product or quotient.

Question 13.
-5 • 11
Answer:
Given,
-5 • 11
minus × plus = minus
So, the result will be negative
-5 × 11 = -55

Question 14.
-30 • (-4)
Answer:
Given,
-30 • (-4)
minus × minus = plus
30 × 4 = 120

Question 15.
144 ÷ (-6)
Answer:
Given,
144 ÷ (-6)
144 ÷ 6 = 24
Put negative sign to the obtained answer.
144 ÷ (-6) = -24

Question 16.
-48 ÷ (-3)
Answer:
Given,
-48 ÷ (-3)
First cancel the negative signs
We get
48 ÷ 3 = 16
Thus -48 ÷ (-3) = 161

Question 17.
-126 ÷ 9
Answer:
Given,
-126 ÷ 9
Remove the negative sign and perform division operation
126 ÷ 9 = 14
Put a negative sign to the obtained answer.
-126 ÷ 9 = -14

Question 18.
104 ÷ (-8)
Answer:
Given,
104 ÷ (-8)
Remove the negative sign and perform division operation
104 ÷ 8 = 13
Put a negative sign to the obtained answer.
104 ÷ (-8) = -13

Question 19.
–\(\frac{5}{8}\) • \(\frac{8}{15}\)
Answer:
Given,
–\(\frac{5}{8}\) • \(\frac{8}{15}\)
Cancel 8 and 8 we get 1 and cancel 5 by 15 we get 3.
So, the answer is –\(\frac{1}{3}\)

Question 20.
–\(\frac{3}{4}\) • \(\left(-1 \frac{2}{3}\right)\)
Answer:
Given,
–\(\frac{3}{4}\) • 1 \(\frac{2}{3}\)
–\(\frac{3}{4}\) • 1 \(\frac{2}{3}\) = –\(\frac{3}{4}\) × \(\frac{5}{3}\)
–\(\frac{3}{4}\) × \(\frac{5}{3}\) = \(\frac{15}{12}\) = \(\frac{5}{4}\)
\(\frac{5}{4}\) can be written as 1 \(\frac{1}{4}\)

Question 21.
5\(\frac{1}{4}\) ÷ \(\left(-\frac{7}{12}\right)\)
Answer:
Given,
5\(\frac{1}{4}\) ÷ \(\left(-\frac{7}{12}\right)\)
\(\frac{21}{4}\) ÷ –\(\frac{7}{12}\)
= (21 × 12)/(4 × 7)
= -252/28
= -9
5\(\frac{1}{4}\) ÷ \(\left(-\frac{7}{12}\right)\) = -9

Question 22.
-4\(\frac{4}{5}\) ÷ 1\(\frac{1}{3}\)
Answer:
Given,
-4\(\frac{4}{5}\) ÷ 1\(\frac{1}{3}\)
\(\frac{24}{5}\) ÷ \(\frac{4}{3}\)
= (24 × 3)/(5 × 4)
= 72/20
= 3 \(\frac{3}{5}\)

Question 23.

Answer:
Given,

First cancel the negative signs
\(\frac{2}{5}\) ÷ \(\frac{8}{15}\)
(2 × 15) ÷ (5 × 8)
30 ÷ 40
= 3/4

Question 24.

Answer:
Given,

\(\frac{10}{3}\) ÷ \(\frac{20}{9}\)
(10 × 9)/(3 × 20)
90/60 = 9/6 = 3/2
1 \(\frac{1}{2}\)

Evaluate each expression.

Question 25.
12.3 – 8.1 + 2\(\frac{1}{10}\) • 0.4 – 1.6
Answer:
Given,
12.3 – 8.1 + 2\(\frac{1}{10}\) • 0.4 – 1.6
4.2 + \(\frac{21}{10}\) × \(\frac{4}{10}\) – 1.6
4.2 + \(\frac{82}{10}\) – 1.6
4.2 + 8.2 – 1.6
12.4 – 1.6 = 10.8

Question 26.
(25.7 + 4) ÷ 3 + 0.82
Answer:
Given,
(25.7 + 4) ÷ 3 + 0.82
29.4 ÷ 3 + 0.82
9.8 + 0.82 = 10.62

Question 27.
10 – 32.86 ÷ 5.3 + 7\(\left(\frac{81}{100}\right)\)
Answer:
Given,
10 – 32.86 ÷ 5.3 + 7\(\left(\frac{81}{100}\right)\)
10 – 32.86 ÷ 5.3 + 7(0.81) = 9.47

Question 28.
3.25(0.9 – 0.74) + 6.3
Answer:
Given,
3.25(0.9 – 0.74) + 6.3
3.25 (0.16) + 6.3
= 0.52 + 6.3
= 6.82

Question 29.

Answer:
Given,

\(\frac{1}{3}\) – \(\frac{1}{4}\)
LCM of 3 and 4 is 12
\(\frac{4}{12}\) – \(\frac{3}{12}\) = \(\frac{1}{12}\)
\(\frac{1}{8}\) + \(\frac{1}{2}\)
LCM of 8 and 2 is 8
\(\frac{1}{8}\) + \(\frac{4}{8}\) = \(\frac{5}{8}\)
\(\frac{1}{12}\) ÷ \(\frac{5}{8}\)
(1 × 8)/(12 × 5)
\(\frac{8}{60}\)
= \(\frac{2}{15}\)

Question 30.

Answer:
Given,

–\(\frac{1}{6}\) ÷ \(\frac{5}{18}\)
= –\(\frac{3}{5}\)
8.5 – (-\(\frac{3}{5}\))
\(\frac{85}{10}\) + \(\frac{3}{5}\)
LCM of 10 and 5 is 10.
\(\frac{85}{10}\) + \(\frac{6}{10}\) = \(\frac{91}{10}\) = 9.1

Problem Solving

Solve. Show your work.

Question 31.
When you wake up on Monday, the temperature is -18°F. During the day, the temperature rises 13°F. By the time you wake up on Tuesday, it has dropped 19°F. What is the temperature when you wake up on Tuesday?
Answer:-24°F.

Question 32.
Tim dug a hole that was 16\(\frac{1}{2}\) inches deep. He left a pile of dirt next to the hole that was 8\(\frac{3}{4}\) inches high. Show how you could use subtraction to find the distance from the top of the pile of dirt to the bottom of the hole.
Answer:
Given,
Length of the hole = 16\(\frac{1}{2}\) inches
Length of the dirt = 8\(\frac{3}{4}\) inches
The distance between the top of the pile to the bottom of the hole = ?
Since the dirt is beside the hole and not inside the hole, we can find it’s length using addition.
Distance from the top to the bottom = length of dirt + length of the hole
Length of dirt = 8×\(\frac{3}{4}\) = 6 inches
Length of the hole = 16 × \(\frac{1}{2}\) = 8 inches
Distance from the top of the dirt to the bottom of the hole = (6 + 8) inches
Distance from the top of the dirt to the bottom of the hole = 14 inches
Distance left = length of hole – length of dirt
Distance left = 8 – 6 = 2 inches

Question 33.
Daniel bought four bags of potatoes. The weight of the first bag was 2.6 pounds. The second bag weighed 0.4 pound less than twice the weight of the first bag. The third bag weighed 0.6 pound more than the first bag. The fourth bag weighed 0.3 pound less than the weight of the second bag. What is the average weight of the bags of potatoes that Daniel bought? Round your answer to the nearest tenth.
Answer:
Given,
Weight of the first bag = 2.6 pounds
Weight of the second bag is 0.4 pounds less than twice the weight of the first bag.
W2 = 2W1 – 0.4 = 2(2.6 – 0.4) = 5.2 – 0.4 = 4.8 pounds
Weight of the third bag is 0.6 pounds more than that of the first bag.
W3 = W1 + 0.6 = 2.6 + 0.6 = 3.2 pounds
Weight of the fourth bag is 0.3 pounds less than that of the second bag.
W4 = W2 – 0.3 = 4.8 – 0.3 = 4.5 pounds
Therefore, the average weight of the bags of potatoes is given as the sum of all the weights and then divide the sum by 4.
Average weight = (W1 + W2 + W3 + W4)/4
= (2.6 + 4.8 + 3.2 + 4.5)/4
= 15.1/4
= 3.775

Question 34.
A hiker descended 320 feet in 40 minutes. Find the hiker’s average change in elevation per minute.
Answer:
Given,
A hiker descended 320 feet in 40 minutes.
We have to find,
The hiker’s average change in elevation per minute.
According to the question.
We know that average speed is defined as distance divided by time.
Therefore,
Speed = Distance/Time
Here, the value of the distance is 320 feet and the value of time is 40 minutes.
Now, we have to put the values in the given equation and solve it further.
Speed = 320/40 = 8
Hence, the hiker’s average change in elevation per minute is 8.

Question 35.
A hot air balloon descends 305 feet per minute for 4 minutes and then ascends at a rate of 215 feet per minute for another 2 minutes. Find the total change in the balloon’s altitude.
Answer:
Given,
A hot air balloon descends 305 feet per minute for 4 minutes and then ascends at a rate of 215 feet per minute for another 2 minutes.
305 × 4 = 1220
215 × 2 = 430
1220 – 430 = 790
The change in the altitude of the balloon is 790 feet.

Question 36.
Suppose you deposit $12.50 into your savings account each week for 4 weeks and then withdraw $4.80 each week for the next two weeks. Find the total change in the amount of money in your account.
Answer:
Given,
Amount of money deposited each week = $12.50
Amount of money withdrawn each week = $4.80
Amount of money deposited in 4 weeks = 12.50 * 4 = $50
Amount of money withdrawn in 2 weeks = 4.80 * 2 = $9.6
Now, amount of money left in the account is the difference between the two amounts.
50 – 9.6 = $40.4
Therefore, the total change in the amount of money in my account is given as:
Total change = Initial amount after 4 weeks – Final amount in the account.
Total change = $ 50 – $40.4 = $ 9.6

Question 37.
A game show awards 30 points for each correct answer and deducts 50 points for each incorrect answer. A contestant answers 2 questions incorrectly and 3 questions correctly. What is his final score?
Answer:
Given,
Let us say Initial number of points = 0
He answers 2 incorrectly = 0 – 50 – 50
= -100
He answers 3 correctly =-100 + 30 + 30 + 30
His final score = -100 + 30 + 30 + 30
= -10 points

Question 38.
The price of a stock falls $1.50 each day for 7 days.
a) Find the total change in the price of the stock.
Answer:
Given,
Price of the stock = $36
stock price fall per day = $1.50
number of days price fall = 7 days
the price of the stock changes by = $1.50 x 7 = $10.5
The price of stock decreased by $10.5

b) If the value of the stock was $36 before the price of the stock started falling for 7 days, find the price of the stock after those 7 days.
Answer:
Price of stock after 7 days
= $36 – $10.5
= $25.5
Thus, the value of stock after 7 days is equal to $25.5

Question 39.
Martin uses 24 boards that are each 5\(\frac{3}{4}\) feet long to build a treehouse. The wood costs $1.65 per foot. Find the total cost of the wood.
Answer:
Given,
Martin uses 24 boards that are each 5\(\frac{3}{4}\) feet long to build a treehouse.
The wood costs $1.65 per foot.
we know the amount per foot of wood $1.65. each piece is 5 3/4 (which is also 5.75) ft, so multiply these two numbers to see how much each piece costs.
1.65×5.75=9.4875
now to know how much total, we need to multiply by 24 (since we have 24 pieces)
9.4875×24=227.70
So, he spent $227.70 on the wood

Question 40.
James bought 8 baseball caps for $12.99 each before sales tax. The sales tax in his state is 6%. How much must James pay in total?
Answer:
Given,
James bought 8 baseball caps for $12.99 each before sales tax.
The sales tax in his state is 6%.
Amount due before taxes: 8($12.99) = $103.92
Multiplying this total by 1.06 will produce the final, with tax, amount: 1.06($103.92) = $110.16

Question 41.
Over a period of 5 years, the enrollment at a college changes from 12,000 students to 14,000 students. Find the percent change ¡n enrollment.
Answer:
Given,
Over a period of 5 years, the enrollment at a college changes from 12,000 students to 14,000 students.
(14,000 – 12,000)/5
2000/5 × 100
100% change in the enrollment.

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 2 Lesson 2.6 Operations with Decimals to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 2 Lesson 2.6 Answer Key Operations with Decimals

Math in Focus Grade 7 Chapter 2 Lesson 2.6 Guided Practice Answer Key

Copy and complete.

Question 1.
2.35 + (-6.13)
Using absolute values,
– = – Subtract the lesser absolute value from the greater absolute value.
= Simplify.
2.35 + (-6.13) = Use a sign, because has a greater absolute value.
Answer:
2.35 – 6.13 = 6.13 – 2.35 Subtract the lesser absolute value from the greater absolute value.
= 3.78 Simplify.
2.35 + (-6.13) = 3.78 Use a negative sign, because 6.13 has a greater absolute value.

Solve.

Question 2.
-8.6 – 3.27
Answer:
negative plus negative is negative
– × – = +
So we have to add the given numbers
-8.6 – 3.27 = -11.87

Question 3.
3.38 + (-5.6)
Answer:
3.38 – 5.6 = 5.6 – 3.38
= 2.22
Th greatest number has negative sign so we have to put negative sign to the resultant numbr.
3.38 + (-5.6) = -2.22

Solve.

Question 4.
At noon, the temperature was 2.7°F. By midnight, the temperature had dropped 7.5°F. Then, during the morning, the temperature rose 3.8°F. Find the final temperature.
Answer:
2.7 + (-7.5) + 3.8 = (2.7 + 3.8) + (-7.5)
= 6.5 + (-7.5), /6.5/</-7.5/, /-7.5/-/6.5/ = -1°F

Evaluate each product.

Question 5.
-7.23 • 4.6
Answer:
-7.23 • 4.6
– × + = –
-7.23 • 4.6 = -33.258

Question 6.
-37 • (-9.2)
Answer:
-37 • (-9.2)
– × – = +
-37 • (-9.2) = 340.4

Question 7.
8% of $230
Answer:
Given,
8% of $230
8% = 8/100 = 0.08
0.08 × 230 = 18.4

Tell whether each quotient is positive or negative. Then evaluate the quotient.

Question 8.
-21.7 ÷ 0.7
Answer: -31
As we know that – × + = –
The quotient will be negative.

Question 9.
-31.92 ÷ (-4.2)
Answer:
We know that -×-=+. So the quotient will be positive.
First we have to cancel negative signs.
31.92 ÷ 4.2 = 7.6

Solve.

Question 10.
The temperature in a certain town drops by 1.6°F per hour for 1.2 hours. It then drops by 0.8°F per hour for 2.5 hours. Find the total change in temperature.
You can use a negative number to represent the hourly drop in temperature.

Total change in temperature:
1.6 • + (-0.8) • = +
=
The total change in temperature is °F.

Answer:
Total change in temperature:
1.6 • 1.2 + (-0.8) • 2.5 = 1.92 + (-2)
= -0.8
The total change in temperature is -0.8 °F.

Question 11.
Mrs. Thompson usually uses 0.5 cup of sugar to bake a raisin cake. To bake a healthier raisin cake using less sugar, she decreases the amount of sugar by 20%. What ¡s the amount of sugar that Mrs. Thompson uses for baking the healthier raisin cake?
0.5 – ( • ) = 0.5 – Multiply.
= Add.
The amount of sugar that she uses is cup.
Answer:
0.5 – (0.5 • 0.2) = 0.5 – 0.1 Multiply.
= 0.4

Question 12.
Janice buys four boxes of paper clips. She pays with a $10 bill and receives $6.08 in change. What is the price of one box of paper clips?
Answer:
Given,
Janice buys four boxes of paper clips. She pays with a $10 bill and receives $6.08 in change.
10 – 6.08 = 3.92
3.92 ÷ 4 = 0.98
Thus the cost of each paper clip is $0.98

Question 13.
According to the 2000 census and the 2010 census, the population of the United States changed from 281.4 million to 308.7 million. Find the percent change in the population of the United States over the 10-year period. Round your answer to the nearest tenth.
Answer:
Given,
According to the 2000 census and the 2010 census, the population of the United States changed from 281.4 million to 308.7 million.
308.7 – 281.4 = 27.3
27.3/281.4 = 0.97 = 9.7%
9.7 to the nearest tenth is 10.

Question 14.
Stratosphere Tower in Las Vegas, Nevada, is the tallest freestanding observation tower in United States. Its height is 350.2 meters. The Eiffel Tower in Paris, France, is the country’s tallest building. Its height ¡s 324 meters. Find the difference in their heights.

Answer:
Given,
Stratosphere Tower in Las Vegas, Nevada, is the tallest freestanding observation tower in United States. Its height is 350.2 meters.
The Eiffel Tower in Paris, France, is the country’s tallest building. Its height is 324 meters.
350.2 – 324 = 26.2 meters
Thus the difference between the two towers is 26.2 meters.

Math in Focus Course 2A Practice 2.6 Answer Key

Solve. Show your work.

Evaluate each sum or difference.

Question 1.
-6.25 + 3.9
Answer:
6.25 – 3.9 = 2.35
Here the greatest value has negative sign so the difference of two numbers is -2.35
thus -6.25 + 3.9 = -2.35

Question 2.
-2.074 + 1.8
Answer:
2.074 – 1.8 = 0.274
Here the greatest value has a negative sign so the difference of the two numbers is -0.274

Question 3.
-11.52 – 6.3
Answer:
The signs of both the numbers are same so we have to add the numbers.
11.52 + 6.3 = 17.82
-11.52 – 6.3 = -17.82

Question 4.
-29.4 – (-7.21)
Answer:
-29.4 + 7.21 = 29.4 – 7.21
= 22.19
Here the greatest value has negative sign so the difference of two numbers is -22.19

Question 5.
-8.106 – 0.98
Answer:
The signs of both the numbers are same so we have to add the numbers.
8.106 + 0.98 = 9.086
Now put the negative sign to the answer.
-8.106 – 0.98 = -9.086

Evaluate each product.

Question 6.
0.3 • (-4.8)
Answer:
Plus × minus = minus
0.3 • (-4.8) = -1.44

Question 7.
-1.6 • 2.9
Answer:
Plus × minus = minus
1.6 × 2.9 = 4.64
Now put negative sign to the resultant.
-1.6 • 2.9 = -4.64

Question 8.

-3.25 • (-1.7)
Answer:
Minus × minus = plus
3.25 × 1.7 = 5.525

Question 9.
2.03 • (-5.4)
Answer:
Plus × minus = minus
2.03 × 5.4 = 10.962
Now put negative sign to the resultant.
2.03 • (-5.4) = -10.962

Question 10.
-0.08 • 3.2
Answer:
Plus × minus = minus
0.08 • 3.2 = 0.256
Now put negative sign to the resultant.
-0.08 • 3.2 = -0.256

Evaluate each quotient.

Question 11.
-29.52 ÷ 3.6
Answer:
29.52 ÷ 3.6 = 8.2
Now put negative sign to the quotient
-29.52 ÷ 3.6 = -8.2
Thus the quotient is -8.2

Question 12.
107.64 ÷ (-2.3)
Answer:
107.64 ÷ (-2.3)
Now put negative sign to the quotient
107.64 ÷ (2.3) = 46.8
107.64 ÷ (-2.3) = -46.8
Thus the quotient is -46.8

Question 13.
-40.56 ÷ (-5.2)
Answer:
-40.56 ÷ (-5.2) = 40.56 ÷ 5.2
= 7.8
Thus the quotient is 7.8

Question 14.

9.758 ÷ 0.41
Answer:
Given,
9.758 ÷ 0.41 = 23.8
Thus the quotient is 23.8

Evaluate each expression.

Question 15.
-0.59 – 1.2 – 3.4
Answer:
All the signs in the given expression is same.
So we have to add the numbers.
0.59 + 1.2 + 3.4 = 5.19
Now put the negative sign to the obtained answer.
-0.59 – 1.2 – 3.4 = -5.19

Question 16.
-2.38 + 15.6 – 140.05
Answer:
Given,
-2.38 + 15.6 – 140.05
-2.38 – 140.05 + 15.6
-142.43 + 15.6
=-126.83

Question 17.
38.92 – 6.7 – (-12.04)
Answer:
Given,
38.92 – 6.7 – (-12.04)
38.92 – 6.7 + 12.04
38.92 + 12.08 – 6.7
51 – 6.7 = 44.3

Question 18.
712.14 – 356.8 – (-9.03)
Answer:
Given,
712.14 – 356.8 – (-9.03)
712.14 – 356.8 + 9.03
First add the positive numbers
712.14 + 9.03 – 356.8
721.17 – 356.8 = 364.37

Question 19.
3 11.3 – 5.1 + 3.1 • 0.2 – 1.1
Answer:
Given,
3 11.3 – 5.1 + 3.1 • 0.2 – 1.1
311.3 – 5.1 + 0.62 – 1.1
311.3 + 0.62 – 5.1 – 1.1
311.3 + 0.62 – 6.2
305.72

Question 20.
(29.3 + 4) ÷ 3 + 0.5 • 2
Answer:
Given,
(29.3 + 4) ÷ 3 + 0.5 • 2
(33.3) ÷ 3 + 0.5 • 2
11.1 + 1
12.1

Solve. Show your work.

Question 21.
In Arizona, a minimum temperature of -40.0°F was recorded at Hawley Lake in 1971. A maximum recorded temperature of 53.3°F was recorded at Lake Havasu City in 1994. Find the difference between these maximum and minimum temperatures.
Answer:
Given,
A minimum temperature of -40.0°F was recorded at Hawley Lake in 1971
A maximum recorded temperature of 53.3°F was recorded at Lake Havasu City in 1994.
The difference between these maximum and minimum temperatures is 53.3°F – (-40.0°F)
53.3°F + 40°F
93.3°F

Question 22.
A shop owner buys 5 handbags to sell in his shop. The owner pays $39.75 for each handbag. Later, the owner has to sell the handbags at a loss. If he charges $27.79 for each handbag, what is his total loss for the 5 handbags?
Answer:
Given,
A shop owner buys 5 handbags to sell in his shop.
The owner pays $39.75 for each handbag.
5 x 39.75 = 198.75
Later, the owner has to sell the handbags at a loss.
he charges $27.79 for each handbag.
5 x 27.79 = 138.95
198.75 – 138.95 = 59.80
His total loss is $59.80

Question 23.
The original price of a football helmet was $78.60. If Peter was given a 15% discount, how much did he pay for the football helmet?

Answer:
Given,
The original price of a football helmet was $78.60.
First, you have to find out what one percent of the price is by dividing 78.6 by 100.
One percent is 0.786.
You want to know what 15 percent of the price is so that you can subtract this as a discount, you do this by multiplying 0.786 by 15.
78.6 – 11.79 = 66.81
Thus peter pays $66.81 for the football helmet.

Question 24.
The state sales tax in New York is 4.25%. Jean spends $208 at a department store, but only half of the merchandise she purchases is taxed. What is her total bill?
Answer:
Given,
The total amount of money spent by her = $208
Tax rate = 4.25%
The amount that was taxed = half of the merchandise bought by her.
Total bill = Initial bill + Tax amount
Tax = (Half of money spend by her * 4.25)/100
Tax = (208/2 x 4.25)/100
Tax = 104 x 4.25/100
Tax = 1.04 x 4.25 = $4.42
Thus the total amount of bill = initial bill + tax amount = $208 + $ 4.42 = $212.42

Question 25.
Sarah bought some T-shirts and a pair of shorts for $66.30. The pair of shorts costs $15.90 and each T-shirt costs $5.60. How many T-shirts did she buy?
Answer:
Given,
Sarah bought some T-shirts and a pair of shorts for $66.30.
The pair of shorts costs $15.90 and each T-shirt costs $5.60
66.3 – 15.9 = 50.4.
50.4 ÷ 5.6 = 9
Thus the Sarah bought 9 T-shirts

Question 26.
Margaret wants to buy 10 books. Six of them cost $12.50 each and the rest cost $26.35 each. If she only has $150, how much is she short?
Answer:
Given,
Margaret wants to buy 10 books.
Six of them cost $12.50 each and the rest cost $26.35 each.
6 x 12.50=75
4 x 26.35=105.4
75 + 105.4=180.4
150 – 180.4= -30.4

Question 27.
The recommended calcium intake for men and women is about 1.2 grams per day. A glass of milk contains about 0.27 gram of calcium. If a man drinks 3 glasses of milk, how much additional calcium does he need from other food sources?
Answer:
Given,
The recommended calcium intake for men and women is about 1.2 grams per day.
A glass of milk contains about 0.27 grams of calcium.
0.27 x 3 is 0.60 + 0.21=0.81
then 1.2-0.81=0.39

Question 28.
Math Journal Susannah evaluated an expression as follows:

She made a common mistake when applying the order of operations. Explain her mistake and help her solve the problem correctly.
Answer:
48 ÷ 2(0.9 + 0.3)
48 ÷ 2 (0.12)
48 ÷ 0.6 = 80

Question 29.
One day in February, the temperature at 9 A.M. is -6.8°F. At 3 P.M. on the same day, the temperature is 1.72°F.
a) Find the change in temperature.
Answer:
One day in February, the temperature at 9 A.M. is -6.8°F. At 3 P.M.
On the same day, the temperature is 1.72°F.
-6.8 + 1.72 = -5.08
Thus the change in temperature is -5.08°F.

b) Find the average hourly rate of change in temperature.
Answer:

question 30.
A submarine was cruising at 1,328.4 feet below sea level. It then rose at a rate of 14.76 feet per minute for 15 minutes.
a) Find the submarine’s depth after it rose for 15 minutes.
Answer:
Let us first calculate the total number of feet the submarine rose in 15 minutes using the rate of rise.
rate = 14.76 feet per minute
This means that at every minute, the submarine rose by 14.76 feet.
1 minute = 14.76 feet
Therefore 15 minutes = 14.76 × 15 = 221.4 feet

b) If the submarine continued to rise at this same rate, find the time it took to reach the surface from the depth you found in a).
Answer:
To find the new depth, we will subtract the number of feet risen from the initial depth.
initial depth = 1,328.4 feet
rise after 15 minutes = 221.4 feet
New depth = 1,328.4 – 221.4 = 1,107 feet

Question 31.
James is mountain climbing. Using a rope, James climbs down from the top of a steep cliff for 4 minutes at a rate of 12.2 feet per minute. He then climbs back up for 10 minutes at a rate of 3.6 feet per minute. How far from the top of the cliff is he after 14 minutes?
Answer:
Given,
James is mountain climbing. Using a rope, James climbs down from the top of a steep cliff for 4 minutes at a rate of 12.2 feet per minute.
12.2 × 4 = 48.8
He then climbs back up for 10 minutes at a rate of 3.6 feet per minute.
3.6 × 10 = 36
48.8 + 36 = 84.8 feet

Question 32.
Salina has 120 shares in a shipyard company. On Monday, the value of each share dropped by $0.38. On Tuesday, the value of each share rose by $0.16. Find the total change in the value of Salina’s 120 shares.
Answer:
Given,
Salina has 120 shares in a shipyard company.
On Monday, the value of each share dropped by $0.38.
On Tuesday, the value of each share rose by $0.16.
120(0.38 + 0.16)
120 (0.54) = $64.8

Question 33.
An organization that raises funds for charity raised $2.45 million last year and $1.96 million this year. Find the percent change in the amount raised.
Answer:
Given,
An organization that raises funds for charity raised $2.45 million last year and $1.96 million this year.
2.45 – 1.96 = $ 0.49 million
Thus the percent change in the amount raised is $0.49 million

Question 34.
A company suffered a loss of $5.4 million in its first year. It lost another $3.1 million in the second year. It made a profit of $4.9 million in the third year.

a) Find the average profit or loss for the first three years.
Answer:
A company suffered a loss of $5.4 million in its first year. It lost another $3.1 million in the second year.
$5.4 – $3.1 = $2.3 million
It made a profit of $4.9 million in the third year.
$4.9 – $2.3 = $2.6 million

b) After its fourth year of business, the company’s combined profit for all four years was $0. Find the company’s profit or loss during the fourth year.
Answer:
Let the Company’s loss or profit for the fourth year be x
$Company\ combined\ profit\ for\ all\ the\ fourth years\ is\ $0
-5.4 – 3.1 + 4.9 + x = 0
-36 + x = 0 Simplify
-3.6 + x + 3.6 = 0 + 3.6 Add 3.6 to both sides
x = 3.6
Therefore,\ Company’s\ made\ a\ profit\ of\ $3.6\ million\ during\ the\ fourth\ year$

Brain Work

Question 1.
The average of seven rational numbers is -5.16.
a) Find the sum of the rational numbers.
Answer:

b) If six of the numbers each equal -5.48, find the seventh number.
Answer:

Question 2.
The temperature of dry air decreases by about 0.98°F for every 100-meter increase in altitude.
a) The temperature above a town is 16°F on a dry day. Find the temperature of an aircraft 3.6 kilometers above the town.
Answer:

b) The temperature outside an aircraft 1.8 kilometers above the town is -5.64°F. Find the temperature in the town.
Answer:

Question 3.
Julie finds a way to use mental math to find the averages of these numbers:
15, 19, 18, 12, 20
she guesses that the mean is about 17, and uses mental math to find how far above or below this value each data item is:
-2, 2, 1, -5,3
she uses mental math to add these amounts:
-2 + 2 + 1 + (-5) + 3 = -1
she then divides -1 by 5 to get an average of -0.2. she says this means that the average of the numbers is 0.2 less than 17, the number she estimated. Check that Julie’s method gives the correct average. Then use it to find the average of these 4 numbers:
32, 35, 38, 36
Answer:
15 +  19 +  18 + 12 + 20 = 84/5 = 16.8 approx 17
-2 + 2 + 1 – 5 + 3 = -1
-1/5 = -0.2
Julies method is correct