Math in Focus

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 2 Lesson 2.3 Multiplying and Dividing in Scientific Notation to finish your assignments.

Math in Focus Grade 8 Course 3 A Chapter 2 Lesson 2.3 Answer Key Multiplying and Dividing in Scientific Notation

Math in Focus Grade 8 Chapter 2 Lesson 2.3 Guided Practice Answer Key

Complete.

Question 1.
In the 19th century, the Law Courts of Brussels was the largest building ever built. Its base area measures about 1.6 • 10² meters by 1.5 • 10² meters. Find the approximate base area of the building.
Approximate base area =
Length • Width

The area enclosed by the outer wall is approximately square meters.
Answer:
Given that Brussels was the largest building ever built.
Its base area measures about 1.6 × 102 meters by 1.5 × 102 meters it means
Length = 1.6 × 10²
Width = 1.5 × 10²
We know that
Base area = length × width
Base area = 1.6 × 1 0² × 1.5 × 10²
= 1.6 × 1.5 × 10⁴
= 2.4 × 10⁴ m²
The area enclosed by the outer Wall is approximately 2.4 × 10⁴ square meters.

Question 2.
The outer wall of Angkor Wat, a World Heritage site in Cambodia, encloses an area of about 1.02 • 10³ meters by 8.02 • 10² meters. Find the approximate area enclosed by the outer wall.
Approximate area enclosed by outer wall
= Length • Width

The area enclosed by the outer wall ¡s approximately square meters.
Answer:
Given that the length of a world Heritage site in Cambodia is 1.02 × 10³
The width of a world Heritage site in Cambodia is 8.02 × 10²
Area enclosed by the outer Wall = length × width
= 1.02 × 10³ × 8.02 × 10²
= 1.02 × 8.02 × 10⁵
= 8.1804 × 10⁵
The area enclosed by the outer Wall is approximately 8.1804 × 10⁵

Complete. Round each coefficient answer to the nearest tenth.

Question 3.
The Jean-Luc Lagardere plant in France is the second largest building in the world. It has an approximate volume of 5.6 • 10⁶ cubic meters. The NASA vehicle assembly building in Florida has a volume of about 3.7 • 10⁶ cubic meters. How many times as great as the volume of the NASA vehicle assembly building is the volume of the Jean-Luc Lagardere plant?

The volume of the Jean-Luc Lagardere plant is about times as great as the volume of the NASA vehicle assembly building.
Answer:
Given that the volume of Jean-Luc Lagardere plant in France is 5.6 × 10⁶ cubic meters
And the volume of the NASA vehicle assembly building is 3.7 × 10⁶ cubic meters
Now the volume of Jean-Luc Lagardere plant /volume of NASA vehicles assembly building is 5.6 × 10⁶/3.7 × 10⁶
= 5.6/3.7 × 10⁶/10⁶
= 20.72 cubic meters
The volume of the Jean-Luc Lagardere plant is 20.72 cubic meters great as the volume of the NASA vehicle assembly building.

Question 4.
The Abraj Al-Bait towers in Saudi Arabia has a floor area of about 1.5 • 10⁶ square meters. The Palazzo in Las Vegas has an approximate floor area of 6.5 • 10⁵ square meters. How many times as great as the floor area of the Palazzo is the floor area of the Abraj Al-Bait towers?

The floor area of the Abraj Al-Bait towers is approximately times greater than the floor area of the Palazzo.
Answer:
The floor area of Abraj Al-Bait towers in saudi Arabia is 1.5 × 10⁶ m²
The floor area of Palazzo in Las Vegas is 6.5 × 10⁵ m²
Therefore the floor area of Abraj AL-Bait towers/floor area of Palazzo
= 1.5 × 10⁶/6.5 × 10⁵
= 1.5/ 6.5 × 10⁶/10⁵
= 0.23 × 10¹
= 2.3 m²
The floor area of the Abraj Al-Bait Towers is approximately 2.3 m² times greater than the floor area of the Palazzo.

Math in Focus Course 3A Practice 2.3 Answer Key

Evaluate each expression in scientific notation, and round the coefficient to the nearest tenth.

Question 1.
7.45 • 10⁶ • 5.4 • 10^-6
Answer:
7.45 • 10⁶ • 5.4 • 10-6
Bases are equal powers should be added
= 7.45 • 5.4
= 40.23
40.23 rounded to the nearest tenth is 40

Question 2.
6.84 • 10^-5 • 4.7 • 10¹⁰
Answer:
6.84 • 10-5 • 4.7 • 1010
Bases are equal powers should be added.
6.84 • 4.7 • 10⁵
32.148 • 10⁵
32.148
32.148 rounded to the nearest tenth is 32.1

Question 3.
5.75 • 10^-5 ÷ (7.15 • 10⁷)
Answer:
Given that
5.75 • 10-5 ÷ (7.15 • 107)
Here 10-5 /107 = 1/10²
So, 5.75 ÷ 7.15 × 10-2
0.804 × 10-2
0.804 × 10-2 is rounded to the nearest tenth is 0.8 × 10-2

Question 4.
8.45 • 10¹¹ ÷ (1.69 • 10^-8)
Answer:
Given that
8.45 • 1011 ÷ (1.69 • 10-8)
Here 1011 /10-8 = 10³
So, 8.45 × 10³ ÷ 1.69
5 × 10³
5 × 10³ rounded to the nearest is 5 × 10³

The table shows the approximate volumes of some planets. Use the information to answer questions 5 to 7. Round your answers to the nearest tenth.

Question 5.
About how many times as great as the volume of Mars is the volume of Venus?
Answer:
Given that the volume of Mars is 1.6 × 10¹¹.
And the volume of Venus is 9.4 × 10¹¹
To find which one is great for that subtract the volume of Mars from the volume of Venus
That is 9.4 × 10¹¹/1.6 × 10¹¹
= 9.4/1.6 × 10¹¹/10¹¹
= 5.875
Therefore the volume of Venus is 5.875 times as great as Mars.
5.875 rounded to the nearest tenth of 6

Question 6.
About how many times as great as the volume of Mars is the volume of Earth?
Answer:
Given that the volume of Mars is 1.6 × 10¹¹.
And the volume of earth is 1.1 × 10¹²
To find which one is great for that we subtract the volume of earth from the volume of Mars.
That is 1.6 × 10¹¹ / 1.1 × 10¹²
= 1.6/1.1 × 10¹¹/10¹²
= 1.45 × 1/10¹
= 1.45 × 0.1
= 0.145
Therefore the volume of Mars is 0.145 as great as the Earth.
0.145 rounded to the nearest tenth is 0.1

Question 7.
About how many times as great as the volume of Venus is the volume of Earth?
Answer:
Given that the volume of Venus is 9.4 × 10¹¹
And the volume of earth is 1.1 × 10¹²
To find which one is great for that we subtract the volume of earth from the volume of Mars
That is 9.4 × 10¹¹ / 1.1 × 10¹²
= 9.4/1.1 × 10¹¹/10¹²
= 8.54 × 1/10¹
= 8.54 × 0.1
= 0.854
Therefore the volume of earth is 0.854 as great as Venus.
0.854 rounded to the nearest tenth is 0.9

Solve. Show your work.

Question 8.
Suzanne’s digital camera has a resolution of 2560 • 1920 pixels. Douglas’ digital camera has a resolution of 3264 • 2448 pixels.
a) Express the resolution of the digital cameras in prefix form to the nearest whole unit. Use the most appropriate unit.
Answer:
Suzanne: 2560 ∙ 1920 We are given the resolutions:
Douglas: 3264 ∙ 2448
2560 ∙ 1920 = 4,915, 200 ≈ 4.92 ∙ 10⁶ pixeli a) We express the resolution of Suzannes camera in prefix form:
= 4.92 megapixeli
3264 ∙ 2448 = 7, 990, 272 ≈ 7.99 ∙ 10⁶ pixeli We express the resolution of Douglas camera in prefix form:
= 7.99 megapixeli
4.99 < 7.99 b) the two numbers have the same exponent We compare the coefficients:
4.99. 10⁶ < 7.99. 10⁶

b) Whose camera has a higher resolution?
Answer:
Given that Suzanne’s digital camera has a resolution of 2560 × 1920 pixels.
= 49,15,200
And the Douglas digital camera has a resolution of 3264 × 2448 pixels.
= 79,90,272
Therefore Douglas digital camera has a higher resolution

Question 9.
Bobby downloaded pictures of a cruise ship and a ski run from the internet. The file size of the cruise ship is about 794 kilobytes while the file size of the ski run is about 2.6 megabytes.
a) What is the total file size, in megabytes and in kilobytes, of a file containing the two pictures?
Answer:
Given that the file size of the cruise ship is 794 kilobytes.
And the file size of the ski run is 2.6 megabytes.
The total file size of two pictures is 794 kilobytes + 2.6 megabytes
1 kilobyte = 0.001 megabyte
794 kilobytes = 0.794 megabytes
Therefore 0.794 + 2.6 = 3.394 megabytes.
The total file size of two pictures in megabytes is 3.394 megabytes.
1 megabyte = 1000 kilobytes
2.6 kilobytes = 2.6 × 1000 = 2600 kilobytes
Therefore the total file size of two pictures in kilobytes is 2600 kilobytes.

b) Calculate the difference in file size, in megabytes and in kilobytes, between the two pictures.
Answer:
Given that the file size of the cruise ship is 794 kilobytes.
1 kilobyte = 0.001 megabyte
794 kilobytes = 0.794 megabytes
And the file size of the ski run is 2.6 megabytes.
1 megabyte = 1000 kilobytes
2.6 megabytes = 2.6 × 1000 = 2600 kilobytes
Therefore the file size of the cruise ship is 794 kilobytes.
And the file size of the ski run is 2600 kilobytes.
The difference between the two pictures in kilobytes is 2600 – 794 = 1806
The file size of the cruise ship is 0.794 megabytes
And the file size of the ski run is 2.6 megabytes.
The difference between the two pictures in megabytes is 2.6 – 0.794 = 1.806

c) To the nearest tenth, about how many times as great as the file size of the ski run picture is the file size of the ship picture?
Answer:
Given that the file size of the cruise ship is 794 kilobytes.
Here 794 nearest to the tenth place is 790 kilobytes
1 kilobyte = 0.001 megabyte
790 kilobytes = 0.001 × 790 = 0.79 megabytes
And the file size of the ski run is 2.6 megabytes
2.6 nearest to the tenth is 3 megabytes
Therefore 3 megabytes – 0.79 megabytes
= 2.21 megabytes
The file size of the ski run picture is 2.21 megabytes great as the file size of the cruise ship.

d) Bobby saved the two pictures on a thumb drive with a capacity of 256 megabytes. Find the remaining free capacity of the thumb drive to the nearest tenth megabyte after Bobby saved the two pictures in it.
Answer:
Given that, Bobby saved two pictures on the thumb drive with a capacity of 256 megabytes.
256 nearest to the tenth is
First look at the tens place it is 5 and the digit to the right is 6.
Here the digit 6 is above 5. So, we add 1 to the tens place and place 0 on the ones place.
Therefore 256 nearest to the tenth place is 260

Question 10.
The Georgia Aquarium in Atlanta is about 2.63 • 10³ inches long, 1.26 • 10² inches wide, and 3 • 10¹ inches deep at its largest point. Find its approximate volume.
Answer:
Given that the length of a Georgia Aquarium in Atlanta is 2.63 × 10³.
The width of a Georgia Aquarium in Atlanta is 1.26 × 10².
The depth of the Georgia Aquarium in Atlanta is 3 × 10¹.
We know that the volume formula for a rectangle is length × width × height.
Georgia Aquarium is in the shape of a rectangle
Volume = 2.63 × 10³ × 1.26 × 10² × 3 × 10¹
Bases are equal powers should be added
= 2.63 × 1.26 × 3 × 10⁶
= 9.9414 × 10⁶.

Question 11.
The square base of the Great Pyramid of Khufu has a length of approximately 1.476 • 10³ feet. Its height is about 2.17 • 10² feet. Find the approximate volume of the pyramid. Write your answer in scientific notation. Round the coefficient to the nearest tenth.

Answer:
Given that the length of a Great Pyramid of Khufu is 1.476 × 10³ feet.
And the height of the great Pyramid of Khufu is 2.17 × 10² feet.
Volume of a pyramid = ⅓ × bh
b = 1.476 × 10³
h = 2.17 × 10²
= ⅓ × 1.476 × 10³ × 2.17 × 10²
⅓ × 1.476 × 2.17 × 10⁵
1.067 × 10⁵
= 1,06,700
1,06,700 nearest to the tenth is 106700.

Question 12.
The Tropical Islands Resort is housed inside a former airplane hangar approximately 1.18 • 10³ feet long, 6.89 • 10² feet wide, and 3.51 • 10² feet high. Use the formula for the volume of a rectangular prism to approximate the volume enclosed by the resort. Round the coefficient to the nearest tenth.
Answer:
Given that the length of a tropical island resort is housed inside a former airplane hangar is 1.18 × 10³.
The wide of a tropical island resort housed inside a former airplane hangar is 6.89 × 10².
The height of a tropical island resort housed inside a former airplane hangar is 3.51 × 10².
We know that the volume of the rectangular prism is width × height × length.
Volume of the rectangular prism = 1.18 × 10³ × 6.89 × 10² × 3.51 × 10²
Bases are same powers should be added
1.18 × 6.89 × 3.51 × 10⁷
= 28.537 × 10⁷
= 28.537 × 10⁷ nearest to the tenth is 30 × 10⁷

Question 13.
The time light takes to. travel one meter in a vacuum is about 3.3 nanoseconds. To travel one mile it takes about 5.4 microseconds.
a) Find the difference, in microseconds, between the times taken by light to travel one meter and one mile in a vacuum.
Answer:
Given that, the time light takes to travel one meter in a vacuum is 3.3 nanoseconds.
The time light takes to travel one mile in a vacuum is 5.4 microseconds.
1 microsecond = 1000 nanoseconds
5.4 microseconds = 5.4 × 1000 = 5400
Difference in microseconds is 5400 – 3.3 = 5396.7

b) How many times longer, to the nearest tenth, does it take light to travel one mile than one meter?
Answer:

Question 14.
A spherical particle was found to have a radius of 3.5 • 10^-10 meter.
a) Express the diameter in the prefix form using picometers.
Answer:
Diameter of a spherical D = 2r
D = 2 × 3.5 × 10-10
= 7 × 10-8 × 10-2 meters
0.00000007 millimeters.

b) Use your answer in a), express the circumference in the prefix form using nanometers. Use 3.14 as an approximation for π.
Answer:
We know that the circumference of a spherical is C = 2πr
C = 2 × 3.14 × 3.5 × 10-10
C = 21.98 × 10-1 × 10-9
C = 21.98 × 10-1 nanometers.

Brain @ Work

Question 1.
Find the cube root of 2.7 • 10¹⁰.
Answer:
Given that 2.7 • 1010
The cube root is (2.7 • 10¹⁰) is
= (2.7 • 10,00,00,00,000)
= (27000000000)
= 3000
Therefore the cube root of 2.7 • 1010 is 3000.

Question 2.
Given that a = 3 • 10³ and b = 4 • 10², find each value.
a) 2a + b
Answer:
Given equation is 2a + b
Here a = 3 • 103
b = 4 • 102
Substitute a,b in the above given equation is
2(3 • 103) + (4 • 102)
= 2(3000)+400
= 6000+400
= 6400

b) \(\frac{2a}{b}\)
Answer:
The given equation is 2ab
Here a = 3 • 103
b = 4 • 102
Substitute a,b in the above given equation is
2(3 • 103)×(4 • 102)
2(3000)×(400)
6000×400
2400000

Question 3.
Solve each of the following. Write your answer in scientific notation using the basic unit.
a) 80 micrograms + 200 nanograms
Answer:
Convert micrograms into nanograms
1 microgram equal to 1000 nanograms
So, 80 micrograms = 1000 × 80 = 80,000 nanograms
Therefore 80,000 nanograms + 200 nanograms = 80,200 nanograms

b) 3 gigabytes – 700 megabytes
Answer:
Convert gigabytes into megabytes
1 gigabyte equal to 1024 megabytes
So, 3 gigabytes equal to 3 × 1024 = 3072 megabytes
Therefore, 3072 megabytes – 700 megabytes = 2372 megabytes.

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 2 Lesson 2.2 Adding and Subtracting in Scientific Notation to finish your assignments.

Math in Focus Grade 8 Course 3 A Chapter 2 Lesson 2.2 Answer Key Adding and Subtracting in Scientific Notation

Math in Focus Grade 8 Chapter 2 Lesson 2.2 Guided Practice Answer Key

Complete.

Question 1.
The population of Washington, D.C., is about 5.9 • 10⁵. South Dakota has a population of approximately 8 • 10⁵.

a) Find the sum of the populations.
Sum of populations
= Population of Washington D.C. + Population of South Dakota

The sum of the populations is about .
Answer:
Sum of populations
= Population of Washington D.C. + Population of South Dakota
5.9 • 10⁵ + 8 • 10⁵.
Substitute the value 10⁵. from each term
Add within the parentheses
(5.9 + 8) • 10⁵.
13.9 • 10⁵.
write 13.9 in the scientific notation.
1.39 • 10¹.• 10⁵.
Use the product of powers property.
1.39 • 10⁶.

b) Find the difference in the populations.
Difference in the populations
= Population of South Dakota – Population of Washington, D.C.

The difference in the populations is about .
Answer:
Population of South Dakota – Population of Washington, D.C.
8 • 10⁵ – 5.9 • 10⁵.
Substitute the value 10⁵. from each term
Add within the parentheses
(8 – 5.9) • 10⁵.
2.1 • 10⁵.
write 13.9 in the scientific notation.
21 • 10¹.• 10⁵.
Use the product of powers property.
21 • 10⁶.

Question 2.
The approximate length of the smallest salamander is 1.7 • 10^-2 meter. The smallest lizard is about 1.6 • 10^-2 meter long.

a) What is the sum of the lengths of the salamander and the lizard?
Sum of the lengths of the salamander and the lizard
= Length of salamander + Length of lizard
= 1.7 • 10^-2 + 1.6 • 10^-2 Substitute.
= ( + ) • Factor from each term.
= • m within parentheses.
The sum of the lengths is about meter.
Answer:
Sum of the lengths of the salamander and the lizard
= Length of salamander + Length of lizard
= 1.7 • 10^-2 + 1.6 • 10^-2 Substitute.
= (1.7 + 1.6) • 10^-2
= (3.3)• 10^-2
The sum of the lengths is about (3.3)• 10^-2 meter.

b) What is the difference ¡n the length of the reptiles?

The salamander is about meter longer than the lizard.
Answer:
Difference in length between the salamander and lizard.
= Length of salamander – Length of lizard
= 1.7 • 10^-2 – 1.6 • 10^-2 Substitute.
= (1.7 – 1.6) • 10^-2
= 0.1 • 10^-2
= 1 • 10^-1 • 10^-2
= 1 • 10^-3

Question 3.
The approximate area of the continent of Australia is 9 • 10⁶ square kilometers.
The area of the continent of Antarctica is about 1,37 • 10⁷ square kilometers.
a) Find the approximate sum of the land areas of the two continents.

The sum of the land areas is about square kilometers.
Answer:
Approximate sum of the land areas of the two continents
Area of Australia + Area of Antarctica
9 • 10⁶ + 1.37 • 10⁷
9 • 10⁶ + 1.37 • 10⁶ • 10¹
(9 + 13.7)  • 10⁶
22.7  • 10⁶
2.27  • 10⁷  square kilometers

b) What is the difference in the areas of the two continents?
Difference in the land areas
= Area of Antarctica – Area of Australia

The land area of Antarctica is about square kilometers larger than the land area of Australia.
Answer:
The difference in the land areas
= Area of Antarctica – Area of Australia
9 • 10⁶ – 1.37 • 10⁷
1.37 • 10⁶ – 9 • 10⁶
(13.7 – 9)  • 10⁶
4.7 • 10⁶ square kilometers

Solve. Write your answers in scientific notation.

Question 4.
A custom-made invitation using a 10-pt card stock is about 2.54 • 10^-4 meter thick. It is placed inside a tissue paper insert that is approximately 6.0 • 10^-6 meter thick.
a) How thick is the invitation when placed in the tissue paper insert?
Answer:
2.54 • 10^-4+ 6.0 • 10^-6 meters thick
2.54 • 10^-4+ 0.06 • 10^-4 meters thick
(2.54 + 0.06) • 10^-4 meters thick
2.6 • 10^-4 meters

b) How much thicker is the invitation than the tissue paper insert?
Answer:
Let x is a variable here representing the number of times thicker.
Thickness of the card stock is x times as thick as tissue.
2.54 • 10^-4= x • 6.0 • 10^-6
x = 2.54 • 10^-4/6.0 • 10^-6
x = 0.423 • 10²
x = 4.23 • 10²

Complete.

Question 5.
On average, Pluto orbits the Sun at a distance of approximately 4,802 gigameters. Uranus’s average distance from the Sun is about 2.992 • 10⁹ kilometers. Which planet is farther from the Sun? How much farther?

Distance of Pluto from the Sun:
Gm = • km Write in scientific notation.
Difference in distance of Pluto and Uranus from the Sun
= Distance of from the Sun – Distance of from the Sun
= • – • Substitute.
= ( – ) • Factor from each term.
= • km within parentheses.
So, is kilometers farther from the Sun.
Answer:
Given,
On average, Pluto orbits the Sun at a distance of approximately 4,802 gigameters.
Uranus’s average distance from the Sun is about 2.992 • 10⁹ kilometers.
1 gigameter = 10⁶ kilometers.
4,802 gigameters = 4,802 • 10⁶ kilometers.
Difference in distance of Pluto and Uranus from the Sun
= Distance of Pluto from the Sun – Distance of Uranus from the Sun
4,802 • 10⁶ kilometers – 2.992 • 10⁹ kilometers
= 4,802 • 10⁶ kilometers – 2,992 • 10⁶ kilometers
= (4802 – 2992) • 10⁶ kilometers
= 1810 • 10⁶
So, Pluto is 1810 • 10⁶ kilometers farther from the Sun.

Math in Focus Course 3A Practice 2.2 Answer Key

Solve. Show your work. Round the coefficient to the nearest tenth.

Question 1.
6.3 • 10^-2 + 4.9 • 10^-2
Answer:
(6.3 + 4.9) • 10^-2
(11.2) • 10^-2
Now, Round the coefficient to the nearest tenth.
11 • 10^-2

Question 2.
7.2 • 10² – 3.5 • 10²
Answer:
7.2 • 10² – 3.5 • 10²
(7.2 – 3.5) • 10²
3.7 • 10²
Now, Round the coefficient to the nearest tenth.
4 • 10²

Question 3.
3.8 • 10³ + 5.2 • 10⁴
Answer:
3.8 • 10³ + 5.2 • 10⁴
3.8 • 10³ + 5.2 • 10³ • 10¹
(3.8 + 52) • 10³
55.8 • 10³
Now, Round the coefficient to the nearest tenth.
56 • 10³

Question 4.
8.1 • 10⁵ – 2.8 • 10⁴
Answer:
8.1 • 10⁵ – 2.8 • 10⁴
81 • 10⁴ – 2.8 • 10⁴
(81 – 2.8) • 10⁴
78.2 • 10⁴
Now, Round the coefficient to the nearest tenth.
78 • 10⁴

Use the table to answer questions 5 to 9.

The table shows the amounts of energy, in Calories, contained in various foods.

Question 5.
Find the total energy in each food combination. Write your answer in scientific notation. Round coefficients to the nearest tenth.
a) Chicken breast and cabbage
Answer:
Chicken breast: 1.71 • 10⁴
cabbage: 2.5 • 10⁴
Total energy in each food combination is
1.71 • 10⁴ + 2.5 • 10⁴
(1.7 + 2.5) • 10⁴
4.2 • 10⁴
4 • 10⁴

b) Cabbage and raw potato
Answer:
cabbage: 2.5 • 10⁴
Raw potato: 7.7 • 10
Total energy in each food combination is
2500 • 10 + 7.7 • 10
2507.7 • 10
2510 • 10

Question 6.
How many more Calories are in chicken breast than in salmon?
Answer:
Chicken breast: 1.71 • 10⁴
Salmon: 1.67 • 10⁵
1.67 • 10⁵ – 1.71 • 10⁴
(16.7 – 1.71) • 10⁴
14.99 • 10⁴

Question 7.
How many more Calories are in salmon than in cabbage?
Answer:
Salmon: 1.67 • 10⁵
cabbage: 2.5 • 10⁴
1.67 • 10⁵ – 2.5 • 10⁴
(16.7 – 2.5) • 10⁴
14.2 • 10⁴

Solve. Show your work.

Question 8.
A flight from Singapore to New York includes a stopover at Hawaii. The distance between Singapore and Hawaii is about 6.7 • 10³ miles. The distance between New York and Hawaii is about 4.9 • 10³ miles. Write each sum or difference in scientific notation.
a) Find the total distance from Singapore to New York.
Answer:
The distance between Singapore and Hawaii is about 6.7 • 10³ miles.
The distance between New York and Hawaii is about 4.9 • 10³ miles.
6.7 • 10³ miles + 4.9 • 10³ miles
(6.7  + 4.9) • 10³ miles
11.6 • 10³ miles

b) Find the difference in the length of the two flights.
Answer:
The distance between Singapore and Hawaii is about 6.7 • 10³ miles.
The distance between New York and Hawaii is about 4.9 • 10³ miles.
6.7 • 10³ miles – 4.9 • 10³ miles
(6.7  – 4.9) • 10³ miles
1.8 • 10³ miles

Question 9.
Angora wool, obtained from rabbits, has fibers with a diameter of about 1 • 10^-6 meter. Cashmere, obtained from goats, has fibers with a diameter of about 1.45 • 10^-5 meter. Write your answers in the appropriate unit in prefix form.
a) Find the sum of the diameters of the two types of fiber.
Answer:
Angora wool, obtained from rabbits, has fibers with a diameter of about 1 • 10^-6 meter.
Cashmere, obtained from goats, has fibers with a diameter of about 1.45 • 10^-5 meter.
1.45 • 10^-5 meter + 1 • 10^-6 meter.
14.5 • 10^-6 meter + 1 • 10^-6 meter.
(14.5 + 1) • 10^-6 meter.
15.5 • 10^-6 meter.
1.55 • 10^-5 meter.

b) How much wider is the cashmere fiber than the angora fiber?
Answer:
Angora wool, obtained from rabbits, has fibers with a diameter of about 1 • 10^-6 meter.
Cashmere, obtained from goats, has fibers with a diameter of about 1.45 • 10^-5 meter.
1.45 • 10^-5 meter – 1 • 10^-6 meter.
14.5 • 10^-6 meter – 1 • 10^-6 meter.
(14.5 – 1) • 10^-6 meter.
13.5 • 10^-6 meter.
1.35 • 10^-5 meter.

The average distances of three planets from the Sun are shown in the diagram. Use this information for questions 10 to 13. Express your answers in kilometers.

Question 10.
What is the closest Mercury comes to Earth when both are at an average distance from the Sun?
Answer:
Mercury: 5.83 • 10¹⁰
Earth: 1.5 • 10⁸ km = 1.5 • 10⁸ • 10³ m = 1.5 • 10¹⁰• 10¹
Difference between the distance of Earth from Sun to distance of Mercury from Sun
15 • 10¹⁰ – 5.83 • 10¹⁰
(15 – 5.83) • 10¹⁰
9.17 • 10¹⁰

Question 11.
What is the closest Saturn comes to Mercury when both are at an average distance from the Sun?
Answer:
Mercury: 5.83 • 10¹⁰
Saturn: 1.43 • 10¹²
Difference between the distance of Saturn from Sun to distance of Mercury from Sun
143 • 10¹⁰ – 5.83 • 10¹⁰
(143 – 5.83) • 10¹⁰
137.17 • 10¹⁰

Question 12.
What is the closest Saturn comes to Earth when both are at an average distance from the Sun?
Answer:
Earth: 1.5 • 10⁸ km = 1.5 • 10⁸ • 10³ m = 1.5 • 10¹¹
Saturn: 1.43 • 10¹²
Difference between the distance of Saturn from Sun to distance of Mercury from Sun
14.3 • 10¹¹ – 1.5 • 10¹¹
(14.3 – 1.5) • 10¹¹
12.8• 10¹¹

Question 13.
Is the distance you found in 12 greater or less than the average distance from Earth to the Sun? Explain.
Answer: Yes the distance of Saturn from the Sun to the distance of Mercury from the Sun is 12.8• 10¹¹

Solve. Show your work.

Question 14.
Factories A and B produce potato chips. They use the same basic ingredients: potatoes, oil, and salt. Last year, each factory used different amounts of these ingredients, as shown in the table.

a) Which factory used more potatoes last year? How many more potatoes did it use?
Answer: By seeing the above table we can say that Factory A has used more potatoes last year than Factor B.
Potato Factory A Used: 4.87 • 10⁶
Potato Factory B Used: 3,309 • 10³
Potato Factory A Used: 4870 • 10³
Potatoes Used Last Year: 4870 • 10³–  3,309 • 10³
(4870 – 3309) • 10³
1561 • 10³

b) Which factory used more oil last year? How much more oil did it use than the other factory?
Answer:
By seeing the above table we can say that Factory B has used more oil last year than Factor A.
Oil Factory A Used: 356,000 = 356 • 10³
Oil Factory B Used: 5.61 • 10⁵ = 561 • 10³
Oil Used Last Year: 561 • 10³–  356• 10³
(561- 356) • 10³
205• 10³

c) Find the total weight of the ingredients used by each factory. Write your answer in scientific notation.
Answer:
Factory A:
Potato Factory A Used: 4870 • 10³
Oil Factory A Used: 356,000 = 356 • 10³
Salt Factory A Used: 2.87  • 10⁵ = 287 • 10³
4870 • 10³ + 356 • 10³ + 287 • 10³
(4870 + 356 + 287) • 10³
5513 • 10³
Factory B:
Potato Factory B Used: 3,309 • 10³
Oil Factory B Used: 561 • 10³
Salt Factory B Used: 193500 = 193.5  • 10³ 
3309 • 10³ + 561 • 10³ + 193.5 • 10³
(3309+ 561 + 193.5) • 10³
4063.5 • 10³

Question 15.
Math journal The approximate population of the following countries in North America in 2011 are shown in the table. Explain how to use scientific notation to find the total population of the countries.

Answer:
Mexico: 110,000,000 = 11 • 10⁷
Haiti: 9,700 000 = 97 • 10⁵
Costa Rica: 4,600,000 = 46 • 10⁵
United States: 310,000,000 = 31 • 10⁷
11 • 10⁷ + 31 • 10⁷ + 97 • 10⁵ + 46 • 10⁵
4 •  10⁷ + 143 • 10⁵

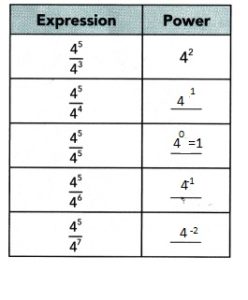
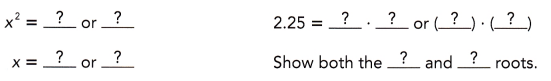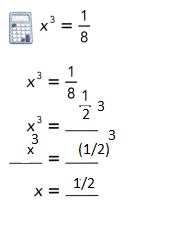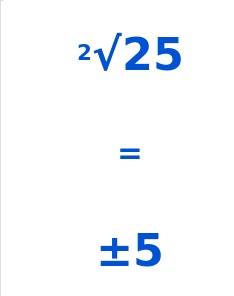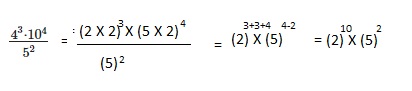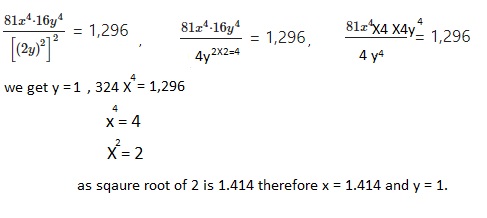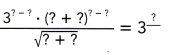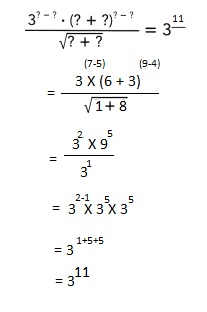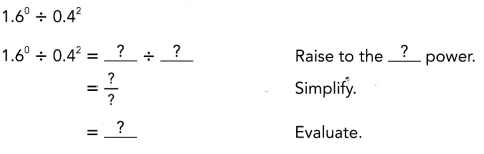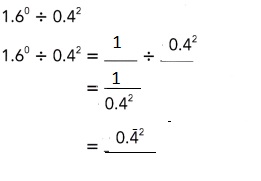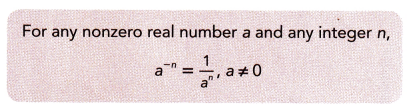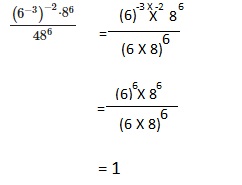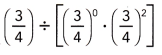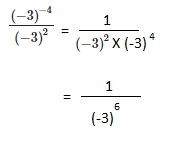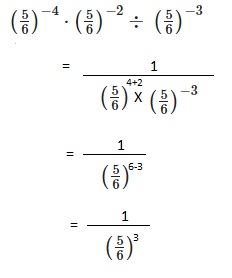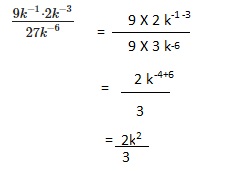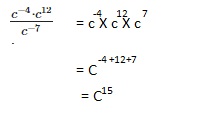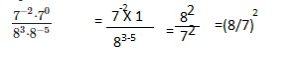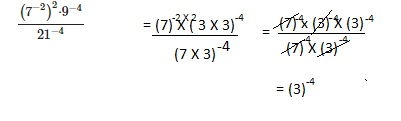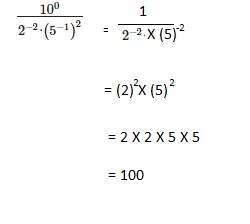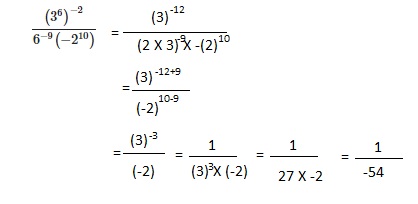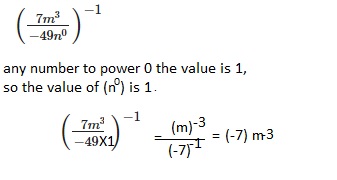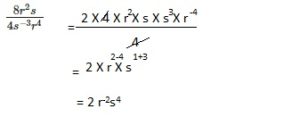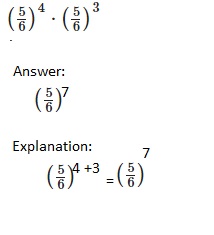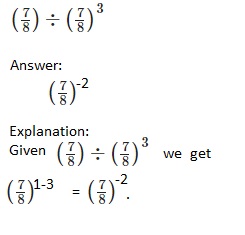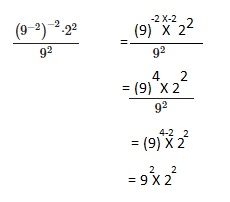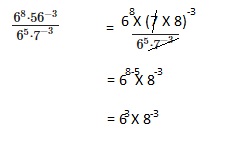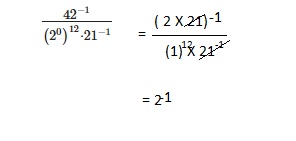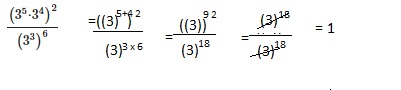Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 2 Lesson 2.1 Understanding Scientific Notation to finish your assignments.

Math in Focus Grade 8 Course 3 A Chapter 2 Lesson 2.1 Answer Key Understanding Scientific Notation

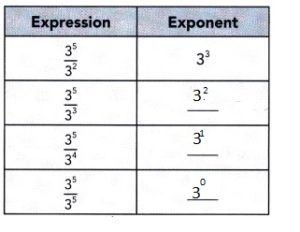
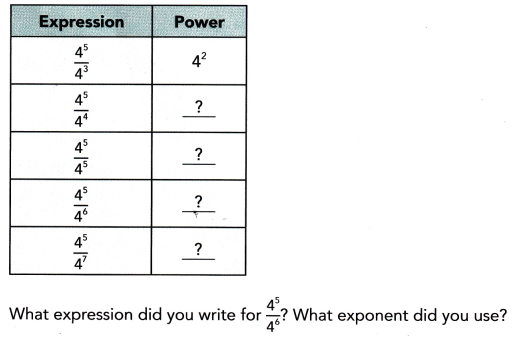
Math in Focus Grade 8 Chapter 2 Lesson 2.1 Guided Practice Answer Key

Tell whether each number is written correctly in scientific notation. If it is incorrectly written, state the reason.

Question 1.
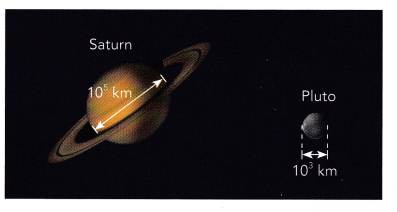
A Brazilian gold frog is about 9.6 • 10° millimeters long.
Answer:
Given,
A Brazilian gold frog is about 9.6 • 10° millimeters long.
9.6 × 1 = 9.6 millimeters
The given statement is correct because the length of a Brazilian gold frog is about 9.6 mm

Question 2.
The wavelength of green light is about 4.15 • 10^-7 meter.
Answer: The wavelength of green light is measured in a nanometer. Thus the above statement is incorrect.

Question 3.
Mars is approximately 0.2244 • 10⁷ kilometers from the Sun.
Answer: The above statement is correct.

Write each number in scientific notation.

Question 4.
856.2
856.2 = • Move the decimal point places to the left and multiply by .
= • Rewrite as a power of 10.
Answer:
856.2 = 8562 • 10^-1 Move the decimal point 1 place to the left and multiply by 8562 • 10^-1
= 8562 • 10^-1

Question 5.
0.06
Answer:
6  • 10^-2 Move the decimal point 2 places to the left and multiply 6 by 10^-2

Write each number in standard form.

Question 6.
9 • 10⁴
9 • 10⁴ = • Evaluate the power.
= Multiply by .
Answer:
9 • 10⁴
• indicates product of two numbers.
9 × 10⁴
9 × 10000 = 90,000
9 multiply by 10000.

Question 7.
2.5 • 10^-2
2.5 • 10^-2 = • Evaluate the power.
= Divide by .
Answer:
2.5 • 10^-2 = 2.5 • 10^-2 Evaluate the power.
= 2.5 Divide by 1/100

Identify the lesser number in each pair of numbers. Justify your reasoning.

Question 8.
4.2 • 10² and 6.5 • 10¹
< Compare the .
<  .
So, is the lesser number.
Answer:
6.5 • 10¹  < 4.2 • 10² Compare the decimals.
6.5 • 10¹  < 4.2 • 10²
So, 6.5 • 10¹ is the lesser number.

Question 9.
3.6 • 10^-3 and 8.4 • 10^-3
The are the same.
< Compare the .
< .
So, is the lesser number.
Answer:
The exponents are the same.
3.6 • 10^-3 < 8.4 • 10^-3
3.6 < 8.4
So, 3.6 is the lesser number

Complete.

Question 10.
An actor has 75,126 fans on a social network. A musician has 8.58 • 104 fans. Who has more fans on the social network?

Method 1
8.58 • 10⁴ =
>
So, the has more fans on the social network.

Method 2
75,126 = •
Compare and .
The are the same.
> Compare the coefficients.
So, the has more fans on the social network.
Answer:
Given,
An actor has 75,126 fans on a social network. A musician has 8.58 • 10⁴ fans.
We have to find who has more fans on the social network.
When you multiply a decimal by a positive power of 10, the decimal point to the right.
8.58 • 10⁴ = 858 × 10²
= 85800 fans
75,126 is less than 85800
Therefore we can say that the musician has more fans on the social network.

Question 11.
The average diameter of a type of round shaped bacteria is 0.0000037 meter. The spacing between two of these bacteria is 2.1 • 10^-9 meter. Which length is shorter?
Answer:
Given,
The average diameter of a type of round shaped bacteria is 0.0000037 meter.
The spacing between two of these bacteria is 2.1 • 10^-9 meter.
0.0000037 meter can be written as
0.37 × 1/100000
0.37 × 10^-5 meter
3.7 ×10 ^-6 meter
37 × 10^-7 meter
2.1 • 10^-9 meter is shorter than 37 • 10^-7 meter

Question 12.
There are 5.816 • 10⁴ spectators in a stadium watching a football game. In a theater, 1,150 people attend an opera. Which venue has more people?
Answer:
Given,
There are 5.816 • 10⁴ spectators in a stadium watching a football game.
In a theater, 1,150 people attend an opera.
We know that,
When you multiply a decimal by a positive power of 10, the decimal point to the right.
5.816 • 10⁴ = 5.816  • 10000
= 5816 × 10
= 58160
1,150
58160 is greater than 1150
Thus the stadium watching a football game has more people than people attend an opera.

Math in Focus Course 3A Practice 2.1 Answer Key

Tell whether each number is written correctly in scientific notation. If incorrectly written, state the reason.

Question 1
71 • 10²²
Answer:
71 • 10²²
No the above number is not written in the scientific notation

Question 2.
8 • 10^-2
Answer:
8 • 10^-2
= 8 × 1/100
= 0.08
No the above number is not written in the scientific notation

Question 3.
0.99 • 10^-3
Answer:
0.99 • 10^-3
= 9.9 × 10^-4
Yes the above number is written in the scientific notation

Question 4.
1.2 • 10^-4
Answer:
1.2 • 10^-4
Yes the above number is written in the scientific notation

Write each number in scientific notation.

Question 5.
533,000
Answer:
We can write the very large number in the standard form as the product of a number between 1 and 10 inclusive of 1 and an integer power of 10.
For the numbers greater than 1 we can use a positive exponent.
533 • 10³

Question 6.
327.8
Answer:
We can write the very large number in the standard form as the product of a number between 1 and 10 inclusive of 1 and an integer power of 10.
For the numbers less than 1 we use a negative exponent.
3278 • 10^-1

Question 7.
0.0034
Answer:
We can write the very large number in the standard form as the product of a number between 1 and 10 inclusive of 1 and an integer power of 10.
For the numbers less than 1 we use a negative exponent.
34 • 10^-4

Question 8.
0.00000728
Answer:
We can write the very large number in the standard form as the product of a number between 1 and 10 inclusive of 1 and an integer power of 10.
For the numbers less than 1 we use a negative exponent.
728 • 10^-8

Write each number in standard form.

Question 9.
7.36 • 10³
Answer: 7360

Question 10.
2.431 • 10⁴
Answer: 24310

Question 11.
5.27 • 10^-2
Answer: 0.0527

Question 12.
4.04 • 10^-4
Answer: 0.000404

Identify the lesser number in each pair of numbers. Justify your reasoning.

Question 13.
8.7 • 10⁶ and 5.9 • 10³
Answer: 5.9 • 10³ < 8.7 • 10⁶

Question 14.
4.8 • 10³ and 9.6 • 10⁷
Answer: 4.8 • 10³ < 9.6 • 10⁷

Question 15.
3.1 • 10^-5 and 7.5 • 10^-5
Answer: 3.1 • 10^-5 < 7.5 • 10^-5

Question 16.
6.9 • 10^-3 and 4.3 • 10^-3
Answer: 4.3 • 10^-3 < 6.9 • 10^-3

Solve. Show your work.

Question 17.
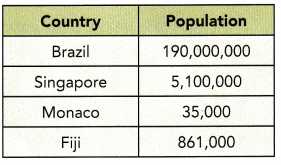
The table shows population data for some countries. Write each population ¡n scientific notation.

Answer:
From the above table, we can write the population in scientific notation.
Brazil – 190,000,000
19 • 10⁷
Singapore – 5,100,000
51 • 10⁵
Monaco – 35,000
35 • 10³
Fiji – 861,000
861 • 10³

Question 18.
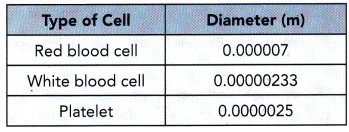
Human blood contains red blood cells, white blood cells, and platelets. The table shows the approximate diameters of each of these cells in fractions of a meter. Write each diameter in scientific notation.

Answer:
Given,
Human blood contains red blood cells, white blood cells, and platelets.
The table shows the approximate diameters of each of these cells in fractions of a meter.
Red blood cell – 0.000007
= 7 • 10^-6
White blood cell – 0.00000233
= 233 • 10^-8
Platelet – 0.0000025
= 25 • 10^-7

Question 19.
A praying mantis is approximately 15 centimeters long. A caterpillar is about 76 millimeters long.
a) Write both lengths in millimeters in scientific notation.
b) Write both lengths in centimeters in scientific notation.
How does writing the numbers using the same units help you compare them?
Answer:
a) Write both lengths in millimeters in scientific notation.
Given,
A praying mantis is approximately 15 centimeters long.
15 × 10 millimeters
A caterpillar is about 76 millimeters long.
b) Write both lengths in centimeters in scientific notation.
A praying mantis is approximately 15 centimeters long.
76 × 10^-1 centimeter

Question 20.
A technician reads and records the air pressure from several pressure gauges. The table shows each air pressure reading in pascals (Pa). A pascal is a unit used to measure the amount of force applied on a given area by air or other gases.

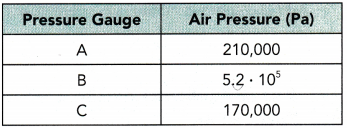
a) Which pressure gauge has the greatest reading?
Answer:
Pressure Gauge B has the greatest readings is 5.2 × 10⁵ = 520000

b) Which pressure gauge has the lowest reading?
Answer:
Pressure gauge C has the lowest reading is 170,000

c) The atmospheric pressure when these readings were made was 1.1 • 10⁵ pascals. Which gauge(s) showed a reading greater than the atmospheric pressure?
Answer:
All the gauges A, B, C are showed a greater reading than the atmospheric pressure.
210000 = 2.1 × 10⁵
520000 = 5.2 × 10⁵
170000 = 1.7 × 10⁵

Question 21.
Math Journal The table shows some numbers written in standard form and in the equivalent scientific notation. Describe the relationship between the pair of variables described in a) and b).

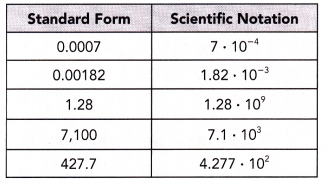
a) The value of the positive number in standard form and the sign of the exponent when expressed in scientific notation.
Answer:
When a number is written in scientific notation, the exponent tells you if the term is a large or a small number. A positive exponent indicates a large number and a negative exponent indicates a small number that is between 0 and 1.

b) The sign of the exponent when expressed in scientific notation and the direction the decimal point moves to express the number in standard form.
Answer:
In order to go between scientific notation and decimals, the decimal point is moved to the number of spaces indicated by the exponent. A negative exponent tells you to move the decimal point to the right, while a positive exponent tells you to move it to the left.

Question 22.
Math Journal When visible light passes through a prism the light waves refract, or bend and the colors that make up the light can be seen. Each color has a different wavelength, as shown in the diagram, which is refracted to a different degree.

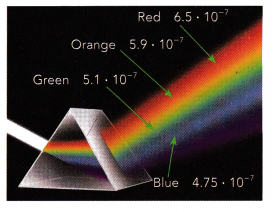
a) Shorter wavelengths refract more than longer wavelengths. Which color of light wave shows the most refraction? Which color of light wave shows the least refraction?
Answer:
Here the red light shows the longer wavelength is 6.5 × 10^-7, so the red color of the lightwave shows the most reflection. Blue color light shows the least reflection because the wavelength is

b) The frequency of a light wave is the number of waves that travel a given distance in a given amount of time. The shorter the wavelength, the greater the frequency. Order the wavelengths, in order of their frequencies, from least to greatest.
Answer:
Blue: 4.75 • 10^-7
Green: 5.1  • 10^-7
Orange: 5.9  • 10^-7
Red: 6.5 × 10^-7

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 2 Scientific Notation to finish your assignments.

Math in Focus Grade 8 Course 3 A Chapter 2 Answer Key Scientific Notation

Math in Focus Grade 8 Chapter 2 Quick Check Answer Key

Evaluate.

Question 1.
1.8 • 100
Answer: 180

Explanation:
Here the • indicates the product.
Here the decimal point moves to the right because we are multiplying the decimal number with the whole number 100.
when 1.8 is multiplied by 100 then we get 180.

Question 2.
-0.28 • 10³
Answer: 280

Explanation:
Here the • indicates the product.
Here the decimal point moves to the right because we are multiplying the decimal number with 10³.
-0.28 is multiplied by 10³ gives 280.

Question 3.
1.3 • 10⁴
Answer: 13000

Explanation:
Here the • indicates the product.
Here the decimal point moves to the right because we are multiplying the decimal number with 10⁴.
1.3 is multiplied by 10⁴ gives the result 13000.

Question 4.
74.5 ÷ 1,000
Answer: 0.0745

Explanation:
Here the ÷ indicates the division.
Here the decimal point moves to the left because we are dividing the decimal number by 1000.
74.5 is divided by 1000 gives the result 0.0745.

Question 5.
-3.8 ÷ 10
Answer: 0.38

Explanation:
Here the ÷ indicates the division.
Here the decimal point moves to the left because we are dividing the decimal number by 10.
-3.8 is divided by 10 gives the result -0.38.

Question 6.
2.81 ÷ 10²
Answer: 0.0281

Explanation:
Here the ÷ indicates the division.
Here the decimal point moves to the left because we are dividing the decimal number by 10².
2.81 is divided by 10² gives the result 0.0281.

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 1 Lesson 1.2 The Product and the Quotient of Powers to finish your assignments.

Math in Focus Grade 7 Course 3 A Chapter 1 Lesson 1.2 Answer Key Exponential Notation

Math in Focus Grade 8 Chapter 1 Lesson 1.2 Guided Practice Answer Key

Simplify each expression. Write your answer in exponential notation.

Question 1.
6⁴ • 6³ =
6⁴ • 6³ = Use the of powers property.
= Simplify.
Answer:
6⁷,

Explanation:
Given 6⁴ • 6³ using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base, So  6⁴ • 6³ = 6^{4 + 3} = 6⁷.

Question 2.
(-5) • (-5)⁵
(-5) • (-5)⁵ = Use the of powers property.
= Simplify the exponent.
= Simplify.
Answer:
(-5)⁶,

Explanation:
Given (-5) • (-5)⁵ using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base, So  (-5) • (-5)⁵ =(-5) ^{1 + 5} = (-5)⁶.

Question 3.

Answer:

Explanation:
Given \(\left(\frac{1}{5}\right)^{3}\) • \(\left(\frac{1}{5}\right)^{4}\)
using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base \(\left(\frac{1}{5}\right)^{3}\) • \(\left(\frac{1}{5}\right)^{4}\) =
\(\left(\frac{1}{5}\right)^{3 +4}\) = \(\left(\frac{1}{5}\right)^{7}\).

Simplify each expression. Write your answer in exponential notation.

Question 4.
p³ • p⁶
p³ • p⁶ = Use the of powers property.
= Simplify.
Answer:
p³ • p⁶ = p^{3 + 6} = p⁹,

Explanation:
Given \({p}^{3}\) • \({p}^{6}\)
using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base \({p}^{3}\) • \({p}^{6}\) =
\({p}^{3 + 6}\) = \({p}^{9}\).

Question 5.
(-c)⁴ • (-c)² 
Answer:
(-c)⁴ • (-c)² = (-c)⁴⁺² = (-c)⁶,

Explanation:
Given \({-c}^{4}\) • \({-c}^{2}\)
using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base \({-c}^{4}\) • \({-c}^{2}\) =
\({-c}^{4 + 2}\) = \({-c}^{6}\).

Question 6.
(3s)⁵ • (3s)
Answer:
(3s)⁵ • (3s) = (3s)⁵⁺¹ = (3s)⁶,

Explanation:
Given \({3s}^{5}\) • \({3s}^{1}\)
using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base \({3s}^{5}\) • \({3s}\) =
\({3s}^{5 + 1}\) = \({3s}^{6}\).

Simplify each expression. Write your answer in exponential notation.

Question 7.
pq³ • p⁵q²

Answer:

Explanation:
Given \({p}{q}^{1}{3}\) • \({p}{q}^{5}{2}\)
using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base \({p}^{1 + 5}\) • \({q}^{3 + 2}\) =
\({p}^{6}\) • \({q}^{5}\).

Question 8.
4s⁴t³ • 5s⁴t⁶

Answer:

Explanation:
Given 4. \({s}{t}^{4}{3}\) • 5 . \({s}{t}^{4}{5}\)
using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base 20 . \({s}^{4+ 4}\) •\({t}^{3 + 6}\) =
20 . \({s}^{8}\) • \({t}^{9}\).

Simplify each expression. Write your answer in exponential notation.

Question 9.
10⁸ ÷ 10⁵
10⁸ ÷ 10⁵ = Use the of powers property.
= Simplify.
Answer:
10⁸ ÷ 10⁵ = 10³,

Explanation:
Given to find 10⁸ ÷ 10⁵  dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take 10⁸ ÷ 10⁵ = 10^8-5= 10³.

Explanation:
Given to find 2.7⁹ ÷ 2.7⁶ dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent), means we take 2.7⁹ ÷ 2.7⁶ = 2.7^9-6= 2.7³.

Question 11.
\(\left(\frac{5}{8}\right)^{6}\) ÷ \(\left(\frac{5}{8}\right)\)

= Use the of powers property.
=
Simplify.
Answer:
\(\left(\frac{5}{8}\right)^{5}\),

Explanation:
Given \(\left(\frac{5}{8}\right)^{6}\) ÷ \(\left(\frac{5}{8}\right)\)
dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent) means we take as
\(\left(\frac{5}{8}\right)^{6-1}\) = \(\left(\frac{5}{8}\right)^{5}\).

Simplify each expression. Write your answer in exponential notation.

Question 12.
q⁷ ÷ q²
q⁷ ÷ q² =
= Simplify
Answer:
\({q}^{5}\),

Explanation:
Given to find q⁷ ÷  q²  dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take q⁷ ÷ q² = q^7-2= q⁵.

Question 13.
(-p)⁵ ÷ (-p)³
Answer:
\({-p}^{2}\),

Explanation:
Given to find (-p)⁵ ÷ (-p)²  dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take (-p)⁵ ÷ (-p)³ = (-p)^5-3= (-p)².

Question 14.

Answer:
(r)³ . (s)²,  

Explanation:
Given to find (r)⁸ (s)⁶ ÷ (r)⁵ (s)⁴ dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take
(r)⁸ (s)⁶ ÷ (r)⁵ (s)⁴ = (r)^8-5 . (s)^6-4 = (r)³ . (s)².  

Question 15.

Answer:

Explanation:
Given to find 63 (x)⁹ (y)⁷ ÷ 9.(x)³ (y)⁴ dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take
63 (x)⁹ (y)⁷ ÷ 9 (x)³ (y)⁴ = 7 . (x)^9-3 . (y)^7-4 = 7. (x)⁶ (y)³ .  

Simplify each expression. Write your answer in exponential notation.

Question 16.

Answer:
\({6}^{2}\),

Explanation:
Given to find (6)⁷ (6)³ (6)² ÷ (6)¹ (6)⁴ (6)⁵ dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take
(6)⁷ (6)³ (6)² ÷ (6)¹ (6)⁴ (6)⁵ = (6)⁷⁺³⁺²÷ (6)¹⁺⁴⁺⁵ =
(6)¹² ÷ (6)¹⁰=(6)^12-10 = (6)².

Question 17.

Answer:
\({7.5}^{2}\),

Explanation:
Given to find (7.5)⁵ (7.5)³ (7.5)¹ ÷ (7.5)² (7.5)¹ (7.5)⁴ dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take
(7.5)⁵ (7.5)³ (7.5)¹ ÷ (7.5)² (7.5)¹ (7.5)⁴ = (7.5)⁵⁺³⁺¹÷ (7.5)²⁺¹⁺⁴ =
(7.5)⁹ ÷ (7.5)⁷=(7.5)^9-7 = (7.5)².

Question 18.

Answer:

Explanation:
Given to find (b)⁵ (4a)⁴ (9a)³ ÷ (2a)² (b)² (6a)² dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take
(9).(4).(a)⁴⁺³.(b)⁵ ÷ (2).(6).(a)²⁺² (b)³ = ((36).(a)⁷ .(b)⁵ )÷ (12). (a)⁴.(b)² =
(3)(a)^7-4 (b)^5-2=(3)(a)³ (b)³.

Solve. Show your work.

Question 19.
Jupiter is approximately 108 kilometers from the Sun.
The dwarf planet Eris is about 101° kilometers from the Sun.
How many times as far as Jupiter is Eris from the Sun?

Answer:
Eris is 100 times as far as Jupiter from the Sun,

Explanation:

Math in Focus Course 3A Practice 1.2 Answer Key

Question 1.
(-2)⁶ • (-2)²
Answer:
(-2)⁸ ,

Explanation:
Given (-2)⁶ • (-2)² using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base, So  (-2)⁶ • (-2)² =(-2) ^{6 + 2} = (-2)⁸.

Question 2.
7.²3 • 7.2⁴
Answer:
7.2³ . 7.2⁴ = 7.2³⁺⁴ = 7.2⁷,

Explanation:
Given to find 7.2³ . 7.2⁴ using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base, So 7.2³ . 7.2⁴ = 7.2³⁺⁴= 7.2⁷.

Question 3.
10⁵ • 10⁴
Answer:
10⁹

Explanation:
Given 10⁵ • 10⁴ using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base, So 10⁵ • 10⁴ = 10⁵⁺⁴ = 10⁹.

Question 4.
\(\left(\frac{2}{3}\right) \cdot\left(\frac{2}{3}\right)^{5}\)
Answer:
\(\left(\frac{2}{3}\right)^{6}\),

Explanation:
Given \(\left(\frac{2}{3}\right)^{1}\) • \(\left(\frac{2}{3}\right)^{5}\)
using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base \(\left(\frac{2}{3}\right)^{1}\) • \(\left(\frac{2}{3}\right)^{5}\) =
\(\left(\frac{2}{3}\right)^{1 +5}\) = \(\left(\frac{2}{3}\right)^{6}\).

Question 5.
p • p⁸
Answer:
p¹ • p⁸ = p^{1 + 8} = p⁹,

Explanation:
Given \({p}^{1}\) • \({p}^{8}\)
using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base \({p}^{1}\) • \({p}^{8}\) =
\({p}^{1 + 8}\) = \({p}^{9}\).

Question 6.
q⁸ ÷ q
Answer:
\({q}^{7}\),

Explanation:
Given to find q⁸ ÷  q¹  dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take q⁸ ÷ q¹ = q^8-1= q⁷.

Question 7.
xy² • x⁴y³
Answer:
\({x}^{5}\) • \({y}^{5}\),

Explanation:
Given xy² • x⁴y³
using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base \({x}^{1 + 4}\) • \({y}^{2 + 3}\) =
\({x}^{5}\) • \({y}^{5}\).

Question 8.
2x²y⁴ • 5x⁵y
Answer:
10 X \({x}^{7}\) • \({y}^{5}\),

Explanation:
Given 2x²y⁴ • 5x⁵y using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base (2 X 5) X \({x}^{2 + 5}\) • \({y}^{4 + 1}\) =
10 X \({x}^{7}\) • \({y}^{5}\).

Question 9.
2.5x³y⁶ • 3x²y⁴
Answer:
7.5 X \({x}^{5}\) • \({y}^{10}\),

Explanation:
Given 2.5 X x³y⁶ • 5x²y⁴ using the Product of Powers Property states that when
multiplying two exponents with the same base, we add the exponents and
keep the base (2.5 X 3) X \({x}^{3 + 2}\) • \({y}^{6 + 4}\) =
7.5 X \({x}^{5}\) • \({y}^{10}\).

Question 10.
(-3)⁴ ÷ (-3)²
Answer:
(-3)² ,

Explanation:
Given to find (-3)⁴ ÷  (-3)²  dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take (-3)⁴ ÷ (-3)² = (-3)^4-2= (-3)².

Question 11.
2¹⁰ ÷ 2⁵
Answer:
2⁵,

Explanation:
Given to find 2¹⁰ ÷  2⁵  dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take 2¹⁰ ÷ 2⁵ = 2^10-5= 2⁵.

Question 12.
\(\left(-\frac{1}{6}\right)^{5} \div\left(-\frac{1}{6}\right)^{2}\)
Answer:
\(\left(-\frac{1}{6}\right)^{3}\),

Explanation:
Given \(\left(-\frac{1}{6}\right)^{5}\) ÷ \(\left(-\frac{1}{6}\right)^{2}\)
dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent) means we take as
\(\left(-\frac{1}{6}\right)^{5-2}\) = \(\left(-\frac{1}{6}\right)^{3}\).

Question 13.
63y³z⁵ ÷ 9
Answer:
7y³z⁵,

Explanation:
Given to find 63 (y)³ (z)⁵ ÷ 9 dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take
63 (y)³ (z)⁵ ÷ 9 = 7. (y)³ (z)⁵ .  

Question 14.
h²k⁵ ÷ hk⁴
Answer:
hk,

Explanation:
Given to find  (h)² (k)⁵ ÷ h.(k)⁴ dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take
(h)² (k)⁵ ÷  h. (k)⁴ = (h)^2-1 . (k)^5-4 = hk.  

Question 15.
64a⁸b⁵ ÷ 4a³b²
Answer:
16a⁵b³,

Explanation:
Given to find 64 (a)⁸ (b)⁵ ÷ 4.(a)³ (b)² dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take
64 (a)⁵ ( b)³ ÷ 4 (a)³ (b)² = 16 . (a)^8-3 . (b)^5-2 = 16. a⁵b³ . 

Question 16.
\(\frac{5^{9} \cdot 5^{7} \cdot 5^{8}}{5^{3} \cdot 5^{2} \cdot 5}\)
Answer:
5¹⁸,

Explanation:
Given to find (5)⁹ (5)⁷ (5)⁸ ÷ (5)³ (5)² (5)¹ dividing them with the exponent value in
(5)⁹ (5)⁷ (5)⁸ ÷ (5)³ (5)² (5)¹ the numerator (the top exponent) and
subtract the exponent value of the denominator (the bottom exponent).
Here that means we take (5)⁹⁺⁷⁺⁸ ÷ (5)³⁺²⁺¹ = (5)²⁴ ÷ (5)⁶=(5)^24-6 = (5)¹⁸.

Question 17.

Answer:
\(\left(\frac{4}{9}\right)^{5}\),

Explanation:
Given to find \(\left(\frac{4}{9}\right)^{6}\). \(\left(\frac{4}{9}\right)^{5}\).
\(\left(\frac{4}{9}\right)^{4}\)  ÷ \(\left(\frac{4}{9}\right)^{3}\). \(\left(\frac{4}{9}\right)^{3}\). \(\left(\frac{4}{9}\right)^{4}\) dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take
\(\left(\frac{4}{9}\right)^{6+5+4}\) ÷ \(\left(\frac{4}{9}\right)^{3 +3+4}\),
\(\left(\frac{4}{9}\right)^{15}\) ÷ \(\left(\frac{4}{9}\right)^{10}\),
\(\left(\frac{4}{9}\right)^{15-10}\) = \(\left(\frac{4}{9}\right)^{5}\).

Question 18.
\(\frac{a^{9} \cdot a^{2} \cdot a^{3}}{a^{6} \cdot a^{3} \cdot a^{4}}\)
Answer:
a,

Explanation:
Given \(\frac{a^{9} \cdot a^{2} \cdot a^{3}}{a^{6} \cdot a^{3} \cdot a^{4}}\)
to find dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take
\(\frac{a^{9+2+3} \cdot}{a^{6+3+4} \cdot}\) =
\(\frac{a^{14} \cdot}{a^{13} \cdot}\) = (a)^14-13 = = a.

Question 19.
\(\frac{b^{4} \cdot b^{6} \cdot b}{b^{3} \cdot b^{3} \cdot b^{3}}\)
Answer:
(b)²,

Explanation:
Given \(\frac{b^{4} \cdot b^{6} \cdot b}{b^{3} \cdot b^{3} \cdot b^{3}}\)
to find dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take
\(\frac{b^{4+6+1} \cdot}{a^{3+3+3} \cdot}\) =
\(\frac{b^{11} \cdot}{b^{9} \cdot}\) = (b)^11-9 = (b)².

Question 20.
\(\frac{3 x^{3} \cdot z^{4} \cdot 4 x^{3}}{2 x \cdot x \cdot 3 z}\)
Answer:
2x⁴z³,

Explanation:
Given to find 3.(x)³ (z)⁴ . 4(x)³ ÷ 2.(x)(x) (z) dividing them with the exponent value in
the numerator (the top exponent) and subtract the exponent value of the
denominator (the bottom exponent). Here that means we take
12 (x)⁶ (z)⁴ ÷ 6 (x)² (z) = 2 . (x)^6-2 . (z)^4-1 = 2. (x)⁴ (z)³ .  

Question 21.
\(\frac{4 c^{6} \cdot 3 b^{4} \cdot 9 c^{5}}{b^{3} \cdot 6 c^{3} \cdot 2 c^{3}}\)
Answer:
9bc⁵,

Explanation:
Given to find \(\frac{4 c^{6} \cdot 3 b^{4} \cdot 9 c^{5}}{b^{3} \cdot 6 c^{3} \cdot 2 c^{3}}\)
dividing them with the exponent value in the numerator (the top exponent) and
subtract the exponent value of the denominator (the bottom exponent).
Here that means we take 4(c)⁶. 3(b)⁴ . 9(c)⁵  ÷ (b)³ . 6 (c)³ . 2(c)³  =
9 . (b)^4-3 . (c)^11-6 = 9.(b).(c)⁵ .  

Solve. Show your work.

Question 22.
Pluto has a diameter of about 103 kilometers. The diameter of Saturn is
approximately 105 kilometers.
How many times as great as Pluto’s diameter is Saturn’s diameter?

Answer:
100 times as great as Pluto’s diameter is Saturn’s diameter,

Explanation:
Given Pluto has a diameter of about (10)³ kilometers.
The diameter of Saturn is approximately (10)⁵ kilometers.
So number of times as great as Pluto’s diameter is Saturn’s diameter is
(10)^5-3 = (10)²,
therefore 100 times as great as Pluto’s diameter is Saturn’s diameter.

Question 23.
Use the rectangular prism shown.
a) Express the volume of the rectangular prism using exponential notation.
Answer:
6(x)³,

Explanation:
Given width of the rectangular prism as 2x units,
height as x units and length as 3x units so the
volume of the rectangular prism using exponential notation is
w X h X l = 2x X x X 3x =6(x)¹⁺¹⁺¹ = 6(x)³.

b) Another prism has dimensions that are twice the dimensions of the prism shown.
Express the volume of that prism using exponential notation.
Answer:

Explanation:
Given another prism has dimensions that are twice the dimensions of the prism shown.
Expressing the volume of that prism using exponential notation is
width of the rectangular prism as 2x X 2x = 4x¹⁺¹  = 4x² units,
height as 2 X x = 2x units and length as 3x X 3 x = 9x¹⁺¹ = 9x² units,
So the volume of the rectangular prism using exponential notation is
w X h X l = 4x² X 2x X 9x² = 72 (x)²⁺¹⁺² = 72(x)⁵.

c) How many times greater is the volume of the larger prism than the volume of the smaller prism?
Answer:
12x² times greater is the volume of the larger prism than the volume of the smaller prism,

Explanation:
To know number of times greater is the volume of the larger prism than the
volume of the smaller prism, we divide 72(x)⁵ ÷ 6(x)³ = 12(x)^5-3 = 12(x)².

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 1 Lesson 1.3 The Power of a Power to finish your assignments.

Math in Focus Grade 7 Course 3 A Chapter 1 Lesson 1.3 Answer Key The Power of a Power

Math in Focus Grade 8 Chapter 1 Lesson 1.3 Guided Practice Answer Key

Hands-On Activity

Materials:

• three stacks of five cards, each labeled with a number from

Explore The Power

In this activity, you and your partner will play a game in which you write and
evaluate expressions in the form (a^m)ⁿ.
You will get a point for each expression you write, and the person with the greater score wins.

Step 1.
Shuffle each stack of number cards and place them in a pile. Each player randomly draws three cards, one from each pile.

Step 2
Use your three cards to write an expression in the form (a^m)ⁿ.
For instance, if you draw 2, 4, and 5, you could write (2⁴)⁵,(4²)⁵, or another expression.
Write as many expressions as you can. You may want to use a calculator to evaluate your expression.
For instance, to evaluate (2⁴)⁵, you can use these keystrokes:

Step 3.
Record your expressions and their values.
Your partner should also record his or her expressions and their values.
Check your partner’s work.

Step 4.
Continue the game by replacing the cards you used and shuffling the piles.
Repeat Step 1 to Step 2 several more times. When you are finished,
find each player’s score by counting the number of correct expressions that
each player has written. The player with the greater score wins.

Math Journal Is it correct to assume that using the greatest number drawn as
the base will give the expression with the greatest possible value?
Explain or give an example.
Answer:
Yes,
Example: Drawing numbers 7,3,8,

Explanation:
Yes it is correct to assume that using the greatest number drawn as
the base will give the expression with the greatest possible value example
if we draw 7,3,8 we could write (8⁷)³,(7⁸)³.

Simplify each expression. Write your answer in exponential notation.

Question 1.
(5³)⁴
(5³)⁴ = Use the of a power property.
= Simplify.
Answer:
(5)¹²,

Explanation:
Given (5³)⁴ used the power of a power property and simplified as
(5)^3X4 = (5)¹².

Question 2.
(2.3⁴)²
(2.3⁴)² = Use the of a power property.
= Simplify.
Answer:
(2.3)⁸,

Explanation:
Given (2.3⁴)² used the power of a power property and simplified as
(2.3)^{4 X 2} = (2.3)⁸.

Question 3.
[(3p)⁵]⁴
Answer:
(3p)²⁰,

Explanation:
Given [(3p)⁵]⁴ used the power of a power property and simplified as
(3p)^{5 X 4} = (3p)²⁰.

Question 4.
[(-y)⁴]⁷
Answer:
(-y)²⁸,

Explanation:
Given (-y⁴)⁷ used the power of a power property and simplified as
(-y)^4X7 = (-y)²⁸.

Simplify each expression. Write your answer in exponential notation.

Question 5.
[(-3) • (-3)⁶]²

Answer:
(-3)¹⁴,

Explanation:

Question 6.
[p⁴ • p²]⁵

Answer:
(p)³⁰,

Explanation:

Question 7.
(6³ • 6³]⁷ ÷ 6¹⁰

Answer:
(6)³²,

Explanation:

Question 8.

Answer:
(x)⁶,

Explanation:

Math in Focus Course 3A Practice 1.3 Answer Key

Simplify each expression. Write your answer in exponential notation.

Question 1.
(2⁶)²
Answer:
(2)¹²,

Explanation:
Given (2⁶)² used the power of a power property and simplified as
(2)^{6 X 2} = (2)¹².

Question 2.
(3⁴)³
Answer:
(3)¹²,

Explanation:
Given (3⁴)³ used the power of a power property and simplified as
(3)^{4 X 3} = (3)¹².

Question 3.
(10⁵)⁴
Answer:
(10)²⁰,

Explanation:
Given (10⁵)⁴ used the power of a power property and simplified as
(10)^{5 X 4} = (10)²⁰.

Question 4.
(10⁷)²
Answer:
(10)¹⁴,

Explanation:
Given (10⁷)² used the power of a power property and simplified as
(10)^{7X 2} = (10)¹⁴.

Question 5.
(25³)³
Answer:
(25)⁹,

Explanation:
Given (25³)³ used the power of a power property and simplified as
(25)^{3X 3} = (25)⁹.

Question 6.
(x⁶)³
Answer:
(x)¹⁸,

Explanation:
Given (x⁶)³ used the power of a power property and simplified as
(x)^{6 X 3} = (x)¹⁸.

Question 7.
\(\left[\left(\frac{1}{8}\right)^{3}\right]^{6}\)
Answer:
\([\left(\frac{1}{8}\right)^{18}\),

Explanation:
Given \([\left(\frac{1}{8}\right)^{3}]^{6}\)
used the power of a power property and simplified as
\([\left(\frac{1}{8}\right)^{3 X 6}\) =
\([\left(\frac{1}{8}\right)^{18}\).

Question 8.
\(\left[\left(\frac{4}{5}\right)^{2}\right]^{4}\)
Answer:
\([\left(\frac{4}{5}\right)^{8}\),

Explanation:
Given \(\left[\left(\frac{4}{5}\right)^{2}\right]^{4}\)
used the power of a power property and simplified as
\([\left(\frac{4}{5}\right)^{2X4}\) =
\([\left(\frac{4}{5}\right)^{8}\).

Question 9.
[(2y)³]⁸
Answer:
(2y)²⁴,

Explanation:
Given [(2y)³)]⁸ used the power of a power property and simplified as
(2y)^3X8 = (2y)²⁴.

Question 10.
[(57p)⁴]⁴
Answer:
(57p)¹⁶,

Explanation:
Given [(57p)⁴)⁴ used the power of a power property and simplified as
(57p)^{4 X 4} = (57)¹⁶.

Question 11.
[(-6)⁴]³
Answer:
(-6)¹²,

Explanation:
Given [(-6)⁴)³ used the power of a power property and simplified as
(-6)^4X3 = (-6)¹².

Question 12.
[(-p)²]¹¹
Answer:
(-p)²²,

Explanation:
Given [(-p)²]¹¹ used the power of a power property and simplified as
(-p)^2X11 = (-p)²².

Question 13.
Math Journal Michael thinks that (a³)² = a⁵. Is he correct? Why?

Answer:
No, Michael is not correct as [(a)³]² = (a)⁶≠(a)⁵,

Explanation:
Given (a³)² = a⁵ used the power of a power property and simplified as
(a)^3X2 = (a)⁶≠(a)⁵. Therefore Michael is incorrect.

Simplify each expression. Write your answer in exponential notation.

Question 14.
(5⁵ • 5⁶)²
Answer:
(5)²²,

Explanation:
Given ((5⁵ • 5⁶)² used the product of a power property as
(5⁵⁺⁶)² = (5¹¹)² and using power of power property simplified as
(5)^11X2 = (5)²².

Question 15.
(p⁴ • p²)⁶
Answer:
(p)⁴⁸,

Explanation:
Given ((5⁵ • 5⁶)² used the product of a power property as
(5⁵⁺⁶)² = (5¹¹)² and using power of power property simplified as
(5)^11X2 = (5)²².

Question 16.
\(\left[\left(\frac{1}{2}\right) \cdot\left(\frac{1}{2}\right)^{3}\right]^{5}\)
Answer:
\(\left[(\frac{1}{2}\right)^{20}\),

Explanation:
Given \(\left[\left(\frac{1}{2}\right) \cdot\left(\frac{1}{2}\right)^{3}\right]^{5}\)
Using the product of a power property as \(\left[\left(\frac{1}{2}\right)^{1+
3}\right]^{5}\) = \(\left[\left(\frac{1}{2}\right)^{4}\right]^{5}\) and using power of power property simplified as \(\left(\frac{1}{2}\right)^{4 X 5}\) = \(\left(\frac{1}{2}\right)^{20}\).

Question 17.
\(\left[\left(-\frac{4}{9}\right)^{2} \cdot\left(-\frac{4}{9}\right)^{3}\right]^{2}\)
Answer:
\(\left[(-\frac{4}{9}\right)^{10}\),

Explanation:
Given \(\left[\left(-\frac{4}{9}\right)^{2} \cdot\left(-\frac{4}{9}\right)^{3}\right]^{2}\)
Using the product of a power property as \(\left[\left(-\frac{4}{9}\right)^{2+
3}\right]^{2}\) = \(\left[\left(-\frac{4}{9}\right)^{5}\right]^{2}\) and using power of power property simplified as \(\left(-\frac{4}{9}\right)^{5 X 2}\) = \(\left(-\frac{4}{9}\right)^{10}\).

Question 18.
(2² • 2⁴)³ ÷ 2⁸
Answer:
2¹⁰,

Explanation:
Given (2² • 2⁴)³ ÷ 2⁸ used the product of a power property as
(2²⁺⁴)³  ÷ 2⁸  = (2⁶)³ ÷ 2⁸ and using power of power property simplified as
(2)^6X3 ÷ 2⁸  = ( 2)¹⁸ ÷2⁸ using division of power property ( 2)^18-8 = (2)¹⁰.

Question 19.
(7 • 7²)⁵ ÷ 7³
Answer:
^{( 7)12,}

Explanation:
Given (7 • 7²)⁵ ÷ 7³ used the product of a power property as
(7¹⁺²)⁵  ÷ 7³  = (7³)⁵ ÷ 7³ and using power of power property simplified as
(7)^3X5 ÷ 7³  = ( 7)¹⁵ ÷7³ using division of power property ( 7)^15-3 = ( 7)¹².

Question 20.
(s⁶ • s²) ÷ s⁴
Answer:
(s)⁴,

Explanation:
Given (s⁶ • s²) ÷ s⁴ used the product of a power property as
(s⁶⁺²) ÷ s⁴  = (s⁸) ÷ s⁴  using division of power property ( s)^8-4 = ( s)⁴.

Question 21.
(t⁴ • t⁴) ÷ t⁴
Answer:
(t)⁴,

Explanation:
Given (t⁴ • t⁴) ÷ t⁴ used the product of a power property as
(t⁴⁺⁴) ÷ t⁴  = (t⁸) ÷ t⁴  using division of power property (t)^8-4 = ( t)⁴.

Question 22.
\(\frac{\left(8^{8} \cdot 8^{3}\right)^{2}}{\left(8^{5}\right)^{4}}\)
Answer:
8²,

Explanation:
Given \(\frac{\left(8^{8} \cdot 8^{3}\right)^{2}}{\left(8^{5}\right)^{4}}\)  used the product of a power property as \(\frac{\left(8^{8+3}\right)^{2}}{\left(8^{5}\right)^{4}}\)
and using power of power property simplified as \(\frac{(8)^{11 X 2}}{(8)^{5 X 4}}\)
 using division of power property (8)^22-20 = (8)².

Question 23.
\(\frac{\left(3^{4} \cdot 3^{2}\right)^{4}}{\left(3^{5}\right)^{2}}\)
Answer:
3¹⁴,

Explanation:
Given \(\frac{\left(3^{4} \cdot 3^{2}\right)^{4}}{\left(3^{5}\right)^{2}}\) used the product of a power property as \(\frac{\left(3^{4+2}\right)^{4}}{\left(3^{5}\right)^{2}}\)
and using power of power property simplified as \(\frac{(3)^{6 X 4}}{(3)^{5 X 2}}\)
 using division of power property (3)^24-10 = (3)¹⁴.

Question 24.
\(\frac{\left(b \cdot b^{3}\right)^{5}}{\left(b^{2}\right)^{4}}\)
Answer:
b¹²,

Explanation:
Given \(\frac{\left(b \cdot b^{3}\right)^{5}}{\left(b^{2}\right)^{4}}\) used the product of a power property as \(\frac{\left(b^{1+3}\right)^{5}}{\left(b^{2}\right)^{4}}\)
and using power of power property simplified as \(\frac{(b)^{4 X 5}}{(b)^{2X 4}}\)
 using division of power property (b)^20-8 = (b)¹².

Question 25.
\(\frac{\left(h^{6} \cdot h^{6}\right)^{2}}{\left(h^{3}\right)^{5}}\)
Answer:
h⁹,

Explanation:
Given \(\frac{\left(h^{6} \cdot h^{6}\right)^{2}}{\left(h^{3}\right)^{5}}\) used the product of a power property as \(\frac{\left(h^{6+6}\right)^{2}}{\left(h^{3}\right)^{5}}\)
and using power of power property simplified as \(\frac{(h)^{12 X 2}}{(h)^{3X 5}}\)
 using division of power property (h)^24-15 = (h)⁹.

Question 26.
(q⁵ • q²)³) ÷ 5q⁵
Answer:
(q)¹⁶÷ 5 or 1/5 . q¹⁶,

Explanation:
Given ((q⁵ • q²)³) ÷ 5q⁵  used the product of a power property as
((q⁵⁺²)³) ÷ 5q⁵  and using power of power property simplified as ((q)^{7 X 3} ) ÷ 5q⁵  using
division of power property (q)^21-5 ÷ 5 = (q)¹⁶÷ 5 or 1/5 . q¹⁶.

Question 27.
(c⁷ • q³)⁴ ÷ 6c²
Answer:
(c²⁶• q¹²) ÷ 6 or 1/6 . q¹⁶,

Explanation:
Given ((c⁷ • q³)⁴) ÷ 6c² using power of power property simplified as
((c)^{7 X4} • q^3X4) ÷ 6c²  using division of power property ((c)^28-2 • q¹² ) ÷ 6 =
(c²⁶• q¹²) ÷ 6 or 1/6 . q¹⁶.

Question 28.

Answer:
\(\left(\frac{2}{3}\right)^{2}\),

Explanation:
Given (\(\left[(\frac{2}{3}\right)^{2}\) . \(\left[(\frac{2}{3}\right)^{6}\))÷\(\left[(\frac{2}{3}\right)^{2 X 3}\)] using product of power property simplified as
\(\left(\frac{2}{3}\right)^{2+ 6}\) ÷\(\left(\frac{2}{3}\right)^{6}\) using
division of power property \(\left[(\frac{2}{3}\right)^{8-6}\)] we get
\(\left(\frac{2}{3}\right)^{2}\).

Question 29.

Answer:
\(\left(\frac{x}{2}\right)^{1}\),

Explanation:
Given (\(\left[(\frac{x}{2}\right)^{3}\) . \(\left[(\frac{x}{2}\right)^{4}\))÷\(\left[(\frac{x}{2}\right)^{3 X 2}\)] using product of power property simplified as
\(\left(\frac{x}{2}\right)^{3+ 4}\) ÷\(\left(\frac{x}{2}\right)^{6}\) using
division of power property \(\left[(\frac{x}{2}\right)^{7-6}\)] we get
\(\left(\frac{x}{2}\right)^{1}\).

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 1 Exponents to finish your assignments.

Math in Focus Grade 8 Course 3 A Chapter 1 Answer Key Exponents

Math in Focus Grade 8 Chapter 1 Quick Check Answer Key

Identify the integers in the list below.

Question 1.
4.31, -6, 8.12, 58, -211,43
Answer:
-211,-6,43 and 58,

Explanation:
Integers are positive,negative and zero but not decimal numbers therefore
from the given numbers 4.31 and 8.12 are not integers
the integers are -211,-6,43 and 58.

Write each rational number as a terminating decimal.

Question 2.
\(\frac{3}{5}\)
Answer:
0.6,

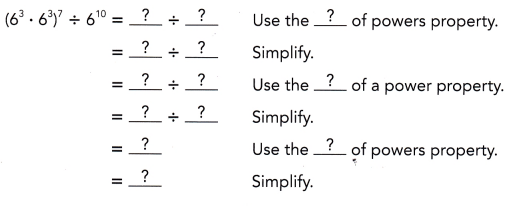
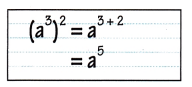
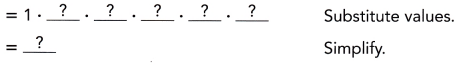
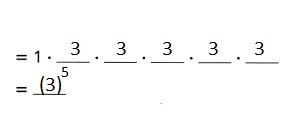
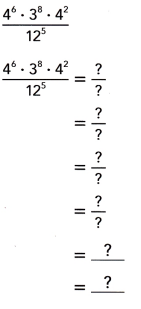
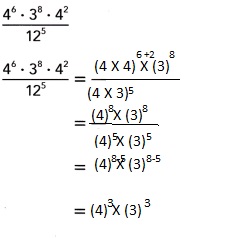
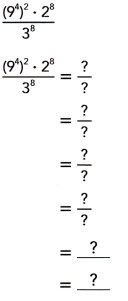
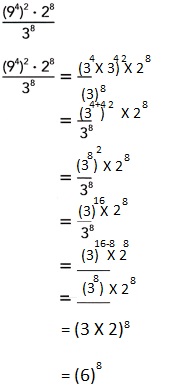
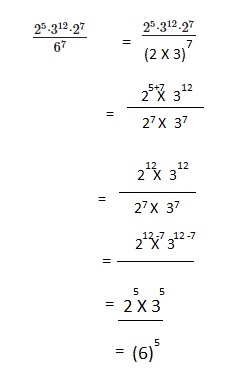
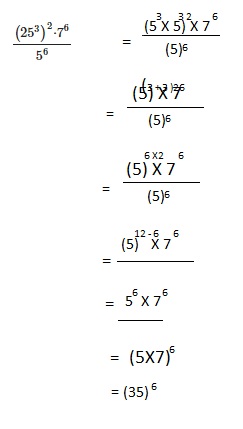
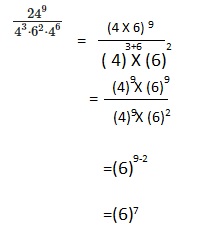
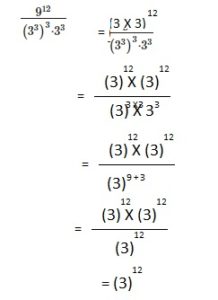
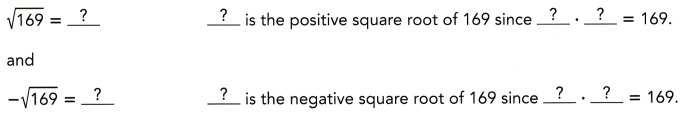
Explanation:

when we divide 3 by 5 we get terminating decimal as 0.6.

Question 3.
4\(\frac{1}{4}\)
Answer:
4.25,

Explanation:
Given 4\(\frac{1}{4}\) we get \(\frac{4 x 4 + 1}{4}\) =
\(\frac{17}{4}\)
the terminating decimal is 4.25.

Write each rational number as a repeating decimal.

Question 4.
\(\frac{6}{11}\)
Answer:
The repeating decimal of 6/11 is 0.5363636 and so on,

Explanation:
Given to find \(\frac{6}{11}\) we get

the repeating decimal of 6/11 is 0.5363636 and so on.

Question 5.
\(\frac{5}{12}\)
Answer:
The repeating decimal of 5/12 is 0.4166 so on,

Explanation:

The repeating decimal of 5/12 is 0.4166 so on.

Locate each irrational number on a number line using rational approximation.

Question 6.

Answer:

Explanation:
Located irrational number cube root of -47 on the
number line – 3.6 using rational approximation.

Question 7.
\(\sqrt{19}\)
Answer:

Explanation:
Located irrational number square root of 19 on the
number line 4.35 using rational approximation.

Evaluate each expression.

Question 8.
-3 + (-4)
Answer:
-7,

Explanation:
Adding  -3 to -4 we get -7.

Question 4.
-4 – (-2)
Answer:
-6,

Explanation:
Adding -4 to -2 we get -6.

Evaluate each expression.

Question 10.
(-7) • (-3)
Answer:
21,

Explanation:
Given -7 multiplied by -3 we get – 7 X -3 = 21.

Question 11.
(-12) ÷ 3
Answer:
-4,

Explanation:
Given to divide (-12) with 3 we get -4.

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 1 Lesson 1.4 The Power of a Product and the Power of a Quotient to finish your assignments.

Math in Focus Grade 7 Course 3 A Chapter 1 Lesson 1.4 Answer Key The Power of a Product and the Power of a Quotient

Math in Focus Grade 8 Chapter 1 Lesson 1.4 Guided Practice Answer Key

Simplify each expression. Write your answer in exponential notation.

Question 1.
6³ • 7³
6³ • 7³ = Use the power of a property.
= Simplify.
Answer:
(6 X 7)³ = (42)³,

Explanation:
Given 6³ • 7³  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(6 X 7)³ = (42)³.

Question 2.

Answer:
(5/24)⁴,

Explanation:
Given (-5/6)⁴. (- 1/4)⁴ when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product and quotients of a property,
(-5/6 X -1/4)⁴ = (5/24)⁴.

Question 3.
(1.8)² • (0.75)²
(1.8)² • (0.75)² = Use the power of a property.
= Simplify.
Answer:
((1.8) • (0.75))²,

Explanation:
Given (1.8)² • (0.75)² when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product of a property,
((1.8) • (0.75))².

Simplify each expression. Write your answer in exponential notation.

Question 4.
p⁶ • q⁶
p⁶ • q⁶ = Use the power of a property.
= Simplify.
Answer:
(p X q)⁶ ,

Explanation:
Given p⁶ • q⁶  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(p X q)⁶ .

Question 5.
(3a)⁴ • (4b)⁴
(3a)⁴ • (4b)⁴ = Use the power of a property.
= Simplify.
Answer:
(3a X 4b)⁴ ,

Explanation:
Given (3a)⁴ • (4b)⁴  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property we get (3aX 4b)⁴.

Question 6.
(-3y²)³ • \(\left(\frac{1}{12 y}\right)^{3}\)
Answer:
\(\left(-\frac{y}{4}\right)^{3}\),

Explanation:
Given (-3y²)³ • \(\left(\frac{1}{12 y}\right)^{3}\) on simplification
(-y)^{2 X 3} • \(\left(\frac{1}{4 y}\right)^{3}\) = (-y)^6-3 • \(\left(\frac{1}{4}\right)^{3}\) =
(-y)³ • \(\left(\frac{1}{4}\right)^{3}\) = \(\left(-\frac{y}{4}\right)^{3}\).

Simplify each expression. Write your answer in exponential notation.

Question 7.
2⁵ ÷ 4⁵

Answer:
\(\left(\frac{1}{2}\right)^{5}\),

Explanation:
Given 2⁵ ÷ 4⁵  as 4 can be written as (2 X 2) so 2⁵ ÷ (2 X 2)⁵ upon simplification
we get 1/2⁵ or \(\left(\frac{1}{2}\right)^{5}\).

Question 8.
(-9)³ ÷ (-3)³

Answer:
(3)³,

Explanation:
Given(-9)³ ÷ (-3)³  as (-9) can be written as (-3 X 3) so (-3 X 3)³ ÷ (-3)³
on simplification we get (3)³.

Simplify each expression. Write your answer in exponential notation.

Question 9.
x⁴ ÷ y⁴

Answer:
\(\left(\frac{x}{y}\right)^{4}\),

Explanation:
Given x⁴ ÷ y⁴ when the variable bases are different and the
powers are the same, the bases are simplified first as (x ÷ y)⁴ and solved.

Question 10.
(8p)⁵ ÷ (3q)⁵
Answer:
(8p ÷ 3q)⁵,

Explanation:
Given (8p)⁵ ÷ (3q)⁵ when the variable bases are different and the
powers are the same, the bases are simplified first as (8p ÷ 3q)⁵ and solved.

Simplify each expression. Write your answer in exponential notation.

Question 11.

Answer:
(2)⁷,

Explanation:

Question 12.

Answer:
(4)³ X (3)³,

Explanation:

Question 13.

Answer:
(6)⁸,

Explanation:

Question 14.
\(\frac{2^{5} \cdot 3^{12} \cdot 2^{7}}{6^{7}}\)
Answer:
(6)⁵,

Explanation:
Given \(\frac{2^{5} \cdot 3^{12} \cdot 2^{7}}{6^{7}}\),
6 can be written as 2 X 3 so \(\frac{2^{5} \cdot 3^{12} \cdot 2^{7}}{({2 X 3})^{7}}\),

Question 15.
\(\frac{\left(25^{3}\right)^{2} \cdot 7^{6}}{5^{6}}\)
Answer:
(35)⁶,

Explanation:
Given \(\frac{\left(25^{3}\right)^{2} \cdot 7^{6}}{5^{6}}\)

Math in Focus Course 3A Practice 1.4 Answer Key

Simplify each expression. Write your answer in exponential notation.

Question 1.
5⁴ • 6⁴
Answer:
(5 X 6)⁴ = (30)⁴,

Explanation:
Given 5⁴ • 6⁴  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(5 X 6)⁴ = (30)⁴.

Question 2.
5.4³ • 4.5³
Answer:
(5.4 X 4.5)³ = (24.3)³,

Explanation:
Given 5.4³ • 4.5³  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(5.4 X 4.5)³ = (24.3)³.

Question 3.
2⁵ • 10⁵
Answer:
(2 X 10)⁵ = (20)⁵,

Explanation:
Given 2⁵ • 10⁵  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(2 X 10)⁵ = (20)⁵.

Question 4.
a³ • b³
Answer:
(a X b)³ = (ab)³,

Explanation:
Given a³ • b³  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(a X b)³ = (ab)³.

Question 5.
(2x)⁵ • (3y)⁵
Answer:
(2x X 3y)⁵ = (6xy)⁵,

Explanation:
Given (2x)⁵ • (3y)⁵  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(2x X3y)⁵ = (6xy)⁵.

Question 6.
(2.5a)⁶ • (1.6b)⁶
Answer:
(2.5a X 1.6b)⁶ = (4ab)⁶,

Explanation:
Given (2.5a)⁶ • (1.6b)⁶  when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property,
(2.5a X 1.6b)⁶ = (4ab)⁶.

Question 7.
\(\left(-\frac{1}{3}\right)^{4} \cdot\left(-\frac{2}{5}\right)^{4}\)
Answer:
\(\left(\frac{2}{15}\right)^{4}\),

Explanation:
Given \(\left(-\frac{1}{3}\right)^{4} \cdot\left(-\frac{2}{5}\right)^{4}\)
when the variable bases are different and the powers are the same,
the bases are multiplied first,Used the powers of product property,
\(\left(\frac{-1 X -2}{3X 5}\right)^{4}\) = \(\left(\frac{2}{15}\right)^{4}\).

Question 8.
9² ÷ 3²
Answer:
(3)²,

Explanation:
Given (9)² ÷ (3)²  as 9 = 3 X 3 can be written as (3²)² so (3)⁴ ÷ (3)²
on simplification we get (3)^4-2 = (3)².

Question 9.
10⁶ ÷ 5⁶
Answer:
(2)⁶,

Explanation:
Given (10)⁶ ÷ (5)⁶  as 10 can be written as (5 x 2)⁶ so (5)⁶ .(2)⁶ ÷ (5)⁶
on simplification we get (2)⁶.

Question 10.
2.8⁷ ÷ 0.7⁷
Answer:
(4)⁷,

Explanation:
Given (2.8)⁷ ÷ (0.7)⁷  as 2.8 ÷ 0.7 = 4 so can be written as (4)⁷ .

Question 11.
15² ÷ 25²
Answer:
\(\left(\frac{3}{5}\right)^{2}\),

Explanation:
Given 15² ÷ 25², 15² can be written as (5 X 3)² and 25²  as (5 X 5)²  ,
upon simplification we get \(\left(\frac{3}{5}\right)^{2}\).

Question 12.
7.2⁹ ÷ 2.4⁹
Answer:
(3)⁹,

Explanation:
Given (7.2)⁹ ÷ (2.4)⁹  as 7.2 ÷ 2.4 = 3, so can be written as (3)⁹.

Question 13.
(3.2x)⁹ ÷ (1.1y)⁹
Answer:
(3.2x ÷ 1.1y)⁹,

Explanation:
Given (3.2x)⁹ ÷ (1.1y)⁹ when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property (3.2x ÷ 1.1y)⁹.

Question 14.
(-6)⁸ ÷ (-2)⁸
Answer:
(3)⁸,

Explanation:
Given (-6)⁸ ÷ (-2)⁸  as -6 can be written as (-2 x 3)⁸ so (-2)⁸ .(3)⁸ ÷ (-2)⁸
on simplification we get (3)⁸.

Question 15.
s⁵ ÷ r⁵
Answer:
\(\left(\frac{s}{r}\right)^{5}\),

Explanation:
Given s⁵ ÷ r⁵ the variable bases are different and the
powers are the same, the bases are divided first,upon simplification we get
\(\left(\frac{s}{r}\right)^{5}\).

Question 16.
(3a)⁶ ÷ (2b)⁶
Answer:
\(\left(\frac{3a}{2b}\right)^{6}\),

Explanation:
Given (3a)⁶ ÷ (2b)⁶ the variable bases are different and the
powers are the same, the bases are divided first, upon simplification we get
\(\left(\frac{3a}{2b}\right)^{6}\).

Question 17.
(h²k⁵)⁴
Answer:
h⁸k²⁰,

Explanation:
Given (h²k⁵)⁴ when the variable bases are different and the
powers are the same,Used the powers of product and
quotients of a property we get h^{2X 4} X k^5X4 = h⁸k²⁰.

Question 18.
\(\left(\frac{32 m^{6}}{4 n^{4}}\right)^{2}\)
Answer:
\(\left(\frac{8 m^{6}}{4n^{4}}\right)^{2}\),

Explanation:
Given \(\left(\frac{32 m^{6}}{4 n^{4}}\right)^{2}\) upon simplification
we get \(\left(\frac{8 m^{6}}{4n^{4}}\right)^{2}\).

Question 19.
\(\frac{9^{2} \cdot 9^{7}}{3^{5} \cdot 3^{4}}\)
Answer:
(3)⁹,

Explanation:
Given \(\frac{9^{2} \cdot 9^{7}}{3^{5} \cdot 3^{4}}\)
9 can be written as \(\frac{3 X 3 ^{2} \cdot 3 X 3^{7}}{3^{5} \cdot 3^{4}}\)
when bases are same powers are added \(\frac{3^{2+2+7+7}}{3^{5+4}}\) =
\(\frac{3^{18}}{3^{9}}\) on further simplification we get (3)^18-9 = (3)^9.

Question 20.
\(\frac{6^{5} \cdot 2^{3} \cdot 6^{4}}{12^{3}}\)
Answer:
(6)⁶,

Explanation:
Given\(\frac{6^{5} \cdot 2^{3} \cdot 6^{4}}{12^{3}}\) upon simplification
\(\frac{6^{5+4} \cdot 2^{3} }{6 X 2^{3}}\) = \(\frac{6^{9} \cdot 2^{3} }{(6 X 2)^{3}}\)=
(6)^9-3 = (6)⁶.

Question 21.
\(\frac{\left(5^{4}\right)^{2} \cdot 6^{8}}{10^{8}}\)
Answer:
(3)⁸,

Explanation:
Given \(\frac{\left(5^{4}\right)^{2} \cdot 6^{8}}{10^{8}}\) as denominator
10 can be written as 5 X 2 so \(\frac{\left(5\right)^{8} \cdot 6^{8}}{(5 X 2)^{8}}\) we get
\(\frac{6^{8}}{2^{8}}\) = \(\frac{(2 X 3)^{8}}{2^{8}}\) = (3)⁸.

Question 22.
\(\frac{\left(6^{3}\right)^{3} \cdot 4^{9}}{8^{9}}\)
Answer:
(3)⁹,

Explanation:
Given \(\frac{\left(6^{3}\right)^{3} \cdot 4^{9}}{8^{9}}\) as denominator
8 can be written as 4 X 2 so  we get
\(\frac{\left((2 X 3)^{3}\right)^{3} \cdot 4^{9}}{(4 X 2)^{9}}\) = (3)⁹.

Question 23.
\(\frac{24^{9}}{4^{3} \cdot 6^{2} \cdot 4^{6}}\)
Answer:
(6)⁷,

Explanation:
Given \(\frac{24^{9}}{4^{3} \cdot 6^{2} \cdot 4^{6}}\) as
24 in numerator can be written as 4 X 6 so

Question 24.
\(\frac{9^{12}}{\left(3^{3}\right)^{3} \cdot 3^{3}}\)
Answer:
(3)¹²,

Explanation:

Question 25.
Math Joural Charles thinks that a³ • b³ = ab⁶. Is he correct? Why?
Answer:
No, Charles is incorrect,

Explanation:
a³ • b³ ≠ ab⁶ it should be (ab)³ as when the variable bases are different and the
powers are the same, the bases are multiplied first,
Used the powers of product property we get (aX b)³ ≠ ab⁶.

Solve. Show your work.

Question 26.
At the beginning of January, Mr. Howard gives his niece $1 to start a savings account.
For each month that she can triple the amount in the account,
Mr. Howard will double the amount in the account at the end of each month.
How much does Mr. Howard’s niece have in her account at the beginning of May?
Answer:
$7,776 Mr. Howard’s niece have in her account at the beginning of May,

Explanation:
Given at the beginning of January, Mr. Howard gives his niece $1 to start a savings account.
For each month that she can triple the amount in the account,
Mr. Howard will double the amount in the account at the end of each month.
So at the beginning of January it is

therefore,$7,776 Mr. Howard’s niece have in her account at the beginning of May.

Go through the Math in Focus Grade 8 Workbook Answer Key Chapter 1 Lesson 1.6 Real-World Problems: Squares and Cubes to finish your assignments.

Math in Focus Grade 7 Course 3 A Chapter 1 Lesson 1.6 Answer Key Real-World Problems: Squares and Cubes

Math in Focus Grade 8 Chapter 1 Lesson 1.6 Guided Practice Answer Key

Solve. Show your work.

Question 1.
Find the two square roots of 169.

Answer:
Explanation:
Given to find two square roots of 169 and -169,So using prime factorization
we get for 169 it is 13 and for – 169 it is -13

Solve. Show your work.

Question 2.
Find the cube root of \(\frac{1}{729}\).

Answer:
1/9,

Explanation:

Solve. Show your work.

Question 3.
x² = 2.25
x² = 2.25

Answer:
1.5,

Explanation:

Solve. Show your work.

Question 4.

Answer:
x = (1/2),

Explanation:

Question 5.
A square field has an area of 98.01 square meters. Find the length of each side of the field.
Let the length of each side be x meters.
x² = Translate into an equation.
= Solve for x by taking the positive root of both sides.
x = m Use a calculator to find the square root.
The length of each side is meters.
Answer:
x² = 98.01 We translate into an equation:
\(\sqrt{x^{2}}\) = \(\sqrt{98.01}\) We solve for x by taking the positive square root of both sides:
x = 9.9m We use a calculator to find the square root:
The length of each side is 9.9 meters.
9.9 meters

Solve. Show your work.

Question 6.
Robin bought a crystal globe that has a volume of 1,774\(\frac{2}{3} \pi\)ir cubic centimeters. Find the radius of the crystal globe.
Let the radius of the crystal globe be r centimeters.

Answer:
The radius of the crystal globe is 29.7 cms,

Explanation:

Question 7.
A spherical waterme’on has a volume of 562.5π cubic centimeters. What is the diameter of the watermelon?

Let the radius of the watermelon be r centimeters.

Answer:
The diameter of the watermelon is 15 centimeters,

Explanation:

Math in Focus Course 3A Practice 1.6 Answer Key

Find the two square roots of each number. Round your answer to the nearest tenth when you can.

Question 1.
25
Answer:
5, or -5,

Explanation:
Given to find sqaure roots of 25
1. 5 X 5 = 25,
2. -5 X -5 = 25,
so 5, or -5.

Question 2.
64
Answer:
8 or -8,

Explanation:
Given to find sqaure roots of 64
1. 8 X 8 = 64,
2. -8 X -8 = 64,
so 8, or -8.

Question 3.
80
Answer:
8.944 or -8.944,

Explanation:
Given to find sqaure roots of 64
1. 8.944 X 8.944 = 80,
2. -8.944 X -8.944 = 80,
so 8.944, or -8.944.

Question 4.
120
Answer:
10.9544 or -10.9544,

Explanation:
Given to find sqaure roots of 64
1. 10.9554 X 10.9554 = 120,
2. -10.9554X -10.9554 = 120,
so 10.9554, or -10.5994.

Find the cube root of each number. Round your answer to the nearest tenth when you can.

Question 5.
512
Answer:
8

Explanation:

Question 6.
1,000
Answer:
10

Explanation:

Question 7.
999
Answer:
9.997,

Explanation:

Question 8.
\(\frac{64}{343}\)
Answer:
\(\frac{4}{7}\),

Explanation:
As

 

 

So Cube root of \(\frac{64}{343}\) is \(\frac{4}{7}\).

Solve each equation involving a variable that ¡s squared.
Round your answer to the nearest tenth when you can.

Question 9.
a² = 46.24
Answer:
a= 6.8,

Explanation:

Question 10.
b² = \(\frac{25}{49}\)
Answer:
b= \(\frac{5}{7}\),

Explanation:
Given b² = \(\frac{25}{49}\) as b² = \(\frac{5X5}{7X7}\),
therefore b = square root of \(\frac{5X 5}{7 X 7}\) = \(\frac{5}{7}\),

Question 11.
m² = 196
Answer:
m = 14,

Explanation:

Therefore m = 14.

Question 12.
n² = 35o
Answer:
n= 18.708,

Explanation:

therefore n = 18.708.

Solve each equation involving a variable that is cubed.
Write fractions in simplest form, and round decimal answers
to the nearest tenth.

Question 13.
x³ = 74.088
Answer:
x =4.2,

Explanation:

the cube root of 74.088 is 4.2.

Question 14.
x³ = \(\frac{216}{729}\)
Answer:
x = \(\frac{6}{9}\),

Explanation:

the cube root of x³ = \(\frac{216}{729}\) so x = \(\frac{6}{9}\).

Question 15.
x³ = 1,728
Answer:
x= 12,

Explanation:

Question 16.
x³ = 2,500
Answer:
x= 13.572,

Explanation:

the cube root x = 13.572088083.

Solve. Show your work. Round to the nearest tenth.

Question 17.
The volume of a spherical tank is 790.272π cubic feet.
What is the diameter of the container?

Answer:
The diameter of the container is 16.8 ft,

Explanation:
Given the volume of a spherical tank is 790.272π cubic feet.
so radius is 4/3 pi r³ = 790.272π,
r³ = (790.272 X 3)/4 = 592.704,
r= 8.4,

diameter of the container is 2r = 2 X 8.4 = 16.8 ft.

Question 18.
An orchard planted on a square plot of land has 3,136 apple trees.
If each tree requires an area of 4 square meters to grow,
find the length of each side of the plot of land.

Answer:
The length of each side of plot is 112 meters,

Explanation:
Given an orchard planted on a square plot of land has 3,136 apple trees.
If each tree requires an area of 4 square meters to grow,
the length of each side of the plot of land of square root of 3136 X 4
sqaure root of 12544 = 112 meters.

Question 19.
Mr. Berman deposited $2,500 in a savings account. Three years later there
was $2,812.16 in the savings account. Use the formula A = P(1 + r)ⁿ to find
the rate of interest, r percent, that he was paid. A represents the final amount of the
investment, P is the original principal, and n is the number of years it was invested.
Answer:
Rate of intreset is 5.78%,

Explanation:
Given Mr. Berman deposited $2,500 in a savings account. Three years later there
was $2,812.16 in the savings account. Using the formula A = P(1 + r)ⁿ to find
the rate of interest, r percent, that he was paid. A represents the final amount of the
investment, P is the original principal, and n is the number of years it was invested,
$2812.16 = $2,500(1 + r)³
$2812.16 – $2,500 = (1 + r)³
(1 + r)³ = $312.16
1 + r = cube root of $312.16,

1 + r = 6.7835,
therefore r = 6.7835 – 1 = 5.7835.

Brain @ Work

Question 1.
Evaluate \(\frac{4^{3} \cdot 10^{4}}{5^{2}}\) without using a calculator.
Answer:
2¹⁰ X 5²,

Explanation:

Question 2.
Find the values of x and y that make the equation \(\frac{81 x^{4} \cdot 16 y^{4}}{\left[(2 y)^{2}\right]^{2}}\) = 1,296 true,
Answer:
X = 1.414 and y = 1,

Explanation:

Question 3.
Use each of the numbers 1 to 9 exactly once to fill in the blanks.

Answer:
3¹¹,

Explanation:
Used each of the numbers 1 to 9 exactly once to fill the blanks

Question 4.
Jeremy wants to measure the radius of a marble. He uses a tank and
filled the tank with 360 identical marbles shown below, If the volume of the
tank is 9,720 cubic inches, find the radius of each marble.

Answer:
Radius is 3 inches,

Explanation:
Given Jeremy wants to measure the radius of a marble. He uses a tank and
filled the tank with 360 identical marbles shown below, If the volume of the
tank is 9,720 cubic inches, volume of each cube is 9,720 ÷ 360 = 27,
radius is cube root of 27 = 3 inches.