Hillary

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 7 Lesson 7.2 Constructing Perpendicular Bisectors to score better marks in the exam.

Math in Focus Grade 7 Course 2 B Chapter 7 Lesson 7.2 Answer Key Constructing Perpendicular Bisectors

Math in Focus Grade 7 Chapter 7 Lesson 7.2 Guided Practice Answer Key

Hands-On Activity

Materials:

• ruler

Explore The Distance Between Points On The Perpendicular Bisector Of A Segment And The Endpoints Of The Segment

Work in pairs.

Line XY is the perpendicular bisector of line segment AB. Points W, X, Y, and Z are four points on the perpendicular bisector of \(\overline{\mathrm{AB}}\).

Measure and record each length to the nearest tenth of a centimeter.

Step 2.
Compare the lengths of \(\overline{A W}\) and \(\overline{B W}\). Then compare the lengths of each of the following pairs of segments: \(\overline{A X}\) and \(\overline{B X}\), \(\overline{A Y}\) and \(\overline{B Y}\), and \(\overline{A Z}\) and \(\overline{B Z}\). What do you notice about each pair of line segment lengths?
Answer:

Math Journal
Suppose you choose any point on the perpendicular bisector and measure the distances from that point to points A and B. What do you predict about the distances? What conclusion can you make?

From the activity, any point on the perpendicular bisector of a line segment is equidistant from the two endpoints of the line segment.

Complete.

Question 1.
Copy or trace triangle XYZ. Then draw the perpendicular bisector of line segment XY.

Answer:

Copy the triangle and complete.

Question 2.
A trucking company has most of its business in Cities P, Q, and R. Where should it locate its new facility so that it is equidistant from all three cities? Mark the location of the facility on a copy of the map.

Answer:

Math in Focus Course 2B Practice 7.2 Answer Key

Draw each line segment and construct its perpendicular bisector.

Question 1.
XY = 5 cm
Answer:

Question 2.
PQ = 6.8
Answer:

Question 3.
AB = 8.8 cm
Answer:

Question 4.
MN = 11 cm
Answer:

Question 5.
Draw a line segment between 4 inches and 5 inches and label the endpoints M and N. Construct the perpendicular bisector of \(\overline{\mathrm{MN}}\). Explain briefly if you could construct a different perpendicular bisector of \(\overline{\mathrm{MN}}\).
Answer:

Question 6.
Math Journal
In the diagram below, point M is the midpoint of \(\overline{\mathrm{AB}}\). Ben drew line segment XY through point M. He labeled it as the perpendicular bisector of \(\overline{\mathrm{AB}}\). Do you agree with Ben? Give a reason for your answer.

Answer:
Yes, I do agree with Ben.

Explanation:
In the given diagram, point M is the midpoint of \(\overline{\mathrm{AB}}\). Ben also drew line segment XY through point M. So Ben labeled it as the perpendicular bisector of \(\overline{\mathrm{AB}}\). A perpendicular bisector is a line that bisects another line at a right angle, through the intersection point. Hence I agree with Ben.

Question 7.

Answer:

Question 8.
Draw the perpendicular bisectors of \(\overline{\mathrm{PQ}}\) and \(\overline{\mathrm{PR}}\) on a copy of each polygon. Label the point where the two perpendicular bisectors meet as W.

Answer:

Question 9.
The point that is equidistant from points W, X, and Y. On a copy of WXYZ, mark the points that are described, if possible. Otherwise, explain why you cannot.
Answer:
We are given the polygon:

The point equidistant from points W, X and Y is the intersection of the perpendicular bisectors of the segments \(\overline{W X}\), \(\overline{X Y}\) and \(\overline{Y W}\).

It is enough to draw two of the perpendicular bisectors as the three of them intersect in the same point.
We draw the perpendicuLar bisectors on \(\overline{X Y}\) and \(\overline{W X}\):

They intersect in point A. therefore A is the point that is equidistant from points W, X and Y.

Question 10.
The point that is equidistant from \(\overline{W X}\), \(\overline{W Z}\), and \(\overline{X Y}\).
Answer:

The points equidistant from \(\overline{W X}\) and \(\overline{W Z}\) are on the angle bisector of ∠XWZ.
The points equidistant from \(\overline{W X}\) and \(\overline{X Y}\) are on the angle bisector of ∠WXY.
Therefore the point equidistant from \(\overline{W X}\), \(\overline{W Z}\) and \(\overline{X Y}\) is the intersection of the two angle bisectors.
We draw the angle bisector of ∠XYZ:

We draw the angle bisector of ∠WXY:

They intersect in point B, therefore B is the point that is equidistant from \(\overline{W X}\), \(\overline{W Z}\) and \(\overline{X Y}\):

Question 11.
The point that is equidistant from \(\overline{W X}\) and \(\overline{W Z}\), and also from points X and Y.
Answer:
We are given the polygon:

The points equidistant from \(\overline{W X}\) and \(\overline{W Z}\) are on the angle bisector of ∠XYZ.
The points equidistant from the points X and Y are on the perpendicular bisector of \(\overline{X Y}\).
Therefore the point equidistant from \(\overline{W X}\) and \(\overline{W Z}\) and from points X and Y is the intersection between the angle bisector of ∠XWZ and the perpendicular bisector of \(\overline{XY}\).
We draw the angle bisector of ∠XWZ:

We draw the perpendicular bisector of \(\overline{XY}\):

They intersect in point C, therefore C is the point that ¡s equidistant from \(\overline{W X}\) and \(\overline{W Z}\) and points X, Y.

Solve.

Question 12.
Mark the point on \(\overline{Q R}\) that is equidistant from points Q and R on a copy of triangle POR.

Answer:

Question 13.
Mr. Smith wants to put a circular water sprinkler in his triangular-shaped garden. His garden has a tree at each vertex. The water sprinkler is to be equidistant from the trees. Copy or trace the given triangle. Mark point W to show where Mr. Smith should put the water sprinkler.

Answer:
We are given:

The point equidistant from the 3 trees is the intersection of the perpendicuLar bisectors of the triangles edges

It is enough to draw two of the perpendicular bisectors as the three of them intersect in the same point
We draw the perpendicular bisectors on two edges:

They intersect in point A. therefore A is the point that is equidistant from the 3 trees.

Question 14.
Math Journal
Melissa was asked to bisect a very long line segment using a compass and a straightedge. Melissa opened the compass to the widest possible setting. She found that it was not wide enough to do the standard construction that she had learned in math class. Is it possible for Melissa to bisect the very long line segment with only her compass and a straightedge? Explain and give a suggestion.
Answer:
Let \(\overline{A B}\) be the initial very long segment.
In order to be able to use an opening of the compass greater than half of a segment, she should ‘decrease the length of the given long segment as much as possible. For this, she places the compass, with its greatest opening, in point A and draw an arc which intersects \(\overline{A B}\) in X₁. With the same opening she places the compass in B and draw an arc which intersects \(\overline{A B}\) in Y₁.. She got a smaller segment \(\overline{X_{1} Y_{1}}\).

She continues placing the compass in X₁ and Y₁ and drawing arcs until she gets a segment \(\overline{X_{n} Y_{n}}\),  for which she can construct the perpendicular bisector.

She constructs the perpendicular bisector of \(\overline{X_{n} Y_{n}}\), which is also the perpendicular bisector of \(\overline{A B}\) because AX_n = BY_n.

Decrease the length of the segment with equal values until the procedure of constructing the perpendicular bisector can be applied.

Question 15.
Math Journal
Copy the rectangle shown. Use the least possible number of arcs and lines to construct the perpendicular bisectors of each side of the rectangle. Explain how you know you have used the least possible number.

Answer:

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 4 Lesson 4.1 Understanding Equivalent Equations to score better marks in the exam.

Math in Focus Grade 7 Course 2 A Chapter 4 Lesson 4.1 Answer Key Understanding Equivalent Equations

Math in Focus Grade 7 Chapter 4 Lesson 4.1 Guided Practice Answer Key

Copy and complete to state whether each pair of equations are equivalent equations. Give a reason for your answer.

Question 1.

x – 3 + 4x = 5 and 5x = 2
x – 3 + 4x = 5
5x – 3 = 5 Group like terms.
5x – 3 + = 5 + Add to both sides.
5x = Simplify.
x – 3 + 4x = 5 be rewritten as 5x = 2.
So, the equations have solutions and are
Answer:
No, they are not equivalent equations.

Explanation:
Given 1st equation, x – 3 + 4x = 5

It can also be written as 5x – 3 =5

Add 3 to both sides, 5x – 3 + 3 = 5 + 3

5x = 8

So, equation x – 3 + 4x = 5  cannot be written as 5x = 2

Question 2.
x + 7 = 12 and 2x = 10
First solve x + 7 = 12.
x + 7 = 12
x + 7 – = 12 – Subtract from both sides.
x = Simplify.
Then check to see if is the solution of the equation 2x = 10.
If x = , 2x = 2 • Substitute for x.
= a solution.
Because the equations have the solution, they are equations.
Answer:
Yes, Both are equivalent equations.

Explanation:
First, let’s solve x + 7 = 12

Subtract 7 on both sides.

x + 7 – 7 = 12 -7

x = 5

Lets consider second equation 2x = 10

substitute x= 5 which we got by solving  the 1st equation in the 2nd equation.

2.(5) = 10

Hence proved.

Question 3.
1.2x = 2.4 and x – 6 = 8
First solve x – 6 = 8.
x – 6 = 8
x – 6 + = 8 + Add to both sides,
x = Simplify.
Then check to see if is the solution of the equation 1.2x = 2.4.
If x = , 1.2x = 1.2 • Substitute for x.
= a solution.
Because the equations have solutions, they are equations.
Answer:
No, they are not equivalent equations.

Explanation:
First, lets consider x – 6 = 8

Add 6 on both sides

x – 6 + 6 = 8 + 6

x = 14

Lets substitute x = 14  in the first equation.

1.2 x = 2.4

1.2(14) = 16.8

Both the equations are not equivalent equations.

Question 4.
\(\frac{2}{5}\)x = 4 and x = 10.
If x = 10, \(\frac{2}{5}\)x = \(\frac{2}{5}\) • 10 Substitute 10 for x.
= a solution.
Because the equations have the solution, they are equations.
Answer:
Yes, both the equations have the same solution, they are equivalent equations.

Explanation:
Let’s consider first equation, (2/5)x =4

Let us  substitute the second equation, x =10 in first equation.

(2/5) × 10 = 4

Hence proved.

Both the equations have the same solution, they are equivalent equations.

Math in Focus Course 2A Practice 4.1 Answer Key

Tell whether each pair of equations are equivalent. Give a reason for your answer.

Question 1.
2x = 4 and 4x + 5 = 13
Answer:
Yes, Both the equations are equivalent.

Explanation:
Let us consider second equation, 4x + 5 = 13

Subtract 5 on both sides.

4x + 5 – 5 = 13 – 5

4x = 8

x = 8 ÷ 4

x = 2

Substitute x=2 in the first equation, 2x = 4

2(2) = 4

Hence proved.

Both the equations are equivalent.

Question 2.
-2x + 9 = 7 and —2x = 2
Answer:
No, both the equations are not equivalent.

Explanation:
Lets solve the first equation, -2x + 9 = 7

Subtract 9  on both sides.

-2x + 9 – 9 = 7 – 9

-2x = -2

The second equation is -2x = 2

So, both the equations are not equivalent.

Question 3.
5x – 4 + 3x = 8 and 8x = 12
Answer:
Both are equivalent equations.

Explanation:
Lets us consider first equation, 5x – 4 + 3x = 8

8x – 4 = 8

8x = 8 + 4

8x = 12

As we derived second equation from the first equation, both are equivalent equations.

Question 4.
\(\frac{3}{4}\)x – 7 = 2 and x = 12
Answer:
Yes, both are equivalent equations.

Explanation:
Let us consider first equation, (3/4)x = 2

Substitute, the second equation, x = 12 in the first equation.

(3/4)(12) – 7 = (3).(3) – 7

=9 – 7

=2

Hence proved. Both are equivalent equations.

Match each equation with an equivalent equation.

Answer:
5 – d
6 – c
7 – e
8 – a
9 – g
10 – f
11 – b

Explanation:
5.  0.5x + 1 = 1.5

0.5x = 1.5 – 1 = 0.5

x = 0.5 ÷ 0.5

x = 1

We can match 5th equation with equation (d) on the other side.

6. 9 + 3.5x = 16

Let us solve the equation

3.5x = 16 – 9

3.5x = 7

x = 7 ÷ 3.5

x = 2

We can match the equation (3/2)x = 3

x = 3 × (2/3)

x = 2

Hence both are same.

7. (4/5)x =4

4x = 20

x =5

We can match 7th equation with equation (e) on the other side.

2x =10

x =5

Hence Matched.

8.  2x + (1/2) = (7/2)

2x = (7/2) – (1/2)

2x = (6/2)

2x = 3

x = 3/2

As option (a) is 6x =9

It can be also written as 3/2 as both are dividends of 3.

9. x – 8.3 = 1.3

x = 1.3 + 8.3

x = 9.6

Option (g) is  (1/2)x = 4.8

x =9.6

Hence matched.

10. 13.9 = 2.5x

x = 13.9 ÷ 2.5

x = 5.56

Option (f) is 1.2 + x = 6.76

x = 6.76 – 1.2

x =5.56

Hence proved.

11. 4x = (4/9)

x = 1/9

We can match with option (b).

(3/5)x = (1/15)

x = (1/9)

Solve.

Question 12.
Math Journal Max was asked to write to \(\frac{2}{3}\)x = 3 – x. He wrote the following:
\(\frac{2}{3}\)x = 3 – x
\(\frac{2}{3}\)x ∙ 3 = 3 ∙ 3 – x
2x = 9 – x
He concluded that \(\frac{2}{3}\)x = 3 – x and 2x = 9 \(\frac{2}{3}\) x are equivalent equations. Do you agree with his conclusion? Give a reason for your answer.
Answer:
No, I don’t agree with Max, both are not equivalent equations.

Explanation:
Let us consider first equation, (2/3)x = 3 – x

2x = 9 -3x (Max gave the equation 2x = 9 – x which is wrong, if we multiplied 3 on both sides not only it is multiplied with 3 it is also multiplies with x. so it is 2x = 9 -3x)

5x = 9

x = 9/5

x = 1.8

The second equation, 9(2/3)x =2x

substitute x =1.8 in the second equation

2 (1.8) = 9(2/3)(1.8)

3.6 = 10.8

Hence the both the equations are not equivalent.

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 4 Algebraic Equations and Inequalities to score better marks in the exam.

Math in Focus Grade 7 Course 2 A Chapter 4 Answer Key Algebraic Equations and Inequalities

Math in Focus Grade 7 Chapter 4 Quick Check Answer Key

Solve each equation.

Question 1.
x + 4 = 10
Answer:
6

Explanation:
x + 4 = 10
x = 10 -4

x = 6

Question 2.
x – \(\frac{1}{2}\) = 2
Answer:
2(1/2)

Explanation:
x – (1/2) = 2

x = 2 + (1/2)

x = 2 (1/2)

Question 3.
\(\frac{1}{5}\)x = 3
Answer:
15

Explanation:
(1/5)x = 3
x=  3 × 5

x = 15

Question 4.
1.2x = 2.4
Answer:
2

Explanation:
1.2x=2.4

x= 2.4 ÷ 1.2

x= 2

State whether each statement is True or False.

Question 5.
x = 1 gives the solution of the algebraic equation 3x + 5 = 8.
Answer:
True

Explanation:
3x + 5 = 8

Given, x = 1. Substitute x= 1 in the equation.

3(1) + 5  = 8

8 = 8

Hence proved.

Question 6.
y = 2 gives the solution of the algebraic equation 6y – 3 = 8.
Answer:
False

Explanation:
6y – 3 = 8

Given y = 2, substitute in the equation.

6(2) – 3 = 8

12 – 3 = 8

9 ≠ 8

So False.

Question 7.
z = 6 gives the solution of the algebraic equation \(\frac{z}{3}\) = 3.
Answer:
False

Explanation:
\(\frac{z}{3}\) = 3

(z/3) = 3

Given, z = 6, Substitute it in the equation.

(6/3) = 3

2 ≠ 3

So  false.

Question 8.
w = 3 gives the solution of the algebraic equation 2w = 6.
Answer:
True

Explanation:
Given equation, 2w = 6.

Given w=3, substitute it in the equation.

2(3) = 6

6 = 6

So the equation is true.

Draw a number line to represent each inequality.

Question 9.
x ≥ 3.5
Answer:

Explanation:
Given equation, x ≥ 3.5

In the equation , x can be any number which is equal to (or) more than 3.5.

It is represented in the number line as given above.

Question 10.
y < \(\frac{1}{2}\)
Answer:

Explanation:
Given equation, y < (1/2)

In the equation, y is a number which is less than (1/2)

It is represented in the number line as given above.

Complete each with =, >, or <.

Question 11.
11 12
Answer:
11 < 12

Question 12.
-9 -7
Answer:
-9  <  -7

Question 13.
25 ∙ (-1) (-1) ∙ 25
Answer:
25 ∙ (-1)  =  (-1) ∙ 25

Question 14.
3 ÷ (-1) (-1) ÷ 3
Answer:
3 ÷ (-1) = (-1) ÷ 3

Use x to represent the unknown quantity. Write an algebraic inequality for each statement.

Question 15.
The box can hold less than 70 pounds.
Answer:
x < 70

Explanation:
Let us consider the box be “x”.

As the box can hold less than 70 pounds.

Hence the equation x < 70 .

Question 16.
You have to be at least 17 years old to qualify for the contest.
Answer:
x ≥ 17

Explanation:
“At least” means it should be minimum of 17 or more than that.

Given, you have to be at least 17 years old to qualify for the contest.

Hence the equation, x ≥ 17.

Question 17.
The width of luggage that you can carry onto the plane is at most 17 inches.
Answer:
y ≤ 17

Explanation:
“At most” means it should be maximum of 17 nor less than that, but not more than 17.

As, The width of luggage that you can carry onto the plane is at most 17 inches.

Hence the equation, y ≤ 17

Question 18.
There are more than 120 people standing in line for the roller coaster.
Answer:
y > 120

Explanation:
The statement states “There are more than 120 people standing in line for the roller coaster” i.e, higher than 120.

Hence the equation, y > 120

Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 3 Review Test to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 3 Review Test Answer Key

Concepts and Skills
Simplify each expression.
Question 1.
1.4w – 0.6w
Answer:
1.4w – 0.6w = 0.8w.

Explanation:
1.4w – 0.6w
= 0.8w.

Question 2.
\(\frac{3}{4}\)m + \(\frac{4}{5}\)m
Answer:
\(\frac{3}{4}\)m + \(\frac{4}{5}\)m = \(\frac{31}{20}\)m.

Explanation:
\(\frac{3}{4}\)m + \(\frac{4}{5}\)m
LCD of 4 n 5 = 20.
= [(3 × 5) + (4 × 4)]m ÷ 20
= (15 + 16)m ÷ 20
= 31m ÷ 20 or \(\frac{31}{20}\)m.

Question 3.
\(\frac{1}{6}\)y + \(\frac{1}{2}\)y + \(\frac{1}{3}\)y
Answer:
\(\frac{1}{6}\)y + \(\frac{1}{2}\)y + \(\frac{1}{3}\)y = y.

Explanation:
\(\frac{1}{6}\)y + \(\frac{1}{2}\)y + \(\frac{1}{3}\)y = y.
LCD of 6 n 2 = 6.
= [(1 × 1) + (1 × 3)]y ÷ 6] +  \(\frac{1}{3}\)y
= [(1 + 3)y ÷ 6] + \(\frac{1}{3}\)y
= (4y ÷ 6) + \(\frac{1}{3}\)y
= \(\frac{2}{3}\)y+ \(\frac{1}{3}\)y
= (2 + 1)y ÷ 3
= 3y ÷ 3
= y.

Question 4.
1.8m – 0.2m – 7m
Answer:
1.8m – 0.2m – 7m = -5.4m.

Explanation:
1.8m – 0.2m – 7m
= 1.6m – 7m
= -5.4m.

Question 5.
1.3a – 0.8b + 2.2b – a
Answer:
1.3a – 0.8b + 2.2b – a = 0.3a + 1.4b.

Explanation:
1.3a – 0.8b + 2.2b – a
= 1.3a – a – 0.8b + 2.2b
= 0.3a – 0.8b + 2.2b
= 0.3a + 1.4b.

Question 6.
1 + \(\frac{1}{5}\)a + \(\frac{3}{5}\)b + \(\frac{4}{5}\)a
Answer:
1 + \(\frac{1}{5}\)a + \(\frac{3}{5}\)b + \(\frac{4}{5}\)a = 1 + a + \(\frac{3}{5}\)b.

Explanation:
1 + \(\frac{1}{5}\)a + \(\frac{3}{5}\)b + \(\frac{4}{5}\)a
= 1 + \(\frac{1}{5}\)a + \(\frac{4}{5}\)a + \(\frac{3}{5}\)b
= 1 + [(1 + 4)a ÷ 5] + \(\frac{3}{5}\)b
= 1 + (5a ÷ 5) + \(\frac{3}{5}\)b
= 1 + a + \(\frac{3}{5}\)b.

Expand each expression. Then simplify when you can.
Question 7.
1.2(2p – 3)
Answer:
1.2(2p – 3) = 2.4p – 3.6.

Explanation:
1.2(2p – 3)
= (1.2 × 2p) – (3 × 1.2)
= 2.4p – 3.6.

Question 8.
\(\frac{1}{3}\)(12p + 9q)
Answer:
\(\frac{1}{3}\)(12p + 9q) = 4p + 3q.

Explanation:
\(\frac{1}{3}\)(12p + 9q)
= [12p × \(\frac{1}{3}\)] + [ 9q × \(\frac{1}{3}\)]
= 4p + 3q.

Question 9.
\(\frac{1}{5}\)\(\left(\frac{t}{3}+\frac{1}{2}\right)\)
Answer:
\(\frac{1}{5}\)\(\left(\frac{t}{3}+\frac{1}{2}\right)\) = \(\frac{t}{15}\) + \(\frac{1}{10}\).

Explanation:
\(\frac{1}{5}\)\(\left(\frac{t}{3}+\frac{1}{2}\right)\)
= [\(\frac{t}{3}\) × \(\frac{1}{5}\)] + [\(\frac{1}{2}\) × \(\frac{1}{5}\)]
= \(\frac{t}{15}\) + \(\frac{1}{10}\).

Question 10.
-4(-2q + 2.5)
Answer:
-4(-2q + 2.5) = 8q – 10.

Explanation:
-4(-2q + 2.5)
= (-4 × -2q) + (2.5 × -4)
= 8q – 10.

Question 11.
–\(\frac{2}{3}\)(6x + 3)
Answer:
–\(\frac{2}{3}\)(6x + 3) = 4x – 2.

Explanation:
–\(\frac{2}{3}\)(6x + 3)
= (6x × –\(\frac{2}{3}\)) + (3 × –\(\frac{2}{3}\))
= (2x × 2) + (1 × -2)
= 4x – 2.

Question 12.
-0.5(2m – 4n)
Answer:
-0.5(2m – 4n) = -m + 0.5n.

Explanation:
-0.5(2m – 4n)
= (2m × -0.5) – (1n × -0.5)
= -1m – (-0.5n)
= -m + 0.5n.

Question 13.
3(a + 3) + 2a
Answer:
3(a + 3) + 2a = 5a + 9.

Explanation:
3(a + 3) + 2a
= [(3 × a) + (3 × 3)] + 2a
= 3a + 9 + 2a
= 3a + 2a + 9
= 5a + 9.

Question 14.
4(2p – 3) – 3(p + 2)
Answer:
4(2p – 3) – 3(p + 2) = 5p – 6.

Explanation:
4(2p – 3) – 3(p + 2)
= [(2p × 4) – (3 × 4)] – [(3 × p) + (2 × 3)]
= (8p – 12) – (3p + 6)
= 8p – 12 – 3p – 6
= 8p – 3p – 12 – 6
= 5p – 6.

Question 15.
2.5(m – 2) + 5.6m
Answer:
2.5(m – 2) + 5.6m = 8.1m – 5.

Explanation:
2.5(m – 2) + 5.6m
= [(m × 2.5) – (2 × 2.5)] + 5.6m
= (2.5m – 5) + 5.6m
= 2.5m – 5 + 5.6m
= 2.5m + 5.6m – 5
= 8.1m – 5.

Question 16.
4(0.6n – 3) – 0.2(2n – 3)
Answer:
4(0.6n – 3) – 0.2(2n – 3) = 2n – 12.6.

Explanation:
4(0.6n – 3) – 0.2(2n – 3)
= 2.4n – 12 – 0.4n + 0.6
= 2.4n – 0.4n – 12 – 0.6
= 2n – 12.6.

Factor each expression.
Question 17.
4t – 20s
Answer:
4t – 20s = 4(t – 5s).

Explanation:
4t – 20s
= 4(t – 5s).

Question 18.
-6p – 21q
Answer:
-6p – 21q = -3(2p + 7q).

Explanation:
-6p – 21q
= -3(2p + 7q).

Question 19.
8i + 12 + 4j
Answer:
8i + 12 + 4j = 4(2i + 3 + j).

Explanation:
8i + 12 + 4j
= 4(2i + 3 + j)

Question 20.
6a + 10b – 20
Answer:
6a + 10b – 20 = 2(3a + 5b – 10).

Explanation:
6a + 10b – 20
= 2(3a + 5b – 10).

Question 21.
-9m – 3n – 6
Answer:
-9m – 3n – 6 = -3(3m + n + 2).

Explanation:
-9m – 3n – 6
= -3(3m + n + 2).

Question 22.
-15x – 6 – 12y
Answer:
-15x – 6 – 12y = -3(5x + 2 + 4y).

Explanation:
-15x – 6 – 12y
= -3(5x + 2 + 4y).

Translate each verbal description into an algebraic expression. Then simplify when you can.
Question 23.
One-fourth x less than the sum of 7 and 2x.
Answer:
\(\frac{x}{4}\) – (7 + 2x) = – \(\frac{7}{4}\)x – 7.

Explanation:
One-fourth x less than the sum of 7 and 2x.
=> \(\frac{x}{4}\) – (7 + 2x)
=> \(\frac{x}{4}\) – 7 – 2x
=> \(\frac{x}{4}\) – 2x – 7.
=> [(x – 8x) ÷ 4 ] – 7.
=> (-7x ÷ 4) – 7
=> – \(\frac{7}{4}\)x – 7.

Question 24.
4 times 5y divided by 18.
Answer:
(4 × 5y ) ÷ 18 = \(\frac{10}{9}\)y.

Explanation:
4 times 5y divided by 18
=> (4 × 5y ) ÷ 18
=> 20y ÷ 18
=> 10y ÷ 9 or \(\frac{10}{9}\)y.

Question 25.
Five-ninths of (3p + 1) subtracted from one-third of (q + p).
Answer:
[\(\frac{5}{9}\) × (3p + 1) ] – [\(\frac{1}{3}\) × (q + p)] = 2p – \(\frac{1}{3}\)q + \(\frac{5}{9}\)

Explanation:
Five-ninths of (3p + 1) subtracted from one-third of (q + p)
=> [\(\frac{5}{9}\) × (3p + 1) ] – [\(\frac{1}{3}\) × (q + p)]
=> \(\frac{15}{9}\)p + \(\frac{5}{9}\) – \(\frac{1}{3}\)q + \(\frac{1}{3}\)p.
=> \(\frac{15}{9}\)p + \(\frac{1}{3}\)p – \(\frac{1}{3}\)q + \(\frac{5}{9}\)
= LCD of 9 n 3 = 9.
= [(15 + 3)p ÷ 9 ] – \(\frac{1}{3}\)q + \(\frac{5}{9}\)
= (18p ÷ 9) – \(\frac{1}{3}\)q + \(\frac{5}{9}\)
= (2p ÷ 1) – \(\frac{1}{3}\)q + \(\frac{5}{9}\)
= 2p – \(\frac{1}{3}\)q + \(\frac{5}{9}\)

Problem Solving
Solve. Show your work.
Question 26.
After 14 boys leave a concert, the ratio of boys to girls is 3 : 10. If there are p girls at the concert, write an algebraic expression for the number of boys at the beginning of the concert in terms of p.
Answer:
An algebraic expression for the number of boys at the beginning of the concert in terms of p =
0.3 p + 14.

Explanation:
Number of girls in the concert = p.
After 14 boys leave a concert, the ratio of boys to girls is 3 : 10.
Let total number of boys be b.
Ratio of boys after 14 boys leave:
=> \(\frac{b – 14}{p}\) = \(\frac{3}{10}\)
=> 3 × p = 10( b – 14)
=> 3 p = 10 b – 140
=>  10 b = 3 p + 140
= >  b = 0.3 p + 14

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 6 Lesson 6.4 Interior and Exterior Angles to score better marks in the exam.

Math in Focus Grade 7 Course 2 B Chapter 6 Lesson 6.4 Answer Key Interior and Exterior Angles

Math in Focus Grade 7 Chapter 6 Lesson 6.4 Guided Practice Answer Key

Hands-On Activity

Materials:

• scissors
• ruler

Explore The Sum Of The Angles In A Triangle

Work in pairs.

Step 1.
Draw and cut out a triangle. Label the three angles of the triangle as 1, 2, and 3.

Step 2.
Cut the triangle into three pieces, so that each piece contains a vertex.

Step 3.
Rearrange the cut pieces on a straight line. What do you notice about the sum of the measures of the three interior angles?

Complete.

Question 1.
Find the value of p.

Answer:
p° = 88°

Explanation:

∠RPQ + ∠QRP + ∠PQR = 180°
35° + p° + 57° = 180°
p° + 92° = 180°
p° = 180° – 92°
p° = 88°

Complete.

Question 2.
Triangle XYZ is an isosceles triangle and m∠XYZ = 55°. Find the value of x.

Answer:
∠XYZ + ∠XZY + ∠YXZ = 180°
55° + 55° + x° = 180°
110° +x° = 180°
x° = 180° – 110°
x° = 70°

Find the value of each variable.

Question 3.

Answer:
x° = 70°

Explanation:

x° + 62° = 132°
x° = 132° – 62°
x° = 70°

Question 4.

Answer:
x° = 76°

Explanation:

x° + 35°= 70° + 41°
x° + 35° = 111°
x° = 111° – 35°
x° = 76°

Complete.

Question 5.
Triangle ABC is an isosceles triangle. Find the measures of ∠1 and ∠2.
AB = AC
m∠ACB = m∠ABC

Answer:
∠1 = 255°, ∠2 = 95°

Explanation:
m∠ACB = m∠ABC
∠1 = 75° + 180°
∠1 = 255°
∠2 = 180° – 75°
∠2 = 95°

Question 6.
Triangle EFG is an isosceles triangle and \(\overleftrightarrow{E F}\) is parallel to \(\overleftrightarrow{H I}\). Find the value of x.

Answer:
x° = 120°

Explanation:

∠FEG = ∠IGJ
= 30°
∠FGE = ∠FEG
= 30°
∠FEG + ∠FGE + ∠EFG = 180°
30° + 30° + x° = 180°
x° + 60° = 180°
x° = 180° -60°
x° = 120°

Math in Focus Course 2B Practice 6.4 Answer Key

Find the value of y.

Question 1.

Answer:
y° = 61°

Explanation:
y° + 52° + 67° = 180°
y° + 119° = 180°
y° = 180° -119°
y° = 61°

Question 2.

Answer:
y° + 26° + 18° = 180°
y° + 44° = 180°
y° = 180° – 44°
y° = 136°

Question 3.

Answer:
20° + y° = 90° + 42°
20° + y° = 132°
y° = 132° -20°
y° = 112°

Question 4.

Answer:
90° + 27° + x° = 180°
117° + x° = 180°
x° = 180° -117°
x° = 63°
63° + 51° + y° = 180°
114° + y° = 180°
y° = 180° – 114°
y° = 66°

Question 5.

Answer:
y° = 122°

Explanation:
y° + 28° + 30° = 180°
y° + 58° = 180°
y° = 180° – 58°
y° = 122°

Question 6.

Answer:
x°  = 57° , y° = 67°

Explanation:
x°  + 123°  = 180°
x°  = 180° -123°
x°  = 57°
56°  + 57° + y° = 180°
y°  + 113° = 180°
y° = 180° – 113°
y° = 67°

Find m∠1 and m∠2 in each diagram.

Question 7.

Answer:
62° + 90° + m∠1 = 18o° ∠s sum in triangle:
152° + m∠1 = 180° Simplify:
152° + m∠1 — 152° = 180° — 152° Subtract 152° from both sides:
m∠1 = 28° Simplify:
m∠2 = 90° + m∠1 Exterior ∠ of triangle:
m∠2 = 90° + 28° substitute
m∠2 = 118° simplify
m∠1 = 28°
m∠2 = 118°

Question 8.

Answer:
∠1 = 76°, ∠2 = 114°

Explanation:
∠1 + 28° + 76° = 180°
∠1 + 104° = 180°
∠1 = 180° – 104°
∠1 = 76°
76° + 38° + x° = 180°
114° + x° = 180°
x° = 180° – 114°
x° = 66°
x° + ∠2 = 180°
66° + ∠2 = 180°
∠2 = 180° – 66°
∠2 = 114°

Question 9.

Answer:
50° + 70° + m∠1 = 180° Corresponding ∠s and ∠s sum in triangle:
120° + m∠1 = 180° Simplify:
120° + m∠1 – 120° = 180° – 120° Subtract 120° from both sides:
m∠1 = 60° Simplify:
m∠2 = 50° + 70° Exterior ∠ of triangle:
m∠2 = 120° simplify
m∠1 = 60°
m∠2 = 120°

Question 10.

Answer:
70° = 43° + m∠1 Alternate interior ∠s
70° – 43° = 43° + m∠1 – 43° Subtract 43° from both sides:
m∠1 = 27° Simplify:
m∠2 + m∠1 + 43° = 180° ∠s sum of triangle:
m∠2 + 27° + 43° = 180°
m∠2 + 70° = 180° Simplify:
m∠2 + 70° — 70° = 180° — 70° Subtract 70° from both sides:
m∠2 = 110° Simplify:
m∠1 = 27
m∠2 = 110°

Use an equation to find the value of y.

Question 11.

Answer::
3y° = y° + 80° Exterior ∠ of triangle:
3y = y + 80 The equation for y is:
3y – y = y + 80 – y Subtract y from both sides:
2y = 80 Simplify:
\(\frac{2 y}{2}\) = \(\frac{80}{2}\) Divide by 2
y = 40 simplify
3y = y + 80
y = 40

Question 12.

Answer:
Let’s note by x° the measure of the congruent angles of the isosceles triangle
x° = 2y° Alternate interior ∠s
x° + 3y° = 180° Supplementary ∠s:
2y° + 3y° = 180° Substitute:
5y° = 180° Simplify:
\(\frac{5 y^{\circ}}{5}\) = \(\frac{180^{\circ}}{5}\) Divide by 5
y = 36 simplify
2y + 3y = 180
y = 36

Find the value of x and name the type of triangle that is shown.

Question 13.

Answer:
x° = 60°, x° = 60°

Explanation:
x° + x° + 60° = 180°
2x° + 60° = 180°
2x° = 180° – 60°
2x° = 120°
x° = 120 ÷ 2
x = 60°

Question 14.

Answer:
x° = 36°, x° = 36°

Explanation:
x°+ x°+ 108° = 180°
2x° + 108° = 180°
2x° = 180° – 108°
2x° = 72°
x° = 72÷2
x° = 36°

Question 15.

Answer:
x° = 8°

Explanation:
We all know that all the angles in a triangle add up to 180 degrees.
In the given figure, each triangle has 3 angles.  Thus, we have the sum of three angles as shown:
A° + B° +C° = 180°
62°+ 90°+ x° = 180°
x°+ 172° = 180°
x° = 180° – 172°
x° = 8°

Find the measure of each numbered angle.

Question 16.

Answer:
m∠2 = 148° Corresponding ∠s:
m∠2 = m∠3 + 63° Vertical ∠s and exterior ∠ of triangle:
148° = m∠3 + 63° Substitute:
148° – 63° = m∠3 + 63° – 63° Subtract 63° from both sides:
m∠3 = 85° Simplify:
m∠1 + 63° = 180° supplementary ∠s
m∠1 + 63° – 63° = 180° – 63° subtract 63° from both sides
m∠1 = 117° simplify
m∠1 = 117°
m∠2 = 148°
m∠3 = 85°

Question 17.

Answer:
m∠1 + 140° = 180° Supplementary ∠s
m∠1 + 140° — 140° = 180° – 140° Subtract 140° from both sides:
m∠1 = 40° Simplify:
m∠2 + 15° + 40° = 180° Alternate interior ∠s and ∠s sum of triangle:
m∠2 + 55° = 180° Simplify:
m∠2 + 55° – 55° = 180° – 55° subtract 55° from both sides
m∠2 = 125° simplify
m∠1 = 40°
m∠2 = 125°

Find the measure of each numbered angle.

Question 18.

Answer:

We are given
m∠5 = 50° Corresponding ∠s
m∠3 = m∠5 = 50° Corresponding ∠s
m∠4 = 50° Alternate Interior ∠s
m∠4 + m∠2 + 77° = 180° substitute
m∠2 + 127° = 180° simplify
m∠2 + 127° – 127° = 180° — 127° Subtract 127° from both sides:
m∠2 = 53° Simplify:
114° = m∠1 + m∠4 Exterior ∠ of triangle:
114° = m∠1 + 50° Substitute:
114° – 50° = m∠1 + 50° + 50° Substitute 50° from both sides
m∠1 = 64° simplify
m∠1 = 64°
m∠2 = 53°
m∠3 = 50°

Question 19.

Answer:

we are given
m∠1 + 67° + 53° = 180° Sum of ∠s in triangle:
m∠1 + 120° = 180° Simplify:
m∠1 + 120° – 120° = 180° — 120° Subtract 120° from both sides:
m∠1 = 60° Simplify:
m∠3 = 67° Alternate interior ∠s
m∠2 = m∠1 + m∠3 vertical ∠s
m∠2 = 60° + 67° substitute
m∠2 = 127° simplify
m∠1 = 60°
m∠2 = 127°

Solve.

Question 20.
\(\overleftrightarrow{\mathrm{BE}}\) is parallel to \(\overleftrightarrow{\mathrm{FH}}\). Find the measure of A
∠CAD in terms of ∠1 and ∠2.

Answer:
m∠ADE = m∠2 Corresponding ∠s:
m∠ADE = m∠CAD + m∠1 Exterior ∠ of triangle:
m∠2 = m∠CAD + m∠1 Substitute:
m∠2 — m∠1 = m∠CAD + m∠1 — m∠1 subtract m∠1 from both sides:
m∠CAD = m∠2 – m∠1 Simplify:
m∠CAD = m∠2 – m∠1

Question 21.
Math Journal
Explain why each of the following statement is true.
a) A triangle cannot have two right angles.
Answer:
m∠A = m∠B = 90° a) Let’s assume that a triangle ABC has two right angles:
m∠A + m∠B + m∠C = 180° Sum of ∠s in triangle:
90° + 90° + m∠C = 180° Substitute:
180° + m∠C = 180° Simplify:
180° + m∠C – 180° = 180° – 180° Subtract 180° from both sides:
m∠C = 0° Simplify:
We got a false statement as the triangle does not exist in this case. Therefore we assumed a wrong statement So a triangle cannot have two right angles.

b) The interior angle measures of an isosceles triangle cannot be 96°, 43°, and 43°.
Answer:
Lets assume that a triangle has the measures of its angles 96°, 43°, 43°
96° + 43° + 43° = 182° We compute the sum of the angles’ measures:
But the sum of a triangle’s angles measures is 180°. We got 182° ≠ 180°, therefore the statement that we assumed is false. So the interior measures of a triangle cannot be 96°, 43°, 43°.
See proofs (sum of the measures of the triangle’s angles)

Question 22.
m∠1 = 2x°, m∠2 = (x – 5)°, and m∠3 = 100°. Use an equation to find the value of x and then find the measures of ∠1 and ∠2.

Answer:
∠1 = 80°, ∠2 = 35°

Explanation:
∠1 + ∠3 = 180°
2x° + 100° = 180°
2x° = 180° – 100°
2x° = 80°
x° = 80°÷2
x° = 40°
∠1 = 2×40 = 80°
∠2 = 40 – 5 =35°

Use an equation to find the value of x.

Question 23.

Answer:
x° = 56°

Explanation:
x° + 94°+ 30° = 180°
x° + 124° = 180°
x° = 180° – 124°
x° = 56°

Question 24.

Answer:
x° = 59°, 2x° = 118°

Explanation:
2x° + 62° = 180°
2x° = 180° – 62°
2x° = 118°
x° = 118°÷2
x° = 59°
x + 13 = 59° + 13° = 72°

Use an equation to find the value of x.

Question 25.

Answer:
x° = 50°, y° = 65°

Explanation:
y° + 115° = 180°
y° = 180° -115°
y° = 65°
65° + 65° + x° = 180°
x° + 130° = 180°
x° = 180° – 130°
x° = 50°

Question 26.

Answer:
x° + x° + 12° = 180°
2x° + 12° = 180°
2x° = 180° – 12°
2x° = 68°
x° = 68 ÷ 2
x° = 34°

Brain@Work

ABCD is a rhombus, and the measure of ∠BCD is 68°. BDE is a triangle where the measure of ∠BED is 36° and the measure of ∠BDE is 73°. Find m∠EBC. Show how you obtain your answer.

Answer:
m∠EBD + 36° + 73° = 180° Sum of ∠s in triangle:
m∠EBD + 109° = 180° Simplify:
m∠EBD + 109° — 109° = 180° — 109° Subtract 109° from both sides:
m∠EBD = 71° Simplify:
\(\overline{B C}\) = \(\overline{D C}\) ABCD rhombus
m∠CDB = m∠CBD ∆BCD isosceles:
68° + m∠CDB + m∠CBD = 180° Sum of ∠s in triangle:
68° + 2m∠CBD = 180°
68° + 2m∠CBD — 68° = 180° — 68° Subtract 68° from both sides:
2m∠CBD = 112° Simplify:

Divide by 2
m∠CBD = 56° Simplify:
m∠EBC = m∠EBD — m∠CBD Substitute:
m∠EBC = 71° — 56°
= 15°

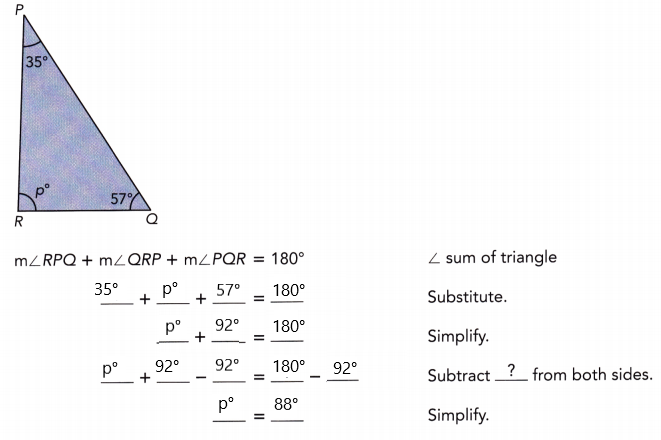
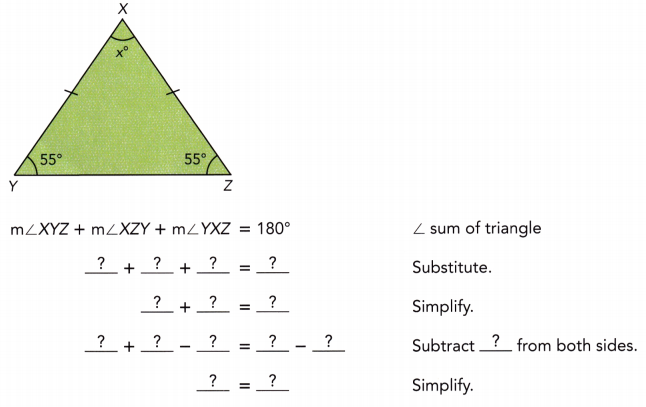
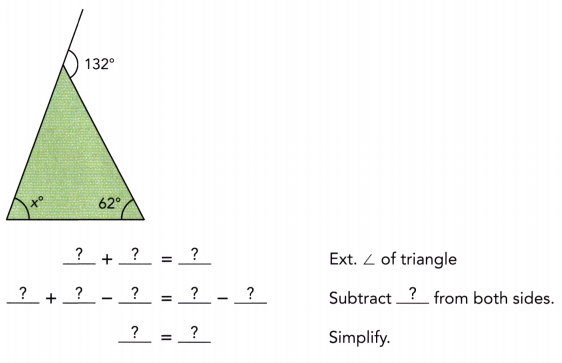
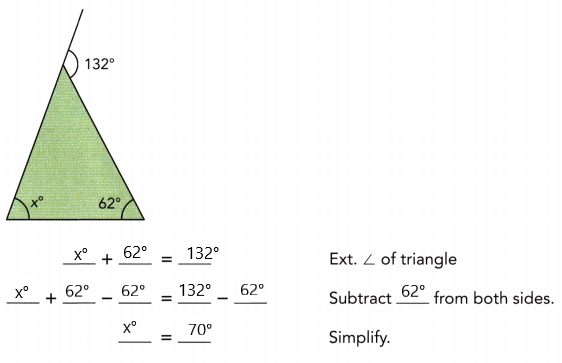
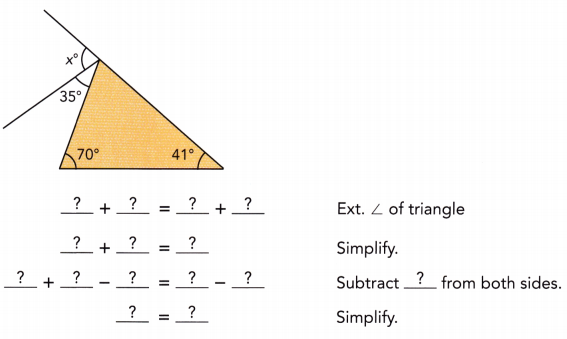
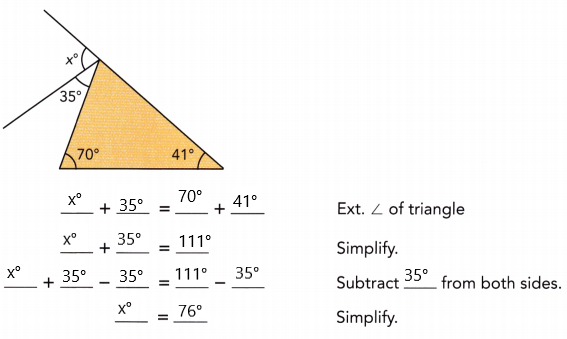
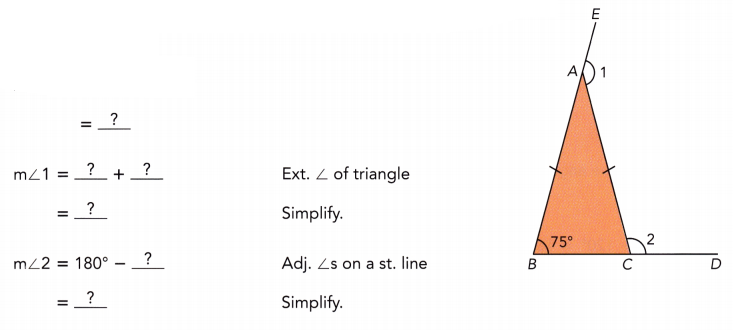
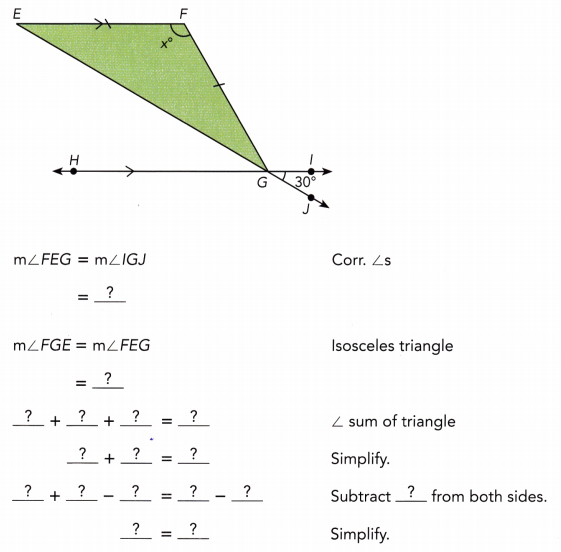
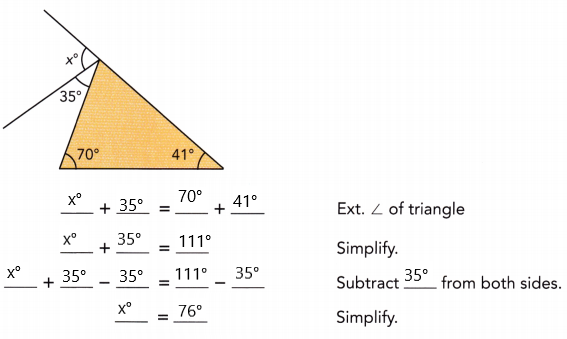
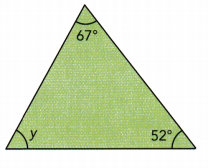
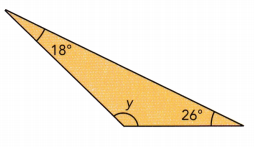
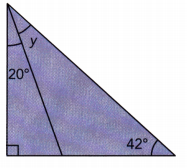
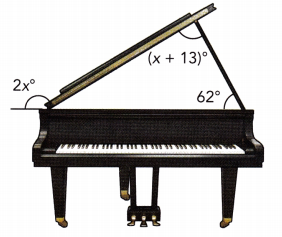
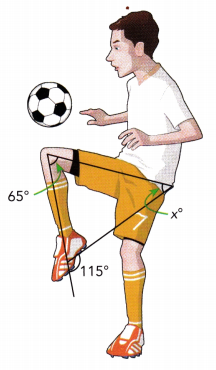
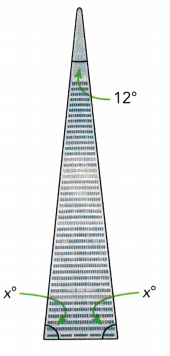
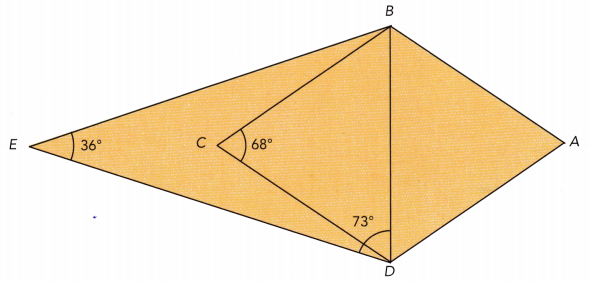
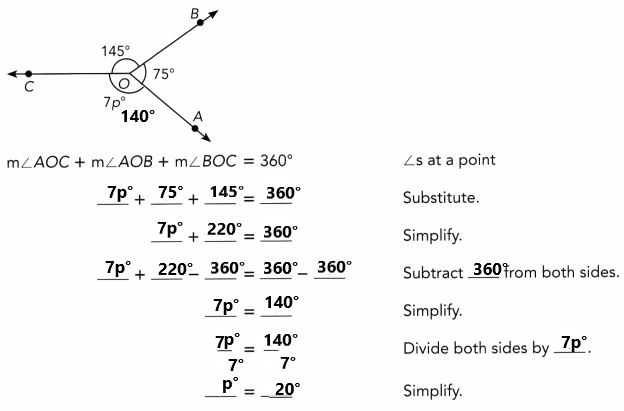
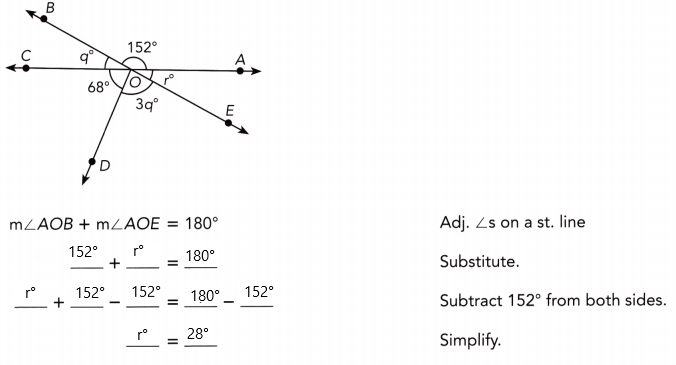
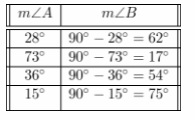
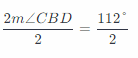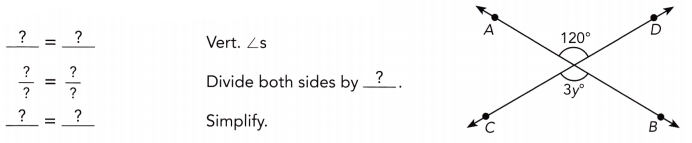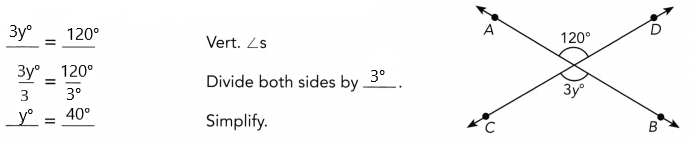Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 6 Lesson 6.3 Alternate Interior, Alternate Exterior, and Corresponding Angles to score better marks in the exam.

Math in Focus Grade 7 Course 2 B Chapter 6 Lesson 6.3 Answer Key Alternate Interior, Alternate Exterior, and Corresponding Angles

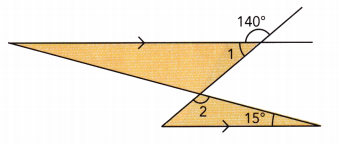
Math in Focus Grade 7 Chapter 6 Lesson 6.3 Guided Practice Answer Key

Hands-On Activity

Materials:

• protractor

Explore The Angles Formed By Parallel Lines And A Transversal Using A Protractor

Work in pairs.

Step 1.
On a piece of paper, draw a pair of parallel lines, \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\), as shown. Draw a transversal \(\overleftrightarrow{P Q}\) that intersects the pair of parallel lines. Use a protractor to measure the angles in the diagram.

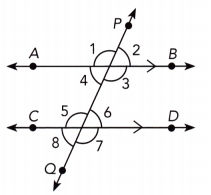
Step 2.
Record your results in a table like the one shown.

Math Journal
What do you notice about the measures of these angle pairs: Alternate interior angles, alternate exterior angles, and corresponding angles? Make a conjecture about the angle measures for each pair.

Math Journal
Compare the conjecture that you have made for corresponding angles, alternate interior angles, and alternate exterior angles with the conjectures made by other students. What do you observe?

When two parallel lines are cut by a transversal,

• the alternate interior angles are always congruent (alt. int. ∠s, || lines).
• the alternate exterior angles are always congruent (alt. ext. ∠s, || lines).
• the corresponding angles are always congruent (corr. ∠s, || lines).

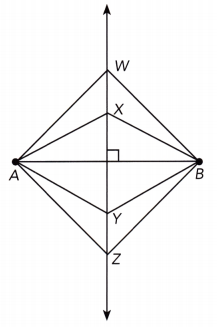
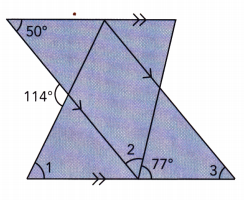
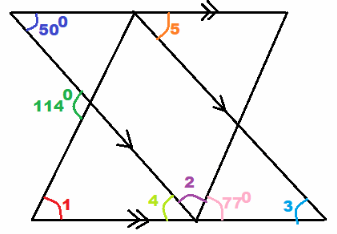
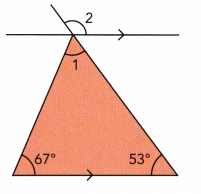
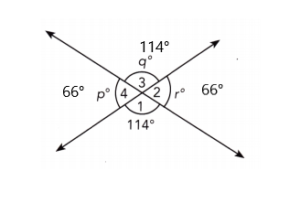
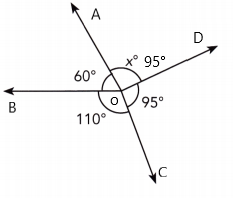
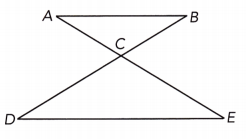
Use the diagram at the right to complete the following questions.

Question 1.
\(\overleftrightarrow{\mathrm{AD}}\), \(\overleftrightarrow{\mathrm{EH}}\), \(\overleftrightarrow{\mathrm{XY}}\), and \(\overleftrightarrow{\mathrm{WZ}}\) are straight lines and \(\overleftrightarrow{\mathrm{XY}}\) is parallel to \(\overleftrightarrow{\mathrm{WZ}}\). Identify all the pairs of angles formed by the intersection of \(\overleftrightarrow{\mathrm{AD}}\) with \(\overleftrightarrow{\mathrm{XY}}\) and \(\overleftrightarrow{\mathrm{WZ}}\).

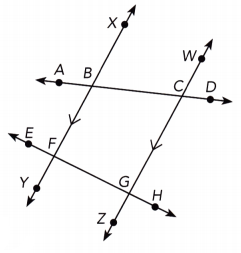
Answer:
\(\overline{X Y}\) || \(\overline{W Z}\) a) We are given:
∠ABX and ∠BCW Pairs of corresponding angles:
∠XBC and ∠WCD
∠EFB and ∠FGC
∠BFG and ∠CGH
∠XBC and ∠BCG b) Alternate interior angles:
∠FBC and ∠BCW

a) Corresponding angles: ∠ABX and ∠BCW;
Answer:
∠XBC and ∠WCD
∠EFB and ∠FGC
∠BFG and ∠CGH

b) Alternate interior angles: ∠XBC and ∠BCG;
Answer:
∠FBC and ∠BCW

Question 2.
Name another transversal of the parallel lines in the diagram.
Answer:
\(\overline{X Y}\) || \(\overline{W Z}\) we are given
A transversal of the parallel lines \(\overline{X Y}\) and \(\overline{W Z}\) other than \(\overline{A D}\) is \(\overline{E H}\).
\(\overline{E H}\)

Question 3.
Identify one pair of each of the following angles formed by the intersection of \(\overleftrightarrow{\mathrm{EH}}\) with \(\overleftrightarrow{\mathrm{XY}}\) and \(\overleftrightarrow{\mathrm{WZ}}\).
a) Corresponding angles
Answer:
\(\overline{X Y}\) || \(\overline{W Z}\) We are given:
∠EFY and ∠FOZ a) Identify a pair of corresponding angles formed by the intersection of \(\overline{E H}\) with \(\overline{X Y}\) and \(\overline{W Z}\):

b) Alternate interior angles
Answer:
∠BFG and ∠FGZ b) Identify a pair of alterrate interior angles formed by the intersection of \(\overline{E H}\) with \(\overline{X Y}\) and \(\overline{W Z}\):

c) Alternate exterior angles
Answer:
∠EFY and ∠CGR c) Identity a pair of aiterrate exterior angles formed by the intersection of \(\overline{E H}\) with \(\overline{X Y}\) and \(\overline{W Z}\):
a) ∠EFY and ∠FGZ
b) ∠BFG and ∠FGZ
c) ∠EFY and ∠CGH

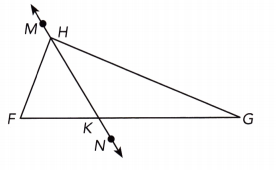
Complete.

Question 4.
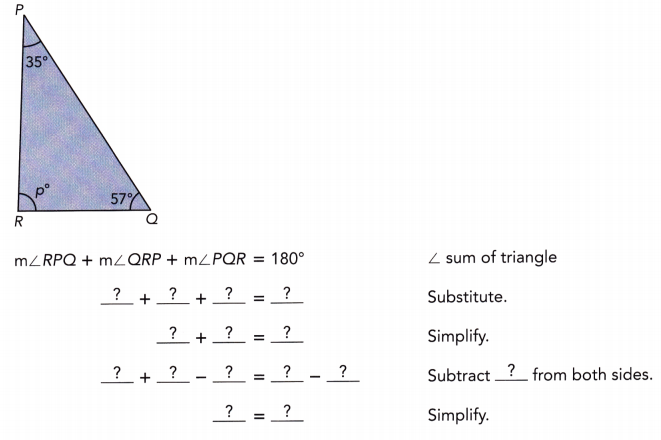
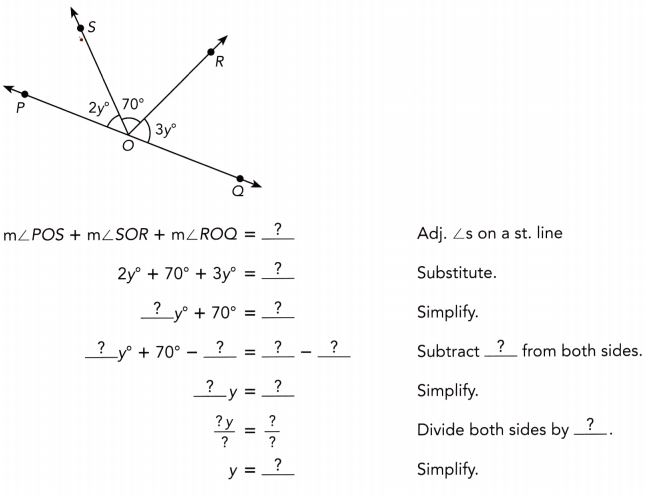
In the diagram, \(\overleftrightarrow{\mathrm{MN}}\) is parallel to \(\overleftrightarrow{\mathrm{PQ}}\). Find the measures of ∠1, ∠2, and ∠3.

Answer:
\(\overline{M N}\) || \(\overline{P Q}\) We are given:
m∠1 = 81° Alternate interior ∠s:
m∠2 = 81° : Corresponding ∠s:
m∠3 + m∠2 = 180° Supplementary ∠s:
m∠3 + 81° = Substitute m∠2 = 81°:
m∠3 + 81° — 81° = 180° — 81° Subtract 81° from bothsides:
m∠3 = 99° simplify
81° ; 81° ; m∠2 ; 81° ; 81° ; 81° ; 81° ; 81° ; 99°

Math in Focus Course 2B Practice 6.3 Answer Key

\(\overleftrightarrow{\mathrm{MN}}\) is parallel to \(\overleftrightarrow{\mathrm{PQ}}\). Identify each pair of angles as corresponding, alternate interior, alternate exterior angles, or none of the above.

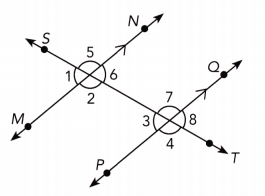
Question 1.
∠3, ∠6
Answer:
\(\overline{M N}\) || \(\overline{P Q}\) We are given:
∠3 and ∠6 are alternate interior angles because they lie inside the pair of parallel lines and on the opposite sides of the transversal.
Alternate interior angles

Question 2.
∠5, ∠7
Answer:
\(\overline{M N}\) || \(\overline{P Q}\) We are given:
∠5 and ∠7 are corresponding angles because they lie in matching corners on same side of the transversal \(\overline{S T}\).
corresponding angles

Question 3.
∠1, ∠2
Answer:
\(\overline{M N}\) || \(\overline{P Q}\) We are given:
∠1 and ∠2 are neither alternate interior, nor alternate exterior or corresponding, therefore none of the above.
None of the above

Question 4.
∠1, ∠8
Answer:
\(\overline{M N}\) || \(\overline{P Q}\) We are given:
∠1 and ∠8 are alternate exterior angles because they lie outside the pair of parallel lines and on the opposite sides of the transversal \(\overline{S T}\).
Alternate exterior angles

Question 5.
∠8, ∠6
Answer:
\(\overline{M N}\) || \(\overline{P Q}\) We are given:
∠8 and ∠6 are corresponding angles because they lie in matching corners on same side of the transversal \(\overline{S T}\).
corresponding angles

Question 6.
∠4, ∠7
Answer:
\(\overline{M N}\) || \(\overline{P Q}\) We are given:
∠4 and ∠7 are neither alternate interior, nor alternate exterior or corresponding, therefore none of the above.
None of the above

Question 7.
∠2, ∠7
Answer:
\(\overline{M N}\) || \(\overline{P Q}\) We are given:
∠2 and ∠7 are alternate interior angles because they lie inside the pair of parallel lines and on the opposite sides of the transversal \(\overline{S T}\).
Alternate interior angles

Question 8.
∠6, ∠7
Answer:
\(\overline{M N}\) || \(\overline{P Q}\) We are given:
∠6 and ∠7 are neither alternate interior, nor alternate exterior or corresponding, therefore none of the above.
None of the above

\(\overleftrightarrow{\mathrm{AB}}\) is parallel to \(\overleftrightarrow{\mathrm{CD}}\). Use the diagram to answer the following.

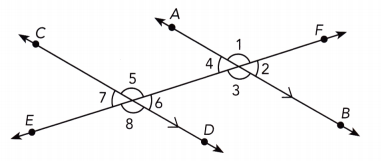
Question 9.
Name two angles that have the same measure as ∠2.
Answer:
\(\overline{A B}\) || \(\overline{C D}\) We are given:
m∠7 = m∠2 ∠2 and ∠7 are alternate exterior angles because they lie outside the pair of parallel lines and on the opposite sides of the transversal \(\overline{E F}\).
m∠6 = m∠2 ∠2 and ∠6 are corresponding angles because they lie in matching corners on the same side of the transversal \(\overline{E F}\).
∠6, ∠7

Question 10.
Name an angle that is supplementary to ∠6.
Answer:
\(\overline{A B}\) || \(\overline{C D}\) We are given:
∠5, ∠8, ∠3, ∠1 We identify supplementary angles to ∠6:
∠5, ∠8, ∠3, ∠1

Question 11.
If m∠4 = 46°, find m∠5.
Answer:
\(\overline{A B}\) || \(\overline{C D}\) We are given:
m∠6 = m∠4 Alternate interior ∠s:
m∠6 = 46° substitute:
m∠5 + m∠6 = 180° supplementary ∠s:
m∠5 + 46° = 180° substitute
m∠5 + 46° – 46° = 180° – 46° subtract 46° from both sides
m∠5 = 134° simplify
134°

Question 12.
If m∠1 = 131°, find m∠7.
Answer:
\(\overline{A B}\) || \(\overline{C D}\) We are given:
Corresponding ∠s:
m∠5 = m∠1 corresponding ∠s:
m∠5 = 131° Substitute:
m∠5 + m∠7 = 180° Supplementary ∠s:
131° + m∠7 = 180° Substitute:
131° + m∠7 – 131° = 180° – 131° Subtract 131° from both sides:
m∠7 = 49° Simplify:
49°

Find the measure of each numbered angle.

Question 13.
\(\overleftrightarrow{M N}\) is parallel to \(\overleftrightarrow{P Q}\).

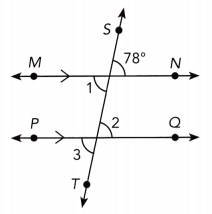
Answer:
\(\overline{M N}\) || \(\overline{P Q}\) We are given:
m∠1 = 78° vertical ∠s:
m∠1 = m∠2 Alternate interior ∠s:
m∠2 = 78° Substitute:
m∠3 = m∠2 vertical ∠s:
m∠3 = 78° Substitute:
m∠1 = 78° ;m∠2 = 78° ; m∠3 = 78°

Question 14.
\(\overleftrightarrow{M N}\) is parallel to \(\overleftrightarrow{P Q}\).

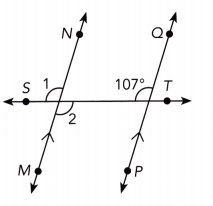
Answer:
\(\overline{M N}\) || \(\overline{P Q}\) We are given:
m∠1 = 107° vertical ∠s:
m∠1 = m∠2 corresponding ∠s:
m∠1 = m∠2 vertical ∠s:
m∠2 = 107° Substitute:
m∠1 = 107° ;m∠2 = 107°

Question 15.
\(\overleftrightarrow{P Q}\) is parallel to \(\overleftrightarrow{R S}\).

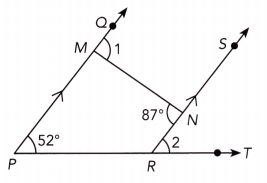
Answer:
\(\overline{P Q}\) || \(\overline{R S}\) We are given:
m∠1 = 87° Alternate interior ∠s:
m∠2 = 52° corresponding ∠s:
m∠1 = 87° ; m∠2 = 52°

Question 16.
\(\overleftrightarrow{P Q}\) is parallel to \(\overleftrightarrow{R S}\).

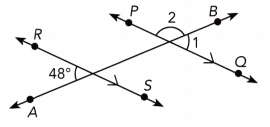
Answer:
\(\overline{P Q}\) || \(\overline{R S}\) We are given:
m∠1 = 48° Alternate exterior ∠s:
m∠1 + m∠2 = 180° supplementary ∠s:
48° + m∠2 = 180° substitute
48° + m∠2 – 48° = 180° – 48° subtract 48° from both sides
m∠2 = 132° simplify
m∠1 = 48° ; m∠2 = 132°

Question 17.
\(\overleftrightarrow{A B}\) is parallel to \(\overleftrightarrow{C D}\) and \(\overleftrightarrow{M N}\) is parallel to \(\overleftrightarrow{P Q}\).

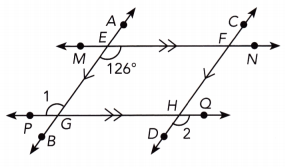
Answer:
\(\overline{M N}\) || \(\overline{P Q}\) We are given:
m∠1 = 126° Alternate interior ∠s:(transversal \(\overline{A B}\))
\(\overline{A B}\) || \(\overline{C D}\) we are given
m∠2 = m∠1 Alternate exterior ∠s:(transversal \(\overline{P Q}\))
m∠2 = 126° substitute
m∠1 = 126° ; m∠2 = 126°

Question 18.
\(\overleftrightarrow{A B}\) is parallel to \(\overleftrightarrow{C D}\) and \(\overleftrightarrow{M N}\) is parallel to \(\overleftrightarrow{P Q}\).

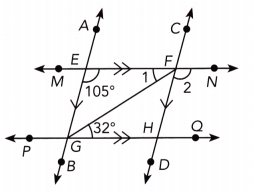
Answer:
\(\overline{M N}\) || \(\overline{P Q}\) We are given:
m∠1 = 32° Alternate interior ∠s:(transversal \(\overline{G F}\))
\(\overline{A B}\) || \(\overline{C D}\) we are given
m∠2 = 105° corresponding ∠s:(transversal \(\overline{M N}\))
m∠1 = 32° ; m∠2 = 105°

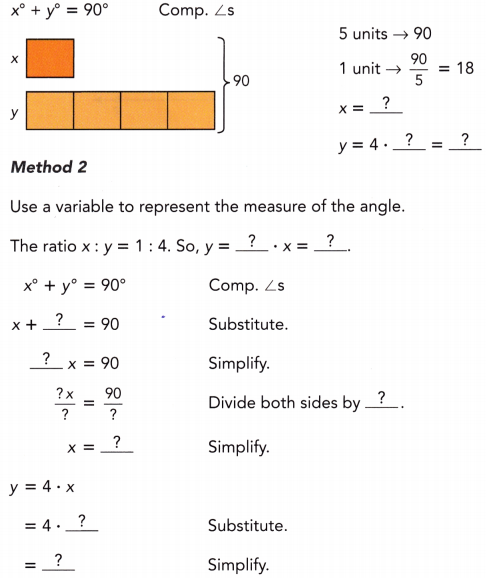
Find the value of each variable.

Question 19.
\(\overleftrightarrow{P Q}\) is parallel to \(\overleftrightarrow{R S}\).

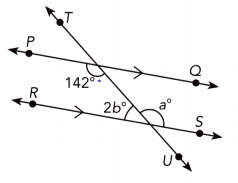
Answer:
\(\overline{P Q}\) || \(\overline{R S}\) We are given:
a = 142 Alternate interior ∠s (transversal \(\overline{T U}\)):
a = 142
2b° + a° = 180° Supplementary ∠s
2b° + 142° = 180° Substitute:
2b° + 142° — 142° = 180° — 142° Subtract 142° from both sides:
2b° = 38°
\(\frac{2 b^{\circ}}{2}\) = \(\frac{38^{\circ}}{2}\) Divide by 2:
b = 19 simplify
a = 142
b = 19

Question 20.
\(\overleftrightarrow{P Q}\) is parallel to \(\overleftrightarrow{R S}\).

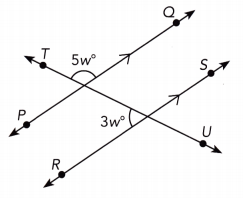
Answer:
\(\overline{P Q}\) || \(\overline{R S}\) We are given:
Let’s note by X the intersection between the lines \(\overline{T U}\) and \(\overline{R S}\).
m∠TXS = Corresponding ∠s (transversal \(\overline{T U}\)):
m∠TXS + m∠TXR = 180° Supplementary ∠s
5w° + 3w° = 180° Substitute:
8w° = 180° Simplify:
\(\frac{8 w^{\circ}}{8}\) = \(\frac{180^{\circ}}{8}\) Divide by 8
w = 22.5° simplify
w = 22.5°

MathJournal
Determine whether \(\overleftrightarrow{A B}\) is parallel to \(\overleftrightarrow{C D}\). Use the fact that two lines are parallel if a pair of corresponding angles formed by a transversal are congruent. Explain your answer.

Question 21.

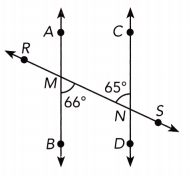
Answer:
m∠BMN = 66° ∠BMN and ∠MNC are alternate interior ∠s We have:
m∠BMN ≠ m∠MNC As 66° ≠ 65°, we have

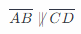
This means the lines \(\overline{A B}\) and \(\overline{C D}\) are not parallel:

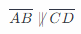
Question 22.

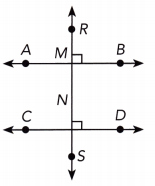
Answer:
m∠MND = 90° ∠RMB and ∠MND are corresponding ∠s. We have:
m∠MND = 90°
m∠RMB = m∠MND We get:
\(\overline{A B}\) = \(\overline{C D}\) This means the lines \(\overline{A B}\) and \(\overline{C D}\) are parallel:
\(\overline{A B}\) || \(\overline{C D}\)

Question 23.

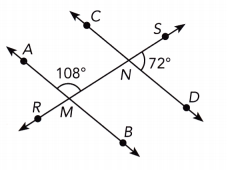
Answer:
m∠AMN + m∠NMB = 180° Supptementary ∠s
108° + m∠NMB = 180° Substitute:
108° + m∠NMB — 108° = 180° — 108° Subtract 108° from both sides:
m∠NMB = 72° Simplify:
m∠NMB = 72° ∠SND and ∠NMB are corresponding ∠s. We have:
m∠SND = m∠NMB we got
\(\overline{A B}\) = \(\overline{C D}\) This means the lines \(\overline{A B}\) and \(\overline{C D}\) are parallel
\(\overline{A B}\) || \(\overline{C D}\)

\(\overline{M N}\) is parallel to \(\overline{P Q}\). Find each unknown angle measure.

Question 24.

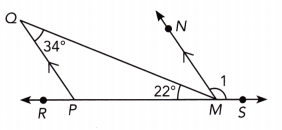
Answer:
m∠QMN = m∠PQM AS \(\overline{M N}\) || \(\overline{M N}\), ∠PQM and ∠QMN are alternate interior ∠s. We hava
m∠QMN = 34° Substitute
∠RMQ + m∠QMN + m∠1 = 180° ∠RMS straight angle
22° + 34° + m∠1 = 180°
56° + m∠1 = 180° Simplify
56° + m∠1 – 56° = 180° – 56° subtract 56° from both sides
m∠1 = 124° simplify
m∠1 = 124°

Question 25.

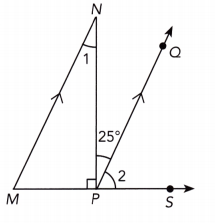
Answer:
m∠1 = m∠NPQ As \(\overline{M N}\) and \(\overline{P Q}\), ∠1 and ∠NPQ are alternate interior ∠s. We have:
m∠1 = 25° Substitute:
m∠MPN + m∠NPQ + m∠2 = 180° ∠MPS straight:
90° + 25° + m∠2 = 180° Substitute:
115° + m∠2 = 180° Simplify:
115° + m∠2 – 115° = 180° – 115° subtract 115° from both sides
m∠2 = 65° simplify
m∠1 = 25°
m∠2 = 65°

Question 26.

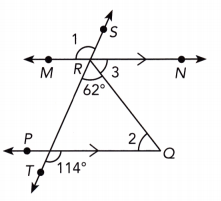
Answer:
m∠TRN = 114° As \(\overline{M N}\) || \(\overline{P Q}\), a pair of corresponding angles is:
62° + m∠3 = 114° Substitute:
62° + m∠3 – 62° = 114° — 62° Subtract 62° from both sides:
m∠3 = 52° simplify
m∠2 = m∠3 alternate interior ∠s
m∠2 = 52°
m∠1 = 114° Alternate exterior ∠s
m∠1 = 114°
m∠2 = 52°
m∠3 = 52°

Question 27.

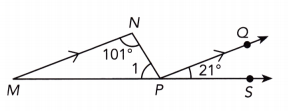
Answer:
m∠NPQ = m∠MNP As \(\overline{M N}\) || \(\overline{P Q}\), ∠MNP and ∠NPQ are alternate interior angles
m∠NPQ = 101° Substitute:
m∠1 + m∠NPQ + m∠QPS = 180° ∠MPS is a straight line
m∠1 + 101° + 21° = 180° substitute
m∠1 + 122° = 180° simplify
m∠1 + 122° – 122° = 180° – 122° subtract 122° from both sides
m∠1 = 58° simplify
m∠1 = 58°

Question 28.

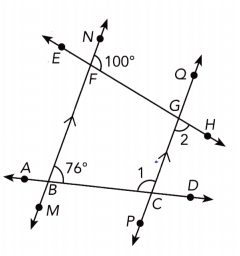
Answer:
m∠DCQ = m∠DBN As \(\overline{M N}\) || \(\overline{P Q}\), a pair of a corresponding angles is :
m∠DCQ = 76° Substitute
m∠1 + m∠DCQ = 180° ∠ACD is straight
m∠1 + 76° = 180° substitute
m∠1 + 76° – 76° = 180° – 76° subtract 76° from both sides
m∠1 = 104° simplify
m∠MFH + m∠HFN = 180° m∠MFH straight line
m∠MFH + 100° = 180° substitute
m∠MFH + 100° – 100° = 180° Subtract 100° from both sides:
m∠MFH = 80° Simplify:
m∠PGH = m∠MFH ∠MFH and ∠PGH corresponding angles:
m∠2 = 80° Substitute:
m∠1 = 104°
m∠2 = 80°

Question 29.

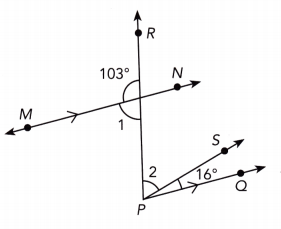
Answer:
m∠1 + 103° = 180° Straight ∠
m∠1 + 103° — 103° = 180° — 103° Subtract 103° from both sides:
m∠1 = 77° Simplify:
m∠1 = m∠2 + 16° As \(\overline{M N}\) || \(\overline{P Q}\), a pair of alternate interior angles is:
77° = m∠2 + 16° Substitute:
77° – 16° = m∠2 + 16 — 16° Subtract 16° from both sides:
m∠2 = 61° Simplify:
m∠1 = 77°
m∠2 = 61°

\(\overline{\mathbf{A B}}\) is parallel to \(\overline{\mathbf{C D}}\). Find the value of x.

Solve. Show your work.

Question 30.

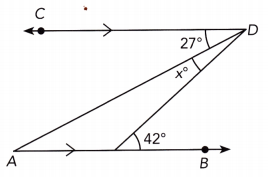
Answer:
27° + x° = 42 As \(\overline{A B}\) || \(\overline{C D}\), a pair of alternate interior angles is:
27° + x° — 27° = 42° — 27° Subtract 27° from both sides:
x° = 15° Simplify:
x = 15

Question 31.

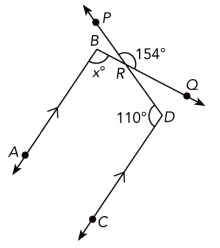
Answer:

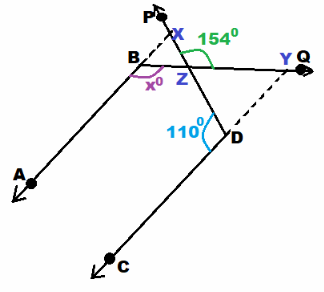
we are given
Let X be the intersection of the Lines \(\overline{A B}\) and \(\overline{P D}\), Y be the intersection of the lines \(\overline{C D}\) and \(\overline{B Q}\) and Z be the intersection of the lines \(\overline{P D}\) || \(\overline{B Q}\).
110° + m∠PDY = 180° ∠CDY is straight
110° + m∠PDY = 180° – 110° subtract 110° from both sides
m∠PDY = 70° simplify
m∠DZY + 154° = 180° ∠PZD is straight
m∠DZY + 154° – 154 = 180° — 134° Subtract 154° from both sides:
m∠DZY = 26° Simplify:
m∠DZY + m∠PDY + m∠BYD = 180° Sum of the angles in ∆ZDY:
26° + 70° + m∠BYD = 180° Substitute:
96° + m∠BYD = 180° Simplify:
96° + m∠BYD – 96° = 180° — 96° Subtract 96° from both sides:
m∠BYD = 84° Simplify:
m∠BYD + m∠DYQ = 180° ∠BYQ is straight:
84° + m∠DYQ = 180° Substitute:
84° + m∠DYQ – 84° = 180° – 84° Subtract 84° from both sides:
m∠DYQ = 96° Simplify:
m∠ABQ = m∠DYQ As \(\overline{A B}\) || \(\overline{C D}\), a pair of corresponding angles is:
x° = 96° Substitute:
x = 96

Question 32.

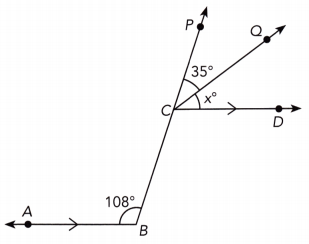
Answer:
m∠BCD = m∠ABC As \(\overline{A B}\) || \(\overline{C D}\), a pair of alternate interior angles is:
m∠BCD = 108° Substitute:
m∠BCD + m∠DCQ + m∠QCP = 180° ∠BCP is straight:
108° + x° + 35° = 180° Substitute:
143° + x° = 180° Simplify:
143° + x° — 143° = 180° – 143° Substitute:
x = 37 Simplify:
x = 37

Question 33.

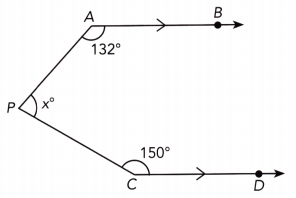
Answer:

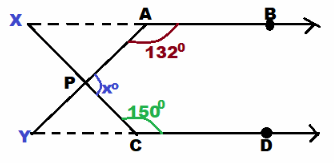
we are given
Let X be the intersection of the lines \(\overline{A B}\) and \(\overline{P C}\), Y be the intersection of the lines \(\overline{C D}\) and \(\overline{A P}\).
150° + m∠XCY = 180° ∠YCD is straight:
150° + m∠XCY — 150° = 180° — 150° Subtract 150° from both sides:
m∠XCY = 30° Simplify:
m∠XAP + 132° = 180° ∠XAB is straight:
m∠XAP = 48° simplify
m∠XAP = m∠PYC As \(\overline{A B}\) || \(\overline{C D}\), a pair of alternate interior angles is:
m∠PYC = 48° Substitute:
m∠PYC + m∠XCY + m∠YPC = Sum of the ∠s in a triangle:
48° + 30° + m∠YPC = 180° Substitute:
78° + m∠YPC = Simplify:
78° + m∠YPC — 78° = 180° — 78° Subtract 78° from both sides:
m∠YPC = 102° Simplify:
m∠YPC + x° = 180° ∠APY straight:
102 + x° = 180° Substitute:
102° + x° – 102° = 180° — 102 Subtract 102° from both sides:
x° = 78° simplify
x = 78

Solve. Show your work.

Question 34.
In the diagram below, \(\overleftrightarrow{M N}\) is parallel to \(\overleftrightarrow{P Q}\). m∠1 = (x + 28)° and m∠2 = (3x + 14)°. Write and solve an equation to find the measures of ∠1 and ∠2.

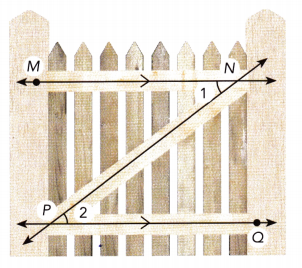
Answer:
m∠1 = m∠2 As \(\overline{M N}\) || \(\overline{P Q}\), a pair of alternate interior angles is:
x + 28 = 3x + 11 substitute
x + 28 – x = 3x + 14 – x Subtract x from both sides:
28 = 2x + 14 simplify
28 — 14 = 2x + 14 — 14 Subtract 14 from both sides:
2x = 14 Simplify:
\(\frac{2 x}{2}\) = \(\frac{14}{2}\) Divide by 2:
x = 7 Simplify:
m∠1 = m∠2 = (7 + 28)° = 35° Determine m∠1, m∠2:
x + 28 = 3x + 14
m∠1 = 35° ;m∠2 = 35°

Question 35.
Math Journal
In a plane, if a line is perpendicular to one of two parallel lines, is it also perpendicular to the other? Explain your reasoning.
Answer:
\(\overline{A B}\) || \(\overline{C D}\) We are given:
\(\overline{E F}\) ⊥ \(\overline{A B}\)
m∠EMB = 90°: \(\overline{E F}\) ⊥ \(\overline{A B}\)
m∠MND = m∠EMB As \(\overline{A B}\) || \(\overline{C D}\), a pair of corresponding angles is:
m∠MND = 90° Substitute:
\(\overline{E F}\) ⊥ \(\overline{C D}\) m∠MND = 90°
yes

Question 36.
The diagram below contains examples of parallel lines cut by transversals. Line MN is parallel to line PQ and line AB is parallel to line CO.

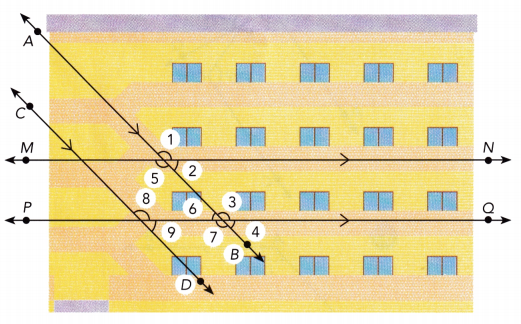
a) Name two pairs of corresponding angles.
Answer:
∠1 and ∠3 a) As \(\overline{A B}\) || \(\overline{P Q}\), pairs of corresponding angles are (transversal \(\overline{A B}\)):
∠2 and ∠4
∠5 and ∠7

b) Name all the angles that have the same measure as ∠1.
Answer:
m∠5 = m∠1 b) vertical ∠s:
m∠3 = m∠1 corresponding ∠s:
m∠8 = m∠3 = m∠1
m∠7 = m∠5 = m∠1
a) ∠1 and ∠3
∠2 and ∠4
∠5 and ∠7
b) ∠1, ∠3, ∠5, ∠7 = ∠8

Question 37.
The two mirrors used in a periscope are parallel to each other as shown. m∠1 = 3x°, m∠2 = (60 – x)°, and m∠3 = 90°. Write and solve an equation to find the value of x. Then find the measure of ∠4.

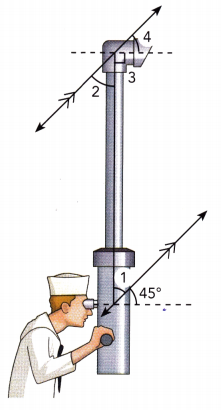
Answer:
m∠1 = 3x° We are given:
m∠2 = (60 – x)°
m∠3 = 90°
m∠1 = m∠2 Alternate interior ∠s
3x° = (60 – x)°
3x = 60 — x Substitute:
3x + x = 60 – x + x Add x to both sides:
4x = 60 Simplify:
\(\frac{4 x}{4}\) = \(\frac{60}{4}\) Divide by 4:
x = 15 Simplify:
m∠2 + m∠3 + m∠4 = 180° Straight ∠:
Substitute:
(60 – x)° + 90° + m∠4 = 180°
(60 – 15)° + 90° + m∠4 = 180°
45° + 90° + m∠4 = 180°
135° + m∠4 = 180° Simplify:
135° + m∠4 – 135° = 180° — 135° Subtract 135° from both sides:
m∠4 = 45° Simplify:
x = 15
m∠4 = 45°

Question 38.
MathJournal
Use a diagram to illustrate each of the following: transversal, corresponding angles, alternate exterior angles, and alternate interior angles. Label your diagram and explain which angles are congruent.
Answer:

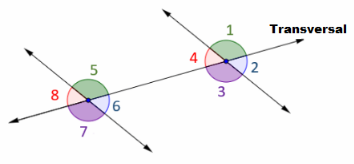
We draw the diagram of 2 parallel lines cut by a transversal:
m∠1 = m∠5 Pairs of corresponding angles:
m∠2 = m∠6
m∠3 = m∠7
m∠4 = m∠8
m∠1 = m∠7 Pairs of alternate exterior aigles
m∠2 = m∠8
m∠3 = m∠5 Pairs of alternate Interior angles
m∠4 = m∠6
See diagram

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 6 Lesson 6.2 Angles that Share a Vertex to score better marks in the exam.

Math in Focus Grade 7 Course 2 B Chapter 6 Lesson 6.2 Answer Key Angles that Share a Vertex

Math in Focus Grade 7 Chapter 6 Lesson 6.2 Guided Practice Answer Key

Complete.

Question 1.
Find the value of p in the diagram.

Answer:
p° = 20°

Explanation:

7 p°+ 75° + 145° = 360°
7 p° + 220° = 360°
7p° + 220° – 360° = 360°-360°
7p° = 140°
p°  = 140 ÷ 7
p° = 20°

Solve.

Question 2.
\(\overleftrightarrow{B E}\) and \(\overleftrightarrow{C A}\) are straight lines. Find the value of each variable.


Answer:
r°=28°, q°=28°, 3q°=84°

Explanation:


∠BOA + ∠AOE = 180°
152°+r°=180°
r = 180°-152°
r= 28°
∠BOC + ∠COD + ∠DOE = 180°
q°+ 68°+3q° = 180°
4q°+68° = 180°
4q° = 180°-68°
4q° = 112°
q°= 112÷4
q°= 28°
3q°= 84°

Question 3.
\(\overleftrightarrow{P Q}\) is a straight line. Find the value of each variable.

Answer:
m°=31°, n°=17°, 3m°=93°

Explanation:

m°+149° = 180°
m° = 180°-149°
m° = 31°
3m°= 93°
n°+3m°+70°=180°
n°+93°+70°=180°
n°=180°-163°
n°= 17°

Complete.

Question 4.
In the diagram at the right, the ratio a: b: c = 1: 3 : 5. Find the values of a, b, and c.
The ratio a : b : c = 1 : 3 : 5. So, b = 3 • a and c = 5 • a.


Answer:
a°= 40°, b°=120°, c°=200°

Explanation:
The ratio given is a : b : c = 1 : 3 : 5. Let a=1a, b=3a, c=5a

Technology Activity

Materials:

• geometry software

Explore The Relationship Among Vertical Angles Using Geometry Software

Work in pairs.

Step 1.
Construct intersecting line segments, \(\overline{A B}\) and \(\overline{C D}\), as shown.

Step 2.
Select ∠AOD and find its measure.

Step 3.
Select ∠COB and find its measure.

Step 4.
Then select ∠AOC and ∠BOD and find their measures.

Step 5.
Select point D and drag it so that you change the measures of ∠AOD and ∠AOC. As the measure of ∠AOD changes, what do you notice about the measure of ∠AOC?

Math Journal
Describe what you notice about the measures of the vertical angles.
Answer:
Vertical angles are always equal to one another and are always congruent. The four angles all together always sum to a full angle 360°.

Complete.

Question 5.
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are straight lines. Find the value of y.

Answer:
3y°=120°

Explanation:

∠COB = ∠AOD
3y°=120°
y°= 120°÷3
y° = 40°

Complete.

Question 6.
In the diagram, two straight lines intersect to form angles 1, 2, 3, and 4. Find the value of each variable if m∠1 = 114°.

m∠1 + m∠2 = 180° Supp. ∠S

Answer:
r°=66°, p°=66°, q°=114°

Explanation:


114°+r°=180°
r°=180°-114
r°=66°
∠3=∠1
q°=114°
∠4=∠2
p°=r°
as r°=66°
p°=66°

Math in Focus Course 2B Practice 6.2 Answer Key

Find the value of each variable.

Question 1.

Answer:
x°=307°

Explanation:

x°+53°=360°
x°=360°-53°
x°=307°

Question 2.

Answer:
x°=257°

Explanation:

x°+33°=290°
x°=290°-33°
x°=257°

Question 3.

Answer:
x°=100°

Explanation:

x°+110°+150°=360°
x°+260°=360°
x°=100°

Question 4.

Answer:
x°=95°

Explanation:

∠AOD+∠BOC+∠AOD = 360°
x°+110°+95°+60°=360°
x°+265°=360°
x°=360°-265°
x°=95°

Question 5.
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are straight lines.

Answer:
p°= 34°

Explanation:

∠COA = ∠BOD
34° = p°
Hence p° = 34°

Question 6.
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are straight lines.

Answer:
r°=16°

Explanation:

In the image given below, we can observe that CD and AB are two straight lines. Here, ∠AOB and ∠COD are vertical angles.
a°= 164°
a°+r°=180°
164°+r°=180°
r°=180°-164°
r°=16°

Question 7.
\(\overleftrightarrow{A B}\), \(\overleftrightarrow{C D}\) and \(\overleftrightarrow{E F}\) are straight lines.

Answer:
a° = 35°, b° = 106°

Explanation:

∠FOD = ∠COE
a° = 35° (vertically opposite angles)
∠EOB = ∠AOF
b° = 106° (Vertically opposite angles)

Question 8.
\(\overleftrightarrow{A B}\), \(\overleftrightarrow{C D}\) and \(\overleftrightarrow{E F}\) are straight lines.

Answer:
b° = 126°, a° = 31°

Explanation:
∠AOF = ∠EOB
b° = 126° (vertically opposite angles)
∠AOC = ∠DOB
31° = a° (vertically opposite angles)

Question 9.
\(\overleftrightarrow{A B}\), \(\overleftrightarrow{C D}\) and \(\overleftrightarrow{E F}\) are straight lines.

Answer:
x° = 119°, y°= 122°

Explanation:

∠COE + ∠AOC = 180°
y°+ 58° = 180°
y° = 180°-58°
y° = 122°
∠DOB + ∠FOD = 180°
x° + 61° = 180°
x° = 180°-61°
x° = 119°

Question 10.
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are straight lines.

Answer:
w + 90° = 168° Vertical ∠s:
w° + 90° – 90° = 168° – 90° Subtract 90° from both sides:
w° = 78° Simplify:
w = 78

Find the value of k.

Question 11.
The ratio ∠1 : ∠2 : ∠3 : ∠4 = 3 : 2 : 1 : 3.

Answer:
k° = 40°

Explanation:

Let the assume given ratio be x
Now, the ratio is 3x: 2x: x: 3x
The sum of all angles at one point is 360°
Now add 3x+ 2x + x + 3x = 360°
9x = 360°
x = 360 ÷ 9
x° = 40°
3x° = 120°
2x° = 80°
3x° = 120°
Now we need to calculate the numbered angle 3 which is named as k° that is 40°

Question 12.
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are straight lines.

Answer:
4k°= 84°, 3k° = 63

Explanation:

∠COE +∠EOF = 174°
4k°+ 90° = 174°
4k° = 174-90
4k°= 84°
k° = 84÷4
k° = 21°
3k°= 21×3
3k° = 63°

Question 13.

Answer:
2k°+5k°+3k°+130°=180°
10k°+130°=360°
10k° = 360°-130°
10k° = 230°
k° = 23°
IF k°=23° then 2k° = 2×23 = 46°, 3k° = 3×23=69°
5k° = 5×23=115°

Name the pairs of vertical angles.

Question 14.

Answer:
AE and DB are a pair of non-adjacent angles that are formed when two lines intersect.

Explanation:
Vertical lines are a pair of non-adjacent angles formed when two lines intersect.

Question 15.

Answer:
Vertical angles are a pair of opposite angles formed by intersecting lines.
∠MKF and ∠NKG Lines \(\overline{M N}\) and \(\overline{F G}\) intersect in K.
∠FKN and ∠MKC We identify the pairs of vertical angles:
∠MKF and ∠NKG
∠FKN and ∠MKC

Question 16.
\(\overleftrightarrow{P S}\) and \(\overleftrightarrow{R N}\) are straight lines.

Answer:
Vertical angles are a pair of opposite angles formed by ¡ntersecting tines.
∠SOR ard ∠NOP Lines \(\overline{P S}\) and \(\overline{R N}\) intersect in O.
∠SON and ∠ROP We identify the pairs of vertical angles:
∠SOR and ∠NOP
∠SON ard ∠ROP

Find the value of each variable.

Question 17.

Answer:
64°+23°+3e°=360°
87°+3e°=360°
3e°=360°-87°
3e°=273°
e°=273°÷ 3°
e° = 91°

Question 18.
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are straight lines.

Answer:
2p°=88, q°= 92°, r°=2°

Explanation:

∠DOA = ∠BOC
2p°=88
p°= 88÷2
p°= 44
∠DOE+∠EOB+∠BOC= 180°
r°+2p°+88 = 180°
r°+88+88 = 180°
r°+178°=180°
r°=180°-178°
r°=2°
2p°+q°=180°
88+q°=180°
q°=180-88
q°= 92°

Question 19.
\(\overleftrightarrow{A B}\), \(\overleftrightarrow{C D}\) and \(\overleftrightarrow{E F}\) are straight lines. The ratio a : b : c = 1 : 2 : 2.

Answer:
a° = 36°, b = 72°, c = 72°

Explanation:

Let the ratio be x
The sum of the ratio be x + 2x + 2x = 5x
∠AOC = ∠DOB (vertically opposite angles are equal)
∠FOD + ∠DOB + ∠EOB = 180°
c°+a°+b° = 180°
2x + x° + 2x° = 180°
5x° = 180°
x° = 180÷5
x° = 36°
2x°= 72°

Question 20.
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are straight lines.

Answer:
f° = 40° Vertical ∠s:
f = 40
e° + f° = 180° Straight ∠:
e° + 40° = 1800 Substitute:
e° + 40° – 40° = 180° – 40° Subtract 40° from both sides:
e = 140 Simplify:
d° + 90° + 15° = e° Vertical ∠s:
d° + 105° = 140° Simplify:
d° + 105° — 105° = 140° – 105° Subtract 105° from both sides:
d = 35 Simplify:
f = 40
e = 140
d = 35

Answer each of the following.

Question 21.
In the diagram, the ratio p: q: r = 1: 2 : 3. Find the values of p, q, and r.

Answer:
p = 60°, q = 120°, r = 180°

Explanation:

p: q: r = 1: 2 : 3
x+2x+3x = 360°
6x = 360°
x = 360° ÷ 6
x = 60°
2x= 120°
3x = 180°
p = 60°, q = 120°, r = 180°

Question 22.
If ∠P and ∠N are angles at a point and m∠P = 149°, what is the m∠N?
Answer:
m∠N = 31°

Explanation:
The sum of angles at a point is 180°
Given angles are ∠P = 149°
Here we need to calculate ∠N
∠P + ∠N = 180°
149° + ∠N = 180°
∠N = 180°-149°
∠N = 31°

Question 23.
If 67°, 102°, 1 5°, and x° are angles at a point, what is the value of x?
Answer:
x° = 176°

Explanation:
67°+102°+15°+x°=360°
184°+x° = 360°
x°=360° -184°
x° = 176°

In the diagram below, \(\overleftrightarrow{M P}\) and \(\overleftrightarrow{Q R}\) are straight lines. Answer each of the following.

Question 24.
Name the angle that is vertical to ∠MNR.
Answer:
∠QNP

Explanation:
Vertical angles mean the angles that are opposite to each other. By observing from the given figure the angle ∠QNP is vertical to ∠MNR.

Question 25.
What kind of angles are ∠RNP and ∠PNS?
Answer:
∠RNP and ∠PNS are adjacent angles because they have a common vertex (N) and a common side (\(\overline{N P}\)) and they do not overlap.
Adjacent angles

Question 26.
Find the measure of ∠QNS.
Answer:
m∠QNS + m∠SNP = m∠MNR Vertical ∠s:
m∠QNS + 61° = Substitute:
m∠QNS + 61° – 61° = 138° – 61° Subtract 61° from both sides:
m∠QNS = 77° Simplify:
m∠QNS = 77°

Question 27.
Find the measure of ∠PNR.
Answer:
m∠MNP = 180° Straight ∠
m∠PNR + 138° = 180° Substitute:
m∠PNR + 138° — 138° = 180° — 138° Subtract 138° from both sides:
m∠PNR = 42° Simplify:
m∠PNR = 42°

Use an equation to find the value of each variable.

Question 28.
\(\overleftrightarrow{\mathrm{AB}}\) is a straight line.

Answer:
x°=30°, y°=150°, w°=120°

Explanation:

∠COE + ∠BOE =90°
2x°+x°= 90°
3x°=90
x°=30°
2x°=60°
∠AOC + ∠COE = 180°
w°+2x°=180°
w°+60°=180°
w°=180°-60°
w°=120°
∠AOE + ∠BOE = 180°
y°+x°=180°
y°+30°=180°
y°=180°-30°
y°=150°

Question 29.
\(\overleftrightarrow{\mathrm{AB}}\) and \(\overleftrightarrow{\mathrm{CD}}\) is a straight line.

Answer:
3b° = 90°, b° = 30°, c° = 60°

Explanation:

3b°=90°
b°=90÷3
b°=30°
∠DOB = ∠AOC (vertically opposite angles)
∠AOC = c
∠DOB = c°
∠AOD = 120°
∠DOB + ∠AOD = 180°
c°+120° = 180°
c° = 180°- 120°
c° = 60°

\(\overleftrightarrow{\mathrm{AB}}\) and \(\overleftrightarrow{\mathrm{CD}}\) are straight lines.

Question 30.
The ratio ∠1 : ∠2 = 3 : 1

Answer:
p°= 45°, q°= 135°

Explanation:
Let the given ratio be x
The sum of angles in a traingle is 180°
∠AOD +∠AOC = 180°
The ratio ∠1 : ∠2 = 3x : 1x
3x + x = 180°
4x = 180°
x°= 180÷4
x°= 45°
3x = 135°
∠1 = ∠3 vertically opposite angles
∠2 = ∠4 vertically opposite angles
∠3 = q°= 135°
∠4= p°= 45°

Question 31.

Answer:
p°=50°, q°= 80°, 2p° = 100°

Explanation:

∠AOC = ∠DOB
2p° = p+50
2p°-p° = 50
p°=50°
∠DOB = 100°
∠DOB+∠COB = 180°
P+50 = 50+50 = 100°
100°+q°=180°
q°=180°-100°
q°= 80°

Solve.

Question 32.
The diagram below shows the flag of the Philippines, m∠ADB = 60° and m∠ADC = m∠BDC. Find the measures of ∠ADC and ∠BDC.

Answer:
∠ADB = 60°, ∠BDC = 150°

Explanation:
∠ADB = 60°
∠ADC = ∠BDC
∠ADB + ∠ADC +∠BDC = 360°
60° + ∠ADC + ∠ADC = 360°
60 + 2 ∠ADC = 360°
2 ∠ADC = 360°-60°
2∠ADC = 300°
∠ADC = 300÷2
∠ADC = 150°
∠BDC = 150°

Question 33.
Math Journal
The diagram shows a pattern on a carpet.
a) Are ∠4 and ∠6 vertical angles? Explain why or why not.
Answer:
No.
When two lines cross then vertical angles are opposite to each other.

Explanation:
The angles ∠4 and ∠6 are not vertical angles. Because the vertical angles are opposite to each other but by observing the angles from the given figure the angles given are not opposite to each other.

b) Suppose m∠4 = m∠6. Are ∠4 and ∠5 supplementary angles? Explain your answer.

Answer:
Yes, angles ∠4 and ∠5 are supplementary angles.

Explanation:
Two angles are supplementary when if they add up to 180°. If we add up the given angles ∠4 and ∠5 then the angles add up to 180°

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 6 Lesson 6.1 Complementary, Supplementary, and Adjacent Angles to score better marks in the exam.

Math in Focus Grade 7 Course 2 B Chapter 6 Lesson 6.1 Answer Key Complementary, Supplementary, and Adjacent Angles

Math in Focus Grade 7 Chapter 6 Lesson 6.1 Guided Practice Answer Key

Technology Activity

Materials:

• geometry software

Explore The Relationship Of Complementary Angles Using Geometry Software

Work in pairs.

Step 1.
Construct \(\overline{\mathrm{AB}}\). Then construct a second line segment, \(\overline{\mathrm{BC}}\), that is perpendicular to \(\overline{\mathrm{AB}}\). Finally, construct line segment \(\overline{\mathrm{BD}}\).

Step 2.
Select ∠ABC and find
Step 3.
Select ∠ABD and find its measure. Then select ∠DBC and find its measure.
Step 4.
Use the calculate function of the program to find the sum of the measures of ∠ABD and ∠DBC. What do you notice about the sum of their measures?
Step 5.
Select the point D and drag it so that you change the measures of ∠ABD and ∠DBC. Record your results in a table as shown below.

Step 6.
As the angle measures change, how does the sum of the angle measures change?

Math Journal
Describe what you notice about the sum of the measures of complementary angles.

Solve.

Question 1.
Name three pairs of complementary angles.

Answer:
m∠ABC = 61° We have:
m∠PQR = 29°
m∠ABC + m∠PQR = 61° + 29° = 90° we add the measures of the two angles:
Since the sum of their measures is 90° ∠ABC and ∠PQR are complementary angles
m∠DEF = 38° We have:
m∠MNO = 52°
m∠DEF + m∠MNO = 38° + 52° = 90° we add the measures of the two angles:
Since the sum of their measures is 90°, ∠DEF and ∠MNO are complementary angles
m∠GIH = 21° We have:
m∠JKL = 69°
m∠GIH + m∠JKL = 21° + 69° = 90° We add the measures of the two angles:
Since the sum of their measures is 90°, ∠GIH and ∠JKL are complementary angles
∠ABC and ∠PQR
∠DEF and ∠MNO
∠GIH and ∠JKL
Copy and complete the table.

Question 2.
Angles A and 8 are complementary. Find m∠B for each measure of ∠A.

Answer:
m∠A + m∠B = 90° We are given:

We determine each measure of ∠A:
62° ;17° ;54° ; 75°

Technology Activity

Materials:

• geometry software

Explore The Relationship Of Supplementary Angles Using Geometry Software

Work in pairs.

Step 1.
Construct \(\overline{P R}\). Then construct a second line segment, \(\overline{S Q}\), as shown below.

Step 2.
Select ∠PQR and find its measure.
Step 3.
Select ∠SQP and find its measure. Then select ∠SQR and find its measure.
Step 4.
Use the calculate function of the program to find the sum of the measures of ∠SQP and ∠SQR. What do you notice about the sum of their measures?
Step 5.
Select the point S and drag it so that you change the measures of ∠SQP and ∠SQR. Record your results in a table as shown below.

Step 6.
As the angle measures change, how does the sum of the angle measures change?

MathJournal
Describe what you notice about the sum of the measures of supplementary angles.

Solve.

Question 3.
Tell whether each pair of angles is supplementary.
a) m∠X = 32° and m∠Y = 108°
Answer:
m∠X = 32° a) We are given:
m∠Y = 108°
m∠X + m∠Y = 32° + 108° = 140° Add the measures of the two angles:
As m∠X + m∠Y ≠ 180°. ∠X and ∠Y are not supplementary

b) m∠A = 45° and m∠B = 45°
Answer:
m∠A = 45° b) We are given:
m∠B = 45°
m∠A + m∠B = 45° + 45° = 90° Add the measures of the two angles:
As m∠A + m∠B ≠ 180°, ∠A and ∠B are not supplementary.

c) m∠D = 12° and m∠E = 168°
Answer:
m∠D = 12° c) We are given:
m∠E = 168°
m∠D + m∠E = 12° + 168° = 180° Add the measures of the two angles:
As m∠D + m∠E = 180°, ∠D and ∠E are supplementary.

d) m∠V = 85° and m∠W = 95°
Answer:
m∠V = 85° d) We are given:
m∠W = 95°
m∠V + m∠W = 85° + 95° = 180° Add the measures of the two angles:
As m∠V + m∠W = 180°. ∠V and ∠W are supplementary.

Copy and complete the table.

Question 4.
Angles A and B are supplementary. Find m∠B for each measure of ∠A.

Answer:
m∠A + m∠B = 180° We are given:

We determine each measure of ∠A:
98°; 154°; 44°; 75°

Complete.

Question 5.
In the diagram, m∠ABC = 90°. Find the value of x.

Answer:

We are given
m∠ABD + m∠DBC = 90° Complementary angles:
x° + 23° = 90° Substitute:
x + 23° – 23° = 90° — 23° Subtract 23° from bothsides:
x = 67 Simplify:
x = 67

Given that \(\overleftrightarrow{P Q}\) is a straight line, find the value of y.

Question 6.

Answer:

we are given
m∠PQR + m∠ROQ = 180° Adjacent angles on a straight line:
37° + y° = 180° Substitute:
37° + y° – 37° = 180° – 37° Subtract 37° from both sides:
y = 143 Simplify:
y = 143

Question 7.

Answer:

we are given
m∠POS + m∠SQR + m∠ROQ = 180° Adjacent angles on a straight line:
2y° + 70° + 3y° = 180° substitute
5y° + 70° = 180° Simplify:
5y° + 70° – 70° = 180° — 70° Subtract 70° from both sides:
5g = 110 Simplify:
\(\frac{5 y}{5}\) = \(\frac{110}{5}\) Divide both sides by 5:
y = 22 Simplify:
y = 22

Complete.

Question 8.
In the diagram, m∠PQR = 90° and the ratio x : y = 1: 4. Find the values of x and y.
Method I

Use bar models.

Answer:

m∠PQR = 90°
x : y = 1 : 4
we are given

x° + y° = 90° Method 1; use bar models
Complementary angles:

We use bar models:
5 units → 90 We have:
1 unit → \(\frac{90}{5}\) = 18
x = 18
y = 4 ∙ 18 = 72

Method 2; use a variable to represent the measure of the angle
y = 4 • x = 4x The ratio x : y = 1 : 4 So we have:
x° + y° = 90° Complementary angles
x + 4x = 90 Substitute:
5x = 90 Simplify:
\(\frac{5 x}{5}\) = \(\frac{90}{5}\) Divide both sides by 5:
x = 18 Simplify:
y = 4 • x Substitute:
= 4 • 18
= 72 Simptify:
x = 18; y = 72

Math in Focus Course 2B Practice 6.1 Answer Key

Tell whether each pair of angles is complementary.

Question 1.
m∠A = 25° and m∠B = 65°
Answer:
m∠A = 25° We are given:
m∠B = 65°
m∠A + m∠B = 25° + 65° = 90° We compute the sum:
Because the sum of the measures of the two angles is exactly 90°, the given angles are complementary.
Yes

Question 2.
m∠C = 105° and m∠D = 7°
Answer:
m∠C = 105° We are given:
m∠D = 7°
m∠C + m∠D = 105° + 7° = 112° We compute the sum:
Because the sum of the measures of the two angles is not exactly 90°, the given angles are not complementary.
No

Question 3.
m∠E = 112° and m∠F = 68°
Answer:
m∠E = 112° We are given:
m∠F = 68°
m∠E + m∠F = 112° + 68° = 180° We compute the sum:
Because the sum of the measures of the two angles is not exactly 90° the given angles are not complementary.
No

Question 4.
m∠G = 45° and m∠H = 45°
Answer:
m∠G = 45° We are given:
m∠H = 45°
m∠G + m∠H = 45° + 45° = 90° We compute the sum:
Because the sum of the measures of the two angles is exactly 90°, the given angles are complementary.
Yes

Tell whether each pair of angles is supplementary.

Question 5.
m∠A = 130° and m∠8 = 50°
Answer:
m∠A = 130° We are given:
m∠B = 50°
m∠A + m∠B = 130° + 50° = 180° We compute the sum:
Because the sum of the measures of the two angles is exactly 180°, the given angles are supplementary.
Yes

Question 6.
m∠C = 90° and m∠D = 80°
Answer:
m∠C = 90° We are given:
m∠D = 80°
m∠C + m∠D = 90° + 80° = 170° We compute the sum:
Because the sum of the measures of the two angles is exactly 180°, the given angles are not supplementary.
No

Question 7.
m∠E = 120° and m∠F = 60°
Answer:
m∠E = 120° We are given:
m∠F = 60°
m∠E + m∠F = 120° + 60° = 180° We compute the sum:
Because the sum of the measures of the two angles is exactly 180°, the given angles are supplementary.
yes

Question 8.
m∠G = 60° and m∠H = 30°
Answer:
m∠G = 60° We are given:
m∠H = 30°
m∠G + m∠H = 60° + 30° = 90° We compute the sum:
Because the sum of the measures of the two angles is exactly 180°, the given angles are not supplementary.
yes

Find the measure of the complement of the angle with the given measure.

Question 9.
19°
Answer:
m∠θ = 19° We are given:
90° – m∠θ = 90° – 19 = 71° We determine the measure of the complement of the angle with the given
measure:
71°

Question 10.
64°
Answer:
m∠θ = 64° We are given:
90° – m∠θ = 90° – 64° = 26° We determine the measure of the complement of the angle with the given
measure:
26°

Question 11.
7°
Answer:
m∠θ = 7° We are given:
90° – m∠θ = 90° – 7° = 83° We determine the measure of the complement of the angle with the given
measure:
83°

Question 12.
35°
Answer:
m∠θ = 35° We are given the angle:
90° – m∠θ = 90° – 35° = 55° We determine the measure of the complement of the angle with the given
measure:
55°

Find the measure of the supplement of the angle with the given measure.

Question 13.
78°
Answer:
m∠θ = 78° We are given the angle:
180° – m∠θ = 180° – 78° = 102° We determine the measure of the complement of the angle with the given measure:
102°

Question 14.
4°
Answer:
m∠θ = 4° We are given the angle:
180° – m∠θ = 180° – 78° = 102° We determine the measure of the complement of the angle with the given measure:
176°

Question 15.
153°
Answer:
m∠θ = 153° We are given the angle:
180° – m∠θ = 180° – 153° = 27° We determine the measure of the complement of the angle with the given measure:
27°

Question 16.
101°
Answer:
m∠θ = 101° We are given the angle:
180° – m∠θ = 180° – 101° = 79° We determine the measure of the complement of the angle with the given measure:
79°

∠ABD and ∠DBC are complementary angles. Find the value of x.

Question 17.

Answer:
m∠ABD + m∠DBC = 90° ∠ABD and ∠DBC complementary:
65 + x = 90 Substitute:
65 + x – 65 = 90 – 65 Subtract 65 from both sides:
x = 25 Simplify:
x = 25

Question 18.

Answer:
m∠ABD + m∠DBC = 90° ∠ABD and ∠DBC complementary:
8 + x = 90 Substitute:
8 + x – 8 = 90 – 8 Subtract 8 from both sides:
x = 82 Simplify:
x = 82

∠PQS and ∠SQR are complementary angles. Find the value of m.

Question 19.

Answer:
m∠PQS + m∠SQR = 90° ∠PQS and ∠SQR supplementary:
m + 29 = 180 Substitute:
m + 29 – 29 = 180 – 29 Subtract 29 from both sides:
x = 151 Simplify:
x = 151

Question 20.

Answer:
m∠PQS + m∠SQR = 180° ∠PQS and ∠SQR supplementary:
152 + m = 180 Substitute:
152 + m – 152 = 180 – 152 Subtract 152 from both sides:
m = 28 Simplify:
m = 28

Answer each of the following.

Question 21.
The measure of an angle is 7°. Find the measure of its complement.
Answer:
m∠θ = 7° We are given the angle:
90° – m∠θ = 90° – 7° = 83° We determine the measure of the complement of the angle with the given measure:
83°

Question 22.
The measure of an angle is 84°. Find the measure of its supplement.
Answer:
m∠θ = 84° We are given the angle:
180° – m∠θ = 180° – 84° = 96° We determine the measure of the supplement of the angle with the given measure:
83°

Question 23.
Math Journal
a) Find the measures of the complement and the supplement of each of the following angles, where possible.
m∠W = 2° m∠X = 40° m∠Y = 32° m∠Z = 115°
Answer:
m∠W = 2° a) we are given the angle:
90° – m∠W = 90° – 2° = 88° We determine the complement of ∠W:
180° – m∠W = 180° – 2° = 178° We determine the supplement of ∠W:
m∠X = 40° We are given the angle:
90° — m∠X = 90° – 40° = 50° We determine the complement of ∠X:
180° — m∠X = 180° – 40° = 140° We determine the supplement of ∠X:
m∠Y = 32° We are given the angle:
90° — m∠Y = 90° — 32° = 58° We determine the complement of ∠Y:
180° — m∠Y = 180° — 32° = 148° We determine the supplement of ∠Y:
m∠Z = 115° We are given the angle:
As m∠Z > 90°: ∠Z has no complement
180° — m∠Z = 180 — 115° = 65° We determinethe supplement of ∠Z:

b) Which angle in a) does not have both a complement and a supplement?
Answer:
∠Z does not have both complement and supplement

c) In general, what must be true about the measure of an angle that has both a complement and a supplement?
Answer:
In order that an angle has both complement and supplement, its measure must be greater or equal than 0° and less or equal than 90°.

Question 24.
Math Journal Identify all the angles in each diagram. Tell which angles are adjacent. Explain your reasoning.

The measure of ∠ABC = 90°. Find the value of x.
Answer:
∠GOH We identify all the angles in the first diagram:
∠HOK
∠GOK
∠GOH and ∠HOK The adjacent angles in the diagram is the pair of angles which have a common side and a common vertex and don’t overlap:

∠WOX We identify all the angles in the second diagram:
∠XOY
∠YOZ
∠WOY
∠XOZ
∠WOZ
∠WOX and ∠XOY (common side OX, common vertex O) We identify the adjacent angles in the second diagram:
∠XOY and ∠YOZ (common side OY, common vertex O)
∠WOY and ∠YOZ (common side OY, common vertex O)
∠WOX and ∠XOZ (common side OX, common vertex O)

Question 25.

Answer:
m∠ABC = 90° We are given:
x° + 42° + 30° = 90° we have
x + 72° = 90°
x + 72 – 72 = 90 – 72 Subtract 72 from both sides
x = 18 simplify
x = 18

Question 26.

Answer:
m∠ABC = 90° We are given:
2x° + 22° = 90° we have
2x + 22 – 22 = 90 – 22 Subtract 22 from both sides
2x = 68 simplify
\(\frac{2 x}{2}\) = \(\frac{68}{2}\) Divide by 2:
x = 34 simplify:
x = 34

Question 27.

Answer:
m∠ABC = 90° We are given:
2x° + 45° + 21° = 90° we have
2x° + 66 = 90°
2x + 66 — 66 = 90 — 66 Subtract 66 from both sides:
2x = 24 Simplify:
\(\frac{2 x}{2}\) = \(\frac{24}{2}\) Divide by 2:
x = 12 Simplify:
x = 12

Question 28.

Answer:
m∠ABC = 90° We are given:
18° + 3x° + 21° = 90° we have
39° + 3x° = 90°
39 + 3x — 39 = 90 — 39 Subtract 39 from both sides:
3x = 51 Simplify:
\(\frac{3 x}{3}\) = \(\frac{51}{3}\) Divide by 3:
x = 17 Simplify:
x = 17

\(\overleftrightarrow{P R}\) is a straight line. Find the value of m.

Question 29.

Answer:
m∠PQR = 90° Because \(\overline{P R}\) is a straight line, we have
m∠PQT + m∠TQS + m∠SQR = m∠PQR we have
49° + m° + 57° = 180° substitute
106° + m° = 180°
106 + m – 106 = 180 – 106 subtract 106 from both sides
m = 74

Question 30.

Answer:
m∠PQR = 180° Because \(\overline{P R}\) is a straight line, we have
m∠PQT + m∠TQS + m∠SQR = m∠PQR we have
20° + m° + 87° = 180° substitute
150° + m° = 180°
150 + m – 150 = 180 – 150 subtract 150 from both sides
m = 30 Simplify:
m = 30

In the diagram, the ratio a: b = 2: 3. Find the values of a and b.

Question 31.

Answer:
a : b = 2 : 3 we are given
\(\frac{a}{b}\) = \(\frac{2}{3}\) we rewrite the ratio
3a = 2b cross-multiply
\(\frac{3 a}{3}\) = \(\frac{2 b}{3}\) Divide both sides by 3
a = \(\frac{2 b}{3}\)
m∠RQS + m∠SQP = 90° ∠RQS and ∠SQP are complementary
b + a = 90
b + \(\frac{2 b}{3}\) = 90 substitute
\(\frac{3 b+2 b}{3}\) = 90 Determine b
\(\frac{5 b}{3}\) = 90
5b = 3 ∙ 90
5b = 270
\(\frac{5 b}{5}\) = \(\frac{270}{5}\)
b = 54
a = \(\frac{2 \cdot 54}{3}\) = 36 Determine a
a = 36
b = 54

Question 32.
\(\overleftrightarrow{P R}\) is a straight line.

Answer:
a : b = 2 : 3 we are given
\(\frac{a}{b}\) = \(\frac{2}{3}\) we rewrite the ratio
3a = 2b cross-multiply
\(\frac{3 a}{3}\) = \(\frac{2 b}{3}\) Divide bothsides by 3
a = \(\frac{2 b}{3}\)
m∠RQS + m∠SQP = 180° ∠RQS and ∠SQP are supplementary
b + a = 180 substitute
b + \(\frac{2 b}{3}\) = 180
\(\frac{3 b+2 b}{3}\) = 180
\(\frac{5 b}{3}\) = 180
5b = 3 ∙ 180
5b = 540
\(\frac{5 b}{5}\) = \(\frac{540}{5}\)
b = 108
a = \(\frac{2 \cdot 108}{3}\) = 72
a = 72
b = 108

Solve.

Question 33.
The diagram shows the pattern on a stained glass window. \(\overleftrightarrow{A C}\) is a straight line. ∠EBD and ∠DBA are complementary angles and m∠DBA = 30°. Find the measures of ∠EBD and ∠CBD.

Answer:

we are given
m∠EBD + m∠DBA = 90° ∠EBD and ∠DBA complementary:

m∠EBD + 30° = 90° Substitute:
m∠EBD + 30° — 30° = 90° – 30° Subtract 30° from both sides:
m∠EBD = 60° Simplify:
m∠CBD + m∠DBA = 180° \(\overline{A C}\) straight line:
m∠CBD + 30° = 180° Substitute
m∠CBD + 30° – 30° = 180° – 30° Subtract 30° from both sides
m∠CBD = 150° Simplify
m∠EBD = 60°
m∠CBD = 150°

Question 34.
The diagram shows a kite. The two diagonals \(\overline{M P}\) and \(\overline{Q T}\) are perpendicular to each other. Identify all pairs of complementary angles and all pairs of supplementary angles that are not pairs of right angles.

Answer:
\(\overline{M P}\) ⊥ \(\overline{Q T}\) We are given:
∠MNR and ∠RNQ We identify the pairs of complementary angles:
∠QNS and ∠SNP
∠NMQ and ∠MQN
∠NQP and ∠QPN
∠TMN and ∠MTN
∠NTP and ∠NPT
∠MNR and ∠RNQ We identify the pairs of supplementary angLes that are not pairs of right angles:
∠MNS and ∠SNP
Complementary angles: ∠MNR and ∠RNQ
∠QNS and ∠SNP
∠NMQ and ∠MQN
∠NQP and ∠QPN
∠TMN and ∠MTN
∠NTP and ∠NPT
Supplementary angles: ∠MNR and ∠RNP
∠MNS and ∠SNP

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 6 Angle Properties and Straight Lines to score better marks in the exam.

Math in Focus Grade 7 Course 2 B Chapter 6 Answer Key Angle Properties and Straight Lines

Math in Focus Grade 7 Chapter 6 Quick Check Answer Key

Tell whether each angle is an acute, right, obtuse, or straight angle.

Question 1.

Answer:
Right angle triangle.

Explanation:
A right-angled triangle is a triangle with one of the angles as 90 degrees.

Question 2.

Answer:
Acute angle triangle.

Explanation:
An acute-angled triangle is a type of triangle in which all the three internal angles of the triangle measures less than 90°.

Question 3.

Answer:
90° < 154° < 180° We have
The given angle is obtuse because Its measure is greater than 90°, but Less than 180°.
obtuse

Question 4.

Answer:
straight angle.

Explanation:
The 180-degree angle is known as a straight angle. The sides of the angle are opposite to each other and they make a straight angle.

Question 5.
m∠w = 86°
Answer:
Acute angle

Explanation:

Question 6.
m∠y = 90°
Answer:
Right angle triangle.

Explanation:

Identify each pair of parallel line segments.

Question 7.

Answer:
RS∥UT

Explanation:
The lines will not meet each other at any point in the given figure. Hence parallel line will never intersect.

Question 8.

Answer:
WX∥ZY

Explanation:
The lines that do not intersect or meet each other at any point in a plane. Parallel lines will never intersect.

Identify each pair of perpendicular line segments.

Question 9.
ABCD is a rectangle.

Answer:
There are four right angles, and 2 pairs of perpendicular lines.

Explanation:
A rectangle has lines that are perpendicular to two other lines and it also has four right angles.

Question 10.

Answer:
The given figure is a right-angle triangle and has two perpendicular lines.

Explanation:
A triangle has three sides and three angles. Only one type of triangle is a right-angle triangle that has two perpendicular line segments.

Question 11.

Answer:
The given figure has two perpendicular line segments.

Explanation:
Perpendicular lines are lines, segments that intersect to form right angles.

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Chapter 5 Review Test to score better marks in the exam.

Math in Focus Grade 7 Course 2 A Chapter 5 Review Test Answer Key

Concepts and Skills

Tell whether each table, graph, or equation represents a direct proportion, an inverse proportion, or neither.

Question 1.

Answer:

Direct Proportion :
For each pair of values x and y →
\(\frac{y}{x}\) = \(\frac{4.5}{3}\) = 1.5
\(\frac{y}{x}\) = \(\frac{7.5}{5}\) = 1.5
\(\frac{y}{x}\) = \(\frac{10.5}{7}\) = 1.5
\(\frac{y}{x}\) is a constant so x and y is direct proportional

Inverse Proportion :
For each pair of values x and y →
xy = 3 ∙ 4.5 = 13.5
xy = 5 . 7.5 = 37.5
xy = 7 ∙ 10.5 = 73.5
xy is not a constant so y is not inversely proportional to x

NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten a. xy = k or y = \(\frac{k}{x}\)
Direct proportion

Question 2.

Answer:

Direct Proportion :
For each pair of valties x and y →
\(\frac{y}{x}\) = \(\frac{50}{2}\) = 25
\(\frac{y}{x}\) = \(\frac{25}{4}\) = 6.25
\(\frac{y}{x}\) = \(\frac{12.5}{8}\) = 1.56
\(\frac{y}{x}\) is not a constant so x and y does not represent direct proportion

Inverse Proportion :
For each pair of values x and y →
xy = 2 ∙ 50 = 100
xy = 4 ∙ 25 = 100
xy = 8 ∙ 12.5 = 100
The product of x and y is a constant so y is inversely proportional to x

NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Inverse Proportion

Question 3.

Answer:

Direct Proportion :
For each pair of values x and y →
\(\frac{y}{x}\) = \(\frac{12}{6}\) = 2
\(\frac{y}{x}\) = \(\frac{9}{8}\) = 1.125
\(\frac{y}{x}\) = \(\frac{3.5}{2.4}\) = 0.145
\(\frac{y}{x}\) is not a constant so x and y is not direct proportion.

Inverse Proportion :
For each pair of values x and y →
xy = 6 ∙ 12 = 72
xy = 8 ∙ 9 = 72
xy = 24 ∙ 3.5 = 84
The product of z and y is not a constant so y is not inversely proportional to z

NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Neither Direct Proportion nor Inverse Proportion

Question 4.

Answer:

Direct Proportion :
For each pair of values x and y →
\(\frac{y}{x}\) = \(\frac{5}{2.5}\) = 2
\(\frac{y}{x}\) = \(\frac{10}{5}\) = 2
\(\frac{y}{x}\) = \(\frac{15}{7.5}\) = 2
\(\frac{y}{x}\) is a constant so x and y is direct proportional

Inverse Proportion :
For each pair of values x and y →
xy = 2.5 ∙ 5 = 12.5
xy = 5 ∙ 10 = 50
xy = 7.5 ∙ 15 = 112.5
The product of x and y is not a constant so x is not inversely proportional to x

NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Direct Proportion

Question 5.

Answer:
Direct Proportion :
The given graph is a straight line that does not lie along
the x — axis or y — axis but does not pass through the origin.
So, the given graph does not represents a direct proportion.

Inverse Proportion :
$Use\graph\: $
x ∙ y = 3 ∙ 1 = 2
x ∙ y = 2 ∙ 2 = 4
x ∙ y = 1 ∙ 3 = 3
The product of x and y is not a constant so x and y does not represent a inverse proportion.
Neither direct proportion nor inverse proportion

Question 6.

Answer:
Direct Proportion :
The given graph is a straight line that does not lie along the x — axis or y — axis and it pass through the origin.
So. the given graph represents a direct proportion.

Inverse Proportion :
$Use\graph\: $
x ∙ y = 1 ∙ 1 = 1
x ∙ y = 2 ∙ 2 = 4
x ∙ y = 3 ∙ 3 = 9
The product of x and y is not a constant so x and y does not ‘represent a inverse proportion.
Direct Proportion

Question 7.

Answer:
Direct Proportion :
The given graph is not a straight line and it lie along the x — axis or y — axis and does not pass through the origin.
So. the given graph does not ‘represents a direct proportion.

Inverse Proportion:
$Use\ graph\: $
x ∙ y = 4 ∙ 1 = 4
x ∙ y = 2 ∙ 2 = 4
x ∙ y = 1 ∙ 4 = 4
The product of x and y is a constant so x and y represents a inverse proportion.
Inverse Proportion

Question 8.

Answer:
Direct Proportion :
The given graph is not a straight line and it lie along the x — axis but it pass through the origin.
So, the given graph does not represents a direct proportion.

Inverse Proportion :
$Use\graph\: $
x ∙ y = 1 ∙ 2 = 2
x ∙ y = 2 ∙ 4 = 8
x ∙ y = 3 ∙ 2 = 6
The product of x and y is not a constant so x and y does not represent a inverse proportion.
Neither direct proportion nor inverse proportion

Question 9.
y = \(\frac{1}{2}\)x + 5
Answer:
y = \(\frac{1}{2} x\) + 5
Direct Proportion:
y = \(\frac{1}{2} x\) + 5
Because the original equation y = y = \(\frac{1}{2} x\) + 5 cannot be rewritten as an equivalent
equation in the form y = kx, it does not represent a direct proportion.

Inverse Proportion :
y = \(\frac{1}{2} x\) + 5

Because the original equation y = \(\frac{1}{2} x\) + 5 cannot be rewritten as an equivalent
equation in the form xy = k, it does not represent an inverse proportion.

NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten xy = k or y = \(\frac{k}{x}\)
Neither Direct Proportion nor Inverse Proportion

Question 10.
\(\frac{y}{4}\) = 7x
Answer:
\(\frac{y}{4}\) = 7x
4 ∙ \(\frac{y}{4}\) = 4 ∙ 7x
y = 28x
Because the original equation \(\frac{y}{4}\) = x can be rewritten as an equivalent equation in the form y = kx, it represent a direct proportion.

Inverse Proportion :
\(\frac{y}{4}\) = 7x
4 ∙ \(\frac{y}{4}\) = 4 ∙ 7x
y = 28x
Because the original equation \(\frac{y}{4}\) = x cannot be re’wrítten as an equivalent
equation in the form xy = k, it does not represent an inverse proportion.

NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k. and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k. and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Direct Proportion

Question 11.
-3 + x = y
Answer:
-3 + x = y
Direct Proportion :
-3 + x = y
-3 + x – x = y – x Subtract x from both sides
y – x = -3
Because the original equation -3 + x = y cannot be rewritten as an equivalent equation in the form y = kx, it does not represent a direct proportion.
Inverse Proportion :
-3 + x = y
-3 + x — x = y — x Subtract x from both sides
y – x = -3
Because the original equation — 3 + x = y cannot be rewritten as an equivalent equation in the form xy = k, it does not represent an inverse proportion.

NOTE :
Direct Proportion : y is directly proportional to z then they have a constant
of proportionality k, and it crin be rewritten as y = kz or \(\frac{y}{x}\) = k
Inverse Proportion : z and y are in inverse proportion thìen their product is a constant of proportionality k, and it can be rewritten as zy = k or y = \(\frac{k}{x}\)
Neither Direct Proportion nor inverse Proportion

Question 12.
\(\frac{y}{2}\) = \(\frac{3}{x}\)
Answer:
\(\frac{y}{2}\) = \(\frac{3}{x}\)
Direct Proportion :
\(\frac{y}{2}\) = \(\frac{3}{x}\)
x ∙ y = 3 ∙ 2 Cross Multiplication
xy = 6
Because the original equation \(\frac{y}{2}\) = \(\frac{3}{x}\) cannot be rewritten as an equivalent equation in the form y = kx, it does not represent a direct proportion.

Inverse Proportion :
\(\frac{y}{2}\) = \(\frac{3}{x}\)
x ∙ y = 3 ∙ 2 Cross Multiplication
xy = 6
Because the original equation \(\frac{y}{2}\) = \(\frac{3}{x}\) can be rewritten as an equivalent equation in the form xy = k, it does represent an inverse proportion.

NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it crin be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant
of proportionality k. and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Inverse proportion

In each table, y is directly proportional to x. Find the constant of proportionality. Then copy and complete the table.

Question 13.

Answer:

y is directly proportional to z :
\(\frac{y}{x}\) = \(\frac{16}{4}\)
\(\frac{y}{x}\) = 4 Simplify
x ∙ \(\frac{y}{x}\) = 4 ∙ x Multiply both sides by x
y = 4x
Find missing value in the table.
When y = 25 find x.
y = 4x
25 = 4x Evaluate y = 25
\(\frac{25}{4}\) = \(\frac{4x}{4}\) Divide both sides by 4
x = 6.25 Simplify
When x = 2 find y,
y = 4x
y = 4 ∙ 2 Evaluate x = 2
y = 8 Simplify

The missing number are 8 and 6.25

Question 14.

Answer:

y is directly proportional to x :
\(\frac{y}{x}\) = \(\frac{2.5}{5}\)
\(\frac{y}{x}\) = \(\frac{1}{2}\) Simplify
x ∙ \(\frac{y}{x}\) = \(\frac{1}{2}\) ∙ x Multiply both sides by x
y = \(\frac{1}{2}\)x

Find missing value in the table.
When y = 3 find x,
y = \(\frac{1}{2}\)x
3 = \(\frac{1}{2}\)x Evaluate y = 3
2 ∙ 3 = 2 ∙ \(\frac{1}{2}\)x Multiply both sides by 2
x = 6 Simplify
When x = 3 find y,
y = \(\frac{1}{2}\)x
y = \(\frac{1}{2}\) ∙ 3 Evaluate x = 3
y = 1.5 simplify

The missing number are y = 1.5 and x = 6

In each table, y is inversely proportional to x. Find the constant of proportionality. Then copy and complete the table.

Question 15.

Answer:

y is inversely proportional to x :
xy = 2 ∙ 30
xy = 60 Simplify
Find missing value in the table.
When x = 4 find y.
xy = 60
4 ∙ y = 60 Evaluate x = 4
\(\frac{4 y}{4}\) = \(\frac{60}{4}\) Divide both sides by 4
y = 15 Simplify
When y = 10 find x.
x ∙ 10 = 60 Evaluate y = 10
\(\frac{10 x}{10}\) = \(\frac{60}{10}\) Divide both sides by 10
x = 6 Simplify

The missing number are y = 15 and x = 6

Question 16.

Answer:

y is inversely proportional to x :
xy = 5 ∙ 1.6
xy = 8 Simplify
Find missing value in the table.
When x = 2.5 find y.
xy = 8
2.5 ∙ y = 8 Evaluate x = 2.5
\(\frac{2.5 y}{2.5}\) = \(\frac{8}{2.5}\) Divide both sides by 2.5
y = 3.2 simplify
when y = 2 find x,
x ∙ 2 = 8 Evaluate y = 2
\(\frac{2 x}{2}\) = \(\frac{8}{2}\) Divide both sides by 2.
x = 4 simplify

The missing number are y = 3.2 and x = 4

Solve using proportionality reasoning.

Question 17.
y is directly proportional to x, and y = 56 when x = 7. Find the value of y when x = 4.
Answer:
x = 7 and y = 56
y is directly proportional to x:
\(\frac{y}{x}\) = \(\frac{56}{7}\)
\(\frac{y}{x}\) = 8
x ∙ \(\frac{y}{x}\) = 8 ∙ x Multiply both sides by x
y = 8x
Find the value of y when x = 4
We know y = 8x,
y = 8 ∙ 4 Evaluate y = 8x when x = 4
y = 32 Simplify
y = 32

Question 18.
y is inversely proportional to x, and y = 12 when x = 4. Find the value of x when y = 8.
Answer:
x = 4 and y = 12
y is inversely proportional to x :
xy = 4 ∙ 12
xy = 48
\(\frac{x y}{y}\) = \(\frac{48}{y}\) Divide both sides by y
x = \(\frac{48}{y}\)
Find the value of x when y = 8
We know x = \(\frac{48}{y}\),
x = \(\frac{48}{8}\) Evaluate x = \(\frac{48}{y}\) when y = 8
x = 6 simplify
x = 6

Problem Solving

Use a proportion to solve each question. Show your work.

Question 19.
The graph shows that the cost of gasoline, y dollars, is directly proportional to x gallons of gasoline.

a) Find the constant of proportionality. What does this value represent in the context of the problem?
Answer:
y is directly proportional to x :
\(\frac{y}{x}\) = \(\frac{4}{1}\)
\(\frac{y}{x}\) = 4 simplify
Constant of Proportionality = 4
It represents the unit cost per gallons of gasoline.

b) Write a direct proportion equation.
Answer:
y is directly proportional to x :
\(\frac{y}{x}\) = \(\frac{4}{1}\) = 4 Simplify
\(\frac{y}{x}\) = \(\frac{8}{2}\) = 4 Simplify
\(\frac{y}{x}\) = \(\frac{12}{3}\) = 4 Simplify
x ∙ \(\frac{y}{x}\) = 4 ∙ x Multiply both sides by x
y = 4x

c) If Umberto spent $24 for gasoline, how many gallons of gasoline did he buy?
Answer:
y = 4x
24 = 4x Evaluate y = 24
\(\frac{24}{4}\) = \(\frac{4 x}{4}\) Divide both sides by 4
x = 6
Umberto will get 6 gallons of gasoline if he spent $24.

Question 20.
Out of every $100 that Judy earns at her part-time job, she saves $25 for college. The amount she saves is directly proportional to the amount she earns. If she earns $3,880 in one year, how much will she save for college?
Answer:
Amount of money she saves = y
Amount of money she earns = x
Find Direct Proportion Equation :
Amount of money she saves is directly proportional to Amount of money she earns :
\(\frac{y}{x}\) = \(\frac{25}{100}\)
\(\frac{y}{x}\) = \(\frac{1}{4}\) simplify
x ∙ \(\frac{y}{x}\) = x ∙ \(\frac{1}{4}\) Multiply both sides x
y = \(\frac{1}{4}\)x

If she earns $3880 in one year, how much she will save :
y = \(\frac{1}{4}\)x
y = \(\frac{1}{4}\) ∙ 3880 Evaluate x = 3880
y = 970
She will save $970 in one year if she earns $3880.

Question 21.
Harry made fruit punch using 2 parts orange juice to 3 parts soda water. The amount of soda water that Harry used is directly proportional to the amount of orange juice he used. How many cups of orange juice should Harry use with 18 cups of soda water?
Answer:
Amount of soda water = y
Amount of orange juice = x
Find Direct Proportion Equation :
Amount of soda water is directly proportional to Amount of orange juice :
\(\frac{y}{x}\) = \(\frac{3}{2}\)
\(\frac{y}{x}\) = 1.5 simplify
x ∙ \(\frac{y}{x}\) = x ∙ 1.5 Multiply both sides by x
y = 1.5x
How many cups of orange juice should Harry use with 18 cups of soda water :
y = 1.5z
18 = 1.5x Evaluate y = 18
\(\frac{18}{1.5}\) = \(\frac{1.5 x}{1.5}\) Divide both sides by 1.5
x = 12
Harry should ‘use 12 cups of orange juice with 18 cups of soda water.
12 cups

Use a graph paper. Solve.

Question 22.
An initial amount of money deposited in a bank account that earns interest is called the principal. In the table below, P stands for the principal, and l stands for the interest earned by that principal for a period of one year at a particular bank. P is directly proportional to l. Graph the direct proportion relationship between P and l. Use 1 unit on the horizontal axis to represent 1 dollar and 1 unit on the vertical axis to represent $50.

Answer:

a) Using the graph, find the interest earned when the principal is $350.
Answer:
$From\ the\ graph,\ for\ $350\ Principal,\ Interest\ earned\ is\ $7 $

b) Write an equation relating P and I. Then find the principal when the interest earned is $15.
Answer:
P is directly proportional to I :
\(\frac{P}{I}\) = \(\frac{100}{2}\)
\(\frac{P}{I}\) = 50 Simplifying
I ∙ \(\frac{P}{I}\) = I ∙ 50 Multiplying both sides by I
P = 50I
Find the principal when the Interest earned is $15 :
P = 50I
P = 50 ∙ 15 Substituting I = 15
P = 750

Use a proportion to solve each question. Show your work.

Question 23.
The time taken by some students to deliver 500 flyers, t hours, is inversely proportional to the number of students, n. The graph shows the relationship between n and t.

a) Find the constant of proportionality graphically.
Answer:
$Since,\ the\ line\ is\ passing\ through\ the\ point\ (6,\ 2) $
So, the constant of proportionality is 6 × 2 = 12
Constant of Proportionality = 12

b) Write an equation relating n and t.
Answer:
Number of hours (t) to delivers the flyers is inversely proportional to the ‘number of students
n ∙ t = 6 ∙ 2
nt = 12

c) Describe the relationship between the number of students and the time needed to deliver the flyers.
Answer:
Since t is inversely proportional to n
The number of students increases as the amount of time to deliver the flyers decreases.

d) Explain what the point (6, 2) represents in this situation.
Answer:
6 students take 2 hours to deliver 500 flyers.

Question 24.
Jerry has set aside a certain amount of money to download applications for his new smart phone. The number of applications he can afford to download is inversely proportional to the cost of each download. With his money, he can afford to download 12 applications that cost $2 each. How many applications can he afford to download if he finds less expensive applications that cost only $1.50 each?
Answer:
Number of application he can afford to download = x
Cost of each download = y
Find Inverse Proportion equation :
$He\ has\ the\ amount\ of\ money\ to\ download\ 12\ application\ which\ cost\ $2\ each\
Number of applications he can afford to download is inversely proportional to Cost of each download \ :
xy=12\cdot2
xy = 24 $
How many applications he can afford to download if cost of each application is $1.50 :
xy = 24
1.50 = 24 Substitute y = 1.50
\(\frac{1.50 x}{1.50}\) = \(\frac{24}{1.50}\) Divide both sides by 1.50
x = 16
$He\ can\ afford\ to\ download\ 16\ applications\ if\ each\ applications\ cost\ $1.50 $
16 application