Hillary

This handy Math in Focus Grade 1 Workbook Answer Key Chapter 3 Practice 2 Ways to Add detailed solutions for the textbook questions.

Math in Focus Grade 1 Chapter 3 Practice 2 Answer Key Ways to Add

Complete the number bonds. Then fill in the blanks.

Example

Question 1.

Answer:

Explanation:
8 + 2 = 10
2 + 8 = 10
The combination of numbers gives the same sum
to make a number bond of 10
used 8 and 2 numbers and made different combinations.

Question 2.

Answer:

Explanation:

Question 3.

Answer:

Explanation:

Complete the number bonds. Then fill in the blanks.

Question 4.

Answer:

Explanation:

Question 5.

Answer:

Explanation:

Question 6.

Answer:

Explanation:

Question 7.

Answer:

Explanation:

Question 8.

Answer:

Explanation:

Question 9.

Answer:

Explanation:

Help each Momma Butterfly find her babies! Color the small butterflies that match her number.

Question 10.

Answer:

Explanation:

Question 11.

Answer:

Explanation:

Question 12.

Answer:

Explanation:

Question 13.

Answer:

Explanation:

Question 14.

Answer:

Explanation:

Add.
You can draw number bonds to help you.

Question 15.

Answer:

Explanation:

Now color the train cars above. Then fill in the table with your answers.

Question 16.

Answer:


Explanation:

Solve.

Question 17.
A ball falls into the number machine. Which ball is it? Write the correct number on the ball below.

Answer:
Explanation:

Go through the Math in Focus Grade 2 Workbook Answer Key Chapter 2 Practice 1 Addition Without Regrouping to finish your assignments.

Math in Focus Grade 2 Chapter 2 Practice 1 Answer Key Addition Without Regrouping

Add.

Question 1.
232 + 645 = ?
Add the ones.
2 ones + 5 ones = 7 ones
Add the tens.
3 tens + 4 tens = _________ tens
Add the hundreds.
2 hundreds + 6 hundreds = _______ hundreds
232 ÷ 645 = _______

Answer:

Add the ones.
2 ones + 5 ones = 7 ones
Add the tens.
3 tens + 4 tens = 7 tens
Add the hundreds.
2 hundreds + 6 hundreds = 8 hundreds

Question 2.

Answer:

Explanation:
Add the ones.
8 ones + 1 ones = 9 ones
Add the tens.
0 tens + 7 tens = 7 tens
Add the hundreds.
1 hundreds + 8 hundreds = 9 hundreds

Question 3.

Answer:

Explanation:
Add the ones.
9 ones + 0 ones = 9 ones
Add the tens.
7 tens + 2 tens = 9 tens
Add the hundreds.
8 hundreds = 8 hundreds

Question 4.
122 + 473 = ___

Answer:

Explanation:
The sum of 122 + 473 = 595

Question 5.
217 + 771 = ___

Answer:

Explanation:
The sum of 217 + 771 = 988

Add.

Question 6.
Three friends have some addition cards. Some answers will win prizes. Help them add to find their prizes.

Answer:

Explanation:
First friend has bear
second friend has book
third friend has hat

Go through the Math in Focus Grade 2 Workbook Answer Key Chapter 2 Addition up to 1,000 to finish your assignments.

Math in Focus Grade 2 Chapter 2 Answer Key Addition up to 1,000

Put on Your Thinking cap!

challenging practice

Write the missing numbers.

Question 1.

Answer:

Explanation:
In ones place 3 and 1 makes 4
so, missing number is 3

Question 2.

Answer:

Explanation:
In hundreds place 6 hundreds and 2 hundreds make 8 hundreds

Question 3.

Answer:

Explanation:
In tens place 0 tens  + 9 tens  is 9 tens

Question 4.

Answer:

Explanation:
In tens place 2 tens and 4 tens make 6 tens

Question 5.

Answer:

Explanation:
7 ones + 5 ones = 12
1 tens and 2 ones
In tens place 3 tens 9 tens and 1 ten = 13 tens

Question 6.

Answer:

Explanation:
In ones place 3 ones and 9 ones make 12 ones
That is 1 tens and 2 ones
1 ten will be carry
So, 8 ten +5 ten + 1 ten ten = 8 + 6 = 14 tens

Do these.

Question 7.

Answer:

Explanation:
The numbers are written in least to greatest

a. Order the numbers from greatest to least.
Answer:

Explanation:
The number are written in Decending order

b. Add 100 to the least number. Show your work.
Answer: 554
Explanation:
The least number in the given numbers is 454 + 100 = 554

Put On Your Thinking Cap!

problem Solving

Make two 3-digit numbers from the numbers below. Use each number only once. What are the two 3-digit numbers that give the greatest answer when you add them?

____ ____ _____
Answer:

Explanation:
5, 1, 2 = 5 + 1 + 2 = 8
and 4, 3, 0 = 4 + 3 + 0 = 7
are the two 3-digit numbers that give the greatest answer when you add them

Chapter Review/Test

Vocabulary

Fill in the blanks with words from the box.
The words may be used more than once.

Question 1.


Step 1
Add the _____
2 ones + 8 ones = 10 ones
__________ the ones.
10 ones = 1 ten 0 ones

Explanation:
Add the ones
2 ones + 8 ones = 10 ones
Regroup the ones.
10 ones = 1 ten 0 ones
Step 2

Add the ________
1 ten + 6 tens + 6 tens = 13 tens
___________ the tens.
13 tens = 1 _________ 3 ____

Explanation:
Add the tens
1 ten + 6 tens + 6 tens = 13 tens
Regroup the tens.
13 tens = 1tens 3 ones
Step 3

Add the ____
1 hundred + 4 hundreds + 2 hundreds
= 7 hundreds
462 + 268 = 730

Explanation:
Add the hundreds
1 hundred + 4 hundreds + 2 hundreds
= 7 hundreds
462 + 268 = 730

Concepts and Skills

Add.
Then match the problems with the same answer.

Question 2.

Answer:

Explanation:
The addition of three digits number is found on both sides
And matched the sum of numbers

Problem Solving

Solve.

Question 3.
Mr. Thomas drives 173 miles on Monday. On Tuesday, he drives 216 miles. How many miles does he drive in all?
He drives ___ miles in all.
Answer:
He drives ___ miles in all.
Explanation:
Mr. Thomas drives 173 miles on Monday.
On Tuesday, he drives 216 miles.
173 + 216 = 389 miles does he drive in all

Question 4.
A carpenter has 362 pieces of lumber. He needs another 228 pieces of lumber to build a bridge. How many pieces of lumber does he need to build the bridge?
He needs ___ pieces of lumber to build the bridge.
Answer:
He needs ___ pieces of lumber to build the bridge
Explanation:
A carpenter has 362 pieces of lumber.
He needs another 228 pieces of lumber to build a bridge.
362 + 228 = 590 pieces of lumber does he need to build the bridge

Solve.

Question 5.
A movie theater sells 294- tickets to the first show. It sells 457 tickets to the second show. How many tickets does it sell in all?
It sells ___ tickets in all.
Answer:
It sells ___ tickets in all
Explanation:
A movie theater sells 294- tickets to the first show.
It sells 457 tickets to the second show.
294 + 457 = 751 tickets does it sell in all

Question 6.
Shantel has 546 stickers in her collection. She has 278 fewer stickers than Sherice. How many stickers does Sherice have in her collection?
Shantel has ___ stickers in her collection.
Answer:
Shantel has ___ stickers in her collection
Explanation:
Shantel has 546 stickers in her collection.
She has 278 fewer stickers than Sherice.
546 + 278 = 824 stickers does Sherice have in her collection

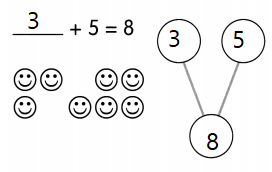
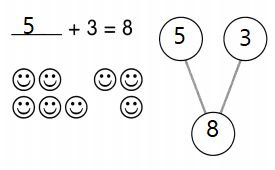
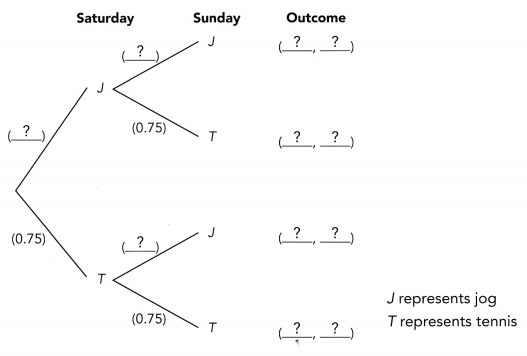
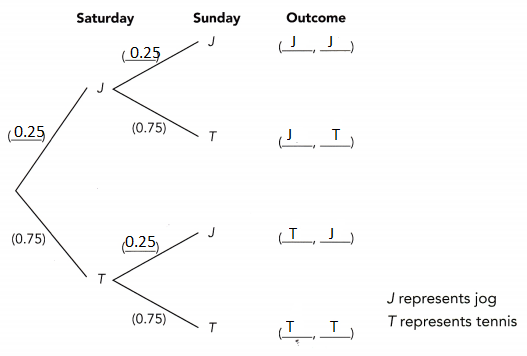
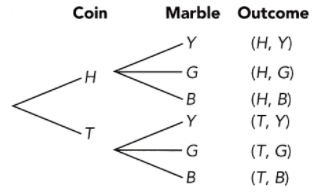
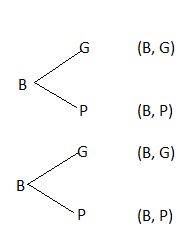
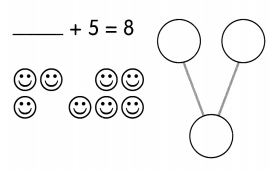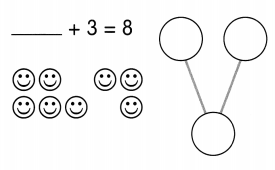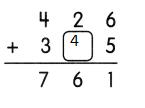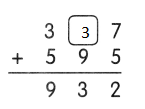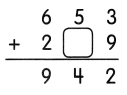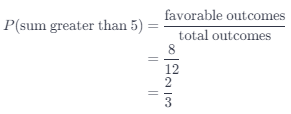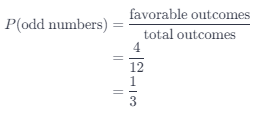This handy Math in Focus Grade 8 Workbook Answer Key Cumulative Review Chapters 10-11 detailed solutions for the textbook questions.

Math in Focus Grade 8 Course 3 B Cumulative Review Chapters 10-11 Answer Key

Construct a scatter plot for each table of bivariate data. Identify any outliers. (Lesson 10.1)

Question 1.
Use 1 centimeter on the horizontal axis to represent 1 unit and 1 centimeter on the vertical axis to represent 100 units.

Answer:

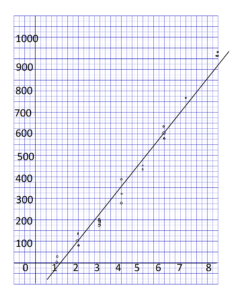
Question 2.
Use 1 centimeter on the horizontal axis to represent 0.2 units for x interval from 36.0 to 38.0 and 1 centimeter on the vertical axis to represent 2 units for y interval from 230 to 252.

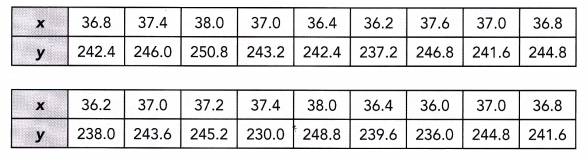
Answer:

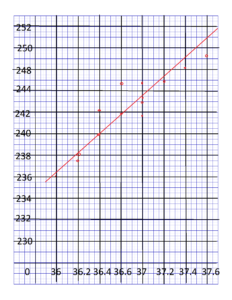
Describe any association between the bivariate data in each scatter plot. (Lesson 10.1)

Question 3.

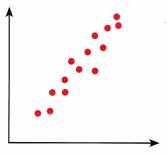
Answer:
One variable increasing with another has a positive association, otherwise, it is negative. If the scatter plot follows a straight line then it is the linear association, otherwise, it is nonlinear association. If it is hard to find the arrangement of the variables then it has a weak association, otherwise, it has a strong association. In this case, the graph has positive, strong and linear associations.

Question 4.

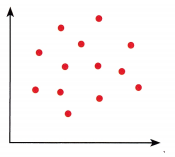
Answer:
If it is hard to identify the arrangement of the variables then it has a weak association and when it seems it has no pattern at all then it has no association. For this case, the graph has no association at all.

State the line that represents a line of best fit for each scatter plot. (Lesson 10.2)

Question 5.

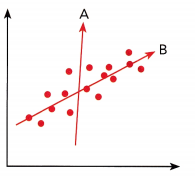
Answer:
Line B fits the scatter plot, as it is the straight line that shows the data on scatter plot when compared with the Line A.

Question 6.

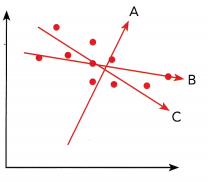
Answer:
Line C fits the scatter plot, It is the most possible straight line that shows the data on a scatter plot in comparison with Line A and Line B.

Construct each scatter plot and draw a line of best fit for the given table of bivariate data. (Lesson 10.2)

Question 7.
Use 1 centimeter on the horizontal axis to represent 1 unit and 1 centimeter on the vertical axis to represent 2 units.

Answer:

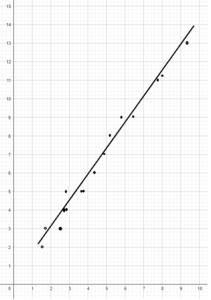
Question 8.
Use 1 centimeter to represent 1 unit on both axes.

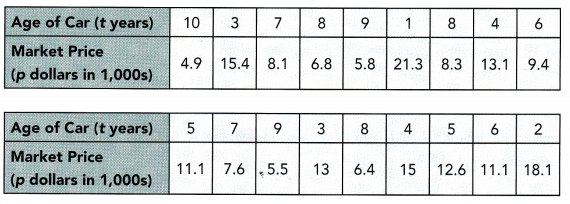
Answer:

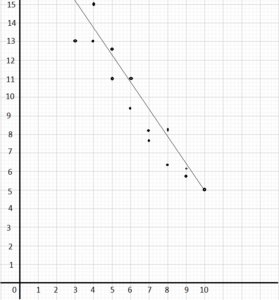
Identify whether the given data is qualitative or quantitative. (Lesson 10.3)

Question 9.
Number of eggs hatched
Answer: Quantitative

Question 10.
Ice cream flavors
Answer: Qualitative

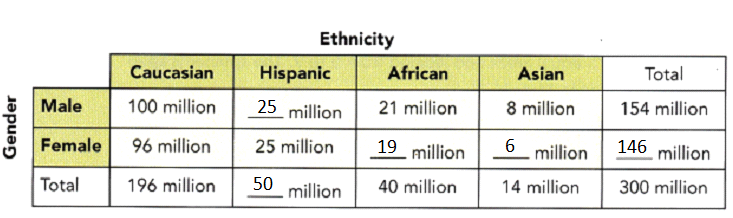
Copy and fill in the missing information in the two-way table. (Lesson 10.3)

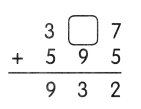
Question 11.

Answer:

Construct a two-way table using the given data. (Lesson 10.3)

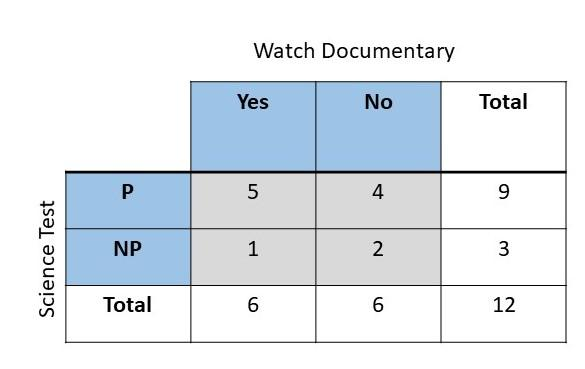
Question 12.

W represents watch the documentary
NW represents did not watch the documentary
P represents passed the science test
NP represents did not pass the science test
Answer:

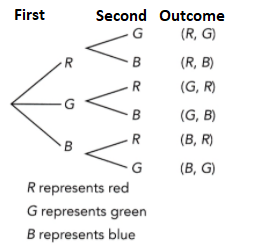
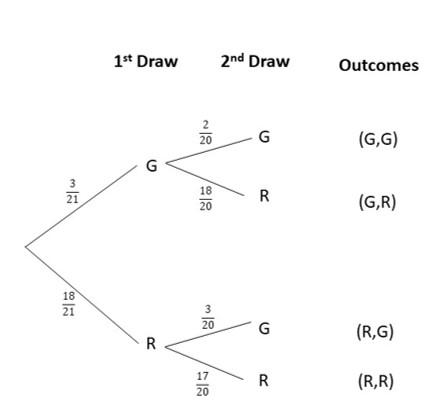
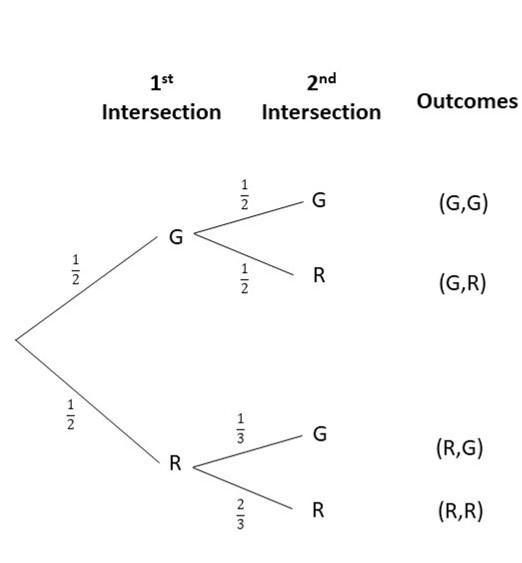
Tell whether the outcomes described are from a simple or compound event. If it is a compound event, identify the simple events that form the compound event. (Lesson 11.1)

Question 13.
Drawing a blue marble followed by a green marble, without replacing the first marble, from a box containing 2 red, 5 blue, and 3 green marbles.
Answer:
Compound event is composed of more than 1 simple event, Since there are two draws, the first draw to obtain a blue marble and the second one is to pick the green marble. Therefore, this is a compound event.

Question 14.
Getting a number between 2 and 5 when rolling a fair six-sided number die.
Answer:
Rolling a die to obtain a number between 2 and 5 once is one single event. It is possible to get in one single event, therefore this is a simple event.

Question 15.
Getting a product of 12 when rolling two fair six-sided number dice.
Answer:
Since there are two dices to roll, the first roll is the first event and the second dice is rolled to get 12 when the digit obtained is multiplied is the second event. Therefore, this is a compound event.

Solve. Show your work.

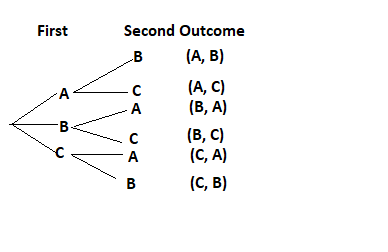
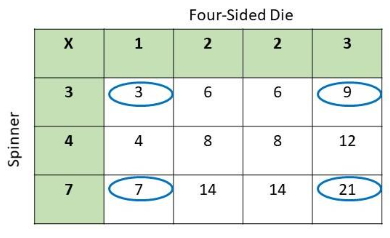
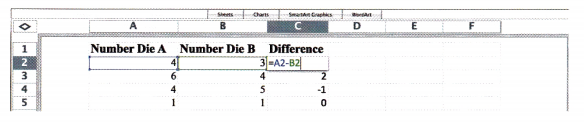
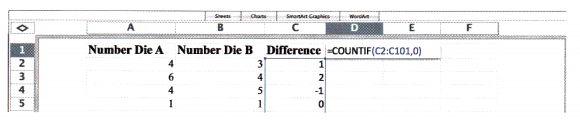
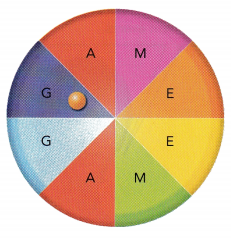
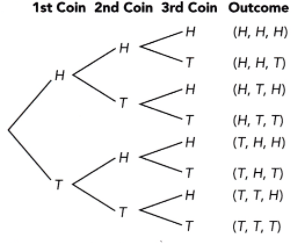
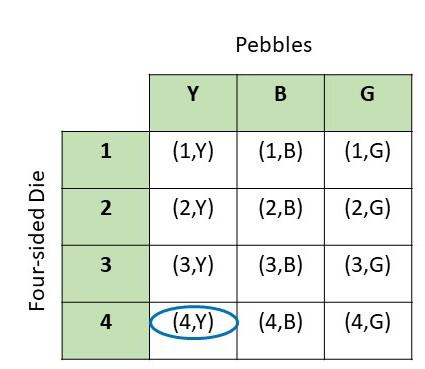
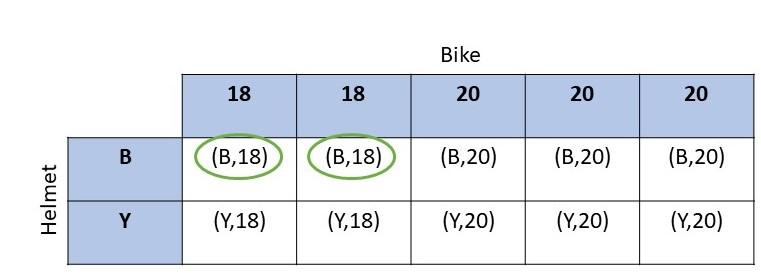
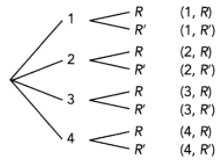
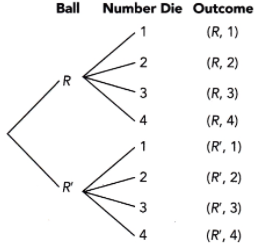
Question 16.
A fair four-sided number die, labeled 4 to 7, and a letter cube, labeled A, B, C, D, E, and E, are rolled. (Lessons 11.1, 11.2)
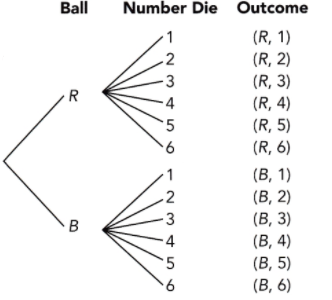
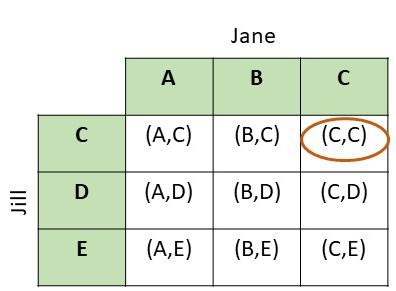
a) Draw a possibility diagram to represent the possible outcomes.
Answer:

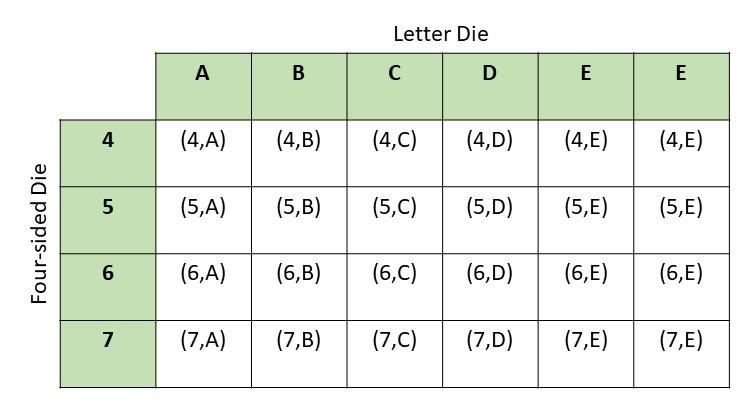
b) Find the probability of getting the letter E.
Answer:
There are 24 possible outcomes and 8 have E,
Probability = favorable outcomes / total outcomes
= 8/24
= 1/3

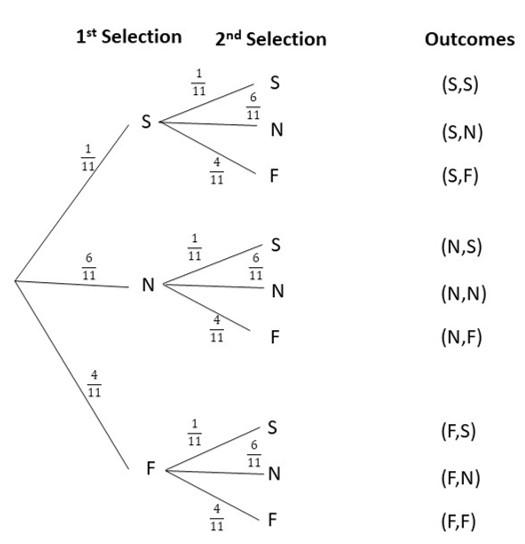
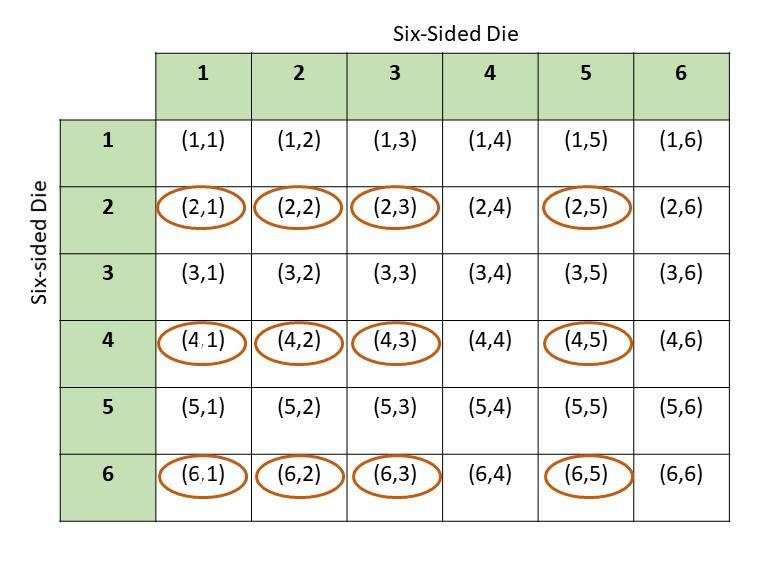
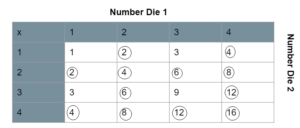
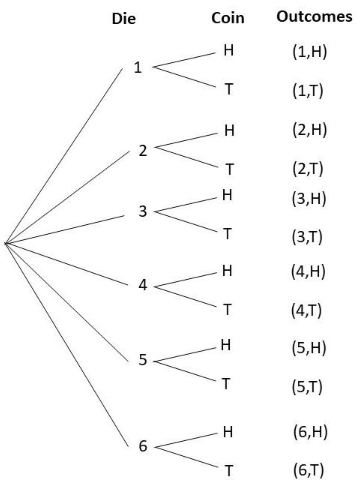
Question 17.
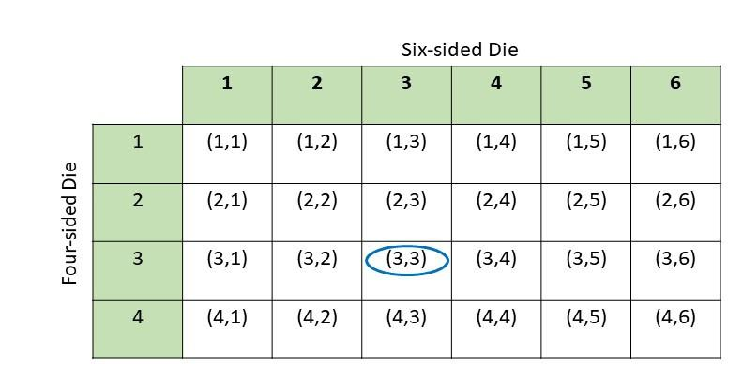
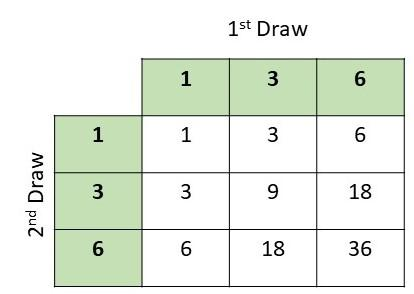
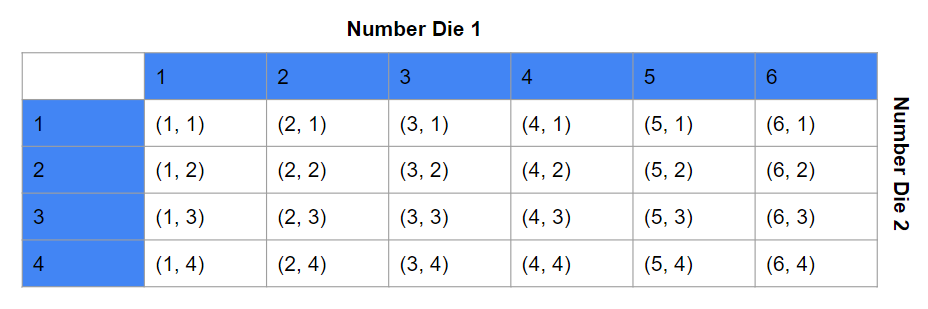
Two fair six-sided number dice numbered 1 to 6 are rolled. (Lessons 11.1, 11.2)
a) Draw a possibility diagram to represent the possible outcomes.
Answer:

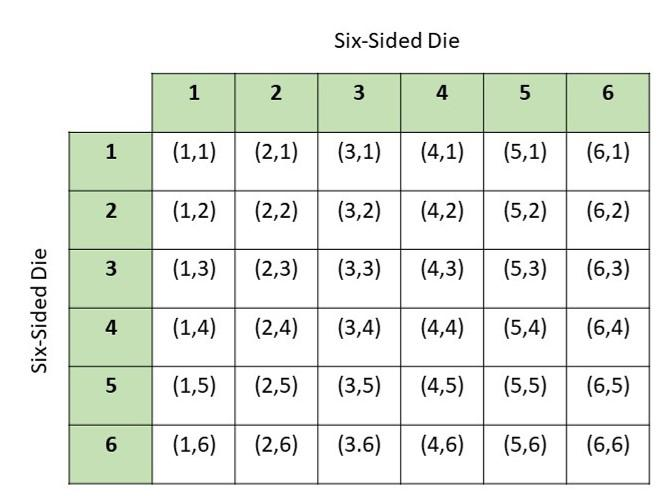
b) Find the probability that the outcomes for both six-sided number dice are even.
Answer:
There are total of 36 possibe outcomes and 9 obtained even numbers on both the dice
Probability = favorable outcomes/total outcomes
= 9/36
= 1/4

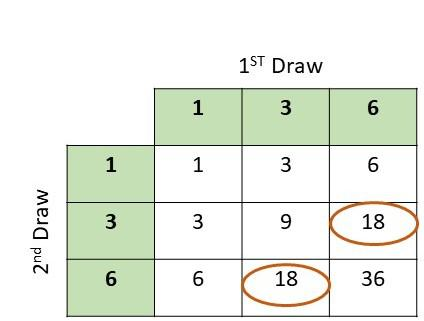
c) Find the probability that the product of the two numbers is a prime number.
Answer:
There are total of 36 possibe outcomes and 6 obtained prime numbers on both the dice
Probability = favorable outcomes/total outcomes
= 6/36
= 1/6

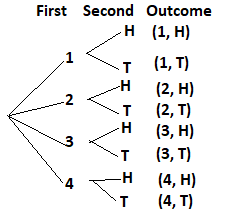
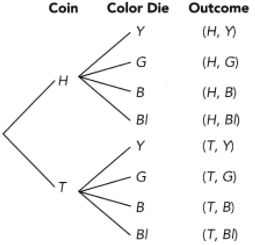
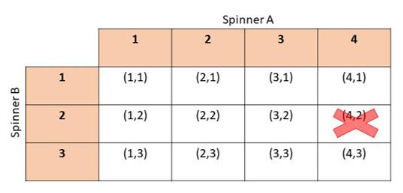
Question 18.
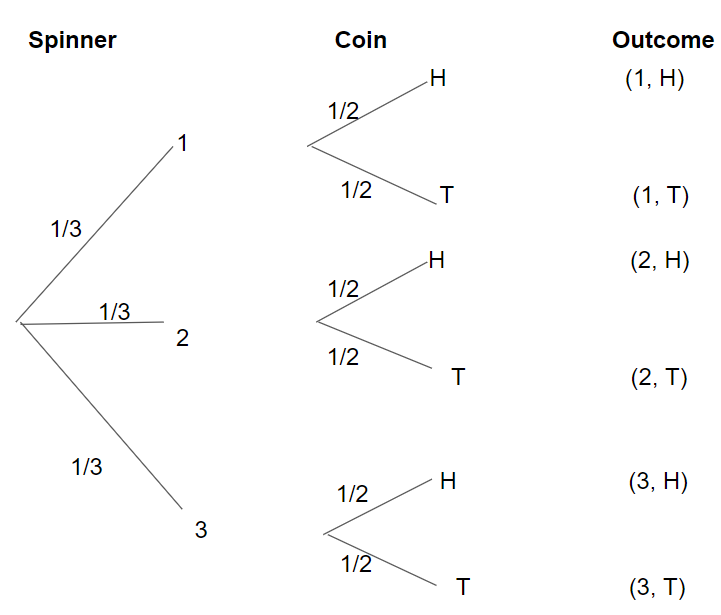
Spinner P is divided into 5 equal areas and labeled from 5 to 9. The spinner is spun and a coin is tossed. (Lessons 11.1, 11.2)
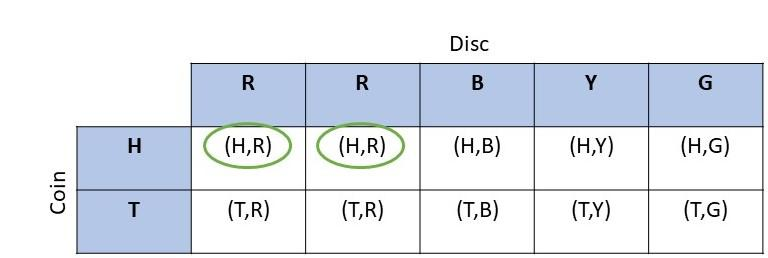
a) Draw a possibility diagram to represent the possible outcomes.
Answer:

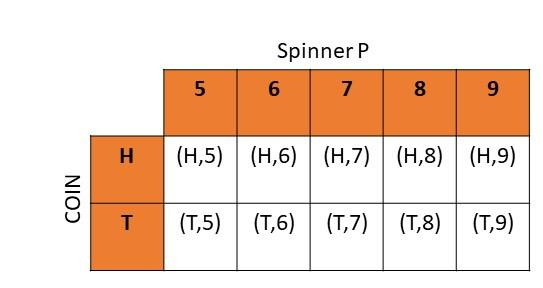
b) Find the probability of getting heads and an even number.
Answer:
There are total of 10 possibe outcomes and 2 results have head and even numbers in it
Probability = favorable outcomes/total outcomes
= 2/10
= 1/5

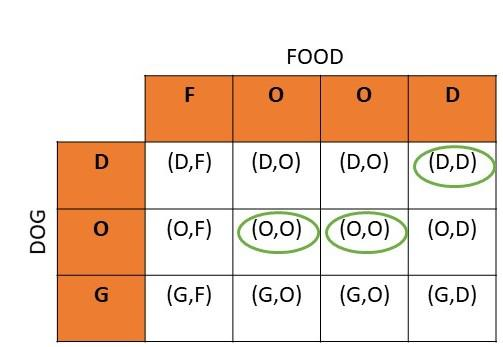
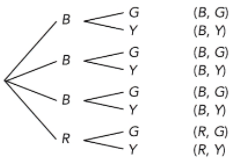
Question 19.
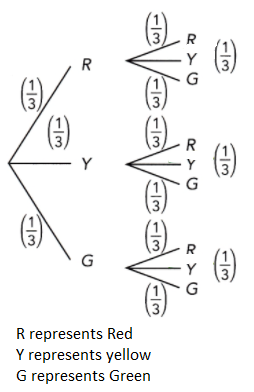
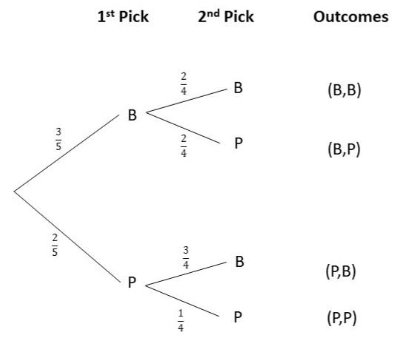
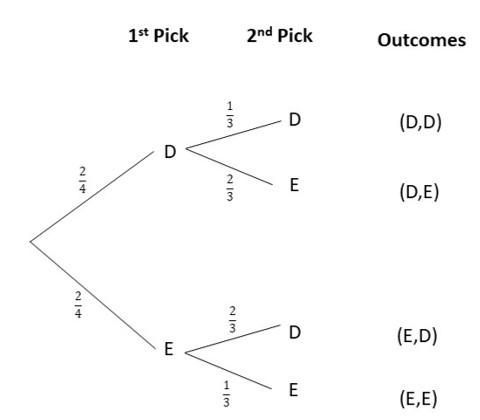
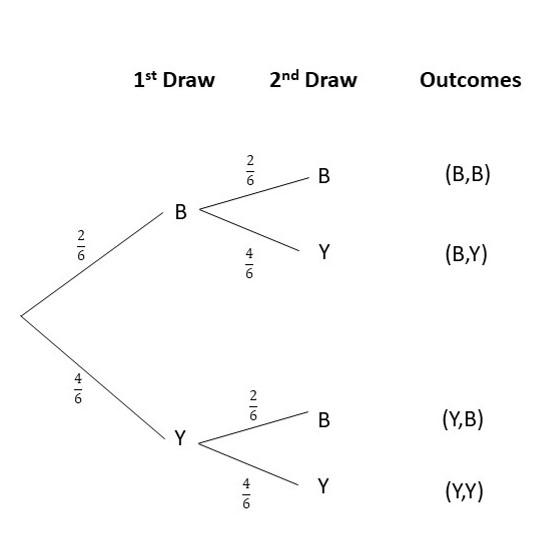
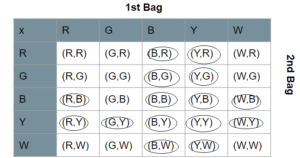
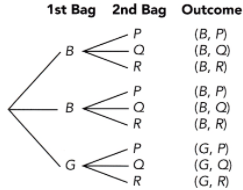
There are 4 yellow highlighters, 2 blue highlighters, and 3 purple highlighters in bag A. There are 2 white balls and 4 blue balls in bag B. A highlighter is randomly drawn from bag A, and then a ball is randomly drawn from bag B. (Lesson 11.3)
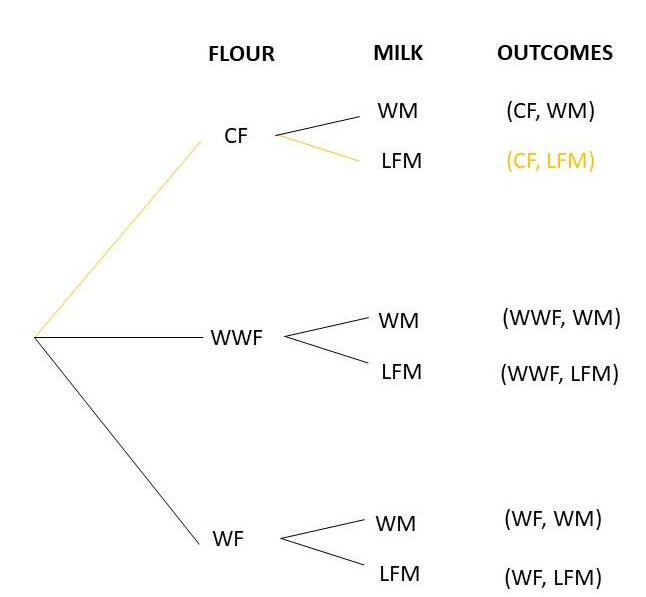
a) Draw a tree diagram to represent the possible outcomes and their corresponding probabilities.
Answer:

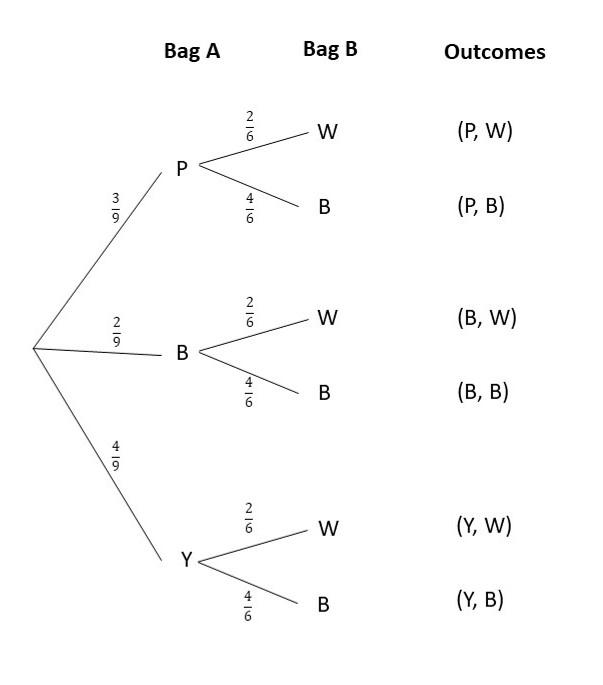
b) What is the probability of drawing a yellow highlighter and a blue ball?
Answer:
For the probability of obtaining a blue ball after obtaining a yellow highlighter denoted as P(Y,B), the probability of getting a yellow highlighter in the Bag A is 4/9 while the probability of selecting a blue ball in the Bag B is P(B) after getting a yellow highlighter is 4/6 then,
Probability = P(Y) x P(B)
= 4/9 x 4/6
= 16/54
= 8/27

c) What is the probability of drawing a highlighter and a ball that are the same color?
Answer:
For the probability of obtaining a blue highlighter followed by a blue ball denoted as P(B,B), the probability of getting a blue highlighter in the Bag A P(B) is 2/9 while the probability of selecting a blue ball in the Bag B is P(B) is 4/6 then,
Probability = P(Y) x P(B)
= 2/9 x 4/6
= 8/54
= 4/27

d) What is the probability of drawing exactly one blue item?
Answer:
The probability of selecting one blue item is the probability of getting one purple highlighter and a blue ball P(P,B) or the probability of selecting yellow highlighter and a blue ball P(Y,B) or the probability of obtaining a blue highlighter and white ball P(B,W)
P(P,B)+P(Y,B)+P(B,W)
= P(P) . P(B) + P(Y) . P(B) + P(B) . P(W)
= 3/9 x 4/6 + 4/9 x 4/6 + 2/9 x 2/6
= 12/54 + 16/54 + 4/54
= 32/54
= 16/27

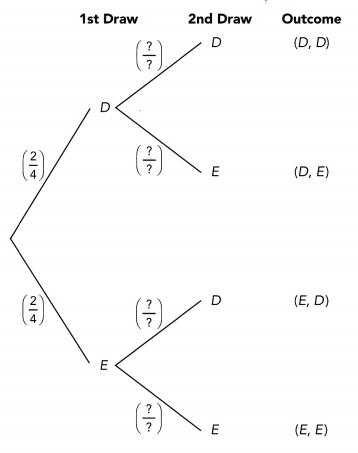
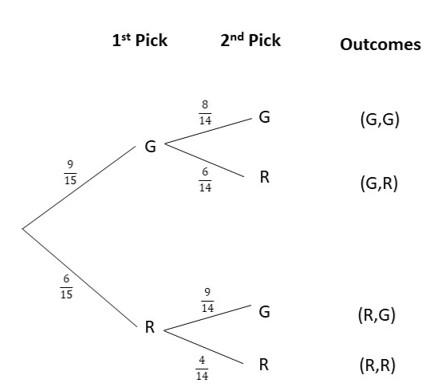
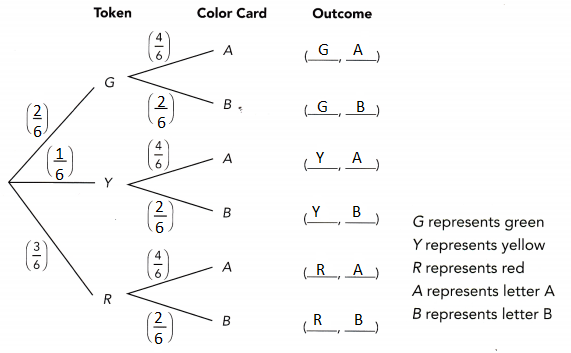
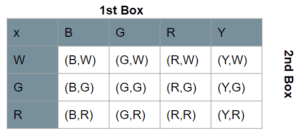
Question 20.
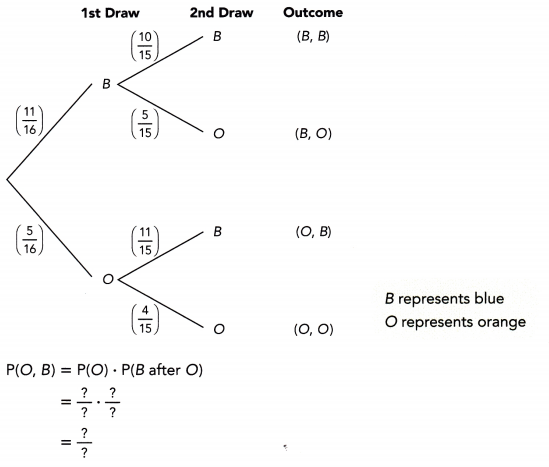
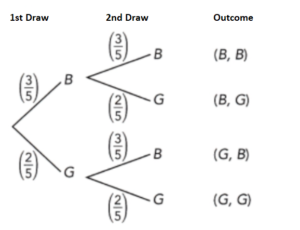
A box contains 16 color cards: 5 red, 4 blue, and 7 green. Two cards are picked at random from the box, one after another without replacement. The tree diagram shows the possible outcomes and the corresponding probabilities. (Lesson 11.4)

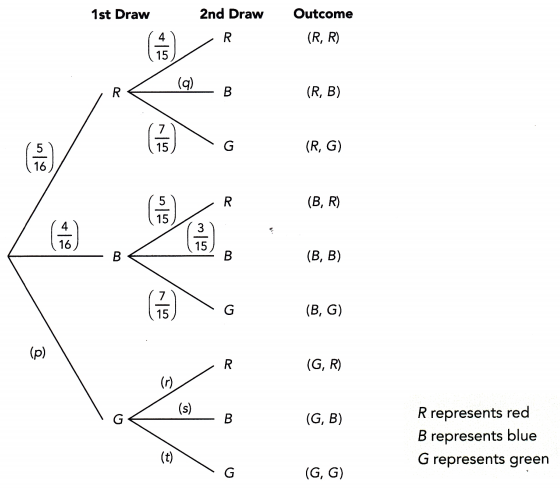
a) Find the values of p, q, r, s, and t.
Answer:
To find the value of p:
P(B) + P(R) + p = 1
4/16 + 5/16 + p = 1
9/16 + p = 1
p = 1 – 9/16
p = 7/16
To find the value of q:
P(G) + P(R) +p = 1
7/15 + 4/15 + p = 1
11/15 + p = 1
p = 1 – 11/15
p = 4/15
To find the value of r:
The probability of obtaining red in the second pick is 5/15 or 1/3.
To find the value of s:
The probability of obtaining blue denoted as s in the second pick is 4/15.
To find the value of t:
The probability of obtaining green denoted as t in the second pick is 6/15.

b) Find the probability that both cards are green.
Answer:
P(G,G) = P(G) x P(G)
= 7/16 x 6/15
= 42/240
= 7/40

c) Find the probability that both cards are the same color.
Answer:
P(G,G) + P(B,B) + P(R,R)
=P(G) x P(G) + P(B) x P(B) + P(R) x P(R)
=7/16 x 6/15 + 4/16 x 3/15 + 5/16 x 4/15
= 42/240 + 12/240 + 20/240
= 74/240
= 37/120

d) Find the probability that both cards are different colors.
Answer:
P(M) + P(NM) = 1
37/120 + P(NM) = 1
P(NM) = 1 – 37/120
P(NM) = 83/120

e) Find the probability that both cards are blue or both are green.
Answer:
P(G,G) or P(B,B) = P(G,G) + P(B,B)
= P(G) x P(G) + P(B) x P(B)
= 7/16 x 6/15 + 4/16 x 4/15
= 42/240 + 12/240
= 54/240
= 9/40

Problem Solving

Solve. Show your work.

Question 21.
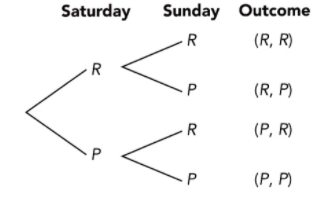
Alan has 3 pencils in a box: 1 blue, 1 red, and 1 orange. He has 1 blue marker and 2 red markers in another box. Alan randomly selects a pencil and a marker. Use a possibility diagram to represent the possible outcomes. Then find the probability of getting the same colors for the pencil and marker. (Chapter 11)
Answer:

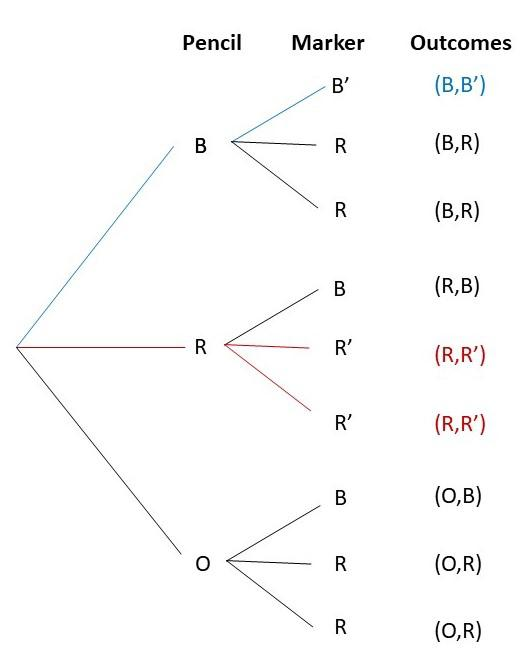
There are total of 9 outcomes and 3 favorable outcomes, then
Probability = favorable outcomes / total outcomes
= 3/9
= 1/3

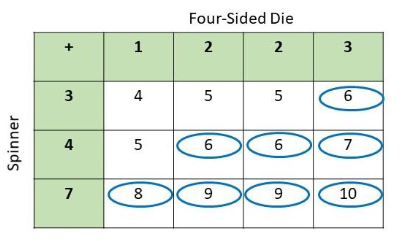
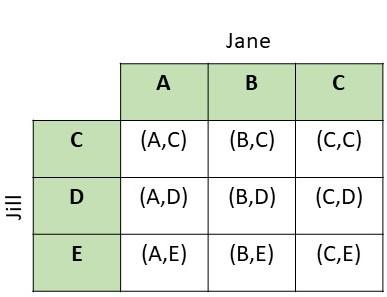
Question 22.
Joyce rolled a fair six-sided number die labeled 1 to 6 and a fair four-sided number die labeled 2 to 5. Use a possibility diagram to find the probability that the product of the two resulting numbers is at least 20. (Chapter 11)
Answer:

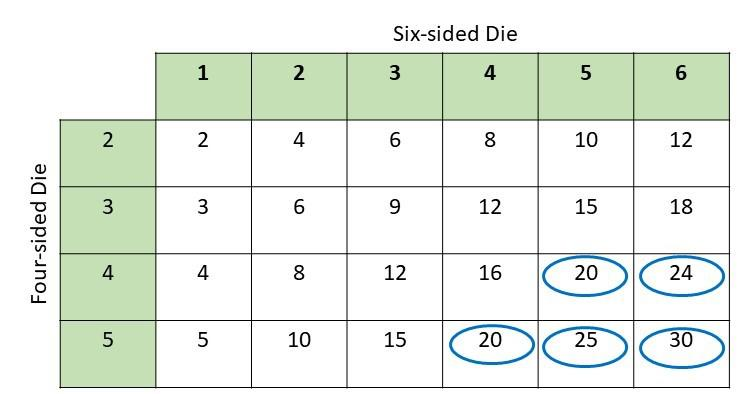
Explanation:
There are 36 total outcomes and 5 are greater than or equal to 20 then,
Probability = favorable outcomes / total outcomes
= 5/36

Refer to the scenario below to answer questions 23 to 28.

The data below shows the amount of electricity consumption and cost for some households in a particular month. (Chapter 10)

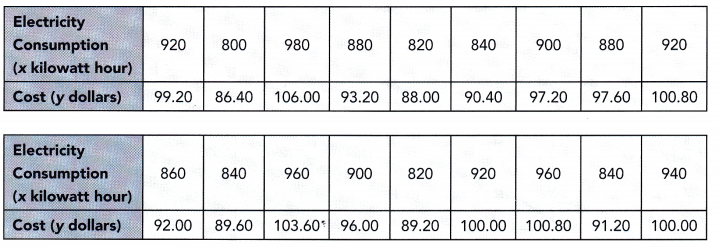
Question 23.
Construct a scatter plot for the given bivariate data. Use 1 centimeter on the horizontal axis to represent 20 kilowatt-hour for the x interval from 800 to 1,000 and 1 centimeter on the vertical axis to represent 2 dollars for the y interval from 86 to 108.
Answer:

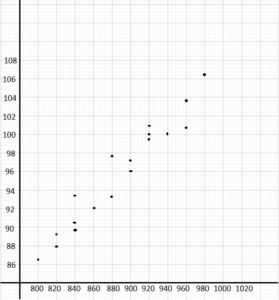
Question 24.
Describe the association between the electricity consumption and the cost.
Answer: The variable have a positive and linear association. Then, a high electricity usage corresponds to a high cost and a low consumption means a lower price.

Question 25.
Draw a line of best fit.
Answer:

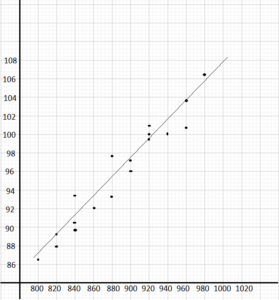
Question 26.
Write an equation for the line of best fit. Use points (820, 88) and (900, 97).
Answer:
For the equation of the line that best fits , using the points that best fits line passes through (820,88) and (900,97) to solve the slope of the line.
Slope of the line m = y2 – y1/ x2 – x1
m = 97 – 88 / 900 – 820
m = 9 / 80
m = 0.11
Using the slope intercept form given by y = mx + b, where m is the slope, b is the y intercept
y = mx + b
88 = (0.11)820 + b
88 = 90.2 + b
b = 90.2 – 88
b = 2.2
Therefore, the equation of line best fits is y = 0.11x + 2.2

Question 27.
Using the equation in 26, predict the cost per month for an electricity consumption of 888 kilowatt hour in that particular month.
Answer:
To estimate the price x given the electricity usage y, study the graph and the line of best fit at the point y at 888 kw. The point is on (888, 96.8).
Therefore, a household with 888 kw per hour consumption will pay around $96.8

Question 28.
Using the equation in 26, predict the cost per month for an electricity consumption of 1,000 kilowatt hour in that particular month.
Answer:
By using the equation of the line the cost of electricity consumption of 1000 kw per hour is calculated as
y = mx + b
y = 0.11(1000) + 2.2
y = 110 + 2.2
y = 112.2

Solve. Show your work.

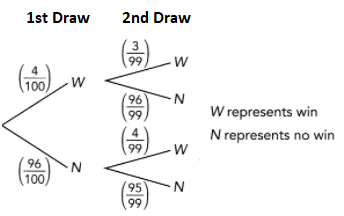
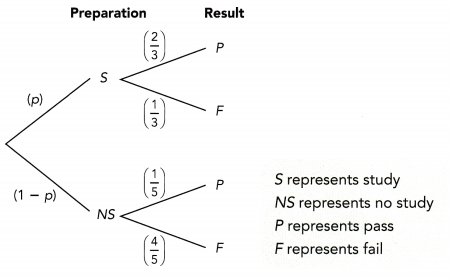
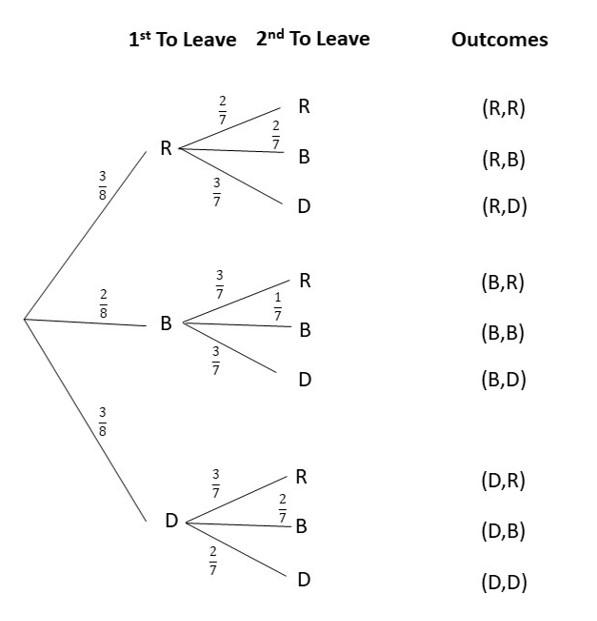
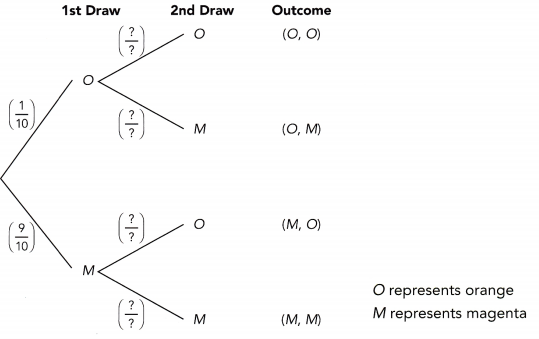
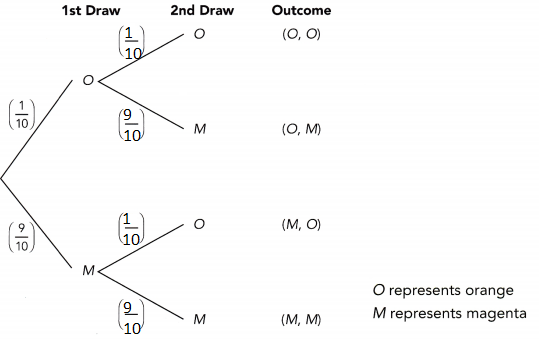
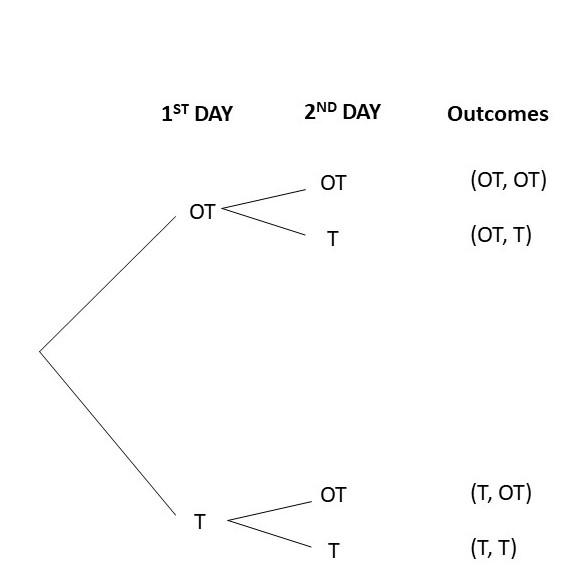
Question 29.
Bag A contains 25 tomatoes, 4 of which are rotten. Bag B contains 15 tomatoes, 6 of which are rotten. Jamie randomly selects a tomato from bag A followed by another random selection from bag B. (Chapter 11)
a) Draw a tree diagram to represent the possible outcomes and their corresponding probabilities.
Answer:

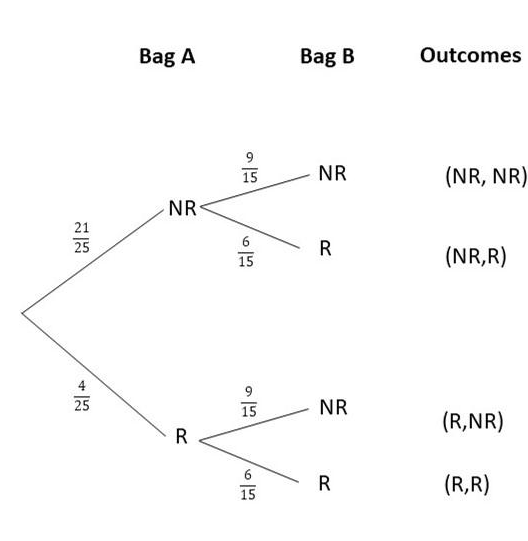
b) What is the probability that both tomatoes are rotten?
Answer:
P(R,R) = P(R) x P (R)
= 4/25 x 6/15
=24/375
= 8/125

c) What is the probability that exactly one tomato is rotten?
Answer:
P(NR,R) or P(R,NR) = P(NR,R) + P(R,NR)
= P(NR) x P(R) + P(R) x P(NR)
= 21/25 x 6/15 + 4/25 x 9/15
= 126/375 + 36/375
= 162/375
= 54/375

d) What is the probability that at least one tomato is not rotten?
Answer:
P(R,NR) + P(NR,R) + P(R,R)
= P(R) x P(NR) + P(NR) x P(R) + P(R) x P(R)
= 4/25 x 9/15 + 21/25 x 6/15 + 4/25 x 6/15
= 36/375 + 126/375 + 24/375
= 186/375
= 62/125

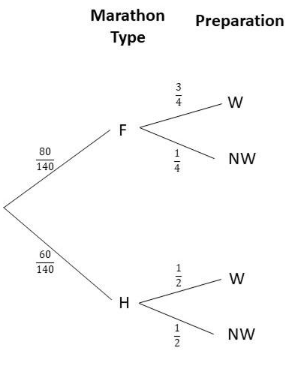
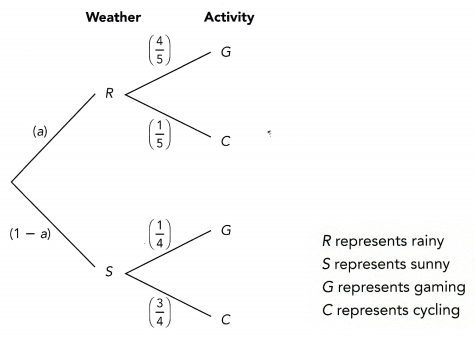
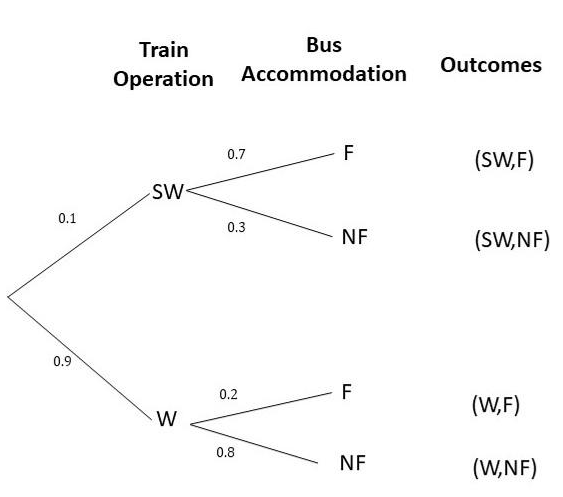
Question 30.
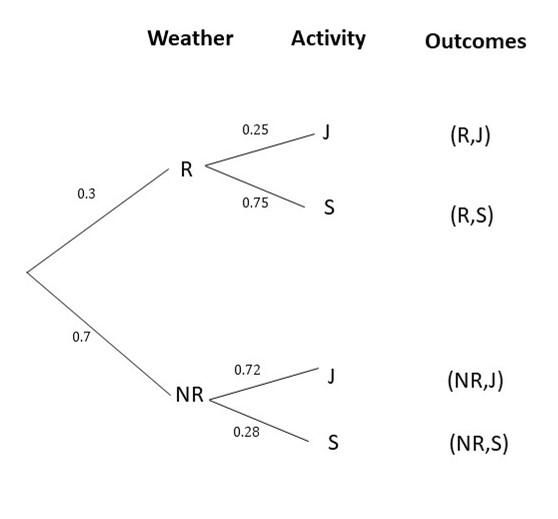
The probability that Jeremy wakes up late is 0.3. Jeremy can choose to cycle, take a bus, or drive a car to the gym. If he does not wake up late, the probability that he cycles is 0.5, takes a bus is 0.4, and drives a car is 0.1. If he wakes up late, the probability that he cycles is 0.05, takes a bus is 0.2, and drives a car is 0.75. (Chapter 11)
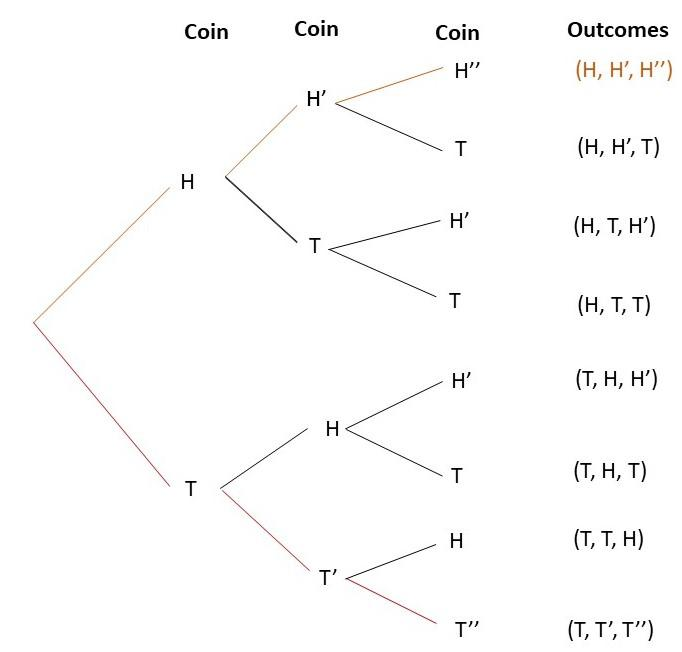
a) Draw a tree diagram to represent the possible outcomes and their corresponding probabilities.
Answer:

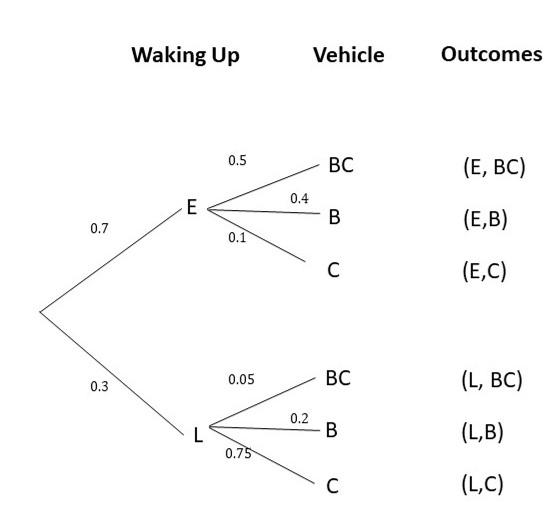
b) Find the probability that Jeremy will wake up and cycle to the gym.
Answer:
P(L,BC) = P(L) x P(BC)
= 0.3 x 0.05
= 0.015

c) Find the probability that Jeremy will not wake up late and will drive a car to the gym.
Answer:
P(E,C) = P(E) x P(C)
= 0.7 x 0.1
= 0.07

d) Find the probability that Jeremy will take a bus to the gym.
Answer:
P(E,B) or P(L,B) = P(E,B) + P(L,B)
= P(E) x P(B) + P(L) x P(B)
= 0.7 x 0.4 + 0.3 x 0.2
= 0.28 + 0.06
= 0.34

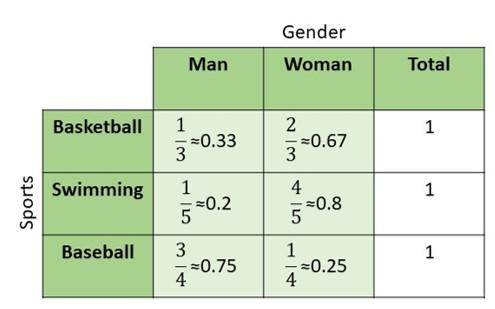
Refer to the scenario below to answer questions 31 to 34.

The data below shows the gender and favorite sport of 12 students surveyed. (Chapter 10)

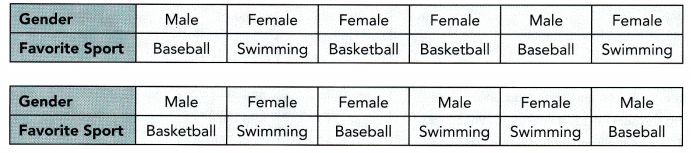
Question 31.
Construct a two-way table using the above data.
Answer:

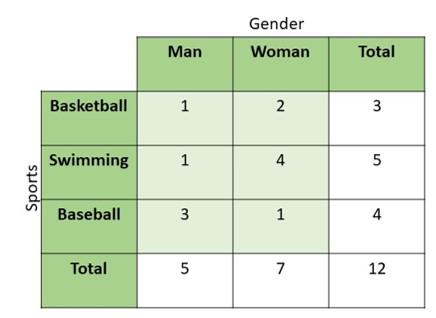
Question 32.
Describe the association between genders and favorite sports based on the given data.
Answer:
The total number of female who answers the survey is greater than the number of boys who accomplished the same activity. Swimming got the most number of votes compared to the other two. Therefore, more female students engage to sports compared to the male population and the most favorite sport is swimming.

Question 33.
Copy and find the relative frequencies (to the nearest hundredth) to compare the distribution of the genders among the different favorite sports (columns).
Answer:

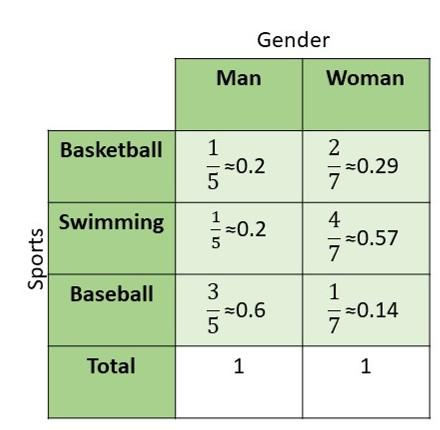
Question 34.
Copy and find the relative frequencies (to the nearest hundredth) to compare the distribution of the favorite sports among the genders (rows).
Answer:

This handy Math in Focus Grade 8 Workbook Answer Key Chapter 11 Review Test detailed solutions for the textbook questions.

Math in Focus Grade 8 Course 3 B Chapter 11 Review Test Answer Key

Concepts and Skills

State whether each event is a simple or compound event.

Question 1.
Drawing 2 yellow marbles ¡n a row from a bag of yellow and green marbles.
Answer:
Drawing 2 yellow marbles in a row from a bag of yellow and green marbles are compound events. Because the number of marbles is 3 so, the result is the number of outcomes.

Question 2.
Drawing 1 red pebble and 1 yellow pebble in a row from a bag of red and yellow pebbles.
Answer:
Drawing 1 red pebble and 1 yellow pebble in a row from a bag of red and yellow pebbles is compound. Because the number of pebbles is 2 so, the result is the number of outcomes

Question 3.
Tossing a coin once.
Answer:
Tossing a coin once is a simple event because it has a result of one outcome.

Draw the possibility diagram and state the number of possible outcomes for each compound event.

Question 4.
From three cards labeled A, B, and C, draw two cards, one at a time with replacement.
Answer:

Question 5.
From a pencil case with 1 red pen, 1 green pen, and 1 blue pen, select two pens, one at a time without replacement.
Answer:

Question 6.
Toss a fair four-sided number die, labeled 1 to 4, and a coin.
Answer:

Draw the tree diagram for each compound event.

Question 7.
Spinning a spinner divided into 4 equal areas labeled 1 to 4, and tossing a coin.
Answer:

Question 8.
Picking two green apples randomly from a basket of red and green apples.
Answer:
The probability of picking red and green apples is 1/2.

State whether each compound event consists of independent events or dependent events.

Question 9.
From a pencil case, two-color pencils are randomly drawn, one at a time without replacement.
Answer: Dependent event

Question 10.
From two classes of 30 students, one student ¡s selected randomly from each class for a survey.
Answer: Independent event

Problem Solving

Solve. Show your work.

Question 11.
There are two tables in a room. There are 2 history textbooks and 1 math textbook on the first table. There are 1 history workbook and 1 math workbook on the second table. Use a possibility diagram to find the probability of randomly selecting a history textbook from the first table and a math workbook from the second table.
Answer:
Given,
There are two tables in a room. There are 2 history textbooks and 1 math textbook on the first table.
1 + 2 = 3
The probability of randomly selecting a history textbook from the first table and a math workbook from the second table is 1/3.

Question 12.
A fair four-sided number die is marked 1, 2, 2, and 3. A spinner equally divided into 3 sectors is marked 3, 4, and 7. Jamie tosses the number die and spins the spinner.
a) Use a possibility diagram to find the probability that the sum of the two resulting numbers is greater than 5.
Answer:
Note that there are 4 possible outcomes in rolling a die which is 1, 2, 2, and 3, and 3 outcomes for the spinner which are 3, 4 and 7. Add these possible resuLts, then mark the answers that are bigger the 5.

Observe that there are 12 possible outcomes and 8 are greater than 5 then

Therefore, the probability of obtaining a number that is larger than 5 is \(\frac{2}{3}\).

b) Use a possibility diagram to find the probability that the product of the two resulting numbers is odd.
Answer:
Notice that there are 4 possible outcomes in rolling a die which is 1, 2, 2. and 3, and 3 outcomes for the spinner which are 3, 4 and 7. Multiply these possible results, then mark the answers that odd numbers.

Observe that there are 12 possibLe outcomes and 4 are odd numbers then

Therefore, the probability of obtaining an odd number is \(\frac{1}{3}\).

Question 13.
A juggler is giving a performance by juggling a red ball, a yellow ball, and a green ball. All 3 balls have equal chance of dropping. If one ball drops, the juggler will stop and pick up the ball and resume juggling. If another ball drops again, the juggler will stop the performance.
a) Draw a tree diagram to represent the possible outcomes and the corresponding probabilities.
Answer:

b) Find the probability of dropping the same colored ball twice.
Answer: 1/3

c) Find the probability of dropping one green and one yellow ball.
Answer:
P(G)P(R) = 1/3 × 1/3= 1/9

Question 14.
In a marathon, there is a half-marathon and a full-marathon. There are 60 students who participated in the half-marathon and 80 participated in the full-marathon. Half of the students in the half-marathon warm up before the run, while three-quarters of the students in the full-marathon warm up. Assume that warming up and not warming up are mutually exclusive and complementary.
a) Draw a tree diagram to represent the possible outcomes and the corresponding probabilities.
Answer:
Since, there are 2 types of marathon, then start the tree diagram with 2 branches. Now, at the end of these branches put the possible outcomes: H for half-marathon, and F for full marathon. Note that the probability of full marathon is \(\frac{80}{140}\) and the probability of half-marathon is \(\frac{60}{140}\). Next, there are a group who warms up and who does not, then make another 2 branches. At the end of these branches put the possible outcomes: W for warming up and NW for not warming up. Finally, conclude the possible results. Therefore, the tree diagram for the said event is as depicted below.

b) What is the probability of randomly picking a marathon participant who warms up before running a full-marathon?
Answer: full marathon: 80 runners

c) What is the probability of randomly picking a marathon participant who does not warm up before running?
Answer:
80 + 60 = 140
total: 140 runners; 90 warm-up.
The probability that a randomly selected runner warms up is 90/140.

Question 15.
The probability of Cindy waking up after 8 A.M. on a weekend day is p. Assume the events of Cindy waking up after 8 A.M. and by 8 A.M. are mutually exclusive and complementary.
a) If p = 0.3, find the probability that she will wake up after 8 A.M. on two consecutive weekend days.
Answer:
P(waking up after 8 A.M. two weekend days in a row) = p²
If p=0.3
p² = (0.3)²
p² = 0.09

b) If p = 0.56, find the probability that she will wake up by 8 A.M. on two consecutive weekend days.
Answer:
P(waking up before 8 A.M two weekend days in a row) = (1 – p)²
If p = 0.56, 1-p = 0.44 and
(1 – p)² = (0.44)² = 0.1936.

Question 16.
In a jar, there are 2 raisin cookies and 3 oat cookies. Steven takes two cookies one after another without replacement.
a) Draw a tree diagram to represent the possible outcomes and the corresponding probabilities.
Answer:
Since there are two different kinds of muffins, which are bran and pumpkin, then start the tree diagram with 2 branches. Now, at the end of these branches put the possible outcomes: P for pumpkin muffin, and B for bran muffins. Note that there are 2 pumpkin muffins out of the total of 5 muffins, and 3 bran muffins out of the 5 total muffins. So the probability for selecting a pumpkin is \(\frac{2}{5}\), and the probability of selecting a bran is \(\frac{3}{5}\).

Next, there are stilt 2 different kinds of muffins, then again, at the end of these branches put the possible outcomes: P for pumpkin muffin, and B for bran muffins. If a pumpkin muffin is obtained in the first pick, then on the second pick, there are now 1 pumpkin muffin and a totat of 4 muffins left since a muffin is already taken, then the probability of choosing a pumpkin is \(\frac{1}{4}\). Also, there are still 3 bran muffin out of 4 muffins left, thus, the probability of selecting a bran muffin is \(\frac{3}{4}\).

If a bran muffin is obtained in the first pick, then on the second pick, there are still a pumpkin muffin and a total of 4 muffins left since a muffin is already taken, then the probability of choosing a pumpkin is \(\frac{2}{4}\). Also, there are only 2 bran muffin left out of 4 muffins, thus, the probability of selecting a bran muffin is \(\frac{2}{4}\). Therefore, the tree diagram for the said event is as depicted below.

b) Find the probability of Steven randomly getting two of the same type of cookie.
Answer:
The probability of seLecting 2 muffins of a matching type is the probability of obtaining 2 pumpkin muffins, P(P, P), or the probability of choosing 2 bran muffins, P(B, B), then
P(P, P) or P(B, B) = P(P, P) + (B, B)
= P(P) · P(P) +P(B) · P(B)
= \(\frac{2}{5}\) · \(\frac{1}{4}\) + \(\frac{3}{5}\) · \(\frac{2}{4}\)
= \(\frac{2}{20}\) + \(\frac{6}{20}\)
= \(\frac{8}{20}\)
Therefore, the probability of picking 2 muffins of a matching type is \(\frac{8}{20}\).

c) Find the probability of Steven randomly getting at least one raisin cookie.
Answer:
For, the probability of selecting a minimum of one pumpkin muffin, note that the probability of choosing 2 bran muffins, P(B, B), and the probability of picking at least one pumpkin muffin is complementary.
P(B, B) + P(Minimum of One Pumpkin) = 1
P(Minimiun of One Pumpkin) = 1 – P(B, B)
P(Minimum of One Pumpkin) = 1 – P(B) · P(B)
P(Minimum of One Pumpkin) = 1 – \(\frac{3}{5}\) · \(\frac{2}{4}\)
P(minimum of One Pumpkin) = 1 – \(\frac{6}{20}\)
P(Minimum of One Pumpkin) = \(\frac{7}{10}\)
Therefore, the probabiUty of picking a minimum of one pumpkin is \(\frac{7}{10}\).

Question 17.
Out of 100 raffle tickets, 4 are marked with a prize. Matthew randomly selects two tickets from the box.
a) Draw a tree diagram to represent the possible outcomes and the corresponding probabilities.
Answer:

b) What is the probability that Matthew does not win any prizes?
Answer: 152/165

c) What is the probability that Matthew gets exactly one of the prizes?
Answer: 64/825

Question 18.
The tree diagram shows the probability of how Shane spends his day gaming or cycling, depending on the weather. The probability of rain is denoted by a. Assume that gaming and cycling are mutually exclusive.

a) If a = 0.4, find the probability that he will spend his day gaming.
Answer:
Given that a = 0.4
Here the G represents gaming.
The probability that he will spend his day on gaming =(1- 0.4) × 1/4 = 0.15.

b) If a = 0.75, find the probability that he will spend his day cycling.
Answer:
Given that a = 0.75
Here C represents cycling.
The probability that he will spend his day in cycling = (1-0.75) × 3/4 = 0.1875.

This handy Math in Focus Grade 8 Workbook Answer Key Chapter 11 Lesson 11.4 Dependent Events detailed solutions for the textbook questions.

Math in Focus Grade 8 Course 3 B Chapter 11 Lesson 11.4 Answer Key Dependent Events

Math in Focus Grade 8 Chapter 11 Lesson 11.4 Guided Practice Answer Key

Solve. Show your work.

Question 1.
A deck of four cards with the letters D, E, E, D are placed facing down on a table. Two cards are turned at random to show the letter. Draw a tree diagram to represent the possible outcomes in this compound event.

Let D represent letter D and E represent letter E.
1st draw
P(D) = \(\frac{2}{4}\)
P(E) = \(\frac{2}{4}\)

2nd draw
P(D after D)4 = \(\frac{?}{?}\) There is D left after 1 D is drawn.
P(E after D) = \(\frac{?}{?}\) There are E still after 1 D is drawn.
P(D after E) = \(\frac{?}{?}\) There are D still after 1 E is drawn.
P(E after E) = \(\frac{?}{?}\) There is E left after 1 E is drawn.

Answer:

P(D after D)4 = There is 1/3 D left after 1 D is drawn.
P(E after D) = There are 2/3 E still after 1 D is drawn.
P(D after E) = There are 2/3 D still after 1 E is drawn.
P(E after E) = There is 1/3 E left after 1 E is drawn

Question 2.
There are 16 different color pebbles in a jar. 11 of them are blue and the rest are orange. Two pebbles are randomly selected from the jar, one at a time without replacement.
a) Find the probability of taking an orange pebble followed by a blue pebble.

The probability of randomly taking an orange pebble followed by a blue pebble is
Answer:
P(B,O) = P(B) x P(O)
= 11/16 x 5/15
= 55/240
= 11/48
~0.23
Therefore, the probability of selecting a blue than a orange pebble is 11/48 or approx 0.23.

b) Find the probability of taking two orange pebbles.
P(O, O) = P(O) • P(O after O)
= \(\frac{?}{?} \cdot \frac{?}{?}\)
= \(\frac{?}{?}\)
The probability of randomly taking two orange pebbles is .
Answer:
P(O, O) = P(O) • P(O)
= 5/16 x 4/15
= 20/240
= 1/12
~0.08
Therefore, the probability of selecting two orange pebbles is 1/12 or approx 0.08.

c) Find the probability of taking two blue pebbles.
P(B, B) = P(B) • P(B after 8)
= \(\frac{?}{?} \cdot \frac{?}{?}\)
= \(\frac{?}{?}\)
The probability of randomly taking two blue pebbles is .
Answer:
P(B, B) = P(B) • P(B)
= 11/16 x 10/15
= 110/240
= 11/24
~0.46
The probability of randomly taking two blue pebbles is 11/24 or approx 0.46.

Question 3.
The tree diagram below shows how passing an examination depends on whether a student studies (S) or does not study (NS) for the exam. The probability that a student studies is denoted by p. Assume that S and NS are mutually exclusive events.

a) If p = 0.4, find the probability that a student passes the examination.
P(S) = \(\frac{?}{?}\) Write the fraction for 0.4.
P(NS) = 1 – P(S) Events S and NS are complementary.
= 1 – \(\frac{?}{?}\)
= \(\frac{?}{?}\)
P(P) = \(\frac{?}{?}\) • \(\frac{?}{?}\) + \(\frac{?}{?}\) • \(\frac{?}{?}\) Evaluate P(S, P) + P(NS, P).
= \(\frac{?}{?}\)
If the probability of studying is 0.4, then the probability of passing is .
Answer:
P(NS) + P(S) = 1
P(NS) = 1 – P(S)
P(NS) = 1 – 4/10
P(NS) = 6/10
Therefore, the probability of not studying is 6/10.
P(Pa) = P(S,P) + P(NS,P)
= P(S) x P(P) + P(NS) x P(P)
= 4/10 x 2/3 + 6/10 x 1/5
= 8/30 + 6/50
= 29/75
~0.39
Therefore, the probability of passing the exam is 29/75 or approx 0.39.

b) If p = 0.75, find the probability that a student fails the examination.
P(S) = \(\frac{?}{?}\) Write the fraction for 0.75.
P(NS) = 1 – P(S) Events S and NS are complementary.
= 1 – \(\frac{?}{?}\)
= \(\frac{?}{?}\)
P(F) = \(\frac{?}{?}\) • \(\frac{?}{?}\) + \(\frac{?}{?}\) • \(\frac{?}{?}\) Evaluate P(S, F) + P(NS, F).
= \(\frac{?}{?}\)
If the probability of studying is 0.75, then the probability of failing is .
Answer:
P(NS) + P(S) = 1
P(NS) = 1 – P(S)
P(NS) = 1 – 3/4
P(NS) = 1/4
Therefore, the probability of not studying is 1/4.
P(Fa) = P(S,F) + P(NS,F)
= P(S) x P(F) + P(NS) x P(F)
= 3/4 x 1/3 + 1/4 x 4/5
= 3/12 + 4/20
= 9/20
= 0.45
Therefore, the probability of failing the exam is 9/20 or approx is 0.45

Math in Focus Course 3B Practice 11.4 Answer Key

State whether each event is a dependent or independent event.

Question 1.
Drawing 2 red balls randomly, one at a time without replacement, from a bag of six balls.
Answer: Dependent event

Question 2.
Tossing a coin twice.
Answer: Independent event

Question 3.
Reaching school late or on time for two consecutive days.
Answer: Independent event

Question 4.
Flooding of roads during rainy or sunny days.
Answer: Dependent event

Draw the tree diagram for each compound event.

Question 5.
2 balls are drawn at random, one at a time without replacement, from a bag of 3 green balls and 18 red balls.
Answer:

Question 6.
The probability of rain on a particular day is 0.3. If it rains, then the probability that Renee goes shopping is 0.75. If it does not rain, then the probability that she goes jogging is 0.72. Assume that shopping and jogging are mutually exclusive and that rain and no rain are complementary.
Answer:
The probability of raining is 0.3, and the probability of raining P(R) and the probability of not raining P(NR) is equal to 1, then
P(NR) + P(R) = 1
P(NR) = 1 – P(R)
P(NR) = 1 – 0.3
P(NR) = 0.7
Therefore, the probability of not raining is 0.7
The probability of shopping when rain comes is 0.75, and the probability of shopping P(S), when it rains and the probability of jogging P(J) during rainy day is equal to 1, then
P(S) + P(J) = 1
P(J) = 1 – P(S)
P(J) = 1 – 0.75
P(J) = 0.25
Therefore, the probability of jogging when rains is 0.25
The probability of jogging when the rain did not come is 0.72, and the probability of shopping P(S) when it did not rain and the probability of jogging P(J) during a non-rainy day is equal to 1, then
P(S) + P(J) = 1
P(S) = 1 – P(J)
P(S) = 1 – 0.72
P(S) = 0.28
Therefore, the probability of shopping when it did not rain is 0.28.

Solve. Show your work.

Question 7.
Geraldine has a box of 13 colored pens: 3 blue, 4 red, and the rest black. What is the probability of drawing two blue pens randomly, one at a time without replacement?

Answer:
P(B, B) = P(B) x P(B)
= 3/13 x 2/12
= 1/26.
Therefore, the probability of picking blue pens twice is 1/26.

Question 8.
A box contains 8 dimes, 15 quarters, and 27 nickels. A student is to randomly pick two items, one at a time without replacement, from the bag. Find the probability that 2 quarters are picked.
Answer:
P(Q,Q) = P(Q) x P(Q)
= 15/50 x 14/49
= 210/2450
= 3/35
Therefore, the probability of picking a quarter twice is 3/35.

Question 9.
There are 9 green, 2 yellow, and 5 blue cards in a deck. Players A and B each randomly pick a card from the deck. Player A picks a card first before player B picks. Find the probability that both players pick the same color cards.
Answer:
P(B,B) or P(Y,Y) or P(G,G) = P(B,B) + P(Y,Y) + P(G,G)
= P(B) x P(B) + P(Y) x P(Y) + P(G) x P(G)
= 5/16 x 4/15 + 2/16 x 1/15 + 9/16 x 8/15
= 20/240 + 2/240 + 72/240
= 94/240
= 47/120
Therefore, the probability of obtaining a matching color of cards is 47/120.

Question 10.
The probability diagram below shows the probability of Xavier going to library or park depending if the weather is sunny or rainy. The probability of rain on a particular day is denoted by a. Assume that going to the library and going to the park are mutually exclusive and complementary.

a) If a = 0.3, find the probability that Xavier goes to the park on any day.
Answer:
To convert decimals into fractions,
= 0.3/1
Multiplying both numerator and denominator to 100
= 0.3/1 x 100/100
= 30/100
= 3/10
Therefore, 0.3 is 3/10 in fractional form.
P(S) + P(R) = 1
P(S) = 1 – P(R)
P(S) = 1- 3/10
P(S) = 7/10
Therefore, the probability of having a sunny day is 7/10.
P(L) + P(P) = 1
P(P) = 1 – P(L)
P(P) = 1 – 1/5
P(P) = 4/5
Therefore, the probability of going to the park during the sunny day is 4/5.
P(S,P) or P(R,P) = P(S,P) + P(R,P)
= P(S) x P(P) + P(R) x P(P)
= 7/10 x 4/5 + 3/10 x 1/3
= 28/50 + 3/30
= 33/30
= 0.66
Therefore, the probability of going to park at any day is 0.66.

b) If a = 0.75, find the probability that he goes to the library on any day.
Answer:
Converting the decimals into fractions,
= 0.75/1
Multiply both the numerator and denominator to 100,
= 0.75/1 x 100/100
= 75/100
= 3/4
Therefore, 3/4 is the fractional form of 0.75
P(S) + P(R) = 1
P(S) = 1 – P(R)
P(S) = 1 – 3/4
P(S) = 1/4
Therefore, the probability of having a sunny day is 1/4.
P(S,L) or P(R,L) = P(S,L) + P(R,L)
= P(S) x P(L) + P(R) x P(L)
= 1/4 x 1/5 + 3/4 x 2/3
= 1/20 + 6/12
= 11/20
= 0.55
Therefore, the probability of going to library at any day is 0.55.

Question 11.
There are 15 apples in a fruit basket. 6 of them are red apples and the rest green apples. Two apples are picked randomly, one at a time without replacement.

a) Draw a tree diagram to represent the possible outcomes.
Answer:

b) Find the probability of picking a green apple and then a red apple.
Answer:
P(G,R) = P(G) x P(R)
= 9/15 x 6/14
= 54/210
= 9/35
Therefore, the probability of picking a green apple then a red apple is 9/35.

c) Find the probability of picking two green apples.
Answer:
P(G,G) = P(G) x P(G)
= 9/15 x 8/14
= 72/210
= 12/35
Therefore, the probability of getting two green apples is 12/35.

d) Find the probability of picking two red apples.
Answer:
P(R,R) = P(R) x P(R)
= 6/15 x 5/14
= 30/210
= 1/70
Therefore, the probability of obtaining two red apples is 1/7.

Question 12.
There are 8 people in a room: 3 of them have red hair, 2 have blonde hair, and the rest have dark hair. Two people are randomly selected to leave the room, one after another, and they do not re-enter the room.
a) Draw a tree diagram to represent the possible outcomes.
Answer:

b) What is the probability of a person with dark hair leaving the room first?
Answer:
P(D,D) or P(D,R) or P(D,B) = P(D,D) + P(D,R) + P(D,B)
= P(D) x P(D) + P(D) x P(R) + P(D) x P(B)
= 3/8 x 2/7 + 3/8 x 3/7 + 3/8 x 2/7
= 6/56 + 9/56 + 6/56
= 21/56
= 3/8
Therefore, the probability that a dark haired person is the first one to leave is 3/8

c) What is the probability of a person with red hair leaving the room, followed by a person with blonde hair?
Answer:
P(R,B) = P(R) x P(B)
= 3/8 x 2/7
= 6/56
= 3/28
Therefore, the probability that a red haired person is the first one to leave then a blonde is 3/28.

d) What is the probability of two people with the same hair color leaving the room?
Answer:
P(D,D) or P(R,R) or P(B,B) = P(D,D) + P(R,R) + P(B,B)
= P(D) x P(D) + P(R) x P(R) + P(B) x P(B)
= 3/8 x 2/7 + 3/8 x 2/7 + 2/8 x 1/7
= 6/56 + 9/56 + 2/56
= 17/56
Therefore, the probability that a dark haired person is the first to leave is 17/56.

Question 13.
Along a stretch of road there are 2 traffic light intersections. Having red or green light for the first intersection is equally likely. Having a red light at the second intersection is twice as likely as a green light, if the first intersection traffic light was red. What is the probability of having a red light on the first intersection and a green light on the second intersection? Draw a tree diagram to show the possible outcomes.
Answer:

P(R,G) = P(R) x P(G)
= 1/2 x 1/3
= 1/6
Therefore, the probability of encountering a red then a green light is 1/6.

Question 14.
To get to work, Mr. Killiney needs to take a train and then a bus. The probability that the train breaks down is 0.1. When the train breaks down, there is a 0.7 probability that the bus will be overcrowded. When the train is operating normally, there is a 0.2 probability that the bus will be overcrowded. What is the probability of getting a seat in the bus? Draw a tree diagram to show the possible outcomes.
Answer:
P(SW) + P(W) = 1
P(W) = 1 – P(SW)
P(W) = 1 – 0.1
P(W) = 0.9
Therefore, the probability of the train working normally is 0.9.
P(NF) + P(F) = 1
P(NF) = 1 – P(F)
P(NF) = 1 – 0.7
P(NF) = 0.3
Therefore, the probability that the bus is not full is 0.3 when the train is not working properly.
P(NF) + P(F) = 1
P(NF) = 1- P(F)
P(NF) = 1 – 0.2
P(NF) = 0.8
Therefore, the probability that the bus is not full is 0.8 when the train is not working properly.

P(SW,NF) or P(W,NF) = P(SW) x P(NF) + P(W) x P(NF)
= 0.1 x 0.3 + 0.9 x 0.8
= 0.03 + 0.72
= 0.75
Therefore, the probability that the bus is not full is 0.75.

Brain @ Work

Question 1.
If there are 12 green and 6 red apples, find the probability of randomly choosing three apples of the same color in a row, without replacement. Show your work.
Answer:
P(G,G,G) = P(G) x P(G) x P(G)
= 12/18 x 11/17 x 10/16
= 55/204
Therefore, the probability of obtaining green apples is 55/204.
P(R,R,R) = P(R) x P(R) x P(R)
= 6/18 x 5/17 x 4/16
= 5/204
Therefore, the probability of obtaining red apples is 5/204.
P(R,R,R) or P(G,G,G) = P(R) x P(R) x P(R) + P(G) x P(G) x P(G)
= 5/204 + 55/204
= 60/204
= 5/17
Therefore, the probability of obtaining of picking 3 apples of a matching color is 5/17.

Question 2.
William has five $1 bills, ten $10 bills, and three $20 bills in his wallet. He picks three bills randomly in a row, without replacement. What is the probability of him picking three of the same type of bills? $how your work.
Answer:
P($20,$20,$20) = P($20) x P($20) x P($20)
= 3/18 x 2/17 x 1/16
= 6/4896
= 1/816
Therefore, the probability of obtaining three $20 bills is $1/816.
P($10,$10,$10) = P($10) x P($10) x P($10)
= 10/18 x 9/17 x 8/16
= 720/4896
= 5/34
Therefore, the probability of obtaining three $10 bills is $5/34.
P($1,$1,$1) = P($1) x P($1) x P($1)
= 5/18 x 4/17 x 3/16
= 60/4896
= 5/408
Therefore, the probability of obtaining three $1 bills is 5/408.
P($20,$20,$20) or P($10,$10,$10) or P($1,$1,$1) = P($20,$20,$20) + P($10,$10,$10) + P($1,$1,$1)
= 1/816 + 5/34 + 5/408
= 131/816
Therefore, the probability of having three bills of a matching type is 131/816.

Question 3.
Daniel plans to visit Australia. Whether he goes alone or with a companion is equally likely. If he travels with a companion there is a 40% chance of joining a guided tour. If he travels alone, there is an 80% chance of joining a guided tour.

a) What is the probability of traveling with a companion and not joining a guided tour?
Answer:
P(NT) + P(T) = 1
P(NT) = 1 – P(T)
P(NT) = 1 – 0.4
P(NT) = 0.6
Therefore, the probability of not going to tour is 0.6 if he travels with others.
P(NT) + P(T) = 1
P(NT) = 1 – P(T)
P(NT) = 1 – 0.8
P(NT) = 0.2
Therefore, the probability of not going to tour is 0.2 if he travels without the other.
P(C,NT) = P(C) x P(NT)
= 0.5 x 0.6
= 0.3
Therefore, the probability of travelling with others and not going with a tour is 0.3.

b) What is the chance of joining a guided tour?
Answer:
P(C,T) or P(WC,T) = P(C) x P(T) + P(WC) x P(T)
= 0.5 x 0.4 + 0.5 x 0.8
= 0.2 + 0.4
= 0.6
Therefore, the probability of being in a tour is 0.6

This handy Math in Focus Grade 8 Workbook Answer Key Chapter 11 Lesson 11.3 Independent Events detailed solutions for the textbook questions.

Math in Focus Grade 8 Course 3 B Chapter 11 Lesson 11.3 Answer Key Independent Events

Math in Focus Grade 8 Chapter 11 Lesson 11.3 Guided Practice Answer Key

Solve. Show your work.

Question 1.
A game is played with a bag of 6 color tokens and a bag of 6 letter tiles. The 6 tokens consist of 2 green tokens, 1 yellow token, and 3 red tokens. The 6 letter tiles consist of 4 tiles of letter A and 2 tiles of letter B. To win the game, you need to randomly get a yellow token and a tile of letter B from a random selection in each bag.
a) Copy and complete the tree diagram.

Answer:

b) Use the multiplication rule of probability to find the probability of winning the game in one try.
P(winning the game) = P(Y, B)
= P(Y) • P(B)
= •
=
The probability of winning the game is .
Answer:
P(winning the game) = P(Y, B)
= P(Y) • P(B)
P(Y) = 1/6 and P(B) = 2/6
= 1/6 • 2/6
= 2/36
= 1/18
The probability of winning the game is 1/18.

Technology Activity

Materials:
spreadsheet software

SIMULATE RANDOMNESS

Work in pairs.

Background
Two fair six-sided number dice are thrown. Using a spreadsheet, data will be generated to investigate how frequently the outcome of doubles (1 and 1, 2 and 2, … , 6 and 6) occurs.
STEP 1: Label your spreadsheet as shown.

STEP 2: To generate a random integer between 1 and 6, in cell A2, enter the formula = INT(RAND()*6 + 1) to simulate rolling a die. A random number from 1 to 6 should appear in the cell.

STEP 3: To model 100 rolls, select cells A2 to A101 and choose Fill Down from the Edit menu.

STEP 4: Repeat STEP 2 and STEP 3 for cells B2 to B101.

STEP 5: In cell C2, enter the formula = A2 – B2. Select cells C2 to C101 and choose Fill Down from the Edit menu. This column serves as a check to see if the random numbers generated in columns A and B are the same. If the numbers are the same, their difference is 0. A zero difference indicates doubles outcome.

STEP 6: To see how many times the data shows double occurring, in cell E1, enter the formula = COUNTIF(C2:C101,0).

STEP 7: Find the experimental probability of the occurrence of two number dice showing the same number by dividing the number you get in cell E1 by the total, 100 rolls.

Math Journal Find the theoretical probability of rolling doubles with 2 fair number dice. Compare this theoretical probability with the experimental probability you obtained in the spreadsheet simulation. Are these two values the same?

Answer:

Question 2.
In a bag, there are 9 magenta balls and 1 orange ball. Two balls are randomly drawn, one at a time with replacement.
a) Find the probability of drawing two magenta balls.

P(M, M) = P(M) • P(M)
= •
=
The probability drawing two magenta balls is .
Answer:

P(M) = 9/10
P(M, M) = P(M) • P(M)
= 9/10 • 9/10
= 81/100
The probability drawing two magenta balls is 81/100.

b) Find the probability of drawing an orange ball followed by a magenta ball.
P(O, M) = P(O) • P(M)
= •
=
The probability drawing an orange ball followed by a magenta ball is .
Answer:
P(O) = 1/10
P(M) = 9/10
P(O, M) = P(O) • P(M)
= 1/10 • 9/10
= 9/100
The probability drawing an orange ball followed by a magenta ball is .

c) Find the probability of drawing both orange balls.
P(O, O) = P(O) • P(O)
= •
=
The probability drawing both orange balls is .
Answer:
P(O) = 1/10
P(O, O) = P(O) • P(O)
= 1/10 • 1/10
= 1/100
The probability drawing both orange balls is 1/100.

Question 3.
On weekends, Carli either jogs (J) or plays tennis (T) each day, but never both. The probability of her playing tennis is 0.75.
a) Find the probability that Carli jogs on both days.
Because J and T are complementary,
P(J) = 1 – P(T)
= 1 –
=

P(J, J) = P(J) • P(J)
P(J, J) = •
=
The probability that Carli jogs both days is .
Answer:
P(J) = 1 – P(T)
= 1 – 0.75
= 0.25

P(J, J) = P(J) • P(J)
P(J, J) = 0.25 • 0.25
= 0.0625
The probability that Carli jogs both days is 0.0625.

b) Find the probability that Carli jogs on exactly one of the days.
Using the addition rule of probability:
P(J, J) + P(T, J) = P(J) • P(T) + P(T) • P(J)
= • + •
=
The probability that Carli jogs on exactly one of the days is .
Answer:
Using the addition rule of probability:
P(J, J) + P(T, J) = P(J) • P(T) + P(T) • P(J)
= 0.25 • 0.75 + 0.75 • 0.25
= 0.125 + 0.125
= 0.25
The probability that Carli jogs on exactly one of the days is 0.25.

Math in Focus Course 3B Practice 11.3 Answer Key

Draw a tree diagram to represent each compound event.

Question 1.
Tossing a fair coin followed by drawing a marble from a bag of 3 marbles:
1 yellow, 1 green, and 1 blue.
Answer:

H represents heads
T represents  tails
Y represents yellow
G represents green
B represents blue

Question 2.
Drawing two balls randomly with replacement from a bag with 1 green ball and 1 purple ball.
Answer:

B represents ball
G represents green ball
P represents purple ball

Question 3.
Drawing a ball randomly from a bag containing 1 red ball and 1 blue ball, followed by tossing a fair six-sided number die.
Answer:

R represents red ball
B represents blue ball

Question 4.
Tossing a fair coin twice.
Answer:
If we toss a fair coin twice, we have the following possible outcomes, or events: {(H,H), (H,T),(T,H), (T,T). The total number of possible outcomes is therefore 4 and the number of outcomes where the result is two heads is 1. The probability of getting two heads in tossing a fair coin twice is therefore 1/4.

Question 5.
Reading or playing on each day of a weekend.
Answer:

R represents reading
P represents playing

Question 6.
On time or tardy for school for two consecutive days.
Answer:

Solve. Show your work.

Question 7.
Mindy is playing a game that uses the spinner shown below and a fair coin. An outcome of 3 on the spinner and heads on the coin wins the game.

a) Draw a tree diagram to represent the possible outcomes of this game.
Answer:

H represents Heads
T represents Tails

b) Find the probability of winning the game in one try.
Answer:
1/2 × 1/3 = 1/6
Thus the probability of winning the game in one try is 1/6.

c) Find the probability of losing the game in one try.
Answer:
1/2 + 1/3
= 3/6 + 2/6
= 5/6
Thus the probability of losing the game in one try is 5/6.

Question 8.
There are 2 blue balls and 4 yellow balls in a bag. A ball is randomly drawn from the bag, and it is replaced before a second ball is randomly drawn.
a) Draw a tree diagram to represent the possible outcomes.
Answer:

b) Find the probability that a yellow ball is drawn first, followed by another yellow ball.
Answer:
The probability of obtaining 2 yellow balls is 4/9.
Explanation:
P(Y,Y) = P(Y) x P(Y)
= 4/6 x 4/6
= 16/36
= 4/9

c) Find the probability that a yellow ball is drawn after a blue ball is drawn first.
Answer:
The probability of picking a blue than a yellow ball is 2/9.
Explanation:
P(B,Y) = P(B) x P(Y)
= 2/6 x 4/6
= 8/36
= 2/9

Question 9.
Jasmine has 3 blue pens and 2 green pens in her pencil case. She randomly selects a pen from her pencil case, and replaces it before she randomly selects again.
a) Draw a tree diagram to represent the possible outcomes.
Answer:

B represents blue
G represents green

b) Find the probability that she selects 2 blue pens.
Answer:
P(B) =3/5
P(B) × P(B) = 3/5 × 3/5 = 9/25

c) Find the probability that she selects 2 green pens.
Answer:
P(G) = 2/5
P(G) × P(G) = 2/5 × 2/5 = 4/25
Thus the probability that she selects 2 green pens is 4/25

d) Find the probability that she selects 2 pens of the same color.
Answer:
P(B, B) + P(G, G) = 9/25 + 4/25 = 13/25
Therefore the probability that she selects 2 pens of the same color is 13/25

Question 10.
Henry has 4 fiction books, 6 non-fiction books, and 1 Spanish book on his bookshelf. He randomly selects two books with replacement.

a) Draw a tree diagram to represent the possible outcomes.
Answer:

b) Find the probability that he selects a fiction book twice.
Answer:
The probability of obtaining 2 fictional books is 16/121 or around 0.13
Explanation:
P(F,F) = P(F) x P(F)
= 4/11 x 4/11
= 16/121
~ 0.13

c) Find the probability that he first selects a non-fiction book, and then a Spanish book.
Answer:
The probability of obtaining a non-fiction book and a spanish book is 6/121 or around 0.05
Explanation:
P(N,S) = P(N) x P(S)
= 6/11 x 1/11
= 6/121
~ 0.05

d) Find the probability that he first selects a fiction book, and then a non-fiction book.
Answer:
The probability of obtaining a fiction book and a non-fiction book is 24/121 or around 0.20
P(F,N) = P(F) x P(N)
= 4/11 x 6/11
= 24/121
~ 0.20

Question 11.
Andy tosses a fair six-sided number die twice. What is the probability of tossing an even number on the first toss and a prime number on the second toss?

Answer:

There are 36 total possible outcomes and 12 of them are favorable outcomes
P(E,P) = favorable outcomes/total outcomes
= 12/36
=1/3
Therefore, the probability of obtaining an even number and a prime number on the 2 tosses is 1/3.

Question 12.
The probability that Fiona wakes up before 8 A.M. when she does not need to set her alarm is \(\frac{4}{10}\). On any two consecutive days that Fiona does not need to set her alarm, what is the probability of her waking up before 8 A.M. for at least one of the days?
Answer:
The probability of waking up earlier than 8 AM at least once is 0.64.
Explanation:
P(E) + P(L) = 1
P(L) = 1 – P(E)
P(L) = 1 – 2/5
P(L) = 3/5
Therefore, the probability of that she will wakeup late is 3/5.
The probability of Fiona waking up late two days consecutively is 0.36
P(L,L) = P(L) x P(L)
= 3/5 x 3/5
= 9/25
= 0.36
The probability of waking up earlier than 8 AM at least once
A = 1 – P(L,L)
A = 1 – 0.36
A = 0.64

Question 13.
A globe is spinning on a globe stand. The globe surface is painted with 30% yellow, 10% green, and the rest is painted blue. Two times Danny randomly points to a spot on the globe while it spins. The color he points to each time is recorded.
a) What is the probability that he points to the same color on both spins?
Answer:
The probability of getting to the same color on both spins is 0.46
Explanation:
P(M) = P(Y,Y) + P(G,G) + P(B,B)
= P(Y) x P(Y) + P(G) x P(G) + P(B) x P(B)
= 0.3 x 0.3 + 0.1 x 0.1 + 0.6 x 0.6
= 0.09 + 0.01 + 0.36
= 0.46

b) What is the probability that he points to yellow at least one time?

Answer:
The probability of selecting yellow at least once is 0.51
Explanation:
P(NY) + P(Y) = 1
P(NY) = 1 – P(Y)
P(NY) = 1 – 0.3
P(NY) = 0.7
Therefore, the probability of not selecting yellow is 0.7
P(NY,NY) = P(NY) x P(NY)
P(NY,NY) = 0.7 x 0.7
P(NY,NY) = 0.49
Therefore, the probability of selecting twice is 0.49
P(A) + P(NY, NY) = 1
P(A) = 1 – 0.49
P(A) = 0.51
Therefore, the probability of selecting yellow at least once is 0.51.

Question 14.
Math Journal Sally thinks that for two independent events, because the occurrence of one event will not have any impact on the probability of the other event, they are also mutually exclusive. Do you agree with her? Explain your reasoning using an example.
Answer:
In an independent event, the existence of one does not affect the others. For example, eating chocolates and watching TV as they both are not mutually exclusive. Mutually exclusive events are two (or more) events that cannot be done at the same time. Thus independent events are not mutually exclusive.

Question 15.
A game is designed so that a player wins when the game piece lands on the letter A. The game piece begins on letter G. A fair six-sided number die is tossed. If the number tossed is odd, the game piece moves one step counterclockwise. If the number tossed is even, the game piece moves one step clockwise.
a) What is the probability that a player will win after tossing the number die once?
Answer:
Winning with one roll of die means getting an even number, say P(E). A number die has 6 possible results and 3 of these are even so the probability of getting even number die is the same as the probability of winning in one roll of the number die, which is 3/6 or 1/2.

b) What is the probability that a player will win after tossing the number die twice?

Answer:
The probability of arriving on A with two rolls of the dice is 1/4.
Explanation:
P(O,O) = P(O) x P(O)
P(O,O) = 1/2 x 1/2
P(O,O) = 1/4
Therefore, the probability of arriving on A with two rolls of the dice is 1/4.

This handy Math in Focus Grade 8 Workbook Answer Key Chapter 11 Lesson 11.2 Probability of Compound Events detailed solutions for the textbook questions.

Math in Focus Grade 8 Course 3 B Chapter 11 Lesson 11.2 Answer Key Probability of Compound Events

Math in Focus Grade 8 Chapter 11 Lesson 11.2 Guided Practice Answer Key

Use a possibility diagram to find each probability.

Question 1.
Two fair four-sided number dice, each numbered 1 to 4 are rolled together. The result recorded is the number facing down. Find the probability that the product of the two numbers is divisible by 2.
Answer:
Given,
Two fair four-sided number dice, each numbered 1 to 4 are rolled together.
The result recorded is the number facing down.

3/4

Question 2.
One colored disc is randomly drawn from each of two bags. Both bags each have 5 colored discs: 1 red, 1 green, 1 blue, 1 yellow, and 1 white. Find the probability of drawing a blue or yellow disc.
Answer:
Given,
One colored disc is randomly drawn from each of two bags. Both bags each have 5 colored discs: 1 red, 1 green, 1 blue, 1 yellow, and 1 white.

R represents red
G represents green
B represents blue
Y represents yellow
W represents white
16/25

Question 3.
A box has 1 black, 1 green, 1 red, and 1 yellow marble. Another box has 1 white, 1 green, and 1 red marble. A marble is taken at random from each box. Find the probability that a red marble is not drawn.
Answer:
Given,
A box has 1 black, 1 green, 1 red, and 1 yellow marble.
Another box has 1 white, 1 green, and 1 red marble.
Marble is taken at random from each box.

B represents black
R represents red
G represents green
Y represents yellow
W represents white
1/2

Solve. Show your work.

Question 4.
Three fair coins are tossed together.
a) Draw a tree diagram to represent the possible outcomes.
Answer:

H represents Heads
T represents tails

b) Using your answer in a), find the probability of getting all heads.
Answer:
Total outcomes = 24
Number of getting all heads = 3
3/24 = 1/8
The probability of getting all heads = 1/8

c) Using your answer in a), find the probability of getting at least two tails.
Answer:
Total outcomes = 24
1/2
The probability of getting at least two tails = 1/2

Math in Focus Course 3B Practice 11.2 Answer Key

Solve. Show your work

Question 1.
A bag contains 2 blue balls and 1 red ball. Winnie randomly draws a ball from the bag and replaces it before she draws a second ball. Use a possibility diagram to find the probability that the balls drawn are different colors.
Answer:
Given,
A bag contains 2 blue balls and 1 red ball = 3
P(red) = 1/3
P(blue) = 2/3
possible outcomes = 4
Thus the probability that the balls drawn are different colors = 4/6

Question 2.
A letter is randomly chosen from the word FOOD, followed by randomly choosing a letter from the word DOG. Draw a tree diagram to find the probability that both letters chosen are the same.
Answer:

There are 12 possible outcomes and 3 among them are favorable outcomes, then
Probability = favorable outcomes/total outcomes
= 3/12
= 1/4
Therefore, the probability of getting two similar letters is 1/4.

Question 3.
Three pebbles are placed in a bag: 1 blue, 1 green, and 1 yellow. First a pebble is randomly drawn from the bag. Then a fair four-sided number die labeled from 1 to 4 is rolled. The result recorded is the number facing down. Use a possibility diagram to find the probability of drawing a yellow pebble and getting a 4.
Answer:

As there are 12 possible outcomes and 1 favorable outcome, then
Probability = favorable outcomes/total outcomes
= 1/12
Therefore, the probability of getting (4,y) is 1/12.

Question 4.
Thomas rolled a fair six-sided number die and a fair four-sided number die labeled 1 to 4 together. Use a possibility diagram to find the probability of rolling the number 3 on both.

Answer:

As there are total of 24 possible outcomes and 1 favorable outcome, then
Probability = favorable outcome/total outcomes
= 1/24
Therefore, the probability of getting (3,3) is 1/24.

Question 5.
At a bike shop, there are 3 bikes with 20-speed gears and 2 bikes with 18-speed gears. The bike shop also sells 1 blue helmet and 1 yellow helmet. Use a possibility diagram to find the probability of getting an 18-speed bicycle and a blue helmet if randomly selecting one bike and one helmet from among these.

Answer:

As there are 10 possible outcomes and 2 of them are favorable outcomes, then
Probability = favorable outcomes/total outcomes
= 2/10
= 1/5
Therefore, the probability of getting (B,18) is 1/5.

Question 6.
Susan randomly draws a card from three number cards: 1, 3, and 6. After replacing the card, Susan randomly draws another number card. The product of the two numbers drawn is recorded.

a) Use a possibility diagram to represent the possible outcomes.
Answer:

b) Using your answer in a), what is the probability of forming a number larger than 10 but less than 30?
Answer:

There are 9 possible outcomes and 2 of them are favorable outcomes,then
Probability(>10<30) = favorable outcomes/total outcomes
= 2/9
Therefore, the probability of getting greater than 10 and less than 30 is 2/9.

Question 7.
Jane and Jill watch television together for 2 hours. Jane selects the channel for the first hour, and Jill selects the channel for the second hour. Jane’s remote control randomly selects from Channels A, B, and C. Jill’s remote control randomly selects from Channels C, D, and E.
a) Use a possibility diagram to represent the possible outcomes for the channels they watch on television for 2 hours.
Answer:

b) Using your answer in a), what is the probability of watching the same channel both hours?
Answer:

As there are 9 possible outcomes and 1 favorable outcome, then
Probability = favorable outcomes/total outcomes
= 1/9

Question 8.
A color disc is randomly drawn from a bag that contains the following discs.

After a disc is drawn, a fair coin is tossed. Use a possibility diagram to find the probability of drawing a red disc and landing on heads.
Answer:

As there are 10 possible outcomes and 2 of them are favorable outcomes, then
Probability = favorable outcomes/total outcomes
= 2/10
= 1/5
Therefore, the probability of getting a red disc and head is 1/5.

Question 9.
Karen tosses a fair coin three times. Draw a tree diagram to find the probability of getting the same result in all three tosses.
Answer:

As there are total of 8 possible outcomes and 2 favorable outcomes, then
Probability = favorable outcomes/total outcomes
= 2/8
= 1/4
Therefore, the probability of acquiring a (H,H’,H”) and (T,T’,T”) is 1/4.

Question 10.
Mrs. Bridget’s recipes require her to put in some fine maize flour in bowl 1, followed by wheat flour in bowl 2, and rice flour in bowl 3. However, the jars of flour are not labeled, so she randomly guesses which flour to put in which bowl.
a) Draw a tree diagram to represent the possible outcomes.
Answer:

b) Using your answer in a), find the probability of getting the correct flour in the correct order.

Answer:
There are total of 6 possible outcomes and 1 favorable outcomes, then
Probability = favorable outcomes/total outcomes
= 1/6
Therefore, the probability of selecting a cornmeal flour and low fat milk is 1/6.

This handy Math in Focus Grade 8 Workbook Answer Key Chapter 11 Lesson 11.1 Compound Events detailed solutions for the textbook questions.

Math in Focus Grade 8 Course 3 B Chapter 11 Lesson 11.1 Answer Key Compound Events

Math in Focus Grade 8 Chapter 11 Lesson 11.1 Guided Practice Answer Key

Tell whether the outcomes described are from a simple or compound event. If it is a compound event, identify the simple events that form the compound event.

Question 1.
Obtaining two heads when two coins are tossed
Answer:
There are two simple events each consisting of tossing a coin.
Thus it is a compound event

Question 2.
Winning a football game
Answer:
Simple event

Question 3.
Getting a number less than 4 or getting a number greater than 5 when a fair six-sided number die is rolled
Answer: Simple event

Question 4.
Rolling two fair six-sided number dice and obtaining a sum of 10 from the throws
Answer: There are two simple events each consisting of rolling a fair number die.

Represent and tell the number of possible outcomes for each compound event described.

Question 5.
Two fair coins are tossed together.
Answer:
The possibilities of tossing two coins are {(HH), (TT), (H,T), (T, H)}
Thus there are 4 outcomes of tossing two fair coins.

Question 6.
The results of rolling two fair six-sided number dice are multiplied.
Answer:
(1, 1), (1, 2) (1, 3), (1, 4) (1, 5) (1, 6)
(2, 1), (2, 2) (2, 3), (2, 4) (2, 5) (2, 6)
(3, 1), (3, 2) (3, 3), (3, 4) (3, 5) (3, 6)
(4, 1), (4, 2) (4, 3), (, 4) (4, 5) (4, 6)
(5, 1), (5, 2) (5, 3), (5, 4) (5, 5) (2, 6)
(6, 1), (6, 2) (6, 3), (6, 4) (6, 5) (6, 6)
The possible outcomes are 36.

Question 7.
A fair six-sided number die and a fair four-sided number die labeled 1 to 4 are rolled. The results that face down on both number dice are recorded.

Answer:

For each compound event, draw a tree diagram to represent the possible outcomes. Then tell the number of possible outcomes.

Question 8.
Joshua has two bags. In the first bag, there are 2 blue beads and 1 green bead. In the second bag, there are 3 lettered cards with the letters P, Q, and R. Joshua randomly takes an item from the first bag, and then from the second bag.
Answer:

The possible outcomes are 9
Where,
B represents blue
G represents Green
P represents letter P
Q represents letter Q
R represents letter R

Question 9.
A fair coin is tossed then a fair four-sided color die with faces painted yellow, green, blue, and black is rolled. The color facing down is the result recorded.
Answer:

The possible outcomes are 8.
Where,
H represents heads
T represents tails
Y represents yellow
G represents green
B represents blue
B represents black

Math in Focus Course 3B Practice 11.1 Answer Key

Tell whether each statement is True or False.

Question 1.
Selecting letter A from the word PROBABILITY is a compound event.
Answer:
P – 1
R – 1
O – 1
B – 2
A – 1
I – 2
L – 1
T – 1
Y – 1
So, the statement is false.

Question 2.
Selecting letter B from the word BASEBALL and ABLE is a simple event.
Answer:
B – 2
A – 2
S – 1
E – 1
L – 2
The statement is false
ABLE is a simple event

Question 3.
Tossing a fair six-sided number die to get either an even number or a five is a compound event.
Answer:
Rolling an even number: {2, 4, 6}
Rolling a 5: {5}
The statement “Tossing a fair six-sided number die to get either an even number or a five is a compound event” is false.

Question 4.
Umberto has 3 red cards and 4 blue cards. Drawing two red cards in a row, without replacing the first card before drawing the second card, is a compound event.
Answer: true

Tell whether the outcomes described are from a simple or compound event. If it is a compound event, identify the simple events that form the compound event.

Question 5.
Getting a 6 when a fair six-sided number die is rolled.
Answer:
Rolling a 6: {6}
A simple event is an event with only one outcome.

Question 6.
Rolling three fair six-sided number dice and obtaining a sum of 18 from the throws.
Answer:
There are 3 possible outcomes.
A compound event is an event with more than one outcome.

Question 7.
Getting an eighteen when a fair twenty-sided number die is rolled.

Answer:
There is one possible outcome thus it is a simple event.

Question 8.
Susan has 3 red cards and 4 blue cards. She first draws a blue card. Without replacing the first card, she then draws another blue card.
Answer: Compound event

Solve. Show your work.

Question 9.
In the top drawer, there are two battery operated flash lights, one red and one yellow. In the second drawer, there are three packages of batteries: small, medium, and large. A flashlight and a package of batteries are randomly selected.
a) Use a possibility diagram to represent the possible outcomes.
Answer:

R represents red
Y represents yellow
S represents small
M represents medium
L represents large

b) How many possible outcomes are there?
Answer: 6 outcomes

Question 10.
Two electronic spinners, A and B, are spun by pressing a button. Spinner A has four sectors labeled 1 to 4, while B has three sectors, labeled 1 to 3. Spinner B, due to technical error, will never land on number 2 if spinner A lands on a 4.
a) Use a possibility diagram to represent the possible outcomes.
Answer:
The target of this task is to analyze the events of turning two spinners labelled t 2, 3, and 4, and 1, 2, and 3 then make a diagram that shows all its possibLe outcomes then determine the number of its possible outcomes given a condition of not being able to get (4, 2).

Since there are two spinners A and B, marked from 1 – 4 and 1 – 3 then the illustration for the possible outcomes would be as depicted in the table.

b) How many possible outcomes are there?
Answer:
The possible outcomes are (1, 1), (2, 1), (3, 1), (4, 1), (1, 2), (2, 2), (3, 2), (1, 3), (2, 3), (3, 3). and (4, 3)Therefore, there are 11 possible outcomes.

Question 11.
Winston has two boxes. The first box has 3 black pens and 1 red pen. The second box has 1 green ball and 1 yellow ball. Use a tree diagram to represent the possible outcomes for randomly drawing a pen and a ball. Then tell the number of possible outcomes.

Answer:

8 outcomes
R represents red
Y represents yellow
G represents green
B represents black

Question 12.
Seraphina first tosses a fair six-sided number die. She then tosses a fair coin. Use a tree diagram to represent the possible outcomes.
Answer:
The objective of this task is to make a tree diagram for the possibLe outcomes for tossing a number die and flipping a coin.

Observe that rolling a die has 6 possible outcomes, then start the tree diagram with 6 branches. Now, at the end of these branches put the possible outcomes: 1, 2, 3, 4, 5 and 6. Next in tossing a coin, since there are 2 possible outcomes then for each number, make another 2 branches. At the end of these branches put the possibLe outcomes: H for head and T for tail. Finally, conclude the possible results. The tree diagram for this event would be as depicted below.

Question 13.
A game was designed such that a participant needs to accomplish 2 rounds to be considered the overall winner. The first round is to roll a 4 from a fair four-sided number die labeled 1 to 4. The result recorded is the number facing down. The second round is to randomly draw a red ball from a box of 2 differently colored balls.
a) Draw a tree diagram to represent the possible outcomes.
Answer:

R represents red
R’ represents not red

b) How many possible outcomes are there?
Answer: 8 outcomes

c) Math Journal If the participant first draws the colored ball and then rolls the four-sided number die, will the number of possible outcomes be the same? Use a diagram to explain your reasoning.
Answer: Yes, there are still 8 outcomes

R represents red
R’ represents not red

Question 14.
Zoe first rolls a fair four-sided number die labeled 1 to 4. Then she rolls another fair four-sided number die labeled 2 to 5. The result recorded is the number facing down.

a) Use a possibility diagram to find the number of favorable outcomes for an odd sum.
Answer:
Note that there are 4 possible outcomes for born toss of the die, add these results, then the outcomes in tossing a die twice and adding their result would be as depicted in the table. Mark the sum that are odd.

Observe that there are 16 possib[e outcomes and 8 are odd then

Therefore, the probability of obtaining an odd sum is \(\frac{1}{2}\).

b) Use a possibility diagram to find the number of favorable outcomes for a difference greater than 2.
Answer:
Since there are 4 possible outcomes for both toss of the die, subtract these results, then the outcomes in tossing a die twice and subtracting their result would be as depicted in the table. Mark the difference that are bigger than 2.

Notice that there are 16 possible outcomes and only 1 is larger than 2 then

Therefore, the probability of obtaining a difference greater than 2 is \(\frac{1}{16}\).

This handy Math in Focus Grade 8 Workbook Answer Key Chapter 11 Probability detailed solutions for the textbook questions.

Math in Focus Grade 8 Course 3 B Chapter 11 Answer Key Probability

Math in Focus Grade 8 Chapter 11 Quick Check Answer Key

Solve. Show your work.

A box has 2 black balls, 7 red balls, and 3 green balls. A ball is randomly chosen from the box.

Question 1.
What is the probability of choosing a green ball?
Answer:
Given,
A box has 2 black balls, 7 red balls, and 3 green balls.
Total number of balls = 2 + 7 + 3 = 12
We have to find the probability of choosing a green ball.
Number of green balls = 3
Probability of choosing green balls = 3/12 = 1/4
Thus the Probability of choosing green balls is 1/4.

Question 2.
What is the probability of choosing a black ball?
Answer:
Given,
A box has 2 black balls, 7 red balls, and 3 green balls.
Total number of balls = 2 + 7 + 3 = 12
We have to find the probability of choosing a black ball.
Number of green balls = 2
Probability of choosing green balls = 2/12 = 1/6
Thus the Probability of choosing green balls is 1/6.

Question 3.
What is the probability of choosing a blue ball?
Answer:
Given,
A box has 2 black balls, 7 red balls, and 3 green balls.
Total number of balls = 2 + 7 + 3 = 12
We have to find the probability of choosing a black ball.
Number of blue balls = 0
Thus the Probability of choosing blue balls is 0.

Question 4.
What is the probability of choosing a ball that is not red?
Answer:
A box has 2 black balls, 7 red balls, and 3 green balls.
Total number of balls = 2 + 7 + 3 = 12
We have to find the probability of choosing a ball that is not red.
Number of red balls = 7
The number of balls that are not red is 5
So, the probability of choosing a ball that is not red is 5/12.

Question 5.
What is the probability of choosing a red or green ball?
Answer:
Given that,
A box has 2 black balls, 7 red balls, and 3 green balls.
Total number of balls = 2 + 7 + 3 = 12
Find the probability of choosing a red or green ball.
Number of green balls = 2
Probability of choosing green balls = 2/12 = 1/6
Thus the Probability of choosing green balls is 1/6.
Number of red balls = 7
Probability of choosing green balls = 7/12
The probability of choosing a red or green ball is 9/12 = 3/4.

Tell whether the events X and Y are mutually exclusive events.

Question 6.
A fair coin and a fair six-sided number die are tossed. X is the event that a head is obtained. Y is the event that a six is obtained.
Answer:
Given,
A fair coin and a fair six-sided number die are tossed.
X is the event that a head is obtained.
The probability of getting heads is p(A) = 1
Y is the event that a six is obtained.
The probability of getting six is p(B) = 1
Yes the events X and Y are not mutually exclusive events.

Question 7.
A fair six-sided number die is rolled. X is the event of obtaining a three. Y is the event of obtaining a five.
Answer:
A fair six-sided number die is rolled.
X is the event of obtaining a three.
Y is the event of obtaining a five.
Events 3 and 5 are mutually exclusive because we cannot get 3 and 5 at the same time.

Question 8.
Two fair six-sided number dice are tossed. X is the event that the sum of the score is six. Y is the event that the sum of the score is 10.
Answer:
Given,
Two fair six-sided number dice are tossed.
X is the event that the sum of the score is six.
Y is the event that the sum of the score is 10.
Total number of possible results from two six-sided dice is 6 × 6 = 36.
The possibility of the sum of the score is six is (1, 5) (2, 4) (3, 3) (4, 1) (5, 1) = 5/36
The sum of the score is 10 is (4, 6) (5, 5) (6, 4) = 3/36 = 1/12
Thus they are mutually exclusive events.

Question 9.
X is the event consisting of the factors of 24. Y is the event consisting of multiples of 6 less than 20.
Answer:
Factors of 24 is (1, 24), (2, 12) (3, 8) and (4, 6).
Multiples of 6 less than 20 is 6, 12, 18.
Thus they are mutually exclusive events.