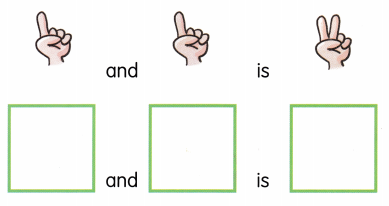
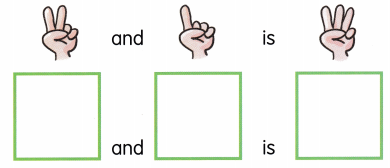
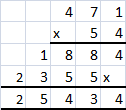
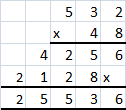
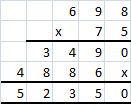
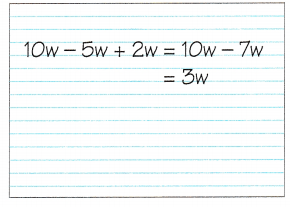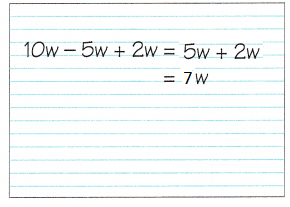Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 7 Lesson 7.3 Simplifying Algebraic Expressions to score better marks in the exam.
Math in Focus Grade 6 Course 1 A Chapter 7 Lesson 7.3 Answer Key Simplifying Algebraic Expressions
Math in Focus Grade 6 Chapter 7 Lesson 7.3 Guided Practice Answer Key
Simplify each expression. Then state the coefficient of the variable In the expression.
Question 1.
x + x + x + x + x
Answer:
5x
Explanation:
x is the variable or constant,
add all the variables, we get 5x.
So, 5 is the coefficient of the variable x.
Question 2.
y + y + 6
Answer:
2y + 6
Explanation:
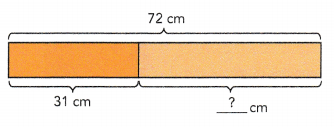
y is the variable, add all the variables
y + y + 6
2y + 6
So, 25 is the coefficient of the variable y
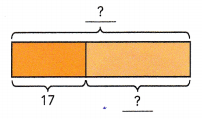
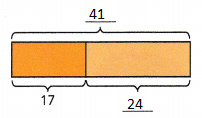
Question 3.
m + m + m + 5 + 4
Answer:
3m + 9
Explanation:
3 is the coefficient of the variable m,
add of the variables.
m + m + m + 5 + 4
3m+9
Question 4.
n + n + n + n + n + n + 12 – 8
Answer:
6n + 4
Explanation:
n is the variable, add all the variables at first.
n + n + n + n + n + n + 12 – 8
6n + 4
6 is the coefficient of the variable 2
Solve.
Question 5.
A square has sides of length x centimeters. Find the perimeter of the square in terms of x.
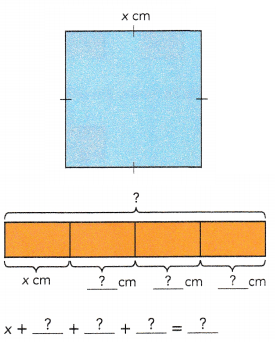
The perimeter of the square is  centimeters.
centimeters.
Answer:
4x
Explanation:
x + x + x + x = 4x
The perimeter of the square is 4x centimeters.
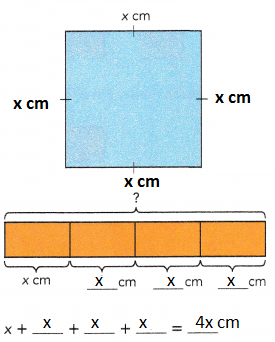
Question 6.
The figure shows a trapezoid. The length of each side is given as shown. Find the perimeter of the trapezoid in terms of w.
10cm
The perimeter of the trapezoid is 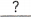 centimeters.
centimeters.
Answer:
3w + 10 cm
Explanation:
The perimeter of the trapezoid is 3w + 10 centimeters.
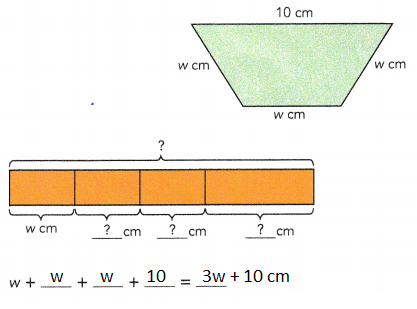
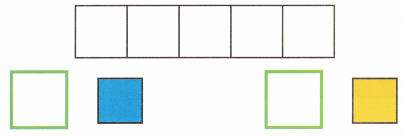
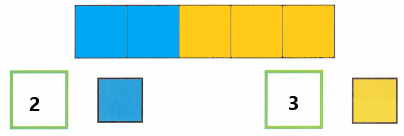
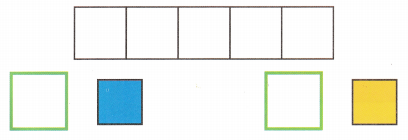
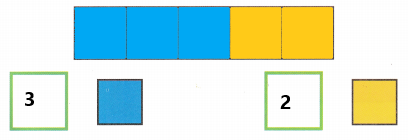
Hands-On Activity
Materials:
RECOGNIZE SIMPLIFIED EXPRESSIONS ARE EQ UIVALENT)
Work in pairs.
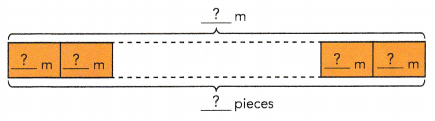
STEP 1: Make the following set of paper strips.
Let the length of the shortest strip be m units. Make and label 5 such strips.

Make and label 4 more strips of lengths 2m units, 3m units, 4m units, and 5m units.
STEP 2: Take one of the longer strips and place it horizontally.

STEP 3: Ask your partner to use the pieces of the shortest strips to match the length of the chosen strip in STEP 2.
Example
STEP 4: Write an algebraic expression to describe the number of short strips used, and simplify it. For example in STEP 3, write m + m + m = 3m.
STEP 5: Repeat the activity with other lengths of strips.
Activity 1:
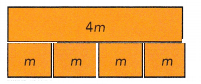
m + m + m + m = 4m
Activity 2:
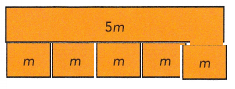
m + m + m + m + m = 5m
Math Journal How do the lengths of the strips show that the expressions are equivalent?
Answer:
We use the fraction strips to show differences between different fractions.
Explanation:
For example;
We start with halves and quarters.
Ask each student to pull out a 1/2 foot strip.
Now ask them to clear their desks of everything but the 1/4 pieces and the one 1/2 strip.
Then ask them to put down enough quarter pieces to make the same length as the half piece.
We can show the lengths of the strips are equivalent with expressions.
Complete.
Question 7.
Simplify x + 8x.
x + 8x = 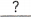

Answer:
9x
Explanation:
We use the fraction strips to show differences between different fractions.

Simplify each expression.
Question 8.
3r + 2r
Answer: 5r
Explanation:
r is the variable in the given expression
3r + 2r
= r + r + r + r + r
= 5r
5 is the coefficient of the variable r.
Question 9.
5y + 6y
Answer:
11y
Explanation:
y is the variable in the given expression.
y + y + y + y + y + y +y + y + y + y + y = 11y
11 is the coefficient of the variable y.
State whether each pair of expressions are equivalent.
Question 10.
3a and a + a + a
Answer:
YES, pair of expressions are equivalent.
Explanation:
3a can be expanded as a + a + a = 3a
a + a + a = 3a
So, the given statement is correct.
Question 11.
2h + 2h and 4h
Answer:
YES, pair of expressions are equivalent.
Explanation:
2h can be expanded as h + h
2h + 2h = 4h
h + h + h + h = 4h
Question 12.
2k + 5 and (k + k) • 5
Answer:
NO, pair of expressions are not equivalent.
Explanation:
2k + 5 and (k + k) • 5
2k + 5 is not equal to 2k.5
2k + 5 is not equal to 10k
Question 13.
6z + 4z and 10 + 2z
Answer:
NO, pair of expressions are notequivalent.
Explanation:
6z + 4z = 10z
10 + 2z is another expression
10z not equal to 10 + 2z
Question 14.
1p + 3p and 13p
Answer:
NO, pair of expressions are not equivalent.
Explanation:
1p + 3p = 4p
4p is not equal to 13p
Question 15.
3n + 2 + 4n and 2 + 7n
Answer:
YES, pair of expressions are equivalent.
Explanation:
both are equal
3n + 2 + 4n
= 3n + 4n + 2
= 7n + 2
Complete
Question 16.
Simplify 4s – s
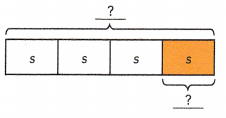
4s – s = 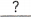
Answer:
3s
Explanation:
We use the fraction strips to show differences between different fractions.

Simplify each expression.
Question 17.
12z – 7z
Answer:
5z
Explanation:
Subtract 12 from 7
12z – 7z = 5z
Question 18.
3p – 3p
Answer:
0
Explanation:
Subtracting 3p from 39 we get 0
3p – 3p = 0
State whether each pair of expressions are equivalent.
Question 19.
f – 6 and 6 – f
Answer:
NO, pair of expressions are not equivalent.
Explanation:
f- 6 is positive if f > 6
6-f is negative for the above f value.
Question 20.
5c – 5c and a – a
Answer:
YES, pair of expressions are equivalent.
Explanation:
5c – 5c = 0
a – a = 0
both are correct.
Simplify each expression.
Question 21.
(j + 3j) + 2j = 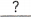 + 2j
+ 2j
= 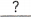
Answer:
6j
Explanation:
(j + 3j) + 2j
= 4j + 2j
= 6j
Question 22.
4j + 5j + 2j
Answer:
11j
Explanation:
4j + 5j + 2j
= 9j + 2j
= 11j
Question 23.
9t – 3t – 4t
Answer:
2t
Explanation:
9t – 3t – 4t
= 6t – 4t
= 2t
Question 24.
5t – t – 4t
Answer:
0
Explanation:
5t – t – 4t
= 4t – 4t = 0
Question 25.
8w – 6w + 3w
Answer:
5w
Explanation:
8w – 6w + 3w
= 2w + 3w
= 5w
Question 26.
7w + 2w – 6w
Answer:
3w
Explanation:
7w + 2w – 6w
= 9w – 6w = 3w
Complete.
Question 27.
The figure shows a quadrilateral. Find the perimeter of the quadrilateral.
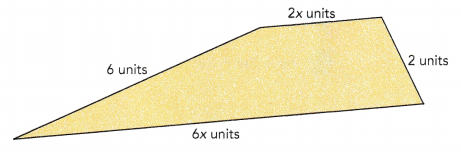
6x + 6 + 2x + 2 = 6x + 2x + 6 + 2
= 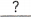 +
+ 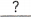
The perimeter of the quadrilateral is 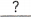 units.
units.
Answer:
8x + 8 units
Explanation:
6x + 6 + 2x + 2
= 6x + 2x + 6 + 2
= 8x + 8 units
The perimeter of the quadrilateral is 8x + 8 units.
Simplify each expression.
Question 28.
4x – 3 + 3x
Answer:
7x – 3
Explanation:
4x – 3 + 3x
= 4x + 3x – 3
= 7x – 3
Question 29.
5y + 4 = 2y
Answer:
3y + 4 =0
Explanation:
5y + 4 = 2y
5y – 2y + 4
3y + 4 = 0
Question 30.
8y – 7 – 4y
Answer:
4y – 7
Explanation:
8y – 7 – 4y
subtract the variables first,
= 4y – 7
Question 31.
7z + 9 – 2z – 2
Answer:
5z + 7
Explanation:
7z + 9 – 2z – 2
Bring all the variables and coefficients to one side.
= 7z – 2z +9 – 2
= 5z + 7
Question 32.
5 + 11 z – 4 + 6z
Answer:
1 + 17z
Explanation:
5 + 11 z – 4 + 6z
Bring all the variables and coefficients to one side.
= 5 – 4 + 11 z + 6z
= 1 + 17z
Question 33.
8g + 10 – 3g + 7
Answer:
5g + 17
Explanation:
8g + 10 – 3g + 7
Bring all the variables and coefficients to one side.
=8g – 3g + 10 + 7
=5g + 17
Question 34.
12 + 6g – 5 – 4g
Answer:
7 – 2g
Explanation:
12 + 6g – 5 – 4g
Bring all the variables and coefficients to one side.
=12 – 5 + 6g – 4g
=7 – 2g
Question 35.
27 + 3r – 9 + 15r
Answer:
18 +18r
Explanation:
27 + 3r – 9 + 15r
Bring all the variables and coefficients to one side.
=27 – 9 +3r + 15r
=18 +18r
Math in Focus Course 1A Practice 7.3 Answer Key
Simplify each expression. Then state the coefficient of the variable in each expression.
Question 1.
u + u + u + u
Answer:
4u
Explanation:
Add all the variable to get the sum
u + u + u + u = 4u
Question 2.
v + v + 5 – 2
Answer:
2v + 3
Explanation:
v + v + 5 – 2
Add all the variable at first,
then subtract the coefficient.
Finally, write an algebraic expression.
= 2v + 5 – 2
= 2v + 3
Question 3.
w + w + w + w + w + w + 15 – 7
Answer:
6w + 8
Explanation:
Add all the variable at first,
then subtract the coefficient.
Finally, write an algebraic expression.
w + w + w + w + w + w + 15 – 7
= 6w + 15 – 7
= 6w + 8
Simplify each expression.
Question 4.
3p + p
Answer:
4p
Explanation:
3p + p
Expand the variables at first, then add.
= p + p + p + p
= 4p
Question 5.
4p + 5p
Answer:
9p
Explanation:
4p + 5p
Expand the variables at first, then add.
p + p + p + p + p + p + p + p + p
= 9p
Question 6.
7p – 2p
Answer:
5p
Explanation:
7p -2 p
Expand the variables at first, then subtract.
= (p + p + p + p + p + p + p) – (p + p)
= 5p
Question 7.
3p – 2p + 5p
Answer:
6p
Explanation:
3p – 2p + 5p
3p – 2p = 1p
1p + 5p = 6p
Question 8.
2p + 3p + 4p + 5p – 6p – 7p
Answer:
p
Explanation:
2p + 3p + 4p + 5p – 6p – 7p
14p – 13p = p
State whether each pair of expressions are equivalent.
Question 9.
5x and x + x + 3x
Answer:
YES, pair of expressions are equivalent.
Explanation:
x + x + 3x = 5x
So, 5x and x + x + 3x are equivalent.
Question 10.
4y + 2y + y and 5y + y
Answer:
NO, pair of expressions are not equivalent.
Explanation:
4y + 2y + y and 5y + y
4y+2y+y = 7y
5y+y=6y
7y is not equal to 6y
Question 11.
2z + 5 and z + 8 + z – 3
Answer:
YES, pair of expressions are equivalent.
Explanation:
2z + 5 and z + 8 + z – 3
2z + 5
z + 8 + z – 3 = 2z+5
both are equal
Question 12.
2w – 5 and 5 – 2w
Answer:
No, pair of expressions are not equivalent.
Explanation:
2w – 5 and 5 – 2w
2w – 5, here coefficient is negative and variable is positive.
-2w + 5, here coefficient is positive and variable is negative.
Question 13.
11u – 4u and 11 – 4 + u
Answer:
No, pair of expressions are not equivalent.
Explanation:
11u – 4u and 11 – 4 + u
11u – 4u = 7u
11 – 4 + 4 = 7 + u
7 + u is not 7u
Question 14.
3v + v and \(\frac{12v}{3}\)
Answer:
Yes, pair of expressions are equivalent.
Explanation:
3v + v and \(\frac{12v}{3}\)
3v + v = 4v
\(\frac{12v}{3}\) = 4v
4v is equal \(\frac{12v}{3}\)
Simplify each expression.
Question 15.
3x + 5 + 4x + 6
Answer:
7x + 11
Explanation:
3x + 5 + 4x + 6
Add all the variables and coefficients.
= 3x + 4x + 5 + 6
= 7x + 11
Question 16.
3x + 2x + 3x + 2
Answer:
8x + 2
Explanation:
3x + 2x + 3x + 2
Add all the variables at first,
= 8x + 2
Question 17.
17 + 4w – 12 – w
Answer:
5 + 3w
Explanation:
17 + 4w – 12 – w
= 17 -12 + 4w – w
= 5 + 3w
Question 18.
9 + 5u + 6u – 7 – 8u + 4
Answer:
6 + 3u
Explanation:
9 + 5u + 6u – 7 – 8u + 4
= 9 – 7 + 4 + 5u + 6u – 8u
= 6 + 3u
Solve.
Question 19.
A book has a length of (b + 2) inches and a width of b inches. Write a simplified expression for the perimeter of the book.

Answer:
4b + 4 inches
Explanation:
A book has a length of (b + 2) inches and a width of b inches.
Perimeter = 2(length + width)
= b + 2 + b + b + 2 + b
Add all the variables and coefficients to write an equation.
= 4b + 4 inches is the perimeter of the book.
Question 20.
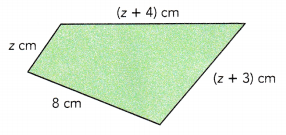
The figure shows a quadrilateral. The length of each side is given as shown. Find the perimeter of the quadrilateral in terms of z.
Answer:
3z + 15 cm
Explanation:
The length of each side is given as shown.
The perimeter of the quadrilateral in terms of z.
p = z + 8 + z + 3 + z + 4
= 3z + 15 cm
Question 21.
Anne is currently h years old. Bill is currently 2h years old and Charles is currently 8 years old. Find an expression for each person’s age after h years. Then find an expression for the sum of their ages after h years.
Answer:
8 + h years
Explanation:
Anne h years
Bill is 2h years
Charles is 8 years
an expression for each person’s age after h years
Anne h + h = 2h years
Bill is 2h + h = 3h years
Charles is 8 + h years
Question 22.
There are 18 boys in a class. There are w fewer boys than girls. How many students are there in the class?
Answer:
36 – w
Explanation:
Boys = 18
Girls = 18 – w
Total number of students = 18 + 18 – w
= 36 – w
Question 23.
A rectangular garden has a length of (y + 2) yards and a width of (4y – 1) yards. Find the perimeter of the garden in terms of y.
Answer:
10y + 2
Explanation:
A rectangular garden has a length of (y + 2) yards and a width of (4y – 1) yards.
The perimeter of the garden in terms of y.
p = y + 2 + 4y – 1 + y + 2 + 4y – 1
p = 10y + 2
the perimeter of the garden in terms of y is = 10y + 2
Question 24.
Kayla had 64b dollars. She gave \(\frac{1}{8}\) of it to Luke and spent $45. How much money did Kayla have left? Express your answer in terms of b.
Answer:
\(\frac{520b -360} {8}\)
Explanation:
Kayla had 64b dollars.
She gave \(\frac{1}{8}\) of it to Luke and spent $45.
64b- \(\frac{1}{8}\) -45
= \(\frac{64b x 8 + 8b -45 x 8} {8}\)
= \(\frac{520b – 360} {8}\)
Question 25.
A rectangle has a length of (2m + 1) units and a width of (10 – m) units. A square has sides of length \(\frac{2 m+1}{2}\) units.
a) Find the perimeter of the rectangle.
Answer:
2m + 22
Explanation:
length of (2m + 1) units and a width of (10 – m) units
the perimeter of the rectangle is
= 2m + 1 + 10 – m + 2m + 1 + 10 – m
= 2m + 22
b) Find the perimeter of the square.
Answer:
4 x \(\frac{2 m+1}{2}\) units
Explanation:
length \(\frac{2 m+1}{2}\) units
Perimeter of a square =4 x \(\frac{2 m+1}{2}\) units
c) Find the sum of the perimeters of the two figures if m = 6.
Answer:
26 units
Explanation:
the perimeters of the two figures if m = 6
Perimeter of a square = 4 x \(\frac{2 m+1}{2}\) units
= 4 x \(\frac{2 x 6+1}{2}\) units
= 4 x \(\frac{13}{2}\) units
= 26 units
the perimeter of the rectangle is = 2m + 22 units
=2 x 9 + 22
= 18 + 22
= 40 units
d) If m – 6, the perimeter of the rectangle is greater than the perimeter of the square. Find how many units greater the rectangle’s perimeter is than the square’s perimeter.
Answer:
40 units
Explanation:
the perimeters of the two figures if m = 6
Perimeter of a square = 26 units
the perimeter of the rectangle is = 40 units
Question 26.
Math Journal Rita simplified the expression 10w – 5w + 2w in this way:
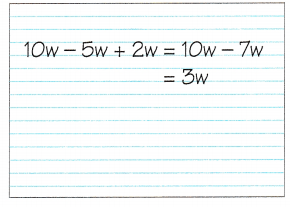
Is Rita’s answer correct? If not, explain why it is incorrect.
Answer:
Is Rita’s answer Wrong
Explanation:
In the above math journal of Rita,
she wrote the express as -5w + 2w = – 7
where as the correct express is 10w – 5w = 5w
5w + 2w = 7w
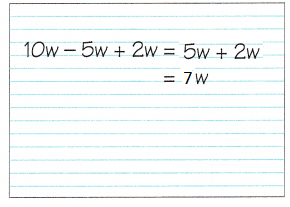
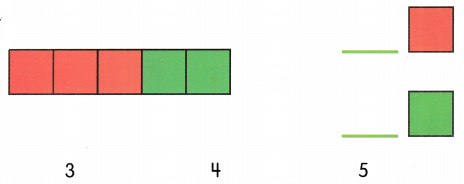
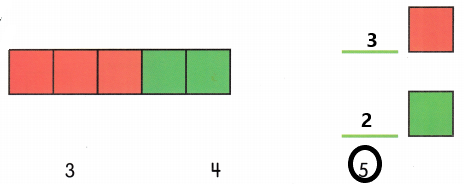
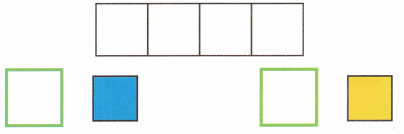
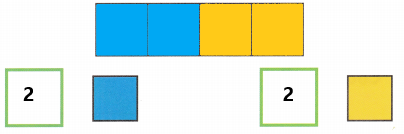


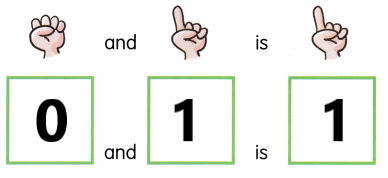
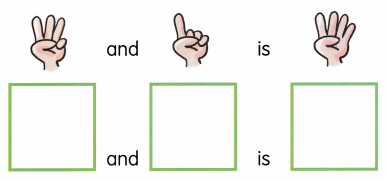
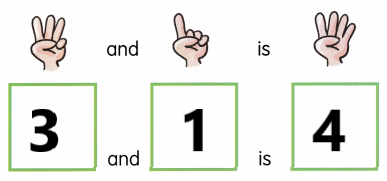
![]() . Count and write.
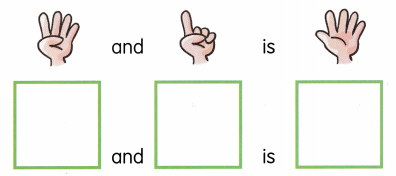
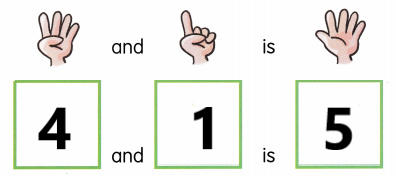
. Count and write.