Hillary

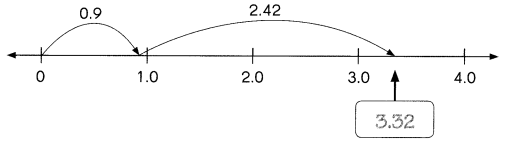
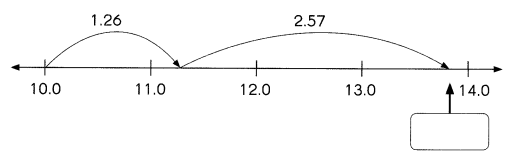
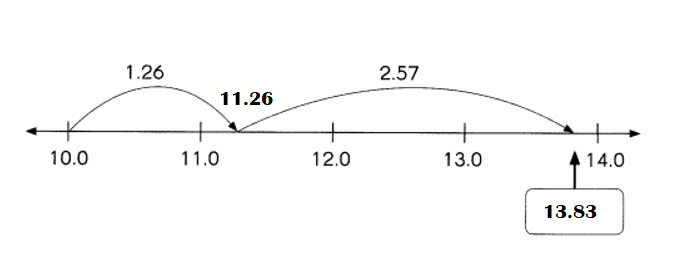
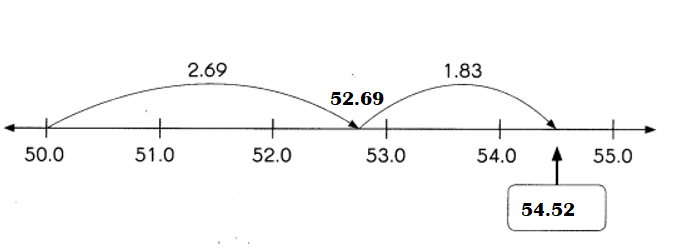
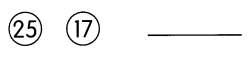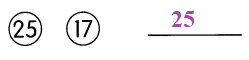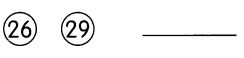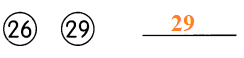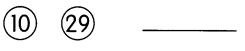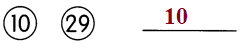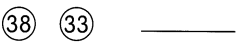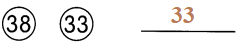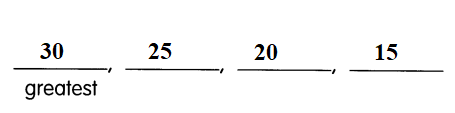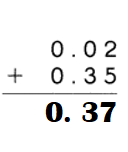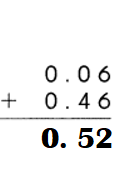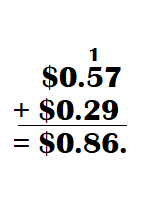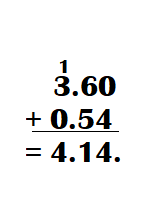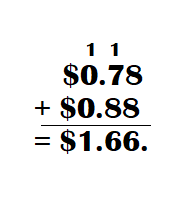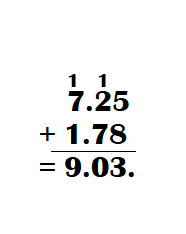This handy Math in Focus Grade 7 Workbook Answer Key Chapter 10 Lesson 10.3 Approximating Probability and Relative Frequency detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Chapter 10 Lesson 10.3 Answer Key Approximating Probability and Relative Frequency

Hands-On Activity

Materials

• a coin

FIND RELATIVE FREQUENCIES OF FLIPPING A COIN

Work in pairs.

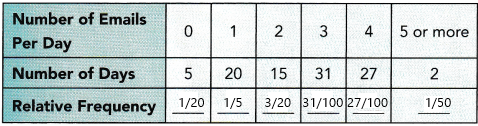
Step 1: Flip a coin 20 times. Record whether it lands heads or tails after each flip. The table below shows that the number of times the coin landed heads and the number of times it landed tails.

The observed frequency is the number of observations of a data value. It refers to how many times a data value appears in the chance process.

Step 2: What is the observed frequency of the coin landing on heads? What is the observed frequency of the coin landing on tails?
The relative frequency of a data value is the ratio of the observed frequency to the total number of observations in a chance process. Relative frequency can be calculated from the observed frequency.

Step 3: What is the relative frequency of the coin landing on heads? What ¡s the relative frequency of the coin landing on tails?

Step 4: What is the sum of the relative frequencies?

Math in Focus Grade 7 Chapter 10 Lesson 10.3 Guided Practice Answer Key

Complete.

Question 1.
The table shows the relative frequencies for three sizes of monitors sold during a sale at a computer store. 640 monitors were sold during the sale.

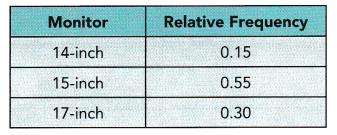
Each relative frequency represents a fraction of the total number of monitors sold. The sum of the relative frequencies is 1. 0.15 + 0.55 + 0.30 = 1
a) How many 17-inch monitors were sold during the sale?
The relative frequency 0.30 means that \(\frac{30}{100}\) of the 640 monitors sold were 17-inch monitors.
• 640 =
Multiply the relative frequency for 17-inch monitors by the total number of monitors sold.
17-inch monitors were sold during the sale.
Answer: 0.30;192
Explanation:
The number of times an event occurs is called a frequency. Relative frequency is an experimental one, but not a theoretical one. Since it is an experimental one, it is possible to obtain different relative frequencies when we repeat the experiments. To calculate the frequency we need
– Frequency count for the total population
– Frequency count for a subgroup of the population
We can find the relative frequency probability in the following way if we know the above two frequencies. The formula for a subgroup is
Relative Frequency = Subgroup Count / Total Count
The relative frequency 0.30 means that \(\frac{30}{100}\) of the 640 monitors sold were 17-inch monitors: 0.30*640=192.
Therefore, 192 17-inch monitors were sold during the sale.

b) How many fewer 14-inch monitors were sold than 15-inch monitors?
• 640 = Find the number of 14-inch monitors.
• 640 = Find the number of 15-inch monitors.
– = Subtract the number of 14-inch monitors from the number of 15-inch monitors.
There are fewer 14-inch monitors sold than 15-inch monitors.
Answer:
The relative frequency of 14-inch monitor=0.15
the relative frequency of a 15-inch monitor=0.55
Now we need to find out the number of monitors that were sold.
The number of 14-inch monitors=0.15*640=96
The number of 15-inch monitors=0.55*640=352
To know the number of fewer 14-inch monitors were sold than 15-inch monitors. We need to subtract.
: 352-96=256
therefore, 256 fewer 14-inch monitors sold than 15-inch monitors.

Copy and complete. Solve.

Question 2.
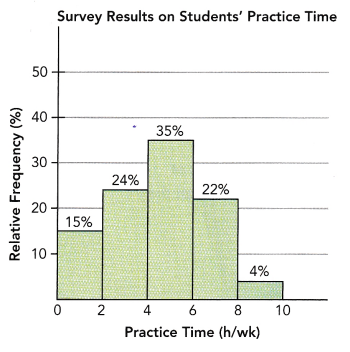
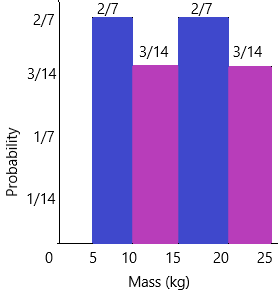
Alexis and Joe caught 40 fish over the weekend. The histogram shows the masses of the fish they caught. On the histogram, the interval 14-16 includes data for fish that have a mass of at least 14 kilograms, but less than 16 kilograms.

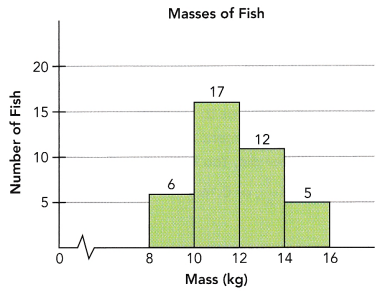
a) Find the relative frequency for fish that have a mass of at least 8 kilograms but less than 10 kilograms. Give your answer as a percent.
There are fish that have a mass of at least 8 kilograms but less than 10 kilograms.
= Write out of 40 fish as a fraction and simplify.
∙ 100% = Multiply by 100%
The relative frequency for fish that have a mass of at least 8 kilograms but less than 10 kilograms is %.
Answer:
According to the above-given histogram:
There are 6 fish that have a mass of at least 8 kilograms but less than 10 kilograms.
Infractions, 6/40 is equal to 3/20.
To convert into percentage multiply by100%
=3/20*100
=15%
Therefore, the relative frequency for fish that have a mass of at least 8 kilograms but less than 10 kilograms is

b) Draw a relative frequency histogram using percent.
∙ 100% =
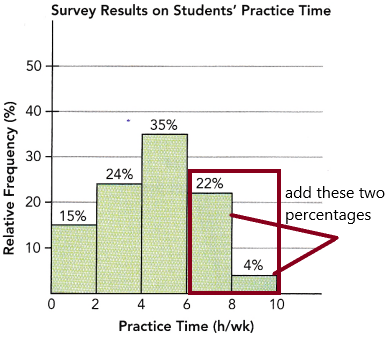
Find the relative frequency of fish that have a mass of at least 10 kilograms but less than 12 kilograms.

∙ 100% =
Find the relative frequency of fish that have a mass of at least 12 kilograms but less than 14 kilograms.

∙ 100% = Find the relative frequency of fish that have a mass of at least 14 kilograms but less than 16 kilograms.

Answer:

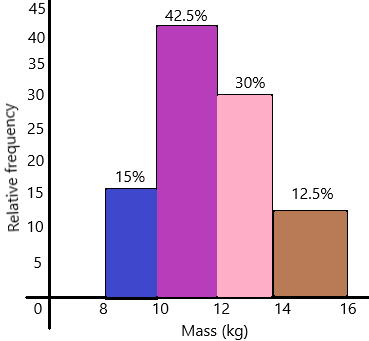
The relative frequency using percentage:
1. 6/40*100=15%
2. The relative frequency of fish that have a mass of at least 10 kilograms but less than 12 kilograms.
: 17/40*100=42.5%
3. The relative frequency of fish that have a mass of at least 12 kilograms but less than 14 kilograms.
: 12/40*100=30%
4. The relative frequency of fish that have a mass of at least 14 kilograms but less than 16 kilograms.
: 5/40*100=12.5%

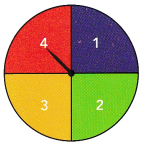
Question 3.
Lucas made a dartboard as shown in the diagram. He threw a dart at the dartboard 100 times. He recorded the number of times the dart landed on each color. The number of times he missed hitting the dartboard was also recorded.

a) Find the relative frequency, expressed as a decimal, for each event.
= Find the relative frequency of landing on red.
= Write the fraction as a decimal.

= Find the relative of landing on yellow.
= Write the fraction as a decimal.

= Find the relative frequency of landing on blue.
= Write the fraction as a decimal.

= Find the relative frequency of misses.
= Write the fraction as a decimal.
Answer:
Formula:
Relative frequency=subgroup count/total count
The relative frequency of landing on red=10/100
Therefore, the relative frequency is 1/10
In decimal, we can write as 0.1
The relative frequency of landing on yellow=35/100
Therefore, the relative frequency is 7/20
In decimal, we can write as 0.35
The relative frequency of landing on blue=48/100
Therefore, the relative frequency is 12/25
In decimal, we can write as 0.48
The relative frequency of misses=7/100
Therefore, the relative frequency is 7/100
In decimal, we can write as 0.07

b) Explain what the relative frequency of the dart landing in the red region means.
The event of landing in the red region has a relative frequency of , which means that the dart landed in the red region about of the time.
Answer:0.1 and 10%
The event of landing in the red region has a relative frequency of 0.1, which means that the dart landed in the red region about of the time.

c) If Lucas throws the dart again, predict in which region the dart is most likely to land.
The dart is most likely to land in the region, because it has the greatest relative frequency of .
Answer: blue, o.48
Explanation:
The relative frequency of red is 0.1
The relative frequency of yellow is 0.35
The relative frequency of blue is 0.48
By comparing all the frequencies, definitely, the dart is most likely to land in the blue region because it has the highest relative frequency of 0.48.

Hands-On Activity

Materials:

• 10 counters (5 red,
• 3 blue, and 2 green)
• a paper bag

Work in pairs.

Step 1: Place the 10 counters into the bag. Shake the bag to mix the counters. Without looking into the bag, select a counter randomly. Record its color in a tally chart, and then put the counter back in the bag. Repeat this procedure 20 times.

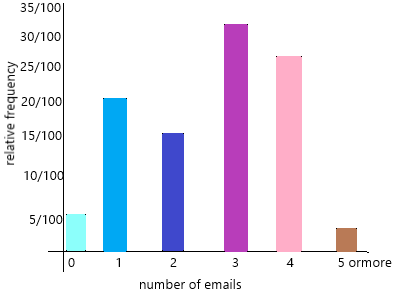
Step 2: Combine your group’s data from Step 1 with data from other groups. Use the class data to make a relative frequency table like the one shown below.

Step 3: Find the theoretical probabilities for the colors. Copy and complete the table below.

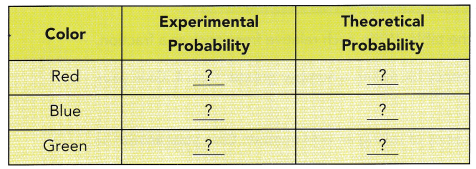
Step 4: Compare the experimental and the theoretical probabilities for each color. What do you observe?

Math in Focus Course 2B Practice 10.3 Answer Key

Solve.

Question 1.
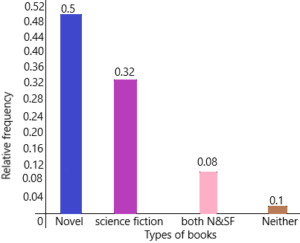
A library conducted a survey on 2,000 library users about the types of books they usually borrow. The table shows the relative frequencies of the types of books borrowed.

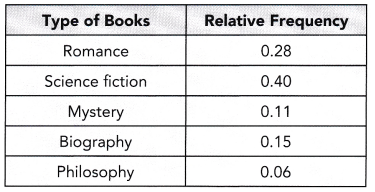
a) How many library users borrowed biography titles?
Answer:
Relative frequency=observed frequency of data value/total number of observations
Here we know the relative frequency and observed frequency data.
Number of library users borrowed biography tiles=X
this can be write as:
0.15=2000/X
Send ‘X’ on the left side and bring relative frequency to the right side.
X=2000*0.15
X=300
therefore, 300 biography titles were borrowed.

b) What percent of the library users borrowed mystery titles?
Answer:
The relative frequency of mystery tiles=0.11
The observed frequency data=2000
The per cent of the library users borrowed mystery tiles=Y
Relative frequency=observed frequency of data value/total number of observations
Y=0.11*100
Y=11%

c) What percent of the library users borrowed romance or science fiction titles?
Answer:
the relative frequency of romance=0.28
the relative frequency of science fiction titles=0.40
The percent of the library users borrowed romance or science fiction titles=Z
Z=0.28+0.40
Z=0.68
This we can write in percentages by multiplying 100
Z=0.68*100
Z=68%
therefore, 68% of the library users borrowed romance and science fiction titles.

Question 2.
A coin is tossed 66 times and lands on heads 36 times.
a) Find the relative frequency of the coin landing on heads.
Answer:
Formula:
Relative frequency=observed frequency of data value/total number of observations
The total number of observations=66
Observed frequency=36
Relative frequency=X
According to the formula, substitute the above-given values:
X=36/66
X=6/11
In decimal, we can write as 0.54

b) Find the relative frequency of the coin landing on tails.
Answer:
Relative frequency=observed frequency of data value/total number of observations
The total number of observations=66
Observed frequency for the coin landing on head=36
Observed frequency for the coin landing on tail=66-36=30
Relative frequency of the coin landing on tails=Y
Y=30/66
Y=5/11
In decimal, we can write as 0.45

Question 3.
A number die is rolled 50 times. After each roll, the result is recorded. The table gives the observed frequency for each number on the die.

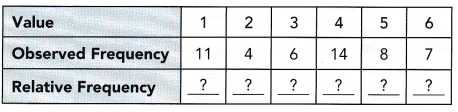
a) Copy and complete the table. Write each relative frequency as a fraction.
Answer:
The total frequency=50
The observed frequencies are 11, 4, 6, 14, 8, 7
Now we have to find relative frequency:
Relative frequency=observed frequency of data value/total number of observations
The relative frequency of value 1 = 11/50
The relative frequency of value 2 = 4/50=2/25
The relative frequency of value 3 = 6/50=3/25
The relative frequency of value 4 = 14/50=7/25
The relative frequency of value 5 = 8/50=4/25
The relative frequency of value 6 = 7/50

b) Find the relative frequency for rolling a number greater than 4. Give your answer as a fraction.
Answer:3/10
Explanation:
The dice greater than 4 is 5 and 6
The observed frequency of 5 is 8
The observed frequency of 6 is 7
Now add these two frequencies
8+7=15
Relative frequency=observed frequency of data value/total number of observations
Relative frequency=15/50
Relative frequency=3/10
Therefore, 3/10 is the relative frequency for rolling a number greater than 4.

c) Find the relative frequency of rolling an odd number. Give your answer as a fraction.
Answer:1/2
Explanation:
– We will write the probability of rolling an odd number on dice as a fraction.
– The odd numbers are 1, 3, and 5
– This is 3 of the 6 sides of the dice
– The probability of rolling an odd number on a dice is 3/6
– 3/6 is the same as the 1/2
– you can expect an odd number to be rolled half of the time.
The observed frequency of 1 is 11
The observed frequency of 3 is 6
The observed frequency of 5 is 8
Now add these three frequencies
11+6+8=25
Relative frequency=observed frequency of data value/total number of observations
Relative frequency=25/50
Relative frequency=1/2

Question 4.
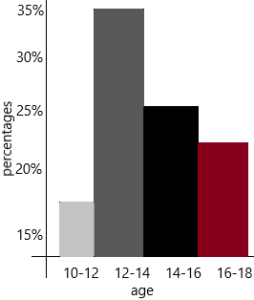
The ice hockey team Blue Thunder played 25 times during the winter season. The team had 14 wins, 8 losses, and 3 ties.

a) Find the relative frequency for each of the following: wins, losses, ties. Give your answers as percents.
Answer:
The number of wins a team had=14
Relative frequency of wins=14/25
In percentage, we can write as:14/25*100=56%
The number of losses a team had=8
Relative frequency of losses=8/25
In percentage, we can write as:8/25*100=32%
The number of ties a team had=3
Relative frequency of losses=3/25
In percentage, we can write as:3/25*100=12%

b) Draw a relative frequency bar graph that uses percents.
Answer:

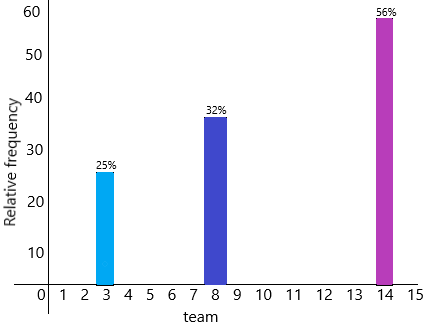
c) What percent of the total number of games ended in a loss or a tie?
Answer:
The number of losses a team had=8
Relative frequency of losses=8/25
In percentage, we can write as:8/25*100=32%
The number of ties a team had=3
Relative frequency of losses=3/25
In percentage, we can write as:3/25*100=12%

Question 5.
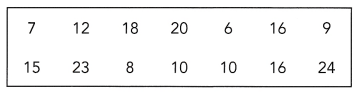
You are given a deck of 52 cards showing scenes of the four seasons of the year. There are 13 cards for each season. You randomly select a card from the deck 100 times. After each selection, you record the season shown on the card and replace it in the deck for the next selection. The results are given in the table below.

a) Find the relative frequency of the appearance of each season.
Answer:
The total number of observations=100
The observed frequencies=23, 34, 19, 24
Relative frequency=observed frequency of data value/total number of observations
The relative frequency of the spring=23/100
The relative frequency of the summer=34/100=17/50
The relative frequency of the fall=19/100
The relative frequency of the winter=24/100=6/25

b) What is the experimental probability of selecting a card with a summer scene?
Answer:
Experimental probability: Experimental probability, also known as Empirical probability, is based on actual experiments and adequate recordings of the happening of events. To determine the occurrence of any event, a series of actual experiments are conducted. Experiments that do not have a fixed result are known as random experiments. The outcome of such experiments is uncertain. Random experiments are repeated multiple times to determine their likelihood. An experiment is repeated a fixed number of times and each repetition is known as a trial. Mathematically, the formula for the experimental probability is defined by;
Probability of an Event P(E) = Number of times an event occurs / Total number of trials.
The observed frequency of the summer=34
According to the above definition:
P(E)=34/100
p(E)=17/50

c) What is the theoretical probability of selecting a card with a summer scene?
Answer:
In probability, the theoretical probability is used to find the probability of an event. Theoretical probability does not require any experiments to conduct. Instead of that, we should know about the situation to find the probability of an event occurring. Mathematically, the theoretical probability is described as the number of favourable outcomes divided by the number of possible outcomes.
Probability of Event P(E) = No. of. Favourable outcomes/ No. of. Possible outcomes.
N0.of favourable outcomes of summer=1
No.of possible outcomes=4 (4 seasons)
P(E)=1/4

d) Math journal The experimental and the theoretical probabilities J of selecting a card with a summer scene are not equal. Describe some
factors that cause the two probabilities to be different.
Answer:
Some possible factors are as follows: The cards may not be well-shuffled; different people choose a card in different ways. How the cards are placed may make a difference; The theoretical probability may have assumptions that cannot be achieved from experiments.

e) Suppose that the spring and summer cards have a red background and the fall and winter cards have a black background. What is the experimental probability of selecting a card with a black background?
Answer:43/100
The total number of observations=100
The observed frequencies=23, 34, 19, 24
Relative frequency=observed frequency of data value/total number of observations
The relative frequency of the spring=23/100
The relative frequency of the summer=34/100=17/50
The relative frequency of the fall=19/100
The relative frequency of the winter=24/100=6/25
Experimental probability:
Probability of an Event P(E) = Number of times an event occurs / Total number of trials.
Now add the fall and winter cards:
Calculation:

100 is the least common multiple of denominators 100 and 25. Use it to convert to equivalent fractions with this common denominator.
Therefore, the experimental probability of selecting a card with a black background is 43/100.

f) What is the theoretical probability of selecting a card with a red background?
Answer:1/2
In the above question given that the spring and summer cards have a red background. According to that we need to calculate the probability.
In probability, the theoretical probability is used to find the probability of an event. Theoretical probability does not require any experiments to conduct. Instead of that, we should know about the situation to find the probability of an event occurring. Mathematically, the theoretical probability is described as the number of favourable outcomes divided by the number of possible outcomes.
Probability of Event P(E) = No. of. Favourable outcomes/ No. of. Possible outcomes.
The number of favourable outcomes=1
the number of possible outcomes=2
P(E)=1/2

Question 6.
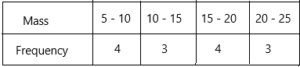
A group of researchers catch and measure the length offish before releasing them back to a river. The lengths of the 50 fish are categorized in the table below.

a) Find the relative frequency of each category of fish.
Answer:
The total number of observations=50
The observed frequencies=16, 23, 11
Relative frequency=observed frequency of data value/total number of observations
The relative frequency of length of the fish (L<7)=16/50=8/25
The relative frequency of length of the fish 7less than or equal to L < 14=23/50
The relative frequency of length of the fish 14 less than or equal to L < 21=11/50

b) If the researchers catch and measure one more fish, what is the probability of catching a fish that is less than 7 inches long?
Answer:
The probability of catching fish is less than 7 and the possible outcomes are 1, 2, 3, 4, 5, 6
P(E)=N(P)/N(T)
P(E)=5/50
P(E)=1/10
Therefore, the probability of catching a fish that is less than 7 inches long is 1/10.

c) What is the probability that the next fish caught will be at least 7 inches long?
Answer:
The probability of catching fish is less than 7 and the possible outcomes are 1, 2, 3, 4, 5, 6,7
P(E)=N(P)/N(T)
P(E)=7/50
Therefore, the probability of catching a fish that is less than 7 inches long is 7/10.

d) Draw a relative frequency histogram using percent.
Answer:
The total number of observations=50
The observed frequencies=16, 23, 11
Relative frequency=observed frequency of data value/total number of observations
The relative frequency of length of the fish (L<7)=16/50=8/25
In percentages, we can write 8/25*100=8%
The relative frequency of length of the fish 7less than or equal to L < 14=23/50
In percentages, we can write 23/50*100=11.5%
The relative frequency of length of the fish 14 less than or equal to L < 21=11/50
In percentages, we can write 11/50*100=5.5%

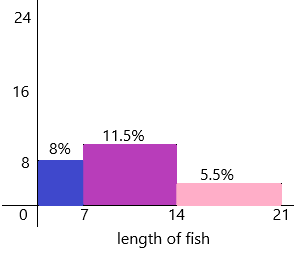
Question 7.
A car dealership has sold 75 new cars this year. The histogram below shows frequencies for cars sold in different price ranges.

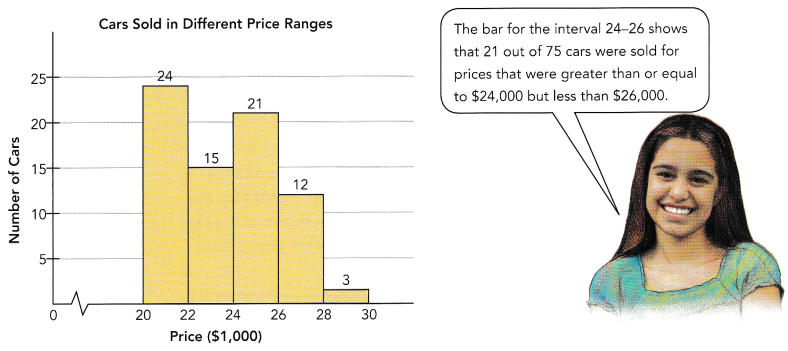
a) Find the relative frequency of the cars sold in the price range of $26,000 to $28,000. Give your answer as a percent.
Answer:
The total number of observations=75
The observed frequencies=24, 15, 21, 12, 3
Relative frequency=observed frequency of data value/total number of observations
Relative frequency=12/75=0.16
In percentages, we can write 0.16*100=16%
Therefore, the relative frequency of the cars sold in the price range of $26,000 to $28,000 is 16%.

b) Find the relative frequency of the cars sold in the price range of $20,000 to $24,000. Give your answer as a percent.
Answer:
The total number of observations=75
The observed frequencies=24, 15, 21, 12, 3
Relative frequency=observed frequency of data value/total number of observations
The relative frequency of the cars sold in the price range of $20,000 to $24,000=X
X=24+15/75
X=39/75
X=0.52
In percentages, we can write 0.52*100=52%

c) What is the probability that the next car will be sold in the price range of $28,000 to $30,000?
Answer:
the probability of the next car will be sold in the price range of $28,000 to $30,000=3/75=0.04
In percentages, we can write 0.04*100=4%.

Question 8.
A light bulb manufacturer estimates that 10% of a shipment of 600 bulbs will have a lifespan greater than or equal to 1,000 hours, but less than 2,000 hours. The manufacturer also estimates that 240 of the bulbs will have a lifespan greater than or equal to 2,000 hours, but less than 3,000 hours, and that the remaining light bulbs will have a lifespan greater than or equal to 3,000 hours, but less than 4,000 hours.
a) Copy and complete the table below.

Answer:

Explanation:
The number of bulbs will have a lifespan greater than or equal to 1,000 hours, but less than 2,000 hours
:10% of 600=60 bulbs
10*600/100=60 bulbs.
So I had written 60 in the first box.
Already given 240 bulbs are given for second box.
The remaining boxes =X
X=240+60=300
Now subtract the total bulbs and the life span of the present boxes.
X=600-300
X=300
The remaining bulbs are 300.

b) Draw a frequency histogram for the three lifespans shown in the table.
Answer:

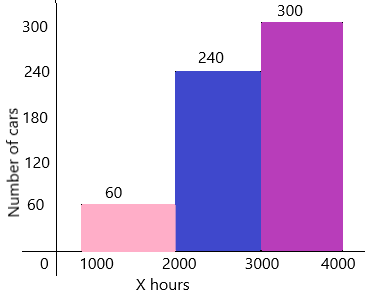
A histogram is a graphical representation of a grouped frequency distribution with continuous classes. It is an area diagram and can be defined as a set of rectangles with bases along with the intervals between class boundaries and with areas proportional to frequencies in the corresponding classes. In such representations, all the rectangles are adjacent since the base covers the intervals between class boundaries. The heights of rectangles are proportional to corresponding frequencies of similar classes and for different classes, the heights will be proportional to corresponding frequency densities.
In other words, a histogram is a diagram involving rectangles whose area is proportional to the frequency of a variable and width is equal to the class interval.

c) Find the relative frequency for the bulbs with each of the lifespans. Then draw a relative frequency histogram using percents.
Answer:
The total frequency=100
The observations are=60,240,300
The relative frequency of bulbs will have a lifespan greater than or equal to 1,000 hours, but less than 2,000 hours=60/600=0.6
In percentages, we can write 0.6*100=60%
The relative frequency of the bulbs will have a lifespan greater than or equal to 2,000 hours, but less than 3,000 hours=240/600=0.4
In percentages, we can write 0.4*100=40%
The relative frequency of the bulbs will have a lifespan greater than or equal to 3,000 hours, but less than 4,000 hours=300/600=0.5
In percentages, we can write 0.5*100=50%

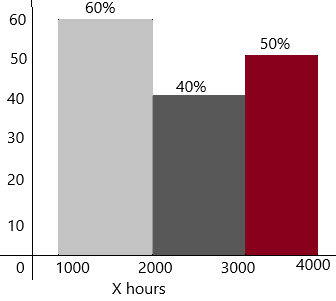
d) If you buy a light bulb from this shipment, what do you predict is the most likely lifespan of your light bulb? Explain your answer using experimental probability.
Answer:
First, compare the life span of the bulbs:
The bulbs will have a lifespan greater than or equal to 1,000 hours, but less than 2,000 hours=60
The bulbs will have a lifespan greater than or equal to 2,000 hours, but less than 3,000 hours=240
The bulbs will have a lifespan greater than or equal to 3,000 hours, but less than 4,000 hours=300
The highest lifespan is 300 so definitely, everyone will predict that it will be the most likely one.
Experimental probability: Experimental probability, also known as Empirical probability, is based on actual experiments and adequate recordings of the happening of events. To determine the occurrence of any event, a series of actual experiments are conducted. Experiments that do not have a fixed result are known as random experiments. The outcome of such experiments is uncertain. Random experiments are repeated multiple times to determine their likelihood. An experiment is repeated a fixed number of times and each repetition is known as a trial. Mathematically, the formula for the experimental probability is defined by;
Probability of an Event P(E) = Number of times an event occurs / Total number of trials.
P(E)=300/600
P(E)=1/2.

This handy Math in Focus Grade 7 Workbook Answer Key Chapter 10 Review Test detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Chapter 10 Review Test Answer Key

Concepts and Skills

Solve.

Question 1.
You select a card at random from 50 cards numbered from 1 to 50. What are the possible outcomes for the event of choosing a number that is a multiple of 6?
Answer:
The numbers are:1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50.
This formula is the number of favourable outcomes to the total number of all the possible outcomes that we have already decided in the Sample Space.
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
The total number of outcomes=50
The possible outcomes are 6, 12, 18, 24, 30, 36, 42, 48.
the event is choosing a number that is multiple of 6.
the numbers which are multiple of 6 are 6, 12, 18, 24, 30, 36, 42, 48.

Question 2.
Three fair coins are tossed together once. List the outcomes that are favorable for the event of only two of the coins landing on heads.
Answer:
When 3 coins are tossed, the possible outcomes are HHH, TTT, HTT, THT, TTH, THH, HTH, HHT.
The sample space is S = { HHH, TTT, HTT, THT, TTH, THH, HTH, HHT}
Number of elements in sample space, n(S) = 8
Let E₂ denotes the event of getting two heads.
E₂ = {HHT, HTH, THH}
n(E₂) = 3
P(getting two heads) = n(E₂)/ n(S)
= 3/8
Hence the required probability is 3/8.

Question 3.
Daniel wants to write all the 2-digit numbers with no repeating digits that can be formed using the digits 5, 6, and 7.
a) List all the possible outcomes.
Answer:
The above-given numbers are 5, 6, and 7
The possible numbers will come without repeating digits that can be formed 2-digit numbers=56, 57, 65, 67, 75, 76

b) X is the event that the 2-digit number is divisible by 5. How many of the outcomes are favorable to event X?
Answer: 2 outcomes.
Explanation:
The possible outcomes we got in the above question=56, 57, 65, 67, 75, 76
Event X is the numbers divisible by 5.
The favourable outcomes we need to find.
5*12=65
5*15=75
E(X)=65, 75
Therefore, the number of outcomes is 2

Question 4.
Amy writes a computer program that will choose two letters from her own name to make a two-letter “string.” The order of the letters matters. For example, AM and MA are different strings.
a) List all the possible outcomes for forming a two-letter string.
Answer:
The above-given name: Amy
If we choose the letters A and Y then the possible outcomes for forming a two-letter string are:
AY and YA.

b) What is the probability that Amy forms a two-letter string with the letter M in it?
Answer:
The above-given name: Amy
Now letter M is given
This formula is the number of favourable outcomes to the total number of all the possible outcomes that we have already decided in the Sample Space.
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
The outcomes are 2 [AM, MY]
The total number of letters in the name=3
P(A)=2/3
therefore, the probability is 2/3.

Question 5.
Two-digit numbers are formed using digits 2, 3, and 4, with no repeating digits.
a) List all the possible outcomes.
Answer:
The above-given numbers are 2, 3, and 4
The possible numbers will come without repeating digits that can be formed 2-digit numbers=23, 24, 32, 34, 42, 43

b) What is the probability of forming a number greater than 32?
Answer:
This formula is the number of favourable outcomes to the total number of all the possible outcomes that we have already decided in the Sample Space.
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
The numbers we formed using the 2, 3, and 4 are 23, 24, 32, 34, 42, 43
The numbers greater than 32 are 34, 42, 43
the possible outcomes are 3
The total number of outcomes=6
P(greater than 32)=3/6
P(greater than 32)=1/2=0.5
therefore, the probability is 0.5 or 1/2.

Question 6.
Tim has three DVDs. One is a science fiction movie, one is an action movie, and the other is a documentary. If he stacks the DVDs randomly, what is the probability that the science fiction movie is on top, the action movie is in the middle, and the documentary is on the bottom?
Answer:1/3
The above-given data:
The DVDs Tim has science fiction movies, action movies, documentaries.
If he kept randomly on the shelves then the probability of the DVDs keeping in a given order.
This formula is the number of favourable outcomes to the total number of all the possible outcomes that we have already decided in the Sample Space.
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
the total number of DVDs=3
The possible number of outcomes keeping in the DVDs=1
P(science fiction)=1/3
P(action movie)=1/3
P(documentaries)=1/3

Question 7.
A ribbon is selected at random out of a total of 4 orange ribbons, 5 yellow ribbons, and 3 red ribbons. What is the probability of selecting an orange ribbon?
Answer:
The total ribbons=12
This formula is the number of favourable outcomes to the total number of all the possible outcomes that we have already decided in the Sample Space.
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
The possible outcomes of orange ribbons=4
P(orange ribbons)=4/12
P(orange ribbons)=1/3
Therefore, the probability of orange ribbons=1/3.

Question 8.
Use the spinner shown.

a) What is the probability of landing on an even number?
Answer:1/2
The above-given numbers 1, 2, 3, and 4
the even numbers are 2 and 4
the possibilities are 2
the total number of outcomes=4
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
P(even number)=2/4
P(even number)=1/2
therefore, the probability of landing an even number is 1/2 or 0.5

b) What is the probability of landing on a number less than 4?
Answer:
The above-given numbers 1, 2, 3, and 4
the numbers less than 4 are 1, 2, 3
the possibilities are 3
the total number of outcomes=4
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
P(less than 4)=3/4
therefore, the probability is 3/4.

Problem Solving

Solve.

Question 9.
Olivia and Jackie played a game with the spinner shown.

Olivia spun a 2 on 12 spins out of 50, while Jackie spun a 2 on 19 spins out of 100.
a) Find each person’s experimental probability of spinning a 2. Express your answers as decimals.
Answer:0.24; 0.19
explanation:
The above-given data
Olivia spun 12 spins on 2 out of 50.
While Jackie spun 19 spins on 2 out of 2
Experimental Probability is the probability of an event based on exact recordings or experiments of an event. The calculation is done by dividing the number of times an event occurred by the total number of trials in an experiment. We can express experimental probability mathematically as,
Experimental Probability = Number of times a particular event occurs/ Number of total trials)
The number of times a particular event occurs for Olivia=12
The number of times a particular event occurs for Jackie=19
The total number of spins of Olivia=50
the total number of spins of Jackie=100
P(Olivia)=12/50
P(Olivia)=6/25
P(Olivia)=0.24
P(Jackie)=19/100
P(Jackie)=0.19

b) Suppose the spinner is fair, meaning that it is equally likely to land on any of the numbers. What is the theoretical probability of spinning a 2?
Answer:1/6
Theoretical Probability describes the probability of the happening of certain events that are not in an experimental way of an occurrence. An example of this is drawing a red stone out of a bag etc. We can express theoretical probability mathematically as,
theoretical Probability = Total number of desired outcomes/ Total number of outcomes
Total number of the desired outcomes=1
Total number of outcomes=6
Theoretical probability=1/6
therefore, the probability of spinning 2 is 1/6.

c) Assuming the spinner is fair, what do you predict will happen to the experimental probability of getting a 2 if the spinner is spun 500 times?
Answer:
It is closer to the theoretical probability.
Theoretical Probability describes the probability of the happening of certain events that are not in an experimental way of an occurrence. An example of this is drawing a red stone out of a bag etc. We can express theoretical probability mathematically as,
theoretical Probability = Total number of desired outcomes/ Total number of outcomes.

Question 10.
A red number die and a green number die each have faces labeled 1 to 6. Suppose you roll the number dice and record the values for each die as an ordered pair of numbers: (red value, green value). The event E is the event of getting a pair of values in which the number on the green die is greater than the number on the red die.
a) Find all the outcomes favorable to event E.
Answer:
The numbers are on the green die=1, 2, 3, 4, 5, 6
The numbers are on the red die=1, 2, 3, 4, 5, 6
The possible outcomes are:
{ (2, 1) (3, 2) (3, 1) (4, 1) (4, 2) (4, 3) (5, 1) (5, 2) (5, 3) (5, 4) (6, 1) (6, 2) (6, 3) (6, 4) (6, 50)}

b) Find P(E).
Answer:
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
The event E is the event of getting a pair of values in which the number on the green die is greater than the number on the red die.
the number of favourable outcomes=5 (2, 3, 4, 5, 6)
The total number of possible outcomes=15
{ (2, 1) (3, 2) (3, 1) (4, 1) (4, 2) (4, 3) (5, 1) (5, 2) (5, 3) (5, 4) (6, 1) (6, 2) (6, 3) (6, 4) (6, 50)}
P(E)=5/15
P(E)=1/3
In decimals, we can write as 0.3
Therefore, the probability is 0.3 or 1/3.

Question 11.
Two fair counters are tossed together. One of the counters is white on one side and black on the other side, the other counter is white on one side, and red on the other side. They are tossed together and the face up colors of the two counters are noted. Let F be the event that red and black appear, and F be the event that at least one is white.
a) Define the sample space of the experiment.
Answer:
A sample space is a collection of a set of possible outcomes of a random experiment. The sample space is represented using the symbol, “S”. The subset of possible outcomes of an experiment is called events. A sample space may contain a number of outcomes that depends on the experiment. If it contains a finite number of outcomes, then it is known as discrete or finite sample spaces.
The samples spaces for a random experiment is written within curly braces “ { } “. There is a difference between the sample space and the events. For rolling a die, we will get the sample space, S as {1, 2, 3, 4, 5, 6 } whereas the event can be written as {1, 3, 5 } which represents the set of odd numbers and { 2, 4, 6 } which represents the set of even numbers. The outcomes of an experiment are random and the sample space becomes the universal set for some particular experiments.
Let W, B and R represent white, black and red respectively.
the sample space is {WW, WR, BW, BR}.

b) Calculate the probability of each outcome.
Answer:1/4
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
Total number of possible outcomes=4
The number of a favourable outcomes for red=1
The number of a favourable outcome for black=1
The number of a favourable outcome for white=1
P(red)=1/4
P(black)=1/4
P(white)=1/4

c) Construct the probability distribution table. Is it a uniform probability model?
Answer:
A probability distribution table is a table that displays the probability that a random variable takes on certain values.

Uniform in Probability. A discrete uniform probability distribution is one in which all elementary events in the sample space have an equal opportunity of occurring. As a result, for a finite sample space of size n, the probability of an elementary event occurring is 1/ n.
yes, all the outcomes have an equal probability of occurring.

d) Draw a Venn diagram for events E and F. Are they mutually exclusive?
Answer:
A diagram is used to represent all possible relations of different sets. A Venn diagram can be represented by any closed figure, whether it be a Circle or a Polygon (square, hexagon, etc.). But usually, we use circles to represent each set.

In probability theory, two events are said to be mutually exclusive if they cannot occur at the same time or simultaneously. In other words, mutually exclusive events are called disjoint events. If two events are considered disjoint events, then the probability of both events occurring at the same time will be zero.
Probability of Disjoint (or) Mutually Exclusive Event = P ( A and B) = 0
According to the above definition:
Yes, the events are mutually exclusive.

e) Calculate P(E) and P(F).
Answer:
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
The number of favourable outcomes of event E=1
The total number of possible outcomes=4
P(E)=1/4
The number of favourable outcomes of event F=1
P(F)=3/4

Question 12.
Joan keeps track of the number of emails she receives each day for 100 days. She then makes a table showing how many days she received 0 emails, 1 email, 2 emails, and so on, as shown in the table.

a) Copy and complete the table above by finding each relative frequency.
Answer:
The number of times an event occurs is called a frequency. The number of times an event occurs is called a frequency. Relative frequency is an experimental one, but not a theoretical one. Since it is an experimental one, it is possible to obtain different relative frequencies when we repeat the experiments. To calculate the frequency we need
– Frequency count for the total population
– Frequency count for a subgroup of the population
We can find the relative frequency probability in the following way if we know the above two frequencies. The formula for a subgroup is;
Relative Frequency = Subgroup Count / Total Count

The relative frequency of the number of days(5)=5/100=1/20
The relative frequency of the number of days(20)=20/100=1/5
The relative frequency of the number of days(15)=15/100=3/20
The relative frequency of the number of days(31)=31/100
The relative frequency of the number of days(27)=27/100
The relative frequency of the number of days(22)=2/100=1/50

b) Present the relative frequencies in a bar graph.
Answer:
Relative Frequency Graph Maker A relative frequency graph shows the relative frequencies corresponding to the values in a sample, with respect to the total sample data.

Question 13.
At a music school, 400 students were given a survey on the number of hours they practice each week. The results of this survey are shown in the relative frequency histogram.

a) How many students practiced at least 2 hours but less than 4 hours per week?
Answer: 96
Explanation:
The above-given question:
The total number of students was given a survey on the number of hours they practise each week=400
The number of students practised at least 2 hours but less than 4 hours per week=X
at least 2 means 2 or more than 2.
The percentage of students practised at least 2 hours but less than 4 hours per week=24%
By using the given data we need to calculate the number of students practised between the given time in the question
X=24*400/100
X=96.
Therefore, the number of students practised at least 2 hours but less than 4 hours per week is 96.

b) One of the students is selected at random. What is the probability that this student has practiced 6 or more hours per week?
Answer:0.26 or 13/50
Explanation:
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.

The probability that this student has practised 6 or more hours per week=P(A)
The total number of students (total possible outcomes)=n(S)=400
The number of favourable outcomes(6 0r more)=22%+4%=26%
26% of 400
=26*400/100
=104
P(A)=104/400
P(A)=13/50
In decimals, we can write as 0.26
Therefore, the probability is 0.26 or 13/50

Question 14.
Fifty students at a school kept track of how many books they read last semester. Each student wrote the number of books he or she read in a table provided by the school librarian.

a) Copy and complete the frequency table.

Answer:
Frequency table: Frequency means the number of times a value appears in the data. A table can quickly show us how many times each value appears. If the data has many different values, it is easier to use intervals of values to present them in a table.

b) Copy and complete the probability distribution table below.

Answer:
A probability distribution table is a table that displays the probability that a random variable takes on certain values.

The probability of students read books 0-5=15/50=0.3
The probability of students read books 6-10=15/50=0.3
The probability of students reading books 11-15=8/50=0.16
The probability of students reading books 16-20=6/50=0.12
The probability of students reading books 21-25=3/50=0.06
The probability of students reading books 21-25=3/50=0.06

c) Suppose the librarian selects one of the students at random. What is the probability that the student has read at least 6 books but not more than 15 books?
Answer:23/50 or 0.46
Explanation:
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
the probability that the student has read at least 6 books but not more than 15 books=P(A)
The number of outcomes (6-15)=15+8=23=n(E)
the total number of students=50=n(S)
P(A)=23/50
In decimals, we can write as 0.46

d) What per cent of the students had read 10 or fewer books?
Answer: 30%
The above-given question:
The per cent of the students had read 10 or fewer books=X
10 or fewer means 10 and 10 below books.
Now observe the frequency table above:
0-10 there are total 30 books (15+15)
Now calculate the percentage.
X=15/50*100
X=3/10*100
X=30%
therefore, 30% of the students had read 10 or fewer books.

e) Present the probability distribution in a bar graph.
Answer:
Probability distribution yields the possible outcomes for any random event. It is also defined based on the underlying sample space as a set of possible outcomes of any random experiment. These settings could be a set of real numbers or a set of vectors or a set of any entities. It is a part of probability and statistics.

This handy Math in Focus Grade 7 Workbook Answer Key Cumulative Review Chapters 9-10 detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Cumulative Review Chapters 9-10 Answer Key

Concepts and Skills

Find the range, the three quartiles, and the interquartile range. (Lesson 9.1)

Question 1.
32, 65, 90, 25, 46, 81, 30, 57, 85, 104, 33, 48
Answer:
To calculate range follow the below steps:
1. List the elements of your data set.
2. Identify the highest and lowest numbers in the set.
3. Subtract the smallest number in your data set from the largest number.
4. Label the range clearly.
In the given set the highest number is 104
the lowest number is 25
Now subtract highest number-lowest number
104-25=79
therefore, the range is 79.
The three quartiles:
1. Order your data set from lowest to highest values
2. Find the median. This is the second quartile Q₂.
3. At Q₂ split the ordered data set into two halves.
4. The lower quartile Q₁ is the median of the lower half of the data.
5. The upper quartile Q₃ is the median of the upper half of the data.
the given data: 32, 65, 90, 25, 46, 81, 30, 57, 85, 104, 33, 48
write in ascending order:
25, 30, 32, 33, 46, 48, 57, 65, 81, 85, 90, 104
Now finding the median:
Q2=46, 48, 57, 65
Now add the middle values and divide by 2.
Q2=48+57/2
Q2=105/2
Q2=52.5
Now, look at the bottom half of the data. The median of this half is found between the second and fifth values:
25, 30, 32, 33, 46, 48
Thus the first quartile is found to equal Q₁ = (32 +33)/2
Q1=65/2
Q1=32.5
To find the third quartile, look at the top half of the original data set. We need to find the median of:
57, 65, 81, 85, 90, 104
Here the median is (81 + 85)/2 = 83. Thus the third quartile Q₃ = 83.
Interquartile range=Q3-Q1
Interquartile range=83-32.5
Interquartile range=50.5

Question 2.
12.6, 13.0, 15.5, 18.6, 14.4, 12.0, 11.0, 11.0, 15.6, 15.9
Answer:
11.0, 11.0, 12.0, 12.6, 13.0, 14.4, 15.5, 15.6, 15.9, 18.6
To calculate range follow the below steps:
1. List the elements of your data set.
2. Identify the highest and lowest numbers in the set.
3. Subtract the smallest number in your data set from the largest number.
4. Label the range clearly.
In the given set the highest number is 18.6
the lowest number is 11.0
Now subtract highest number-lowest number
18.6-11.0=7.6
therefore, the range is 7.6
The three quartiles:
1. Order your data set from lowest to highest values
2. Find the median. This is the second quartile Q₂.
3. At Q₂ split the ordered data set into two halves.
4. The lower quartile Q₁ is the median of the lower half of the data.
5. The upper quartile Q₃ is the median of the upper half of the data.
the given data: 12.6, 13.0, 15.5, 18.6, 14.4, 12.0, 11.0, 11.0, 15.6, 15.9
write in ascending order:
11.0, 11.0, 12.0, 12.6, 13.0, 14.4, 15.5, 15.6, 15.9, 18.6
Now finding the median:
Q2= 13.0, 14.4
Now add the middle values and divide by 2.
Q2=13.0+14.4/2
Q2=27.4/2
Q2=13.7
Now, look at the bottom half of the data. The median of this half is found between the second and fifth values:
11.0, 11.0, 12.0, 12.6, 13.0
Thus the first quartile is found to equal Q₁ = 12.0
Q1=12.0
Note: If the size of the data set is odd, do not include the median when finding the first and third quartiles.
To find the third quartile, look at the top half of the original data set. We need to find the median of:
14.4, 15.5, 15.6, 15.9, 18.6
Here the median is 15.6. Thus the third quartile Q₃ = 15.6.
Interquartile range=Q3-Q1
Interquartile range=15.6-12.0
Interquartile range=3.6

Find the mean absolute deviation. Round to the nearest hundredth. (Lesson 9.3)

Question 3.
103, 111, 150, 165, 192, 144, 144, 163, 121
Answer:
The mean absolute deviation (MAD) of a data set is the average distance between each data value and the mean.
Mean absolute deviation helps us get a sense of how “spread out” the values in a data set are.
Formula to calculate mean absolute deviation:
– Start by finding the mean of the data set.
– Find the absolute value of the difference between each data value and the mean.
– Find the sum of the absolute values and divide the sum by the number of data values.
the given values:
103, 111, 150, 165, 192, 144, 144, 163, 121
We’ll begin by finding the mean of the data set.
Mean: The word average mean middle or central point. Most of the time when we are required to calculate the average of a list of data we are supposed to calculate the ‘mean’ of the given data.
Formula to calculate average (mean) for ungrouped data:
Average is calculated by dividing the sum of the given data by the count of the same data.

n=9
Mean=103+111+150+165+192+144+144+163+121/9
Mean=1293/9
Mean=143.666666667
Mean=144
Then find the absolute value of the difference between each data value and the mean
1. |103-144|=41
2. |111-144|=33
3. |150-144|=6
4. |165-144|=21
5. |192-144|=48
6. |144-144|=0
7. |144-144|=0
8. |163-144|=19
9. |121-144|=23
Lastly, find the sum of the absolute values and divide by the number of the values.
MD=41+33+6+21+48+0+0+19+23/9
MD=191/2
MD=21.222

Question 4.
2.0, 3.2, 4.5, 5.6, 7.0, 7.9, 8.6, 9.1, 10.2, 12.3
Answer:
The mean absolute deviation (MAD) of a data set is the average distance between each data value and the mean.
Mean absolute deviation helps us get a sense of how “spread out” the values in a data set are.
Formula to calculate mean absolute deviation:
– Start by finding the mean of the data set.
– Find the absolute value of the difference between each data value and the mean.
– Find the sum of the absolute values and divide the sum by the number of data values.
the given values:
2.0, 3.2, 4.5, 5.6, 7.0, 7.9, 8.6, 9.1, 10.2, 12.3
We’ll begin by finding the mean of the data set.
Mean: The word average mean middle or central point. Most of the time when we are required to calculate the average of a list of data we are supposed to calculate the ‘mean’ of the given data.
Formula to calculate average (mean) for ungrouped data:
Average is calculated by dividing the sum of the given data by the count of the same data.
Average=X1+X2+…+Xn/n
n=10
Mean=2.0+3.2+4.5+5.6+7.0+7.9+8.6+9.1+10.2+12.3/10
Mean=70.4
Mean=7.04
Mean=7 (rounded to 100)
Then find the absolute value of the difference between each data value and the mean
1. |2.0-7|=5
2. |3.2-7|=3.8
3. |4.5-7|=2.5
4. |5.6-7|=1.4
5. |7.0-7|=0
6. |7.9-7|=0.9
7. |8.6-7|=1.6
8. |9.1-7|=2.1
9. |10.2-7|=3.2
10. |12.3-7|=5.3
Lastly, find the sum of the absolute values and divide by the number of the values.
MD=5+3.8+2.5+1.4+0+0.9+1.6+2.1+3.2+5.3/10
MD=25.8/10
MD=2.58

Use the information below to answer questions 5 to 10. (Lessons 9.1, 9.2)

The heights of plants, in centimeters, are shown in a stem-and-leaf plot.

Question 5.
Find the range of the data.
Answer:
To calculate range follow the below steps:
1. List the elements of your data set.
2. Identify the highest and lowest numbers in the set.
3. Subtract the smallest number in your data set from the largest number.
4. Label the range clearly.
You can use a stem-and-leaf plot to figure out the range of a set of data. The range is the difference between the maximum score and the minimum score.
Let’s look at the above diagram:
The smallest number in the stem-and-leaf plot is 10.5. You can see that by looking at the first stem and the first leaf. The greatest number is the last stem and the last leaf on the chart. In this case, the largest number is 15.9
To find the range, subtract the smallest number from the largest number. This difference will give you the range.
15.9-10.5=5.4 cm
The range is 5.4 for this set of data.

Question 6.
Find the mode of the data.
Answer:
Mode: The mode is the value that appears most often in a set of data. The mode of a discrete probability distribution is the value x at which its probability mass function takes its maximum value. In other words, it is the value that is most likely to be sampled.
1. Now write the numbers in the data set:
{10.5, 10.7, 10.7, 11.0, 11.3, 11.4, 11.5, 11.8, 12.0, 12.0, 12.6, 12.6, 12.7, 12.9, 14.3, 14.3, 14.3, 14.8, 15.0, 15.0, 15.1, 15.7, 15.7, 15.8, 15.9}
2. Order the numbers from smallest to largest:
{10.5, 10.7, 10.7, 11.0, 11.3, 11.4, 11.5, 11.8, 12.0, 12.0, 12.6, 12.6, 12.7, 12.9, 14.3, 14.3, 14.3, 14.8, 15.0, 15.0, 15.1, 15.7, 15.7, 15.8, 15.9}
3. Count the number of times each number is repeated:
10.5 – 1; 10.7 – 2; 11.0 – 1; 11.3 – 1; 11.4 – 1; 11.5 – 1; 11.8 – 1; 12.0 – 2; 12.6 – 2; 12.7 – 1; 12.9 – 1; 14.3 – 3; 14.8 – 1; 15.0 – 2;
15.1 – 1; 15.7 – 2; 15.8 – 1; 15.9 – 1}
4. Identify the value(or values) that occur most often:
When you know how many times each value occurs in your data set, find the value that occurs the greatest number of times. This is your data set’s mode. Note that there can be more than one mode in a data set. If the two values are tied for being the most common values in the set, the data set can be said to be bimodal, whereas if three values are tied, the set is trimodal, and so on.
– In the above-given data set, 14.3 occurs more times than any other value, 14.3 is the mode.
– If a value besides 14.3 had also occurred three times, (like, for instance, if there were one more 15.0 in the data set), 14.3 and this other number would both be the mode.

Question 7.
Find the median height.
Answer:
Median: The median is the value separating the higher half of a data sample, a population, or a probability distribution, from the lower half. In simple terms, it may be thought of as the “middle” value of a data set.
The given data set:
{10.5, 10.7, 10.7, 11.0, 11.3, 11.4, 11.5, 11.8, 12.0, 12.0, 12.6, 12.6, 12.7, 12.9, 14.3, 14.3, 14.3, 14.8, 15.0, 15.0, 15.1, 15.7, 15.7, 15.8, 15.9}
The number of data set=25
Now divide the numbers bottom half and lower half.
{10.5, 10.7, 10.7, 11.0, 11.3, 11.4, 11.5, 11.8, 12.0, 12.0, 12.6, 12.6, 12.7, 12.9, 14.3, 14.3, 14.3, 14.8, 15.0, 15.0, 15.1, 15.7, 15.7, 15.8, 15.9}
– The bottom half is 12 and the lower half is 12.
– And the median is the middle number that is 12.7
Therefore, 12.7 is the median.

Question 8.
Find the mean height.
Answer:
Mean: The word average mean middle or central point. Most of the time when we are required to calculate the average of a list of data we are supposed to calculate the ‘mean’ of the given data.
Formula to calculate average (mean) for ungrouped data:
Average is calculated by dividing the sum of the given data by the count of the same data.
Average=X1+X2+…+Xn/n
n=25
Average=10.5+10.7+10.7+11.0+11.3+11.4+11.5+11.8+12.0+12.0+12.6+12.6+12.7+12.9+14.3+14.3+14.3+14.8+15.0+15.0+15.1+15.7+15.7+15.8+15.9/25
Average=410.8/25
Average (mean)=16.432

Question 9.
Calculate Q₁ and Q₃.
Answer:
The three quartiles:
1. Order your data set from lowest to highest values
2. Find the median. This is the second quartile Q₂.
3. At Q₂ split the ordered data set into two halves.
4. The lower quartile Q₁ is the median of the lower half of the data.
5. The upper quartile Q₃ is the median of the upper half of the data.
the given data: {10.5, 10.7, 10.7, 11.0, 11.3, 11.4, 11.5, 11.8, 12.0, 12.0, 12.6, 12.6, 12.7, 12.9, 14.3, 14.3, 14.3, 14.8, 15.0, 15.0, 15.1, 15.7, 15.7, 15.8, 15.9}
write in ascending order:
{10.5, 10.7, 10.7, 11.0, 11.3, 11.4, 11.5, 11.8, 12.0, 12.0, 12.6, 12.6, 12.7, 12.9, 14.3, 14.3, 14.3, 14.8, 15.0, 15.0, 15.1, 15.7, 15.7, 15.8, 15.9}
The second quartile Q₂ is easy to find. It is the median of any data set and it divides an ordered data set into upper and lower halves.
The first quartile Q₁ is the median of the lower half not including the value of Q₂. The third quartile Q₃ is the median of the upper half not including the value of Q₂.
Data set divided for finding Q1: 10.5, 10.7, 10.7, 11.0, 11.3, 11.4, 11.5, 11.8, 12.0, 12.0, 12.6, 12.6
Q1=11.4+11.5/2
Q1=22.9/2
Q1=11.45
Q2 data set: 12.7, 12.9, 14.3, 14.3, 14.3, 14.8, 15.0, 15.0, 15.1, 15.7, 15.7, 15.8, 15.9
n=13 (odd); If the size of the data set is odd, do not include the median when finding the first and third quartiles.
Q3=15.0 cm

Question 10.
Find the interquartile range.
Answer:
The interquartile range IQR is the range in values from the first quartile Q₁ to the third quartile Q₃. Find the IQR by subtracting Q1 from Q3.
IQR=Q3-Q1
IQR=15.0-11.45
IQR=3.55

Use the following information to answer questions 11 to 14. (Lessons 9.1, 9.3)

The history test scores of twenty students are tabulated below.

Question 11.
Find the range of the scores.
Answer:
To calculate range follow the below steps:
1. List the elements of your data set.
2. Identify the highest and lowest numbers in the set.
3. Subtract the smallest number in your data set from the largest number.
4. Label the range clearly.
The highest number is:92
The lowest number is: 50
range=highest number-lowest number
range=92-50
range=42

Question 12.
Find the 3 quartiles of the scores.
Answer:
the given data set: 75, 92, 56, 60, 50, 60, 67, 87, 88, 74, 60, 78, 90, 61, 64, 92, 50, 75, 58, 70.
1. Order your data set from lowest to highest values
2. Find the median. This is the second quartile Q₂.
3. At Q₂ split the ordered data set into two halves.
4. The lower quartile Q₁ is the median of the lower half of the data.
5. The upper quartile Q₃ is the median of the upper half of the data.
Now write in an ascending order:
50, 50, 56, 58, 60, 60, 60, 61, 64, 67, 70, 74, 75, 75, 78, 87, 88, 90, 92, 92.
Q2=67+70/2
Q2=137/2
Q2=68.5
The first quartile Q₁ is the median of the lower half not including the value of Q₂. The third quartile Q₃ is the median of the upper half not including the value of Q₂.
Now, look at the bottom half of the data.
50, 50, 56, 58, 60, 60, 60, 61, 64, 67
Q1=60+60/2
Q1=120/2
Q1=60
Thus the first quartile is found to equal Q₁ = 60
Q3 data set: 70, 74, 75, 75, 78, 87, 88, 90, 92, 92
Q3=78+87/2
Q3=165/2
Q3=82.5
Thus the third quartile is found to equal Q3 = 82.5

Question 13.
Find the interquartile range of the scores.
Answer:
The interquartile range IQR is the range in values from the first quartile Q₁ to the third quartile Q₃. Find the IQR by subtracting Q1 from Q3.
IQR=Q3-Q1
IQR=82.5-60
IQR=22.5

Question 14.
Find the mean absolute deviation of the scores. Round to the nearest hundredth.
Answer:
The mean absolute deviation (MAD) of a data set is the average distance between each data value and the mean.
Mean absolute deviation helps us get a sense of how “spread out” the values in a data set are.
Formula to calculate mean absolute deviation:
– Start by finding the mean of the data set.
– Find the absolute value of the difference between each data value and the mean.
– Find the sum of the absolute values and divide the sum by the number of data values.
the given values:
50, 50, 56, 58, 60, 60, 60, 61, 64, 67, 70, 74, 75, 75, 78, 87, 88, 90, 92, 92.
We’ll begin by finding the mean of the data set.
Mean: The word average mean middle or central point. Most of the time when we are required to calculate the average of a list of data we are supposed to calculate the ‘mean’ of the given data.
Formula to calculate average (mean) for ungrouped data:
Average is calculated by dividing the sum of the given data by the count of the same data.
Average=x1+x2+…+x3/n
n=20
Mean=50+50+56+58+60+60+60+61+64+67+70+74+75+75+78+87+88+90+92+92/20
Mean=1407/20
Mean=70.35
Mean=70 (round to 100)
Then find the absolute value of the difference between each data value and the mean
|50-70| = 20
|50-70| = 20
|56-70| = 14
|58-70| = 12
|60-70| = 10
|60-70| = 10
|60-70| = 10
|61-70| = 9
|64-70| = 6
|67-70| = 3
|70-70| = 0
|74-70| = 4
|75-70| = 5
|75-70| = 5
|78-70| = 8
|87-70| = 17
|88-70| = 18
|90-70| = 20
|92-70| = 22
|92-70| = 22
Lastly, find the sum of the absolute values and divide by the number of the values.
MD=20+20+14+12+10+10+10+9+6+3+0+4+5+5+8+17+18+20+22+22/20
MD=235/20
MD=11.75

Use the data in the table to answer questions 15 to 17. (Lesson 9.3)

The table shows the speeds, ¡n miles per hour, of twelve vehicles.

Question 15.
Calculate Q₁, Q₂, and Q₃.
Answer:
The given data set: 80, 65, 72, 58, 60, 70, 75, 68, 48, 51, 88, 90
1. Order your data set from lowest to highest values
2. Find the median. This is the second quartile Q₂.
3. At Q₂ split the ordered data set into two halves.
4. The lower quartile Q₁ is the median of the lower half of the data.
5. The upper quartile Q₃ is the median of the upper half of the data.
Now write in ascending order:
48, 51, 58, 60, 65, 68, 70, 72, 75, 80, 88, 90.
The second quartile Q₂ is easy to find. It is the median of any data set and it divides an ordered data set into upper and lower halves.
Q2=68+70/2
Q2=138/2
Q2=69
Now calculate Q1 and Q3
The first quartile Q₁ is the median of the lower half not including the value of Q₂. The third quartile Q₃ is the median of the upper half not including the value of Q₂.
Q1 data set: 48, 51, 58, 60, 65, 68
Q1=58+60/2
Q1=118/2
Q1=59
Thus, the first quartile is found to equal Q₁ = 59
Q3 data set: 70, 72, 75, 80, 88, 90
Q3=75+80/2
Q3=155/2
Q3=77.5
Thus, the third quartile is found to equal Q3 = 77.5

Question 16.
Draw a box plot of the speeds of the vehicles.
Answer:
The given data set: 80, 65, 72, 58, 60, 70, 75, 68, 48, 51, 88, 90
Now write in ascending order:
48, 51, 58, 60, 65, 68, 70, 72, 75, 80, 88, 90.
Q1=59, Q2=60, Q3=77.5

Question 17.
Calculate the mean absolute deviation of the speeds of vehicles. Round to the nearest hundredth.
Answer:
The mean absolute deviation (MAD) of a data set is the average distance between each data value and the mean.
Mean absolute deviation helps us get a sense of how “spread out” the values in a data set are.
Formula to calculate mean absolute deviation:
– Start by finding the mean of the data set.
– Find the absolute value of the difference between each data value and the mean.
– Find the sum of the absolute values and divide the sum by the number of data values.
the given values:
80, 65, 72, 58, 60, 70, 75, 68, 48, 51, 88, 90
We’ll begin by finding the mean of the data set.
Mean: The word average mean middle or central point. Most of the time when we are required to calculate the average of a list of data we are supposed to calculate the ‘mean’ of the given data.
Formula to calculate average (mean) for ungrouped data:
Average is calculated by dividing the sum of the given data by the count of the same data.
Average=x1+x2+…+x3/n
n=12
Mean=80+65+72+58+60+70+75+68+48+51+88+90/12
Mean=825/12
Mean=68.75
Mean=69 (round to nearest 100)
Then find the absolute value of the difference between each data value and the mean
|80-69| = 11
|65-69| = 4
|72-69| = 3
|58-69| = 11
|60-69| = 9
|70-69| = 1
|75-69| = 6
|68-69| = 1
|48-69| = 21
|51-69| = 18
|88-69| = 19
|90-69| = 21
Lastly, find the sum of the absolute values and divide by the number of the values.
MD=11+4+3+11+9+1+6+1+21+18+19+21/12
MD=125/12
MD=10.41

Use the box plot to answer questions 18 to 20 (Lesson 9.3)

The box plot below summarizes the reaction times, in seconds, of 300 drivers in an experiment.

Question 18.
State the 5-point summary.
Answer:
– When we display the data distribution in a standardized way using 5 summary – minimum, Q1 (First Quartile), median, Q3(third Quartile), and maximum, it is called a Box plot.
– The method to summarize a set of data that is measured using an interval scale is called a box and whisker plot. These are the maximum used for data analysis.
– It does not show the distribution in particular as much as a stem and leaf plot or histogram does.
– In simple words, we can define the box plot in terms of descriptive statistics related concepts. That means box or whiskers plot is a method used for depicting groups of numerical data through their quartiles graphically.
– These may also have some lines extending from the boxes or whiskers which indicates the variability outside the lower and upper quartiles, hence the terms box-and-whisker plot and box-and-whisker diagram. Outliers can be indicated as individual points.
– It helps to find out how much the data values vary or spread out with the help of graphs. As we need more information than just knowing the measures of central tendency, this is where the box plot helps. This also takes less space. It is also a type of pictorial representation of data.
From the above-given box plot, we need to summarize the points.
according to the definition:
The first point represents the minimum, the point is 1.5
The second point represents Q1 (First Quartile), the Q1 point is 2.0
The third point represents Q2 (Median), the Q2 point is 2.5
The fourth point represents Q3 (third quartile), the Q3 point is 2.7
The fifth point represents the maximum, Thus the maximum point is 3.1

Question 19.
How many drivers have reaction time more than 2 seconds?
Answer: 225 drivers.

Question 20.
If a driver with reaction time less than 2 seconds is considered fast, how many drivers are fast?
Answer:

Solve. Show your work. (Lesson 9.5)

Question 21.
Six random samples of inner diameters, in millimeters, of metal pipes were collected. The sample means are 112, 103.5, 98.4, 106.2, 110, and 99.7. Use the 6 sample means to generate a mean length to estimate the population mean diameter of the pipes. Round your answer to the nearest tenth.
Answer:
The given sample means are 112, 103.5, 98.4, 106.2, 110, and 99.7
Mean length=112+103.5+98.4+106.2+110+99.7/6
Mean length=629.8/6
Mean length=104.96
Therefore, mean length=105 mm (round to nearest 10).

Question 22.
A bag contains 5 red cards, 4 yellow cards, and 7 blue cards. A card is randomly drawn from the bag. (Lessons 10.1, 10.2)
a) How many outcomes are in the sample space?
Answer:
The total number of cards=16 cards.
The number of red cards=5
The number of yellow cards=4
The number of blue cards=7
A sample space is a collection of a set of possible outcomes of a random experiment. The sample space is represented using the symbol, “S”. The subset of possible outcomes of an experiment is called events. A sample space may contain a number of outcomes that depends on the experiment. If it contains a finite number of outcomes, then it is known as discrete or finite sample spaces.
The outcomes are {R, R, R, R, R, Y, Y, Y, Y, B, B, B, B, B, B, B}
the number of possibles is 16

b) If X is the event of drawing a card which is not yellow, what are the outcomes favorable to X?
Answer:
If not drawing yellow means then there is the chance of taking blue and red
The possible outcome of event x is { R, R, R, R, R, B, B, B, B, B, B, B}

c) Find P(X).
Answer:
This formula is the number of favourable outcomes to the total number of all the possible outcomes that we have already decided in the Sample Space.
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
The possible outcome of event x is { R, R, R, R, R, B, B, B, B, B, B, B}
the total number of possible outcomes=16
the favourable outcomes=12
P(X)=n(E)/n(S)
P(X)=12/16
P(X)=3/4
P(X)=0.75
Therefore, the probability of event X is 0.75

d) If Y is the event of drawing a blue card, what does the complement of Y mean?
Answer:
If the probability of occurring an event is P(A) then the probability of not occurring an event is
P(A’) = 1- P(A)
P(Y)=7/16
The number of favourable outcomes is 7
We need to find out the not occurring of an event.
The complement of event Y is:
P(Y’)=1-P(Y)
P(Y’)=1-7/16
P(Y’)=16-7/16
P(Y’)=9/16
P(Y’)=0.5

Question 23.
The numbers in the Venn diagram indicate the number of outcomes favorable to the events. For example, there are 12 outcomes favorable to event A. (Lesson 10.2)

a) What is the total number of possible outcomes?
Answer: 48
Explanation:
The number of outcomes to event A=12
The number of outcomes to event B=21
the number of outcomes that are not event A and event B=15
Now add all the outcomes=12+21+15
The total number of possible outcomes are 48.

b) Find P(A), P(B), and P(B’).
Answer:
This formula is the number of favourable outcomes to the total number of all the possible outcomes that we have already decided in the Sample Space.
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
The total number of possible outcomes=48
The number of favourable outcomes of event A=12
P(A)=12/48
P(A)=1/4
The number of favourable outcomes of event B=21
P(B)=21/48
P(B)=7/16
If the probability of occurring an event is P(B) then the probability of not occurring an event is
P(B’) = 1- P( B)
Here we know P(B) is 7/16, then we can find the complement of B.
P(B’)=1-7/16
P(Y’)=16-7/16
P(Y’)=9/16
P(Y’)=0.5

c) Copy and complete the table.

Answer:
The number of outcomes to event A=12
The number of outcomes to event B=21
the number of outcomes that are not event A and event B=15
Now add all the outcomes=12+21+15
The total number of possible outcomes is 48.
Definition of Mutually Non-Exclusive Events: Two events A and B are said to be mutually non-exclusive events if both events A and B have at least one common outcome between them. The event of getting an ‘odd-face’ and the event of getting ‘less than 4’ occur when we get either 1 or 3.
In logic and probability theory, two events (or propositions) are mutually exclusive or disjoint if they cannot both occur at the same time. A clear example is the set of outcomes of a single coin toss, which can result in either heads or tails, but not both.
according to the above definitions we can fill the table:

Question 24.
A coin is flipped repeatedly and the outcomes are HTTHHHTHTHTHTHHTHHTH. What is the experimental probability that the coin lands on heads when you flip the coin again? (Lesson 10.3)
Answer:
The total outcomes came when the coin was flipped repeatedly=20
The number of times coin lands on the head when the coin is flipped again=12
Experimental Probability is the probability of an event based on exact recordings or experiments of an event. The calculation is done by dividing the number of times an event occurred by the total number of trials in an experiment. We can express experimental probability mathematically as,
experimental probability=Number of times a particular event occurs/Number of total trails.
P(Heads)=12/20
P(Heads)=3/5
P(Heads0=0.6
Therefore, the experimental probability that the coin lands on heads when you flip the coin again is 0.6 or 3/5

Question 25.
A spinner with outcomes A, E, O, and B is spun and the letter at which the arrow is pointing is recorded. After spinning the spinner several times, it generates the following outcomes: OABBBEAOOBAA. What is the experimental probability that the arrow points at a vowel if you spin the spinner again? (Lesson 10.3)
Answer:
Experimental Probability is the probability of an event based on exact recordings or experiments of an event. The calculation is done by dividing the number of times an event occurred by the total number of trials in an experiment. We can express experimental probability mathematically as
experimental probability=Number of times a particular event occurs/Number of total trails.
The total number of outcomes=12
The number of times a particular event occurs=8 (favourable outcomes of vowels)
According to the definition:
P(Vowels)=8/12
P(Vowels)=2/3

Problem Solving

Solve. Show your work.

Question 26.
The table shows 100 responses on the level of satisfaction of a service. Customers evaluate their experiences, as 1 very dissatisfied, 2 somewhat dissatisfied, 3 neutral, 4 somewhat satisfied or 5 very satisfied. (Chapters 9, 10)

a) Find the lower quartile, median, and upper quartile.
Answer:
the given data set: 7, 18, 27, 23, 25.
1. Order your data set from lowest to highest values
2. Find the median. This is the second quartile Q₂.
3. At Q₂ split the ordered data set into two halves.
4. The lower quartile Q₁ is the median of the lower half of the data.
5. The upper quartile Q₃ is the median of the upper half of the data.
Now write in ascending order:
7, 18, 23, 25, 27
Q2=23
The first quartile Q₁ is the median of the lower half not including the value of Q₂. The third quartile Q₃ is the median of the upper half not including the value of Q₂.
Now, look at the bottom half of the data.
Q1=7+8/2
Q1=25/2
Q1=12.5
Thus the first quartile is found to equal Q₁ = 12.5
Q3=25+27/2
Q3=52/2
Q3=26
Thus the third quartile is found to equal Q3 = 26

b) Draw a box plot of the level of satisfaction.
Answer:
– When we display the data distribution in a standardized way using 5 summary – minimum, Q1 (First Quartile), median, Q3(third Quartile), and maximum, it is called a Box plot.
– The method to summarize a set of data that is measured using an interval scale is called a box and whisker plot. These are the maximum used for data analysis.

c) If a customer’s response is randomly selected, what is the probability that the level of satisfaction is at least 4?
Answer:
The frequency of 4 and 5 are 23 and 25
The favourable outcomes are 2
The total outcomes are 23+25=48
This formula is the number of favourable outcomes to the total number of all the possible outcomes that we have already decided in the Sample Space.
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
P(satisfaction)=2/48
P(satisfaction)=1/24
In decimals, we can write as 0.04
Therefore, the probability that the level of satisfaction is at least 4 is 1/24 or 0.04

d) Construct a relative frequency table. Write each relative frequency as a percent.
Answer:
The number of times an event occurs is called a frequency. Relative frequency is an experimental one, but not a theoretical one. Since it is an experimental one, it is possible to obtain different relative frequencies when we repeat the experiments. To calculate the frequency we need
– Frequency count for the total population
– Frequency count for a subgroup of the population
We can find the relative frequency probability in the following way if we know the above two frequencies. The formula for a subgroup is;
Relative Frequency = Subgroup Count / Total Count
The relative frequency of very dissatisfied=1/7
The relative frequency of dissatisfied=2/18=1/9
The relative frequency of neutral=3/27=1/9
The relative frequency of somewhat satisfied=4/23
the relative frequency of very satisfied=5/25=1/5

e) Present the relative frequency in a bar graph.
Answer:
The relative frequency of very dissatisfied=1/7=0.14
The relative frequency of dissatisfied=2/18=1/9=0.11
The relative frequency of neutral=3/27=1/9=0.11
The relative frequency of somewhat satisfied=4/23=0.17
the relative frequency of very satisfied=5/25=1/5=0.2

Question 27.
A survey was conducted on 100 randomly selected people about the types of books they usually read. The survey results show that 58 people read novels, 40 people read science fiction, and 10 people read neither. (Chapter 10)
a) Find the number of people surveyed who read both novels and science fiction.
Answer:8
The number of people who read novels is 58
The number of people who reads science fiction is 40
The number of people read none=10
Therefore, 100-10=90
The remaining people are 90.
If we subtract science fiction people from the remaining people then we get the people who read novels.
90-40=50
Thus, 50 people read novels.
But we have 58 people read the novel
: 58-50=8
8 people read both novels and science fiction.
So, a number of people who read only science fiction: 40-8=32.

b) Draw a Venn diagram to represent the different types of books read.
Answer:
A diagram used to represent all possible relations of different sets. A Venn diagram can be represented by any closed figure, whether it be a Circle or a Polygon (square, hexagon, etc.). But usually, we use circles to represent each set.

c) Copy and complete the following relative frequency table. Write each relative frequency as a decimal.

Answer:
relative frequency: We come across repetitive data in observation all the time. When repetitive data is given, then the number of times it has been in the observation is called its frequency. Relative frequency is the comparison between the number of times a number has been repeated to the total frequencies of all the numbers. Mathematically speaking, relative frequency is the division between the individual frequency of an item by the total number of repetition that has occurred.
The formula for the relative frequency is given as:
relative frequency=f/n
Here,
f is the number of times the data occurred in an observation
n  = total frequencies
The relative frequency of reading novel=50/100=0.5
The relative frequency of science fiction=32/100=0.32
The relative frequency of both novel and science fiction=8/100=0.08
The relative frequency of reading neither=10/100=0.1

d) Draw a relative frequency bar graph using decimals.
Answer:
The line plot is a useful graph for examining small sets of data. It’s especially helpful as a device for learning basic statistical ideas. But for larger data sets, it can be awkward to create, since for each data value there is a corresponding dot. That’s a lot of dots for data sets with hundreds or thousands of values! You can, however, replace a line plot with a frequency bar graph.

e) If a person is randomly selected from this population to do the survey, what is the probability that the selected person reads novels?
Answer: 0.58
Explanation:
This formula is the number of favourable outcomes to the total number of all the possible outcomes that we have already decided in the Sample Space.
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
the number of people who read novels=58
The total number of people=100
P(novels)=58/100
P(novels)=0.58
Therefore, the probability is o.58

Question 28.
The table shows the number of children surveyed for each age group. (Chapter 10)

a) Construct a probability model. Express each probability of the age groups as a percent.
Answer:
A probability model is a mathematical representation of a random phenomenon. It is defined by its sample space, events within the sample space, and probabilities associated with each event. The sample space S for a probability model is the set of all possible outcomes.
The probability 0f age group 10 to 12=14/80=0.175=17.5%
The probability of age group 12 to 14=28/80=0.35=35%
The probability of age group 14 to 16=20/80=0.25=25%
The probability of age group 16 to 18=18/80=0.225=22.5%

b) If a child is randomly selected, what is the probability that the selected child is at least 10 years old but not yet 14 years old?
Answer:
The probability 0f age group 10 to 12=14
The probability 0f age group 12 to 14=28
here asked the question that we need to find out the probability that the selected child is at least 10 years old but not yet 14 years old.
This formula is the number of favourable outcomes to the total number of all the possible outcomes that we have already decided in the Sample Space.
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
The number of favourable outcomes is 14+28=42
The total number of possible outcomes=80
P(age)=42/80
P(age)=0.525
Therefore, the probability is 0.525

c) Display the probability distribution in a histogram using percent.
Answer:
Probability distribution yields the possible outcomes for any random event. It is also defined based on the underlying sample space as a set of possible outcomes of any random experiment. These settings could be a set of real numbers or a set of vectors or a set of any entities. It is a part of probability and statistics.

Question 29.
The data show the masses, in kilograms, of 14 grass carps. (Chapters 9, 10)

a) Construct a stem-and-leaf plot of the masses of the grass carps.
Answer:
Definition: The Stem and Leaf plot is a way of organizing data into a form that makes it easy to see the frequency of different values. In other words, we can say that a Stem and Leaf Plot is a table in which each data value is split into a “stem” and a “leaf.” The “stem” is the left-hand column that has the tens of digits. The “leaves” are listed in the right-hand column, showing all the ones digit for each of the tens, the twenties, thirties, and forties.
Remember that Stem and Leaf plots are a pictorial representation of grouped data, but they can also be called a modal representation. Because, by quick visual inspection at the Stem and Leaf plot, we can determine the mode.
Steps for making stem-and-leaf plot:
– First, determine the smallest and largest number in the data.
– Identify the stems.
– Draw a with two columns and name them as “Stem” and “Leaf”.
– Fill in the leaf data.
– Remember, a Stem and Leaf plot can have multiple sets of leaves.
By using the above-given data, we can make a stem-and-leaf plot:

b) Make a frequency table. Group the data into 4 intervals: 5-10, 10-15, 15-20, and 20 — 25. Note: The interval 5 — 10 includes masses greater than or equal to 5 kilograms, but less than 10 kilograms.
Answer:
Frequency refers to the number of times an event or a value occurs.  A frequency table is a table that lists items and shows the number of times the items occur. We represent the frequency by the English alphabet ‘f’.
Creating a frequency table:
Step 1: Make three columns. The first column carries the data values in ascending order (from lesser to large values).
Step 2: The second column contains the number of times the data value occurs using tally marks. Count for every row in the table. Use tally marks for counting.
Step 3:  Count the number of tally marks for each data value and write it in the third column.

c) Draw a probability model. Give probabilities in fractions.
Answer:
A probability model is a mathematical representation of a random phenomenon. It is defined by its sample space, events within the sample space, and probabilities associated with each event. The sample space S for a probability model is the set of all possible outcomes.
– Identify every outcome.
– Determine the total number of possible outcomes.
– Compare each outcome to the total number of possible outcomes.
The probability of mass 5-10 is 4/14=2/7
The probability of mass 10-15 is 3/14
The probability of mass 15-20 is 4/14=2/7
The probability of mass 20-25 is 3/14

d) Present the probability distribution, in fractions, in a histogram.
Answer:
Probability distribution yields the possible outcomes for any random event. It is also defined based on the underlying sample space as a set of possible outcomes of any random experiment. These settings could be a set of real numbers or a set of vectors or a set of any entities. It is a part of probability and statistics.

e) Is the model a uniform probability model? Explain your answer.
Answer: No, all possible outcomes do not have the same relative frequency.
A discrete uniform probability distribution is one in which all elementary events in the sample space have an equal opportunity of occurring. As a result, for a finite sample space of size n, the probability of an elementary event occurring is 1/n. Uniform distributions are very common for initial studies of probability. The histogram of this distribution will look rectangular in shape.

Question 30.
In a game, the scores given to each student are in multiples of 5 up to a maximum of 25. The bar graph and dot plot show the scores of Groups A and B, respectively. (Chapters 9, 10)

a) Calculate the mean score of each group.
Answer:
Mean: The word average mean middle or central point. Most of the time when we are required to calculate the average of a list of data we are supposed to calculate the ‘mean’ of the given data.
Formula to calculate average (mean) for ungrouped data:
Average is calculated by dividing the sum of the given data by the count of the same data.
Average=X1+X2+…+Xn/n
n=5
Finding mean for Group A:
The given data is 2, 5, 8, 4, 1
Mean=2+5+8+4+1/5
Mean=20/5
Mean of group A=4
Finding mean for group B:
The given data is 4, 7, 2, 4, 3
Mean=4+7+2+4+3/5
mean=20/5
Mean of group B=4

b) Calculate the mean absolute deviation of the scores of each group.
Answer:
The mean absolute deviation (MAD) of a data set is the average distance between each data value and the mean.
Mean absolute deviation helps us get a sense of how “spread out” the values in a data set are.
Formula to calculate mean absolute deviation:
– Start by finding the mean of the data set.
– Find the absolute value of the difference between each data value and the mean.
– Find the sum of the absolute values and divide the sum by the number of data values.
the given values of group A: 2, 5, 8, 4, 1
Mean=4
|2 – 4|=2
|5 – 4|=1
|8 – 4|=4
|4 – 4|=0
|1 – 4|=3
MAD=2+1+4+0+3/5
MAD=10/5
MAD of group A=2
The given values of group B: 4, 7, 2, 4, 3
Mean=4
|4 – 4|=0
|7 – 4|=3|
|2 – 4|=2
|4 – 4|=0
|3 – 4|=1
MAD=0+3+2+0+1/5
MAD=6/5
MAD of group B is 1.2

c) Which group’s scores deviate more about its mean score?
Answer:
The mean of group A is 4
The mean of group B is 4
The mean deviation of group A is 2
The mean deviation of Group B is 1.2
By comparing all these Group A score deviate is more.

d) A randomly selected student from one of these groups has a score of 10 or 15. Which group is the student likely to be selected from? Explain your answer using probability.
Answer:
This formula is the number of favourable outcomes to the total number of all the possible outcomes that we have already decided in the Sample Space.
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
The number of students of 10 or 15 in group A is 5+8=13
the number of students 0f 10 or 15 in group B is 7+2=9
The favourable outcomes of group A are 13
The total number of students=20
P(Group A)=13/20
The favourable outcomes of group B are 9
The total number of students =20
P(Group B)=9/20

Question 31.
The table shows the place of origin of incoming freshman students at a university. (Chapter 9)

Describe how you would conduct a stratified random sampling of 500 of the 6,000 incoming freshman, considering the student distribution within their place of origins.
Answer:
Use the per cent to determine how many of the 500-student samples will be selected from each region. Then conduct a simple random sampling within each region. The total number of students sampled will be 500.

Practice the problems of Math in Focus Grade 1 Workbook Answer Key Chapter 12 Practice 1 Counting to 40 to score better marks in the exam.

Math in Focus Grade 1 Chapter 12 Practice 1 Answer Key Counting to 40

First make tens, then count on. Fill in the missing numbers.

Example

Question 1.

____, . . . 20, . . . _____, 31, ____, ______
_______
Answer: 10, . . . 20, . . . 30, 31, 32, 33,34

Question 2.

10, . . . ____, . . . ____, ____, _____
33, ____, _____, 36
Answer:10, . . .20, . . . 30,31, 32,33, 34, 35, 36

Circle groups of 10. Then count and write the numbers.

Question 3.

Answer:

Question 4.

Answer:

Question 5.

Answer:

Question 6.

Answer:

Question 7.

Answer:

Count the s and write the numbers.

Question 8.

Answer:

Question 9.

Answer:

Question 10.

Answer:

Question 11.

Answer:

Write the numbers.

Question 12.
twenty-five _______
Answer: twenty-five in numeric is 25

Question 13.
thirty-nine ____
Answer: thirty-nine in numeric is 39

Question 14.
thirty-two ____
Answer: thirty-two in numeric is 32

Question 15.
twenty-nine ____
Answer: twenty-nine in numeric is 29

Write the numbers in words.

Question 16.
21 _______________
Answer: 21 in words is twenty one

Question 17.
37 ________________
Answer: 37 in words is thirty seven

Question 18.
22 ____________
Answer: 22 in words is twenty two

Question 19.
40 _______________
Answer:40 in words is forty

Question 20.
35 _______________
Answer: 35 in words is thirty five

Question 21.
31 _______________
Answer: 31 in words is thirty one

Fill in the missing numbers.

Question 22.
20 + 3 = ____
Answer: 20 + 3 = 23

Question 23.
8 + 30 = ____
Answer: 8 + 30 = 38

Question 24.
_____ + 9 = 39
Answer: 30 + 9 = 39

Question 25.
30 and 5 make ___.
Answer: 30 and 5 make 35

Question 26.
7 and 20 make ___.
Answer: 7 and 20 make 27

Question 27.
___ and 2 make 32.
Answer: 30 and 2 make 32.

Question 28.
___ and 8 make 28.
Answer: 20 and 8 make 28.

Question 29.
___ and 6 make 36.
Answer: 30 and 6 make 36.

Practice the problems of Math in Focus Grade 1 Workbook Answer Key Chapter 12 Numbers to 40 to score better marks in the exam.

Math in Focus Grade 1 Chapter 12 Answer Key Numbers to 40

Put On Your Thinking Cap!

Challenging Practice

Fill in the blanks.

Wayne has four cards. Each card has a number on it.

Question 1.
Use two cards to form the least number. Do not begin with 0.
____________________
Answer: card number 1 and card number 2 makes a value 12 which is the least number when not starting with 0

Question 2.
Use two cards to form the greatest number.
____________________
Answer: card number 3 and card number 2 makes a value 32 which is the greatest number

Question 3.
Use two cards to form a number less than 30. Do not begin with 0.
____________________
Answer: card 2 and card 3 will make a number 23 which is a number that is less than 30 and which does not start with 0

Question 4.
Use two cards to form a number greater than 25.
____________________
Answer: card number 3 and card number 2 makes a value 32 which is the greatest number when compares to 25

There is more than one correct answer for Exercises 3 and 4

Put on your Thinking Cap!

Problem Solving

Fill in the blanks.

Jan uses tiles to make shapes that form a pattern.

Answer:

Question 1.
Draw Shape 4.
Answer:

Question 2.
Jan needs _______ more tiles to make Shape 4.
Answer: Jan needs four more tiles to make Shape 4.

Question 3.
Complete the table.

Answer:

Question 4.
Complete the number pattern.
1, 5, 9, ___, ___, _____
Answer: 1, 5, 9, 13, 17, 21

Chapter Review/Test

Vocabulary

Match.

Question 1.

Answer:

Concepts and Skills

Count to find how many.

Question 2.

Answer:

Question 3.

Answer:

Write the numbers.

Question 4.
twenty-four _____
Answer: twenty-four is 24

Question 5.
thirty _____
Answer: thirty is 30

Write the number that ¡s greater.

Question 6.

Answer:

Question 7.

Answer:

Write the number that is less.

Question 8.

Answer:

Question 9.

Answer:

Compare the numbers. Then fill in the blanks.

Question 10.
Which number is greatest? _____
Answer: 35 is the greatest when compared to all the rest

Question 11.
Which number is least? ________
Answer: 9 is the lest when compares to all the other numbers

Order the numbers from greatest to least.

Question 12.

Answer:

Complete the number pattern.

Question 13.
17, 20, 23, ___, ___, 32
Answer:
17,20,23,26,29,32

Fill in the blanks.

Question 14.
2 less than 25 is ____.
Answer: 2 less than 25 is 23.

Question 15.
________ is 3 more than 18.
Answer: 21 is 3 more than 18.

Question 16.
24 = ________ tens 4 ones
Answer: 24 = 2 tens 4 ones

Question 17.
18 = 1 ten _______ ones
Answer: 18 = 1 ten 8 ones

Practice the problems of Math in Focus Grade 4 Workbook Answer Key Chapter 7 Practice 3 Comparing Decimals to score better marks in the exam.

Math in Focus Grade 4 Chapter 7 Practice 3 Answer Key Comparing Decimals

Use the number line. Find the number that is described.

Question 1.
0.1 more than 0.2. _________
Answer:

Explanation:
0.1 more than 0.2 = 0.1 + 0.2 = 0.3.

Question 2.
0.3 more than 0.5. ________
Answer:

Explanation:
0.3 more than 0.5 = 0.3 + 0.5 = 0.8.

Question 3.
0.1 less than 0.6. ___________
Answer:

Explanation:
0.1 less than 0.6 = 0.6 – 0.1 = 0.5.

Question 4.
0.2 less than 0.9. __________
Answer:

Explanation:
0.2 less than 0.9 = 0.9 – 0.2 = 0.7.

Use the number line. Find the number that is described.

Question 5.
0.01 more than 0.13. __________
Answer:

Explanation:
0.01 more than 0.13 = 0.01 + 0.13 = 0.14.

Question 6.
0.04 more than 0.16. ______
Answer:

Explanation:
0.04 more than 0.16 = 0.04 + 0.16 = 0.20.

Question 7.
0.01 less than 0.18. _________
Answer:

Explanation:
0.01 less than 0.18 = 0.18 – 0.01 = 0.17.

Question 8.
0.05 less than 0.17. _______
Answer:

Explanation:
0.05 less than 0.17 = 0.17 – 0.05 = 0.12.

Fill in the missing numbers.
Question 9.

Answer:

Explanation:
0.1 more than 4.7 = 0.1 + 4.7 = 4.8.
0.1 less than 4.7 = 4.7 – 0.1 = 4.6.

Question 10.

Answer:

Explanation:
0.1 more than 2.05 = 0.1 + 2.05 = 2.15.
0.1 less than 2.05 = 2.05 – 0.1 = 1.95.

Question 11.

Answer:

Explanation:
0.01 more than 0.94 = 0.01 + 0.94 = 0.95.
0.01 less than 0.94 = 0.94 – 0.01 = 0.93.

Question 12.

Answer:

Explanation:
0.01 more than 3.8 = 0.01 + 3.8 = 3.81.
0.01 less than 3.8 = 3.8 – 0.01 = 3.79.

Complete the number patterns. Use the number line to help you.

Question 13.
0.2 0.4 0.6 _________ _________
Answer:
0.2     0.4    0.6   0.8   1.0

Explanation:
0.2     0.4    0.6   0.8   1.0
Difference: 0.4 – 0.2 = 0.2.
0.2 + 0.2 = 0.4.
0.4 + 0.2 = 0.6.
0.6 + 0.2 = 0.8.
0.8 + 0.2 = 1.0

Question 14.
1.1 0.9 0.7 _________ ___
Answer:
1.1    0.9    0.7    0.5     0.3

Explanation:
1.1    0.9    0.7    0.5     0.3
Difference: 1.1 – 0.9 = 0.2.
1.1 – 0.2 = 0.9.
0.9 – 0.2 = 0.7.
0.7 – 0.2 = 0.5.
0.5 – 0.2 = 0.3.

Question 15.
0.1 0.4 ________ 1.0 _______
Answer:
0.1    0.4     0.7     1.0     1.3.

Explanation:
0.1    0.4     0.7     1.0     1.3.
Difference: 0.4 – 0.1 = 0.3.
0.1 + 0.3 = 0.4.
0.4 + 0.3 = 0.7.
0.7 + 0.3 = 1.0.
1.0 + 0.3 = 1.3.

Question 16.
2.0 _________ _________ 0.8 0.4
Answer:
2.0      1.6      1.2     0.8      0.4

Explanation:
2.0      1.6      1.2     0.8      0.4
Difference: 0.8 – 0.4 = 0.4.
2.0 – 0.4 = 1.6.
1.6 – 0.4 = 1.2.
1.2 – 0.4 = 0.8.
0.8 – 0.4 = 0.4.

Continue the number patterns.
Question 17.

Answer:
0.03     0.06    0.09     0.12     0.15

Explanation:
0.03     0.06    0.09     0.12     0.15
Difference: 0.06 – 0.03 = 0.03.
0.03 + 0.03 = 0.06.
0.06 + 0.03 = 0.09.
0.09 + 0.03 = 0.12.
0.12 + 0.03 = 0.15.

Question 18.

Answer:
0.24     0.20     0.16      0.12      0.08

Explanation:
0.24     0.20     0.16      0.12      0.08
Difference: 0.24 – 0.20 = 0.04.
0.24 – 0.04 = 0.20.
0.20 – 0.04 = 0.16.
0.16 – 0.04 = 0.12.
0.12 – 0.04 = 0.08.

Practice the problems of Math in Focus Grade 4 Workbook Answer Key Chapter 8 Practice 4 Real-World Problems: Decimals to score better marks in the exam.

Math in Focus Grade 4 Chapter 8 Practice 4 Answer Key Real-World Problems: Decimals

Solve. Show your work.

Example
1 pound of grapes costs $1.79 and 1 pound of peaches costs $1.49. What is the total cost of 1 pound of grapes and 1 pound of peaches?
Cost of grapes + cost of peaches
$1,79 + $1,49 = $3,20
The total cost of 1 pound of grapes and 1 pound of peaches is $323.

Question 1.
A tank is full of water. After 16.5 liters of water are used, 8.75 liters of water are left. How much water was in the full tank?
Answer:
Number of liters of water was in the full tank = 25.25.

Explanation:
Number of liters of water are used = 16.5.
Number of liters of water are left = 8.75.
Number of liters of water was in the full tank = Number of liters of water are used  +  Number of liters of water are left
= 16.5 + 8.75
= 25.25.

Question 2.
A piece of fabric is 4.5 yards long. A customer buys 2.35 yards of the fabric. How many yards of fabric are left?
Answer:
Number of yards of  fabric are left = 2.15.

Explanation:
Number of yards of a piece of fabric = 4.5 yards.
Number of yards of the fabric a customer buys = 2.35 yards.
Number of yards of  fabric are left = Number of yards of a piece of fabric – Number of yards of the fabric a customer buys
= 4.5 – 2.35
= 2.15.

Question 3.
Mr. Larson lives 8.7 miles from school. He was driving home from school and stopped 3.5 miles along the way at a supermarket. How much farther does he have to drive before he reaches home?
Answer:
Number of miles he have to drive before he reaches home = 5.2.

Explanation:
Number of miles Mr. Larson lives from school = 8.7.
Number of miles he was driving home from school and stopped along the way at a supermarket = = 3.5.
Number of miles he have to drive before he reaches home = Number of miles Mr. Larson lives from school – Number of miles he was driving home from school and stopped along the way at a supermarket
= 8.7 – 3.5
= 5.2.

Question 4.
A grocery store is having a sale. A loaf of wheat bread regularly costs $2.29, but the sale price is $1.79. The store is also offering 50¢ off on a gallon of fresh milk. If Mrs. Larson buys a gallon of fresh milk and a loaf of wheat bread, how much does she save on her purchases?
Answer:
Amount of money she save on her purchases = $1.0.

Explanation:
Cost price of a loaf of wheat bread regularly = $2.29.
Selling price of the loaf of wheat bread = $1.79.
Cost of fresh milk a store offering = 50¢.
Amount of money she save on her purchases = (Cost price of a loaf of wheat bread regularly – Selling price of the loaf of wheat bread ) + Cost of fresh milk a store offering
= ($2.29 – $1.79) + 50¢
= $0.5 + 50¢
= $1.0

Question 5.
Lily bought a skirt for $25.90 and a shirt for $19.50. She paid the cashier $50. How much change did she receive?
Answer:
Amount of change she received = $4.6.

Explanation:
Cost of a skirt Lily bought = $25.90.
Cost of a shirt Lily bought = $19.50.
Amount of money she paid the cashier = $50.
Amount of change she received = Amount of money she paid the cashier – (Cost of a skirt Lily bought  + Cost of a shirt Lily bought)
= $50 – ( $25.90 + $19.50)
= $50 – $45.40
= $4.6.

Question 6.
Shannon collects rainwater to water her flowers. She has one bucket with 3.4 gallons of water and another with 1.85 gallons less. She uses both buckets to water the flowers. How many gallons of water does she use?
Answer:
Number of gallons she uses both buckets to water the flowers = 4.95.

Explanation:
Number of gallons one bucket she has = 3.4 gallons.
She has one bucket with 3.4 gallons of water and another with 1.85 gallons less.
=> Number of gallons other bucket she has = Number of gallons one bucket she has – 1.85
=> 3.4 – 1.85
=> 1.55.
Number of gallons she uses both buckets to water the flowers = Number of gallons one bucket she has + Number of gallons other bucket she has
= 3.4 + 1.55
= 4.95.

Practice the problems of Math in Focus Grade 4 Workbook Answer Key Chapter 8 Practice 2 Adding Decimals to score better marks in the exam.

Math in Focus Grade 4 Chapter 8 Practice 2 Answer Key Adding Decimals

Fill in the blanks. Write each sum as a decimal.

Example
0.02 + 0.04 = 2 hundredths + 4 hundredths
= 6 hundredths
= 0.06

Question 1.
0.03 + 0.07 = ___ hundredths + ____ hundredths
= ____ hundreths
= _____
Answer:
0.03 + 0.07 = 0.10.

Explanation:
0.03 + 0.07 = 3 hundredths + 7 hundredths
= 10 hundreths
= 0.10.

Question 2.
0.06 + 0.08 = ___ hundredths + ____ hundredths
= ____ hundreths
= _____
Answer:
0.06 + 0.08 = 0.14.

Explanation:
0.06 + 0.08 = 6 hundredths + 8 hundredths
= 14 hundreths.
= 0.14.

Question 3.
0.09 + 0.05 = ___ hundredths + ____ hundredths
= ____ hundreths
= _____
Answer:
0.09 + 0.05 = 0.14.

Explanation:
0.09 + 0.05 = 9 hundredths + 5 hundredths
= 14 hundreths.
= 0.14.

Fill in the blanks.
Question 4.

Add the hundredths.
4 hundredths + 7 hundredths
= ___ hundredths
Regroup the hundredths.
___ hundredths = ___ tenth ___ hundredth
Step 2

Add the tenths.
3 tenths + 8 tenths + ___ tenth = ___ tenths
Regroup the tenths.
___ tenths = ___ one and ___ tenths
Step 3

Add the ones.
2 ones + 0 ones + ___ one = ___ ones
So, 2.34 + 0.87 = ___.
Answer:
2.34 + 0.87 = 3.21.

Explanation:
Step 1:

Add the hundredths.
4 hundredths + 7 hundredths
= 11 hundredths.
Regroup the hundredths.
11 hundredths = 1 tenth 1 hundredth.
Step 2:

Add the tenths.
3 tenths + 8 tenths + 1 tenth = 12 tenths.
Regroup the tenths.
12 tenths = 1 one and 2 tenths.
Step 3:

Add the ones.
2 ones + 0 ones + 1 one = 3 ones.

Add.
Question 5.

Answer:
0.02 + 0.35 = 0.37.

Explanation:
Step 1:

Add the hundredths.
2 hundredths + 5 hundredths
= 7 hundredths.
Step 2:

Add the tenths.
0 tenths + 3 tenths = 3 tenths.
Step 3:

Add the ones.
0 ones + 0 ones = 0 ones.

Question 6.

Answer:
0.06 + 0.46 = 0.52.

Explanation:
Step 1:

Add the hundredths.
6 hundredths + 6 hundredths
= 12 hundredths.
Regroup the hundredths.
12 hundredths = 1 tenth 2 hundredth.
Step 2:

Add the tenths.
0 tenths + 4 tenths + 1 tenth = 5 tenths.
Step 3:

Add the ones.
0 ones + 0 ones  = 0 ones

Write in vertical form. Then add.
Question 7.
$0.57 + $0.29 = $ _____
Answer:
$0.57 + $0.29 = $0.86.

Explanation:

Question 8.
3.6 + 0.54 = ____
Answer:
3.6 + 0.54 = 4.14.

Explanation:

Question 9.
$0.78 + $0.88 = $____
Answer:
$0.78 + $0.88 = $1.66.

Explanation:

Question 10.
7.25 + 1.78 = ___
Answer:
7.25 + 1.78 = 9.03.

Explanation:

Derek hops two steps on each number line. Which decimal does he land on? Write the correct decimal in each box.
Example

Question 11.

Answer:

Explanation:
10.0 + 1.26 + 2.57
=11.26 + 2.57
= 13.83.

Question 12.

Answer:

Explanation:
50.0 + 2.69 + 1.83
= 52.69 + 1.83
= 54.52.

Question 13.

Answer:

Explanation:
1.2 + 0.36 + 0.38
= 1.56 + 0.38
= 1.94.

This handy Math in Focus Grade 4 Workbook Answer Key Chapter 12 Practice 2 Rectangles and Squares detailed solutions for the textbook questions.

Math in Focus Grade 4 Chapter 12 Practice 2 Answer Key Rectangles and Squares

Find the perimeter of each figure.

Example

Perimeter of rectangle
= 7 + 4 + 7 + 4
= 22 cm
The perimeter of the rectangle is 22 centimeters.

Question 1.

Perimeter of square = 4 × ___________
= _________ in.
The perimeter of the square is ___________inches.
Answer:
In square all four sides are equal.
Perimeter of square = 4 × 6 in
= 24 in.
The perimeter of the square is 24 inches.

Solve. Show your work.

Example

The perimeter of a square flower garden is 20 feet. Find the length of one side of the flower garden.

Length of one side = perimeter ÷ 4
= 20 ÷ 4
= 5 ft
The length of one side of the flower garden so 5 feet.

Question 2.
The perimeter of a square building is 160 yards. Find the length of one side of the building.

Answer:
Perimeter = 160 yards
Length of one side = perimeter ÷ 4
= 160 yards ÷ 4
= 40 yards
The length of one side of the building is 40 yards.

Solve. Show your work.

Question 3.
A square field has a perimeter of 44 meters. Find the length of one side of the field.

Answer:
Perimeter = 44 m
Length of one side = perimeter ÷ 4
= 44 m ÷ 4
= 11 m
The length of one side of the field is 11 m.

Question 4.
The perimeter of a rectangular town is 32 miles. Its width is 5 miles. Find the length.

Answer:
From the above image we can have a data of width and perimeter.
Length = ?
width = 5 mi
perimeter = 32 mi
Perimeter of the rectangular town = length + width + length + width
32 mi = l + 5 mi + l + 5 mi
32 mi = 2l + 10 mi
32 mi – 10 mi = 2l
22 mi = 2l
11 mi = l
The length of the rectangular town is 11 miles.

Solve. Show your work.

Question 5.
The perimeter of a rectangle is 24 centimeters. Its length is 9 centimeters. Find the width.

Answer:
From the above image we can have a data of length and perimeter.
Length = 9 cm
width = ?
perimeter = 24 cm
Perimeter of the rectangle = length + width + length + width
24 cm = 9 cm + w + 9 cm + w
24 cm= 18 cm + 2w
24 cm – 18 cm = 2w
6 cm = 2w
3 cm = w
The width of the rectangle is 3 cm.

Question 6.
The perimeter of a rectangular garden is 18 yards. Its length is 6 yards. Find the width.

Answer:
From the above image we can have a data of length and perimeter.
Length = 6 yards
width = ?
perimeter = 18 yards
Perimeter of the rectangular garden = length + width + length + width
18 yards = 6 yards + w + 6 yards + w
18 yards = 12 yards + 2w
18 yards – 12 yards = 2w
6 yards = 2w
3 yards = w
The width of the rectangular garden is 3 yards.

This handy Math in Focus Grade 7 Workbook Answer Key Chapter 9 Lesson 9.4 Understanding Random Sampling Methods detailed solutions for the textbook questions.

Math in Focus Grade 7 Course 2 B Chapter 9 Lesson 9.4 Answer Key Understanding Random Sampling Methods

Hands-On Activity

Materials:

• list of names of 40 students
• a random number table

EXPLORE HOW A RANDOM SAMPLING PROCESS AFFECTS DATA COLLECTION

Work in groups of four or five.

STEP 1: Choose 40 students to participate in this activity. They will be asked how long it took them to get to school today.

STEP 2: Assign each of the 40 students a 2-digit number from 01 to 40.

STEP 3: Use the random number table to pick five 2-digit numbers. Discard any 2-digit numbers greater than 40.

STEP 4: Ask the 5 students whose numbers match those you picked in STEP 3 the following question and record the results. About how many minutes did it take you to commute to school today?

STEP 5: Find the mean and the mean absolute deviation of the data you collected in STEP 4.

STEP 6: Repeat STEP 3 to STEP 5 to generate new random samples, and to collect and analyze the data from each sample.

Math Journal Does the mean number of minutes vary greatly from sample to sample? Does the mean absolute deviation vary greatly from sample to sample? What are some problems you encountered in the random sampling process? Describe.
Answer:
We got by adding those two-digit numers:
Mean=sum of observations/number of observations.
Mean=4+18+19+27+37/5
Mean=105/5
Mean=21
Now calculate the Mean absolute deviation.
First, subtract the data set values from the mean
|4-21|=17
|18-21|=3
|19-21|=2
|27-21|=6
|37-21|=16
MAD=17+3+2+6+16/5
MAD=44/5
MAD=8.8
Mean varies greatly from sample to sample. comparing to mean MAD varies less.
It is easy to get the data wrong just as it is easy to get right.
The application of random sampling is only effective when all potential respondents are included within the large sampling frame. Everyone or everything that is within the demographic or group being analyzed must be included for the random sampling to be accurate. If the sampling frame is exclusionary, even in a way that is unintended, then the effectiveness of the data can be called into question and the results can no longer be generalized to the larger group.

Hands-On Activity

Materials:

• computer
• relevant books

COMPARE THE STRENGTHS AND WEAKNESSES OF RANDOM SAMPLING METHODS

Work in pairs.

Back ground
Every sampling method has its own strengths and weaknesses. Each method is designed for specific purposes. Sometimes you may find more than one method can be used in a particular situation. At another time, you may find it necessary to combine two methods to obtain the best possible random sample.
Be creative when you apply a random sampling method!

STEP 1: Research the strengths and weaknesses of the three random sampling methods.
STEP 2: Compile the information in a table shown below.

Math Journal Do you find that a weakness of one method can be addressed by another method? Explain.
Answer:
strengths of stratified:
– Has greater ability to make inferences within a stratum and comparisons across strata.
– Has slightly smaller random sampling errors for samples of the same sample size, thereby requiring smaller sample sizes for the same margin of error
– Obtains a more representative sample because it ensures that elements from each stratum are represented in the sample.
Weaknesses:
– Requires information on the proportion of the total population that belongs to each stratum
– Information on stratification variables is required for each element in the population. If such information is not readily available, it may be costly to compile.
– More expensive, time-consuming, and complicated than simple random sampling.
Simple random sampling:
Compared to other probability sampling procedures, simple random sampling has several strengths that should be considered in choosing the type of probability sample design to use Some of these include:
• Advanced auxiliary information on the elements in the population is not required. Such information is required for other probability sampling procedures, such as stratified sampling.
• Each selection is independent of other selections, and every possible combination of sampling units has an equal and independent chance of being selected. In systematic sampling, the chances of being selected are not independent of each other.
• It is generally easier than other probability sampling procedures (such as multistage cluster sampling) to understand and communicate to others.
• Statistical procedures required to analyze data and compute errors are easier than those required of other probability sampling procedures.
On the other hand, simple random sampling has important weaknesses. Compared to other probability sampling procedures, simple random samplings have the following weaknesses:
• A sampling frame of elements in the target population is required. An appropriate sampling frame may not exist for the population that is targeted, and it may not be feasible or practical to construct one. Alternative sampling procedures, such as cluster sampling, do not require a sampling frame of the elements of the target population.
• Simple random sampling tends to have larger sampling errors and less precision than stratified samples of the same sample size. Respondents may be widely dispersed; hence, data collection costs might be higher than those for other probability sample designs such as cluster sampling.
• Simple random sampling may not yield sufficient numbers of elements in small subgroups. This would not make simple random sampling a good choice for studies requiring comparative analysis of small categories of the population with much larger categories of the population
Strengths of systematic random sampling:
1. If the selection process is manual, systematic sampling is easier, simpler, less time-consuming, and more economical.
2. The target population need not be numbered and a sampling frame compiled if there is a physical representation.
3. If the ordering of the elements in the sampling frame is randomized, systematic sampling may yield results similar to simple random sampling.
Weaknesses:
1. If the sampling interval is related to the periodic ordering of the elements in the sampling frame, increased variability may result.
2. Combinations of elements have different probabilities of being selected.
3. Technically, only the selection of the first element is a probability selection since for subsequent selections, there will be elements of the target population that will have a zero chance of being selected.

Math in Focus Grade 7 Chapter 9 Lesson 9.4 Guided Practice Answer Key

Determine which sampling method is best suited for each situation.

Question 1.
Describe how you would carry out the sampling process. You may use a combination of methods, if you see fIt. Justify your process.
Scenario 1
A truck load of 3OOO oranges were delivered to a wholesale market. You are allowed to check 1% of the oranges as a random sample before deciding whether to accept the shipment.

Scenario 2
A grocer would like to find what items the store should carry to attract more customers. The grocer wants to survey loo people in the neighbourhood.
Answer:
Scenario 1:  Systematic random sampling: Scenario 1 uses random sampling because you want the sample to cover a wide range of oranges in the shipment.
Scenario 2: Simple random sampling: Scenario 2 uses simple random sampling because it is just an opinion poll of people in the neighbourhood.

Math in Focus Course 2B Practice 9.5 Answer Key

Answer the following.

Question 1.
Explain what a random sampling process is.
Answer:
Random sampling is a method of choosing a sample of observations from a population to make assumptions about the population. It is also called probability sampling. The counterpart of this sampling is Non-probability sampling or Non-random sampling. The primary types of this sampling are simple random sampling, stratified sampling, cluster sampling, and multistage sampling. In the sampling methods, samples that are not arbitrary are typically called convenience samples.
The primary feature of probability sampling is that the choice of observations must occur in a ‘random’ way such that they do not differ in any significant way from observations, which are not sampled. We assume here that statistical experiments contain data that is gathered through random sampling.

Question 2.
Give an example of how a random sampling process is used in a real-world situation.
Answer:
– At a birthday party, teams for a game are chosen by putting everyone’s name into a jar, and then choosing the names at random for each team.
– On an assembly line, each employee is assigned a random number using computer software. The same software is used periodically to choose a number of the employees to be observed to ensure they are employing best practices.
– A restaurant leaves a fishbowl on the counter for diners to drop their business cards. Once a month, a business card is pulled out to award one lucky diner with a free meal.
– At a bingo game, balls with every possible number are placed inside a mechanical cage. The caller rotates the cage, tumbling around the balls inside. Then, she selects one of the balls at random to be called, like B-12 or O-65.
– A pharmaceutical company wants to test the effectiveness of a new drug. Volunteers are assigned randomly to one of two groups. The first group will receive the new drug; the second group will receive a placebo.

Question 3.
Why do people want to use random samples to collect information about a population?
Answer:
Random sampling offers two primary advantages. Because individuals who make up the subset of the larger group are chosen at random, each individual in the large population set has the same probability of being selected. This creates, in most cases, a balanced subset that carries the greatest potential for representing the larger group as a whole.
Moreover, they want to collect information to understand the characteristics of the population.

Question 4.
Explain why a biased sample is not an appropriate sample.
Answer:
Sampling bias occurs when some members of a population are systematically more likely to be selected in a sample than others. It is also called ascertainment bias in medical fields. Sampling bias limits the generalizability of findings because it is a threat to external validity, specifically population validity. In other words, findings from biased samples can only be generalized to populations that share characteristics with the sample.

State which sampling method is being described.

Question 5.
A frozen yogurt store sells 5 flavors: vanilla, chocolate, strawberry, macadamia nut, and peppermint. To check the quality of the frozen yogurt, 5 tubs of each flavor were sampled.

Answer: Stratified random sampling.
Definition: In this sampling method, a population is divided into subgroups to obtain a simple random sample from each group and complete the sampling process (for example, number of girls in a class of 50 strength). These small groups are called strata. The small group is created based on a few features in the population. After dividing the population into smaller groups, the researcher randomly selects the sample.

Question 6.
A group of students conducted an online poll of Internet users by randomly selecting 500 Internet users.
Answer: Clustered sampling
Definition:
Cluster sampling is similar to stratified sampling, besides the population is divided into a large number of subgroups (for example, hundreds of thousands of strata or subgroups). After that, some of these subgroups are chosen at random and simple random samples are then gathered within these subgroups. These subgroups are known as clusters. It is basically utilised to lessen the cost of data compilation.

Question 7.
To check the freshness of the bagels at a bakery, the baker randomly picked 5 bagels at an interval of every hour.
Answer: Systematic random sampling
In this method, the items are chosen from the destination population by choosing the random selecting point and picking the other methods after a fixed sample period. It is equal to the ratio of the total population size and the required population size.

Question 8.
Unique numbers were assigned to the members of a country club. The club manager used a random number generator to choose 150 numbers that were matched to members of the club.
Answer: Stratified random sampling.
In this sampling method, a population is divided into subgroups to obtain a simple random sample from each group and complete the sampling process (for example, number of girls in a class of 50 strength). These small groups are called strata. The small group is created based on a few features in the population. After dividing the population into smaller groups, the researcher randomly selects the sample.

Question 9.
Out of 100 students, the teachers randomly choose the first student and every sixth student thereafter.
Answer: Systematic random sampling
In this method, the items are chosen from the destination population by choosing the random selecting point and picking the other methods after a fixed sample period. It is equal to the ratio of the total population size and the required population size.

Question 10.
To assess pollution levels in a region, water samples are taken from 5 rivers and 2 lakes for analysis.
Answer: Stratified random sampling.
In this sampling method, a population is divided into subgroups to obtain a simple random sample from each group and complete the sampling process (for example, number of girls in a class of 50 strength). These small groups are called strata. The small group is created based on a few features in the population. After dividing the population into smaller groups, the researcher randomly selects the sample.

Refer to the situation to answer the following.

Question 11.
Math Journal A corn field is divided into five areas. To determine whether the corn plants are healthy, you are asked to collect a random sample of 100 ears of corn for analysis.
a) If you use a stratified random sampling method, describe how you will go about collecting the random sample.
Answer:
In this sampling method, a population is divided into subgroups to obtain a simple random sample from each group and complete the sampling process (for example, number of girls in a class of 50 strength). These small groups are called strata. The small group is created based on a few features in the population. After dividing the population into smaller groups, the researcher randomly selects the sample.
according to the definition, we can write:
The 5 areas of the cornfield constitute 5 groups of corn plants. 20 ears of corn are randomly selected from each group.

b) Explain why the stratified random sampling method is preferred.
Answer:
It gives a fair representation of each of the five areas that’s why the stratified random sampling method is preferred.

Question 12.
Math Journal Explain why the simple sampling method may not give you a representative sample.
Answer:
When a sample is not representative, we will have a sampling error known as the margin of error. If we want to have a representative sample of 100 employees, we must choose a similar number of men and women. For example, if we have a sample inclined to a specific genre, then we will have an error in the sample.
The sample size is essential, but it does not guarantee that it accurately represents the population that we need. More than size, representativeness is related to the sampling frame, that is, to the list from which people are selected, for example, part of a survey. Therefore, we must take care that people from our target audience are included in that list to say that it is a representative sample.

Refer to the situation below to answer the following.

2,000 runners participated in a marathon. You want to randomly choose 60 of the runners to find out how long ¡t took each one to run the race.

Question 13.
Describe how you would select the 60 runners if you use a simple random sampling method.
Answer:
In this sampling method, each item in the population has an equal and likely possibility of getting selected in the sample (for example, each member in a group is marked with a specific number). Since the selection of item completely depends on the possibility, therefore this method is called the “Method of chance Selection”. Also, the sample size is large, and the item is selected randomly. Thus it is known as “Representative Sampling”.
According to the definition:
Pick runners randomly in the marathon to interview until 60 runners have been interviewed.

Question 14.
Describe how you would select the 60 runners if you use a systematic random sampling method.
Answer:
In this method, the items are chosen from the destination population by choosing the random selecting point and picking the other methods after a fixed sample period. It is equal to the ratio of the total population size and the required population size.
according to the definition:
Picking a few numbers out of a hat, but you can use any number of runners as long as you have a minimum size.

Question 15.
Describe how you would select the 60 runners if you use the stratified random sampling method.
Answer:
In this sampling method, a population is divided into subgroups to obtain a simple random sample from each group and complete the sampling process (for example, number of girls in a class of 50 strength). These small groups are called strata. The small group is created based on a few features in the population. After dividing the population into smaller groups, the researcher randomly selects the sample.
According to the definition:
Use age bands, for example, select randomly 15 runners from each of the 4 age bands. Below 20, 20 to 30, 30 to 40, and above 40.

Refer to the situation below to answer the following.

There are 1,650 trees growing in 5 areas within a park. The trees are numbered from 1 to 1,650. A systematic random sample of 40 trees is needed to check whether there are fungi causing root rot among the trees.

Question 16.
Describe how you would carry out a systematic random sampling.
Answer:
In this method, the items are chosen from the destination population by choosing the random selecting point and picking the other methods after a fixed sample period. It is equal to the ratio of the total population size and the required population size.
According to the definition:
Out of 1,650 trees, the researchers randomly choose the first tree and every sixth tree thereafter. Likewise, they select the fixed sample tree and check the trees if they are fungi causing root among the trees.

Question 17.
Describe how you would carry out a stratified random sampling.
Answer:
In this sampling method, a population is divided into subgroups to obtain a simple random sample from each group and complete the sampling process (for example, number of girls in a class of 50 strength). These small groups are called strata. The small group is created based on a few features in the population. After dividing the population into smaller groups, the researcher randomly selects the sample.
According to the definition:
Use the 5 areas of 5 groups of trees in the park and randomly select 8 trees within each area.

Refer to the situation below to answer the following.

Question 18.
A poll is taken in a small town to find out which candidate voters will choose in an election. A stratified sampling method is used to generate a random sample of 500 residents. The table shows the town population and the sample size within each group.

a) The stratified random sample has been criticized for not being representative of the population. What could possibly be the problem with the random sample?
Answer:
In the stratified random sampling method, we divide the groups into subgroups but in the representative the sample size is large, and the item is selected randomly. Moreover, the problem with the random sample is below:
1. No additional knowledge is taken into consideration.
Here a number of residents are more: 5000-men; 8000 women. From this, we need to select 500 residents in total.
Although random sampling removes an unconscious bias that exists, it does not remove an intentional bias from the process. Researchers can choose regions for random sampling where they believe specific results can be obtained to support their own personal bias. No additional knowledge is given consideration from the random sampling, but the additional knowledge offered by the researcher gathering the data is not always removed.
2. It is a complex and time-consuming method of research. With random sampling, every person or thing must be individually interviewed or reviewed so that the data can be properly collected. When individuals are in groups, their answers tend to be influenced by the answers of others. This means a researcher must work with every individual on a 1-on-1 basis. This requires more resources, reduces efficiencies, and takes more time than other research methods when it is done correctly.

b) How would you improve the above stratified random sampling?
Answer:
1. Stratified Random Sampling provides better precision as it takes the samples proportional to the random population.
2. Stratified Random Sampling helps minimize the biasness in selecting the samples.
3. Stratified Random Sampling ensures that no section of the population is underrepresented or overrepresented.
4. As this method provides greater precision, a greater level of accuracy can be achieved even by using a small size of samples. This saves resources.