Hillary

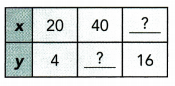
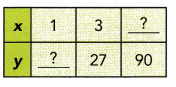
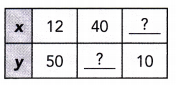
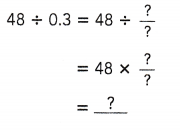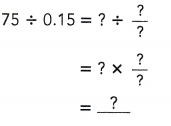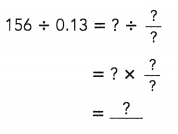Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 6 Lesson 6.2 Fractions, Decimals, and Percents to score better marks in the exam.

Math in Focus Grade 6 Course 1 A Chapter 6 Lesson 6.2 Answer Key Fractions, Decimals, and Percents

Hands-On Activity

EXPRESSING FRACTIONS OR MIXED NUMBERS AS PERCENTS

Work in pairs.

Use these fractions and mixed numbers.

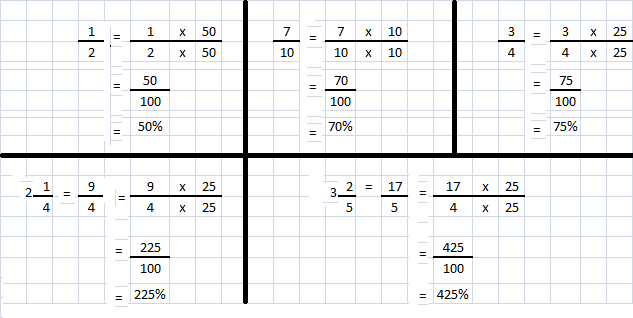
STEP 1: Find which of the fractions or mixed numbers can be expressed as percents using the method of writing an equivalent fraction. List the fractions that cannot be expressed as percents using this method.
Example

Answer:

STEP 2: If you want to use the method of writing an equivalent fraction to express a fraction as a percent, what must be true of the fraction or mixed number?
Explanation:
The denominator must me 100 in the fraction,
then the fraction in the numerator is expressed as percentage.
fractions with denominator with 9, 8 , 6, 3 can not be expressed as 100 in the denominator.

Math Journal Explain how you would express 1\(\frac{3}{4}\) as a percent.
Answer:
175%
Explanation:
Express 1\(\frac{3}{4}\) as a percent.
\(\frac{7}{4}\)
To express the fraction with denominator 100,
multiply both the numerator and denominator with 25
= \(\frac{175}{100}\)
= 175%

Math in Focus Grade 6 Chapter 6 Lesson 6.2 Guided Practice Answer Key

Express each fraction or mixed number as a percent.

Question 1.
\(\frac{4}{7}\) = \(\frac{4}{7}\) × %
= \(\frac{?}{?}\) %
= %
Answer:
57%
Explanation:
\(\frac{4}{7}\) = \(\frac{4}{7}\) × 100%
= \(\frac{400}{7}\) %
= 57%

Question 2.
1\(\frac{5}{9}\) = 1\(\frac{5}{9}\) × %
= \(\frac{?}{9}\) × %
= %
Answer:
155%
Explanation:
1\(\frac{5}{9}\) =1 \(\frac{5}{9}\) × 100%
= \(\frac{14}{9}\) x 100%
= 155%

Question 3.
\(\frac{5}{6}\)
Answer:
83%
Explanation:
\(\frac{5}{6}\) = \(\frac{5}{6}\) × 100%
= \(\frac{500}{6}\) %
= 83%

Question 4.
1\(\frac{7}{8}\)
Answer:
187.5%
Explanation:
1\(\frac{7}{8}\) = 1\(\frac{7}{8}\) × 100%
= \(\frac{15}{8}\) x 100 %
= 187.5%

Complete.

Question 5.
Express 0.82 as a percent.
Method 1
0.82 = \(\frac{?}{100}\)
=

Method 2
0.82 = \(\frac{?}{9}\) × 100 %
=
Answer:
82%
Explanation:
Express 0.82 as a percent.
Method 1
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
0.82 = \(\frac{82}{100}\)
= 0.82

Express each decimal as a percent.

Question 6.
0.04
Answer:
4%
Explanation:
Express 0.04 as a percent.
Method 1
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
0.04 = \(\frac{4}{100}\)
= 0.04

Question 7.
0.98
Answer:
98%
Explanation:
Express 0.98 as a percent.
Method 1
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
0.98 = \(\frac{98}{100}\)
= 0.98

Question 8.
0.6
Answer:
60%
Explanation:
Express 0.6 as a percent.
Method 1
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
0.6 = \(\frac{60}{100}\)
= 0.6

Express each percent as a fraction in simplest form.

Question 9.
83\(\frac{1}{3}\) %
Answer:
8333.33
Explanation:
83 \(\frac{1}{3}\)%
= \(\frac{250}{3}\) x 100
= 8333.33

Question 10.
84.4%
Answer:
\(\frac{211}{250}\)
Explanation:
84.4% = \(\frac{84.4}{100}\)
multiply the numerator and denominator with 10,
as numerator has decimal
= \(\frac{844}{1000}\)
Divided numerator and denominator with 2 to simplify
= \(\frac{211}{250}\)

Math in Focus Course 1A Practice 6.2 Answer Key

Express each fraction or mixed number as a percent.

Question 1.
\(\frac{3}{5}\)
Answer:
60%
Explanation:
Simplify the given fraction
\(\frac{3}{5}\) = 0.6
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
0.6 x 100 = 60%

Question 2.
\(\frac{3}{8}\)
Answer:
37.5%
Explanation:
Simplify the given fraction
\(\frac{3}{8}\) = 0.375
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
0.375 x 100 = 37.5%

Question 3.
\(\frac{1}{3}\)
Answer:
33%
Explanation:
Simplify the given fraction
\(\frac{1}{3}\) = 0.33
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
0.33 x 100 = 33%

Question 4.
2\(\frac{1}{5}\)
Answer:
220%
Explanation:
Simplify the given fraction
2\(\frac{1}{5}\)
= \(\frac{11}{5}\) = 2.2
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
2.2 x 100 = 220%

Question 5.
7\(\frac{3}{4}\)
Answer:
442%
Explanation:
Simplify the given fraction
7\(\frac{3}{4}\)
\(\frac{31}{7}\) = 4.42
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
4.42 x 100 = 442%

Question 6.
9\(\frac{7}{8}\)
Answer:
987%
Explanation:
Simplify the given fraction
9\(\frac{7}{8}\)
\(\frac{79}{8}\) = 9.87
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
9.87 x 100 = 987%

Express each decimal as a percent.

Question 7.
0.46
Answer:
46%
Explanation:
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
0.46 x 100 = 46%

Question 8.
0.7
Answer:
70%
Explanation:
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
0.7 x 100 = 70%

Question 9.
0.06
Answer:
6%
Explanation:
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
0.06 x 100 = 6%

Question 10.
1.52
Answer:
152%
Explanation:
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
1.52 x 100 = 152%

Question 11.
6.03
Answer:
603%
Explanation:
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
6.03 x 100 = 603%

Question 12.
8.9
Answer:
890%
Explanation:
Converting from a decimal to a percentage is done by multiplying the decimal value by 100 and adding %.
8.9 x 100 = 890%

Express each percent as a fraction in simplest form.

Question 13.
5.75%
Answer:
\(\frac{23}{400}\)
Explanation:
5.75% can be written as \(\frac{5.75}{100}\)
To convert percent as a fraction in simplest form,
multiply with 100 on both numerator and denominator.
\(\frac{5.75}{100}\) X \(\frac{100}{100}\)
= \(\frac{575}{10000}\)
Simplify the fraction divided with the greatest common factor 5 on both sides.
= \(\frac{23}{400}\)

Question 14.
25.5%
Answer:
\(\frac{51}{200}\)
Explanation:
25.5% can be written as \(\frac{25.5}{100}\)
To convert percent as a fraction in simplest form,
multiply with 10 on both numerator and denominator.
\(\frac{25.5}{100}\) X \(\frac{100}{100}\)
= \(\frac{255}{1000}\)
Simplify the fraction divided with the greatest common factor 5 on both sides.
= \(\frac{51}{200}\)

Question 15.
85.25%
Answer:
\(\frac{341}{400}\)
Explanation:
85.25% can be written as \(\frac{85.25}{100}\)
To convert percent as a fraction in simplest form,
multiply with 100 on both numerator and denominator.
\(\frac{85.25}{100}\) X \(\frac{100}{100}\)
= \(\frac{8525}{10000}\)
Simplify the fraction divided with the greatest common factor 5 on both sides.
= \(\frac{341}{400}\)

Question 16.
16\(\frac{2}{3}\) %
Answer:
\(\frac{1}{6}\)
Explanation:
16\(\frac{2}{3}\) %
= \(\frac{50}{3}\) %
= \(\frac{50}{3}\) X \(\frac{100}{100}\)
= \(\frac{1}{6}\)

Question 17.
42\(\frac{3}{8}\)%
Answer:
\(\frac{339}{800}\)
Explanation:
42\(\frac{3}{8}\) %
= \(\frac{339}{8}\) %
= \(\frac{339}{8}\) X \(\frac{100}{100}\)
= \(\frac{339}{800}\)

Question 18.
79\(\frac{5}{6}\) %
Answer:
\(\frac{479}{600}\)
Explanation:
79\(\frac{5}{6}\) %
= \(\frac{479}{6}\) %
= \(\frac{479}{6}\) X \(\frac{100}{100}\)
= \(\frac{479}{600}\)

Express each fraction as a percent. Round your answer to the nearest whole number.

Question 19.
\(\frac{76}{125}\)
Answer:
61%
Explanation:
\(\frac{76}{125}\) = 0.608
Round 0.608 to the nearest whole number = 61
So, percentage of fraction = 61%

Question 20.
\(\frac{98}{230}\)
Answer:
43%
Explanation:
\(\frac{98}{230}\) = 0.426
Round 0.426 to the nearest whole number = 43
So, percentage of fraction = 43%

Question 21.
\(\frac{102}{350}\)
Answer:
29%
Explanation:
\(\frac{102}{350}\) = 0.291
Round 0.291 to the nearest whole number = 29
So, percentage of fraction = 29%

Find the missing fractions and decimals.

Question 22.

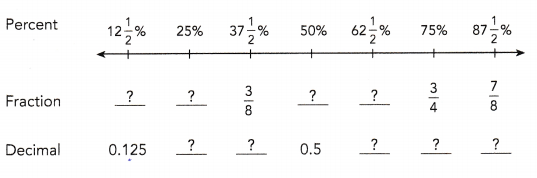
Answer:

Explanation:
The below fractions are missing fractions.
a)12\(\frac{1}{2}\) %
= \(\frac{25}{2}\) %
= \(\frac{25}{2}\) X 100
= \(\frac{25}{200}\)
= \(\frac{1}{8}\)

b) 25%
= \(\frac{25}{100}\) %
= \(\frac{25}{100}\)
= \(\frac{1}{4}\)

c) 37\(\frac{1}{2}\) %
= \(\frac{75}{2}\) %
= \(\frac{75}{2}\) X \(\frac{100}{100}\)
= \(\frac{75}{200}\)
= \(\frac{3}{8}\)

d) 50%
= \(\frac{50}{100}\)
= \(\frac{1}{2}\)

e) 62\(\frac{1}{2}\) %
= \(\frac{125}{2}\) %
= \(\frac{125}{2}\) X \(\frac{100}{1}\)
= \(\frac{125}{200}\)
= \(\frac{5}{8}\)

f) 75%
= \(\frac{75}{100}\)
= \(\frac{3}{4}\)

g) 87\(\frac{1}{2}\) %
= \(\frac{175}{2}\) %
= \(\frac{175}{2}\) X \(\frac{100}{1}\)
= \(\frac{175}{200}\)
= \(\frac{7}{8}\)

Below are the missing decimals.
a) 25%
\(\frac{25}{100}\) = 0.25
b) \(\frac{3}{8}\) = 0.375
c) \(\frac{5}{8}\) = 0.625
d) \(\frac{3}{4}\) = 0.75
e) \(\frac{7}{8}\) = 0.87

Solve. Show your work.

Question 23.
Math Journal School A has 450 seniors, and 432 of them plan to go to college. School B has 380 seniors, and 361 of them plan to go to college. In which school does a greater percent of students plan to go to college? Justify your reasoning.
Answer:
In School A
Explanation:
School A has 450 seniors, and 432 of them plan to go to college.
A = \(\frac{432}{450}\)
percentage of the students = \(\frac{432}{450}\) X 100 = 96%
School B has 380 seniors, and 361 of them plan to go to college.
B = \(\frac{361}{380}\)
percentage of the students = \(\frac{361}{380}\) = 95%
So, greater percent of students plan to go to college are School A.

Practice the problems of Math in Focus Grade 7 Workbook Answer Key Cumulative Review Chapters 3-5 to score better marks in the exam.

Math in Focus Grade 7 Course 2 A Cumulative Review Chapters 3-5 Answer Key

Concepts and Skills

Simplify each expression. (Lessons 3.1, 3.2, 3.3)

Question 1.
3.9p + 0.9p – 1.8p
Answer:
3.9p + 0.9p – 1.8p
= 4.8p – 1.8p
= 3.0p

Question 2.
\(\frac{8}{3}\)x – \(\frac{3}{5}\)y + \(\frac{2}{5}\)x + \(\frac{7}{4}\)y
Answer:
\(\frac{8}{3}\)x – \(\frac{3}{5}\)y + \(\frac{2}{5}\)x + \(\frac{7}{4}\)y

= \(\frac{8}{3}\)x + \(\frac{2}{5}\)x + \(\frac{7}{4}\)y – \(\frac{3}{5}\)y

= \(\frac{(8 x 5) + (2 x 3)}{(3 x 5)}\)x + \(\frac{(7 x 5) – (3 x 4)}{(4 x 5)}\)y

= \(\frac{(40) + (6)}{15}\)x + \(\frac{(35) – (12)}{20}\)y

= \(\frac{46}{15}\)x + \(\frac{23}{20}\)y

Expand and simplify each expression. (Lesson 3.4)

Question 3.
-0.2(0.8q – 4)
Answer:
-0.2(0.8q – 4)
= (-0.2) x (0.8q) + (-0.2) x (-4)
= – 0.16q + 0.8

Question 4.
–\(\frac{2}{3}\)(-\(\frac{3}{4}\)y – \(\frac{1}{2}\))
Answer:
–\(\frac{2}{3}\)(-\(\frac{3}{4}\)y – \(\frac{1}{2}\))

= \(\frac{-2}{3}\)(\(\frac{-3}{4}\)y + \(\frac{-1}{2}\))

=(\(\frac{-2 X -3}{3 X 4}\)y) + (\(\frac{-2 X -1}{3 X 2}\))

=\(\frac{2}{4}\)y + \(\frac{1}{3}\)

=\(\frac{1}{2}\)y + \(\frac{1}{3}\)

Question 5.
5(\(\frac{1}{15}\)x – 6y) – \(\frac{1}{3}\)x
Answer:
5(\(\frac{1}{15}\)x – 6y) – \(\frac{1}{3}\)x

=\(\frac{5 X 1}{15}\)x – (5 X 6)y – \(\frac{1}{3}\)x

= \(\frac{5}{15}\)x – 30y – \(\frac{1}{3}\)x

= \(\frac{5}{5 X 3}\)x – 30y – \(\frac{1}{3}\)x

= \(\frac{1}{3}\)x – 30y – \(\frac{1}{3}\)x

= \(\frac{1}{3}\)x – \(\frac{1}{3}\)x – 30y

= -30y

Question 6.
2(m – n) – 6(n – 2m)
Answer:
2(m – n) – 6(n – 2m)
=2m – 2n -6n + 12m
=2m + 12m -2n-6n
=14m-8n

Write an algebraic expression for the shaded area shown in questions 7 and 8. Then expand and simplify the expression. (Lesson 3.4)

Question 7.

Answer:
Length = x in
Base = (y + x) in
Height = 5 m
Area of Trapezium = \(\frac{5}{2}\)(x + y + x) m²
\(\frac{5}{2}\)(x + y + x) m²
= \(\frac{5}{2}\)(2x + y) m² Add like terms
= \(\frac{5}{2}\)(2x) + \(\frac{5}{2}\)(y) m² Use Distributive Property
= (5x + \(\frac{5}{2}\)y)m² Multiply

Question 8.

Answer:
Big Rectangle :
Length = 12 + x + x = (12 + 2x) m
width = 10 in
Area of Big Rectangle = Length × Width = (12 + 2x) ∙ (10)
= 12(10) + 2x(10) = (120 + 20x) m²
Small Rectangle :
Length = 12 m
Width = 2x m
Area of Small Rectangle = Length × Width = 12 ∙ 2x = 24x m²
Area of shaded area = (120 + 20x) – 24x m²
= (120 + 20x) – 24x
= 120 + 20x – 24x
= (120 – 4x) m²
Area = (120 + 20x — 24x) m² = (120 – 4x) m²

Factor each expression. (Lesson 3.5)

Question 9.
-4k – 36
Answer:
-4k – 36
= (-4)k + (-4)(9)
= -4(k + 9)

Question 10.
9 + 15m – 21n
Answer:
9 + 15m – 21n
=(3)(3) + (3)(5)m – (3)(7)n
= 3(3 + 5m – 7n)

Translate each verbal description into an algebraic expression. Simplify the expression when you can. (Lesson 3.6)

Question 11.
50% of one-twentieth of the product of 12 and 5z + 5.
Answer:
50% of one-twentieth of the product of 12 and 5z + 5

=(50%) X (\(\frac{1}{20}\)) X (12) X (5z + 5)

= (\(\frac{50}{100}\)) X (\(\frac{1}{20}\)) X (12) X (5z + 5)

= (\(\frac{1}{2}\)) X (\(\frac{1}{20}\)) X (12) X (5z + 5)

= (\(\frac{1 X 1 X 12}{2 X 20}\)) X (5z + 5)

= (\(\frac{12}{40}\)) X (5z + 5)

= (\(\frac{12}{40}\)) X (5z + 5)

= (\(\frac{3}{10}\)) X (5z + 5)

= (\(\frac{3}{10}\)) X (5)(z + 1)

=(\(\frac{3 X 5}{10}\)) X (z + 1)

=(\(\frac{3}{2}\)) X (z + 1)

=\(\frac{3}{2}\)z +\(\frac{3}{2}\)

Question 12.
21 plus 6p minus two-thirds the sum of 14p and 3q.
Answer:
21 plus 6p minus two-thirds the sum of 14p and 3q
= 21 + 6p – \(\frac{2}{3}\)(14p + 3q)

= 21 + 6p – \(\frac{2 X 14p}{3}\) – \(\frac{2 X 3q}{3}\)

= 21 + 6p – \(\frac{2 X 14p}{3}\) – \(\frac{2 X 3q}{3}\)

= 21 + 6p – \(\frac{28p}{3}\) – 2q

= 21 + \(\frac{3 X 6p}{3}\) – \(\frac{28p}{3}\) – 2q

= 21 + \(\frac{18p}{3}\) – \(\frac{28p}{3}\) – 2q

= 21 + \(\frac{18p-28p}{3}\)– 2q

= 21 + \(\frac{-10p}{3}\)– 2q

= 21 – \(\frac{10}{3}\)p- 2q

Tell whether each pair of equations are equivalent. (Lesson 4.1)

Question 13.
x – 7 = 1 and x = 6
Answer:
The above equations are not equivalent
If x = 6, and if we substitute it in
x – 7 = 1
(6) – 7 = 1
-1 = 1  -> False

Hence they are not equivalent.

Question 14.
0.2x = 0.6 and 3x + 1 =10
Answer:
The above equations are equivalent.
Equation 1
0.2x = 0.6
2x = 6
x = 3

Equation 2
3x + 1 = 10
3(3) + 1 = 10
9 + 1 = 10
10 = 10  -> True

Hence they are equivalent.

Solve each equation. (Lesson 4.2)

Question 15.
11 + 4k = 7
Answer:
11 + 4k = 7
4k = 7 – 11
4k = -4
k = -1

Question 16.
5p + \(\frac{2}{15}\) = \(\frac{3}{5}\) + \(\frac{4}{5}\)p
Answer:

5p + \(\frac{2}{15}\) = \(\frac{3}{5}\) + \(\frac{4}{5}\)p

5p – \(\frac{4}{5}\)p = \(\frac{3}{5}\) – \(\frac{2}{15}\)

\(\frac{5 X 5}{5}\)p – \(\frac{4}{5}\)p = \(\frac{3 X 3}{5 X 3}\) – \(\frac{2}{15}\)

\(\frac{25}{5}\)p – \(\frac{4}{5}\)p = \(\frac{9}{15}\) – \(\frac{2}{15}\)

\(\frac{21}{5}\)p = \(\frac{7}{15}\)

\(\frac{7 X 3}{5}\)p = \(\frac{7}{5 X 3}\)

\(\frac{3}{1}\)p = \(\frac{1}{3}\)

3p = \(\frac{1}{3}\)

p = \(\frac{1}{3 X 3}\)

p = \(\frac{1}{9}\)

Question 17.
\(\frac{8}{9}\)(4x – 3) = \(\frac{2}{3}\)
Answer:
\(\frac{8}{9}\)(4x – 3) = \(\frac{2}{3}\)

\(\frac{4 X 2}{3 X 3}\)(4x – 3) = \(\frac{2}{3}\)

\(\frac{4}{3}\)(4x – 3) = \(\frac{2 X 3}{3 X 2}\)

\(\frac{4}{3}\)(4x – 3) = \(\frac{1}{1}\)

\(\frac{4}{3}\)(4x – 3) = 1

4(4x – 3) = 3
(4)(4x) – (4)(3) = 3
16x – 12 = 3
16x = 3 + 12
16x = 15

x = \(\frac{15}{16}\)

Question 18.
7(x + 5) – 3x = x – 7
Answer:
7(x + 5) – 3x = x – 7
7x + 35 – 3x = x – 7
7x  – 3x – x = – 7 – 35
7x – 4x = -42
3x = – 42
x = -14

Solve each inequality. Then graph each solution set on a number line. (Lesson 4.4)

Question 19.
8x – 7 > 9
Answer:
8x – 7 > 9
8x > 9 + 7
8x > 16
x > 2

Question 20.
6 + \(\frac{2}{5}\)y ≤ \(\frac{1}{3}\)y + 6\(\frac{1}{3}\)
Answer:

6 + \(\frac{2}{5}\)y ≤ \(\frac{1}{3}\)y + 6\(\frac{1}{3}\)

\(\frac{2}{5}\)y – \(\frac{1}{3}\)y ≤ 6\(\frac{1}{3}\) – 6

\(\frac{2}{5}\)y – \(\frac{1}{3}\)y ≤ \(\frac{1}{3}\)

\(\frac{2 X 3}{5 X 3}\)y – \(\frac{1 X 5}{3 X 5}\)y ≤ \(\frac{1}{3}\)

\(\frac{6}{15}\)y – \(\frac{5}{15}\)y ≤ \(\frac{1}{3}\)

\(\frac{1}{15}\)y ≤ \(\frac{1}{3}\)

y ≤ \(\frac{15}{3}\)

y ≤ \(\frac{5 X 3}{3}\)

y ≤ 5

Question 21.
1.8(x – 5) ≥ 0.2(x – 13)
Answer:
1.8(x – 5) ≥ 0.2(x – 13)
(10)(1.8)(x – 5) ≥ (10)(0.2)(x – 13)
18(x – 5) ≥ 2(x – 13)
9(x – 5) ≥ 1(x – 13)
9x – 45 ≥ x – 13
9x – x ≥ -13 + 45
8x ≥ 32
x ≥ 4

Question 22.
2(3 – r) + 4(1 + 3r) > – 2(3 – 7r)
Answer:
2(3 — r) + 4(1 + 3r) > —2(3 — 7r)
2(3) + 2(—r) + 4(1) + 4(3r) > —2(3) + (—2)(—7r) Use Distributive Property
6 — 2r + 4 + 12r > —6 + 14r Multiply
10r + 10 > —6 + 14r Combine like terms
10r + 10 — 10 > —6 + 14r — 10 Subtract 10 from both sides
10r > -16 + 14r Simplify
10r – 14r > -16 + 14r – 14r Subtract 14r from both sides
-4r > -16 Simplify
-4r > -16
\(\frac{-4}{-4} r\) > \(\frac{-16}{-4}\) Divide both sides by -4 and reverse sign of inequality
r < 4

Use shaded circle for ≥ or ≤ and empty circle for < or >
The number line for r < 4 is shown

Tell whether each table, equation, or graph represents a direct proportion, an inverse proportion, or neither. Find the constant of proportionality for the direct and inverse proportion identified. (Lessons 5.1, 5.2, 5.4)

Question 23.

Answer:

Direct Proportion :
For each pair of values x and y →
\(\frac{y}{x}\) = \(\frac{12}{1.5}\) = 8
\(\frac{y}{x}\) = \(\frac{20}{2.5}\) = 8
\(\frac{y}{x}\) = \(\frac{28}{3.5}\) = 8
\(\frac{y}{x}\) is a constant so x and y is direct proportional
Inverse proportion :
For each pair of values x and y →
xy = 1.5 ∙ 12 = 18
xy = 2.5 ∙ 20 = 50
xy = 3.5 ∙ 28 = 98
xy is not a constant so y is not inversely proportional to x
NOTE:
Direct proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in Inverse proportion then their product is a constant of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Direct Proportion

Question 24.

Answer:

Direct Proportion :
For each pair of values x and y →
\(\frac{y}{x}\) = \(\frac{90}{10}\) = 9
\(\frac{y}{x}\) = \(\frac{45}{20}\) = 2.25
\(\frac{y}{x}\) = \(\frac{30}{30}\) = 1
\(\frac{y}{x}\) is not a constant so x and y is not direct proportional

Inverse Proportion :
For each pair of values x and y →
xy = 10 ∙ 90 = 900
xy = 20 ∙ 45 = 900
xy = 30 ∙ 30 = 900
xy is a constant so y is inversely proportional to x

NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Inverse proportion

Question 25.

Answer:

Direct Proportion :
For each pair of valtes x and y →
\(\frac{y}{x}\) = \(\frac{36}{3}\) = 12
\(\frac{y}{x}\) = \(\frac{60}{6}\) = 10
\(\frac{y}{x}\) = \(\frac{84}{9}\) = 9.33
\(\frac{y}{x}\) is not a constant so x and y is not direct proportional

Inverse Proportion :
For each pair of values x and y →
xy = 3 ∙ 36 = 108
xy = 6 ∙ 60 = 360
xy = 9 ∙ 84 = 756
xy is not a constant so y is not inversely proportzonal to x

NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Neither

Question 26.
y = 1.8x + 3.6
Answer:
y = 1.8x + 3.6
Direct proportion :
y = 1.8x + 3.6
Because the original equation y = 1.8x + 3.6 cannot be rewritten as an equivalent equation in the form y = kx, it does not represent a direct proportion.

Inverse Proportion :
y = 1.8x + 3.6
Because the original equation y = 1.8x + 3.6 cannot be rewritten as an equivalent equation in the form xy = k, it does not represent an inverse proportion.

NOTE :
Direct Proportion : y is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Neither Direct Proportion nor Inverse Proportion

Question 27.
\(\frac{2}{5}\)y = \(\frac{1}{2}\)x
Answer:
\(\frac{2}{5}\)y = \(\frac{1}{2}\)x

Direct proportion :
\(\frac{2}{5}\)y = \(\frac{1}{2}\)
\(\frac{5}{2}\) ∙ \(\frac{2}{5}\)y = \(\frac{5}{2}\) ∙ \(\frac{1}{2}\)x Multiply both sides by \(\frac{5}{2}\)
y = \(\frac{5}{4}\)x
Because the original equation \(\frac{2}{5}\)y = \(\frac{1}{2}\)x can be rewritten as an equivalent equation in the form y = kx, it represent a direct proportion.

Inverse Proportion :
\(\frac{2}{5}\)y = \(\frac{1}{2}\)x
\(\frac{5}{2}\) ∙ \(\frac{2}{5}\)y = \(\frac{5}{2}\) ∙ \(\frac{1}{2}\)x Multiply both sides by \(\frac{5}{2}\)y

Because the original equation \(\frac{2}{5}\)y = \(\frac{1}{2}\)x cannot be rewritten as an equivalent equation in the form xy = k, it does not represent an inverse proportion.

NOTE:
Direct Proportion : y ‘is directly proportional to x then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant of proportionality k, and it can be rewritten as y = k or y = \(\frac{k}{x}\)
Direct proportion

Question 28.
3y = \(\frac{18}{x}\)
Answer:
3y = \(\frac{18}{x}\)
Direct Proportion :
3y = \(\frac{18}{x}\)
\(\frac{x}{3}\) ∙ 3y = \(\frac{x}{3}\) ∙ \(\frac{18}{3}\) Multiply both sides by \(\frac{x}{3}\)
Because the original equation 3y = \(\frac{18}{3}\) cannot be rewritten as an eqnivalent equation in the form y = kx, it does not represent a direct proportion.

Inverse Proportion :
3y = \(\frac{18}{3}\)
\(\frac{x}{3}\) ∙ 3y = \(\frac{x}{3}\) ∙ \(\frac{18}{3}\) Multiply both sides by \(\frac{x}{3}\)
xy = 6
18
Because the original eqtiation 3y = \(\frac{18}{x}\) can be rewritten as an equivalent equation in the form xy = k, il represent an inverse proportion.

NOTE :
Direct Proportion : y is directly proportional to z then they have a constant of proportionality k, and it can be rewritten as y = kx or \(\frac{y}{x}\) = k
Inverse Proportion : x and y are in inverse proportion then their product is a constant
of proportionality k, and it can be rewritten as xy = k or y = \(\frac{k}{x}\)
Inverse Proportion

Question 29.

Answer:
Direct Proportion :
$From\ the\ graph$
\(\frac{y}{x}\) = \(\frac{5}{1}\) = 5
\(\frac{y}{x}\) = \(\frac{10}{2}\) = 5
\(\frac{y}{x}\) = Constant
The given graph is a straight line that does not lie along the x — axis or y — axis and does pass through the origin.
So, the given graph represents a direct proportion.
Inverse Proportion :
$Use\graph\: $
x ∙ y = 1 ∙ 5 = 5
x ∙ y = 2 ∙ 10 = 20
The product of x and y is not a constant so x and y does not represent an inverse proportion.
Direct proportion

Question 30.

Answer:

Question 31.

Answer:
Direct Proportion:
The given graph is not a straight tine that does tie along the x — axis and don not pass through the origin.
So, the given graph does not represents a direct proportion.

Inverse Proportion:
Use graph
x ∙ y = 1 ∙ 30 = 30
x ∙ y = 3 ∙ 10 = 30
The product of x and y is a constant so x and y represent an inverse proportion.
Inverse Proportion

In each table, y is directly proportional to x. Find the constant of proportionality and then complete the table. (Lesson 5.3)

Question 32.

Answer:

Find Constant of Proportionality :
y is directly proportional to x :
\(\frac{y}{x}\) = \(\frac{4}{20}\)
\(\frac{y}{x}\) = \(\frac{1}{5}\) simplify
Constant of proportionality = \(\frac{1}{5}\)

Find Missing numbers :
Find y when x = 40
\(\frac{y}{x}\) = \(\frac{1}{5}\)
\(\frac{y}{40}\) = \(\frac{1}{5}\) Multiply both sides by 40
40 ∙ \(\frac{y}{40}\) = 40 ∙ \(\frac{y}{40}\)
y = 8
Find x when y = 16
\(\frac{y}{x}\) = \(\frac{1}{5}\)
\(\frac{16}{x}\) = \(\frac{1}{5}\) Evaluate y = 16
5 ∙ 16 = x ∙ 1 Cross Muttipliction
x = 80

Constant of proportionality = \(\frac{1}{5}\)
The missing number are 8 and 80 respectively

Question 33.

Answer:

y is directly proportional lo x :
\(\frac{y}{x}\) = \(\frac{27}{3}\)
\(\frac{y}{x}\) = 9 simplify
Constant of Proportionality = 9
Find Missing Numbers :
Find y when x = 1
\(\frac{y}{x}\) = 9
\(\frac{y}{1}\) = 9 Evaluate x = 1
y = 9
Find x when y = 90
\(\frac{y}{x}\) = 9
\(\frac{90}{x}\) = 9 Evaluate y = 90
\(\frac{x}{90}\) ∙ \(\frac{90}{x}\) = \(\frac{x}{9}\) ∙ 9 Multiply both sides by \(\frac{x}{9}\)
x = 10

Constant of Proportionality = 9
The missing numbers are 9 and 10 respectively

In each table, y is inversely proportional to x. Find the constant of proportionality and then complete the table. (Lesson 5.4)

Question 34.

Answer:

Find Constant of Proportionality
y is Inversely proportional to x:
xy = 12 • 50
xy = 600 Slmplif y
Find missing value in tite table.
when x = 40 find y.
xy = 600
40 • y = 600 Evaluate x = 40
\(\frac{40 y}{40}\) = \(\frac{600}{40}\) Divide both sides by 4
y = 15 Simplify
when y = 10 find x,
x ∙ 10 = 600 Evaluate y = 10
\(\frac{10 x}{10}\) = \(\frac{600}{10}\) Divide both sides by 10
x = 60 Simplify

Constant of Proportionality = 600
The missing number are y = 15 and x = 60

Question 35.

Answer:

Find Constant of Proportionality
y is inversely proportional to x:
xy = 2 ∙ 4.5
xy = 9 Simplify
Find missing value in the table.
When x = 1 find y,
xy = 9
1 ∙ y = 9 Evaluate x = 1
y = 9 Simplify
When y = 3 find x,
x ∙ 3 = 9 Evaltate y = 3
\(\frac{3 x}{3}\) = \(\frac{9}{3}\) Divide both sides by 3
x = 3 Simplify

Constant of Proportionality = 9
The missing number are y = 9 and x = 3

Solve using proportional reasoning. (Lessons 5.3, 5.4)

Question 36.
y varies directly as x, and y = 4.8 when x = 0.2. Find y when x = 0.8.
Answer:
y = 4.8 and x = 0.2
y is directly proportional to x :
\(\frac{y}{x}\) = \(\frac{4.8}{0.2}\)
\(\frac{y}{x}\) = 24
x ∙ \(\frac{y}{x}\) = 24 ∙ x Multiply both sides by x
y = 24x
Find the value of y when x = 0.8
We know y = 24x,
y = 24 ∙ 0.8 Substituting x = 0.8
y = 19.2 Simplify

Question 37.
P is inversely proportional to Q, and P = \(\frac{1}{4}\) when Q = \(\frac{1}{2}\). Find P when Q = 2 \(\frac{1}{2}\).
Answer:
P = \(\frac{1}{4}\) and Q = \(\frac{1}{2}\)
Write an inverse proportion equation :
P is inversely proportional to Q :
P ∙ Q = \(\frac{1}{4}\) ∙ \(\frac{1}{2}\)
PQ = \(\frac{1}{8}\)

Find the value of P when Q = 2\(\frac{1}{2}\)
PQ = \(\frac{1}{8}\)
P ∙ 2\(\frac{1}{2}\) = \(\frac{1}{8}\) Substituting Q = 2\(\frac{1}{2}\)
\(\frac{5}{2}\)P = \(\frac{1}{8}\) Simplifying
\(\frac{2}{5}\) ∙ \(\frac{5}{2}\)P = \(\frac{1}{8}\) ∙ \(\frac{2}{5}\) Multiplying both sides by \(\frac{2}{5}\)
P = \(\frac{1}{20}\)

Problem Solving

Solve. Show your work.

Question 38.
The table shows the relationship between the capacity in quarts, x, and the capacity in cups, y. Graph the relationship between y and x. Use 1 unit on the horizontal axis to represent 1 quart and 1 unit on the vertical axis to represent 4 cups. (Chapter 5)

Answer:


a) Is the number of cups directly proportional to the number of quarts? If so, find the constant of proportionality.
Answer:
The graph is a straight line through the origin, and It does not lie along the x – axis or y – axis.
So, it represents a direct proportion.
Yes the number of cups is directly proportional to the number of quarts
Find the Constant of Proportionality :
\(\frac{y}{x}\) = \(\frac{4}{1}\) = 4
\(\frac{y}{x}\) = \(\frac{8}{2}\) = 4
\(\frac{y}{x}\) = \(\frac{12}{3}\) = 4
\(\frac{y}{x}\) = \(\frac{16}{4}\) = 4
The Constant of Proportionality is 4

b) A soup recipe calls for 5 quarts of stock. How many cups of stock does the soup recipe need?
Answer:
$We \know$
\(\frac{y}{x}\) = 4
\(\frac{y}{5}\) = 4 Substituting x = 5
5 ∙ \(\frac{y}{5}\) = 5 ∙ 4 Multiplying bothsides by 5
y = 20
The recipe will need 20 cups of stocks

c) Convert 24 cups of water to quarts of water.
Answer:
$We\ know$
\(\frac{y}{x}\) = 4
\(\frac{24}{x}\) = 4 Substituting x = 24
\(\frac{x}{4}\) ∙ \(\frac{24}{x}\) = \(\frac{x}{4}\) ∙ 4 Multiplying bothsides by \(\frac{x}{4}\)
x = 6
24 cups of water = 6 quarts of water

Question 39.
A printer takes 2.4 seconds longer to print a page in color than a page in black and white. A page in black and white can be printed in 4 seconds.
There are (-\(\frac{5}{8}\)w + 6) color pages and (1.2w + 5) black and white pages to print. (Chapters 3, 4)
Answer:
The printer takes 4 seconds to print a page in black and white.
So, to print a page in color, the printer wilitake = 4 + 2.4 = 6.4 seconds
Number of pages to print in Blackund White 1.2w+ 5
Number of pages to print in Color = \(\frac{5}{8}\)w + 6

a) How long does it take to print all the pages?
Answer:
4 (1.2w + 5) + 6.4 (\(\frac{5}{8}\)w + 6)
= 4(1.2w) + 4(5) + 6.4 (\(\frac{5}{8}\)w) + 6.4(6) Use Distributive Property
= 4.8w + 20 + 4w + 38.4 Multiply
= 4.8w + 4w + 20 + 38.4 Group like terms
= (8.8w + 58.4) seconds

b) If w = 40, how long does it take to print all the pages?
Answer:
8.8w + 58.4
= 8.8(40) + 58.4 Substituting w = 40
= 352 + 58.4 Multiply
= 410.4 seconds

Question 40.
Jason has to choose between two offers of a gym club membership as shown below. (Chapter 4)

Answer:
Gym A = $55 per month membership fee plus $15 per hour of training with a personal trainer.
${\color{#4257b2} Gym\ B) = $220\ per\ month\ membership\ fee\ and\ training\ with\ a\ personal\ trainer\ at\ no\ extra\ cost $
a) After how many hours of training per month would Gym B be a better deal than Gym A?
Answer:
55 + 15x > 220
55 + 15x – 55 > 220 — 55 Subtract 35 from both sides
15x > 165 Simplify
\(\frac{15 x}{15}\) > \(\frac{165}{15}\) Divide both sides by 15
x > 11
After 11 hours of training per month Gym B would be a better deal than Gym A

b) If Jason plans to train for at least 12 hours per month, which gym club membership should he take up? Explain your answers.
Answer:
Gym A:
55 + 15 • 12
= 55 + 180 Multiply
= 235
Gym B:
220
Jason should take membership of Gym B since it is cheaper if he plans to train for at least 12 hours per month

Question 41.
A commission is an amount of money earned by a sales person, based on the amount of sales the person makes. At a particular home-improvement store, the commission made, C, is directly proportional to the amount of sales, S. A sales person earns $198 when he makes total sales of $3,600. (Chapter 5)
Answer:
Commission (C) = $198
Sales (S) = $3600

a) Write a direct proportion equation that relates C and 5. Then express the store’s commission rate as a percent.
Answer:
C is directly proportional to S :
\(\frac{C}{S}\) = \(\frac{198}{3600}\)
\(\frac{C}{S}\) = \(\frac{11}{200}\)
S ∙ \(\frac{C}{S}\) = \(\frac{11}{200}\) ∙ S Multiply both sides by S
C = \(\frac{11}{200}\)S
Express the store’s commission rate as a percent
C is directly proportional to S :
\(\frac{C}{S}\) = \(\frac{11}{200}\)
\(\frac{C}{S}\) = 0.055
\(\frac{C}{S}\) = 0.055 ∙ 100
\(\frac{C}{S}\) = 5.5%

b) Find the amount of sales made if his commission is $297.
Answer:
We know C = \(\frac{11}{200}\)S,
297 = \(\frac{11}{200}\)S Substituting C = 297
\(\frac{200}{11}\) ∙ 297 = \(\frac{200}{11}\) ∙\(\frac{11}{200}\)S Multiplying both sides by \(\frac{200}{11}\)
S = 5400 Simplify
He made a saie of amount $5400 if his commission is $297

Question 42.
Amy and her friends want to equally share the cost of David’s birthday gift. They plan to buy a baseball glove that costs $79.98. The amount of money that each has to contribute, C, is inversely proportional to the number of people sharing the cost, n. (Chapter 5)
Answer:
Cost of baseball gloves = $79.98
Amount of money that each has to contribute = C
Number of people sharing the cost = n
a) Write an inverse proportion equation that relates C and n.
Answer:
Inverse proportion equation :
C ∙ n = 79.98
Cn = 79.98 Multiplying
\(\frac{C n}{n}\) = \(\frac{79.98}{n}\) Divide both sides by n
C = \(\frac{79.98}{n}\)

b) How much will each person have to pay if 6 people are sharing the cost?
Answer:
n = 6 and C = \(\frac{79.98}{n}\),
C = \(\frac{79.98}{6}\) Substituting n = 6
C = 13.33
Each person has to contribute $13.33 if 6 person are sharing the cost.

Question 43.
The time it takes Tim to cycle to his destination varies inversely as his cycling speed in miles per hour. The graph shows the relationship between y and x. (Chapter 5)

a) Find the constant of proportionality. What does this value represent in this situation?
Answer:
Use the point (1, 12) from the graph to find the constant of proportionality.
x • y = 1 • 12 Choose the point (1, 12)
xy = 12 Multiply
The constant of proportionality is 12
This value represents the distance’ traveled by Tim

b) Write an equation that relates speed and time taken.
Answer:
Use the point (1, 12) from the graph to find the constant of proportionality.
x • y = 1 • 12 Choose the point (1, 12)
xy = 12 Multiply

c) Explain what the point (1, 12) represents in this situation.
Answer:
It means that when Tim cycle at a speed of 12 miles per hour he will reach his destination in 1 hour.

d) How long does it take Tim to reach his destination if he decreases his speed to 6 miles per hour?
Answer:
From the graph :
If Tim cycle at a speed of 6 miles per hour he will reach his destination in 2 hour.

Question 44.
Two-thirds of the capacity of jar A is equivalent to eight-fifteenths of the capacity of jar B. Suppose the full capacity of jar B is (6x – 3) liters. (Chapters 3, 4)
a) What is the full capacity of jar A in terms of x?
Answer:
Let the full capacity of Tank A be A
Let the full capacity of Tank B be B

Two — third of the capacity of Jar A is equivalent to eight — fifteenths of the capacity of jar B :
\(\frac{2}{3}\) ∙ A = \(\frac{8}{15}\) ∙ B Multiplying both sides by \(\frac{3}{2}\)
A = \(\frac{4}{5}\) ∙ B Simplifying
A = \(\frac{4}{5}\) ∙ (6x – 3) Substituting B = (6x – 3)
A = \(\frac{4}{5}\)(6x) – \(\frac{4}{5}\)(3) Using Distributive Property
A = \(\frac{24}{5}\)x – \(\frac{12}{5}\) Multiplying
A = \(\frac{24 x-12}{5}\)

b) If the capacity of jar A is 18 liters, what is the value of x?
Answer:
A = \(\frac{24 x-12}{5}\)
A = \(\frac{24 x-12}{5}\) Substituting A = 18
5 ∙ 18 = 5 ∙ \(\frac{24 x-12}{5}\) Multiplying both sides by 5
90 = 24x – 12 Simplifying
90 + 12 = 24x – 12 + 12 Add 12 to both sides
24x = 102 Simplifying
\(\frac{24 x}{24}\) = \(\frac{102}{24}\) Divide both sides by 24
x = 4.25

Question 45.
A rectangle measures 12 inches by 8 inches. The length of the rectangle is increased by r percent while the width remains unchanged. (Chapters 3, 4)
Answer:
Expanded Length = (12 + \(\frac{12}{100}\)r) inches
Width = 8 inches
a) Write an algebraic expression of the area of the expanded rectangle.
Answer:
Algebraic Expression for the area of the expanded rectangle
Area
= Length ∙ Width
= (12 + \(\frac{12}{100}\)r) ∙ 8
= (12 + 0.12r) ∙ 8
= 8(12) + 8(0.12r)
= (96 + 0.96r) square inches

b) If the area of the expanded rectangle is 120 square inches, find the value of r.
Answer:
Area = 120 square inches
96 + 0.96r = 120
96 + 0.96r – 96 = 120 – 96 Subtract 96 from both suies
0.96r = 24 Simplify
\(\frac{0.96 r}{0.96}\) = \(\frac{24}{0.96}\)
Divide both sides by 0.96
r = 25

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 18 Practice 1 Classifying Polygons provides detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 18 Practice 1 Answer Key Classifying Polygons

Circle the polygons.

Question 1.

Answer:

Explanation:
The above figure contains 5 polygons.
A polygon is a closed two-dimensional shape that is formed by enclosing line segments.
A minimum of three line segments are required to make a polygon.

Mark the angles. Label the parts of each polygon.

Question 2.

Answer:

Explanation:
Given figure is a polygon.
The line segments forming a polygon are called its sides.
Sides are AB, BC, CD  and DA .
The meeting point of a pair of sides is called its vertex.

Question 3.

Answer:

Explanation:
Given picture is called a polygon.
The line segments forming a polygon are called its sides.
Sides are AB, BC, CD, DE and EA .
The meeting point of a pair of sides is called its vertex.

Identify each polygon.

Question 4.

Answer: Square

Explanation:
Given figure is a polygon. Square in shape.
The line segments forming a polygon are called its sides.
Sides are AB, BC, CD  and DA .
The meeting point of a pair of sides is called its vertex.

Question 5.

Answer: Pentagon

Explanation:
Given picture is called a polygon. Pentagon in shape.
The line segments forming a polygon are called its sides.
Sides are AB, BC, CD, DE and EA .
The meeting point of a pair of sides is called its vertex.

Question 6.

Answer: Octagon

Explanation:
Given picture is called a polygon. Octagon in shape.
The line segments forming a polygon are called its sides.
What are the sides of polygon ABCDEFGH
Sides are AB, BC, CD, DE , EF and FG, GH and HA .
The meeting point of a pair of sides is called its vertex.

Question 7.

Answer: Square

Explanation:
Given figure is a polygon. Square in shape.
The line segments forming a polygon are called its sides.
Sides are AB, BC, CD  and DA .
The meeting point of a pair of sides is called its vertex.

Question 8.

Answer: Hexagon

Explanation:
Given picture is called a polygon. Hexagon in shape.
The line segments forming a polygon are called its sides.
What are the sides of polygon ABCDEF
Sides are AB, BC, CD, DE , EF and FA .
The meeting point of a pair of sides is called its vertex.

Question 9.

Answer: Trapezoid

Explanation:
Given figure is a polygon. Trapezoid in shape.
The line segments forming a polygon are called its sides.
Sides are AB, BC, CD  and DA .
The meeting point of a pair of sides is called its vertex.

Complete the table. Then answer the question.

Question 10.

Answer:

Explanation:
A Square is a regular quadrilateral or polygon.
which has all the four sides of equal length, four vertices and,
four angles with right angle triangles.
Octagon is a polygon in geometry, which has 8 sides, 8 vertices and 8 angles.
That means the number of vertices is 8 and the number of edges is 8.
So, octagon is a 8-sided polygon and it is a two dimensional plane figure.
All the sides are joined with each other end-to-end to form a shape.
In geometry, a hexagon can be defined as a polygon with six sides.
The two-dimensional shape has 6 sides, 6 vertices and 6 angles.

Answer:

Explanation:
The above Triangle is polygon.
A triangle has three sides, 3 vertices and
3 angles sum to 180 degrees.
The above figure rectangular polygon,
it has four sides, four vertices and four angles, with 90 degrees.
And the angles are right angle triangles.
A pentagon is a five-sided polygon with five straight sides,
five vertices and five interior angles that sum up to 540°540°.
A pentagon shape is a plane figure, or flat (two-dimensional) 5-sided geometric shape.

Answer:

Explanation:
Parallelogram is a four-sided closed figure with opposite sides are equal and opposites angles are equal.
A parallelogram has 4 sides, 4 vertices and 4 angles.
A rhombus is a quadrilateral whose four sides have the same length.
Every rhombus has two diagonals connecting pairs of opposite vertices, and two pairs of parallel sides.
Opposite angles of a rhombus have equal length.
A trapezoid is a quadrilateral with exactly one pair of parallel sides.
The sum of the interior angles of a trapezoid equals 360 degrees,
So, it has four angles and four vertices, also called corners.

Question 11.
Which figures have the same number of sides, vertices and angles?

Answer:
All the above mentioned polygons have sides, vertices and angles.
Explanation:
Polygons are named according to the number of sides and angles they have.
The most familiar polygons are the triangle, the rectangle, and the square.
A regular polygon is one that has equal sides.
Some special polygons have equal sides, vertices and angles.

Are these statements correct? Write true or false.

Question 12.
A hexagon has seven sides and six angles. ____________
Answer: False
Explanation:
hexa means six
In geometry, a hexagon can be defined as a polygon with six sides.
The two-dimensional shape has 6 sides, 6 vertices and 6 angles.

Question 13.
All polygons have four sides. ____________
Answer: False
Explanation:
A plane figure that is described by a finite number of straight line segments connected to form a closed polygon.
Polygons are named according to the number of sides and angles they have.

Question 14.
All parallelograms, squares, and trapezoids have four angles. ____________
Answer: True
Explanation:
All parallelograms, squares, and trapezoids have four angles,
4 sides and 4 vertices as mentioned above.

Question 15.
An octagon has eight vertices and seven sides. ____________
Answer: False
Explanation:
Octagon is a polygon in geometry, which has 8 sides, 8 vertices and 8 angles.
That means the number of vertices is 8 and the number of edges is 8.
So, octagon is a 8-sided polygon and it is a two dimensional plane figure.
All the sides are joined with each other end-to-end to form a shape.

Question 16.
A pentagon has six angles. ____________
Answer: False
Explanation:
A pentagon is a five-sided polygon with five straight sides,
five vertices and five interior angles that sum up to 540°540°.
A pentagon shape is a plane figure, or flat (two-dimensional) 5-sided geometric shape.

Question 17.
A triangle has two vertices. ____________
Answer: False
Explanation:
A triangle has three sides, 3 vertices and
3 angles sum to 180 degrees.

Question 18.
A parallelogram can be separated into 4 triangles. ____________
Answer: True
Explanation:
Parallelogram is a four-sided closed figure with opposite sides are equal and opposites angles are equal.
A parallelogram has 4 sides, 4 vertices and 4 angles.

Question 19.
A rectangle has four right angles. ____________
Answer: True
Explanation:
A rectangle has four sides, four vertices and four angles, with 90 degrees.
And the angles are right angle triangles.

Cut out the tangram below and complete the table.

Question 20.

Answer:

Explanation:
Answer may vary,
We can write all polygons like square, triangle, rectangle and pentagon …. so on.
Polygons are named according to the number of sides and angles they have.
The most familiar polygons are the triangle, the rectangle, and the square.
A regular polygon is one that has equal sides.
Some special polygons have equal sides, vertices and angles.

Use at least 5 polygons to make a figure. Complete the table.

Question 21.

Answer:


Explanation:
All types of polygons be used.
here in the above figure we used 5 polygons
i) Pentagon
ii) Triangle
iii) Rhombus
iv) Trapezoid
v) Rectangle
As we know polygon is a two-dimensional geometric figure that has a finite number of sides and a closed figure.
Polygons are named according to the number of sides and angles they have.
A regular polygon is one that has equal sides.
Some special polygons have equal sides, vertices and angles.

Question 22.
Name the figure that you have made.

Answer:

Explanation:
From the above figure,
we can cut 4 triangles, 1 parallelogram and 1 rectangle.

Solve.

Question 23.
I am a polygon. I have 1 more angle than a rectangle has. What am I? ___________
Answer:
Pentagon
Explanation:
A pentagon is a five-sided polygon with five straight sides,
five vertices and five interior angles that sum up to 540°540°.
A pentagon shape is a plane figure, or flat (two-dimensional) 5-sided geometric shape.

Question 24.
I am a polygon. I have 1 more side than a pentagon has. What am I? ___________
Answer:
Hexagon
Explanation:
hexa means six
In geometry, a hexagon can be defined as a polygon with six sides.
The two-dimensional shape has 6 sides, 6 vertices and 6 angles.

Question 25.
I am a polygon. I have 1 more vertex than a triangle has. What am I? ___________
Answer:
Rectangle
Explanation:
A rectangle has four sides, four vertices and four angles, with 90 degrees.
And the angles are right angle triangles.

Question 26.
Add one more polygon to the shape below to make it a hexagon.

Answer:

Explanation:
The above drawn figure is Hexagon, hexa means six.
In geometry, a hexagon can be defined as a polygon with six sides.
The two-dimensional shape has 6 sides, 6 vertices and 6 angles.

Identify each quadrilateral. Then explain your answer.

Example

This is a rectangle. A rectangle has 2 pairs of opposite sides that are parallel. Only the opposite sides of a rectangle need to be of equal length. All 4 angles of a rectangle are right angles.

Question 27.

This is a ____________________
Answer:
This is a parallelogram.
Explanation:
A parallelogram has 2 pairs of opposite sides that are parallel.
Only the opposite sides of a rectangle need to be of equal length.
All 4 angles of a rectangle are right angles.

Question 28.

This is a ____________________
Answer:
This is a rhombus.
Explanation:
A rhombus has 2 pairs of opposite sides that are parallel.
Only the opposite sides of a rectangle need to be of equal length.
All 4 angles of a rectangle are right angles.

Question 29.

This is a ____________________
Answer:
This is a Trapezoid.
Explanation:
A trapezoid has 2 pairs of opposite sides that are parallel.
Only the opposite sides of a rectangle need to be of equal length.
All 4 angles of a rectangle are right angles.

Write P for a parallelogram, R for rhombus, or T for trapezoid on the shapes.

Question 30.

Answer:

Explanation:
As we all ready know that clearly about Parallelogram, Rhombus and Trapezoid in the above question no.27,
identify the Parallelogram, Rhombus and Trapezoid and mention with their initials.

Question 31.
How is a trapezoid different from a parallelogram?
Answer:

Both are quadrilaterals.
Explanation:
A parallelogram has two pairs of parallel sides.
A trapezoid only has to have one pair of parallel sides.
So a parallelogram is a trapezoid (a special case of one), but a trapezoid is not, in general, a parallelogram.

Question 32.
How is a trapezoid similar to a parallelogram?
Answer:

Explanation:
A trapezoid has one pair of parallel sides and a parallelogram has two pairs of parallel sides.
So a parallelogram is also a trapezoid.

This handy Math in Focus Grade 3 Workbook Answer Key End of Year Review detailed solutions for the textbook questions.

Math in Focus Grade 3 End of Year Review Answer Key

Test Prep

Multiple Choice

Fill in the circle next to the correct answer.

Question 1.
John spends $1.35 on bus fare and $2.50 on food each day. How much does he spend in two days? (Lesson 10.1)
(A) $3.85
(B) $6.60
(C) $6.70
(D) $7.70
Answer:
Option(D)
Explanation:
John spends $1.35 on bus fare and
$2.50 on food each day.
Total amount he spend in two days
$2.50 + $1.35 = 3.85
3.85 x 2 = 7.7

Question 2.
Paige jogs around a 400-meter track 3 times a day. What is the distance she jogs each day? (Lesson 11.2)
(A) 400 m
(B) 1 km 200 m
(C) 1 km 400 m
(D) 10 km 200 m
Answer:
Option(B)
Explanation:
Paige jogs around a 400-meter track 3 times a day.
The distance she jogs each day
400 x 3 = 1200 m

Question 3.
Which mass is not the same as the others? (Lesson 11.3)
(A) 7,220 g
(B) 7,022 g
(C) 7,000 g + 22 g
(D) 7 kg 22 g
Answer:
Option(A)
Explanation:
7,220 g is not same as the other,
other three are 7kg + 22g or 7022g or 7000g + 22g represent same.

Question 4.
Which is incorrect? (Lesson 14.3)

Answer:
Option(C)
Explanation:
A, B and D are correct fractions.
C is incorrect fraction.
As \(\frac{2}{3}\) is not a perfect division.

Question 5.
Look at the measuring cups. (Lesson 11.4)

Which is correct?
(A) There is 500 milliliters more water in X than Y.
(B) There is a total of 1,500 milliliters of water in X and Y.
(C) Z contains 180 milliliters less water than X.
(D) The difference in the volume of water in Y and Z is 170 milliliters.
Answer:
Option(D)
Explanation:
The amount of space in an object is known as volume.
Compare both the volumes in Y and Z,
The difference in the volume of water in Y and Z is 170 milliliters.
V = Y – Z = 200 – 30 = 170 milliliters.

Question 6.
What fraction of the figure is shaded? (Lesson 14.1)

(A) \(\frac{1}{5}\)
(B) \(\frac{2}{5}\)
(C) \(\frac{6}{13}\)
(D) \(\frac{2}{3}\)
Answer:
Option(B)
Explanation:
Total shaded regions are 4 and total regions are 10, and the fraction form is written as follows
\(\frac{4}{10}\) = \(\frac{2}{5}\)

Question 7.
Look at the line segments. (Lesson 17.6)

Which line segments are parallel?
(A) Segments AB and AF
(B) Segments BC and EF
(C) Segments AF and BC
(D) Segments AB and CD
Answer: D
Explanation:
Two lines or line segments can either intersect (cross) each other or be parallel.
Parallel line segments never meet, no matter how far they are extended.
So, Segments AB and CD

Question 8.
Which is a polygon? (Lesson 18.1)

(A) Figure W
(B) Figure X
(C) Figure Y
(D) Figure Z
Answer:
Option(D)
Explanation:
A polygon is defined as a flat or plane, two-dimensional closed shape with straight sides.
It does not have curved sides.
So, figure Z is polygon.

Question 9.
Which tarts weigh the same? (Lesson 15.2)

(A) Lemon and Strawberry
(B) Lemon and Peach
(C) Blueberry and Strawberry
(D) Blueberry and Peach
Answer:
Option(B)
Explanation:
1 pound = 16 ounce
Lemon = 2 pounds
Peach = 32 ounces
2 x 16 = 32
So, Lemon and Peach weigh the same.

Question 10.
8 of the 20 buttons in a box are gray. The rest are white. What fraction of the buttons are white? (Lesson 14.6)

(A) \(\frac{2}{5}\)
(B) \(\frac{3}{5}\)
(C) \(\frac{4}{5}\)
(D) \(\frac{3}{7}\)
Answer:
Option(A)
Explanation:
8 of the 20 buttons in a box are gray.
The rest are white.
\(\frac{8}{20}\)
Divide both numerator and denominator with 4 to simplify.
\(\frac{2}{5}\) fraction of the buttons are white.

Short Answer

Read the questions carefully. Write your answers in the space provided.

Question 11.
Order the fractions from greatest to least. (Lesson 14.4)
\(\frac{1}{4}\), \(\frac{7}{8}\), \(\frac{3}{4}\)
Answer:
\(\frac{7}{8}\), \(\frac{3}{4}\), \(\frac{1}{4}\)
Explanation:
Simplify,
\(\frac{1}{4}\) = 0.25,
\(\frac{7}{8}\) = 0.87,
\(\frac{3}{4}\) = 0.75,
So, when we arrange the fractions greatest to least
\(\frac{7}{8}\), \(\frac{3}{4}\), \(\frac{1}{4}\)

Question 12.
String A is 28 inches long. String B is 4 feet long. Which is longer? (Lesson 15.1)
String ____________
Answer:
String B is longer than A.
Explanation:
String A is 28 inches long.
String B is 4 feet long.
1 feet = 12 inches
4 feet = 12 x 4 = 48 inches
So, string B is longer.

Question 13.
George starts on his science project at 8:25 A.M. He finishes at 10:10 A.M. How long did he take? (Lesson 16.5)
__________ h ___________ min
Answer:
1 hrs 85 min
Explanation:
George starts on his science project at 8:25 A.M.
He finishes at 10:10 A.M.
Total time he took
10:10 A.M – 8:25 A.M = 1 hrs 85 min

Question 14.
Mrs. Freeman puts 3 cups of lemon juice in a punch bowl. She adds 6 pints of water. How many cups of liquid are there in total? (Lesson 15.3)
____________ cups
Answer: 6 cups
Explanation:
Mrs. Freeman puts 3 cups of lemon juice in a punch bowl.
She adds 6 pints of water.
1 cup = 0.5 pints
6 pints = 0.5 x 6 = 3 cups
Already 3 cups are there, so she adds 3 more
Total cups of liquid in bowl 3 + 3 = 6

Question 15.
Which angles in the figure are less than a right angle? (Lesson 17.3)

Angles ___________ and ___________
Answer:
Angles F and D
Explanation:
Angle F and D are less then 90 degrees ,
So F and D are angles in the figure are less than a right angle.

Look at the figures to answer Exercises 16 and 17. (Lesson 19.4)

Question 16.
Which figure has a greater area?
Figure ____________
Answer:
Figure B has a greater area
Explanation:
Figure A has 6 in.²
Figure B 7 in.²,
when compare both the figures the area of B is greater.
Question 17.
How much greater?
__________ in.²
Answer: 1 in.²
Explanation:
Figure A has 6 in.²
Figure B 7 in.²,
when compare both the figures the area of B is greater.
Question 18.
Which figures are congruent? (Lesson 18.2)

Figures __________ and ___________
Answer:
Figures A and C
Explanation:
If two figures or objects have the same shape and size or known as congruent,
or if one has the same shape and size as the mirror image of the other.

Look at the line plot to answer Exercises 19 and 20.

Beth surveyed her friends on the number of books they read last week. She drew a line plot to show her data. (Lesson 13.3)

Question 19.
How many friends did she survey?
Answer:
13 friends
Explanation:
Beth surveyed her friends on the number of books they read last week.
The above line plot tells that she surveyed on 13 friends.

Question 20.
How many friends read more than three books last week?
Answer:
4 friends
Explanation:
Beth surveyed her friends on the number of books they read last week.
The above line plot tells that she surveyed on 13 friends.
Among them 4 of her friends read more than three books last week.

Extended Response

The table and the bar graph show the number of books checked out of a library over five days. Some of the bars on the bar graph were incorrectly drawn.

Look at the table and bar graph to answer Exercises 21 to 26.

Question 21.
Complete the bar graph for Tuesday.
Answer:

Explanation:
The table show the number of books checked out of a library over five days.
On Tuesday the number of books checked out are 25.

Question 22.
One bar on the bar graph was incorrectly drawn for one of the days. On which day is it?
Answer: Tuesday
Explanation:
The table show the number of books checked out of a library over five days.
On Friday the number of books checked out are 40.
But the graph drawn in correctly as 35.

Question 23.
Show the correct number of books checked out for that day in the bar graph.
Answer:
40 b00ks
Explanation:

Question 24.
How many books were checked out during that week?
____________ books
Answer:
150 books
Explanation:
Number of books on Monday = 20
Number of books on Tuesday = 25
Number of books on Wednesday = 30
Number of books on Thursday = 35
Number of books on Friday = 40
Total number of books checked that week
20 + 25 + 30 + 35 + 40 = 150

Question 25.
On which day was the number of books checked out twice as many as Monday?
Answer:
Friday
Explanation:
Information given in the table tells,
Number of books checked on Monday are 20
Number of books checked on Friday are 40
So, on Friday the number of books checked out twice as many as Monday.

Question 26.
Look at the number of books checked out from Monday to Friday. What is the pattern?
Answer:
Ascending order
Explanation:
When we observe the number of books checked on each day,
5 books increased on each day,
following ascending order.
Ascending order means to arrange numbers in increasing order, that is, from smallest to largest.

Solve. Show your work.

Question 27.
After a garage sale, Norman makes $105.50. Julie makes $38.75 more than Norman. Lana makes $19.20 less than Julie. How much does Lana make?
Answer:
$163.45
Explanation:
Norman makes $105.50.
Julie makes $38.75 more than Norman.
$105.50 + 38.75 = $144.25
Lana makes $19.20 less than Julie
$144.25 + $ 19.20 = $163.45

Question 28.
Colin uses a wire to make a square. Each side is 6 centimeters long. He then uses the same wire to make a triangle of three equal sides. How long is each side of the triangle?

Answer: 8 cm
Explanation:
Perimeter of Square P = 4 x s = 4 x 6 = 24 cm
Perimeter of the Triangle = 3s
P = 3s = 24
s = \(\frac{24}{3}\) = 8 cm

Solve. Show your work.

Question 29.
Pauline went to a party. She spends 3 hours 25 minutes there. She goes home at 2:15 P.M. What time did she go to the party?

Answer:
10 : 50 AM

Explanation:
time line diagram as shown above
Pauline went to party and she spends 3hr 25 min and she goes home at 2:15 pm
2 : 15 – 3 :25 = 10 :50
Pauline go to party at 10:50 AM
10:50 + 3:25 = 2:15 PM

Solve. Show your work.

Question 30.
A family has two dogs, a husky and a terrier. The husky’s mass is 23 kilograms. If he gains 7 kilograms, his mass will be five times that of the terrier. What is the mass of the terrier?
Answer: 6kg
Explanation:
Husky’s mass is 23 kilograms
Terrier mass is x
23 + 7 = 5x
30 = 5 x
x = \(\frac{30}{5}\)
x= 6 kg

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 4 Lesson 4.3 Real-World Problems: Ratios to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 4 Lesson 4.3 Answer Key Real-World Problems: Ratios

Math in Focus Grade 6 Chapter 4 Lesson 4.3 Guided Practice Answer Key

Solve.

Question 1.
A box contains baseball and football cards. The number of baseball cards to the number of football cards is in the ratio 5:1.
a) If the total number of cards is 1,380, find the number of each type of cards.

The number of baseball cards is .
Answer:
1,150 baseball cards.
Explanation:

Total number of units is = 5 + 1 = 6
6 units => 1,380
1 unit = 1,380/6 = 230
number of foot ball cards = 230
5 units x 230 = 1,150
The number of baseball cards is 1,150.

b) Suppose the number of baseball cards is 950, find the number of football cards.

The number of football cards is .
Answer:
190 football cards.
Explanation:

5 units => 950
1 unit = 950 / 5 = 190

Question 2.
A school raised $18,000 at a charity event. The money raised was shared among three charities, A, B, and C, in the ratio 1: 2: 3. How much money did each charity receive?

Total number of units = + +
=
units → $
1 unit → $\(\frac{?}{?}\) = $
A received $

Answer:
$9,000
Explanation:
Total number of units = 1 +2 + 3 = 6
6 units → $18,000
1 unit → $\(\frac{18,000}{6}\) = $ 3,000
A received $ 3,000

Question 3.
The number of coins collected by Xavier, Yohann, and Zachary is in the ratio 2:5:8. Yohann collected 85 coins.

a) Find the number of coins Zachary collected.
5 units → coins
1 unit → $\(\frac{?}{?}\) = coins
units → × = coins
Zachary collected coins.
Answer:
136 coins
Explanation:

the number of coins Zachary collected.
5 units → 136 coins
1 unit → $\(\frac{136}{8}\) = 17 coins
8 units → 17 × 8 = 136 coins
Zachary collected 136 coins.

b) Find the number of coins collected by the three boys altogether.
Total number of units = + +
=
units → × = coins
The three boys collected coins altogether.
Answer:
255 coins
Explanation:
the number of coins collected by the three boys altogether.
Total number of units = 2 + 5 + 8
= 15
15 units → 17 ×  = 15 coins
The three boys collected 255 coins altogether.

Question 4.
At Stacey’s middle school, students either ride bikes to school, walk, or take a bus. The ratio of the number of students who ride bikes to the number who walk is 3 : 4. The ratio of the number of students who walk to the number who take a bus is 12 : 7. There are 560 students in all.
a) Find the number of students who ride bikes to school.

So, Ride bike : Walk : Take bus = : : .
Total number of units = + +
=
units → 560 students
1 unit → \(\frac{?}{?}\) = students
9 units → × = students
The number of students who ride bikes is .
Answer:
180 bike rides
Explanation:

Ride : Walk        Walk : bus
3:4 = 9:12              12  :  7
So, Ride bike : Walk : Take bus = 9 : 12 : 7.
Total number of units = 9 + 12 +  7 = 28
28 units → 560 students
1 unit → \(\frac{560}{28}\) = 20 students
9 units → 9 × 20 = 180 students
The number of students who ride bikes is 180.

b) Find the number of students who walk to school.
units → × = students
The number of students who walk is .
Answer: 240
Explanation:
12 units → 12 × 20 = 240 students
The number of students who walk is 240.

c) Find the number of students who take a bus to school.
units → × = students
The number of students who take a bus is .
Answer: 140
Explanation:
7 units → 7 × 20 = 140 students
The number of students who take a bus is 140.

Question 5.
Claire keeps some green and red plates in a cabinet. The ratio of the number of green plates to the number of red plates is 2 : 1. She adds 18 more red plates in the cabinet and the ratio becomes 4 : 5.
Before
The ratio of the number of green plates to the number of red plates is : .

After
The ratio of the number of green plates to the number of red plates becomes : .
The length of the model for plates does not change. The model for plates is divided into units.
The model for red plates is divided into units of the same size and additional units are added to make the total length units.
The additional units represent the red plates Claire adds in the cabinet.

Answer:
Before
The ratio of the number of green plates to the number of red plates is 2 : 1.

After
The ratio of the number of green plates to the number of red plates becomes 2 : 15.
The length of the model for green plates does not change. The model for green plates is divided into 2 units.
The model for red plates is divided into units of the same size and additional units are added to make the total length 5 units.
The additional units represent the 6 red plates Claire adds in the cabinet.

a) How many green plates are there in the cabinet?
3 units → plates
1 unit → \(\frac{?}{?}\) = plates
units → × = plates
There are green plates in the cabinet.
Answer:
8 green plates
Explanation:
3 units → 6 plates
1 unit → \(\frac{6}{3}\) = 2 plates
4 units → 4 × 2 =8plates
There are 8 green plates in the cabinet.

b) How many red plates are there in the cabinet in the end?
units → × = plates
There are red plates in the cabinet in the end.
Answer:
30 Red plates
Explanation:
5units → 5 ×6 =30 plates
There are 30 red plates in the cabinet in the end.

Math in Focus Course 1A Practice 4.3 Answer Key

Solve. Show your work.

Question 1.
A rope is cut into three pieces P, Q, and R. The lengths of the pieces are in the ratio 3 : 5 : 7. If the rope is 33 feet 9 inches long, find the lengths of P, Q, and R.
Answer:
P = 81in , Q = 135in, R = 189in.
Explanation:
First convert 33 feet 9 inches into inches,
 There are 12 inches in 1 foot,
33 × 12 = 396.
= 396 + 9 = 405
3 : 5 : 7 = 405
3x + 5x + 7x = 405
15x = 405
x = 27
3x = 3 x 27 = 81
5x = 5 x 27 = 135
7x = 7 x 27 = 189
P = 81 , Q = 135 , R = 189.

Question 2.
Alice, Bernice, and Cheryl shared some stamps in the ratio 8 : 9 : 18. Alice received 184 stamps. Find the number of stamps that Bernice and Cheryl each received.
Answer:
Bernice 207 and Cheryl 230
Explanation:
Consider the ratios in parts
Alice 8 parts = 184
184 ÷ 8 = 23
So, 1 part = 23 stamps
Bernice has 9 parts,
9 x 23 = 207 stamps
Cheryl has 10 parts,
10 x 23 = 230 stamps.

Question 3.
Alan, Gil, and Deb’s point score in a video game was in the ratio 2 : 3 : 4. Deb scored 114,400 points.
a) How many points did Gil score?
Answer:
85,800 points
Explanation:
Let the points scored by Alan, Gil and Deb be
2x, 3x, and 4x
Deb scored 114,400
So, 4x = 114400
x = 28600
Gil scored 3x = 85800

b) How many points did they score in all?
Answer:
257,400 points
Explanation:
Let the points scored by Alan, Gil and Deb be
2x, 3x, and 4x
Deb scored 114,400
So, 4x = 114400
x = 28600
Alan scored 2x = 2 x 28600 = 57200
Gil scored 3x = 85800
Alan scored 57200 + Gil scored 85800 + Deb scored 114400 = 257,400

Question 4.
Lara has three cats: Socks, Princess, and Luna. The ratio of Socks weight to Princess’s weight is 4 : 5. The ratio of Princess’s weight to Luna’s weight is 6 : 7. What is the ratio of Socks weight to Luna’s weight?
Answer:
Ratio of Socks weight to Luna’s weight = 24 : 35
Explanation:
Let Socks weight = s
Princess weight = p
Luna’s weight = l
The ratio of Socks weight to princess weight is 4 : 5 s : p = 4 : 5
s / p = 4 / 5
The ratio of princesses weight to Luna’s weight is 6 : 7
p : l = 6 : 7
p / l = 6 / 7
the ratio of socks weight to Luna’s weight,
Multiply both given ratios (s / p) X (p / l) = (4 / 5) X (6 / 7)
s / l = 24 / 35
s : l = 24 : 35
Ratio of socks weight to Luna’s weight is 24 : 35

Question 5.
Danny poured 78 liters of water into containers X, Y, and Z. The ratio of the volume of water in Container X to the volume of water in Container Y is 5 : 2. The ratio of the volume of water in Container Y to the volume of water in Container Z is 8 : 11.
a) How much water was poured into Container X?
Answer:
40 liters
Explanation:
x + y + z = 78
The ratio of the volume of water in Container X to the volume of water in Container Y is 5 : 2.
x : y = 5 : 2
The ratio of the volume of water in Container Y to the volume of water in Container Z is 8 : 11.
y : z = 8 : 11
x : y = 20 : 8 , and y : z = 8 : 11
Now, both ratios we can rewrite as one,
x : y : z = 20 : 8 : 11
20 + 8 + 11 = 39 units
Three containers contain 78 liters and that is 39 units, let’s find how many litters in 1 unit.
78 / 39 = 2 litters per unit
x = 20 x 2 = 40

b) How much more water was poured into Container X than Container Z?
Answer:
18 liters
Explanation:
x + y + z = 78
The ratio of the volume of water in Container X to the volume of water in Container Y is 5 : 2.
x : y = 5 : 2
The ratio of the volume of water in Container Y to the volume of water in Container Z is 8 : 11.
y : z = 8 : 11
x : y = 20 : 8 , and y : z = 8 : 11
Now, both ratios we can rewrite as one,
x : y : z = 20 : 8 : 11
20 + 8 + 11 = 39 units
Three containers contain 78 liters and that is 39 units, let’s find how many litters in 1 unit.
78 / 39 = 2 litters per unit
x = 20 x 2 = 40
y = 8 x 2 = 16
z = 11 x 2 = 22
x – z = 40 – 22 = 18

Question 6.
The ratio of the number of mystery books to the number of science fiction books is 4 : 3. The ratio of the number of science fiction books to the number of biographies is 4 : 5. If there are 48 science fiction books, find the total number of books.
Answer:
172 books
Explanation:
The ratio of the number of mystery books to the number of science fiction books is 4 : 3.
Mystery  books = 48 / 3 = 16
16 x 4 = 64
Biography books = 48 / 4 = 12
12 x 5 = 60
The ratio of the number of science fiction books to the number of biographies is 4 : 5.
If there are 48 science fiction books
The total number of books = 60 + 64 + 48 = 172

Question 7.
In a music room, the ratio of the number of clarinets to the number of flutes was 3 : 4. After the school bought another 24 flutes, the ratio became 3 : 8. How many clarinets were there in the music room?
Answer:
18 clarinets
Explanation:
The ratio of the number of clarinets to the number of flutes was 3 : 4.
clarinets (c) : flutes (f) = 3 : 4
4c = 3f
After the school bought another 24 flutes, the ratio became 3 : 8.
\(\frac{c}{(f + 24)}\) = \(\frac{3}{8}\)
Number of clarinets in music room
⇒ 8c  =3f + 72 (3f = 4c)
⇒ 8c = 4c + 72
⇒ 4c = 72
∴c = 18

Question 8.
In a school gym, the ratio of the number of boys to the number of girls was 4 : 3. After 160 boys left the gym, the ratio became 4 : 5. How many girls were there in the gym?
Answer:
300 girls
Explanation:
The ratio of the number of boys to the number of girls was 4 : 3.
b/g = 4/3
After 160 boys left the gym, the ratio became 4 : 5.
(b-160)/g = 4/5
g = 300

Question 9.
The ratio of the number of men to the number of women on a bus was 2 : 3. At a bus stop, 4 women got off and the ratio became 4 : 5.
a) How many men were on the bus?
Answer:
16 men

b) How many women were on the bus in the end?
Answer:
20 women
Explanation:
ratio of men to women is 2:3
2 and 3 have to be multiplied by some number, call it x, to determine the exact number of men and women
2x/3x is how to write the ratio
4 women got off the bus
2x is the number of men and 3x – 4 is the number of women
2x/(3x – 4) is the ratio now which equals 4/5
2x/(3x – 4) = 4/5
cross multiply
5(2x) = 4(3x – 4)
10x = 12x – 16
10x – 12x = – 16
-2x = -16
2x = 16
x = 16/2
x = 8
2 x 8 = 16 and 3 x 8 = 24,
so the original ratio was 16/24 which is 2/3
4 women got off the bus
16 men and 24 – 4 = 20 women

Question 10.
CD The number of chickens to the number of ducks on a farm was 6 : 5. After 63 ducks were sold, there were 3 times as many chickens as ducks left,
a) How many chickens were there on the farm?
Answer:
126 chickens
Explanation:
Let there be $6x$ chickens and $5x$ ducks
Ratio of chickens and ducks = $6:5$.
When 63 ducks are sold, by given condition,
\(\frac{6x}{(5x – 63)}\) = \(\frac{3}{1}\)
6x = 15x – 189
9x = 189
x = \(\frac{189}{9}\)
x = 21
6x = 6 x 21 = 126
Therefore, $126$ chickens were there in the farm.

b) How many chickens and ducks were there altogether on the farm in the end?
Answer:
168 ducks
Explanation:
Total number of chickens and ducks in the end are
$\left(6x\right)+(5x-63)=11x-63=\mathrm{11\; x}21-63=231-63=168$

Question 11.
The ratio of the volume of fruit juice to the volume of smoothies served at a party was 4\(\frac{1}{2}\) : 2.4. There were 35 liters more fruit juice served than smoothies. Find the volume of smoothies served.
Answer:
40 liters
Explanation:
4\(\frac{1}{2}\) : 2.4
35 liters more fruit juice served than smoothies
4\(\frac{1}{2}\) = \(\frac{9}{2}\) = 4.5
4.5 : 2.4  ::  x + 35 : x
4.5 x :: 2.4 (x + 35)
4.5 x :: 2.4x + 84
4.5x – 2.4x :: 84
2.1 x = 84
x = 84/2.1
x = 40

Question 12.
A piece of ribbon is cut into two shorter pieces in the ratio 2.8 : 1.25. The difference in the length of the two shorter pieces is 80.6 centimeters. What is the length of the original piece of ribbon?
Answer:
210.6cm
Explanation:
The lengths of the two pieces are in the ratio 2.8 : 1.25,
the lengths are 2.8x and 1.25x, for some positive number, x.
2.8x – 1.25x = 80.6
1.55x = 80.6
x = 52
Length of larger piece = 2.8x = 2.8 X 52 = 145.6 cm
Length of smaller piece = 1.25x = 1.25 X 52) = 65 cm
length of the original piece of ribbon = 145.6 + 65 = 210.6cm

Question 13.
Math journal The ratio of the number of beads collected by Jane to the number of beads collected by Jill is 7 : 3. Jane gave some beads to Jill. Is it possible for both Jane and Jill to have the same number of beads after Jane gave some beads to Jill? Explain why you think so.
Answer:
YES
Explanation:
The ratio of the number of beads collected by Jane to the number of beads collected by Jill is 7 : 3
7x : 3x
Let ratio coefficient is = x  , So Jane have total beads  = 7 x and Jill have total beads  = 3 x 
Now we assume that Jane gave ‘ y ‘ beads to Jill to have same number of beads for both , So
7x – y = 3x + y
7x – 3 x = y + y
4x = 2y
y = 2x
yes, it possible for both Jane and Jill to have the same number of beads after Jane gave some beads to Jill.

Question 14.
Today the ratio of Elinor’s age to her mother’s age is 3 : 8. After 15 years, the ratio will become 6 : 11.
a) Find Elinor’s age today.
Answer:
15 years
Explanation:
Today the ratio of Elinor’s age to her mother’s age is 3 : 8
3x + 15 : 8x + 15 = 6 : 11
(3x + 15 ) x 11 = (8x + 15) x 6
33x + 165 = 48x + 90
48x -33x = 165 – 90
15x = 75
x = 75 / 15
x = 5

b) Find her mother’s age after 15 years.
Answer:
55 years
Explanation
3x + 15 : 8x + 15 = 6 : 11
her mother’s age after 15 years.
11x = 11 x 5
= 55 years

Question 15.
The ratio of Mike’s savings to Nick’s savings was 4 : 3. After Mike saved another $120 and Nick saved another $60, the ratio became 8 : 5. What was their combined savings before each of them saved the additional money?
Answer:
$210
Explanation:
The ratio of Mike’s savings to Nick’s savings was 4 : 3
4 : 3
4x : 3x
4x + 120 : 3x + 60 = 8 : 5
4x + 120 = 8x
4x = 120
x = 120/4
x = 30
4 x 30 + 3 x 30 = 120+90 = $210

Brain @ Work

Question 1.
ABCD is a rectangle. BD is a straight line that cuts the rectangle into equal halves. The ratio of the area of P to the area of Q is 2 : 5, and the ratio of the area R to the area of S is 4 : 3. The area of S is 9 square centimeters.
a) Find the ratio of the area of R to the area of the rectangle.
Answer:
12 square centimeter
Explanation:
The ratio of the area of P to the area of Q is 2 : 5,
the ratio of the area R to the area of S is 4 : 3. The area of S is 9 square centimeters.
P : Q :: 2 : 5
R : S :: 4 : 3
R : 9 :: 4 : 3
R = (9 x 4) / 3
R =  12 square centimeter

b) Find the area of the rectangle.

Answer:
42 square centimeters
Explanation:
Area of  rectangle
S+R = P + Q
9 + 12 = P + Q
P + Q = 21
Area of  rectangle
S+R + P + Q
21 + 21 = 42 square centimeters

Question 2.
A farmer raises chickens and sheep on his farm. The ratio of the total number of legs of the chickens to the total number of legs of the sheep is 4 : 7. Find the minimum number of chickens and sheep on his farm. Copy and complete the table to solve the problem. (Hint: Make a list and solve the problem using guess and check.)

Answer:
1 : 2
Explanation:
The ratio of the total number of legs of the chickens to the total number of legs of the sheep is 4 : 7

1 chicken has 2 legs
1 sheep has 4 legs
So, the ratio of chicken legs and sheep legs are 2 : 4 = 1 : 2

Go through the Math in Focus Grade 6 Workbook Answer Key Cumulative Review Chapters 1-3 to finish your assignments.

Math in Focus Grade 6 Course 1 A Cumulative Review Chapters 1-3 Answer Key

Concepts and Skills

Draw a horizontal number line to represent each set of numbers. (Lesson 1.1)

Question 1.
Mixed numbers from 3 to 7, with an interval of \(\frac{1}{3}\) between each pair of mixed numbers
Answer:

Explanation:
Mixed Fractions on Number Line Mixed fractions have two parts,
one whole number and one proper fraction.
To represent mixed fractions on a number line,
first, mark two points: the whole number part on the left and its successor on the right.

Question 2.
Decimals between 4.2 and 5.4, with an interval of 0.3 between each pair of decimals
Answer:

Explanation:
To represent a decimal on a number line,
divide each segment of the number line into ten equal parts.
Then mark the numbers with given intervals.

Express each number as a product of its prime factors. (Lesson 1.2)

Question 3.
84
Answer:
Factors of 84 are  1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 and 84.
The prime factorization of 84 is 2 × 2 × 3 × 7 or 2² × 3 × 7.
Explanation:
Factors of 84 are the numbers that divide the original number evenly,
since 84 divided by 2 is equal to 42,
42 divided by 2 is equal to 21,
21 divided by 3 is equal to 7.
So, The prime factorization of 84 is 2 × 2 × 3 × 7 or 2² × 3 × 7.
where 2, 3 and 7 are the prime numbers.

Find the greatest common factor of each pair of numbers. (Lesson 1.3)

Question 5.
16 and 60
Answer:
GCF = 4
Explanation:
Find the prime factorization of 16
16 = 2 × 2 × 2 × 2
Find the prime factorization of 60
60 = 2 × 2 × 3 × 5
To find the GCF, multiply all the prime factors common to both numbers.
Therefore, GCF = 2 × 2
GCF = 4

Question 6.
63 and 96
Answer:
GCF = 3
Explanation:
The factors of 63 are 1,3,7,9,21,63;
The factors of 96 are 1,2,3,4,6,8,12,16,24,32,48,96.
To find the GCF, take the common factor to both numbers.
3 is the greatest number that 63 and 96 divides into.
Therefore, GCF = 3

Find the least common multiple of each pair of numbers. (Lesson 1.3)

Question 7.
9 and 12
Answer:
LCM = 36
Explanation:
To find the least common multiple of 9 and 12,
we need to find the multiples of 9 and 12
multiples of 9 = 9, 18, 27, 36;
multiples of 12 = 12, 24, 36, 48
choose the smallest multiple that is exactly divisible by 9 and 12, i.e., 36.
So, the LCM of 9 and 12 is 36.

Question 8.
15 and 18
Answer:
LCM = 90
Explanation:
To find the least common multiple of 15 and 18,
we need to find the multiples of 15 and 18.
multiples of 15 = 15, 30, 45, 60, 75, 90;
multiples of 18 = 18, 36, 54, 72, 90.
choose the smallest multiple that is exactly divisible by 15 and 18, i.e., 90.
So, the LCM of 15 and 18 is 90.

Find the square root of each number. (Lesson 1.4)

Question 9.
256
Answer:
The square root of 256 is 16.
Explanation:
Determine the prime factors using prime factorization.
Prime factorization of 256 =  2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
 Group the prime factors obtained for 256 in pairs.
Pick one factor from each pair and they can be written in the form:
256 = (2 × 2 × 2 × 2)²
 we get, √256 = √(16²)
The square root of 256 is 16.

Question 10.
676
Answer:
The square root of 676 is 26.
Explanation:
676 is a perfect square hence,
we can express it as (2 × 2 × 13 × 13).
The numbers within square root which get repeated are 2 and 13.
Hence, the square root of 676 is 2 × 13 = 26 .

Find the cube root of each number. (Lesson 1.5)

Question 11.
1,728
Answer:
The cube root of 1,728 is 12
Explanation:
To find the cube root of 1728 through the prime factorization method,
1728 = 2 × 2 ×2 × 2 × 2 × 2 ×3 × 3 × 3
Pair the similar factors in a group of them and represent them as cubes.
1728 =  (2 × 2 × 2) × (2 × 2 × 2 ) × (3 × 3 ×3)
1728 = 2³ × 2³ × 3³
1728 = 2 x 2 x 3 = 12
Hence, the cube root of 1,728 is 12.

Question 12.
5,832
Answer:
The cube root of 5,832 is 18.
Explanation:
To find the cube root of 1728 through the prime factorization method,
1728 = 2 × 2 × 2 × 3 × 3 × 3 ×3 × 3 × 3
Pair the similar factors in a group of them and represent them as cubes.
1728 =  (2 × 2 × 2) × (3 × 3 × 3 ) × (3 × 3 ×3)
1728 = 2³ × 3³ × 3³
1728 = 2 x 3 x 3 = 18
Hence, the cube root of 5,832 is 18.

Find the value of each of the following. (Lesson 1.5)

Question 13.
5³ – 11² + 7³
Answer: 347
Explanation:
Write the cubes  and square roots of given numbers.
5³ = 5 x 5 x 5 = 125
7³ = 7 x 7 x 7 = 343
11² = 11 x 11 = 121
According to BOADMAS first add the numbers of positive integers and then subtract the negative integers.
5³  + 7³ = 468
5³ – 11² + 7³ = 468 – 121 = 347

Question 14.
4³ ÷ 8² × 12³
Answer: 1,728
Explanation:
Apply the order of mathematical operations,
BODMAS stands for B-Brackets, O-Orders, D-Division, M-Multiplication, A-Addition, S-Subtraction.
4³ ÷ 8²
4x4x4 = 64
8×8 = 64
So, 64 ÷ 64 = 1
12³  = 12 x 12 12 = 1,728
4³ ÷ 8² × 12³ = 1,728
Solve. (Lesson 1.5).

Question 15.
Given that 56² = 3,136, find the square of 112.
Answer:
112 x 112 = 12,544
Explanation:
Square root is the number that we multiply by itself to get the original number.
56 x 56 = 3,136
112 x 112 = 12,544

Question 16.
Given that 13³ = 2,197, find the cube root of 17,576.
Answer:
The cube root of 17,576 is 26.
Explanation:
To find the cube root of 17,576 through the prime factorization method,
17,576 = 2 × 2 × 2 × 13 x 13 x 13
Pair the similar factors in a group of them and represent them as cubes.
17,576 =  (2 × 2 × 2) × (13 × 13 × 13 )
17,576 = 2³ × 13³ 
17,576 = 2 x 13 = 26
Hence, the cube root of 17,576 is 26.

Draw a vertical number line to represent each set of numbers. (Lessons 1.3, 2.1)

Question 17.
Multiples of 3 between 81 and 110
Answer:
84, 87, 90, 93, 96, 99, 102, 105, 108.
Explanation:

3 x 28 = 84
3 x 29 = 87
3 x 30 = 90
3 x 31 = 93
3 x 32 = 96
3 x 33 = 99
3 x 34 = 102
3 x 35 = 105
3 x 36 = 108

Question 18.
Even numbers greater than -37 but less than -25
Answer:
-36, -34,  -32. -30, -28, -26
Explanation:
Even numbers after -37 and -25 given number are
-36
-36+2 = -34
-34 + 2 = -32
-32 + 2 = 30
-30 + 2 = 28
-28 + 2 = -26

Write a positive or negative number to represent each situation. (Lesson 2.1)

Question 19.
Getting a pay raise of $320 per year
Answer:
Getting a pay raise of $320 per year, means increase to the previous pay.
Explanation:
positive number
Pay raise of $320 per year
it means adding to the previous number

Question 20.
214°F below zero
Answer:
-214°F
Explanation:
Measurement of temperature
0 degrees Fahrenheit is equal to -17.77778 degrees Celsius:
0°F = -17.77778 °C

The temperature T in degrees Celsius (°C) is equal to 214 degrees Fahrenheit (°F) minus 32, times 5/9. To convert 214 Fahrenheit to Celsius we can use the formula below:

Question 21.
Riding an elevator down 15 floors
Answer:
negative number
Explanation:
It means Elevator is moving down.
Elevator down from 15, to 14 , 13 …….. to zero (it means ground floor)

Copy and complete each inequality using > or <. (Lesson 2.1)

Question 22.
121 -388
Answer:
121 > -388
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number,
smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.

Question 23.
-795 347
Answer:
-795 < 347
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number,
smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.

Question 24.
-78 -132
Answer:
-78 > -132
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number, smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.

Question 25.
-234 -243
Answer:
-234 > -243
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number, smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.

Write an inequality for each of the following statements using > or <. (Lesson 2.1)

Question 26.
185°F is colder than 209°F.
Answer:
Yes,
Explanation:
According to the Fahrenheit scale 185°F is less then 209°F, according to the number system 185 is less then the 209, hence the 185°F is colder then 209°F

Question 27.
Town A, which is 84 kilometers from Town B, is farther from Town B than Town C, which is 76 kilometers from Town B.
Answer:

Copy and complete each inequality using > or <. (Lesson 2.2)

Question 28.
|-356| |368|
Answer:
356 < 368
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number, smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.

Question 29.
|232| |-324|
Answer:
232 < 324
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number, smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.

Question 30.
|264| |246|
Answer:
264 > 246
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number, smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.

Question 31.
|-311| |-389|
Answer:
311 < 389
Explanation:
Important symbol or signs used to identify the numbers to understand the bigger number, smaller number and the number that is equal.
When one number is bigger than the other number; we use greater than sign >.
When one number is smaller than the other number; we use less than sign <.

Divide. (Lesson 3.1)

Question 32.
28 ÷ \(\frac{1}{5}\)
Answer: 140
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.

28 ÷ \(\frac{1}{5}\)

\(\frac{28}{1}\) x \(\frac{5}{1}\)

28 x 5 = 140

Question 33.
42 ÷ \(\frac{2}{3}\)
Answer: 63
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.

42 ÷ \(\frac{2}{3}\)

\(\frac{42}{2}\) x \(\frac{3}{1}\)

\(\frac{126}{2}\) = 63

Question 34.
\(\frac{3}{8}\) ÷ 12
Answer: 32
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.

\(\frac{3}{8}\) ÷ 12

\(\frac{96}{3}\) = 32

Question 35.
\(\frac{5}{14}\) ÷ \(\frac{10}{21}\)
Answer: 0.75
Explanation:
Dividing fractions is equal to the multiplication of a fraction by the reciprocal of another fraction. A fraction has a numerator and a denominator.
When we divide one fraction by another, we almost multiply the fractions.

\(\frac{5}{14}\) ÷ \(\frac{10}{21}\)

\(\frac{105}{140}\) = 0.75

Multiply. (Lesson 3.2)

Question 36.
0.3 × 3.8
Answer: 1.14
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
and then the number of decimal places in the product is equal to the total number of decimal places in the given numbers.

Question 37.
6.3 × 4.7
Answer: 29.61
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
and then the number of decimal places in the product is equal to the total number of decimal places in the given numbers.
Question 38.
0.28 × 474
Answer: 132.72
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
and then the number of decimal places in the product is equal to the total number of decimal places in the given numbers.

Question 39.
8.23 × 9.107
Answer: 74.95061
Explanation:
Multiplication of decimals is done by ignoring the decimal point and multiply the numbers,
and then the number of decimal places in the product is equal to the total number of decimal places in the given numbers.

Divide. (Lesson 3.3)

Question 40.
72 ÷ 0.3
Answer: 240
Explanation:
When we divide decimals,
we change the divisor to a whole number by moving the decimal point all the way to the right.
Then, we move the decimal point of the dividend up to the same number of places to the right,
and divide the resultant numbers in the normal way as we do regular division.

Question 41.
8.1 ÷ 0.3
Answer: 27
Explanation:
When we divide decimals,
we change the divisor to a whole number by moving the decimal point all the way to the right.
Then, we move the decimal point of the dividend up to the same number of places to the right,
and divide the resultant numbers in the normal way as we do regular division.

Question 42.
2.88 ÷ 1.2
Answer: 240
Explanation:
When we divide decimals,
we change the divisor to a whole number by moving the decimal point all the way to the right.
Then, we move the decimal point of the dividend up to the same number of places to the right,
and divide the resultant numbers in the normal way as we do regular division.

Question 43.
128 ÷ 0.02
Answer: 6,400
Explanation:
When we divide decimals,
we change the divisor to a whole number by moving the decimal point all the way to the right.
Then, we move the decimal point of the dividend up to the same number of places to the right,
and divide the resultant numbers in the normal way as we do regular division.

Problem Solving

Solve. Show your work.

Question 44.
Alison paid $21.75 for a number of packs of rice crackers. Three packs of rice crackers cost $1.45. How many packs of rice crackers did Alison buy? If she were to buy 60 packs of the same rice crackers, would $30 be enough to pay for them? (Chapter 3)
Answer:
60 packs
Explanation:
Find the x, the unit price 3x = 1.45
\(\frac{3x}{3}\)

= \(\frac{1.45}{3x}\)

x = 0.483 cost per pack.
the number of packs bought 21.75 = 0.483 x 0.483x = 21.75
0.483x / 0.483 = 21.75 / 0.483 x = 45 packs bought
total cost of 60 packs x = 0.483(60) x = 28.98 is the total cost.
$30 is more than enough to pay for 60 packs.

Question 45.
Find two consecutive numbers whose cubes differ by 169. (Chapter 1)
Answer:
8 and 7 are 2 consecutive numbers.
Explanation:
cube of 8 = 8 x 8 x 8 = 512
cube of 7 = 7 x 7 x 7 = 343
Difference of 8 cube and 7 cube
512 – 343 = 169

Question 46.
Two light houses flash their lights every 30 seconds and 40 seconds respectively. Given that they last flashed together at 10:40 A.M., when will they next flash together? (Chapter 1)
Answer:
10:42 AM
Explanation:
for every 120 seconds the lights will flash together
30 x 4 = 120 sec
40 x 3 = 120 sec
10:40 AM flash
10:42 AM

Question 47.
\(\frac{7}{8}\) of a rectangle is colored red. Damien cuts this red part into a number of pieces so that each piece is \(\frac{1}{24}\) of the whole rectangle. Find the number of red pieces Damien has. (Chapter 3)
Answer:
21 red pieces
Explanation:
\(\frac{7}{8}\) of a rectangle is colored red.
Damien cuts this red part into a number of pieces so that each piece is \(\frac{1}{24}\) The number of red pieces Damien has
\(\frac{7}{8}\) ÷ \(\frac{1}{24}\)

\(\frac{7×24}{8}\) = \(\frac{168}{8}\) = 21

Question 48.
Jon spent \(\frac{1}{3}\) of his allowance on baseball cards, \(\frac{1}{4}\) on baseball souvenirs, and \(\frac{3}{8}\) on a baseball ticket. If he had $5 left, how much allowance did he have to start with? (Chapter 3)
Answer:
$120
Explanation:
Let x is total allowance Jan started
Allowance spent on baseball = \(\frac{1}{3}\)

Allowance spent on baseball souvenirs = \(\frac{3}{4}\)

Allowance spent on baseball ticket = \(\frac{3}{8}\)
Remaining allowances = Total allowance – baseball – souvenirs – ticket
= x -(\(\frac{1}{3}\)) x  – (\(\frac{3}{4}\))x – (\(\frac{3}{8}\)) x

= x – \(\frac{x}{3}\) – \(\frac{x}{4}\) – \(\frac{3x}{8}\)

L.C.M of the denominators = 24
Multiply each term with 24
24x – 8x – 6x – 9x ÷ 24
Jane left with $5
\(\frac{x}{24}\) = 5
Multiply 24 on both sides
\(\frac{x}{24}\) x 24 = 5 x 24
= 120

Question 49.
A baker baked some loaves of bread. 240 loaves were sold by the end of the day. The baker was then left with \(\frac{9}{25}\) of the number of loaves that were baked. How many loaves of bread did the baker bake on that day? (Chapter 3)
Answer:
375 loaves
Explanation:
x- 240 = \(\frac{x9}{25}\)

x –  \(\frac{x9}{25}\) = 240
25 x -9x = 240 x 25
16x = 6000
x = 6000/25
x = 375

Question 50.
Front and back row tickets to a performance are available. There are 18 front rows with 39 seats in each row, and 27 back rows with 4 seats in each row. If \(\frac{5}{6}\) of all the front row seats and \(\frac{7}{9}\) of the back row seats are sold, how much is the total ticket sales? (Chapter 3)
Answer:
669 seats
Explanation:
18 front rows with 39 seats in each row =
=18 x 39 = 702
702 x \(\frac{5}{6}\) = 585 seats

27 back rows with 4 seats in each row
27 x 4 = 108
108x\(\frac{7}{9}\)
=84
the total ticket sales
= 585 + 84
= 669 seats

Question 51.
A charitable organization packed 195 bags of rice, 325 blankets, and 455 bottles of water equally into boxes. (Chapter 1)
a) Find the greatest possible number of boxes that the items can be packed into.
Answer:
5 boxes
Explanation:
195/5 = 35
325/5 =65
445/5= 91
packed 195 bags of rice, 325 blankets, and 455 bottles of water equally into 5 boxes.

b) Find the number of bags of rice, blankets, and bottles of water in each box.
Answer:
35 rice bags, 65 blankets and 91 water bottles.
Explanation:
195/5 = 35 rice
325/5 =65 blankets
445/5= 91 water bottles

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 3 Lesson 3.3 Dividing Decimals to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 3 Lesson 3.3 Answer Key Dividing Decimals

Math in Focus Grade 6 Chapter 3 Lesson 3.3 Guided Practice Answer Key

Complete.

Question 1.
Find 1 ÷ 0.5
Method 1

Answer:
There are two 0.5s in 1 whole.

Explanation:
There are two 0.5s are in 1 whole.

Method 2
1 ÷ 0.5 = 1 ÷ \(\frac{5}{10}\)
= 1 × \(\frac{10}{5}\)
= 2.

Question 2.
Find 48 ÷ 0.3

Answer:
48 ÷ 0.3 = 160.

Explanation:
48 ÷ 0.3 = 48 ÷ \(\frac{3}{10}\)
= 48 × \(\frac{10}{3}\)
= 16 × 10
= 160.

Complete.

Question 3.
Complete the model to show the division expression 98 ÷ 0.14.

Answer:
98 ÷ 0.14 = 700.

Explanation:

Method 2
98 ÷ 0.14 = 98 ÷ \(\frac{14}{100}\)
= 98 × \(\frac{100}{14}\)
= 7 × 100
= 700.

Divide.

Question 4.

Answer:
75 ÷ 0.15 = 500.

Explanation:
75 ÷ 0.15 = 75 ÷ \(\frac{15}{100}\)
= 75 × \(\frac{100}{15}\)
= 5 × 100
= 500.

Question 5.

Answer:
156 ÷ 0.13 = 1200.

Explanation:
Given the division expression is 156 ÷ 0.13,
156 ÷ 0.13 = 156 ÷ \(\frac{13}{100}\)
= 156 × \(\frac{100}{13}\)
= 12 × 100
= 1200.

Complete.

Question 6.
Find 0.9 ÷ 0.3.

Answer:
There are three 0.3s in 0.9.

Explanation:
Given the division expression is 0.9 ÷ 0.3,
0.9 ÷ 0.3 = \(\frac{9}{10}\) ÷ \(\frac{3}{10}\)
= \(\frac{9}{10}\) × \(\frac{10}{3}\)
= 3.
So each small interval represents 0.3 and there are 3 intervals.

Complete.

Question 7.
Find 0.72 ÷ 0.03.
Method 1

Answer:
0.72 ÷ 0.03 = 24.

Explanation:
Given the division expression is 0.72 ÷ 0.03,
Method 1
0.72 = \(\frac{72}{100}\)  and 0.03 = \(\frac{3}{100}\)
= \(\frac{72}{100}\) ÷ \(\frac{3}{100}\)
= \(\frac{72}{100}\) × \(\frac{100}{3}\)
= 24.

Method 2
0.72 ÷ 0.03 = \(\frac{0.72}{0.03}\)
= \(\frac{0.72}{0.03}\) × \(\frac{100}{100}\)
= \(\frac{72}{3}\)
= 24.

Complete.

Question 8.
Find 0.78 ÷ 0.6.

Answer:
0.78 ÷ 0.6 = 1.3.

Explanation:
Given the division expression is 0.78 ÷ 0.6,
Method 1
0.78 = \(\frac{78}{100}\)  and 0.6 = \(\frac{6}{10}\)
= \(\frac{78}{100}\) ÷ \(\frac{6}{10}\)
= \(\frac{78}{100}\) × \(\frac{10}{6}\)
= \(\frac{13}{10}\)
= 1.3.

Method 2
0.78 ÷ 0.6 = \(\frac{0.78}{0.6}\)
= \(\frac{0.78}{0.6}\) × \(\frac{10}{10}\)
= \(\frac{7.8}{6}\)
= 1.3.

Question 9.
Find 6.75 ÷ 0.3.

Answer:

Explanation:
Given the division expression is 6.75 ÷ 0.3,
Method 1
6.75 = \(\frac{675}{100}\)  and 0.3 = \(\frac{3}{10}\)
= \(\frac{675}{100}\) ÷ \(\frac{3}{10}\)
= \(\frac{675}{100}\) × \(\frac{10}{3}\)
= \(\frac{225}{10}\)
= 22.5.

Method 2
6.75 ÷ 0.3 = \(\frac{6.75}{0.3}\)
= \(\frac{6.75}{0.3}\) × \(\frac{10}{10}\)
= \(\frac{67.5}{3}\)
= 22.5

Math in Focus Course 1A Practice 3.3 Answer Key

Write a division expression that represents each model.

Question 1.

Answer:
1 ÷ 0.2 = 5.

Explanation:
In 1 whole there are five 0.2s, so the division expression will be 1 ÷ 0.2 which is 5.

Question 2.

Answer:
3 ÷ 0.2 = 15.

Explanation:
In 3 wholes there are 15 0.2s, so the division expression will be 3 ÷ 0.2 which is 15.

Divide.

Question 3.
2 ÷ 0.4
Answer:
2 ÷ 0.4 = 5.

Explanation:
Given the division expression is 2 ÷ 0.4,
2 ÷ 0.4 = 2 ÷ \(\frac{4}{10}\)
= 2 × \(\frac{10}{4}\)
= 5.

Question 4.
4 ÷ 0.5
Answer:
4 ÷ 0.5 = 8.

Explanation:
Given the division expression is 4 ÷ 0.5,
4 ÷ 0.5 = 4 ÷ \(\frac{5}{10}\)
= 4 × \(\frac{10}{5}\)
= 8.

Question 5.
5 ÷ 0.2
Answer:
5 ÷ 0.2 = 25.

Explanation:
Given the division expression is 5 ÷ 0.2,
5 ÷ 0.2 = 5 ÷ \(\frac{2}{10}\)
= 5 × \(\frac{10}{2}\)
= 5 × 5
= 25.

Question 6.
8 ÷ 0.8
Answer:
8 ÷ 0.8 = 10.

Explanation:
Given the division expression is 8 ÷ 0.8,
8 ÷ 0.8 = 8 ÷ \(\frac{8}{10}\)
= 8 × \(\frac{10}{8}\)
= 10.

Question 7.
9 ÷ 0.3
Answer:
9 ÷ 0.3 = 30.

Explanation:
Given the division expression is 9 ÷ 0.3,
9 ÷ 0.3 = 9 ÷ \(\frac{3}{10}\)
= 9 × \(\frac{10}{3}\)
= 3 × 10
= 30.

Question 8.
7 ÷ 0.4
Answer:
7 ÷ 0.4 = 17.5.

Explanation:
Given the division expression is 7 ÷ 0.4,
7 ÷ 0.4 = 7 ÷ \(\frac{4}{10}\)
= 7 × \(\frac{10}{4}\)
= 7 × \(\frac{5}{2}\)
= \(\frac{35}{2}\)
= 17.5.

Question 9.
12 ÷ 0.3
Answer:
12 ÷ 0.3 = 40.

Explanation:
Given the division expression is 12 ÷ 0.3,
12 ÷ 0.3 = 12 ÷ \(\frac{3}{10}\)
= 12 × \(\frac{10}{3}\)
= 4 × 10
= 40.

Question 10.
42 ÷ 0.7
Answer:
42 ÷ 0.7 = 60.

Explanation:
Given the division expression is 42 ÷ 0.7,
42 ÷ 0.7 = 42 ÷ \(\frac{7}{10}\)
= 42 × \(\frac{10}{7}\)
= 6 × 10
= 60.

Question 11.
55 ÷ 0.5
Answer:
55 ÷ 0.5 = 110.

Explanation:
Given the division expression is 55 ÷ 0.5,
55 ÷ 0.5 = 55 ÷ \(\frac{5}{10}\)
= 55 × \(\frac{10}{5}\)
= 11 × 10
= 110.

Question 12.
69 ÷ 0.2
Answer:
69 ÷ 0.2 = 345

Explanation:
Given the division expression is 69 ÷ 0.2,
69 ÷ 0.2 = 69 ÷ \(\frac{2}{10}\)
= 69 × \(\frac{10}{2}\)
= 69 × 5
= 345.

Question 13.
86 ÷ 0.5
Answer:
86 ÷ 0.5 = 172

Explanation:
Given the division expression is 86 ÷ 0.5,
86 ÷ 0.5 = 86 ÷ \(\frac{5}{10}\)
= 86 × \(\frac{10}{5}\)
= 86 × 2
= 172.

Question 14.
93 ÷ 0.4
Answer:

Explanation:
Given the division expression is 93 ÷ 0.4,
93 ÷ 0.4 = 93 ÷ \(\frac{4}{10}\)
= 93 × \(\frac{10}{4}\)
= 93 × \(\frac{5}{2}\)
= \(\frac{465}{2}\)
= 232.5.

Question 15.
1 ÷ 0.02
Answer:
1 ÷ 0.02 = 50.

Explanation:
Given the division expression is 1 ÷ 0.02,
1 ÷ 0.02 = 1 ÷ \(\frac{2}{100}\)
= 1 × \(\frac{100}{2}\)
= 50.

Question 16.
3 ÷ 0.06
Answer:
3 ÷ 0.06 = 50.

Explanation:
Given the division expression is 3 ÷ 0.06,
3 ÷ 0.06 = 3 ÷ \(\frac{6}{100}\)
= 3 × \(\frac{100}{6}\)
= \(\frac{100}{2}\)
= 50.

Question 17.
6 ÷ 0.15
Answer:
6 ÷ 0.15 = 40.

Explanation:
Given the division expression is 6 ÷ 0.15,
6 ÷ 0.15 = 6 ÷ \(\frac{15}{100}\)
= 6 × \(\frac{100}{15}\)
= 2 × \(\frac{100}{5}\)
= 2 × 20
= 40.

Question 18.
7 ÷ 0.35
Answer:
7 ÷ 0.35 = 20.

Explanation:
Given the division expression is 7 ÷ 0.35,
7 ÷ 0.35 = 7 ÷ \(\frac{35}{100}\)
= 7 × \(\frac{100}{35}\)
= 20.

Question 19.
8 ÷ 0.32
Answer:
8 ÷ 0.32 = 25.

Explanation:
Given the division expression is 8 ÷ 0.32,
8 ÷ 0.32 = 8 ÷ \(\frac{32}{100}\)
= 8 × \(\frac{100}{32}\)
= 25.

Question 20.
9 ÷ 0.72
Answer:
9 ÷ 0.72 = 12.5.

Explanation:
Given the division expression is 9 ÷ 0.72,
9 ÷ 0.72 = 9 ÷ \(\frac{72}{100}\)
= 9 × \(\frac{100}{72}\)
= 12.5.

Draw a model to show each division expression.

Question 21.
2 ÷ 0.5
Answer:
2 ÷ 0.5 = 4.

Explanation:
Given the division expression is 2 ÷ 0.5,
2 ÷ 0.5 = 2 ÷ \(\frac{5}{10}\)
= 2 × \(\frac{10}{5}\)
= 4.

Question 22
5 ÷ o.2
Answer:
5 ÷ o.2 = 10.

Explanation:
Given the division expression is 5 ÷ o.2,
5 ÷ o.2 = 5 ÷ \(\frac{2}{10}\)
= 5 × \(\frac{10}{5}\)
= 10.

Divide.

Question 23.
36 ÷ 0.36
Answer:
36 ÷ 0.36 = 100.

Explanation:
Given the division expression is 36 ÷ 0.36,
36 ÷ 0.36 = 36 ÷ \(\frac{36}{100}\)
= 36 × \(\frac{100}{36}\)
= 100.

Question 24.
49 ÷ 0.14
Answer:
49 ÷ 0.14 = 350.

Explanation:
Given the division expression is 49 ÷ 0.14,
49 ÷ 0.14 = 49 ÷ \(\frac{14}{100}\)
= 49 × \(\frac{100}{14}\)
= 49 × 50
= 350.

Question 25.
56 ÷ 0.28
Answer:
56 ÷ 0.28 = 200.

Explanation:
Given the division expression is 56 ÷ 0.28,
56 ÷ 0.28 = 56 ÷ \(\frac{28}{100}\)
= 56 × \(\frac{100}{28}\)
= 2 × 100
= 200.

Question 26.
72 ÷ 0.20
Answer:
72 ÷ 0.20 = 360.

Explanation:
Given the division expression is 72 ÷ 0.20,
72 ÷ 0.20 = 72 ÷ \(\frac{20}{100}\)
= 72 × \(\frac{100}{20}\)
= 72 × 5
= 360.

Question 27.
81 ÷ 0.54
Answer:
81 ÷ 0.54 = 150.

Explanation:
Given the division expression is 81 ÷ 0.54,
81 ÷ 0.54 = 81 ÷ \(\frac{54}{100}\)
= 81 × \(\frac{100}{54}\)
= 3 × \(\frac{100}{2}\)
= 3 × 50
= 150.

Question 28.
256 ÷ 0.64
Answer:
256 ÷ 0.64 = 400.

Explanation:
Given the division expression is 256 ÷ 0.64,
256 ÷ 0.64 = 256 ÷ \(\frac{64}{100}\)
= 256 × \(\frac{100}{64}\)
= 4 × 100
= 400.

Question 29.
749 ÷ 0.7
Answer:
749 ÷ 0.7 = 1,070.

Explanation:
Given the division expression is 749 ÷ 0.7,
749 ÷ 0.7 = 749 ÷ \(\frac{7}{10}\)
= 749 × \(\frac{10}{7}\)
= 107 × 10
= 1,070.

Question 30.
972 ÷ 0.8
Answer:
972 ÷ 0.8 = 1,215.

Explanation:
Given the division expression is 972 ÷ 0.8,
972 ÷ 0.8 = 972 ÷ \(\frac{8}{10}\)
= 972 × \(\frac{10}{8}\)
= 972 × \(\frac{5}{4}\)
= 243 × 5
= 1,215.

Question 31.
96 ÷ 0.16
Answer:
96 ÷ 0.16 = 1600.

Explanation:
Given the division expression is 96 ÷ 0.16,
96 ÷ 0.16 = 96 ÷ \(\frac{16}{100}\)
= 96 × \(\frac{100}{16}\)
= 16 × 100
= 1600.

Question 32.
545 ÷ 0.25
Answer:
545 ÷ 0.25 = 218.

Explanation:
Given the division expression is 545 ÷ 0.25,
545 ÷ 0.25 = 545 ÷ \(\frac{25}{10}\)
= 545 × \(\frac{10}{25}\)
= 545 × \(\frac{2}{5}\)
= 109 × 2
= 218.

Question 33.
0.6 ÷ 0.3
Answer:
0.6 ÷ 0.3 = 2.

Explanation:
Given the division expression is 0.6 ÷ 0.3,
0.6 ÷ 0.3 = \(\frac{6}{10}\) ÷ \(\frac{3}{10}\)
= \(\frac{6}{10}\) × \(\frac{10}{3}\)
= 2.

Question 34.
0.64 ÷ 0.04
Answer:
0.64 ÷ 0.04 = 64.

Explanation:
Given the division expression is 4 ÷ 0.5,
0.64 ÷ 0.04 = \(\frac{64}{100}\) ÷ \(\frac{4}{100}\)
= \(\frac{64}{100}\) × \(\frac{100}{4}\)
= 16.

Question 35.
0.78 ÷ 0.06
Answer:
0.78 ÷ 0.06 = 13.

Explanation:
Given the division expression is 0.78 ÷ 0.06,
0.78 ÷ 0.06 = \(\frac{78}{100}\) ÷ \(\frac{6}{100}\)
=\(\frac{78}{100}\) × \(\frac{100}{6}\)
= 13.

Question 36.
0.85 ÷ 0.5
Answer:
0.85 ÷ 0.5 = 17.

Explanation:
Given the division expression is 0.85 ÷ 0.5,
0.85 ÷ 0.5 = \(\frac{85}{100}\) ÷ \(\frac{5}{10}\)
= \(\frac{85}{10}\)× \(\frac{10}{5}\)
= 17.

Question 37.
0.025 ÷ 0.5
Answer:
0.025 ÷ 0.5 = 0.05.

Explanation:
Given the division expression is 0.025 ÷ 0.5,
0.025 ÷ 0.5 = \(\frac{25}{1000}\) ÷ \(\frac{5}{10}\)
= \(\frac{25}{1000}\) × \(\frac{10}{5}\)
= \(\frac{5}{100}\)
= 0.05.

Question 38.
0.816 ÷ 0.34
Answer:
0.816 ÷ 0.34 = 2.4.

Explanation:
Given the division expression is 0.816 ÷ 0.34,
0.816 ÷ 0.34 = \(\frac{816}{1000}\) ÷ \(\frac{34}{100}\)
= \(\frac{816}{1000}\) × \(\frac{100}{34}\)
= \(\frac{24}{10}\)
= 2.4.

Question 39.
4.5 ÷ 0.2
Answer:
4.5 ÷ 0.2 = 22.5.

Explanation:
Given the division expression is 4.5 ÷ 0.2,
4.5 ÷ 0.2 = \(\frac{45}{10}\) ÷ \(\frac{2}{10}\)
= \(\frac{45}{10}\) × \(\frac{10}{2}\)
= \(\frac{45}{2}\)
= 22.5.

Question 40.
8.82 ÷ 0.6
Answer:
8.82 ÷ 0.6 = 14.7.

Explanation:
Given the division expression is 8.82 ÷ 0.6,
8.82 ÷ 0.6 = \(\frac{882}{100}\) ÷ \(\frac{6}{10}\)
= \(\frac{882}{100}\) × \(\frac{10}{6}\)
= \(\frac{147}{10}\)
= 14.7.

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 2 Lesson 2.1 Negative Numbers to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 2 Lesson 2.1 Answer Key Negative Numbers

Math in Focus Grade 6 Chapter 2 Lesson 2.1 Guided Practice Answer Key

Write a positive or negative number to represent each situation.

Question 1.
36°F below zero
Answer:
-36°F
Explanation:
The given situation is 36°F below zero. The word ‘below zero’ represents negative sign. The given situation is represented with negative number -36°F.

Question 2.
A debit of $10,540
Answer:
-$10,540
Explanation:
The given situation is a debit of $10,540. The word debit is represented with negative sign and credit is represented with positive sign. The given situation is represented with negative number -$10,540.

Question 3.
29,035 feet below sea level
Answer:
-29,035 feet
Explanation:
The given situation is 29,035 feet below sea level. The word ‘below sea level’ is represented with negative sign. So, the given situation is represented with negative number -29,035 feet.

Question 4.
A gain of 45 yards
Answer:
45 yards
Explanation:
The given situation is a gain of 45 yards. The word ‘gain’ is represented with positive sign. The word ‘loss’ is represented with negative sign. So, the given situation is represented with positive number 45 yards.

Answer the questions.

The table shows the elevations of four locations compared to sea level.

Question 5.
New Orleans is 8 feet sea level.
Answer:
New Orleans is 8 feet below sea level.

Question 6.
Mount Davidson is feet above sea level.
Answer:
Mount Davidson is 928 feet above sea level.

Question 7.
The deepest location among the four locations is .
Answer:
The deepest location among the four locations is Death Valley.

Question 8.
The highest location among the four locations is
Answer:
The highest location among the four locations is Pilot Mountain.

Question 9.
The location nearest to sea level is .
Answer:
The location nearest to sea level is New Orleans.

Copy and complete each inequality using > or <.

Question 10.

Answer:

-13 < -12 < -11 < -10 < -9 < -8 < -7 < -6 < -5 < -4
Explanation:
The missing numbers on the horizontal number line are -13, -11, -9, -6. On a horizontal number line, the numbers become greater as you move to the right, and less as you move to the left as we can observe in the above image.

Draw a horizontal number line to represent each set of numbers.

Question 11.
-8, -5, -4, -2, 2, 5, 7
Answer:

The given numbers -8, -5, -4, -2, 2, 5, 7 are represented in the above horizontal number line. On a horizontal number line, the numbers become greater as you move to the right, and less as you move to the left.

Question 12.
-16, -19, -20, -22, -25
Answer:

The given numbers -16, -19, -20, -22, -25 are represented in the above horizontal number line. On a horizontal number line, the numbers become greater as you move to the right, and less as you move to the left.

Write the opposite of each number.

Question 13.
-14
Answer:
The opposite number of -14 is 14.

Question 14.
-9
Answer:
The opposite number of -9 is 9.

Question 15.
-17
Answer:
The opposite number of -17 is 17.

Question 16.
27
Answer:
The opposite number of 27 is -27.

Question 17.
-23
Answer:
The opposite number of -23 is 23.

Question 18.
46
Answer:
The opposite number of 46 is -46.

Copy and complete each Inequality using > or <.

Question 19.
-15 -6
Answer:
-15  -6
Explanation:
The given numbers are -15 and -6. Here we have to compare both the numbers. By comparing the above given numbers the number -15 is less than -6.

Question 20.
-20 -23
Answer:
-20  -23
The given numbers are -20 and -23. Here we have to compare both the numbers. By comparing the above given numbers the number -20 is greater than -23.

Question 21.
-30 -3
Answer:
-30 -3
The given numbers are -30 and -3. Here we have to compare both the numbers. By comparing the above given numbers the number -30 is less than -3.

Question 22.
-19 0
Answer:
-19   0
The given numbers are -19 and 0. Here we have to compare both the numbers. By comparing the above given numbers the number -19 is less than 0.

Question 23.
12 -31
Answer:
12 -31
The given numbers are 12 and -31. Here we have to compare both the numbers. By comparing the above given numbers the number 12 is greater than -31.

Question 24.
-75 46
Answer:
-75  46
The given numbers are -75 and 46. Here we have to compare both the numbers. By comparing the above given numbers the number -75 is less than 46.

Hands-On Activity

Materials:

• number cards

Work in pairs. Your teacher will give you and your partner a set of number cards with these numbers on them:

Step 1.
Draw a number line and divide it into ten equal intervals. Label the endpoints -100 and 0. Shuffle the cards and place them face down on a flat surface.
Step 2.
Choose one card and turn it over. Mark the number shown on the card on the drawn number line.
Step 3.
Have your partner choose another card and mark the number shown on the number line.
Step 4.
Work together to write a statement of inequality for the two numbers you represented on the number line.
Step 5.
Repeat Step 2 through Step 4 using the other number cards.

Interpret and explain statements of order for positive and negative numbers in real-world situations.

a) The table shows the lowest recorded temperature in Alaska for each month from July through December.

September’s lowest recorded temperature of -13°F is lower than August’s lowest recorded temperature of 8°F.
To compare these two temperatures using an inequality, you can write -13°F < 8°F.
Answer:

b) The table shows the elevations of some natural features.

The elevation of Death Valley, which is -282 feet, ¡s greater than the elevation of Lake Assai, which is -509 feet.
To compare the two elevations using an inequality, you can write -282 ft > -509 ft.
The elevation of Lake Assai, which is -509 feet, is less than the elevation of Driskill Mountain, which has an elevation of 535 feet.
To compare the two elevations using an inequality, you can write -509 ft < 535 ft.

You can also write the inequalities above as -509ft < -282 ft and 535 ft > -509 ft.

Write an inequality for each statement using > or <.

Question 25.
0°C is warmer, than -5°C.
Answer:
0°C > -5°C
Explanation:
The given statement is 0°C is warmer, than -5°C. Here we have to compare both the temperatures. After comparing the temperatures 0°C is greater than -5°C.

Question 26.
The elevation of the Valdes Peninsula, which is -131 feet, is less than the elevation of the Caspian Sea, which is -92 feet.
Answer:
-131 feet < -92 feet
Explanation:
The elevation of the Valdes Peninsula is -131 feet.
The elevation of the Caspian Sea is -92 feet.
After comparing both the elevations -131 feet is less than -92 feet.

Write a statement to describe each inequality.

Question 27.
-61 °F < -47°F
Answer:
The lowest recorded temperature yesterday was -61°F, which is colder than today’s lowest recorded temperature of -47°F.

Question 28. –
520 feet > -893 feet
Answer:
A dog is standing on a cliff, 520 feet above sea level which is greater than a dolphin which is swimming 893 feet below sea level.

Math in Focus Course 1A Practice 2.1 Answer Key

Write a positive or negative number to represent each situation.

Question 1.
438°C above zero
Answer:
438°C
Explanation:
The given situation is 438°C above zero. The word ‘below zero’ represents negative number and ‘above zero’ represents positive number. So the situation is represented with positive number 438°C, which is above zero.

Question 2.
164°F below zero
Answer:
-164°F
Explanation:
The given situation is 164°F below zero. The word ‘below zero’ represents negative number and ‘above zero’ represents positive number. So the situation is represented with negative number -164°F, which is below zero.

Question 3.
8,327 feet below sea level
Answer:
-8,327 feet
Explanation:
The given situation is 8,327 feet below sea level. The word ‘below sea level’ represents negative number and ‘above sea level’ represents positive number. So the situation is represented with negative number -8,327 feet, which is below sea level.

Question 4.
12,316 feet above sea level
Answer:
12,316 feet
Explanation:
The given situation is 12,316 feet above sea level. The word ‘below sea level’ represents negative number and ‘above sea level’ represents positive number. So the situation is represented with positive number 12,316 feet, which is above sea level.

Question 5.
A loss of 20 yards
Answer:
-20 yards
Explanation:
The given situation is a loss of 20 yards. In general loss is represented with negative number and gain is represented with positive number. So the given situation is represented with negative number -20 yards.

Question 6.
A credit of $3,401
Answer:
$3,401
Explanation:
The given situation is a credit of $3,401. In general debit is represented with ‘negative sign’ and credit is represented with ‘positive sign’. So, the given situation is represented with positive number $3,401.

Copy and complete each number line by filling in the missing numbers.

Question 7.

Answer:

Explanation:
The missing numbers are -11, -9, -7, -3. The above number line is filled with the missing numbers as we can observe in the above image.

Question 8.

Answer:

Explanation:
The missing numbers are -35, -33, -32, -29. The above number line is filled with the missing numbers as we can observe in the above image.

Write the opposite of each number.

Question 9.
8
Answer:
The opposite number of 8 is -8.

Question 10.
-5
Answer:
The opposite number of -5 is 5.

Question 11.
21
Answer:
The opposite number of 21 is -21.

Question 12.
-29
Answer:
The opposite number of -29 is 29.

Question 13.
24
Answer:
The opposite number of 24 is -24.

Question 14.
-106
Answer:
The opposite number of -106 is 106.

Draw a horizontal number line to represent each set of numbers.

Question 15.
Even negative numbers from -24 to -1o
Answer:
Even negative numbers from -24 to -1o are -24, -22, -20 ,-18, -16, -14, -12, -10.

Explanation:
The even negative numbers are  -24, -22, -20 ,-18, -16, -14, -12, -10 are represented in the above horizontal number line. On a horizontal number line, the numbers become greater as you move to the right, and less as you move to the left.

Question 16.
The opposites of the whole numbers from 35 to 45
Answer:
The opposites of the whole numbers from 35 to 45 are -35, -36, -37, -38, -39, -40, -41, -42, -43, -44, -45.

Explanation:
The opposites of the whole numbers from 35 to 45 are -35, -36, -37, -38, -39, -40, -41, -42, -43, -44, -45 are represented in the above horizontal number line. On a horizontal number line, the numbers become greater as you move to the right, and less as you move to the left.

Draw a vertical number line to represent each set of numbers.

Question 17.
Odd numbers between -91 and -103
Answer:
Odd numbers between -91 and -103 are -93, -95, -97, -99, -101.

Explanation:
The odd numbers between -91 and -103 are -93, -95, -97, -99, -101 are represented in the above vertical number line. On a vertical number line, the numbers become greater as you move up, and lesser as you move down.

Question 18.
Even numbers greater than -6 but less than 12
Answer:
Even numbers greater than -6 but less than 12 are -4, -2, 0, 2 , 4, 6, 8, 10.

Explanation:
Even numbers greater than -6 but less than 12 are -4, -2, 0, 2 , 4, 6, 8, 10 are represented in the above vertical number line. On a vertical number line, the numbers become greater as you move up, and lesser as you move down.

Use the number line to compare each pair of numbers using > or <.

Question 19.
-9 -2
Answer:
-9  -2
Explanation:
In the above horizontal number line, the numbers become greater as you move to the right, and less as you move to the left.
Here -9 is to the left of -2.
So, -9 < -2.

Question 20.
-10 -4
Answer:
-10  -4
Explanation:
In the above horizontal number line, the numbers become greater as you move to the right, and less as you move to the left.
Here -10 is to the left of -4.
So, -10 < -4.

Question 21.
-5 4
Answer:
-5  4
Explanation:
In the above horizontal number line, the numbers become greater as you move to the right, and less as you move to the left.
Here -5 is to the left of 4.
So, -5 < 4.

Question 22.
2 -6
Answer:
2  -6
Explanation:
In the above horizontal number line, the numbers become greater as you move to the right, and less as you move to the left.
Here 2 is to the right of -6.
So, 2 > -6.

Question 23.
-5 -12
Answer:
-5  -12
Explanation:
In the above horizontal number line, the numbers become greater as you move to the right, and less as you move to the left.
Here -5 is to the right of -12.
So, -5 > -12.

Question 24.
-10 3
Answer:
-10 3
Explanation:
In the above horizontal number line, the numbers become greater as you move to the right, and less as you move to the left.
Here -10 is to the left of 3.
So, -10 < 3.

Copy and complete each inequality using > or <.

Question 25.
-27 -3
Answer:
-27  -3
Explanation:
The given numbers are -27 and -3. Here we have to compare both the numbers. By comparing the above given numbers the number -27 is less than -3.

Question 26.
-45 15
Answer:
-45  15
Explanation:
The given numbers are -45 and 15. Here we have to compare both the numbers. By comparing the above given numbers the number -45 is less than 15.

Question 27.
25 -25
Answer:
25  -25
Explanation:
The given numbers are 25 and -25. Here we have to compare both the numbers. By comparing the above given numbers the number 25 is greater than -25.

Question 28.
19 -15
Answer:
19  -15
Explanation:
The given numbers are 19 and -15. Here we have to compare both the numbers. By comparing the above given numbers the number 19 is greater than -15.

Question 29.
14 -16
Answer:
14  -16
Explanation:
The given numbers are 14 and -16. Here we have to compare both the numbers. By comparing the above given numbers the number 14 is greater than -16.

Question 30.
-81 -80
Answer:
-81  -80
Explanation:
The given numbers are -81 and -80. Here we have to compare both the numbers. By comparing the above given numbers the number -81 is less than -80.

Order the numbers in each set from least to greatest.

Question 31.
3, 7, -2, -9, 0, -5
Answer:
The above given numbers from least to greatest are -9, -5, -2, 0, 3, 7.

Question 32.
-10, 8, 34, -13, 10, -17
Answer:
The above given numbers from least to greatest are -17, -13, -10, 8, 10, 34.

Order the numbers in each set from greatest to least.

Question 33.
-14, 43, -20, -57, 19, 31
Answer:
The above given numbers from greatest to least are 43, 31, 19, -14, -20, -57.

Question 34.
98, -101, -76, 125, -92, 113
Answer:
The above given numbers from greatest to least are 125, 113, 98, -76, -92, -101.

Answer the questions.

Question 35.
Name two numbers that are each 2 units away from -7. Give the opposites of these two numbers.
Answer:

Question 36.
Math Journal Is the opposite of a number always negative? Explain
Answer:
No. The opposite of a negative integer is a positive number. For example, the opposite of -1 is 1.
Explanation:
The opposite of any positive integer is negative. The opposite of any negative integer is positive. Zero is its own opposite.

Question 37.
Write an inequality using > or < for the following statement: -22°C is colder than -4°C.
Answer:
-22°C < -4°C
Explanation:
The given statement is -22°C is colder than -4°C. Here we have to compare both the temperatures. After comparing the temperatures -22°C is less than -4°C.

Question 38.
Your friend says that the statement 0 < -15 is correct. Explain why the statement is incorrect.
Answer:
The statement 0 < -15 is incorrect.
-15 is the negative integer.
0 is the positive integer.
Explanation:
Consider a horizontal number line, In that line the numbers become greater as you move to the right, and less as you move to the left.
Here -15 is to the left of 0.
So, -15 < 0.

Question 39.
The elevation of the deepest part of the Pacific Ocean is -36,200 feet. The elevation of the deepest part of the Indian Ocean is -24,442 feet.
Write an inequality to compare the elevations. In which of the two oceans is the deepest part farther from sea level?

Answer:
The elevation of the deepest part of the Pacific Ocean is -36,200 feet.
The elevation of the deepest part of the Indian Ocean is -24,442 feet.
 -36,200 ft < -24,442 ft
Pacific ocean is the deepest part farther from seal level.

Question 40.
The temperature at which a substance boils is called its boiling point. The boiling points of two elements are shown in the table.

Write an inequality to compare the two boiling points. Which element has the greater boiling point?
Answer:
The boiling point of the oxygen is -183°C.
The boiling point of the Nitrogen is -196 °C.
-183°C > -196 °C
The oxygen has the greatest boiling point with -183°C.

Write a statement to describe each inequality.

Question 41.
-45 feet > -80 feet
Answer:
The given inequality is -45 feet > -80 feet. The statement for the given inequality is the elevation of the deepest part of the North Atlantic ocean is -45 feet which is greater than the elevation of the deepest part of the South Atlantic Ocean is -80 feet.

Question 42.
-436°F < -271 °F
Answer:
The given inequality is -436°F < -271 °F. The statement for the given inequality is –436°F is colder than -271 °F.

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 1 Lesson 1.4 Squares and Square Roots to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 1 Lesson 1.4 Answer Key Squares and Square Roots

Math in Focus Grade 6 Chapter 1 Lesson 1.4 Guided Practice Answer Key

Find the square of each number.

Question 1.
2
Answer:
2 x 2 = 4

Explanation:
The square of 2 is 4.

Question 2.
6
Answer:
6 x 6 = 36

Explanation:
The square of 6 is 36.

Question 3.
9
Answer:
9 x 9 = 81

Explanation:
The square of 9 is 81.

Question 4.
11
Answer:
11 x 11 = 121

Explanation:
The square of 11 is 121.

Find a square root of a perfect square.

a) A square has an area of 9 square inches. Find the length of each side of the square.

You know that
Area of square = length × length.
To find the length of a side of the square, you need to find the number whose square is 9.
Recalling the multiplication facts of 3, you know that 3 × 3 = 9.
So, the length of each side of the square is 3 inches.
3 is called a square root of 9. This can be written as \(\sqrt{9}\) = 3.
You read this as “the square root of 9 equals 3”.

b) Find the square root of 100.

I can relate this to finding the length of the side of a square, given that it has an area of 1oo units².

Method 1
Recalling the multiplication facts of 10, you know that
10 × 10 = 100
So, \(\sqrt{100}\) = 10.

Method 2
By prime factorization,

Find the square root of each number.

Question 5.
25
Answer:
5

Explanation:
Recalling the multiplication facts of 25, you know that
25 = 5 x 5
= 5²
So, \(\sqrt{25}\) = 5

Question 6.
64
Answer:
8

Explanation:
Recalling the multiplication facts of 64, you know that
64 = 8 x 8
= 8²
So, \(\sqrt{64}\) = 8

Question 7.
144
Answer:
12

Explanation:
Recalling the multiplication facts of 144, you know that
144 = 12 x 12
= 12²
So, \(\sqrt{144}\) = 12

Question 8.
196
Answer:
13

Explanation:
Recalling the multiplication facts of 169, you know that
169 = 13 x 13
= 13²
So, \(\sqrt{169}\) = 13

Math in Focus Course 1A Practice 1.4 Answer Key

Find the square of each number.

Question 1.
3
Answer:
3 x 3 = 9

Explanation:
The square of 3 is 9.

Question 2.
7
Answer:
7 x 7 = 49

Explanation:
The square of 7 is 49.

Question 3.
12
Answer:
144

Explanation:
The square of 12 is 144.

Question 4.
10
Answer:
100

Explanation:
The square of 10 is 100.

Find the square root of each number.

Question 5.
36
Answer:
6

Explanation:
Recalling the multiplication facts of 36, you know that
36 = 6 x 6
= 6²
So, \(\sqrt{36}\) = 6

Question 6.
81
Answer:
9

Explanation:
Recalling the multiplication facts of 81, you know that
81 = 9 x 9
= 9²
So, \(\sqrt{81}\) = 9

Question 7.
121
Answer:
11

Explanation:
Recalling the multiplication facts of 121, you know that
121 = 11 x 11
= 11²
So, \(\sqrt{121}\) = 11

Question 8.
49
Answer:
7

Explanation:
Recalling the multiplication facts of 49, you know that
49 = 7 x 7
= 7²
So, \(\sqrt{49}\) = 7

Solve.

Question 9.
List the perfect squares that are between 25 and 100.
Answer:

Find the value of each of the following.

Question 10.
35²
Answer:

35 x 35 = 1225

Explanation:
The square of 35 is 1225.

Question 11.
56²
Answer:

56 x 56 = 3136

Explanation:
The square of 56 is 3136.

Question 12.
64²
Answer:

64 x 64 = 4096

Explanation:
The square of 64 is 4096.

Question 13.
\(\sqrt{289}\)
Answer:
17

Explanation:
Recalling the multiplication facts of 289, you know that
289 = 17 x 17
= 17²
So, \(\sqrt{289}\) = 17

Question 14.
\(\sqrt{400}\)
Answer:
20

Explanation:
Recalling the multiplication facts of 400, you know that
400 = 20 x 20
= 20²
So, \(\sqrt{400}\) = 20

Question 15.
\(\sqrt{484}\)
Answer:
22

Explanation:
Recalling the multiplication facts of 484, you know that
484 = 22 x 22
= 22²
So, \(\sqrt{484}\) = 22

Solve.

Question 16.
Given that 41² = 1,681, find the square of 410.
Answer:
168100

Explanation:
If 41² = 1,681 then 410² = 168100.

Question 17.
Given that 51² = 2,601, find the square root of 260,100.
Answer:
510

Explanation:
If 51² = 2601 then the square root of 260100 will be 510.

Question 18.
Given that \(\sqrt{676}\) = 26, evaluate \(\sqrt{2,704}\).
Answer:
52

Explanation:
Recalling the multiplication facts of 400, you know that
2704 = 52 x 52
= 52²
So, \(\sqrt{2704}\) = 52

Question 19.
Given that \(\sqrt{1,521}\) = 39, evaluate 390².
Answer:
152100

Explanation:
If \(\sqrt{1,521}\) = 39 then 390² = 152100.

Question 20.
Heather wants to make a giant square quilt with sides of length 28 feet. She uses square patches of fabric that have sides of length 4 feet. How many patches of fabric will Heather need to make the giant square quilt?

Answer:
7 patches of fabric Heather will need to make the giant square quilt.

Explanation:
Heather wants to make a giant square quilt with sides of length 28 feet.
She uses square patches of fabric that have sides of length 4 feet.
4 x 7 = 28
So, 7 patches of fabric Heather will need to make the giant square quilt.

Question 21.
This week, customers at a carpet store pay $3 for a square foot of carpet. Next week the store will be having a sale. During the sale, each square foot of carpet will cost only $2. Neil wants to carpet two square rooms in his house. The floor in one room is 10 feet by 10 feet. The floor in the other room is 14 feet by 14 feet. How much money will Neil save if he waits to buy carpet during the sale?
Answer:
296

Explanation:
Neil wants to carpet two square rooms in his house.
The floor in one room is 10 feet by 10 feet.
10 x 10 = 100 square feet
The floor in the other room is 14 feet by 14 feet
14 x 14 = 196
Neil wants to carpet two square rooms in his house
100+196=296
During the sale, each square foot of carpet is reduced by 1 so, $296 Neil will save.

Go through the Math in Focus Grade 6 Workbook Answer Key Chapter 1 Positive Numbers and the Number Line to finish your assignments.

Math in Focus Grade 6 Course 1 A Chapter 1 Answer Key Positive Numbers and the Number Line

Math in Focus Grade 6 Chapter 1 Quick Check Answer Key

Find the factors of each number.

Question 1.
30
Answer:
30 = 1 x 30, 30 = 2 x 15,
30 = 3 x 10, 30 = 5 x 6

Explanation:
1, 2, 3, 5, 6, 10, 15 and 30 are the factors of number 30.
a number or algebraic expression that divides another number or expression evenly,
with no remainder.

Question 2.
63
Answer:
1 x 63 = 63, 3 x 21 = 63, 7 x 9 = 63.

Explanation:
1, 3, 7, 9, 21 and 63 are the factors of number 63.
a number or algebraic expression that divides another number or expression evenly,
with no remainder.

Question 3.
56
Answer:
1 x 56 = 56, 2 x 28 = 56
4 x 14 = 56, 7 x 8 = 56

Explanation:
1, 2, 4, 7, 8, 14, 28 and 56 are the factors of number 56.
a number or algebraic expression that divides another number or expression evenly,
with no remainder.

Question 4.
84
Answer:
1 x 84 = 84, 2 x 42 = 84, 3 x 28 = 84
4 x 21 = 84, 6 x 14 = 84, 7 x 12 = 84

Explanation:
1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 and 84 are the factors of number 84.
a number or algebraic expression that divides another number or expression evenly,
with no remainder.

Find the first five multiples of each number.

Question 5.
4
Answer:
4, 8, 12, 16 and 20

Explanation:
4 x 1 = 4, 4 x 2 = 8, 4 x 3 = 12, 4 x 4  = 16, 4 x 5 = 20
4, 8, 12, 16 and 20 are the first five multiples of number 4.

Question 6.
6
Answer:
6, 12, 18, 24 and 30

Explanation:
6 x 1 = 6, 6x 2 = 12, 6 x 3 = 18, 6 x 4 = 24, 6 x 5 = 30
6, 12, 18, 24 and 30 are the first five multiples of number 6.

Question 7.
9
Answer:
9, 18, 27, 36 and 45

Explanation:
9 x 1 = 9, 9 x 2 = 18, 9 x 3 = 27, 9 x 4 = 36,9 x 5 = 45
9, 18, 27, 36 and 45 are the first five multiples of number 9.

Question 8.
13
Answer:
13, 26, 6, 52, 65

Explanation:
13 x 1 = 13, 13 x 2 = 26, 13 x 3 = 36, 13 x 4 = 52, 13 x 5 = 65
13, 26, 39, 52 and 65 are the first five multiples of number 13.

Complete.

Question 9.
Identify all the prime numbers in the following set of numbers.
2, 5, 13, 21, 23, 39, 47, 51, 53, 57
Answer:
2, 5, 13, 23, 47, 53.

Explanation:
2, 5, 13, 23, 47, 53 are the prime numbers in the given set.

Simplify.

Question 10.
(40 – 28) + 8 × 7
Answer:
68

Explanation:
(40-28) + 8 x 7
=12 + 56
=68
(40 – 28) + 8 × 7 = 68.

Question 11.
75 × (45 ÷ 5) – 70
Answer:
605

Explanation:
75 (45 ÷  5) – 70
=75 (9) – 70
=675 – 70
=605
75 × (45 ÷ 5) – 70 = 605.