Math in Focus

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 17 Practice 2 Right Angles provides detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 17 Practice 2 Answer Key Right Angles

Look at these angles. Use a piece of folded paper
to help you answer the questions.

Question 1.
Which angle is less than a right angle?
Angle ________________
Answer:

Angle  C, D and E are angles less then a right angle.
Explanation:
Angle less than a right angles are Acute angles.

Question 2.
Which angle is greater than a right angle?
Angle ________________
Answer:

Angle A is greater then a right angle.
Explanation:
Angle greater than a right angles are Obtuse angles.

Question 3.
Which angles are the same size as right angles?
Angles _________________
Answer:

Angle A and F are the same as right angles.
Explanation:
The angle bounded by two lines perpendicular to each other.
A right triangle has one angle exactly equal to 90 degrees.

Mark all the right angles in each figure.

Question 4.

Answer:

Explanation:
The above figure has,
One right angle is there, which is marked blue color.
The angle bounded by two lines perpendicular to each other.
A right triangle has one angle exactly equal to 90 degrees.

Question 5.

Answer:

Explanation:
The above figure has,
One right angle is there, which is marked blue color.
The angle bounded by two lines perpendicular to each other.
A right triangle has one angle exactly equal to 90 degrees.

Question 6.

Answer:

Explanation:
The above figure has,
One right angle is there, which is marked blue color.
The angle bounded by two lines perpendicular to each other.
A right triangle has one angle exactly equal to 90 degrees.

Question 7.

Answer:

Explanation:
The above figure has,
One right angle triangles , the angle is marked blue color.
The angle bounded by two lines perpendicular to each other.
A right triangle has one angle exactly equal to 90 degrees.

Question 8.

Answer:

Explanation:
The above figure has,
Two right angle are there, which are marked blue color.
The angle bounded by two lines perpendicular to each other.
A right triangle has one angle exactly equal to 90 degrees.

Question 9.

Answer:

Explanation:
The given figure has,
Two right angle are there, which are marked in blue color.
The angle bounded by two lines perpendicular to each other.
A right triangle has one angle exactly equal to 90 degrees.

This handy Math in Focus Grade 5 Workbook Answer Key Chapter 15 Surface Area and Volume provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 15 Answer Key Surface Area and Volume

Math Journal

This rectangular container is \(\frac{2}{5}\)-filled with water.
How much more water is needed to increase the height of the water level to 3 centimeters?

Show two methods of solving this problem. Which method do you prefer? Why?
Answer:
Given rectangular tank has volume 8 cm X 10 cm X 5 cm = 400 cm³,
Method 1:
Knowing the volume of tank and water filled in it
as the rectangular container is \(\frac{2}{5}\)-filled with water.
\(\frac{2}{5}\) X 400 cm³ = 160 cm³, filled with water.
as 1 cubic centimeter is equal to 1 milliliters,

Put on Your Thinking Cap!

Challenging Practice

Question 1.
A rectangular tank is half-filled with water.
Another 650 cubic centimeters of water are needed to make it \(\frac{3}{5}\) full.
How much water will be in the tank when it is \(\frac{3}{5}\) full?
Answer:
3,900 cubic centimeters of water will be in the tank when it is \(\frac{3}{5}\) full,

Explanation:
Given a rectangular tank is half-filled with water.
Another 650 cubic centimeters of water are needed to make it \(\frac{3}{5}\) full.
Let x cubic centimeters of water so \(\frac{1}{2}\)x + \(\frac{3}{5}\)x = 650 cm³ + x,
\(\frac{5x + 6x}{10}\) = 650 cm³ + x,
\(\frac{11x}{10}\) = 650 cm³ + x,
11 x = 10 X (650 cm³ + x),
11 x =  6500 cm³ + 10 x,
11x – 10 x = 6,500 cm³,
x = 6,500 cm³,
So, water will be in the tank when it is \(\frac{3}{5}\) full is
\(\frac{3}{5}\) x 6,500 cm³ = \(\frac{3 X 6,500}{5}\) cm³,
\(\frac{19,500}{5}\) cm³ = 3,900 cm³,
therefore 3,900 cubic centimeters of water will be in the tank when it is \(\frac{3}{5}\) full.

Question 2.
A cube has a surface area of 21 6 square centimeters.
A second cube has edges that are 3 times as long.
How much greater is the surface area of the second cube than the first cube?
Answer:
1,728 cm² greater is the surface area of the second cube than the first cube,

Explanation:
Given a cube has a surface area of 216 square centimeters as
surface area of cube is 6 X a²= 216 cm²,
a² = 36 cm² = 6 cm X 6 cm,
edge a    = 6 cm,
A second cube has edges that are 3 times long as
6 cm X 3 = 18 cm, Surface area of second cube is 6 x (18)² =
6 X 18 cm X 18 cm = 1,944 cm², Now compairing much greater is the
surface area of the second cube than the first cube is 1,944 cm² – 216 cm² = 1,728 cm².

Put on Your Thinking Cap!

Problem Solving

A prism has a square base whose edges each measure 5 centimeters.
The ratio of its height to its width is 4 : 1.
Find the volume of the rectangular prism in cubic centimeters.

Answer:
Given a prism has a square base whose edge each measure 5 centimeters.
height = 4 cm
width = 1 cm
Volume of the rectangular prism = 2l × 2w × 2h
V = 2 × 5 × 2 × 1 × 2 × 4
V = 80 cubic centimeters

This handy Math in Focus Grade 5 Workbook Answer Key Chapter 15 Practice 4 Understanding and Measuring Volume provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 15 Practice 4 Answer Key Understanding and Measuring Volume

These solids are formed by stacking unit cubes in the corner of a room.
Find the volume of each solid.

Question 1.

Volume = _________ cubic units
Answer:
Volume of give cube has 27 cubic units,

Explanation:
As we know volume of  solid is l X w X h,
so given cube  has 3 unit X 3 unit X 3 unit = 27 cubic units.

Question 2.

Volume = _________ cubic units
Answer:
Volume of give cube has 32 cubic units,

Explanation:
As we know the volume of solid is l X w X h,
so the given cube has 4 units X 4 units X 2 units = 32 cubic units.

Question 3.

Volume = _________ cubic units
Answer:
Volume of given cube has  16 cubic units,

Explanation:
As we know the volume of  solid is l X w X h,
Given cube contains 2 fewer small unit cubes so first we
calculate the total surface and subtract missing cubic units,
Total surface area has 3 units X 2 units X 3 units = 18 cubic units.
the surface area of small unit cubes is 1 unit X 1 unit X 2 units = 2 cubic units,
therefore the volume of the given cube is 18 cubic units – 2 cubic units = 16 cubic units.

Question 4.

Volume = _________ cubic units
Answer:
Volume of 9 cubic units,

Explanation:
Given solid cube has 9 unit cubes with 1 unit X 1 unit X 1 unit each,
So the volume of given cube is 9 X (1 unit X 1 unit X 1 unit)  = 9 cubic units.

These solids are formed by stacking 1-centimeter cubes in the corner of a room.
Find the volume of each solid.

Question 5.

Volume = ______ cm³
Answer:
Volume 11 cm³,

Explanation:
Given solid cube has 11 units cms with 1 cm X 1 cm X 1 cm each,
So the volume of given cubes is 11 X (1 cm X 1 cm X 1 cm)  = 11 cm³.

Question 6.

Volume = _________ cm³
Answer:
Volume 8 cm³,

Explanation:
Given solid cube has 8 units cms with 1 cm X 1 cm X 1 cm each,
So the volume of given cubes is 8 X (1 cm X 1 cm X 1 cm)  = 8 cm³.

Question 7.

Volume = _________ cm³
Answer:
Volume 10 cm³,

Explanation:
Given solid cube has 10 units cms with 1 cm X 1 cm X 1 cm each,
So the volume of given cubes is 10 X (1 cm X 1 cm X 1 cm)  = 10 cm³.

Question 8.

Volume = ______ cm³
Answer:
Volume 12 cm³,

Explanation:
Given solid cube has 12 units cms with 1 cm X 1 cm X 1 cm each,
So the volume of given cubes is 12 X (1 cm X 1 cm X 1 cm)  = 12 cm³.

Question 9.

Volume = _________ cm³
Answer:
Volume 7 cm³,

Explanation:
Given solid cube has 7 units cms with 1 cm X 1 cm X 1 cm each,
So the volume of given cubes is 7 X (1 cm X 1 cm X 1 cm)  = 7 cm³.

Question 10.

Volume = _________ cm³
Answer:
Volume 11 cm³,

Explanation:
Given solid cube has 11 units cms with 1 cm X 1 cm X 1 cm each,
So the volume of given cubes is 11 X (1 cm X 1 cm X 1 cm)  = 11 cm³.

These solids are built using 1-centimeter cubes. Find the volume of each solid.
Then compare their volumes and fill in the blanks.

Question 11.

Solid _________ has a greater volume than solid _________.
Answer:

Solid B has a greater volume than solid A,

Explanation:
Given solid cube A has 5 units cms with 1 cm X 1 cm X 1 cm each,
So the volume of given cubes is 5 X (1 cm X 1 cm X 1 cm)  = 5 cm³,
and given solid cube B has 8 units cms with 1 cm X 1 cm X 1 cm each,
So the volume of given cubes is 8 X (1 cm X 1 cm X 1 cm)  = 8 cm³.
Solid B has a greater volume than solid A.

These solids are built using 1-meter cubes. Find the volume of each solid.
Then compare their volumes and fill in the blanks.

Question 12.

Solid _________ has less volume than solid _________.
Answer:

Solid 8 m³ has less volume that solid 11 m³,

Explanation:
Given solid cube C has 8 units m’s with 1 m X 1 m X 1 m each,
So the volume of given cubes is 8 X (1 m X 1 m X 1 m)  = 8 m³,
and given solid cube D has 11 units m’s with 1 m X 1 m X 1 m each,
So the volume of given cubes is 11 X (1 m X 1 m X 1 m)  = 11 m³.
Solid 8 m³ has less volume that solid 11 m³.

These solids are built using 1-inch cubes.
Find the volume of each solid.
Then compare their volumes and f411 in the blanks.

Question 13.

Length = __________ in.
Width = __________ in.
Height = _________ in.
Volume = _________ in.³

Length = __________ in.
Width = __________ in.
Height = _________ in.
Volume = _________ in.³
Solid _________ has less volume than solid _________.
Answer:
Solid E has less volume than solid F,

Explanation:
Given the solid cube of E which has a length of 2 in, width 2 in and height 3 in,
so the volume of cube E is 12 in.³,
Given solid cube of F which has a length of 4 in, width of 2 in, and height of 2 in,
so volume of cube F is 16 in.³.
Solid E has less volume than solid F.

These solids are built using 1-foot cubes. Find the volumes of each solid.
Then compare their volumes and fill in the blanks.

Question 14.

Length = _____2_____ ft.
Width = ______2____ ft.
Height = _____2____ ft.
Volume = _____8____ ft.³

Length = ____4______ ft.
Width = _____4_____ ft.
Height = _____4____ ft.
Volume = _____64____ ft.³
Solid _________ has a greater volume than solid _________.
Answer:
Solid H has greater volume than solid G,

Explanation:
Given the solid cube of  G which has a length 2 ft, width 2 ft, and height 2 ft,
so volume of cube G is 8 ft.³,
Given the solid cube of H which has a length 4 ft, width 4 ft and height 4 ft,
so volume of cube H is 64 in.³.
Solid H has a greater volume than solid G.

This handy Math in Focus Grade 5 Workbook Answer Key Chapter 15 Practice 5 Volume of a Rectangular Prism and Liquid provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 15 Practice 5 Answer Key Volume of a Rectangular Prism and Liquid

Write the length, width, and height of each rectangular prism or cube.

Example

Answer:
Volume of given rectangular prism is 240 cm³,

Explanation:
Given Length = 5 cm, Width = 8 cm and Height = 6 cm,
Volume of the rectangular prism is lwh = 5 cm X 8 cm X 6 cm = 240 cm³.

Question 1.

Length = _____12_______ ft
Width = _______12_____ ft
Height = _______20_____ ft
Answer:
Volume of the recangular prism is cube is 2,880 ft³,

Explanation:
Given rectangular prism has length 12 ft, width 12 ft and height 20 ft,
so volume of the rectangular prism is 12 ft X 12 ft X 20 ft = 2,880 ft³.

Question 2.

Length = ____12________ in.
Width = ______25______ in.
Height = _______16_____ in.
Answer:
Volume of the recangular prism is 4,800 in³,

Explanation:
Given rectangular prism has length 12 in, width 25 in and height 16 in,
so volume of the rectangular prism is 12 in X 25 in X 16 in = 4,800 in³.

Question 3.

Length = _____18_______ m
Width = ______18______ m
Height = ______18______ m
Answer:
Volume of the cube is 5832 m³,

Explanation:
Given cube has length 18 m, width 18 m and height 18 m,
so volume of the cube is 18 m X 18 m X 18 m = 5832  m³.

Find the volume of each rectangular prism.

Question 4.

The length of the rectangular prism is _______12_____ centimeters.
The width of the rectangular prism is _______5_____ centimeters.
The height of the rectangular prism is _______9_____ centimeters.
Volume of the rectangular prism = length × width × height
= _____12_______ × _____5_______ ×______9______
= ______540______ cm³
Answer:
Volume of the recangular prism is cube is 540 cm³,

Explanation:
Given rectangular prism has length 12 cm, width 5 cm and height 9 cm,
so volume of the rectangular prism is 12 cm X 5 cm X 9 cm = 540 cm³.

Question 5.

Volume = _____24_______in³
Answer:
Volume of the recangular prism is 24 in³,

Explanation:
Given rectangular prism has length 3 in, width 4 in and height 2 in,
so volume of the rectangular prism is 3 in X 4 in X 2 in = 24 in³.

Question 6.

Volume = _____120_______ yd³,
Answer:
Volume of the recangular prism is 120 yd³,

Explanation:
Given rectangular prism has length 5 yd, width 8 yd and height 3 yd,
so volume of the rectangular prism is 5 yd X 8 yd X 3 yd = 120 yd³.

Find the volume of each rectangular prism or cube.

Question 7.

Volume = _____120_______ft³,
Answer:
Volume of the recangular prism is cube is 120 ft³,

Explanation:
Given rectangular prism has length 4 ft, width 6 ft and height 5 ft,
so volume of the rectangular prism is 4 ft X 6 ft X 5 ft = 2,880 ft³.

Question 8.

Volume = ______4,096______m³,
Answer:
Volume of the cube is 4,096 m³,

Explanation:
Given cube has length 18 m, width 18 m and height 18 m,
so volume of the cube is 16 m X 16 m X 16 m = 4,096 m³.

Question 9.

Volume = _____384_______cm³,

Answer:
Volume of the recangular prism is cube is 384 cm³,

Explanation:
Given rectangular prism has length 4 cm, width 24 cm and height 4 cm,
so volume of the rectangular prism is 4 cm X 24 cm X 4 cm = 384 cm³.

Question 10.

Volume = _____189_______ in³,
Answer:
Volume of the recangular prism is 189 in³,

Explanation:
Given rectangular prism has length 7 in, width 9 in and height 3 in,
so volume of the rectangular prism is 7 in X 9 in X 3 in = 189 in³.

Question 11.

Volume = ______448______ in³,
Answer:
Volume of the recangular prism is 448 in³,

Explanation:
Given rectangular prism has length 8 in, width 8 in and height 7 in,
so volume of the rectangular prism is 8 in X 8 in X 7 in = 448 in³.

Question 12.

Volume = _____120_______ m³,
Answer:
Volume of the recangular prism is 120 m³,

Explanation:
Given rectangular prism has length 8 m, width 3 m and height 5 m,
so volume of the rectangular prism is 8 m X 3 m X 5 m = 120 m³.

Find the volume of each rectangular prism.

Question 13.
Length = 5 cm
Width = 12 cm
Height = 9 cm
Volume = ______540_______ cm³,
Answer:
Volume of the recangular prism is 540 cm³,

Explanation:
Given rectangular prism has length 5 cm, width 12 cm and height 9 cm,
so volume of the rectangular prism is 5 cm X 12 cm X 9 cm = 540 cm³.

Question 14.
Length = 10 in.
Width = 25 in.
Height = 14 in.
Volume = ______3,500_______ in³,
Answer:
Volume of the recangular prism is 3,500 in³,

Explanation:
Given rectangular prism has length 10 in, width 25 in and height 14 in,
so volume of the rectangular prism is 10 in X 25 in X 14 in = 3,500 in ³.

Question 15.
Length = 7 m
Width = 12 m
Height = 8 m
Volume = _____672________ m³,
Answer:
Volume of the recangular prism is 672 m³,

Explanation:
Given rectangular prism has length 7 m, width 12 m and height 8 m,
so volume of the rectangular prism is 7 m X 12 m X 8 m = 672 m³.

Question 16.
Length = 24 ft
Width = 10 ft
Height = 15 ft
Volume = ______3,600_______ ft³,
Answer:
Volume of the recangular prism is 3,600 ft³,

Explanation:
Given rectangular prism has length 24 ft, width 10 ft and height 15 ft,
so volume of the rectangular prism is 24 ft X 10 ft X 15 ft = 3,600 ft³.

Solve. Show your work.

Question 17.
Find the volume of a cube with edges measuring 9 centimeters.
Answer:
Volume of the cube is 729 cm³,

Explanation:
Given cube has edges measuring 9 centimeters each
means length 9 cm, width 9 cm and height 9 cm,
so volume of the cube is 9 cm X 9 cm X 9 cm = 729 cm³.

Question 18.
A rectangular prism has a width of 8 feet and a height of 5 feet.
Its length is twice its width.
Find the volume of the rectangular prism.
Answer:
Volume of the recangular prism is 640 ft³,

Explanation:
Given rectangular prism has width 8 feet and height 5 feet,
its length is twice its width so length is 2 X 8 feet = 16 feet,
so volume of the rectangular prism is 16 ft X 8 ft X 5 ft =640 ft³.

Question 19.
The base of a rectangular prism is a square whose sides each measure 9 inches.
The height of the rectangular prism is 11 inches. Find its volume.
Answer:
Volume of the recangular prism is 891 in³,

Explanation:
Given the base of a rectangular prism is a square whose sides are each measure 9 inches.
The height of the rectangular prism is 11 inches.
So the rectangular prism has length 9 inches, width 9 inches and height 11 inches,
therefore, volume of the rectangular prism is 9 inches X 9 inches X 11 inches = 891 in³.

This handy Math in Focus Grade 5 Workbook Answer Key Chapter 15 Practice 3 Nets and Surface Area provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 15 Practice 3 Answer Key Nets and Surface Area

Find the surface area of each cube.

Example

3 × 3 = 9
6 × 9 = 54
Surface area of cube = 54 cm²

Question 1.

Answer:
S.A = 150 in.²,

Explanation:
As we know surface area (S.A) of cube is 6 X (side X side),
Given cube has 5 in side therefore S.A = 6 X (5 in X 5 in) =
6 X (25 in.²) = 150 in.².

Question 2.

Answer:
S.A = 864 in.²,

Explanation:
As we know surface area (S.A) of cube is 6 X (side X side),
Given cube has 12 in side therefore S.A = 6 X (12 in X 12 in) =
6 X (144 in.²) = 864 in.².

Question 3.

Answer:
S.A = 1924 cm²,

Explanation:
As we know surface area (S.A) of cube is 6 X (side X side),
Given cube has 18 in side therefore S.A = 6 X (18 cm X 18 cm) =
6 X (324 cm²) = 1924 cm².

Find the surface area of each rectangular prism.

Example

2 × 8 × 4 = 64
2 × 22 × 4 = 176
2 × 22 × 8= 352
64 + 176 + 352 = 592
Surface area of rectangular prism = 592 in.²

Question 4.

Answer:
The surface area of rectangular prism is 684 in.²,

Explanation:
As the surface area of rectangular prism is
2 X [(width X length) + (height X length) + (height X width)],
= 2 X [(12 in X 15 in) + (6 in X 15 in) + (6 in X 12 in)],
= 2 X [(180 in.²) + (90 in.²) + (72 in.²)]
= 2 X [ 342 in.²],
= 684 in.².

Question 5.

Answer:
The surface area of rectangular prism is 952 m.²,

Explanation:
As the surface area of rectangular prism is
2 X [(width X length) + (height X length) + (height X width)],
= 2 X [(8 m X 19 m) + (12 m X 19 m) + ( 12 m X  8 m)],
= 2 X [(152 m.²) + (228 m.²) + (96 m.²)]
= 2 X [ 476 m.²],
= 952 m.².

Find the surface area of each triangular prism.

Example

Answer:
Surface area of triangular prism = 228 in.²

Explanation:
2 × \(\frac{1}{2}\) × 3 in × 4 in = 12 in.²
4 in × 18 in = 72 in.²
3 in × 18 in = 54 in.²
5 in × 18 in = 90 in.²
12 in.²+ 72  in.² + 54 in.² + 90 in.² = 228 in.²
Surface area of triangular prism = 228 in.²

Question 6.

Answer:

Explanation:
The formula for the surface area of triangular prism is:
Surface area = bh + (l X w + w X h + l X h),
= (5 cm X 35 cm) + (13 cm X 24 cm + 24 cm X 5 cm + 13 cm X 35 cm),
= 175  cm²+ ( 312 cm²+ 120 cm²+ 455 cm²)
= 1,062 cm².

Solve. Show your work.

Question 7.

Jeffrey cuts out the net of a box he wants to make.
Find the surface area of the box.

Answer:
The surface area of Jeffrey box is 684 in.²,

Explanation:
Jeffrey box contains 1 square of 8 in side,
2 rectangles of length 15 in and 8 in width,
2 rectangles of length 15 in and 10 in width,
1 rectangle of length 10 in and 8 in width,
So the surface area of Jeffrey box is
8 in X 8 in = 64 in.²
2 X (15 in X 8 in) = 2 X 120 in.²= 240 in.²
2 X (15 in X 10 in) = 2 X 150 in.²= 300 in.²
1 X (10 in X 8 in) = 80 in.²
surface area = 64 in.²+ 240 in.² + 300 in.²+ 80 in.²,
surface area = 684 in.².

Solve. Show your work.

Question 8.
This glass fish tank does not have a cover. Find the total area of the
glass panels used to make the tank.

Answer:
The total area of the glass panels used to make the tank is = 288 cm²,

Explanation:
Given glass fish tank that does not have a cover. The total area of the
glass panels used is in the shape of cuboid,
therefore to make the tank we need
2(lw + lh + hw) = 2 X [(24 cm + 21 cm) + (24 cm + 27 cm) + (27 cm + 21 cm)],
= 2 X (45 cm² + 51 cm² + 48 cm²),
= 2 X (144 cm²),
= 288 cm².

Question 9.
The tank shown is made of steel. It does not have a cover.
Find the area of steel sheet used to make the tank.

Answer:
The total area of the steel sheet is 190 ft²,

Explanation:
Given tank shown is made of steel,
The total area of the steel sheet used is in the shape of rectangular prism,
therefore to make the tank we need
2(lw + lh + hw) = 2 X [(6 1/2 ft + 28 ft) + (6 1/2 ft + 13 ft) + (13 ft + 28 ft)],
= 2 X (34 1/2 ft² + 19 1/2 ft² + 41 ft²),
= 2 X (95 ft²),
= 190 ft².

Question 10.
A rectangular piece of poster board measures 60 centimeters by 80 centimeters.
Linn draws the net of a box on the poster board and cuts it out.
If the box measures 10 centimeters by 16 centimeters by 27 centimeters,
what is the area of the poster board left?
Answer:
The area of the poster board left 3076 cm²,

Explanation:
Given a rectangular piece of poster board measures 60 centimeters by 80 centimeters.
Area of poster board is 60 cm X 80  cm = 4800 cm².
Linn draws the net of a box on the poster board and cuts it out.
If the box measures 10 centimeters by 16 centimeters by 27 centimeters,
the surface area of the box is
2(lw + lh + hw) = 2 X [(10 cm + 16 cm) + (16 cm + 27 cm) + (27 cm + 10 cm)],
= 2 X (160 cm² + 432 cm² + 270 cm²),
= 2 X (862 cm²),
= 1724 cm²,
therefore 4800 cm²– 1724 cm² = 3076 cm².

This handy Math in Focus Grade 5 Workbook Answer Key Chapter 15 Practice 2 Drawing Cubes and Rectangular Prisms provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 15 Practice 2 Answer Key Drawing Cubes and Rectangular Prisms

Draw on dot paper.

Question 1.
Draw a unit cube.

Answer:

Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
Shown the volume of a unit cube = Side × Side × Side,
= 1 unit × 1 unit × 1 unit,
= 1 unit cubes.

Question 2.
Draw two different views of a rectangular prism made up of 2 unit cubes.

Answer:

Explanation:
Drawn two different views of a rectangular prism made up of 2 unit cubes,
A unit cube has all its sides of length 1 unit
and 2 unit cubes shows the volume of a 2 unit cubes = 2 X (Sides × Side × Side),
= 2 X (1 unit × 1 unit × 1 unit),
= 2 unit cubes.

Question 3.
Draw two different solids made up of 3 unit cubes each.

Answer:

Explanation:
Drawn two different views of a rectangular prism made up of 3 unit cubes,
A unit cube has all its sides of length 1 unit
and 3 unit cubes shows the volume of a 3 unit cubes = 3 X (Sides × Side × Side),
= 3 X (1 unit × 1 unit × 1 unit),
= 3 unit cubes.

Draw each cube or rectangular prism on the dot paper.

Example

Question 4.

Answer:

Explanation:
Drawn one cube on the dot paper,
As given cube has 4 units shown the volume of cube =
side X side X side = 4 units X 4 units X 4 units = 64 unit cubes.

Question 5.

Answer:

Explanation:
Drawn one rectangular prism on the dot paper,
As given rectangular prism has 4 units X 4 units  X 1 unit =
16 unit cubes rectangular prism.

Question 6.

Answer:

Explanation:
Drawn one rectangular prism on the dot paper,
As given rectangular prism has 4 units X 2 units  X 2 units =
16 unit cubes rectangular prism.

Draw each cube or rectangular prism on the dot paper.

Question 7.

Answer:

Explanation:
Drawn one rectangular prism on the dot paper,
As given rectangular prism has 2 units X 2 units  X 2 units =
8 unit cubes rectangular prism.

Question 8.

Answer:

Explanation:
Drawn one rectangular prism on the dot paper,
As given rectangular prism has 3 units X 1 unit  X 1 unit =
3 unit cubes rectangular prism.

Draw a cube with edges 4 times as long as the edges of this unit cube.

Question 9.

Answer:

Explanation:
Given 1 unit cube with volume 1 unit X 1 unit X 1 unit = 1 cubic unit and
Drawn a cube with edges 4 times as long as the given edge so the volume is
4 units X 4 units X 4 units = 64 cubic units.

Complete the drawing of each cube or rectangular prism.

Question 10.

Answer:

Explanation:
Completed the drawing of given cube as shown above
which has 2 units.

Question 11.

Answer:

Explanation:
Completed the drawing of given cube as shown above
which has 3 units.

Question 12.

Answer:

Explanation:
Completed the drawing of given rectangular prism as shown above
which has 2 units.

Question 13.

Answer:

Explanation:
Completed the drawing of given cube as shown above
which has 3 units.

This handy Math in Focus Grade 5 Workbook Answer Key Chapter 15 Practice 1 Building Solids Using Unit Cubes provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 15 Practice 1 Answer Key Building Solids Using Unit Cubes

Find the number of unit cubes used to build each solid.

Question 1.

__________ unit cubes
Answer:
5 unit cubes,

Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
we have 5 unit cubes,
So, the volume of a 5 unit cubes = 5 X (Side × Side × Side),
= 5 X (1 unit × 1 unit × 1 unit),
= 5 X (unit cubes).

Question 2.

__________ unit cubes
Answer:
7 unit cubes,

Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
we have 7 unit cubes,
So, the volume of a 7 unit cubes = 7 X (Side × Side × Side),
= 7 X (1 unit × 1 unit × 1 unit),
= 7 unit cubes.

Question 3.

__________ unit cubes
Answer:
8 unit cubes,

Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
we have 8 unit cubes,
So, the volume of a 8 unit cubes = 8 X (Side × Side × Side),
= 8 X ( 1 unit × 1 unit × 1 unit),
= 8 unit cubes.

Question 4.

__________ unit cubes
Answer:
6 unit cubes,

Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
we have 6 unit cubes,
So, the volume of a 6 unit cubes = 6 X (Side × Side × Side),
=6 X (1 unit × 1 unit × 1 unit),
= 6 unit cubes.

Question 5.

__________ unit cubes
Answer:
8 unit cubes,

Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
we have 8 unit cubes,
So, the volume of a 8 unit cubes = 8 X (Side × Side × Side),
= 8 X (1 unit × 1 unit × 1 unit),
= 8 unit cubes.

Question 6.

__________ unit cubes
Answer:
9 unit cubes,

Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
we have 9 unit cubes,
So, the volume of a 9 unit cubes = 9 X (Side × Side × Side),
= 9 X (1 unit × 1 unit × 1 unit),
= 9 unit cubes.

Find the number of unit cubes used to build each solid.

Question 7.

__________ unit cubes
Answer:
7 unit cubes,

Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
we have 7 unit cubes,
So, the volume of a 7 unit cubes = 7 X (Side × Side × Side),
= 7 X ( 1 unit × 1 unit × 1 unit),
= 7 unit cubes.

Question 8.

__________ unit cubes
Answer:
9 unit cubes,

Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
we have 9 unit cubes,
So, the volume of a 9 unit cubes = 9 X (Side × Side × Side),
= 9 X (1 unit × 1 unit × 1 unit),
= 9 unit cubes.

Question 9.

__________ unit cubes
Answer:
7 unit cubes,

Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
we have 7 unit cubes,
So, the volume of a 7 unit cubes = 7 X (Side × Side × Side),
= 7 X (1 unit × 1 unit × 1 unit),
= 7 unit cubes.

Question 10.

__________ unit cubes
Answer:
10 unit cubes,

Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
we have 10 unit cubes,
So, the volume of a 10 unit cubes = 10 X (Side × Side × Side),
= 10 X (1 unit × 1 unit × 1 unit),
= 10 unit cubes.

Question 11.

__________ unit cubes
Answer:
15 unit cubes,

Explanation:
As a cube has all its sides of the same length.
A unit cube has all its sides of length 1 unit.
we have 15 unit cubes,
So, the volume of a 15 unit cubes = 15 X (Side × Side × Side),
= 15 X (1 unit × 1 unit × 1 unit),
= 15 unit cubes.

Go through the Math in Focus Grade 5 Workbook Answer Key Chapter 3 Practice 1 Adding Unlike Fractions to finish your assignments.

Math in Focus Grade 5 Chapter 3 Practice 1 Answer Key Adding Unlike Fractions

Find two equivalent fractions for each fraction.

Example

Question 1.
\(\frac{3}{4}\) = ___ = ____
Answer:

Question 2.
\(\frac{2}{5}\) = ___ = ____
Answer:

Question 3.
\(\frac{5}{6}\) = ___ = ____
Answer:

Question 4.
\(\frac{1}{7}\) = ___ = ____
Answer:

Express each fraction in simplest form.

Question 5.
\(\frac{6}{8}\) = ___
Answer:

Question 6.
\(\frac{8}{20}\) = ___
Answer:

Question 7.
\(\frac{10}{15}\) = ___
Answer:

Question 8.
\(\frac{9}{21}\) = ___
Answer:

Rewrite each pair of unlike fractions as like fractions.

Example

Question 9.
\(\frac{1}{4}\) = ___ \(\frac{5}{12}\) = ___
Answer:

Question 10.
\(\frac{1}{10}\) = ___ \(\frac{2}{5}\) = ___
Answer:

Question 11.
\(\frac{5}{9}\) = ___ \(\frac{2}{3}\) = ___
Answer:

Question 12.
\(\frac{3}{8}\) = ___ \(\frac{9}{16}\) = ___
Answer:

Write equivalent fractions for each fraction. Then find the least common denominator of the fractions.

Example
\(\frac{1}{2}\) = \(\frac{2}{4}\) = \(\frac{3}{6}\)
\(\frac{2}{3}\) = \(\frac{4}{6}\)
The least common denominator is 6.

Question 13.
\(\frac{2}{3}\) =
\(\frac{3}{4}\) =
The least common denominator is ____
Answer:

Question 14.
\(\frac{1}{4}\) =
\(\frac{5}{6}\) =
The least common denominator is ____
Answer:

Question 15.
\(\frac{5}{6}\) = ____
\(\frac{3}{8}\) = ____
The least common denominator is ____
Answer:

Shade and label each model to show the tractions. Then complete the addition sentence.

Example

Question 16.
\(\frac{1}{5}\), \(\frac{1}{2}\)

Answer:

Look at the model. Write two addition sentences.

Question 17.
\(\frac{1}{6}\), \(\frac{1}{4}\)

\(\frac{1}{6}\) + \(\frac{1}{4}\) = ___ + ___
= ____
Answer:

Question 18.
\(\frac{1}{5}\), \(\frac{2}{3}\)

\(\frac{1}{5}\) + \(\frac{2}{3}\) = ____ + ___
= ____
Answer:

Question 19.
Addition sentence 1:

Answer:

Question 20.
Addition sentence 2 (fractions in simplest form):
____ + ____ = ____
Answer:

Add. Express each sum in simplest form.

Question 21.
\(\frac{1}{3}\) + \(\frac{1}{9}\) =
Answer:

Question 22.
\(\frac{5}{8}\) + \(\frac{2}{4}\) =

Question 23.
\(\frac{1}{2}\) + \(\frac{6}{7}\) =
Answer:

Question 24.
\(\frac{4}{8}\) + \(\frac{1}{5}\) =
Answer:

Use benchmarks to estimate each sum.

Example

Question 25.
\(\frac{2}{3}\) + \(\frac{2}{9}\)
Answer:

Question 26.
\(\frac{7}{9}\) + \(\frac{1}{7}\) + \(\frac{3}{5}\)
Answer:

Go through the Math in Focus Grade 5 Workbook Answer Key Chapter 1 Practice 3 Place Value to finish your assignments.

Math in Focus Grade 5 Chapter 1 Practice 3 Answer Key Place Value

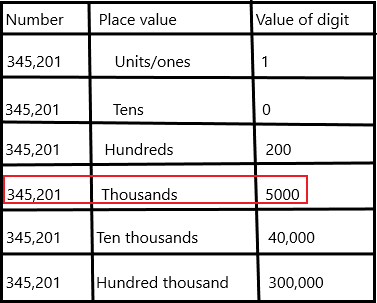
Complete. Use the place-value chart.

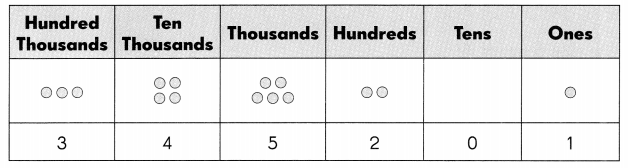
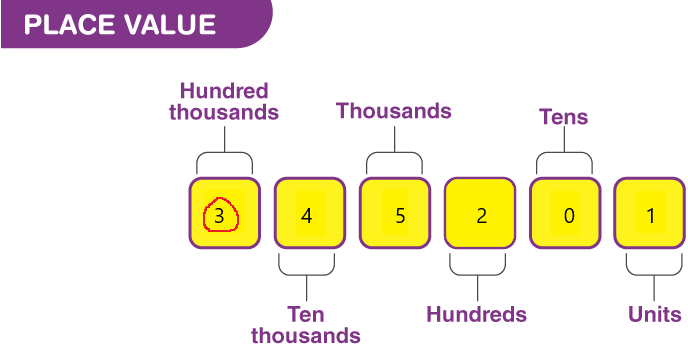
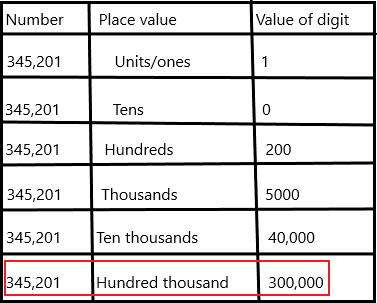
In 345,201:

Question 1.
a. the digit 3 stands for ___________
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.

The digit 3 stands for a hundred thousand.

b. the value of the digit 3 is _____
Answer:
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.
The value of the digit is 300,000.

Question 2.
a. the digit 4 stands for ___.
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.

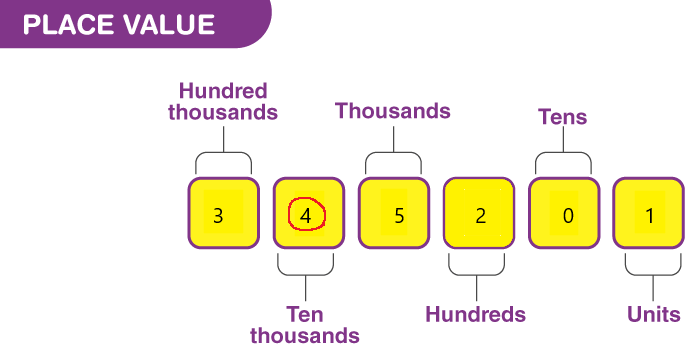
The digit 4 stands for ten thousand.

b. the value of the digit 4 is ______
Answer:
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.
The value of digit 4 is 40,000.

Question 3.
a. the digit 5 stands for ___.
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.

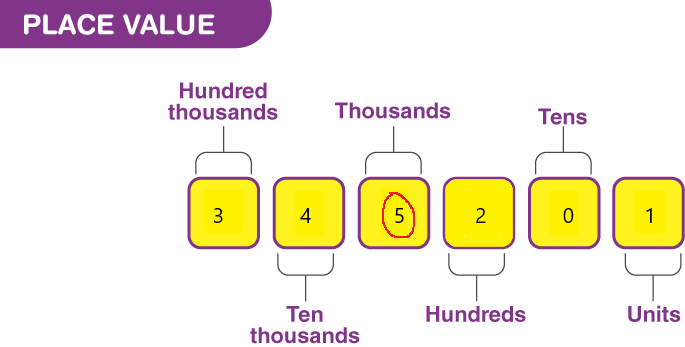
The digit 5 stands for thousands.

b. the value of the digit 5 is ______
Answer:
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.
The value of digit 5 is 5000.

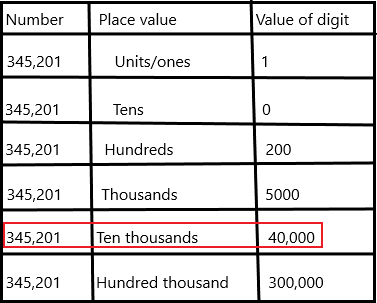
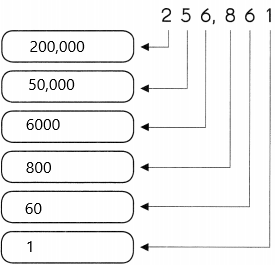
Write the value of each digit in the correct box.

Question 4.

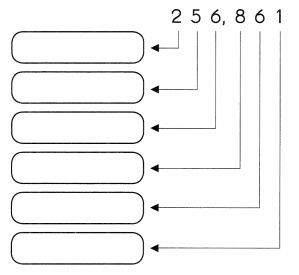
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.

Complete.

In 346,812:

Question 5.
the digit 3 stands for ____
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.

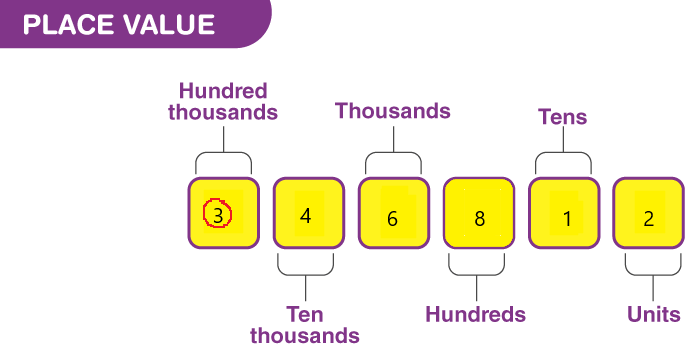
The digit 3 stands for a hundred thousand.

Question 6.
the digit 6 stands for ____
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.

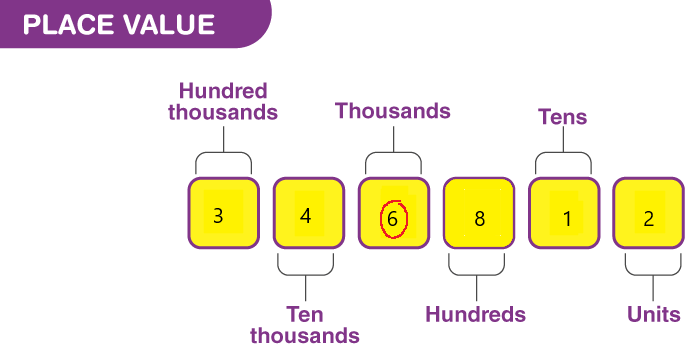
The digit 6 stands for thousand.

Write the value of the digit 2 in each number.

Question 7.
329,051 ____
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.

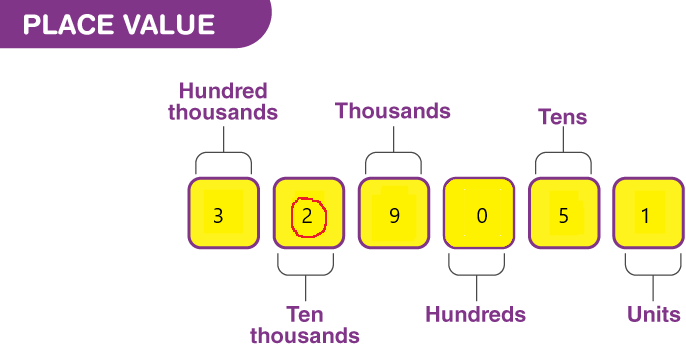
The value of digit 2 is 20,000 because it represents the ten thousand places.

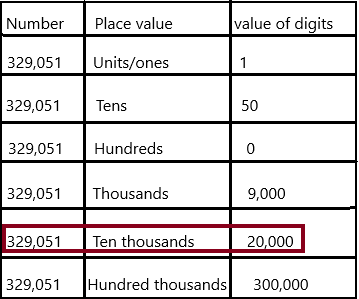
Question 8.
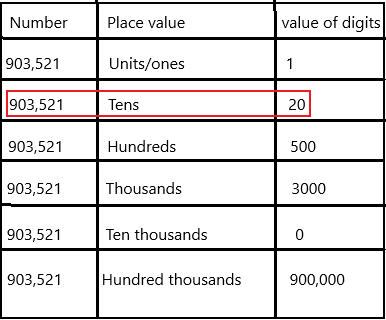
903,521 ____
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.

The value of digit 2 is 20 because it represents the tens place.

Question 9.
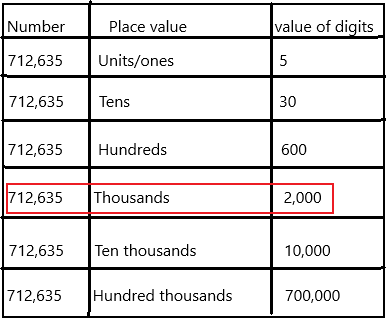
712,635 ___
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.

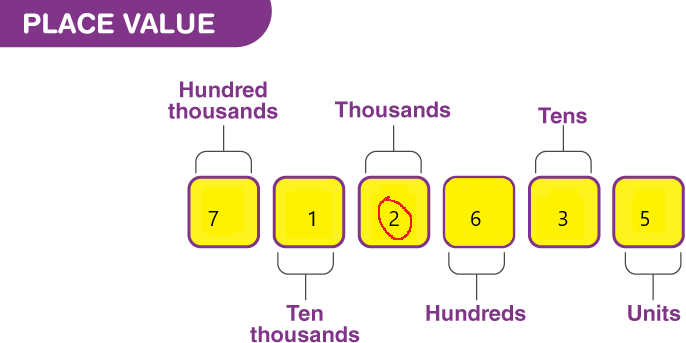
The value of digit 2 is 2000 because it represents the thousands place.

Question 10.
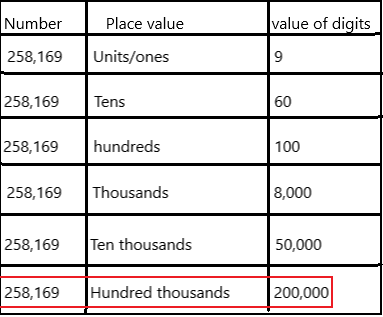
258,169 ____
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.

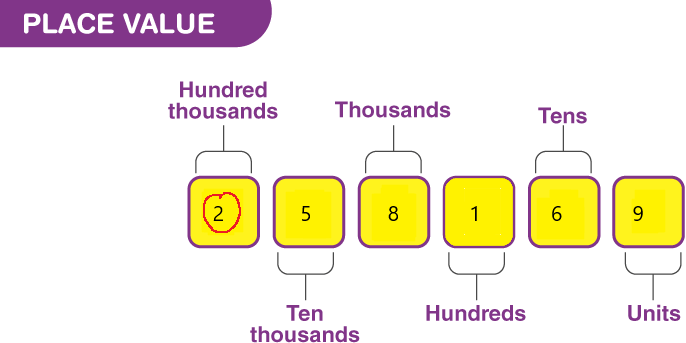
The value of digit 2 is 200,000 because it represents the hundred thousand place.

Complete.

Question 11.
In 320,1 87, the digit ___ is in the thousands place.
Answer: 0
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.

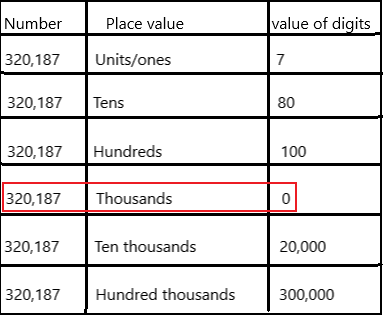
The value of digit present in the thousands place is 0.

Question 12.
In 835,129, the digit 8 is in the ____ place.
Answer: Hundred thousand place.
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.

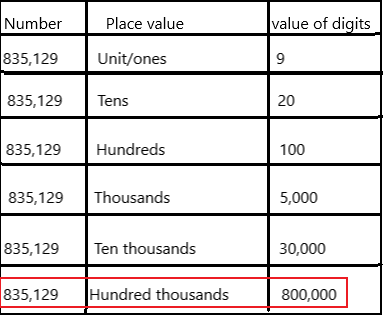
The place value of 8 in the given number is a hundred thousand and its digit value is 800,000.

Question 13.
In 348,792, the digit 4 is in the ____ place.
Answer: Ten thousand place.
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.

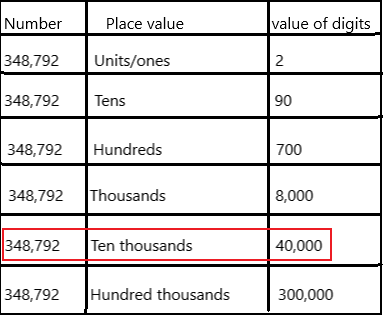
The place value of the 4 in the given number is ten thousands place and its digit value is 40,000.

Complete to express each number in expanded form.

Question 14.
153,420 = 100,000 + ___ + 3,000 + 400 + 20
Answer:
Expanded form definition: The expanded form of the numbers helps to determine the place value of each digit in the given number. It means that the expansion of numbers is based on the place value. The expanded form splits the number, and it represents the number in units, tens, hundreds and thousands form.
How to write numbers in expanded form:
Go through the below steps to write the numbers in expanded form:
Step 1: Get the standard form of the number.
Step 2: Identify the place value of the given number using the place value chart.
Step 3: Multiply the given digit by its place value and represent the number in the form of (digit × place value).
Step 4: Finally, represent all the numbers as the sum of (digit × place value) form, which is the expanded form of the number.
Now write the expanded form for the given number by using the above steps:
Step 1: The standard form of the number is 153,420.
Step 2: The place value of the given number is:
1 – Hundred thousand
5 – Ten thousand
3 – Thousands
4 – Hundreds
2 – Tens
0 – Ones
Step 3: Multiply the given number by its place value.
(i.e., 1×100,000, 5×10,000, 3×1000, 4×100, 2×10, 0×1
Step 4: Expanded form is 100,000+50,000+3000+400+20+0
Finally, the expanded form of the number 100,000+50,000+3000+400+20+0.

Question 15.
760,300 = ____ + 60,000 + 300
Answer: 700,000
Expanded form definition: The expanded form of the numbers helps to determine the place value of each digit in the given number. It means that the expansion of numbers is based on the place value. The expanded form splits the number, and it represents the number in units, tens, hundreds and thousands form.
Step 1: The standard form of the number is 760,300.
Step 2: The place value of the given number is:
7 – Hundred thousand
6 – Ten thousand
0 – Thousands
3 – Hundreds
0 – Tens
0 – Ones
Step 3: Multiply the given number by its place value.
(i.e., 7×100,000, 6×10,000, 0×1000, 3×100, 0×10, 0×1
Step 4: Expanded form is 700,000+60,000+0+300+0+0
Finally, the expanded form of the number 700,000+60,000+300.

Question 16.
700,000 + 8,000 + 500 + 4 = ____
Answer: 708,504
Expanded form definition: The expanded form of the numbers helps to determine the place value of each digit in the given number. It means that the expansion of numbers is based on the place value. The expanded form splits the number, and it represents the number in units, tens, hundreds and thousands form.
Step 1: The standard form of the number is 760,300.
Step 2: The place value of the given number is:
7 – Hundred thousand
0 – Ten thousand
8 – Thousands
5 – Hundreds
0 – Tens
4 – Ones
Step 3: Multiply the given number by its place value.
(i.e., 7×100,000, 0×10,000, 8×1000, 5×100, 0×10, 4×1
Step 4: Expanded form is 700,000+0+8000+500+0+4
Finally, the expanded form of the number 700,000+8000+500+4.
The number is 708,504.

Question 17.
200,000 + 2,000 + 10 = ____
Answer:
Expanded form definition: The expanded form of the numbers helps to determine the place value of each digit in the given number. It means that the expansion of numbers is based on the place value. The expanded form splits the number, and it represents the number in units, tens, hundreds and thousands form.
Step 1: The standard form of the number is 202,010.
Step 2: The place value of the given number is:
2 – Hundred thousand
0 – Ten thousand
2 – Thousands
0 – Hundreds
1 – Tens
0 – Ones
Step 3: Multiply the given number by its place value.
(i.e., 2×100,000, 0×10,000, 2×1000, 0×100, 1×10, 0×1
Step 4: Expanded form is 200,000+0+2000+0+10+0
Finally, the expanded form of the number 200,000+2000+10
The number is 202,010.

Complete. Use the place-value chart.

In 1,508,369.
Question 18.
a. the digit 1 stands for ____
Answer:
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.

The place value of the 1 in the given number 1,508,369 is millions.

b. the value of the digit 1 is ____
Answer: 1,000,000.
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use

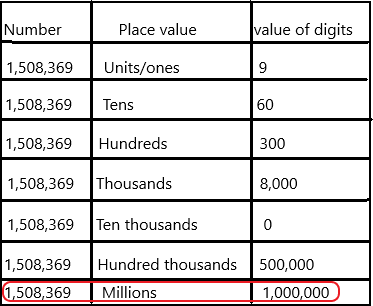
The value of digit of 1 in the given number 1,508,369 is 1,000,000.

Complete

Question 19.
a. the digit 8 stands for _____
Answer: Thousands place.
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.

The place value of 8 in the given number 1,508,369 is thousand place.

b. the value of the digit 8 is ________________
Answer: 8000
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.

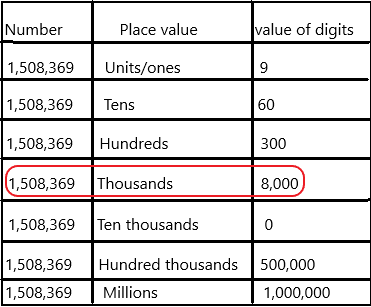
The value of digit 8 in the given number 1,508,369 is 8000.

Question 20.
the digit 0 is in the ___ place.
Answer:
In Mathematics, place value charts help us to make sure that the digits are in the correct places. To identify the positional values of numbers accurately, first, write the digits in the place value chart and then write the numbers in the usual and the standard form.

The digit 0 in the given number 1,508,369 is ten thousands place.

Write the value of each digit in the correct box.

Question 21.

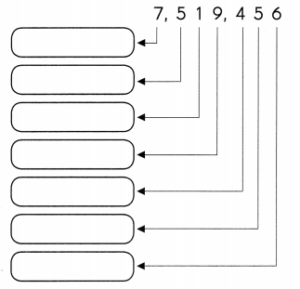
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.

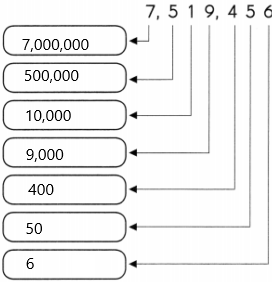
Complete

Question 22.
In 5,420,000, the digit 5 is in the ____ place.
Answer: Millions place.
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.

The place value of the 5 in the given number 5,420,000 is millions place.

Question 23.
In 1,077,215, the digit in the hundred thousand place is ____
Answer: 0
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.

In the given number 1,077,215, the hundred thousand place is 0.

Question 24.
In 9,400,210, the digit 9 stands for _____
Answer: Millions place.
1. Place value tells you how much each digit stands for
2. Use a hyphen when you use words to write 2-digit numbers greater than 20 that have a digit other than zero in the one’s place.
3. A place-value chart tells you how many hundreds, tens, and ones to use.

The place value of the 9 in the given number 9,400,210 is millions place.

Complete to express each number in expanded form.

Question 25.
4,130,000 = ___ + 100,000 + 30,000
Answer: 4,000,000
Expanded form definition: The expanded form of the numbers helps to determine the place value of each digit in the given number. It means that the expansion of numbers is based on the place value. The expanded form splits the number, and it represents the number in units, tens, hundreds and thousands form.
Step 1: The standard form of the number is 4,130,000.
Step 2: The place value of the given number is:
4 – Millions
1 – Hundred thousand
3 – Ten thousand
0 – Thousands
0 – Hundreds
0 – Tens
0 – Ones
Step 3: Multiply the given number by its place value.
(i.e., 4×1,000,000,  1×100,000, 3×10,000, 0×1000, 0×100, 0×10, 0×1)
Step 4: Expanded form is 4,000,0000+100,000+30,000+0+0+0+0
Finally, the expanded form of the number 4,000,0000+100,000+30,000
The number is 4,130,000.

Question 26.
6,123,750 = 6,000,000 + 100,000 + 20,000 + 3,000 + 700 + ____
Answer: 50
Expanded form definition: The expanded form of the numbers helps to determine the place value of each digit in the given number. It means that the expansion of numbers is based on the place value. The expanded form splits the number, and it represents the number in units, tens, hundreds and thousands form.
Step 1: The standard form of the number is 6,123,570.
Step 2: The place value of the given number is:
6 – Millions
1 – Hundred thousand
2 – Ten thousand
3 – Thousands
5 – Hundreds
7 – Tens
0 – Ones
Step 3: Multiply the given number by its place value.
(i.e., 6×1,000,000,  1×100,000, 2×10,000, 3×1000, 7×100, 5×10, 0×1)
Step 4: Expanded form is 6,000,0000+100,000+20,000+3,000+700+50+0
Finally, the expanded form of the number 6,000,0000+100,000+20,000+3,000+700+50
The number is 6,123,750.

Question 27.
7,550,100 = 7,000,000 + ___ + 50,000 + 100
Answer: 500,000
Expanded form definition: The expanded form of the numbers helps to determine the place value of each digit in the given number. It means that the expansion of numbers is based on the place value. The expanded form splits the number, and it represents the number in units, tens, hundreds and thousands form.
Step 1: The standard form of the number is 7,550,100.
Step 2: The place value of the given number is:
7 – Millions
5 – Hundred thousand
5 – Ten thousand
0 – Thousands
1 – Hundreds
0 – Tens
0 – Ones
Step 3: Multiply the given number by its place value.
(i.e., 7×1,000,000,  5×100,000, 5×10,000, 0×1000, 1×100, 0×10, 0×1)
Step 4: Expanded form is 7,000,0000+500,000+50,000+0+100+0+0
Finally, the expanded form of the number 7,000,0000+500,000+50,000+100.
The number is 7,550,100.

Question 28.
5,000,000 + 200,000 + 7,000 + 70 = ____
Answer: 5,207,070.
Expanded form definition: The expanded form of the numbers helps to determine the place value of each digit in the given number. It means that the expansion of numbers is based on the place value. The expanded form splits the number, and it represents the number in units, tens, hundreds and thousands form.
Step 1: The standard form of the number is 5,207,070.
Step 2: The place value of the given number is:
5 – Millions
2 – Hundred thousand
0 – Ten thousand
7 – Thousands
0 – Hundreds
7 – Tens
0 – Ones
Step 3: Multiply the given number by its place value.
(i.e., 5×1,000,000,  2×100,000, 0×10,000, 7×1000, 0×100, 7×10, 0×1)
Step 4: Expanded form is 5,000,0000+200,000+0+7,000+0+70+0
Finally, the expanded form of the number 5,000,000+200,000+7,000+70
The number is 5,207,070.

Question 29.
3,000,000 + 20,000 + 9,000 + 100 + 5 = ____
Answer: 3,029,105.
Expanded form definition: The expanded form of the numbers helps to determine the place value of each digit in the given number. It means that the expansion of numbers is based on the place value. The expanded form splits the number, and it represents the number in units, tens, hundreds and thousands form.
Step 1: The standard form of the number is 3,029,105.
Step 2: The place value of the given number is:
3 – Millions
0 – Hundred thousand
2 – Ten thousand
9 – Thousands
1 – Hundreds
0 – Tens
5 – Ones
Step 3: Multiply the given number by its place value.
(i.e., 3×1,000,000,  0×100,000, 2×10,000, 9×1000, 1×100, 0×10, 5×1)
Step 4: Expanded form is 3,000,0000+0+20,000+9,000+100+0+5
Finally, the expanded form of the number 3,000,000+20,000+9,000+100+5
The number is 3,029,105.

Read the clues to find the number.

It is a 7-digit number.
The value of the digit 7 is 700.
The greatest digit is in the millions place.
The digit 1 is next to the digit in the millions place. The value of the digit 8 is 8 tens.
The value of the digit 3 is 3 ones.
The digit 5 is in the thousands place.
The digit 6 stands for 60,000.

Question 30.
The number is ____
Answer: 8,165,783
The greatest digit in the given clue is the number 8. So I kept 8 in the millions place.
The hundred thousand place is the digit 1. In the clue already given that 1 is next to the millions place.
The ten thousand place is the digit 6.
The thousands place is the digit 5.
The hundreds place is the digit 7.
The tens place is the digit 8.
The units place is the digit 3.

This handy Math in Focus Grade 4 Workbook Answer Key Chapter 13 Practice 3 Making Symmetric Shapes and Patterns detailed solutions for the textbook questions.

Math in Focus Grade 4 Chapter 13 Practice 3 Answer Key Making Symmetric Shapes and Patterns

Each figure below is half of a symmetric shape with the dotted line as a line of symmetry. Complete each symmetric shape.

Example

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

Each figure below is half of a symmetric shape with the dotted line as a line of symmetry. Complete each symmetric shape.

Question 4.

Answer:

Question 5.

Answer:

Shade four more squares in each figure so that the pattern of shaded squares has rotational symmetry.

Example

Question 6.

Answer:

Question 7.

Answer:

Question 8.

Answer:

Shade four more squares in each figure so that the pattern of shaded squares has rotational symmetry.

Example

Question 9.

Answer:

Question 10.

Answer:

Question 11.

Answer: