Math in Focus

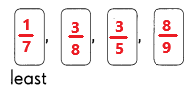
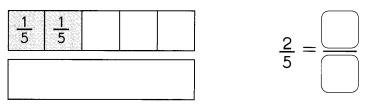
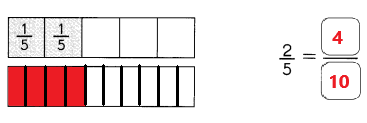
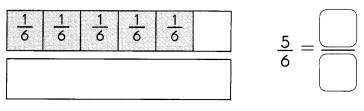
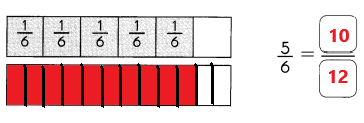
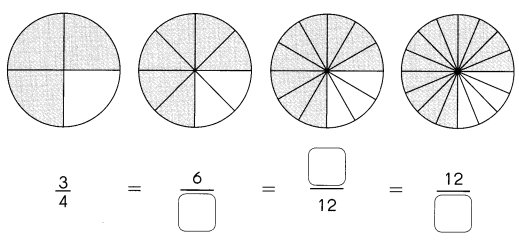
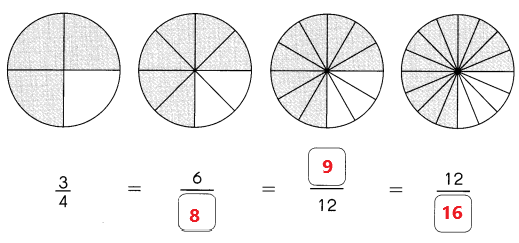
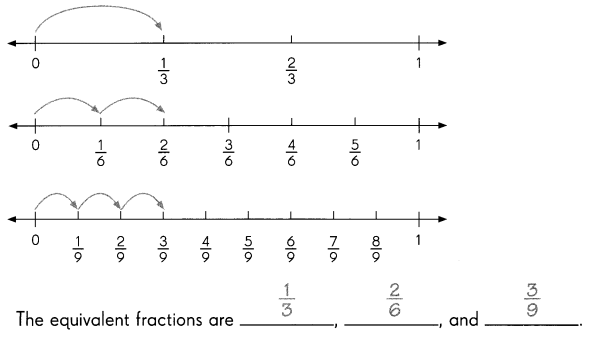
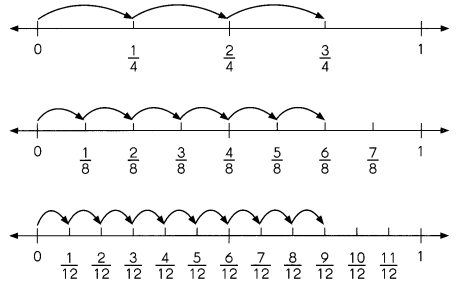
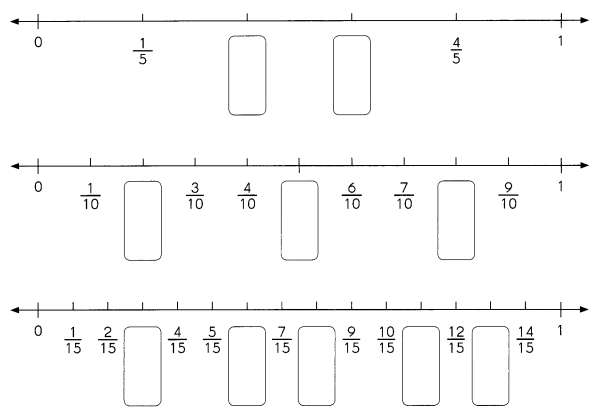
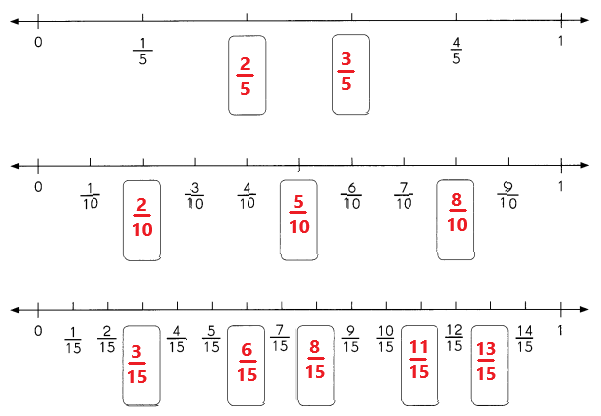
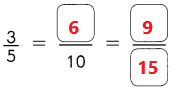
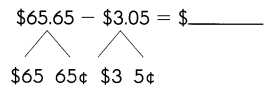
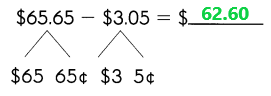
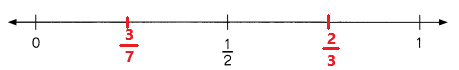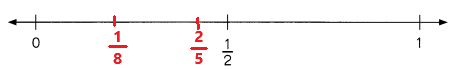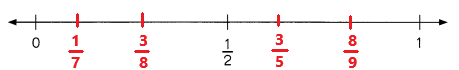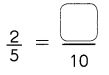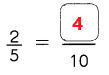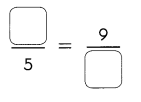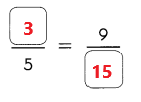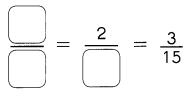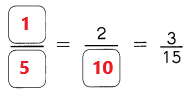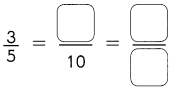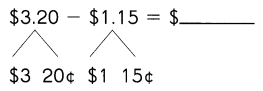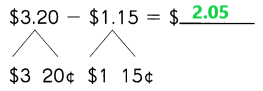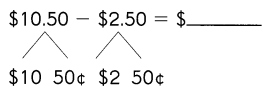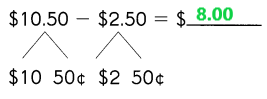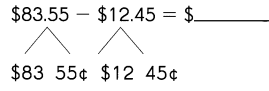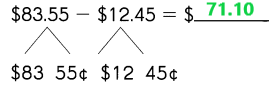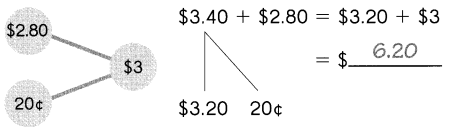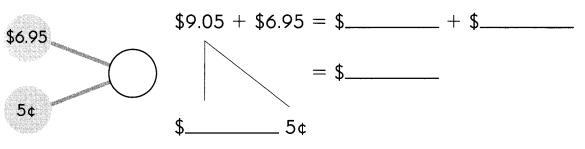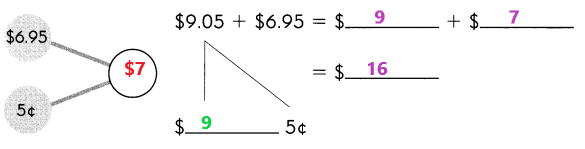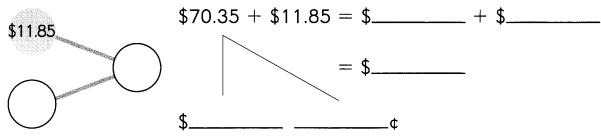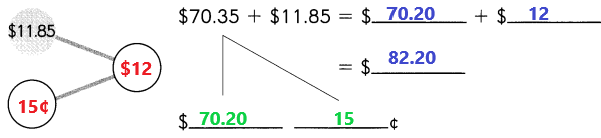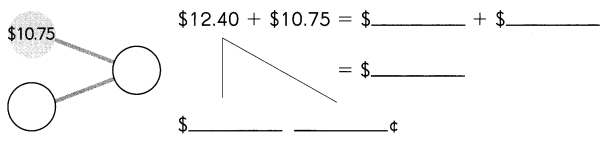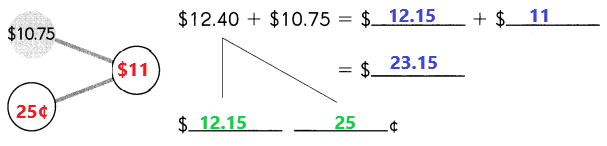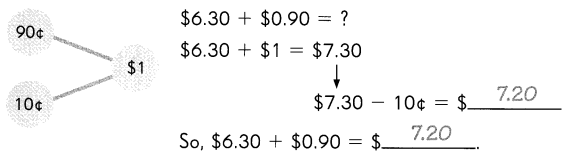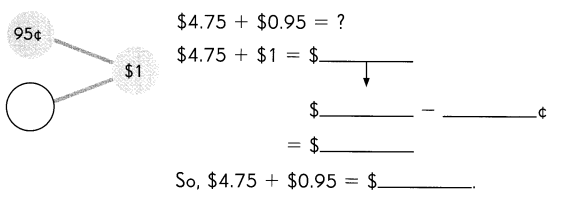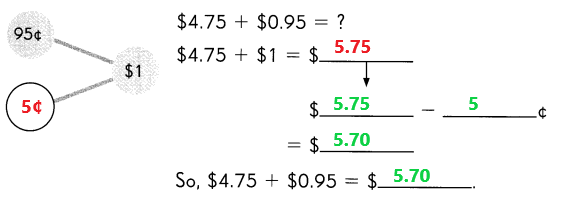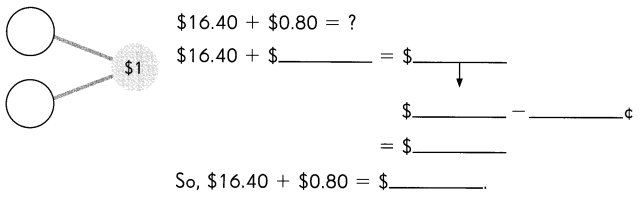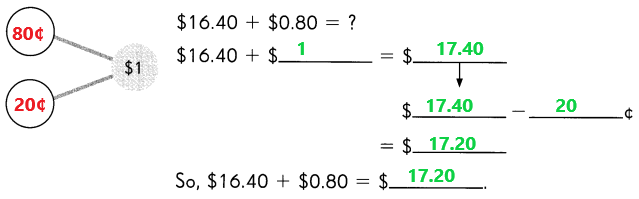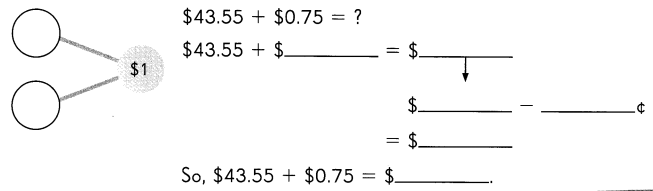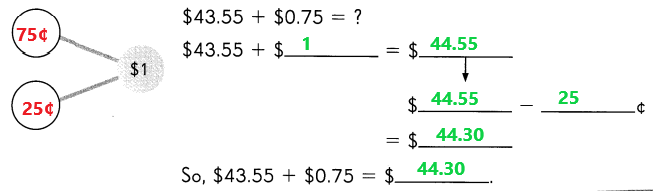Go through the Math in Focus Grade 1 Workbook Answer Key Chapter 16 Numbers to 100 to finish your assignments.

Math in Focus Grade 1 Chapter 16 Answer Key Numbers to 100

Put On Your Thinking Cap!

Challenging Practice.

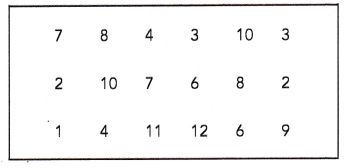
Read each clue. Cross out the numbers that are incorrect. Fill in the blanks.

Question 1.

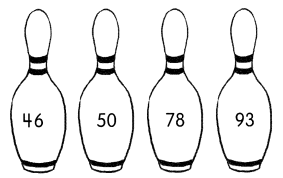
The mystery number is less than 90. It is greater 56.
The mystery number is ___________.
Answer:
The mystery number is 78.

Explanation:
Given that the mystery number is less than 90 and it is greater 56. So the number will be 78.

Question 2.

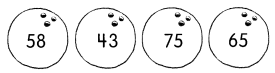
The mystery number is greater than 50 but less than 70. It is 5 more than 60.
The mystery number is ____________.
Answer:
The mystery number is 65.

Explanation:
Given that the mystery number is greater than 50 but less than 70 and it is 5 more than 60. So the number will be 60+5 which is 65.

Question 3.

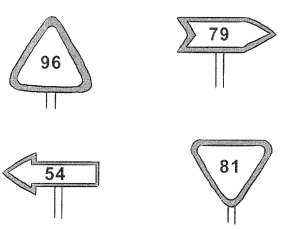
The mystery number is less than 90 but greater than 63. It is 1 less than 80.
The mystery number is ____________.
Answer:
The mystery number is 79.

Explanation:
Given that the mystery number is less than 90 but greater than 63 and it is 1 less than 80 which is 80-1 = 79.

Put on Your Thinking Cap!

Problem Solving

Use the chart to complete the following number patterns. Explain the rule for the number pattern.

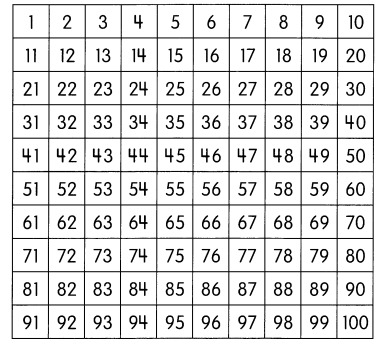
Example

Question 1.
41, 46, 51, 56, __________, __________, __________
Rule: ______________________ ___________
Answer:
41,46,51,56,61,66,71.

Explanation:
The rule is Counting on in steps of 5 from the number before it or Adding 5 to the number before it.
41,46,51,56,61,66,71.

Question 2.
30, 36, 42, 48, __________, __________, __________
Rule: ___________________________ _________
Answer:
30,36,42,48,54,60,66.

Explanation:
The rule is Counting on in steps of 6 from the number before it or Adding 6 to the number before it.
30,36,42,48,54,60,66.

Question 3.
10, 20, 30, 40, __________, __________, __________
Rule: ____________________________ __________
Answer:
10,20,30,40,50,60,70.

Explanation:
The rule is Counting on in steps of 10 from the number before it or Adding 10 to the number before it.
10,20,30,40,50,60,70.

Question 4.
81, 78, 75, 72, , __________, __________, __________
Rule: ____________ ___________________________
Answer:
81,78,75,72,69,66,63.

Explanation:
The rule is Count back 3 from the number or Subtract 3 to the number.
81,78,75,72,69,66,63.

Question 5.
90, 85, 80, 75, __________, __________, __________
Rule: ____________ ___________________________
Answer:
90,85,80,75,70,65,60,55.

Explanation:
The rule is Count back 5 from the number or Subtract 5 to the number.
90,85,80,75,70,65,60,55.

Chapter Review/Test

Vocabulary

Choose the correct word.

Question 1.
You _____________ numbers by finding which number is greater than or less than the other.
Answer:
You compare numbers by finding which number is greater than or less than the other.

Question 2.
When you do not need an exact number, you can _____________.
Answer:
When you do not need an exact number, you can estimate.

Question 3.
A ____________ is used to compare numbers.
Answer:
A number line is used to compare numbers.

Concepts and Skills

Fill in the blanks.

Question 4.
Write ninety-eight as a number. ____________
Answer:
99.

Explanation:
Ninety-eight as a number is 99.

Question 5.
Write 74 in word form. ____________
Answer:
Seventy-four.

Explanation:
The number 74 in words is Seventy-four.

Question 6.
80 and 7 make ____________.
Answer:
87.

Explanation:
80 and 7 make 87.

Question 7.
64 = __________ tens _________ ones
Answer:
64 = 6 tens 4 ones.

Explanation:
The number 64 has 6 tens and 4 ones.

Question 8.
____________ is 6 more than 54.
Answer:
60 is 6 more than 54.

Explanation:
Given that 6 more than 54 which is 54+6 = 60.

Compare.

Question 9.
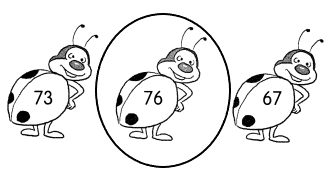
Circle the greatest number.

Answer:
76.

Explanation:
The greatest number is 76.

Question 10.
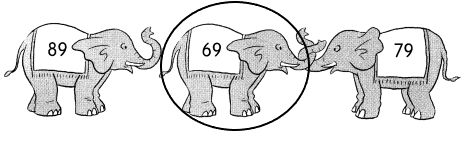
Circle the least number.

Answer:
69.

Explanation:
The least number is 69.

Estimate then count.

Question 11.
Estimate the number of bowling pins. Then count the exact number.

Estimate: _____________
Count: ____________
Answer:
Estimate: 30
Count: 25.

Explanation:
In the above image, estimated bowling pins are 30 and the actual count is 25.

Practice the problems of Math in Focus Grade 2 Workbook Answer Key Chapter 8 Practice 3 Measuring in Grams to score better marks in the exam.

Math in Focus Grade 2 Chapter 8 Practice 3 Answer Key Measuring in Grams

Fill in the blanks.

The mass of each is 1 gram.

Question 1.

The cap of a pen has a mass of ___ grams.
Answer: 4 grams.
Explanation:
Observe the picture carefully, there is a pen cap on one side and there are grams on another side.
There are 4 1 grams are present. Add all the grams it becomes 4.
Therefore, the weight of the pen cap is 4 grams.

Question 2.

The pencil has a mass of __ grams.
Answer: 9 grams.
First, notice that you are looking for weight. A pencil weighs more than a paperclip but less than a kitten. This means it would be best measured in grams. The answer is the weight of a pencil would be best measured in grams.
Add all the grams present over there. Then we get 9 ‘1’ grams are there.
Therefore, the pencil has a mass of 9 grams.

Question 3.

The sharpener has a mass of ___ grams.
Answer: 7 grams.
Explanation:
1. we will compare the weights of the sharpener and grams by placing them on each end of the scale.
2. The scale remains the same at a certain angle.
3. Add the grams and then write the mass of the sharpener.
4. Therefore, the sharpener has a mass of 7 grams.

Question 4.

The eraser has a mass of ___ grams.
Answer: 16 grams.
Explanation:
1. we will compare the weights of the eraser and grams by placing them on each end of the scale.
2. The scale remains the same at a certain angle.
3. Add the grams and then write the mass of the eraser.
4. Therefore, the eraser has a mass of 16 grams.

Fill in the blanks.

Question 5.

Answer:

Explanation:
1. Start at 0 and count the lines.
2. From 0 count the next line it is 5.
3. After 5 it will be 10 and the next it will be 15. It was like multiples of 5.
4. According to that count the grams and fill the blanks according to that.

Question 6.

Answer:

Explanation:
1. Start at 0 and count the lines. Each line represents the 10
2. From 0 count the next line it is 10.
3. After 10 the next line will be 20, 30, 40, and so on…
4. According to that count the grams and write the blanks.

Question 7.

Answer:

Explanation:
1. Start at 0 and count the lines. Each line represents the 1
2. From 0 count the next line it is 1.
3. After 1 the next line will be 2, 3, 4, and so on… it is like multiples of 1.
4. According to that count the grams and write the blanks.

Fill in the missing numbers.

Question 8.

Answer:

1. Start at 0 and count the lines. Each line represents the 10
2. From 0 count the next line it is 10.
3. After 10 the next line will be 20, 30, 40, and so on…
4. According to that count the grams and write the blanks.

Fill in the blanks.

Question 9.

The sandwich has a mass of __ grams.
Answer: 100  grams.
The measuring scale is showing 100 grams.
Explanation:
1. Choose a scale that measures in grams. Make sure the scale can handle the size of objects you plan on weighing. Since a gram is a metric unit of measurement, your scale needs to use the metric system. Scales are available in digital and mechanical models.
2. Weigh an empty container first before putting an item in it. If you plan to measure something you can’t put directly on the scale, weigh the container before putting the item in it.
3. Press the tare button to zero out the scale. The mysterious button labelled “tare” on digital scales is a reset button. Press the tare button after each item you measure on the scale. If you weighed a container, you can fill it now.
4. Set the object you wish to measure on the scale. Place your object in the centre of the scale. If you measured a container first, you can now put the object you wish to measure inside the container. The scale will then calculate the heaviness of your object.
5. Finish weighing the object on the scale. Wait for the scale’s digital display or needle to come to a stop. When it finishes moving, read the number to find out how heavy the object is. Make sure that the weight is in grams. Then, remove your object and hit the tare button again to reset the scale.

Question 10.

The box of crackers has a mass of __ grams.
Answer: 400 grams.
The measuring scale is showing 400 grams.
Explanation:
1. Choose a scale that measures in grams. Make sure the scale can handle the size of objects you plan on weighing. Since a gram is a metric unit of measurement, your scale needs to use the metric system. Scales are available in digital and mechanical models.
2. Weigh an empty container first before putting an item in it. If you plan to measure something you can’t put directly on the scale, weigh the container before putting the item in it.
3. Press the tare button to zero out the scale. The mysterious button labelled “tare” on digital scales is a reset button. Press the tare button after each item you measure on the scale. If you weighed a container, you can fill it now.
4. Set the object you wish to measure on the scale. Place your object in the centre of the scale. If you measured a container first, you can now put the object you wish to measure inside the container. The scale will then calculate the heaviness of your object.
5. Finish weighing the object on the scale. Wait for the scale’s digital display or needle to come to a stop. When it finishes moving, read the number to find out how heavy the object is. Make sure that the weight is in grams. Then, remove your object and hit the tare button again to reset the scale.

Fill in the blanks.

Question 11.

The pencil case has a mass of ___ grams.
Answer:250 grams.
The measuring scale is showing 250 grams.
Explanation:
1. Choose a scale that measures in grams. Make sure the scale can handle the size of objects you plan on weighing. Since a gram is a metric unit of measurement, your scale needs to use the metric system. Scales are available in digital and mechanical models.
2. Weigh an empty container first before putting an item in it. If you plan to measure something you can’t put directly on the scale, weigh the container before putting the item in it.
3. Press the tare button to zero out the scale. The mysterious button labelled “tare” on digital scales is a reset button. Press the tare button after each item you measure on the scale. If you weighed a container, you can fill it now.
4. Set the object you wish to measure on the scale. Place your object in the centre of the scale. If you measured a container first, you can now put the object you wish to measure inside the container. The scale will then calculate the heaviness of your object.
5. Finish weighing the object on the scale. Wait for the scale’s digital display or needle to come to a stop. When it finishes moving, read the number to find out how heavy the object is. Make sure that the weight is in grams. Then, remove your object and hit the tare button again to reset the scale.

Question 12.

The water bottle has a mass of ___ grams.
Answer:250 grams.
The measuring scale is showing 250 grams.
Explanation:
1. Choose a scale that measures in grams. Make sure the scale can handle the size of objects you plan on weighing. Since a gram is a metric unit of measurement, your scale needs to use the metric system. Scales are available in digital and mechanical models.
2. Weigh an empty container first before putting an item in it. If you plan to measure something you can’t put directly on the scale, weigh the container before putting the item in it.
3. Press the tare button to zero out the scale. The mysterious button labelled “tare” on digital scales is a reset button. Press the tare button after each item you measure on the scale. If you weighed a container, you can fill it now.
4. Set the object you wish to measure on the scale. Place your object in the centre of the scale. If you measured a container first, you can now put the object you wish to measure inside the container. The scale will then calculate the heaviness of your object.
5. Finish weighing the object on the scale. Wait for the scale’s digital display or needle to come to a stop. When it finishes moving, read the number to find out how heavy the object is. Make sure that the weight is in grams. Then, remove your object and hit the tare button again to reset the scale.

Fill in the blanks.

Question 13.

The bag of peanuts has a mass of ___ grams.
Answer:170 grams.
The bag of peanuts has a mass of 170 grams.
The measuring scale is showing 170 grams.
Explanation:
1. Choose a scale that measures in grams. Make sure the scale can handle the size of objects you plan on weighing. Since a gram is a metric unit of measurement, your scale needs to use the metric system. Scales are available in digital and mechanical models.
2. Weigh an empty container first before putting an item in it. If you plan to measure something you can’t put directly on the scale, weigh the container before putting the item in it.
3. Press the tare button to zero out the scale. The mysterious button labelled “tare” on digital scales is a reset button. Press the tare button after each item you measure on the scale. If you weighed a container, you can fill it now.
4. Set the object you wish to measure on the scale. Place your object in the centre of the scale. If you measured a container first, you can now put the object you wish to measure inside the container. The scale will then calculate the heaviness of your object.
5. Finish weighing the object on the scale. Wait for the scale’s digital display or needle to come to a stop. When it finishes moving, read the number to find out how heavy the object is. Make sure that the weight is in grams. Then, remove your object and hit the tare button again to reset the scale.

Question 14.

The box of crackers has a mass of ___ grams.
Answer: 370 grams.
The box of crackers has a mass of 370 grams.
The measuring scale is showing 370 grams.
Explanation:
1. Choose a scale that measures in grams. Make sure the scale can handle the size of objects you plan on weighing. Since a gram is a metric unit of measurement, your scale needs to use the metric system. Scales are available in digital and mechanical models.
2. Weigh an empty container first before putting an item in it. If you plan to measure something you can’t put directly on the scale, weigh the container before putting the item in it.
3. Press the tare button to zero out the scale. The mysterious button labelled “tare” on digital scales is a reset button. Press the tare button after each item you measure on the scale. If you weighed a container, you can fill it now.
4. Set the object you wish to measure on the scale. Place your object in the centre of the scale. If you measured a container first, you can now put the object you wish to measure inside the container. The scale will then calculate the heaviness of your object.
5. Finish weighing the object on the scale. Wait for the scale’s digital display or needle to come to a stop. When it finishes moving, read the number to find out how heavy the object is. Make sure that the weight is in grams. Then, remove your object and hit the tare button again to reset the scale.

Fill in the blanks.

Question 15.
The empty bowl has a mass of ___ grams.
Answer: 300 grams.
Already given the mass of empty bowl.

Question 16.
Some marbles are put into the bowl.
The bowl and the marbles have a mass of __ grams
Answer: 480 grams.
The measuring scale is showing 480 grams.
Explanation:
1. Choose a scale that measures in grams. Make sure the scale can handle the size of objects you plan on weighing. Since a gram is a metric unit of measurement, your scale needs to use the metric system. Scales are available in digital and mechanical models.
2. Weigh an empty container first before putting an item in it. If you plan to measure something you can’t put directly on the scale, weigh the container before putting the item in it.
3. Press the tare button to zero out the scale. The mysterious button labelled “tare” on digital scales is a reset button. Press the tare button after each item you measure on the scale. If you weighed a container, you can fill it now.
4. Set the object you wish to measure on the scale. Place your object in the centre of the scale. If you measured a container first, you can now put the object you wish to measure inside the container. The scale will then calculate the heaviness of your object.
5. Finish weighing the object on the scale. Wait for the scale’s digital display or needle to come to a stop. When it finishes moving, read the number to find out how heavy the object is. Make sure that the weight is in grams. Then, remove your object and hit the tare button again to reset the scale.

Question 17.
What is the mass of the marbles? ___ grams
Answer: 180 grams.
Explanation:
The mass of the empty bottle=300 grams.
The total mass of marbles and empty bottle combine is 480 grams.
Now we need to calculate the mass of the marbles. Assume it as X.
Subtract the total mass and mass of the empty bottle.
X=480-300
X=180
Therefore, the mass of marbles is 180 grams.

Practice the problems of Math in Focus Grade 2 Workbook Answer Key Chapter 8 Practice 4 Comparing Masses in Grams to score better marks in the exam.

Math in Focus Grade 2 Chapter 8 Practice 4 Answer Key Comparing Masses in Grams

Find the mass of each vegetable. Then fill in the blanks.

Question 1.
The ___ is the heaviest.
Answer: Pumpkin
The pumpkin is having 750 grams. So it is the heaviest.

Question 2.
The ___ are the lightest.
Answer: peppers.
The mass of peppers is 100 grams which are the lightest.

Question 3.
The pumpkin is ____ grams heavier than the celery.
Answer: 500 grams.
The mass of the pumpkin is 750 grams.
The mass of celery is 250 grams.
The number of more grams the pumpkin is heavier than celery=X
Subtract the mass of pumpkin and mass of celery.
X=750-250
X=500
Therefore, 500 grams more than celery.

Question 4.
The ___ is heavier than the bag of peppers but lighter than the bag of carrots.
Answer: celery.
The mass of peppers=100 grams.
The mass of carrots=250 grams.
we need to calculate the thing which is heavier than peppers and lighter than carrots.
Now observe the masses of vegetables. Compare all the vegetables to each other.
The mass of celery is 200 grams.
It is the only one which is lighter than carrots and heavier than peppers.

Look at the boxes. Then fill in the blanks.

Question 5.
Which is the heaviest? Box ____
Answer: Box C
Explanation:
The mass of box A is 180 g
The mass of box B is 250 g
The mass of box C is 800 g
The mass of box D is 430 g
Now observe which is having the highest mass.
The heaviest box is 800 grams which are box C.

Question 6.
Which is the lightest? Box ___
Answer: Box A.
Explanation:
The mass of box A is 180 g
The mass of box B is 250 g
The mass of box C is 800 g
The mass of box D is 430 g
Now observe which is having the lightest mass.
The lightest box is 180 grams which are a box A.

Write heavier or lighter.

Question 7.
Box B is _____________ than Box D.
Answer: Lighter.
Explanation:
The mass of box B is 250 g
The mass of box D is 430 g
Box B is lesser than box D.
Therefore, box B is lighter than box D.

Question 8.
Box D is ____________ than Box A.
Answer: heavier
Explanation:
The mass of box D is 430 g
The mass of box A is 180 g
Box D is greater than box A.
Therefore, box D is heavier than box A.

Fill in the blanks.

Question 9.
Box C is ___ grams heavier than Box B.
Answer:
The mass of box B is 250 g
The mass of box C is 800 g
To calculate the number of more grams heavier than box B. Assume it as X.
X=800-250
X=550
Therefore, Box C is 550 grams heavier than Box B.

Question 10.
Box A is ___ grams lighter than Box C.
Answer: 620 grams.
Explanation:
The mass of box A is 180 g
The mass of box C is 800 g
To calculate Box A is how much lighter than Box C. Assume it as X
X=800-180
X=620
therefore, Box A is 620 grams lighter than Box C.

Question 11.
Order the boxes from the lightest to the heaviest.

Answer:

Explanation:
The mass of box A is 180 g
The mass of box B is 250 g
The mass of box C is 800 g
The mass of box D is 430 g
It was like an ascending order. It means we have to arrange from lightest to heaviest.

Practice the problems of Math in Focus Grade 3 Workbook Answer Key Chapter 14 Fractions to score better marks in the exam.

Math in Focus Grade 3 Chapter 14 Answer Key Fractions

Put On Your Thinking Cap!

Challenging Practice

Question 1.
Write a fraction with denominator 9. The fraction should be less than \(\frac{1}{2}\).
Answer:
The fraction with denominator 9 and less than 1/2 are 1/9, 2/9, 3/9, 4/9.

Mark the number lines to help you.

Question 2.

Which is greater, \(\frac{3}{7}\) or \(\frac{2}{3}\)?
__________ > __________
Answer:

2/3 > 3/7
Explanation:
The fraction 2/3 is greater than 3/7.

Question 3.

Which is less, \(\frac{1}{8}\) or \(\frac{2}{5}\)?
__________ < __________
Answer:

1/8 < 2/5
Explanation:
The fraction 1/8 is lees than 2/5.

Question 4.

Order \(\frac{1}{7}, \frac{3}{5}, \frac{3}{8}\), and \(\frac{8}{9}\) from least to greatest.

Answer:


Explanation:
The fractions from least to greatest are 1/7, 3/8, 3/5, 8/9.

Put On Your Thinking Cap!

Problem Solving

Question 1.
Shade to show a fraction greater than \(\frac{1}{4}\) but less than \(\frac{1}{2}\).

Answer:

Explanation:
In the above image we can observe the shaded part is greater than 1/4 and less than 1/2.
Question 2.
Sam wants to shade \(\frac{2}{3}\) of the figure. He has already shaded 4 squares. How many more squares must he shade? Help him shade.

Answer:

Explanation:
Sam wants to shade 2/3 of the figure. He has already shaded 4 squares. He shaded 4 more squares.

Question 3.
Shade the figure to show each fraction below. Use a different color for shading each fraction.
\(\frac{1}{3}, \frac{1}{4}, \frac{1}{12}\)

What fraction of the figure is unshaded?
___________ of the figure is unshaded.
Answer:

Explanation:
1/3 of 12 = 4
1/4 of 12 = 3
1/12 of 12 = 1
4/12 of the figure is unshaded.

Practice the problems of Math in Focus Grade 3 Workbook Answer Key Chapter 14 Practice 2 Understanding Equivalent Fractions to score better marks in the exam.

Math in Focus Grade 3 Chapter 14 Practice 2 Answer Key Understanding Equivalent Fractions

Example

Shade the part(s) to show fractions equivalent to \(\frac{1}{4}\). Then write the fractions.

Question 1.
Shade the part(s) to show fractions equivalent to \(\frac{1}{5}\). Then write the fractions.

Answer:

Explanation:
In the above diagram we can observe 3 images.
In first image we can observe one – fifth part is shaded.
The given fraction is 1/5. Multiply numerator and denominator with 2. The equivalent fraction for 1/5 is 2/10. So, 2/10 part is shaded in second image.
The given fraction is 1/5. Multiply numerator and denominator with 3. The equivalent fraction for 1/5 is 3/15. So, 3/15 part is shaded in third image.

Question 2.
Divide the second bar into 10 equal parts. Shade the part(s) to show a fraction equivalent to \(\frac{2}{5}\). Write the fraction.

Answer:

Explanation:
In the above image we can observe two bars.
The first bar is divided into 5 equal parts. In the first bar 2/5 part is shaded.
We have to divide second bar into 10 equal parts. The equivalent fraction for 2/5 is 4/10. In second bar 4/10 part is shaded with red color.

Question 3.
Divide the second bar into 12 equal parts. Shade the part(s) to show a fraction equivalent to \(\frac{5}{6}\). Write the fraction.

Answer:

Explanation:
In the above image we can observe two bars.
The first bar is divided into 6 equal parts. In the first bar 5/6 part is shaded.
We have to divide second bar into 12 equal parts. The equivalent fraction for 5/6 is 10/12. In second bar 10/12 part is shaded with red color.

Question 4.
Find the missing numerator or denominator.

Answer:

Explanation:
In the above diagram we can observe four images.
In first image 3/4 part is shaded.
In second image 6/8 part is shaded. The missing denominator is 8.
In third image 9/12 part is shaded. The missing numerator is 9.
In fourth image 12/16 part is shaded. The missing denominator is 16.

Use number lines to find equivalent fractions.

Example

Question 5.

The equivalent fractions are __________, _________, and __________.
Answer:
The equivalent fractions are 3/4, 6/8, and 9/12.
Explanation:
In the above image we can observe three number lines.
In first number line we can observe 3/4. In the second number line we can observe 6/8. In third number line we can observe 9/12. The equivalent fractions are 3/4, 6/8, and 9/12.
Fill in the missing tractions on the number lines Then use the number lines to find the missing numerators and denominators.

Question 6.

Answer:

Explanation:
In the above image we can observe three number lines.
In first number line we can observe some fractions are missing. The missing fractions are 2/5 and 3/5.
In second number line also we can observe some fractions are missing. The missing fractions are 2/10, 5/10 and 8/10.
In third number line also we can observe some fractions are missing. The missing fractions are 3/15, 6/15, 8/15, 11/15 and 13/15.

Question 7.

Answer:

Explanation:
In first number line we can observe 2/5. In second number line we can observe 4/10 exactly below to the fraction 2/5. The equivalent fraction for 2/5 is 4/10.The missing numerator is 4.

Question 8.

Answer:

Explanation:
In first number line we can observe 3/5. In third number line we can observe 9/15 exactly below to the fraction 3/5. The equivalent fraction for 3/5 is 9/15.The missing numerator is 3. The missing denominator is 15.

Question 9.

Answer:

Explanation:
In third number line we can observe 3/15. In second number line we can observe 2/10 exactly above to the fraction 3/15. The missing denominator is 10.
In first number line we can observe 1/5 exactly above to the fraction 2/10. The equivalent fractions for 3/15 is 2/10 and 1/5.The missing numerator is 1. The missing denominator is 5.

Question 10.

Answer:

Explanation:
In first number line we can observe 3/5. In second number line we can observe 6/10 exactly below to the fraction 3/5. The missing numerator is 6.
In third number line we can observe 9/15 exactly below to the fraction 6/10. The equivalent fractions for 3/5 is 6/10 and 9/15.The missing numerator is 9. The missing denominator is 15.

Practice the problems of Math in Focus Grade 3 Workbook Answer Key Chapter 10 Practice 4 Subtraction to score better marks in the exam.

Math in Focus Grade 3 Chapter 10 Practice 4 Answer Key Subtraction

Subtract. Color the answers on the picture.

Question 1.
$6.35 – $6.00 = $___________
Answer:
$6.35 – $6.00 = $0.35
Explanation:
Perform subtraction operation on above two numbers. Subtract $6.00 from $6.35 the difference is $0.35.

Question 2.
$8.35 – $5.00 = $___________
Answer:
$8.35 – $5.00 = $3.35
Explanation:
Perform subtraction operation on above two numbers. Subtract $5.00 from $8.35 the difference is $3.35.

Question 3.
$98.20 – $8.00 = $___________
Answer:
$98.20 – $8.00 = $90.20
Explanation:
Perform subtraction operation on above two numbers. Subtract $8.00 from $98.20 the difference is $90.20.

Question 4.
$76.65 – $12.00 = $___________
Answer:
$76.65 – $12.00 = $64.65
Explanation:
Perform subtraction operation on above two numbers. Subtract $12.00 from $76.65 the difference is $64.65.

Question 5.
$26.40 – $9.00 = $___________
Answer:
$26.40 – $9.00 = $17.40
Explanation:
Perform subtraction operation on above two numbers. Subtract $9.00 from $26.40 the difference is $17.40.

Question 6.
$45.60 – $39.00 = $___________
Answer:
$45.60 – $39.00 = $6.60
Explanation:
Perform subtraction operation on above two numbers. Subtract $39.00 from $45.60 the difference is $6.60.

Question 7.
$5.25 – $0.05 = $___________
Answer:
$5.25 – $0.05 = $5.20
Explanation:
Perform subtraction operation on above two numbers. Subtract $0.05 from $5.25 the difference is $5.20.

Question 8.
$1.45 – $0.35 = $___________
Answer:
$1.45 – $0.35 = $1.10
Explanation:
Perform subtraction operation on above two numbers. Subtract $0.35 from $1.45 the difference is $1.10.

Question 9.
$14.90 – $0.70 = $___________
Answer:
$14.90 – $0.70 = $14.20
Explanation:
Perform subtraction operation on above two numbers. Subtract $0.70 from $14.90 the difference is $14.20.

Question 10.
$20.75 – $0.30 = $___________
Answer:
$20.75 – $0.30 = $20.45
Explanation:
Perform subtraction operation on above two numbers. Subtract $0.30 from $20.75 the difference is $20.45.

Question 11.
$15.60 – $0.35 = $___________
Answer:
$15.60 – $0.35 = $15.25
Explanation:
Perform subtraction operation on above two numbers. Subtract $0.35 from $15.60 the difference is $15.25.

Question 12.
$26.70 – $0.45 = $___________
Answer:
$26.70 – $0.45 = $26.25
Explanation:
Perform subtraction operation on above two numbers. Subtract $0.45 from $26.70 the difference is $26.25.

Answer:

Explanation:
The above answers are colored on the picture.

Subtract.

Question 13.

$3 – $1 =$___________
20¢ – 15¢ = ___________¢
$___________ + ___________¢ = $___________
Answer:

$3 – $1 = $2
20¢ – 15¢ = 5¢
$2 + 5¢ = $2.05
Explanation:
In the above image we can observe that $3.20 is divided into $3 and 20¢. The $1.15 is divided into $1 and 15¢.
Subtract the dollars.
$3 – $1 = $2
Subtract the cents.
20¢ – 15¢ = 5¢
Add the cents to the dollars.
$2 + 5¢ = $2.05

Question 14.

$___________ – $___________ = $___________
___________¢ – ___________¢ = ___________¢
$___________ + ___________¢ = $___________
Answer:

$10 – $2 = $8
50¢ – 50¢ = 0¢
$8 + 0¢ = $8.00
Explanation:
In the above image we can observe that $10.50 is divided into $10 and 50¢. The $2.50 is divided into $2 and 50¢.
Subtract the dollars.
$10 – $2 = $8
Subtract the cents.
50¢ – 50¢ = 0¢
Add the cents to the dollars.
$8 + 0¢ = $8.00

Question 15.

$___________ – $___________ = $___________
___________¢ – ___________¢ = ___________¢
$___________ + ___________¢ = $___________
Answer:

$65 – $3 = $62
65¢ – 5¢ =60¢
$62 + 60¢ = $62.60
Explanation:
In the above image we can observe that $65.65 is divided into $65 and 65¢. The $3.05 is divided into $3 and 5¢.
Subtract the dollars.
$65 – $3 = $62
Subtract the cents.
65¢ – 5¢ =60¢
Add the cents to the dollars.
$62 + 60¢ = $62.60

Question 16.

$___________ – $___________ = $___________
___________¢ – ___________¢ = ___________¢
$___________ + ___________¢ = $___________
Answer:

$83 – $12 = $71
55¢ – 45¢ = 10¢
$71 + 10¢ = $71.10
Explanation:
In the above image we can observe that $83.55 is divided into $83 and 55¢. The $12.45 is divided into $12 and 45¢.
Subtract the dollars.
$83 – $12 = $71
Subtract the cents.
55¢ – 45¢ = 10¢
Add the cents to the dollars.
$71 + 10¢ = $71.10

Practice the problems of Math in Focus Grade 3 Workbook Answer Key Chapter 10 Practice 2 Addition to score better marks in the exam.

Math in Focus Grade 3 Chapter 10 Practice 2 Answer Key Addition

Complete each number bond. Then add.

Example

Question 1.

Answer:

Explanation:
To make $6.95 to the nearest integer we have to add required ¢ to the $6.95.
A number bond is a simple addition of two numbers that add up to give the sum. Add these two numbers $6.95 and 5¢ the sum is $7.
The number $9.05 is divided into two parts as $9 and 5¢.
In place of $9.05 and $6.95 we have to use $9 and $7.
Add $9 with $7 the sum is $16.

Question 2.

Answer:

Explanation:
To make $11.85 to the nearest integer we have to add required ¢ to the $11.85.
A number bond is a simple addition of two numbers that add up to give the sum. Add these two numbers $11.85 and 15¢ the sum is $12.
The number $70.35 is divided into two parts as $70.20 and 15¢.
In place of $70.35 and $11.85 we have to use $70.20 and $12.
Add $70.20 with $12 the sum is $82.20.

Question 3.

Answer:

Explanation:
To make $10.75 to the nearest integer we have to add required ¢ to the $10.75.
A number bond is a simple addition of two numbers that add up to give the sum. Add these two numbers $10.75 and 25¢ the sum is $11.
The number $12.40 is divided into two parts as $12.150 and 25¢.
In place of $12.40 and $10.75 we have to use $12.15 and $11.
Add $12.15 with $11 the sum is $23.15.

Complete each number bond. Then add.

Example

Question 4.

Answer:

Explanation:
To make $0.95 to the nearest integer we have to add required ¢ to the $0.95.
A number bond is a simple addition of two numbers that add up to give the sum. Add these two numbers 95¢ and 5¢ the sum is $1.
In place of $0.95 we have to use $1. Add $4.75 with $1 the sum is $5.75.
The ¢ which are added to the given number $0.95 to make nearest integer are subtracted from the above sum.
Subtract 5¢ from $5.75 the difference is $5.70.
By adding $4.75 with $0.95 the sum is also $5.70.

Question 5.

Answer:

Explanation:
To make $0.80 to the nearest integer we have to add required ¢ to the $0.80.
A number bond is a simple addition of two numbers that add up to give the sum. Add these two numbers 80¢ and 20¢ the sum is $1.
In place of $0.80 we have to use $1. Add $16.40 with $1 the sum is $17.40.
The ¢ which are added to the given number $0.80 to make nearest integer are subtracted from the above sum.
Subtract 20¢ from $17.40 the difference is $17.20.
By adding $16.40 with $0.80 the sum is also $17.20.

Question 6.

Answer:

Explanation:
To make $0.75 to the nearest integer we have to add required ¢ to the $0.75.
A number bond is a simple addition of two numbers that add up to give the sum. Add these two numbers 75¢ and 25¢ the sum is $1.
In place of $0.75 we have to use $1. Add $43.55 with $1 the sum is $44.55.
The ¢ which are added to the given number $0.75 to make nearest integer are subtracted from the above sum.
Subtract 25¢ from $44.55 the difference is $44.30.
By adding $43.55 with $0.75 the sum is also $44.30.

Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 7 Practice 3 Real-World Problems: Ratios to score better marks in the exam.

Math in Focus Grade 5 Chapter 7 Practice 3 Answer Key Real-World Problems: Ratios

Solve. Show your work.

Question 1.
Ms. Grande bought 24 apples and 1 8 oranges for a party after a class play. Find the ratio of the number of apples to the total pieces of fruit Ms. Grande bought.
Answer:
24 : 42 = 4 : 7
Explanation:
Given,
Ms. Grande bought 24 apples and 18 oranges for a party,
Total number of fruits we get,
By adding 24 with 18 we get 42,
The ratio of the number of apples to the total number of number of fruits is 24 : 42,
To get into simplest form 24 and 42 can be divisible by 6 we get 4 : 7

Question 2.
There are 44 chicken and fish filets altogether in a freezer. There are 1 2 chicken filets. What is the ratio of the number of chicken filets to the number of fish filets in the freezer?
Answer:12 : 32 = 3 : 8
Explanation:
Given,
There are 44 chicken and fish fillets altogether in a freezer,
There are 12 chicken filets,
By subtracting 12 from 44 we get 32,
So there are 32 fish filets,
The ratio of number of chicken filets to the number of fish filets in the freezer is 12 : 32.
To get into simplest form 12 and 32 can be divisible by 4 we get 3 : 8.

Solve. Show your work.

Question 3.
There were 1 2 boys and 1 8 girls in a class. Then, 3 more boys joined the class and 2 girls left. What is the ratio of the number of boys to the number of girls in the class now?
Answer:15 : 16
Explanation:
Given,
There were 12 boys and 3 more boys joined the class, by adding 12 with 3 we get 15,
There were 18 girls and 2 girls left, by subtracting 2 from 18 we get 16,
The ratio of the number of boys to the number of girls in the class is 15 : 16

Question 4.
Monica had $42 and Naomi had $18 at first. Monica then gave $6 to Naomi. What is the ratio of the amount of money Monica has to the amount of money Naomi has in the end?
Answer:36 : 24 = 3 : 2
Explanation:
Given,
Monica had $42 and gave $6 to Naomi, by subtracting 6 from 42 we get 36
Naomi had $18 and by adding 18 with 6 we get 24,
The ratio of the amount of money Monica has to the amount of money Naomi is 36 : 24,
To get into simplest form 36 and 24 can be divisible by 12 we get 3 : 2.

Solve. Show your work.

Question 5.
In a competition, the ratio of the number of tickets Mark collected to the number of tickets Julia collected is 4 : 3. Julia collected 36 tickets. How many tickets did they collect altogether?
Answer:84 tickets
Explanation:
Given,
The ratio of number of tickets Mark collected to the number of tickets Julia collected is 4 : 3,
Julia collected is 36 tickets,
1 unit is equal to 12 tickets,
So 3 units is equal to 36 tickets which Julia has and 4 units is equal to 48 tickets which Mark has,
By adding 48 with 36 we get 84,
So Mark and Julia collected 84 tickets altogether.

Question 6.
The ratio of the number of stamps Calvin has to the number of stamps Roger has is 7 : 3. Roger has 18 stamps. How many stamps do they have altogether?
Answer:60 stamps
Explanation:
Given,
The ratio of the number of stamps Calvin to the number of stamps Roger is 7 : 3,
Roger has 18 stamps,
1 unit is equal to 6 stamps,
So 3 units is equal to 18 tickets which Roger has and 7 units is equal to 42 tickets which Calvin has,
By adding 42 with 18 we get 60,
So Calvin and Roger have 60 tickets altogether.

Solve. Show your work.

Question 7.
On a Saturday, the ratio of the amount of water used by Household A to the amount of water used by Household B was 13:5. Household A used 260 gallons of water for that day. Find the total amount of water used by the two households on that Saturday.
Answer: 360 Gallons
Explanation:
Given,
The ratio of the amount of water used by Household A to the amount of water used by Household B was 13 : 5,
Household A used 260 gallons of water,
1 unit is equal to 20 gallons,
So 13 units is equal to 260 gallons of water used by Household A and 5 units is equal to 100 gallons of water used by Household B,
By adding 260 with 100 we get 360,
So the total amount of water used by two households is 360 gallons of water.

Question 8.
A cleaning solution and water are mixed in the ratio 4 : 15. The amount of water in the mixture is 1,200 milliliters. What is the total volume of the mixture?
Answer:1520 milliliters
Explanation:
Given,
A cleaning solution and water are mixed in the ratio is 4 : 5,
The amount of water in the mixture is 1200 milliliters,
1 unit is equal to 80,
So 4 units is equal to 320 milliliters and 15 units is equal to 1200 milliliters,
By adding 320 with 1200 we get 1520,
So the total volume of the mixture is 1520 milliliters.

Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 7 Ratio to score better marks in the exam.

Math in Focus Grade 5 Chapter 7 Answer Key Ratio

Math Journal

Andy and Clara each drew a model to solve this word problem.

Mr. Marcos bought chicken and beef from the butcher and fish from the fish market for a barbecue. The ratio of the weight of chicken to the weight of beef to the weight of fish he bought was 3 : 1 : 5. He bought 10 pounds of fish.
What was the total weight of meat he bought from the butcher?

Both models however are incorrect.
Explain the mistakes that they each made.

Draw the correct model. Then solve the problem.

Answer:
8 pounds
Explanation:
Given,
Ratio of the weight of chicken to the weight of beef to the weight of fish is = 3 : 1 : 5
Mr. Marcos bought fish of = 10 pounds,
Total ratio = 3 + 1 + 5 = 9
Total pounds of chicken, beef and fish bought = X
Equation for pounds of fish bought = 5 / 9 x X = 10
=> X = 10 x 9 / 5
=> X = 2 x 9
=> X = 18
Pounds of chicken bought = 3 / 9 x 18 = 6 pounds
Pounds of beef bought = 1 / 9 x 18 = 2 pounds
Total weight of meat bought = 6 + 2 = 8 pounds
Therefore, Total weight of meat bought is 8 pounds.

Put on Your Thinking cap!

Challenging Practice

Question 1.
A small square with an area of 16 square centimeters is cut from a larger square with sides that measure 6 centimeters. Find the ratio of the area of the small square to the area of the remaining part of the larger square.

Answer:

Explanation:
Given,
Area of small square = 16 square centimeters
Side of larger square = 6 centimeters
Area of small sqaure : Area of remaining part
16 square centimeters : ?
Area of remaining part = Area of large square – Area of small square
= 6 x 6 – 16
= 36 – 16
= 20 square centimeters
Ratio = area of small square : area of remaining part
= 16 : 20
= 4 : 5

Question 2.
The perimeters of two squares are in the ratio 2 : 4. The perimeter of the larger square is 16 centimeters.

a. What is the perimeter of the smaller square?
Answer: The perimeter of smaller square is 8 cm
Explanation:
Given,
The ratio of two squares are 2 : 4,
The perimeter of larger square is 16 centimeters,
By multiplying 2 and 4 with 4 we get the ratio 8 : 16,
Therefore, the perimeter of smaller square is 8 cm

b. What is the length of one side of the smaller square?
Answer: The length of one side of the smaller sqaure is 2 cm

Put on Your Thinking Cap!

Problem Solving

Solve.

Question 1.
The ratio of the number of plants Trish bought to the number of plants Sarah bought is 2 : 5. Trish bought 16 plants.
a. What is the total number of plants Trish and Sarah bought altogether?
Answer: The total number of plants Trish and Sarah bought are 56 plants
Explanation:
Given,
Ratio of plants Trish and Sarah bought are = 2 : 5,
Trish bought number of plants = 16,
By multiplying both the ratios 2 : 5 with 8, then we get 16 : 40,
By adding 16 with 40 we get 56,
Therefore, the total number of plants Trish and Sarah bought are 56 plants.

b. If each plant cost $1 7, what is the total cost of the plants Trish and Sarah bought?
Answer: The total cost of the plants Trish and Sarah bought is $952.
Explanation:
Given,
Number of plants Trish and Sarah bought are = 56,
Each plant costs = $17,
By multiplying 56 with 17 we get the sum as 952,
Therefore, the total cost of 56 plants is $952.

Question 2.
The ratio of the number of boys to the number of girls at a town fair is 5 : 8 There are 60 boys at the fair.

a. What is the total number of boys and girls at the fair?
Answer:The total number of boys and girls at the fair is 156.
Explanation:
Given,
The ratio of number of boys to the number of girls = 5 : 8,
The number of boys at the fair = 60,
Total number of boys and girls = 5 : 8
By multiplying both 5 and 8 with 12 we get the ratio as 60 : 96,
Therefore, there are 60 boys and 96 girls,
By adding 60 with 96 we get the sum as 156.

b. The admission fee for each child is $3. Find the total admission fees for the boys and girls.
Answer: The total admission fees for the boys and girls is $468.
Explanation:
Given,
Number of boys and girls = 156,
Admission fee for each child is = $3,
By multiplying 156 with 3 we get the sum as 468,
Therefore, the total admission fees for the boys and girls is $468.

This handy Math in Focus Grade 6 Workbook Answer Key Chapter 13 Lesson 13.2 Dot Plots detailed solutions for the textbook questions.

Math in Focus Grade 6 Course 1 B Chapter 13 Lesson 13.2 Answer Key Dot Plots

Math in Focus Grade 6 Chapter 13 Lesson 13.2 Guided Practice Answer Key

Math in Focus Course 1B Practice 13.2 Answer Key

Question 1.
A group of 15 students was asked how many times they have traveled on a plane. The results are recorded in the table.

Answer:

Explanation:
A dot plot is a graphical display of data using dots.
In a dot plot, data points (dots) are stacked in a column over a category.
The height of the column represents the frequency of observations in a given category.
These graphs stack dots along the horizontal X-axis to represent the frequencies of  values.
More dots indicate greater frequency.
Each dot represents a set number of observations.
Title the dot plot based on the problem.

Question 2.
The results of the high jumps at a track meet are recorded in the table.

Answer:

Explanation:
A dot plot is a graphical display of data using dots.
In a dot plot, data points (dots) are stacked in a column over a category.
The height of the column represents the frequency of observations in a given category.
These graphs stack dots along the horizontal X-axis to represent the frequencies of  values.
More dots indicate greater frequency.
Each dot represents a set number of observations.
Title the dot plot based on the problem.

Describe the data.

Question 3.
The weekly savings (in dollars) of 10 students in a class are shown in the dot plot. Briefly describe the distribution of the weekly savings of the students.

Answer:

Explanation:
Given that, the weekly savings (in dollars) of 10 students in a class are shown in the dot plot.
So, there are 10 students in the class as per the dots on the dot plot.
The distribution of the weekly savings of the students are:
$0 weekly savings = 0 students
$1 weekly savings = 1 student
$2 weekly savings = 2 students
$3 weekly savings = 2 students
$4 weekly savings = 4 students
$5 weekly savings = 1 student

Question 4.
The number of points scored by 12 members of a volleyball team in a game is shown in the dot plot. Briefly describe the number of points scored by the group of players.

Answer:

Explanation:
Given that, The number of points scored by 12 members of a volleyball team in a game is shown in the above dot plot.
So, there are 12 members of a volleyball team in a game.
The different players scored different points are listed on the above table.

Hands-On Activity

CONSTRUCTING A DISTRIBUTION

Materials:

• 2 number cubes, numbered 1-6
• blank table

Work in pairs.
Step 1: Toss two number cubes. Record the difference between the two numbers in a tally chart.
Step 2: Repeat 20 times and add your results to another group’s results. Record the results for 40 tosses in a copy of the table below.

Step 3: Represent the data with a dot plot.
Step 4: Repeat Step 1 to Step 3, but record the SUM of the two numbers each time.

Answer:
Step 1: Toss two number cubes. Record the difference between the two numbers in a tally chart.

Step 2: Repeat 20 times and add your results to another group’s results.

Record the results for 40 tosses in a copy of the table below.

the results for 40 tosses in a copy of the table below.

Represent the data with a dot plot.

a) What is the least sum you can get?
Answer:
2

Explanation:
Toss two number cubes and record the difference between the two numbers in a tally chart,
ass shown above.
Repeat 20 times and add results to another group’s results.
Record the results for 40 tosses.
So, the lest sum we get after tossing is only 2 times of 4 number toss recorded after 40 experiments.

b) What is the greatest sum you can get?
Answer:
11

Explanation:
Toss two number cubes and record the difference between the two numbers in a tally chart,
ass shown above.
Repeat 20 times and add results to another group’s results.
Record the results for 40 tosses.
The difference between the two cubes is 0 and 2 are 11  times 4 number toss recorded after 40 experiments.

Math journal
a) Describe the distribution of the differences.
Answer:
The Sampling Distribution of the Difference between two Means shows the distribution of means of two samples drawn from the two independent populations, such that the difference between the population means can possibly be evaluated by the difference between the sample means.

Explanation:
To find the distribution of the differences between two numbers,
subtract the number with the smallest value from the number with the largest value.
The product of this sum is the difference between the two numbers.
for example; the difference between 45 and 100 is 55.

b) Describe the distribution of the sums.
Answer:
We can form new distributions by combining random variables.
If we know the mean and standard deviation of the original distributions,
we can use that information to find the mean and standard deviation of the resulting distribution.

Explanation:
So, the normal distribution has a mean equal to the original mean multiplied by the sample size and a standard deviation.

c) Discuss with your partner why one distribution is skewed, and the other is symmetric (or nearly so). Why are the shapes of the two distributions different?
Answer:
In a symmetrical distribution the two sides of the distribution are a mirror image of each other.

Explanation:
A distribution of data item values may be symmetrical or asymmetrical.
Two common examples of symmetry and asymmetry are the normal distribution and the skewed distribution.
In a symmetrical distribution the two sides of the distribution are a mirror image of each other.

Math in Focus Course 1B Practice 13.2 Answer Key

Represent each set of data with a dot plot.

Question 1.
The years of service for each of the 18 employees in a company are as follows:

Answer:

Explanation:
A dot plot is a graphical display of data using dots.
In a dot plot, data points (dots) are stacked in a column over a category.
The height of the column represents the frequency of observations in a given category.
These graphs stack dots along the horizontal X-axis to represent the frequencies of  values.
More dots indicate greater frequency.
Each dot represents a set number of observations.
Title the dot plot based on the problem.
Dot plot drawn with the data given in the table,
as years of service for each of the 18 employees in a company.
Each data is one employee, there are total 18 employees.

Question 2.
A group of 24 students was asked how many states they have visited. The results are recorded in the table.

Answer:

Explanation:
A dot plot is a graphical display of data using dots.
In a dot plot, data points (dots) are stacked in a column over a category.
The height of the column represents the frequency of observations in a given category.
These graphs stack dots along the horizontal X-axis to represent the frequencies of  values.
More dots indicate greater frequency.
Each dot represents a set number of observations.
Title the dot plot based on the problem.
Dot plot drawn with the data given in the table,
a group of 24 students was asked how many states they have visited.

A group of teens was asked to indicate how many pairs of shoes they have in their closet. The results are shown in the dot plot. Use the dot plot to answer questions 3 to 5.

Question 3.
How many data values are there?
Answer:
2 data values.

Explanation:
Number of pairs of shoes and Number of teens.

Question 4.
What conclusions can you draw with regard to the number of pairs of shoes the teens have?
Answer:
More number of teens have 2 pairs of shoes.

Explanation:
As per the dot plot more dots or more teens are marked in orange who consists 2 pairs of shoes.
The conclusion is more number of teens have 2 pairs of shoes.

Question 5.
What percent of the teens indicated 3 pairs of shoes in their closet?
Answer:
25%

Explanation:
Total number of teens are 20.
The teens who indicated 3 pairs of shoes are 5.
5/20 = 0.25
0.25 X 100 =25%

The dot plot shows the number of weeks each movie that was number 1 at the box office during one year stayed in the number 1 position. Use the dot plot to answer questions 6 and 7.

Question 6.
How many movies are represented by the dots altogether?
Answer:
20 movies.

Explanation:
In the above dot plot, total 20 dots present,
it means 20 movies are represented by the dots altogether.

Question 7.
Give a reason why more dots are above the numbers 1 to 3 than above the numbers 4 and 5 on the horizontal axis.
Answer:
More dots on plot shows the number of weeks each movie that was number 1 at the box office during one year stayed in the number 1 position between the numbers 1 to 3 than above the numbers 4 and 5 on the horizontal axis.

Explanation:
A dot plot is a graphical display of data using dots.
In a dot plot, data points (dots) are stacked in a column over a category.
The height of the column represents the frequency of observations in a given category.
These graphs stack dots along the horizontal X-axis to represent the frequencies of  values.
More dots indicate greater frequency.
Each dot represents a set number of observations.
Title the dot plot based on the problem.

Copy and complete the dot plot. Use the dot plot to answer each question.

Question 8.
The incomplete dot plot shows the result of a survey in which each student was asked how many dimes were in their pockets or wallets. The results for “4 dimes” are not shown. Each dot represents one student. It is known that 12.5% of the students had one dime.

a) Find the number of students surveyed. Then complete the dot plot.
Answer:
32 students were surveyed.
So, dots for 4 dimes is 3.

Explanation:
let x be the number of students surveyed,
If 12.5% of the students had one dime,
then, 0.125x = students had one dime.
From the dot plot, 4 students had one dime.
So, 0.125x = 4
Dividing both sides by 0.125 gives,
x= 4/0.125
x = 32
Therefore 32 students were surveyed.
Counting the total number of dots in the incomplete dot plot gives:
2 + 4 + 8 + 9 + 4 + 2 = 29
Hence there must be 32 dots in all to represent all 32 of the students.
Then there should be
32 − 29 = 3
dots for “4 dimes” are 3.

b) What percent of the students had either 0 or 6 dimes?
Answer:
6.25% students have 0 or 6 dimes in their pocket.

Explanation:
Total dots = 32
percent of the students had either 0 or 6 dimes,
2 students have either 0 or 6 dimes in their pocket.
2/32 = 0.625
0.625 x 100 = 6.25%

c) What percent of the students had either 1 or 5 dimes?
Answer:
12.5% students have 1 or 5 dimes in their pocket.

Explanation:
Total dots = 32
percent of the students had either 1 or 5 dimes,
4 students have either 1 or 5 dimes in their pocket.
4/32 = 0.125
0.125 x 100 = 12.5%

d) Briefly describe the distribution of the data.

Answer:
The distribution of the data given in the dot plot is number of students and the number of dimes in their pocket.

Explanation:
The distribution of the data given in the dot plot is number of students and the number of dimes in their pocket.
2 students have no dimes in their pocket.
4 students have 1 dime in their pocket.
8 students have 2 dimes in their pocket.
9 students have 3 dimes in their pocket.
4 students have 4 dimes in their pocket.
5 students have 5 dimes in their pocket.
2 students have 6 dimes in their pocket.