Hillary

Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 9 Multiplying and Dividing Decimals to score better marks in the exam.

Math in Focus Grade 5 Chapter 9 Answer Key Multiplying and Dividing Decimals

Math Journal

Solve. Show your work.

Question 1.
James has a square piece of paper. He wants to cut it into 20 strips of equal width. He says This piece of paper is about 48 centimeters wide.’ How can he find out the width of each strip without measuring? Is this width accurate?
Answer:
2.4 centimeter wide.
Explanation:
By dividing the 48 cm in to 20 equal strips of 2.4cm
\(\frac{48}{20}\) = 2.4

Is this width accurate?
Yes
Explanation:
The strip is equally divided without leaving any remainder.
\(\frac{48}{20}\) = 2.4 centimeter wide

Question 2.
James takes a ruler and measures the width of the piece of paper. He finds that the actual width is 48.8 centimeters. Find the width of each strip. How can you check if your answer is reasonable?
Answer:
2.44 cenimetres
Explanation:
The actual width is 48.8 centimeters
and it is cut in to 20 strips of equal pieces
\(\frac{48.8}{20}\) = 2.44 cm

Put on Your Thinking!

Challenging Practice

Solve. Show your work.

Question 1.
A plumber has two pipes. One pipe is 7 times as long as the other pipe. He cuts 2.2 meters from the longer pipe. The remaining length of this pipe is 3 times that of the shorter pipe. Find the length of the shorter pipe in meters.
Answer:
0.55 meters short.
Explanation:
One pipe is of length x
Other pipe length is 7x
7x – 2.2 =3x
7x – 3x = 2.2
4x = 2.2
x= 2.2
\(\frac{2.2}{4}\) = 0.55m

Question 2.
At a farmer’s market, 5 pounds of strawberries cost $21.50. At a supermarket, 3 pounds of the same quality strawberries cost $15.75.

a. Which is a better buy?
Answer:
At a farmer’s market is a better buy.
Explanation:
1 pound of strawberries cost $4.3
At farmer market,
5 pounds of strawberries cost $21.50
for 1 pound= \(\frac{21.50}{5}\) = $ 4.3
At supermarket
3 pounds of strawberries cost $15.75
for 1 pound= \(\frac{15.75}{3}\) = $ 5.25

b. How much can you save by buying 20 pounds of the strawberries that are the better buy?
Answer: $19
Explanation:
The difference between the farmer’s market cost and the supermarket cost is
$5.25 – $4.3 = $0.95 for one pound of strawberries
20 x $0.95 = $19
$19 save by buying 20 pounds of the strawberries that are the better buy

Put On Your Thinking!

Problem Solving

Solve. Show your work.

Question 1.
Sam buys 10 oranges and 11 apples for $10.05. The total cost of 1 orange and 1 apple is $0.94. How much does an apple cost?
Answer: $5.17
Explanation:
Cost of 1 orange and 1 apple is $0.94
\(\frac{0.94}{2}\) = $ 0.47
an apple cost = 11 * $0.47= $5.17

Question 2.
A bucket filled with sand has a mass of 11.15 kilograms. When it is filled with water, the mass is 5.95 kilograms. The mass of the sand is twice that of the water. Find the mass of the bucket in grams.
Answer: 400 grams
Explanation:
Mass of bucket filled with sand is 11.5 kg
Mass of bucket filled with water is 5.95 kg
It is given that the mass of sand is twice that of the water.
So if mass of water is x kg, then mass of sand is 2x kg.
Let the mass of bucket be y kg, then as per given condition we get,  
 2x+y=11.5    ....(1)     
x+ y=5.95    ..….(2)
Subtract (2)  from (1)   
 2x+y=11.5      x+ y=5.95    −   −    −               x=5.55
Put this value in (2) to get,   
5.55+y=5.95        y=5.95−5.55        y=0.4
So the mass of bucket in grams is     0.4×1000=400 grams.

Solve. Show your work.

Question 3.
The total capacity of 6 pitchers and 12 glasses is 21 liters. The capacity of a pitcher is 5 times that of a glass. Find the capacity of each glass. Give your answer in liters.
Answer:
The capacity of each glass is 0.5 liters.
Explanation:
one picture = 5 glass
Total capacity = 6 pitchers + 12 glasses = 21 liters
= 30 glasses + 12 glasses = 21 liters
= 42 glasses = 21 liters
So, 21/42 = 0.5 liters.

Solve. Show your work.

Question 4.
Dahlia has just enough money to buy either 6 pears and 20 oranges or 12 oranges and 11 pears. A pear costs $0.80. How much does an orange cost?
Answer:
Orange cost is $0.5
Explanation:
let Pear is p and Orange is q
6p + 20q = 11p + 12q
11p – 6p = 20q – 12q
5p = 8q
q = 5p/8
q =  5 x 0.80 / 8
q = $0.50

Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 10 Practice 1 Percent to score better marks in the exam.

Math in Focus Grade 5 Chapter 10 Practice 1 Answer Key Percent

Each large square is divided into 100 parts. Fill in the blanks to describe each large square.

Question 1.

___ out of 100 equal parts are shaded.
___ % of the large square is shaded.
___ out of 100 equal parts are not shaded.
____ % of the large square is not shaded.
Answer:
46 out of 100 equal parts are shaded.
46 % of the large square is shaded.
54 out of 100 equal parts are not shaded.
54 % of the large square is not shaded.
Explanation:
Each large scale is divided into 100 squares,
out of which 46 are shaded and 54 are not shaded.
So the percentage of large scale are 46%  and 54%

Question 2.

___ out of 100 equal parts are shaded.
___ % of the large square is shaded.
___ out of 100 equal parts are not shaded.
____ % of the large square is not shaded.
Answer:
78 out of 100 equal parts are shaded.
78 % of the large square is shaded.
22 out of 100 equal parts are not shaded.
22 % of the large square is not shaded.
Explanation:
Each large scale is divided into 100 squares,
out of which 78 are shaded and 22 are not shaded.
So the percentage of large scale are 78%  and 22%

Express each decimal as a percent

Example
\(\frac{38}{100}\) = 38%

Question 3.
\(\frac{7}{100}\) = ___ %
Answer:
7%
Explanation:
To convert a fraction to a percent,
first divide the numerator by the denominator.
Then multiply the decimal by 100.
The fraction \(\frac{7}{100}\) can be converted to decimal by dividing 7 by 100.
It can be converted to percent by multiplying the decimal by 100.
7 ÷ 100 = 0.07×100 = 7
So, the fraction \(\frac{7}{100}\) is equivalent to 7%

Question 4.
\(\frac{7}{100}\) = ___ %
Answer:
7%
Explanation:
To convert a fraction to a percent,
first divide the numerator by the denominator.
Then multiply the decimal by 100.
The fraction \(\frac{7}{100}\) can be converted to decimal by dividing 7 by 100.
It can be converted to percent by multiplying the decimal by 100.
7 ÷ 100 = 0.07×100 = 7
So, the fraction \(\frac{7}{100}\) is equivalent to 7%

Question 5.
\(\frac{19}{100}\) = ___ %
Answer:
19%
Explanation:
To convert a fraction to a percent,
first divide the numerator by the denominator.
Then multiply the decimal by 100.
The fraction \(\frac{19}{100}\) can be converted to decimal by dividing 19 by 100.
It can be converted to percent by multiplying the decimal by 100.
19 ÷ 100 = 0.19×100 = 19
So, the fraction \(\frac{19}{100}\) is equivalent to 19%

Question 6.
\(\frac{6}{10}\) = ___ %
Answer:
60%
Explanation:
To convert a fraction to a percent,
first divide the numerator by the denominator.
Then multiply the decimal by 100.
The fraction \(\frac{6}{10}\) can be converted to decimal by dividing 6 by 10.
It can be converted to percent by multiplying the decimal by 100.
6 ÷ 10 = 0.6×100 = 60
So, the fraction \(\frac{6}{10}\) is equivalent to 60%

Question 7.
\(\frac{4}{10}\) = ___ %
Answer:
40%
Explanation:
To convert a fraction to a percent,
first divide the numerator by the denominator.
Then multiply the decimal by 100.
The fraction \(\frac{4}{10}\) can be converted to decimal by dividing 4 by 10.
It can be converted to percent by multiplying the decimal by 100.
4 ÷ 10 = 0.4×100 = 40
So, the fraction \(\frac{4}{10}\) is equivalent to 40%

Express each decimal as a percent.

Example

Question 8.

Answer: 28%
Explanation:
To convert a decimal to a fraction, place the decimal number over its place value.
First divide the numerator by the denominator.
Then multiply the decimal by 100, to convert a fraction to a percent.

Question 9.
0.07 = _________%
Answer: 7%
Explanation:
To convert a decimal to a fraction, place the decimal number over its place value.
First divide the numerator by the denominator.
Then multiply the decimal by 100, to convert a fraction to a percent.

Question 10.
0.01 = _________%
Answer: 1%
Explanation:
To convert a decimal to a fraction, place the decimal number over its place value.
First divide the numerator by the denominator.
Then multiply the decimal by 100, to convert a fraction to a percent.

Question 11.
0.08 _________%
Answer: 8%
Explanation:
To convert a decimal to a fraction, place the decimal number over its place value.
First divide the numerator by the denominator.
Then multiply the decimal by 100, to convert a fraction to a percent.

Question 12.
0.5 = _________%
Answer: 50%
Explanation:
To convert a decimal to a fraction, place the decimal number over its place value.
First divide the numerator by the denominator.
Then multiply the decimal by 100, to convert a fraction to a percent.

Question 13.
0.9 = _________%
Answer: 90%
Explanation:
To convert a decimal to a fraction, place the decimal number over its place value.
First divide the numerator by the denominator.
Then multiply the decimal by 100, to convert a fraction to a percent.

Question 14.
0.8 = _________%
Answer: 80%
Explanation:
To convert a decimal to a fraction, place the decimal number over its place value.
First divide the numerator by the denominator.
Then multiply the decimal by 100, to convert a fraction to a percent.

Express each percent as a fraction with a denominator of 100.

Example

Question 15.

Answer:

Explanation:
To convert a percent to a fraction,
we have to remove the percent sign and divide the given number by 100.

Question 16.

Answer:

Explanation:
To convert a percent to a fraction,
we have to remove the percent sign and divide the given number by 100.

Question 17.

Answer:

Explanation:
To convert a percent to a fraction,
we have to remove the percent sign and divide the given number by 100.

Question 18.

Answer:

Explanation:
To convert a percent to a fraction,
we have to remove the percent sign and divide the given number by 100.

Question 19.

Answer:

Explanation:
To convert a percent to a fraction,
we have to remove the percent sign and divide the given number by 100.

Express each percent as a fraction with a denominator of 100.

Example

Question 20.

Answer:

Explanation:
To convert a percent to a fraction,
we have to remove the percent sign and divide the given number by 100.
And, then we express the fractional form of the percentage in the simplest form.

Question 21.

Answer:

Explanation:
To convert a percent to a fraction,
we have to remove the percent sign and divide the given number by 100.
And, then we express the fractional form of the percentage in the simplest form.

Question 22.

Answer:

Explanation:
To convert a percent to a fraction,
we have to remove the percent sign and divide the given number by 100.
And, then we express the fractional form of the percentage in the simplest form.

Question 23.
46% =
Answer:

Explanation:
To convert a percent to a fraction,
we have to remove the percent sign and divide the given number by 100.
And, then we express the fractional form of the percentage in the simplest form.

Question 24.
55% =
Answer:

Explanation:
To convert a percent to a fraction,
we have to remove the percent sign and divide the given number by 100.
And, then we express the fractional form of the percentage in the simplest form.

Express each percent as a decimal.

Question 25.

Answer:

Explanation:
First remove the percent sign to convert from a percent to a decimal.
Divide the number by 100 and the out put is in the form of decimal.

Question 26.
9% = ___
Answer:

Explanation:
First remove the percent sign to convert from a percent to a decimal.
Divide the number by 100 and the out put is in the form of decimal.

Question 27.
1% = ___
Answer:

Explanation:
First remove the percent sign to convert from a percent to a decimal.
Divide the number by 100 and the out put is in the form of decimal.

Write each ratio as a fraction and then as a percent.

Question 28.

Answer:

Explanation:
Ratios are smaller to fractions, and each fraction can be written as a fraction.
Divide the first number 23 by the second number 100.
Multiply by 100 to convert to a percentage.
Add the percent symbol (%) to the output.

Question 29.

Answer:

Explanation:
Ratios are smaller to fractions, and each fraction can be written as a fraction.
Divide the first number 9 by the second number 100.
Multiply by 100 to convert to a percentage.
Add the percent symbol (%) to the output

Express each percent as a decimal. Then mark ✗ to show where each decimal is located on the number line.

Question 30.
71% = ______
Answer:

Explanation:
To convert a decimal to a percentage, multiply by 100,
just move the decimal point 2 places to the right.

Question 31.
19% = ___
Answer:

Explanation:
To convert a decimal to a percentage, multiply by 100,
just move the decimal point 2 places to the right.

Question 32.
44%= ____
Answer:

Explanation:
To convert a decimal to a percentage, multiply by 100,
just move the decimal point 2 places to the right.

Solve. Show your work.

Question 33.
There are 100 students in a drawing contest, and 58 of them are girls.
a. What percent of the students in the contest are girls?
Answer: 58%
Explanation:
To convert a fraction to a percent,
first divide the numerator by the denominator.
Then multiply the decimal by 100.
The fraction \(\frac{58}{100}\) can be converted to decimal by dividing 58 by 100.
It can be converted to percent by multiplying the decimal by 100.
58 ÷ 100 = 0.58×100 = 58
So, the fraction \(\frac{58}{100}\) is equivalent to 58%

b. What percent of the students in the contest are boys?
Answer: 42%
Explanation:
To convert a fraction to a percent,
first divide the numerator by the denominator.
Then multiply the decimal by 100.
The fraction \(\frac{42}{100}\) can be converted to decimal by dividing 42 by 100.
It can be converted to percent by multiplying the decimal by 100.
42 ÷ 100 = 0.42×100 = 42
So, the fraction \(\frac{42}{100}\) is equivalent to 42%

Question 34.
A jogging route is 10 kilometers long. Lee Ming has jogged 4 kilometers of the route.

a. What percent of the route has Lee Ming jogged?
Answer: 40%
Explanation:
A jogging route is 10 kilometers long.
Lee Ming has jogged 4 kilometers of the route.
To convert a fraction to a percent,
first divide the numerator by the denominator.
Then multiply the decimal by 100.
The fraction \(\frac{4}{10}\) can be converted to decimal by dividing 4 by 10.
It can be converted to percent by multiplying the decimal by 100.
4 ÷ 10 = 0.4×100 = 40
So, the fraction \(\frac{4}{10}\) is equivalent to 40%

b. What percent of the route does Lee Ming have to jog to complete the whole route?
Answer: 60%
Explanation:
A jogging route is 10 kilometers long.
Lee Ming has jogged 4 kilometers of the route.
To convert a fraction to a percent,
first divide the numerator by the denominator.
Then multiply the decimal by 100.
The fraction \(\frac{6}{10}\) can be converted to decimal by dividing 6 by 10.
It can be converted to percent by multiplying the decimal by 100.
6 ÷ 10 = 0.6×100 = 60
So, the fraction \(\frac{6}{10}\) is equivalent to 60%

This handy Math in Focus Grade 5 Workbook Answer Key Chapter 11 Practice 1 Making and Interpreting Double Bar Graphs provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 11 Practice 1 Answer Key Making and Interpreting Double Bar Graphs

Complete. Use the data in the graph.

The double bar graph shows the number of boys and girls in two classes, 5A and 5B.

Question 1.
There are ___________ students in 5A and ___________ students in 5B.
Answer:
24 students in 5A and 20 students in 5B
Explanation:
The above graph shows number of boys and girls.
Number of students on y-axis and sections on y-axis.
number of boys in 5A = 10
number of girls in 5A = 14
total boys and girls in 5A = 10 + 14 = 24
Similarly,
number of boys in 5B = 10
number of girls in 5B = 10
total boys and girls in 5B = 10 + 10 = 20

Question 2.
There are ___________ more girls than boys in 5A.
Answer:
4 more girls than boys in 5A
Explanation:
number of boys in 5A = 10
number of girls in 5A = 14
number of more girls than boys in 5A = 14 – 10 = 4

Question 3.
Class ___________ has an equal number of boys and girls.
Answer:
5B has an equal number of boys and girls
Explanation:
The above graph shows number of boys and girls.
number of boys in 5B = 10
number of girls in 5B = 10
total boys and girls in 5B = 10 + 10 = 20

Question 4.
There are ___ girls altogether in 5A and 5B.
Answer:
24 girls altogether in 5A and 5B
Explanation:
The above graph shows number of boys and girls.
number of girls in 5A = 14
number of girls in 5B = 10
total girls in 5A and 5B = 14 + 10 = 24

Question 5.
There are ___ boys altogether in 5A and 5B.
Answer:
20 boys altogether in 5A and 5B
Explanation:
The above graph shows number of boys and girls.
number of boys in 5A = 10
number of boys in 5B = 10
total boys in 5A and 5B = 10 + 10 = 20

Question 6.
The average number of students in the two classes is ___
Answer: 22
Explanation:
The average number of students in the two classes is = 22
Average = sum/number of events
Average = \( \frac {24 + 20} {2} \)
= \( \frac {44} {2} \)
= 22

Complete the bar graph using the data in the table. Then answer the questions.

Question 7.
The table shows the number of bags of apples and oranges sold by a grocer on three days.

Answer:

Explanation:
The above graph shows number of apples and oranges sold on Thursday, Friday and Saturday.
y-axis represents the number of bags of apples and oranges.
x-axis represents the apples and oranges sold on particular days.

Question 8.
On Friday, ___ more bags of oranges than apples were sold.
Answer:
On Friday 15 more bags of oranges than apples were sold.
Explanation:
The above graph shows number of apples and oranges sold on Friday.
number of apples sold = 20
number of oranges sold = 35
number of more bags of oranges than apples = 35 – 20 = 15

Question 9.
On Saturday, ___ fewer bags of apples than oranges were sold.
Answer:
On Saturday, 20 fewer bags of apples than oranges were sold.
Explanation:
The above graph shows number of apples and oranges sold on Saturday.
number of apples sold = 25
number of oranges sold = 55
number of less bags of apples than oranges = 45 – 25 = 20

Question 10.
The total number of bags of apples and oranges sold was the greatest on ___________.
Answer:
The total number of bags of apples and oranges sold was the greatest on Saturday.
Explanation:
The above graph shows number of apples and oranges sold on Thursday, Friday and Saturday.
Comparing on the three days apples and oranges were sold more on Saturday.

Question 11.
The difference between the number of bags of apples and oranges sold was the least on ____.
Answer:
The difference between the number of bags of apples and oranges sold was the least on Thursday.
Explanation:
The above graph shows number of apples and oranges sold on Thursday, Friday and Saturday.
Comparing on the three days apples and oranges were sold less on Thursday.

This handy Math in Focus Grade 5 Workbook Answer Key Chapter 12 Practice 3 Vertical Angles provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 12 Practice 3 Answer Key Vertical Angles

Complete.

Question 1.
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) meet at O. Use a protractor to find unknown angle measure

m∠w = _______
m∠x = __________
m∠y = _____
m∠z = __________
m∠____ = m∠______
∠___________ and ∠___________ are vertical angles.
m∠____ = m∠______
∠___________ and ∠___________ are vertical angles.
Answer:
m∠w = 50°
m∠x = 130° = 180 ° – 50°
m∠y = 50°
m∠z = 130°
m∠w = m∠y
Vertical angles are a pair of opposite angles formed by intersecting lines
∠w  and ∠y are vertical angles.
m∠x = m∠z
∠x  and ∠z are vertical angles.
Explanation:
As can be seen from the figure above, when two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.

Question 2.
\(\overleftrightarrow{X Z}\) and \(\overleftrightarrow{V W}\) meet at Y. Use a protractor to find unknown angle measures.

m∠XYW = _______
m∠WYU = __________
m∠UYZ = _____
m∠ZYV = __________
m∠VYX = ______
∠___________ and ∠___________ are vertical ongles.
∠___________ and ∠___________ are vertical angles.
Answer:

m∠XYW = 40°
m∠WYU = 90°
m∠UYZ = 50°
m∠ZYV = 40°
m∠VYX = 140°
∠XYW and ∠VYZ are vertical ongles.
∠WYZ and ∠XYV are vertical angles.
Explanation:
As can be seen from the figure above, when two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.

Complete.

Question 3.
Look at the star and its marked angles. In the table below, write three sets of:
a. angles on a line,
b. angles at a point,
c. vertical angles.


Answer:

Draw.

Explanation:
The common point where two rays meet is called the vertex and the rays are called arms of the angle or Angle on lines.
Angles on line add upto 180°
An angle is measured with reference to a circle with its center at the common endpoint of the rays.
Hence, the sum of angles at a point is always 360°
When two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.

Question 4.
Draw rays at P to form
a. an angle whose measure forms a sum of 180° with the measure of ∠x,
Answer:
x= 30°
30° x 6 = 180°

Explanation:
The common point where two rays meet is called the vertex and the rays are called arms of the angle or Angle on lines.
Angles on line add upto 180°

b. an angle whose measure is equal to the measure of ∠x.
(Do not use a protractor to draw the angles.)

a.

b.
Answer: 30°
Explanation:
An angle measures less than 90 degrees is called acute angle.

Find the unknown angle measures.

Question 5.
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) meet at O. Find the measure of ∠COB.

Answer:
m∠COB = 130°

Explanation:
180 – 130 = 50°
Vertical angles are a pair of opposite angles formed by intersecting lines.
∠AOD  and ∠COB are vertical angles.
m∠AOD = m∠COB = 130°

Question 6.
\(\overleftrightarrow{E F}\) and \(\overleftrightarrow{G H}\) meet at O. Find the measures of ∠GOF and ∠EOH.

Answer:
m∠GOF = 132° and
m∠EOH = 132°
Explanation:

180° – 48° = 132°
Vertical angles are a pair of opposite angles formed by intersecting lines
∠GOF  and ∠EOH are vertical angles.
m∠GOF = m∠EOH = 132°

Question 7.
\(\overleftrightarrow{R S}\) and \(\overleftrightarrow{P Q}\) meet at N. Find the measures of ∠PNR, ∠RNQ, and ∠QNS.

Answer:
m∠PNR = 20°
m∠RNQ = 160°
m∠QNS = 20°
Explanation:
∠PNR = 180° – 160° = 20°
Vertical angles are a pair of opposite angles formed by intersecting lines

Find the unknown angle measures.

Question 8.
\(\overleftrightarrow{J K}\) and \(\overleftrightarrow{L M}\) meet at O. Find the measure of ∠NOK.

Answer:
∠NOK = 56°
Explanation:

∠LOJ = 180° – 108° = 72°
∠NOK = 180° -(52° + 72°)
=180° – 124°
=56°

Question 9.
\(\overleftrightarrow{A B}\), \(\overleftrightarrow{C D}\) and \(\overleftrightarrow{E F}\) meet at O. Find the measure of ∠x.

Answer:
m∠x = 120°
Explanation:
As can be seen from the figure below, when two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.
∠AOF and ∠EOB are vertical angles

Question 10.
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) meet at O. Find the measure of ∠w.

Answer:
m∠w = 75°
Explanation:

As can be seen from the figure above, when two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.

Find the unknown angle measures.

Question 11.
\(\overleftrightarrow{Q R}\) and \(\overleftrightarrow{S T}\)meet at O. Find the measures of ∠QOS, ∠TOR, and ∠SOR.

Answer:
m∠QOS = 20°
m∠TOR= 20°
m∠SOR = 160°
Explanation:
As can be seen from the figure below, when two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.

Question 12.
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\)meet at O. Find the measures of ∠p, ∠q, and ∠r.

m∠p = ____
m∠q = ____
m∠r = ____
Answer:
m∠p = 25°
m∠q = 155°
m∠r = 65°
Explanation:
As can be seen from the figure below, when two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.

Question 13.
\(\overleftrightarrow{U V}\), \(\overleftrightarrow{W X}\), and \(\overleftrightarrow{Y Z}\) meet at O. Find the measure of ∠UOW.

Answer:

Explanation:
when two lines intersect, four angles are formed.
Each opposite pair are called vertical angles and are always congruent.
68° + 72° = 140
∠UOW = 180° -140° = 40°

Question 14.
\(\overleftrightarrow{A B}\), \(\overleftrightarrow{C D}\), and \(\overleftrightarrow{E F}\) meet at O. Find the measures of ∠x and ∠y.

Answer:
m∠x = 30°
m∠y = 60°
Explanation:
∠AOB  = 180° – (∠AOC + ∠FOB)
= 180° – (90° + 60°)
= 180° – 150° = 30°

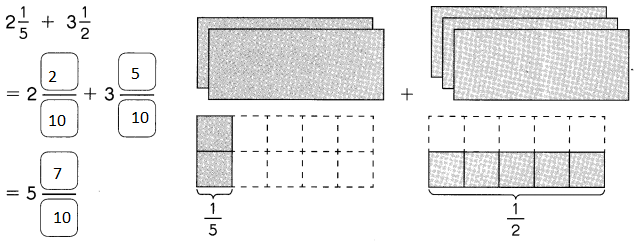
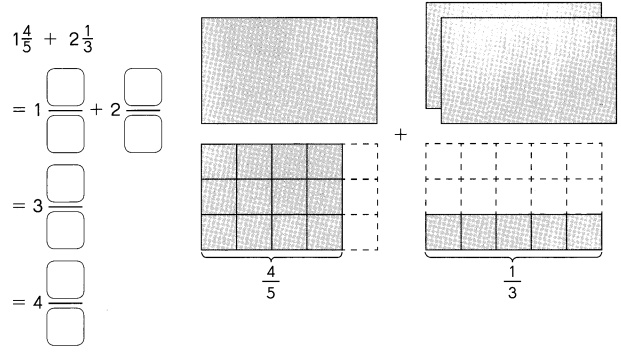
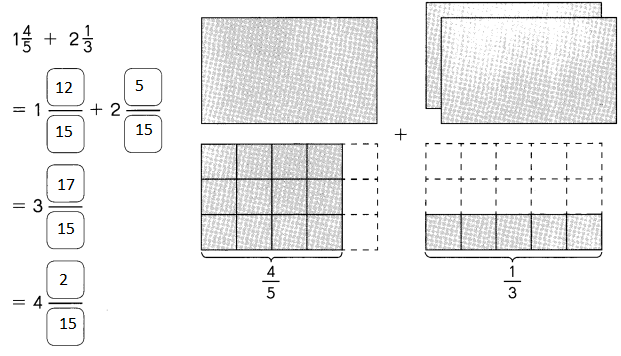
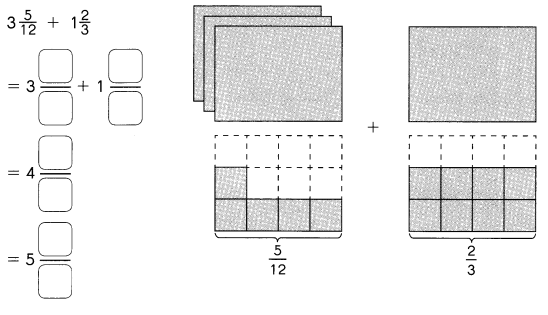
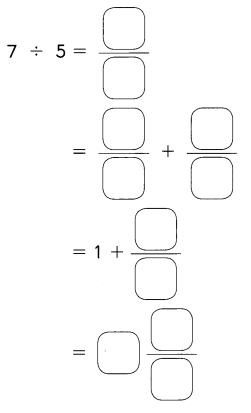
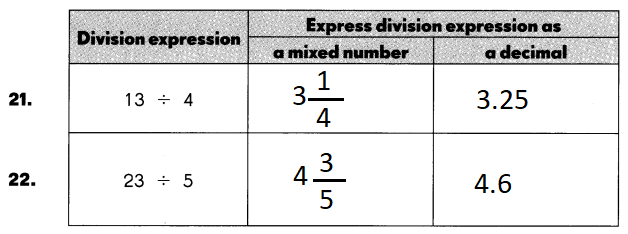
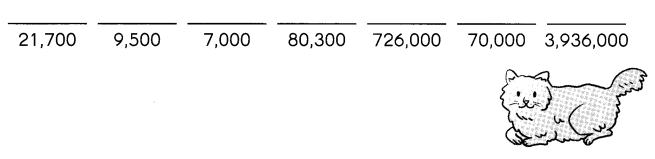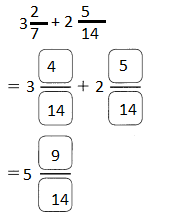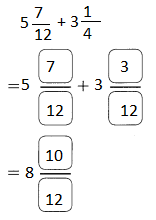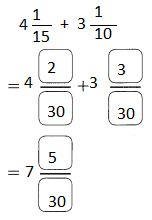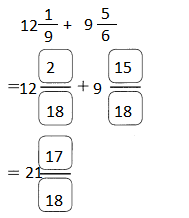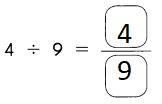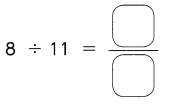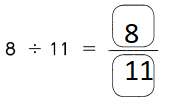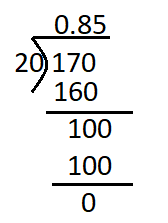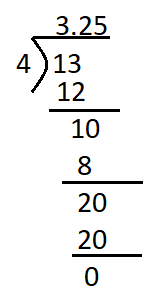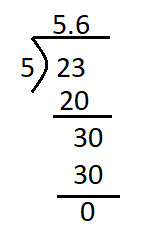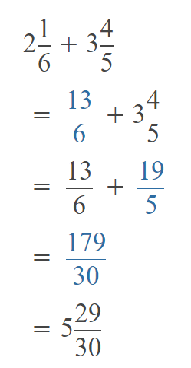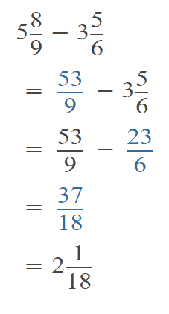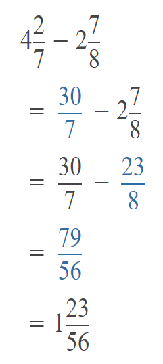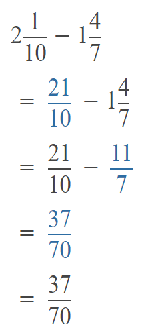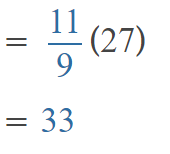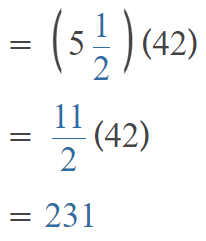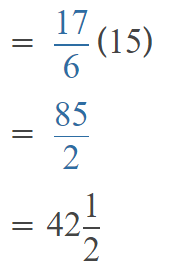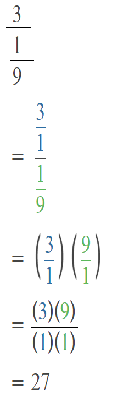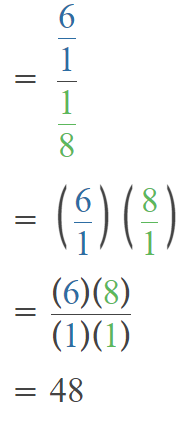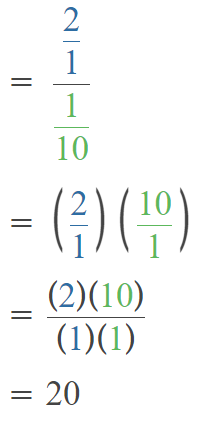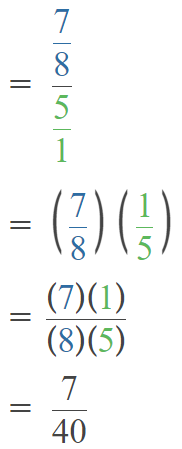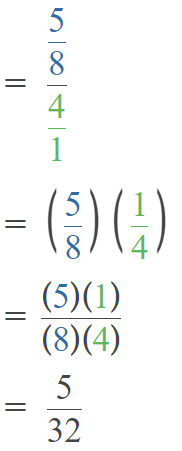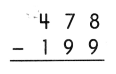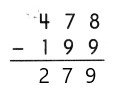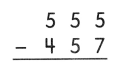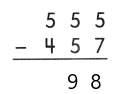Go through the Math in Focus Grade 5 Workbook Answer Key Chapter 2 Practice 2 Multiplying by Tens, Hundreds, or Thousands to finish your assignments.

Math in Focus Grade 5 Chapter 2 Practice 2 Answer Key Multiplying by Tens, Hundreds, or Thousands

Multiply.

Question 1.
47 × 10 = ___
Answer:
47 X 10 = 470,

Explanation:
Given 47 multiplied by 10 we get zero at units place and
we increment towards left side as shown,
so 47 X 10 = 470.

Question 2.
38 × 10 = ___
Answer:
38 X 10 = 380,

Explanation:
Given 38 multiplied by 10 we get zero at units place and
we increment towards left side as shown,
so 38 X 10 = 380.

Question 3.
109 × 10 = ___
Answer:
109 X 10 = 1,090,

Explanation:
Given 109 multiplied by 10 we get zero at units place and
we increment towards left side as shown,
so 109 X 10 = 1,090.

Question 4.
521 × 10 = ___
Answer:
521 X 10 = 5,210,

Explanation:
Given 521 multiplied by 10 we get zero at units place and
we increment towards left side as shown,
so 521 X 10 = 5,210.

Question 5.
7,140 × 10 = ___
Answer:
7,140 X 10 = 71,400,

Explanation:
Given 7,140 multiplied by 10 we get zero at units place and
we increment towards left side as shown,
so 7,140 X 10 = 71,400.

Question 6.
1,503 × 10 = ___
Answer:
1,503 X 10 = 15,030,

Explanation:
Given 1,503 multiplied by 10 we get zero at units place and
we increment towards left side as shown,
so 1,503 X 10 = 15,030.

Question 7.
3,702 × 10 = ___
Answer:
3,702 X 10 = 37,020,

Explanation:
Given 3,702 multiplied by 10 we get zero at units place and
we increment towards left side as shown,
so 3,702 X 10 = 37,020.

Question 8.
9,342 × 10 = ___
Answer:
9,342 X 10 = 93,420,

Explanation:
Given 9,342 multiplied by 10 we get zero at units place and
we increment towards left side as shown,
so 9,342 X 10 = 93,420.

Find the missing factors.

Question 9.
96 × __ = 960
Answer:
96 X __10__ = 960,

Explanation:
As given 96 X _____ = 960 to find missing factors we divide
960 by 96 we get 10, so answer is 96 X __10 ___ = 960.

Question 10.
___ × 10 = 700
Answer:
__70 __ X 10 = 700,

Explanation:
As given  _____ X 10 = 700 to find missing factors we divide
700 by 10 we get 70, so answer is  __70 _ X 10 = 700.

Question 11.
514 × __ = 5,140
Answer:
514 X __10 __= 5,140,

Explanation:
As given 514 X _____ = 5,140 to find missing factors we divide
5,140 by 514 we get 10, so answer is 514 X __10 ___ = 5,140.

Question 12.
___ × 10 = 5,000
Answer:
__500 __ X 10 = 5,000,

Explanation:
As given  _____ X 10 = 5,000 to find missing factors we divide
5,000 by 10 we get 500, so answer is  __500_ X 10 = 5,000.

Question 13.
308 × ___ = 3,080
Answer:
308 X __10_ = 3,080,

Explanation:
As given 308 X _____ = 3,080 to find missing factors we divide
308 by 3,080 we get 10, so answer is 308 X __10 ___ = 3,080.

Question 14.
___ × 10 = 4,020
Answer:
__402__ X 10 = 4,020,

Explanation:
As given _____ X 10 = 4,020 to find missing factors we divide
4,020 by 10 we get 402, so answer is __402 ___ X 10 = 4,020.

Question 15.
2,096 × ___ = 20,960
Answer:
2,096 X __10 ___ = 20,960,

Explanation:
As given 2,096 X _____ = 20,960 to find missing factors we divide
20,960 by 2,096 we get 10, so answer is 2,096 X __10 ___ = 20,096.

Question 16.
___ × 10 = 91,760
Answer:
__9,176__ X 10 = 91,760,

Explanation:
As given _____ X 10 = 91,760 to find missing factors we divide
91,760 by 10 we get 9,176, so answer is __9,176 ___ X 10 = 91,760.

Complete.

Example.

65 × 40 = (65 × 4) × 10
= 260 × 10
= 2,600
Answer:
65 X 40 = 2,600,

Explanation:
Given 65 X 40  as 40 can be divided as 4 X 10,
So (65 X _4_) X 10,
__260__ X 10,
_2,600_,
therefore 65 X 40 = 2,600.

Question 17.
39 × 30
= (39 × _3__) × 10
= _117_ × 10
= _1,170___
Answer:
39 X 30 = 1,170,

Explanation:
Given 39 X 30 as 30 can be divided as 3 X 10,
So (39 X _3_) X 10,
__117__ X 10,
_1,170_,
therefore 39 X 30 = 1,170.

Question 18.
143 × 90
= (143 × _9_) × __10__
= __1,287__ × __10__
= _12,870___
Answer:
143 X 90 = 12,870,

Explanation:
Given 143 X 90 as 90 can be divided as 9 X 10,
So (143 X _9_) X 10,
__1,287__ X 10,
_12,870_,
therefore 143 X 90 = 12,870.

Question 19.
360 × 30
= (360 × _3__) × __10__
= _1,080__ × __10__
= __10,800__
Answer:
360 X 30 = 10,800,

Explanation:
Given 360 X 3 as 30 can be divided as 3 X 10,
So(360 X _3_) X 10,
__1,080__ X 10,
_10,800_,
therefore 360 X 30 = 10,800.

Question 20.
285 × 80
= (285 × _8_) × _10__
= _2,280___ × _10__
= _22,800__
Answer:
285 X 80 = 22,800,

Explanation:
Given 285 X 80 as 80 can be divided as 8 X 10,
So(285 X _8_) X 10,
__2,280__ X 10,
_22,800_,
therefore 39 X 30 = 1,170.

Multiply.

Question 21.
7 × 1,000 = ___
Answer:
7,000 ,

Explanation:
Given to find multiplication of 7 with thousand we get
7,000 .

Question 22.
86 × 100 = ___
Answer:
8,600

Explanation:
Given to find multiplication of 86 with hundred we get
8,600 .

Question 23.
70 × 1,000 = ___
Answer:
70,000 ,

Explanation:
Given to find multiplication of 70 with thousand we get
70,000.

Question 24.
95 × 100 = __
Answer:
9,500,
Explanation:
Given to find multiplication of 9,500 with hundred we get
9,500.

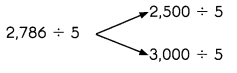
Question 25.
400 × 1,000 = ____4,00,000_____
Answer:
4,00,000 ,

Explanation:
Given to find multiplication of 400 with thousand we get
4,00,000.

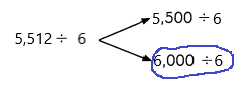
Question 26.
217 × 100 = ___21,700_____
Answer:
21,700,

Explanation:
Given to find multiplication of 217 with hundred we get
217 X 100 = 21,700.

Question 27.
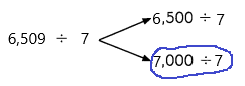
726 × 1,000 = ___72,60,000______

Answer:
72,60,000 ,

Explanation:
Given to find multiplication of 726 with thousand we get
72,60,000 .

Question 28.
803 × 100 = _____80,300____
Answer:
80,300 ,

Explanation:
Given to find multiplication of 803 with hundred we get
80,300.

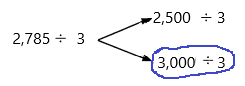
Question 29.
8,032 × 1,000 = ____80,32,000_______
Answer:
80,32,000 ,

Explanation:
Given to find multiplication of 8,032 with thousand we get
80,32,000.

Question 30.
3,810 × 100 = ___3,81,000______
Answer:
3,81,000,

Explanation:
Given to find multiplication of 3,810 with hundred we get
3,81,000 .

Question 31.
3,936 × 1,000 = ___39,36,000________
Answer:
39,36,000 ,

Explanation:
Given to find multiplication of 3,936 with thousand we get
39,36,000.

What cat has long, fine hair, and a snubbed nose?
Write the letters that match the answers below to find out.

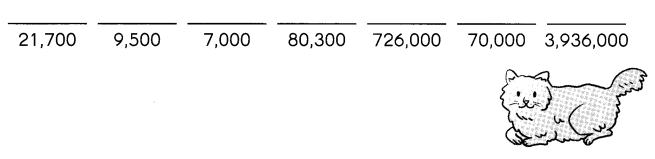
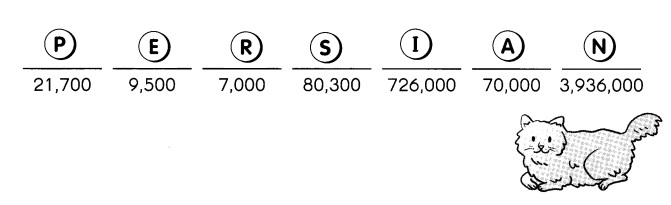
PERSIAN cat has long, fine hair and a snubbed nose,

Explanation:
Persian cat has long, fine hair, and a snubbed nose,
the letters that match the answers above are written above as
P – 21,700,
E – 9,500,
R – 7,000,
S – 80,300,
I – 7,26,000,
A – 70,000,
N – 3,936,000.

Find the missing factors.

Question 32.
17 × ___100____ = 1,700

Answer:
17 X 100 = 1,700,

Explanation:
Given 17 X ____ = 1,700,
to find missing factor we divide 1,700 by 17 we get
1,700 ÷ 17 = 100.

Question 33.
_25__ × 1,000 = 25,000
Answer:
__25__ X 1,000 = 25,000,

Explanation:
Given ____ X 1,000 = 25,000,
to find missing factor we divide 25,000 by 1,000 we get
25,000 ÷ 1,000 = 25.

Question 34.
____4,78_____ × 1,000 = 4,78,000
Answer:
__4,78___ X 1,000 = 4,78,000,

Explanation:
Given ____ X 1,000 = 4,78,000,
to find missing factor we divide 4,78,000 by 1,000 we get
4,78,000 ÷ 1,000 = 4,78.

Question 35.
320 × _1,000_ = 3,20,000
Answer:
320 X __1,000__ = 3,20,000,

Explanation:
Given 320 X __1,000___ = 3,20,000,
to find missing factor we divide 3,20,000 by 320 we get
3,20,000 ÷ 320 = 1,000.

Question 36.
1,315 × ____100____ = 131,500
Answer:
1,315  X __100___ = 131,500,

Explanation:
Given 1,315 X _ 100_ = 131,500
to find missing factor we divide 131,500 by 1,315 we get
131,500 ÷ 1,315 = 100.

Question 37.
_2,662__ × 1,000 = 2,662,000
Answer:
__2,662__ X 1,000 = 2,662,000,

Explanation:
Given ____ X 1,000 = 2,662,000,
to find missing factor we divide 2,662,000 by 1,000 we get
2,662,000 ÷ 1,000 = 2,662.

Question 38.
4,668 × ___100___ = 4,66,800
Answer:
4,668  X __100__ = 4,66,800,

Explanation:
Given 4,668 X _ 100_ = 4,66,800
to find missing factor we divide 4,668 by 100 we get
4,66,800 ÷ 4,668 = 100.

Question 39
___25_____ × 1,000 = 25,000
Answer:
__25___ X 1,000 = 25,000,

Explanation:
Given ____ X 1,000 = 25,000,
to find missing factor we divide 25,000 by 1,000 we get
25,000 ÷ 1,000 = 25.

Complete.

Example.
4 × 300 = (4 × 3) × 100
= 12 × 100
= 1,200

Question 40.
12 × 500 =
= (12 × _5__) × 100
= ___60___ × 100
= __6,000__
Answer:
12 X 500 = 6,000,

Explanation:
Given to find 12 X 500 so
=  (12 X __5__) X 100,
= __60__ X 100,
= __6,000_.

Question 41.
700 × 900 = (700 × __9_) × 1oo
= ___6,300___ × 100
= _6,30,000___
Answer:
700 X 900 = (700 X __9__) X 100,

Explanation:
Given to find 700 X 900 so
= (700 X __9__) X 100,
= ___6,300___ X 100,
= ___ 6,30,000__.

Complete.

Question 42.
814 × 700 =
= (814 × __7_) × 100
= __5,698____ × 100
= 5,69,800
Answer:
814 X 700 = 5,69,800,

Explanation:
Given to find 814 X 700 so
(814 X __7 __) X 100,
= __5,698___ X 100,
= 5,69,800.

Question 43.
5,400 × 800 =
= (5,400 × _8__) × 100
= __43,200____ × 100
= _4,320,000__
Answer:
5,400 X 800= 43,200,

Explanation:
Given to find 5,400 X 800 so
= __43,200__ X 100,
= __4,320,000__.

Question 44.
5 × 7,000
= (5 × _7_) × 1,000
= ___35____ × 1,000
= __35,000__
Answer:
5 X 7,000 = 35,000,

Explanation:
Given to find 5 X 7,000  so
= (5 X _7_) X 1,000,
= __35___ X 1,000,
= 35,000.

Question 45.
8 × 5,000
= (8 × _5_) × 1,000
= ___40___ × 1,000
= __40,000__
Answer:
8 X 5,000 = 40,000,

Explanation:
Given to find 8 X 5,000 so
= 8 X 5 X 1,000,
= 40 X 1,000,
= 40,000.

Question 46.
12 × 3,000
= (12 × __3_) × 1,000
= _36__ × 1,000
= __36,000___
Answer:
12 X 3,000 = 36,000,

Explanation:
Given to find 12 X 3,000 so
=(12 X __3__) X 1,000,
= __36__ X 1,000,
= __36,000__.

Question 47.
15 × 2,000
= (15 × __2_) × 1,000
= ___30____ × 1,000
= __30,000___
Answer:
15 X 2,000 = 30,000,

Explanation:
Given to find 15 X 2,000 so
15 X 2 X 1000,
= 30 X 1,000,
= 30,000.

Question 48.
300 × 4,000
= (300 × __4_) × _1,000___
= _1,200_ × 1,000
= _12,00,000___
Answer:
300 X 4,000 = 12,00,000,

Explanation:
Given to find 300 X 4,000 we get
300 x 4 X 1,000,
= 12,00 X 1,000,
=  12,00,000.

Question 49.
663 × 6,000
= (663 × _6_) × 1,000
= _3,978__ × 1,000
= _39,78,000___
Answer:
663 X 6,000 =39,78,000,

Explanation:
Given to find 663 X 6,000 so
663 X 6 X 1,000,
= 3,978 X 1,000,
= 39,78,000.

Multiply.

Question 50.

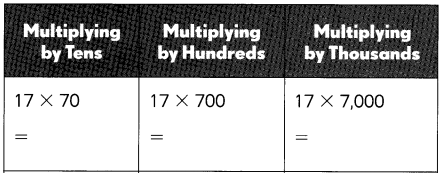
Answer:

Explanation:
Multiplying by Tens we get 17 X 70 as 17 X 7 X 10 = 1,190,
Multplying by Hundreds we get 17 X 700 as 17 X 7 X 100 = 11,900,
Multiplying by Thousands we get 17 X 7,000 = 17 X 7 X 1,000 = 1,19,000.

Question 51.

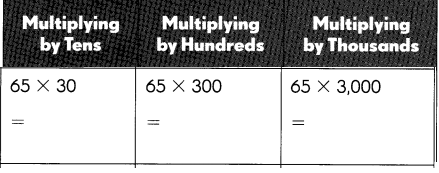
Answer:

Explanation:
Multiplying by Tens we get 65 X 30 as 65 X 3 X 10 = 1,950,
Multplying by Hundreds we get 65 X 300 as 65 X 3 X 100 = 19,500,
Multiplying by Thousands we get 65 X 3,000 = 65 X 3 X 1,000 = 1,95,000.

Question 52.

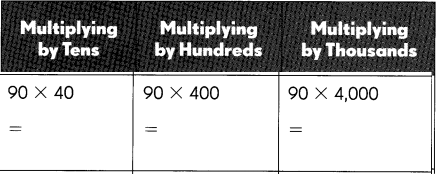
Answer:

Explanation:
Multiplying by Tens we get 90 X 40 as 9 X 4 X 10 = 3,600,
Multplying by Hundreds we get 90 X 400 as 90 X 4 X 100 = 36,000,
Multiplying by Thousands we get 90 X 4,000 = 90 X 4 X 1,000 = 3,60,000.

Question 53.

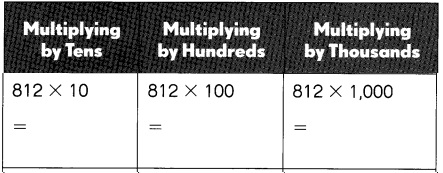
Answer:

Explanation:
Multiplying by Tens we get 812 X 10 as 812 X 10 = 8,120,
Multplying by Hundreds we get 812 X 100 as 812 X 100 = 81,200,
Multiplying by Thousands we get 812 X 1,000 = 812 X 1,000 = 8,12,000.

Question 54.

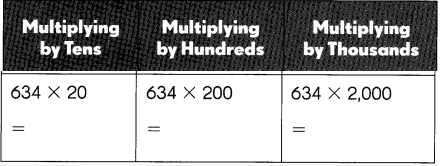
Answer:

Explanation:
Multiplying by Tens we get 634 X 20 as 634 X 2 X 10 = 12,680,
Multplying by Hundreds we get 634 X 200 as 634 X 2 X 100 = 1,26,800,
Multiplying by Thousands we get 634 X 200 = 634 X 2 X 1,000 = 12,68,000.

Find the missing factors.

Question 55.
31 × ___100_____ = 3,100
Answer:
31 X 100 = 3,100,

Explanation:
Given to find 31 X ___ = 3,100,
the missing factor is 3,100 ÷ 31 = 100.

Question 56.
30 × ___3,000______ = 90,000
Answer:
30 X ___3,000___ = 90,000,

Explanation:
Given to find 30 X _____ = 90,000,
So we divide 90,000 by 30 we get 90,000 ÷ 30 = 3,000.

Question 57.
103 × ___30_____ = 3,090
Answer:
103 X _30 ___ = 3,090,

Explanation:
Given to find 103 X _____ = 3,090,
So we divide 3,090 by 103 we get 3,090 ÷ 103  = 30.

Question 58.
25 × ____200_____ = 5,000
Answer:
25 X __200__ = 5,000,

Given to find 25 X _____ = 5,000,
So we divide 5,000 by 25 we get 5,000 ÷ 25 = 200.

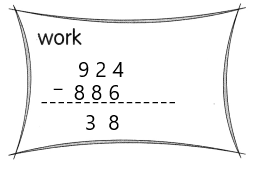
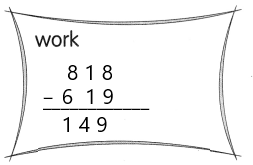
The owner of on electronics store wants to estimate the amount she will receive from the soles of these items:

58 all-in-one printers at $219 each.
652 radio clocks at $73 each.
99 portable audio players at $217 each.
39 plasma television sets at $4,156 each.

Answer:
The owner of the electronics store will receive $19,38,025,

Explanation:
Given the owner of an electronics store wants to estimate the amount she
will receive from the soles of these items:
58 all-in-one printers at $219 each.
652 radio clocks at $73 each.
99 portable audio players at $217 each.
39 plasma television sets at $4,156 each are
So for all-in-one printers it is 58 X $219 = $12,702,
for radio clocks it is 652 X $73 = $47,596 for
portable audio players it is 99 X $217 = $21,483 and
for 39 plasma television sets it is 39 X $47,596 = $18,56,244.
Therefore the owner will receive
$12,702 + $47,596 + $21,483 + $18,56,244 = $19,38,025.

Estimate the amount she receives for each type of item by rounding to the greatest place value. Then, estimate the total amount from the sales of the items.

Question 59.
58 × $219 rounds to ___60______ × $___220______ = $4,400
Answer:
$4,400,

Explanation:
When 58 X $219 rounds to 60 X $220 we get $4,400.

Question 60.
652 × $73 rounds to ___650______ × $ ___70___ = $45,500
Answer:
$45,500,

Explanation:
When 652 X $73 rounds to 650 X $70 we get $45,500.

Question 61.
99 × $217 rounds to ____100______ × $ __220_______ = $22,000
Answer:
$22,000,

Explanation:
When 99 X $217 rounds to 100 X $220 we get $22,000.

Question 62.
39 × $4156 rounds to ___40______ × $ ___4,160______ = $1,66,400
Answer:
$1,66,400,

Explanation:
When 39 X $4156 rounds to 40 X $4,160 = $1,66,400.

Question 63.
The total estimated amount is
$ _4,400____ +$ __45,500___ +$ __22,000___ +$1,66,400
= $ _2,38,300_____
Answer:
$2,38,300,

Explanation:
The given total estimated amount is $4,400 + $45,500 + $22,000 + $1,66,400 =
$2,38,300,

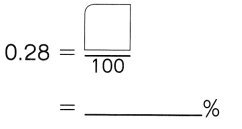
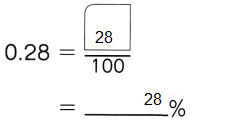
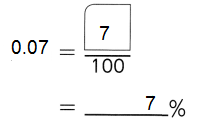
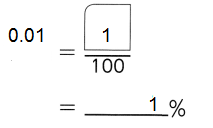
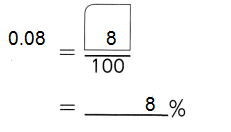
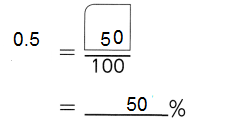
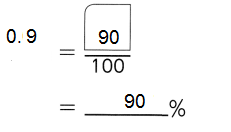
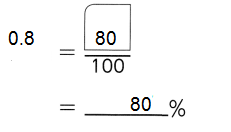
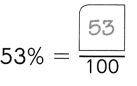
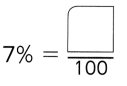
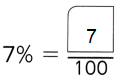
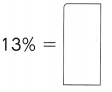
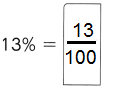
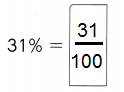
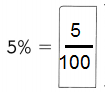
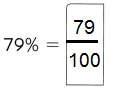
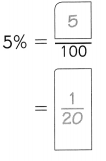
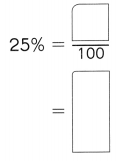
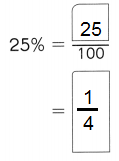
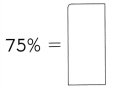
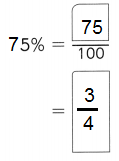
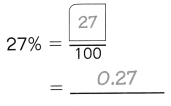
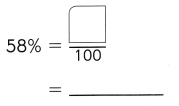
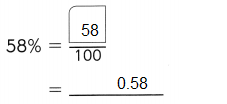
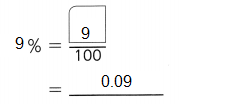
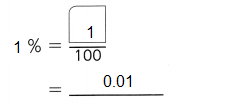
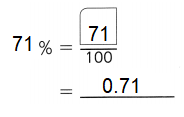
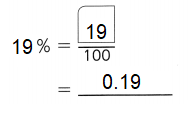
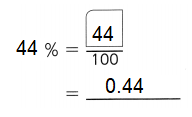
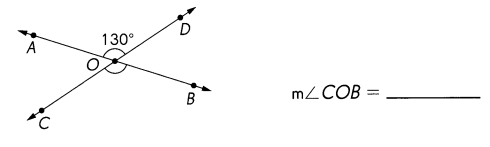
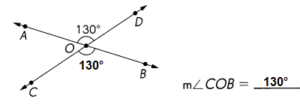
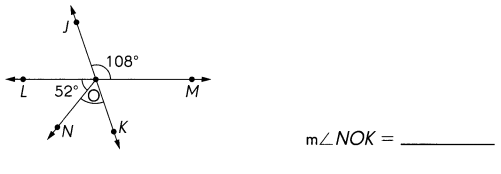
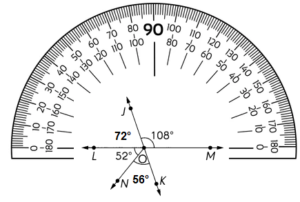
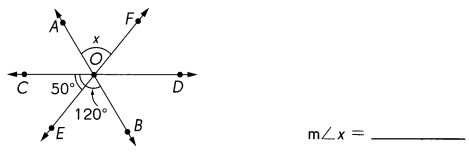
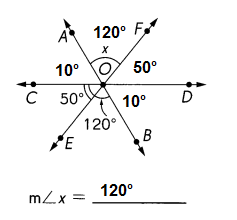
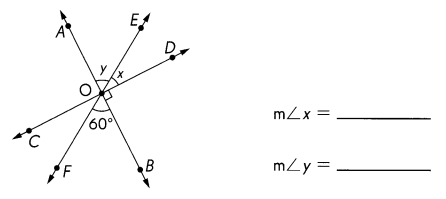
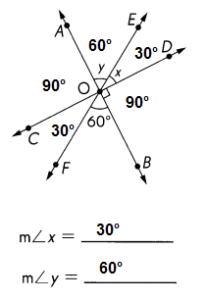
Go through the Math in Focus Grade 5 Workbook Answer Key Chapter 1 Practice 5 Rounding and Estimating to finish your assignments.

Math in Focus Grade 5 Chapter 1 Practice 5 Answer Key Rounding and Estimating

Mark an ✗ to show where each number is located on the number line. Then round each number.

Example

656 rounded to the nearest ten is 660

Question 1.

9,709 rounded to the nearest hundred is ____
Answer: 9,700
Rounding is a way of simplifying numbers to make them easier to understand or work with. Rounding can be used when an exact number isn’t needed, and an approximate answer will do.
When rounding a number such as 9709 to the nearest hundred, we use the following rules:
A) We round the number up to the nearest hundred if the last two digits in the number are 50 or above.
B) We round the number down to the nearest hundred if the last two digits in the number are 49 or below.
C) If the last two digits are 00, then we do not have to do any rounding, because it is already to the hundred.
In this case, Rule B applies and 9709 rounded to the nearest hundred is: 9,700

9,709 rounded to the nearest hundred is 9,700.

Question 2.

31,600 rounded to the nearest thousand is ___
Answer: 32,000
Rounding off the numbers means shortening the length of the number from long digits by replacing it with the nearest value. Round of to the nearest 1000 means minimizing the given decimal number to its nearest 1000 value.
How to round off the numbers to the nearest 1000:
Based on the below steps, we can easily round the numbers to the nearest 1000.
1. First, Find out the thousand’s digit in the number.
2. Next, choose the next smallest number (that is the hundredth digit of the number).
3. Now, check the hundred’s digit is either <5 (That means 0, 1, 2, 3, 4) or > = 5 (That is 5, 6, 7, 8, 9).
(i) If the digit is < 5, then the hundreds place is replaced with the digit ‘0’.
(ii) If the digit is > = 5, then the hundred’s digit is replaced with the digit ‘0’, and the thousand’s place digit is increased by 1 digit.
Number 31,600 Round to the Nearest 1000
Step 1: Thousand’s digit of the number is 1.
Step 2: Hundred’s digit of the number is 0.
Step 3: The hundred’s digit ‘0’ is <5, then we have to apply 3(i) conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
31,600 rounding of the nearest 1000 is equal to 32,000.

Round each number to the nearest thousand.

Question 3.
5,637 ____
Answer: 6000
Explanation:
Rounding off the numbers means shortening the length of the number from long digits by replacing it with the nearest value. Round of to the nearest 1000 means minimizing the given decimal number to its nearest 1000 value.
How to round off the numbers to the nearest 1000:
Based on the below steps, we can easily round the numbers to the nearest 1000.
1. First, Find out the thousand’s digit in the number.
2. Next, choose the next smallest number (that is the hundredth digit of the number).
3. Now, check the hundred’s digit is either <5 (That means 0, 1, 2, 3, 4) or > = 5 (That is 5, 6, 7, 8, 9).
(i) If the digit is < 5, then the hundreds place is replaced with the digit ‘0’.
(ii) If the digit is > = 5, then the hundred’s digit is replaced with the digit ‘0’, and the thousand’s place digit is increased by 1 digit.
Number 5,637 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 5.
Step 2: Hundred’s digit of the number is 6.
Step 3: The hundred’s digit ‘6’ is >5, then we have to apply 3(ii) conditions. That is, the hundred’s placed is replaced with the digit ‘0’and the thousand’s place digit is increased by 1 digit.
5,637 rounding of the nearest 1000 is equal to 6000.

Question 4.
9,541 ____
Answer: 10,000
Explanation:
Number 9,541 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 9.
Step 2: Hundred’s digit of the number is 5.
Step 3: The hundred’s digit ‘5’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’and the thousand’s place digit is increased by 1 digit.
9,541 rounding of the nearest 1000 is equal to 10,000.

Question 5.
1,399 ___
Answer: 1000
Explanation:
Number 1,399 Round to the Nearest 1000
Step 1: Thousand’s digit of the number is 1.
Step 2: Hundred’s digit of the number is 3.
Step 3: The hundred’s digit ‘3’ is <5, then we have to apply conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
1,399 rounding of the nearest 1000 is equal to 1000.

Question 6.
72,245 ____
Answer:  72000
Explanation:
Number 72,245 Round to the Nearest 1000
Step 1: Thousand’s digit of the number is 2.
Step 2: Hundred’s digit of the number is 2.
Step 3: The hundred’s digit ‘2’ is <5, then we have to apply conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
72,245 rounding of the nearest 1000 is equal to 72,000.

Question 7.
473,075 _________
Answer: 473,000
Explanation:
Number 473,075 Round to the Nearest 1000
Step 1: Thousand’s digit of the number is 3.
Step 2: Hundred’s digit of the number is 0.
Step 3: The hundred’s digit ‘0’ is <5, then we have to apply conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
473,075 rounding of the nearest 1000 is equal to 473,000.

Question 8.

69,547 ___
Answer: 70,000
Explanation:
Number 69,547 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 9.
Step 2: Hundred’s digit of the number is 5.
Step 3: The hundred’s digit ‘5’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’and the thousand’s place digit is increased by 1 digit.
69,547 rounding of the nearest 1000 is equal to 70,000.

Question 9.
20,100 ____
Answer: 20,000
Explanation:
Number 20,100 Round to the Nearest 1000
Step 1: Thousand’s digit of the number is 0.
Step 2: Hundred’s digit of the number is 1.
Step 3: The hundred’s digit ‘1’ is <5, then we have to apply conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
20,100 rounding of the nearest 1000 is equal to 20,000.

Question 10.
756,715 ____
Answer: 757000
Explanation:
Number 756,715 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 6.
Step 2: Hundred’s digit of the number is 7.
Step 3: The hundred’s digit ‘7’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’and the thousand’s place digit is increased by 1 digit.
756,715 rounding of the nearest 1000 is equal to 757,000.

Answer each question. Use the number line to help you.

Example
Rounding to the nearest thousand, what is the least and the greatest number that rounds to 3,000?

Least number: 2,500
Greatest number: 3,499

Question 11.
Rounding to the nearest thousand, what is
a. the least number that rounds to 5,000?

_______
Answer: The least number of 5000 is 4,500.
Explanation:
Number 4,500 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 4.
Step 2: Hundred’s digit of the number is 5.
Step 3: The hundred’s digit ‘5’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’and the thousand’s place digit is increased by 1 digit.
4,500 rounding of the nearest 1000 is equal to 5,000.
So, the least number to round up 5000 is 4,500.

b. the greatest number that rounds to 90,000?

Answer:90,499
Explanation:
Number 90,000 Round to the Nearest 1000
Step 1: Thousand’s digit of the number is 0.
Step 2: Hundred’s digit of the number is 0.
Step 3: The hundred’s digit ‘0’ is <5, then we have to apply conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
But here the greatest number is asked to round up the 90,000 that means the number we need to find out to get the 90,000 if we calculate the nearest values to that number.
If I take 90,499.
Step 1: The thousand’s place is 0.
Step 2: Hundred’s place is 4.
Step 3: The hundred’s digit ‘4’ is <5 then we have to apply conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
Finally, if we calculate 90,499 with the nearest 1000 with the above rules then the number will be 90,000.

Round each number to the nearest thousand. Then estimate the sum.

Example
9,286 + 5.703
9,286 rounds to 9,000.
5,703 rounds to 6,000.
9,000 + 6,000 = 15,000

Question 12.
6,789 + 4,200
Answer:11000.
Explanation:
Number 6,789 and 4,200 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 6 and 4.
Step 2: Hundred’s digit of the number is 7 and 2.
Step 3: The hundred’s digit ‘7’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’and the thousand’s place digit is increased by 1 digit.
Step 4: The hundred’s digit ‘2’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’
6,789 rounding of the nearest 1000 is equal to 7000.
4,200 rounding of the nearest 1000 is equal to 4000.
Now add the rounded figures: 7000+4000=11000.

Question 13.
7,264 + 7,153
Answer:14000
Explanation:
Number 7,264 and 7,153 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 7 and 7.
Step 2: Hundred’s digit of the number is 2 and 1.
Step 3: The hundred’s digit ‘2’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
Step 4: The hundred’s digit ‘1’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
7,264 rounding of the nearest 1000 is equal to 7000.
7,153 rounding of the nearest 1000 is equal to 7000.
Now add the rounded figures: 7000+7000=14000.

Question 14.
4,885 + 6,075
Answer: 11000
Number 4,885 and 6,075 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 4 and 6.
Step 2: Hundred’s digit of the number is 8 and 0.
Step 3: The hundred’s digit ‘8’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
Step 4: The hundred’s digit ‘1’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
4,885 rounding of the nearest 1000 is equal to 5000.
6,075 rounding of the nearest 1000 is equal to 6000.
Now add the rounded figures: 5000+6000=11000.

Question 15.
3,105 + 9,940
Answer: 13000
Number 3,105 and 9,940 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 3 and 9.
Step 2: Hundred’s digit of the number is 1 and 9.
Step 3: The hundred’s digit ‘9’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
Step 4: The hundred’s digit ‘1’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
3,105 rounding of the nearest 1000 is equal to 3000.
9,940 rounding of the nearest 1000 is equal to 10000.
Now add the rounded figures: 3000+10000=13,000.

Question 16.
7,083 + 2,607
Answer:10,000
Number 3,105 and 9,940 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 7 and 2.
Step 2: Hundred’s digit of the number is 0 and 6.
Step 3: The hundred’s digit ‘0’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
Step 4: The hundred’s digit ‘6’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
7,083 rounding of the nearest 1000 is equal to 7000.
2,607 rounding of the nearest 1000 is equal to 3000.
Now add the rounded figures: 7000+3000=10,000.

Round each number to the nearest thousand. Then estimate the difference

Example
8,156 – 6,109
8,156 rounds to 8,000.
6,109 rounds to 6,000.
8,000 – 6,00 = 2,000

Question 17.
4,924 – 4,127
Answer: 1000
Number 4,924 and 4,127 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 4 and 4.
Step 2: Hundred’s digit of the number is 9 and 1.
Step 3: The hundred’s digit ‘1’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
Step 4: The hundred’s digit ‘9’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
4,924 rounding of the nearest 1000 is equal to 5000.
4,127 rounding of the nearest 1000 is equal to 4000.
Now add the rounded figures: 5000-4000=1,000.

Question 18.
7,105 – 3,940
Answer:3000
Number 7,105 and 3,940 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 7 and 3.
Step 2: Hundred’s digit of the number is 9 and 1.
Step 3: The hundred’s digit ‘1’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
Step 4: The hundred’s digit ‘9’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
7,105 rounding of the nearest 1000 is equal to 7000.
3,940 rounding of the nearest 1000 is equal to 4000.
Now add the rounded figures: 7000-4000=3000.

Question 19.
4,885 – 1,075 ____
Answer:4000.
Number 4,885 and 1,075 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 4 and 1.
Step 2: Hundred’s digit of the number is 8 and 0.
Step 3: The hundred’s digit ‘0’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
Step 4: The hundred’s digit ‘8’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
4,885 rounding of the nearest 1000 is equal to 5000.
1,075 rounding of the nearest 1000 is equal to 4000.
Now add the rounded figures: 5000-4000=1000.

Question 20.
3,522 – 2,815
Answer:1000
Step 1: Thousand’s digit of the number is 3 and 2.
Step 2: Hundred’s digit of the number is 5 and 8.
Step 3: The hundred’s digit ‘8 and 5’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
3,522 rounding of the nearest 1000 is equal to 4000.
2,815 rounding of the nearest 1000 is equal to 3000.
Now add the rounded figures: 4000-3000=1000.

Question 21.
6,480 – 1,397
Answer: 5000
Number 6,480 and 1,397 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 6 and 1.
Step 2: Hundred’s digit of the number is 4 and 3.
Step 3: The hundred’s digit ‘4 and 3’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
6,480 rounding of the nearest 1000 is equal to 6000.
1,397 rounding of the nearest 1000 is equal to 1000.
Now add the rounded figures: 6000-1000=5000.

Use front-end estimation with adjustment to estimate each sum.

Example
1,963 + 3,290 + 7,837
1,000 + 3,000 + 7,000
= 11,000
900 + 200 – &00
= 1,900
To the nearest thousanci:
1,900 → 2,000
11,000 + 2,000 = 13,000

Question 22.
2,541 + 6,061 + 1,681
Answer: 11000
With front end estimation, we only round and add the numbers in the leftmost place or the very last number on the left. This means that all numbers in other places will be zeros except the number in the leftmost place after the numbers are rounded. Having said that, if the numbers have two digits, round to the tens place before adding the leftmost digits or numbers.
Explanation:
Number 2,541, 6,061 and 1,681 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 2, 6, and 1.
Step 2: Hundred’s digit of the number is 5, 0, and 6.
Step 3: The hundred’s digit  ‘0’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
Step 4: The hundred’s digit ‘5 and 6’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
2,541 rounding of the nearest 1000 is equal to 3000.
6,061 rounding of the nearest 1000 is equal to 6000.
1,681 rounding of the nearest 1000 is equal to 2000
The front end estimations are 3000, 6000, 2000.
Now add all those estimations:3000+6000+2000=11000.

Question 23.
7,823 + 6,848 + 3,310
Answer:
With front end estimation, we only round and add the numbers in the leftmost place or the very last number on the left. This means that all numbers in other places will be zeros except the number in the leftmost place after the numbers are rounded. Having said that, if the numbers have two digits, round to the tens place before adding the leftmost digits or numbers.
Explanation:
Number 7,823, 6,848 and 3,310 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 7, 6, and 3.
Step 2: Hundred’s digit of the number is 8, 8, and 3.
Step 3: The hundred’s digit  ‘3’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
Step 4: The hundred’s digit ‘8 and 8’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
7,823 rounding of the nearest 1000 is equal to 8000.
6,848 rounding of the nearest 1000 is equal to 7000.
3,310 rounding of the nearest 1000 is equal to 3000
The front end estimations are 8000, 7000, 3000.
Now add all those estimations:8000+7000+3000=18000.

Question 24.
4,197 + 8,936 + 2,226
Answer:
With front end estimation, we only round and add the numbers in the leftmost place or the very last number on the left. This means that all numbers in other places will be zeros except the number in the leftmost place after the numbers are rounded. Having said that, if the numbers have two digits, round to the tens place before adding the leftmost digits or numbers.
Explanation:
Number 4,197, 8,936 and 2,226 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 4, 8, and 2.
Step 2: Hundred’s digit of the number is 1, 9, and 2.
Step 3: The hundred’s digit  ‘1 and 2’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
Step 4: The hundred’s digit ‘9’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
4,197 rounding of the nearest 1000 is equal to 4000.
8,936 rounding of the nearest 1000 is equal to 9000.
2,226 rounding of the nearest 1000 is equal to 2000
The front end estimations are 4000, 9000, 2000.
Now add all those estimations:4000+9000+2000=15000.

Use front-end estimation with adjustment to estimate each difference.

Example .
2,943 – 1,272
2,000 – 1,000
= 1,000
900 – 200 = 700
To the nearest thousand:
700 → 1,000
1,000 + 1,000 = 2,000

Question 25.
6,770 – 3,081
Answer: 4000
Explanation:
With front end estimation, we only round and subtract the numbers in the leftmost place or the very last number on the left. This means that all numbers in other places will be zeros except the number in the leftmost place after the numbers are rounded. Having said that, if the numbers have two digits, round to the tens place before adding the leftmost digits or numbers.
Number 6,770 and 3,081 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 6 and 3.
Step 2: Hundred’s digit of the number is 7 and 0.
Step 3: The hundred’s digit ‘7 and 5’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
Step 4: The hundred’s digit  ‘0’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
6,770 rounding of the nearest 1000 is equal to 7000.
3,081 rounding of the nearest 1000 is equal to 3000.
The front end estimations are 7000, 3000.
Now add all those estimations:7000-3000=4000.

Question 26.
8,764 – 3,589
Answer: 5000
Explanation:
With front end estimation, we only round and subtract the numbers in the leftmost place or the very last number on the left. This means that all numbers in other places will be zeros except the number in the leftmost place after the numbers are rounded. Having said that, if the numbers have two digits, round to the tens place before adding the leftmost digits or numbers.
Number 8,764and 3,589 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 8 and 3.
Step 2: Hundred’s digit of the number is 7 and 5.
Step 3: The hundred’s digit ‘7 and 5’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
8,764 rounding of the nearest 1000 is equal to 9000.
3,589 rounding of the nearest 1000 is equal to 4000.
The front end estimations are 9000, 4000.
Now subtract all those estimations:9000-4000=5000.

Question 27.
7,802 – 4,396
Answer: 4000
Explanation:
With front end estimation, we only round and subtract the numbers in the leftmost place or the very last number on the left. This means that all numbers in other places will be zeros except the number in the leftmost place after the numbers are rounded. Having said that, if the numbers have two digits, round to the tens place before adding the leftmost digits or numbers.
Number 7,802 and 4,396 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 7 and 4.
Step 2: Hundred’s digit of the number is 8 and 3.
Step 3: The hundred’s digit ‘8’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
Step 4: The hundred’s digit  ‘3’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
7,802 rounding of the nearest 1000 is equal to 8000.
4,396 rounding of the nearest 1000 is equal to 4000.
The front end estimations are 8000, 4000.
Now subtract all those estimations:8000-4000=4000.

Use front-end estimation with adjustment to estimate each difference.

Example
7,594 – 2,831
7,000 – 2,000 = 5,000
800 – 500 = 300
To the nearest thouari:
300 → 0
5,000 – 0 = 5,000

Question 28.
5,780 – 3,962
Answer: 2000
Explanation:
With front end estimation, we only round and subtract the numbers in the leftmost place or the very last number on the left. This means that all numbers in other places will be zeros except the number in the leftmost place after the numbers are rounded. Having said that, if the numbers have two digits, round to the tens place before adding the leftmost digits or numbers.
Number 5,780 and 3,962 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 5 and 3.
Step 2: Hundred’s digit of the number is 7 and 9.
Step 3: The hundred’s digit ‘7 and 9’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
5,780 rounding of the nearest 1000 is equal to 6000.
3,962 rounding of the nearest 1000 is equal to 4000.
The front end estimations are 6000, 4000.
Now subtract all those estimations:6000-4000=2000.

Question 29.
9,119 – 4,852
Answer; 4000
Explanation:
With front end estimation, we only round and subtract the numbers in the leftmost place or the very last number on the left. This means that all numbers in other places will be zeros except the number in the leftmost place after the numbers are rounded. Having said that, if the numbers have two digits, round to the tens place before adding the leftmost digits or numbers.
Number 9,119 and 4,852 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 9 and 4.
Step 2: Hundred’s digit of the number is 1 and 8.
Step 3: The hundred’s digit ‘8’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
Step 4: The hundred’s digit  ‘1’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
9,119 rounding of the nearest 1000 is equal to 9000.
4,852 rounding of the nearest 1000 is equal to 5000.
The front end estimations are 9000, 5000.
Now subtract all those estimations:9000-5000=4000.

Question 30.
8,254 – 4,836
Answer: 3000
Explanation:
With front end estimation, we only round and subtract the numbers in the leftmost place or the very last number on the left. This means that all numbers in other places will be zeros except the number in the leftmost place after the numbers are rounded. Having said that, if the numbers have two digits, round to the tens place before adding the leftmost digits or numbers.
Number 8,254 and 4,836 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 8 and 4.
Step 2: Hundred’s digit of the number is 2 and 8.
Step 3: The hundred’s digit ‘8’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
Step 4: The hundred’s digit  ‘2’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
8,254 rounding of the nearest 1000 is equal to 8000.
4,836 rounding of the nearest 1000 is equal to 5000.
The front end estimations are 8000, 5000.
Now subtract all those estimations:8000-5000=3000.

Estimate each product.

Example
4,512 × 2
4,512 rounds to 5,000.
5,000 × 2 = 10,000

Question 31
3,765 × 7
Answer: 8000
Number 3,765 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 3.
Step 2: Hundred’s digit of the number is 7.
Step 3: The hundred’s digit ‘7’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
3,765 rounding of the nearest 1000 is equal to 4000.
The estimation is 4000
Now multiply with the given number that is 7:
4000×2=8000

Question 32.
2,521 × 5
Answer: 15000
Explanation:
Number 2,521 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 2.
Step 2: Hundred’s digit of the number is 5.
Step 3: The hundred’s digit ‘5’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
2,521 rounding of the nearest 1000 is equal to 3000.
The estimation is 3000
Now multiply with the given number that is 5:
3000×5=15000.

Question 33.
5,108 × 6
Answer: 30,000
Explanation:
Number 5,108 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 5.
Step 2: Hundred’s digit of the number is 1.
Step 3: The hundred’s digit  ‘1’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
5,108 rounding of the nearest 1000 is equal to 5000.
The estimation is 5000
Now multiply with the given number that is 6:
5000×6=30,000.

Question 34.
8,497 × 9
Answer: 72,000
Explanation:
Number 8,497 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 8.
Step 2: Hundred’s digit of the number is 4.
Step 3: The hundred’s digit  ‘4’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
8,497 rounding of the nearest 1000 is equal to 8000.
The estimation is 8000
Now multiply with the given number that is 9:
8000×9=72,000.

Question 35.
6,060 × 3
Answer:
Explanation:
Number 6,060 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 6.
Step 2: Hundred’s digit of the number is 0.
Step 3: The hundred’s digit  ‘0’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
6,060 rounding of the nearest 1000 is equal to 6000.
The estimation is 6000
Now multiply with the given number that is 3:
6000×3=18,000.

Estimate each quotient.

2,786 ÷ 5
2,500 ÷ 5
2,786 rounds to 3,000.
3,000 ÷ 5 = 600

Look for compatible numbers.

Which number is nearer to 2,786?

Question 36
6,509 ÷ 7
Answer: 1000
Explanation:

Why I choose 7000 to the nearest number I will explain below:
Number 6,509 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 6.
Step 2: Hundred’s digit of the number is 5.
Step 3: The hundred’s digit ‘5’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
6,509 rounding of the nearest 1000 is equal to 7000.
The estimation is 7000
Now divide with the given number that is 7:
7000÷7=1000.

Question 37.
5,512 ÷ 6
Answer: 1000

Explanation:
Why I choose 6000 to the nearest number I will explain below:
Number 5,512 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 5.
Step 2: Hundred’s digit of the number is 5.
Step 3: The hundred’s digit ‘5’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
5,512 rounding of the nearest 1000 is equal to 6000.
The estimation is 6000
Now divide with the given number that is 6:
6000÷6=1000.

Question 38.
2,785 ÷ 3
Answer: 1000
Explanation:

Number 2,785 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 2.
Step 2: Hundred’s digit of the number is 7.
Step 3: The hundred’s digit ‘7’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
2,785 rounding of the nearest 1000 is equal to 3000.
The estimation is 3000
Now divide with the given number that is 3:
3000÷3=1000.

Question 39.
6,287 ÷ 8
Answer: 750
Explanation:

Number 6,287 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 6.
Step 2: Hundred’s digit of the number is 2.
Step 3: The hundred’s digit ‘2’ is <5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’.
6,287 rounding of the nearest 1000 is equal to 6000.
The estimation is 6000
Now divide with the given number that is 8:
6000÷8=750.

Question 40.
2,963 ÷ 9
Answer: 333.33
Explanation:

Number 2,963 Round to the Nearest 1000:
Step 1: Thousand’s digit of the number is 2.
Step 2: Hundred’s digit of the number is 9.
Step 3: The hundred’s digit ‘9’ is >=5, then we have to apply some conditions. That is, the hundred’s placed is replaced with the digit ‘0’ and the thousand’s place digit is increased by 1 digit.
2,963 rounding of the nearest 1000 is equal to 3000.
The estimation is 3000
Now divide with the given number that is 9:
3000÷9=333.33.

Go through the Math in Focus Grade 5 Workbook Answer Key Chapter 3 Practice 4 Expressing Fractions, Division Expressions, and Mixed Numbers as Decimals to finish your assignments.

Math in Focus Grade 5 Chapter 3 Practice 4 Answer Key Expressing Fractions, Division Expressions, and Mixed Numbers as Decimals

Write each fraction as a decimal.

Example

\(\frac{3}{5}\) = \(\frac{3}{5}\)
= 0.6

Question 1.
\(\frac{13}{20}\) = ____
= _____
Answer:
\(\frac{13}{20}\) = \(\frac{13}{20}\)
= 0.65
Explanation:
Written the fraction as a decimal.

Question 2.
\(\frac{19}{25}\) = ____
= _____
Answer:
\(\frac{19}{25}\) =\(\frac{19}{25}\)
= 0.76
Explanation:
Written the fraction as a decimal.

Question 3.
\(\frac{47}{50}\) = ____
= _____
Answer:
\(\frac{47}{50}\) = \(\frac{47}{50}\)
= 0.94
Explanation:
Written the fraction as a decimal.

Express each division expression as a mixed number in simplest form and as a decimal.

Explanation:

Question 4.
7 ÷ 2
Answer:
7 ÷ 2 = \(\frac{6}{2}\) + \(\frac{1}{2}\)
= 3 + \(\frac{1}{2}\)
= 3 + 0.5
= 3.5

Explanation:
Converted division expression into mixed fraction and decimal

Question 5.
9 ÷ 4
Answer:
\(\frac{8}{4}\) + \(\frac{1}{4}\)
= 2 + \(\frac{1}{4}\)
= 2 + 0.25
= 2.25

Explanation:
Converted division expression into mixed fraction and decimal

Question 6.
21 ÷ 5
Answer:
\(\frac{20}{5}\) + \(\frac{1}{5}\)
= 4 + \(\frac{1}{5}\)
= 4 + 0.2
= 4.2

Explanation:
Converted division expression into mixed fraction and decimal

Question 7.
101 ÷ 25
Answer:
\(\frac{100}{25}\) + \(\frac{1}{25}\)
= 1 + \(\frac{1}{25}\)
= 4 + 0.04
= 4.04

Explanation:
Converted division expression into mixed fraction and decimal

Express each improper fraction as a decimal.

Example
\(\frac{3}{2}\) = \(\frac{2}{2}\) + \(\frac{1}{2}\)
= 1 + \(\frac{1}{2}\)
= 1 + 0.5
= 1.5
Explanation:
Converted each improper fraction into decimal

Question 8.
\(\frac{22}{5}\)
Answer:
\(\frac{20}{5}\) + \(\frac{2}{5}\)
= 4 + \(\frac{2}{5}\)
= 4 + 0.4
= 4.4
Explanation:
Converted each improper fraction into decimal

Question 9.
\(\frac{47}{20}\)
Answer:
\(\frac{40}{20}\) + \(\frac{7}{20}\)
= 2 + \(\frac{7}{20}\)
= 2 + 0.35
= 2.35
Explanation:
Converted each improper fraction into decimal

Question 10.
\(\frac{32}{25}\)
Answer:
\(\frac{25}{25}\) + \(\frac{7}{25}\)
= 1 + \(\frac{7}{25}\)
= 1 + 0.28
= 1.28
Explanation:
Converted each improper fraction into decimal

Solve. Show your work.

Question 11.
A coil of rope 603 feet long is cut into 25 equal pieces. What is the length of each piece? Express your answer as a mixed number and as a decimal.
Answer:
24.12 in decimal
24\(\frac{3}{25}\) in mixed fraction.
Explanation:
A coil of rope 603 feet long is cut into 25 equal pieces.
603 ÷  25 = \(\frac{600}{25}\) + \(\frac{3}{25}\)
= 24 + \(\frac{3}{25}\)
= 24\(\frac{3}{25}\)
= 24 + 0.12
= 24 .12
24.12 is the length of each piece

Go through the Math in Focus Grade 5 Workbook Answer Key Chapter 3 Practice 5 Adding Mixed Numbers to finish your assignments.

Math in Focus Grade 5 Chapter 3 Practice 5 Answer Key Adding Mixed Numbers

Add. Express each sum in simplest form.

Example

Question 1.

Answer:

Explanation:
Made the unlike denominators to like denominators
then added the mixed fractions.

Question 2.

Answer:

Explanation:
Made the unlike denominators to like denominators
then added the mixed fractions.

Add. Express each sum in simplest form

Question 3.
3\(\frac{2}{7}\) + 2\(\frac{5}{14}\)
Answer:

Explanation:
Made the unlike denominators to like denominators
then added the mixed fractions.

Question 4.
5\(\frac{7}{12}\) + 3\(\frac{1}{4}\)
Answer:

Explanation:
Made the unlike denominators to like denominators
then added the mixed fractions.

Question 5.
4\(\frac{1}{15}\) + 1\(\frac{3}{10}\)
Answer:

Explanation:
Made the unlike denominators to like denominators
then added the mixed fractions.

Question 6.
12\(\frac{1}{9}\) + 9\(\frac{5}{6}\)
Answer:

Explanation:
Made the unlike denominators to like denominators
then added the mixed fractions.

Add. Express each sum in simplest form.

Question 7.

Answer:

Explanation:
Made the unlike denominators to like denominators
then added the mixed fractions.

Question 8.

Answer:

Explanation:
Made the unlike denominators to like denominators
then added the mixed fractions.

Question 9.
2\(\frac{3}{4}\) + 3\(\frac{2}{5}\)
Answer:

Explanation:
Made the unlike denominators to like denominators
then added the mixed fractions.

Question 10.
2\(\frac{5}{9}\) + 1\(\frac{5}{6}\)
Answer:

Explanation:
Made the unlike denominators to like denominators
then added the mixed fractions.

Question 11.
7\(\frac{8}{9}\) + 9\(\frac{5}{12}\)
Answer:

Explanation:
Made the unlike denominators to like denominators
then added the mixed fractions.

Question 12.
5\(\frac{7}{12}\) + 1\(\frac{3}{4}\)
Answer:

Explanation:
Made the unlike denominators to like denominators
then added the mixed fractions.

Use benchmarks to estimate each sum.

Example

Question 13.
9\(\frac{6}{7}\) + 7\(\frac{5}{12}\)
Answer:
17\(\frac{1}{2}\)
Explanation:
\(\frac{6}{7}\) is near to the benchmark 1
\(\frac{5}{12}\) is near to the bench mark \(\frac{1}{2}\)
9 + 1 = 10
10 + 7 \(\frac{1}{2}\)
17\(\frac{1}{2}\)

Question 14.
4\(\frac{7}{12}\) + 10\(\frac{1}{9}\)
Answer:
14 \(\frac{1}{2}\)
Explanation:
\(\frac{7}{12}\) is near to the benchmark \(\frac{1}{2}\)
\(\frac{1}{12}\) is near to the bench mark 0
10 + 0 = 10
4\(\frac{1}{2}\) + 10
= 14 \(\frac{1}{2}\)

Go through the Math in Focus Grade 5 Workbook Answer Key Cumulative Review Chapters 3 and 4 to finish your assignments.

Math in Focus Grade 5 Cumulative Review Chapters 3 and 4 Answer Key

Concepts and Skills
Shade and label the model to show the sum of \(\frac{1}{3}\) and \(\frac{3}{5}\).
Then complete the addition sentence. (Lesson 3.1)

Question 1.

Answer:
\(\frac{1}{3}\) + \(\frac{3}{5}\) =
\(\frac{5}{15}\) + \(\frac{9}{15}\).=
\(\frac{14}{15}\)
Explanation:
Making unlike denominators to like denominators.

Explanation:
Making unlike denominators to like denominators.

Add. Express each sum in simplest form. (Lesson 3.1)

Question 2.
\(\frac{3}{4}\) + \(\frac{1}{12}\) =
Answer:
\(\frac{3}{4}\) + \(\frac{1}{12}\) =
\(\frac{9}{12}\) + \(\frac{1}{12}\) =
\(\frac{10}{12}\)
Explanation:
Making unlike denominators to like denominators.
And added the fractions

Question 3.
\(\frac{3}{5}\) + \(\frac{2}{7}\) =
Answer:
\(\frac{3}{5}\) + \(\frac{2}{7}\) =
\(\frac{21}{35}\) + \(\frac{10}{35}\) =
\(\frac{31}{35}\)
Explanation:
Making unlike denominators to like denominators.
and added the fractions

Estimate each sum by using the benchmarks, 0, \(\frac{1}{2}\) or 1. (Lesson 3.1)

Question 4.
\(\frac{8}{9}\) + \(\frac{2}{5}\) =
Answer:
= \(\frac{3}{2}\)
Explanation:
Estimating \(\frac{8}{9}\) as 1
and \(\frac{2}{5}\)  as \(\frac{1}{2}\)
1 + \(\frac{1}{2}\)
= \(\frac{3}{2}\)

Question 5.
\(\frac{1}{8}\) + \(\frac{6}{7}\) + \(\frac{1}{6}\) =
Answer:
\(\frac{1}{8}\) + \(\frac{6}{7}\) + \(\frac{1}{6}\) =
Estimated answer = 1
Explanation:
Estimating the bench marks
\(\frac{1}{8}\) = 0
\(\frac{6}{7}\) = 1
\(\frac{1}{6}\) = 0
0 + 1  + 0 = 1

Shade and label the model to show the difference between \(\frac{4}{5}\) and \(\frac{2}{3}\). Then complete the subtraction sentence. (Lesson 3.2)

Question 6.

Answer:

Explanation:
Simplified the fractions.

Subtract. Express each difference in simplest form. (Lesson 3.2)

Question 7.
\(\frac{3}{4}\) – \(\frac{1}{12}\) = \(\frac{2}{3}\)
Answer:
\(\frac{3}{4}\) – \(\frac{1}{12}\) = \(\frac{2}{3}\)
Explanation:

Question 8.
\(\frac{3}{5}\) – \(\frac{3}{9}\) =
Answer:
\(\frac{3}{5}\) – \(\frac{3}{9}\) = \(\frac{4}{15}\)
Explanation:

Estimate each difference by using the benchmarks, 0, \(\frac{1}{2}\) or 1. (Lesson 3.2)

Question 9.
\(\frac{4}{5}\) – \(\frac{3}{8}\)
Answer:
\(\frac{4}{5}\) – \(\frac{3}{8}\) = \(\frac{1}{2}\)
Explanation:
Estimating the fractions to bench marks
\(\frac{4}{5}\) = 1
\(\frac{3}{8}\) = \(\frac{1}{2}\)
1 – \(\frac{1}{2}\)  = \(\frac{1}{2}\)

Question 10.
\(\frac{7}{12}\) – \(\frac{5}{9}\)
Answer:
\(\frac{7}{12}\) – \(\frac{5}{9}\) = 1
Explanation:
Estimating the fractions to bench marks
\(\frac{7}{12}\)  = \(\frac{1}{2}\)
\(\frac{5}{9}\) = \(\frac{1}{2}\)
\(\frac{1}{2}\)  + \(\frac{1}{2}\)  = 1

Write each fraction as a division expression. (Lesson 3.3)

Question 11.

Answer:

Explanation:
\(\frac{4}{9}\)
Fraction into expression.

Question 12.

Answer:

Explanation:
\(\frac{8}{11}\)
Fraction into expression.

Write each division expression as a fraction. (Lesson 3.3)

Question 13.
\(\frac{5}{6}\) = ___ ÷ ___
Answer:
5 ÷ 6
\(\frac{5}{6}\) = 5 ÷ 6
Explanation:
converting division expression as a fraction.

Question 14.
\(\frac{7}{12}\) = ___ ÷ ___
Answer:
7 ÷ 12
\(\frac{7}{12}\) = 7 ÷ 12
Explanation:
converting division expression as a fraction.

Complete. (Lesson 3.3)

Question 15.

Answer:

Explanation:
Converting the division expression to a mixed fraction

Question 16.

Answer:

Explanation:
Converting the division expression to a mixed fraction

Divide. Express each quotient as a mixed number in simplest form. (Lesson 3.3)

Question 17.

Answer:

Explanation:
Converting the division expression to a mixed fraction

Question 18.

Answer:

Explanation:
Converting the division expression to a mixed fraction

Express each fraction as a decimal. (Lesson 3.4)

Question 19.
\(\frac{4}{5}\) = ____
= _________
Answer:
\(\frac{4}{5}\) = 0.8
Explanation:

Question 20.
\(\frac{17}{20}\) = ____
= _________
Answer:

Explanation:
\(\frac{17}{20}\) = 0.85

Express each division expression as a mixed number and as a decimal. (Lessons 3.3 and 3.4)

Explanation:

Question 21.
13 ÷ 4 = 3\(\frac{1}{4}\)
Answer:

Explanation:
13 ÷ 4 = 3.25

Question 22.
23 ÷ 5
Answer:

Explanation:
23 ÷ 5 = 5.6

Add. Express each sum in simplest form. (Lesson 3.5)

Question 23.
2\(\frac{2}{7}\) + 3\(\frac{1}{2}\)
Answer:

2\(\frac{2}{7}\) + 3\(\frac{1}{2}\) = 5\(\frac{11}{14}\)

Question 24.
1\(\frac{1}{2}\) + 1\(\frac{5}{9}\)
Answer:

Explanation:
1\(\frac{1}{2}\) + 1\(\frac{5}{9}\) = 3\(\frac{1}{18}\)

Estimate each sum by using the nearest whole number or half. (Lesson 3.5)

Question 25.
1\(\frac{5}{8}\) + 1\(\frac{1}{5}\)
Answer:

Explanation:
1\(\frac{5}{8}\) + 1\(\frac{1}{5}\) = 3\(\frac{1}{18}\) = 3 + 0 = 3
Converting the fraction into a whole number.

Question 26.
2\(\frac{1}{6}\) + 3\(\frac{4}{5}\)
Answer:

Explanation:
2\(\frac{1}{6}\) + 3\(\frac{4}{5}\) = 5\(\frac{29}{30}\)
Converting the fraction into a whole number.
5 + 1 = 6

Subtract. Express each difference in simplest form. (Lesson 3.6)

Question 27.
5\(\frac{8}{9}\) – 3\(\frac{5}{6}\)
Answer:

Explanation:
5\(\frac{8}{9}\) – 3\(\frac{5}{6}\) = 2\(\frac{1}{18}\)
2 + 0 = 2

Question 28.
4\(\frac{2}{7}\) – 2\(\frac{7}{8}\)
Answer:

Explanation:
4\(\frac{2}{7}\) – 2\(\frac{7}{8}\) = 1\(\frac{23}{56}\)
= 1 + \(\frac{1}{2}\)
= \(\frac{3}{2}\)

Estimate difference by using the nearest whole number or half. (Lesson 3.6)

Question 29.
2\(\frac{1}{10}\) – 1\(\frac{4}{7}\)
Answer:

Explanation:
2\(\frac{1}{10}\) – 1\(\frac{4}{7}\) = \(\frac{37}{70}\) = \(\frac{1}{2}\)
Converting the fraction into a half

Question 30.
3\(\frac{3}{8}\) – 1\(\frac{7}{12}\)
Answer:

Explanation:
3\(\frac{3}{8}\) – 1\(\frac{7}{12}\) = 1\(\frac{19}{24}\)
= 1 + 1 = 2

Find the product in simplest form. (Lesson 4.1)

Question 31.
\(\frac{6}{7}\) × \(\frac{5}{8}\) =
Answer:

Explanation:
\(\frac{6}{7}\) × \(\frac{5}{8}\) = \(\frac{15}{28}\)
Multiplication in fractions we have to directly multiply
Numerator x Numerator
and Denominator x Denominator.

Question 32.
\(\frac{4}{5}\) × \(\frac{10}{12}\) =
Answer:

Explanation:
\(\frac{4}{5}\) × \(\frac{10}{12}\) = \(\frac{2}{3}\)
Multiplication in fractions we have to directly multiply
Numerator x Numerator
and Denominator x Denominator.

Question 33.
\(\frac{2}{5}\) of \(\frac{10}{11}\) =
Answer:

Explanation:
\(\frac{2}{5}\) of \(\frac{10}{11}\) =\(\frac{4}{11}\)
Multiplication in fractions we have to directly multiply
Numerator x Numerator
and Denominator x Denominator.

Question 34.
\(\frac{8}{9}\) of \(\frac{5}{12}\) =
Answer:

Explanation:
\(\frac{8}{9}\) of \(\frac{5}{12}\)  = \(\frac{10}{27}\)
Multiplication in fractions we have to directly multiply
Numerator x Numerator
and Denominator x Denominator.

Multiply. Express the product in simplest form. (Lesson 4.3)

Question 35.
\(\frac{2}{5}\) × \(\frac{15}{7}\) =
Answer:

Explanation:
\(\frac{2}{5}\) × \(\frac{15}{7}\) = \(\frac{6}{7}\)
Multiplication in fractions we have to directly multiply
Numerator x Numerator
and Denominator x Denominator.

Question 36.
\(\frac{9}{5}\) × \(\frac{5}{12}\) =
Answer:

Explanation:
\(\frac{9}{5}\) × \(\frac{5}{12}\) = \(\frac{3}{4}\)
Multiplication in fractions we have to directly multiply
Numerator x Numerator
and Denominator x Denominator.

Multiply. Express the product as a whole number or a mixed number in simplest form. (Lesson 4.3)

Question 37.
\(\frac{4}{3}\) × \(\frac{7}{6}\) =
Answer:

Explanation:
\(\frac{4}{3}\) × \(\frac{7}{6}\) = \(\frac{14}{9}\)
Multiplication in fractions we have to directly multiply
Numerator x Numerator
and Denominator x Denominator.

Question 38.
\(\frac{8}{3}\) × \(\frac{9}{12}\) =
Answer:

Explanation:
\(\frac{8}{3}\) × \(\frac{9}{12}\)= 2
Multiplication in fractions we have to directly multiply
Numerator x Numerator
and Denominator x Denominator.

Question 39.
\(\frac{7}{8}\) × \(\frac{6}{5}\) =
Answer:

Explanation:
\(\frac{7}{8}\) × \(\frac{6}{5}\) = \(\frac{21}{20}\)
Multiplication in fractions we have to directly multiply
Numerator x Numerator
and Denominator x Denominator.

Question 40.
\(\frac{25}{4}\) × \(\frac{10}{8}\) =
Answer:

Explanation:
\(\frac{25}{4}\) × \(\frac{10}{8}\) = \(\frac{125}{16}\)
Multiplication in fractions we have to directly multiply
Numerator x Numerator
and Denominator x Denominator.

Multiply. Express the product as a whole number or a mixed number in simplest form. (Lesson 4.4)

Question 41.
2\(\frac{1}{4}\) × 16 =
Answer:

Explanation:
Converting the mixed fraction in to a fraction then multiply with 16
And done the simplest form to make into a whole number

Question 42.
27 × 1\(\frac{2}{9}\) =
Answer:

Explanation:
Converting the mixed fraction in to a fraction then multiply with 27
And done the simplest form to make into a whole number

Multiply. Express the product as a whole number or a mixed number in simplest form. (Lesson 4.4)

Question 43.
5\(\frac{3}{6}\) × 42 =
Answer:

Explanation:
Converting the mixed fraction in to a fraction then multiply with 42
And done the simplest form to make into a whole number

Question 44.
2\(\frac{5}{6}\) × 15 =
Answer:

Explanation:
Converting the mixed fraction in to a fraction then multiply with 15
And done the simplest form to make into a whole number

Divide. Express each quotient in simplest form. (Lesson 4.6)

Question 45.
3 ÷ \(\frac{1}{9}\) =
Answer:

Explanation:
Converting the whole number as a fraction
To divide a fraction with a whole number,
we multiply the given whole number with the denominator of the fraction.

Question 46.
6 ÷ \(\frac{1}{8}\) =
Answer:

Explanation:
Converting the whole number as a fraction
To divide a fraction with a whole number,
we multiply the given whole number with the denominator of the fraction.

Question 47.
5 ÷ \(\frac{1}{5}\) =
Answer:

Explanation:
Converting the whole number as a fraction
To divide a fraction with a whole number,
we multiply the given whole number with the denominator of the fraction.

Question 48.
2 ÷ \(\frac{1}{10}\) =
Answer:

Explanation:
Converting the whole number as a fraction
To divide a fraction with a whole number,
we multiply the given whole number with the denominator of the fraction.

Question 49.
\(\frac{7}{8}\) ÷ 5 =
Answer:

Explanation:
Converting the whole number as a fraction
To divide a fraction with a whole number,
we multiply the given whole number with the denominator of the fraction.

Question 50.
\(\frac{5}{8}\) ÷ 4 =
Answer:

Explanation:
Converting the whole number as a fraction
To divide a fraction with a whole number,
we multiply the given whole number with the denominator of the fraction.

Question 51.
\(\frac{4}{7}\) ÷ 12 =
Answer:

Explanation:
Converting the whole number as a fraction
To divide a fraction with a whole number,
we multiply the given whole number with the denominator of the fraction.

Question 52.
\(\frac{2}{9}\) ÷ 6 =
Answer:

Explanation:
Converting the whole number as a fraction
To divide a fraction with a whole number,
we multiply the given whole number with the denominator of the fraction.

Problem Solving

Solve. Show your work.

Question 53.
Ron used \(\frac{3}{5}\) pound of flour to bake bread and \(\frac{2}{7}\) pound of flour to bake scones. How many more pounds of flour did he use to bake bread than scones?
Answer: \(\frac{11}{35}\) more pounds of flour he used to bake bread than scones
Explanation:
Subtract them…
But to subtract fractions you need a common denominator (the smallest thing that 5 and 7 both go into)
Remember when making equivalent fractions with your common denominator (which is 7×5 = 35) make sure you multiply the top by whatever you multiplied the bottom by.

Question 54.
Tina uses 4\(\frac{5}{12}\) yards of wire for her science project. Kelvin uses 1\(\frac{2}{3}\) yards of wire for his project. How many yards of wire do they use altogether?
Answer: 6\(\frac{1}{12}\) yards of wire used altogether
Explanation:

Solve. Show your work

Question 55.
Rosa poured 1\(\frac{3}{4}\) quarts of grape juice into a container. She added 3\(\frac{1}{3}\) quarts of apple juice. She then poured 2\(\frac{2}{3}\) quarts of the mixed juice into a pitcher. How many quarts of mixed juice were left in the container?
Answer: 2\(\frac{5}{12}\)
Explanation:
1\(\frac{3}{4}\) =1\(\frac{9}{12}\)
3\(\frac{1}{3}\) = 3\(\frac{4}{12}\)

1\(\frac{9}{12}\)+ 3\(\frac{4}{12}\) = 4\(\frac{13}{12}\) = 5\(\frac{1}{12}\)

4\(\frac{13}{12}\) – 2\(\frac{8}{12}\) = 2\(\frac{5}{12}\)

Question 56.
A race was \(\frac{11}{12}\) mile long. Hamish ran \(\frac{4}{5}\) of the distance.

a. Without multiplying, explain how you know that the answer must be less than \(\frac{11}{12}\).
Answer:
With the help of bench mark. Both the values are lesser than 1. So he ran less than \(\frac{11}{12}\).

b. How far did he run?
Answer: \(\frac{7}{60}\)
Explanation:

Solve. Show your work.

Question 57.
Ashley uses \(\frac{1}{4}\) package of raisins for o fruit cake. She then uses \(\frac{1}{9}\) of the remainder for muffins. What fraction of the package of raisins does she have left?
Answer: \(\frac{23}{36}\) of the package of raisins she have left
Explanation:

Question 58.
Mrs. Vernon used 4\(\frac{3}{8}\) pounds of meat in each of her 12 pots of soup. How many pounds of meat did she use for the 12 pots of soup?
Answer: 52\(\frac{1}{2}\) pounds of meat she used.
Explanation:

Solve. Show your work.

Question 59.
A custodian pours \(\frac{1}{8}\) gallon of cleaning solution into each pail of water that she uses.

a. How many pails of water and cleaning solution can the custodian make using 16 gallons of cleaning solution?
Answer:

b. Find the volume of solution in two of these pails.
Answer:

Question 60.
A carnival sold 135 bottles of juice in one day. They sold \(\frac{1}{3}\) of the bottles in the first hour and \(\frac{2}{5}\) of the bottles in the second hour. How many bottles of juice did they sell altogether in these two hours?
Answer: 99 bottles sold altogether in these two hours
Explanation:

Solve. Show your work.

Question 61.
Ms. Li spent $840 on a vacation. She spent \(\frac{2}{3}\) of the amount on a plane ticket and \(\frac{1}{2}\) of the remaining amount on food. How much did she spend on the ticket and food altogether?
Answer: So she spent $560+$140 = $ 700  on the ticket and food altogether
Explanation:
Ms. Li spent $840 on a vacation. She spent \(\frac{2}{3}\) of the amount on a plane ticket. So she spent $560 for plane ticket.

She spent \(\frac{1}{2}\) of the remaining amount on food.
Remaining amount is $280.
So she spent $ 140 on food

So she spent $560+$140 = $ 700  on the ticket and food altogether

Question 62.
Sam traveled \(\frac{3}{4}\) of a journey by bus. He jogged \(\frac{1}{2}\) the remaining distance and walked the rest of the way. If he walked 800 feet, what was the total distance he traveled?
Answer: 6400 feet he traveled
Explanation:
Total Distance = x
Sam traveled \(\frac{3}{4}\) of a journey by bus. So it is \(\frac{3}{4}\) x
So remaining distance is x – \(\frac{3}{4}\) x =\(\frac{1}{4}\) x
He jogged \(\frac{1}{2}\) the remaining distance. So he jogged \(\frac{1}{8}\) x

walked the rest of the way . So remining is x – \(\frac{3}{4}\) x + \(\frac{1}{8}\) x  =800

Solve. Show your work.

Question 63.
Matthew used \(\frac{1}{5}\) of a box of flour for cooking and \(\frac{3}{4}\) of the remainder to make bread. The rest of the flour was packed equally into 5 containers. What fraction of the total amount of flour was in each container? r
Answer: \(\frac{1}{100}\) fraction of the total amount of flour was in each container
Explanation:
Matthew used \(\frac{1}{5}\) of a box of flour for cooking. So remaining flour is

\(\frac{3}{4}\) of the remainder to make bread

The rest of the flour was packed equally into 5 containers

Question 64.
A bus driver filled up \(\frac{7}{8}\) of her fuel tank for a trip. She used \(\frac{6}{7}\) of the fuel by the end of the trip. The capacity of her tank is 70 gallons. How much fuel did she use for the trip? Express your answer as a decimal.
Answer: 52.5gallons of fuel she used for the trip
Explanation:
The capacity of her tank is 70 gallons.
A bus driver filled up \(\frac{7}{8}\) of her fuel tank for a trip

So she filled 61.25 gallons of fuel in tank.
She used \(\frac{6}{7}\) of the fuel by the end of the trip.

Question 65.
Sergio walked to and from school on \(\frac{3}{5}\) of the days in one month. He got a ride to school on \(\frac{7}{8}\) of the remaining days. On the one remaining school day that month, he stayed home with a cold. How many school days were there that month?
Answer: 20 days
Explanation:
Total Days = x
Sergio walked to and from school on \(\frac{3}{5}\) of the days in one month = \(\frac{3}{5}\)x
So remaining days = x – \(\frac{3}{5}\)x = \(\frac{2}{5}\)x
He got a ride to school on \(\frac{7}{8}\) of the remaining days. = \(\frac{7}{20}\)x .Since

On the one remaining school day that month, he stayed home with a cold.
So

x =20

Go through the Math in Focus Grade 2 Workbook Answer Key Chapter 3 Practice 7 Subtraction with Regrouping in Hundreds, Tens, and Ones to finish your assignments.

Math in Focus Grade 2 Chapter 3 Practice 7 Answer Key Subtraction with Regrouping in Hundreds, Tens, and Ones

Regroup.
Then subtract.

Question 1.
241 – 173 = ?
241 – 173
= 2 hundreds 4 tens 1 one – 1 hundred 7 tens 3 ones
= 2 hundreds ________ tens 11 ones – 1 hundred 7 tens 3 ones
= _________ hundred 13 tens 11 ones – 1 hundred 7 tens 3 ones
= _________ hundreds _________ tens _________ ones
241 – 173 = ____
Use addition to check your answer.

Answer:
241-173 = 68,
173+68 = 241.

Explanation:
Given that 241 – 173 which is 68. So to check the answer we will perform addition, which is 173+68 = 241.
241 – 173
= 2 hundreds 4 tens 1 one – 1 hundred 7 tens 3 ones
= 2 hundreds 3 tens 11 ones – 1 hundred 7 tens 3 ones
= 1 hundred 13 tens 11 ones – 1 hundred 7 tens 3 ones
= 0 hundreds 6 tens 8 ones.

Question 2.

Answer:
478 – 199 = 279,
279+199 = 478.

Explanation:
Given that 478 – 199 which is 279. So to check the answer we will perform addition, which is
279+199 = 478.

Question 3.

Answer:
555-457 = 98,
457+98 = 555.

Explanation:
Given that 555 – 457 which is 98. So to check the answer we will perform addition, which is
457+98 = 555.

Question 4.
924 – 886 = ___

Answer:
924-886 = 38,
38+886 = 924.

Explanation:
Given that 924-886 which is 38. So to check the answer we will perform addition, which is
38+886 = 924.

Question 5.
818 – 669 = ___

Answer:
818-669 = 149,
149+669 = 818.

Explanation:
Given that 818-669 which is 149. So to check the answer we will perform addition, which is
149+669 = 818.

Help Daryl ride past these rocks to reach the shore. Subtract and write the correct answer on each rock.

Question 6.

Answer: