Hillary

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 18 Practice 2 Congruent Figures provides detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 18 Practice 2 Answer Key Congruent Figures

Does Figure A show a flip of Figure B? Write yes or no.

Question 1.

Answer: No
Explanation:
A flip is also called a reflection,
which rotates an object end over end.
So, A and B are not flip.

Question 2.

Answer: Yes
Explanation:
A flip is also called a reflection,
which rotates an object end over end.
So, A and B are flip. and figure B is flip of figure A

Does Figure C show a slide of Figure D? Write yes or no.

Question 3.

Answer: YES
Explanation:
Slides are the simplest transformation–just moving something from one place to another.  In primary grades, we usually describe a slide using relative position words, such as “slide down” or “slide to the right and down”
So, figure C slides right to form figure D.

Question 4.

Answer: YES
Explanation:
Slides are the simplest transformation–just moving something from one place to another.  In primary grades, we usually describe a slide using relative position words, such as “slide down” or “slide to the right and down”
So, figure C slides right to form figure D.

Does Figure E show a turn of Figure F? Write yes or no.

Question 5.

Answer: Yes
Explanation:
A turn or a rotation describes the motion of turning a shape as if it were drawn on a piece of paper.
The usual primary-grades vocabulary is a “turn” and the usual middle-grades vocabulary is “rotation”.

Question 6.

Answer: YES
Explanation:
A turn or a rotation describes the motion of turning a shape as if it were drawn on a piece of paper.
The usual primary-grades vocabulary is a “turn” and the usual middle-grades vocabulary is “rotation”.

Look at the pairs of figures. Identify and explain which pair is congruent and which is not.

Example

The two shapes are not congruent because they do not have the same shape.

Question 7.

The figures are ____________ because _________________.
Answer:
The figures are congruent because they have the same shape.
Explanation:
When two things are said to be congruent, it means that all of their measurements are identical.
So, the above figures are congruent.

Question 8.

The figures are ____________ because _________________.
Answer:
The figures are not congruent because they do not have the same shape.
Explanation:
When two things are said to be congruent, it means that all of their measurements are identical.
So, the above figures are not congruent.

Circle the pairs of congruent shapes.

Question 9.

Answer:
The figures are congruent because they have the same shape.
Explanation:
When two things are said to be congruent, it means that all of their measurements are identical.
So, the above figures are congruent.

Question 10.

Answer:
The figures are congruent because they have the same shape.
Explanation:
When two things are said to be congruent, it means that all of their measurements are identical.
So, the above figures are congruent.

Question 11.

Answer:
The figures are congruent because they have the same shape.
Explanation:
When two things are said to be congruent, it means that all of their measurements are identical.
So, the above figures are congruent.

Circle the congruent figures.

Question 12.

Answer:

Explanation:
When two things are said to be congruent, it means that all of their measurements are identical.
So, the 3rd figure is congruent to the given pentagon.

Question 13.

Answer:

Explanation:
When two things are said to be congruent, it means that all of their measurements are identical.
So, the 1st figure is congruent to the given Arrow Mark.

Draw congruent figures. Trace the shape. Cut it out and draw a congruent figure by sliding it from left to right.

Question 14.

Answer:

Explanation:
When two things are said to be congruent, it means that all of their measurements are identical.

Question 15.

Answer:

Explanation:
When two things are said to be congruent, it means that all of their measurements are identical.

Circle the figure that shows a flip.

Question 16.

Answer:

Explanation:
A flip is also called a reflection,
which rotates an object end over end.
So, in the above figure 1st letter is a flip of S.
Question 17.

Answer:

Explanation:
A flip is also called a reflection,
which rotates an object end over end.
So, in the above figure 3rd one is a flip of triangle.

Question 18.

Answer:

Explanation:
A flip is also called a reflection,
which rotates an object end over end.
So, in the above figure 3rd one is a flip of pentagon.

Circle the figure that shows a turn.

Question 19.

Answer:

Explanation:
A turn or a rotation describes the motion of turning a shape as if it were drawn on a piece of paper.
The usual primary-grades vocabulary is a “turn” and the usual middle-grades vocabulary is “rotation”.

Question 20.

Answer:

Explanation:
A turn or a rotation describes the motion of turning a shape as if it were drawn on a piece of paper.
The usual primary-grades vocabulary is a “turn” and the usual middle-grades vocabulary is “rotation”.

Question 21.

Answer:

Explanation:
A turn or a rotation describes the motion of turning a shape as if it were drawn on a piece of paper.
The usual primary-grades vocabulary is a “turn” and the usual middle-grades vocabulary is “rotation”.

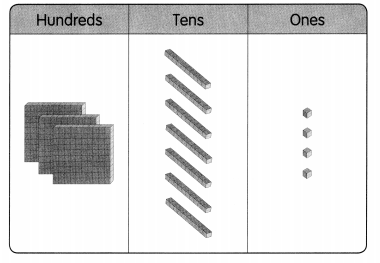
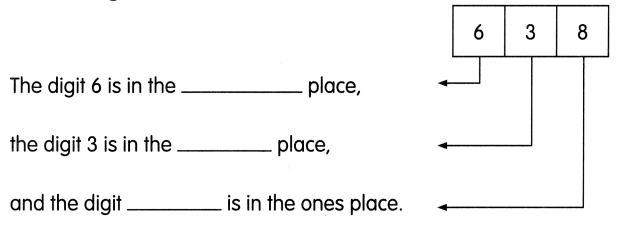
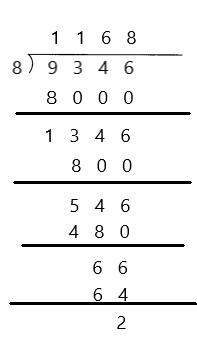
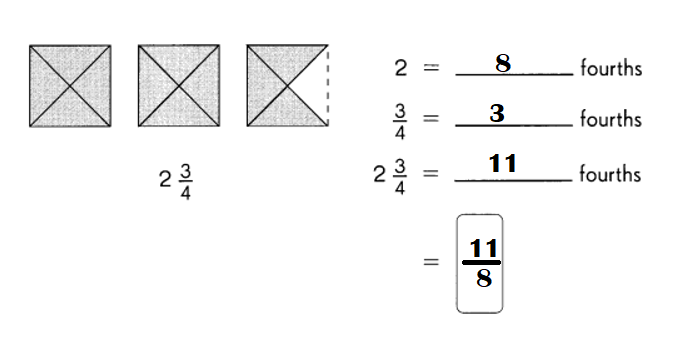
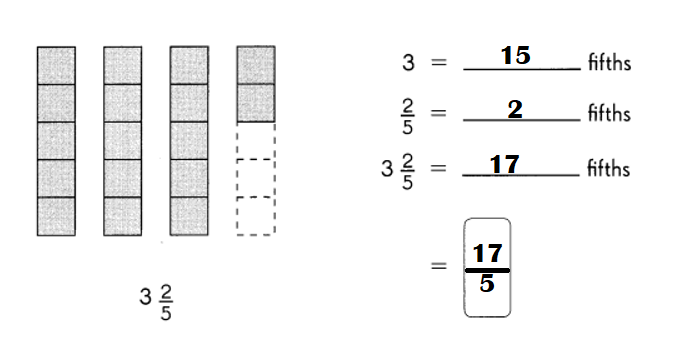
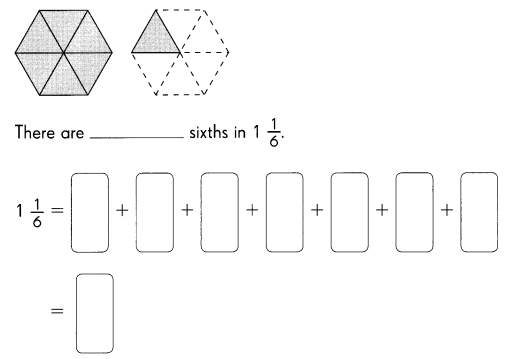
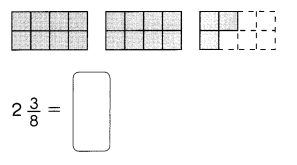
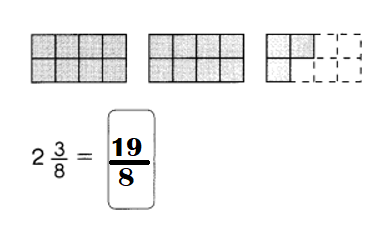
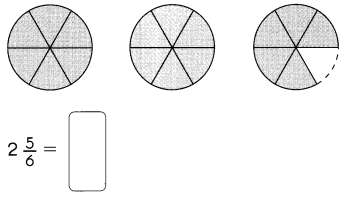
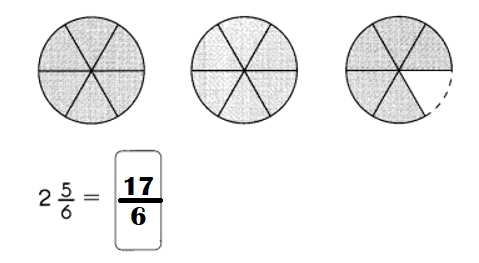
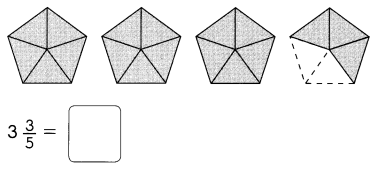
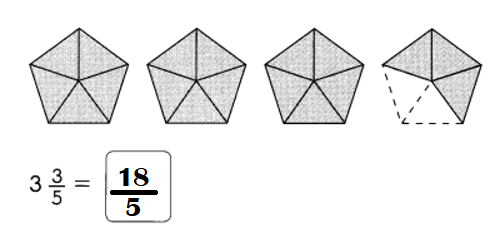
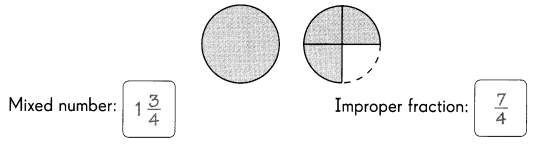
Go through the Math in Focus Grade 7 Workbook Answer Key Chapter 1 Lesson 1.5 Introducing Significant Digits to finish your assignments.

Math in Focus Grade 7 Course 2 A Chapter 1 Lesson 1.5 Answer Key Introducing Significant Digits

Math in Focus Grade 7 Chapter 1 Lesson 1.5 Guided Practice Answer Key

List the significant digits for each number. Then write the number of significant digits.

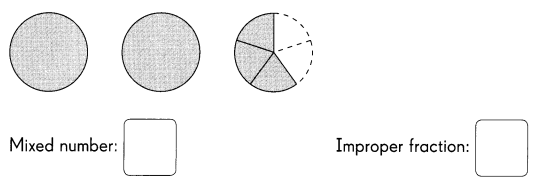
Question 1.
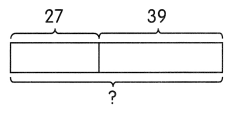
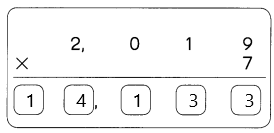
23,005
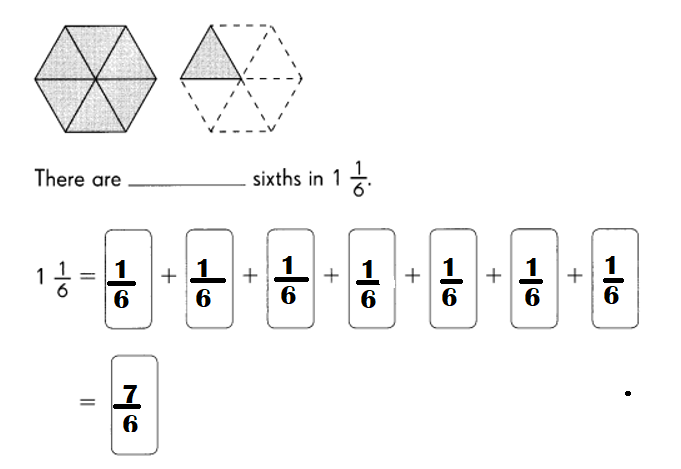
The two zeros are in between nonzero digits. Using RULES 1 and 2, 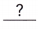are significant digits.
There are 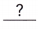significant digits.
Answer:
There are 3 rules to find the significant figures. They are
Non zero digits are always significant figures.
Any zeros between the two significant figures are also significant.
The zeros in the decimal portion is also significant.
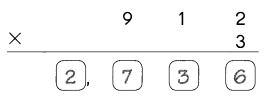
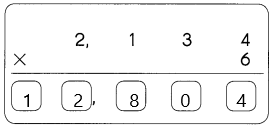
23005 has 5 significant figures.
The 5 significant figures are 2, 3, 0, 0, 5.

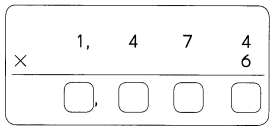
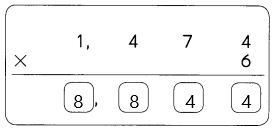
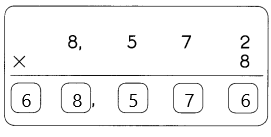
Question 2.
367.9410
The trailing zero in the decimal is 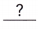. Using RULES 1 and 3, 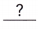are significant digits.
There are 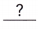significant digits.
Answer:
There are 3 rules to find the significant figures. They are
Non zero digits are always significant figures.
Any zeros between the two significant figures are also significant.
The zeros in the decimal portion is also significant.
All the digits in the 367.9410 is significant.
It has 7 significant figures they are 3, 6, 7, 9, 4, 1, 0.

Question 3.
0.094
Answer:
There are 3 rules to find the significant figures. They are
Non zero digits are always significant figures.
Any zeros between the two significant figures are also significant.
The zeros in the decimal portion is also significant.
The number 0.094 has 2 significant figures. They are 9 and 4.

Question 4.
450.0
Answer:
There are 3 rules to find the significant figures. They are
Non zero digits are always significant figures.
Any zeros between the two significant figures are also significant.
The zeros in the decimal portion is also significant.
The number 450.0 has 4 significant figures. They are 4, 5, 0, 0.

Complete.

Question 5.
Round 346 to 2 significant digits.
The third significant digit is 6, which is 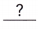than 5.
346 is closer to 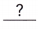than to .
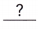So, the integer rounded to 2 significant digits is .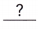
Answer:
The third significant digit is 6, which is greater than 5.
346 is closer to 350 than to 340
So, the integer rounded to 2 significant digits is 350

Round each integer to the number of significant digits given.

Question 6.
16,890 (3 significant digits)
Answer:
In the integer after 3 digits the tens place is greater than 5 so it is written as 16900.
The integer 16890 rounded to the 3 significant digits is 16900.
In the number 16900 the 3 significant numbers are 1,6,9.

Question 7.
96,500,100 (2 significant digits)
Answer:
In the integer after 2 digits the lakhs place is equal to 5 then it is written has 97000000
The integer 96,500,100 rounded to the 2 significant digits is 97000000.
Tn the number 97000000 The 2 significant digits are 9 and 7.

Question 8.
8,253,611 (4 significant digits)
Answer:
In the integer after 4 digits the hundred place is greater than 5 then it is written has 8254000
The integer 8253611 rounded to the 4 significant digits is 8254000.
Tn the number 8254000 The 4 significant digits are 8, 2, 5, 4.

Question 9.
7,462 (1 significant digits)
Answer:
In the integer after 1 digit the hundred place is less than 5 then it is written has 7000
The integer 7462 rounded to the 1 significant digits is 7000.
In the number 7000 The 1 significant digits are 7.

Solve.

The integer 6,590,000 is obtained after rounding a number to the hundreds place.
The integer 200,000 is obtained after rounding another number to the ten thousands place.

Question 10.
List the significant digits in each integer.
Answer:
There are 3 rules to find the significant figures. They are
Non zero digits are always significant figures.
Any zeros between the two significant figures are also significant.
The zeros in the decimal portion is also significant.
In the number 65,90,000 the significant figures are 6,5,9.
In the number 200000 The significant figure 1s 2.

Question 11.
State the number of significant digits in each integer.
Answer:
The integer 6,590,000 has 3 significant figures. They are 6,5,9.
The integer 200,00 has 1 significant figures. They are 2.

Complete.

Question 12.
Round 1,230.320 to 5 significant digits.
Using RULE 3, all the digits in 1,230.320 are significant. Only 5 significant digits are required. The sixth significant digit is 2, which is 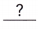than 5. So, the decimal rounded to 5 significant digits is .
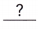Answer:
In the given number after 5 digits from the left the tens place is less than 5 then it is written has 1,230.3
The number 1,230.320 rounded to the 5 significant digits is 1230.3.
In the number 1230.3. The 5 significant digits are 1,2,3,0,3.

Question 13.
Round 0.8765421 to 3 significant digits.
Using RULES 1 and 4, only the digits after the decimal point are significant. Only 3 significant digits are required. The fourth significant digit is 5, which is 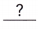5. So, the decimal rounded to 3 significant digits is .
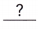Answer:
In the given number after 3 digits from the left the ten thousands place is greater than 5 then it is written has 0.977
The number 0.8765421 rounded to the 3 significant digits is 0.977.
In the number 0.977. The 5 significant digits are 9,7,7.

Round each decimal to the number of significant digits given.

Question 14.
35.0997 (4 significant digits)
Answer:
In the given number 35.0997 after 4 digits from the left the tens place is less than 5 then it is written has 35.10
The number 35.997 rounded to the 4 significant digits is 35.10.
In the number 35.997. The 4 significant digits are 3,5,1,0.

Question 15.
0.008010002 (5 significant digits)
Answer:
In the given number 0.008010002 after 5 digits from the left the ten thousands place is less than 5 then it is written has 0.0080100.
The number 0.008010002 rounded to the 5 significant digits is 0.0080100.
In the number 0.0080100. The 5 significant digits are 0,0,8,0,1.

Question 16.
74.015 (3 significant digits)
Answer:
In the given number 74.015 after 3 digits from the left the tens place is less than 5 then it is written has 74.0.
The number 74.015 rounded to the 3 significant digits is 74.0.
In the number 74.0. The 3 significant digits are 7,4,0.

Solve.

Question 17.
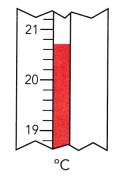
A reading of a thermometer in Celsius is shown.
a) List the digits in the reading that are certain.
Answer:
Looking closely at the given thermometer, we found the reading in the thermometer is 20.6°C
The digits that are certain are 2, 0, and 6

b) List the digit that is not certain, the estimated digit. Write an approximate reading with two decimal places.
Answer:
The reading is in between 20.6° C and 20.7° C
The approximate reading with two decimal places is 20.65°C

c) State the number of significant digits the reading has.

Answer:
There are 4 significant digits in 20.65°C

Solve.

Question 18.
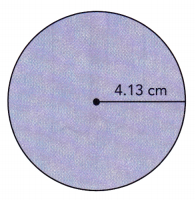
The area of a circle is given by the expression πr². The radius of a circle is 4.13 centimeters.
a) Calculate the area of the circle.
b) State the area of the circle correct to 3 significant digits.

Answer:
Given that,
The radius of the circle is 4.13 centimeters.
The area of the circle is A = πr²
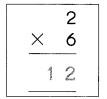
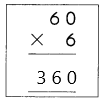
A = 3.14 x(4.13)²
A = 53.5

Math in Focus Course 2A Practice 1.5 Answer Key

List the significant digits for each number. Then count the number of significant digits.

Question 1.
0.0017
Answer:
There are 3 rules to find the significant figures. They are
Non zero digits are always significant figures.
Any zeros between the two significant figures are also significant.
The zeros in the decimal portion is also significant.
The number 0.0017 has 2 significant figures. They are 1 and 7.

Question 2.
82.005
Answer:
There are 3 rules to find the significant figures. They are
Non zero digits are always significant figures.
Any zeros between the two significant figures are also significant.
The zeros in the decimal portion is also significant.
The number 82.005 has 5 significant figures. They are 8, 2, 0, 0, 5.

Question 3.
300.0
Answer:
There are 3 rules to find the significant figures. They are
Non zero digits are always significant figures.
Any zeros between the two significant figures are also significant.
The zeros in the decimal portion is also significant.
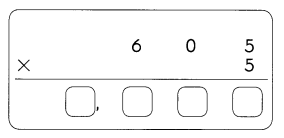
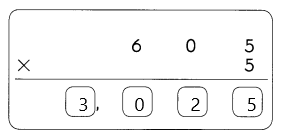
The number 300.0 has 4 significant figures. They are 3,0,0,0.

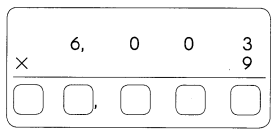
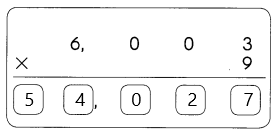
Question 4.
0.0600
Answer:
Rules to Identify Significant Digits in a Given Numbers :
RULE 1 → All nonzero digits are significant.
RULE 2 → Zeros in between nonzero digits are significant.
RULE 3 → Trailing zeros in a decimal are significant.
RULE 4 → Zeros on the left of the first nonzero digit are NOT significant.
RULE 5 → Trailing zeros in any integer may or may not be significant due to rounding.

0.0600

Zeros on the left of the first nonzero digit are not significant,
Using Rule 4, <u> 6, 0 and 0 </u> are significant digits.
There are <u>three</u> significant digits.

6, 0, and 0; Three

Question 5.
45.13
Answer:
There are 3 rules to find the significant figures. They are
Non-zero digits are always significant figures.
Any zeros between the two significant figures are also significant.
The zeros in the decimal portion are also significant.
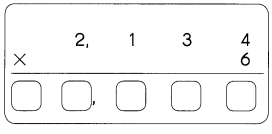
The number 45.13 has 4 significant figures. They are 4,5,1,3.

Question 6.
2.002
Answer:
There are 3 rules to find the significant figures. They are
Non-zero digits are always significant figures.
Any zeros between the two significant figures are also significant.
The zeros in the decimal portion are also significant.
The number 2.002 has 4 significant figures. They are 2,0,0,2.

Round each integer to the number of significant digits stated in the parentheses.

Question 7.
8,496 (to 2 significant digits)
Answer:
In the given number after 2 digits from the left, the tens place is greater than 5 then it is written as 8500.
The number 8496 rounded to the 2 significant digits is 8500.
In the number 8500, The 2 significant digits are 8,5.

Question 8.
187,204 (to 3 significant digits)
Answer:
In the given number after 3 digits from the left, the hundred places are less than 5 then it is written has 187000.
The number 187204 rounded to the 3 significant digits is 187000.
In the number 187000. The 3 significant digits are 1,8,7.

Question 9.
39,148 (to 3 significant digits)
Answer:
In the given number after 3 digits from the left, the tens place is less than 5 then it is written as 39100.
The number 39148 rounded to the 3 significant digits is 39100.
In the number 39100. The 5 significant digits are 3,9,1.

Question 10.
40,100 (to 2 significant digits)
Answer:
In the given number after 2 digits from the left, the hundred places are less than 5 then it is written as 40000.
The number 40,100 rounded to the 2 significant digits is 40000.
In the number 40000. The 2 significant digits are 4,0.

Question 11.
5,300,924 (to 4 significant digits)
Answer:
In the given number after 4 digits from the left the hundred places is greater than 5 then it is written as 5301000
The number 5300924 rounded to the 4 significant digits is 5301000.
In the number 5301000. The 4 significant digits are 5,3,0,1.

Question 12.
111,111 (to 4 significant digits)
Answer:
In the given number after 4 digits from the left, the tens place is less than 5 then it is written as 111100
The number 111,111 rounded to the 4 significant digits is 111100.
In the number 111100. The 4 significant digits are 1,1,1,1.

Question 13.
99,000 (to 3 significant digits)
Answer:
In the given number after 3 digits from the left, the tens place is less than 5 then it is written as 990
The number 99000 rounded to the 3 significant digits is 990.
In the number 990. The 5 significant digits are 9,9,0.

Question 14.
820,635 (to 1 significant digit)
Answer:
In the given number after 1 digit from the left, the ten thousand places is less than 5 then it is written as 9000000.
The number 820,635 rounded to the 1 significant digit is 9000000.
In the number 9000000. The 5 significant digits are 9.

Round each decimal to the given number of significant digits.

Question 15.
0.7621 (to 1 significant digit)
Answer:
In the given number after 1 digits from the left the thousand place is greater than 5 then it is written has 0.8.
The number 0.7621 rounded to the 2 significant digits is 0.8.
In the number 0.8. The 2 significant digits are 8,0.

Question 16.
1 .0087 (to 2 significant digits)
Answer:
In the given number after 2 digits from the left the hundred place is less than 5 then it is written has 1.0.
The number 1.0087 rounded to the 2 significant digits is 1.0.
In the number 1.0. The 2 significant digits are 1,0.

Question 17.
45.91082 (to 5 significant digits)
Answer:
In the given number after 5 digits from the left, the tens place is greater than 5 then it is written
45.911.
The number 45.91082 rounded to the 5 significant digits is 45.911.
In the number 45.911. The 5 significant digits are 5,4,9,1,1.

Question 18.
0.08507 (to 3 significant digits)
Answer:
In the given number after 3 digits from the left, the hundreds place is equal to 5 then it is written as 0.0851.
The number 0.08507 rounded to the 3 significant digits is 0.0851.
In the number 0.0851. The 3 significant digits are 8,5,1.

Question 19.
520.8 (to 3 significant digits)
Answer:
In the given number after 3 digits from the left the ones place is greater than 5 then it is written has 521.
The number 520.8 rounded to the 3 significant digits is 521.
In the number 521 The 3 significant digits are 5,2,1.

Question 20.
4.381 (to 2 significant digit)
Answer:
In the given number after 2 digits from the left the tens place is greater than 5 then it is written has 4.4.
The number 4.381 rounded to the 2 significant digits is 4.4.
In the number 4.4. The 2 significant digits are 4,4.

Solve.

Question 21.
Round 0.09845 and 109,530 to the given number of significant digits.
a) 1 significant digit
b) 2 significant digits
c) 3 significant digits
Answer:
a) 0.09845 rounded to 1 significant digit is 0.10.
109530 rounded to 1 significant digit is 100000.
b) 0.09845 rounded to 2 significant digit is 0.098.
109,530 rounded to 2 significant digit is 0.098.
c) 0.09845 rounded to 3 significant digit is 0.0985
109530 rounded to 3 significant digit is 110000.

Question 22.
The touchpad that Mike hits at the end of a swimming race is calibrated to measure the time to the nearest hundredth of a second. John claims that Mike won the race by 0.005 second. Jacqui says that Mike won by 0.05 second. Whose claim is more reliable? State your reason.

Answer:
John claims : Mike won the race by 0.005 seconds.
Jacqui claims : Mike won the race by 0.05 seconds.
So, 0.05 second is much more reliable than 0.005 seconds.
Hence, Jacqui claim is much more reliable.

Question 23.
Table A measures 2 feet long and table B measures 2.0 feet long.
a) How many significant digits are there in each measurement?
Answer:
Given that,
The table A measures 2 feet long.
There are 1 significant digit in the 2 feet long.
The table B measures 2.0 feet long.
There are 2 significant figures in the 2.0 feet long.

b) Do you think that the measurements are rounded values? Explain your answer.
Answer:
If we round Table 2 measurement of 2.0 feet long to 1 significant digit, we see that is rounded to 2 feet long, which is same as Table A measurement.
Thus, the measurement of Table A and Table B are rounded value.
Yes

Question 24.
A bag of potatoes weighs 9.42 pounds on a weighing scale. Which of the significant digits in the scale reading is the least reliable? Explain your answer.
Answer:
A bag of potatoes weighs 9.42 pounds
The significant digits are 9, 4, and 2
Since, the significant digit 2 is the hundredth reading so, it is least reliable.
2

Question 25.
The thickness of a ream of 500 sheets of paper is 57.15 millimeters. What is the thickness of one sheet of paper correct to 2 significant digits?
Answer:
Given that,
The thickness of a ream of 500 sheets of paper is 57.15 millimeters.
The thickness of 1 sheet is 500/57.15 is 8.7489.
The correct to the 2 significant digits is 8.7.

Question 26.
Given a rectangle of length 36.80 centimeters and width 13.4 centimeters, find the area of the rectangle correct to 3 significant digits.
Answer:
Given that,
The length of a rectangle is 36.80 centimeters.
The width of the rectangle is 13.4 centimeters.
The area of the rectangle is length l x B = 36.80 x 13.4 = 13.4 centimeter.
The 13.4 is correct to the 3 significant digit.

Question 27.
The temperature ranges from 43.5°C to 44.5°C in an experiment. You want to find the average of the two extreme temperature readings.
a) What would you write as the value of the average temperature?
Answer:
Given that,
The temperature range is 43.5°C to 44.5°C.
The average temperature is 44.5°C – 43.5°C = 1°C.

b) How many significant digits will the value of the average temperature have?
Answer:
In the 1°C the number of significant digits are one they are 1.

Question 28.
The average distance of the Sun from the Earth is about 93,000,000 miles. How many of the trailing zeros could be significant? State your reason.
Answer:
Given that,
The distance of the sun from from the earth is 9300000 miles.
The trailing zeros means no numbers after continues zero.
The trailing zeros of the number 93000000 is 000000 are 6 zeros.

Brain Work

Use the decimal representation of π, 3.141592653…, to answer the following questions.

a) Describe an irrational number, a, which is at a distance of 0.0001 unit from π.
Answer:
3.141592653
Irrational number at a distance of 0.0001 unit from π
3.141592653 + 0.0001 = 3.141692653

b) Describe another irrational number, b, which is even closer to π than the previous answer.
Answer:
Another irrational number which is closer to π than previous answer :
Any irrational number between 3.141592653 and 3.141692653 is the answer.
Thus, 3.141592754 is closer to π than 3.141692653
3.141592754

c) Graph the positions of n and the two irrational numbers on a real number line.
Answer:

d) What can you conclude about the irrational numbers on the real number line?
Answer:

Go through the Math in Focus Grade 2 Workbook Answer Key Chapter 4 Practice 1 Using Part-Part-Whole in Addition and Subtraction to finish your assignments.

Math in Focus Grade 2 Chapter 4 Practice 1 Answer Key Using Part-Part-Whole in Addition and Subtraction

Solve.

Use the bar models to help you.

Question 1.
Miss Lucy has 27 students in her morning ballet class. She has 39 students in her afternoon ballet class. How many students does she have in both classes?

27 + 39 = ____
She has ____ students in both classes.
Answer:
She has 66 students in both classes.

Explanation:
Given that Miss Lucy has 27 students in her morning ballet class and she has 39 students in her afternoon ballet class. So the number of students does she have in both classes is 27+39 which is 66 students.

Question 2.
Rani collects 365 beads in January. She collects 419 beads in April. How many beads does she collect in January and April?

She collects ___ beads in January and April.
Answer:
She collects 784 beads in January and April.

Explanation:
Given that Rani collects 365 beads in January and she collects 419 beads in April. So the number of beads does she collect in January and April is 365+419 which is 784 beads.

Solve.

Draw bar models to help you.

Question 3.
Mr. Jackson drove 427 miles last week. This week, he drove 215 miles. How many miles did he drive in the two weeks?

He drove ___ miles in the two weeks.
Answer:
He drove 642 miles in the two weeks.

Explanation:
Given that Mr. Jackson drove 427 miles last week and this week, he drove 215 miles. So the number of miles did he drive in the two weeks is 427+215 which is 642 miles.

Question 4.
143 men and 62 women go to a concert. How many adults go to the concert?
____ adults are at the concert.
Answer:
205 adults are at the concert.

Explanation:
Given that 143 men and 62 women go to a concert. So the number of adults who attended to the concert is 143+62 which is 205 adults.

Solve.

Use the bar models to help you.

Question 5.
There are 278 people at a camp. 26 of them are teachers and the rest are children. How many children are there?

278 – 26 = ____
There are ___ children.
Answer:
There are 252 children.

Explanation:
Given that there are 278 people at a camp and 26 of them are teachers and the rest are children. So the number of children is 278-26 which is 252 children.

Question 6.
Mr. Wilson packs 431 files in two boxes. He packs 216 files in the first box. How many files does he pack in the second box?

He packs ___ files in the second box.
Answer:
He packs 215 files in the second box.

Explanation:
Given that Mr. Wilson packs 431 files in two boxes and he packs 216 files in the first box. So the number of files does he pack in the second box is 431-216 which is 215 boxes.

Solve.

Draw bar models to help you.

Question 7.
A letter carrier delivers 999 letters in two days. The carrier delivers 306 letters on Monday and the rest of the letters on Tuesday. How many letters does the carrier deliver on Tuesday?

The carrier delivers ___ letters on Tuesday.
Answer:
The carrier delivers 693 letters on Tuesday.

Explanation:
Given that a letter carrier delivers 999 letters in two days and the carrier delivers 306 letters on Monday and the rest of the letters on Tuesday. So the number of letters does the carrier delivers on Tuesday is 999-306 which is 693 letters.

Question 8.
A factory makes 674- toys in two days. 325 toys are made on the first day. How many toys does the factory make on the second day?
The factory makes ___ toys on the second day.
Answer:
The factory makes 349 toys on the second day.

Explanation:
Given that a factory makes 674 toys in two days and 325 toys are made on the first day. So the number of toys does the factory makes on the second day is 674-325 which is 349 toys.

Go through the Math in Focus Grade 2 Workbook Answer Key Chapter 1 Numbers to 1,000 to finish your assignments.

Math in Focus Grade 2 Chapter 1 Answer Key Numbers to 1,000

Math Journal

Count on or count back.

Question 1.

Answer:

Explanation:
The pattern is add 1
For every number 1 is added to get 10 more of 132 that is 142

Question 2.

___ is 100 more than ____
Answer:

Explanation:
The pattern is add 10
For every number 10 is added to get 100 more of 0 that is 100

Put On Your Thinking cap!

challenging Practice

Answer the question.
Sunny Snake has swallowed some eggs. The eggs have numbers that follow a pattern. Find the missing numbers.

Answer:

Explanation:
The pattern described in snake is add + 12
For every number 12 is added

Put on Your Thinking cap!

Problem Solving

Answer the question.

Sally and Hans started counting at the same time. Sally counted on by tens from 300. Hans counted back by hundreds. After six counts, they had reached the same number What number did Hans start counting from?

Sally’s counting:
300 + 10 = 310
310 + 10 = 320
320 + 10 = 330
330 + 10 = 340
340 + 10 = 350
350 + 10 = 360
Hans counting
960 he started counting
960 – 100 = 860
860 – 100 = 760
760 – 100 = 660
660 – 100 = 560
560 – 100 = 460
460 – 100 = 360
So, they reached at 360

Chapter Review/Test

Vocabulary

Question 1.
Match.

Answer:

Explanation:
Vocabulary is matched with the appropriate images.

Concepts and Skills

Fill in the blank.

Question 2.

The number shown above is ____
Answer:
The number shown above is 376
Explanation:
1 cube = 100; 3 x 100 = 300
1 line = 10; 7 x 10 = 70
1 dots = 1; 4 x 1 = 4
300 + 70 + 4 = 374

Fill in the blanks.

Question 3.
Five hundred forty-nine is the ___ form of 549.
Answer:
Five hundred forty-nine is the word form of 549.

Question 4.
The standard form of 549 is ___ and the expanded form is ___.
Answer:
The standard form of 549 is 549 and the expanded form is  500 + 40 + 9

Question 5.
In 549, the digit 4 is in the __ place, the digit ___ is in the hundreds place, and the digit 9 is in the ___ place.
Answer:
In 549, the digit 4 is in the tens place, the digit 5 is in the hundreds place, and the digit 9 is in the ones place.

Find the missing numbers or words.

Question 6.

Answer:

Explanation:
Place value is the value of each digit in a number
Place value can be defined as the value represented by a digit in a number on the basis of its position

Fill in the blanks. Use the items in the box to help you.

Question 7.
_______ is greater than ____.
Answer:
969 is greater than 696.
Explanation:
The words are used from vocabulary table

Question 8.
696 ___ 969
Answer:
696 < 969
Explanation:
The symbols are used from vocabulary table

Question 9.
969 ____ 696
Answer:
969 > 696
Explanation:
The symbols are used from vocabulary table

Write the numbers in order from least to greatest.

Question 10.

Answer:

Explanation:
Always start with the largest number. Always make sure the numbers are in order from largest to smallest. Always end with the smallest number

Find the missing numbers.

Question 11.
977 ____ 957 947 ___ ___ 917
Answer:
977 967 957 947 937 927 917
Explanation:
In the above pattern tens place is decreased by 1
that means ten

Problem Solving

Solve.

Question 12.
Taisha has 654 stickers. Jan has 564 stickers and Pedro has 645 stickers. Who has the most stickers and who has the least stickers?
___ has the most stickers and ___ has the least stickers.
Answer:
Taisha has the most stickers and Jan has the least stickers.
Explanation:
Taisha has 654 stickers.
Jan has 564 stickers and Pedro has 645 stickers.
Taisha has more and Pedro has 645
and they are having more than Jan

Question 13.
Winston climbed some steps. With each step he took, he counted on by tens. He started counting from the number 50 (Step 1) and stopped when he counted to 120.

He stopped at step ____
Answer:
At step 8 he stopped
Explanation:
He started at step 1 that is from 50
he added 10 for every step
he stopped at 120

Go through the Math in Focus Grade 4 Workbook Answer Key Chapter 1 Practice 1 Numbers to 10,000 to finish your assignments.

Math in Focus Grade 4 Chapter 1 Practice 1 Answer Key Numbers to 10,000

Write each number in standard form.

Example.
Seventy-two thousand, four hundred sixty 72,460

Question 1.
seventy thousand, eight hundred twenty-three ____
Answer: 70,823
7 is in the ten thousand place
0 is in the thousands place
8 is in the hundreds place
2 is in the tens place
3 is in the one’s place.
By using a place chart we can easily write the number:

According to the place value chart write the number: 70,823

Question 2.
sixty-two thousand, four hundred eighteen ____
Answer: 62,418
6 is in the ten thousand place
2 is in the thousands place
4 is in the hundreds place
1 is in the tens place
8 is in the one’s place.

Question 3.
ninety-seven thousand, four hundred ____
Answer: 97,400
9 is in the ten thousand place
7 is in the thousands place
4 is in the hundreds place
0 is in the tens place
0 is in the one’s place.

Question 4.
thirty thousand, eleven ____
Answer:30,011
3 is in the ten thousand place
0 is in the thousands place
0 is in the hundreds place
1 is in the tens place
1 is in the one’s place.

Write each number in word form.

Example
56,548 fifty-six thousand, five hundred forty-eight

Question 5.
12,021 ______
Answer: twelve thousand, twenty-one
Explanation:
– On beginning with the first digit that is 1. It is present in the place of a ten thousand – 10,000
– The next number to the right side is thousands place – two thousand
– The comma present on the rightmost side represents – twenty-one
– 12,021 in word format is twelve thousand, twenty-one.

Question 6.
70,009 ______
Answer: seventy thousand nine
Explanation:
Explanation:
– On beginning with the first digit that is 1. It is present in the place of a ten thousand – 70,000
– The comma present on the rightmost side represents – nine
– 70,009 in word format is seventy thousand nine

Question 7.
40,807 ______
Answer:
Explanation:
– On beginning with the first digit that is 1. It is present in the place of a ten thousand – 40,000
– The comma present on the rightmost side represents – eight hundred seven
– 40,807 in word format is forty thousand eight hundred seven.

Count on and fill in the blanks.

Question 8.
81,000 82,000 83,000 ____ ____
Answer: 84,000   85,000
A list of numbers that follow a certain sequence is known as patterns or number patterns. The different types of number patterns are algebraic or arithmetic patterns, geometric patterns, Fibonacci patterns and so on. Now, let us take a look at the three different patterns here.
Arithmetic pattern: The arithmetic pattern is also known as the algebraic pattern. In an arithmetic pattern, the sequences are based on the addition or subtraction of the terms. If two or more terms in the sequence are given, we can use addition or subtraction to find the arithmetic pattern.
The above-given sequence, 81,000 82,000 83,000 ____ ____ . Now, we need to find the missing term in the sequence.
Here, we can use the addition process to figure out the missing terms in the patterns.
In the pattern, the rule used is “Add 1000 to the previous term to get the next term”.
In the given above, take the second term (82,000). If we add “1000” to the second term (82,000), we get the third term 83,000.
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 83,000. Therefore, 83,000+1000= 84,000.
Second missing term: The previous term is 84,000. So, 84,000+1000 = 85,000.
Hence, the complete arithmetic pattern is 81,000 82,000 83,000  84,000  85,000.

Question 9.
30,000 40,000 50,000 ___ ___
Answer: 60,000   70,000
A list of numbers that follow a certain sequence is known as patterns or number patterns. The different types of number patterns are algebraic or arithmetic patterns, geometric patterns, Fibonacci patterns and so on. Now, let us take a look at the three different patterns here.
Arithmetic pattern: The arithmetic pattern is also known as the algebraic pattern. In an arithmetic pattern, the sequences are based on the addition or subtraction of the terms. If two or more terms in the sequence are given, we can use addition or subtraction to find the arithmetic pattern.
The above-given sequence, 30,000 40,000 50,000 ___ ___ . Now, we need to find the missing term in the sequence.
Here, we can use the addition process to figure out the missing terms in the patterns.
In the pattern, the rule used is “Add 10,000 to the previous term to get the next term”.
In the given above, take the second term (40,000). If we add “1000” to the second term (40,000), we get the third term of 50,000.
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 50,000. Therefore, 50,000+10,000= 60,000.
Second missing term: The previous term is 60,000. So, 60,000+1000 = 70,000.
Hence, the complete arithmetic pattern is 30,000 40,000 50,000   60,000   70,000

Question 10.
10,000 15,000 20,000 ___ ____
Answer: 25,000   30,000
A list of numbers that follow a certain sequence is known as patterns or number patterns. The different types of number patterns are algebraic or arithmetic patterns, geometric patterns, Fibonacci patterns and so on. Now, let us take a look at the three different patterns here.
Arithmetic pattern: The arithmetic pattern is also known as the algebraic pattern. In an arithmetic pattern, the sequences are based on the addition or subtraction of the terms. If two or more terms in the sequence are given, we can use addition or subtraction to find the arithmetic pattern.
The above-given sequence, 10,000 15,000 20,000 ___ ____ . Now, we need to find the missing term in the sequence.
Here, we can use the addition process to figure out the missing terms in the patterns.
In the pattern, the rule used is “Add 5,000 to the previous term to get the next term”.
In the given above, take the second term (15,000). If we add “5000” to the second term (15,000), we get the third term of 20,000.
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 20,000. Therefore, 20,000+5,000= 25,000.
Second missing term: The previous term is 25,000. So, 25,000+5000 = 30,000.
Hence, the complete arithmetic pattern is 10,000 15,000 20,000  25,000   30,000

Example
two thousand, five hundred twelve 2,512

Question 11.
sixty-one thousand, ____ ___ 1,001
Answer: 61, 001
The word form is sixty-one thousand, one
Explanation:
– On beginning with the first digit that is 6. It is present in the place of a ten thousand – 61,000
– The comma present on the rightmost side represents – one
– 61,001 in word format is sixty-one thousand, one.
The standard form is 61,001.

Question 12.
twenty-four ____, three hundred ten 24,3__0
Answer:24,310
The word form is twenty-four thousand, three hundred ten.
Explanation:
– On beginning with the first digit that is 2. It is present in the place of a ten thousand to thousands – 24,000
– The comma present on the rightmost side represents – three hundred one
– 24,310 in word format is twenty-four thousand, three hundred ten.
The standard form is 24,310.

Question 13.
forty-five thousand, ____ hundred six 4 __,206
Answer: 45,206
Explanation:
– On beginning with the first digit that is 4. It is present in the place of a ten thousand to thousands – 45,000
– The comma present on the rightmost side represents – two hundred six
– 45,206 in word format is forty-five thousand, two hundred six.
The standard form is 45,206.

Question 14.
thirty-six thousand, one hundred. _____ 36,89
Answer: 36,100
Explanation:
– On beginning with the first digit that is 3. It is present in the place of a ten thousand to thousands – 36,000
– The comma present on the rightmost side represents – one hundred
– 36,100 in word, format is thirty-six thousand, one hundred
The standard form is 36,100

Make each 5-digit number using all the cards. Do not begin a number with ‘0’.

Question 15.
An odd number: _______________________________________
Answer: 52,907
Generally, the even and odd numbers are defined as follows:
Definition 1: “Even numbers are those numbers which are divisible by 2 and odd numbers which are not divisible by two”.
Definition 2: “Even numbers are those which when divided by 2 leaves no remainder or as 0 and Odd numbers are those numbers which when divided by 2 leaves a remainder of 1”.
How to check a number is even or odd:
– As we know now that “Even numbers those numbers which end with 0,2,4,6,8 and odd numbers are those numbers which end with 1,3,5,7,9.”
– So, first, look at the number in the one’s place. This single number will tell whether the entire number is odd or even.
Here the above number is 52,907
When it divided by 2 it leaves remainder 1. So it is odd number.

Question 16.
An even number: ________________________________________
Answer:25,970
Generally, the even and odd numbers are defined as follows:
Definition 1: “Even numbers are those numbers which are divisible by 2 and odd numbers which are not divisible by two”.
Definition 2: “Even numbers are those which when divided by 2 leaves no remainder or as 0 and Odd numbers are those numbers which when divided by 2 leaves a remainder of 1”.
How to check a number is even or odd:
– As we know now that “Even numbers those numbers which end with 0,2,4,6,8 and odd numbers are those numbers which end with 1,3,5,7,9.”
– So, first, look at the number in the one’s place. This single number will tell whether the entire number is odd or even.
Here the above number is 25,970
When it is divided by 2 it leaves the remainder 0. So it is an even number.

Question 17.
A number with zero in the hundreds place: _______________________________
Answer: 52,097
By using the above numbers we can write the number having 0 in the hundreds place.
5 hold the ten thousand place.
2 hold the thousands place.
0 holds the hundreds place
9 hold the tens place.
7 holds the one’s place.

Question 18.
A number beginning with the greatest digit: _______________________________
Answer:95,720
By using the above-given numbers are have the highest digit.
that digit is 9.
So we can write with 9 keeping in ten thousand place.
9 hold the ten thousand place.
5 hold the thousands place.
7 holds the hundreds place
2 hold the tens place.
0 holds the one’s place.

Question 19.
A number with 2 in the tens place and 5 in the ones place: _______________________________
Answer:90,725
9 hold the ten thousand place.
0 hold the thousands place.
7 holds the hundreds place
2 hold the tens place.
5 holds the one’s place.

Question 20.
A number ending with 7: _______________________________
Answer: 25,907
5 hold the ten thousand place.
5 hold the thousands place.
9 holds the hundreds place
0 hold the tens place.
7 holds the one’s place.
We can write anyway but the last digit should be 7.

Go through the Math in Focus Grade 4 Workbook Answer Key Chapter 3 Practice 1 Multiplying by a 1-Digit Number to finish your assignments.

Math in Focus Grade 4 Chapter 3 Practice 1 Answer Key Multiplying by a 1-Digit Number

Multiply 962 by 6 and find the missing numbers.

Example
Step 1
2 ones × 6 = 12
= 1 ten 2 ones

Question 1
Step 2
6 tens × 6 = ___ tens
= ___ hundreds ___ tens

Answer:
6 tens × 6 = 36 tens
= 3 hundreds 6 tens

Question 2.
Step 3
9 hundreds × 6 = ___ hundreds
= ___ thousands ___ hundreds

Answer:
9 hundreds × 6 = 54 hundreds
= 5 thousands 4 hundreds

Question 3.

Answer:
962 × 6 = 5,772.

Explanation:
The multiplication of 962 × 6 is 5,772.

Multiply 9,086 by 7 and find the missing numbers.

Question 4.
Step 1
6 ones × 7 = _____ ones
= _____ tens _____ ones

Answer:
6 ones × 7 = 42 ones
= 4 tens 2 ones

Question 5.
Step 2
_____ tens × 7 _____ tens
= ______ hundreds ______ tens

Answer:
8 tens × 7 =  56 tens
= 5 hundreds 6 tens

Question 6.
Step 3
_____ hundreds × 7 = _____ hundreds

Answer:
0 hundreds × 7 = 0 hundreds

Question 7.
Step 4 _____ thousands × 7 _____ thousands
= ______ ten thousands ______ thousands

Answer:
9 thousands × 7 =  63 thousands
= 6 ten thousands 3 thousands

Question 8.

Answer:
9,086 × 7 = 63,602.

Explanation:
The multiplication of 9,086 × 7 is 63,602.

Multiply.

Example.

Question 9.

Answer:
605 × 5 = 3,025.

Explanation:
The multiplication of 605 × 5 = 3,025.

Question 10.

Answer:
2,134 × 6 = 12,804.

Explanation:
The multiplication of 2,134 × 6 = 12,804.

Question 11.

Answer:
6,920 × 4 = 27,680.

Explanation:
The multiplication of 6,920 × 4 = 27,680.

Question 12.

Answer:
2,019 × 7 = 14,133.

Explanation:
The multiplication of 2,019 × 7 = 14,133.

Question 13.

Answer:
1,474 × 6 = 8,844.

Explanation:
The multiplication of 1,474 × 6 is 8,844.

Question 14.

Answer:
8,572 × 8 = 68,576.

Explanation:
The multiplication of 8,572 × 8 is 68,576.

Question 15.

Answer:
6,003 × 9 = 54,027.

Explanation:
The multiplication of 6,003 × 9 is 54,027.

Find each product. Then solve the riddle.

Example
425 × 2 = 2,550

Question 16.
964 × 8 = ____
Answer:
964 × 8 = 7,712.

Explanation:
The multiplication of 964 × 8 is 7,712.

Question 17.
682 × 5 = ____
Answer:
682 × 5 = 3,410.

Explanation:
The multiplication of 682 × 5 is 3,410.

Question 18.
1,685 × 3 = ___
Answer:
1,685 × 3 = 5,055.

Explanation:
The multiplication of 1,685 × 3 is 5,055.

Question 19.
1,936 × 4 = ___
Answer:
1,936 × 4 = 7,774.

Explanation:
The multiplication of 1,936 × 4 is 7,774.

Question 20.
3,270 × 3 = ___
Answer:
3,270 × 3 = 9,810.

Explanation:
The multiplication of 3,270 × 3 is 9,810.

How do you say good-bye to the ocean?
Match the letters to the answers below to find out.

Answer:

Go through the Math in Focus Grade 4 Workbook Answer Key Chapter 3 Practice 4 Dividing by a 1-Digit Number to finish your assignments.

Math in Focus Grade 4 Chapter 3 Practice 4 Answer Key Dividing by a 1-Digit Number

Fill in the blanks to find each quotient.

Example
4,900 ÷ 7 = 49 hundreds ÷ 7
= 7 hundreds
= 700

Question 1.
6,000 ÷ 3 = ___ thousands ÷ 3
= ___ thousands
= ______
Answer:
6,000 ÷ 3 = 2,000.

Explanation:
Given that 6,000 ÷ 3
6,000 ÷ 3 = 6 thousands ÷ 3
= 2 thousands
= 2,000.

Question 2.
8,000 ÷ 2 = ___ thousands ÷ 2
= ____ thousands
= _____
Answer:
8,000 ÷ 2 = 4,000.

Explanation:
Given that 8,000 ÷ 2
8,000 ÷ 2 = 8 thousands ÷ 2
= 4 thousands
= 4,000.

Question 3.
2,400 ÷ 6 = ___ hundreds ÷ 6
= ____ hundreds
= _____
Answer:
2,400 ÷ 6 = 400.

Explanation:
Given that 2,400 ÷ 6
2,400 ÷ 6 = 24 hundreds ÷ 6
= 400 hundreds
= 400.

Estimate each quotient.

Question 4.
64 ÷ 3 is about ___ ÷ 3
= _____
Answer:
The estimated quotient is 20.

Explanation:
Given that 64 ÷ 3 which is about 60 ÷ 3,
So the estimated quotient is 20.

Question 5.
448 ÷ 9 is about ___ ÷ 9
= ____
Answer:
The estimated quotient is 50.

Explanation:
Given that 448 ÷ 9 which is about 450 ÷ 9,
So the estimated quotient is 50.

Question 6.
763 ÷ 4 is about ___ ÷ 4
= ____
Answer:
The estimated quotient is 190.

Explanation:
Given that 763 ÷ 4 which is about 760 ÷ 4,
So the estimated quotient is 190.

Question 7.
127 ÷ 5 is about ___ ÷ 5
= ____
Answer:
The estimated quotient is 25.

Explanation:
Given that 127 ÷ 5 which is about 125 ÷ 5,
So the estimated quotient is 25.

Divide and find the missing numbers:

Example

Question 8.

Answer:

Question 9.

Answer:

Question 10.

Answer:

Divide. Then estimate to check that your answers are reasonable.

Example

Question 11.

Estimate:
_____
Answer:
Estimated answer is 900.

Explanation:
Given that 3,620÷4, as 3,620 is about 3,600. So the estimation will be 3,600÷4 which is 900.

Question 12.

Estimate:
_____
Answer:
Estimated answer is 400.

Explanation:
Given that 2,807 ÷ 7, as 2,807 is about 2,800. So the estimation will be 2,800 ÷ 7 which is 400.

Question 13.

Estimate:
_____
Answer:
Estimated answer is 300.

Explanation:
Given that 1,842 ÷ 6, as 1842 is about 1,800. So the estimation will be 1,800 ÷ 6 which is 300.

Find each quotient. Then estimate to check that your answers are reasonable

Example
1144 ÷ 9 = 127 R 1

Estimate: 1,144 ÷ 9 is
about 900 ÷ 9 = 100.
The answer 127 R 1 is reasonable.

Question 14.
6,514 ÷ 4 = ___ R ____
Answer:
6,514 ÷ 4 = 1,628 R 2.

Explanation:
Given that 6,514 ÷ 4, as 6,514 is about 6,500. So 6,500 ÷ 4 which is 1,625.
6,514 ÷ 4 = 1,628 with remainder 2.

Question 15.
1,340 ÷ 7 = ___ R ____
Answer:
1,340 ÷ 7 = 191 R 3.

Explanation:
Given that 1,340 ÷ 7, as 1,400 is about 1,400. So 1,400 ÷ 7 which is 200.
1,340 ÷ 7 = 191 with remainder 3.

Question 16.
9,346 ÷ 8 = __ R ___
Answer:
9,346 ÷ 8 = 1,125 R 2.

Explanation:
Given that 9,346 ÷ 8, as 9,000 is about 1,125. So 9,000 ÷ 8 which is 1,125.
9,346 ÷ 8 = 1,125 with remainder 2.

Go through the Math in Focus Grade 4 Workbook Answer Key Chapter 5 Practice 6 Real-World Problems: Data and Probability to finish your assignments.

Math in Focus Grade 4 Chapter 5 Practice 6 Answer Key Real-World Problems: Data and Probability

Solve. Show your work.

Example .
In a test, Carl, Sarah, and Dinesh scored an average of 70 points.
Carl scored 65 and Sarah scored 82. How many points did Dinesh get?
Total score of the 3 students = 3 × 70
= 210 points
Carl and Sarah’s total score = 65 + 82
= 147 points
Dinesh’s test score = 210 – 147
= 83 points
Dinesh’s test score was 63 points,

Question 1.
Luis went on a fishing trip from Thursday to Sunday. On average, he caught 12 fish per day. He caught 15 fish on Thursday. How many fish did he catch altogether from Friday to Sunday?
Answer:
The number of fish did he catch altogether from Friday to Sunday is 33 fish.

Explanation:
Given that Luis went on a fishing trip from Thursday to Sunday, on average, he caught 12 fish per day and he caught 15 fish on Thursday. So the number of fishes did he catch altogether from Friday to Sunday is
on average he caught 12 fish per day and the Friday count be X, so
(X+15)/4 = 12
X+15 = 12×4
X+15 = 48
X = 48-15
= 33.

Question 2.
Nicole bought 20 pieces of fabric of different lengths. The average length of 12 pieces is 3 feet. The total length of the other 8 pieces is 44 feet. Find the average length of the 20 pieces of fabric.
Answer:
The average length of the 20 pieces of fabric is 19.4 feet.

Explanation:
Given that Nicole bought 20 pieces of fabric of different lengths and the average length of 12 pieces is 3 feet which are 12×3 =36. The total length of the other 8 pieces is 44 feet which are 8×44 =352 feet. So the total length is 352+36 = 388 feet. So the average length of the 20 pieces of fabric is 388÷20 which is 19.4 feet.

Question 3.
Ron drove his car every day from Monday to Saturday. On Monday and Tuesday, the car used an average of 2 gallons of gas each day. From Wednesday to Saturday, the car used an average of 3 gallons of gas each day. Find the total amount of gas the car used from Monday to Saturday.

Answer:
The total amount of gas the car used from Monday to Saturday is 16 gallons.

Explanation:
Given that Ron drove his car every day from Monday to Saturday and on Monday and Tuesday, the car used an average of 2 gallons of gas each day which is 2×2 = 4 gallons. From Wednesday to Saturday, the car used an average of 3 gallons of gas each day which is 3×4 = 12 gallons. So the total amount of gas the car used from Monday to Saturday is 4 gallons+12 gallons = 16 gallons.

Solve. Show your work. Use bar models to help you.

Example
The average number of students in Class A and Class B is 24. Class A has 4 more students than Class B. How many students are there in each class?
Total number of students in both classes = 2 × 24 = 48

Class A has 26 students, and Class B has 22 students.

Question 4.
Mrs. Johnson buys 2 chickens. The average weight of the 2 chickens is 4 pounds. One of the chickens is 2 pounds heavier than the other. What is the weight of the heavier chicken?

Answer:
The weight of the heavier chicken is 4 pounds.

Explanation:
Given that Mrs. Johnson buys 2 chickens and the average weight of the 2 chickens is 4 pounds and one of the chickens is 2 pounds heavier than the other. So the weight of the heavier chicken is 4 pounds, as the average weight of both chickens is 4, which means the weight of chickens added together than divided by two. The only one that would work is 2. So then we will add 2 to that and it would be four.

Solve. Show your work.

Example
A group of athletes took part in a charity marathon. The table shows the number of kilometers completed by each athlete.

Find the median.

Find the range.
The range is 42 – 28 = 14 kilometers.
Find the mean.
4 × 42 km = 168 km
1 × 36 km = 3 km
3 × 28 km = 84 km
Total = 168 + 36 + 84
= 288 km
The mean is 288 ÷ 8 = 36 kilometers.

Another athlete joins the charity marathon and completes 27 kilometers. Will this athletes distance increase or decrease the mean?
Explain why you think so. Then find the new mean number of kilometers
completed by all the athletes.
The new athlete’s distance will decrease the mean because this new data point is less than the old mean.
288 + 27 = 315 km
315 ÷ 9 = 35 km
The new mean is 35 kilometers.
For every kilometer each athlete completed, $25 would be donated to charity. Find the amount of money raised for charity by the 9 athletes.
315 × $25 = $7,875
The amount raised for charity is $7,875

Question 5.
The scores of 9 players playing 1 8 holes of golf are 65, 72, 70, 69, 72, 67, 70, 72, and 73.
a. Find the median score.
Answer:
The median score is 70.

Explanation:
Given the data is 65, 72, 70, 69, 72, 67, 70, 72, and 73 to find the median we will arrange the numbers in order from least to greatest, and the middle number or the mean of the two middle numbers is the median. So the numbers in order from least to greatest are 65,67,69,70,70,72,72,72,73. So the median score is 70.

b. Find the mode of the scores.
Answer:
The mode of the scores is 72.

Explanation:
To find the mode we will pick the number that appears most often is the mode and there can be more than one mode. So the mode will be 72.

c. Find the range of the set of data.
Answer:
The range of the set of data is 8.

Explanation:
To find the range, we will find the difference between the greatest and the least number.
So the range is 73-65 which is 8.

d. Find the mean of the set of data.
Answer:
The mean of the set of data is 70.

Explanation:
Given that the data is 65,67,69,70,70,72,72,72,73, so the mean will be \(\frac{65+67+69+70+70+72+72+72+73}{9}\) = \(\frac{630}{9}\)
= 70.

e. Another player scores 80. Predict how this player’s score will change the median, mode, range, and mean of the data and explain your reasoning. Then compute each of these measures to check your predictions.
Answer:
The median is 71,
mode is 72,
the range is 15,
mean is 71.

Explanation:
Given that the other player scores 80, the new data set will be 65,67,69,70,70,72,72,72,73,80. So the median will be \(\frac{70+72}{2}\)
= \(\frac{142}{2}\)
= 71.
The mode will not be changed as the number that appears most often is the mode and there can be more than one mode. So the mode will be 72.
The range will be changed, so the range will be 80-65 which is 15.
The mean will be \(\frac{65+67+69+70+70+72+72+72+73+80}{10}\) = \(\frac{710}{10}\)
= 71.

Example
The line plot shows Marilyn’s science test scores during one semester. Each ✗ represents one test.

a. How many tests did she take?
7

b. Find the median, mode, and range of her scores.
Marilyn’s median score is 85
Marilyn’s modal scores are 80 and 90.
The range of her scores is 95 – 75 = 20.

c. Find her mean score.
1 × 75 = 75
2 × 80 = 160
1 × 85 = 85
2 × 90 = 180
1 × 95 = 95
Total = 595
595 ÷ 7 = 85
Her mean score is 85.

d. After Marilyn took another test, her new mean score was 84. What was her latest score?
84 × 6 = 672
672 – 595 = 77
Her latest score was 77.

Question 6.
Kurt recorded the daily temperature highs for a science project. The results are shown in the line plot.

a. On how many days did he record the temperature?
Answer:
9 days.

Explanation:
The number of days did he record the temperature is 9 days.

b. What were the mean and median temperatures?
Answer:
The mean and median temperatures are 29 degrees Fahrenheit.

Explanation:
The median temperature is 29 degrees Fahrenheit and the mean will be \(\frac{27+28+28+28+29+29+30+31+31}{9}\) = \(\frac{261}{9}\)
= 29.

c. The temperature high on another day was included with the data. The new mean temperature changed to 30°F. What was this temperature?
Answer:

d. Find the new median temperature.
Answer:

Question 7.
A restaurant pays its 9 employees these daily wages:
$90, $70, $100, $90, $90, $90, $100, $160, $200
Make a line plot to show the data.
a. Find the mean and median of the set of wages.
Answer:
The mean is $110 and the median is $90.

Explanation:
Given the data is $90, $70, $100, $90, $90, $90, $100, $160, $200. So the mean will be \(\frac{70+90+90+90+90+100+100+160+200}{9}\) = \(\frac{990}{9}\)
= $110.
The median will be $90.

b. Does the mean or the median better describe what a new employee could expect to earn at this restaurant?
Answer:

c. Are there any outliers? If so, what are they?
Answer:

d. How do the mean and median each change if you disregard the outliers? Now does the mean or median better represent what a new employee could expect to earn?
Answer:

Example
During a trip to the beach, 9 children collected seashells. The stem-and-leaf plot shows the number of shells each child collected.

a. If the total number of seashells collected is 681, find the missing number. What is the outlier?
681 – 61 – 61 – 65 -70 -76 -78 – 83 – 88 = 99
The missing number is 99. The outlier is 99 because it is farthest from the other numbers.

b. Find the median of the set of data.
The median is 76

c. Find the mode of the set of data.
The mode is 61.

d. Find the range of the set of data.
99 – 61 = 38
The range is 38.

Question 8.
The stem-and-leaf plot shows the weights of some bowling balls in pounds.

a. How many bowling balls are there?
Answer:
18 balls.

Explanation:
The number of bowling balls are 18.

b. Find the median, mode, and range.
Answer:
The median is 13,
mean is 12.67,
range is 8.

Explanation:
Given the data is 8,8,9,10,10,11,11,12,12,14,14,15,15,15,16,16,16,16. So the mean will be \(\frac{8+8+9+10+10+11+11+12+12+14+14+15+15+15+16+16+16+16}{18}\) = \(\frac{228}{18}\)
= 12.67.
The median will be \(\frac{12+14}{2}\)
= \(\frac{26}{2}\)
= 13.
The range will be 16-8 = 8.

c. What is the least number of bowling balls needed to make the mode 14 pounds?
Answer:

d. Find the total weight of the bowling balls in Exercise 8.c.
Answer:

Find the probability of each outcome on a number line. Then describe the likelihood of each outcome as more likely, less likely, certain, impossible, or equally likely.

Question 9.
The weather forecast in a city is that for every week, 3 days are sunny, 2 are cloudy, and 2 are rainy. On any chosen day, describe the probability of each of these outcomes.
Example
It is a sunny day.

a. It is not a sunny day.
Answer:
\(\frac{4}{7}\).

Explanation:
The probability of not a sunny day is \(\frac{4}{7}\). As 2 days are cloudy and 2 days are rainy.

b. If today is sunny, tomorrow is rainy.
Answer:

Explanation:
If today is sunny, tomorrow is rainy the the probability of not

c. If today is sunny, tomorrow is rainy.
Answer:

Solve.

Question 10.
In a class of 25 students, 10 are girls. The names of the students are written on cards and placed in a box. The names are chosen at random to win prizes donated by a local store.

a. What is the probability that the first student selected is a girl?
Answer:

Explanation:
The probability that the first student selected is a girl is \(\frac{10}{25}\)
= \(\frac{2}{5}\).

b. What is the probability that the first student selected is a boy?
Answer:

Explanation:
The number girl students is 10 and the total number of students is 25. So the total number of boys is 25-10 which is 15. So the probability that the first student selected is a boy is \(\frac{15}{25}\)
= \(\frac{3}{5}\).

c. If the first student selected is a girl, what is the probability that the second student selected is also a girl?
Answer:
\(\frac{2}{5}\).

Explanation:
The probability that the second student selected is a girl is \(\frac{10}{25}\)
= \(\frac{2}{5}\).

Practice the problems of Math in Focus Grade 4 Workbook Answer Key Chapter 6 Practice 4 Improper Fractions to score better marks in the exam.

Math in Focus Grade 4 Chapter 6 Practice 4 Answer Key Improper Fractions

Write each mixed number as an improper fraction.

Example

Question 1.

Answer:

Explanation:
2 = 8 fourths.
\(\frac{3}{4}\) = 3 fourths.
2\(\frac{3}{4}\) = 11 fourths.

Question 2.

Answer:

Explanation:
3 = 15 fifths.
\(\frac{2}{5}\) = 2 fifths.
3\(\frac{2}{5}\) = 17 fifths.

Write the improper fractions for the shaded parts
Question 3.

Answer:

Explanation:
1 = 6 sixths.
Shaded parts = 7 sixths.
= 1 + \(\frac{1}{6}\)
= \(\frac{7}{6}\)

Question 4.

Answer:

Explanation:
1 = 8 eighths.
Shaded parts = 19 eighths.
= 2 + \(\frac{3}{8}\) = 2\(\frac{3}{8}\) .

Question 5.

Answer:

Explanation:
1 = 6 sixths.
Shaded parts = 17 sixths.
= 2 + \(\frac{5}{6}\)
= 2\(\frac{5}{6}\)

Write the improper fraction for the shaded parts.

Question 6.

Answer:

Explanation:
3\(\frac{3}{5}\) = (15 + 3) ÷ 5
= \(\frac{18}{5}\)

Write a mixed number and an improper fraction for each model.
Example

Question 7.

Answer:

Explanation:
Mixed number = 2 + \(\frac{3}{5}\)
= 2\(\frac{3}{5}\).
Improper fraction = 1 + 1 + \(\frac{3}{5}\)
= 2 + \(\frac{3}{5}\)
= (10 + 3) ÷ 5
= \(\frac{13}{5}\) or 13 ÷ 5.

Question 8.

Answer:

Explanation:
Mixed number = 1 + \(\frac{3}{5}\)
= 1\(\frac{3}{5}\).
Improper fraction =  1 + \(\frac{3}{5}\)
= (5 + 3) ÷ 5
= \(\frac{8}{5}\) or 8 ÷ 5.

Write a mixed number and an improper fraction for each model.
Question 9.

Answer:

Explanation:
Mixed number = 1 + 1 + 1 + 1 + \(\frac{1}{4}\)
= 4 + \(\frac{1}{4}\)
= 4 \(\frac{1}{4}\).
Improper fraction = 1 + 1 + 1 + 1 + \(\frac{1}{4}\)
= 4 + \(\frac{1}{4}\)
= (16 + 1) ÷ 4
= \(\frac{17}{4}\) or 17 ÷ 4.

Write the missing improper fraction in each box. Express the answers in simplest form.
Question 10.

Answer:

Explanation:
\(\frac{3}{2}\) – 1 = (3 – 2) ÷ 2
= 1 ÷ 2 or \(\frac{1}{2}\)

= \(\frac{3}{2}\) + \(\frac{1}{2}\)
= (3 + 1) ÷ 2
= 4 ÷ 2 or \(\frac{4}{2}\)

Question 11.

Answer:

Explanation:
\(\frac{11}{8}\) + \(\frac{3}{2}\) = (11 + 12) ÷ 8
= 23 ÷ 8 or \(\frac{23}{8}\)
\(\frac{3}{2}\) + \(\frac{23}{8}\) = (12 + 23) ÷ 8
= 35 ÷ 8 or \(\frac{35}{8}\)
\(\frac{17}{8}\) + \(\frac{9}{4}\) = (17 + 18) ÷ 8
= 35 ÷ 8 or \(\frac{35}{8}\)
\(\frac{9}{4}\) + \(\frac{35}{8}\) = (18 + 35) ÷ 8
= 53 ÷ 8 or \(\frac{53}{8}\)
\(\frac{35}{8}\) + \(\frac{53}{8}\) = (35 + 53) ÷ 8
= 88 ÷ 8
= 11.

Write each improper fraction in a box to show its correct location on the number line.
Question 12.
\(\frac{4}{3}\)
Answer:

Explanation:
\(\frac{4}{3}\) = 1.33.
On number line = \(\frac{12}{9}\) = 1.33.

Question 13.
\(\frac{7}{3}\)
Answer:

Explanation:
\(\frac{7}{3}\) = 2.33.
On number line = \(\frac{21}{9}\)= 2.33.

Question 14.
\(\frac{17}{9}\)
Answer:

Explanation:
\(\frac{17}{9}\) = 1.89.
On number line = \(\frac{17}{9}\) = 1.89.

Practice the problems of Math in Focus Grade 4 Workbook Answer Key Chapter 9 Practice 2 Drawing Angles to 180° to score better marks in the exam.

Math in Focus Grade 4 Chapter 9 Practice 2 Answer Key Drawing Angles to 180°

Use a protractor to draw each angle.

Question 1.
70° using inner scale

Answer:
We have constructed 70° using inner scale.

Explanation:
Here, we have constructed 70° using inner scale. As the angle opens to the right of the protractor.

Question 2.
147° using outer scale

Answer:
We have constructed 147° using outer scale.

Explanation:
Here, we have constructed 147° using outer scale. As the angle opens to the left of the protractor.

Question 3.
35° using outer scale

Answer:
We have constructed 35° using outer scale.

Explanation:
Here, we have constructed 35° using outer scale. As the angle opens to the left of the protractor.

Question 4.
108° using outer scale

Answer:
We have constructed 108° using outer scale.

Explanation:
Here, we have constructed 108° using outer scale. As the angle opens to the left of the protractor.

Join the marked endpoint of each ray to one of the dots to form an angle with the given value. Then label the angle.

Example

Question 5.
Measure of ∠h = 32°

Answer:
Here, we have constructed ∠h = 32°.

Draw an angle that has each measure.

Question 14.
35°
Answer:
Here, we have constructed a 35° angle.

Question 15.
125°
Answer:
Here, we have constructed a 125° angle.