Go through the Math in Focus Grade 4 Workbook Answer Key Chapter 5 Practice 6 Real-World Problems: Data and Probability to finish your assignments.
Math in Focus Grade 4 Chapter 5 Practice 6 Answer Key Real-World Problems: Data and Probability
Solve. Show your work.
Example .
In a test, Carl, Sarah, and Dinesh scored an average of 70 points.
Carl scored 65 and Sarah scored 82. How many points did Dinesh get?
Total score of the 3 students = 3 × 70
= 210 points
Carl and Sarah’s total score = 65 + 82
= 147 points
Dinesh’s test score = 210 – 147
= 83 points
Dinesh’s test score was 63 points,
Question 1.
Luis went on a fishing trip from Thursday to Sunday. On average, he caught 12 fish per day. He caught 15 fish on Thursday. How many fish did he catch altogether from Friday to Sunday?
Answer:
The number of fish did he catch altogether from Friday to Sunday is 33 fish.
Explanation:
Given that Luis went on a fishing trip from Thursday to Sunday, on average, he caught 12 fish per day and he caught 15 fish on Thursday. So the number of fishes did he catch altogether from Friday to Sunday is
on average he caught 12 fish per day and the Friday count be X, so
(X+15)/4 = 12
X+15 = 12×4
X+15 = 48
X = 48-15
= 33.
Question 2.
Nicole bought 20 pieces of fabric of different lengths. The average length of 12 pieces is 3 feet. The total length of the other 8 pieces is 44 feet. Find the average length of the 20 pieces of fabric.
Answer:
The average length of the 20 pieces of fabric is 19.4 feet.
Explanation:
Given that Nicole bought 20 pieces of fabric of different lengths and the average length of 12 pieces is 3 feet which are 12×3 =36. The total length of the other 8 pieces is 44 feet which are 8×44 =352 feet. So the total length is 352+36 = 388 feet. So the average length of the 20 pieces of fabric is 388÷20 which is 19.4 feet.
Question 3.
Ron drove his car every day from Monday to Saturday. On Monday and Tuesday, the car used an average of 2 gallons of gas each day. From Wednesday to Saturday, the car used an average of 3 gallons of gas each day. Find the total amount of gas the car used from Monday to Saturday.
Answer:
The total amount of gas the car used from Monday to Saturday is 16 gallons.
Explanation:
Given that Ron drove his car every day from Monday to Saturday and on Monday and Tuesday, the car used an average of 2 gallons of gas each day which is 2×2 = 4 gallons. From Wednesday to Saturday, the car used an average of 3 gallons of gas each day which is 3×4 = 12 gallons. So the total amount of gas the car used from Monday to Saturday is 4 gallons+12 gallons = 16 gallons.
Solve. Show your work. Use bar models to help you.
Example
The average number of students in Class A and Class B is 24. Class A has 4 more students than Class B. How many students are there in each class?
Total number of students in both classes = 2 × 24 = 48

Class A has 26 students, and Class B has 22 students.
Question 4.
Mrs. Johnson buys 2 chickens. The average weight of the 2 chickens is 4 pounds. One of the chickens is 2 pounds heavier than the other. What is the weight of the heavier chicken?
Answer:
The weight of the heavier chicken is 4 pounds.
Explanation:
Given that Mrs. Johnson buys 2 chickens and the average weight of the 2 chickens is 4 pounds and one of the chickens is 2 pounds heavier than the other. So the weight of the heavier chicken is 4 pounds, as the average weight of both chickens is 4, which means the weight of chickens added together than divided by two. The only one that would work is 2. So then we will add 2 to that and it would be four.
Solve. Show your work.
Example
A group of athletes took part in a charity marathon. The table shows the number of kilometers completed by each athlete.

Find the median.

Find the range.
The range is 42 – 28 = 14 kilometers.
Find the mean.
4 × 42 km = 168 km
1 × 36 km = 3 km
3 × 28 km = 84 km
Total = 168 + 36 + 84
= 288 km
The mean is 288 ÷ 8 = 36 kilometers.
Another athlete joins the charity marathon and completes 27 kilometers. Will this athletes distance increase or decrease the mean?
Explain why you think so. Then find the new mean number of kilometers
completed by all the athletes.
The new athlete’s distance will decrease the mean because this new data point is less than the old mean.
288 + 27 = 315 km
315 ÷ 9 = 35 km
The new mean is 35 kilometers.
For every kilometer each athlete completed, $25 would be donated to charity. Find the amount of money raised for charity by the 9 athletes.
315 × $25 = $7,875
The amount raised for charity is $7,875
Question 5.
The scores of 9 players playing 1 8 holes of golf are 65, 72, 70, 69, 72, 67, 70, 72, and 73.
a. Find the median score.
Answer:
The median score is 70.
Explanation:
Given the data is 65, 72, 70, 69, 72, 67, 70, 72, and 73 to find the median we will arrange the numbers in order from least to greatest, and the middle number or the mean of the two middle numbers is the median. So the numbers in order from least to greatest are 65,67,69,70,70,72,72,72,73. So the median score is 70.
b. Find the mode of the scores.
Answer:
The mode of the scores is 72.
Explanation:
To find the mode we will pick the number that appears most often is the mode and there can be more than one mode. So the mode will be 72.
c. Find the range of the set of data.
Answer:
The range of the set of data is 8.
Explanation:
To find the range, we will find the difference between the greatest and the least number.
So the range is 73-65 which is 8.
d. Find the mean of the set of data.
Answer:
The mean of the set of data is 70.
Explanation:
Given that the data is 65,67,69,70,70,72,72,72,73, so the mean will be \(\frac{65+67+69+70+70+72+72+72+73}{9}\) = \(\frac{630}{9}\)
= 70.
e. Another player scores 80. Predict how this player’s score will change the median, mode, range, and mean of the data and explain your reasoning. Then compute each of these measures to check your predictions.
Answer:
The median is 71,
mode is 72,
the range is 15,
mean is 71.
Explanation:
Given that the other player scores 80, the new data set will be 65,67,69,70,70,72,72,72,73,80. So the median will be \(\frac{70+72}{2}\)
= \(\frac{142}{2}\)
= 71.
The mode will not be changed as the number that appears most often is the mode and there can be more than one mode. So the mode will be 72.
The range will be changed, so the range will be 80-65 which is 15.
The mean will be \(\frac{65+67+69+70+70+72+72+72+73+80}{10}\) = \(\frac{710}{10}\)
= 71.
Example
The line plot shows Marilyn’s science test scores during one semester. Each ✗ represents one test.

a. How many tests did she take?
7
b. Find the median, mode, and range of her scores.
Marilyn’s median score is 85
Marilyn’s modal scores are 80 and 90.
The range of her scores is 95 – 75 = 20.
c. Find her mean score.
1 × 75 = 75
2 × 80 = 160
1 × 85 = 85
2 × 90 = 180
1 × 95 = 95
Total = 595
595 ÷ 7 = 85
Her mean score is 85.
d. After Marilyn took another test, her new mean score was 84. What was her latest score?
84 × 6 = 672
672 – 595 = 77
Her latest score was 77.
Question 6.
Kurt recorded the daily temperature highs for a science project. The results are shown in the line plot.
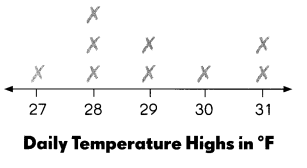
a. On how many days did he record the temperature?
Answer:
9 days.
Explanation:
The number of days did he record the temperature is 9 days.
b. What were the mean and median temperatures?
Answer:
The mean and median temperatures are 29 degrees Fahrenheit.
Explanation:
The median temperature is 29 degrees Fahrenheit and the mean will be \(\frac{27+28+28+28+29+29+30+31+31}{9}\) = \(\frac{261}{9}\)
= 29.
c. The temperature high on another day was included with the data. The new mean temperature changed to 30°F. What was this temperature?
Answer:
d. Find the new median temperature.
Answer:
Question 7.
A restaurant pays its 9 employees these daily wages:
$90, $70, $100, $90, $90, $90, $100, $160, $200
Make a line plot to show the data.
a. Find the mean and median of the set of wages.
Answer:
The mean is $110 and the median is $90.
Explanation:
Given the data is $90, $70, $100, $90, $90, $90, $100, $160, $200. So the mean will be \(\frac{70+90+90+90+90+100+100+160+200}{9}\) = \(\frac{990}{9}\)
= $110.
The median will be $90.
b. Does the mean or the median better describe what a new employee could expect to earn at this restaurant?
Answer:
c. Are there any outliers? If so, what are they?
Answer:
d. How do the mean and median each change if you disregard the outliers? Now does the mean or median better represent what a new employee could expect to earn?
Answer:
Example
During a trip to the beach, 9 children collected seashells. The stem-and-leaf plot shows the number of shells each child collected.

a. If the total number of seashells collected is 681, find the missing number. What is the outlier?
681 – 61 – 61 – 65 -70 -76 -78 – 83 – 88 = 99
The missing number is 99. The outlier is 99 because it is farthest from the other numbers.
b. Find the median of the set of data.
The median is 76
c. Find the mode of the set of data.
The mode is 61.
d. Find the range of the set of data.
99 – 61 = 38
The range is 38.
Question 8.
The stem-and-leaf plot shows the weights of some bowling balls in pounds.
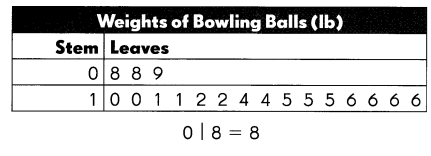
a. How many bowling balls are there?
Answer:
18 balls.
Explanation:
The number of bowling balls are 18.
b. Find the median, mode, and range.
Answer:
The median is 13,
mean is 12.67,
range is 8.
Explanation:
Given the data is 8,8,9,10,10,11,11,12,12,14,14,15,15,15,16,16,16,16. So the mean will be \(\frac{8+8+9+10+10+11+11+12+12+14+14+15+15+15+16+16+16+16}{18}\) = \(\frac{228}{18}\)
= 12.67.
The median will be \(\frac{12+14}{2}\)
= \(\frac{26}{2}\)
= 13.
The range will be 16-8 = 8.
c. What is the least number of bowling balls needed to make the mode 14 pounds?
Answer:
d. Find the total weight of the bowling balls in Exercise 8.c.
Answer:
Find the probability of each outcome on a number line. Then describe the likelihood of each outcome as more likely, less likely, certain, impossible, or equally likely.
Question 9.
The weather forecast in a city is that for every week, 3 days are sunny, 2 are cloudy, and 2 are rainy. On any chosen day, describe the probability of each of these outcomes.
Example
It is a sunny day.
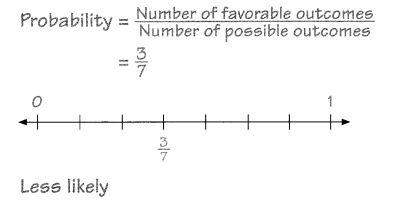
a. It is not a sunny day.
Answer:
\(\frac{4}{7}\).
Explanation:
The probability of not a sunny day is \(\frac{4}{7}\). As 2 days are cloudy and 2 days are rainy.
b. If today is sunny, tomorrow is rainy.
Answer:
Explanation:
If today is sunny, tomorrow is rainy the the probability of not
c. If today is sunny, tomorrow is rainy.
Answer:
Solve.
Question 10.
In a class of 25 students, 10 are girls. The names of the students are written on cards and placed in a box. The names are chosen at random to win prizes donated by a local store.
a. What is the probability that the first student selected is a girl?
Answer:
Explanation:
The probability that the first student selected is a girl is \(\frac{10}{25}\)
= \(\frac{2}{5}\).
b. What is the probability that the first student selected is a boy?
Answer:
Explanation:
The number girl students is 10 and the total number of students is 25. So the total number of boys is 25-10 which is 15. So the probability that the first student selected is a boy is \(\frac{15}{25}\)
= \(\frac{3}{5}\).
c. If the first student selected is a girl, what is the probability that the second student selected is also a girl?
Answer:
\(\frac{2}{5}\).
Explanation:
The probability that the second student selected is a girl is \(\frac{10}{25}\)
= \(\frac{2}{5}\).