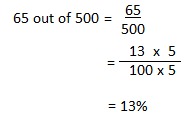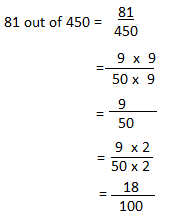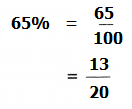Practice the problems of Math in Focus Grade 6 Workbook Answer Key Chapter 6 Lesson 6.5 Percent of Change to score better marks in the exam.
Math in Focus Grade 6 Course 1 A Chapter 6 Lesson 6.5 Answer Key Percent of Change
Math in Focus Grade 6 Chapter 6 Lesson 6.5 Guided Practice Answer Key
Solve.
Question 1.
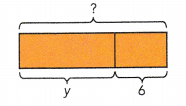
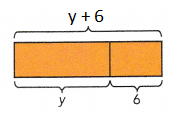
At a post office, the weight of the mail at 10:00 A.M. was 80 pounds. Two hours later, the weight of the mail had increased by 30%. Find the weight of the mail at noon.
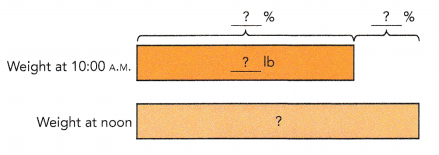
Method 1
30% of 80 = \(\frac{?}{?}\) × 
= 
The weight of the mail had increased by  pounds.
pounds.
80 +  =
= 
The weight of the mail at noon was  pounds.
pounds.
Method 2
100% → 80 lb
1% → 80 ÷ 100 =  lb
lb
 % →
% →  ×
×  =
=  lb
lb
The weight of the mail had increased by  pounds.
pounds.
80 +  =
= 
The weight of the mail at noon was  pounds.
pounds.
Answer:
104 pounds.
Explanation:
At a post office, the weight of the mail at 10:00 A.M. was 80 pounds.
Two hours later, the weight of the mail had increased by 30%.
the weight of the mail at noon,
Method 1
30% of 80 = \(\frac{30}{100}\) × 80
= 24
The weight of the mail had increased by 24 pounds.
80 + 24 = 104
The weight of the mail at noon was 104pounds.
Method 2
100% → 80 lb
1% → 80 ÷ 100 = 0.8lb
10% → 8 × 3 = 24lb
The weight of the mail had increased by 24pounds.
80 + 24 = 104
The weight of the mail at noon was 104 pounds.
Question 2.
The price of a new car was $22,800 in April. However, the price of the car was reduced by 5% in May. Find the price in May.
In May, the price of the car was  % as compared to the price of the car in April.
% as compared to the price of the car in April.
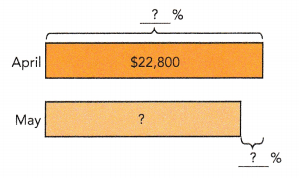
100% → $
1% → $  ÷ 100 = $
÷ 100 = $
 % →
% →  × $
× $  = $
= $
The price of the car in May was $ .
.
Answer:
$21,660
Explanation:
The price of a new car ,was $22,800 in April,
the price of the car was reduced by 5% in May.
100% → $22,800
1% → $ 22,800 ÷ 100 = $22,80
5% → 100 × $ 22,800 = $1140
22,800 – 1140 = 21,660
The price of the car in May was $ 21,660.
Question 3.
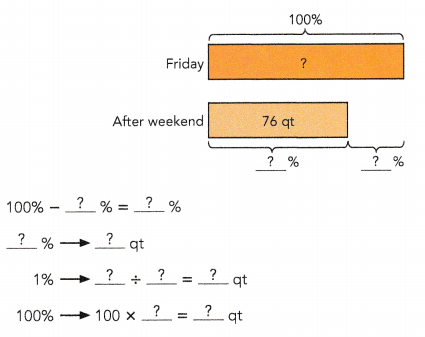
One Friday, a restaurant received enough orange juice for a week. After the weekend, the restaurant’s orange juice supply had decreased by 24% to 76 quarts. After Monday, the supply had further decreased by 20%.
a) What was the original amount of orange juice received?
The original amount of orange juice received was  quarts.
quarts.
Answer:
100qt
Explanation:
One Friday, a restaurant received enough orange juice for a week.
After the weekend, the restaurant’s orange juice supply had decreased by 24% to 76 quarts.
100% – 24% = 76%
24% = 76qt
1% = 76 ÷ 1 = 76qt
100% = 100 x 76 = 7600qt
the original amount of orange juice received
7600 ÷ 76 = 100qt
b) How much orange juice was left after Monday?
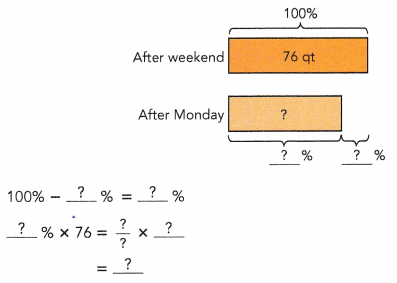
 quarts of orange juice was left after Monday.
quarts of orange juice was left after Monday.
Answer:
\(\frac{?}{?}\) quarts of orange juice was left after Monday.
Explanation:
One Friday, a restaurant received enough orange juice for a week.
After the weekend, the restaurant’s orange juice supply had decreased by 24% to 76 quarts.
After Monday, the supply had further decreased by 20%.
100% – 20 = 80%
100% x 76 = (76 ÷ 1) x (80 ÷ 100)
76(4÷ 5) = 304 ÷ 5
= 60\(\frac{4}{5}\)
Question 4.
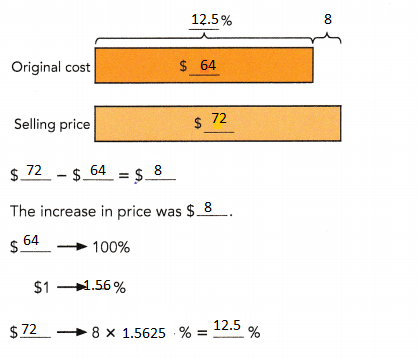
Dennis bought an antique model train for $64. Two years later, he sold it for $72. What was the percent increase in the price of the model train?
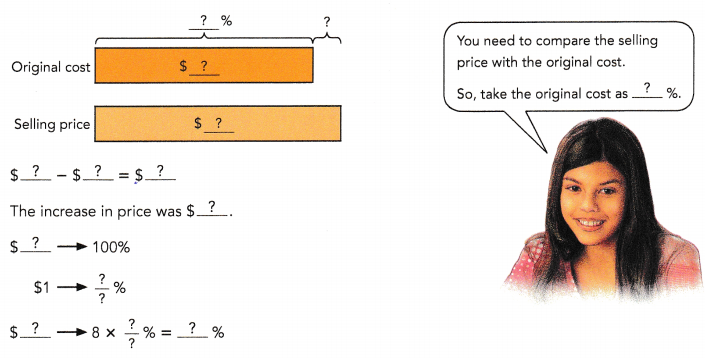
The percent increase in the price of the model train was  %.
%.
Answer:
12.5%
Explanation:
Dennis bought an antique model train for $64.
Two years later, he sold it for $72.
the percent increase in the price of the model train
Question 5.
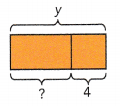
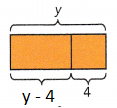
The original length of a spring was 28 millimeters. It was stretched to a length of 35 millimeters. Find the percent increase in its length.
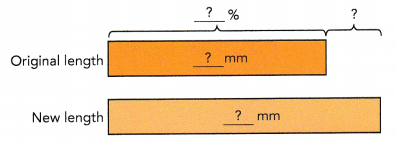
 mm – mm =
mm – mm =  mm
mm
The increase in length was  millimeters.
millimeters.
\(\frac{?}{?}\) × 100% =  %
%
The percent increase in its length was  %.
%.
Answer:
80%
Explanation:
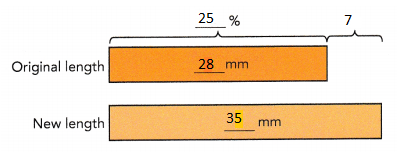
35 mm – 28 mm = 7 mm
The increase in length was 7 millimeters.
\(\frac{7}{28}\) × 100% = 25 %
The percent increase in its length was 25 %.
Question 6.
The amount of the water in a dispenser was 50 liters at first. After 10 minutes, it decreased to 45 liters. Another 15 minutes later, the amount of water had decreased to 40 liters.
a) Find the percent decrease in the amount of water after the first 10 minutes.
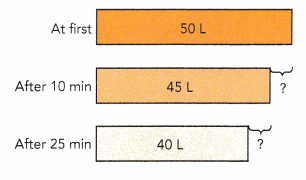
Decrease in amount of water = 50 L – 45 L
=  L
L
\(\frac{?}{?}\) × 100% =  %
%
The percent decrease in the amount of water after the first 10 minutes was  %.
%.
Answer:
10%
Explanation:
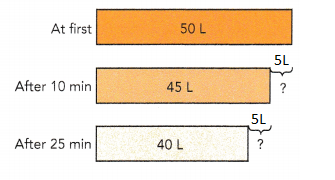
Decrease in amount of water = 50 L – 45 L
= 5 L
\(\frac{5}{50}\) × 100% = 10 %
The percent decrease in the amount of water after the first 10 minutes was 10 %.
b) What was the percent decrease in the amount of water from 45 liters to 40 liters?
Answer:
11.11%
Explanation:
Decrease in amount of water = 45 L – 40 L
= 5 L
\(\frac{5}{45}\) × 100% = 11.11 %
The percent decrease in the amount of water from 45 liters to 40 liters was 11.11 %.
Question 7.
On Monday, Camille scored 120 points in a video game and Emily scored \(\frac{5}{4}\) as many points as Camille. On Tuesday, Emily scored 30% more points than what she scored on Monday. Find the increase in the number of points Emily scored on Tuesday.
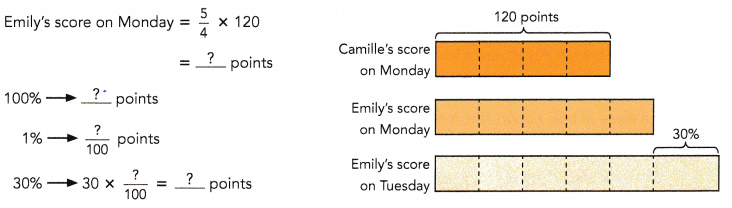
The increase in the number of points Emily scored on Tuesday was  .
.
Answer:
45 points
Explanation:

Math in Focus Course 1A Practice 6.5 Answer Key
Solve. Show your work.
Question 1.
Tom earned $600 last summer delivering newspapers. This summer, he earned 20% more. How much did he earn this summer?
Answer:
$720
Explanation:
Tom earned $600 last summer delivering newspapers.
This summer, he earned 20% more.
20% of 600 = (20 ÷ 100) x 600 = $120
This summer he earned = $600 + $120 = $720
Question 2.
A gift shop buys greeting cards at $3.50 each, and sells them at an 80% markup. At what price does the gift shop sell each greeting card?
Answer:
$6.30
Explanation:
A gift shop buys greeting cards at $3.50 each,
he sells them at an 80% markup.
80% of 3.50 = (80 ÷ 100) x 3.50 = 2.8
price each greeting card,
3.50 + 2.8 = 6.30
Question 3.
Ms. Kendrick earned $3,600 each month last year. This year, she is given a pay raise of 15%. How much more money does she earn each month this year than she earned each month last year?
Answer:
$540
Explanation:
Ms. Kendrick earned $3,600 each month last year.
This year, she is given a pay raise of 15%
more money does she earn each month this year than she earned each month last year
3600 x (15 ÷ 100) = 540
Question 4.
The original price of a computer was $1,250. At a year-end sale, the selling price of the computer was $900. Find the percent discount.
Answer:
28%
Explanation:
The original price of a computer was $1,250.
At a year-end sale, the selling price of the computer was $900.
(n ÷ 100) x 1250 = 900
1250n = 900 x 100
1250n = 90000
n = 90000 ÷ 1250
n = 72
the percent of discount = 100 – 72 = 28%
Question 5.
Last year, Alex earned a monthly salary of $250, and Ben earned a monthly salary of $180. This year, each of them received a pay increase of 25%. This year, how much more did Alex earn in one month than Ben?
Answer:
$17.5
Explanation:
Last year, Alex earned a monthly salary of $250,
This year, each of them received a pay increase of 25%.
(25 ÷ 100) x 250 = 62.5
Ben earned a monthly salary of $180,
This year, each of them received a pay increase of 25%.
(25 ÷ 100) x 180 = 45
This year, how much more did Alex earn in one month than Ben
62.5 – 45 = 17.5
Question 6.
Alan deposited $300 into a savings account. At the end of the first year, the amount of money in the account had increased to $336. At the end of the second year, he had $420.
a) Find the percent increase in the amount of money in his savings account at the end of the first year.
Answer:
12%
Explanation:
Alan deposited $300 into a savings account.
At the end of the first year, the amount of money in the account had increased to $336.
Simple interest = (principal amount x Rate of interest x time) ÷ 100
principal amount = 300
Amount increased = 336
S.I = 336 – 300 = 36
Time = 1 year
36 = (300 x R x 1) ÷ 100
R = (36 x 100) ÷ 300 = 12%
b) Find the percent increase in the amount of money in his savings account from the end of the first year to the end of the second year.
Answer:
25%
Explanation:
From the above explanation in the difference amount is
420 – 336 = 84$
(84/336) x 100 =25%
Question 7.
Linda had an orange ribbon and a blue ribbon. The orange ribbon was 2 meters long. The blue ribbon was \(\frac{4}{5}\) as long as the orange ribbon. Linda cut off a piece of blue ribbon. The length of the piece was 25% of the length of the blue ribbon.
a) What was the length of the blue ribbon before it was cut?
Answer:
1.6 m
Explanation:
The orange ribbon was 2 meters long
The blue ribbon was = 2x\(\frac{4}{5}\) = 1.6m
piece was 25% of the length of the blue ribbon.
2x\(\frac{4}{5}\) x \(\frac{25}{100}\)
= \(\frac{40}{100}\)
= 40%
b) Find the length of the piece of blue ribbon that Linda cut off.
Answer:
0.4 m
Explanation:
piece was 25% of the length of the blue ribbon.
2x\(\frac{4}{5}\) x \(\frac{25}{100}\)
= \(\frac{40}{100}\)
= 0.4
Question 8.
One year, the number of subscribers for Newspaper A was 7,600, and the number of subscribers for Newspaper B was \(\frac{3}{4}\) of the number of subscribers for Newspaper A. The next year, the number of subscribers for Newspaper B increased by 25%. Find the total number of subscribers for Newspaper B the next year.
Answer:
7125 subscribers
Explanation:
subscribers for Newspaper A was 7,600
subscribers for Newspaper B was \(\frac{3}{4}\) x 7,600 = 5,700
\(\frac{25}{100}\) x 5,700 = 1,425
subscribers for Newspaper B increased by 25% = 1,425
the total number of subscribers for Newspaper B the next year.
5,700 + 1,425 = 7,125
Question 9.
Ryan had 240 CDs. Sharon had \(\frac{9}{2}\) of the number of CDs Ryan had. Sharon gave 75 CDs to her friends. Find the percent decrease in the number of CDs Sharon had. Round your answer to 2 decimal places.
Answer:
6.95%
Explanation:
Ryan had 240 CDs.
Sharon had \(\frac{9}{2}\) of the number of CDs Ryan had.
240 x \(\frac{9}{2}\) = 1080
Sharon gave 75 CDs to her friends.
1080 – 75 = 1005
The percent decrease in the number of CDs Sharon had
(1005 ÷ 1080) x 100 = 93.05
100% – 93.05% = 6.95
Question 10.
Shaun collected $925 on the first day of a charity fundraiser. On the second day, he collected $728. By the third day, he had collected a total of $2,538.
a) What was the percent decrease in the amount of money collected from the first day to the second day? Round your answer to 1 decimal place.
Answer:
21.3%
Explanation:
Shaun collected $925 on the first day of a charity fundraiser.
On the second day, he collected $728.
925 – 728 = 197
the percent decrease in the amount of money collected from the first day to the second day
(197 ÷ 925) x 100 = 21.29 = 21.3
b) Find the percent increase or decrease in the amount collected from the second day to the third day. Round your answer to 1 decimal place.
Answer:
21.6%
Explanation:
On the second day, he collected $728.
By the third day, he had collected a total of $2,538.
925 + 728 = 1653
2,538 – 1653 = 885
the percent decrease in the amount of money collected from the second day to the third day
(728 ÷ 885) x 100 = 21.29 = 21.3
Question 11.
Math Journal Jason and Robert each solved the following problem: In a science experiment, Mark had to record the change in the height of a candle when it is lighted. The height of the candle was 25 centimeters at first. After burning for 10 minutes, the height of the candle decreased to 20 centimeters. Another 20 minutes later, the height of the candle decreased to 15 centimeters. Find the percent decrease in its height from 20 centimeters to 15 centimeters.

Whose answer is incorrect? Explain why.
Answer:
Robert’s answer is correct
Explanation:
The question is to find the percent decrease in its height from 20 centimeters to 15 centimeters.

Brain @ Work
Question 1.
A shopping club is having a sale. Members and nonmembers of the club receive different discounts, as shown below.

a) Sally is not a member of the shopping club. She wants to purchase a camcorder that is selling at $580. How much does Sally have to pay for the camcorder?
Answer:
$502
Explanation:
Sally is not a member of the shopping club,
So she will get 10% discount and $20 off with a minimum purchase of $500
She wants to purchase a camcorder that is selling at $580.
Total amount she has to pay for the camcorder
580 x (10 ÷ 100) = 58
580 – 58 = 522
522 – 20 = $502
b) Tabitha is a member of the shopping club. She wants to purchase a computer laptop that is selling at $990. How much does Tabitha have to pay for the computer laptop?
Answer:
$722.5
Explanation:
Tabitha is a member of the shopping club.
She wants to purchase a computer laptop that is selling at $990.
She will get a discount of 25% and $20 off with minimum purchase of $500
Total amount Tabitha have to pay for the computer laptop
990 x (25 ÷ 100) = 247.5
990 – 247.5 = 742.5
742.5 – 20 = $722.5
Question 2.
The figure- the area of the shaded part is 40% of the area of Square P. It is also 20% of the area of Square Q. What percent of the figure is shaded? Round your answer to 2 decimal places. (Hint: Find the ratio of the area of the shaded part to the unshaded part.)
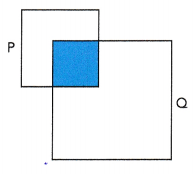
Answer:
16.66 sq mt
Explanation:
P:Q
60 : 40 = 20 : 80
6 : 4 = 2 : 8
3 : 2 = 1 : 4
\(\frac{2}{12}\)
\(\frac{1}{6}\) = 16.66