Hillary

Practice the problems of Math in Focus Grade 1 Workbook Answer Key Chapter 10 Practice 2 Finding the Weight of Things to score better marks in the exam.

Math in Focus Grade 1 Chapter 10 Practice 2 Answer Key Finding the Weight of Things

Fill in the blanks.

Example

The weight of the paper ball is about 3 clothes pins.

Question 1.

The weight of the doll is about ____ toy bricks.
Answer: The weight of the doll is about 15 toy bricks.

Question 2.

The weight of the toy hippo is about ____ toy bricks.
Answer: The weight of the toy hippo is about 20 toy bricks.

Question 3.

The weight of Kitty is more than 15 toy bricks. The weight of Kitty is about ____ toy bricks.
Answer: The weight of Kitty is about 17 toy bricks.

Look at the pictures Then fill in the blanks.

Question 4.
The weight of the tomato is about ____ beads.
Answer: The weight of the tomato is about 15 beads.

Question 5.
The weight of the lemon is about ____ beads.
Answer: The weight of the lemon is about 20 beads.

Question 6.
The weight of the onion is about ____ beads.
Answer: The weight of the onion is about 12 beads.

Question 7.
The tomato is heavier than the ____
Answer: The tomato is heavier than the weight of onion.

Question 8.
The tomato is lighter than the ____
Answer: The tomato is lighter than the weight of lemon.

Question 9.
The ___ is the heaviest.
Answer: The weight of the lemon is the heaviest.

Question 10.
The ____ is the lightest.
Answer: The weight of the onion is the lightest.

Look at the pictures. Then fill in the blanks.

Question 11.
The weight of the pencil case is ___ coins.
Answer: The weight of the pencil case is 10 coins.

Question 12.
The weight of the plastic bottle is ___ coins.
Answer: The weight of the plastic bottle is 6 coins.

Question 13.
The weight of the teddy bear is ___ coins.
Answer: The weight of the teddy bear is 17 coins.

Question 14.
The ____ is heavier than the plastic bottle.
Answer: The weight of the pencil case is heavier than the plastic bottle.

Question 15.
The ____ is lighter than the teddy bear.
Answer: The weight of pencil case is lighter than the teddy bear.

Question 16.
The pencil case is heavier than the ___
Answer: The pencil case is heavier than the plastic bottle.

Question 17.
The ____ is lighter than the ____
Answer: The pencil case is lighter than the teddy bear.

Question 18.
The heaviest thing is the ____
Answer: The heaviest thing is the teddy bear.

Question 19.
The lightest thing is the ____
Answer: The lightest thing is the plastic bottle.

Practice the problems of Math in Focus Grade 1 Workbook Answer Key Chapter 11 Practice 1 Simple Picture Graphs to score better marks in the exam.

Math in Focus Grade 1 Chapter 11 Practice 1 Answer Key Simple Picture Graphs

Daniel draws a picture graph of his friends’ birth months.

Use the graph to answer the questions.

Question 1.
How many friends are born in January? ____
Answer: 3 friends are born in January

Question 2.
In which month are most of his friends born? ____
Answer: Most of the friends are born on the month of April

Look at the picture graph. Then fill in the blanks.

This picture graph shows the flowers in Shana’s garden.

Question 3.
There are ___ sunflowers.
Answer: There are 5 sunflowers

Question 4.
There are ___ roses.
Answer: There are 8 roses.

Question 5.
There are ____ tulips.
Answer: There are 3 tulips.

Question 6.
There are ___ more roses than tulips.
Answer: There are 5 more roses than tulips.

Question 7.
There are ____ fewer tulips than sunflowers.
Answer: There are 3 fewer tulips than sunflowers.

Question 8.
There are ___ flowers in all.
Answer: There are 17 flowers in all.

Look at the picture graph. Then fill in the blanks.

This picture graph shows all the toys in Annie’s toy box.

Question 9.
There are ___ toy planes ¡n Annie’s box.
Answer: There are 3 toy planes ¡n Annie’s box.

Question 10.
There are ___ toy cars.
Answer: There are 10 toy cars.

Question 11.
There are ___ toy trains.
Answer: There are 6 toy trains.

Question 12.
The number of ___________ is the greatest.
Answer: The number of toy car is the greatest.

Question 13.
The number of ___________ is the least.
Answer: The number of toy planes is the least.

Question 14.
Annie has ___ toys in all.
Answer: Annie has 19 toys in all.

Question 15.
There are ________ more toy cars than toy trains.
Answer: There are 4 more toy cars than toy trains.

Question 16.
There are 7 fewer ____________ than ________
Answer: There are 7 fewer toy planes than toy cars

Look at the picture graph. Then fill in the blanks.

This picture graph shows the coins Barry saves in a week.

Question 17.
How many coins does Barry save on Monday? ___ coins
Answer: Barry save 2 coins on Monday

Question 18.
How many coins does he save on Tuesday? ___ coins
Answer: Barry save 4 coins on Tuesday

Question 19.
Barry saves 1 coin on Friday.
He saves ___ more coins on Saturday.
Answer: He saves 2 more coins on Saturday.

Question 20.
How many coins in all does he save from Thursday to Saturday? ___ coins
Answer: From Thursday to Saturday Barry has 17 coins in all

Question 21.
He does not save on ____
Answer: He does not save on Wednesday

Go through the Math in Focus Grade 5 Workbook Answer Key Chapter 5 Algebra to finish your assignments.

Math in Focus Grade 5 Chapter 5 Answer Key Algebra

Math Journal

John’s solutions to the following problems are as shown. Identify and explain the mistakes John has made. Then give the correct solution.

Question 1.
4w + 12w – 10 = 16w – 10
= 6 w
Answer:
4w + 12w – 10 = 16w – 10
Explanation:
John has made a mistake in subtracting number from a variable type of number. So, the correct solution is 16w – 10.

Question 2.
20p – 2p + 4p = 20p – 6 p
= 14p
Answer:
20p – 2p + 4p = 24p – 2p = 22p
Explanation:
John has made a mistake in the order of subtraction and additions. First we should add all the numbers and then subtract the numbers. So, the correct solution is 22p.

Question 3.
6 ÷ q = \(\frac{q}{6}\)
Answer:
6 ÷ q = 6/q
Explanation:
John has made a mistake in putting the numerator and denominator of a division.
The number before the division symbol (÷) should be consider as numerator.
The number after the division symbol (÷) should be consider as denominator.
So, the correct solution is 6/q.

Question 4.
Clarissa bought 3 cartons of milk for y cents each. She gave the cashier $10. How much change did she receive? Express your answer in terms of y.
Answer:
3 × y = 3y
3 cartons of milk cost 3y cents.
$1 = 100 cents
So, $10 = 1,000 cents
Hence, Clarissa received (1,000 – 3y) cents in change.

Put On Your Thinking Cap!

Challenging Practice

Wendy bought 7 handbags. Each handbag costs the same amount. She paid the cashier $100 and received g dollars in change.

a. What was the cost of each handbag in terms of g?
Answer:
Total money paid to cashier is $100.
Total number of handbags bought = 7
Total change received = g $
So, cost of 7 handbags = (100-g)$
Cost of each handbag = (100-g)/7 $

b. If the price of each handbag was more than $1 0, what is the least possible value of g? (Assume that the cost of each handbag is a whole number.)
Answer:
Assume that each handbag costs 10$, then change given is (100-(7×10)) =(100-70)$ = 30$
Assume that each handbag costs 12$, then change given is (100-(7×12)) =(100-84)$ = 16$
Assume that each handbag costs 14$, then change given is (100-(7×14)) =(100-98)$ = 2$
So, the least possible value of g is 2.

Put On Your Thinking Cap

Problem Solving

There are 40 pupils in a class. There are x more girls than boys.

a. How many boys are there in terms of x?
Answer:
Let’s say total number of boys are ‘b’.
Then total number of girls in class will be ‘b+x’
Total number of pupils in class = number of boys + number of girls
40 = b + (b+x).
So, b=(40-x)/2
The number of boys in class un terms of ‘x’ is (40-x)/2

b. If x = 4, how many boys are there?
Answer:
As we know that number of boys = (40-x)/2
So, number of boys = (40-4)/2 = 36/2 =18
Therefore, total number of boys in class is 18.

Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 9 Practice 5 Estimating Decimals to score better marks in the exam.

Math in Focus Grade 5 Chapter 9 Practice 5 Answer Key Estimating Decimals

Round each decimal to the nearest whole number. Then estimate the sum or difference.

Example
7.7 + 12.3
7.7 rounds to 8.
12.3 rounds to 12.
8 + 12 = 20
7.7 + 12.3 is about 20.

21.8 – 11.5
21.8’ rounds to 22.
11.5 rounds to 12.
22 – 12 = 10
21.8 – 11.5 is about 10.

Question 1.
$2.90 + $7.15
Answer: $10.05
Estimate: 10
Explanation:
2.90 + 7.15
2.90 rounds to 3.
7.15 rounds to 7.
3 + 17 = 10
2.90 + 7.15 is about 10.

Question 2.
9.05 + 19.55
Answer: $28.6
Estimate: 29
Explanation:
9.05 + 19.55
9.05 rounds to 9.
19.55 rounds to 20.
9 + 20 = 29
9.05 + 19.55 is about 29.

Question 3.
35.67 – 15.09
Answer: $20.58
Estimate: 21
Explanation:
35.67 – 15.09
35.67 rounds to 36.
15.09 rounds to 15.
36 – 15 = 21
35.67 – 15.09 is about 21.

Question 4.
$15.40 – $5.95
Answer: $9.45
Estimate: 9
Explanation:
15.40 – 5.95
15.40 rounds to 15.
5.95 rounds to 6.
15 – 6 = 9
15.40 – 5.95 is about 9.

Estimate the product by rounding the decimal to the nearest whole number.

Example
4.5 × 4
4.5 rounds to 5.
5 × 4 = 20
4.5 × 4 is about 20.

Question 5.
19.6 × 3
Answer: 58.8
Estimate: 60
Explanation:
19.6 × 3
19.6 rounds to 20.
20 × 3 = 60
19.6 × 3 is about 60.

Question 6.
0.95 × 8
Answer: 7.6
Estimate:800
Explanation:
0.95 × 8
0.95 rounds to 100.
100 x 8 = 800
0.95 × 8 is about 800.

Question 7.
8.25 × 3
Answer: 24.75
Estimate: 2400
Explanation:
8.25 × 3
8.25 rounds to 800.
800 × 3 = 2400
8.25 × 3 is about 2400.

Estimate the quotient by choosing a whole number close to the dividend that can be evenly divided by the divisor.

Example
24.6 ÷ 5
24.6 is about 25.
25 ÷ 5 = 5
24.6 ÷ 5 is about 5.

Question 8.
38.4 ÷ 6
Answer: 6.4
Estimate: 6
Explanation:
38.4 ÷ 6
38.4 is about 36.
36 ÷ 6 = 6
38.4 ÷ 6 is about 6.

Question 9.
71.09 ÷ 8
Answer: 8.8
Estimate: 9
Explanation:
71.09 ÷ 8
71.09 is about 72.
72 ÷ 8 = 9
71.09 ÷ 8 is about 9.

Question 10.
99.75 ÷ 5
Answer: 19.95
Estimate: 20
Explanation:
99.75 ÷ 5
99.75 is about 100.
100 ÷ 5 = 20
99.75 ÷ 5 is about 20.

Round each decimal to the nearest tenth. Then estimate.

Question 11.
0.47 + 15.51
Answer: 15.98
Estimate: 16
Explanation:
0.47 + 15.51
0.47 rounds to 1.
15.51 rounds to 15.
15 + 1 = 16
0.47 + 15.51 is about 16.

Question 12.
9.95 – 1.46
Answer: 8.49
Estimate: 9
Explanation:
9.95 – 1.46
9.95 rounds to 10.
1.46 rounds to 1.
10 – 1 = 9
9.95 – 1.46 is about 9.

Question 13.
2.89 pounds × 4
Answer: 11.56
Estimate: 1200
Explanation:
2.89 × 4
2.89 rounds to 300.
300 × 4 = 1200
2.89 × 4 is about 1200.

Estimate the quotient by choosing a tenth close to the dividend that can be evenly divided by the divisor.

Question 14.
6.34 kilograms ÷ 7
Answer: 0.90
Estimate: 1
Explanation:
6.34 ÷ 7
6.34 is about 7.
7 ÷ 7 = 1
6.34 ÷ 7 is about 1.

Solve. Show your work.

Question 15.
A bag of walnuts sells for $1.95. Estimate the cost of 8 bags of walnuts.
Answer: $15.6
Estimate: 16
Explanation:
1.95 × 8
1.95 rounds to 2.
2 × 8 = 16
1.95 × 8 is about 16.

Question 16.
A piece of plywood is 1 .27 centimeters thick. Find the thickness of a pile of 9 pieces of plywood to the nearest tenth of a centimeter. Estimate to check if your answer is reasonable.
Answer: 11.43 cm
Estimate: 1170
Explanation:
1.27 × 9
1.27 rounds to 130.
130 × 9 = 1170
1.27 × 9 is about 1170.

Practice the problems of Math in Focus Grade 5 Workbook Answer Key Chapter 10 Practice 2 Expressing Fractions as Percents to score better marks in the exam.

Math in Focus Grade 5 Chapter 10 Practice 2 Answer Key Expressing Fractions as Percents

Express each fraction as a percent.

Example

Question 1.
\(\frac{26}{50}\) = ______%
Answer: 15%
Explanation:
To convert a fraction to a percent, first multiply the numerator and the denominator with 5.

Question 2.
\(\frac{4}{5}\) = ______%
Answer: 25%
Explanation:
To convert a fraction to a percent, first multiply the numerator and the denominator with 25.

Question 3.
\(\frac{19}{25}\) = ______%
Answer: 76%
Explanation:
To convert a fraction to a percent, first multiply the numerator and the denominator with 4.

Question 4.
\(\frac{1}{4}\) = ______%
Answer: 25%
Explanation:
To convert a fraction to a percent, first multiply the numerator and the denominator with 25.

Express each fraction as a percent.

Example
\(\frac{1}{5}\) = \(\frac{1}{5}\) × 100% = 20

Question 5.

Answer:

Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the decimal by 100 to express fraction as percentage.

Question 6.

Answer:

Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the decimal by 100 to express fraction as percentage.

Question 7.

Answer:

Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the decimal by 100 to express fraction as percentage.

Express each percent as a fraction in simplest form.

Example

Question 8.

Answer:

Explanation:
To convert a percent to a fraction, we have to remove the percent sign and divide the given number by 100.
And, then we express the fractional form of the percentage in the simplest form.
Divide 100% into 20 parts as each part has 5%.
So, 11 parts is equal to 55%.

Question 9.

Answer:

Explanation:
To convert a percent to a fraction, we have to remove the percent sign and divide the given number by 100.
And, then we express the fractional form of the percentage in the simplest form.
Divide 100% into 25 parts as each part has 4%.
So, 21 parts is equal to 84%.

Express each fraction as a percent.

Question 10.
\(\frac{64}{200}\) = \(\frac{32}{100}\) = ___ %
Answer: 32 %
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .

Question 11.
\(\frac{1300}{400}\) = ___ %
Answer: 325%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .

Question 12.
\(\frac{480}{600}\) = ___ %
Answer: 80%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .

Question 13.
\(\frac{518}{700}\) = ___ %
Answer: 74%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .

Solve. Show your work.

Question 14.
Jeremy finished \(\frac{3}{5}\) of his homework. What percent of his homework did he finish?

Answer: 60%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .

Question 15.
Tracy ran in a marathon, but managed to complete only \(\frac{13}{20}\) of the race.

a. What percent of the marathon did she complete?
Answer: 65%
Explanation:
To convert a fraction to a percent, first divide the numerator by the denominator.
Then multiply the answer by 100 .
It can be converted to percent by multiplying the decimal by 100 .

b. Write each ratio as a fraction and then as a percent.
Answer:
\(\frac{65}{100}\) = 65 %
Explanation:
To convert a fraction to a percent, first multiply the numerator and the denominator with 5.

Solve. Show your work.

Question 16.
Katie bought some flour. She used \(\frac{3}{8}\) of it to bake bread. What percent of the flour is left?

Answer: 62.5%
Explanation:

She used \(\frac{3}{8}\) of it to bake bread, it means 37.5%  used
100% – 37.5% = 62.5% of the flour is left.

Question 17.
There are 800 members in on astronomy club, and 320 of them are females. What percent of the members are males?
Answer: 60%
Explanation:
800 members in on astronomy club, and 320 of them are females.

it means 40% are females.
100 % – 40% = 60% of the members are males.

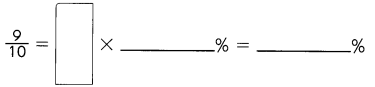
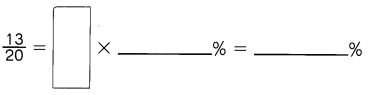
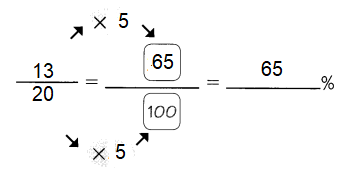
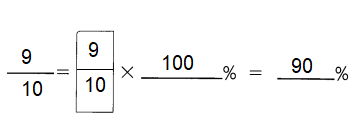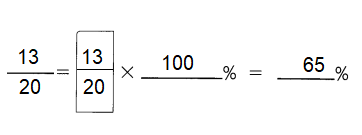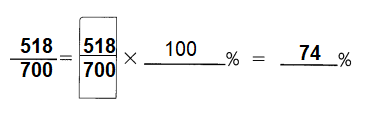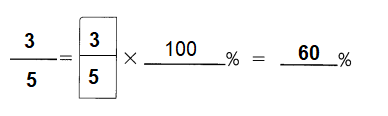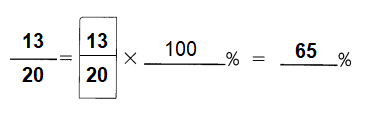This handy Math in Focus Grade 5 Workbook Answer Key Chapter 11 Practice 2 Graphing an Equation provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 11 Practice 2 Answer Key Graphing an Equation

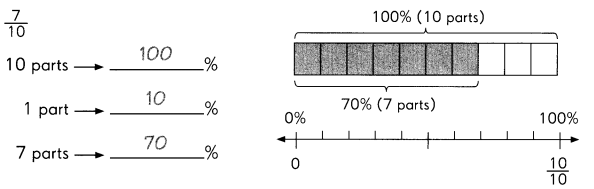
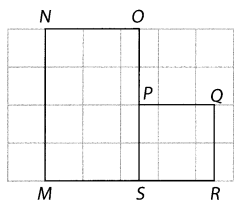
Write the ordered pair for each point.

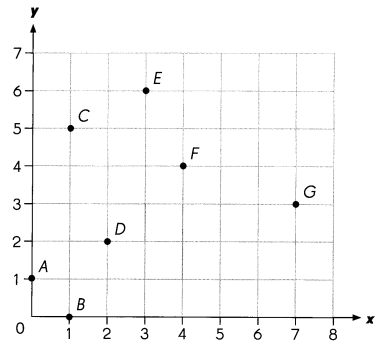
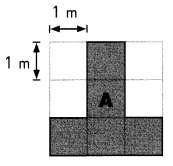
Example
A (0, 1)

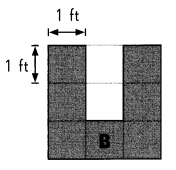
Question 1.
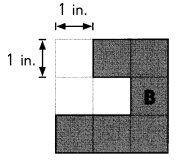
B ___
Answer:
B(1,0)
Explanation:
An ordered pair is used to show the position on a graph,
where the “x” (horizontal) value is first, and the “y” (vertical) value is second.

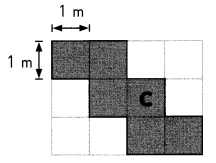
Question 2.
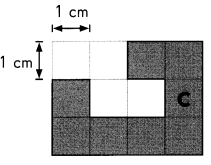
C ____
Answer:
C(1,5)
Explanation:
The numbers on a coordinate grid are used to locate points.
Each point can be identified by an ordered pair of numbers;
that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate.

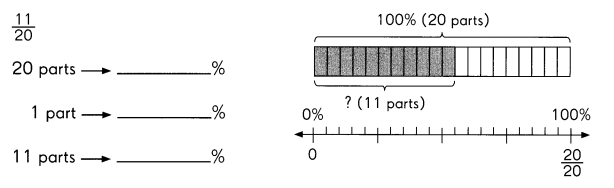
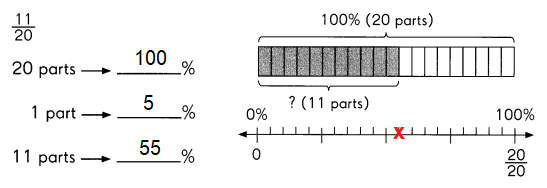
Question 3.
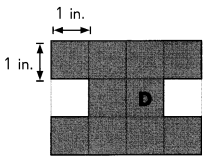
D ___
Answer:
D(2,2)
Explanation:
An ordered pair is used to show the position on a graph,
where the “x” (horizontal) value is first, and the “y” (vertical) value is second.

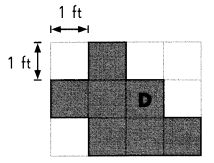
Question 4.
E ____
Answer:
E(3,6)
Explanation:
The numbers on a coordinate grid are used to locate points.
Each point can be identified by an ordered pair of numbers;
that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate.

Question 5.
F ____
Answer:
F(4,4)
Explanation:
An ordered pair is used to show the position on a graph,
where the “x” (horizontal) value is first, and the “y” (vertical) value is second.

Question 6.
G ____
Answer:
G(7,3)
Explanation:
The numbers on a coordinate grid are used to locate points.
Each point can be identified by an ordered pair of numbers;
that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate.

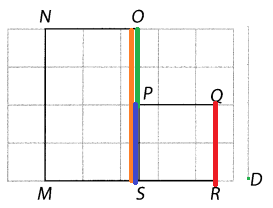
Plot each point on the coordinate grid.

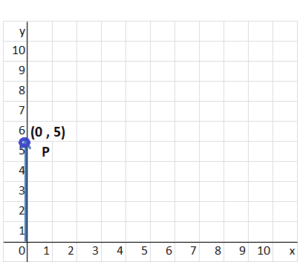
Question 7.
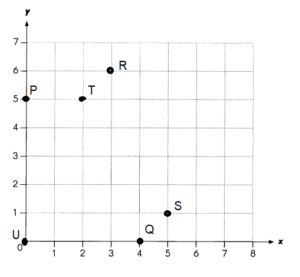
P(0, 5)
Answer:
The location of (0,5) is shown on the coordinate grid below.
The x-coordinate is 0.
The y-coordinate is 5.
To locate (0,5), move 0 units to the right on the x-axis and 5 units up on the y-axis.

Explanation:
The numbers on a coordinate grid are used to locate points.
Each point can be identified by an ordered pair of numbers;
that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate.
P(x,y) = (0,5)

Question 8.
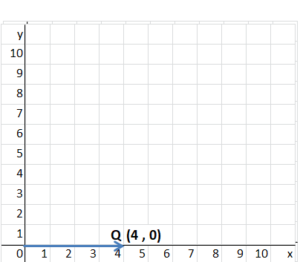
Q(4, 0)
Answer:
The location of (4,0) is shown on the coordinate grid below.
The x-coordinate is 4.
The y-coordinate is 0.
To locate (4,0), move 4 units to the right on the x-axis and 0 units up on the y-axis.

Explanation:
The numbers on a coordinate grid are used to locate points.
Each point can be identified by an ordered pair of numbers;
that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate.
P(x,y) = (4,0)

Question 9.
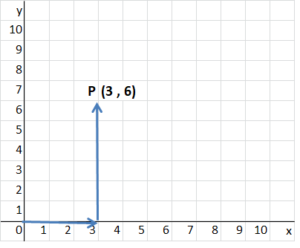
R(3, 6)
Answer:
The location of (3,6) is shown on the coordinate grid below.
The x-coordinate is 4.
The y-coordinate is 0.
To locate (3,6), move 3 units to the right on the x-axis and 6 units up on the y-axis.

Explanation:
The numbers on a coordinate grid are used to locate points.
Each point can be identified by an ordered pair of numbers;
that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate.
R(x,y) = (3,6)

Question 10.
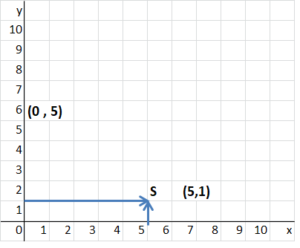
S(5, 1)
Answer:
The location of (5,1) is shown on the coordinate grid below.
The x-coordinate is 5.
The y-coordinate is 1.
To locate (5,1), move 5 units to the right on the x-axis and 1 units up on the y-axis.

Explanation:
The numbers on a coordinate grid are used to locate points.
Each point can be identified by an ordered pair of numbers;
that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate.
S(x,y) = (5,1)

Question 11.
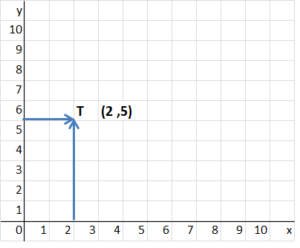
T(2, 5)
Answer:
The location of (2,5) is shown on the coordinate grid below.
The x-coordinate is 2.
The y-coordinate is 5.
To locate (2,5), move 2 units to the right on the x-axis and 5 units up on the y-axis.

Explanation:
The numbers on a coordinate grid are used to locate points.
Each point can be identified by an ordered pair of numbers;
that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate.
T(x,y) = (2,5)

Question 12.
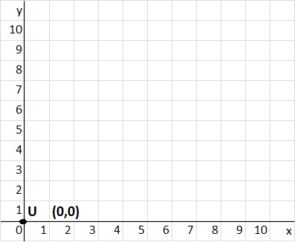
U(0, 0)
Answer:
The location of (0,0) is shown on the coordinate grid below.
The x-coordinate is 0.
The y-coordinate is 0

Explanation:
The numbers on a coordinate grid are used to locate points.
Each point can be identified by an ordered pair of numbers;
that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate.
U(x,y) = (0,0)

The location of (0,0) is shown on the coordinate grid below. The x-coordinate is 0. The y-coordinate is 0

ANSWER:

Explanation:
The numbers on a coordinate grid are used to locate points.
Each point can be identified by an ordered pair of numbers;
that is, a number on the x-axis called an x-coordinate, and a number on the y-axis called a y-coordinate.

Use the graph to answer the questions
The perimeter of a square is P centimeters and the length of each side is s centimeters. A graph of P = 4s is drawn.

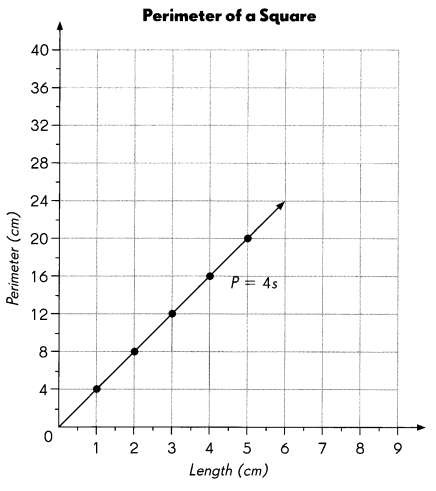
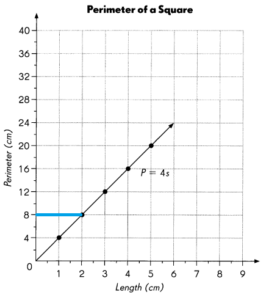
Question 13.
What is the perimeter of a square of side 2 centimeters? ___________
Answer:
8 centimeters
Explanation:
Perimeter of square = 4s
s = 2
P = 4 x 2 = 8 cm

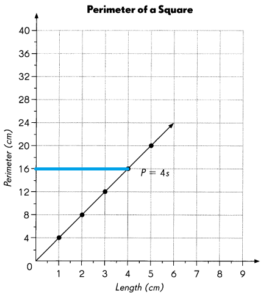
Question 14.
What is the perimeter of a square of side 4.5 centimeters? ___________
Answer:
18 centimeters
Explanation:
P=4s
s = 4.5
P = 4 x 4.5 = 18 cm

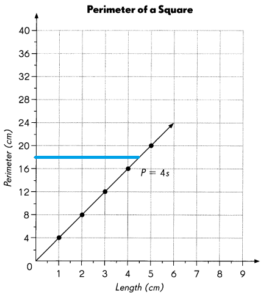
Question 15.
What is the length of a side of a square if its perimeter is 4 centimeters? ____________
Answer:
16 centimeters
Explanation:
Perimeter of square = 4s
s = 4
P = 4 x 4 = 16cm

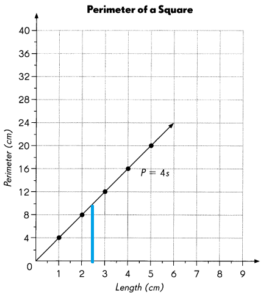
Question 16.
What is the length of a side of a square if its perimeter is 10 centimeters? ____________
Answer:
2.5 centimeter
Explanation:
Perimeter of square = 4s
P=10
10 = 4 x s = 2.5 cm

Question 17.
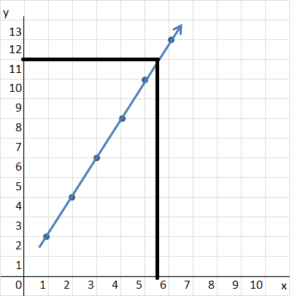
If the point (7, M) is on the graph what is the value of M? ___________
Answer:
M = 28
Explanation:
Perimeter of square = 4s
s = 7
P = 4 x 7 = 28

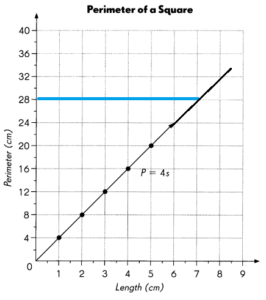
The line starting from (0,0) is extended to upwards, x is 7 and the value is 28

Complete the table.

Question 18.
Each bottle contains 2 liters of cooking oil.

Answer:

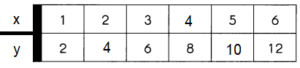
Explanation:
Each bottle contains 2 liters of cooking oil.
Number of bottles are represented with x.
Number of liters are represented with y.
So, y = x X y.

Complete the graph using the data in the table. Then answer the questions.

Question 19.
How many liters of oil are in 3 bottles? _____
Answer:
6 liters
Explanation:
Volume = 2xb is the equation can be used
V = 2 x 3 = 6 liters
on graph

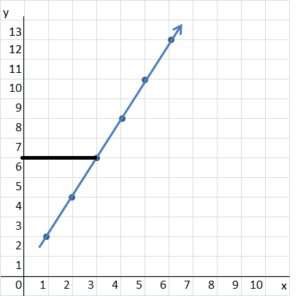
Question 20.
How many liters of oil are in 2.5 bottles? ____
Answer:
5 liters
Explanation:
Volume = 2xb is the equation can be used
V = 2 x 2.5 = 5 liters
on graph

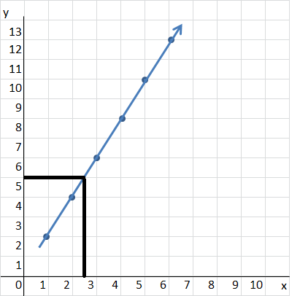
Question 21.
How many bottles contain 8 liters of oil? ____
Answer:
4 bottles
Explanation:
Volume = 2xb is the equation can be used
8 = 2 x b
on graph

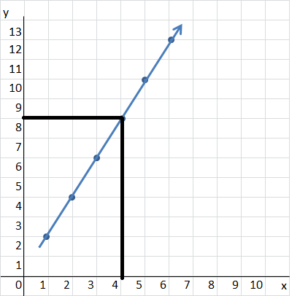
Question 22.
How many bottles contain 7 liters of oil?
Answer:
3.5 bottles
Explanation:
Volume = 2xb is the equation can be used
7 = 2 x b
on graph

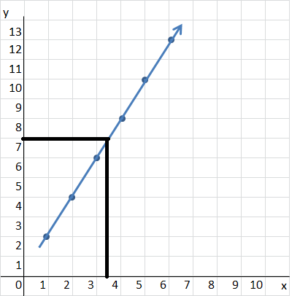
Question 23.
How many bottles contain 11 liters of oil? ___
Answer:
5.5 bottles
Explanation:
Volume = 2xb is the equation can be used
11 = 2 x b = 5.5
on graph

This handy Math in Focus Grade 5 Workbook Answer Key Chapter 11 Practice 3 Combinations provides detailed solutions for the textbook questions.

Math in Focus Grade 5 Chapter 11 Practice 3 Answer Key Combinations

Complete.
A bag has 1 red, 1 blue, and 1 green marble. Another bag has 1 red and 1 blue cube.

Question 1.
List all the possible combinations of choosing 1 marble and 1 cube.

Answer:

Explanation:
A probability is a number that reflects the chance or likelihood that a particular event will occur.
A bag has 1 red, 1 blue, and 1 green marble.
Another bag has 1 red and 1 blue cube.
So, probability may vary from one to one.

Question 2.
There are ___________ combinations.
Answer:
There are 6 combinations.
Explanation:
As we know probability is chance of occurrence,
so there are 6 possible combinations.

Complete.

In a soccer tournament, there are two groups. Each group has three teams. Teams A, B, and C are in Group 1. Teams X, Y, and Z are in Group 2. Each team in Group 1 plays against every team in Group 2.

Question 3.
Complete the table for the games played.

Answer:

Explanation:
In a soccer tournament, there are two groups.
Each group has three teams.
Teams A, B, and C are in Group 1.
Teams X, Y, and Z are in Group 2.
Each team in Group 1 plays against every team in Group 2.
As we know probability is chance of occurrence,
so there are 9 possible combinations.

Question 4.
The number of combinations of games for the six teams is ___.
Answer:
9 combinations
Explanation:
As we know probability is chance of occurrence,
so there are 9 possible combinations of games for 6 teams.

Draw a tree diagram to find the number of combinations.

Question 5.
Ms. Li has 4 different books and 1 red pen, 1 blue pen, and 1 black pen. She is wrapping one book and one pen to give as a gift.
Draw a tree diagram to find the number of combinations she can choose.

There are ___ combinations.
Answer:
12 combinations.

Explanation:
Ms. Li has 4 different books.
She has 1 red pen, 1 blue pen, and 1 black pen.
She is wrapping one book and one pen to give as a gift.
As we know probability is chance of occurrence,
so there are 12 possible combinations.

Find the number of combinations.

Question 6.
Rina has 1 black, 1 red, and 1 yellow skirt. She has 1 white, 1 floral, and 1 striped shirt.

a. Draw a tree diagram to show the possible outfits Rina can wear.
Answer:

Explanation:
A tree diagram is a tool in the fields of general mathematics, probability, and statistics.
It helps to calculate the number of possible outcomes of an event or problem,
and to cite those potential outcomes in an organized way.

b. Find the number of outfits by multiplication.
The number of outfits is ____.
Answer:
The number of outfits is 9
Explanation:
Rina has 1 black, 1 red, and 1 yellow skirt.
She has 1 white, 1 floral, and 1 striped shirt.
All together she has 3 skirts and 3 shirts.
So, the number of outfits she can wear
3 x 3 = 9

Complete.

Question 7.
There are 4 colors on a spinner. There are 6 faces on a number cube, numbered 1 to 6. The spinner is spun and the number cube is tossed.
There are ___________ combinations of color and number.
Answer:
24 combinations of color and number.
Explanation:
There are 24 combinations of color and number.
m x n is the possible combinations of color and number.
m = 4
n = 6
m x n = 4 x 6  = 24

Question 8.
A bookshelf has 10 mathematics books, 8 science books, and 12 history books.

a. There are ___ combinations of a mathematics book and a science book.
Answer:
80 combinations of mathematics and science books.
Explanation:
There are 80 combinations of a mathematics book and a science book.
m x s is the possible combinations of a mathematics book and a science book.
m = 10
s  = 8
m x s = 10 x 8  = 80

b. There are ___________ combinations of a science book and a history book.
Answer:
96 combinations of science and history books.
Explanation:
There are 96 combinations of a History book and a science book.
m x s is the possible combinations of a History book and a science book.
h =  12
s  = 8
h x s = 12 x 8  = 96

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 17 Angles and Lines provides detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 17 Answer Key Angles and Lines

Math Journal

Question 1.
How would you explain perpendicular lines to a second-grader?
Answer:
Two distinct lines intersecting each other at 90° or a right angle are called perpendicular lines.

Explanation:
Draw two straight lines,
which intersect each other.
Measure the angles of intersecting lines, it shows 90°.
So, Two distinct lines intersecting each other at 90° or a right angle are called perpendicular lines.
Question 2.
How would you explain parallel lines to a younger brother or sister?
Answer:
First explain the concept of lines,
then explain them that the lines never meet each other are known ass parallel lines.
Example: Zebra crossing.

Explanation:
Parallel lines can be defined as two lines in the same plane that are at equal distance from each other and never meet.

Question 3.
Lines that meet are perpendicular. Is this statement true? Use figures to explain your answer.
Answer: Yes
Explanation:

A line that splits another line segment (or an angle) into two equal parts is called a “bisector.”
If the intersection between the two line segment is at a right angle, then the two lines are perpendicular,
and the bisector is called a “perpendicular bisector”.

Question 4.
Study the figure.

Line segment CD is not perpendicular to line segment EF. How would you show that they are not parallel?
Answer: YES
Explanation:
CD and EF are not perpendicular lines and,
if CD and EF are extended they will meet at one point C and E end one acute angle will form.

Put On Your Thinking Cap!

Challenging Practice

Draw each shape on the dot grid paper.

Question 1.
A shape with 5 sides and 5 angles

Answer:

Explanation:
5 sides and 5 angles is known as Pentagon.
A regular pentagon is a pentagon whose sides are equal in length, and whose interior angles are equal in measure.
Since each of the interior angles in a regular pentagon are equal in measure.

Question 2.
A shape with 3 sides and 2 angles less than a right angle

Answer:

Explanation:
A triangle is a type of polygon, which has three sides, and 2 angles are less than right angle.
The two sides are joined end to end is called the vertex of the triangle.
An angle is formed between two sides.

Question 3.
A shape with 4 sides and an angle greater than a right angle

Answer:

Explanation:
4 sides and an angle greater than a right angle
Isosceles trapezoid one pair of opposite sides are parallel and the base angles are equal in measure.
Alternative definitions are a quadrilateral with an axis of symmetry bisecting one pair of opposite sides,
or a trapezoid with diagonals of equal length.

Question 4.
A shape with 7 sides and 7 angles, 3 of which are right angles

Answer:
7 sides and 7 angles, 3 of which are right angles

Explanation:
A heptagon is a polygon that has seven sides.
It is a closed figure having 7 vertices.
A heptagon is also sometimes called Septagon.
In Geometry, the shape that is bounded by at least three straight lines or at least three interior angles is called polygon.

Answer the questions.

Question 5.
Name two pairs of perpendicular line segments.

Answer:
AC and BE perpendicular line segments and
AD and EC perpendicular line segments.
Explanation:
The intersection between the two line segment is at a right angle, then the two lines are perpendicular.

Question 6.
Name four line segments parallel to segment NM.

Answer:
OS, OP, PS, QR are four line segments parallel to segment NM.
Explanation:
four line segments parallel to segment NM are shown below;

OS, PS , OP and QR  are parallel lines to NM
Two lines, line segments, or rays are said to be parallel,
if they never meet and are always the same distance apart.

Question 7.
How many pairs of parallel line segments are in the diagram?

There are ____________ pairs of parallel line segments.
Answer:
There are  3 pairs of parallel line segments.
Explanation:
The below picture shows 3 pairs of parallel line segments with 3 different colors.

Two lines, line segments, or rays are said to be parallel,
if they never meet and are always the same distance apart.

Put on Your Thinking Cap!

Problem Solving

Draw shapes on dot grid paper. Then answer the questions.

Question 1.
Draw a triangle with a right angle.

Can you draw a triangle with 2 right angles? __________
Answer:

Explanation:
2 right angles, ∠CDA and ∠CDB
one right angle at C and one right angle at D.

Question 2.
Draw a shape with 4 sides and 2 right angles.

What do you notice about the other angles in the shape?
Answer:

Explanation:
The shape is rectangle with 4 sides and 2 right angles.
It is a type of quadrilateral that has its parallel sides equal to each other and all the four vertices are equal to 90 degrees. Hence, it is also called an equiangular quadrilateral.
Solve.

Question 3.
Five students are walking to school from their houses. Look at the map.

Which student’s house is nearest to the school? Student ___________ Draw a line segment to join this student’s house to the school. What do you notice about this line segment?
Answer:

Explanation:
From the above given information:
Student’s house is nearest to the school is C.
A line segment is bounded by two distinct points on a line.
Or we can say a line segment is part of the line that connects two points.
A line has no endpoints and extends infinitely in both the direction but a line segment has two fixed or definite endpoints.

Question 4.

The pattern is made up of perpendicular line segments. The 1st pattern has 1 right angle. The 2nd pattern has 3 right angles. The 3rd pattern has 5 right angles. How many right angles will the 10th pattern have?
Answer:
19 right angles
Explanation:
From the above information,
in each pattern 2 angles are added.
So, 19 right angles in the 10th pattern.

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 19 Practice 4 Area and Perimeter detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 19 Practice 4 Answer Key Area and Perimeter

Complete. Find the perimeter and area of each shaded figure.

Question 1.

Perimeter of Figure A is __________ centimeters.
Area of Figure A is __________ square centimeters.
Answer:
Perimeter of Figure A is 12 cm centimeters.
Area of Figure A is 6 square centimeters.
Explanation:
Perimeter is the distance around the edge of a shape.
Area is used to define the amount of space taken up by a 2D shape or surface.
We measure area in square units : cm² or m².
Area is calculated by multiplying the length of a shape by its width.

Question 2.

Perimeter of Figure B is __________ inches.
Area of Figure B is __________ square inches.
Answer:
Perimeter of Figure B is 13 inches.
Area of Figure B is 6 square inches.
Explanation:
Perimeter is the distance around the edge of a shape.
Area is used to define the amount of space taken up by a 2D shape or surface.
We measure area in square units : cm² or m².
Area is calculated by multiplying the length of a shape by its width.

Question 3.

Perimeter of Figure C is __________ centimeters.
Area of Figure C is __________ square centimeters.
Answer:
Perimeter of Figure C is 18 centimeters.
Area of Figure C is 8 square centimeters.
Explanation:
Perimeter is the distance around the edge of a shape.
Area is used to define the amount of space taken up by a 2D shape or surface.
We measure area in square units : cm² or m².
Area is calculated by multiplying the length of a shape by its width.

Question 4.

Perimeter of Figure D is __________ inches.
Area of Figure D is __________ square inches.

Answer:
Perimeter of Figure D is 18 inches.
Area of Figure D is 10 square inches.
Explanation:
The perimeter of a two-dimensional figure is the distance covered around it.
It defines the length of shape, whether it is a triangle, square, rectangle or a circle.
Area is the number of unit squares equal in measure to the surface of a figure.

Complete. Find the perimeter and area of each shaded figure.

Question 5.

Perimeter of Figure A is __________ meters.
Area of Figure A is __________ square meters.
Answer:
Perimeter of Figure A is 12 meters.
Area of Figure A is 5 square meters.
Explanation:
Perimeter is the distance around the edge of a shape.
Area is used to define the amount of space taken up by a 2D shape or surface.
We measure area in square units : cm² or m².
Area is calculated by multiplying the length of a shape by its width.

Question 6.

Perimeter of Figure B is __________ feet.
Area of Figure B is __________ square feet.
Answer:
Perimeter of Figure B is 16 feet.
Area of Figure B is 7 square feet.
Explanation:
Perimeter is the distance around the edge of a shape.
Area is used to define the amount of space taken up by a 2D shape or surface.
We measure area in square units : cm² or m².
Area is calculated by multiplying the length of a shape by its width.

Question 7.

Perimeter of Figure C is __________ meters.
Area of Figure C is __________ square meters.
Answer:
Perimeter of Figure C is 14 meters.
Area of Figure C is 6 square meters.
Explanation:
Perimeter is the distance around the edge of a shape.
Area is used to define the amount of space taken up by a 2D shape or surface.
We measure area in square units : cm² or m².
Area is calculated by multiplying the length of a shape by its width.

Question 8.

Perimeter of Figure D is __________ feet.
Area of Figure D is __________ square feet.
Answer:
Perimeter of Figure D is 14 feet.
Area of Figure D is 7 square feet.
Explanation:
Perimeter is the distance around the edge of a shape.
Area is used to define the amount of space taken up by a 2D shape or surface.
We measure area in square units : cm² or m².
Area is calculated by multiplying the length of a shape by its width.

Draw two different figures with an area of 5 square centimeters.

Question 9.

Do they have the same perimeter? _____________
Answer: No
Explanation:
Both have different perimeter,
As, the perimeter of a two-dimensional figure is the distance covered around it.
It defines the length of shape, whether it is a triangle, square, rectangle, circle and so on.

Draw two different figures with a perimeter of 8 centimeters.

Question 10.

Do they have the same area? _____________
Answer:
yes, they have the same area.

Explanation:
Area is the amount of space taken up by a 2D shape or surface.
We measure area in square units : cm² or m².
Area is calculated by multiplying the length of a shape by its width.

Find the perimeter and area of each figure.

Question 11.
Perimeter = ___________
Area = __________
Answer:
Perimeter = 12 m
Area =9 m2
Explanation:
Perimeter is the distance around the edge of a shape.
Area is used to define the amount of space taken up by a 2D shape or surface.
We measure area in square units : cm² or m².
Area is calculated by multiplying the length of a shape by its width.

Question 12.
Perimeter = _____________
Area = ___________
Answer:
Perimeter = 15m
Area = 9 m2
Explanation:
Perimeter is the distance around the edge of a shape.
Area is used to define the amount of space taken up by a 2D shape or surface.
We measure area in square units : cm² or m².
Area is calculated by multiplying the length of a shape by its width.

Write yes or no.

Question 13.
Do Figures A and B have the same area? ___________
Answer: YES
Explanation:
Area is the amount of space taken up by a 2D shape or surface.
Figure A and B have the same are
just by counting the 1×1 m box areas in the given figure will be the area of the figure.

Question 14.
Do Figures A and B have the same perimeter? ___________
Answer: NO
Explanation:
Perimeter is the distance around the edge of a shape.
Figure A and B do not have the same perimeter.
the shape of the figure A and B are different in shape,
the perimeters are also different to each other.

Question 15.
What is different about perimeter and area? Explain.
Answer:
Perimeter is the distance around the outside of a shape.
Area measures the space inside a shape.
Learn how to calculate perimeter and area for various shapes.
Explanation:
Area- Area is defined as space/region occupied by a two-dimensional flat object.
It is measured in square units.
Consider a square having side ‘a’ then the area of the square is given by a².
Perimeter- Perimeter is defined as the length of boundaries of a closed figure.
For example, a square having side length equal to ‘a,’ then the perimeter will be the sum of all its four sides, i.e. ‘4a.’
The measurement of the Perimeter is in the unit.

This handy Math in Focus Grade 3 Workbook Answer Key Chapter 19 Practice 1 Area provides detailed solutions for the textbook questions.

Math in Focus Grade 3 Chapter 19 Practice 1 Answer Key Area

Draw and color two different figures. Use 4 squares (☐) and 2 half-squares (◣) for each figure.

Question 1.

Answer:

Explanation:
Drawings may differ from one to one.
Using the squares in the grid we can draw different shapes.
Use 4 squares (☐) and 2 half-squares (◣) for each figure.
So, to differentiate the full square and half square shade with different colors, and then draw.

The figures are made of square and half-square tiles Write the area of each figure in the table.

Question 2.

Answer:

Explanation:
Area of a square is defined as the number of square units needed to fill a square.
In general, the area is defined as the region occupied inside the boundary of a flat object or 2d figure.
The measurement is done in square units with the standard unit being square meters (m 2).
As, it is mentioned  each square 1 unit square and each half square is half square unit.
So, by calculating each 1 square unit and half square units in the figure, we find Area.
In the figure A the area is 7 square units as it has 5 full squares and 4 half squares.
In the figure B the area is 6 square units as it has 6 full squares.
In the figure C the area is 6 square units as it has 6 full squares.
In the figure D the area is 8 square units as it has 7 full squares and 1 half square.
In the figure E the area is 9 square units as it has 7 full squares and 4 half squares.
In the figure F the area is 12 square units as it has 9 full squares and 6 half squares.

Question 3.
Figure _________ and Figure ________ have the same area.
Answer:
Figure  B and Figure C have the same area.
Explanation:
In the above table, Figure B and C have the same square units.
So, the Area of B and C is 6 square units.
They has 6 full square.

Question 4.
Figure ________ has the largest area.
Answer:
Figure F has the largest area.
Explanation:
In the above table, when compared with all Figures,
Figure F has the largest area.
So, the Area of F is 12 square units.
It has 9 full square and 3 half squares.

Draw two different figures with the same area on the grid.

Question 5.

Answer:
4 x 3 =12 square units or 3 x 4 square units.

Explanation:
Drawings may differ from one to one, depending upon the number of units used in picture.
In the above grid each square is equal to 1 unit.
The area of drawn pictures in the grid is 12 square units.
In figure A it has 4 units vertically and 3 units horizontally.
So, 4 x 3 =12 square units
In figure B it has 3 units vertically and 4 units horizontally.
3 x 4 =12 square units.
4 x 3 =12 square units or 3 x 4 = 12 square units.

Add squares (☐) or half-squares (◣) to each figure to make its area 7 square units.

Question 6.

Answer:
Area of the figures = 7 square units.

Explanation:
Area of a square is defined as the number of square units needed to fill a square.
As, it is mentioned  each square 1 unit square and each half square is half square unit.
So, by calculating each 1 square unit and half square units in the figure, we find Area.
Add 4 full squares to the figure A to make the area as 7 square units.
Add 1 full square and 2 half squares to the figure B to make the area as 7 square units.

Complete. Cut out the triangle tiles. Use all the tiles to make three figures with different areas. Glue them in the spaces below.

Question 7.

Answer:

Explanation:
Area of a square is defined as the number of square units needed to fill a square.
As, it is mentioned  each square 1 unit square and each half square is half square unit.
So, by calculating each 1 square unit and half square units in the figure, we find Area.
In figure A the Area is 3 square units, it consists 6 triangles.
In figure B the Area is 4 square units, it consists 8 triangles.
In figure C the Area is 6 square units, it consists 12 triangles.

Question 8.
Which figure has the smallest area? Figure ____________
Answer:
Figure A
Explanation:
As, figure A consists 6 triangles.
So, the Area is 3 square units.

Question 9.
Which figure has the largest area? Figure _____________
Answer:
Figure C
Explanation:
As, figure C consists 12 triangles.
So, the Area is 6 square units.

Question 10.
Order the figures from smallest to largest area.

Answer:
A, B, C
Explanation:
Compare all the figures and arrange them from least to greatest.
As, figure A consists 6 triangles.
So, the Area is 3 square units.
As, figure B consists 8 triangles.
So, the Area is 4 square units.
As, figure C consists 12 triangles.
So, the Area is 6 square units.